Część 2

9. STATECZNOŚĆ SPRĘŻYSTA UKŁADÓW PRĘTOWYCH

1

9.



9. STATECZNOŚĆ SPRĘŻYSTA UKŁADÓW PRĘTOWYCH

9.1. Wstęp

Omówienie zagadnienia stateczności sprężystej układów prętowych należy rozpocząć od przybliżenia

problemu w sensie fizycznym. Z utratą stateczności mamy do czynienia, gdy niewielka zmiana przyczyny
powoduje bardzo dużą zmianę skutku. Idealnie sprężysty pręt przy pewnej wartości siły ściskającej zmienia w
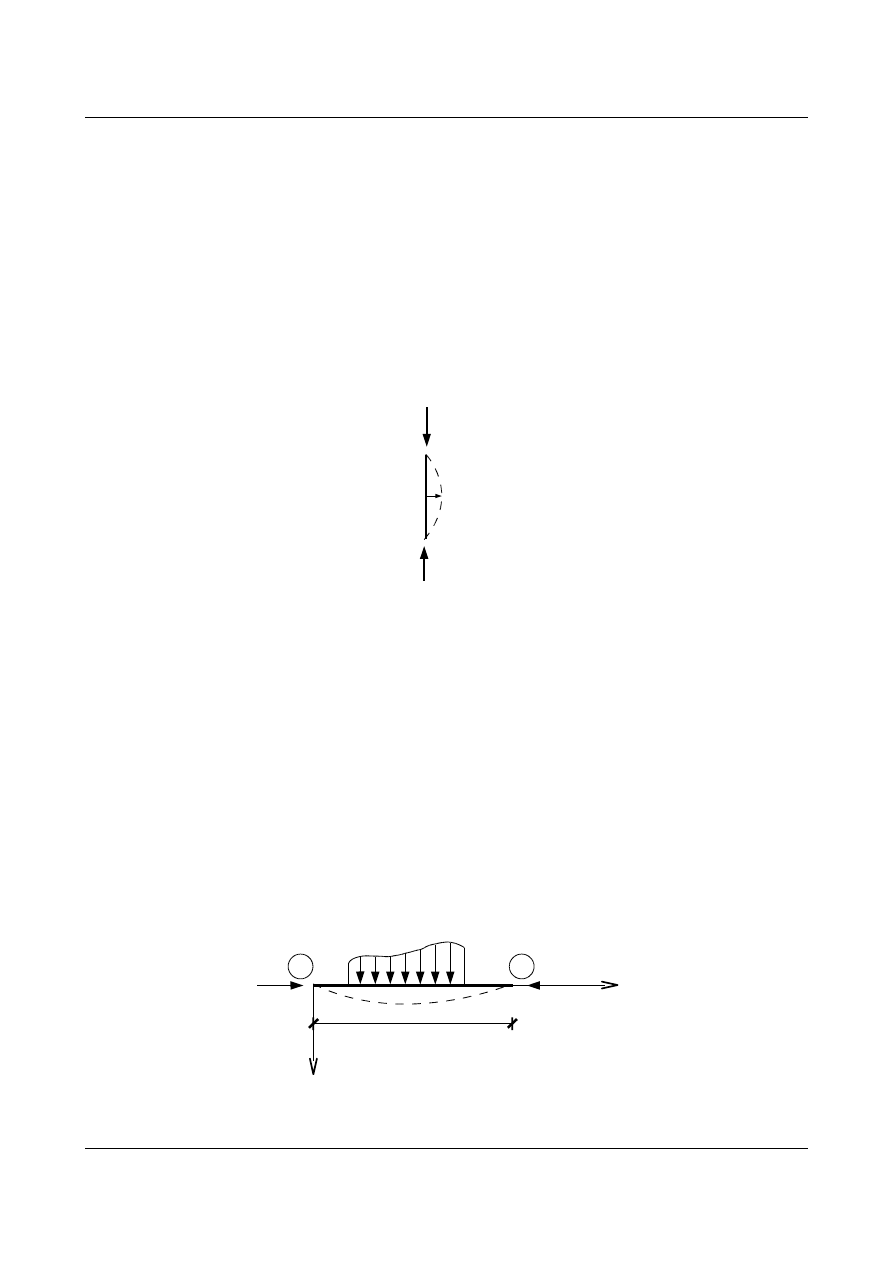
sposób nagły swą prostoliniową postać i przyjmuje położenie wygięte, czyli pręt doznaje wyboczenia
(rys. 9.1).

N

N

w

Rys. 9.1. Postać wyboczenia pod wpływem działania siły osiowej

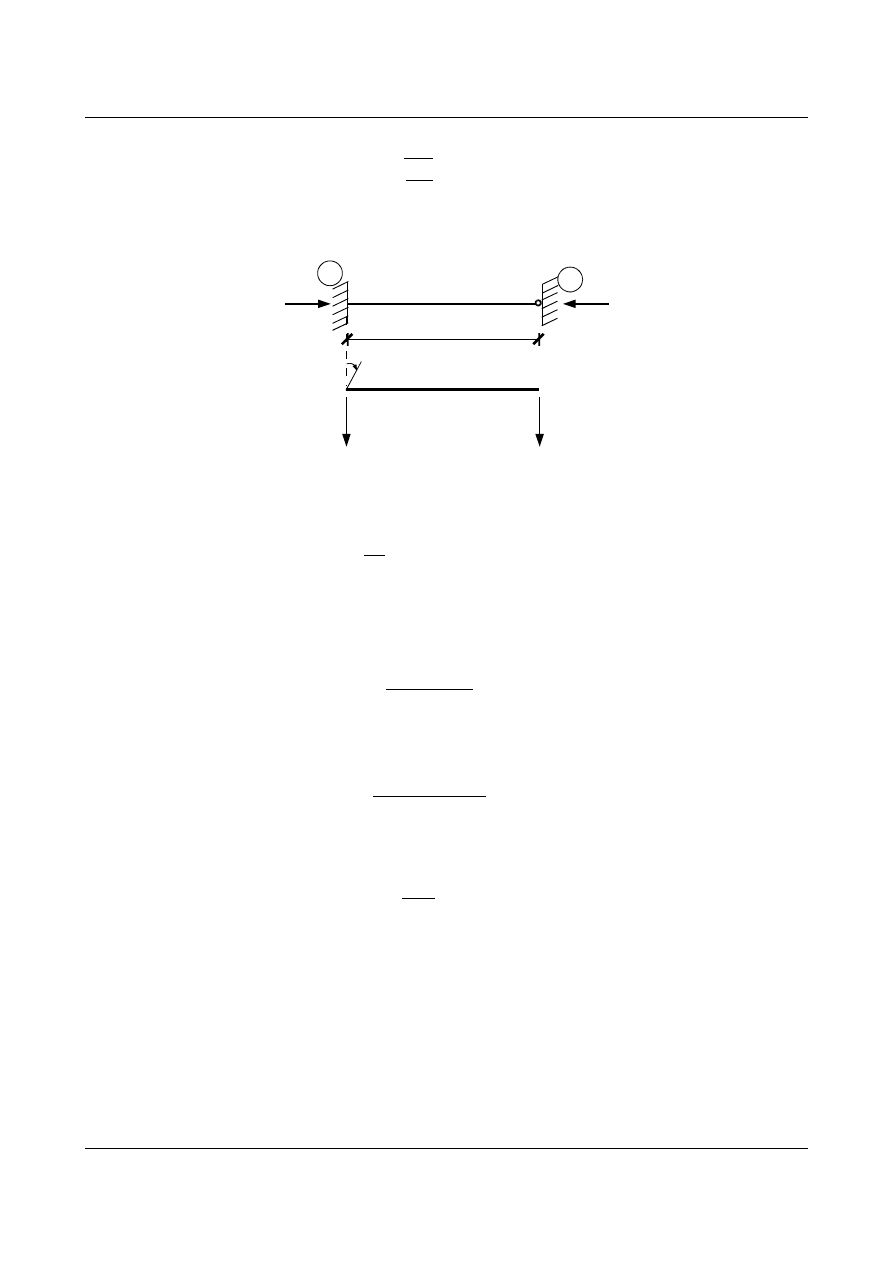
W środku rozpiętości pręta będzie występował moment jako skutek działania siły ściskającej na

pewnym mimośrodzie, na ramieniu równym wartości ugięcia tego pręta

w. Odchodzimy od zasady

zesztywnienia, która zakłada, że ciała przed, jak i po odkształceniu traktowane są jak bryły sztywne,
zajmujące także po obciążeniu konfigurację pierwotną. Utrata stateczności nastąpi po osiągnięciu przez siłę
osiową pewnej wartości krytycznej, której towarzyszą dwa stany równowagi odpowiadające prostoliniowej lub
krzywoliniowej osi pręta. Oznacza to, że dalszy wzrost obciążenia może następować po dwóch ścieżkach
równowagi. Punkt w którym występuje rozdwojenie ścieżki (stanu równowagi) nazywamy punktem bifurkacji.

9.2. Wyznaczanie siły krytycznej

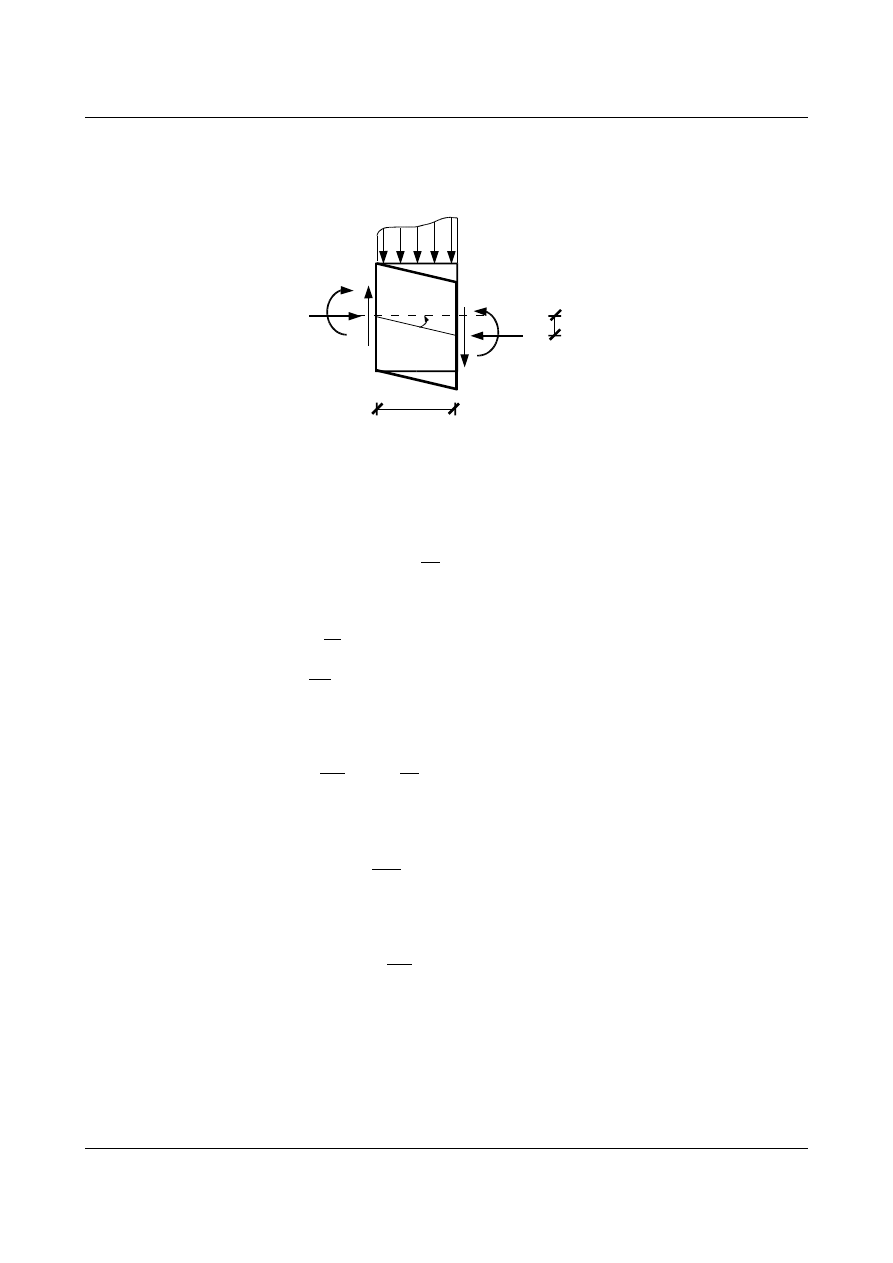
Analizę utraty stateczności (wyboczenia) układów prętowych dokonamy na przykładzie dowolnego

pręta (rys. 9.2), który jest dowolnie zamocowany i obciążony dowolnymi siłami. Do takiego pręta
przykładamy stałą siłę normalną (ściskającą)

N.

i

k

q(x)

EJ

l

y,w

x

N

N

Rys. 9.2. Pręt dowolnie obciążony poddany działaniu siły osiowej N

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 2

9. STATECZNOŚĆ SPRĘŻYSTA UKŁADÓW PRĘTOWYCH

2

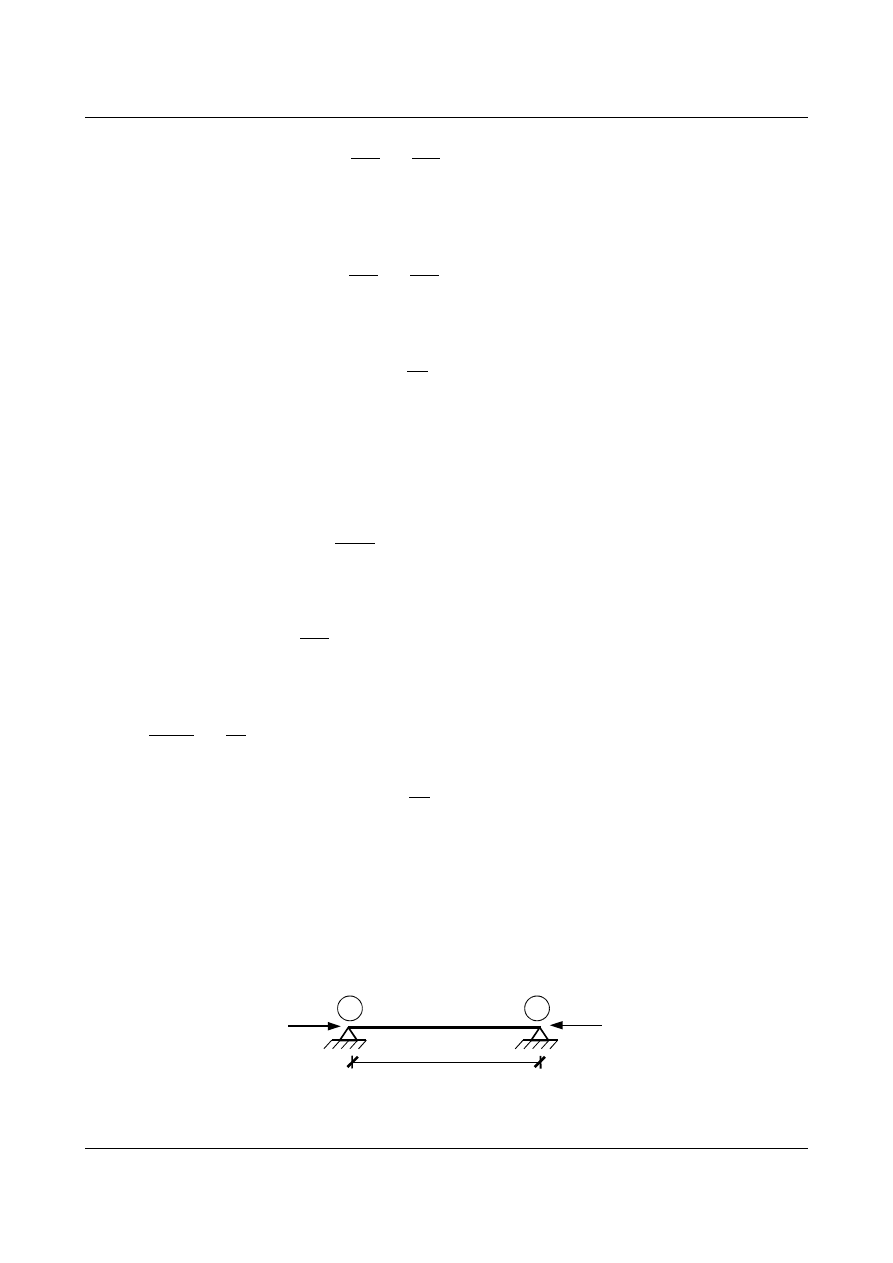
Pod wpływem działania sił układ doznaje pewnego odkształcenia. W stanie odkształconym wycinamy z

układu mały element

dx (rys 9.3) na który działają siły zarówno wewnętrzne jak i zewnętrzne.

q(x)

dx

N

M

T

T+dT

M+dM

N+dN

φ

dw

Rys. 9.3. Nieskończenie mały element poddany działaniu sił wewnętrznych i zewnętrznych

Dla elementu

dx zapisujemy warunki równowagi:

∑

Y

=0

−T qxdxT dT =0

q

 x=−

dT

dx

(9.1)

∑

M

=0

M

q xdx⋅

dx

2





T

dT



dx

−



M

dM



N⋅dw=0

M

q x

dx

2

2

T⋅dxdT⋅dx−M dM N⋅dw=0

pomijając wartości małe wyższego rzędu oraz redukując wyrazy podobne otrzymujemy ostatecznie:

dM

dx

=T N⋅

dw

dx

=T N⋅w'

(9.2)

Ponieważ siła normalna nie ma związku z krzywizną pręta obowiązuje zależność:

EJ

⋅

d

2

w

dx

2

=−M  x

Po zróżniczkowaniu i podstawieniu wyrażenia (9.2) otrzymujemy równanie różniczkowe osi odkształconej:

EJ

⋅w

III

=−

dM

dx

=−T −N⋅w

I

(9.3)

Kolejne różniczkowanie i podstawienie zależności (9.1) daje:

EJ

⋅w

IV

N⋅w

II

=q x

czyli

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 2

9. STATECZNOŚĆ SPRĘŻYSTA UKŁADÓW PRĘTOWYCH

3

EJ

⋅

d

4

w

dx

2

N⋅

d

2

w

dx

2

=qx

Aby rozwiązać równanie różniczkowe najpierw zajmujemy się całką ogólną rozwiązania. Rozwiązujemy
przypadek równania jednorodnego (zakładamy q

 x=0 ):

d

4

w

dx

2



2

⋅

d

2

w

dx

2

=0

(9.4)

gdzie



2

=

N

EJ

Rozwiązanie można przyjąć w postaci wielomianu:

w

 x=C

0

C

1

⋅xC

2

⋅sin  xC

3

⋅cos  x

(9.5)

Na jego podstawie określimy równanie kąta obrotu

x=tg  x=

dw

 x

dx

=C

1

⋅C

2

⋅cos  x−⋅C

3

⋅sin x

(9.6)

i równanie momentu zginającego

M

 x=−

d

2

w

dx

2

⋅EJ =EJ

[



2

⋅C

2

⋅sin x

2

⋅C

3

⋅cos  x

]

(9.7)

Z warunku (9.3) wyznaczymy równanie siły poprzecznej

T

 x=

dM

 x

dx

−N⋅

dw

dx

=EJ

[



3

⋅C

2

⋅cos  x−

3

⋅C

3

⋅sin  x

]

−N⋅

[

C

1

⋅C

2

⋅cos  x−⋅C

3

⋅sin  x

]

=

=EJ 

3

[

C

2

⋅cos  x−C

3

⋅sin  x

]

−N 

[

C

2

⋅cos  x−C

3

⋅sin x

]

−N⋅C

1

=

=

[

C

2

⋅cos x−C

3

⋅sin x

]

⋅



EJ

⋅

N

EJ

⋅−N 



−N⋅C

1

=−N⋅C

1

(9.8)

Stałe

C

i

trzeba wyznaczyć na podstawie warunków brzegowych. Dalsze rozważania przeprowadzimy dla

prętów o zdefiniowanych podporach.

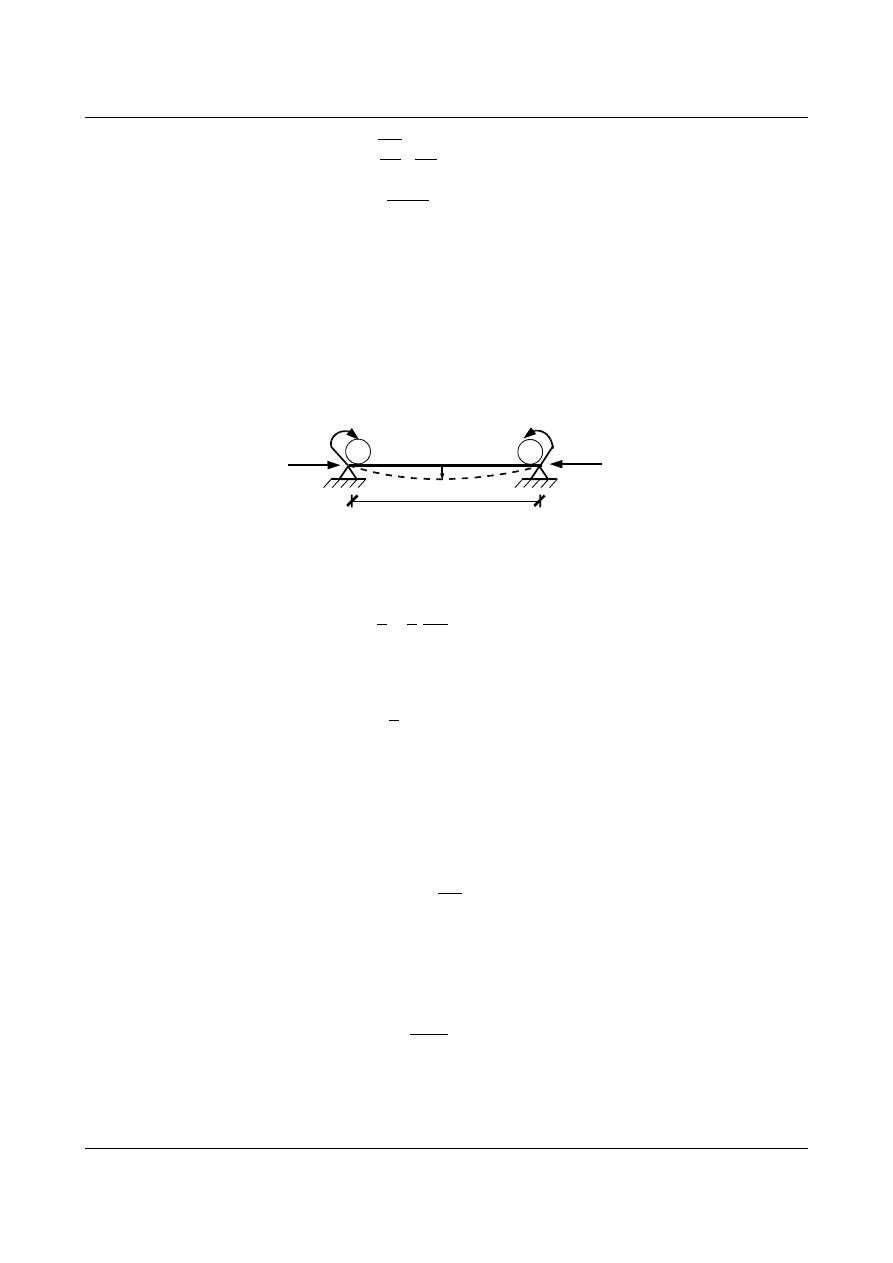
Przykład 1

Określenie stanu równowagi belki wolnopodpartej o jednorodnych warunkach brzegowych (rys. 9.4)

i

k

N

N

l

Rys. 9.4. Belka wolnopodparta poddana działaniu siły osiowej

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

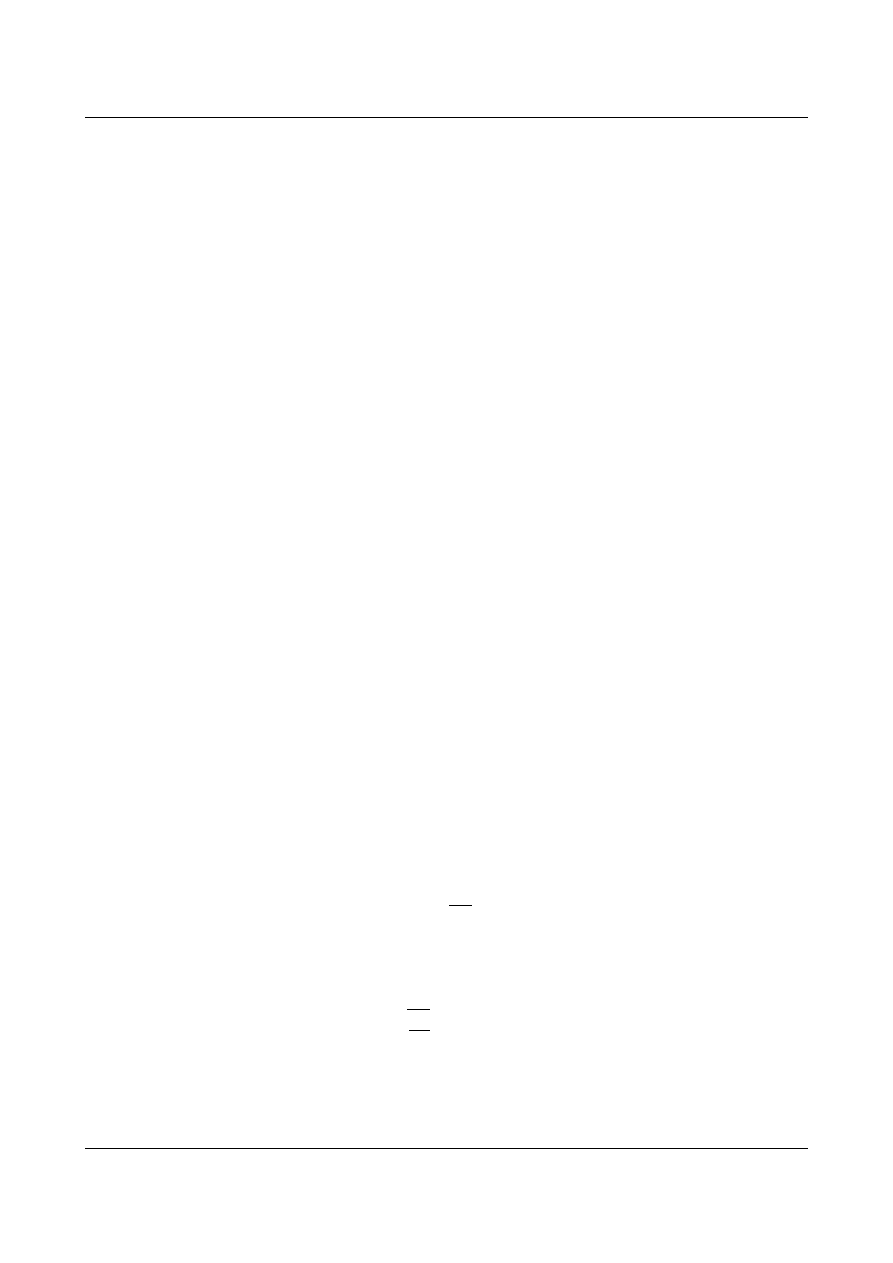
Część 2

9. STATECZNOŚĆ SPRĘŻYSTA UKŁADÓW PRĘTOWYCH

4

Najpierw należy określić warunki brzegowe, które posłużą do wyznaczenia stałych ze wzorów (9.5), (9.6),
(9.7), (9.8):

–

dla

x = 0

w

i

=0

M

ik

=0

–

dla

x = l

w

k

=0

M

ki

=0

Korzystając z równania osi odkształconej

w(x) otrzymujemy zależności:

w

i



x

=0



=0  C

0

C

3

=0

w

k



x

=l



 C

0

C

1

⋅lC

2

⋅sin lC

3

⋅cos l=0

natomiast ze wzoru (9.7) otrzymujemy związki:

M

ik



x

=0



=0  EJ⋅

2

⋅C

3

=0

M

ki



x

=l



=0  EJ

[



2

⋅C

2

⋅sin  l

2

⋅C

3

⋅cos l

]

=0

W ten sposób otrzymaliśmy układ równań algebraicznych jednorodnych z czterema niewiadomymi

C

0

, C

1

, C

2

,

C

3

, dla którego nietrywialne rozwiązanie (trywialne rozwiązanie to

C

0

= C

1

= C

2

= C

3

= 0) uzyskamy, gdy

wyznacznik układu będzie równy zero. Po zredukowaniu równań pierwszego i trzeciego (

C

0

= C

3

= 0)

{

C

1

⋅lC

2

⋅sin l=0

EJ



2

⋅C

2

⋅sin l=0

det

∣

W

∣

=det

∣

l

sin

 l

0 sin

 l

∣

=0

Z przyrównania wyznacznika do zera otrzymujemy równanie charakterystyczne,

l sin

 l=0

a z niego pierwiastki, czyli wartości własne

λ

i

. Ponieważ funkcja sin x osiąga zero dla x = nπ to:

 l=n  =

n



l

(9.9)

gdzie

n określa liczbę naturalną.

Z warunku (9.4) wiemy, że:

=



N

EJ

(9.10)

Wobec tego

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 2

9. STATECZNOŚĆ SPRĘŻYSTA UKŁADÓW PRĘTOWYCH

5



N

EJ

=

n



l

N

=



2

⋅EJ

l

2

⋅n

2

(9.11)

Wartości własnych jest nieskończenie wiele



1

,



2

, ... ,



n

∞

z uwagi na postać funkcji

sin x a każdej

odpowiada jedna postać wyboczenia. Rozważana belka może doznać wyboczenia po przekroczeniu przez siłę
osiową wartości krytycznej określonej wzorem (9.11).

Przykład 2

Wyznaczenie siły krytycznej dla belki poddanej działaniu sił osiowych

N i momentów M (rys. 9.5).

i

k

N

N

l

M

M

δ

Rys. 9.5. Belka wolnopodparta poddana działaniu momentów i siły osiowej

Z równania pracy wirtualnej wyznaczamy wartość ugięcia w środku rozpiętości belki:





l

2



=

1
8

⋅

Ml

2

EJ

Funkcję linii ugięcia wyrażoną przez zmienną bezwymiarową:

x

l

=

(9.12)

przyjmujemy w postaci wielomianu:

w

=C

0

C

1

C

2

⋅sin C

3

⋅cos 

(9.13)

gdzie

=⋅l



2

=

Nl

2

EJ

(9.14)

Określamy warunki brzegowe dla analizowanej belki:

–

dla

x = 0,

=0

w

0=0

w' '

0=−

M

0

EJ

⋅l

2

–

dla

x = l,

=1

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

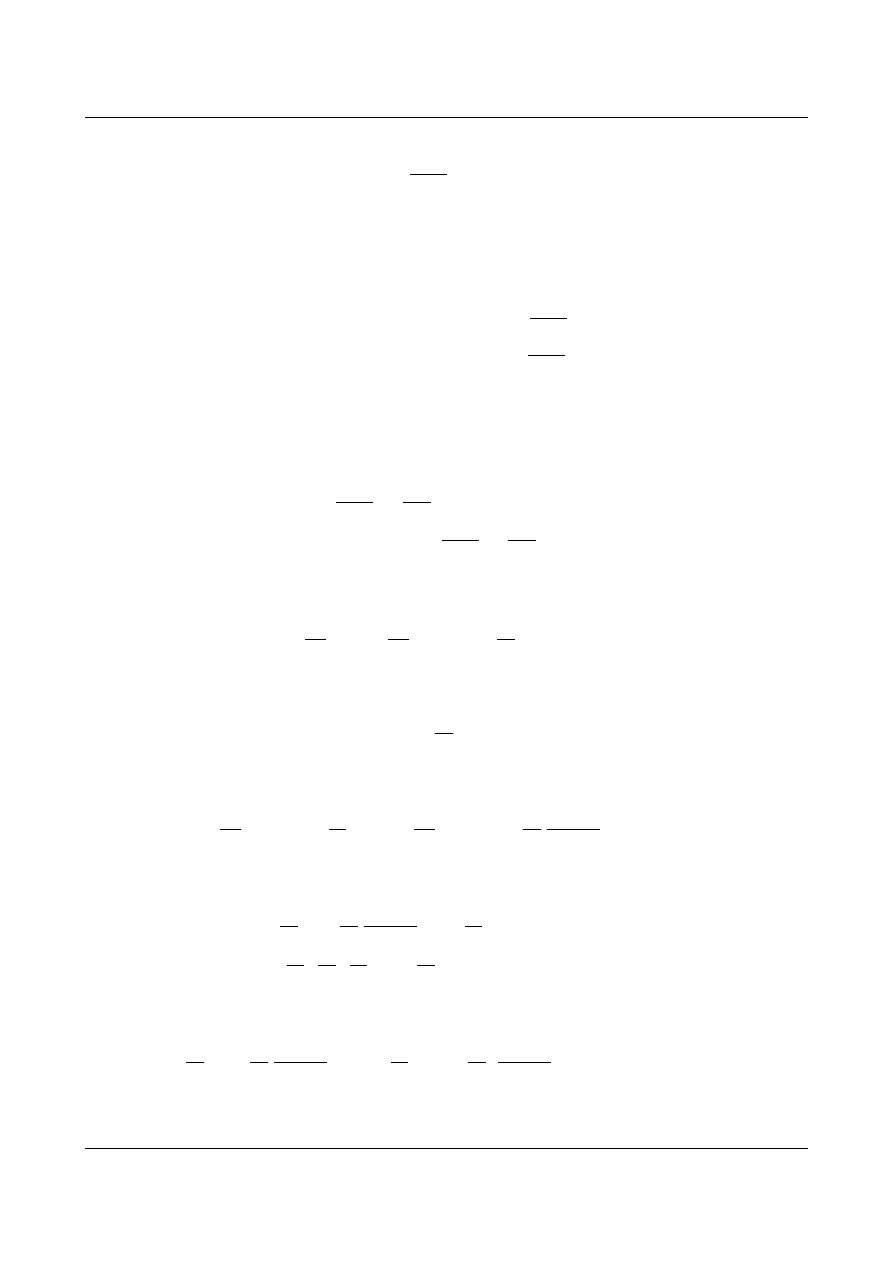
Część 2

9. STATECZNOŚĆ SPRĘŻYSTA UKŁADÓW PRĘTOWYCH

6

w

1=0

w' '

1=−

M

1

EJ

⋅l

2

Wykorzystując wzory (9.5), (9.6), (9.7), (9.8) można wyznaczyć wartości

C

0

, C

1

, C

2

, C

3

z układu równań:

{

w

0=C

0

C

1

⋅0C

2

⋅sin



⋅0



C

3

⋅cos



⋅0



=0

w

1=C

0

C

1

⋅1C

2

⋅sin



⋅1



C

3

⋅cos



⋅1



=0

w' '

0=−





2

⋅C

2

⋅sin



⋅0





2

⋅C

3

⋅cos



⋅0





=−

M

0

EJ

⋅l

2

w' '

1=−





2

⋅C

2

⋅sin



⋅1





2

⋅C

3

⋅cos



⋅1





=−

M

1

EJ

⋅l

2

który po uproszczeniu przyjmuje postać:

{

C

0

C

3

=0

C

0

C

1

C

2

⋅sin C

3

⋅cos =0

−

2

⋅C

3

=−

M

0

EJ

⋅l

2

=−

M

EJ

l

2

−

2



C

2

⋅sin C

3

⋅cos 



=−

M

1

EJ

⋅l

2

=−

M

EJ

l

2

Podstawiając zależność (9.14) możemy z równania trzeciego wyznaczyć wartość

C

3

:

−

N

EJ

⋅l

2

⋅C

3

=−

M

EJ

⋅l

2

 C

3

=

M

N

Następnie na mocy równania pierwszego wyliczamy wartość

C

0

:

C

0

=−C

3

=−

M

N

Z równania czwartego liczymy wartość

C

2

:

−

N

EJ

⋅l

2



C

2

⋅sin 

M

N

⋅cos 



=−

M

EJ

⋅l

2

 C

2

=

M

N

⋅

1

−cos 

sin



Na koniec wyznaczam ostatnią wartość

C

1

:

−

M

N

C

1



M

N

⋅

1

−cos 

sin



⋅sin 

M

N

⋅cos =0

C

1

=

M

N

−

M

N



M

N

⋅cos −

M

N

⋅cos   C

1

=0

Otrzymane wartości pozwolą nam wyznaczyć ostateczne równanie linii ugięcia:

w

=−

M

N

0⋅⋅



M

N

⋅

1

−cos 

sin



⋅sin 





M

N

⋅cos =

M

N

⋅

[

1

−cos 

sin



⋅sin cos −1

]

ponadto podstawiając przekształcone wyrażenie (9.14) możemy zapisać równanie linii ugięcia w lekko

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 2

9. STATECZNOŚĆ SPRĘŻYSTA UKŁADÓW PRĘTOWYCH

7

zmienionej postaci:

w

=

Ml

2

EJ



2

⋅

[

1

−cos 

sin



⋅sincos −1

]

(9.15)

Wartość ugięcia belki dla

=

1
2



x

=

l

2



zależy od parametru

ν, zgodnie z (9.15):

w



1
2



=

Ml

2

EJ



2

⋅

[

1

−cos 

sin



⋅sin



2

cos



2

−1

]

=

Ml

2

EJ



2

⋅

[

1

−cos

2



2

sin

2



2

2 sin



2

⋅cos



2

⋅sin



2

cos



2

−1

]

=

=

Ml

2

EJ



2

⋅

1

−cos

2



2

sin

2



2

2 cos

2



2

−2 cos



2

2 cos



2

=

Ml

2

EJ



2

⋅

1

−cos

2



2

1cos

2



2

−2 cos



2

2 cos



2

=

=

Ml

2

EJ



2

⋅

2

−2 cos



2

2 cos



2

=

Ml

2

EJ



2

⋅

1

−cos



2

cos



2

Ostatecznie wartość linii ugięcia belki w połowie jej rozpiętości wynosi:

w



1
2



= f







=

Ml

2

EJ



2

⋅

1

−cos



2

cos



2

Dla belki nie obciążonej siłą osiową



N

=0  =0



powinniśmy otrzymać wartość

Ml

2

8 EJ

. Ponieważ:

lim

 0

1

−cos



2



2

⋅cos



2

=

1
8

(9.16)

to f



=0



=

Ml

2

8 EJ

.

Przyrównując przemieszczenie wyboczeniowe

f(ν) (belka obciążona siłą N) do przemieszczenia w belce bez

ściskania





l

2



otrzymujemy funkcję:

F

=

f







l

2



=

Ml

2

EJ



2

⋅



1

−cos



2

cos



2



1
8

⋅

Ml

2

EJ

=

8

⋅



1

−cos



2





2

⋅cos



2

(9.17)

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 2

9. STATECZNOŚĆ SPRĘŻYSTA UKŁADÓW PRĘTOWYCH

8

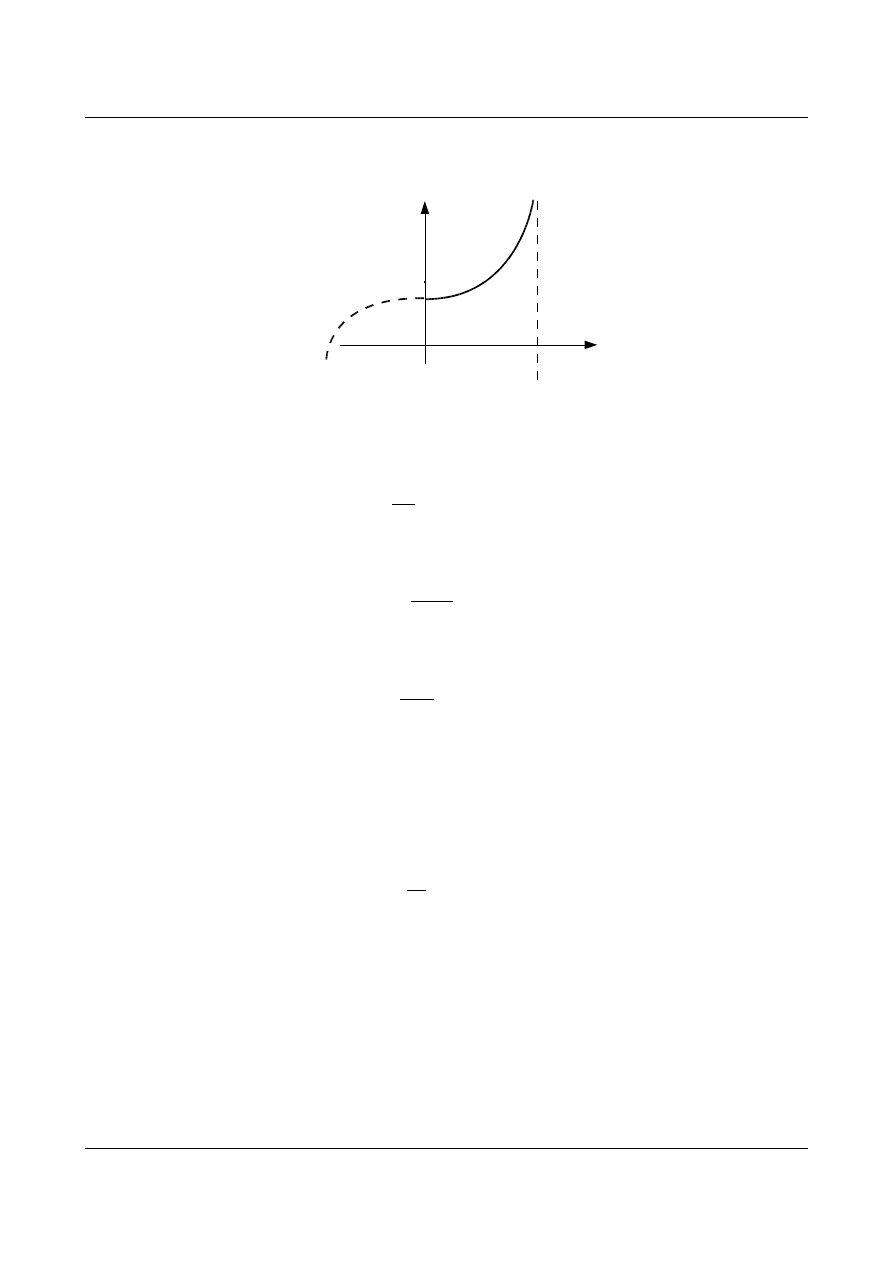
Wykres powyższej funkcji w zależności od wielkości parametru

ν przedstawiono na rys. 9.6.

F(ν)

ν

π

1

Rys. 9.6. Funkcja porównawcza

Funkcja posiada asymptotę dla

ν = π. Wobec tego wyboczenie (duży wzrost przemieszczenia bez zmiany

obciążenia) nastąpi gdy:



2

=

Nl

2

EJ

=

2

(9.18)

Stąd siła krytyczna wynosi:

S

kr

=N =



2

⋅EJ

l

2

(9.19)

Dla siły rozciągającej musimy zmienić znak siły osiowej:



2

=−

Nl

2

EJ

(9.20)

Obliczenia przeprowadzamy analogicznie jak dla siły ściskającej lub też stosując teorię liczb zespolonych
można wprost zastosować wzory transformacyjne wprowadzając w miejsce parametru

ν parametr zastępczy,

który wynosi:

=i⋅

(9.21)

gdzie:

i

=



−1

(9.22)

Dla zmiennych zespolonych wprowadzamy funkcje hiperboliczne,

cos i

=cosh 

sin i

=i sinh 

(9.23)

których pochodne wynoszą odpowiednio:

cosh '=sinh 
sinh '=cosh 

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

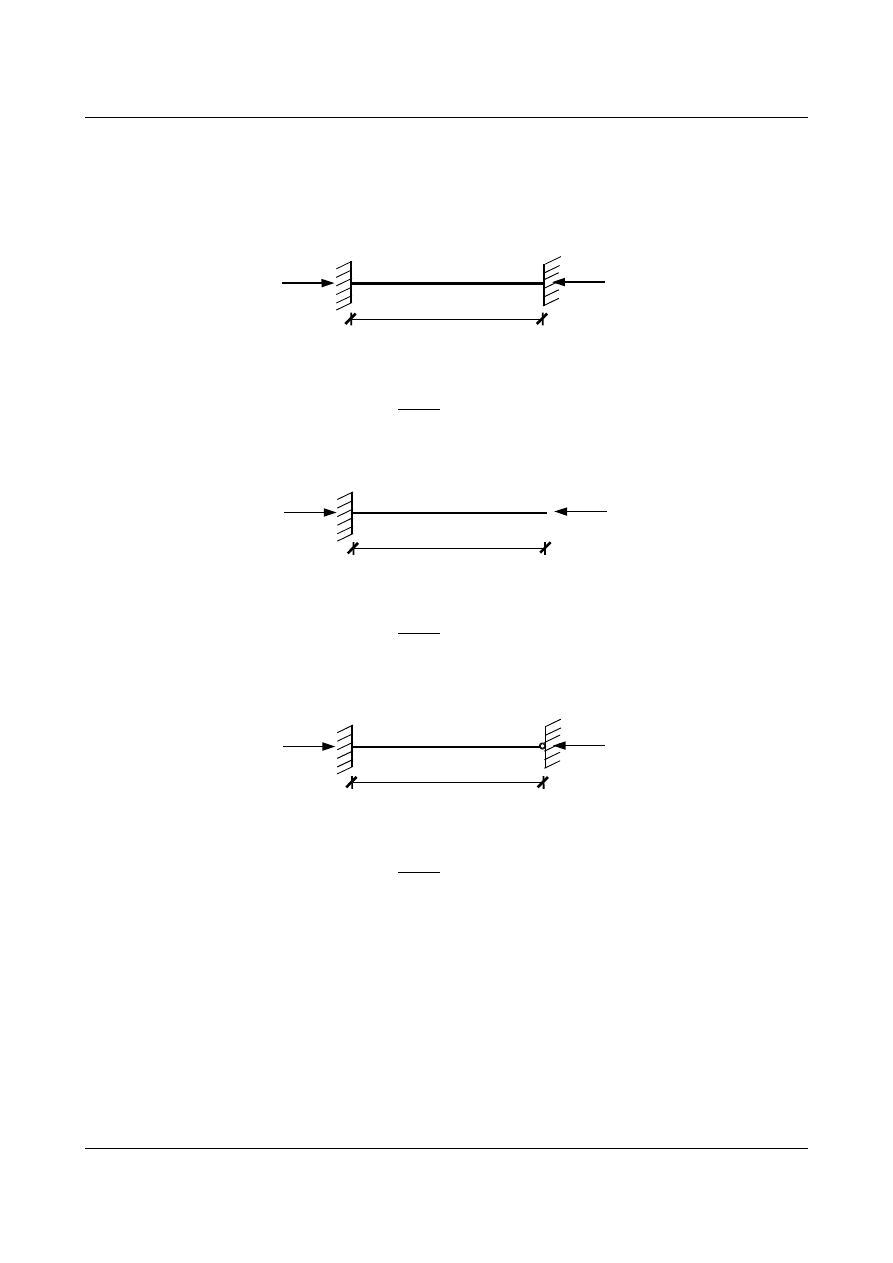
Część 2

9. STATECZNOŚĆ SPRĘŻYSTA UKŁADÓW PRĘTOWYCH

9

Jak wiemy funkcje hiperboliczne (

sinh ν i cosh ν) nie są funkcjami okresowymi, zatem nie istnieje siła

krytyczna dla pręta rozciąganego.

Dla różnego typu belek, w zależności od sposobu podparcia otrzymujemy różne wartości siły krytycznej:

–

belka obustronnie utwierdzona (rys. 9.7):

N

N

l

Rys. 9.7. Belka obustronnie utwierdzona poddana działaniu siły osiowo ściskającej

S

kr

=

EJ

⋅

2



0,5 l



2

(9.24)

–

belka jednostronnie utwierdzona (rys. 9.8):

N

N

l

Rys. 9.8. Belka utwierdzona poddana działaniu siły osiowo ściskającej

S

kr

=

EJ

⋅

2



2 l



2

(9.25)

–

belka utwierdzona i z przegubem (rys. 9.9):

N

N

l

Rys. 9.9. Belka utwierdzona z przegubem na jednym końcu poddana działaniu siły osiowo ściskającej

S

kr

=

EJ

⋅

2



0,7 l



2

(9.26)

Mnożnik, który występuje w mianowniku wyrażenia na siłę krytyczną nazywany jest współczynnikiem
wyboczeniowym

μ.

9.3. Określenie wzorów transformacyjnych dla prętów poddanych działaniu siły normalnej

Wzory transformacyjne metody przemieszczeń, podobnie jak wartość siły krytycznej zależeć będą od

sposobu podparcia belki. Poniżej przedstawiono kilka przykładów różnego sposobu podparć:

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 2

9. STATECZNOŚĆ SPRĘŻYSTA UKŁADÓW PRĘTOWYCH

10

Przykład 3

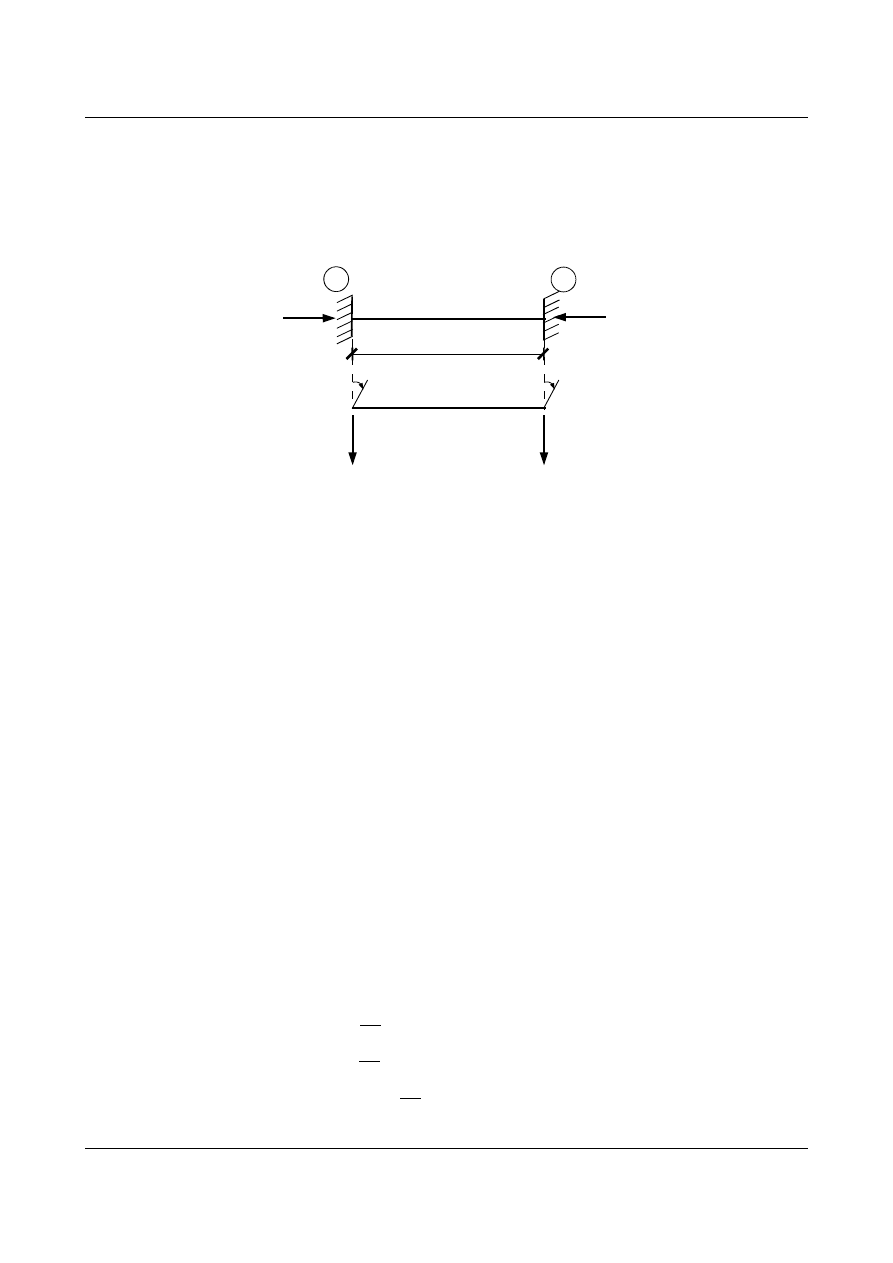
Wyznaczyć wzory transformacyjne dla belki obustronnie utwierdzonej (rys. 9.10).

Należy rozwiązać zadanie niejednorodne. Wartości przemieszczeń przywęzłowych przyjmujemy jako

znane. Zwroty sił i przemieszczeń przyjmujemy jako dodatnie te, które są zaznaczone na rys. 9.10.

N

N

l

i

k

φ

i

φ

k

v

i

φ

i

φ

i

v

k

EJ

Rys. 9.10. Belka obustronnie utwierdzona poddana działaniu siły osiowo ściskającej

Zadanie polega na znalezieniu relacji pomiędzy węzłowymi przemieszczeniami, a siłami przywęzłowymi

(np. M

ik





i

,



k

, v

i

, v

k



). Wyznacza się je z warunków brzegowych, które w tym przypadku wszystkie są

niezerowe:

w

 x=0=v

i

w

 x=l =v

k

 x=0=

i

 x=l =

k

Przyjmujemy funkcję linii ugięcia w postaci wielomianu:

w

 x=C

0

C

1

⋅xC

2

⋅sin xC

3

⋅cos  x

Dalej korzystamy ze związków (9.5) i (9.6), co prowadzi do układu równań niejednorodnych:

{

v

i

=C

0

C

1

⋅0C

2

⋅sin 0C

3

⋅cos 0=C

0

C

3

v

k

=C

0

C

1

⋅lC

2

⋅sin lC

3

⋅cos l



i

=C

1

⋅C

2

⋅cos 0−⋅C

3

⋅sin 0=C

1

⋅C

2



k

=C

1

⋅C

2

⋅cos  l−⋅C

3

⋅sin  l

Z powyższego układu równań wyznaczamy wartości

C

0

, C

1

, C

2

, C

3

. Znając już wartości stałych

C

j

można w

prosty sposób, ze związków (9.7) i (9.8) dojść do wzorów transformacyjnych, które w ogólnej postaci można
zapisać:

M

ik

=M 0=

EJ

l

⋅



'⋅

i

'⋅

k

−'⋅

ik



(9.27)

M

ki

=M l =

EJ

l

⋅



'⋅

i

'⋅

k

−'⋅

ik



(9.28)

T

ik

=T

ki

=T 0=T l =−

EJ

l

2

⋅



'⋅





i



k



−'⋅

ik



(9.29)

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

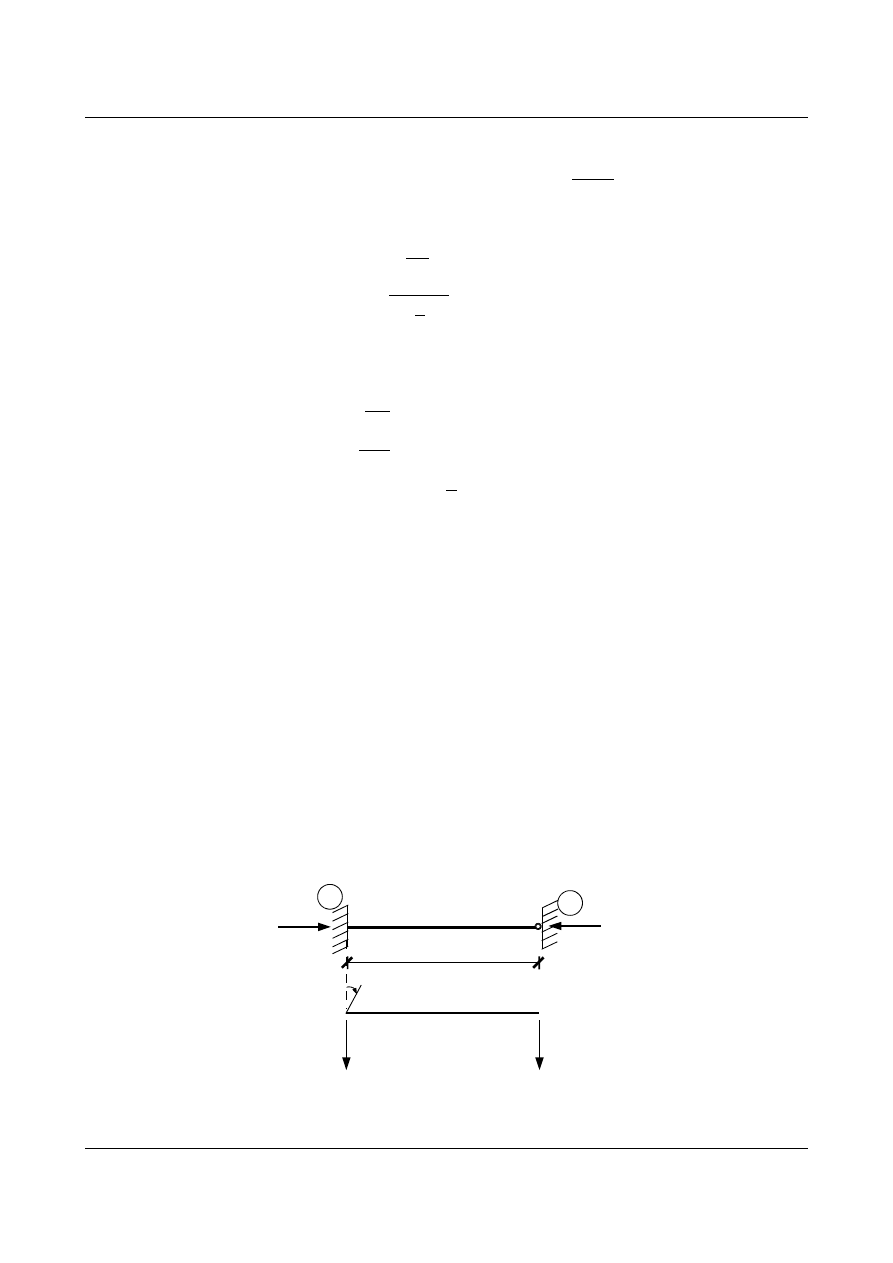
Część 2

9. STATECZNOŚĆ SPRĘŻYSTA UKŁADÓW PRĘTOWYCH

11

Kąt obrotu cięciwy pręta jest zależny od przemieszczeń węzłowych:



ik

=

v

k

−v

i

l

Przyjmując oznaczenia:



2

=

Nl

2

EJ

f



=

1

2 tg



2

−

(9.30)

możemy zapisać współczynniki

α', β', γ', δ' w prostych postaciach:

'=



tg



⋅



tg

−



⋅f



(9.31)

'=



sin



⋅



−sin 



⋅f



(9.32)

'=''=

2

⋅tg



2

⋅f



(9.33)

'=

3

⋅f



(9.34)

Można wykonać przejście graniczne jeżeli przyjmiemy N

=0  =0 , to w prosty lecz bardzo

pracochłonny sposób korzystając z reguły de l'Hospitala możemy policzyć wartości współczynników:

lim

'

 0

=4

(9.35)

lim

'

 0

=2

(9.36)

lim

'

 0

=lim '

 0

lim '

 0

=42=6

(9.37)

lim

'

 0

=12

(9.38)

które pokrywają się z wartościami występującymi we wzorach transformacyjnych pręta utwierdzonego bez
siły osiowej.

Przykład 4

Wyznaczyć wzory transformacyjne dla belki z przegubem (rys. 9.11).

N

N

l

EJ

v

i

φ

i

v

k

i

k

Rys. 9.11. Belka utwierdzona z przegubem na jednym końcu poddana działaniu siły osiowo ściskającej

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 2

9. STATECZNOŚĆ SPRĘŻYSTA UKŁADÓW PRĘTOWYCH

12

Tym razem warunki brzegowe obejmują przemieszczenia i siły (warunki kinematyczne i statyczne):

w

 x=0=v

i

w

 x=l =v

k

 x=0=

i

M

 x=l =0

Na podstawie wzorów (9.5), (9.6), (9.7) tworzymy układ równań:

{

v

i

=C

0

C

1

⋅0C

2

⋅sin 0C

3

⋅cos 0=C

0

C

3

v

k

=C

0

C

1

⋅lC

2

⋅sin  lC

3

⋅cos  l



i

=C

1

⋅C

2

⋅cos 0−⋅C

3

⋅sin 0=C

1

⋅C

2

EJ

[



2

⋅C

2

⋅sin  l

2

⋅C

3

⋅cos l

]

=0

z którego wyznaczamy wartości

C

0

, C

1

, C

2

, C

3

. Na ich podstawie ze wzorów (9.7) i (9.8) tworzymy funkcje:

M

ik

=M 0=

EJ

l

⋅



' '⋅

i

−' '⋅

ik



(9.39)

M

ki

=M l =0

(9.40)

T

ik

=T

ki

=T 0=T l =−

EJ

l

2

⋅



' '⋅

i

−' '⋅

ik



(9.41)

gdzie:

' '=



2

⋅tg 

tg

−

(9.42)

' '=



3

tg

−

(9.43)



2

=

Nl

2

EJ

I tym razem przejście graniczne, gdy N

=0  =0 prowadzi do poprawnych rezultatów.

lim

  0

' '=lim

 0



2

⋅tg 

tg

−

=

H

lim

 0

2

⋅tg 



2

cos

2



1

cos

2



−1

=lim

 0

2

⋅tg ⋅cos

2



2

1

−cos

2



=

=lim

 0

2

⋅tg ⋅cos

2

2−2⋅tg ⋅sin 2 2

sin 2



=lim

 0

2

⋅tg ⋅cos

2

−2 ⋅tg ⋅sin 24 

sin 2



=

=lim

0

2

−2⋅tg ⋅sin 2−2⋅tg ⋅sin 2−

2

⋅sin 2 

cos

2



−4 ⋅cos 2⋅tg 4

2 cos 2



=

=lim

 0

2

−4⋅tg ⋅sin 2 −

2

⋅sin 2

cos

2



−4 ⋅cos 2 ⋅tg 4

2 cos 2



=

[

2

−0−0−04

2

=

6

2

]

=3

(9.44)

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 2

9. STATECZNOŚĆ SPRĘŻYSTA UKŁADÓW PRĘTOWYCH

13

lim

 0

' '=lim

 0



3

tg

−

=

H

lim

3



2

1

cos

2



−1

=lim

 0

3



2

⋅cos

2



1

−cos

2



=

=lim

 0

6

⋅cos

2

−3

2

⋅sin 2 

sin 2



==

H

lim

  0

6

⋅cos

2

−6 ⋅sin 2−6 ⋅sin 2−6 

2

⋅cos 2

2 cos 2



=

=lim

 0

6

⋅cos

2

−12 ⋅sin 2−6 

2

⋅cos 2 

2 cos 2



=

[

6

−0−0

2

=

6

2

]

=3

(9.45)

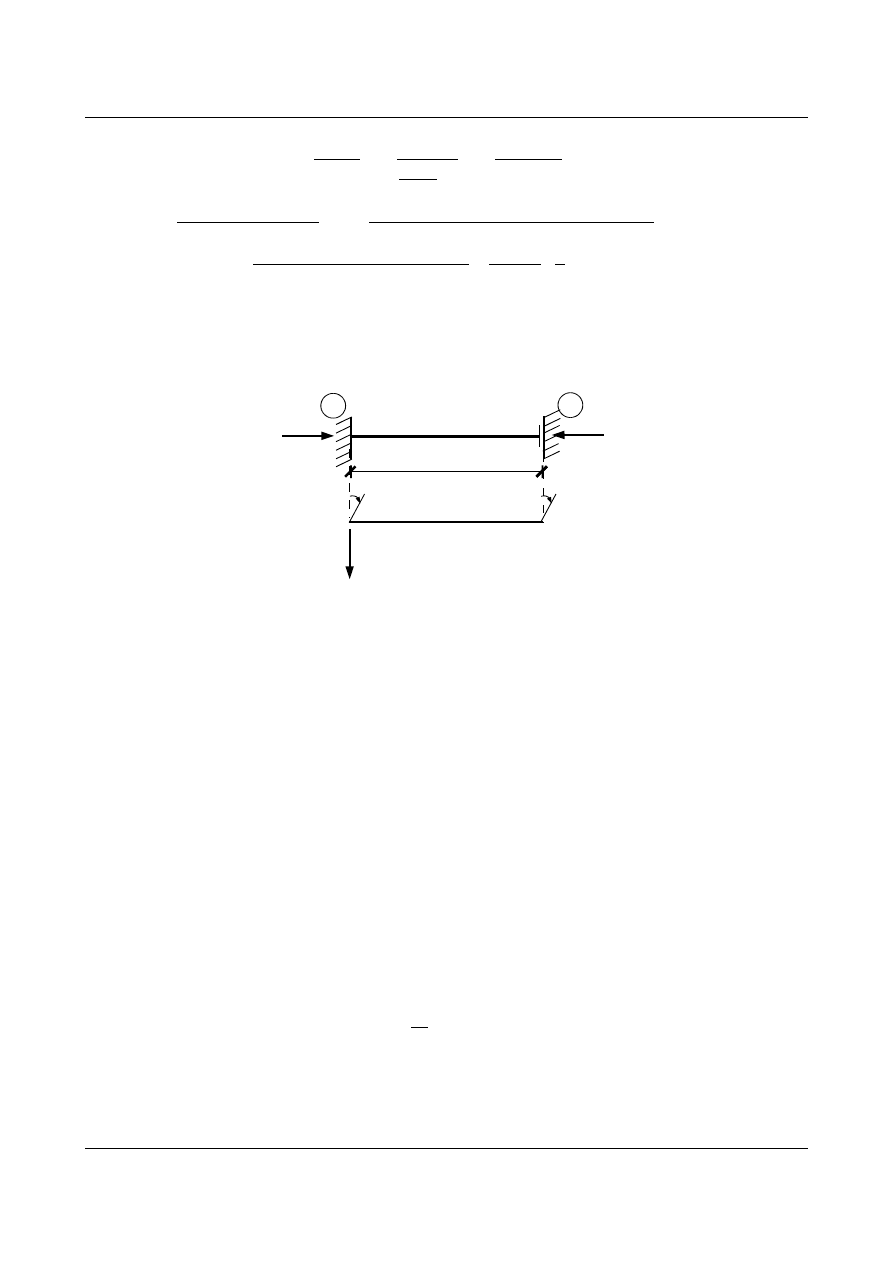
Przykład 5

Wyznaczyć wzory transformacyjne dla belki o schemacie jak na rys. 9.12.

N

N

l

EJ

v

i

φ

i

i

k

φ

k

Rys. 9.12. Belka utwierdzona z podporą ślizgową na jednym końcu poddana działaniu siły osiowo ściskającej

Tak jak w poprzednim zadaniu określamy warunki brzegowe:

w

 x=0=v

i

T

 x=l =0

 x=0=

i

 x=l =

k

W rzeczywistości ugięcie w punkcie

i będzie równe zero, nie ma to jednak wpływu na wartości momentów i sił

poprzecznych dla danej belki, gdyż wartość

C

0

nie występuje we wzorze na

M

ik

i

T

ik

.

Po rozpisaniu powyższych warunków brzegowych otrzymujemy układ równań niejednorodnych:

{

v

i

=C

0

C

1

⋅0C

2

⋅sin0C

3

⋅cos 0=C

0

C

3

=0

−N⋅C

1

=0



i

=C

1

⋅C

2

⋅cos 0−⋅C

3

⋅sin0=C

1

⋅C

2



k

=C

1

⋅C

2

⋅cos l−⋅C

3

⋅sin l

Z powyższych równań wyznaczamy wartości

C

0

, C

1

, C

2

, C

3

. Ponieważ we wzorze na

M

ik

znajdują się tylko

wartości

C

2

i

C

3

, a z drugiego równania brzegowego wiemy, że

C

1

=0, zatem:

C

2

=



i



Podstawiamy powyższą zależność do ostatniego równania brzegowego:

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

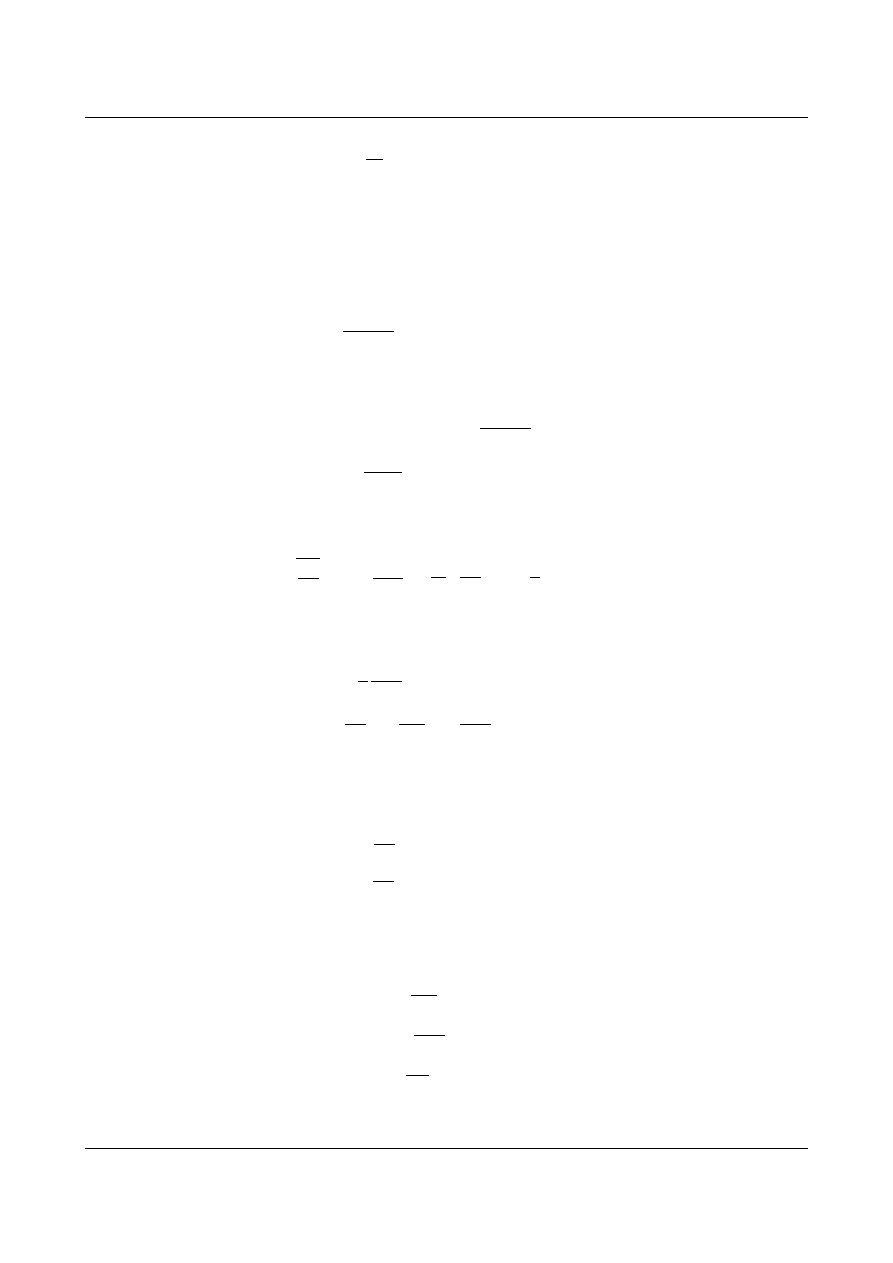
Część 2

9. STATECZNOŚĆ SPRĘŻYSTA UKŁADÓW PRĘTOWYCH

14



k

=0 ⋅



i



⋅cos l−⋅C

3

⋅sinl

i przekształcamy je w następujący sposób:

⋅C

3

⋅sinl=

i

⋅cos l−

k

Otrzymujemy szukaną wartość

C

3

, która wynosi:

C

3

=

1

⋅sinl

⋅





i

⋅cos  l−

k



Podstawiamy wartości

C

2

i

C

3

, do równania na

M

ik

, przy

x = 0:

M

 x=EJ⋅

2

⋅C

2

⋅sin0

2

⋅C

3

⋅cos 0=EJ⋅

[



2

⋅

1

⋅sin  l

⋅





i

⋅cosl−

k



⋅1

]

M

x=EJ⋅

[



sin

 l

⋅





i

⋅cosl−

k



⋅1

]

Zależności określające poszczególne współczynniki:

=



N

EJ



2

=

N

⋅l

2

EJ



2

l

2

=

N

EJ

=



l

podstawiamy do równania na

M

ik

. Otrzymujemy wzór transformacyjny:

M

ik

=EJ⋅

[



l

1

sin



⋅





i

⋅cos −

k



⋅1

]

M

ki

=

EJ

l

⋅





i

⋅



tg



−

k

⋅



sin





Analogicznie postępujemy obliczając wzór na

M

ki

. Ostatecznie wzory transformacyjne dla danej belki możemy

zapisać w następujący sposób:

M

ik

=M 0=

EJ

l

⋅



' ' '⋅

i

' ' '⋅

k



(9.46)

M

ki

=M l =

EJ

l

⋅



' ' '⋅

i

' ' '⋅

k



(9.47)

T

ik

=T

ki

=T 0=T l =0

(9.48)

gdzie:

' ' '=



tg



(9.49)

' ' '=−



sin



(9.50)



2

=

Nl

2

EJ

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

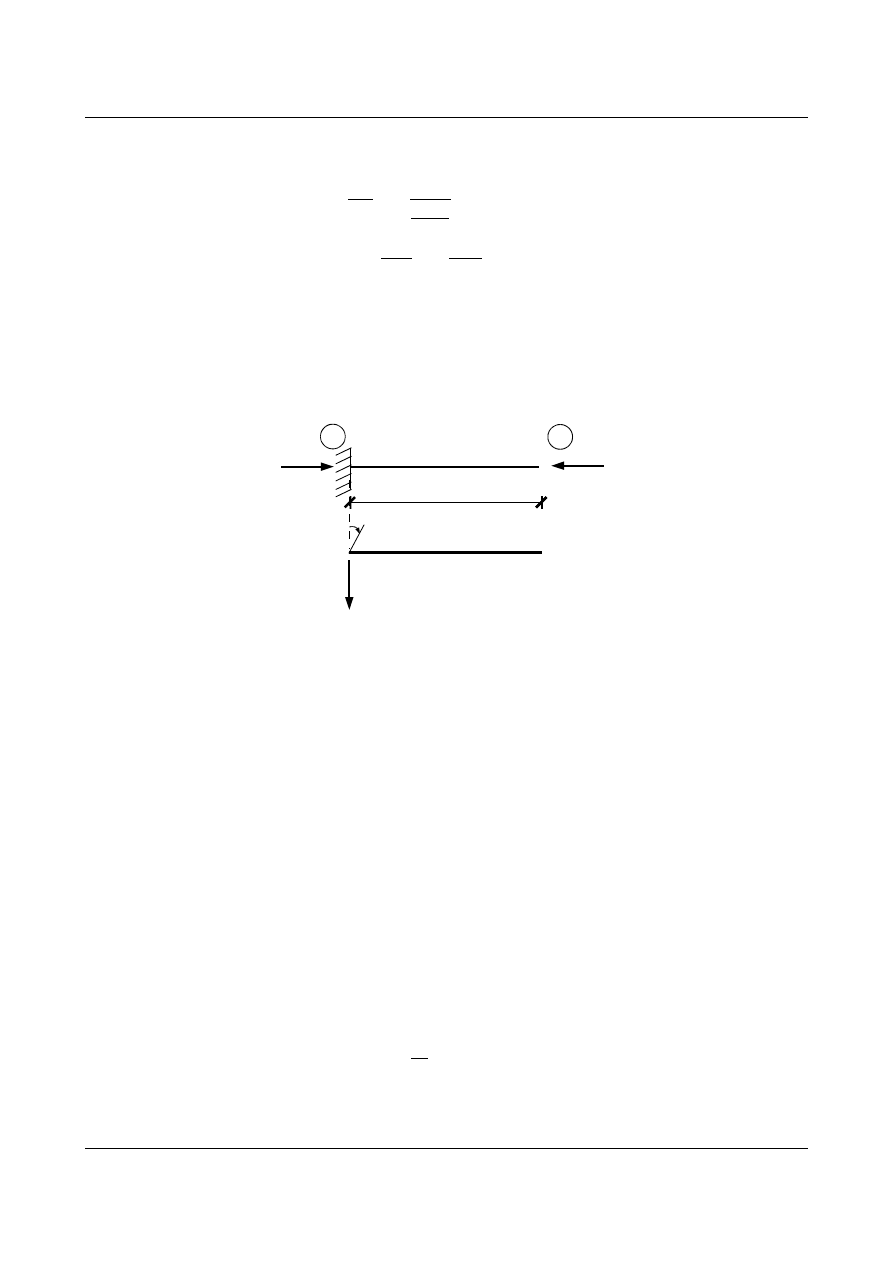
Część 2

9. STATECZNOŚĆ SPRĘŻYSTA UKŁADÓW PRĘTOWYCH

15

Jeżeli przyjmiemy N

=0



=0



, możemy z reguły de l'Hospitala policzyć wartości współczynników:

lim

 0

' ' '=lim

0



tg



=

H

lim

 0

1
1

cos

2



=lim

 0

cos

2

=1

(9.51)

lim

 0

' ' '=lim

 0

−1

sin



=

H

lim

 0

−1

cos



=−1

(9.52)

które są zgodne ze wzorami dla belki bez ściskania.

Przykład 6

Wyznaczyć wzory transformacyjne dla belki lewostronnie utwierdzonej (rys. 9.13).

N

N

l

EJ

v

i

φ

i

i

k

Rys. 9.13. Belka utwierdzona poddana działaniu siły osiowo ściskającej

Tym razem mamy dwa warunki statyczne i dwa kinematyczne:

w

 x=0=v

i

M

 x=l =0

 x=0=

i

T

x=l =0

W rzeczywistości ugięcie w punkcie

i podobnie jak w poprzednim przypadku będzie równe zero i tak samo nie

ma wpływu na wartość momentów i sił poprzecznych dla danej belki.
Podstawiając powyższe zależności do znanych nam już wcześniej wzorów otrzymujemy kolejno równania:

{

v

i

=C

0

C

1

⋅0C

2

⋅sin 0C

3

⋅cos 0=C

0

C

3

=0

EJ

[



2

⋅C

2

⋅sinl

2

⋅C

3

⋅cos l

]

=0



i

=C

1

⋅C

2

⋅cos 0−⋅C

3

⋅sin 0=C

1

⋅C

2

−N⋅C

1

=0

Z układu równań niejednorodnych wyznaczamy wartości

C

0

, C

1

, C

2

, C

3

. Ponieważ we wzorze na

M

ik

znajdują

się tylko wartości

C

2

i

C

3

, a z ostatniego równania brzegowego wiemy, że

C

1

= 0, zatem:

C

2

=



i



Podstawiamy powyższą zależność do równania drugiego:

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

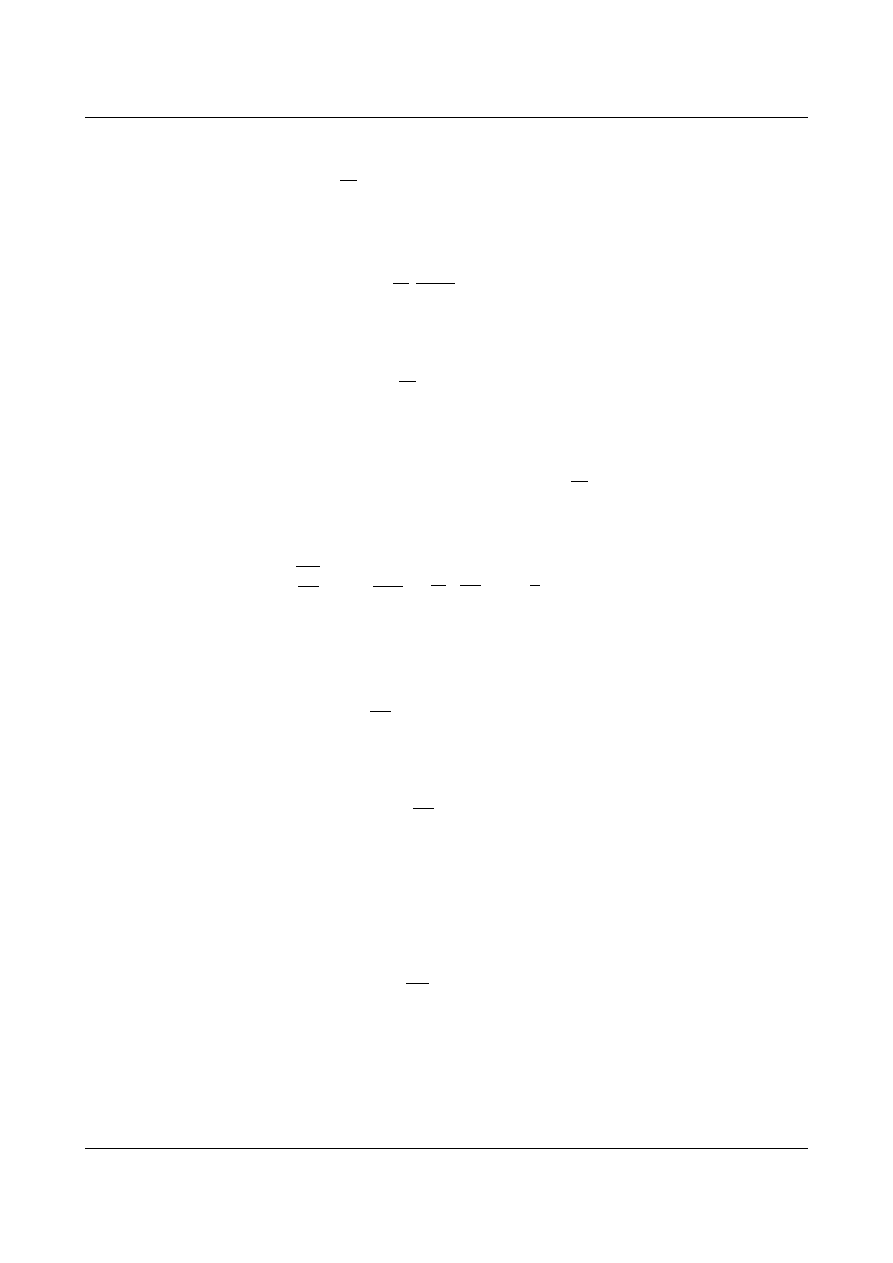
Część 2

9. STATECZNOŚĆ SPRĘŻYSTA UKŁADÓW PRĘTOWYCH

16

EJ

[



2

⋅



i



⋅sin l

2

⋅C

3

⋅cos l

]

=0

oraz dzielimy przez wyrażenie EJ

⋅

2

i przekształcamy:

C

3

=−



i



⋅

sin

 l

cos

l

Otrzymujemy szukaną wartość

C

3

, która wynosi:

C

3

=−



i



⋅tg  l

Podstawiamy wartości

C

2

i

C

3

, do równania na

M

ik

, przy

x=0:

M

ik

=M x=0=EJ⋅

2

⋅C

2

⋅sin0

2

⋅C

3

⋅cos0=EJ⋅

2

⋅



−



i



⋅tg l



Korzystając z zależności:

=



N

EJ



2

=

N

⋅l

2

EJ



2

l

2

=

N

EJ

=



l

otrzymujemy ostateczną postać wzoru transformacyjnego na moment:

M

ik

=EJ⋅⋅



−

i

⋅tg 



M

ik

=

EJ

l

⋅⋅



−

i

⋅tg 



Ostatecznie wzory transformacyjne dla danej belki możemy zapisać w następujący sposób:

M

ik

=M 0=

EJ

l

⋅

IV

⋅

i

(9.53)

M

ki

=M l =0

(9.54)

T

ik

=T

ki

=T 0=T l =0

(9.55)

gdzie:



IV

=−⋅tg 

(9.56)



2

=

Nl

2

EJ

Jeżeli przyjmiemy N

=0



=0



to:

lim

 0



IV

=0

(9.57)

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 2

9. STATECZNOŚĆ SPRĘŻYSTA UKŁADÓW PRĘTOWYCH

17

Przemieszczenie podpory nie powoduje powstania sił wewnętrznych. Natomiast we wsporniku z siłą osiową
występuje zginanie (siła poprzeczna jest zerowa).

Przykład 7

Wyznaczyć wzory transformacyjne dla belki poddanej działaniu siły rozciągającej (rys. 9.14).

N

N

l

EJ

v

i

i

k

φ

k

v

i

Rys. 9.14. Belka z przegubem i z utwierdzeniem ślizgowym poddana działaniu siły osiowo rozciągającej.

W przypadku belki poddanej działaniu siły rozciągającej należy rozwiązać równanie różniczkowe:

d

4

w

dx

2

−

2

⋅

d

2

w

dx

2

=0

(9.58)

Znak “-” oznacza działanie siły rozciągającej, ponadto:



2

=

∣N∣

EJ

l

2

(9.59)

Całkę ogólną w tym przypadku przyjmujemy w postaci wielomianu:

w

 x= 

C

0

 

C

1

⋅x 

C

2

⋅sinh  x 

C

3

⋅cosh  x

(9.60)

Na jego podstawie określimy równanie kąta obrotu

 x=tg x=

dw

 x

dx

= 

C

1

⋅ 

C

2

⋅cosh  x⋅ 

C

3

⋅sinh  x

(9.61)

równanie momentu zginającego

M

 x=

d

2

w

dx

2

⋅EJ =−EJ

[





2

⋅ 

C

2

⋅sinh  x 



2

⋅ 

C

3

⋅cosh  x

]

(9.62)

i równanie siły poprzecznej

T

x=

dM

x

dx

N⋅

dw

dx

=N⋅ 

C

1

(9.63)

Określamy warunki brzegowe:

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 2

9. STATECZNOŚĆ SPRĘŻYSTA UKŁADÓW PRĘTOWYCH

18

w

 x=0=v

i

T

 x=l =0

M

 x=0=0

 x=l =

k

Po rozpisaniu powyższych warunków brzegowych otrzymujemy układ równań niejednorodnych, z których
wyznaczymy wartości 

C

0

, 

C

1

, 

C

2

, 

C

3

:

{

v

i

= 

C

0

 

C

1

⋅0 

C

2

⋅sinh 0 

C

3

⋅cosh 0= 

C

0

 

C

3

=0

−N⋅ 

C

1

=0

−EJ

[





2

⋅ 

C

2

⋅sinh 0 



2

⋅ 

C

3

⋅cosh 0

]

=0



k

= 

C

1

⋅ 

C

2

⋅cosh  l⋅ 

C

3

⋅sinh  l





C

1

=0





C

3

=0

Jak widać wszystkie wartości poza wartością

C

2

znajdującą się we wzorze na

M

ik

są równe zero, zatem:



C

2

=



k

⋅cosh l

Podstawiamy wartość

C

2

do równania na

M

ki

, przy

x = l:

M

ki

=M  x=l =−EJ⋅







2

⋅ 

C

2

⋅sinh  l 



2

⋅ 

C

3

⋅cosh  l



=−EJ⋅

[





2

⋅



k

⋅cosh l

⋅sinh  l

]

=

=−EJ⋅

[

⋅

k

cosh 

l

⋅sinh  l

]

=−EJ⋅

[

⋅

k

⋅tgh  l

]

Korzystając z zależności:

=



N

EJ



2

=

N

⋅l

2

EJ



2

l

2

=

N

EJ

= 



l

otrzymujemy wzór transformacyjny:

M

ki

=−EJ⋅

[



l

⋅

k

⋅tgh 

]

M

ki

=−

EJ

l

⋅



⋅

k

⋅tgh 



Zauważmy, że dla belki o identycznym schemacie statycznym, ale poddanej sile ściskającej otrzymalibyśmy
następujący wzór transformacyjny:

M

ki

=

EJ

l

⋅



⋅

k

⋅tg 



Oznacza to, że możemy w prosty sposób zapisać wzory transformacyjne dla pręta poddanego sile
rozciągającej, na podstawie wzorów otrzymanych dla tego samego pręta, gdy działa na niego siła ściskająca.

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 2

9. STATECZNOŚĆ SPRĘŻYSTA UKŁADÓW PRĘTOWYCH

19

Aby otrzymywane wyrażenie można było łatwo przekształcać, doprowadźmy równanie różniczkowe dla pręta
rozciąganego do postaci identycznej jak dla pręta ściskanego. Wykonujemy podstawienie

=i 

Na podstawie wyrażenia

d

4

w

dx

2

−

2

⋅

d

2

w

dx

2

=0

otrzymujemy

d

4

w

dx

2



2

⋅

d

2

w

dx

2

=0

ponieważ:



2

=−

2

Skoro obydwa równania różniczkowe maja taką samą postać, to rozwiązania otrzymane dla pręta ściskanego,
są prawdziwe (przy odpowiednim podstawieniu) również dla pręta rozciąganego. W tej sytuacji, aby uzyskać
odpowiednią postać równań, należy wykonać następujące podstawienia:

=i 

sin

=sin i =i sinh 

cos

=cos i =cosh 

pamiętając jednocześnie, że i

2

=−1 .

Ostatecznie wzory transformacyjne dla danej belki (rys.9.14) poddanej sile rozciągającej możemy zapisać w
następujący sposób:

M

ik

=M 0=0

(9.64)

M

ki

=M l =−

EJ

l

⋅' ' ' '⋅

k

(9.65)

T

ik

=T

ki

=T 0=T l =0

(9.66)

gdzie:

' ' ' '=⋅tgh 

(9.67)



2

=

Nl

2

EJ

Jeżeli przyjmiemy

N

=0



=0



to:

lim

  0

' ' ' '=0

(9.68)

co oznacza, że moment przywęzłowy

M

ki

w belce nie obciążonej osiowo wynosi zero.

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 2

9. STATECZNOŚĆ SPRĘŻYSTA UKŁADÓW PRĘTOWYCH

20

9.4. Ogólne wzory transformacyjne dla prętów poddanych działaniu siły normalnej

Wyznaczone dotychczas wzory transformacyjne można wyrazić w innej formie:

•

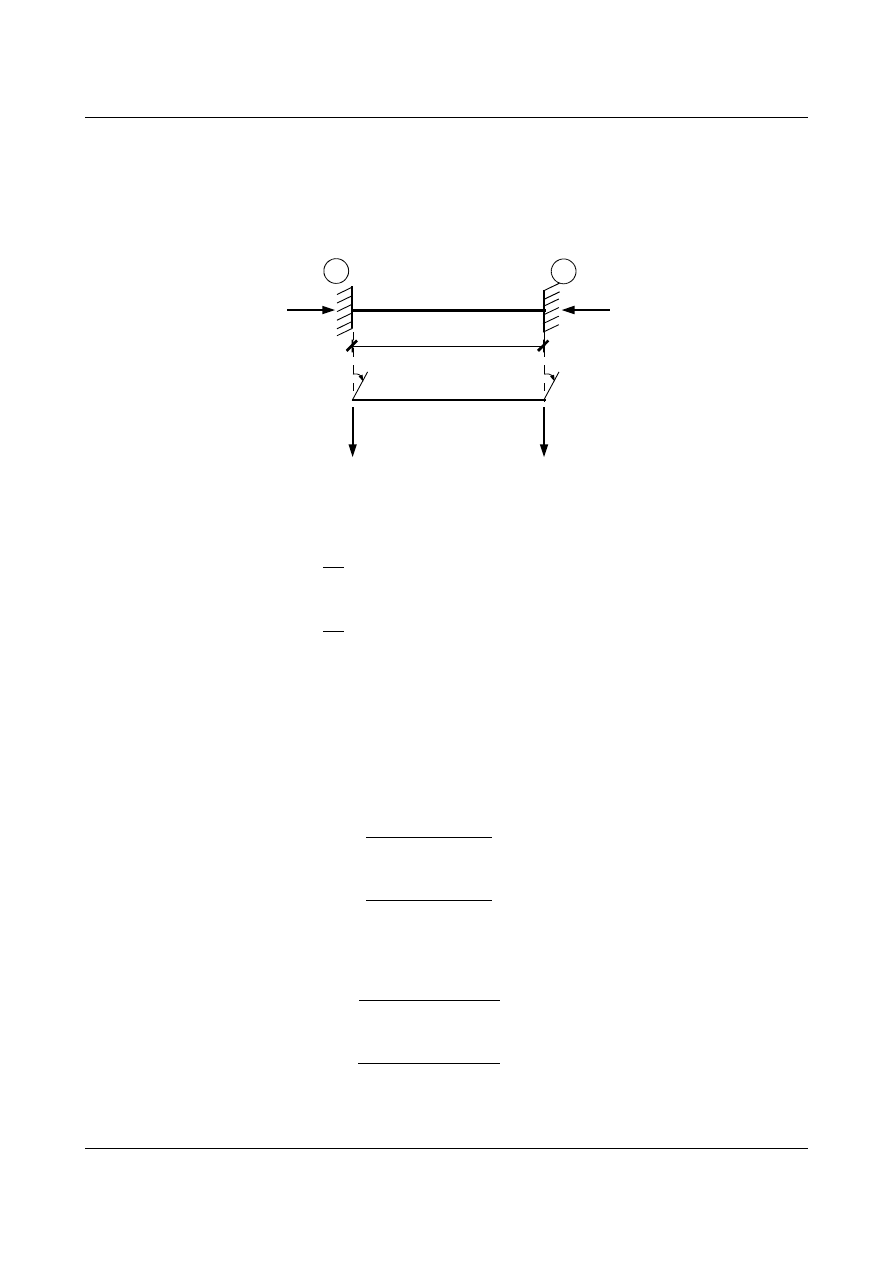
dla pręta obustronnie utwierdzonego (rys 9.15):

l

i

k

φ

i

φ

k

v

i

φ

i

φ

i

v

k

EJ

N

N

Rys. 9.15. Belka obustronnie utwierdzona

Wzory transformacyjne mają postać (jest to inna postać wzorów transformacyjnych z przykładu 3):

M

ik

=

EJ

l

⋅



c



i

s

k

−r

ik



(9.69)

M

ki

=

EJ

l

⋅



s



i

c

k

−r

ik



(9.70)

Pomiędzy współczynnikami zachodzi relacja:

r

=sc

(9.71)

Wartości współczynników możemy wyznaczyć ze wzorów:

–

przy ściskaniu

c

s

=





sin

−⋅cos 



2



1

−cos 



−⋅sin

(9.72)

s

s

=





−sin 



2



1

−cos 



−⋅sin 

(9.73)

–

przy rozciąganiu

c

r

=





sinh

−⋅cosh 



2



cosh

−1



−⋅sinh 

(9.74)

s

r

=





−sinh



2



cosh

−1



−⋅sinh

(9.75)

Bez względu na znak działającej siły osiowej współczynnik

λ wynosi

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 2

9. STATECZNOŚĆ SPRĘŻYSTA UKŁADÓW PRĘTOWYCH

21

=



N l

2

EJ

•

dla pręta z przegubem (rys. 9.16):

l

EJ

v

i

φ

i

v

k

i

k

N

N

Rys. 9.16. Belka utwierdzona z przegubem na jednym końcu

Wzory transformacyjne mają postać (jest to inna postać wzorów transformacyjnych z przykładu 4):

M

ik

=

EJ

l

⋅c⋅





i

−

ik



(9.76)

Wartość współczynnika wyznaczamy w zależności od zwrotu siły osiowej:

–

przy ściskaniu:

c

s

=



2

⋅sin

sin

−⋅cos

(9.77)

–

przy rozciąganiu:

c

r

=



2

⋅sinh

−sinh⋅cosh

(9.78)

Podobnie jak poprzednio parametr

λ nie zależy od znaku siły osiowej



2

=

∣N∣l

2

EJ

ponieważ jej znak uwzględniono w funkcjach trygonometrycznych.

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater