„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 

 
 

 
 
 

MINISTERSTWO EDUKACJI 

NARODOWEJ 

 

 

Antoni Buraczewski 

 

 

 

Projektowanie elementów i układów optycznych 
322[16].Z2.02 

 
 

 

 

 

Poradnik dla ucznia 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Wydawca  

Instytut Technologii Eksploatacji – Państwowy Instytut Badawczy 
Radom 2007 

 

 

 

 

 

 

 

 

 

 

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

  1 

Recenzenci: 

dr inŜ. Marcin Leśniewski 
dr hab. inŜ. Marek Zając 
 

 

Opracowanie redakcyjne: 

mgr inŜ. ElŜbieta Jarosz 

 

 

Konsultacja: 

mgr Małgorzata Sienna 

 

 

 

 

 

 

 

Poradnik  stanowi  obudowę  dydaktyczną  programu  jednostki  modułowej  322[16].Z2.02, 
„Projektowanie  elementów  i  układów  optycznych”,  zawartego  w  modułowym  programie 
nauczania dla zawodu technik optyk. 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
Wydawca 

Instytut Technologii Eksploatacji – Państwowy Instytut Badawczy, Radom  2007 

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

  2 

SPIS TREŚCI 

 
1.

 

Wprowadzenie 

3 

2.

 

Wymagania wstępne 

4 

3.

 

Cele kształcenia  

5 

4.

 

Materiał nauczania 

6 

4.1. Podstawowe prawa optyki geometrycznej i związane z nimi zjawiska   

 świetlne 

6 

 4.1.1. Materiał nauczania 

6 

 4.1.2. Pytania sprawdzające 

14 

 4.1.3. Ćwiczenia 

15 

 4.1.4. Sprawdzian postępów 

16 

4.2. Bieg światła przez powierzchnie elementów optycznych  

18 

 4.2.1. Materiał nauczania 

19 

 4.2.2. Pytania sprawdzające 

42 

 4.2.3. Ćwiczenia 

43 

 4.2.4. Sprawdzian postępów 

44 

4.3. Wykorzystanie falowej natury światła (interferencji, dyfrakcji,  
       polaryzacji i holografii) 

48 

 4.3.1. Materiał nauczania 

48 

 4.3.2. Pytania sprawdzające 

63 

 4.3.3. Ćwiczenia 

64 

 4.3.4. Sprawdzian postępów 

65 

4.4. Fotometria 

67 

 4.4.1. Materiał nauczania 

67 

 4.4.2. Pytania sprawdzające 

70 

 4.4.3. Ćwiczenia 

71 

 4.4.4. Sprawdzian postępów 

72 

5.

 

Sprawdzian osiągnięć 

73 

6.

 

Literatura 

78 

 
 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

  3 

1.

 

WPROWADZENIE  

 

Poradnik  będzie  Ci  pomocny  w  przyswajaniu  wiedzy  o  podstawowych  zjawiskach 

związanych  z  wytwarzaniem,  rozprzestrzenianiem  i  odbieraniem  promieniowania 
świetlnego,  czyli  z  działem  fizyki  zwanym  optyką.  Poznasz  prawa  rządzące  zjawiskami 
optycznymi, terminologię optyczną i zasady konstruowania elementów optycznych oraz ich 
układów w postaci przyrządów optycznych. 

W poradniku znajdziesz: 

−

 

wymagania  wstępne  –  wykaz  umiejętności,  jakie  powinieneś  mieć  ukształtowane,  abyś 
bez problemów mógł korzystać z poradnika, 

−

 

cele kształcenia – wykaz umiejętności, jakie ukształtujesz podczas pracy z poradnikiem, 

−

 

materiał  nauczania  –  wiadomości  teoretyczne  niezbędne  do  opanowania  treści  jednostki 
modułowej, 

−

 

zestaw pytań pozwalający Ci sprawdzić, czy juŜ opanowałeś określone treści, 

−

 

ćwiczenia,  które  pomogą  Ci  ukształtować  wiadomości.  praktyczne  ilustrujące  wiedzę 
teoretyczną, 

−

 

sprawdzian  osiągnięć  w  postaci  zestawu  zadań,  którego  pozytywny  wynik  potwierdzi, 
opanowanie materiału całej jednostki modułowej, 

−

 

wykaz literatury uzupełniającej. 

 
 
 

 

 

 

 

 

 

 

 

 

 

Schemat układu jednostek modułowych 

 

 

 

 

 

 

 

 

 

 

322[16].Z2 

Optyka 

322[16].Z2.02 

Projektowanie elementów 

i układów optycznych 

322[16].Z2.03 

Stosowanie urządzeń, 

przyrządów optycznych 

i optoelektronicznych 

322[16].Z2.01 

Stosowanie i ocena jakości 

 materiałów optycznych 

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

  4 

2.  WYMAGANIA WSTĘPNE 

 

Przystępując do realizacji programu nauczania jednostki modułowej powinieneś umieć: 

−

 

korzystać z róŜnych źródeł informacji, 

−

 

posługiwać  się  podstawowymi  pojęciami    i  wzorami  matematycznymi  oraz  fizycznymi 
w stopniu umoŜliwiającym przeprowadzanie prostych obliczeń, 

−

 

stosować układ jednostek SI. 

−

 

posługiwać  się  podstawowymi  pojęciami  i  wzorami  matematycznymi  oraz  fizycznymi 
w stopniu umoŜliwiającym przeprowadzanie prostych obliczeń, 

−

 

przeliczać jednostki pomiarowe kątów, 

−

 

komunikować się w zespole, 

−

 

posługiwać się materiałem zaczerpniętym z literatury, 

−

 

wyszukiwać,  selekcjonować,  porządkować  przetwarzać  i  przechowywać  informacje 
niezbędne do wykonywania zadań zawodowych, 

−

 

analizować treść zadania, układać plan  i dobierać metody rozwiązania, 

−

 

rozróŜniać rodzaje zjawisk, 

−

 

interpretować wyniki obserwacji i dokonywać uogólnień, 

−

 

dokonywać oceny swoich umiejętności. 

 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

  5 

3.  CELE KSZTAŁCENIA 

 

W wyniku realizacji programu jednostki modułowej powinieneś umieć: 

−

 

zinterpretować prawa optyki geometrycznej, 

−

 

scharakteryzować ośrodki fizyczne pod kątem ich właściwości optycznych, 

−

 

wyznaczyć rozkład cienia w zaleŜności od wielkości i odległości źródła światła, 

−

 

zinterpretować  zjawiska  optyczne  zachodzące  na  granicy  dwu  ośrodków  (załamanie, 
odbicie zewnętrzne i wewnętrzne), 

−

 

rozróŜnić rodzaje powierzchni odbijających światło pod względem kształtu  i właściwości, 

−

 

wyznaczyć miejsce powstawania obrazu w zwierciadle płaskim, 

−

 

wyznaczyć drogę światła przez układy zwierciadeł płaskich, 

−

 

wyznaczyć miejsca powstawania obrazów w zwierciadłach sferycznych, 

−

 

zastosować terminologię dotyczącą zwierciadeł sferycznych, 

−

 

zastosować zjawisko całkowitego wewnętrznego odbicia, 

−

 

zaprojektować płytkę płasko równoległą w zaleŜności od jej roli w układzie optycznym, 

−

 

zaprojektować pryzmat o załoŜonych właściwościach, 

−

 

określić  i  przeanalizować  skład  widma  promieniowania  świetlnego  na  podstawie  jego 
dyspersji, 

−

 

wyznaczyć bieg światła przez powierzchnie kuliste (soczewki i ich układy), 

−

 

określić moc soczewek i ich układów, 

−

 

scharakteryzować układy optyczne róŜnych urządzeń, 

−

 

wyznaczyć gabaryty układów optycznych (apertury i źrenice), 

−

 

scharakteryzować  błędy  odwzorowania  w  układach  optycznych  i przyczyny  ich 
powstawania (aberracje), 

−

 

zdefiniować parametry ruchu falowego, 

−

 

dokonać pomiaru wielkości fizycznych metodami interferencyjnymi, 

−

 

zastosować zjawisko interferencji do pomiarów i projektowania cienkich warstw,  

−

 

zinterpretować obrazy widm dyfrakcyjnych, 

−

 

zaprojektować siatkę dyfrakcyjną pod kątem jej parametrów i zastosowania, 

−

 

zaprojektować układy do obserwacji w świetle spolaryzowanym, 

−

 

zaprojektować  parametry  oświetlenia  i  źródeł  światła  z  zastosowaniem  jednostek 
fotometrycznych, 

−

 

zastosować układy do holograficznej rejestracji i odczytywania obrazów. 

 
 
 
 
 
 
 
 
 
 
 
 
 
 

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

  6 

4.

 

MATERIAŁ NAUCZANIA  

 

4.1.

 

Podstawowe  prawa  optyki  geometrycznej  i  związane  z  nimi 
zjawiska świetlne 

 

4.1.1.

 

Materiał nauczania  

 

Optyka,  jako  część  fizyki  zajmuje  się  zjawiskami  związanymi  z  wytwarzaniem, 

rozchodzeniem  się  i  absorpcją  (pochłanianiem)  światła,  czyli  fal  elektromagnetycznych 
z zakresu  promieniowania  widzialnego  i  jego  sąsiedztwa  –  podczerwieni  i  ultrafioletu. 
Zjawiskami  tymi  ludzkość  zajmowała  się  od  początku  dziejów,  poniewaŜ  ich  znajomość 
i umiejętność  wykorzystywania  warunkowała  przetrwanie.  Pierwsze  próby  opisania  oraz 
wytłumaczenia  zjawisk  optycznych  pojawiły  się  juŜ  w  staroŜytności  i  średniowieczu. 
Prawdziwy  rozwój  tej  dziedziny  fizyki  nastąpił  jednak  po  wynalezieniu  czystego, 
bezbarwnego szkła, które okazało się świetnym, tanim materiałem do konstruowania róŜnych 
elementów  optycznych.  To  z  kolei  pociągnęło  za  sobą  potrzebę  dokładnego  poznania  praw 
rządzących 

zjawiskami 

optycznymi 

i 

zasad 

konstruowania 

coraz 

to 

bardziej 

skomplikowanych przyrządów. 

Coraz dokładniejsze poznawanie zjawisk optycznych doprowadziło do podziału optyki na 

optykę geometryczna i optykę falową. Optyka falowa uwzględnia zjawiska wynikające z tego, 
Ŝe  światło  to  fale  elektromagnetyczne  mogące  na  siebie  oddziaływać  (dyfrakcja 
i interferencja). 

Do projektowania prostych elementów optycznych i złoŜonych z nich układów wystarczy 

znajomość podstawowych formuł optyki  geometrycznej,  geometrii i zasad wytyczania biegu 
promieni  przez  róŜne  ośrodki  optyczne  i  ich  powierzchnie  graniczne.  Pozwoli  to  sporządzić 
i wyjaśnić elementarny opis procesu powstawania obrazu. 

Aby zacząć poznawanie praw i reguł rządzących optyką, konieczna jest znajomość kilku 

podstawowych pojęć. Są to: 

Źródło  światła  –  ciało  wysyłające  światło.  MoŜe  wysyłać  światło  własne  (wytworzone 

przez  siebie)  lub  odbite  (wytworzone  przez  inne  źródło  światła).  Źródła  światła  mogą  być 
naturalne lub sztuczne oraz monochromatyczne (jednobarwne) i złoŜone (wielobarwne) 

Ośrodek optyczny – przestrzeń, w której rozprzestrzenia się światło.  

Ośrodki  optyczne  wykazują  róŜne  zdolności  do  osłabiania  (odbicia,  pochłaniania,  absorpcji) 
przechodzącego przez nie światła i dlatego dzielimy je na trzy rodzaje:

  

−

 

nieprzezroczyste,  

−

 

półprzezroczyste, 

−

 

przezroczyste. 
Ośrodki  optyczne  moŜna  jeszcze  podzielić  na  jednorodne,  wykazujące  jednakowe 

właściwości 

optyczne 

dla 

wszystkich 

kierunków 

rozprzestrzeniania 

się 

światła 

i niejednorodne, w których zaleŜą one od fizyko-chemicznych właściwości ośrodka w danym 
punkcie i od kierunku biegu światła. 

Promień  światła  –  umowna  wielkość  wektorowa  wyznaczająca  kierunek  rozchodzenia 

się  światła.  Promienie  nie  oddziaływają  na  siebie  wzajemnie.  W  zasadzie  nie  istnieją,  nie 
mogą  być  wydzielone  eksperymentalnie.  Jeśli  jednak  potraktujemy  światło  jako  falę 
przestrzenną, która ma swoją powierzchnię (powierzchnia falowa), to linie prostopadłe do tej 
powierzchni moŜna nazwać promieniami – dadzą się narysować. 
 

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

  7 

 

 

 

Rys. 1. Promienie to kierunki rozchodzenia się światła [opracowanie własne] 

 
Zasada  Fermata – Światło przebiegając od punktu do punktu wybiera drogę, na pokonanie 
której  potrzeba  najmniej  czasu.  Oznacza  to,  Ŝe  nie  zawsze  musi  to  być  geometrycznie 
najkrótsza  droga  czyli  linia  prosta.  Zasada  ta  pozwala    wyprowadzić  znane  juŜ  wcześniej 
prawa optyki geometrycznej. 

Prawa te to: 

−

 

Prawo prostoliniowego rozchodzenia się światła (w ośrodkach jednorodnych). 

−

 

Prawo odbicia.  

−

 

Prawo załamania Snelliusa.  

 
Prawo prostoliniowego rozchodzenia się światła 

 

Dzięki  temu  mamy  moŜność  celowania,  powstał  takŜe    przyrząd  zwany  ciemnią  optyczną 
(camera  obscura)  opisany  juŜ  w  średniowieczu,  a  uŜywany  (dzięki  unikatowym  zaletom)  do 
dzisiaj m.in. w technice kosmicznej. Te zalety to szeroki zakres promieniowania, duŜa głębia 
ostrości i brak wady odwzorowania zwanej dystorsją. 

 

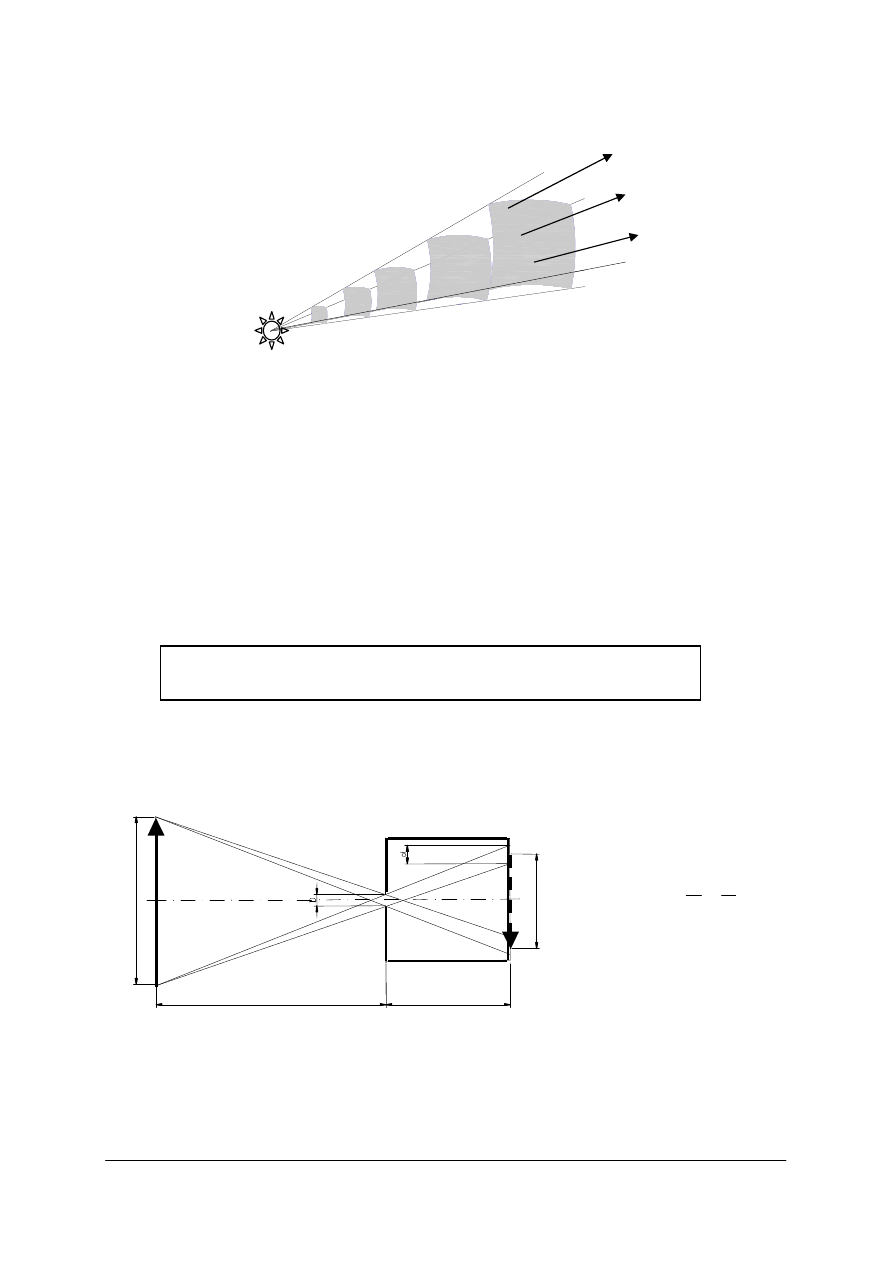
Rys. 2. Rysunek przedstawiający działanie ciemni optycznej, gdzie y – wielkość przedmiotu, y’ – wielkość 

obrazu, x – odległość przedmiotowa, x’ – odległość obrazowa, D – otwór, d – plamka rozmycia  

[opracowanie własne] 

 

Prawo prostoliniowego rozchodzenia się światła wystarcza w zupełności do wyjaśnienia 

zjawiska cienia, o ile będziemy poruszać się w obrębie optyki geometrycznej. 

 

Światło wytworzone przez źródło punktowe w ośrodkach jednorodnych 

rozchodzi się po liniach prostych równomiernie w całej przestrzeni.  

β = Powiększenie poprzeczne 

x

x

y

y

'

'

=

=

β

 

x 

x’ 

y 

y’ 

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

  8 

 

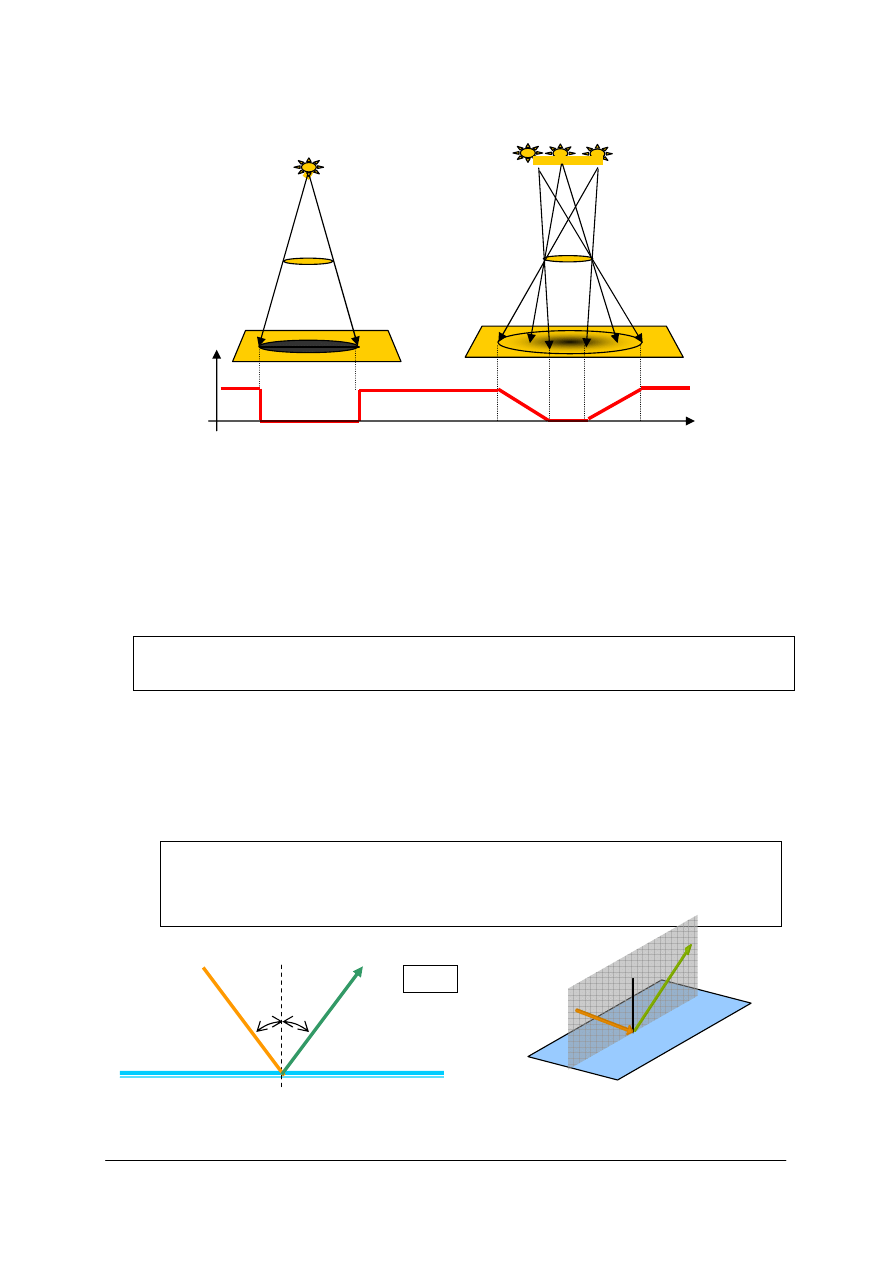
Rozpatrzmy zjawisko w zaleŜności od wielkości źródła światła. 

 

Rys. 3. Cień w zaleŜności od wielkości źródła światła z zaznaczonym na wykresie rozkładem energii 

[opracowanie własne] 

 

Przy  oświetleniu  punktowym  granica  cienia  jest  ostra.  Przy  rozciągłym  źródle  światła 

granica między cieniem a powierzchnią oświetloną pełnym światłem jest płynnie rozciągnięta 
i nosi nazwę półcienia. 
Wykorzystanie  wymienionych  powyŜej  praw  optyki  geometrycznej  i  zjawisk  z  nimi 
związanych pozwala na zaprojektowanie prostych przyrządów optycznych. 

 

O  ciemni  optycznej  i  celownikach  (np.  muszka  i  szczerbinka  w  broni  strzeleckiej)  juŜ 

wspominaliśmy. 

Światło na swojej drodze napotyka róŜne ośrodki optyczne, które w zaleŜności od swoich 

właściwości    optycznych  mogą  róŜnie  oddziaływać  na  bieg  promieni.  Pierwszym  efektem 
takiego  oddziaływania  jest  odbicie  od  powierzchni  rozgraniczającej  ośrodki.  Podlega  ono 
prawu odbicia wynikającemu z zasady Fermata. 

Prawo to jest określone dwoma twierdzeniami: 

Rys. 4. Ilustracja praw odbicia. α – kąt padania, β – kąt odbicia, N – normalna do powierzchni w punkcie 

padania [opracowanie własne] 

−

 

Kąt padania równa się kątowi odbicia (α= β) 

−

 

Promień padający, prosta prostopadła (normalna) do powierzchni odbijającej 

w punkcie padania promienia i promień odbity leŜą w jednej płaszczyźnie. 

N 

N 

α 

β 

α = β 

Dla celów fotometrycznych przyjęto, Ŝe źródło rozciągłe to takie, którego wymiar 
poprzeczny jest większy od 1/20 odległości obserwacji. 

I

max 

I

min 

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

  9 

Drugim  efektem  oddziaływania  powierzchni  oddzielającej  ośrodki  jest  zmiana  kierunku 

promieni  świetlnych  połączona  z  ich  przejściem  do  drugiego  ośrodka.  Nazywa  się  to 
załamaniem i podlega prawu załamania Sneliusa – Kartezjusza (wywodzącemu się równieŜ 
z zasady Fermata), które brzmi:  

 

WyraŜa się ono wzorem: 

n

n

i

i

'

'

sin

sin

=

 gdzie  

,

v

c

n

=

  a    

'

'

v

c

n

=

.  

c

 – oznaczenie prędkości światła w próŜni. 

n i n’ – bezwzględne współczynniki załamania ośrodka pierwszego i drugiego. 

Stosunek  sinusa  kąta  padania  w  pierwszym  ośrodku  do  sinusa  kąta  załamania  w  drugim 
ośrodku nazywamy 

względnym współczynnikiem załamania. Gdy jednym z tych ośrodków 

jest  próŜnia  (n  =  1),  to  współczynnik  nazywamy 

bezwzględnym  współczynnikiem 

załamania. 

 

Rys. 5. Ilustracja prawa załamania. S – ośrodek pierwszy, S’ – ośrodek drugi, v – prędkość w pierwszym 

ośrodku, v’ – prędkość w ośrodku drugim, n – współczynnik załamania ośrodka pierwszego, n’ – współczynnik 

załamania ośrodka drugiego  [opracowanie własne] 

 

 

Konsekwencją tych trzech praw optyki  geometrycznej są zjawiska na  granicy ośrodków 

optycznych. Są to: 

−

 

odbicie, 

−

 

przejście, 

−

 

załamanie, 

−

 

kombinacja tych trzech zjawisk w róŜnych proporcjach. 

Odbicie  światła  moŜe  być:  albo  całkowite  (odbija  wtedy  wszystkie  barwy,  jakie  wysyła 

źródło  światła),  albo  częściowe,  inaczej  selektywne  (odbija  tylko  część  kolorów)  i  dzięki 
temu  przedmioty  oświetlone  światłem  białym  (np.  słonecznym)  mają  róŜne  barwy. 
Przedmioty nie odbijające promieniowania świetlnego są dla nas czarne. 

 
 

Stosunek sinusa kąta padania do sinusa kąta załamania, jest dla dwu graniczących 
ośrodków  (S  i  S’)  wielkością  stałą,  równą  stosunkowi  prędkości  światła  v  i  v’  
w tych ośrodkach. 
Promień  padający,  prostopadła  do  powierzchni  załamującej  w  punkcie  padania  
i promień załamany leŜą w jednej płaszczyźnie. 

 

 i 

i’ 

n’ 

S 

S’ 

v  n 

v’ 

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 10

 

Ze względu na rodzaj powierzchni odbijającej moŜemy sklasyfikować odbicia na: 

−

 

zwierciadlane (lustrzane), 

−

 

dyfuzyjne (rozproszone), 

−

 

mieszane (kombinacja 1 i 2 w róŜnych proporcjach). 

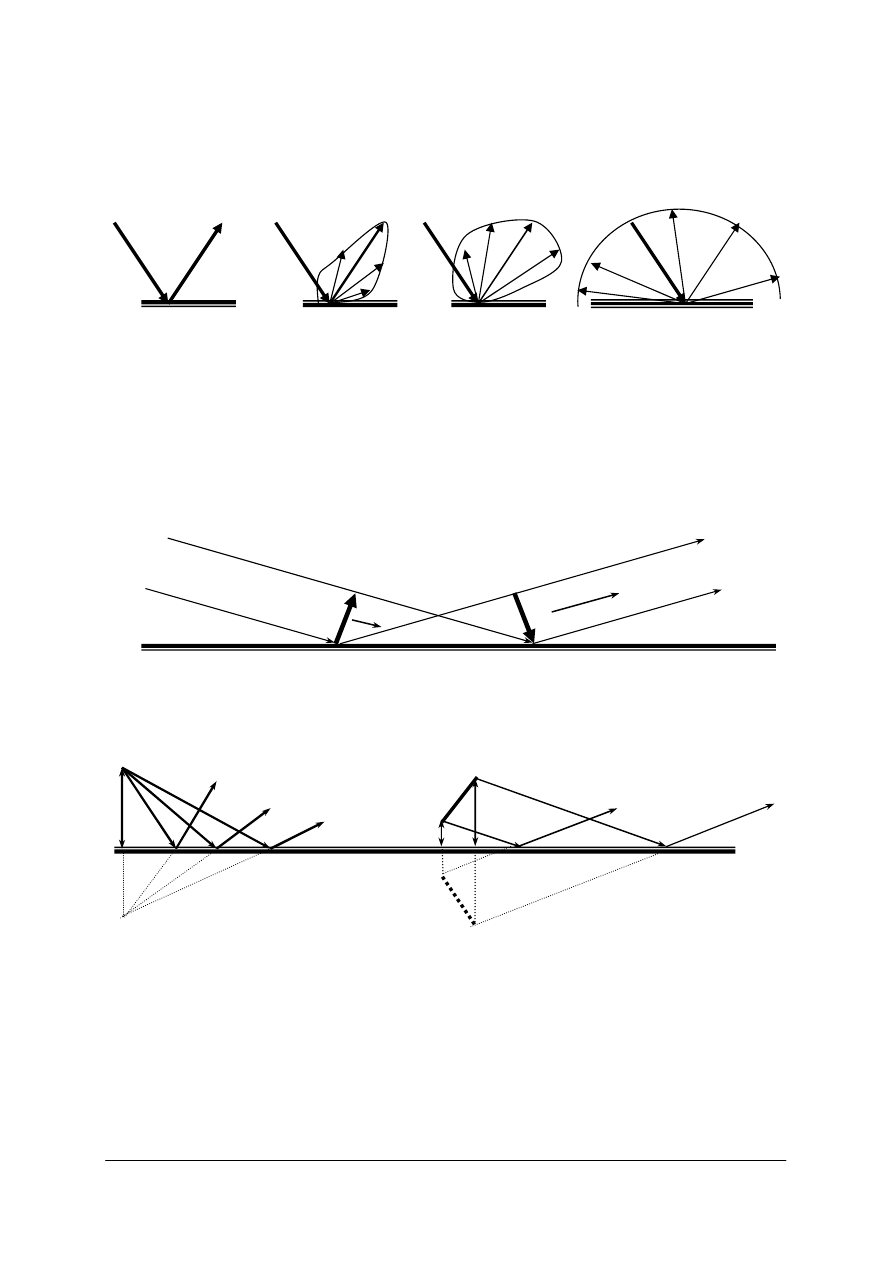
Rys. 6. RóŜne rodzaje odbicia w zaleŜności od gładkości powierzchni  (od zwierciadlanego do w pełni 

dyfuzyjnego) [opracowanie własne] 

 

Przy  pełnym  odbiciu  zwierciadlanym  powierzchnia  odbijająca  jest  niewidzialna.  Przy 

pełnym  rozproszeniu  powierzchnia  odbijająca  jest  dla  obserwatora  jednakowo  jasna,  bez 
względu na kierunek obserwacji. 
Najpowszechniejszym  wykorzystaniem  zjawiska  odbicia  są  wszelkiego  rodzaju  zwierciadła 
płaskie, sferyczne (kuliste) i asferyczne. 

Odbicie od zwierciadła płaskiego 
 

 

Rys. 7. Przy odbiciu od zwierciadła ulega zmianie porządek promieni [opracowanie własne] 

 
 
 

 

Rys. 8. Mechanizm powstawania obrazu w zwierciadle płaskim. Promienie odbite od powierzchni zwierciadła 

docierają do obserwatora z punktów pozornych, leŜących poza tą powierzchnia. Zarówno obraz punktu,  

jak i ich zbioru (np. odcinka) powstaje w miejscu przecięcia przedłuŜeń promieni odbitych  

[opracowanie własne] 

 

A 

A’ 

A 

B 

B’ 

A’ 

1 

2 

2’ 

1’ 

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 11

Rys. 9. ZaleŜność obrazu od połoŜenia zwierciadła. [opracowanie własne] 

Zwierciadło podwójne 
 

Rys. 10. Bieg promienia w zwierciadle podwójnym, gdzie Θ – kąt między zwierciadłami, γ – kąt między 

promieniem wchodzącym i wychodzącym, a δ – kąt odchylenia (dewiacji) promienia [opracowanie własne] 

 

Sześcienny reflektor naroŜny 

Rys. 11. Bieg promienia w sześciennym reflektorze naroŜnym [opracowanie własne] 

Sześcienny  reflektor  naroŜny  to  układ  3  zwierciadeł  ustawionych  pod  kątem  prostym. 

Cechą  jego  jest  to,  Ŝe  wchodzący  do  niego  pod  dowolnym  kątem  promień  wychodzi  jako 

 

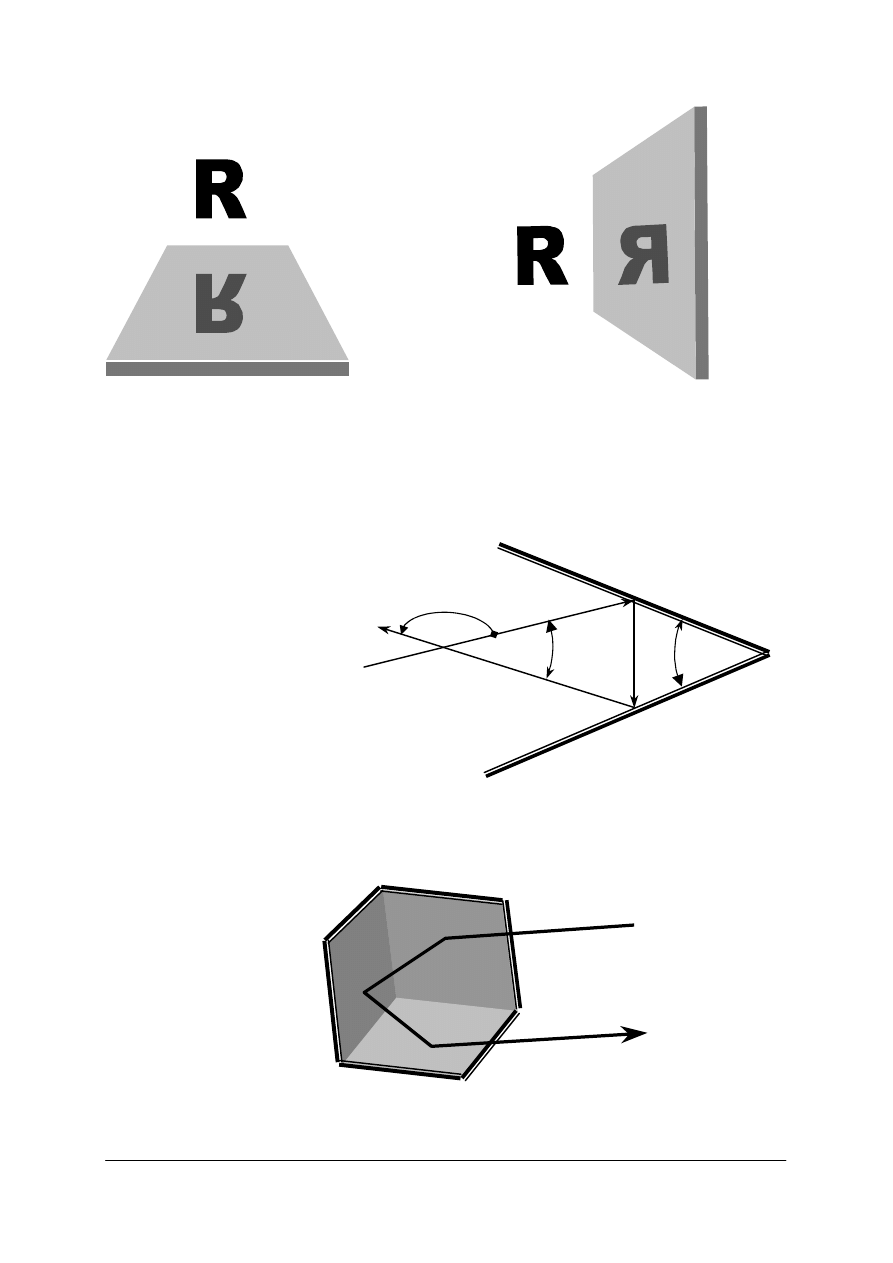
Obraz odwrócony w pionie 

(zamieniony góra – dół), 

 prosty w poziomie. Nieczytelny. 

Obraz odwrócony w poziomie 

(zamieniony prawo – lewo), 

prosty w pionie. Nieczytelny. 

 

 

γ 

Θ 

γ = 180 – 2Θ 

d 

d = 2Θ 

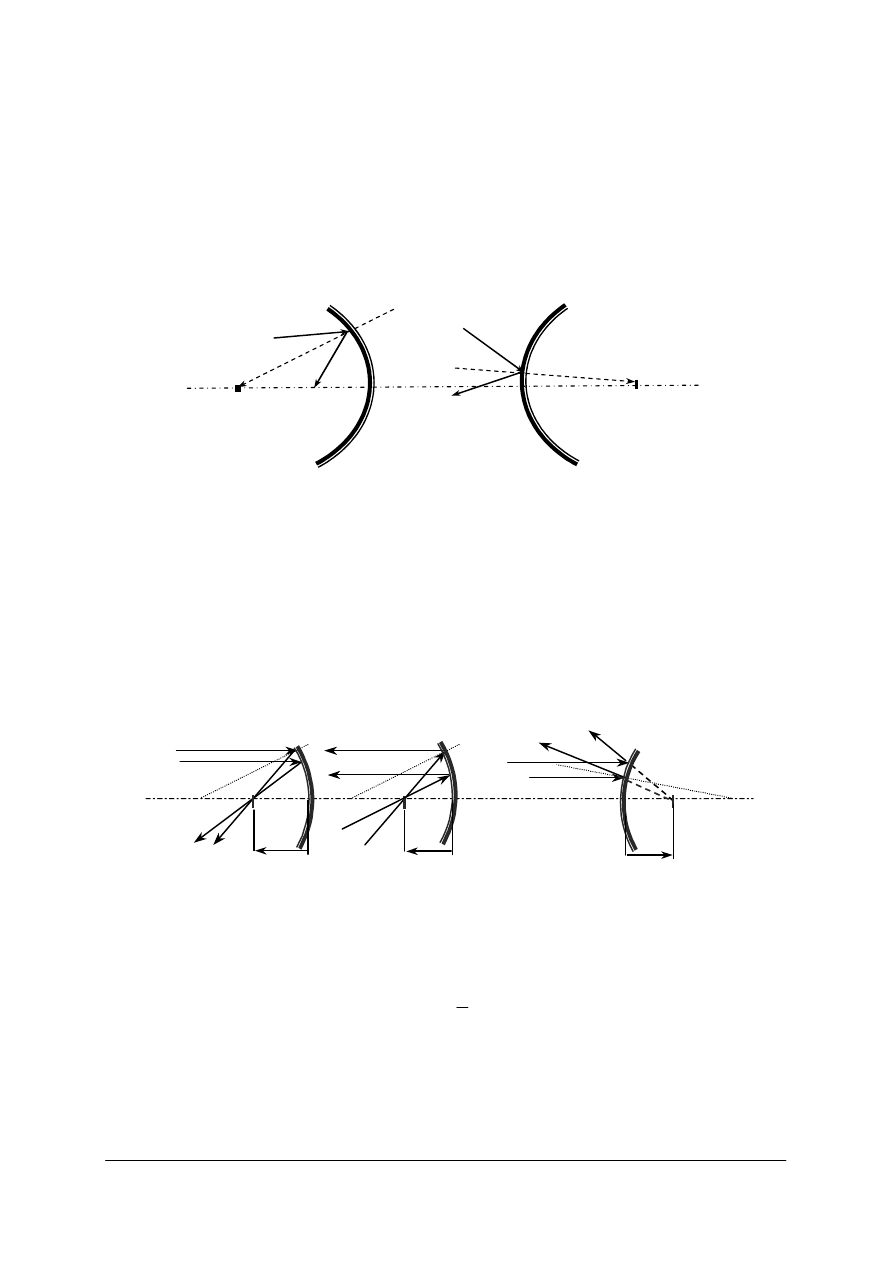
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 12

antyrównoległy.  Układ  ośmiu  takich  reflektorów  stykających  się  zewnętrznymi 
powierzchniami  obejmuje  pełny  kąt  przestrzenny  360°  i  odbija  sygnały  świetlne  w  stronę 
nadajnika bez względu na kierunek z jakiego padają. 

Zwierciadła kuliste (sferyczne) 

Definicje: 

−

 

Zwierciadła,  których  powierzchnie  odbijające  są  fragmentami  powierzchni  kul, 
nazywamy kulistymi lub sferycznymi. Powierzchnie te mogą być wypukłe lub wklęsłe. 

 

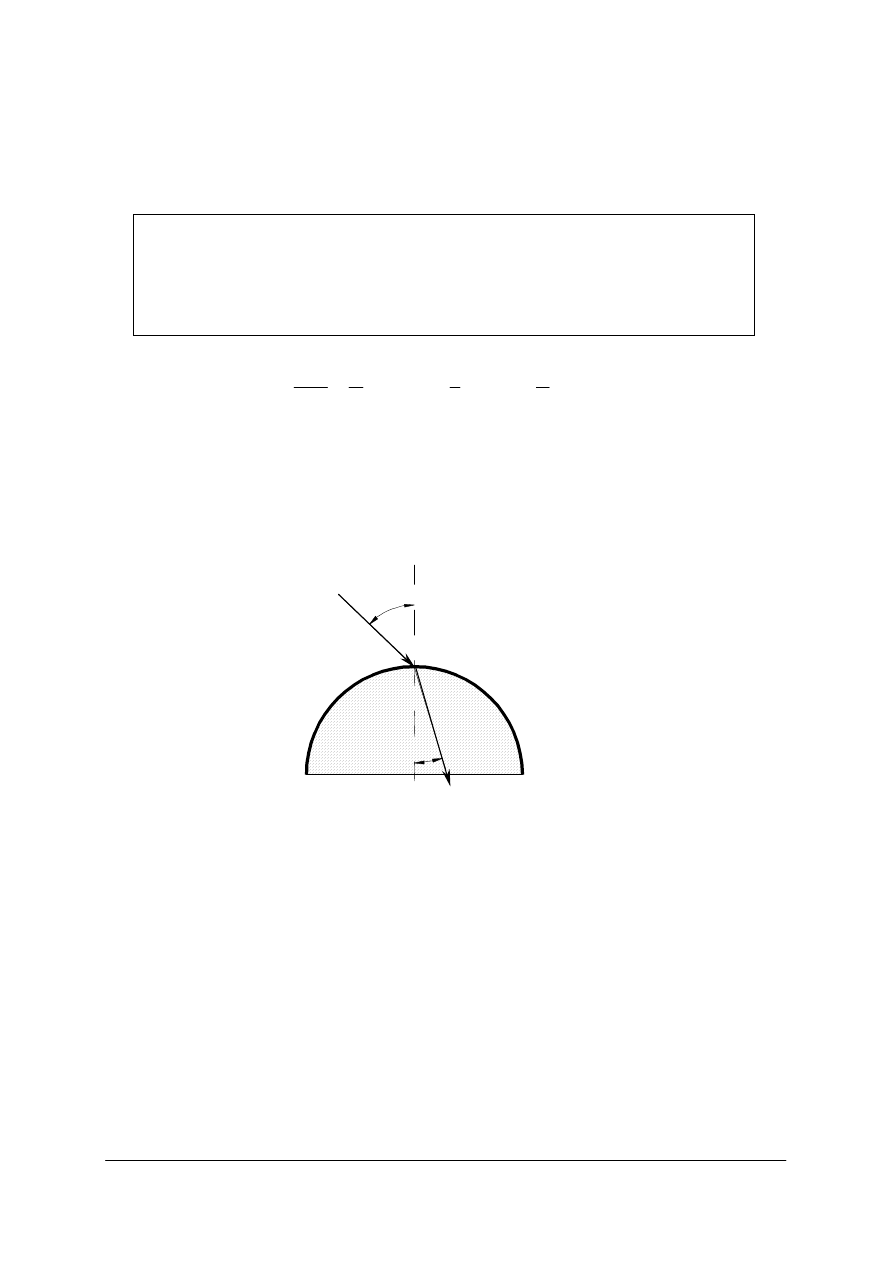
Rys. 12. Podstawowe terminy dotyczące powierzchni sferycznej: R – promień krzywizny, C –  wierzchołek 

krzywizny, S – środek krzywizny, N – normalna do powierzchni w punkcie padania A [opracowanie własne] 

 

−

 

Promień  krzywizny  (R)  –  odcinek  prostopadły  do  powierzchni  w  punkcie  padania 
promienia świetlnego. Łączy ten punkt ze środkiem krzywizny. 

−

 

Oś optyczna (C) –  prosta przechodząca przez środek krzywizny i środek jej obwodu. 

−

 

Promienie zbieŜne – pęk promieni świetlnych skierowanych do jednego punktu. 

−

 

Promienie rozbieŜne – pęk promieni świetlnych skierowanych od jednego punktu. 

−

 

Ogniska (F) – punkty na osi optycznej, do których i od których rozchodzą się odbite od 
powierzchni sferycznej pęki promieni, ale jedynie w przypadku, gdy przed odbiciem albo 
po odbiciu promienie te tworzą wiązki równoległe. Gdy wiązka jest rozbieŜna z ogniska, 
ognisko nazywamy przedmiotowym (F), gdy zbieŜna – obrazowym (F’). 

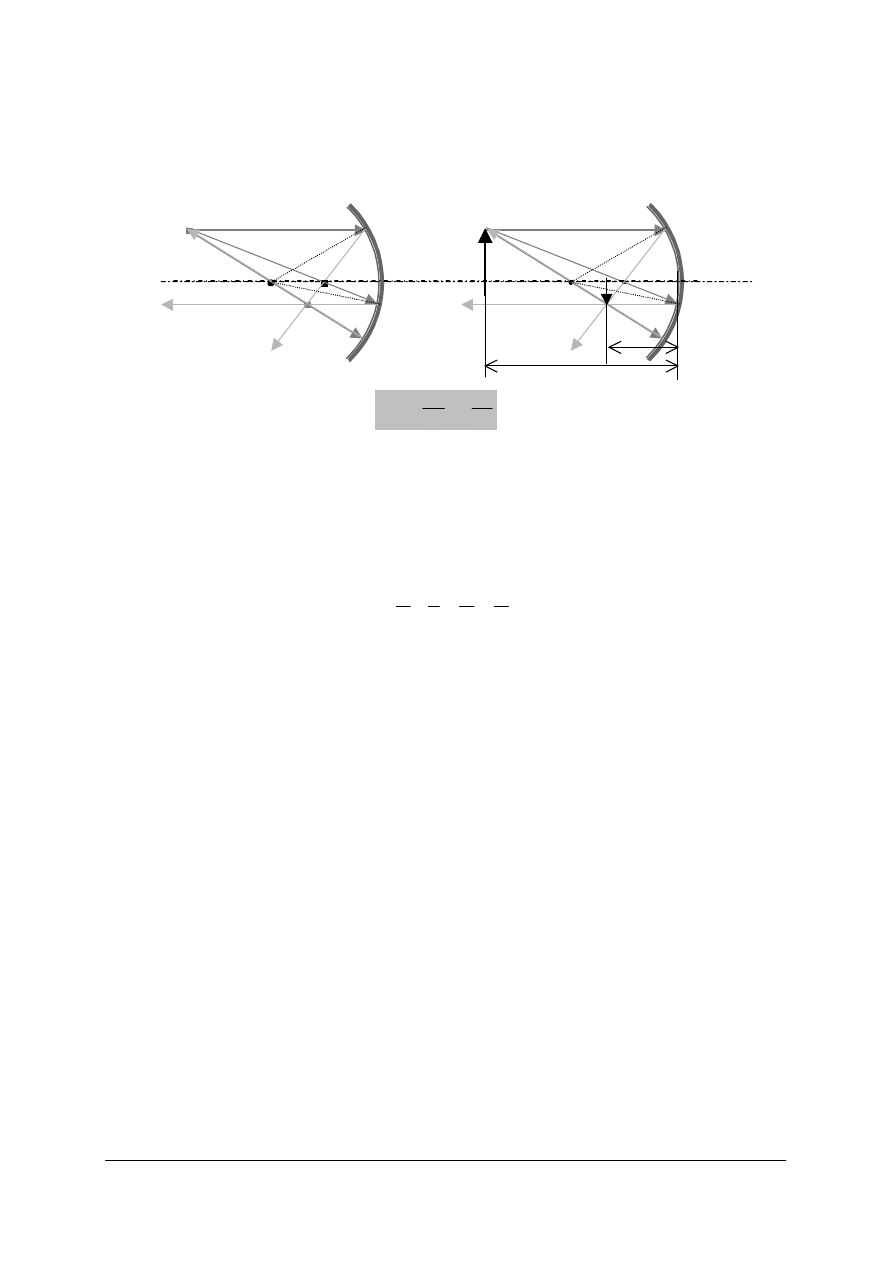
Rys. 13. Ogniska zwierciadeł sferycznych. F – ognisko przedmiotowe, F’ – ognisko obrazowe,  

f – ogniskowa przedmiotowa, f’ – ogniskowa obrazowa [opracowanie własne] 

 

−

 

Ogniskowa  –  Odległość  od  powierzchni  odbijającej  do  ogniska.  Oznaczamy  ją  jako  f, 
jeśli  odnosi  się  do  ogniska  przedmiotowego,  a  f’  jeśli  do  obrazowego.  W zwierciadłach 
sferycznych ogniska pokrywają się, a ogniskowe są równe połowie promienia krzywizny. 

2

r

f

=

 

−

 

Moc  (D)  –    odwrotność  ogniskowej  wyraŜonej  w  metrach,  wyraŜamy  ją  w  dioptriach 
(dptr).  

D =1/f 

 

 

F 

f 

F’ 

f’ 

F’ 

f’ 

C 

C 

N 

N 

R 

R 

A 

A 

S 

S 

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 13

Powstawanie obrazu w zwierciadłach kulistych 

Promienie  świetlne  padając  na  powierzchnie  sferyczna  podlegają  prawom  odbicia,  tak 

samo  jak  w  przypadku  powierzchni  płaskiej.  Wyznaczanie  połoŜenia  obrazu  podlega  więc 
takim samym regułom. 

 

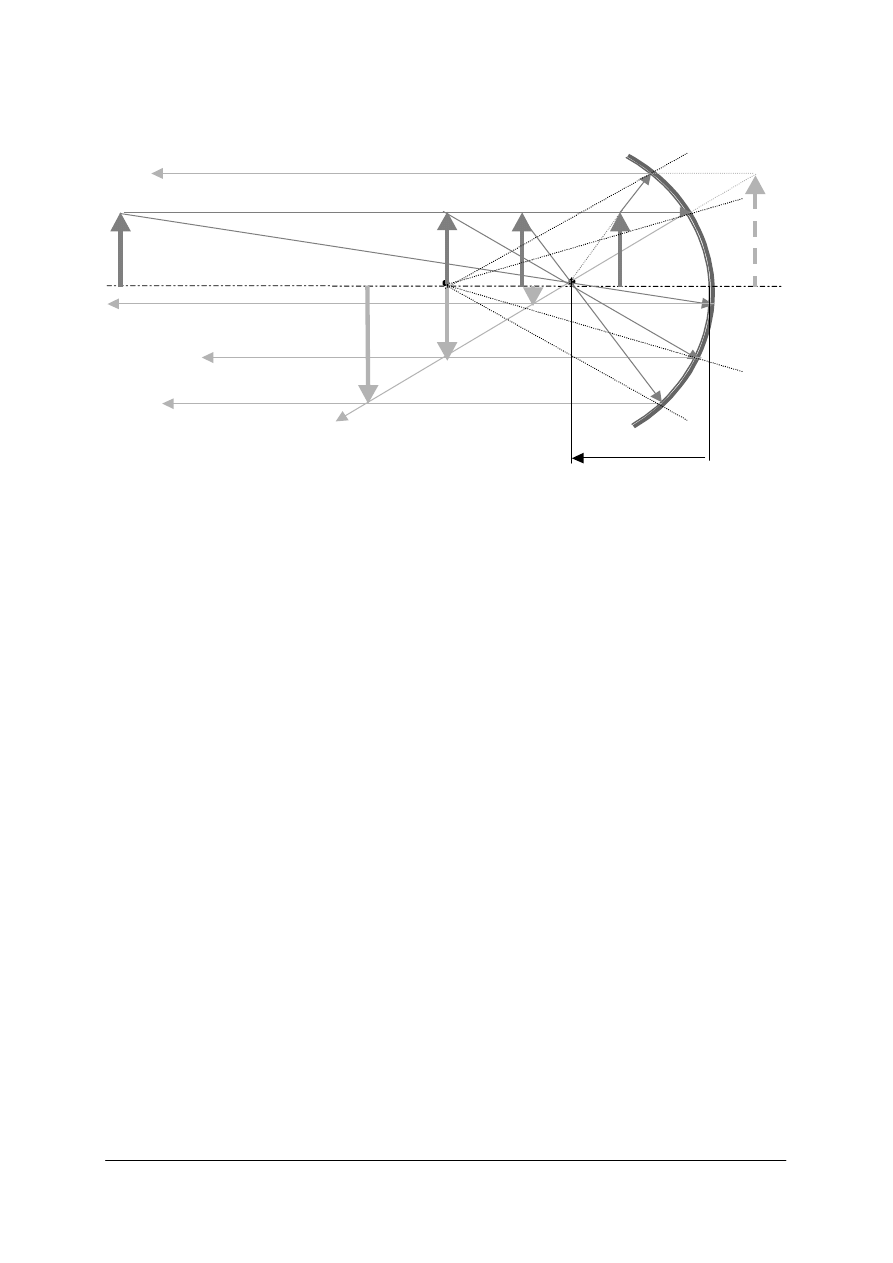
Rys. 14. Schemat powstawania obrazu punktu i odcinka w zwierciadle sferycznym:  

x – odległość przedmiotowa, x’ – odległość obrazowa, y – wielkość przedmiotu, y’ – wielkość obrazu,  

β – powiększenie [opracowanie własne] 

 

 

Metoda  wykreślna  określania  połoŜenia  obrazu  jest  pomocna  jeśli  chodzi  o  wynik 

orientacyjny,  zaleŜy  od  dokładności  rysunku.  Do    wyznaczenia  dokładnych  połoŜeń  obrazu  
i przedmiotu moŜemy posłuŜyć się metodą czysto matematyczną stosując wzór Kartezjusza: 

R

f

x

x

2

1

1

'

1

=

=

−

 

 

Aby  prawidłowo  zastosować  wzór  musimy  przyjąć  następującą  regułę  znaków  dla 

występujących w nim wielkości: 

−

 

Promień  krzywizny  R  i  ogniskowa  f  są  dodatnie  jeśli  kierunek  od  wierzchołka 
krzywizny  C  do  ogniska  F  lub  do  środka  krzywizny  S  jest  zgodny  z  kierunkiem 
promienia odbitego, a ujemne gdy jest przeciwny. 

−

 

Odległość  x  od  wierzchołka  krzywizny  do  przedmiotu  jest  dodatnia,  gdy  jej  kierunek 
jest zgodny z kierunkiem promieni padających. 

−

 

Odległość  x’  od  wierzchołka  krzywizny  do  obrazu  jest  dodatnia,  gdy  jej  kierunek  jest 
zgodny z kierunkiem promieni odbitych. 

−

 

Wymiary  przedmiotu  y  i  obrazu  y’  są  dodatnie,  gdy  znajdują  się  nad  osią  optyczna, 
a ujemne, gdy znajdują się pod nią. 

 
 
 
 
 
 
 
 
 
 
 
 
 
 

 

x

x

y

y

'

'

=

=

β

A 

S 

F 

y’ 

y 

x’ 

A’ 

x 

s

1

P

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 14

Powstawanie obrazu w zaleŜności od połoŜenia przedmiotu 

Zwierciadło wklęsłe. 

Rys. 15.  Schemat powstawania obrazów w zwierciadle wklęsłym w zaleŜności od odległości przedmiotowej, 

gdzie: y

1

 – y

4 – 

kolejne połoŜenia przedmiotu, a  y’

1

- y’

4

 – kolejne, odpowiadające im połoŜenia obrazu.  

Strzałka  z przerywanej linii oznacza obraz pozorny. [opracowanie własne] 

 

4.1.2. Pytania sprawdzające 

 
Odpowiadając na pytania, sprawdzisz, czy jesteś przygotowany do wykonania ćwiczeń. 

1.

 

Jak rozchodzi się światło wytworzone przez źródło punktowe? 

2.

 

Jak działa camera obscura? 

3.

 

Czym róŜnią się cienie powstałe od źródła punktowego i rozciągłego? 

4.

 

Jakie wyróŜniamy ośrodki fizyczne z punktu widzenia optyki? 

5.

 

Jakie zjawiska optyczne zachodzą na granicy ośrodków? 

6.

 

Jak odbija się światło w zaleŜności od rodzaju powierzchni odbijającej? 

7.

 

W  jakim  kolorze  będziemy  oglądali  zieloną  kartkę  papieru  w  pomieszczeniu 
oświetlonym światłem czerwonym? 

8.

 

Czym róŜni się odbicie zwierciadlane od dyfuzyjnego? 

9.

 

Jakie prawa optyki geometrycznej wywodzą się z zasady Fermata? 

10.

 

Jak brzmią prawa odbicia światła? 

11.

 

Jak wyraŜamy prawo załamania światła na granicy ośrodków (prawo Sneliusa)? 

12.

 

Czy  wystąpi  załamanie  na  granicy  cieczy  i  szkła  w  przypadku,  gdy  współczynniki 
załamania obydwu ośrodków są takie same? 

13.

 

Czym charakteryzuje się obraz dawany przez pojedyncze zwierciadło płaskie? 

14.

 

Jak skonstruować układ zwierciadeł, aby dawał obraz prosty? 

15.

 

Jak skonstruować układ zwierciadeł, aby odbijał światło w kierunku źródła bez względu 
na jego ustawienie? 

16.

 

Czy  uzyskanie  promieni  antyrównoległych  jest  moŜliwe  tylko  w  przypadku  ustawienia 
zwierciadeł płaskich pod kątem 90

0

? 

17.

 

Czy przed sferycznym zwierciadłem wypukłym moŜe powstać obraz rzeczywisty? 

18.

 

Kiedy  obraz  dawany  przez  zwierciadło  wklęsłe  jest  rzeczywisty,  odwrócony  i  taki  sam 
wielkościowo jak przedmiot? 

19.

 

Kiedy obraz dawany przez zwierciadło wklęsłe jest pozorny, prosty i powiększony? 

20.

 

Jakie  są  reguły  znaków  dla  określania  połoŜenia  obrazów,  przedmiotów  i  parametrów 
zwierciadeł sferycznych?  

 

 

y’

4 

y

3 

y

4 

y’

2 

f 

y

1 

y

2 

y’

3 

y’

1 

F 

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 15

4.1.3.  Ćwiczenia  

Ćwiczenie 1 

Oblicz,  jaką  długość  powinna  mieć  rurka  o  średnicy  wewnętrznej  20  mm,  aby  patrząc 

przez nią widzieć z odległości 60 m słup telegraficzny o wysokości 10 m, jako jej średnicę.  

 
Sposób wykonania ćwiczenia 
 
Aby wykonać ćwiczenie, powinieneś: 

1)

 

sporządzić szkic z oznaczeniem danych i szukanych, 

2)

 

zapisać wartości liczbowe danych wyjściowych zwracając uwagę na jednostki, 

3)

 

ułoŜyć wzór na obliczenie szukanej wielkości, 

4)

 

podstawić dane i przeprowadzić obliczenia, 

5)

 

napisać odpowiedź z uzyskanym wynikiem. 

 

 WyposaŜenie stanowiska pracy: 

−

 

papier formatu A4, 

−

 

linijka z podziałką, trójkąt kreślarski, ołówek,  

−

 

poradnik dla ucznia, 

−

 

literatura zgodna z punktem 6 poradnika. 

 

Ćwiczenie 2 

Oblicz jakie wymiary powinna mieć camera obscura, aby obraz 20 metrowego drzewa na 

jej tylnej ściance powstał o wymiarze 10 cm. 

 
Sposób wykonania ćwiczenia 

  
 Aby wykonać ćwiczenie, powinieneś: 

1)

 

 sporządzić szkic z oznaczeniem danych i szukanych, 

2)

 

 zapisać wartości liczbowe danych wyjściowych zwracając uwagę na jednostki, 

3)

 

 ułoŜyć wzór na obliczenie szukanej wielkości, 

4)

 

 podstawić dane i przeprowadzić obliczenia, 

5)

 

 napisać odpowiedź z uzyskanym wynikiem. 

 

 WyposaŜenie stanowiska pracy: 

−

 

papier formatu A4, 

−

 

linijka z podziałką, trójkąt kreślarski,  ołówek,  

−

 

literatura zgodna z punktem 6 poradnika. 

 
Ćwiczenie 3 

Posługując  się  linijką  i  ołówkiem  narysuj  szkic  pozwalający  wyznaczyć  najmniejszą 

wielkość  zwierciadła ściennego pozwalającego zobaczyć Ci swoje odbicie w całości. 

 

 Sposób wykonania ćwiczenia 
 
 Aby wykonać ćwiczenie powinieneś 

1)

 

narysować  szkic  sytuacyjny  ilustrujący  symbolicznie  postać  stojąca  przed  lustrem 
i trzymając  się  zasad  wyznaczonych  prawem  odbicia  narysować  bieg  promieni 
w sytuacji, gdy postać moŜe oglądać równocześnie swoje stopy i głowę. 

2)

 

podać wielkość zwierciadła w stosunku do swojego wzrostu. 

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 16

 

WyposaŜenie stanowiska pracy: 

−

 

papier formatu A4, 

−

 

linijka z podziałką, trójkąt kreślarski,  ołówek,  

−

 

literatura zgodna z punktem 6 poradnika. 

 
Ćwiczenie 4 

Określ,  ile  razy  odbije  się  promień  równoległy  do  jednego  z  dwu  zwierciadeł 

ustawionych pod kątem 22

o

30’. 

 
Sposób wykonania ćwiczenia: 
 
 Aby wykonać ćwiczenie powinieneś: 

1)

 

naszkicować układ zwierciadeł i padającego promienia, 

2)

 

przeanalizować bieg promienia na podstawie prawa odbicia i analizy kątów w trójkątach, 

3)

 

sformułować wniosek i podać odpowiedź. 

 
  

WyposaŜenie stanowiska pracy: 

−

 

papier formatu A4, 

−

 

linijka z podziałką, trójkąt kreślarski,  ołówek,  

−

 

literatura zgodna z punktem 6 poradnika. 

 
Ćwiczenie 5 

Oblicz,  jaki  promień  krzywizny  powinno  mieć  zwierciadło  dentystyczne,  aby 

umieszczone 10 mm od zęba dawało obraz pozorny o powiększeniu 2×? 
 

Sposób wykonania ćwiczenia: 
 
 Aby wykonać ćwiczenie, powinieneś: 

1)

 

sporządzić szkic z oznaczeniem danych i szukanych, 

2)

 

zapisać wartości liczbowe danych wyjściowych zwracając uwagę na jednostki, 

3)

 

ułoŜyć wzór na obliczenie szukanej wielkości, 

4)

 

podstawić dane i przeprowadzić obliczenia, 

5)

 

napisać odpowiedź z uzyskanym wynikiem. 

 
 

WyposaŜenie stanowiska pracy: 

−

 

papier formatu A4, 

−

 

linijka z podziałką, trójkąt kreślarski,  ołówek,  

−

 

literatura zgodna z punktem 6 poradnika. 

 
Ćwiczenie 6 

śarnik Ŝarówki projekcyjnej rzutnika ma wymiary 6 × 9 mm. W jakiej odległości naleŜy 

umieścić  zwierciadło  wklęsłe  o  promieniu  krzywizny  R

k

  =  6  cm,  aby  obraz  Ŝarnika  pokrył 

okrąg o średnicy 30 mm? 

 

 Sposób wykonania ćwiczenia: 

Aby wykonać ćwiczenie powinieneś: 

1)

 

sporządzić szkic z oznaczeniem danych i szukanych, 

2)

 

zapisać wartości liczbowe danych wyjściowych zwracając uwagę na jednostki, 

3)

 

ułoŜyć wzór na obliczenie szukanej wielkości, 

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 17

4)

 

podstawić dane i przeprowadzić obliczenia, 

5)

 

napisać odpowiedź z uzyskanym wynikiem. 

 
 

WyposaŜenie stanowiska pracy: 

−

 

papier formatu A4, 

−

 

linijka z podziałką, trójkąt kreślarski,  ołówek,  

−

 

literatura zgodna z punktem 6 poradnika. 

 

4.1.4.  Sprawdzian postępów 

5)

 

wyjaśnić za pomocą szkicu powstanie obrazu w zwierciadle płaskim? 

 

 

6)

 

podać definicję zwierciadła kulistego i terminów optycznych z nim 
związanych? 

 

 

7)

 

wyjaśnić za pomocą szkicu jak powstają obrazy w zwierciadłach 
kulistych? 

 

 

8)

 

zdefiniować pojęcie obrazu pozornego i rzeczywistego? 

 

 

9)

 

podać i zastosować w praktycznych obliczeniach równanie 
zwierciadła kulistego? 

 

 

 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 

 Czy potrafisz: 

 

Tak 

 

Nie 

1)

 

odróŜnić oświetlenie ze źródła punktowego od oświetlenia ze źródła 
rozciągłego? 

 

 

2)

 

określić wymiar źródła światła, aby z określonej odległości mogło 
być traktowane jako punktowe? 

 

 

3)

 

zdefiniować rodzaj ośrodka optycznego? 

 

 

4)

 

określić wymiary camery obscura na podstawie danego 
powiększenia? 

 

 

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 18

4.2.

 

Bieg światła przez powierzchnie elementów optycznych 

 
4.2.1. Materiał nauczania 

Przejście  światła  przez  powierzchnię  graniczną  jest  związane  z  jego  załamaniem. 

Przejście bez załamania moŜe zachodzić, gdy współczynnik załamania obu ośrodków jest taki 
sam, albo gdy kąt padania jest równy 0. Jest to konsekwencja prawa załamania (Snelliusa). 

Jedną  z  konsekwencji  prawa  załamania  jest  zjawisko  przesunięcia  równoległego. 

Występuje  ono  w  sytuacji,  gdy  światło  po  załamaniu  na  pierwszej  powierzchni  i  przejściu 
przez  ośrodek  o  innym  współczynniku  załamania,  wraca  do  poprzedniego  ośrodka  przez 
następną powierzchnię, równoległą do pierwszej. Taki element optyczny, w którym występują 
dwie  równoległe  powierzchnie  załamujące  nazywamy  płytką  płasko–równoległą.  Promień 
wchodzący i wychodzący mają ten sam kierunek. 

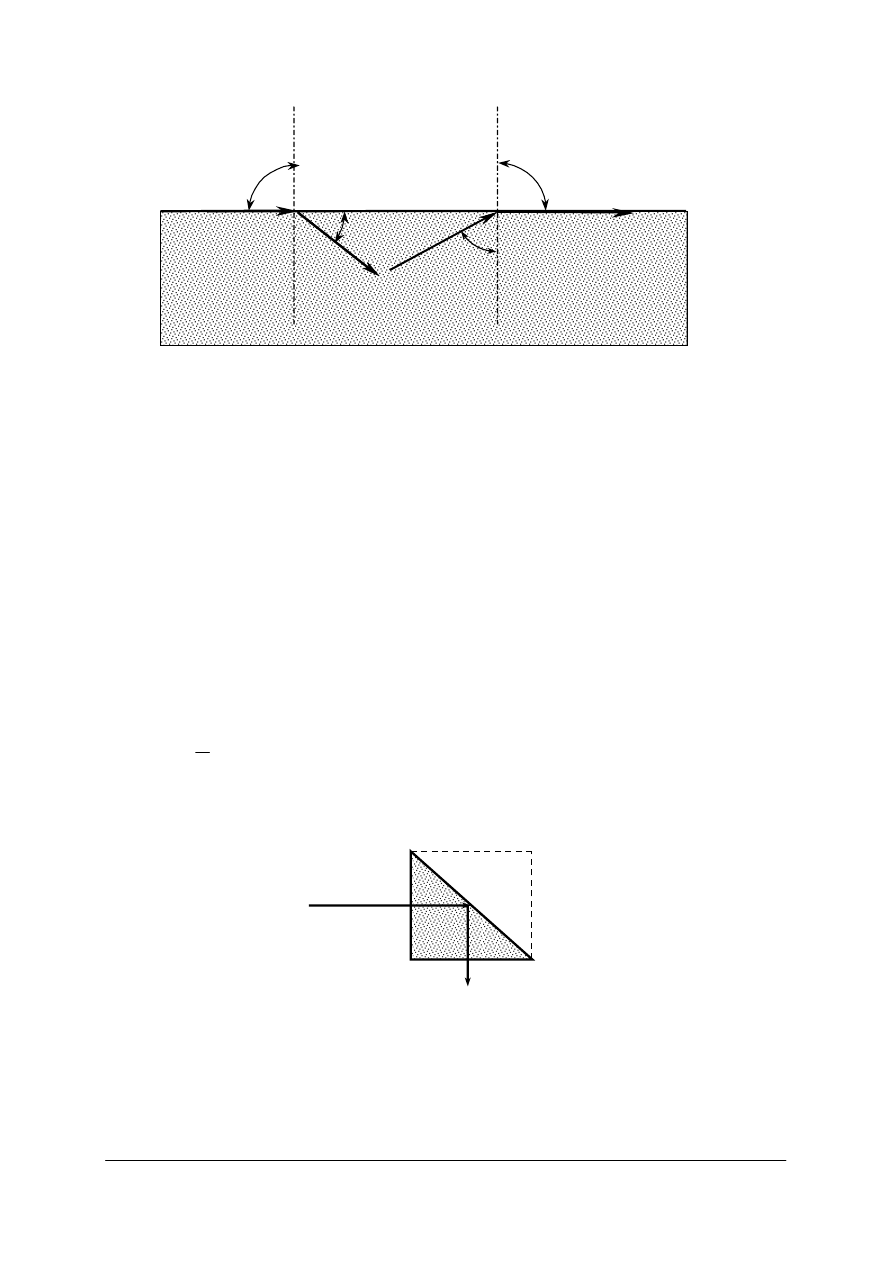
Rys. 16.  Przejście światła przez płytkę płasko równoległą. n – współczynnik załamania otoczenia, 

n’ – współczynnik załamania płytki, d – przesunięcie równoległe [opracowanie własne] 

 

Z  rysunku  ilustrującego  przejście  światła  przez  płytkę  płasko-równoległą  i  prawa 

Snelliusa wynika, Ŝe przesunięcie równoległe będzie tym większe im większa będzie grubość 
płytki i większa róŜnica współczynników załamania.  

W  ośrodku  o  większym  współczynniku  załamania  światło  biegnie  wolniej,  czyli 

przebiegnie w tym samym czasie mniejszą drogę niŜ w ośrodku o mniejszym współczynniku. 
W związku z tym zaistniała konieczność zdefiniowania  tzw. drogi optycznej 

S = L · n 

oraz odległości zredukowanej 

R = 

n

L

 

gdzie:  L oznacza drogę geometryczną, a n – współczynnik załamania. 

Konsekwencją  prawa  załamania  jest  powstanie  zjawiska  granicznego  kąta  załamania 
i granicznego kąta całkowitego wewnętrznego odbicia. 

 

d 

n 

n’ 

n 

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 19

  

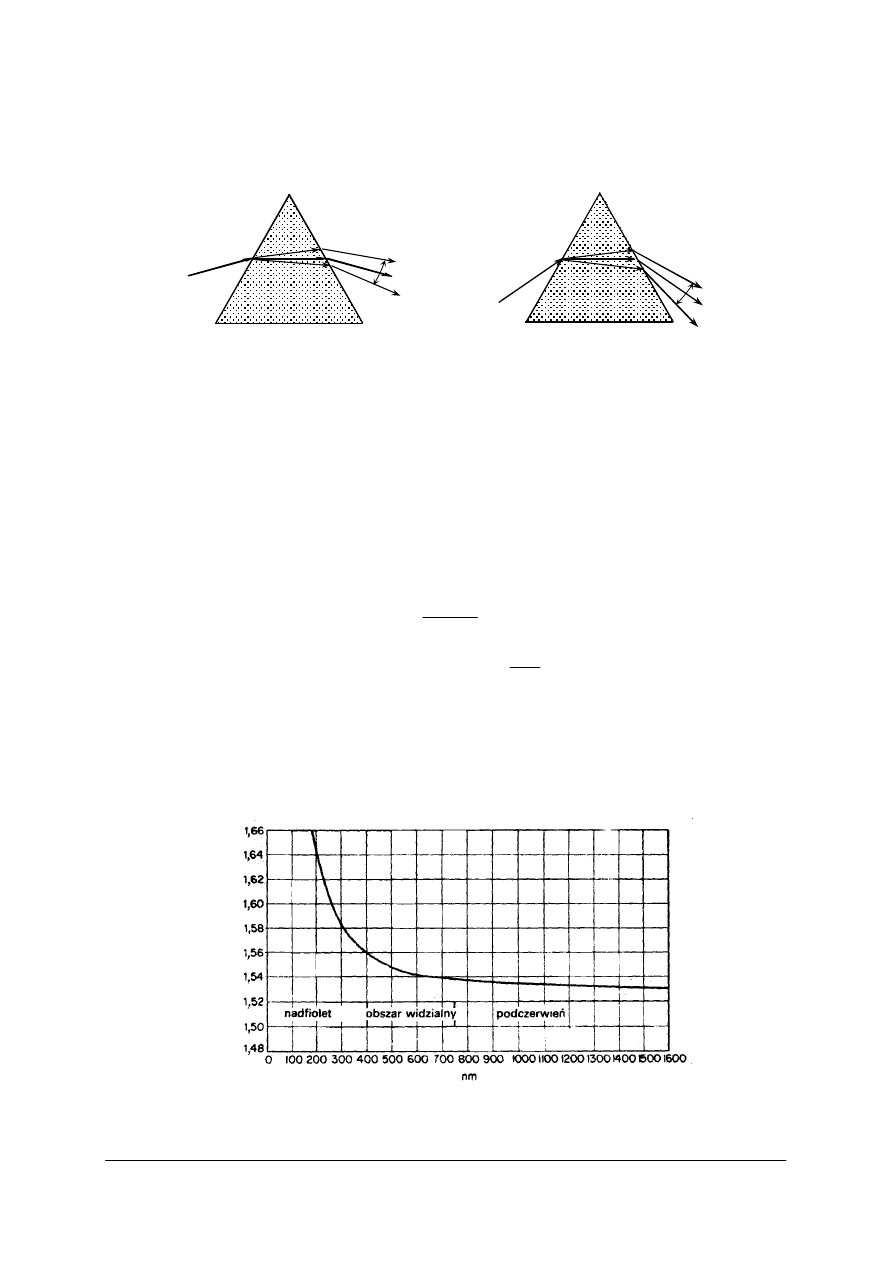
Rys. 17.  Ilustracja zjawiska granicznego kąta załamania (z lewej) i granicznego kąta całkowitego  

wewnętrznego odbicia (z prawej) i – kąty padania, i’ – kąty załamania 

 

Z  granicznym  kątem  załamania  mamy  do  czynienia,  gdy  sinus  kąta  padania  osiągnie 

maksymalną wartość czyli  1 (sin 90

0

), a sinus kąta załamania jeszcze jej nie osiągnie i będzie 

miał  wartość  <1  (czyli  i’  <  90

0

).  Inaczej  mówiąc,  gdy  światło  przechodząc  z  ośrodka  

o  mniejszym  współczynniku  załamania  do  ośrodka  o  większym  współczynniku  pada  pod 
kątem  90°,  wtedy  kąt  załamania  i’  jest  kątem  granicznym.  Zjawisko  jest  m.in. 
wykorzystywane w budowie przyrządów do pomiarów współczynników załamania. 

Graniczny  kąt  całkowitego  wewnętrznego  odbicia  ma  miejsce  w  sytuacji,  gdy  światło 

przechodzi  z  ośrodka  o  większym  współczynniku  załamania  do  ośrodka,  gdzie  jest  on 
mniejszy.  Kąt  padania  jest  wtedy    zawsze  mniejszy  od  kąta  załamania,  który  po  osiągnięciu 
90°  nie  moŜe  juŜ  osiągać  większych  wartości.  Światło  ulega  całkowitemu  wewnętrznemu 
odbiciu od powierzchni granicznej i pozostaje po tej samej jej stronie. 

Zjawisko  to  ma  bardzo  szerokie  zastosowanie  w  budowie  róŜnego  rodzaju  pryzmatów 

odbijających i włókien światłowodowych. 

Kąt graniczny całkowitego wewnętrznego odbicia moŜemy wyznaczyć ze wzoru: 

n

n

i

g

'

sin

=

  ,  gdzie  n’  oznacza  współczynnik  załamania  ośrodka  do  którego  światło 

przechodzi, a n współczynnik z którego wychodzi. 
 
 

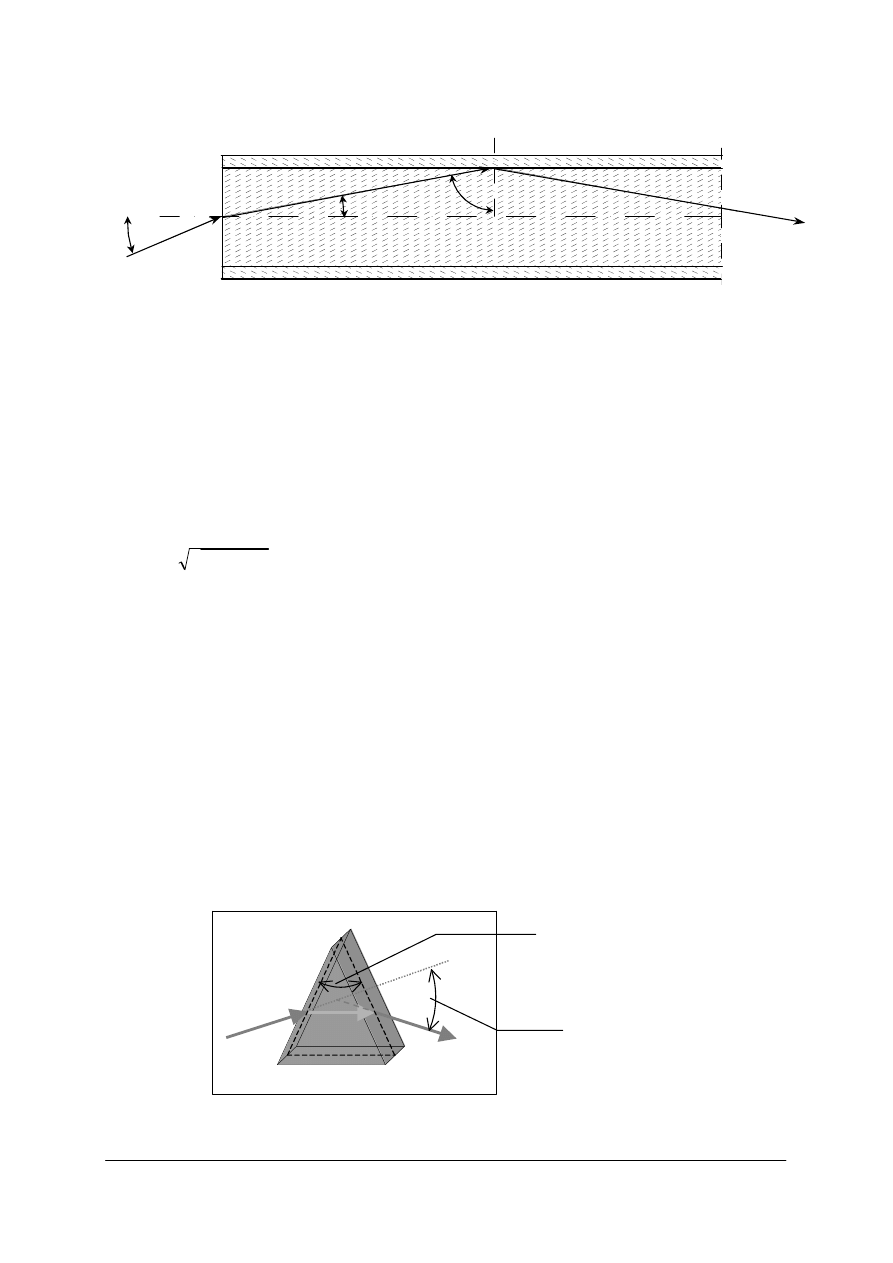
Rys. 18.  Pryzmat prostokątny, w którym światło całkowicie odbija się od przeciwprostokątnej powierzchni 

poniewaŜ nie jest przekroczony graniczny kąt całkowitego wewnętrznego odbicia  

[opracowanie własne] 

i

 

i

 

i’

 

n

 

n’

 

P 

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 20

Rys. 19.  Wykorzystanie zjawiska całkowitego wewnętrznego odbicia we włóknie światłowodowym i pryzmacie 

prostokątnym  i – kąt padania promienia wchodzącego, i’ – kąt załamania na powierzchni wejściowej, 

i

min

 – minimalny kąt całkowitego wewnętrznego odbicia, n

0

 – współczynnik załamania otoczenia,  

n – współczynnik załamania włókna światłowodowego, n’ – współczynnik załamania warstwy 

powlekającej, zmniejszającej kąt graniczny wewnętrznego odbicia, N – normalna do powierzchni  

w punkcie padania [opracowanie własne] 

 

Wartość  kąta  granicznego  wyznacza  stosunek  współczynnika  załamania  warstwy 
powlekającej do współczynnika załamania włókna. 

sin i 

min

 = n’/n 

Na  tej  podstawie  moŜemy  wyznaczyć  maksymalny  kąt  pod  jakim  moŜe  wejść  do 

światłowodu światło, tzw. aperturę numeryczna włókna: 

n

0

 sin i = 

2

2

'

n

n

−

 

Promień gięcia  włókna światłowodowego nie moŜe być zbyt mały, aby  nie przekroczyć 

granicznego  kąta  całkowitego  wewnętrznego  odbicia.  Światło  moŜe  wyjść  poza  światłowód, 
który poza tym moŜe ulec złamaniu. 

Zastosowanie światłowodów: 

−

 

telekomunikacja, 

−

 

mikroskopy światłowodowe i wzierniki,  

−

 

kodowanie i dekodowanie informacji optycznej, 

−

 

koncentracja energii świetlnej. 

 

Następnym elementem optycznym, w którym istotną role odgrywa załamanie światła jest 

pryzmat załamujący. 

W odróŜnieniu od płytki płasko-równoległej, w pryzmacie światło ulega odchyleniu. 

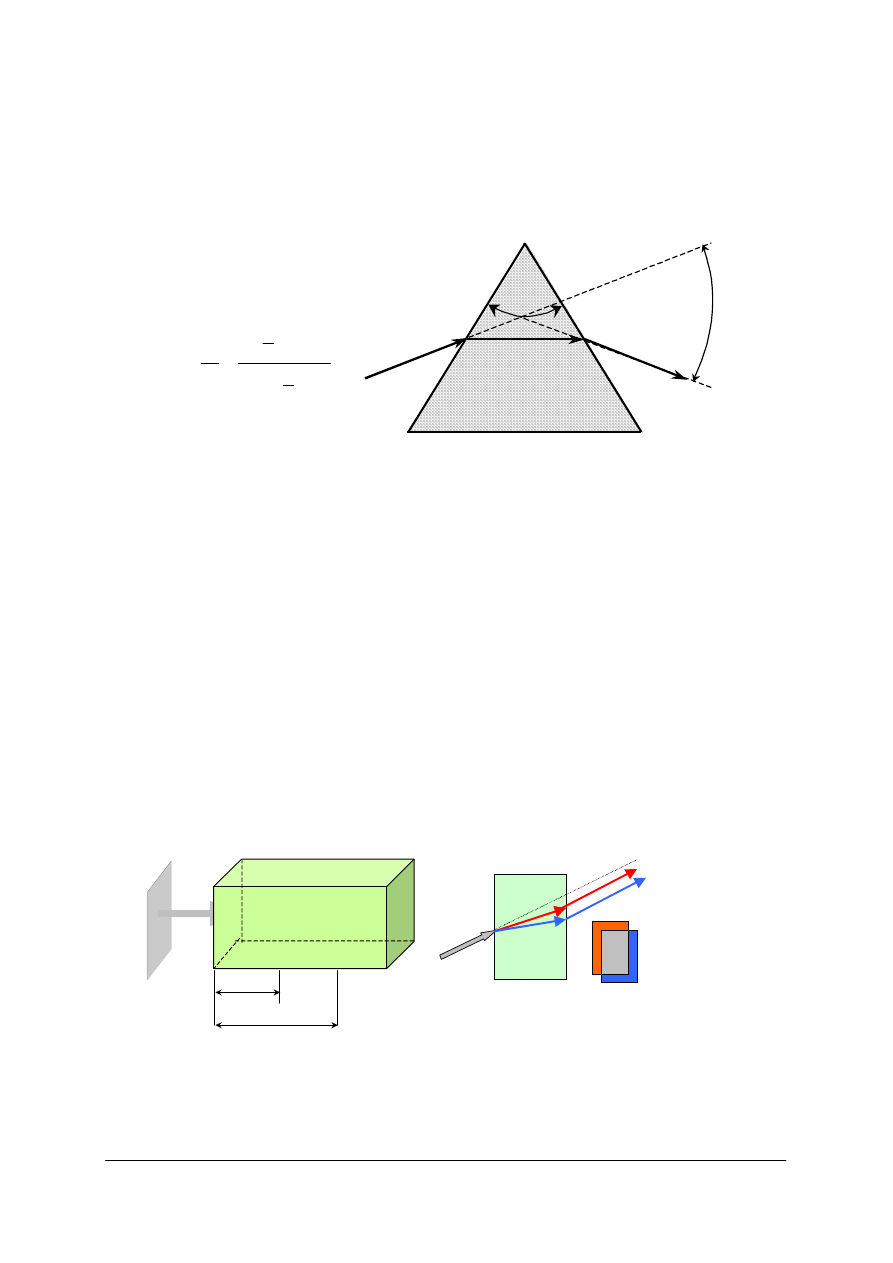
Krawędź  pryzmatu  pomiędzy  powierzchniami  optycznymi  nazywamy  wierzchołkiem.  Kąt 
wierzchołkowy  między  tymi  powierzchniami  nazywamy  kątem  pryzmatu,  albo  kątem 
łamiącym, a powierzchnię przeciwległą do wierzchołka – podstawą pryzmatu. 

Rys. 20. Pryzmat odchylający [opracowanie własne] 

 

 

i 

i’ 

i

min 

N 

n’ 

n

0 

n 

Kąt łamiący Θ 

Kąt odchylenia δ 

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 21

KaŜdy  pryzmat  załamujący  ma  takie  ustawienie  względem  promienia  padającego,  przy 

którym kąt odchylenia jest minimalny. Występuje to w przypadku, gdy promień po załamaniu 
na pierwszej powierzchni jest prostopadły do dwusiecznej kąta łamiącego tego pryzmatu.  
 
Równanie pryzmatu dla minimalnego odchylenia 

 

Rys. 21.  Równanie pryzmatu i szkic z oznaczeniami kątów. n – współczynnik załamania ośrodka pryzmatu, 

n

0

 – współczynnik załamania ośrodka otaczającego pryzmat, Θ – kąt łamiący pryzmatu, δ –kąt 

minimalnego odchylenia pryzmatu [opracowanie własne] 

 

Dla  pryzmatów,  w  których  kąt  łamiący  Θ  jest  bardzo  mały  (kliny  optyczne)  moŜemy 

przyjąć,  Ŝe  sinusy  kątów  są  równe  wartościom  tych  kątów  podanym  w  mierze  łukowej 
(w radianach). Wtedy wzór przybierze postać: 

n ≈ (Θ + δ)/Θ → δ ≈ Θ (n – 1) 

 

Zdolność załamująca jest wielkością wektorową. 

Jednostką  mocy  pryzmatycznej  jest  dioptria  pryzmatyczna  stosowana  do  cienkich 

pryzmatów o małych kątach łamiących. i oznaczana ∆. 

Moc pryzmatyczną równa 1 dioptrii będzie miał pryzmat, który odchyli światło o 1 cm na 

odległości 1 m. 
 
Dyspersja 

Dla  róŜnych  barw  światła  (długości  fal  świetlnych)  stopień  ich  odchylenia  w  pryzmacie 

jest róŜny, bo ich prędkości nie są jednakowe. 

 

 

Rys. 22. W tym samym czasie, róŜne fale świetlne przebędą róŜne drogi , bo róŜne są dla nich współczynniki 

załamania. Dlatego patrząc pod kątem przez grubą płytkę płasko-równoległą,widzimy barwne obwódki na 

konturach oglądanych przedmiotów. S

1

 – droga przebyta w czasie t przez promień niebieski, 

S

2

 – droga przebyta w tym samym czasie przez promień czerwony [opracowanie własne] 

W powietrzu dyspersja jest bardzo mała, a w próŜni Ŝadna. 

 

 

 

 

s

1

=V

1 

x t 

s

2

=V

2 

x t 

Θ

+

Θ

=

2

1

sin

)

(

2

1

sin

0

δ

n

n

 

δ 

n 

n

0 

Θ 

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 22

Newton sądził, Ŝe dyspersja jest proporcjonalna do załamania (to znaczy, Ŝe im większy 

współczynnik  załamania,  tym  większe  rozczepienie),  ale  okazało  się,  Ŝe  nie  istnieje  taki 
prosty  związek.  Materiały  o  małym  współczynniku  załamania  mają  duŜą  dyspersję 
i odwrotnie. 

 

Rys. 23. Przy jednakowej dyspersji moŜe być róŜny kąt odchylenia [opracowanie własne]

 

 

Do opisania wielkości dyspersji wprowadzono miarę liczbową. 
Z  całego  widzialnego  zakresu  widma  wydzielono  łatwe  do  otrzymania  w  postaci 

wyodrębnionej trzy podstawowe długości fal. Dla nich określa się wartości współczynników 
załamania charakteryzujących dany ośrodek. Są to tzw. linie Fraunchofera. 
–  Niebieska linia wodoru F – λ = 486,1 nm → współczynnik załamania n

F  

–  śółta  linia  sodu  (dublet)  D  –  λ  =  589,6  nm  →  współczynnik  załamania  n

D

  Zastępowana 

obecnie Ŝółtą linią helu λ  = 587,6 nm → współczynnik załamania n

d 

–  Czerwona linia wodoru C – λ = 656,3 nm. → współczynnik załamania n

C 

RóŜnicę współczynników załamania ∆n = n

F

 – n

C 

nazywamy dyspersją średnią, a róŜnicę 

n

d

 – 1 nazywamy refrakcją.  

Stosunek  dyspersji  średniej  do  refrakcji 

∆

=

−

−

1

d

C

F

n

n

n

  nazywamy  dyspersją  względną

  lub 

zdolnością  rozczepiającą,  a  jej  odwrotność 

∆

=

1

ν

  →  współczynnikiem  dyspersji 

tzw. liczbą Abbego. 

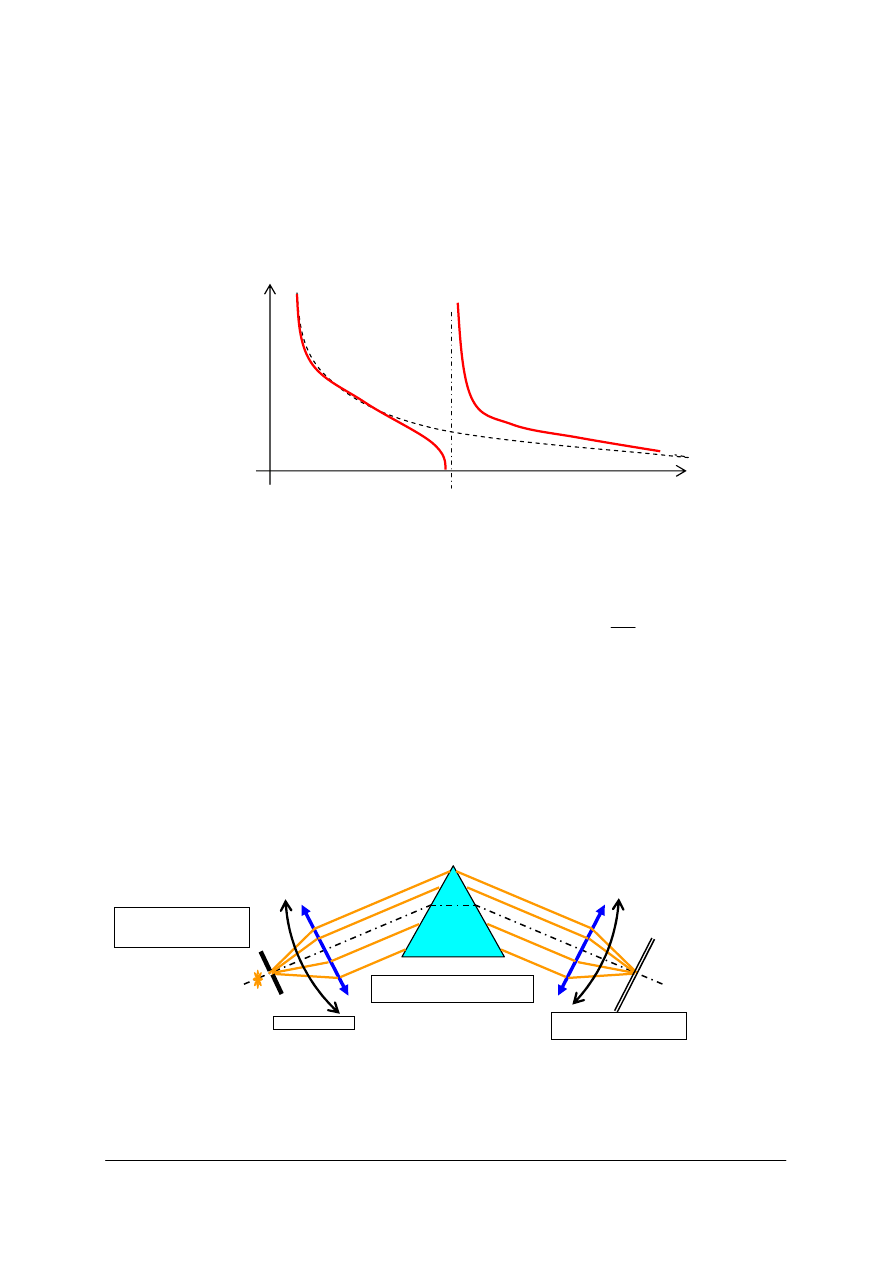
Dyspersję  danego  ośrodka  moŜemy  wyrazić  za  pomocą  krzywej  ukazującej  zmiany 

współczynnika  załamania  w  zaleŜności  od  zmian  długości  fali  świetlnej.  Gdy  zmiany  te 
następują w sposób ciągły, dyspersję nazywamy normalną. Jest to w zasadzie cecha substancji 
bezbarwnych (w zakresie widzialnym). Typowym przykładem moŜe być dyspersja kwarcu. 

 

Rys. 24. Dyspersja kwarcu jako przykład dyspersji normalnej [5, s. 83] 

 

P 

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 23

Na  współczynnik  załamania  ma  wpływ  nie  tylko  długość  fali,  ale  skład  chemiczny, 

temperatura  i  inne  czynniki  fizyczne  działające  na  dany  ośrodek  optyczny.  Temperatura  ma 
większy  wpływ  na  współczynnik  załamania  w  cieczach  i  gazach.  Z  jej  wzrostem 
współczynnik maleje. 
Dyspersja anomalna 

Polega  na  tym,  Ŝe  niektóre  długości  fal  są  przez  ośrodek  pochłaniane  (absorbowane), 

przez co staje się dla nich nie przezroczysty. Dla długości fali przy której następuje absorpcja 
promieniowania obserwujemy skok (nieciągłość) współczynnika załamania. 

Rys. 25. Przykład dyspersji anomalnej. Takich obszarów nieciągłości (absorpcji) moŜe być kilka dla róŜnych 

długości fal [opracowanie własne] 

Zdolność rozdzielcza (rozszczepiająca) pryzmatu 

Chromatyczna  zdolność  rozdzielcza  pryzmatu  jest  to  jego  zdolność  rozróŜnienia  dwu 

sąsiednich  długości  fal.  WyraŜamy  ją  stosunkiem  długości  fali  do  minimalnej  róŜnicy 

długości fal, którą jesteśmy w stanie zarejestrować, czyli wyraŜeniem

λ

λ

∆

 

Dzięki pryzmatom i ich zdolności do rozszczepiania światła wykształciła się nowa gałąź 

optyki  zwana  spektrometrią.  Jest  to  dziedzina  zajmująca  się  badaniem  widm  fal 
elektromagnetycznych z zakresu promieniowania widzialnego i pasm przyległych. 

Głównym  narzędziem  spektrometrii  są  spektrometry  –  przyrządy  najściślej  związane 

z zastosowaniem pryzmatów. 

W zaleŜności od charakteru pracy moŜemy uŜywać: 

−

 

spektroskopów – ułatwiają obserwacje widm, 

−

 

spektrometrów – spektroskopów wyposaŜonych w urządzenia pomiarowe, 

−

 

spektrografów 

– 

spektroskopów 

przystosowanych 

do 

zapisywania 

obrazu 

obserwowanych widm. 

Rys. 26. Schemat spektroskopu [opracowanie własne] 

 
Kolimator i obiektyw z ekranem mogą obracać się wokół wspólnej osi. Widmo badamy 

w połoŜeniu najmniejszego odchylenia – linie są wtedy najcieńsze. 

λ 

n 

Kolimator 

Obiektyw z ekranem 

Źródło badanego 

światła 

Pryzmat rozszczepiający 

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 24

Istnieje  wiele  rozwiązań.  MoŜna  zastąpić  obiektywy  kolimatora  i  teleskopu 

zwierciadłami  sferycznymi.  Rozwiązanie  stosowane  w  monochromatorach  –  urządzeniach 
do wyodrębniania poszczególnych długości fal. 

Spektrometry o wysokiej rozdzielczości są drogie i delikatne. 

W  zaleŜności  od  zakresu  badanego  widma  pryzmaty  mogą  być  wykonane  z  róŜnych 
materiałów:  

−

 

dla podczerwieni – NaCl (sól kuchenna), KCl, Al

2

O

3

 (szafir), 

−

 

dla nadfioletu – kwarc, fluoryt. 

Specjalne typy pryzmatów 

Pryzmaty  achromatyczne  –  dają  odchylenie  kierunku  przebiegu  światła  bez  jego 

rozczepienia Skleja się je z dwu pryzmatów wykonanych z róŜnych materiałów. Odpowiedni 
dobór  materiałów  (pod  względem  współczynników  załamania  i  dyspersji)  dla  pryzmatów 
składowych pozwala na jednakową zmianę kierunku dla wszystkich barw wiązki padającej. 

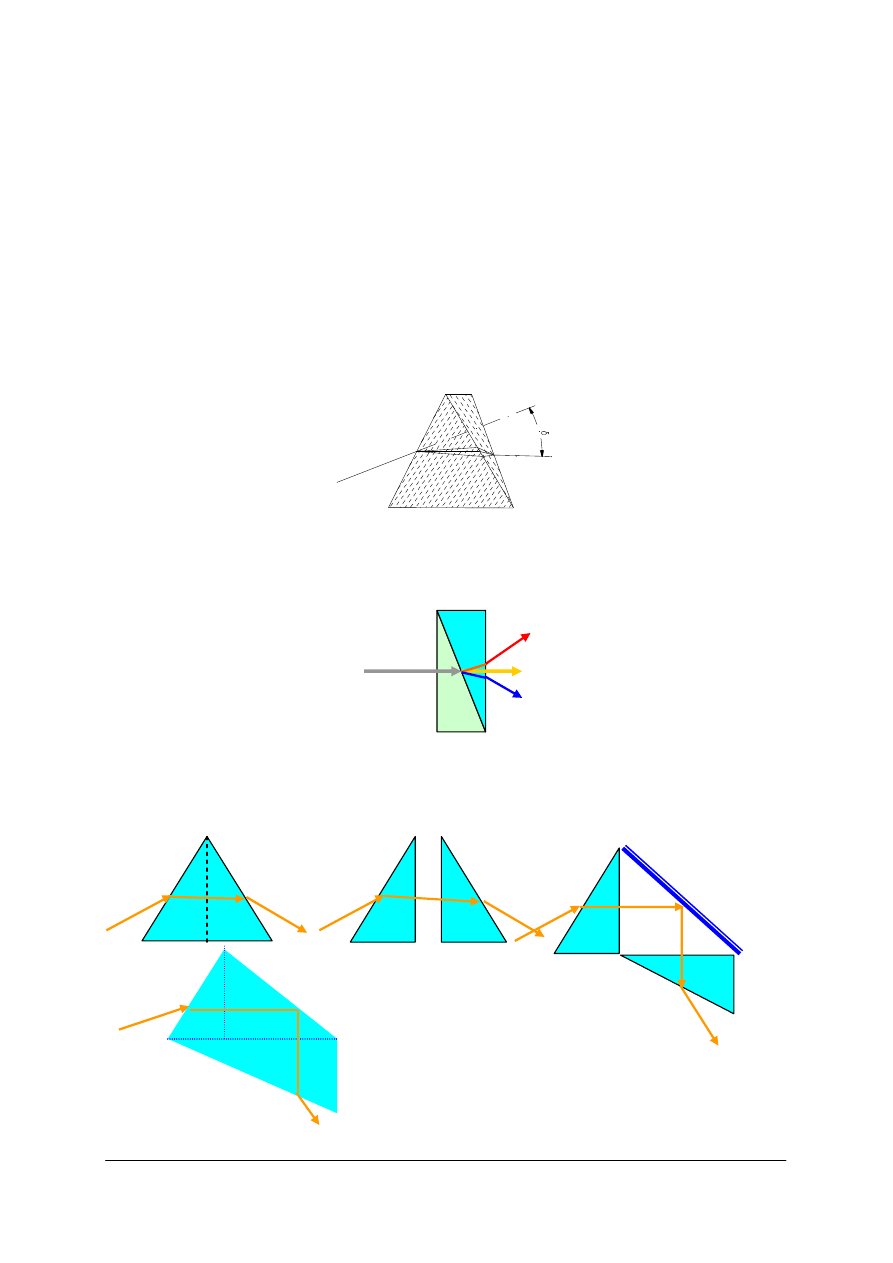
Rys. 27. Pryzmat achromatyczny [opracowanie własne] 

Pryzmaty  nieodchylające  –  dają  rozczepienie  bez  odchylenia  jednej  długości  fali. 

Spotykane  pod  nazwami  „pryzmat  Amiciego”,  „a’  vision  directe”,  „a  direct-vision  prism”. 
Stosowane w prostych spektroskopach ręcznych. 

 

Rys. 28. Pryzmat nieodchylający sklejony z dwu gatunków szkła o odpowiednio dobranych 

współczynnikach załamania i dyspersji. [opracowanie własne] 

 

Pryzmaty  stałego  odchylenia  –  dają  rozczepienie  przy  stałym  kącie  odchylenia,  np. 

pryzmat Pellina-Broca. 

Rys. 29. Konstrukcja pryzmatu Pellina-Broca [opracowanie własne] 

 

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 25

MoŜna go otrzymać rozcinając pryzmat 60 stopniowy i dodając zwierciadło płaskie, ale 

moŜna  teŜ  wykonać  z  jednego  kawałka  szkła  obrabiając  powierzchnie  tak,  jakby  składał  się 
on  z  dwu  pryzmatów  30  stopniowych  i  jednego  prostokątnego  pracującego  w  układzie 
całkowitego wewnętrznego odbicia. 
Bieg światła przez powierzchnie sferyczne (kuliste) i asferyczne 

Światło biegnąć przez granice ośrodków podlega prawu załamania bez względu na kształt 

tej  powierzchni..  Ta  zmienność  kształtu  komplikuje  jednak  wytyczanie  biegu  promieni 
poniewaŜ w kaŜdym punkcie powierzchni mają inny kąt padania. 

Najczęściej  spotykanymi  w  optyce  powierzchniami  są  powierzchnie  kuliste  czyli 

sferyczne.  Do  ich  powszechności  przyczyniała  się  głównie  technologia  ze  względu  na 
stosunkowo łatwą obróbkę szkła zapewniająca wymaganą jakość powierzchni. 

Pojęcia podstawowe dla pojedynczej powierzchni sferycznej: 

−

 

oś optyczna – prosta przechodząca przez środek krzywizny i środek obwodu, 

−

 

punkt wierzchołkowy – punkt, w którym oś optyczna przechodzi przez powierzchnię, 

−

 

odległości przedmiotowe i obrazowe, 

−

 

ogniska przedmiotowe i obrazowe, 

−

 

ogniskowe przedmiotowe i obrazowe, 

−

 

odległości  ogniskowe  przedmiotowe  i  obrazowe  (odległości  od  ognisk)

 

są  zdefiniowane 

tak  jak  przy  zwierciadłach  sferycznych  z  tą  róŜnicą,  Ŝe  ogniska  przedmiotowe  nie 
pokrywają  się  z  obrazowymi  bo  leŜa  po  przeciwnych  stronach  powierzchni  optycznie 
czynnych. Promienie nie odbijają się, ale załamują. 
Wielkości te są zobrazowane i opisane na rys. 30, 31, 32 i 33. 

Rys. 30.

 

Podstawowe elementy sferycznych powierzchni załamujących. C – punkt wierzchołkowy, 

 S – środek krzywizny, R – promień krzywizny [opracowanie własne]

 

 

Lagrange w 1778 r. wprowadził pojęcia: 

−

 

płaszczyzn  ogniskowych  –  płaszczyzn  prostopadłych  do  osi  optycznej  w  miejscu 
połoŜenia ognisk, 

−

 

przestrzeni  przedmiotowej  i  obrazowej  –  przestrzenie  obrazowa  i  przedmiotowa 
rozciągają się od –

∞

 do +

∞

, licząc od powierzchni załamującej w zaleŜności od tego, czy 

promień jest przed, czy po załamaniu, 

−

 

elementów  sprzęŜonych  (punktów,  odległości,  płaszczyzn  i  promieni)  –  kaŜdemu 
elementowi w przestrzeni obrazowej odpowiada element w przestrzeni przedmiotowej. 

 
 
 
 
 

Oś optyczna 

C 

R

 

S

 

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 26

 

Rys. 31. PołoŜenie ognisk i płaszczyzn ogniskowych w przestrzeni przedmiotowej. F – ognisko przedmiotowe, 

π 

– płaszczyzna ogniskowa przedmiotowa, C – punkt wierzchołkowy, f – ogniskowa przedmiotowa dla 

powierzchni wklęsłej ognisko jest pozorne bo przecinają się w nim przedłuŜenia promieni przedmiotowych  

[opracowanie własne] 

 

Rys. 32. PołoŜenie ognisk i płaszczyzn ogniskowych w przestrzeni obrazowej. F’ – ognisko obrazowe, 

π’ - 

płaszczyzna ogniskowa obrazowa, f’ – ogniskowa obrazowa. Dla powierzchni wklęsłej ognisko 

jest pozorne bo przecinają się w nim przedłuŜenia promieni obrazowych [opracowanie własne] 

 
PoniewaŜ  wiązki  ogniskowe  po  przejściu  przez  powierzchnię  stają  się  wiązkami 
równoległymi, więc punkty sprzęŜone z nimi leŜą w nieskończoności. 
 
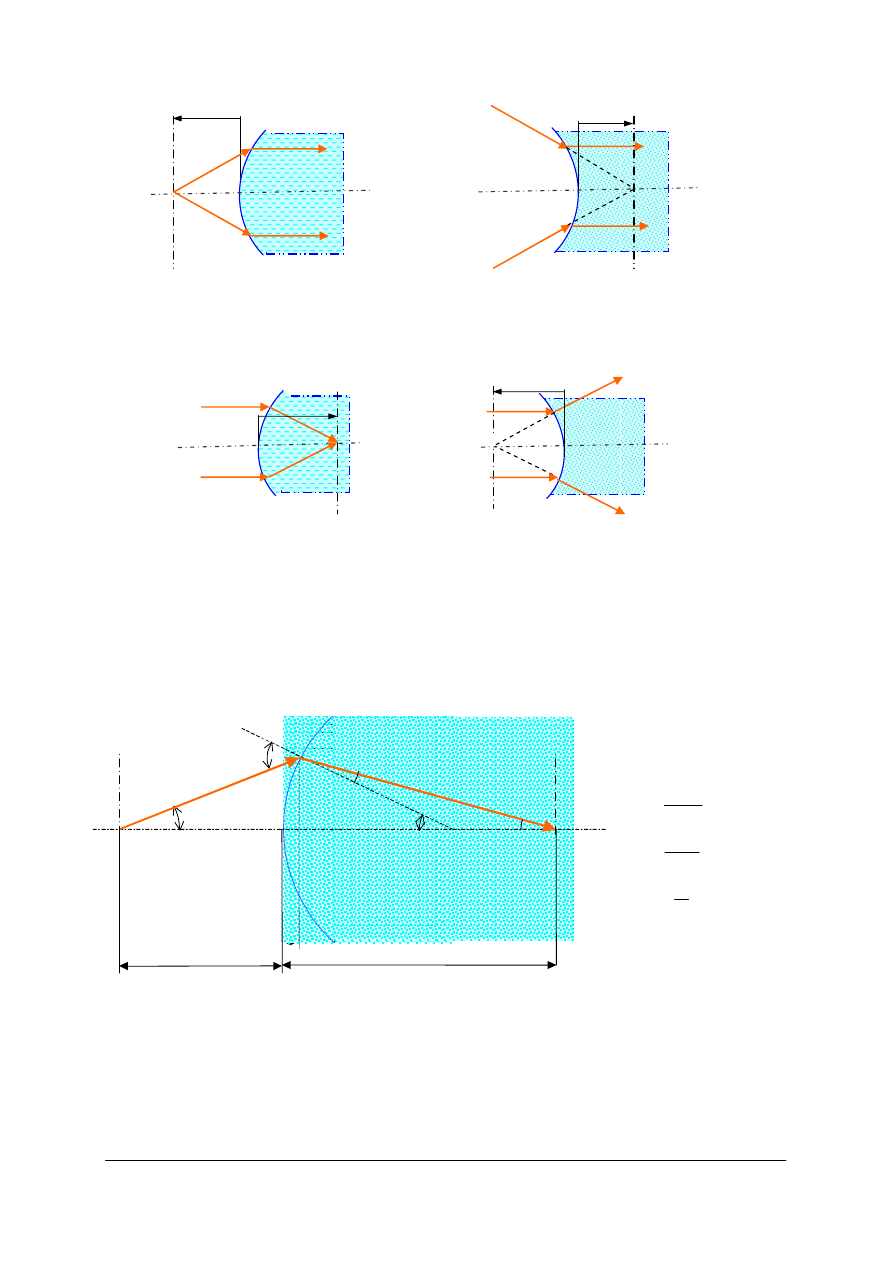
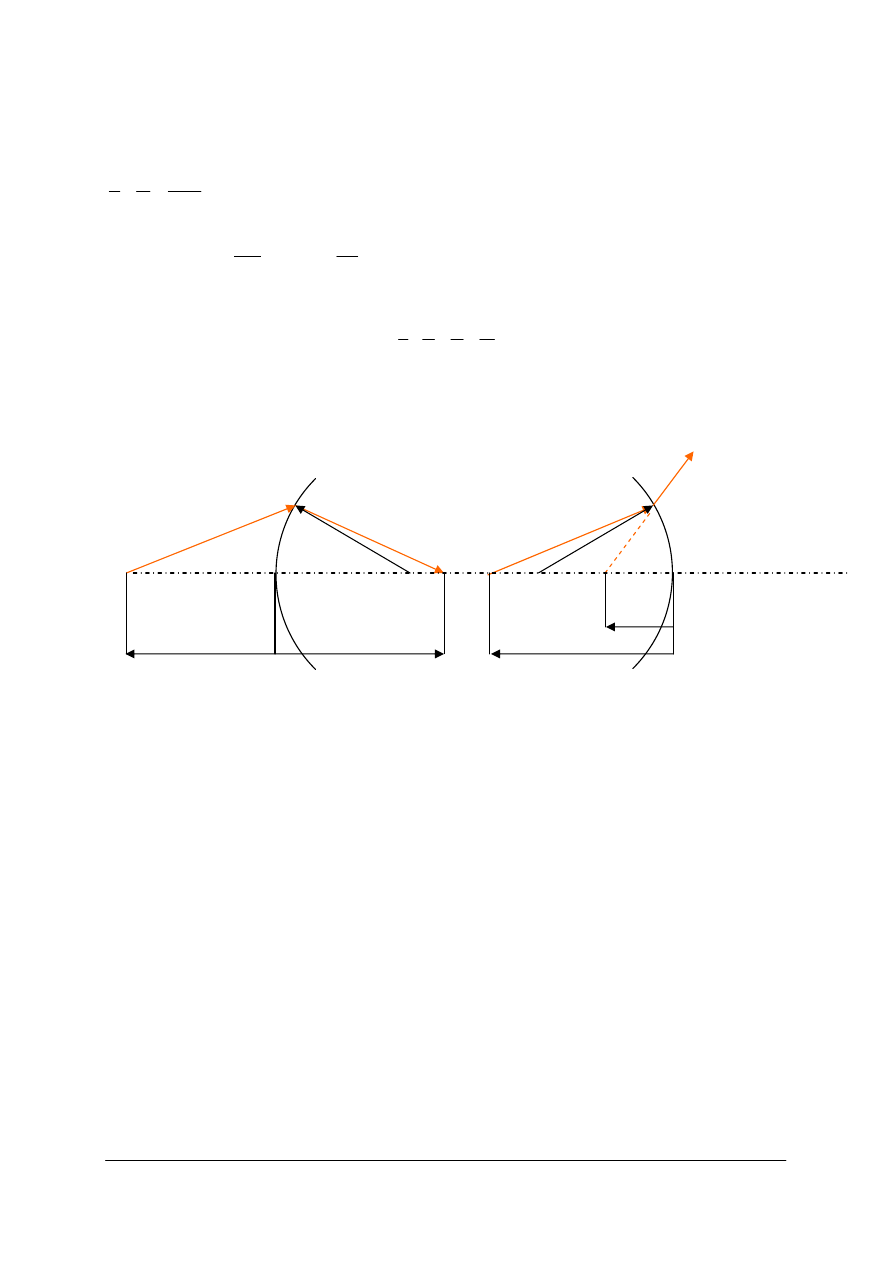
Tworzenie obrazu za pomocą pojedynczej powierzchni sferycznej 
 

i = u + 

φ

 

 

i’ = 

φ

 - u’ 

 

φ

 = i’ + u’ 

d

s

h

tgu

+

=

d

s

h

tgu

−

=

'

'

 

R

h

=

φ

sin

 

 
 
 

 

Rys. 33.  Szkic z danymi wyjściowymi do wyprowadzenia równania pojedynczej powierzchni załamującej (wzór 
Gaussa) gdzie O – punkt przedmiotowy, O’ – obraz punktu O, 

π

p

 – płaszczyzna przedmiotowa, 

π

o 

– płaszczyzna 

obrazowa, C – punkt wierzchołkowy, S – środek krzywizny, A – punkt padania promienia na powierzchnię 

załamującą, h – wysokość padania  promienia, N – normalna do powierzchni w punkcie padania, będąca 

przedłuŜeniem promienia krzywizny R, s – odległość przedmiotowa, s’ – odległość obrazowa, d – strzałka 

krzywizny, u – kąt aperturowy promienia przedmiotowego, u’ – kąt aperturowy promienia obrazowego, Φ – kąt 
między promieniem krzywizny a osią optyczną, i – kąt padania, i’ – kąt załamania, n – współczynnik załamania 

ośrodka pierwszego, n’ – współczynnik załamania ośrodka drugiego [opracowanie własne] 

π

 

F 

π 

F 

C 

C 

f 

f 

π’ 

F’ 

C 

π’ 

F’ 

C 

f’ 

P 

C 

A 

R 

s 

s’ 

u 

i 

i’ 

n 

n’ 

h 

φ

 

u’ 

S 

N 

O

 

d 

O 

π

p 

P 

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 27

Dla małych kątów sin 

≈

 tg 

≈

 kąt w mierze łukowej, a dla przestrzeni przyosiowej moŜna 

teŜ  pominąć  wartość  „d”.  Uwzględniając  te  uproszczenia  i  wykorzystując  prawo  Snelliusa 
otrzymujemy wzór Gaussa dla pojedynczej powierzchni załamującej: 

R

n

n

s

n

s

n

−

=

+

'

'

'

 gdzie n, n’ i R to parametry opisowe, a s i s’ to wielkości funkcyjne. 

Gdy przeniesiemy przedmiot do nieskończoności (s

→

 

∞

), to s’

→

 f’. 

Otrzymamy: 

n

R

n

f

∆

=

'

'

 oraz 

n

nR

f

∆

=

 

Po  przekształceniu  i  podstawieniu  do  wzoru  Gaussa  otrzymamy  wzór  na  odległości 

sprzęŜone dla pojedynczej powierzchni sferycznej: 

'

'

'

'

f

n

f

n

s

n

s

n

=

=

+

 

Dla powierzchni wklęsłych postępujemy tak samo, tylko R ma znak „ – „. 

 
Załamanie światła na powierzchni sferycznej – Reguły znaków 
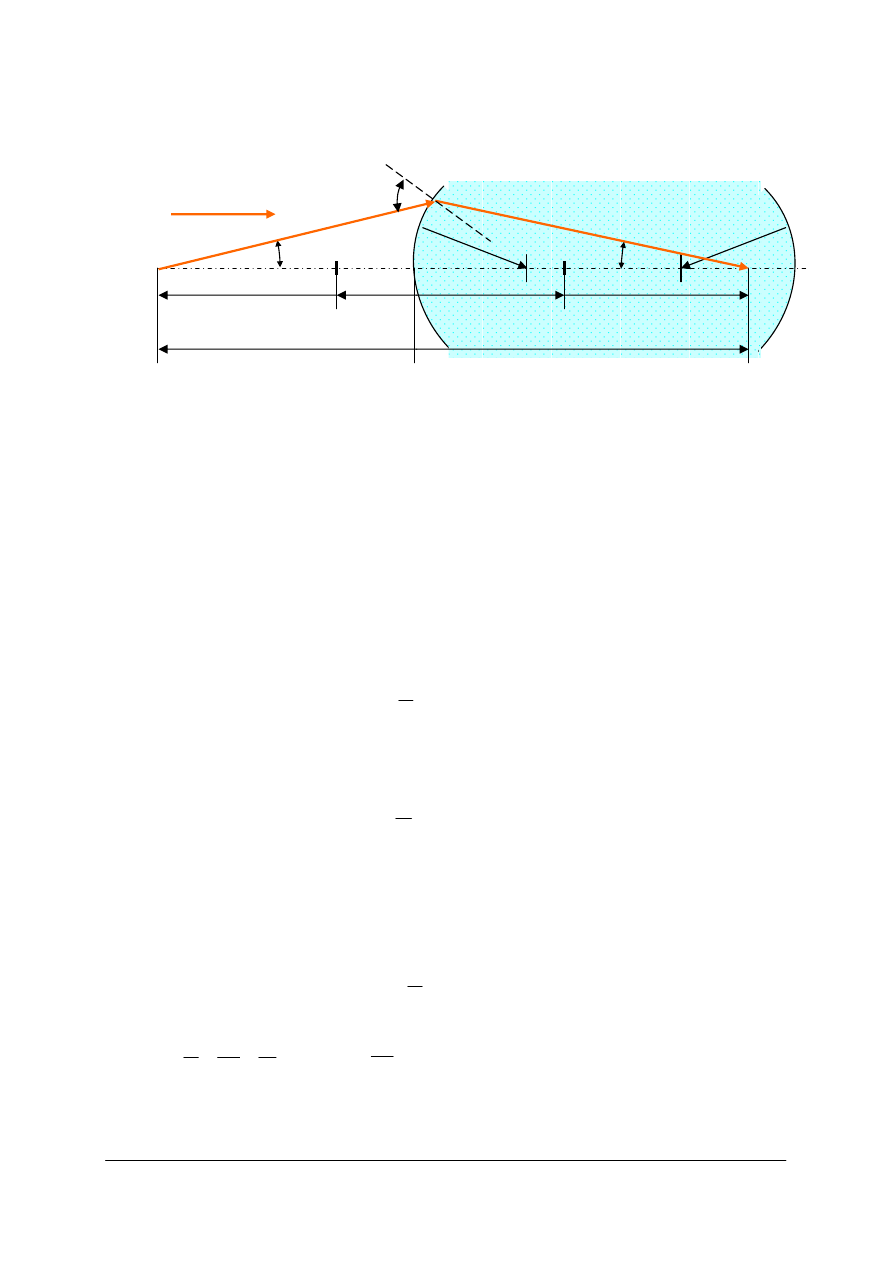
Reguła I – wygodna do stosowania w pojedynczych soczewkach. 

Rys. 34. Szkic z oznaczeniami reguły znaków wg Gaussa [opracowanie własne] 

 

−

 

Odległość przedmiotowa „s” przedmiotu rzeczywistego jest dodatnia „+” 

−

 

Odległość  obrazowa  „s’”  dla  obrazu  rzeczywistego  jest  dodatnia  „+”,  a  dla  obrazu 
pozornego jest ujemna „-”. 

−

 

Ogniskowe są dodatnie dla układu skupiającego, a ujemne dla układu rozpraszającego. 

−

 

Przyjmujemy,  Ŝe  wszystkie  powierzchnie  wypukłe,  patrząc  z  ośrodka  rzadszego 
w kierunku  ośrodka  gęstszego,  bez  względu  na  kierunek  rozchodzenia  się  światła,  mają 
dodatnie promienie krzywizny, a powierzchnie wklęsłe mają promienie ujemne. 

 
 
 
 
 
 
 
 
 
 
 
 
 

O 

O 

O’ 

R(+) 

R(-) 

n 

n’ 

n

<

n’ 

O’ 

n 

n’ 

s (+) 

s’ (+) 

s(+) 

s’(-) 

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 28

s

V

1

=

s

n

V

=

Reguła II – wygodna do stosowania przy obliczaniu układów optycznych. 

 

 

Rys. 35. Reguła znaków przy obliczaniu pojedynczych i złoŜonych układów optycznych – („doskonałych”), 

gdzie pojawiły się nowe wielkości: x – odległość od ogniska przedmiotowego do przedmiotu (odległość 

ogniskowa przedmiotowa), a x’ – odległość od ogniska obrazowego do obrazu [opracowanie własne] 

 

−

 

Światło biegnie „od lewej do prawej”. 

−

 

Odcinki mierzymy od powierzchni (lub płaszczyzn głównych) soczewki, albo od ognisk. 
Powierzchnia ma pierwszeństwo. 

−

 

Odcinki mierzone zgodnie z biegiem światła są dodatnie („+”), a mierzone przeciwnie są 
ujemne („–”). 

−

 

Kąty  są  dodatnie  w  przypadku,  gdy  oś  optyczna  lub  normalna  do  powierzchni,  aby 
pokryć  się  z  promieniem  świetlnym,  musi  obrócić  się  zgodnie  z  ruchem  wskazówek 
zegara. W przeciwnym przypadku kąty są ujemne („-”). 

Skolimowanie  –  opisuje  stopień  nierównoległości  wiązki  światła,  obejmuje  zatem 

zarówno jej

 zbieŜność, jak i rozbieŜność. Decyduje znak. 

 

W najprostszym przypadku:  

 

Po uwzględnieniu współczynnika załamania. 

 

Skolimowanie zredukowane 

 

Znak skolimowania określa się jak znak kąta w punkcie II/4.- reguły znaków. 
 
Moc optyczna 

Mocą  optyczną  (zdolnością  zbierającą,  zdolnością  skupiającą)  powierzchni  nazywamy 

stosunek współczynnika załamania ośrodka do ogniskowej. 

f

n

D

=

 

Im krótsza ogniskowa, tym większa moc. 

PoniewaŜ 

'

'

n

f

n

R

n

f

=

∆

=

  , więc 

R

n

D

∆

=

 – równanie mocy optycznej pojedynczej powierzchni 

załamującej.

 

Pojedyncza powierzchnia załamująca, z reguły nie stanowi jeszcze elementu optycznego, 

muszą być przynajmniej dwie takie powierzchnie (jak np. w płytce płasko-równoległej). 

N 

O 

F 

C 

R(+
) 

S

F’ 

R

2

(-) 

O’ 

x(-
) 

f(-) 

f ’(+) 

x’(+) 

s(-) 

s’(+) 

 
u’(+) 

u(-) 

4.1.1

 

i(-) 

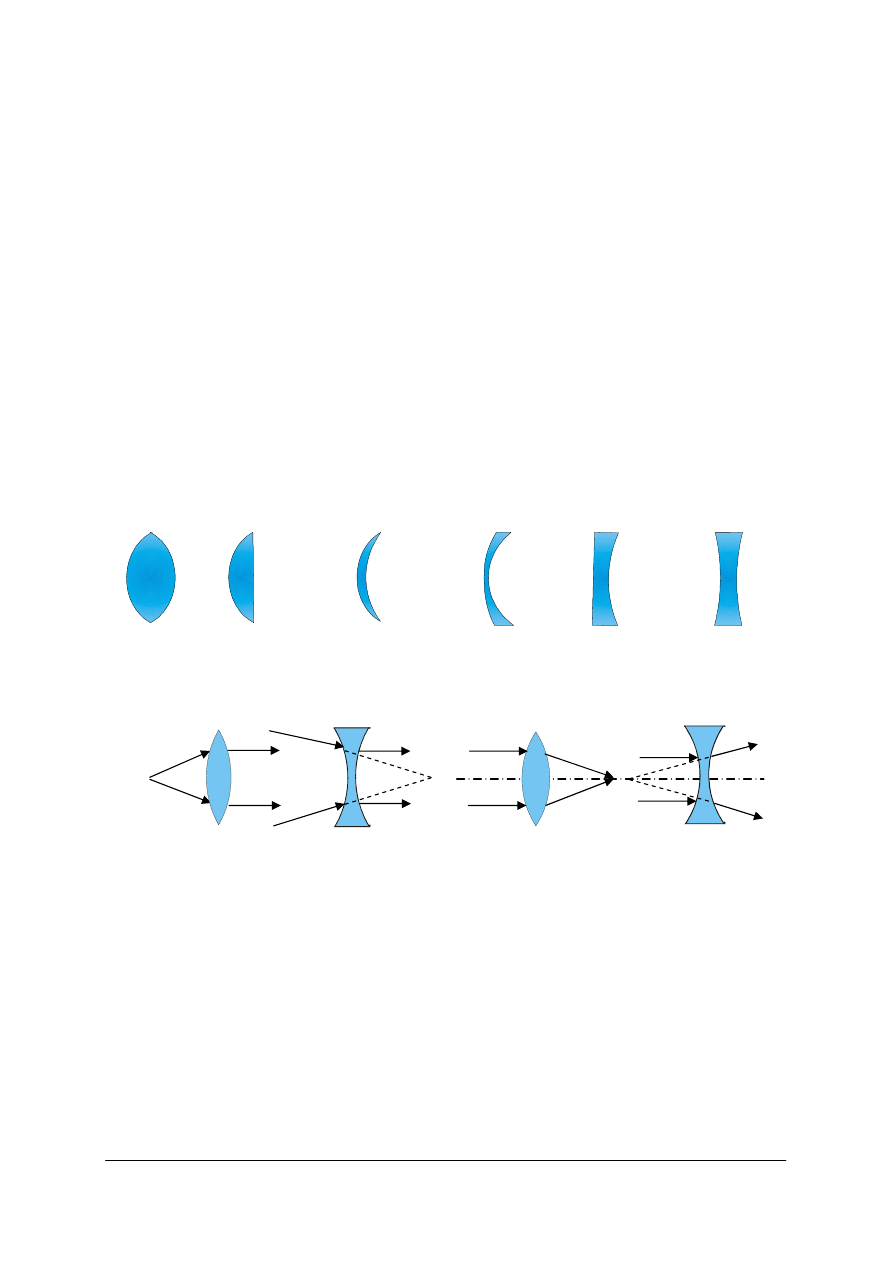
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 29

Elementem, w którym występują dwie powierzchnie załamujące, ale przynajmniej jedna 

nie jest płaska jest  soczewka. 

RozróŜniamy  dwie  zasadnicze  klasy  soczewek,  w  zaleŜności  od  sposobu  ich 

oddziaływania na wiązkę równoległą (Keppler – 1611 r.): 

−

 

soczewki skupiające, czyli dodatnie – grubsze w środku niŜ na brzegu, 

−

 

soczewki rozpraszające, czyli ujemne – cieńsze w środku niŜ na brzegu. 
W  obu  przypadkach  przyjmujemy,  Ŝe  ich  współczynnik  załamania  jest  większy  od 

współczynnika załamania ośrodka otaczającego. 

Soczewka  cienka  jest  elementem  umownym,  w  którym  pomijamy  wartość  drogi 

optycznej pomiędzy powierzchniami załamującymi. MoŜna więc powiedzieć, Ŝe ma moc, ale 
nie ma grubości. 
Moc soczewki jest więc sumą mocy powierzchni. 

W obliczeniach mających charakter orientacyjny moŜna stosować takie uproszczenia. 

Obliczenia  dokładne  wymagają  uwzględnienia  drogi  optycznej  wewnątrz  soczewek  i wtedy 
mówimy, Ŝe prowadzimy obliczenia dla soczewek rzeczywistych (grubych). 

KaŜda  soczewka  sferyczna  ma  dwa  środki  krzywizny  i  dwa  promienie  krzywizny, 

a prosta łącząca środki krzywizn to oś główna soczewki. 
 
 

Dwuwypukła    

    wklęsło-wypukła     

        dwuwklęsła        

płasko-wypukła

wklęsło- wypukła  płasko-wklęsła

Soczewki skupiające

Soczewki rozpraszające

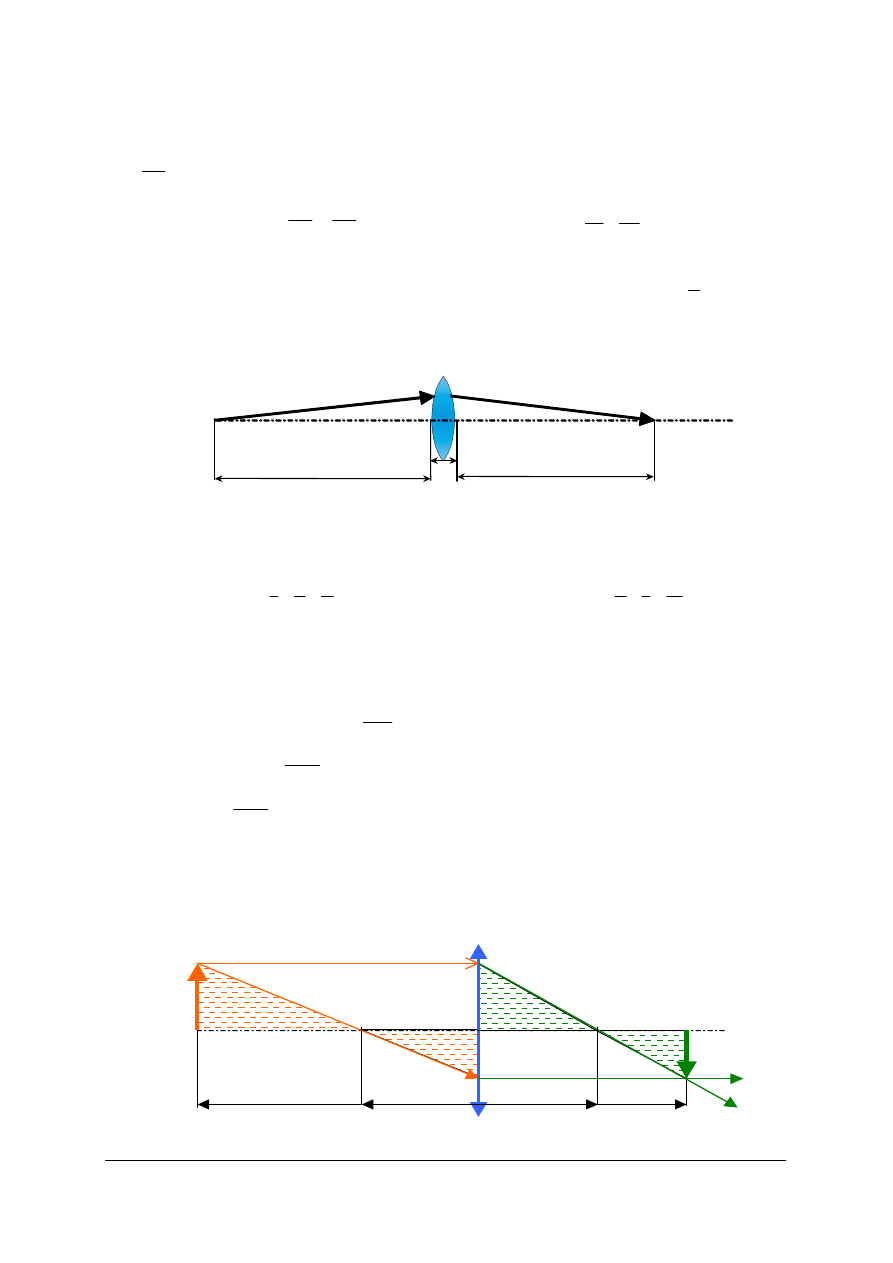
Rys. 36. Rodzaje soczewek

. S

oczewki wklęsło-wypukłe noszą nazwę menisków dodatnich lub ujemnych 

[opracowanie własne]

 

 

 

Rys. 37. PołoŜenie ognisk w soczewkach dodatnich i ujemnych [opracowanie własne] 

 
 

Definicje odległości, płaszczyzn i ognisk są takie same jak dla pojedynczej powierzchni 

z tą  róŜnicą,  Ŝe  pojedyncza  powierzchnia  ma  róŜne  ogniskowe  przedmiotową  i  obrazową, 
a soczewka takie same (o ile za drugą powierzchnią jest ten sam współczynnik załamania co 
przed pierwszą). 

Zadaniem  tak  pojedynczych  soczewek  jak  i  ich  układów  jest  tworzenie  obrazów.  Do 

wyznaczania  połoŜenia  tych  obrazów,  w  zaleŜności  od  połoŜenia  przedmiotu,  słuŜą  róŜne 
wzory. Najprostszymi są wzór Gaussa i wzór Newtona. 

 
 
 
 
 
 

F 

F 

F’ 

F’ 

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 30

O

 

O’

 

s

s’ 

d

n 

Wzór szlifierzy soczewek 
PoniewaŜ  moc  pojedynczej  powierzchni,  tzw.  moc  powierzchniowa  jest  określana  jako 

R

n

D

∆

=

, więc moc pojedynczej soczewki cienkiej będzie sumą mocy jej powierzchni.  

D  =D

1 

+D

2

  czyli 

2

1

R

n

R

n

D

∆

+

∆

=

.  Po  przekształceniu: 

)

1

1

(

2

1

R

R

n

D

+

∆

=

  -  jest  to  wartość 

przybliŜona 

Dla soczewek grubych (rzeczywistych) wzór przybiera postać: 

2

1

2

1

D

D

n

d

D

D

D

−

+

=

, gdzie 

d oznacza grubość soczewki w środku, a n – jej współczynnik załamania. 
Wzory dla soczewki cienkiej w sformułowaniu Gaussa są podobne do wzorów dla  
zwierciadła sferycznego. 

Rys. 38. Oznaczenia do wzoru soczewkowego Gaussa, gdzie O oznacza punkt przedmiotu,  

O’ – sprzęŜony z nim punkt obrazu, s – odległośc  przedmiotową, s’ – odległość obrazową, d – grubość 

soczewki w środku, a n – jej współczynnik załamania [opracowanie własne] 

 

Równanie  soczewki: 

f

s

s

1

'

1

1

=

+

–  (zgodne  z  I  regułą  znaków),  lub

f

s

s

′

=

−

′

1

1

1

  (zgodne  z  II 

regułą  jest  jedynie  teoretyczne  i  odnosi  się  do  przestrzeni  przyosiowej  tj.  takiej,  w  której 
kąty  między  osią  a  promieniami  przedmiotowymi  i obrazowymi  są  na  tyle  małe,  Ŝe  moŜna 
załoŜyć równą wartość sinusa, tangensa i kąta w mierze łukowej. Błąd wynikający z takiego 
uproszczenia jest pomijalnie mały. 
Wtedy odległość przedmiotowa 

f

s

f

s

s

−

=

'

'

, 

 odległość obrazowa 

f

s

sf

s

−

=

'

, 

a ogniskowa 

'

'

s

s

ss

f

+

=

. 

W  niektórych  przypadkach  łatwiej  jest  wyznaczyć  połoŜenie  obrazów  stosując  wzór  dla 

soczewki cienkiej w sformułowaniu Newtona 

RóŜni  się  tym  od  wzoru  Gaussa,  Ŝe  zamiast  odległości  przedmiotowych  i  obrazowych 

wprowadzamy odległości mierzone od odpowiednich ognisk – odległości ogniskowe. 

Wzór soczewkowy Newtona. 

2

'

'

f

xx

−

=

 

Rys. 39. Szkic wyjaśniający wzór Newtona. x – odległość ogniskowa przedmiotowa, n’ – odległośc ogniskowa 

obrazowa [opracowanie własne] 

 

F

 

F ’

 

y’ 

x 

f 

f’ 

x’ 

y 

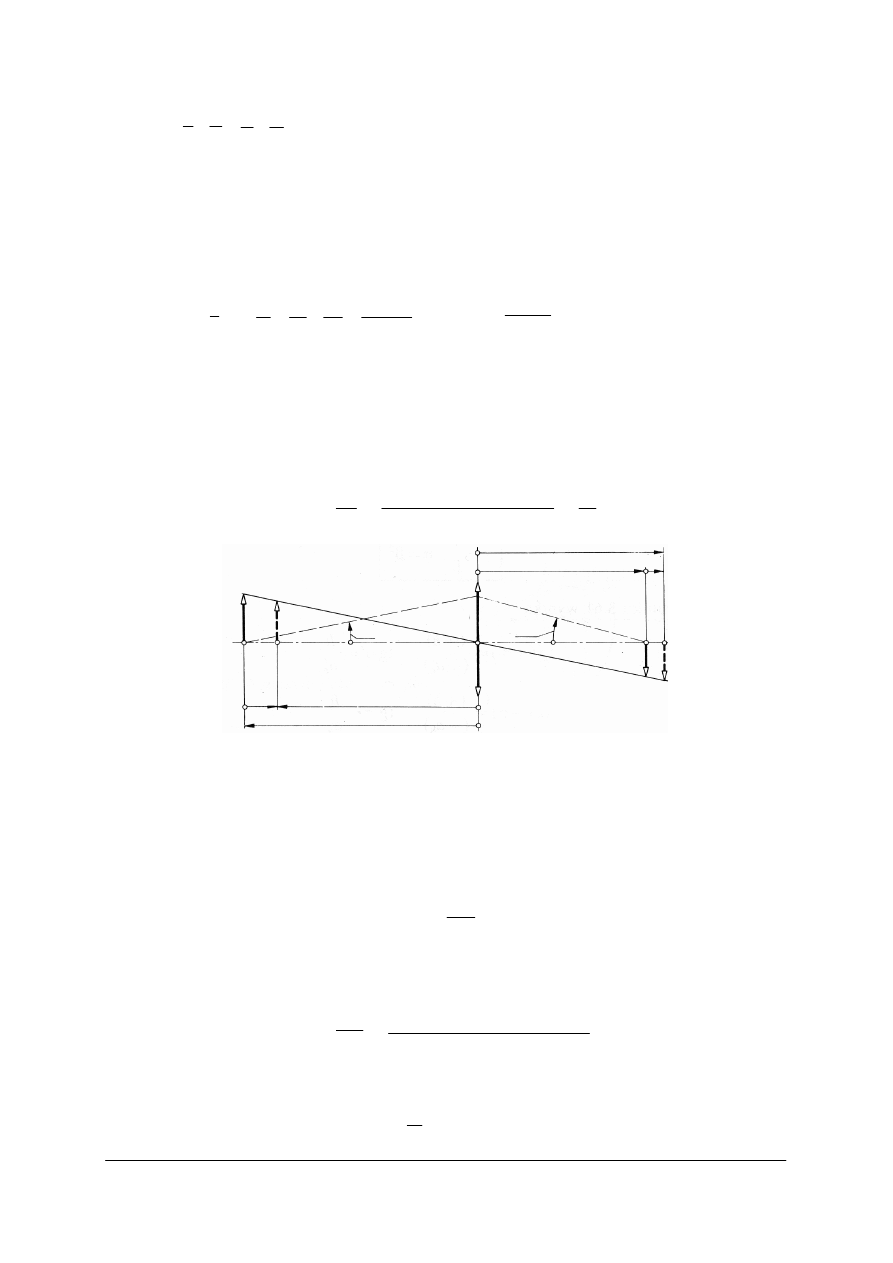
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 31

PoniewaŜ 

f

y

x

y

'

=

 i 

'

'

x

y

f

y

=

 więc xx’=-f’

2 

Soczewki cienkie – układy soczewek, powiększenia, soczewki cylindryczne 

Mówiąc o układzie soczewek cienkich przyjmujemy, Ŝe są one ze sobą w kontakcie. 

Skolimowanie wychodzące z pierwszej jest skolimowaniem wchodzącym drugiej, wychodzące 
drugiej – wchodzącym trzeciej itd. 

Dlatego:  całkowita  moc  optyczna  układu  cienkich  soczewek  jest  równa  sumie  mocy 

soczewek składowych. 
D = D

1

 + D

2

 +.....D

n

 

PoniewaŜ 

f

1

D

=

 , to 

2

1

2

1

2

1

1

1

1

f

f

f

f

f

f

f

+

=

+

=

  więc 

2

1

2

1

f

f

f

f

f

+

=

  Jest  to  słuszne  t

ylko  dla 

soczewek cienkich będących w kontakcie optycznym! 

(stykających się ze sobą). 

Powiększenie 

Termin

  „powiększenie”  mało  precyzyjnie  odzwierciedla  zjawisko  odwzorowania 

przedmiotu w przestrzeni obrazowej. 

Na 

rysunku

  40  litera  y  oznacza  wymiar  przedmiotu,  a  y’  wielkość  obrazu  utworzonego 

przez pojedynczą soczewkę  lub ich układ. Stosunek tych wielkości jest miarą powiększenia 
poprzecznego (liniowego),  mierzonego prostopadle do osi optycznej. 

'

.

.

'

s

s

przedmiotu

wielk

obrazu

wielk

y

y

=

=

=

β

 

 

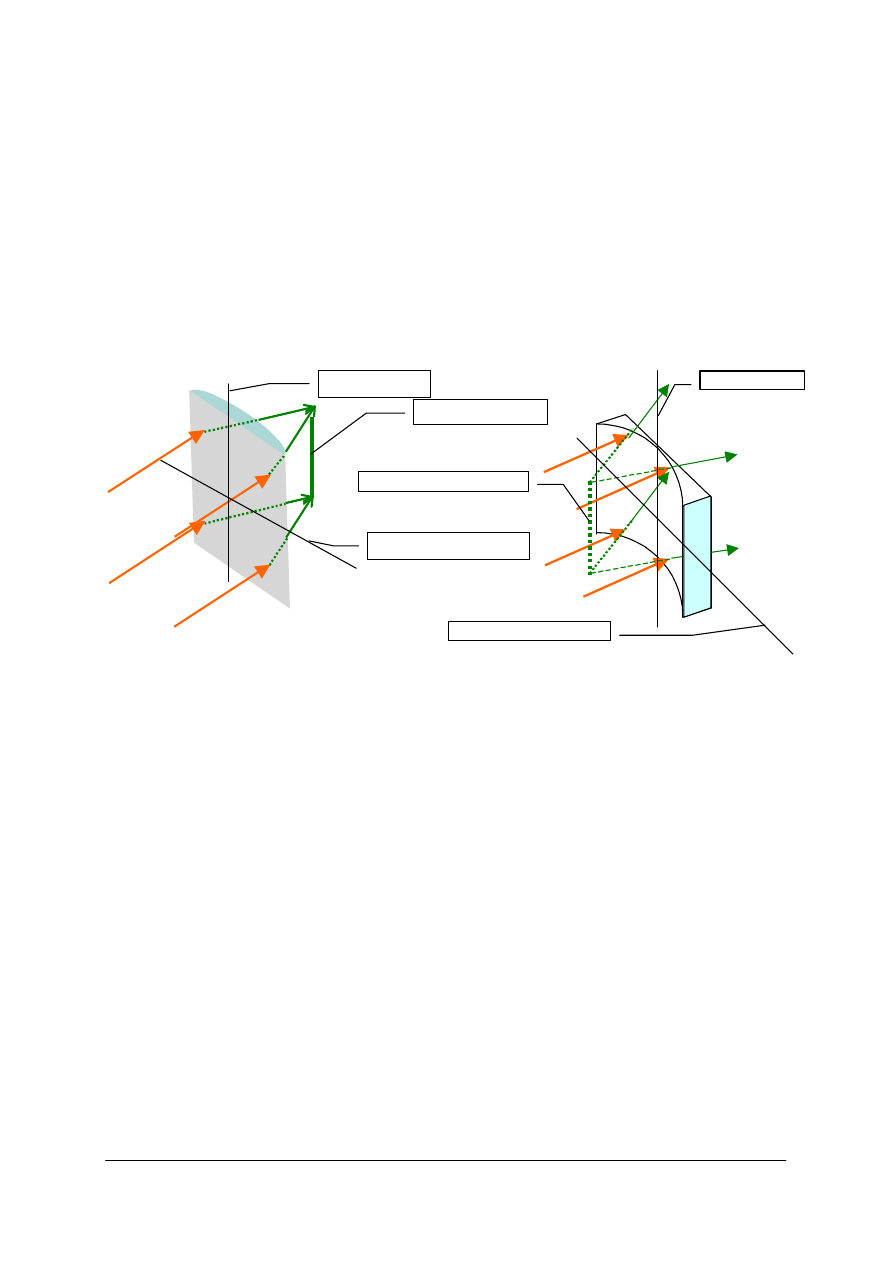
Rys. 41. Rysunek przedstawiający  wielkości określające powiększenia, gdzie y to wielkość przedmiotu, y’ to 

wielkośc obrazu, u – kąt promienia padającego, u’ – kąt  promienia wychodzącego, s

0

 – początkowe połoŜenie 

przedmiotu, s

1

 – końcowe połoŜenie przedmiotu, s’

0

 – początkowe połoŜenie obrazu, s’

1

 – końcowe połoŜenie 

obrazu, ∆s i ∆s’ to przesunięcie przedmiotu i odpowiadające mu przesunięcie obrazu [opracowanie własne] 

 
W 

optyce

 posługujemy się jeszcze innymi rodzajami powiększenia. 

Powiększenie kątowe, określane stosunkiem tangensów kątów u i u’ jakie tworzą z osią 

optyczną promienie wychodzące z układu i padające na układ optyczny, wyraŜone wzorem 

tgu

tgu'

=

γ

 

Jeśli

  przedmiot  przesunie  się  poosiowo  o  wielkość  ∆s,  to  jego  obraz  przesunie  się 

o wielkość    ∆s’.  Stosunek  przesunięcia  obrazu  do  odpowiadającego  mu  przesunięcia 
przedmiotu nazywamy powiększeniem podłuŜnym i wyraŜamy wzorem 

s

s

∆

′

∆

=

α

 = 

przedmiotu

osiowe

przesun

obrazu

osiowe

przesun

.

.

 

 

Pomiędzy powiększeniami zachodzą związki, które wyraŜamy wzorami: 

β

γ

1

=

 oraz

2

β

α

=

 

∆s’ 

y’ 

s

0 

y 

s’

0 

∆s 

s

1

’ 

u

 

 

P 

s

1 

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 32

NaleŜy zwrócić uwagę na fakt, Ŝe wzory określające zaleŜności między powiększeniami 

są słuszne jedynie w przypadku, gdy obraz i przedmiot leŜą w jednakowych ośrodkach. 

 

Przeogniskowanie  –  róŜnica  połoŜenia  (błąd  połoŜenia)  punktu  obrazowego  (lub 

płaszczyzny  obrazowej),  który  moŜna  tolerować  ze  względu  na  pogorszenie  odwzorowania 
(obrazu).  MoŜna  mówić  o  dopuszczalnym  krąŜku  rozproszenia  (plamce  rozproszenia),  który 
jest „rozmytym” obrazem punktu. 

Głębia ostrości – zakres zmian połoŜenia przedmiotu odpowiadający załoŜonej wielkości

 

krąŜka rozproszenia, czyli przeogniskowania. 
 
Soczewki cylindryczne 
 

 

Rys. 42. Szkic przedstawiający terminologię dotyczącą soczewek cylindrycznych. Z lewej soczewka 

cylindryczna dodatnia, z prawej soczewka cylindryczna ujemna [opracowanie własne] 

 
WyróŜniamy dwa prostopadłe do osi optycznej kierunki południkowe – południk osiowy 

i południk mocy optycznej (maksymalnego załamania). 

Powierzchnie cylindryczno-sferyczne nazywamy torycznymi. Obraz punktu występuje tu 

jako twór przestrzenny zwany konoidą Sturma. 

 

Wytyczanie biegu promienia przez pojedynczą powierzchnię 

Przy przejściu przez powierzchnię graniczną zawsze obowiązuje prawo załamania. 
Mamy dwie grupy promieni: 

−

 

południkowe  –  przynajmniej  raz  przecinają  oś  optyczną,  są  łatwe  do  wykreślenia  na 
płaszczyźnie rysunku, 

−

 

skośne – nie przecinają osi ani razu (trygonometria przestrzenna) – teraz moŜna badać ich 
przebieg dzięki symulacji komputerowej. 

 
 
 
 
 
 

Ognisko liniowe 

Ognisko liniowe (pozorne) 

Południk osiowy 

Południk osiowy 

Południk mocy optycznej 

Południk mocy optycznej 

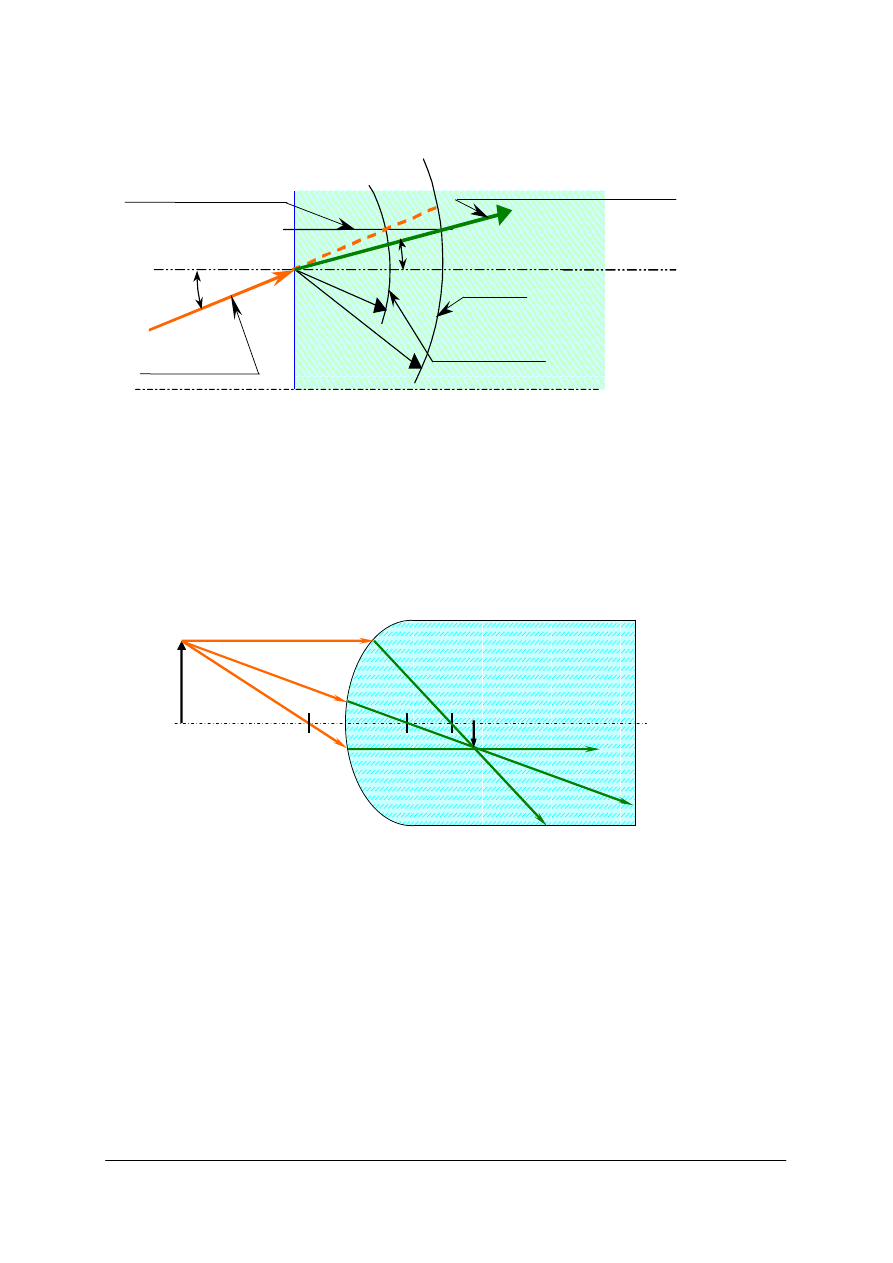
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 33

Wytyczanie biegu promienia przez graniczną powierzchnię płaską 
Metoda promienia równoległego 

 

Rys. 43. Wytyczanie biegu promienia po załamaniu na powierzchni płaskiej. Kolejność postępowania: 

−

 

rysujemy normalną w punkcie padania promienia, 

−

 

z punktu padania wykreślamy dwa łuki o promieniach odpowiadających wartościom współczynników 

załamania n i n’, 

−

 

przez punkt przecięcia łuku R

1

 z przedłuŜeniem promienia padającego prowadzimy równoległą do 

normalnej i przez punkt jej przecięcia z łukiem R

2

 prowadzimy promień załamany [opracowanie własne] 

 
 

Wytyczanie  biegu  promienia  przez  graniczną  powierzchnię  sferyczną  .przeprowadza  się 

analogicznie prowadząc równoległą do promienia krzywizny w punkcie padania. 

Rys. 44. Konstrukcja promieni do wytyczania połoŜenia obrazu dawanego przez pojedynczą powierzchnie 

kulistą [opracowanie własne] 

 
 

Konstrukcja promieni 

−

 

Promień równoległy – jest równoległy do osi optycznej, a po załamaniu przechodzi przez 
ognisko obrazowe. 

−

 

Promień główny – przechodzi przez środek krzywizny i nie ulega załamaniu. 

−

 

Promień  ogniskowy  –  przechodzi  przez  ognisko  przedmiotowe,  po  załamaniu  staje  się 
równoległy do osi optycznej. 

 
 
 
 
 
 

1 

2 

3 

F 

C 

F
’ 

y’ 

y 

Równoległa do

 

normalnej

 

Promień padający

 

Promień wychodzący (załamany)

 

Łuk R

1

 = n 

Łuk R

2

 = n’

 

Normalna do powierzchni w punkcie padania

 

i

 

i'

 

n 

n’ 

Dane: n i n’ ; n 

<

 n’ 

N 

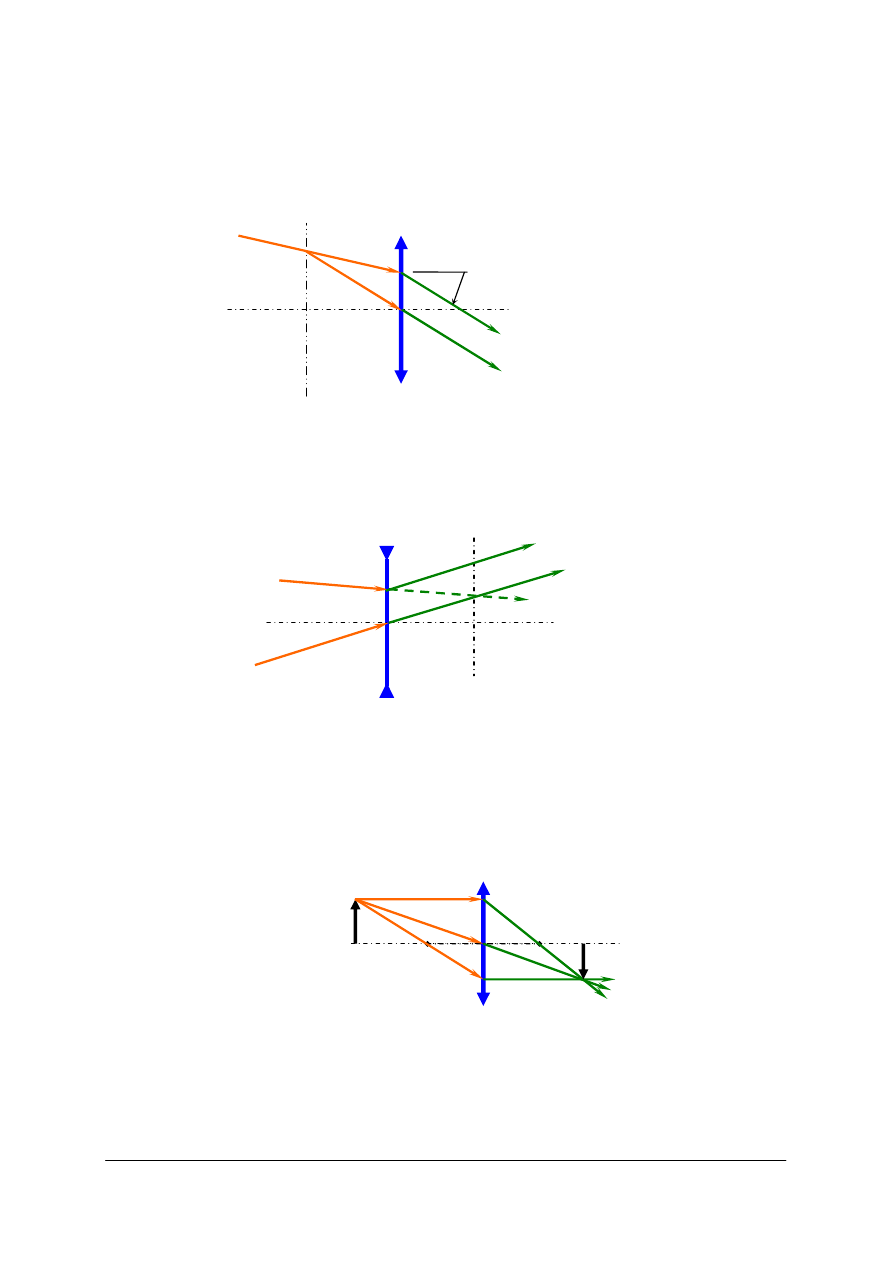
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 34

Wytyczanie biegu promienia przez soczewkę cienką 
 
Soczewka skupiająca (dodatnia). Znana ogniskowa.  

W  uproszczeniu  przedstawiamy  ją  za  pomocą  dwustronnej  strzałki  skierowanej  na 

zewnątrz. 

 

Rys. 45. Wytyczanie biegu promienia przez soczewkę cienką dodatnią gdy znana jest ogniskowa. Promień 

załamany będzie równoległy do promienia głównego wychodzącego z tego samego punktu płaszczyzny 

ogniskowej przedmiotowej [opracowanie własne] 

 

Soczewka rozpraszająca (ujemna) – oznaczamy za pomocą dwustronnej strzałki skierowanej 
do wewnątrz. 

Rys. 46. Wytyczanie biegu promienia przez soczewkę ujemną. Światło skierowane do jakiegokolwiek punktu na 

płaszczyźnie ogniskowej przedmiotowej, po załamaniu będzie równoległy do promienia głównego 

przechodzącego przez ten punkt [opracowanie własne] 

 

Konstrukcja powstawania obrazów przy przejściu światła przez soczewkę 

JeŜeli mamy przedmiot, a nie promień, postępujemy analogicznie jak przy przejściu przez 

pojedynczą  powierzchnię.  Wyznaczamy  przebieg  promienia  równoległego,  głównego 
i ogniskowego.  Na  rysunkach    47–50  przedstawiono  róŜne  warianty  połoŜenia  przedmiotu 
i jego obrazu. 

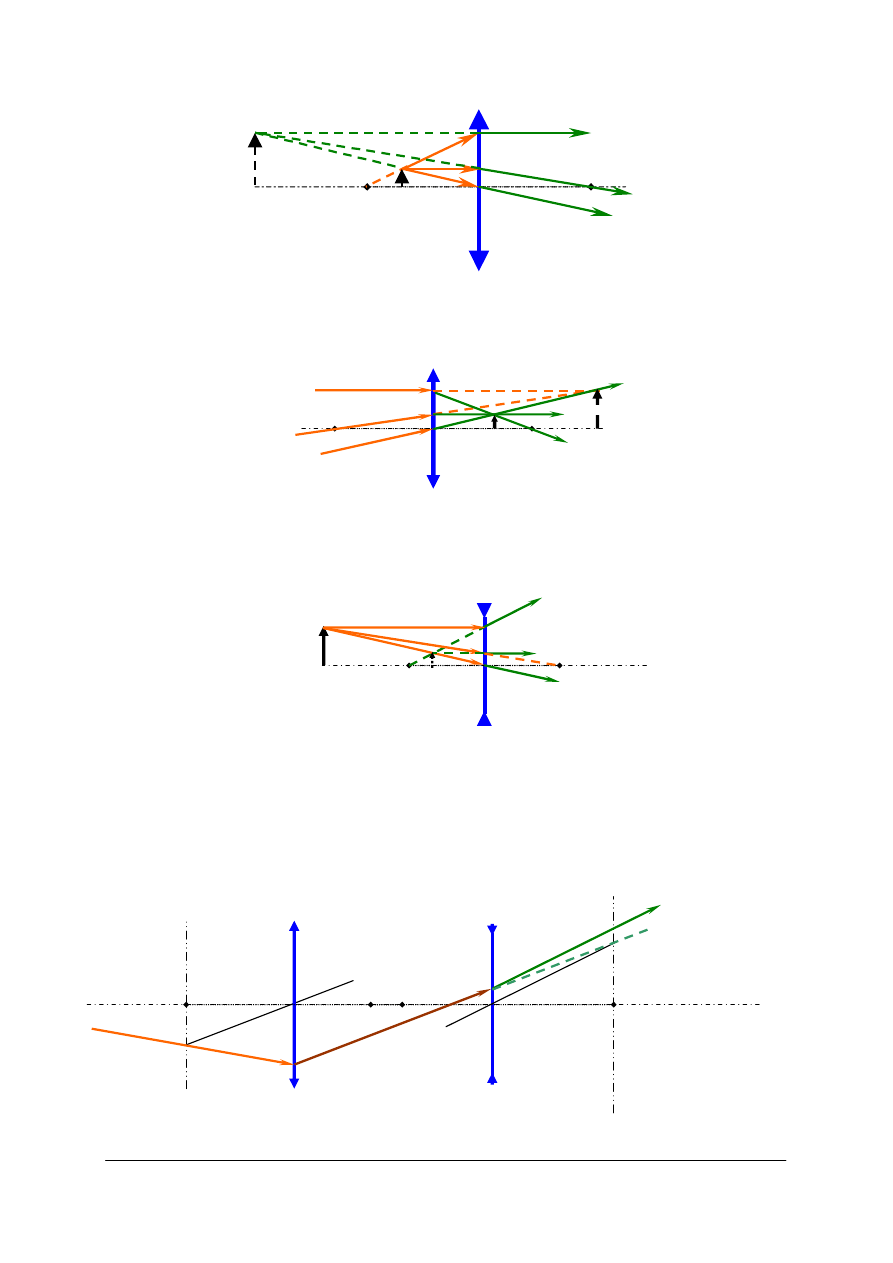
Rys. 47.  JeŜeli przedmiot leŜy dalej niŜ ognisko przedmiotowe otrzymujemy obraz rzeczywisty odwrócony 

[opracowanie własne] 

 
 
 
 
 

ππππ

F 

P 

F 

Promień 
załamany 

ππππ

F 

F 

P 

y 

y’ 

F 

F’ 

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 35

 

Rys. 48.  JeŜeli przedmiot leŜy bliŜej niŜ ognisko przedmiotowe, otrzymujemy obraz pozorny, prosty 

i powiększony [opracowanie własne] 

 
 

 

Rys. 49. JeŜeli przedmiot pozorny jest umieszczony

 

za

 

soczewką dodatnią otrzymujemy obraz rzeczywisty, 

prosty o powiększeniu mniejszym od jedności (pomniejszony) [opracowanie własne] 

 
 

 
 

Rys. 50. JeŜeli soczewka jest ujemna, a przedmiot umieszczony jest przed soczewką, otrzymujemy obraz 

pozorny, prosty i pomniejszony [opracowanie własne] 

 

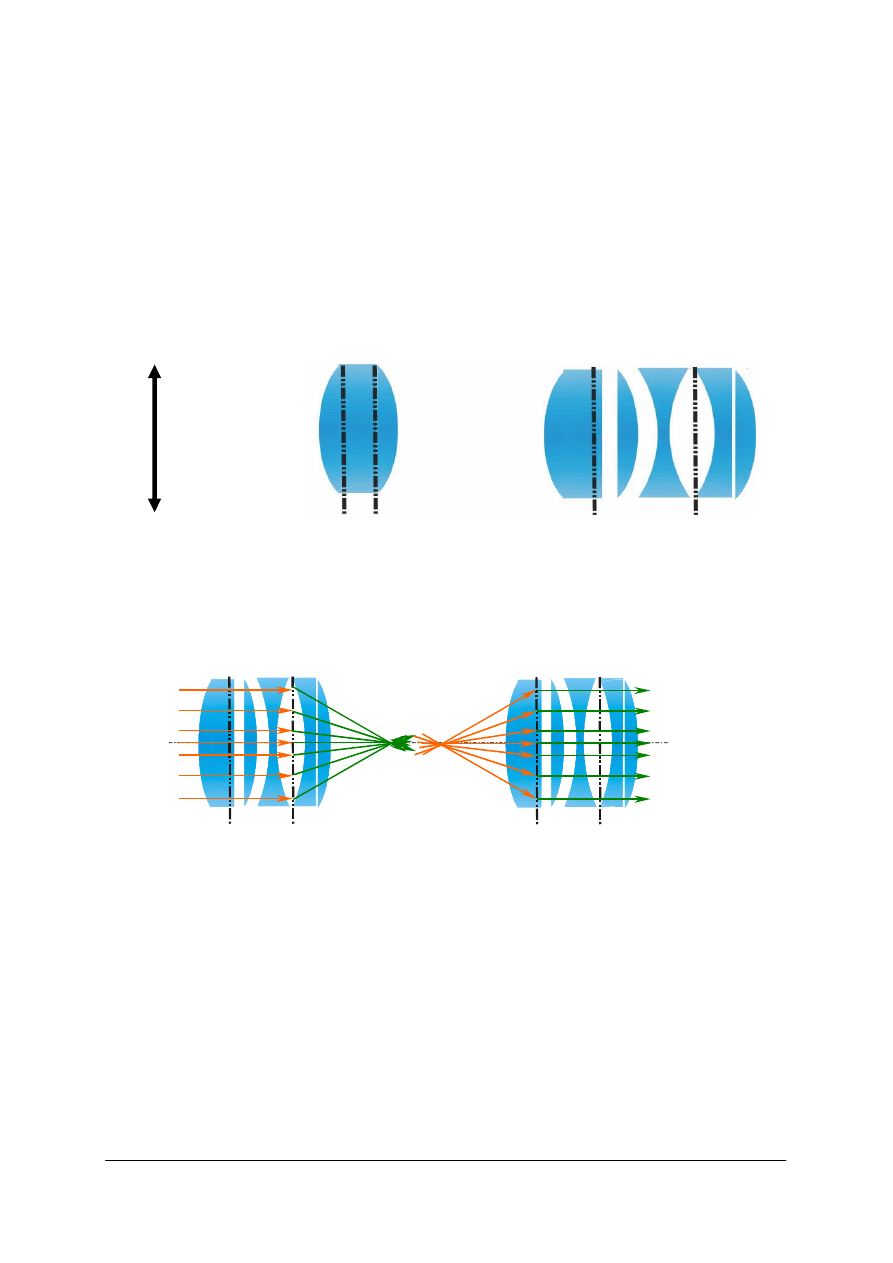
Wytyczanie biegu promienia przez układ  soczewek cienkich 

Przy  kolejnych  soczewkach  postępujemy  tak  jak  przy  pierwszej.  Promień  wychodzący 

z poprzedniej soczewki jest wchodzącym do następnej. 

 

Rys. 51. Wytyczanie biegu promienia przez układ soczewek cienkich w przypadku, gdy jedna z nich jest 

dodatnia, a druga ujemna [opracowanie własne] 

 

F 

F’ 

π

1 

F

1 

I 

II 

F’

2 

F’

1 

F

2 

π

2

 

4

 

P’ 

y’ 

F 

F’ 

y 

y’ 

F

F’ 

y 

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 36

Ten  sposób  postępowania  daje  nam  moŜliwość  przybliŜonego  wyznaczania  połoŜenia 

obrazu dawanego przez układ większej ilości soczewek. 

Do  scharakteryzowania  podstawowych  parametrów  soczewek  rzeczywistych  (grubych) 

i ich  układów  potrzebna  jest  znajomość  połoŜenia  charakterystycznych  punktów  zwanych  
kardynalnymi. 

KaŜda  soczewka  ma    sześć  punktów  kardynalnych:  dwa  ogniska  -  F  i  F’,  dwa  punkty 

główne – H  i H’ oraz dwa punkty węzłowe - N i N’. 
Punkty główne – miejsce przecięcia osi optycznej z płaszczyznami głównymi. 

Płaszczyzny główne – płaszczyzny znajdujące się wewnątrz soczewki lub układu w takim 

miejscu,  gdzie  umownie  skupia  się  cała  moc  tych  elementów,  niezaleŜnie  od  tego,  gdzie  to 
zachodzi w rzeczywistości. 

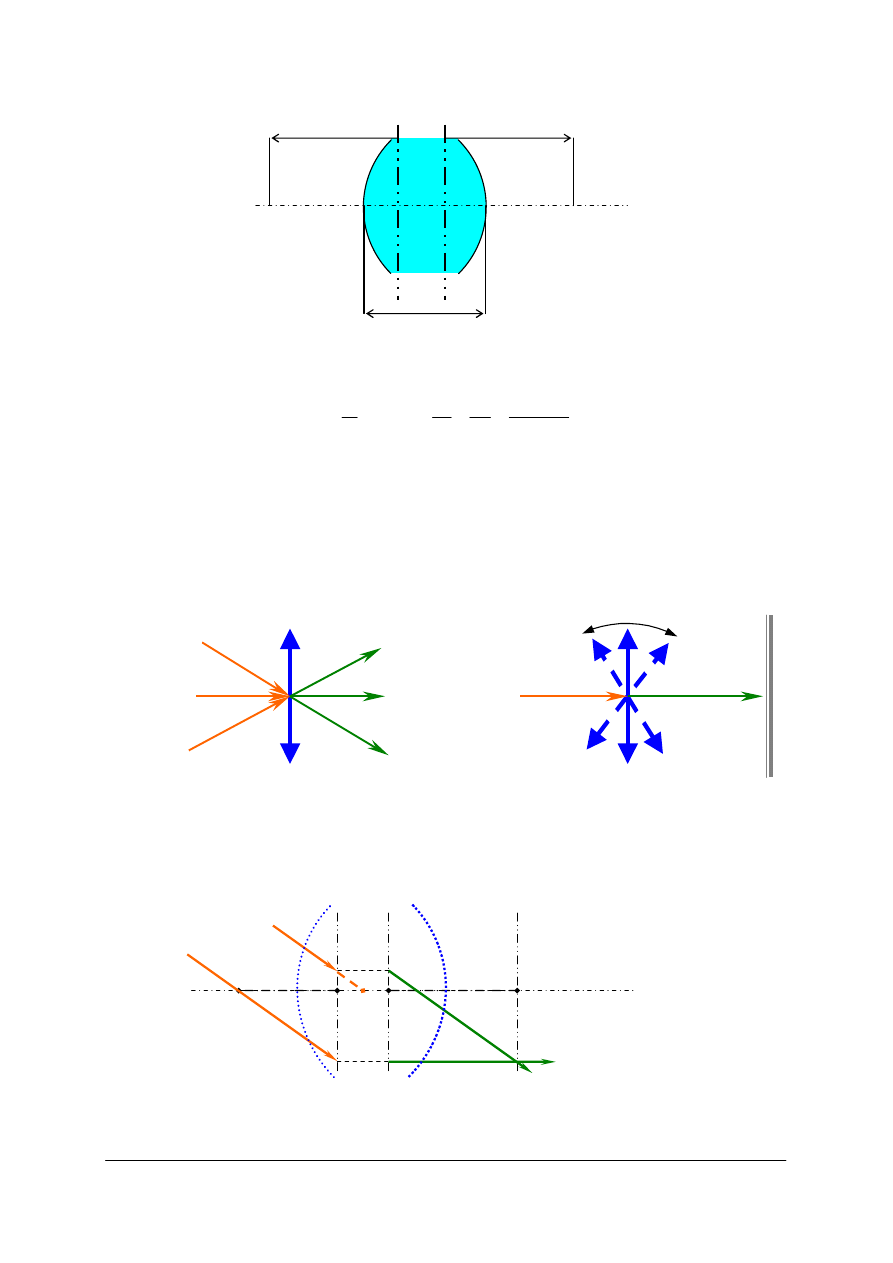
 1)   

 

 

 

 

 

2)   

 

 

 

 

 

 

 

3) 

Rys. 52. PołoŜenie płaszczyzn głównych w zaleŜności od typu soczewki lub układu. 

1) W soczewce cienkiej płaszczyzny pokrywają się, 2) W soczewce grubej są rozsunięte, 

3) W układzie soczewek mogą być rozsunięte i mogą znajdować się poza układem [opracowanie własne] 

 

Znaczenie płaszczyzn głównych. 
Znajomość lokalizacji pomaga w wytyczaniu biegu promieni. 

Rys. 53. Istnieje odpowiedniość punktów (punkt po punkcie) między dwiema płaszczyznami głównymi. – 

KaŜdy z nich jest obrazem prostym (o powiększeniu jednostkowym) odpowiadającego mu punktu z drugiej 

płaszczyzny [opracowanie własne] 

 

Płaszczyzny główne są miejscami geometrycznymi, od których mierzy się ogniskowe. 

 

F’

F 

H 

H’

H 

H’ 

H

H’ 

H 

H 

H’ 

H’ 

P 

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 37

Rys. 54. Soczewka rzeczywista (gruba) z zaznaczonymi ogniskami i płaszczyznami głównymi 

[opracowanie własne] 

 
 













−

+

−

−

=

2

1

2

1

)

1

(

1

1

)

1

(

1

R

nR

n

d

R

R

n

f

 

 

Gdy  znane  jest  połoŜenie  płaszczyzn  głównych,  moŜna  wytyczać  bieg  promieni 

i wyznaczać połoŜenie obrazów (jak w soczewce cienkiej). 

Gdy przejdziemy od soczewki cienkiej do grubej (rzeczywistej), płaszczyzny główne się 

rozdzielą. 

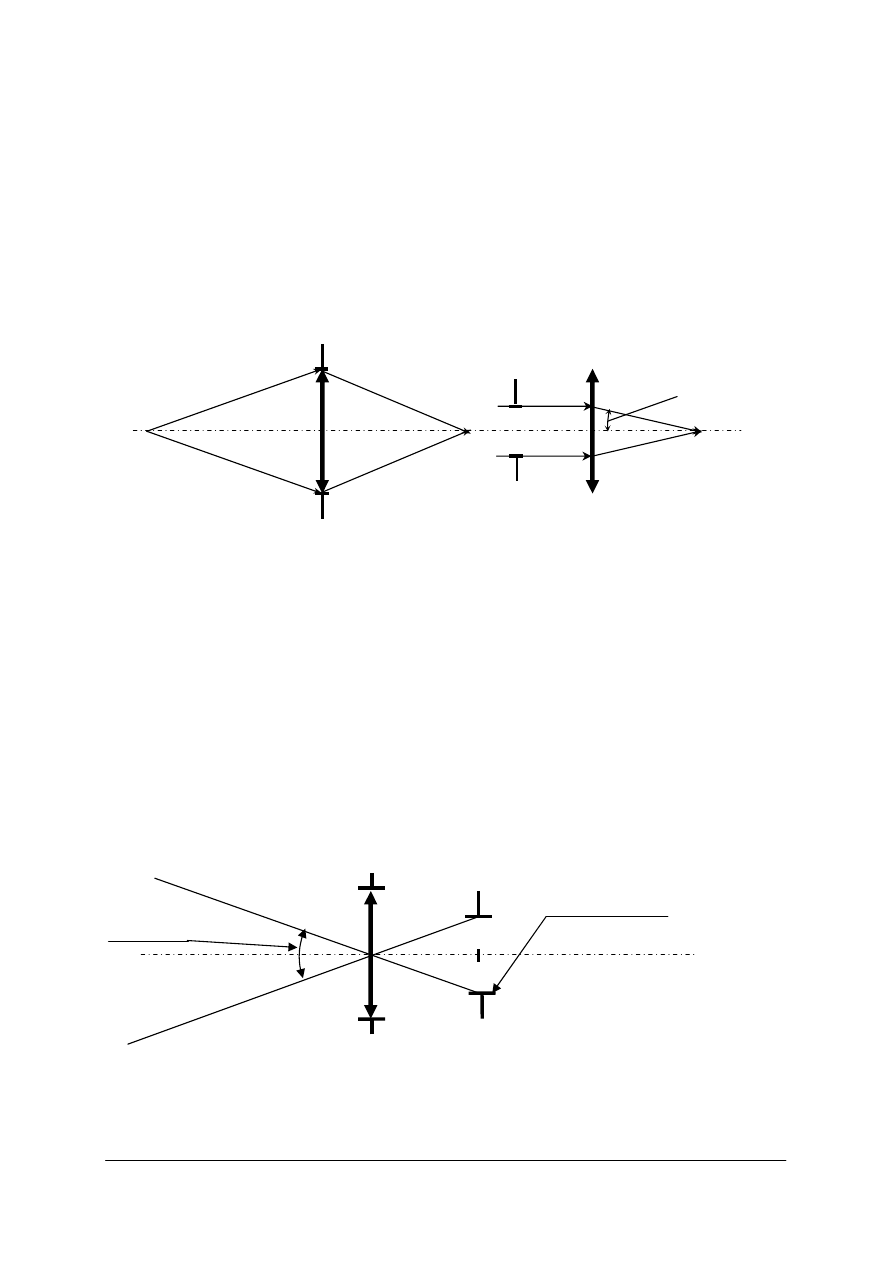
Punkty węzłowe są to punkty, przez które przechodzące światło (promienie) nie zmienia 

kierunku. Dla soczewki cienkiej jest to jej środek. 

Rys.  55. Promienie przechodzące przez środek soczewki cienkiej (punkt jej przecięcia z osią optyczną)  

nie zmieniają swego kierunku (są to promienie główne). Zmieniając kąt padania promienia głównego  

nie powodujemy zmiany jego kierunku. Punkty węzłowe leŜa więc w miejscu przecięcia soczewki cienkiej  

z osią optyczna [opracowanie własne]

 

Rys. 56. Szkic ilustrujący połoŜenie punktów kardynalnych układu rzeczywistego [opracowanie własne]

 

Dla  soczewki  rzeczywistej  istotne  jest  to,  Ŝe  połoŜenie  punktów  N  i  N’  nie  zaleŜy  od 

kierunku promieni padających. Promień przechodzący przez N wychodzi z N’ równolegle do 

F 

F’ 

V 

V’ 

d 

f 

f’ 

H 

H’ 

F 

H 

H’

N 

N’

’ 

F’ 

P’

’ 

N 
N’ 

N 

N’ 

Ekran 

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 38

kierunku padania. Punkty  węzłowe spełniają rolę środka soczewki cienkiej. Dla pojedynczej 
powierzchni sferycznej punktem węzłowym jest środek krzywizny. 
 
Apertury i źrenice 

KaŜda  wiązka  światła  przechodząca  przez  układ  optyczny  jest  ograniczona  jego 

wymiarami  geometrycznymi  (gabarytami).  Otwory  oraz  oprawy  soczewek  i  innych 
elementów  optycznych  nazywamy  przysłonami.  Najistotniejsze  są  dwie  przysłony  – 
aperturowa i polowa nazywane teŜ diafragmą aperturową i diafragmą pola. 

Przysłona  aperturowa  (inaczej:  apertura,  diafragma  aperturowa)  jest  to  przysłona 

ograniczająca  ilość  światła  przechodzącą  przez  układ.  Najprostsza  apertura  to  obrzeŜe 
pojedynczej soczewki lub zwierciadła. 

Rys. 57. Przysłona aperturowa  P

A

 wyznaczona średnicą soczewki i średnicą innego elementu układu 

[opracowanie własne]

 

 

Kąt połówkowy stoŜka wyznaczonego przez aperturę nazywa się aperturą kątową

 

Liczba  otworu  (liczba  przysłony,  przysłona)  jest  to  stosunek  ogniskowej  obrazowej  do 
średnicy apertury. (źrenicy wyjściowej) 

W  układach  o  zmiennej  aperturze  (np.  obiektywy  aparatów  fotograficznych)  liczby 

otworowe  są  tak  dobrane,  aby  kaŜda  następna  wielkość  oznaczała  2  razy  większa 
powierzchnie przysłony, a więc przepuszczała 2 razy więcej światła w tym samym czasie. 

Obrazami  przysłony  aperturowej  są  źrenice.  Źrenica  wejściowa  to  obraz  przysłony 

aperturowej  w  przestrzeni  przedmiotowej,  a  źrenica  wyjściowa  to  jej  obraz  w  przestrzeni 
obrazowej.  Przysłona  aperturowa,  źrenica  wejściowa  i  źrenica  wyjściowa  to  elementy 
sprzęŜone. Inaczej moŜna powiedzieć, Ŝe źrenice są to przysłony lub ich obrazy widziane pod 
najmniejszym  kątem  z  punktu  leŜącego  na  osi,  odpowiednio  w  przestrzeni  przedmiotowej 
lub obrazowej. 
Przysłona  polowa  (inaczej  diafragma  pola)  –  Jest  to  przysłona  regulująca  pole  widzenia 
układu optycznego. 

Rys. 58.  Przysłona polowa określająca kąt pola widzenia [opracowanie własne] 

 

Przysłona  (lub  obraz  przysłony)  w  przestrzeni  przedmiotowej,  którą  widać  pod 

najmniejszym  kątem  ze  środka  źrenicy  wejściowej  nazywamy  luką  wejściową,  a  dla 
przestrzeni  obrazowej  –  luką  wyjściową.  Realną  (materialną)  przysłonę,  której  obrazami  są 
luki, nazywamy przysłona polową. 

Przysłona polowa 
w płaszczyźnie obrazowej 

π’

 

Kąt pola 
widzenia 

P

A 

P

A 

Apertura kątowa 

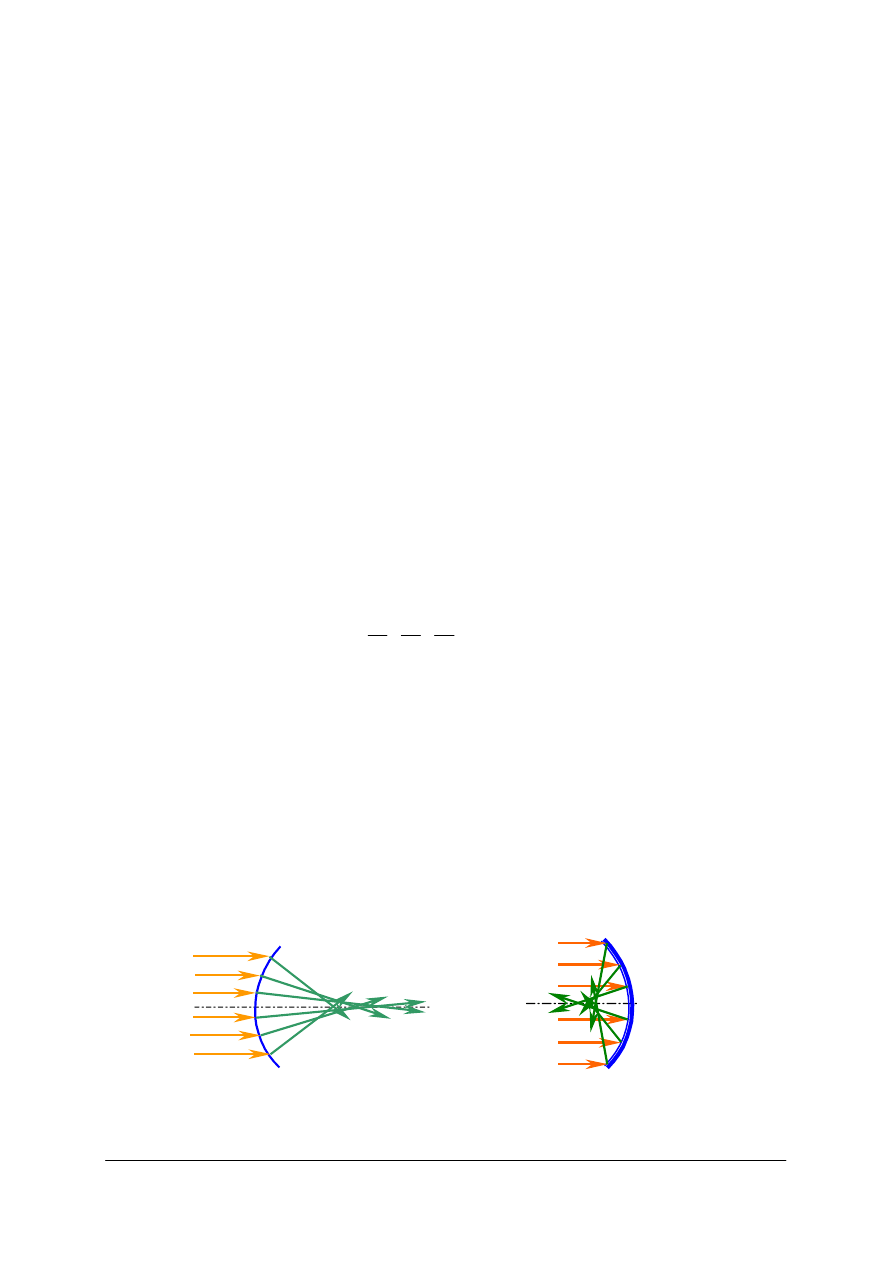
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 39

Promienie wychodzące ze środka płaszczyzny przedmiotowej, to promienie aperturowe, a 

promienie  przechodzące  przez  środek  przysłony  aperturowej  (a  więc  przez  środek  źrenicy 
wejściowej i wyjściowej), to promienie polowe. 

Wszystkie  obrazy  dawane  przez  pojedyncze  soczewki,  albo  ich  układy  są  obarczone 

błędami  odwzorowania.  Inaczej  mówiąc  są  to  niedokładności  odwzorowania  przestrzeni 
przedmiotowej w przestrzeni obrazowej i nazywamy je aberracjami. 

Aberracje mogą być regularne i nieregularne. 

Regularne  –  dające  się  przewidzieć.  Znane  są  przyczyny  ich  powstawania.  MoŜna 

wpływać na ich wartości poprzez odpowiednią konstrukcję układów optycznych. 
Dzielimy  je  na:  aberracje  geometryczne,  tj.  aberrację  sferyczną,  komę,  astygmatyzm, 
krzywiznę  pola  i dystorsję,  oraz  aberracje  chromatyczne  –  chromatyzm  połoŜenia 
i chromatyzm wielkości. 

Nieregularne  –  Wynikają  z  wad  materiałowych  oraz  błędów  konstrukcyjnych 

i wykonawczych. Są nieprzewidywalne. 

Ogólnie moŜemy powiedzieć, Ŝe aberracje są tym większe, im większe są apertury i pola 

rozpatrywanych układów optycznych. 

Projektowanie  układów  optycznych  polega  na  wyznaczaniu  biegu  promieni  świetlnych 

przez  kolejne  powierzchnie  tak,  aby  poprzez  zminimalizowanie  aberracji  zapewnić 
wymaganą jakość odwzorowania. Osiągamy to drogą odpowiednich obliczeń.  

Istotą  obliczeń  jest  to,  Ŝe  w  oparciu  o  prawa  rozchodzenia  się  światła,  wyznaczamy 

geometryczne kształty powierzchni optycznych i odległości między nimi. 

WaŜną  rzeczą  jest  dokładność  z  jaką  określamy  wartość  kątów  i  ich  funkcji 

trygonometrycznych oraz wielkość dróg optycznych między powierzchniami. 

Wartość  sinusa  kąta  moŜemy  przedstawić  w  postaci  szeregu  potęgowego  zwanego 

szeregiem Mac Laurina: 

L

+

−

+

−

=

!

7

!

5

!

3

sin

7

5

3

α

α

α

α

α

 

Widzimy  tutaj,  Ŝe  gdy  mamy  do  czynienia  z  bardzo  małymi  kątami  (promienie  biegną 

przyosiowo i padają prawie prostopadle na powierzchnie załamujące), moŜemy przyjąć, iŜ  
sin  α  =  α,  czyli  pierwszemu  wyrazowi  szeregu.  Mówimy  wtedy,  Ŝe  mamy  do  czynienia 
z optyką pierwszego rzędu lub z optyką Gaussa. (Wzory Gaussa dla pojedynczej powierzchni, 
dla  soczewki  cienkiej,  czy  teŜ  wzór  szlifierzy  soczewek.)  Gdy  sinusy  są  równe  dwu 
pierwszym wyrazom szeregu mówimy o optyce trzeciego rzędu. 

Pierwszy  teorię  aberracji  opracował  niemiecki  matematyk  Ludwig  von  Seidel  

(1821 – 1896), który wprowadził do obliczeń optycznych tzw. „sumy Seidla”. 
Aberracja sferyczna 

Zjawisko polegające na tym, Ŝe promienie świetlne wychodzące z punktu leŜącego na osi 

optycznej powierzchni sferycznej, w przestrzeni obrazowej nie trafiają w jeden punkt osi, lecz 
w róŜne jej punkty. Im większa jest średnica danej powierzchni sferycznej (skrajne promienie 
wiązki mogą padać na powierzchnię dalej od osi), tym zjawisko jest silniejsze. 

 

Rys. 59.   Aberracja sferyczna. Promienie przyosiowe tworzą ognisko dalej od powierzchni niŜ promienie 

skrajne – mówimy wtedy o podłuŜnej aberracji sferycznej dodatniej. Gdy promienie przyosiowe tworzą ognisko 

bliŜej powierzchni niŜ promienie skrajne – aberracja jest ujemna, a soczewka przekorygowana  

[opracowanie własne] 

 

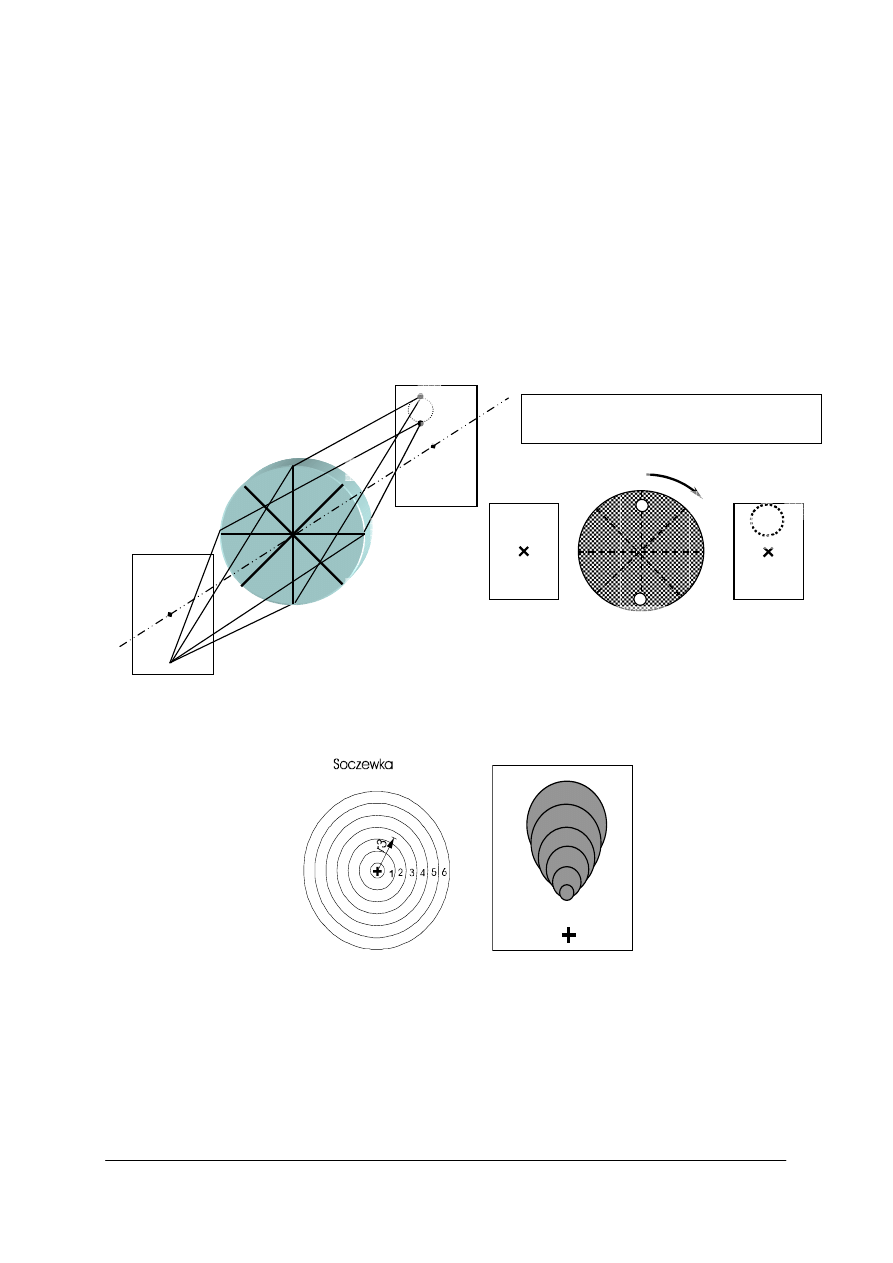
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 40

Aberracji  sferycznej  nie  moŜna  całkowicie  wyeliminować.  W  soczewce  jest  minimalna 

wtedy,  gdy  załamanie  jest  równomiernie  rozłoŜone  między  dwie  powierzchnie.  MoŜna  ją 
minimalizować  poprzez  stosowanie  szkieł  o  wyŜszych  współczynnikach  załamania, 
wprowadzaniu powierzchni asferycznych lub kombinacji soczewek dodatnich i ujemnych. 

 

Aberracja koma 

Polega na tym, Ŝe obraz leŜącego poza osią punktu nie jest punktem, a tworem podobnym 

do ogona komety. 

Przy aberracji sferycznej kolejne strefy soczewki dają ogniska w kolejnych punktach na 

osi optycznej (dla promieni do niej równoległych). 

Obrazy  punktów  leŜących  poza  osią,  pomimo  skorygowania  aberracji  sferycznej,  nie 

będą wyraźne, dopóki nie skorygujemy komy. 
 

 

Rys.  60. Szkic ilustrujący powstawanie aberracji koma. Jeśli dla danej strefy wydzielimy za pomocą przysłony 

dwie leŜące naprzeciw siebie wąskie wiązki światła, to dla wszystkich połoŜeń przysłony światło nie będzie 

ogniskowane w punkcie, lecz na kole zwanym krąŜkiem komatycznym [opracowanie własne] 

 

Rys. 61. 

Jeśli w soczewce wydzielimy kolejne, coraz dalej od osi połoŜone strefy, to kaŜda z nich da obraz punktu 

przedmiotowego w postaci krąŜka komatycznego, leŜącego coraz dalej od osi [

opracowanie własne

] 

 

Promień krąŜka komatycznego jest proporcjonalny do kwadratu promienia odpowiedniej 

strefy (r), tak samo, jak odległość środka krąŜka od osi. Połączenie wszystkich krąŜków daje 
figurę  w  kształcie  ogona  komety.  MoŜe  on  być  skierowany  do  lub  od  osi  optycznej, 
w zaleŜności od typu soczewki. 

Zasadniczą róŜnicą w stosunku do aberracji sferycznej jest to, Ŝe koma nie występuje na 

osi optycznej – jest funkcją kąta nachylenia wiązki. 

Układy wolne od komy i aberracji sferycznej nazywamy aplanatycznymi. 

1 

2 

3 

4 

1 

3 

P 

P

’ 

π 

π’ 

P 

2 

3 

4 

1 

P’ 

1 

2 

3 

4 

Przysłona z dwoma otworkami 
wstawiona przed soczewkę i obracana. 

Punkty obrazowe na krąŜku komatycznym zmieniają połoŜenie o 
kąt 2

x

 większy niŜ punkty przysłony i mają przeciwny kierunek 

obrotu. 

 

1 

2 

3 

6 

5 

4 

 

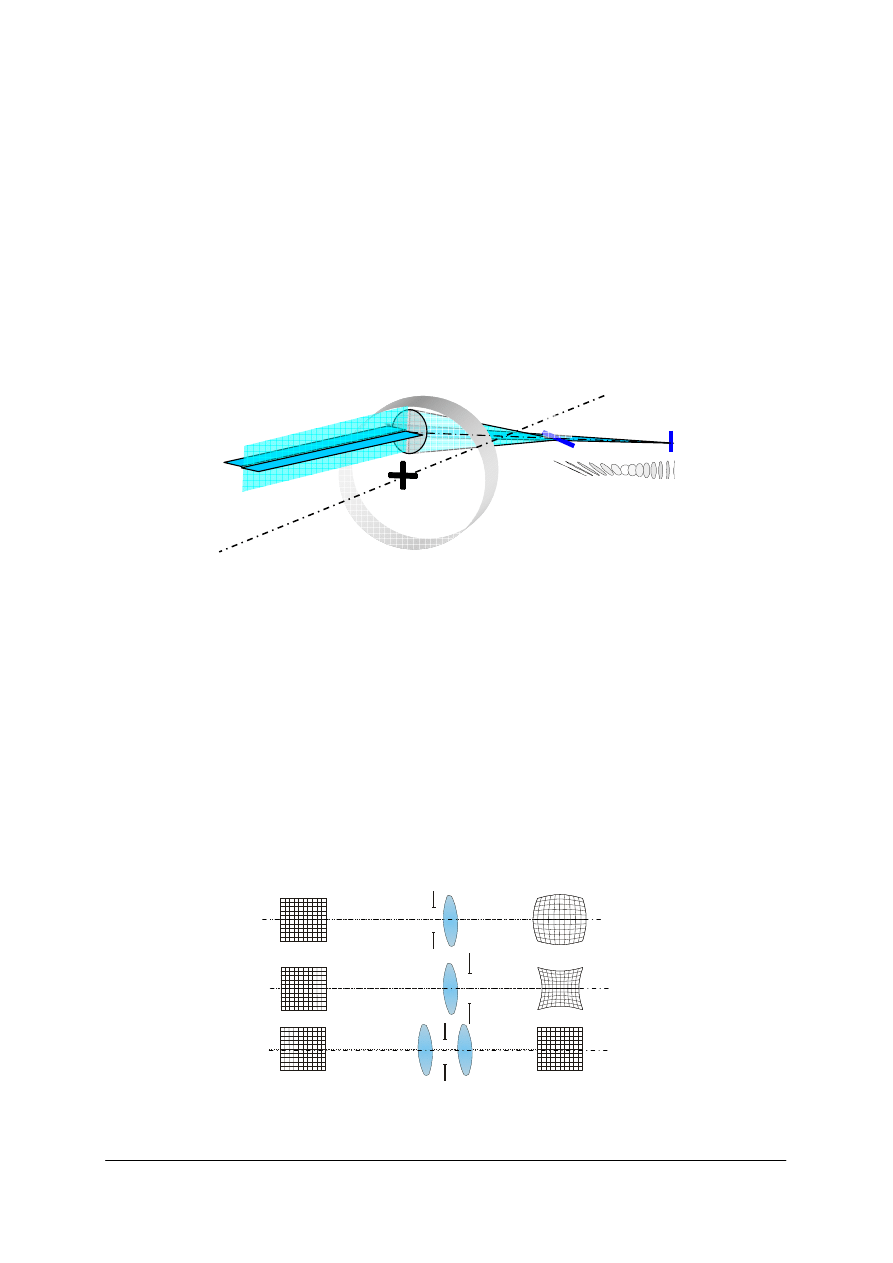
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 41

F’

T 

F’

R 

Astygmatyzm 

Jest to wada polegająca na tym, Ŝe punkt leŜący poza osią układu jest odwzorowany jako 

przestrzenna  bryła  będąca  płynnym  przejściem  od  jednego  do  drugiego,  prostopadłego 
odcinka.  Odcinki  te  są  osiami  głównymi  kolejnych  elips.  W  jednym  z  połoŜeń  osie  są sobie 
równe i tam znajduje się obraz kołowy zwany krąŜkiem najmniejszego rozproszenia. 

Wiązka  światła  o  przekroju  kołowym,  padająca  na  powierzchnię  sferyczną  poza  osią 

optyczną, utworzy linię przenikania podobną do wygiętej w swojej płaszczyźnie elipsy, której

 

oś wielka będzie skierowana w stronę punktu wierzchołkowego sfery, a  mała będzie do niej 
prostopadła. 

Promienie  równoległe  padające  w  płaszczyźnie  osi  wielkiej  utworzą  tzw.  ognisko 

południkowe  (F’

T

),  a  promienie  padające  w  płaszczyźnie  osi  małej  utworzą  ognisko 

równoleŜnikowe (F’

R

). To rozdzielenie ognisk, to właśnie astygmatyzm. 

 

 

Rys. 62. Astygmatyzm Odległość między F’

’T

 a F’

R

 nazywa się interwałem astygmatycznym. (Interwałem 

Sturma). „Najlepszy” obraz jest w płaszczyźnie krąŜka najmniejszego rozproszenia  [opracowanie własne] 

 

Krzywizna pola 

Ten  błąd  odwzorowania  polega  na  tym,  Ŝe  obraz  dokładnie  płaskiego  przedmiotu 

leŜącego  w  prostopadłej  do  osi  optycznej  płaszczyźnie,  nie  jest  odwzorowany  jako  płaski. 
Wada  ta  jest  ściśle  związana  z  astygmatyzmem  i  róŜni  się  od  niego  tym,  Ŝe  nie  zaleŜy  od 
odległości przedmiotowej. 

Zarówno  astygmatyzm,  jak  krzywizna  pola  są  proporcjonalne  do  tangensa  nachylenia 

wiązki i odwrotnie proporcjonalne do kwadratu ogniskowej. 
Dystorsja 

Dystorsja,  tak  jak  koma  jest  aberracją  wtórną,  czyli  skutkiem  innych  aberracji.  Błąd 

odwzorowania  spowodowany  dystorsją  polega  na  tym,  Ŝe  powiększenie  liniowe  obrazu 
zmienia się w miarę oddalania punktów przedmiotowych od osi optycznej. 

Dystorsja  nie  wpływa  na  ostrość  obrazu  i  jest  prawie  nie  widoczna  przy  dostatecznie 

cienkich  soczewkach.  Pojawia  się  w  sytuacjach,  gdy  stosujemy  przysłony  mające  na  celu 
zmniejszenie aberracji sferycznej. 

Rys.  63.  Dystorsja i jej zaleŜność od budowy układu. W zaleŜności od połoŜenia przysłony zmienia się obraz 

kwadratowej siatki na beczkowaty, albo poduszkowaty. MoŜna ją likwidować stosując układy symetryczne 

[opracowanie własne] 

 

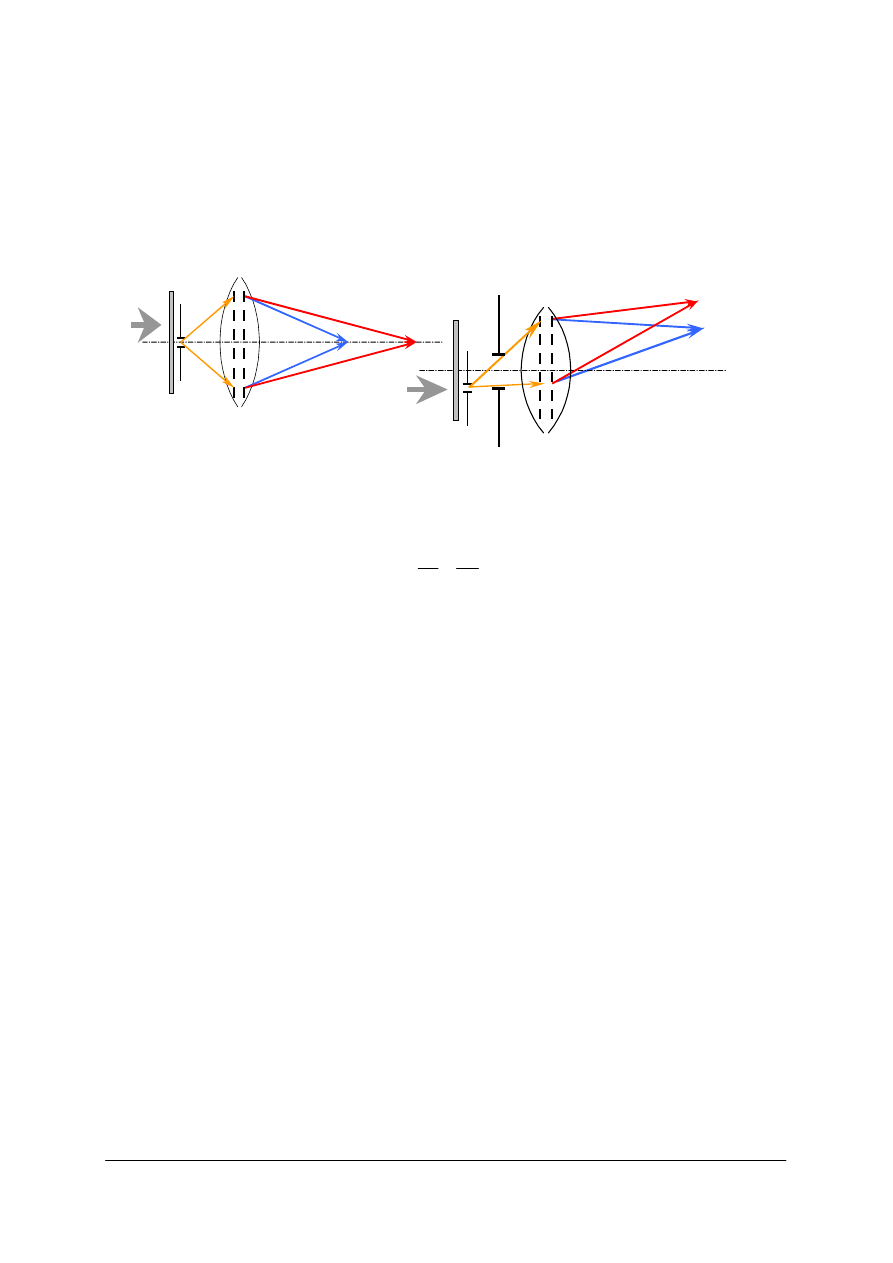
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 42

Aberracja chromatyczna 

Istotą  tej  aberracji  jest  to,  Ŝe  dla  kaŜdej  barwy  światła  soczewka  ma  inną  moc  (inną 

ogniskową)  i  w  związku  z  tym,  dla  kaŜdej  barwy  jest  inna  płaszczyzna  obrazowa  i  inne 
powiększenie dawane przez soczewkę lub układ. Mówi się wtedy o  aberracji chromatycznej 
połoŜenia  (dla  promieni  osiowych),  albo  o  aberracji  chromatycznej  powiększenia  (dla 
promieni wychodzących z punktów leŜących poza osią optyczną). 
 

Rys. 64. Aberracja chromatyczna połoŜenia (z lewej) i aberracja powiększenia (z prawej)[opracowanie własne] 

 

Aberrację  chromatyczną  usuwamy  konstruując  układy  achromatyczne  składające  się  

z  dwu  soczewek,  dodatniej  i  ujemnej  o  odpowiednio  dobranych  mocach  i  współczynnikach 
dyspersji. Układ powinien spełniać warunek wyraŜony równaniem: 

0

2

2

1

1

=

+

ν

ν

D

D

 

w  którym  D1  i  D2  to  moce  soczewek  składowych,  a  ν

1

  i  ν

2

  to  współczynniki  dyspersji 

materiałów, z których wykonano te soczewki. 

Zwierciadła  nie  wykazują  aberracji  chromatycznej,  bo  dla  wszystkich  barw  kąt  padania 

jest równy kątowi odbicia. 

Gdy wiązka przechodzi dwukrotnie, w przeciwnych kierunkach, przez te same powierzchnie, 

to  aberracje  poprzeczne  (koma,  dystorsja,  chromatyzm  wielkości)  częściową  się  znoszą,  
a aberracje podłuŜne (sferyczna, astygmatyzm, chromatyzm połoŜenia) – wzmacniają. 

 

4.2.2. Pytania sprawdzające 

Odpowiadając na pytania, sprawdzisz, czy jesteś przygotowany do wykonania ćwiczeń. 

1.

 

Czym róŜni się kąt graniczny załamania od kąta granicznego całkowitego wewnętrznego 
odbicia? 

2.

 

Od czego zaleŜy wielkość kąta całkowitego wewnętrznego odbicia? 

3.

 

Jakie elementy optyczne wykorzystują zjawisko całkowitego wewnętrznego odbicia? 

4.

 

Kiedy występuje zjawisko przesunięcia równoległego? 

5.

 

Od czego zaleŜy kąt minimalnego odchylenia pryzmatu? 

6.

 

Co to jest dioptria pryzmatyczna? 

7.

 

Co to jest dyspersja światła? 

8.

 

Jakimi parametrami moŜemy określać wielkość dyspersji? 

9.

 

Czym charakteryzuje się dyspersja anomalna? 

10.

 

Na czym polega spektroskopia? 

11.

 

Co to są spektrometry pryzmatyczne i do czego słuŜą.

 

12.

 

Czym charakteryzuje się pryzmat achromatyczny? 

13.

 

Jak  nazywają  się  wszystkie  wielkości  i  parametry  określające  właściwości  elementów 
i układów optycznych? 

14.

 

Co to jest skolimowanie wiązki? 

P’ 

niebieskie

 

P

’ 

czerwone

 

Filtry 

Światło białe

 

Światło białe 

P’ 

niebieskie

 

P’ 

czerwone

 

P 

P 

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 43

15.

 

Co to jest moc optyczna? 

16.

 

Co  to  jest  przestrzeń  przyosiowa  i  soczewka  cienka  oraz  co  się  wiąŜe  ze  stosowaniem 
tych terminów? 

17.

 

Czym róŜni się wzór Gaussa od wzoru Newtona? 

18.

 

Czym róŜni się układ soczewek cienkich od układu soczewek rzeczywistych (grubych)? 

19.

 

Jakie mamy rodzaje powiększeń? 

20.

 

Jaki jest związek przeogniskowania z głębią ostrości? 

21.

 

Co to jest soczewka cylindryczna? 

22.

 

Jak  moŜna  wykreślnie  wyznaczyć  przebieg  promieni  przez  układ  powierzchni 
załamujących i soczewek? 

23.

 

Co to są punkty kardynalne? 

24.

 

Czym róŜni się przysłona aperturowa od polowej? 

25.

 

Jaki jest związek między przysłoną aperturową a liczbą otworową? 

26.

 

Jak nazywamy obrazy przysłony aperturowej? 

27.

 

Jak nazywamy obrazy przysłony polowej? 

28.

 

Jakie są aberracje układów optycznych? 

 

4.2.3. Ćwiczenia 

 
Ćwiczenie 1 

Oblicz,  jaka  gruba  powinna  być  płytka  płasko-równoległa,  wykonana  ze  szkła 

o współczynniku  załamania  n  =  1,52,  aby  przy  skręcaniu  jej  o  ±22°30’,  promień 
przechodzący  miał  przesunięcia  boczne  ±10  mm.  Następnie  oblicz  to  dla  szkła 
o współczynniku załamania n = 1,74. 

 
Sposób wykonania ćwiczenia 
 

 Aby wykonać ćwiczenie powinieneś: 

1)

 

sporządzić szkic z oznaczeniem danych i szukanych, 

2)

 

zapisać wartości liczbowe danych wyjściowych zwracając uwagę na jednostki, 

3)

 

ułoŜyć wzór na obliczenie szukanej wielkości, 

4)

 

podstawić dane i przeprowadzić obliczenia, 

5)

 

napisać odpowiedź z uzyskanym wynikiem. 

 

WyposaŜenie stanowiska pracy: 

−

 

papier formatu A4, 

−

 

linijka z podziałką, trójkąt kreślarski,  ołówek,  

−

 

literatura zgodna z punktem 6 poradnika. 

 

Ćwiczenie 2 

Pryzmat  o  kącie  łamiącym  60°  daje  kąt  minimalnego  odchylenia  δ  =  45°.  Jaki  jest 

współczynnik załamania szkła, z którego wykonano pryzmat. 

 
Sposób wykonania ćwiczenia 
 

 Aby wykonać ćwiczenie powinieneś: 

1)

 

sporządzić szkic z oznaczeniem danych i szukanych, 

2)

 

zapisać wartości liczbowe danych wyjściowych zwracając uwagę na jednostki, 

3)

 

ułoŜyć wzór na obliczenie szukanej wielkości, 

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 44

4)

 

podstawić dane i przeprowadzić obliczenia 

5)

 

napisać odpowiedź z uzyskanym wynikiem. 

 

WyposaŜenie stanowiska pracy: 

−

 

papier formatu A4, 

−

 

linijka z podziałką, trójkąt kreślarski, ołówek,  

−

 

literatura zgodna z punktem 6 poradnika. 

 

Ćwiczenie 3 

Jaki  minimalny  współczynnik  załamania  powinno  mieć  szkło  pryzmatu  prostokątnego, 

aby  promień  padający  prostopadle  na  przyprostokątną  powierzchnię  uległ  następnie 
całkowitemu wewnętrznemu odbiciu? 

 

 Sposób wykonania ćwiczenia 
 

Aby wykonać ćwiczenie powinieneś: 

1)

 

sporządzić szkic z oznaczeniem danych i szukanych, 

2)

 

zapisać wartości liczbowe danych wyjściowych zwracając uwagę na jednostki, 

3)

 

ułoŜyć wzór na obliczenie szukanej wielkości, 

4)

 

podstawić dane i przeprowadzić obliczenia, 

5)

 

napisać odpowiedź z uzyskanym wynikiem. 

 

WyposaŜenie stanowiska pracy: 

−

 

papier formatu A4, 

−

 

linijka z podziałką, trójkąt kreślarski,  ołówek,  

−

 

literatura zgodna z punktem 6 poradnika. 

 
Ćwiczenie 4 

Menisk  dodatni  ma  promienie  krzywizn  R

1 

=  300  mm  i  R

2 

=  600  mm,  a  współczynnik 

załamania szkła wynosi n

D

 = 1,64 

Jaka jest moc optyczna menisku, gdy rozpatrujemy go jako: 

−

 

soczewkę cienką? 

−

 

soczewkę rzeczywistą o grubości d = 3,28 mm? 

 
 Sposób wykonania ćwiczenia 

 

 Aby wykonać ćwiczenie powinieneś: 

1)

 

sporządzić szkic z oznaczeniem danych i szukanych, 

2)

 

zapisać wartości liczbowe danych wyjściowych zwracając uwagę na jednostki, 

3)

 

ułoŜyć wzór na obliczenie szukanej wielkości, 

4)

 

podstawić dane i przeprowadzić obliczenia, 

5)

 

napisać odpowiedź z uzyskanym wynikiem. 

 

WyposaŜenie stanowiska pracy: 

−

 

papier formatu A4, 

−

 

linijka z podziałką, trójkąt kreślarski,  ołówek,  

−

 

literatura zgodna z punktem 6 poradnika. 

 
 
 

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 45

Ćwiczenie 5 

Przedmiot  umieszczony  jest  1,5  ogniskowej  przed  soczewką  o  mocy  4  dptr.  Znajdź 

wykreślnie połoŜenie obrazu oraz odległość obrazową za pomocą równania soczewki cienkiej 

−

 

w postaci podanej przez Gaussa, 

−

 

postaci podanej przez Newtona, 

 

i porównaj z wynikiem otrzymanym metodą wykreślną (ze szkicem). 

 

Sposób wykonania ćwiczenia 

 

Aby wykonać ćwiczenie powinieneś: 

1)

 

sporządzić szkic z oznaczeniem danych i szukanych, 

2)

 

zapisać wartości liczbowe danych wyjściowych zwracając uwagę na jednostki, 

3)

 

ułoŜyć wzór na obliczenie szukanej wielkości, 

4)

 

podstawić dane i przeprowadzić obliczenia, 

5)

 

napisać odpowiedź z uzyskanym wynikiem, 

6)

 

porównać wynik obliczeń z wynikiem otrzymanym wykreślnie i podać wnioski. 

 

WyposaŜenie stanowiska pracy: 

−

 

papier formatu A4, 

−

 

linijka z podziałką, trójkąt kreślarski, ołówek,  

−

 

literatura zgodna z punktem 6 poradnika. 

 
Ćwiczenie 6 

Przedmiot jest umieszczony w odległości 4 m od ekranu. Jaka jest ogniskowa soczewki, 

jeśli na ekranie tworzy obraz rzeczywisty, odwrócony i powiększony liniowo 50

x

? 

 
Sposób wykonania ćwiczenia 
 
Aby wykonać ćwiczenie powinieneś: 

1)

 

sporządzić szkic z oznaczeniem danych i szukanych, 

2)

 

zapisać wartości liczbowe danych wyjściowych zwracając uwagę na jednostki, 

3)

 

ułoŜyć wzór na obliczenie szukanej wielkości, 

4)

 

podstawić dane i przeprowadzić obliczenia, 

5)

 

napisać odpowiedź z uzyskanym wynikiem. 

 

WyposaŜenie stanowiska pracy: 

−

 

papier formatu A4, 

−

 

linijka z podziałką, trójkąt kreślarski,  ołówek,  

−

 

literatura zgodna z punktem 6 poradnika. 

 
Ćwiczenie 7 

Ogniskowa  obiektywu  lunetki  wynosi  200  mm,  jego  średnica  50  mm,  a  ogniskowa 

okularu 2 cm. 

−

 

Jaka jest średnica źrenicy wyjściowej? 

−

 

Jaka jest liczba otworowa obiektywu? 

−

 

Jaki  jest  kąt  pola  widzenia,  jeśli  w  płaszczyźnie  obrazowej  obiektywu  umieścimy 
diafragmę pola o średnicy 15mm ? 

 
 
 

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 46

Sposób wykonania ćwiczenia 
 

 Aby wykonać ćwiczenie powinieneś: 

1)

 

sporządzić szkic z oznaczeniem danych i szukanych, 

2)

 

zapisać wartości liczbowe danych wyjściowych zwracając uwagę na jednostki, 

3)

 

ułoŜyć wzór na obliczenie szukanej wielkości, 

4)

 

podstawić dane i przeprowadzić obliczenia, 

5)

 

napisać odpowiedź z uzyskanym wynikiem. 

 

WyposaŜenie stanowiska pracy: 

−

 

papier formatu A4, 

−

 

linijka z podziałką, trójkąt kreślarski, ołówek,  

−

 

tablice trygonometryczne, albo kalkulator z funkcjami trygonometrycznymi, 

−

 

literatura zgodna z punktem 6 poradnika. 

 

Ćwiczenie 8 

Dodatnia  soczewka  ma  ogniskową  f’

1

  =  200  mm,  za  nią  w  odległości  150  mm 

umieszczono  soczewkę  ujemna  o  ogniskowej  f’

2

  =  –100  mm,  a  za  nią  w  odległości  50  mm 

umieszczono  soczewkę  dodatnią  o  mocy  20  dptr.  Wyznacz  wykreślnie  połoŜenie  ogniska 
układu przy załoŜeniu, Ŝe są to soczewki cienkie. 

 
Sposób wykonania ćwiczenia 

Aby wykonać ćwiczenie powinieneś: 

1)

 

wyrysować w skali bieg wybranego promienia, 

2)

 

zmierzyć odległość od ostatniej soczewki do wyznaczonego graficznie ogniska,  

3)

 

podać wartość ogniskowej, 

4)

 

zapisać dane. 

 

 

WyposaŜenie stanowiska pracy: 

−

 

papier formatu A4 (wskazany milimetrowy), 

−

 

linijka z podziałką, trójkąt kreślarski,  ołówek,  

−

 

literatura zgodna z punktem 6 poradnika. 

 

4.2.4.  Sprawdzenie postępów 

 
Czy potrafisz: 

Tak 

Nie 

1)

 

wyjaśnić za pomocą szkicu powstanie obrazu w zwierciadle płaskim? 

 

 

2)

 

podać  definicję  zwierciadła  kulistego  i  terminów  optycznych  z  nim 
związanych? 

 

 

3)

 

wyjaśnić  za  pomocą  szkicu  jak  powstają  obrazy  w  zwierciadłach 
kulistych? 

 

 

4)

 

zdefiniować pojęcie obrazu pozornego i rzeczywistego? 

 

 

5)

 

podać  i  zastosować  w  praktycznych  obliczeniach  równanie 
zwierciadła kulistego? 

 

 

6)

 

zdefiniować  zjawiska  odbicia  i  załamania  światła  na  granicy 
ośrodków? 

 

 

7)

 

opisać zjawisko odbicia światła w zaleŜności od rodzaju powierzchni 
odbijającej? 

 

 

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 47

8)

 

sformułować i objaśnić prawa odbicia światła? 

 

 

9)

 

podać wzór i wyjaśnić na szkicu prawa załamania światła na granicy 
dwu ośrodków? 

 

 

10)

 

podać  definicje  względnego  i  bezwzględnego  współczynnika 
załamania? 

 

 

11)

 

wytłumaczyć  zjawiska  zachodzące  przy  przejściu  światła  przez 
płytkę płasko-równoleglą 

 

 

12)

 

wytłumaczyć  zjawiska  granicznego  kata  załamania  i  całkowitego 
wewnętrznego odbicia? 

 

 

13)

 

wytłumaczyć działanie światłowodu i podać przykłady zastosowań? 

 

 

14)

 

opisać  budowę  i  podać  definicje  wielkości  charakteryzujących 
pryzmat? 

 

 

15)

 

podać definicję klina optycznego i wzór na jego kąt łamiący? 

 

 

16)

 

podać definicję dioptrii pryzmatycznej? 

 

 

17)

 

opisać  budowę  pryzmatu  całkowicie  odbijającego  i  podać  przykłady 
zastosowań? 

 

 

18)

 

podać definicje drogi optycznej i odległości zredukowanej?  

 

 

19)

 

zinterpretować zjawisko dyspersji? 

 

 

20)

 

objaśnić równanie pryzmatu dla kąta minimalnego odchylenia?  

 

 

21)

 

zdefiniować jednostkę zdolności załamującej pryzmatu?  

 

 

22)

 

wyjaśnić co to są spektrometry pryzmatyczne i do czego słuŜą? 

 

 

23)

 

podać  wzory  i  reguły  znaków  obowiązujące  przy  obliczaniu 
wielkości  dotyczących  pojedynczej  powierzchni  sferycznej,  oraz 
soczewek i ich układów? 

 

 

24)

 

zaprojektować soczewkę o określonej mocy 

 

 

25)

 

wyznaczyć  połoŜenie  obrazu  dawanego  przez  soczewkę  metodą 
obliczeniową? 

 

 

26)

 

wyznaczyć  połoŜenie  obrazu  dawanego  przez  soczewkę  metodą 
wykreślną? 

 

 

27)

 

podać definicję przysłony aperturowej i polowej? 

 

 

28)

 

obliczyć powiększenie dawane przez soczewkę? 

 

 

29)

 

określić  parametry  obiektywu,  okularu  lunety  w  zaleŜności  od 
załoŜonego powiększenia, pola widzenia i liczby otworowej? 

 

 

30)

 

zdefiniować pojęcie aberracji i podać przyczyny ich powstawania? 

 

 

 
 
 
 

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 48

4.3.

 

Wykorzystanie falowej natury światła (interferencji, 
dyfrakcji, polaryzacji i holografii) 

 

4.3.1. Materiał nauczania 

Nie  wszystkie  zjawiska  świetlne  dają  się  wytłumaczyć  prawami  optyki  geometrycznej. 

Odpowiedzi na wiele pytań uzyskano dopiero po odkryciu falowej natury światła. 
 

Okazało  się,  Ŝe  fale  świetlne  są  falami  elektromagnetycznymi  i  podlegają  tym  samym 

zasadom, co inne zjawiska okresowe. Odnoszą się do nich więc te same definicje i pojęcia. 
 

Fala świetlna to rozchodzenie się okresowego zaburzenia pola elektromagnetycznego. 

Definicje 

Amplituda  A  –  odchylenie  zaburzenia  od  połoŜenia  średniego,  moŜe  się  zmieniać 

pomiędzy  wartościami  maksymalnymi  +A  i  –A  przyjmując  kaŜdą  z  wartości  pośrednich 
między nimi. Często jest definiowana jako wychylenie maksymalne. 

NatęŜenie  fali  –  ilość  energii  przepływająca  w  ciągu  sekundy  przez  jednostkową 

powierzchnię prostopadłą do kierunku przepływu. Jest proporcjonalna do kwadratu amplitudy 
(A) i do kwadratu częstotliwości (

ν

). 

Długość  fali 

λ

  –  odległość  odpowiadająca  pełnemu  cyklowi  po  którym  kształt  fali 

powtarza się. Długość fali jest wyraŜona w jednostkach długości, obowiązuje układ SI.  

Okres  T  (miara  czasu)  –    czas  potrzebny  do  tego,  aby  określony  punkt  konfiguracji 

falowej osiągnął kolejną pozycję równowaŜną. 

W ruchu po okręgu okresem jest czas w ciągu którego punkt wykonuje pełny obieg. 

Okres  T  upływa  zawsze  wtedy  gdy  iloczyn  prędkości  kątowej 

ω

  i  czasu  t  wzrośnie  od 

0 do 2

π

. 

ω

T = 2

π

 

T=2

π

/

ω

 

Częstotliwość 

ν

  jest  zdefiniowana  jako  liczba  cykli  (lub  oscylacji)  na  sekundę.  JeŜeli 

oscylujący element (np. wahadło) wykona jedną pełną oscylację (tam i z powrotem) w ciągu 
jednej  sekundy,  to  T  (okres)  =  1  sek.,  a  częstotliwość 

ν

  =  1  oscylacja/1  sek.  Jeśli  mamy  10 

oscylacji w ciągu 1 sek., to T = 1/10 sek., a 

ν

 = 10sek/1, a zatem: 

ν

 = 1/T 

Dla  ruchu  falowego  częstotliwość  jest  stosunkiem  prędkości  w  danym  ośrodku  do 

długości fali w tym ośrodku: 

ν

 =

υ

/

λ

 

Jednostką częstotliwości jest 1Hz (herc) 

Prędkość z jaką rozchodzi się fala jest równa stosunkowi drogi przebytej do czasu, jaki był na 
to potrzebny: 

υ

 = s/t 

PoniewaŜ częstotliwość jest liczbą oscylacji na sekundę, fala będzie przebywać w ciągu 

1sek odległość 

λν

, 

 a w czasie t odległość s, więc: 

s = 

λν

t 

stąd 

υ

 =

λν

 

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 49

Fale  świetlne  (widzialne)  stanowią  jedynie  wąski  wycinek  promieniowania 

elektromagnetycznego. 
 

 

Rys. 65.  Widmo fal elektromagnetycznych [7 – załącznik] 

 

Konsekwencją  falowej  natury  światła  jest  między  innymi  to,  Ŝe  w  sprzyjających 

warunkach  mogą  na  siebie  oddziaływać.  Zachodzi  wtedy  zjawisko  interferencji  czyli 
nakładania się fal.  
Zjawisko to dało początek rozwojowi duŜej gałęzi optyki zwanej interferometrią. 

Podstawą  interferometrii  jest  pomiar  róŜnicy  dróg  optycznych.  RóŜnica  ta  powstaje 

w sytuacji,  gdy  część  wiązki  światła  ma  z  jakiegoś  powodu  inna  drogę  optyczną.  Takim 
powodem  moŜe  być  albo  zmiana  drogi  geometrycznej  (mniejszy  lub  większy  jej  odcinek), 
albo zmiana współczynnika załamania ośrodka przez który biegnie ta część wiązki 

Pamiętasz,  Ŝe  drogą  optyczną  nazywamy  iloczyn  drogi  geometrycznej  przez 

współczynnik  załamania  ośrodka  (S  =  L  x  n),  a  więc  róŜnicę  dróg  moŜemy  wyrazić  albo 
wzorem 
Γ  =  n(L

2

  –  L

1

),  gdy  róŜnią  się  jedynie  drogi  geometryczne,  albo  wzorem  Γ  =  L(n

2

  –  n

1

), 

w przypadku gdy światło biegnie w ośrodkach róŜniących się współczynnikiem załamania. 

RóŜnicę drogi optycznej najwygodniej jest wyrazić uŜywając długości fali jako jednostki. 

Gdy odległość zmienia się o λ, to faza fali sinusoidalnej zmienia się o 2π. 
Jeśli  fale  zmieniają  się  „nie  w  takt”,  to  wówczas  odległość  między  odpowiadającymi  sobie 
punktami jest róŜnicą faz Φ

2

 – Φ

1

 = δ. JeŜeli δ = π,  to fale mają przeciwne fazy. 

π

δλ

2

=

Γ

 

MoŜna więc powiedzieć, Ŝe interferometria to dziedzina obejmująca działania, w których 

są tworzone warunki do zaistnienia zjawiska interferencji. 

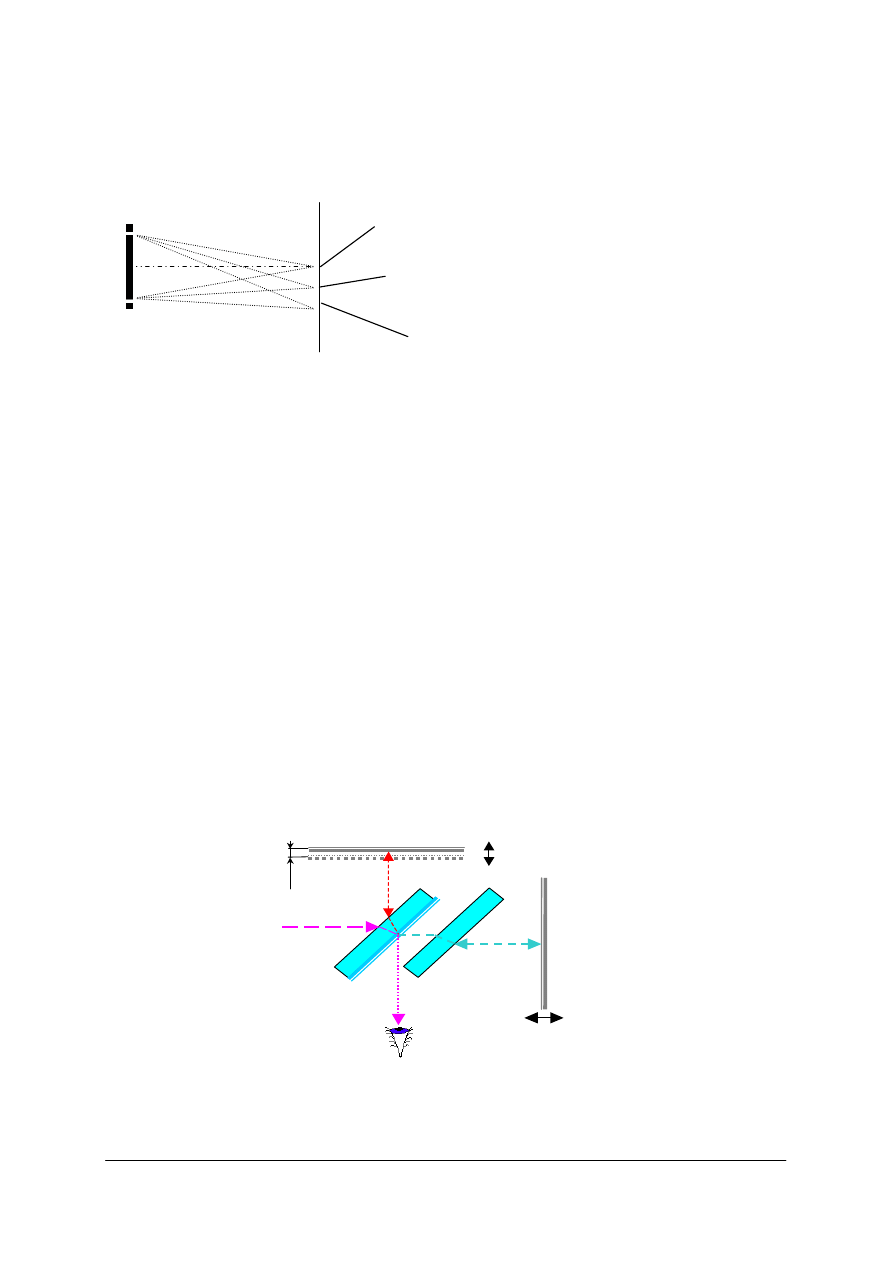
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 50

Takie warunki zostały stworzone w doświadczeniu Thomasa Younga (1773–1829). 
Przepuszczamy  światło  przez  dwie  równoległe  szczeliny  (pierwotnie  były  to  dwa  otworki 
wykonane  szpilką).  Na  ekranie  umieszczonym  za  szczelinami  utworzą  się  ciemne  i  jasne 
prąŜki zwane minimami i maksymami interferencyjnymi. 

Rys. 66. Schemat powstawania kolejnych maksimów interferencyjnych w doświadczeniu Thomasa Younga, 

dzięki któremu moŜemy zaobserwować zjawisko interferencji fal świetlnych. Rysunek przedstawia powstawanie 

kolejnych maksimów tylko w jedną stronę. W rzeczywistości powstają one symetrycznie w obydwie strony od 

maksimum zerowego rzędu.[ opracowanie własne] 

 

RóŜnicę dróg optycznych między kolejnymi maksymami moŜna opisać wzorem  

Γ = mλ   gdzie m = 0, ±1, ±2, ±3 , ....... , ±m 

Ogólne warunki interferencji: 

−

 

Światło powinno być spójne. 

−

 

Wiązki pochodzące z roŜnych źródeł są zazwyczaj niespójne.  (Wyjątkowo – urządzenia 
laserowe). 

−

 

Na ogół termin „prąŜki” odnosi się do interferencji w przestrzeni, ale maksyma i minima 
interferencyjne mogą być równieŜ rejestrowane jako funkcje czasu (heterodynowanie). 

−

 

Obie  interferujące  składowe  powinny  mieć  (w  przybliŜeniu)  jednakowe  amplitudy. 
Zapewnia to maksymalny kontrast (całkowite wygaszanie w minimach). 
W  celu  stworzenia  warunków  do  interferencji  zostały  skonstruowane  przyrządy  zwane 

interferometrami.  Dzielą  się  one  na  dwie  grupy  w  zaleŜności  od  sposobu  podziału  wiązki 
światła.  Podział  ten  moŜe  być  przestrzenny,  w  którym  dzielimy  czoło  fali  (nie  dzielimy 
gęstości energii) – jak w doświadczeniu T. Younga, albo natęŜeniowy (podział amplitudy) –
  na półprzepuszczalnej powierzchni odbijającej. 
Takim  podziałem  wiązki  posłuŜył  się  Albert  Michelson  konstruując  interferometr,  który  do 
dzisiaj uchodzi za wzór wszechstronności i który pomógł mu w badaniach, za które otrzymał 
nagrodę Nobla. 

 

Rys. 67. Schematyczne przedstawienie działania interferometru Michelsona. C – Zwierciadło pierwsze, 

D – zwierciadło drugie, A płytka płasko- równoległa z naniesioną warstwą półprzepuszczalną, 

B – płytka korekcyjna, której pochyleniem moŜna dokładnie regulować długość drogi optycznej w tej gałęzi 

interferometru, C’ – obraz zwierciadła C widziany z kierunku obserwacji [opracowanie własne] 

Maksimum zerowego rzędu Γ = 0 

Maksimum pierwszego rzędu Γ = λ 

Maksimum drugiego rzędu Γ = 2λ 

B  

D  

d  

C ’ 

A  

C 

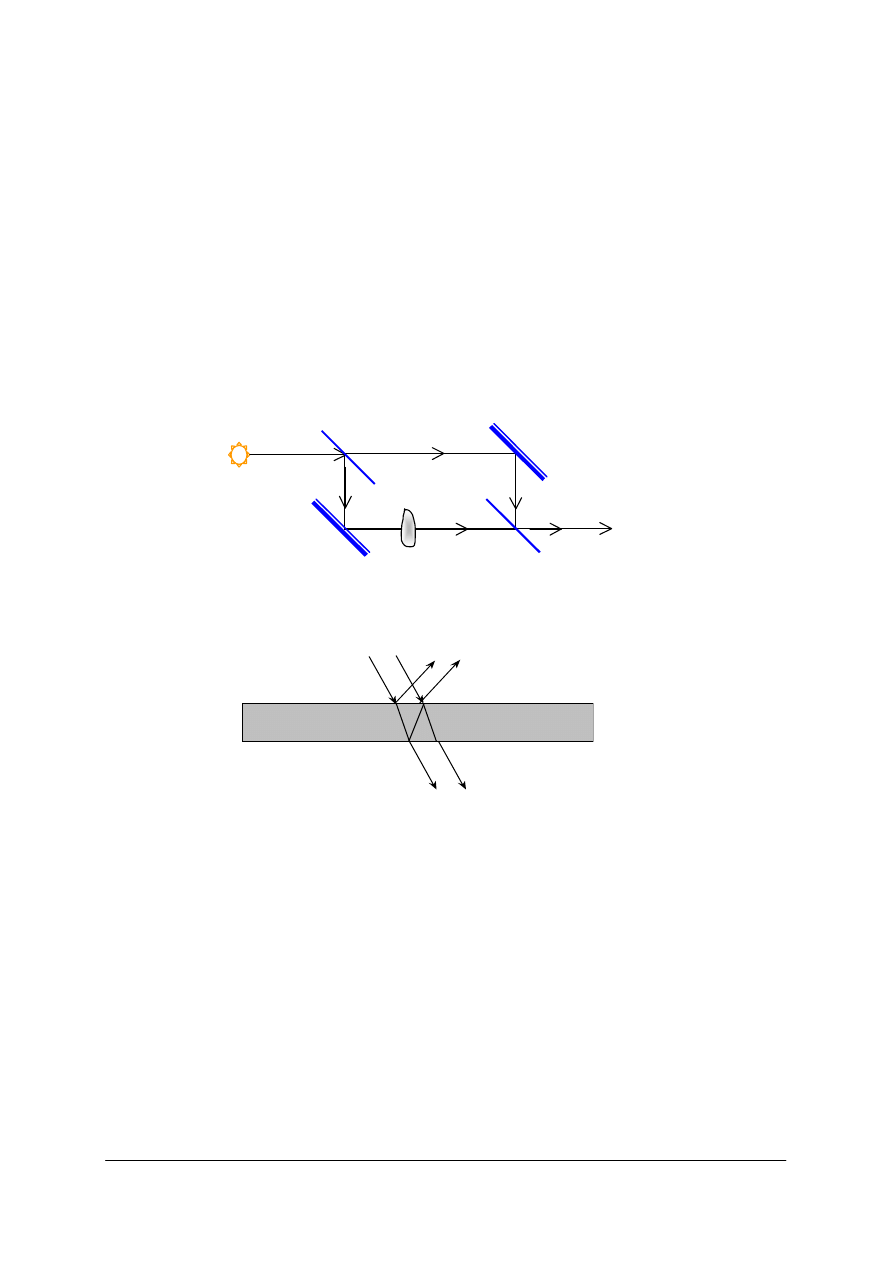
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 51

PoniewaŜ  światło  dwukrotnie  przebiega  odległość  C’D  =  d  i  zmiana  fazy  w  wyniku 

odbicia  wynosi  π  ,więc  warunek  dla  minimów  jest  2d  =  mλ.  Obie  wiązki  docierają  do  A 
w fazie,  ale  faza  wiązki  odbitej  zmienia  się  o  π  –  widać  ciemne  pole.  Jeśli  jedno  ze 
zwierciadeł  przesuniemy  o  ¼  λ,  to  długość  drogi  zmieni  się  o1/2  λ  Jeśli  pierwotnie 
obserwowaliśmy powierzchnię A jako jasną (odbite fale spotykały się w zgodnej fazie), to po 
przemieszczeniu  jednego  ze  zwierciadeł  o  ¼  długości  fali,  obraz  zmieni  się  na  ciemny  (fale 
spotykają się w fazie przeciwnej). 

Tego typu urządzenie pozwala bardzo dokładnie (z dokładnością do ułamka długości fali) 

mierzyć  wszelkie  róŜnice  kształtu  i  połoŜenia  jakie  zaistnieją  między  odbijającymi 
powierzchniami  C  i  D.  Na  tej  zasadzie  powstało  wiele  interferometrów  o  róŜnych 
zastosowaniach. 

Przykładem  innego  sposobu  podziału  i  poprowadzenia  interferujących  wiązek  jest 

interferometr Macha – Zehndera, w którym na drodze wiązki pomiarowej moŜna umieszczać 
elementy  przezroczyste  i  badać  zmiany  ich  współczynników  załamania,  albo  zmiany 
grubości. 

Rys. 68. Schemat interferometru Macha-Zehndera. Konstrukcja pozwala na rozsunięcie wiązek na odległość 

umoŜliwiająca badanie duŜych, przezroczystych elementów [opracowanie własne] 

 

Jeśli  światło  pada  na  cienką  warstwę,  to  między  powierzchniami  zachodzi  zjawisko 

wielokrotnego odbicia. Stwarza to warunki do zaistnienia interferencji w cienkich warstwach.  

Rys. 69. Światło padając na dwie równoległe powierzchnie ulega wielokrotnemu odbiciu i mogą zaistnieć 

warunki do interferencji fal zarówno w świetle przechodzącym jak i odbitym [opracowanie własne] 

 

W zaleŜności od tego, co się zmienia mogą powstawać róŜne rodzaje prąŜków: 

−

 

prąŜki  równej  grubości  –  gdy  światło  rozciągłego  źródła  pada  prawie  prostopadle  na 
nachylone względem siebie płytki, 

−

 

prąŜki równego nachylenia – gdy zmienia się odległość między równoległymi płytkami. 
Obserwator  widzi  koncentryczne  kręgi  rozchodzące  się  lub  zbiegające  się  do  środka. 
ZaleŜy to od tego czy zwiększamy, czy zmniejszamy odległość między płytkami. 

−

 

prąŜki jednakowego rzędu chromatycznego – zmienna długość fali, 
W  przypadku  oświetlenia  światłem  białym  powstają  barwy  interferencyjne.  Jest  to 

konsekwencją wygaszania tych barw, których fale spotykają się w przeciwnych fazach. Efekt 
ten  jest  równieŜ  dostrzegany  w  przypadku  zmiennej  odległości  między  odbijającymi 
powierzchniami. 

 
 
 

 

 

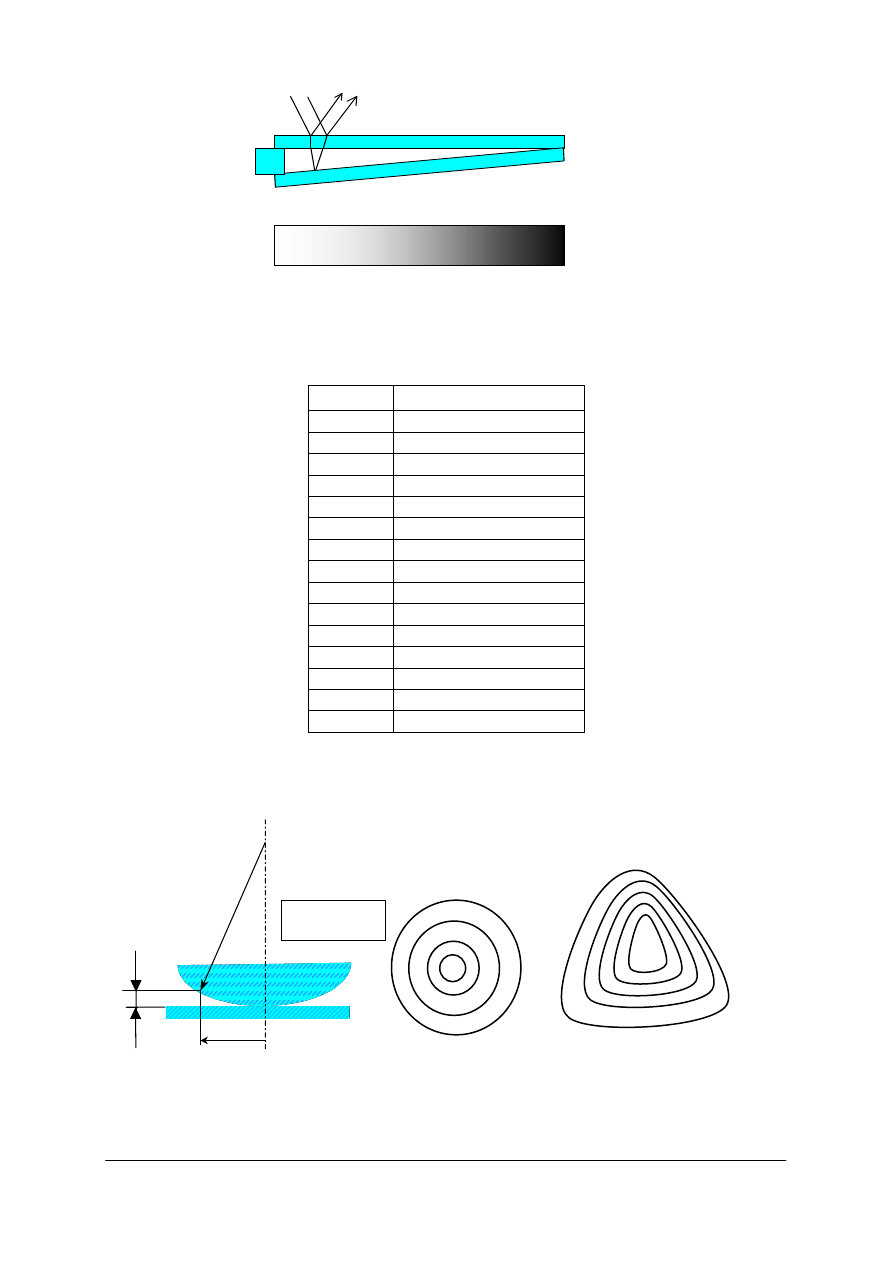
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 52

 

Rys. 70. Klinowe ułoŜenie warstwy powoduje zmianę natęŜenia światła na obserwowanej powierzchni.  

W przypadku oświetlenia światłem białym prąŜki interferencyjne maja róŜne barwy, zaleŜne od grubości 

warstwy [opracowanie własne] 

 

Tablica [5] Barwy interferencyjne powstające przy oświetleniu światłem białym cienkich warstw (n = 1,5): 

d[nm] 

Barwa 

40 

czarna 

55 

szara 

100 

biała 

130 

Ŝółta 

150 

brązowa 

175 

czerwono-purpurowa 

190 

fioletowa 

210 

niebieska 

240 

zielona 

255 

biaława 

260 

Ŝółto-zielona 

280 

Ŝółta 

300 

pomarańczowa 

330 

pomarańczowo-brązowa 

360 

czerwono-fioletowa 

 

Pierścienie  Newtona  powstają  w  pobliŜu  punktu  styku  powierzchni  odbijających.  Są 

wykorzystywane 

do 

pomiarów 

promieni 

krzywizn 

szklanymi 

sprawdzianami 

interferencyjnymi. 

 
 
 
 
 
 
 
 
 
 
 
 

Rys. 71. Z lewej:- Szkic ilustrujący metodę pomiaru krzywizny z wykorzystaniem pierścieni Newtona. Znając  

r i λ moŜna obliczyć R. r – promień m-tego pierścienia (minimum), d – odległość między powierzchniami przy 

 

m-tym pierścieniu. W środku: - Obraz pierścieni na styku z powierzchnią regularną (sferą). Z prawej:  

Obraz pierścieni na styku z powierzchnią nieregularna. [opracowanie własne] 

 

d 

R 

r 

r

2

≈mλR 

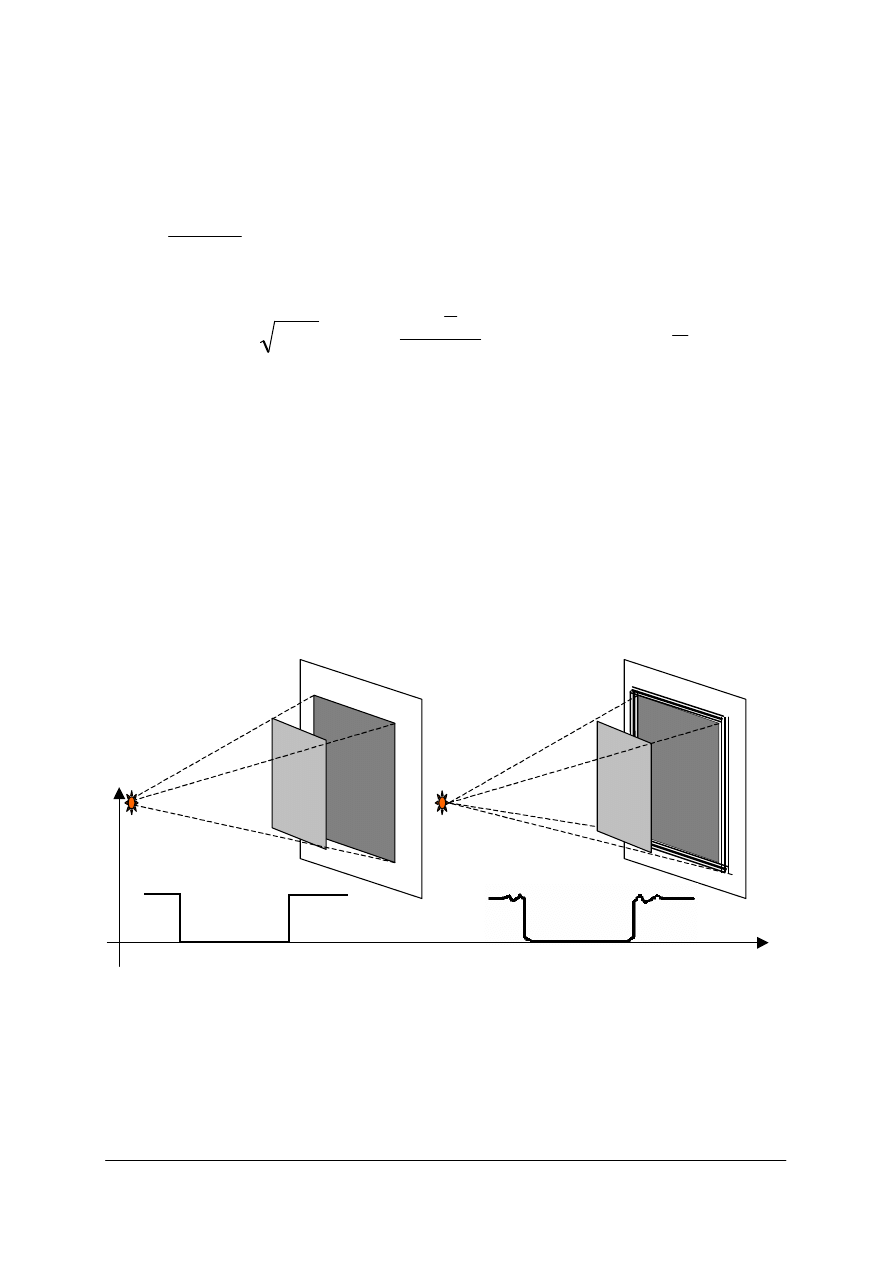
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 53

Interferencja  w  cienkich  warstwach  pomogła  stworzyć  technologię  wytwarzania  warstw 

przeciwodblaskowych  likwidujących  szkodliwe  odbicia  od  powierzchni  elementów 
optycznych. 

Odbicie  od  powierzchni  rozgraniczającej  ośrodki  optyczne  zaleŜy  od  ich 

współczynników załamania i określane jest współczynnikiem odbicia r. 

2

1

2

2

1

)

(

)

(

n

n

n

n

r

+

−

=

 

Warstwy przeciwodblaskowe są nanoszone na powierzchnie elementów optycznych wg 

zasady, Ŝe 

szka

pokr

n

n

=

,     a 

pokr

n

m

d

2

)

2

1

(

λ

+

=

     stąd      

λ

2

1

=

×

d

n

pokr

 

 

We wzorach tych d oznacza grubość nanoszonej warstwy, a λ – długość fali świetlnej. 
Nanosząc odpowiednią kombinacje cienkich warstw moŜemy stworzyć sytuację, w której 

tylko  część  światła  przejdzie  na  drugą  stronę.  Takie  konstrukcje  noszą  nazwę  filtrów 
interferencyjnych. 

Falowa  natura  światła  jest  przyczyną  jeszcze  jednego  zjawiska,  które  nie  dawało  się 

wyjaśnić  prawami  optyki  geometrycznej.  Dokładna  obserwacja  promieni  przechodzących 
przez wąskie szczeliny , czy otwory o bardzo małych średnicach wykazała, Ŝe granica cienia 
nie  jest  ostra,  jakby  wskazywało  na  to  prawo  prostoliniowego  rozchodzenia  się  światła.  Na 
ekranie umieszczonym za szczeliną oświetloną silnym światłem ukazywał się nie tylko jeden 
jasny  prąŜek,  ale  pojawiały  się  teŜ  równoległe  do  niego  następne  prąŜki,  przemiennie  jasne 
i ciemne.    Okazało  się,  Ŝe  jest  to  zjawisko  dyfrakcji,  czyli  ugięcia  fali  na  przeszkodzie 
materialnej. 

 

Rys. 72. Rozkład energii wg optyki geometrycznej – a), i wg optyki falowej – b) [opracowanie własne]

 

 

Mamy dwa rodzaje dyfrakcji: 

−

 

Fraunchofera (1787–1826) – technika optyka, wynalazcy siatki dyfrakcyjnej i odkrywcy 
linii  widmowych  w  świetle  słonecznym  (linie  Fraunchfera).  Fala  osiągająca 
i opuszczająca przeszkodę jest falą płaską. 

−

 

Fresnela  (1788–1827)  –  inŜyniera,  twórcy  pierwszego,  ścisłego,  matematycznego  opisu 
zjawiska dyfrakcji. Opisuje ogólnie zjawisko, bez względu na kształt czoła fali. 

d 

a) 

b) 

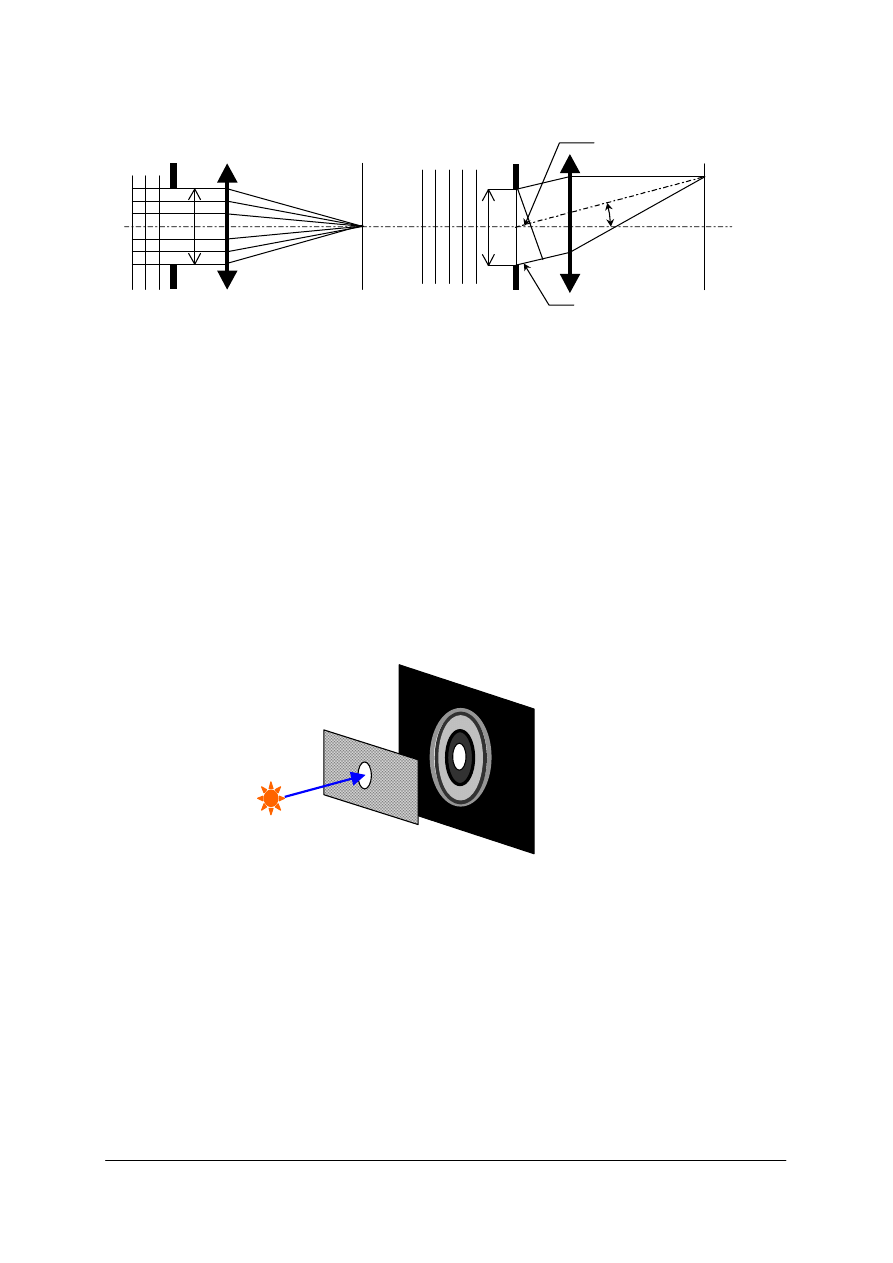
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 54

Dyfrakcja Fraunchofera na pojedynczej szczelinie 

Rys. 73.  Szkic przedstawiający mechanizm powstawania pierwszego minimum dyfrakcyjnego na pojedynczej 

szczelinie. a – szerokość szczeliny, P

0

 – maksimum zerowego rzędu, P

min

 – minimum pierwszego rzędu,  

1, 2, 3 – promienie , Γ

1-2  

i Γ

1-3

 – róŜnice dróg optycznych pomiędzy poszczególnymi promieniami 

[opracowanie własne] 

 
Kolejne  minima  następują,  gdy  róŜnice  dróg  optycznych  stanowią  całkowitą  wielokrotność 
długości fali. 
a sin Θ = mλ , gdzie: a – szerokość szczeliny, Θ – kąt odchylenia wiązki, λ – długość fali,  
a m = 1, 2, 3, .... (kolejne liczby całkowite). 
Jest to ogólny warunek dla minimów dyfrakcyjnych w dyfrakcji Fraunchofera na pojedynczej 
szczelinie.  Z  równania  wynika,  Ŝe  kąt  ugięcia  wzrasta  gdy  maleje  szczelina,  a  więc  gdy 
szczelina  jest    duŜa  ,  kąt  Θ  jest  bardzo  mały.  Z  równania  wynika  równieŜ,  Ŝe  światło 
o większej długości fali jest uginane silniej. 
Dyfrakcja Fraunhofera na otworze kołowym 
WaŜny  przypadek,  poniewaŜ  większość  przysłon  w  przyrządach  optycznych  ma  kształt 
kołowy. Obraz dyfrakcyjny powstający na otworze kołowym nazywamy krąŜkiem Airy’ego. 
 

Rys. 74. Dyfrakcja na otworze kołowym. Maksimum otoczone szeregiem blednących pierścieni - krąŜek 

Airy’ego [opracowanie własne] 

 

Rozkład  energii  na  otworze  kołowym  jest  trochę  inny  niŜ  w  przypadku  szczelin.  RóŜnica 
polega na tym, Ŝe m przybiera wartości inne niŜ kolejne liczby całkowite. 
D sin Θ= mλ , gdzie D – średnica otworka, a m 

1

 = 1,220;. m

2

 

 

= 2,233; m

3

 = 3,238; 

 m

4

 = 4,241 .... 

Dyfrakcja Fraunhofera na innych aperturach 
Wychodzimy  z  załoŜenia  (udowodnionego  matematycznie),  Ŝe  dla  pojedynczej  szerokiej 
szczeliny, prąŜki są blisko siebie i odwrotnie, dla szczeliny wąskiej są one bardziej od siebie 
oddalone. 
Jeśli  otwory  są  wielobokami,  szeregi  maksimów  i  minimów  dyfrakcyjnych  układają  się 
prostopadle do krawędzi otworu. 
 

 

Θ 

P

min

 

P

0

 

P

0 

a 

a 

1 

2 

3 

Γ

1-3 

=λ 

Γ

1-2 

=½λ 

 

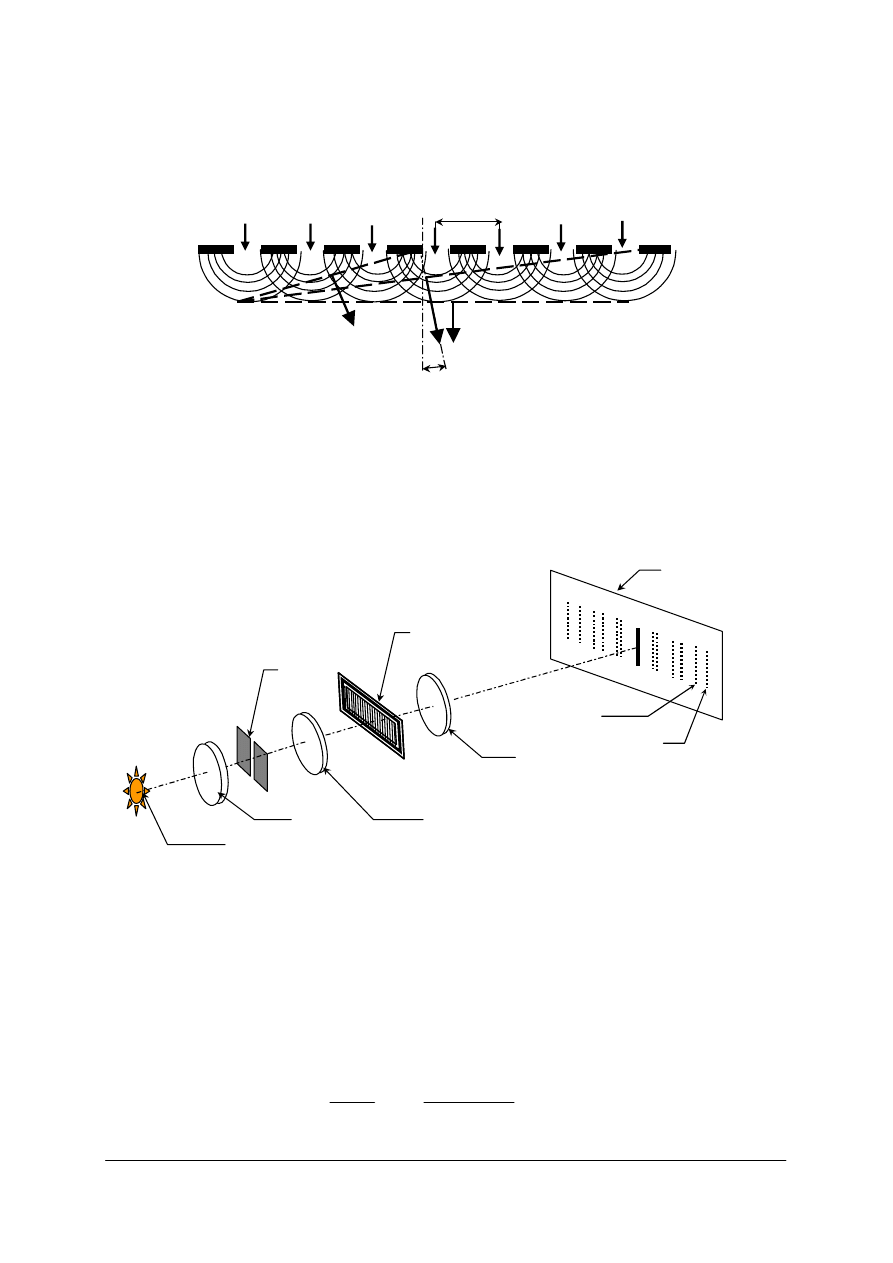
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 55

Siatki dyfrakcyjne 

Siatka  dyfrakcyjna  jest  to  powielenie  doświadczenia  Thomasa  Younga  z  dwoma 

szczelinami.  RóŜnica  polega  na  tym,  Ŝe  zachodzi  interferencja  wielu  fal  z  wielu  szczelin. 
Efektem jest powstanie wyraźniejszych i jaśniejszych prąŜków. 

Rys. 75. Szkic przedstawiający działanie siatki dyfrakcyjnej. Θ – kąt odchylenia, d – odległość między 

szczelinami  [opracowanie własne] 

 

KaŜda  szczelina  to  źródło  fal  wtórnych.  MoŜna  prowadzić  obwiednie  łączące  czoła  fal 

wychodzących z kolejnych szczelin. 

Fale  przechodzące  przez  szczeliny  i  będące  w  jednej  fazie,  będą  się  wzajemnie 

wzmacniać  tam,  gdzie  Γ  =  mλ.  MoŜna  więc  stwierdzić,  Ŝe  połoŜenie  kolejnych  maksimów 
będzie określał wzór: d sin Θ = mλ – Jest to równanie siatki dyfrakcyjnej. 
Powstawanie widm dyfrakcyjnych 

Rys. 76.  Sposób otrzymywania widma liniowego za pomocą siatki dyfrakcyjnej. 1 – źródło promieniowania; 

2 – kondensor oświetlający szczelinę 5; 3 – obiektyw kolimujący wiązkę zerowo; 6 – siatka 

dyfrakcyjna; 4 – obiektyw tworzący obraz na ekranie, 7 – ekran; 1 – 3 to kolejne maksima 

[opracowanie własne] 

 

Większa  część  energii  przechodzi  bez  zakłóceń  (ugięcia)  i  tworzy  silne,  centralne 

maksimum  zerowego  rzędu.  Pozostała  energia,  w  wyniku  ugięcia  kierunku  rozchodzenia  się 
światła,  rozkłada  się  na  kolejne  maksima  wyŜszych  rzędów,  których  liczba  jest  zaleŜna  od 
stałej siatki (d). Gdy d małe, siatka daje mało rzędów interferencji (m), ale szerokie widma 
Dyspersja kątowa siatki 
Dyspersją kątową siatki nazywamy jej zdolność do rozczepiania światła polichromatycznego. 

 

d 

Θ 

 

1 

2 

3 

5 

4 

6 

7 

0 

1 

1  2 

2 

3 

3 

λ΄ > λ 

λ 

λ’ 

Θ

∆

∆Θ

=

cos

d

m

λ

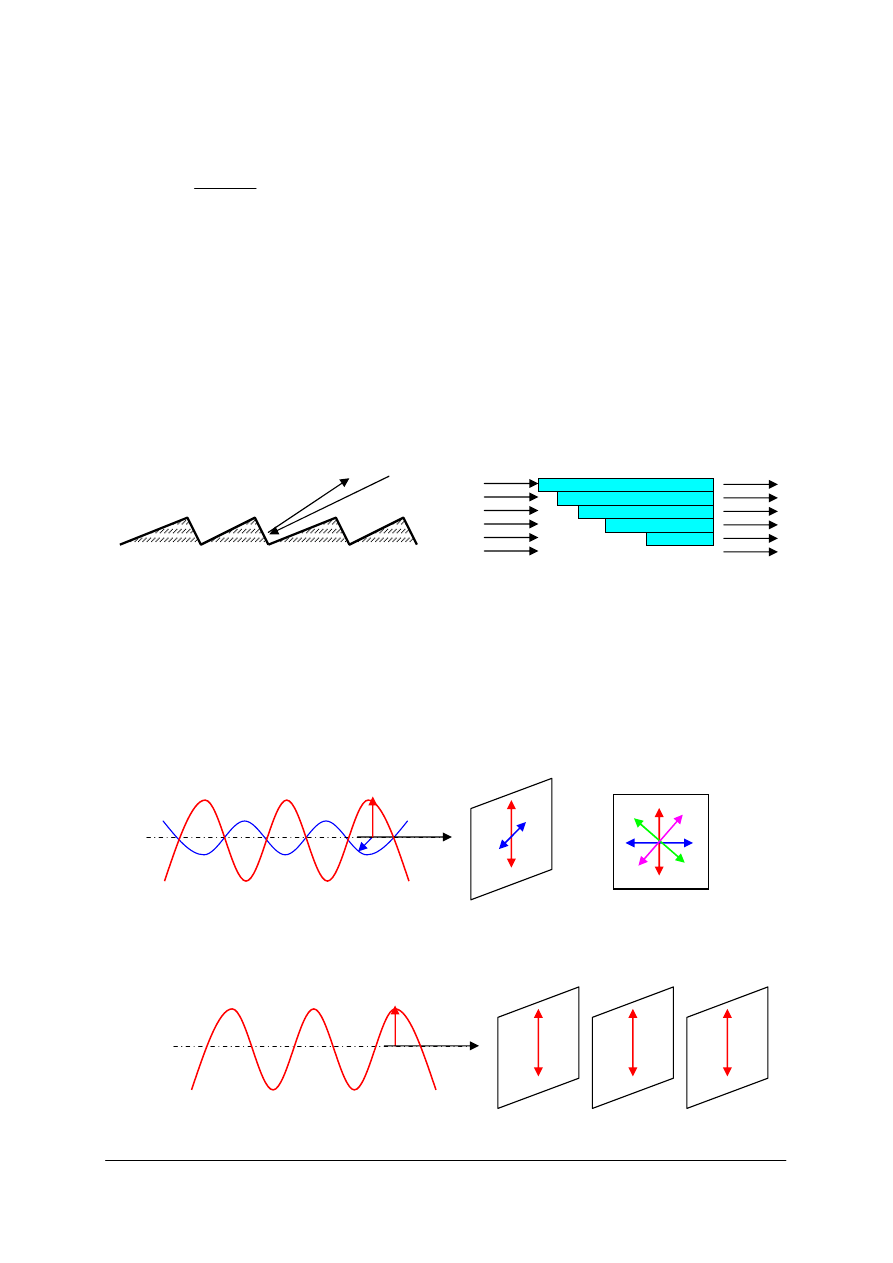
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 56

Nm

=

∆

λ

λ

Chromatyczna  zdolność  rozdzielcza  siatki.  Podobnie  jak  w  przypadku  pryzmatu 
rozczepiającego, określa zdolność do rozdzielania dwu bliskich linii widmowych. 

 

N – liczba szczelin 

 
 

ZaleŜność  ta  określa  najmniejszą  moŜliwą  róŜnicę  długości  fali  ∆λ  jaką  moŜna  rozdzielić  
w m-tym rzędzie przy uŜyciu siatki o N szczelinach. 
Chromatyczna zdolność rozdzielcza siatki jest niezaleŜna od stałej siatki d. 

Rodzaje siatek 

Amplitudowe:  

−

 

Transmisyjne – na szkle nacinane są rysy, a rolę szczelin pełnią przerwy między nimi. 

−

 

Odbiciowe – rysy nacinamy na polerowanej powierzchni odbijającej, a światło odbite od 
powierzchni  między  rysami  daje  takie  same  zjawiska  jak  po  przejściu  przez  siatkę 
transmisyjną. Dobre siatki mają kilkaset  rys/mm 

−

 

Fazowe  –  w  naprzemiennie  leŜących  obszarach  faza  światła  przechodzącego  ulega 
przyspieszeniu lub opóźnieniu. 

 

Rys. 77. Przykładowe rodzaje siatek. Z lewej powierzchnia profilowanej siatki odbiciowe, z prawej siatka 

schodkowa [wg 5, s. 212] 

 

Dokładniejsze badania zjawisk świetlnych  wykazały, Ŝe światło posiada jeszcze jedna  cechę 
tłumaczącą wiele zjawisk. Jest to polaryzacja. 
Odkrycie  i  badanie  zjawiska  polaryzacji  wykazało,  Ŝe  fala  elektromagnetyczne  (a  więc 
i świetlne), muszą być poprzeczne w stosunku do kierunku swojego rozchodzenia się.  

Typy polaryzacji: 

−

 

Światło  niespolaryzowane  –  występuje  w  naturze  najczęściej.  Pokazywanie  go  na 
rysunkach  jako  gwiazdy  wieloramiennej  jest  sposobem  umownym  i  mało  doskonałym, 
nie oddaje bowiem najistotniejszej jego cechy – ciągłej zmiany typu polaryzacji. 

Rys. 78. Schematyczne przedstawienie światła niespolaryzowanego  [opracowanie własne]

 

−

 

Światło spolaryzowane liniowo – wektor elektryczny drga w jednej płaszczyźnie. Wektor 
elektryczny  jest  odpowiedzialny  za  wszystkie  zjawiska  optyczne  oraz  fotograficzne  
i dlatego jego dotyczą rozwaŜania. 

 

Rys. 79. Schematyczne przedstawienie światła spolaryzowanego liniowo [opracowanie własne]

 

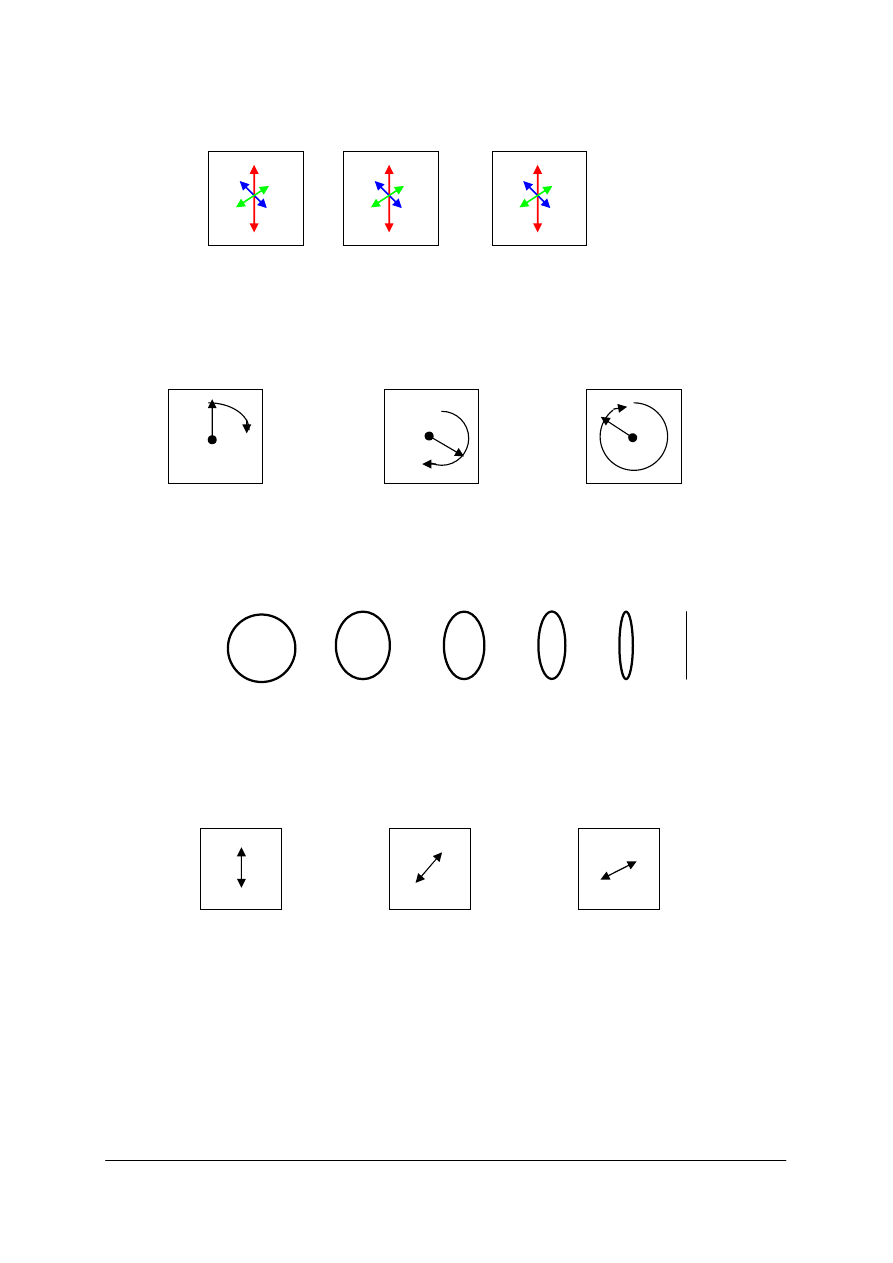
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 57

−

 

Światło  spolaryzowane  częściowo  –  światło  spolaryzowane  liniowo  zawierające 
składową nie spolaryzowaną. 

Rys. 80. Schematyczne przedstawienie światła częściowo spolaryzowanego. Patrząc zgodnie z kierunkiem biegu 

światła, stwierdzamy, Ŝe cześć światła nie jest spolaryzowana [opracowanie własne] 

 

−

 

Polaryzacja kołowa – Koniec wektora elektrycznego nie wykonuje drgań w płaszczyźnie 
lecz  ma  ustaloną  wartość  i  zatacza  okrąg  wokół  kierunku  rozchodzenia  się.  Polaryzacja 
moŜe  być  prawo-  lub  lewoskrętna.  Przestrzennie  polaryzacja  kołowa  jest  polaryzacją 
„śrubową”.  

Rys. 81. Schematyczne przedstawienie światła spolaryzowanego kołowo. Patrząc zgodnie z kierunkiem biegu 

światła stwierdzamy, Ŝe koniec wektora wykonuje ruch śrubowy [opracowanie własne] 

 

−

 

Polaryzacja  eliptyczna  –  najbardziej  ogólny  przypadek  polaryzacji  obejmujący  zakres 
między  polaryzacją  kołową  a  liniową,  które  są  po  prostu  przypadkami  szczególnymi 
(skrajnymi) polaryzacji eliptycznej. 

Rys. 82. Schematyczne przedstawienie światła w róŜnym stopniu spolaryzowanego eliptycznie. Skrajne 

przypadki to polaryzacja kołowa i liniowa [opracowanie własne] 

 

−

 

Rotacja  optyczna  (aktywność  optyczna)  –  powoduje  obrót  płaszczyzny  drgań  światła 
spolaryzowanego  liniowo  lub  eliptycznie  (skręcenie  płaszczyzny  polaryzacji)  w  miarę 
pokonywanej  drogi.  Aktywność  optyczna  jest  właściwością  ośrodka,  w  którym  się 
światło rozchodzi, a nie światła. 

Rys. 83. Schematyczne przedstawienie rotacji optycznej [opracowanie własne]

  

 

Przyrządy  do  otrzymywania  światła  spolaryzowanego  nazywamy  polaryzatorami,  

a przyrządy do obserwacji tego światła nazywamy analizatorami. Analizatory mają tą cechę, 
Ŝe  przepuszczają  tylko  jedna  składową  płaszczyzny  polaryzacji  (kierunku  drgań  wektora). 
Jeśli  płaszczyzna  analizatora  jest  prostopadła  do  płaszczyzny  polaryzacji,  to  światło  nie 
przejdzie, a jeśli płaszczyzny polaryzacji są równoległe, to natęŜenie światła przechodzącego 
będzie maksymalne. Podczas obracania  analizatora względem polaryzatora natęŜenie światła 
będzie się stopniowo zmieniało w myśl prawa Malusa, które jest wyraŜone wzorem: 

 

I

2

= I

1

cos

2

 Θ 

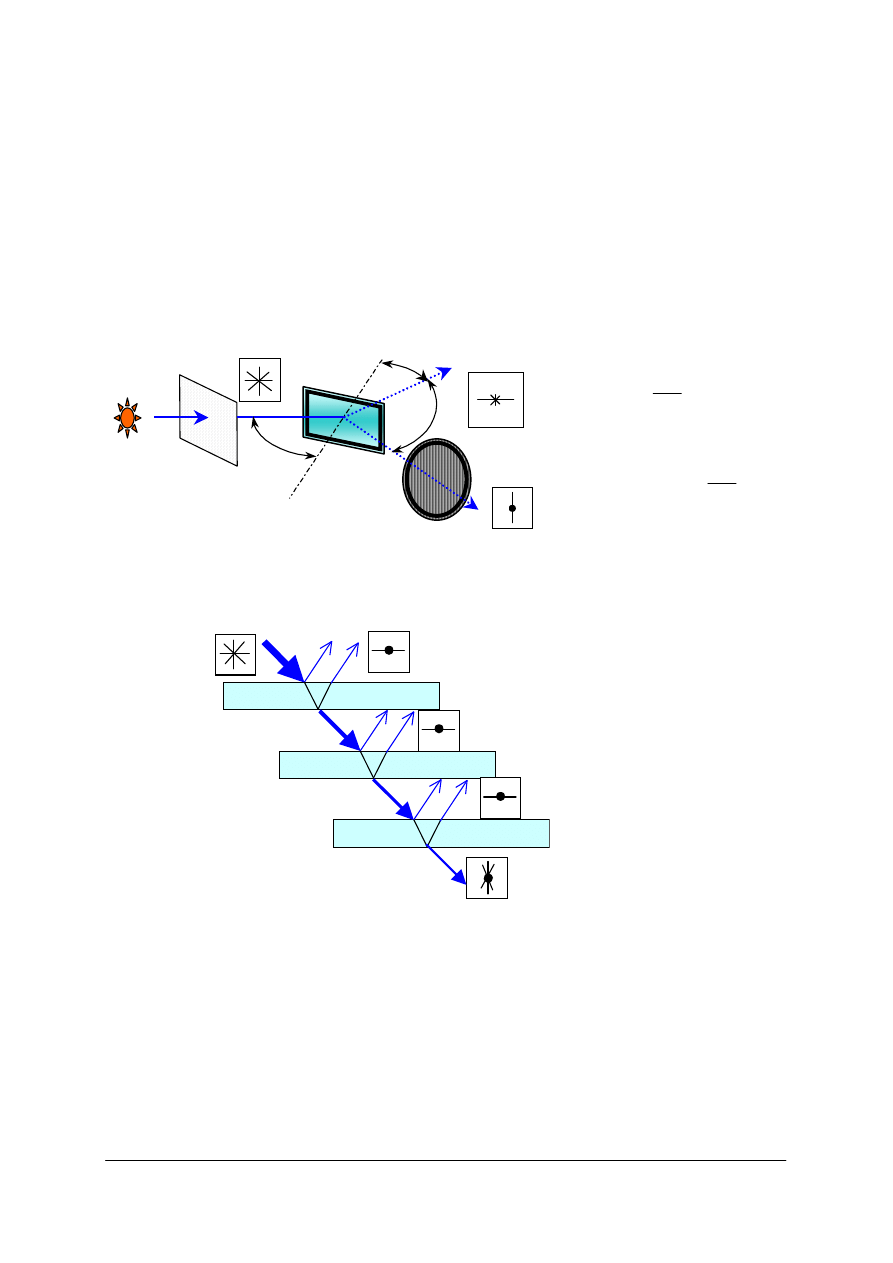
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 58

gdzie I

2

 – to strumień światła przechodzącego, I

1 

 -strumień światła 

przechodzącego przy 

równoległych płaszczyznach polaryzacji polaryzatora i analizatora, 

Θ – kąt między płaszczyznami 

polaryzacji polaryzatora i analizatora.

 

Sposoby otrzymywania światła spolaryzowanego 

−

 

Polaryzacja przez odbicie 
Światło padające na powierzchnię rozgraniczającą dwa ośrodki optyczne ulega częściowo 

załamaniu, a częściowo odbiciu. Obydwie wiązki stają się częściowo spolaryzowane. 
W  1812  r.  Brewster  stwierdził,  Ŝe  najlepszy  efekt  występuje  gdy  kąt  pomiędzy  wiązką 
załamaną, a odbitą wynosi 90°. Jest to tzw.kąt Brewstera określający maksymalną polaryzację 
przy odbiciu (róŜny dla róŜnych długości fali). 
 

 

Rys. 84. Schematyczne przedstawienie sposobu otrzymywania światła spolaryzowanego za pomocą odbicia od 

powierzchni dielektryka [opracowanie własne]

 

 

−

 

Polaryzacja przez załamanie 

Rys. 85. Schematyczne przedstawienie sposobu otrzymywania światła spolaryzowanego za pomocą

 

załamania 

[opracowanie własne] 

 

Światło załamane po stracie składowej odbitej staje się częściowo spolaryzowane, a więc 

po większej liczbie przejść przez płytki płasko-równoległe teŜ moŜe stać się spolaryzowanym. 
Na  kaŜdej  płytce  ubywa  ~8%  spolaryzowanego  w  jednym  kierunku  światła.  Po  przejściu 
przez  10  płytek  światło  jest  spolaryzowane  w  67%,przy  20  płytkach  w  80%,  a  przy  
45 – w 90%. 
 
 
 
 

 

i 

i’ 

N 

90

0 

n

n

arctg

i

n

n

tgi

'

'

=

=

 

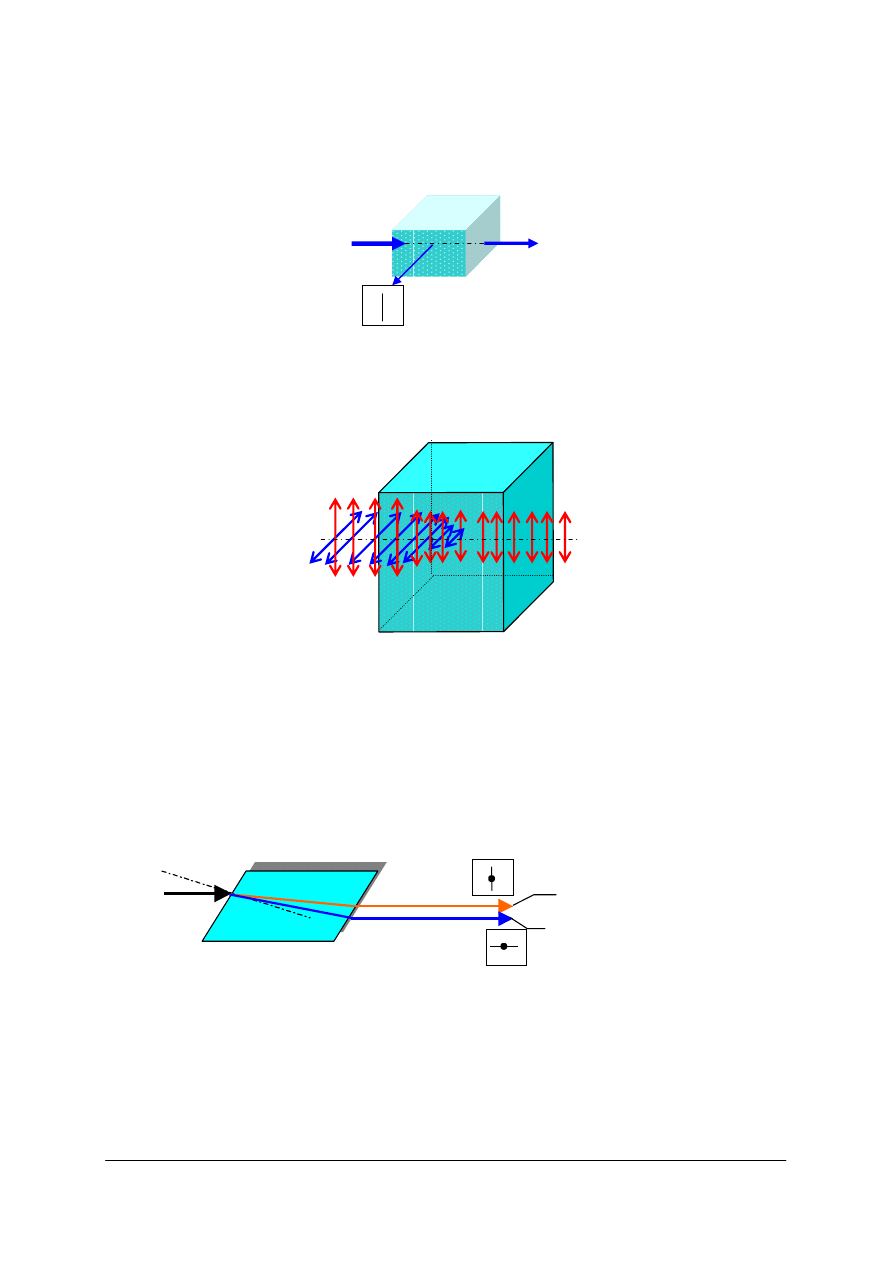
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 59

Polaryzacja przez rozproszenie 

W zawiesinach cząsteczek porównywalnych wielkością z długością fali. Zjawisko moŜna 

zaobserwować oglądając błękitne niebo przez filtr polaryzacyjny, obracając go i patrząc pod 
kątem prostym do kierunku padania światła. 

Rys. 86. Schematyczne przedstawienie sposobu otrzymywania światła spolaryzowanego przez rozproszenie 

[opracowanie własne]

 

 
 
Polaryzacja przez selektywną absorpcję (pochłanianie) 

 

Rys. 87. Schematyczne przedstawienie sposobu otrzymywania światła spolaryzowanego przez selektywną 

absorpcję [opracowanie własne]

 

 

Niektóre kryształy wykazują t. zw. dichroizm np. turmalin.  W 1852 r. William Bird Herapath 

odkrył,  Ŝe  kryształy  jodosiarczanu  chininy  (herpatytu)  przy  odpowiedniej  grubości,  posiadają 
zdolność wygaszania jednej składowej światła niespolaryzowanego Zapoczątkowało to prace nad 
wynalezieniem  folii  polaryzacyjnej  (polaroidu).  –  Najczęściej  stosowanego  obecnie  elementu 
optycznego do otrzymywania światła spolaryzowanego. 

 

Polaryzacja przez podwójne załamanie 

 

Rys. 88

. 

Schematyczne przedstawienie zjawiska dwójłomności

.

 

Płaszczyzny polaryzacji promieni „e” i „o” są 

prostopadłe

 

[opracowanie własne] 

 

Niektóre  ośrodki  wykazują  tzw.  zjawisko  dwójłomności,  polegające  na  tym,  Ŝe  mają 

róŜne współczynniki załamania dla fal o wzajemnie prostopadłych płaszczyznach polaryzacji. 

Ośrodki  w  których  obserwujemy  zjawisko  dwójłomności  nazywamy  anizotropowymi 

(kwarc, mika, cukier, lód, turmalin i wiele innych). 

 

Promień zwyczajny „o” 

Promień nadzwyczajny „e” 

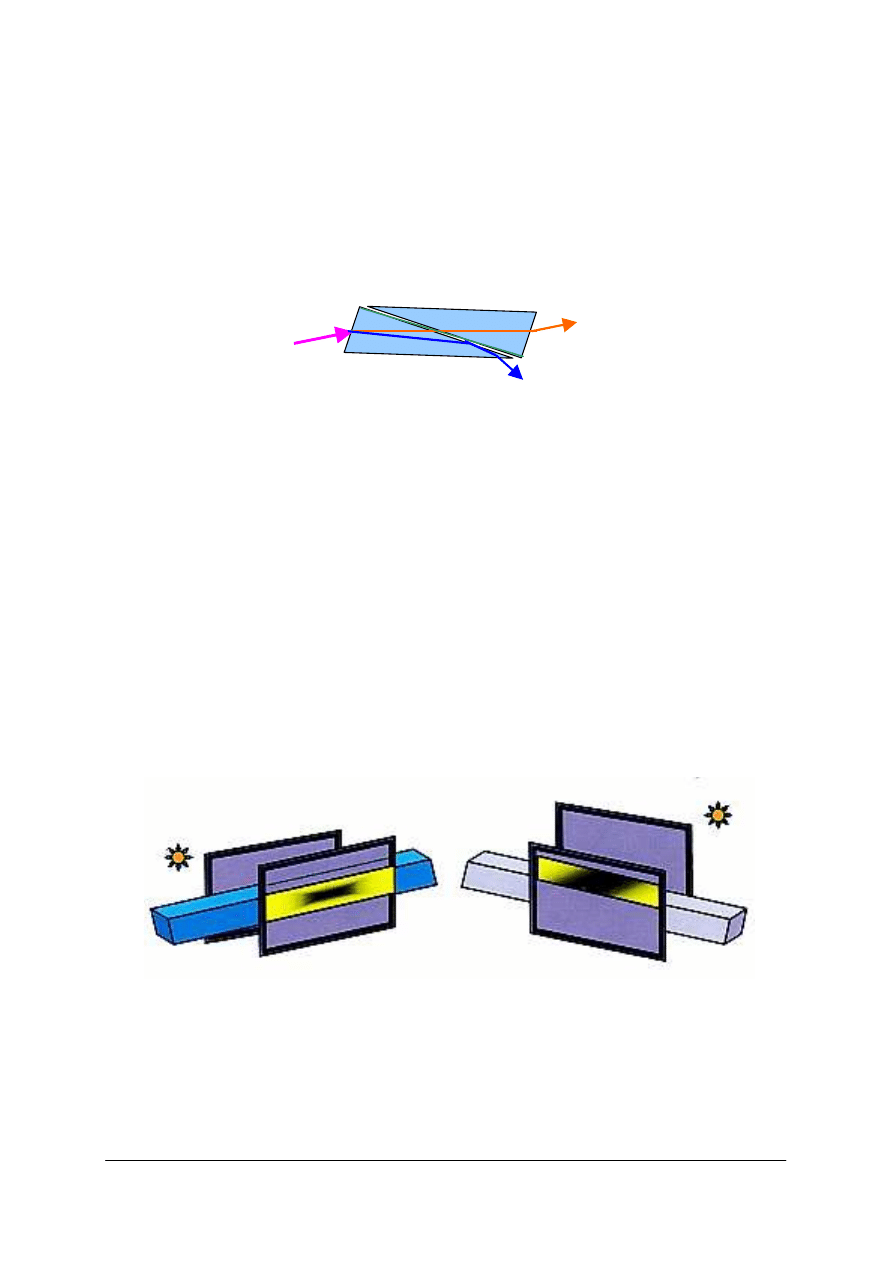
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 60

Materiały  izotropowe  to  większość  gazów,  cieczy  i  niekrystalicznych  ciał  stałych  bez 

napręŜeń.  Ich  współczynniki  załamania  są  jednakowe  dla  wszystkich  kierunków  padania 
światła  i  jego  płaszczyzn  polaryzacji.  Jeśli  wyeliminujemy  jedną  ze  składowych 
to otrzymamy  dobry  polaryzator.  Przykładem  moŜe  być  pryzmat  Nicola.  Dwa  pryzmaty 
prostokątne  wykonane  z  kryształu  kalcytu  (CaCO

3

),  o  kątach  ostrych  22°  i  68°,  sklejone 

balsamem  kanadyjskim,  tworzą  płytkę  równoległoboczną,  która  dzięki  odpowiedniemu 
doborowi kierunków ich osi optycznych, przepuszcza tylko promień nadzwyczajny. Promień 
zwyczajny jest zatrzymywany w pryzmacie. 

Rys. 89. Schematyczne przedstawienie działania pryzmatu Nicola [opracowanie własne] 

 

Pod wpływem działania  sił mechanicznych ciała  izotropowe (jednorodne) mogą stać się 

anizotropowymi (dwójłomnymi). W zaleŜności od tego czy są one ściskane, czy rozciągane, 
mogą  wykazywać  właściwości  dodatniego  lub  ujemnego  kryształu  jednoosiowego,  z  osią 
skierowaną wzdłuŜ działających sił. 

Jest  to  podstawa  elastooptyki  –  dziedziny  zajmującej  się  badaniem  rozkładu  sił  

w róŜnego  rodzaju  konstrukcjach  poddanych  obciąŜeniom.  Obserwuje  się  albo  przejście 
spolaryzowanego  światła  przez  wykonany  z  przeźroczystego  materiału  modelu  konstrukcji, 
albo odbicie tego światła od jej powierzchni pokrytej specjalnym lakierem. Wykorzystywane 
tutaj jest zjawisko aktywności optycznej powodującej skręcenie płaszczyzny polaryzacji. 

Najprostszym  przyrządem  do  badania  napręŜeń  jest  polaryskop  składający  się  z  dwu 

skrzyŜowanych  polaroidów  –  polaryzatora  i  analizatora.  Aktywność  optyczna  materiału 
spowodowana napręŜeniami powoduje skręcenie płaszczyzny polaryzacji, a to jest przyczyną 
pojawienia  się  przepuszczanej  przez  analizator  składowej  światła.  wychodzącego 
z polaryzatora. Przed analizatorem umieszcza się jeszcze dodatkowy filtr zwany płytką czułej 
barwy, której zadaniem jest zwiększyć dokładność obserwacji zmian natęŜenia swiatła. 

 

Rys. 90. Obserwacja napręŜeń za pomocą polaryskopu.  W ośrodkach przeźroczystych (po lewej) i pokrytych 

aktywnym optycznie lakierem (po prawej) [opracowanie własne] 

 
W podobny sposób mogą zachowywać się zarówno ciała stałe, jak i ciecze pod wpływem 

pól elektrycznych, czy magnetycznych.( np. ekrany ciekłokrystaliczne). 
 
 
 

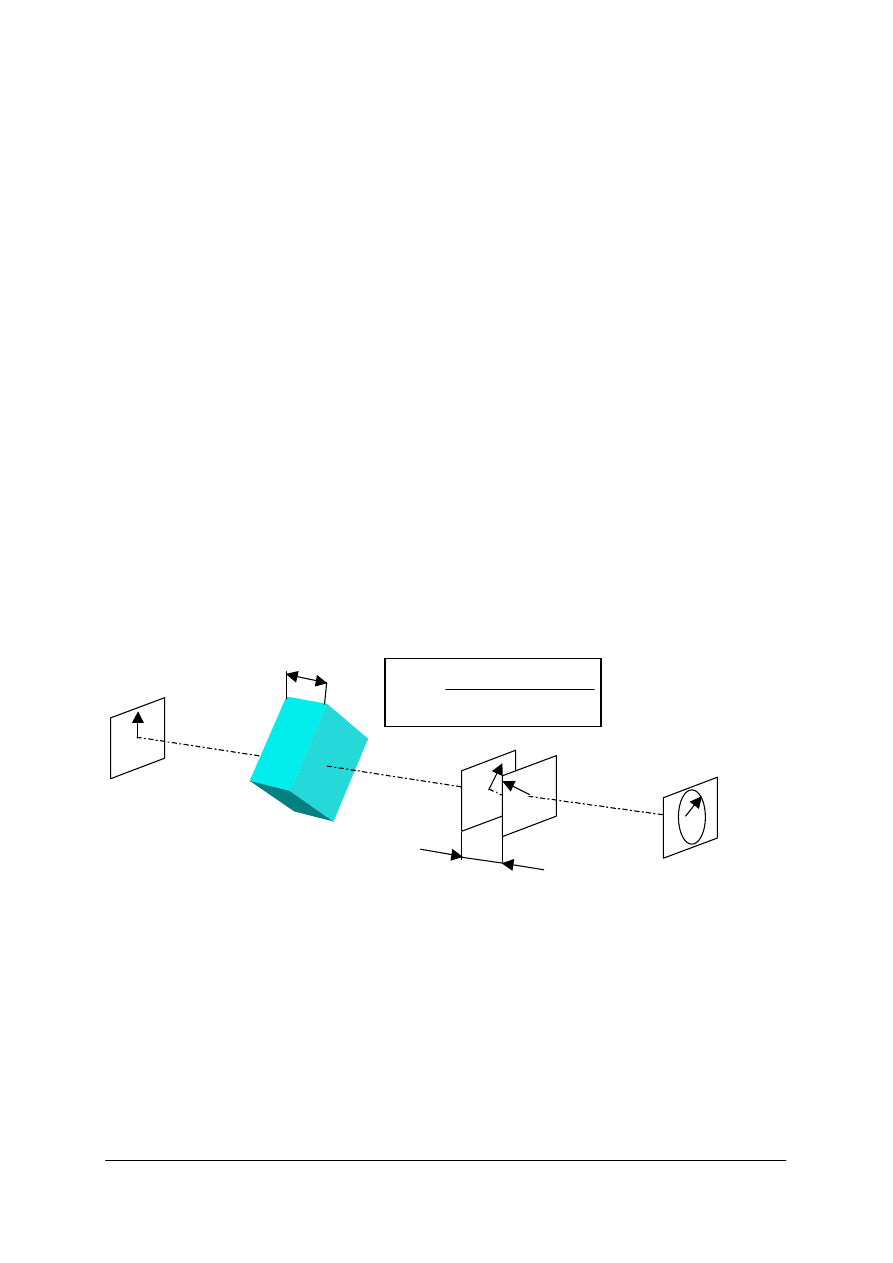
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 61

Polaryzacja i interferencja 
Okazało  się,  Ŝe  polaryzacja  ma  wpływ  na  interferencję  i  moŜe  spowodować,  Ŝe  wiązki 
pozornie spójne nie interferują. 

−

 

Dwie wiązki liniowo spolaryzowanego światła o drganiach prostopadłych nie interferują. 

−

 

Dwie  wiązki  liniowo  spolaryzowanego  światła  o  drganiach  w  tej  samej  płaszczyźnie 
interferują. 

−

 

Dwie  wiązki  liniowo  spolaryzowanego  światła  otrzymane  z  prostopadłych  składowych 
światła  nie  spolaryzowanego,  a  następnie  sprowadzone  do  tej  samej  płaszczyzny  drgań, 
nie interferują. 

−

 

Dwie  wiązki  liniowo  spolaryzowanego  światła  otrzymane  ze  spójnej  wiązki  
i sprowadzone następnie do prostopadłych płaszczyzn drgań, będą ze sobą interferowały 
(moŜe wystąpić zmienny stopień eliptyczności). 

 
Analiza światła o nieznanej polaryzacji 

Obserwujemy  światło  przez  polaryzator.  Jeśli  jest  spolaryzowane  liniowo,  obrót 

polaryzatora  wokół  osi  rozchodzenia  się  światła  spowoduje  zmiany  jego  natęŜenia  od 
minimum,  gdy  oś  polaryzatora  i  płaszczyzna  polaryzacji  światła  są  prostopadłe,  do 
maksimum, gdy są równoległe. 

Pełne  wygaszenie  w  minimum  nastąpi,  gdy  światło  jest  całkowicie  spolaryzowane 

liniowo.  Gdy  obrót  polaryzatora  nie  powoduje  zmian  natęŜenia  przechodzącego  światła,  jest 
ono  albo  niespolaryzowane,  albo  spolaryzowane  kołowo.  Aby  rozróŜnić  te  rozdaje  światła 
musimy  zastosować  jakąś  inną  metodę.  MoŜe  to  być  np.  uŜycie  tzw.  ćwierćfalówki  (płytki 
ćwierćfalowej).  Płytka  plasko-równoległa  wykonana  z  materiału  anizotropowego  tak,  aby 
promień nadzwyczajny był przyspieszony, albo opóźniony w stosunku do zwyczajnego o ¼λ. 

 

 

Rys. 91. Schemat działania płytki ćwierćfalowej. L – grubość płytki obliczana na podstawie róŜnicy 

współczynników załamania dla promienia zwyczajnego i nadzwyczajnego [opracowanie własne] 

 

Płytek  ćwierćfalowych  uŜywa  się  do  konstrukcji  filtrów  polaryzacyjnych  do  fotografii, 

gdy wymagana jest polaryzacja kołowa. 
 
 
 
 
 
 
 
 
 

 

1

/

4

λ 

L 

)

(

4

e

o

n

n

L

−

=

λ

 

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 62

 

 

Wprowadzamy w wiązkę analizator 

Obracamy analizator 

 
 

Zmiany natęŜenia 

NatęŜenie nie zmienia się 

 

 

 

Pełne wygaszanie 

Niepełne wygaszanie 

Wprowadzamy ćwierćfalówkę przed analizator 

 

 

 

 

Brak zmian natęŜenia przy 

obrocie. 

Światło liniowo 

spolaryzowane 

Wprowadzamy 

ćwierćfalówkę przed 

analizator ustawiony na 

maksimum transmisji, tak 

aby jeden z azymutów 

płytki był równoległy do 

płaszczyzny transmisji 
analizatora. Obracamy 

analizator. 

Światło naturalne 

niespolaryzowane. 

Zmiany natęŜenia 

 

 

 

 

Pełne wygaszanie 

Niepełne wygaszanie 

Pełne wygaszanie 

Niepełne wygaszanie 

 

 

 

 

Światło eliptycznie 

spolaryzowane 

 

Światło kołowo 

spolaryzowane 

Mieszanina światła 

spolaryzowanego kołowo i 

światła 

niespolaryzowanego 

Minima natęŜenia światła 

w tej samej pozycji 

analizatora, co przed 

wstawieniem płytki. 

Minima natęŜenia przy 

innej pozycji analizatora. 

 

 

 

 

 

 

Światło częściowo liniowo 

spolaryzowane 

Mieszanina światła 

liniowo i eliptycznie 

spolaryzowanego. 

 

 

 

Rys. 92. Schemat postępowania przy analizie światła o nieznanej polaryzacji [opracowanie własne] 

 

 

W  czasie  poszukiwań  sposobu  skorygowania  naturalnej  aberacji  sferycznej  promieni  X  

w  mikroskopie  elektronowym  Dennis  Gabor  rozpracowywał  zagadnienie  „rekonstrukcji 
powierzchni falowej” nazwane później holografią. 

Holografię  moŜemy  określić  jako  metodę  zapisu  informacji  optycznej  o  przedmiocie  

w  emulsji  z  pominięciem  metod  fotograficznych.  Powstaje  hologram,  z  którego  zapisaną 
informację moŜna odczytać

 

jako obraz przedmiotu. 

Holografia  tym  róŜni  się  od  fotografii,  Ŝe  wykorzystując  interferencję,  dokonuje 

rejestracji  zjawisk  wynikających  z  róŜnicy  fazy,  która  zawiera  informacje  o  przestrzennym 
kształcie holografowanego obiektu. Nie jest konieczne uŜywanie soczewek. 
 
 

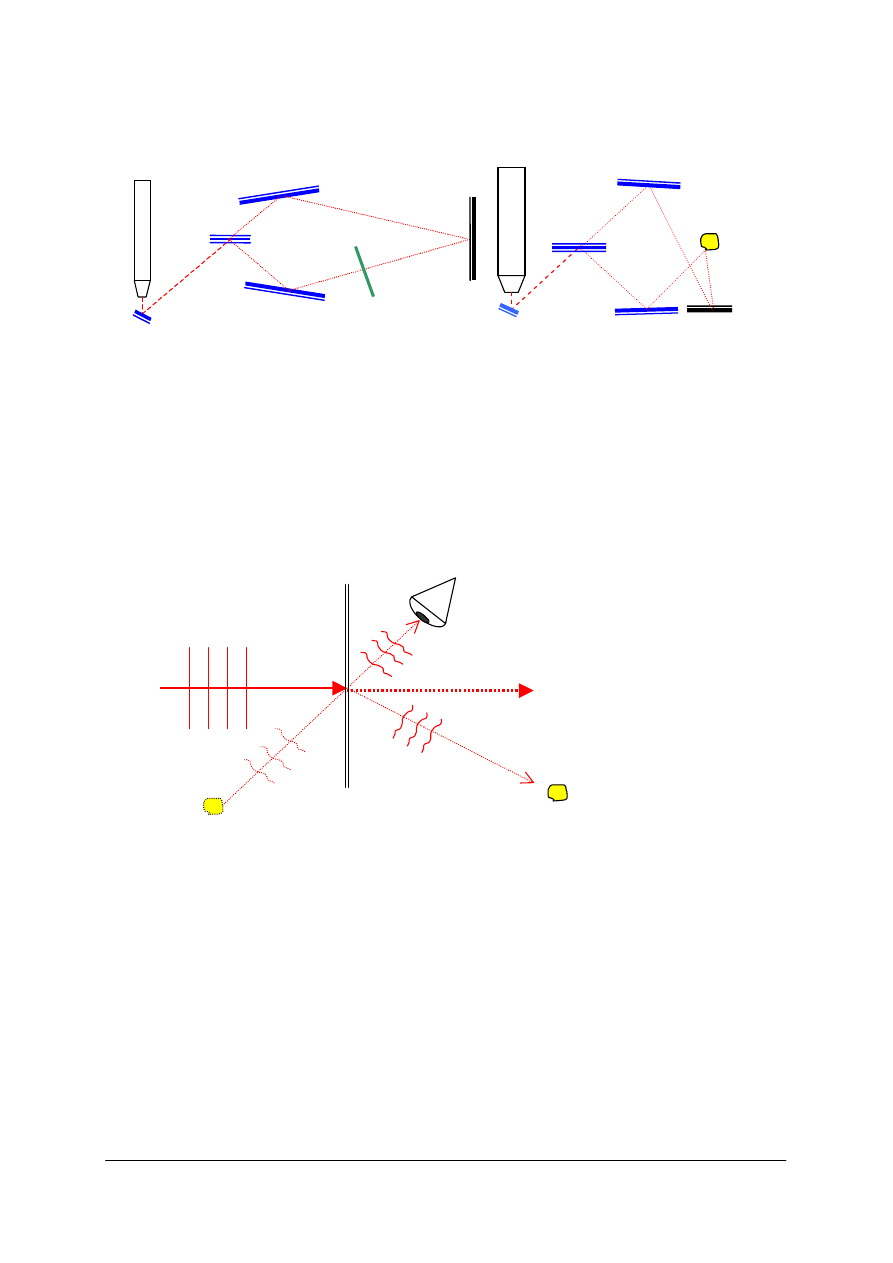
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 63

Wykonywanie hologramów 
 

Rys. 93. Sposób otrzymywania hologramów dla przedmiotów przezroczystych  (z lewej) i odbijających 

(z prawej). L – laser; Z – zwierciadła kierujące wiązkami; Z

p

 – zwierciadła półprzepuszczalne  

[opracowanie własne] 

 

Wszystko zamontowane na cięŜkiej, sztywnej podstawie. zapobiegającej drganiom, 

które mogą spowodować rozmycie rejestrowanego obrazu prąŜków. 

Odtwarzanie hologramu 

Dyfrakcja fali na zarejestrowanych w hologramie prąŜkach tworzących skomplikowaną 

strukturę powoduje powstanie fali o takiej samej fazie, jak fala, która powstała na 
holografowanym przedmiocie i została zarejestrowana w emulsji fotograficznej. 

 

Rys. 94. Sposób odtwarzania  hologramów. Wiązka odtwarzająca przechodząc przez hologram przyjmuje 

amplitudę i fazę wiązki przedmiotowej i dlatego obserwatorowi wydaje się , Ŝe pochodzi z przestrzeni leŜącej 

poza hologramem [opracowanie własne] 

 

4.3.2.

 

Pytania sprawdzające 

 

 Odpowiadając na pytania, sprawdzisz czy jesteś przygotowany do wykonania ćwiczeń. 

1.

 

Jakie wielkości charakteryzują ruch falowy i jakie związki między nimi zachodzą? 

2.

 

Jakie zakresy wyróŜniamy w widmie fal elektromagnetycznych? 

3.

 

Jakim zakresem widma fal elektromagnetycznych zajmuje się optyka? 

4.

 

Co to jest droga optyczna? 

5.

 

Na czym polega dyfrakcja fali świetlnej? 

6.

 

Na  czym  polega  zjawisko  interferencji  fal  świetlnych  i  w  jakich  warunkach  moŜemy  je 
zaobserwować? 

7.

 

Jak moŜna uzyskać iterferujące wiązki światła? 

L 

Z 

Z 

Z 

Z

P 

hologram

 

przedmiot 

odbijający

 

L 

Z 

Z 

Z 

Z

P 

hologram

P 

 

wiązka odtwarzająca 

składowa stała (rząd zerowy) 

obserwator 

obraz pozorny 

obraz rzeczywisty 

hologram 

fala rozproszona na przedmiocie 

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 64

8.

 

Jak działają interferometry? 

9.

 

Co jest istotą pomiarów interferometrycznych? 

10.

 

Jaki jest mechanizm powstawania zjawiska interferencji w cienkich warstwach? 

11.

 

Co to są barwy interferencyjne? 

12.

 

Jak  w  przybliŜeniu  obliczyć  promień  krzywizny  kuli  na  podstawie  pomiaru  pierścieni 
Newtona? 

13.

 

Co to jest współczynnik odbicia? 

14.

 

Jak się projektuje warstwy przeciwodblaskowe? 

15.

 

Jak wygląda obraz dyfrakcyjny szczeliny, a jak otworu kołowego? 

16.

 

Co to jest krąŜek Airy’ego? 

17.

 

Co to jest siatka dyfrakcyjna i jak działa? 

18.

 

Czym  róŜni  się  widmo  światła  białego  dawane  przez  siatkę  dyfrakcyjną  od  widma 
dawanego przez pryzmat rozczepiający? 

19.

 

Jak zapisane jest równanie siatki dyfrakcyjnej? 

20.

 

Od czego zaleŜy chromatyczna zdolność rozdzielcza siatki dyfrakcyjnej? 

21.

 

Jakie mamy rodzaje siatek dyfrakcyjnych? 

22.

 

Czym róŜni się światło nie spolaryzowane o d światła spolaryzowanego? 

23.

 

Jakie mamy rodzaje polaryzacji światła? 

24.

 

Jakie są sposoby otrzymywania światła spolaryzowanego? 

25.

 

Co to jest ćwierćfalówka? 

26.

 

Jak otrzymać światło spolaryzowane kołowo? 

27.

 

Co to jest polaryzator? 

28.

 

Na czym polega zjawisko dwójłomności i gdzie występuje? 

29.

 

Jak działa pryzmat Nikola? 

30.

 

Jak zbudować prosty przyrząd do obserwacji napręŜeń w szkle? 

31.

 

Co to jest hologram ? 

32.

 

Jak  działa  układ  do  rejestracji  hologramów  w  świetle  przechodzącym,  a  jak  w  świetle 
odbitym? 

33.

 

Jakie obrazy moŜemy obserwować odtwarzając hologramy? 

 

4.3.3.

 

Ćwiczenia 

Ćwiczenie 1 

Po  przyłoŜeniu  wypukłej  powierzchni  kulistej  do  płaskiej  powierzchni  otrzymaliśmy 

dokoła punktu styku prąŜki Newtona. Jaki jest w przybliŜeniu promień krzywizny sfery jeśli 
średnica  5  prąŜka  wynosi  4mm,  a  długość  fali  światła  w  jakim  prowadzimy  obserwacje 
wynosi 500 nm? 
 

Sposób wykonania ćwiczenia 
 
Aby wykonać ćwiczenie powinieneś: 

1)

 

sporządzić szkic z oznaczeniem danych i szukanych, 

2)

 

zapisać wartości liczbowe danych wyjściowych zwracając uwagę na jednostki, 

3)

 

ułoŜyć wzór na obliczenie szukanej wielkości, 

4)

 

podstawić dane i przeprowadzić obliczenia, 

5)

 

napisać odpowiedź z uzyskanym wynikiem. 

 

WyposaŜenie stanowiska pracy: 

−

 

papier formatu A4, 

−

 

linijka z podziałką, trójkąt kreślarski, cyrkiel, ołówek,  

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 65

−

 

literatura zgodna z punktem 6 poradnika. 

 
Ćwiczenie 2 
 

Oblicz,  jakie  są  straty  na  odbicie  od  powierzchni  soczewki  wykonanej  ze  szkła 

o współczynniku załamania n = 1,74. Jaki współczynnik załamania powinien mieć materiał na 
warstwę  przeciwodblaskową  i  jaka  powinna  być  jej  grubość,  jeśli  chcielibyśmy  wygasić 
odbicie światła w paśmie λ = 500 nm? 
 

Sposób wykonania ćwiczenia 

 
 

Aby wykonać ćwiczenie powinieneś: 

1)

 

zapisać wartości liczbowe danych wyjściowych zwracając uwagę na jednostki, 

2)

 

napisać wzory na obliczenie szukanych wielkości, 

3)

 

podstawić dane i przeprowadzić obliczenia, 

4)

 

napisać odpowiedź z uzyskanym wynikiem. 

 
 

WyposaŜenie stanowiska pracy: 

−

 

papier formatu A4, 

−

 

literatura zgodna z punktem 6 poradnika. 

 
Ćwiczenie 3 
 

Oblicz, ile szczelin powinna mieć siatka dyfrakcyjna za pomocą której moŜna stwierdzić 

juŜ  na  podstawie  widma  dyfrakcyjnego  pierwszego  rzędu,  Ŝe  Ŝółta  linia  sodu  to  dublet  
o długościach fal λ

1 

= 589,6 nm, λ

2 

= 589,0 nm. 

 
 

Sposób wykonania ćwiczenia. 

 
 

Aby wykonać ćwiczenie powinieneś: 

1)

 

zapisać wartości liczbowe danych wyjściowych zwracając uwagę na jednostki, 

2)

 

zapisać wzór na obliczenie szukanej wielkości, 

3)

 

podstawić dane i przeprowadzić obliczenia, 

4)

 

napisać odpowiedź z uzyskanym wynikiem. 

 
 

WyposaŜenie stanowiska pracy: 

−

 

papier formatu A4, 

−

 

literatura zgodna z punktem 6 poradnika. 

 

4.3.4. Sprawdzian postępów 

Czy potrafisz: 

Tak 

Nie 

1)

 

zdefiniować podstawowe pojęcia ruchu falowego? 

 

 

2)

 

podać zakres widzialnej części widma fal elektromagnetycznych? 

 

 

3)

 

zdefiniować podstawową zasadę pomiarów metodami 
interferencyjnymi? 

 

 

4)

 

objaśnić zasadę działania interferometrów. 

 

 

5)

 

zinterpretować zjawiska występujące podczas interferencji w cienkich 
warstwach? 

 

 

6)

 

zinterpretować zjawisko powstawania pierścieni Newtona? 

 

 

7)

 

zinterpretować kształt pierścieni Newtona powstających na styku 
powierzchni? 

 

 

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 66

8)

 

 obliczyć współczynnik odbicia od powierzchni ośrodka o znanym  
 współczynniku załamania? 

 

 

9)

 

 wyznaczyć grubość cienkiej warstwy na podstawie tabeli barw  
 interferencyjnych? 

 

 

10)

 

 obliczyć grubość warstwy przeciwodblaskowej w zaleŜności od   
 współczynnika załamania podłoŜa? 

 

 

11)

 

 zdefiniować zjawisko dyfrakcji? 

 

 

12)

 

 wyjaśnić, do czego słuŜy siatka dyfrakcyjna? 

 

 

13)

 

 zinterpretować równanie siatki dyfrakcyjnej? 

 

 

14)

 

 zaprojektować siatkę dyfrakcyjna o określonej chromatycznej  
 zdolności rozdzielczej? 

 

 

15)

 

 rozpoznać typ polaryzacji światła ? 

 

 

16)

 

 objaśnić sposoby otrzymywania światła spolaryzowanego? 

 

 

17)

 

 zinterpretować obraz napręŜeń obserwowany pod polaryskopem? 

 

 

18)

 

 zaprojektować układ do obserwacji w świetle spolaryzowanym  
 kołowo? 

 

 

 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 

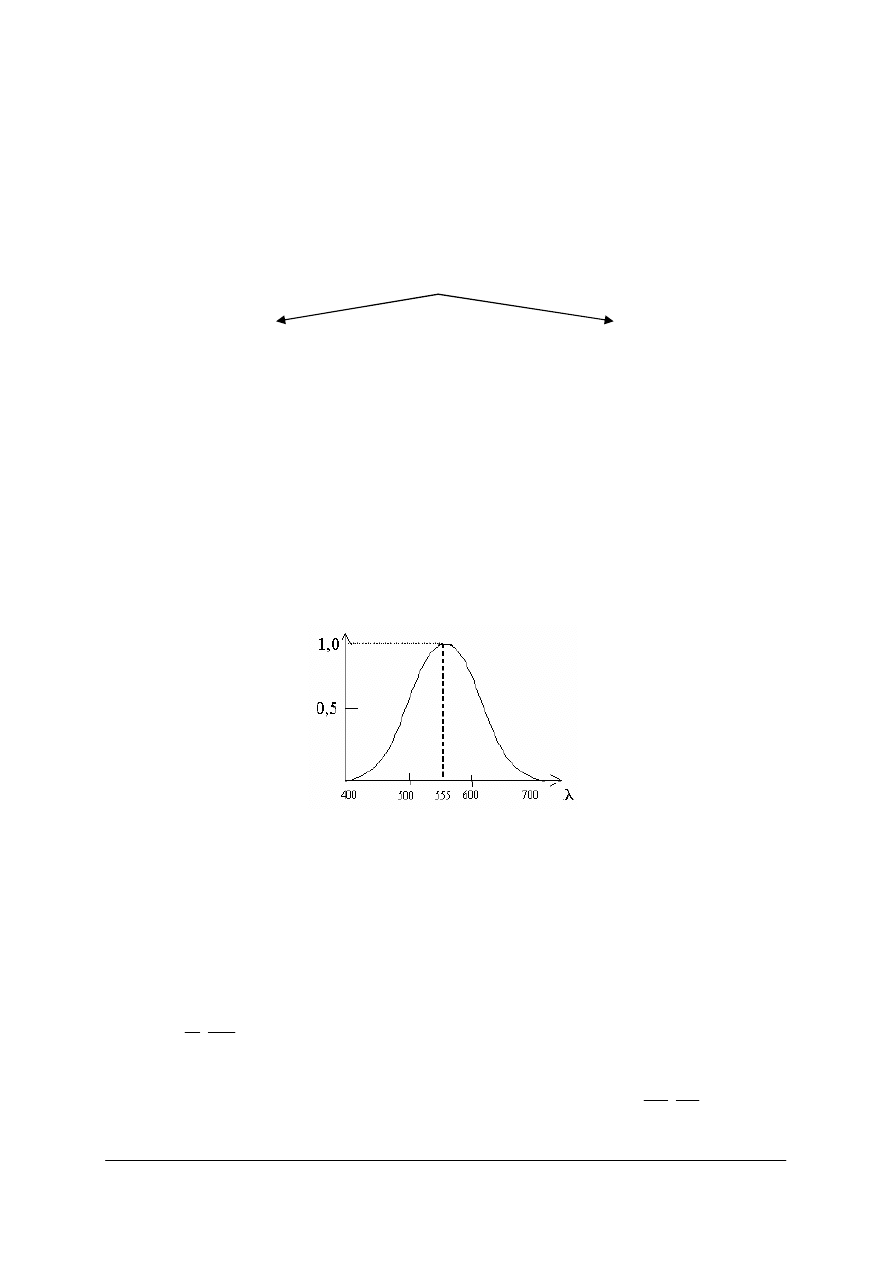
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 67

4.4.

 

Fotometria 

 

4.4.1.

 

Materiał nauczania 

 

Fotometria  jest  to  dział  optyki  zajmujący  się  pomiarami  energii  promieniowania 

elektromagnetycznego  (w  zakresie  widzialnym  i  niewidzialnym)  i  związanych  z  nim  innych 
wielkości. 
 

Fotometria 

 

 

 

 

Fotometria fizyczna, 

obiektywna, energetyczna. 

(Radiometria) 

Rozpatruje promieniowanie 

pod kątem energetycznym, 

wystarczającym z fizycznego 

punktu widzenia. 

 

Fotometria wizualna, 
subiektywna. 
(Fotometria) 
Rozpatruje 
promieniowanie pod 
kątem subiektywnych 
wraŜeń odbiornika 
promieniowania np. 
oka. 

W fotometrii wizualnej istotną rolę odgrywa pojęcie skuteczności (dzielności) świetlnej. 

Jest  to  wielkość  wyraŜana  stosunkiem  strumienia  promieniowania  świetlnego  o danej 
długości fali do strumienia energii tego promieniowania i jest róŜna dla róŜnych długości fal 
światła.  Wykres  obrazujący  tą  zaleŜność  nazywamy  krzywą  czułości  widmowej,  krzywą 
czułości spektralnej lub funkcją widzialności odbiornika (oka). 

Rys. 95. Krzywa czułości spektralnej oka Dla oka ludzkiego maksymalna czułość widmowa przypada na falę  

o długości 555 nm (zieleń) i dlatego w tym zakresie rozróŜniamy najwięcej odcieni [opracowanie własne] 

 
Fotometria – definicje 

Energia  promienista  Q  jest  przenoszona  pod  postacią  fal  elektromagnetycznych  i  jej 

jednostką  jest  dŜul  –  [J]  Dotyczy  to  zarówno  pełnego  zakresu  promieniowania 
elektromagnetycznego  –  Qe,  jak  i  wydzielonego  z  niego  promieniowania  widzialnego 
(świetlnego) – Qw, 

Moc 

promieniowania 

(strumień 

energetyczny) 

– 

stosunek 

ilości 

energii 

wypromieniowanej przez źródło do czasu promieniowania. WyraŜa się ją wzorem 

]

[

sek

J

t

Q

=

Φ

, gdzie 

Q to ilość energii wyraŜona w dŜulach, a t – czas w sekundach. 

NatęŜenie  promieniowania  źródła  jest  to  moc  wysyłana  przez  źródło  punktowe 

w granicach jednostkowego kąta bryłowego i jest wyraŜana wzorem 

]

[

sr

W

I

δω

δ

Φ

=

], gdzie δΦ 

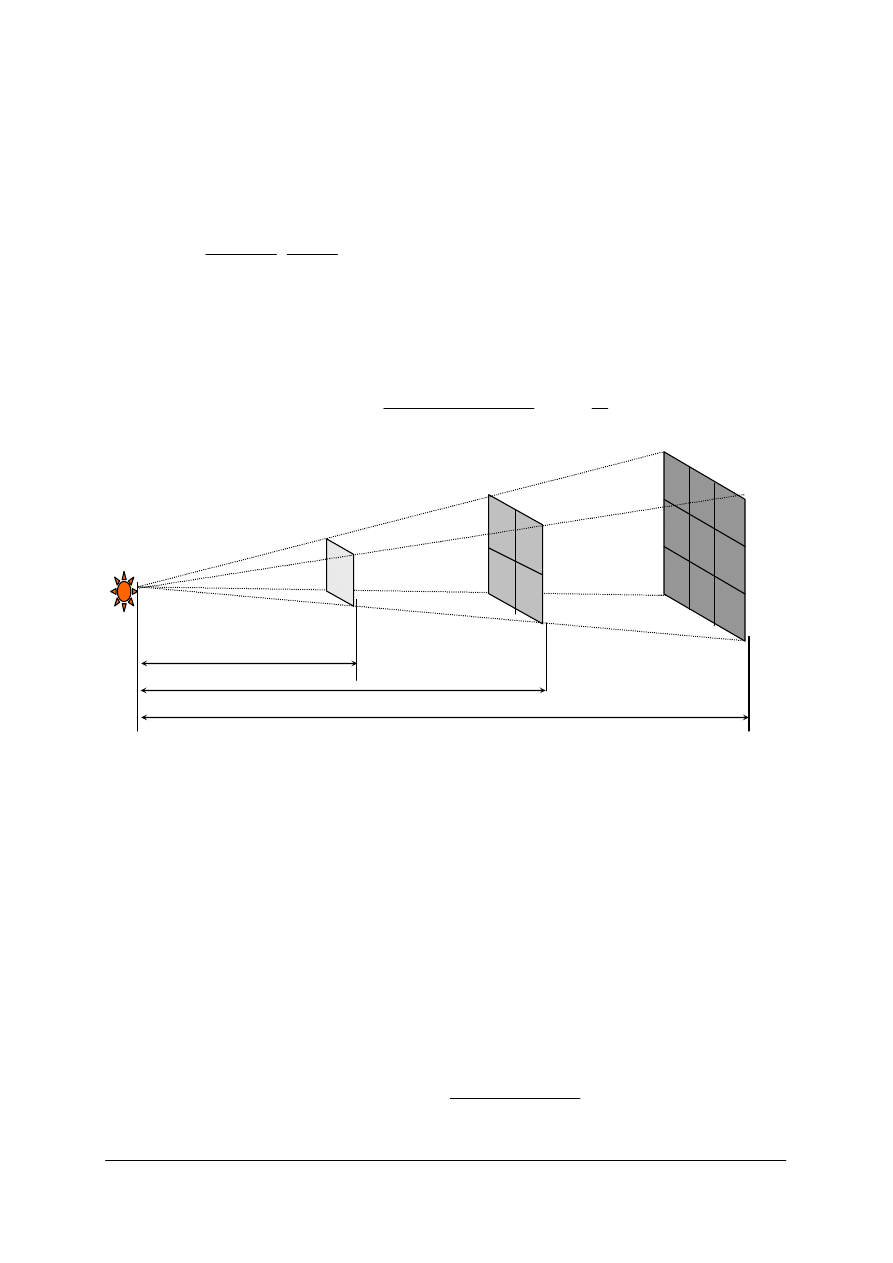
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 68

oznacza  przyrost  mocy  promieniowania,  a  δω  przyrost  kąta  bryłowego,  W  –  (wat)  to 
jednostka mocy, a sr – jednostkowy kąt bryłowy (steradian) 

Luminancja  energetyczna  (gęstość  powierzchniowa  natęŜenia  promieniowania) dotyczy

 

źródła  promieniowania  i  jest  to  stosunek  promieniowania  w  określonym  kierunku  do  pola 
rzutu  powierzchni  emitującej  na  płaszczyznę  prostopadłą  do  tego  kierunku.  WyraŜa  się 

wzorem:

]

[

cos

2

sr

m

W

A

I

L

Θ

=

gdzie I to natęŜenie promieniowania, A – pole powierzchni 

emitującej,  a  Θ  –  kąt  padania  mierzony  od  normalnej.  Luminancja  odnosi  się  do  źródeł 
rozciągłych,  w  przeciwieństwie  do  natęŜenia  promieniowania  źródła,  dotyczącego  źródeł 
punktowych. 

Oświetlenie  powierzchni  jest  równe  mocy  promieniowania  padającego  na  jednostkę 

powierzchni. 

A

E

i

powierzchn

pole

ania

promieniow

moc

e

oswietleni

Φ

=

→

=

 

 

Rys. 96. Ilustracja zmian oświetlenia powierzchni w miarę oddalania jej od punktowego źródła światła. 

A – powierzchnia oświetlana, s – odległość od źródła światła [opracowanie własne] 

 

Wielkość  oświetlenia  dawanego  przez  źródło  punktowe  zmienia  się  odwrotnie 

proporcjonalnie do kwadratu odległości.

 

Ze względu na potrzeby fotometrii wizualnej, traktującej światło z punktu widzenia jego 

odbiorników  (oko,  elementy  optoelektroniczne,  emulsje  fotograficzne,  itp.)  zaistniała 
konieczność  zdefiniowania  innego  układu  jednostek.  Układ  ten  uwzględnia  zjawisko,  Ŝe  ta 
sama  moc  wypromieniowana  ze  źródła  w  postaci  róŜnych  długości  fal,  moŜe  wywoływać 
w odbiorniku róŜne reakcje, zaleŜne od jego krzywej czułości spektralnej. 

Podstawowa  wielkość  fotometrii  wizualnej  to    światłość  (natęŜenie  źródła  światła), 

odpowiednik  natęŜenia  promieniowania  źródła.  Jednostką  światłości  jest  kandela  [cd] 
zdefiniowana  jako  natęŜenie  światła  wypromieniowanego  prostopadle  przez  powierzchnię 
ciała  doskonale  czarnego  o  rozmiarach  1/600000  m

2

,  znajdującą  się  w  temperaturze 

krzepnięcia platyny (ok. 2042°K – 1762°C) pod ciśnieniem 101325 N/m

2 

 

steradian

lumen

kandela

1

1

1

=

 

Jako wzorzec ciała doskonale czarnego przyjęto otwór wnętrza rurki z tlenku toru. 

 

A 

4A 

9A 

s 

3s 

2s 

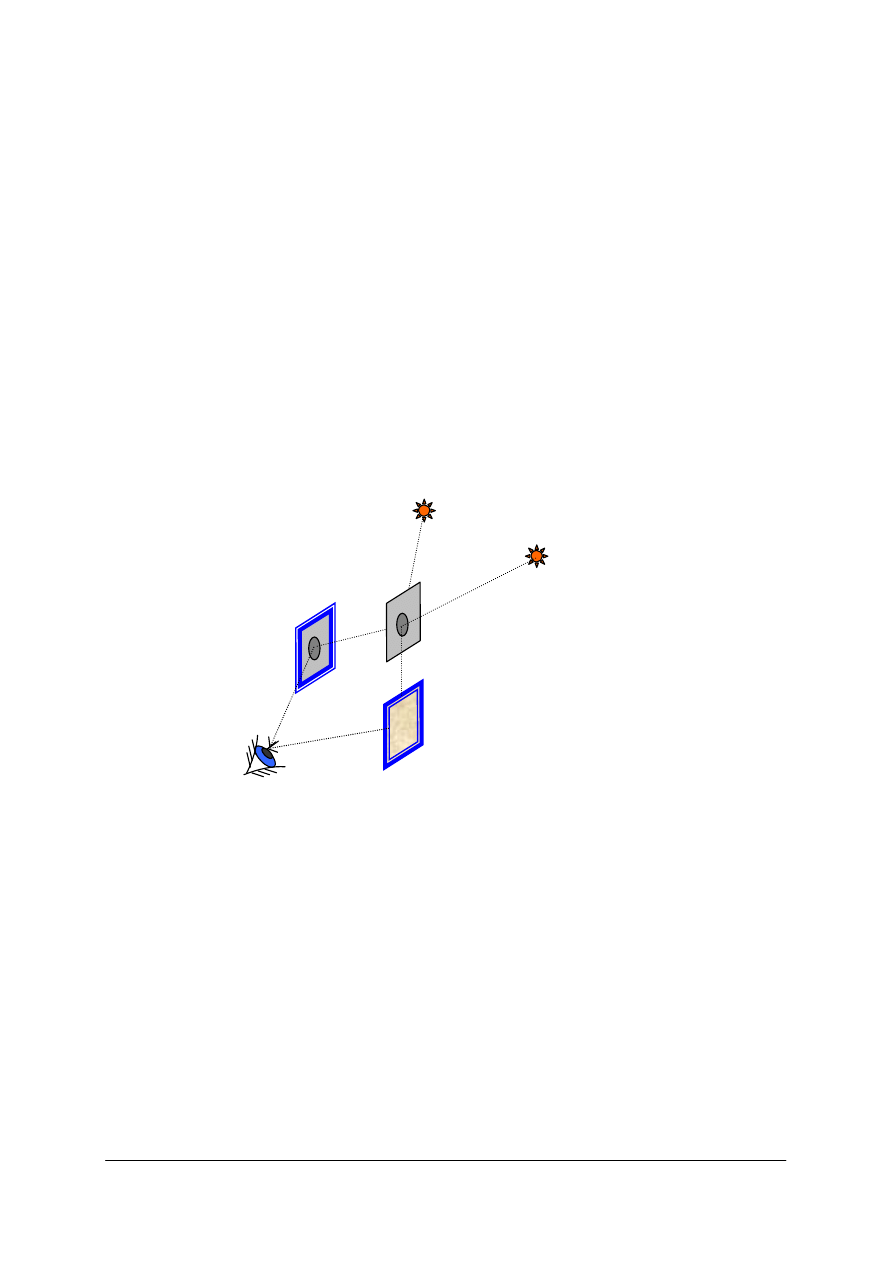
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 69

Z  kandelą  wiąŜe  się  jednostka  luminancji  (jasności)  –  kandela  na  metr  kwadratowy 

(cd/m

2

) – znana pod nazwą nit. 

W fotometrii wizualnej odpowiednikiem mocy  promieniowania jest strumień świetlny –

jest  to  moc  promieniowania  oceniana  na  podstawie  efektu  wywoływanego  przez  nie 
w odbiorniku (oko, światłomierze).wyraŜany w lumenach. 
1 lumen – [1lm] – strumień wysyłany w granicach jednostkowego kąta bryłowego (1 sr) przez 
źródło  punktowe  promieniujące  izotropowo  we  wszystkich  kierunkach  z  natęŜeniem 
1 kandeli. 

Kolejna  wielkością  jest  natęŜenie  oświetlenia.  Jednostką  jest  lux  (lx)  –  natęŜenie 

oświetlenia,  jakie  wywołuje  strumień  świetlny  1  lumena  padający  na  powierzchnię  1  m

2

. 

Jednostką większa jest kilolux. 

NatęŜenie  oświetlenia  oblicza  się  stosunkiem  strumienia  świetlnego  padającego  na  daną 

powierzchnię do pola tej powierzchni – E = I/ s

2

 

Do pomiarów oświetlenia uŜywa się w fotometrii przyrządów zwanych fotometrami. Są 

to  przyrządy  porównujące  natęŜenia  dwóch  źródeł  światła,  z  których  jedno  moŜe  (ale  nie 
musi) być traktowane jako wzorcowe. 

Najprostszym i jednym z najpopularniejszych fotometrów jest fotometr Bunsena. 

 

Rys. 97. Schemat działania fotometru Bunsena. Dwa zwierciadełka (Z

1

 i Z

2

) ustawione w sposób umoŜliwiający 

obserwację arkusza papieru z obu stron równocześnie. Na arkuszu, którego kaŜda ze stron jest oświetlona innym 

źródłem światła (S

1

 i S

2

), znajduje się tłusta plamka znikająca z chwilą, gdy wyrówna się natęŜenie oświetlenia  

po obydwu stronach [opracowanie własne] 

 

Istnieją  równieŜ  fotometry  fotoelektryczne,  w  których  z  sygnałem  wzorcowym 

porównuje się sygnał elektryczny dawany przez fotoczuły odbiornik.  
 
 
 
 
 
 
 
 
 
 
 

S

1 

S

2 

Z

2 

Z

1 

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 70

Tabela 1.  Zestawienie jednostek fotometrycznych [5] 

 

Wielkość 

Symbol 

Jednostka 

Energia promieniowania 

Q

e 

dŜul, 

 [J] 

Gęstość energii 
promieniowania 

W

e 

dŜul/metr

3

, 

 [J/m

3

] 

Moc promieniowania 
(strumień energii) 

Φ

e 

wat, 

 [W] 

Strumień świetlny  

Φ

w 

lumen, 

 [lm] 

NatęŜenie promieniowania 

I

e 

wat/steradian, 

 [W/sr] 

Światłość 

I

w 

kandela, 

 [cd] 

Luminancja energetyczna 

L

e 

wat/metr

2

 × steradian, 

 [W/m

2 

× sr]  

Luminancja (jasność) 

L

w 

kandela/metr

2

 × steradian, 

 [cd/m

2

 × sr] 

Oświetlenie 

E

e 

wat/metr

2

, 

 [W/m

2

] 

NatęŜenie oświetlenia 

E

w 

luks = lumen/metr

2

, 

 [lx] = [lm/m

2

] 

 
 

4.4.2.

 

Pytania sprawdzające 

 

 

Odpowiadając na pytania, sprawdzisz, czy jesteś przygotowany do wykonania ćwiczeń. 

1.

 

Co to jest fotometria i czym się zajmuje? 

2.

 

Co to jest krzywa czułości spektralnej odbiornika? 

3.

 

W jakich jednostkach mierzymy moc promieniowania? 

4.

 

Jakimi jednostkami mierzymy strumień świetlny? 

5.

 

W jakich jednostkach mierzymy natęŜenie promieniowania? 

6.

 

Co to jest kandela? 

7.

 

Jaka jest róŜnica między luminancją (jasnością), a luminancja energetyczną? 

8.

 

W jakich jednostkach mierzymy luminancję? 

9.

 

W jakich jednostkach mierzymy natęŜenie oświetlenia, a w jakich oświetlenie? 

10.

 

Jaka jest definicja natęŜenia oświetlenia? 

11.

 

Jak zmienia się oświetlenie w zaleŜności od źródła światła? 

12.

 

Do czego słuŜą fotometry? 

13.

 

Jak jest zbudowany i jak działa fotometr Bunsena? 

 
 
 
 
 

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 71

4.4.3.

 

Ćwiczenia  

 

Ćwiczenie 1 
 

Nad stołem w odległości 1,5 m wisi Ŝarówka, której luminancja wynosi 2·× 10

6 

cd/m

2

 Na 

stole panuje natęŜenie oświetlenia 50 lx. Wyznaczyć powierzchnię świecącą włókna Ŝarówki, 
światłość Ŝarówki oraz całkowity strumień światła wypromieniowany przez Ŝarówkę. 
 
 

Sposób wykonania ćwiczenia 

 

Aby wykonać ćwiczenie powinieneś: 

1)

 

naszkicować rozmieszczenie elementów i zaznaczyć odległości, 

2)

 

zapisać wartości liczbowe danych wyjściowych zwracając uwagę na jednostki, 

3)

 

napisać wzory na obliczenie szukanych wielkości, 

4)

 

podstawić dane i przeprowadzić obliczenia, 

5)

 

napisać odpowiedź z uzyskanym wynikiem. 

 
 

WyposaŜenie stanowiska pracy: 

−

 

papier formatu A4, 

−

 

linijka z podziałką, trójkąt kreślarski,  ołówek,  

−

 

literatura zgodna z punktem 6 poradnika. 

 

Ćwiczenie 2 
 

KsiąŜkę  trzymamy  w  odległości  3  m  od  punktowego  źródła  światła.  O  ile  zwiększy  się 

natęŜenie oświetlenia, gdy przysuniemy ksiąŜkę na odległość 60 cm od źródła? 

 

 

Sposób wykonania ćwiczenia 

 

 

Aby wykonać ćwiczenie powinieneś: 

1)

 

naszkicować rozmieszczenie elementów i zaznaczyć odległości, 

2)

 

zapisać wartości liczbowe danych wyjściowych zwracając uwagę na jednostki, 

3)

 

napisać wzory na obliczenie szukanych wielkości, 

4)

 

podstawić dane i przeprowadzić obliczenia, 

5)

 

napisać odpowiedź z uzyskanym wynikiem. 

 

 

WyposaŜenie stanowiska pracy: 

−

 

papier formatu A4, 

−

 

linijka z podziałką, trójkąt kreślarski,  ołówek,  

−

 

literatura zgodna z punktem 6 poradnika. 

 

Ćwiczenie 3 
 

Dwa  jednakowe  źródła  światła  są  umieszczone  w  odległości  3  m  od  siebie.  W  jakim 

miejscu między nimi naleŜy umieścić kartkę papieru, aby jedna strona była oświetlona 2 razy 
mocniej niŜ druga? 
 
 

Sposób wykonania ćwiczenia 

 

Aby wykonać ćwiczenie powinieneś: 

1)

 

naszkicować rozmieszczenie elementów i zaznaczyć odległości, 

2)

 

zapisać wartości liczbowe danych wyjściowych zwracając uwagę na jednostki, 

3)

 

napisać wzory na obliczenie szukanych wielkości, 

4)

 

podstawić dane i przeprowadzić obliczenia, 

5)

 

napisać odpowiedź z uzyskanym wynikiem. 

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 72

 

WyposaŜenie stanowiska pracy: 

−

 

papier formatu A4, 

−

 

linijka z podziałka, trójkąt kreślarski,  ołówek,  

−

 

literatura zgodna z punktem 6 poradnika. 

 

4.4.4. Sprawdzian postępów 

 
Czy potrafisz 

Tak 

Nie 

1)

 

zdefiniować jednostki fotometryczne? 

 

 

2)

 

obliczyć natęŜenie oświetlenia? 

 

 

3)

 

zaplanować ustawienie źródeł światła na podstawie załoŜonych róŜnic 
w natęŜeniu oświetlenia? 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 73

5.

 

SPRAWDZIAN OSIĄGNIĘĆ 

 

INSTRUKCJA DLA UCZNIA  

1.

 

Przeczytaj uwaŜnie instrukcję. 

2.

 

Podpisz imieniem i nazwiskiem kartę odpowiedzi. 

3.

 

Zapoznaj się z zestawem zadań testowych. 

4.

 

Test  zawiera  28  zadań.  Do  kaŜdego  zadania  dołączone  są  4  moŜliwości  odpowiedzi. 
Tylko jedna z nich jest prawidłowa 

5.

 

Udzielaj  odpowiedzi  tylko  na  załączonej  karcie  odpowiedzi  stawiając  w  odpowiedniej 
rubryce  znak  X.  W  przypadku  pomyłki  naleŜy  błędną  odpowiedź  zaznaczyć  kółkiem,  a 
następnie ponownie zaznaczyć odpowiedź prawidłową. 

6.

 

W całym teście dopuszczalne są tylko 3 poprawki. 

7.

 

Pracuj samodzielnie, bo tylko wtedy będziesz miał satysfakcję z wykonanego zadania. 

8.

 

JeŜeli udzielenie odpowiedzi będzie Ci sprawiało trudność, wtedy odłóŜ jego rozwiązanie 
na później i wróć do niego, gdy zostanie Ci wolny czas. 

9.

 

Na rozwiązanie testy masz 45 minut. 

 

ZESTAW ZADAŃ TESTOWYCH  
 

1.

 

Ciemnia optyczna (camera obscura) działa dzięki 
a)

 

prawu prostoliniowego rozchodzenia się światła. 

b)

 

zjawisku cienia. 

c)

 

prawu załamania. 

d)

 

zjawisku dyspersji. 

 

2.  Wnętrze  przyrządu  optycznego  pokrywamy  czarnym,  matowym  lakierem  w  celu 

otrzymania powierzchni: 
a)

 

odbijającej selektywnie. 

b)

 

odbijającej dyfuzyjnie. 

c)

 

odbijającej kierunkowo. 

d)

 

nie odbijającej. 

 

3.  Źródło  światła  moŜemy  uznać  jako  punktowe,  jeśli  jego  wymiar  liniowy  mierzony  

poprzecznie do kierunku promieniowania jest mniejszy od 
a)

 

20 mm 

b)

 

1/ 100 odległości od obserwatora. 

c)

 

20 cm 

d)

 

1/20 odległości od obserwatora. 

 

4.  Aby nastąpiło całkowite  wewnętrzne odbicie przy przejściu światła z ośrodka  gęstszego  

do rzadszego kąt padania musi być 
a)

 

większy od kąta granicznego załamania. 

b)

 

mniejszy od kąta granicznego załamania. 

c)

 

większy od kąta całkowitego wewnętrznego odbicia. 

d)

 

mniejszy od kąta całkowitego wewnętrznego odbicia. 

 
 
 
 

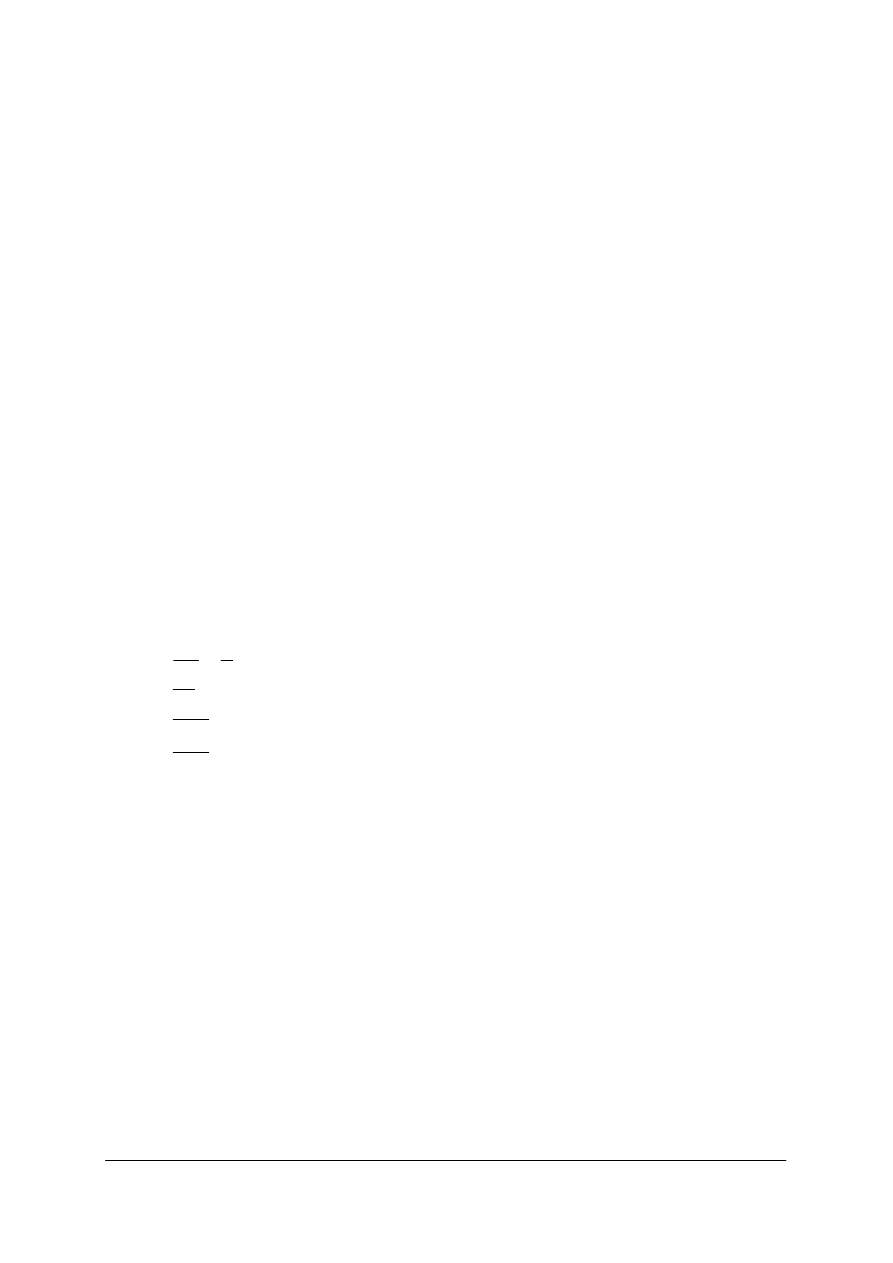
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 74

5.   Zwierciadło płaskie moŜe dać obraz 

a)

 

prosty w poziomie i prosty w pionie. 

b)

 

odwrócony w poziomie i odwrócony w pionie. 

c)

 

nieczytelny. 

d)

 

czytelny. 

 
6.  Przed zwierciadłem sferycznym wypukłym powstaje obraz 

a)

 

rzeczywisty odwrócony. 

b)

 

rzeczywisty  prosty. 

c)

 

pozorny odwrócony. 

d)

 

obraz nie powstaje. 

 
7.  Ogniskowa  wklęsłego  zwierciadła  sferycznego  wynosi  5  cm  przedmiot  umieszczono  

w odległości 10 cm. Obraz przedmiotu dawany przez to zwierciadło będzie 
a)

 

powiększony prosty. 

b)

 

pomniejszony pozorny. 

c)

 

rzeczywisty, taki sam wielkościowo. 

d)

 

pozorny, taki sam wielkościowo. 

 
8.  Kąt odchylenia pryzmatu nie zaleŜy od parametru 

a)

 

kąta łamiącego. 

b)

 

współczynnika załamania. 

c)

 

współczynnika dyspersji. 

d)

 

kąta padania światła. 

 
9.  Dyspersji względnej dotyczy wyraŜenie 

a)

 

n

n

i

i

'

'

sin

sin

=

. 

b)

 

'

'

sin

sin

n

i

i

=

. 

c)

 

∆

=

−

−

1

D

C

F

n

n

n

. 

d)

 

ν

=

−

−

C

F

D

n

n

n

1

. 

 

10.  Mocą optyczna pojedynczej powierzchni nazywamy 

a)

 

odwrotność ogniskowej przedmiotowej. 

b)

 

odwrotność ogniskowej obrazowej. 

c)

 

stosunek róŜnicy współczynników załamania do promienia krzywizny. 

d)

 

stosunek promienia krzywizny do róŜnicy współczynników załamania. 

 

11.  Menisk dodatni to soczewka, która ma pierwszy promień 

a)

 

większy od drugiego i jest grubsza w środku. 

b)

 

mniejszy od drugiego i jest cieńsza w środku. 

c)

 

większy od drugiego i jest grubsza na brzegu. 

d)

 

mniejszy od drugiego i jest grubsza na brzegu. 

 

12.  Odległość obrazowa pojedynczej powierzchni sferycznej to odległość między 

a)

 

płaszczyzną przedmiotową a płaszczyzna obrazową. 

b)

 

punktem wierzchołkowym powierzchni a płaszczyzną obrazową. 

c)

 

ogniskiem obrazowym a punktem wierzchołkowym powierzchni. 

d)

 

płaszczyzną przedmiotową a ogniskiem obrazowym. 

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 75

13.  Wiązka skolimowana ujemnie to wiązka 

a)

 

zbieŜna przychodząca do ogniska obrazowego. 

b)

 

rozbieŜna wychodząca z ogniska przedmiotowego. 

c)

 

równoległa do osi optycznej. 

d)

 

równoległa do promienia głównego. 

 

14.  Do określenia mocy soczewki cienkiej oprócz promieni krzywizn trzeba podać 

a)

 

współczynnik załamania. 

b)

 

współczynnik dyspersji. 

c)

 

grubość w środku. 

d)

 

nic więcej. 

15.  Z pojęciem przysłony aperturowej związana nie jest 

a)

 

liczba otworu. 

b)

 

źrenica wejściowa. 

c)

 

źrenica wyjściowa. 

d)

 

luka wejściowa. 

 

16.  O wielkości pola widzenia układu decyduje średnica 

a)

 

elementu widzianego pod najmniejszym kątem ze środka apertury. 

b)

 

elementu widzianego pod największym kątem ze środka apertury. 

c)

 

pierwszej soczewki. 

d)

 

ostatniej soczewki. 

 

17.  Błąd  odwzorowania  polegający  na  tym,  Ŝe  monochromatyczne  promienie  wychodzące  

 z punktu przedmiotowego na osi tworzą jego obraz rozciągnięty wzdłuŜ osi nazywamy 

a)

 

aberracją sferyczną. 

b)

 

komą. 

c)

 

krzywizną pola. 

d)

 

aberracją chromatyczną. 

 

18.  Aberracją osiową jest wyłącznie aberracja 

a)

 

astygmatyzmu. 

b)

 

koma. 

c)

 

sferyczna. 

d)

 

krzywizny pola. 

 

19.   Wielkość dotycząca ruchu falowego wyraŜana w jednostkach długości to 

a)

 

λ – długość fali 

b)

 

ν – częstotliwość 

c)

 

T – okres 

d)

 

σ – liczba falowa 

 

20.  Interferometry to przyrządy mierzące 

a)

 

częstotliwość fal. 

b)

 

róŜnicę amplitudy. 

c)

 

róŜnicę dróg optycznych. 

d)

 

róŜnicę częstotliwości. 

 
 

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 76

21.  PrąŜki  Newtona  obserwowane  na  styku  powierzchni  badanej  z  płaską  mają  kształt  

 eliptyczny. Świadczy to, Ŝe powierzchnia jest 

a)

 

toryczna. 

b)

 

sferyczna. 

c)

 

cylindryczna. 

d)

 

nieregularna. 

 

22.   Grubość warstwy przeciwodblaskowej na powierzchni szkła jest zaleŜna od 

a)

 

róŜnicy współczynników załamania. 

b)

 

sumy współczynników załamania. 

c)

 

iloczynu współczynników załamania. 

d)

 

ilorazu współczynników załamania. 

 

23.  Przy  fotografowaniu  źródła  światła  przez  obiektyw  posiadający  przysłonę  w  kształcie  

 czworokąta otrzymamy na zdjęciu dyfrakcyjne smugi w postaci gwiazdy 

a)

 

czteroramiennej. 

b)

 

pięcioramiennej. 

c)

 

ośmioramiennej. 

d)

 

dziesięcioramiennej. 

 

24.  Dyfrakcja to zmiana kierunku biegu światła 

a)

 

w wyniku załamania na powierzchni rozgraniczającej dwa ośrodki optyczne. 

b)

 

w wyniku ugięcia na krawędzi przeszkody mechanicznej. 

c)

 

na powierzchni odbijającej. 

d)

 

pod wpływem płynnie zmieniającego się współczynnika załamania ośrodka 

 

25.  Po  wstawieniu  przed  analizator  płytki  ćwierćfalowej,  nie  widać  zmian  natęŜenia  światła  

 przy jej obrocie. Jest to światło 

a)

 

spolaryzowane eliptycznie. 

b)

 

spolaryzowane kołowo. 

c)

 

spolaryzowane liniowo. 

d)

 

naturalne niespolaryzowane. 

 

26.  Jednostką luminancji jest 

a)

 

kandela. 

b)

 

nit. 

c)

 

luks 

d)

 

steradian. 

 

27.  Jeśli zwiększymy odległość powierzchni od źródła światła to oświetlenie powierzchni 

a)

 

zmaleje wprost proporcjonalnie. 

b)

 

zmaleje proporcjonalnie do kwadratu odległości. 

c)

 

wzrośnie wprost proporcjonalnie. 

d)

 

wzrośnie wprost proporcjonalnie do kwadratu odległości. 

 

28.  W holograficznej metodzie rejestracji obrazu nie potrzeba 

a)

 

emulsji fotograficznej. 

b)

 

obiektywu. 

c)

 

zaistnienia interferencji. 

d)

 

róŜnicy dróg optycznych. 

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 77

KARTA ODPOWIEDZI 

 
Imię i nazwisko.......................................................................................... 
 

Projektowanie elementów i układów optycznych 

 
Zakreśl poprawną odpowiedź. 

 

Nr 

zadania 

Odpowiedź 

Punkty 

1

 

 

a 

b 

c 

d 

 

2

 

 

a 

b 

c 

d 

 

3

 

 

a 

b 

c 

d 

 

4

 

 

a 

b 

c 

d 

 

5

 

 

a 

b 

c 

d 

 

6

 

 

a 

b 

c 

d 

 

7

 

 

a 

b 

c 

d 

 

8

 

 

a 

b 

c 

d 

 

9

 

 

a 

b 

c 

d 

 

10

 

 

a 

b 

c 

d 

 

11

 

 

a 

b 

c 

d 

 

12

 

 

a 

b 

c 

d 

 

13

 

 

a 

b 

c 

d 

 

14

 

 

a 

b 

c 

d 

 

15

 

 

a 

b 

c 

d 

 

16

 

 

a 

b 

c 

d 

 

17

 

 

a 

b 

c 

d 

 

18

 

 

a 

b 

c 

d 

 

19

 

 

a 

b 

c 

d 

 

20

 

 

a 

b 

c 

d 

 

21

 

 

a 

b 

c 

d 

 

22

 

 

a 

b 

c 

d 

 

23

 

 

a 

b 

c 

d 

 

24

 

 

a 

b 

c 

d 

 

25

 

 

a 

b 

c 

d 

 

26

 

 

a 

b 

c 

d 

 

27

 

 

a 

b 

c 

d 

 

28

 

 

a 

b 

c 

d 

 

Razem: 

 

 

 

 

 

 

 

 

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego” 

 78

6.

 

LITERATURA    

 
1.

 

Hanc T.: Pomiary optyczne. Wydawnictwo WNT, Warszawa 1964. 

2.

 

Hein  A.,  Sidorowicz  A.,  Wagnerowski  T.:  Oko  i  okulary.  Wydawnictwo  Przemysłu 
Lekkiego i SpoŜywczego, Warszawa 1966 

3.

 

Jóźwicki  R.:  Optyka  instrumentalna.  Wydawnictwo  Naukowo-Techniczne,  Warszawa 
1970 

4.

 

Krawcow  J.A.,  Orłow  J.I.:  Optyka  geometryczna  ośrodków  jednorodnych.  Wydawnictwo 
Naukowo-Techniczne, Warszawa 1993 

5.

 

Meyer-Arendt J.R.: Wstęp do optyki, PWN 1977 

6.

 

Nowak  T.,  Zając  M.:  Optyka  –  kurs  elementarny.  Oficyna  Wydawnicza  Politechniki 
Wrocławskiej, Wrocław 1998 

7.

 

Sojecki A.: Optyka. WSiP Warszawa 1997 

8.

 

Zając M.: Optyka okularowa. Dolnośląskie Wydawnictwo Edukacyjne, Wrocław 2003