3 

 

Spis treści: 
1.Wstęp. 

 

 

 

 

 

 

 

 

 

 

4. 

 

1.1. Podstawa formalna opracowania. 

 

 

 

 

 

4. 

 

1.2. Przedmiot opracowania.  

 

 

 

 

 

 

4. 

 

1.3. Cel i zakres.  

 

 

 

 

 

 

 

 

4. 

 

1.4. Wykorzystane materiały. 

 

 

 

 

 

 

4. 

2. Analiza warunków gruntowo‐wodnych.   

 

 

 

 

 

4. 

3. Ustalenie kategorii geotechnicznej. 

 

 

 

 

 

 

5. 

4. Przyjęcie wartości parametrów geotechnicznych. 

 

 

 

 

5. 

5.Rozkład naprężeń pierwotnych.   

 

 

 

 

 

 

8. 

6. Podział podłoża na warstwy obliczeniowe. 

 

 

 

 

 

10. 

7. Odciążenie podłoża wykopem. 

 

 

 

 

 

 

 

10. 

8. Rozkład naprężeń od obciążenia zewnętrznego.   

 

 

 

 

13. 

9. Wyznaczenie wartości naprężeń dodatkowych i wtórnych. 

 

 

 

16. 

10. Określenie głębokości strefy aktywnej.   

 

 

 

 

 

17. 

11. Rysunek zbiorczy naprężeń. 

 

 

 

 

 

 

 

17. 

12. Obliczenie osiadań. 

 

 

 

 

 

 

 

 

19. 

13. Sprawdzenie warunku drugiego stanu granicznego. 

 

 

 

 

20 

14.Wnioski.   

 

 

 

 

 

 

 

 

 

20 

 

 

4 

 

1. Wstęp. 
 
1.1 Podstawa formalna opracowania: 
 

Niniejsze opracowanie projektowe zostało wykonane w ramach ćwiczeń 

projektowych z mechaniki gruntów I w toku studiów na Wydziale Budownictwa Lądowego i 
Wodnego Politechniki Wrocławskiej. 
 
1.2 Przedmiot opracowania: 
 

Przedmiotem opracowania jest wykop szerokoprzestrzenny zabezpieczony 

deskowaniem oraz grunty znajdujące się pod nim, na których ma być wzniesiony budynek do 
11 kondygnacji. 
Dokładną sytuację projektową pokazano na rys. 1 
 
1.3 Cel i zakres: 
 

Celem opracowania projektowego jest obliczenie osiadania punktu A (rys. 1) 

znajdującego się u podstawy fundamentu. Zadany fundament jest częścią konstrukcji 
budynku którego wysokość nie przekracza 11 kondygnacji. 
W zakres wykonywanych obliczeń wliczono: 
‐ oznaczenie rozkładu naprężeń pierwotnych 
‐ obliczenie odciążenia podłoża wykopem 
‐ oznaczenie rozkładu naprężeń od obciążeń zewnętrznych 
‐ wyznaczenie wartości naprężeń dodatkowych i wtórnych 
‐ obliczenie osiadań 
 
1.4 Wykorzystane materiały 
‐ PN‐EN ISO 14688 
‐ PN‐81/B‐03020 –„Grunty budowlane. Posadowienie bezpośrednie budowli. Obliczenia 
statyczne i projektowe” 
‐ PN‐86/B‐02480 – „Grunty budowlane. Podział, nazwy, symbole i określenia” 

2. Analiza warunków gruntowo – wodnych. 
 

Na podstawie zadanych warunków gruntowych określono stan zawilgocenia 

poszczególnych warstw gruntu. 
Zwierciadło wody gruntowej znajduje się na głębokości 6,8m, t.j. w 1/3 miąższości drugiej 
warstwy gruntu – piasku średniego i jest jedynym zwierciadłem wody gruntowej na badanej 
głębokości. 
 

W związku z powyższym stan zawilgocenia piasku średniego określono jako wilgotny 

(S

r

 = 0,8). Z kolei dla warstwy poniżej, czyli gliny piaszczystej , z uwagi ,że znajduje się poniżej 

zwierciadła wody gruntowej przyjęto stan zawilgocenia – mokry (S

r

 = 1). Warstwa górna – 

warstwa gliny zwięzłej ma stan wilgotności mało wilgotny (S

r

 = 0,4). 

 

Podciąganie kapilarne dla piasku średniego wynosi około 1 m ,więc nie wpłynie na 

zawilgocenie gliny zwięzłej, zalegającej 2,3 m ponad zwierciadłem wody gruntowej. 

5 

 

Stan zawilgocenia gruntów wpływa na ich właściwości i możliwości wykorzystania w 
budownictwie. Warstwa gliny zwięzłej i pisaku średniego mają stany wilgotności optymalne 
do posadowienia na nich budowli. Warstwa gliny piaszczystej jest w stanie mokrym, co 
utrudnia posadowienie konstrukcji na takim podłożu. 

 
3. Ustalenie kategorii geotechnicznej. 
 

Na podstawie normy PN‐B‐02479: 1998 – „Geotechnika. Dokumentowanie 

geotechniczne. Zasady ogólne” ustalono kategorię geotechniczną dla zadanej w ćwiczeniu 
projektowym sytuacji gruntowej.  
Ustalono, że obowiązuje II kategoria geotechniczna. Przy wyborze wzięto pod uwagę rodzaj 
budowli – budynek do 11 kondygnacji , z mało skomplikowanymi przypadkami obciążeń oraz 
występowanie warstw gruntów słabych i niebezpiecznych. W zadanej sytuacji gruntowej 
mamy do czynienia z warstwą gliny piaszczystej w stanie mokrym co znacznie zmienia jej 
cechy wytrzymałościowe. 
 
4. Przyjęcie wartości parametrów geotechnicznych. 
 

Na podstawie zadanych warunków gruntowych określono parametry geotechniczne, 

korzystając z wartości charakterystycznych danych gruntów zamieszczonych w normie PN‐
81/B‐03020 oraz podstawowych zależności korelacyjnych miedzy cechami gruntu. 
Przyjęto metodę B do wyznaczania parametrów geotechnicznych. 
Aby uwzględnić wpływ historii geologicznej na własności inżynierskie gruntów, przyjęto, że 
wszystkie grunty należą do grupy C. 
Wszystkie parametry zamieszczono w tabeli 1. 
 
Do obliczeń przyjęto: 
g = 10 m/s

2

 

ρ

w

 = 1 t/m

3

 

γ

w

 = 10 kN/m

3

 

 
Objaśnienie stosowanych symboli: 
I

L

 – stopień plastyczności gruntu spoistego 

I

D 

– stopień zagęszczenia gruntu sypkiego 

S

R 

– stopień wilgotności gruntu 

ρ

s 

– gęstość właściwa szkieletu gruntowego 

ρ

 

– gęstość objętościowa gruntu 

ρ

d 

– gęstość nasypowa szkieletu gruntowego 

ρ

sat 

– gęstość objętościowa gruntu przy całkowitym nasyceniu wodą 

n – porowatość 
γ

s 

–ciężar właściwy szkieletu gruntowego 

γ

 

– ciężar objętościowy gruntu 

γ

sat 

– ciężar objętościowy gruntu przy całkowitym nasyceniu wodą 

6 

 

w

n

 – wilgotność naturalna 

β – wskaźnik skonsolidowania gruntu 
M

0

 – edometryczny moduł ściśliwości pierwotnej 

M – edometryczny moduł ściśliwości wtórnej 
φ

n

 – kąt tarcia wewnętrznego 

C

u

 – spójność gruntu 

 

 

 

 
Parametr β odczytano z Tablicy 3. Na stronie 15, zaś M

0

 z monogramów 6b dla gruntów 

sypkich i 7b dla gruntów spoistych ze strony 16 i 17 normy PN‐81/B‐03020. 
Podstawowe cechy fizyczne gruntów odczytano z tablicy 1 ze strony 11 normy PN‐81/B‐
03020. 
 
Korzystałem ze wzorów: 
γ

sat

 = (1 ‐ n) ∙ γ

s 

+ n ∙ γ

w

 

I

L 

= 1 – I

C

 

 

 

 

 

 

 

7 

 

Tablica 1. Parametry geotechniczne. 
 

 
 
 
 
 
 

 

 

Symbol 

gruntu wg 

PN‐EN ISO 

14688 

Nazwa 

gruntu wg 

PN‐EN ISO 

14688 

Nazwa 

gruntu wg 

PN‐81‐B‐

03020 

I

L 

I

D

 

ρ

s

 

ρ 

n 

γ

 s

 

γ 

γ

sat

 

w

n

 

β 

M

0

 

M 

φ

u 

C

u

 

[t/m

3

]

[t/m

3

]

[kN/m

3

] [kN/m

3

] [kN/m

3

]

[%] 

[kPa] 

[kPa] 

[ ° ]

[kPa] 

saCl 

Glina 

piaszczysta 

Glina 

zwięzła 

0,4 

‐‐ 

2,69 

2,00 

0,26 

26,9 

19,62 

22,51 

24 

0,75 

24000 

32000 

14,8 

25 

MSa 

Piasek 

średni 

Piasek 

średni 

‐‐ 

0,42 

2,65 

1,85 

0,30 

26,5 

18,15 

21,55 

14 

0,9 

100000 111111

32,2 

‐‐ 

clgrSa 

Piasek 

żwirowy z 

gliną 

Glina 

piaszczysta 

0,7 

‐‐ 

2,67 

2,00 

0,25 

26,7 

19,62 

22,53 

24 

0,75 

14000 

18667 

8,4 

16 

8 

 

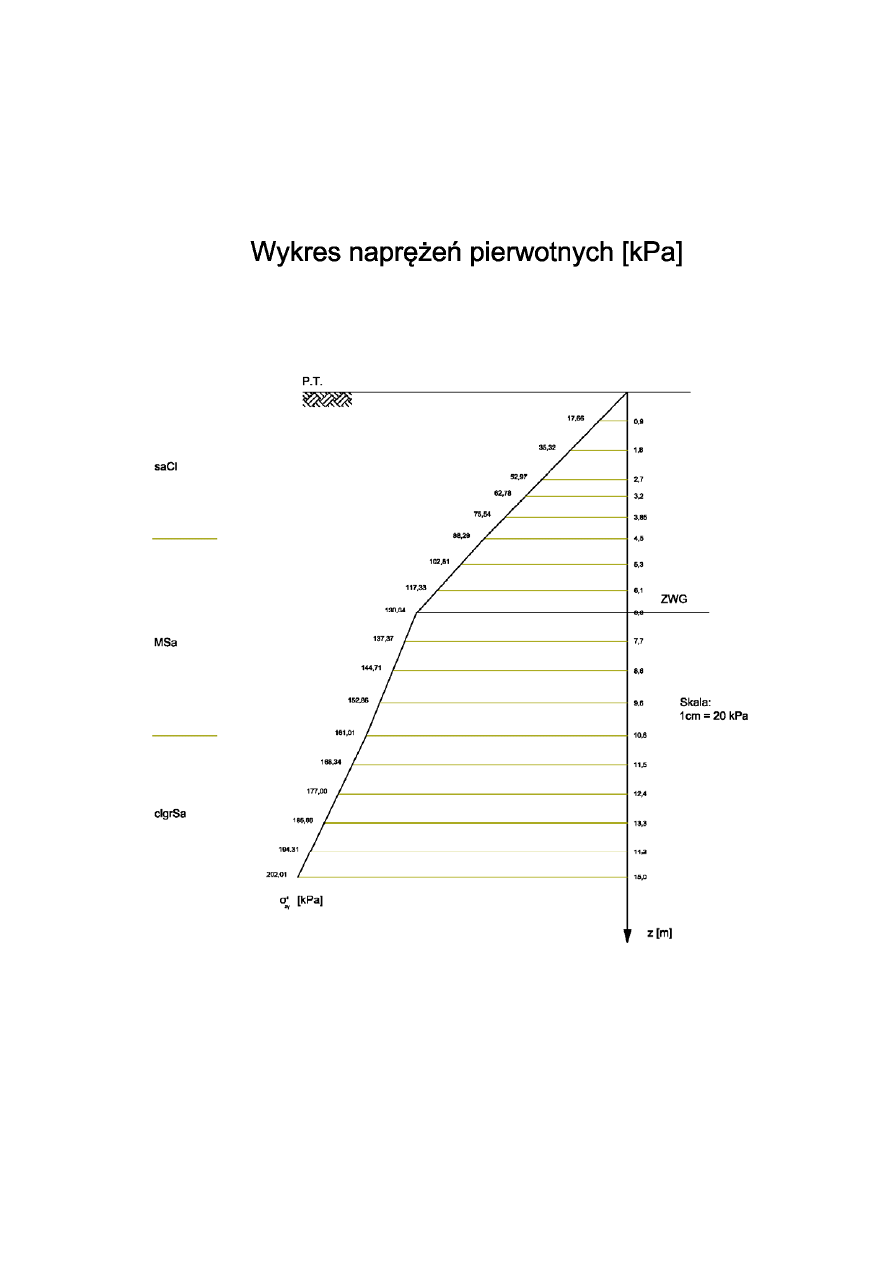
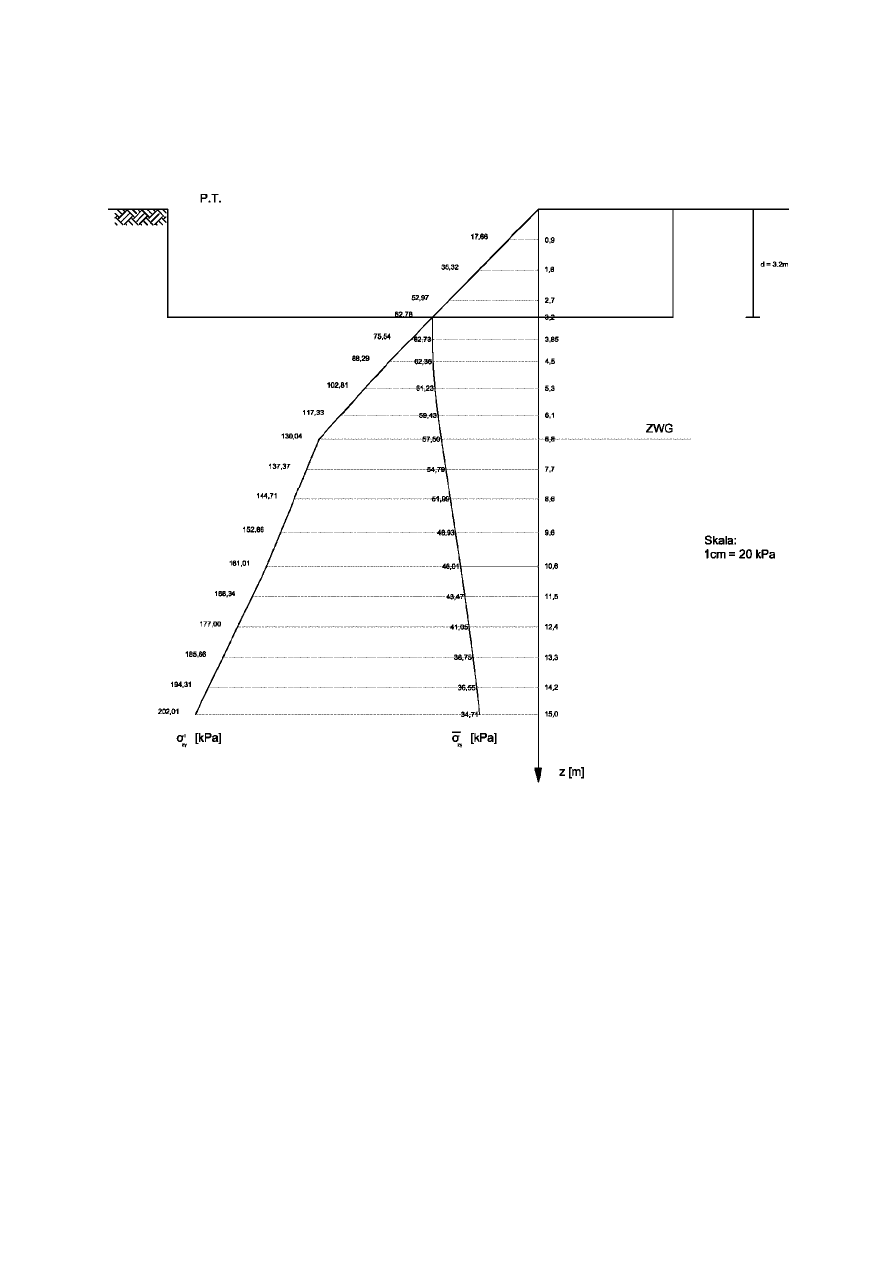
5. Rozkład naprężeń pierwotnych. 
 

Naprężenia pierwotne spowodowane są pionowym naciskiem kolejnych warstw 

gruntu zalegających w podłożu ponad poziomem z. 
Oblicza się je ze wzoru: 
 

 

 

∑

·  

gdzie: 
h

i

 – miąższość i‐tej warstwy 

γ

i

 – ciężar objętościowy gruntu i‐tej warstwy 

 
Obliczeń dokonano wykorzystując zasadę naprężeń efektywnych: 
 

σ = σ’ + u 

gdzie: 
σ – naprężenia całkowite 
σ’ – naprężenia efektywne 
u – ciśnienie porowe wody 
 

u = h

w

 ∙ γ

w

 

gdzie: 
h

w

 – wysokość słupa wody 

γ

w

 – ciężar objętościowy 

 
Tabela 2. Wartości naprężeń pierwotnych: 

Warstwa 

γ

i

 

h

i

 

z

cal

 

σ

zγ

u 

σ

zγ’

 

[kN/m

3

] 

[m] 

[m] 

[kPa] 

[kPa] 

[kPa] 

saCl 

19,62 

0,9 

0,9 

17,66 

0 

17,66 

0,9 

1,8 

35,32 

0 

35,32 

0,9 

2,7 

52,97 

0 

52,97 

0,5 

3,2 

62,78 

0 

62,78 

0,65 

3,85 

75,54 

0 

75,54 

0,65 

4,5 

88,29 

0 

88,29 

MSa 

18,15 

0,8 

5,3 

102,81 

0 

102,81 

0,8 

6,1 

117,33 

0 

117,33 

0,7 

6,8 

130,04 

0 

130,04 

Tu 

γ

sat 

powinno 

być 

wstawione 

0,9 

7,7 

146,37 

9 

137,37 

0,9 

8,6 

162,71 

18 

144,71 

1 

9,6 

180,86 

28 

152,86 

1 

10,6 

199,01 

38 

161,01 

0,9 

11,5 

215,34 

47 

168,34 

clgrSa 

19,62 

0,9 

12,4 

233,00 

56 

177,00 

0,9 

13,3 

250,66 

65 

185,66 

0,9 

14,2 

268,31 

74 

194,31 

0,8 

15 

284,01 

82 

202,01 

9 

 

 

 

 

10 

 

6. Podział podłoża na warstwy obliczeniowe. 
B = 15m 

 

z

max

 = 15m 

 

z ≤ B  , więc h

i

 ≤ B/4 i h

i

 ≤ 1m, 

stąd przyjęto, że h

i 

≤ 1m 

Zwierciadło wody jest granicą warstewek. 
 
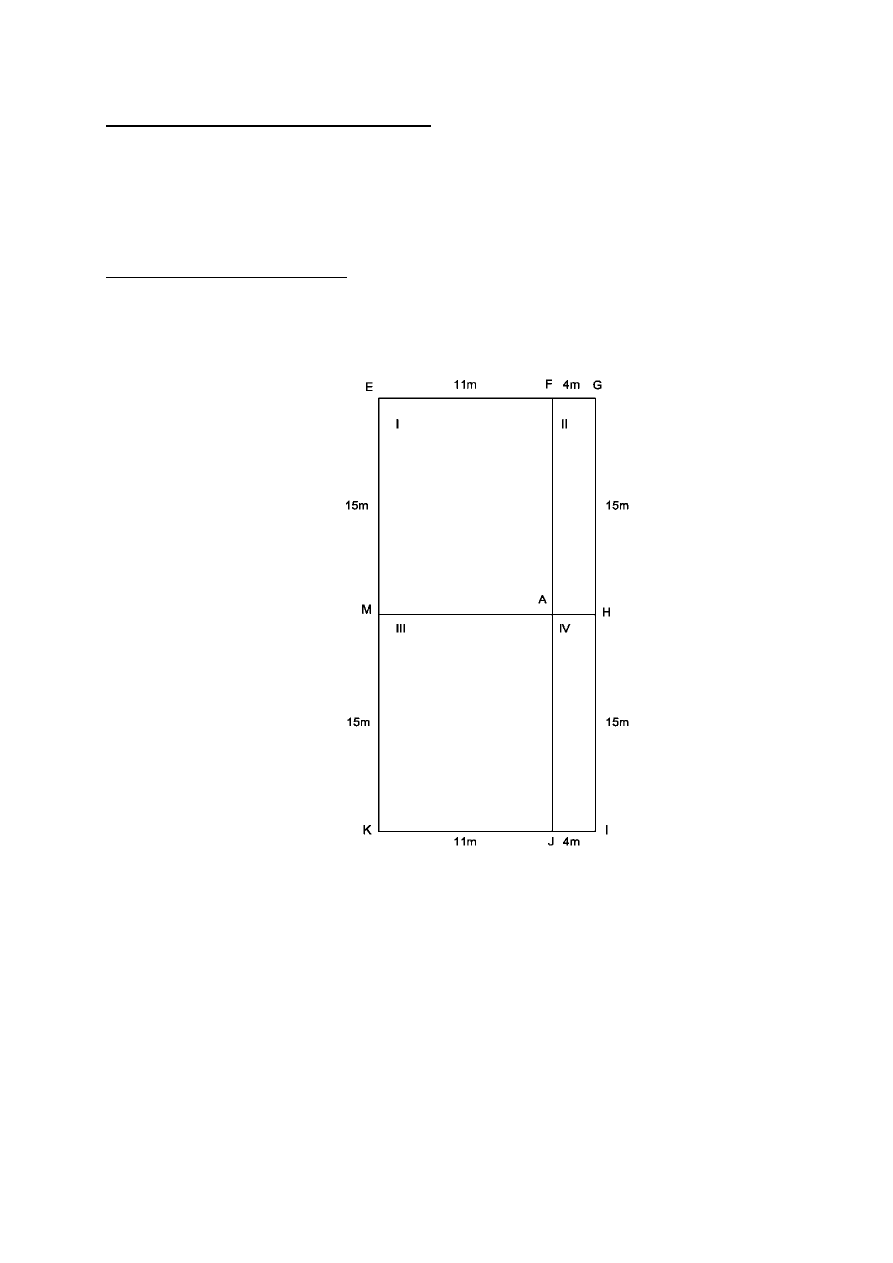
7. Odciążenie podłoża wykopem. 
 

Do obliczeń wykorzystano metodę punktów narożnych. Obszar wykopu dzielimy na 

cztery prostokąty. 

‐ prostokąt EFAM:  

B = 11m 

L= 15m 

L/B = 1,36 

‐ prostokąt FGHA:  

B = 4m  

L= 15m 

L/B = 3,75 

‐ prostokąt AHIJ:  

B = 4m  

L= 15m 

L/B = 3,75 

‐ prostokąt AJKM:  

B = 11m 

L= 15m 

L/B = 1,36 

 
Odciążenie podłoża obliczono ze wzoru: 

·

 

gdzie: 
q

D

 = D ∙ γ

D 

 

11 

 

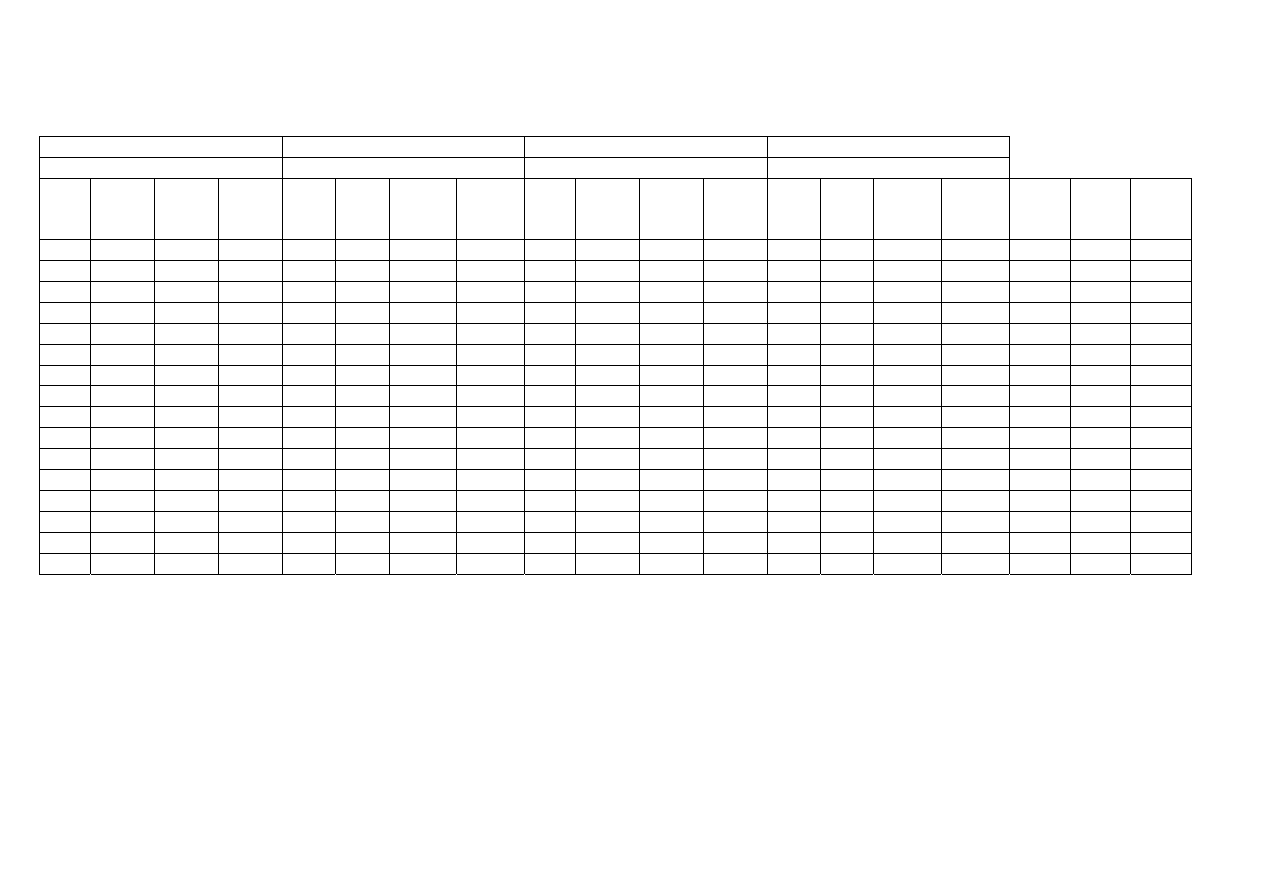
Tabela 3. Wartości naprężeń wywołanych odciążeniem: 

q

D

 = 19,62kN/m

3

 ∙ 3,2m = 62,784 kN/m

3 

 

 

  

 

 

 

 

Prostokąt I 

Prostokąt II 

Prostokąt III 

Prostokąt IV 

 

B = 11,00m     L = 15,00m 

B = 4,00m     L = 15,00m 

B = 11,00m     L = 15,00m 

B = 4,00m     L = 15,00m 

Z/B 

L/B 

η

n

 

 

Z/B 

L/B 

η

n

 

 

Z/B 

L/B 

η

n

 

 

Z/B 

L/B 

η

n

 

 

 

 

 

‐ 

‐ 

‐ 

[kPa] 

‐ 

‐ 

‐ 

[kPa] 

‐ 

‐ 

‐ 

[kPa] 

‐ 

‐ 

‐ 

[kPa] 

‐ 

[kPa] 

[kPa] 

0,00 

1,36 

0,250 

15,70 

0,00 

3,75 

0,250 

15,70 

0,00 

1,36 

0,250 

15,70 

0,00 

3,75 

0,250 

15,70 

1,000 

62,78 

0 

0,06 

1,36 

0,250 

15,70 

0,16 

3,75 

0,250 

15,67 

0,06 

1,36 

0,250 

15,70 

0,16 

3,75 

0,250 

15,67 

0,999 

62,73 

12,80 

0,12 

1,36 

0,250 

15,68 

0,33 

3,75 

0,247 

15,50 

0,12 

1,36 

0,250 

15,68 

0,33 

3,75 

0,247 

15,50 

0,993 

62,36 

25,93 

0,19 

1,36 

0,249 

15,64 

0,53 

3,75 

0,239 

14,97 

0,19 

1,36 

0,249 

15,64 

0,53 

3,75 

0,239 

14,97 

0,975 

61,23 

41,58 

0,26 

1,36 

0,248 

15,55 

0,73 

3,75 

0,226 

14,16 

0,26 

1,36 

0,248 

15,55 

0,73 

3,75 

0,226 

14,16 

0,947 

59,43 

57,90 

0,33 

1,36 

0,246 

15,43 

0,90 

3,75 

0,212 

13,32 

0,33 

1,36 

0,246 

15,43 

0,90 

3,75 

0,212 

13,32 

0,916 

57,50 

72,54 

0,41 

1,36 

0,242 

15,21 

1,13 

3,75 

0,194 

12,18 

0,41 

1,36 

0,242 

15,21 

1,13 

3,75 

0,194 

12,18 

0,873 

54,79 

82,58 

0,49 

1,36 

0,238 

14,92 

1,35 

3,75 

0,176 

11,08 

0,49 

1,36 

0,238 

14,92 

1,35 

3,75 

0,176 

11,08 

0,828 

51,99 

92,72 

0,58 

1,36 

0,231 

14,51 

1,60 

3,75 

0,159 

9,96 

0,58 

1,36 

0,231 

14,51 

1,60 

3,75 

0,159 

9,96 

0,779 

48,93  103,92 

0,67 

1,36 

0,224 

14,03 

1,85 

3,75 

0,143 

8,97 

0,67 

1,36 

0,224 

14,03 

1,85 

3,75 

0,143 

8,97 

0,733 

46,01  115,00 

0,75 

1,36 

0,216 

13,55 

2,08 

3,75 

0,130 

8,19 

0,75 

1,36 

0,216 

13,55 

2,08 

3,75 

0,130 

8,19 

0,692 

43,47  124,87 

0,84 

1,36 

0,208 

13,03 

2,30 

3,75 

0,119 

7,49 

0,84 

1,36 

0,208 

13,03 

2,30 

3,75 

0,119 

7,49 

0,654 

41,05  135,95 

0,92 

1,36 

0,199 

12,50 

2,53 

3,75 

0,110 

6,87 

0,92 

1,36 

0,199 

12,50 

2,53 

3,75 

0,110 

6,87 

0,617 

38,75  146,91 

1,00 

1,36 

0,190 

11,95 

2,75 

3,75 

0,101 

6,32 

1,00 

1,36 

0,190 

11,95 

2,75 

3,75 

0,101 

6,32 

0,582 

36,55  157,76 

1,07 

1,36 

0,183 

11,47 

2,95 

3,75 

0,094 

5,88 

1,07 

1,36 

0,183 

11,47 

2,95 

3,75 

0,094 

5,88 

0,553 

34,71  167,30 

12 

 

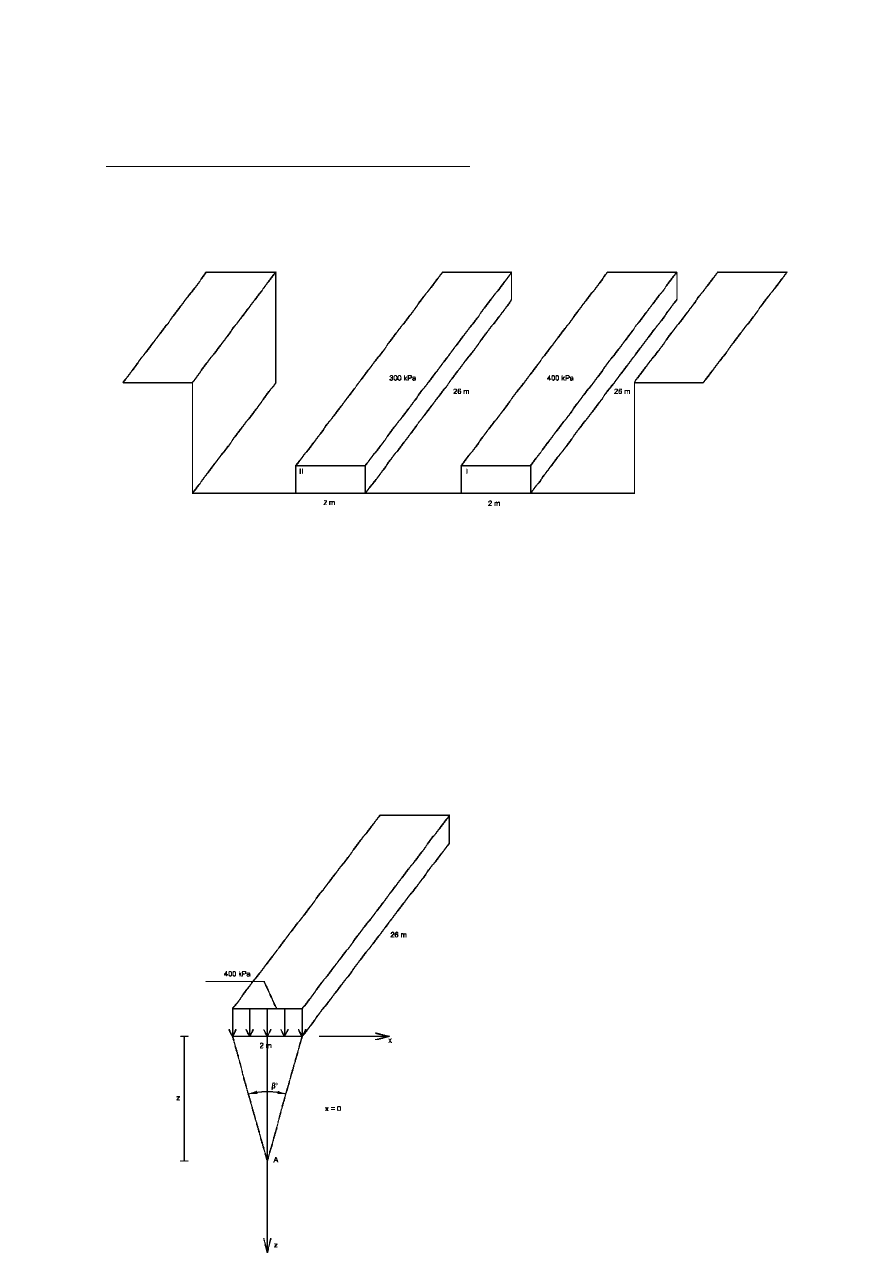
Wykres ilustrujący odciążenie podłoża wykopem [kPa]: 
 

 

 

 

 

 

 

 

 

 

13 

 

 

8. Rozkład naprężeń od obciążenia zewnętrznego. 
 

 

 

Zgodnie z normą PN‐81/B‐03020 jeśli mamy do czynienia z płaskim stanem 

naprężenia, tj. L ≥ 10B i punkt A leży w przekroju przechodzącym w odległości nie większej 
niż 3B od krótszego boku to stosujemy rozkład naprężeń od obciążeń pasmowych. 
 
W przypadki zadanego obciążenia mamy do czynienia z płaskim stanem naprężenia: 
L

I

 = 26 > 20 = 10 ∙ B

I

  

L

II

 = 26 > 20 = 10 ∙ B

II 

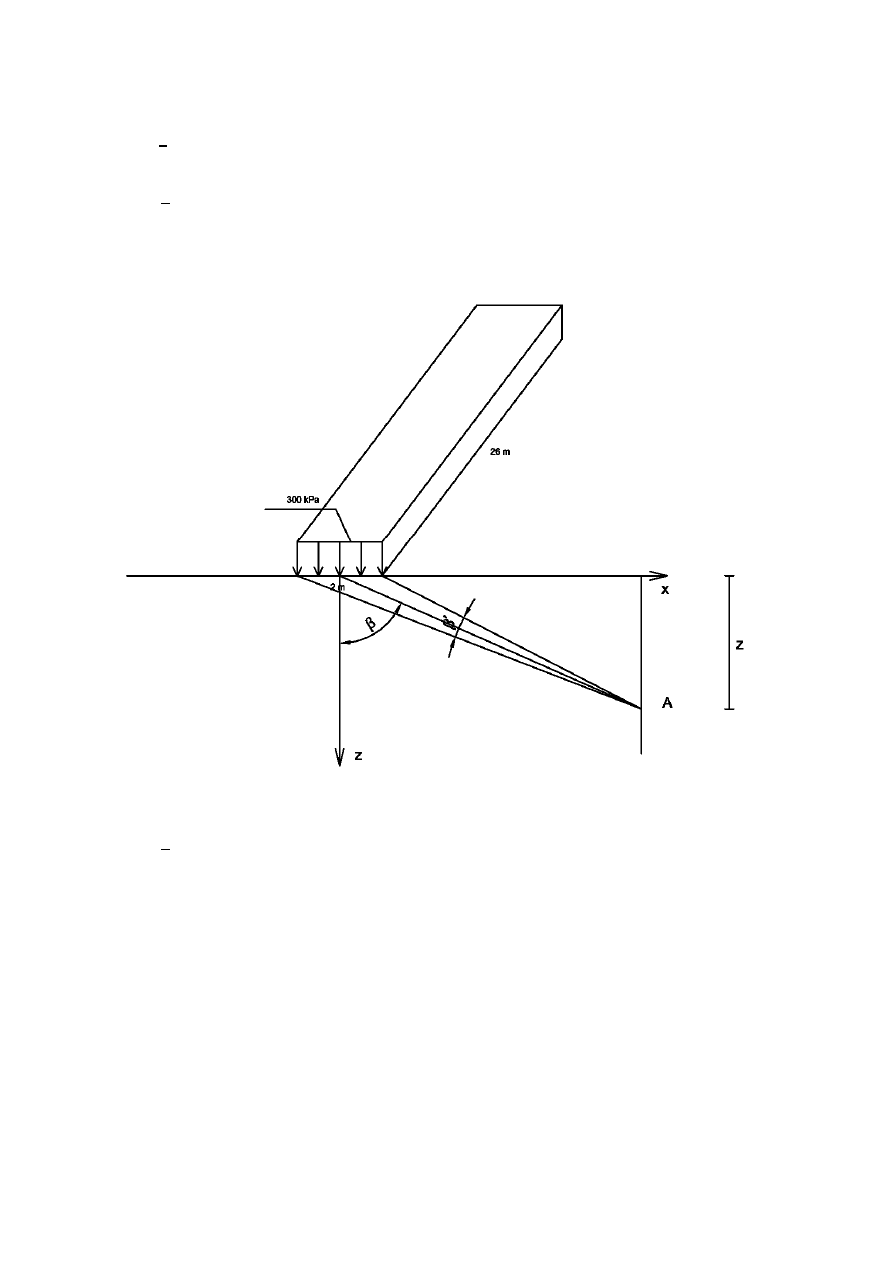
Dla obciążenia I : 

14 

 

Korzystamy ze wzoru:

  

 

 

2   

Po uwzględnieniu warunków zadania wzór przyjmuje postać: 

 

 

 

 

Dla obciążenia II: 

Korzystamy ze wzoru: 

 

 

 

2  

Wyniki zestawiono w tabelach: 4a, 4b i 4c. 
 

 

 

 

 

 

15 

 

 
Tabela 4a. Wartości naprężeń od obciążenia zewnętrznego I. 

z

w

 

q 

β 

β' 

 

[m] 

[kPa] 

[rad] 

[rad] 

[kPa] 

0 

400 

0 

3,141593 

400 

0,65 

0 

1,989675 

369,65 

1,3 

0 

1,310742 

289,93 

2,1 

0 

0,92677 

219,82 

2,9 

0 

0,66497 

163,23 

3,6 

0 

0,541052 

134,47 

4,5 

0 

0,438078 

109,79 

5,4 

0 

0,364774 

91,87 

6,4 

0 

0,310669 

78,48 

7,4 

0 

0,268781 

68,03 

8,3 

0 

0,23911 

60,60 

9,2 

0 

0,216421 

54,90 

10,1 

0 

0,197222 

50,06 

11 

0 

0,181514 

46,10 

11,8 

0 

0,169297 

43,01 

 

Tabela 4b. Wartości naprężeń od obciążenia zewnętrznego II. 

z

w

 

q 

β 

2β 

β' 

 

[m] 

[kPa] 

[rad] 

[rad] 

[rad] 

[kPa] 

0 

300 

1,570796  3,141593 

0 

0 

0,65 

1,480039  2,960078 

0,02618 

0,04 

1,3 

1,389282  2,778564  0,050615 

0,32 

2,1 

1,29678 

2,593559  0,075049 

1,06 

2,9 

1,183333  2,366666  0,099484 

2,72 

3,6 

1,101303  2,202606  0,115192 

4,52 

4,5 

1,00531 

2,010619  0,129154 

7,10 

5,4 

0,919789  1,839577  0,136136 

9,56 

6,4 

0,837758  1,675516  0,141372 

12,09 

7,4 

0,764454  1,528908  0,141372 

14,06 

8,3 

0,706858  1,413717  0,139626 

15,41 

9,2 

0,656244  1,312488  0,136136 

16,31 

10,1 

0,612611  1,225221  0,132645 

16,94 

11 

0,572468  1,144936  0,129154 

17,41 

11,8 

0,541052  1,082104  0,123918 

17,37 

 

 

16 

 

 

Tabela 4c. Wartości naprężeń od całkowitego obciążenia zewnętrznego. 

z

w

 

 

[m] 

[kPa] 

0 

400,00 

0,65 

369,69 

1,3 

290,25 

2,1 

220,87 

2,9 

165,95 

3,6 

138,98 

4,5 

116,89 

5,4 

101,42 

6,4 

90,57 

7,4 

82,10 

8,3 

76,01 

9,2 

71,21 

10,1 

67,00 

11 

63,51 

11,8 

60,38 

Korzystamy ze wzoru: 
 

  

9. Wyznaczenie wartości naprężeń dodatkowych i wtórnych. 

σ

zd

 – naprężenia dodatkowe 

σ

zs

 – naprężenia wtórne 

‐ gdy σ

zq

 > 

 , wtedy: 

 

σ

zs

 = 

 

 

σ

zd

 = σ

zq 

‐ 

 

 

‐ gdy σ

zq

 ≤  

 , wtedy: 

 

σ

zs

 = σ

zq

  

 

σ

zd

 = 0  (nie występują) 

 

 

 

 

 

 

17 

 

 

Tabela 5. Zestawienie naprężeń dodatkowych i wtórnych. 

z

w

 

σ

zs 

σ

zd

 

[m] 

[kPa] 

[kPa] 

0 

62,78 

337,22 

0,65 

62,73 

306,96 

1,3 

62,36 

227,89 

2,1 

61,23 

159,64 

2,9 

59,43 

106,52 

3,6 

57,5 

81,48 

4,5 

54,79 

62,10 

5,4 

51,99 

49,43 

6,4 

48,93 

41,64 

7,4 

46,01 

36,09 

8,3 

43,47 

32,54 

9,2 

41,05 

30,16 

10,1 

38,75 

28,25 

11 

36,55 

26,96 

11,8 

34,71 

25,67 

 
10. Określenie głębokości strefy aktywnej. 
 

Strefa aktywna jest to głębokość na jakiej zachodzi (liczy się) osiadanie. 

Głębokość tej strefy obliczamy wg wzoru: 
0,3 σ

zq max

 = σ

zqi

  

Po podstawieniu do wzoru: 0,3 ∙ 400kPa = 120 kPa 
Więc osiadanie liczymy do 6 warstewki licząc od dna wykopu, tj. do głębokości 4,5 m od dna 
wykopu. 
 
 

 

 

 

 

 

 

11. Zbiorczy wykres naprężeń 

18 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

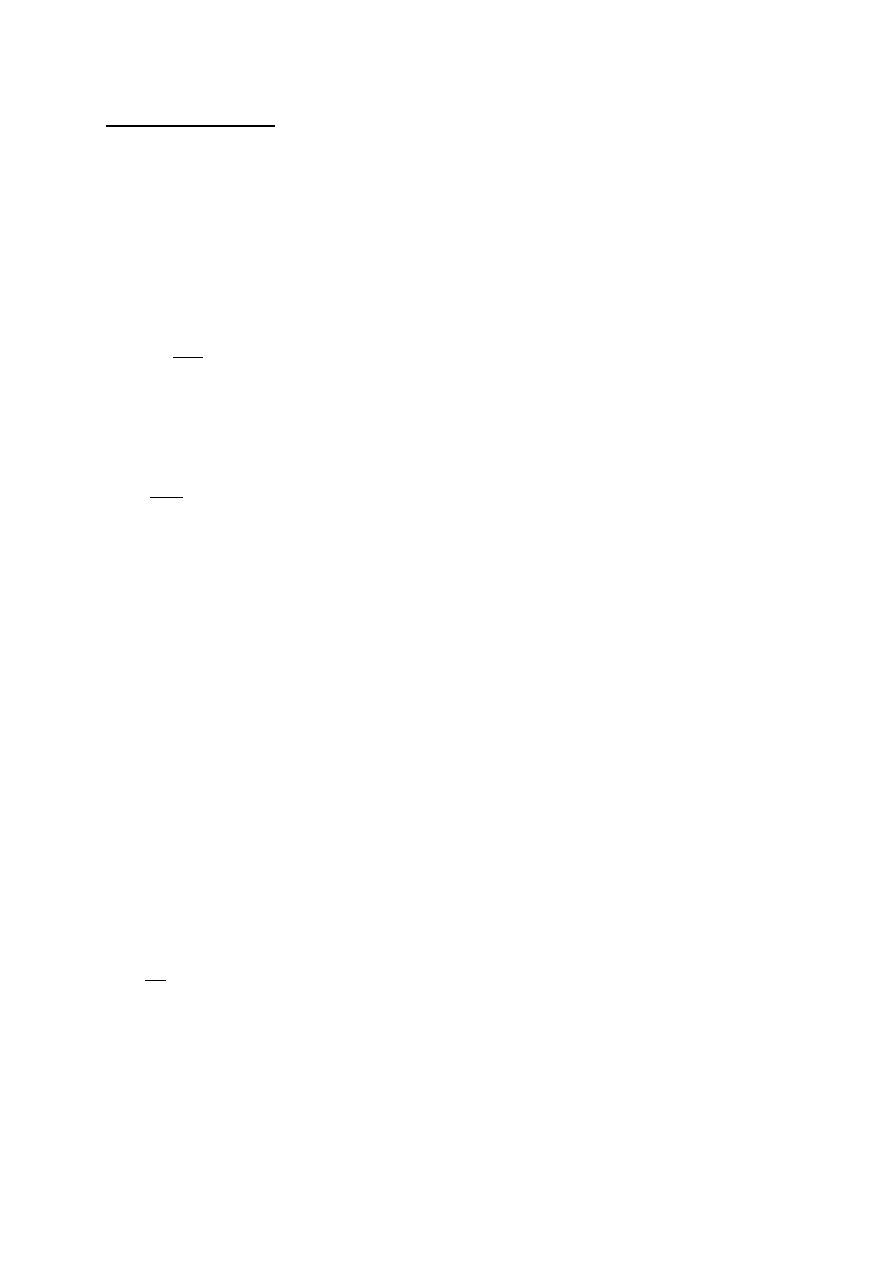
19 

 

12. Obliczenie osiadań. 
Osiadanie obliczono wykorzystując metodę odkształceń jednoosiowych (opartą na analogu 
enometrycznym). 
Sumowanie osiadań przeprowadzono do głębokości z

max

 = 4,5m 

Osiadanie S

i

 i‐tej warstewki obliczono ze wzoru: 

 

 

S

i

 = S

i

’’ + S

i

’ 

gdzie: 
S’’ – osiadanie wtórne i‐tej warstwy [m] 

·

∆

·    [λ=1] 

λ – współczynnik zależny od czasu budowy 

 ‐ naprężenia wtórne w środku warstwy i  

M

i

 – enometryczny moduł ściśliwości wtórnej 

 

∆

·     

 ‐ naprężenia dodatkowe w środku i‐tej warstwy  

M

0i

 – enometryczny moduł ściśliwości pierwotnej 

 
Osiadanie punktu A wyznaczono ze wzoru: 

∑

  

 
Założenia do metody odkształceń jedno‐osiowych: 
‐ stan odkształcenia: 
ε

x

 = ε

y

 = 0 

ε

z

 = 0 

 
‐ stan naprężeń (osiowosymetrycznych): 
σ

x

 = σ

y

   0 

σ

z

   σ

x 

σ

z 

= const.   0 

 
‐ równanie konstytutywne 

∆

  

gdzie: 
ε ‐ odkształcenie 
Δσ – średnia wartość naprężeń 
M – enometryczny moduł ściśliwości 
 
Obliczenia zamieszczono w tabeli 6. 

20 

 

 
Tabela 6. Obliczenie osiadań. 

Grunt  zw 

σ

zs

 

σ

zd

 

σ

zs

* 

σ

zd

* 

h

i

 

M

oi

 

M

i

 

S

i

’ 

S

i

’’ 

 

‐‐‐ 

[m] 

[kPa] 

[kPa] 

[kPa] 

[kPa]  [m]

[kPa] 

[kPa] 

[m] 

[m] 

[m] 

saCl 

0 

62,78  337,22 

‐‐‐ 

‐‐‐ 

‐‐‐ 

‐‐‐ 

‐‐‐ 

‐‐‐ 

‐‐‐ 

‐‐‐ 

62,75  322,09 0,65

24000 

32000 

0,008723 

0,001275 

0,0100 

0,65  62,73  306,96 

62,55  267,42 0,65

24000 

32000 

0,007243 

0,001271 

0,0085 

1,3 

62,36  227,89 

61,80  193,76 0,8 

100000 

111111 

0,001550 

0,000445 

0,0020 

MSa 

2,1 

61,23  159,64 

60,33  133,08 0,8 

100000 

111111 

0,001065 

0,000434 

0,0015 

2,9 

59,43  106,52 

58,47 

94,00  0,7 

100000 

111111 

0,000658 

0,000368 

0,0010 

3,6 

57,5 

81,48 

56,15 

71,79  0,9 

100000 

111111 

0,000646 

0,000455 

0,0011 

4,5 

54,79 

62,10 

 

 

 

 

Suma: 

0,0241 

 

Wg obliczeń zestawionych w tabeli 6. Osiadanie całkowite punktu A pod fundamentem dla 
zadanych warunków wodno – gruntowych wynosi: 
S

A

 = 0,0241m = 2,41 cm 

13. Sprawdzenie warunku drugiego stanu granicznego. 
 

S ≤ S

dop 

S

dop

 ustala się dla danej budowli na podstawie analizy stanów granicznych jaj konstrukcji, 

wymagań użytkowych  i eksploatacyjnych, a także działania połączeń instalacyjnych. 
Wg normy PN‐81/B‐03020 dopuszczalne wartości przemieszczeń liniowych i odkształceń 
zachodzących w fazie eksploatacji budowli dla budynku do 11 kondygnacji wynoszą 7 cm. 

 

 

S

A

 = 2,41 cm, zatem S

A

 < S

dop 

 
Warunek drugiego stanu granicznego został spełniony. 
 
14. Wnioski.