K.Czopek, M.Zazulak – Notatki w internecie. Wstęp do fizyki atomowej i kwantowej.

I.

PROMIENIOWANIE CIEPLNE

- lata '90 XIX wieku

WSTĘP

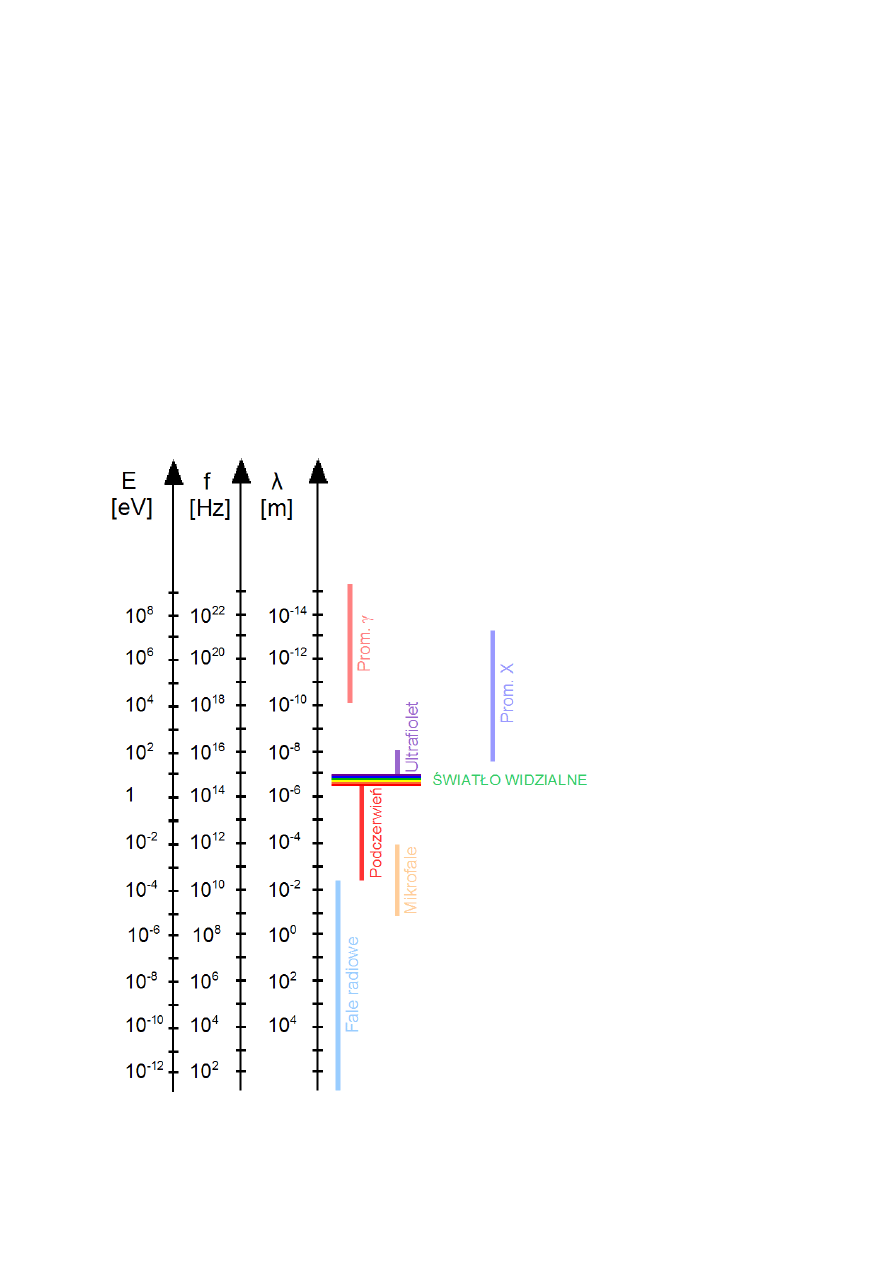
Widmo promieniowania elektromagnetycznego – zakres "pokrycia" różnymi rodzajami fal
elektromagnetycznych promieniowania zawartego w danej wiązce.

rys.I.1. Widmo fal elektromagnetycznych. Dla promieniowania widzialnego (światła) długość fali

λ

mieści się

w zakresie od 380 – 780 nm.

– 1 –

K.Czopek, M.Zazulak – Notatki w internecie. Wstęp do fizyki atomowej i kwantowej.

E ~ f (są skorelowane liniowo)
Im mniejsza energia tym mniejszy wpływ oddziaływania na komórki żywe.
Podczerwień, promieniowanie widzialne i promieniowanie UV są składnikami
promieniowania słonecznego.

I.1. PROMIENIOWANIE PODCZERWONE (CIEPLNE)

–

odegrało znaczącą rolę w rozwoju fizyki kwantowej

–

promieniowanie wysyłane przez ciało ogrzane do pewnej temperatury

–

wszystkie ciała, których temperatura jest różna od zera emitują promieniowanie
termiczne do otoczenia i absorbują je z niego

–

każde ciało dąży do osiągnięcia równowagi termodynamicznej

Zakres energii E i długości fali λ promieniowania cieplnego.

1meV

≤ E ≤ 1 eV

10

-6

m

≤  ≤ 10

-3

m

I.2. ZJAWISKO WYTWARZANIA PROMIENIOWANIA – PROCES EMISJI

(OPIS KLASYCZNY)

Źródłem promieniowania jest ładunek elektryczny

a) ładunek stacjonarny

(

a=0 =>v=0 ∨v=const

),

gdzie a – przyspieszenie, v – prędkość.

Przypadek statyczny:

Wokół ładunku q

0

wytwarza się pole elektryczne

E=

F

q

0

(I.2.1)

gdzie:
F – siła elektrostatyczna

– 2 –

K.Czopek, M.Zazulak – Notatki w internecie. Wstęp do fizyki atomowej i kwantowej.

q

0

0

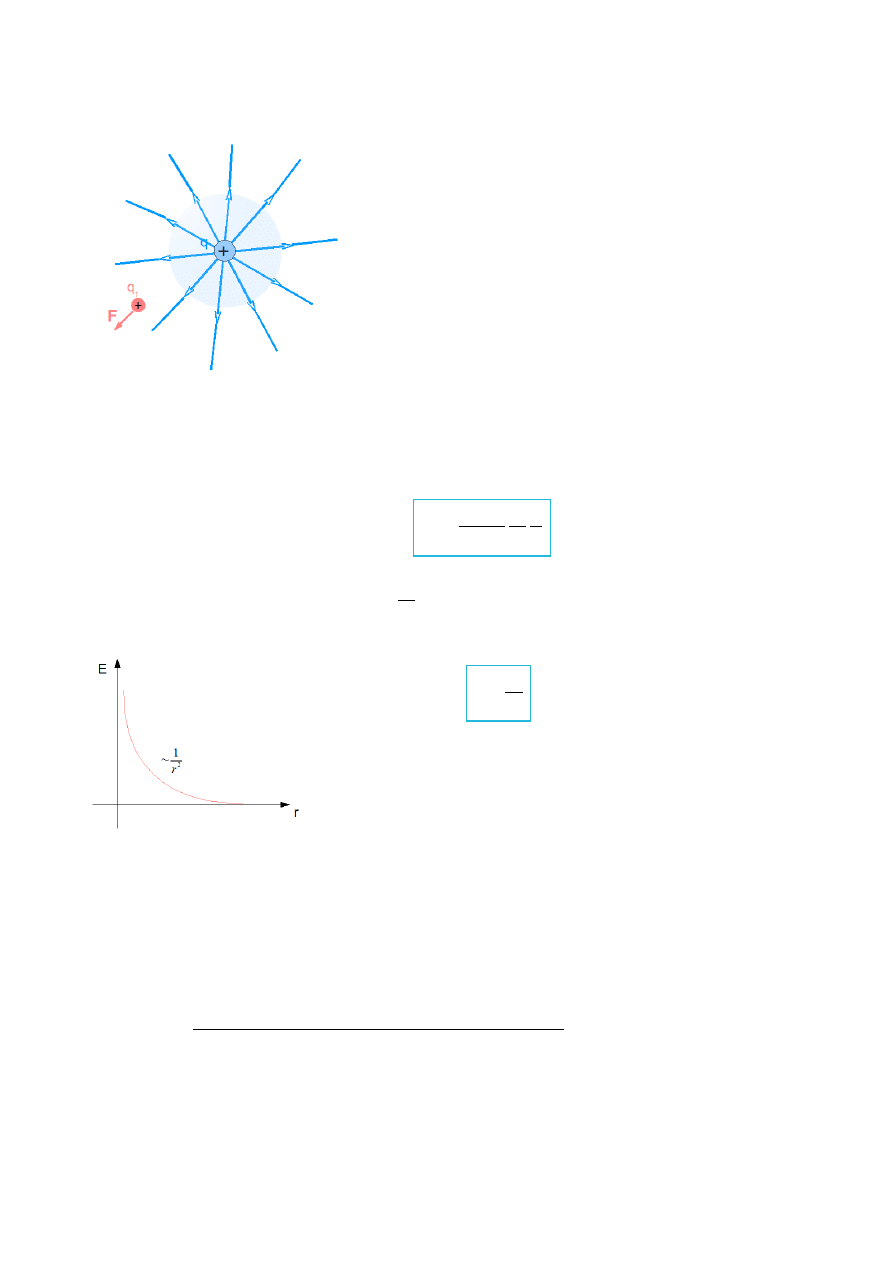
Linie pola: w każdym miejscu są równoległe do natężenia
pola.
Kierunek: wyznaczony przez ruch ładunku dodatniego
umieszczonego w polu elektrycznym.
Natężenia linii pola elektrycznego E jest równe gęstości
linii sił.

rys.I.2. Ruch ładunku dodatniego q

1

w polu elektrycznym pochodzącym od dodatniego ładunku punktowego

q.

Dla ładunku punktowego q w odległości r natężenie pola elektrycznego wyraża się
wzorem:

E

=

1

4

 

0

q

r

2

r

r

(I.2.2)

gdzie

ε

0

=8,854187⋅10

-12

F

m

– przenikalność elektryczna próżni

E

~

1

r

2

(I.2.2a)

rys.I.3. Zależność natężenia pola E od odległości r dla ładunku punktowego.

ρ

E

– gęstość energii pola elektrycznego E

ρ

E

~E

2

Z przestrzeni wokół ładunku stacjonarnego nie jest emitowana fala elektromagnetyczna, z
czego wynika, że energia jest stacjonarna.

b) ładunek poruszający się ze stałą prędkością v.

–

W tym przypadku energia również jest stacjonarna, porusza się wraz z ładunkiem.
Dodatkowo wytwarza się pole magnetyczne o indukcji B:

– 3 –

K.Czopek, M.Zazulak – Notatki w internecie. Wstęp do fizyki atomowej i kwantowej.

B ≠ 0

~B

2

~E

2

B

2

(I.2.3)

Pomimo pojawienia się pola elektromagnetycznego, nie ma emisji promieniowania
(stacjonarne pole elektromagnetyczne).

c) ładunek doznaje przyspieszenia

a ≠ 0

–

Każdy ładunek doznający przyspieszenia emituje promieniowanie.

r >>1,

E

┴

, B

┴

(

E

┴

⊥B

┴

)

 = 0

=2  f t=2



T

t

= t

E = E

0

sin(2

π

ft)

B = B

0

sin(2

π

ft)

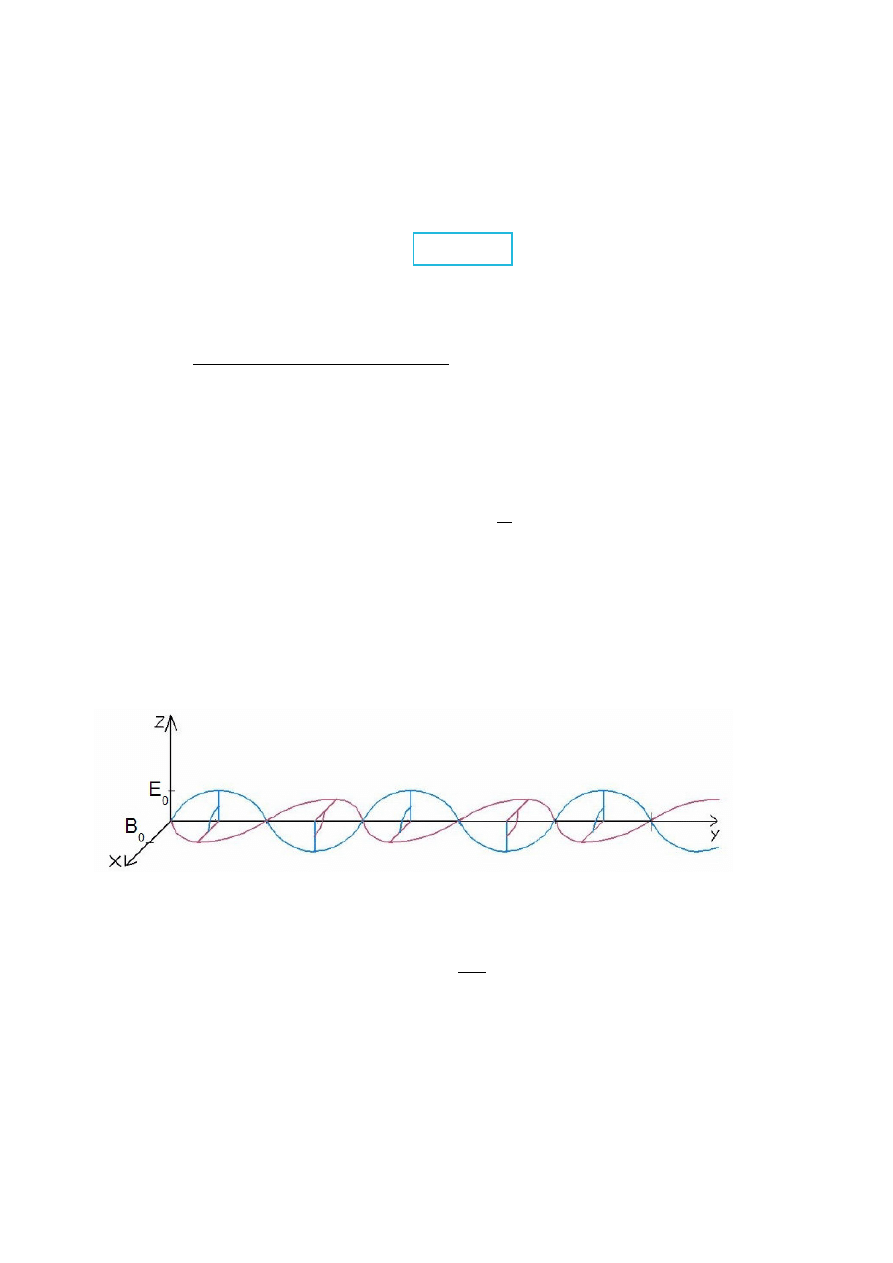
Rys.I.4. Fala elektromagnetyczna jest falą poprzeczną, to znaczy

E i B

są wzajemnie prostopadłe. Fala ta

rozchodzi się w płaszczyźnie XY.

E

= E

0

sin

t  = E

0

sin



2



T

t



= E

0

sin



2

 f t



E

∈z , y

B

∈ x , y

Polaryzacja – uporządkowanie drgań

E i B

– 4 –

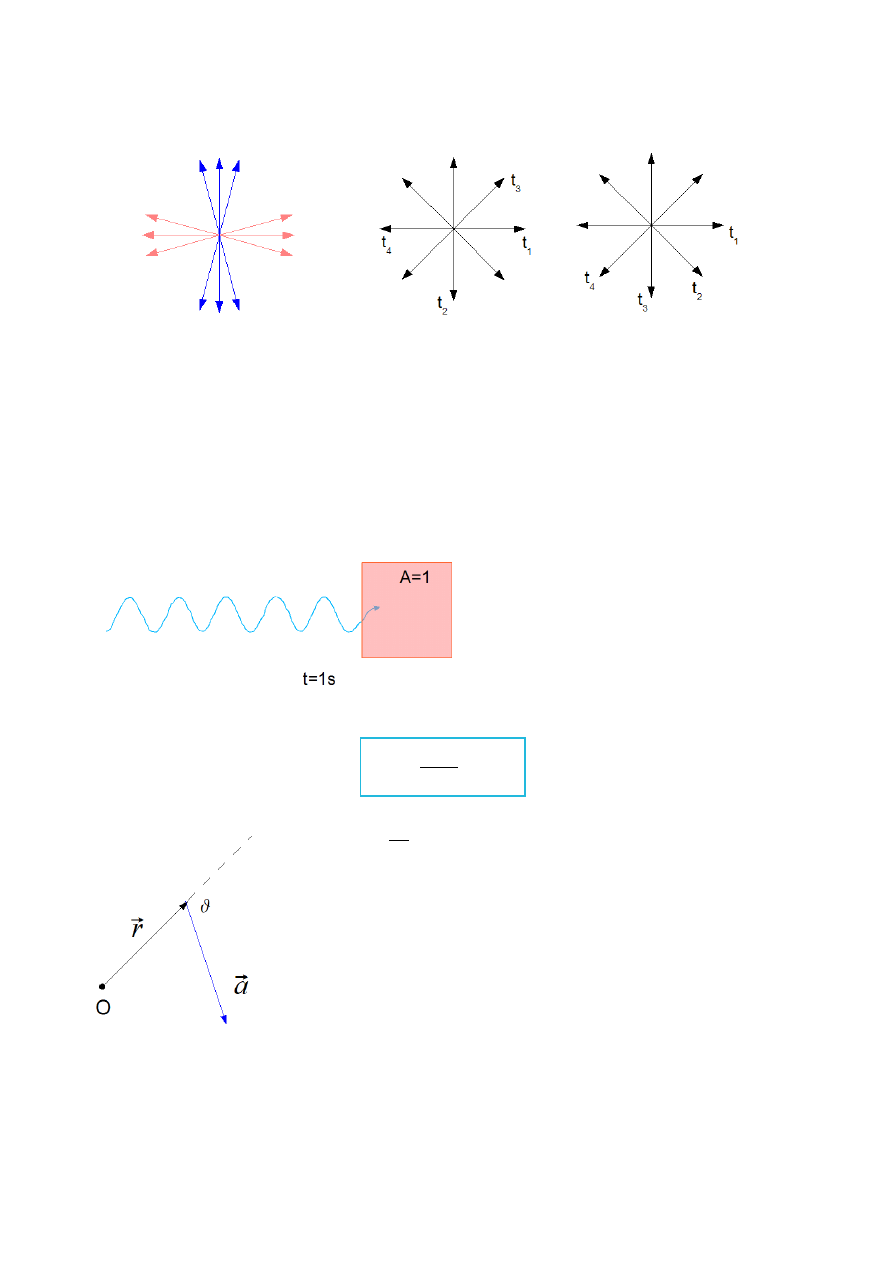
K.Czopek, M.Zazulak – Notatki w internecie. Wstęp do fizyki atomowej i kwantowej.

a)

b)

c)

rys.I.5. a) Częściowa polaryzacja, b) Światło niespolaryzowane – w sposób chaotyczny zmienia się kierunek

drgań (0%PL), c) Polaryzacja kołowa

I.3. NATĘŻENIE EMITOWANEGO PROMIENIOWANIA

–

Jest to energia jaka przechodzi przez jednostkową powierzchnię w czasie 1s.

Rys.I.6. Wiązka promieniowania padająca na jednostkową powierzchnię.

I

=

q

2

a

2

r

2

c

3

sin

2



(I.3.1)

I

~

a

2

r

2

=∢r ,a

rys.I.7. Relacja pomiędzy wektorami r i a.

Natężenie całkowitego promieniowania.

– 5 –

K.Czopek, M.Zazulak – Notatki w internecie. Wstęp do fizyki atomowej i kwantowej.

R

=

∮

I

ds ~

q

2

a

2

c

3

(I.3.2)

Ze wzrostem temperatury wzrasta częstość drgań, co z kolei generuje wzrost
przyspieszenia, a co za tym idzie – większe promieniowanie.

I.4. WPŁYW TEMPERATURY T

Znaleziony eksperymentalnie wpływ temperatury na natężenie promieniowania opisuje
prawo Stefana:

I

T  = e T

4

(I.4.1)

e – zdolność emisyjna (jest tym lepsza, im e bliższe 1)

0

e1

 = 5,7 x10

−8

W

m

2

K

4

– stała Stefana

Ciało emituje promieniowanie w każdej temperaturze (tzn. gdy T > 0 K).
Widmo promieniowania jest ciągłe.

Zjawisko absorpcji – proces odwrotny do emisji.

0

a1

– zdolność absorpcyjna

Powierzchnie gładkie odbijają energię lepiej od matowych.

Prawo Kirchhoffa

e

≡ a

(I.4.2)

– Zdolność emisyjna jest równa zdolności absorpcyjnej promieniowania.

Barwa (kolor) zmienia się od czerwonej do niebieskiej wraz ze wzrostem temperatury.

– 6 –

K.Czopek, M.Zazulak – Notatki w internecie. Wstęp do fizyki atomowej i kwantowej.

I.5. CIAŁO DOSKONALE CZARNE (CDC) – POJĘCIE MODELOWE

Ciała, dla których zdolność absorpcyjna jest równa 1 nazywamy ciałami doskonale
czarnymi.

a =

df

1

(I.5.1)

A zatem całkowicie absorbuje energię.

Ze wzorów (4.2) oraz (5.1) wynika, że

e = 1

Podstawiając tą wartość do wzoru (4.1) otrzymujemy, że

I

T =  T

4

(I.5.2)

Zdolność emisyjna CDC jest uniwersalna.

Modele CDC

a) czarna matowa powierzchnia (sadza)
b) wnęka z małym otworem

Rys.I.8. Wnęka z małym otworem. Promieniowanie wpadające przez otwór po wielokrotnych odbiciach jest
pochłaniane przez wnękę.

Widmo promieniowania CDC – krzywa widmowa

– 7 –

K.Czopek, M.Zazulak – Notatki w internecie. Wstęp do fizyki atomowej i kwantowej.

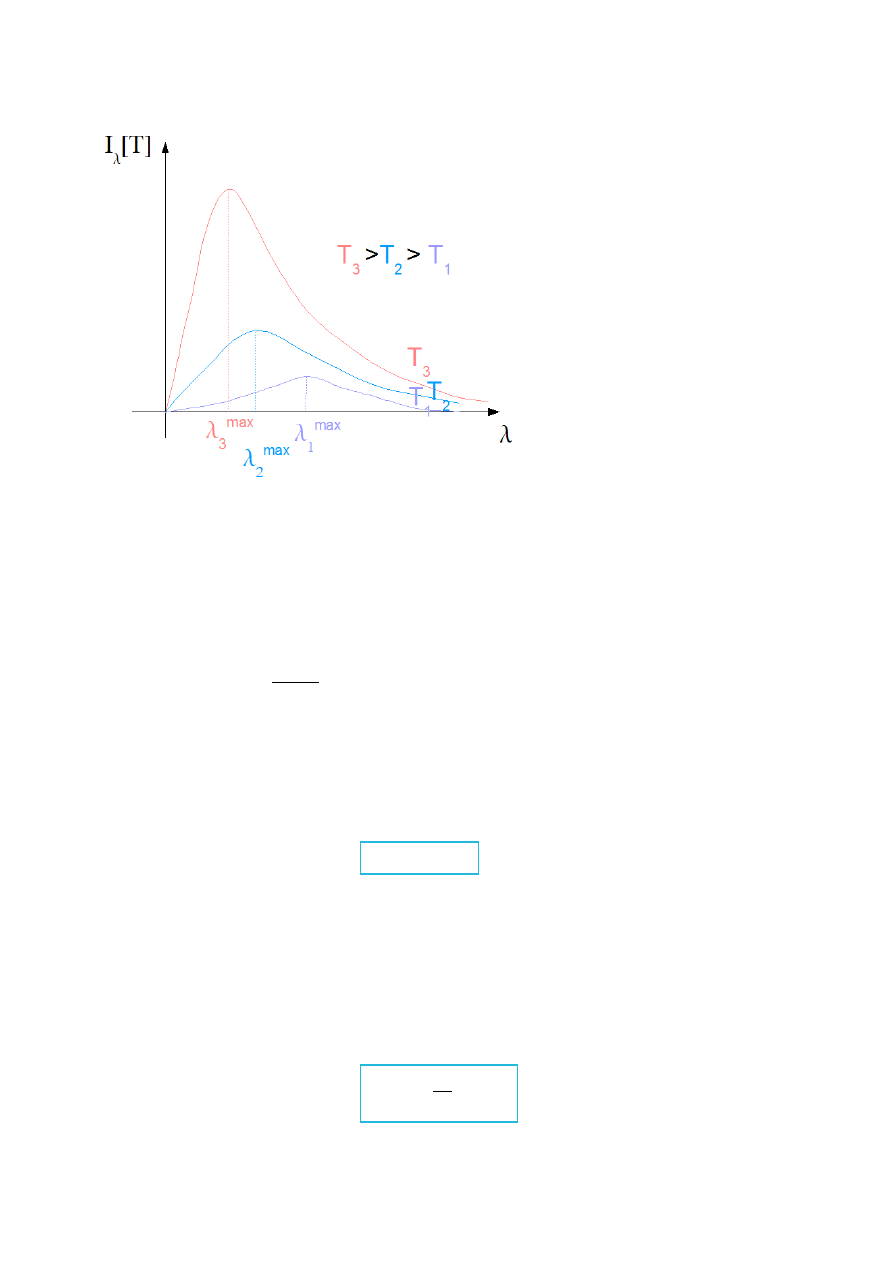
Rys.I.9. Krzywa widmowa ciała doskonale czarnego dla różnych temperatur w funkcji długości fali
promieniowania

Z prawa Stefana wynika, że stosunek natężeń w poszczególnych temperaturach opisuje
relacja:

I

T

1

: I T

2

: I T

3

=T

1

4

: T

2

4

:T

3

4

Jeżeli

T

3

= 3 T

1

, to

I

T

3



I

T

1



=3

4

Ze wzrostem temperatury T



max

maleje (↓), lecz zachowana jest relacja znana jako

prawo przesunięć Wiena (10):

T

1



1

max

=T

2



2

max

=T

3



3

max

=const

T



max

= const

(I.5.3)

I.6. KLASYCZNE TEORIE PROMIENIOWANIA

a) teoria Wiena (1893)



T

W

=

1



5

f

 T 

(I.6.1)

– 8 –

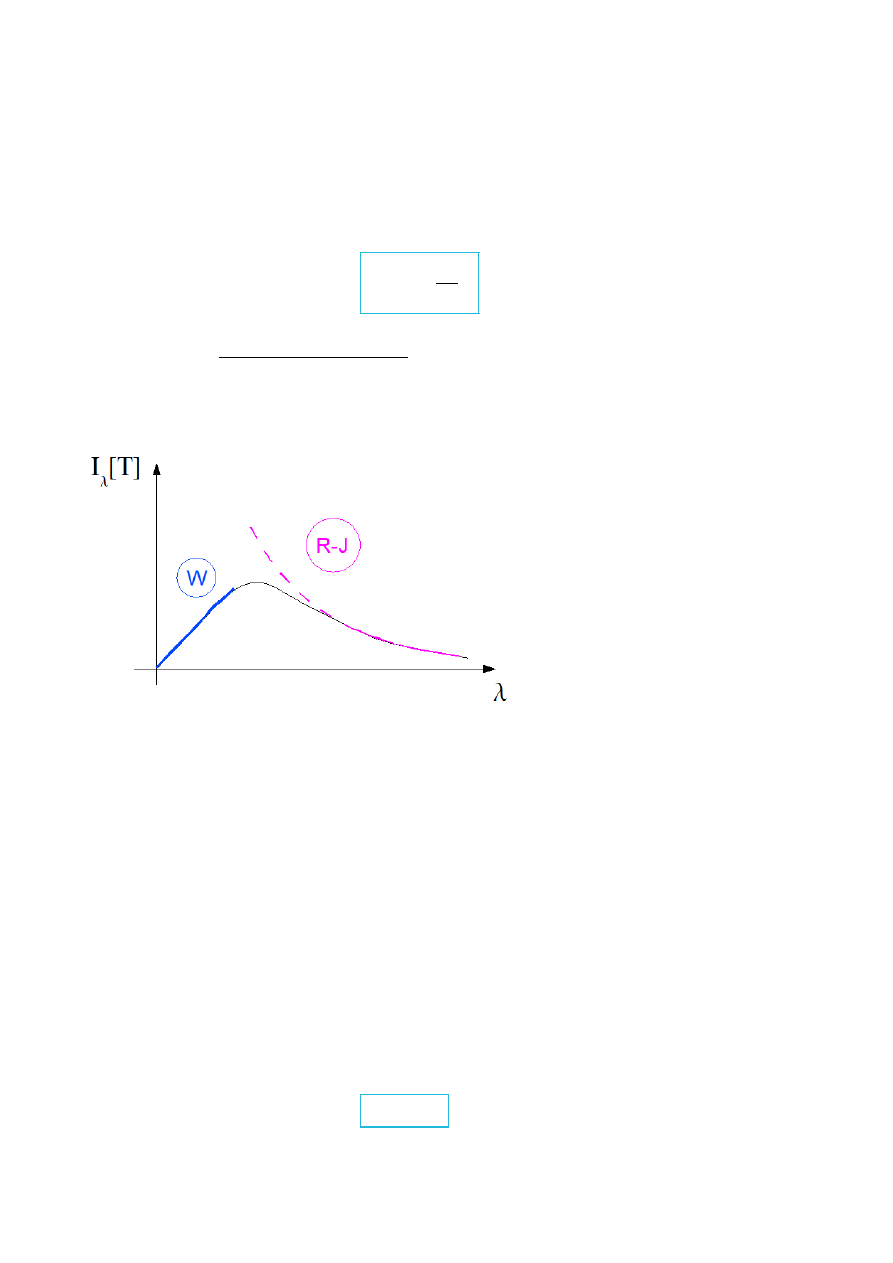
K.Czopek, M.Zazulak – Notatki w internecie. Wstęp do fizyki atomowej i kwantowej.

Przybliżenie opisane wzorem (6.1) jest słuszne, gdy duża energia (małe

l) . Jest to

przybliżenie wysokotemperaturowe.

b) teoria Rayleigha – Jeansa (RJ)



T

RJ

=

C

1

'

λ

4

T

(I.6.2)



T

RJ



∞

0

katastrofa w nadfiolecie

Teoria Wiena opisuje ”lewe zbocze” wykresu z rys.10, natomiast Teoria Rayleigha –
Jeansa opisuje poprawnie “prawe zbocze” tego wykresu.

Rys.I.10. Porównanie krzywej widmowej na podstawie teorii Wiena (niebieska linia), teorii Rayleigha-Jeansa
(różowa linia) z krzywą otrzymaną doświadczalnie dla CDC

Wniosek:
Teoria klasycznie nie potrafiła wyjaśnić w sposób spójny całego widma promieniowania, a
w szczególności jego maksimum.

I.7. TEORIA PLANCKA (KWANTOWA) (1900)

Założenie:
Jeżeli któraś z wielkości opisujących układ zmienia się w sposób harmoniczny, to energia
przyjmuje wartości dyskretne.

x = x

0

cos

2  f t

E

n

= nh f

(I.7.1)

– 9 –

K.Czopek, M.Zazulak – Notatki w internecie. Wstęp do fizyki atomowej i kwantowej.

n = 1, 2, 3, ...

h = 6,6

⋅10

-34

J

⋅s

– kwant działania (stała Plancka)

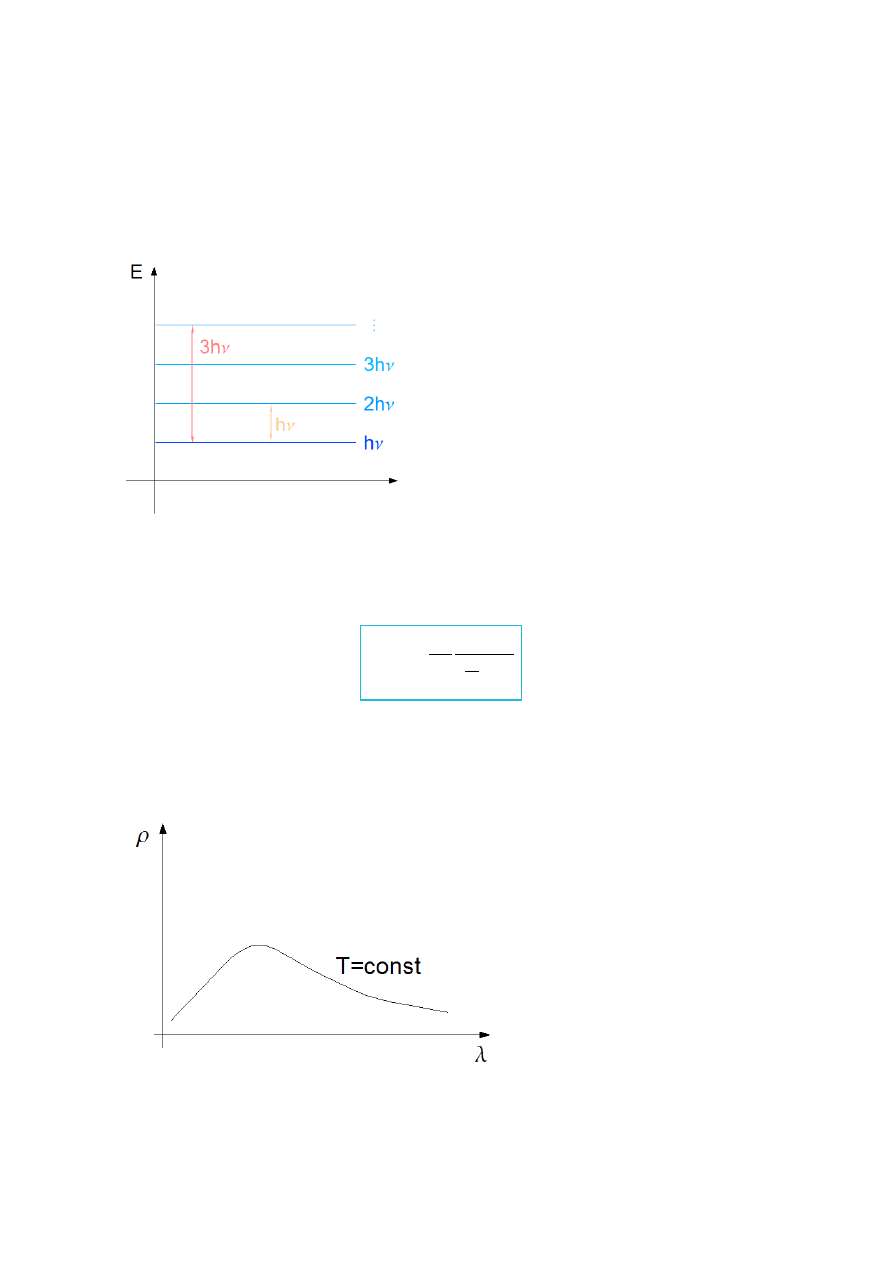
Ze wzoru (7.1) wynika, że widmo energetyczne oscylatora kwantowego jest dyskretne.

Rys.I.11. Schematyczna ilustracja wzoru (13).

Planck traktując atomy emitujące promieniowanie jak zbiór oscylatorów harmonicznych
kwantowych, wyprowadził następujący wzór na gęstość promieniowania:



T

=

C

1



5

1

e

C

2



I

−1

(I.7.2)

Wzór (7.2) poprawnie opisuje widmo promieniowania, a w ekstremalnych warunkach
przechodzi we wzór RJ (gdy hf

≪kT ), oraz we wzór Wiena (gdy hf ≫kT ).

Rys.I.12. Krzywa Plancka przedstawiająca rozkład widmowy promieniowania.

– 10 –