Transformatory 

Transformator trójfazowy ma następujące dane znamionowe: 
 

S

N

 =     MVA 

f

N

 = 50 Hz  

 

U

1N

/U

2N

 =    ±% /    kV 

P

kN

 =     kW 

 poł. -    

u

k%N

 =    % 

Ponadto wiadomo, że: 
 napięcie zwojowe wynosi   u

phN

 

≈ e’ ≈    V/zwój   lub   liczba zwojów   N

XN

 =    zwojów 

 

przekrój kolumny netto wynosi   A

1

η

1

 =     m

2 

 
 
Przykładowe zadania: 
 

1. Obliczyć znamionowe napięcie fazowe i przewodowe strony GN (HV) lub DN (LV) 
2. Obliczyć znamionowy prąd fazowy i przewodowy strony GN (HV) lub DN (LV) 
3. Obliczyć znamionową liczbę zwojów strony GN (HV) lub DN (LV) 
4. Obliczyć znamionowe napięcie zwojowe 
5. Obliczyć znamionową indukcję w kolumnie rdzenia 
6. Obliczyć napięcie przy zmianie przekładni 
7. Wyznaczyć zaczep na który należy przełączyć transformator aby uzyskać napięcie 
8. Obliczyć spadek napięcia pod obciążeniem 

 
 
Rozwiązania: 
 
Podpowiedź: przed przystąpieniem do zadań z obliczaniem wartości przewodowych  

i fazowych polecam wykonanie szkicu skojarzenia uzwojenia z zaznaczeniem 
napięć i prądów (przewodowych i fazowych) 

 

1.  Napięcia znamionowe są napięciami PRZEWODOWYMI 

Napięcia fazowe zależą od skojarzenia uzwojeń !!! 
 
dla połączenia w GWIAZDĘ –  Y  -  y   napięcie fazowe 

 

 

 

 

3

U

U

XN

XphN

=

 

gdzie X oznacza stronę GN (1) lub DN (2) 
 
dla połączenia w TRÓJKĄT –  Δ  -  D  -  d   napięcie fazowe 
 

 

 

 

XN

XphN

U

U

=

 

gdzie X oznacza stronę GN (1) lub DN (2) 

 

2.  Prądy znamionowe są prądami PRZEWODOWYMI 

Znamionowy prąd transformatora 

 

 

 

 

XN

N

XN

U

3

S

I

⋅

=

 

gdzie X oznacza stronę GN (1) lub DN (2) 
 
Prądy fazowe zależą od skojarzenia uzwojeń !!! 
 
dla połączenia w GWIAZDĘ –  Y  -  y   prąd fazowy 
 

 

 

 

XN

XphN

I

I

=

 

gdzie X oznacza stronę GN (1) lub DN (2) 
 

dla połączenia w TRÓJKĄT –  Δ  -  D  -  d   prąd fazowy 

 

 

 

 

3

I

I

XN

XphN

=

 

gdzie X oznacza stronę GN (1) lub DN (2) 

 

3.  Znamionowa liczba zwojów 

 

 

 

 

phN

XphN

XN

u

U

N

=

 

gdzie X oznacza stronę GN (1) lub DN (2) 
UWAGA: do obliczeń używa się wartości fazowych (ph) 

 

4.  Znamionowe napięcie zwojowe 

 

 

 

 

XN

XphN

phN

N

U

u

=

 

gdzie X oznacza stronę GN (1) lub DN (2) 
UWAGA: do obliczeń używa się wartości fazowych (ph) 

 

5.  Znamionowa indukcja w kolumnie rdzenia transformatora 

 

 

 

N

1

1

phN

XN

N

1

1

XphN

mN

f

A

44

,

4

u

N

f

A

44

,

4

U

B

⋅

η

⋅

=

⋅

⋅

η

⋅

=

 

gdzie X oznacza stronę GN (1) lub DN (2) 
UWAGA: do obliczeń używa się wartości fazowych (ph) 

 
 

6. UWAGA: regulacja napięcia (zaczepy) po stronie GN (HV) 

 
Zasilanie od strony GN (HV) napięciem   U

1

 

np. zaczep  +10%  to  przekładnia transformatora 

 

 

 

 

N

2

N

1

N

2

N

1

2

1

U

1

,

1

U

U

%

100

%

10

1

U

U

U

⋅

=

⎟

⎠

⎞

⎜

⎝

⎛ +

⋅

=

 

stąd napięcie przewodowe po stronie DN (LV) 

 

 

 

 

1

,

1

U

U

U

U

N

1

1

N

2

2

⋅

⋅

=

 

 
Zasilanie od strony GN (HV) napięciem   U

1

 

np. zaczep  -10%  to  przekładnia transformatora 

 

 

 

 

N

2

N

1

N

2

N

1

2

1

U

9

,

0

U

U

%

100

%

10

1

U

U

U

⋅

=

⎟

⎠

⎞

⎜

⎝

⎛ −

⋅

=

 

stąd napięcie przewodowe po stronie DN (LV) 

 

 

 

 

9

,

0

U

U

U

U

N

1

1

N

2

2

⋅

⋅

=

 

 

Zasilanie od strony DN (LV) napięciem   U

2

 

np. zaczep  +10%  to  przekładnia transformatora 

 

 

 

 

N

2

N

1

N

2

N

1

2

1

U

1

,

1

U

U

%

100

%

10

1

U

U

U

⋅

=

⎟

⎠

⎞

⎜

⎝

⎛ +

⋅

=

 

stąd napięcie przewodowe po stronie GN (HV) 

 

 

 

 

N

2

2

N

1

1

U

1

,

1

U

U

U

⋅

⋅

=

 

 
Zasilanie od strony DN (LV) napięciem   U

2

 

np. zaczep  -10%  to  przekładnia transformatora 

 

 

 

 

N

2

N

1

N

2

N

1

2

1

U

9

,

0

U

U

%

100

%

10

1

U

U

U

⋅

=

⎟

⎠

⎞

⎜

⎝

⎛ −

⋅

=

 

stąd napięcie przewodowe po stronie GN (HV) 

 

 

 

 

N

2

2

N

1

1

U

9

,

0

U

U

U

⋅

⋅

=

 

 
 

7. UWAGA: regulacja napięcia (zaczepy) po stronie GN (HV) 

 
Np. maksymalne napięcie po stronie DN (LV) przy zasilaniu od strony GN (HV) 
odpowiedź: zaczep –XX%  bo 

 

 

 

 

⎟

⎠

⎞

⎜

⎝

⎛ −

⋅

⋅

=

%

100

%

XX

1

U

U

U

U

N

1

1

N

2

2

 

Np. minimalne napięcie po stronie DN (LV) przy zasilaniu od strony GN (HV) 
odpowiedź: zaczep +XX%  bo 

 

 

 

 

⎟

⎠

⎞

⎜

⎝

⎛ +

⋅

⋅

=

%

100

%

XX

1

U

U

U

U

N

1

1

N

2

2

 

Np. maksymalne napięcie po stronie GN (HV) przy zasilaniu od strony DN (LV) 
odpowiedź: zaczep +XX%  bo 

 

 

 

 

N

2

2

N

1

1

U

%

100

%

XX

1

U

U

U

⎟

⎠

⎞

⎜

⎝

⎛ +

⋅

⋅

=

 

Np. minimalne napięcie po stronie GN (HV) przy zasilaniu od strony DN (LV 
odpowiedź: zaczep -XX%  bo 

 

 

 

 

N

2

2

N

1

1

U

%

100

%

XX

1

U

U

U

⎟

⎠

⎞

⎜

⎝

⎛ −

⋅

⋅

=

 

 

8.  Należy najpierw wyznaczyć znamionowe, względne, procentowe spadki napięć na 

rezystancji (R

kN

)  i reaktancji (X

kN

) zwarcia 

Znamionowy, względny, procentowy czynny spadek napięcia (składowa czynna 
napięcia zwarcia) 

%

100

S

P

%

100

U

3

S

3

U

P

%

100

U

I

3

P

%

100

U

U

u

N

kN

XN

N

XN

kN

XN

XN

kN

XN

kRN

N

%

kR

⋅

=

⋅

⋅

⋅

⋅

=

⋅

⋅

=

⋅

=

 

bo: 

 

 

 

 

XN

kN

XN

kN

kRN

I

3

P

I

R

U

⋅

=

⋅

=

 

gdzie X oznacza stronę GN (1) lub DN (2) 
 
UWAGA: do obliczeń używa się wartości przewodowych 
 
Znamionowy, względny, procentowy bierny spadek napięcia (składowa bierna 
napięcia zwarcia) 
 

 

 

 

2

N

%

kR

2

N

%

k

N

%

kX

u

u

u

−

=

 

 
Procentowa zmiana napięcia przy obciążeniu indukcyjnym,  
przyjmujemy wzór uproszczony 
 

 

 

(

)

.

obc

N

%

kX

.

obc

N

%

kR

%

sin

u

cos

u

u

ϕ

⋅

+

ϕ

⋅

⋅

β

=

Δ

 

gdzie: 

 

XN

X

I

I

=

β

  (stosunek prądu obciążenia do prądu znamionowego danej strony) 

 
Procentowa zmiana napięcia przy obciążeniu pojemnościowym,  
przyjmujemy wzór uproszczony 
 

 

 

(

)

.

obc

N

%

kX

.

obc

N

%

kR

%

sin

u

cos

u

u

ϕ

⋅

−

ϕ

⋅

⋅

β

=

Δ

 

gdzie: 

 

XN

X

I

I

=

β

  (stosunek prądu obciążenia do prądu znamionowego danej strony) 

 
Napięcie po stronie obciążenia (założenie, że zasilanie znamionowe) 

 

 

 

 

⎟

⎠

⎞

⎜

⎝

⎛

Δ

−

⋅

=

%

100

u

1

U

U

%

XN

X

 

UWAGA: do obliczeń używa się wartości przewodowych 
UWAGA: należy uwzględnić znak przy Δu

%

  

 
 

Maszyny Prądu Stałego 

Prądnica bocznikowa prądu stałego o znamionach: 
 

P

N

 =     kW 

n

N

 =     obr/min 

 

U

N

 =      V 

jest wyposażona w uzwojenie kompensacyjne i można przyjąć,  że reakcja poprzeczna 
twornika  jest  w  pełni  skompensowana. 
Dana jest charakterystyka biegu jałowego  E

0

 = f(I

f

)  zmierzona dla  n = n

N

 . W związku  

z pełną kompensacją charakterystyka obciążeniowa  E

a(I

a

=I

aN

)

 = E’

(I

a

=I

aN

)

 = E

0

 = f(I

f

)  (przy 

prądzie twornika  I

a

 =I

aN

 oraz n = n

N

 ) 

Wartości rezystancji obwodu twornika 

ΣR

a

 = 0,006 

Ω

   

i 

uzwojenia 

wzbudzenia 

  R

E1E2

 = 13 

Ω

. 

 
 
Przykładowe zadania: 
 

1. Obliczyć znamionowy prąd twornika i znamionowy prąd wzbudzenia 
2. Obliczyć wartość dodatkowego opornika w obwodzie wzbudzenia dla znamionowych 

warunków pracy prądnicy 

3. Obliczyć rezystancję krytyczną obwodu wzbudzenia 
4. Obliczyć prędkość krytyczną przy  R

f

 = R

E1E2

 

5. Obliczyć napięcie na zaciskach prądnicy przy danym prądzie wzbudzenia  I

f

 

6. Wyznaczyć napięcie na zaciskach prądnicy w stanie jałowym przy danej rezystancji 

wzbudzenia  R

f

 

7. Wyznaczyć prąd wzbudzenia dla uzyskania na zaciskach danego napięcia U 
8.  Przy pracy tej maszyny jako silnik obliczyć prąd pobierany z sieci o napięciu U  

w pierwszej chwili rozruchu 

9.  Przy pracy tej maszyny jako silnik obliczyć wartość opornika dodatkowego w 

obwodzie twornika ograniczającego prąd twornika w pierwszej chwili rozruchu do 
wartości  I

a

 = 1,5 I

aN

 

 
 
Rozwiązania: 
 
Podpowiedź:  polecam wykonanie szkicu schematu połączenia prądnicy z zaznaczeniem 

prądów, siły elektromotorycznej i napięcia 

 

1.  Do obliczania wartości znamionowych prądu twornika i prądu wzbudzenia musimy 

stosować iteracje 
 
I iteracja  -  z braku wiedzy na temat prądu wzbudzenia zakładamy, że prąd twornika 
 

jest równy prądowi znamionowemu prądnicy      

N

a

I

 

 

I

=

 

Prąd znamionowy prądnicy 

 

   

 

 

N

N

N

U

P

I

=

 

UWAGA: prądnica jest znamionowana w mocy elektrycznej na zaciskach 
 
obliczamy siłę elektromotoryczną w tworniku prądnicy 
 

   

 

tc

a

N

N

a

u

2

R

I

U

E

E

Δ

+

⋅

+

=

′

=

∑

 

z charakterystyki odczytujemy dla  

 

 

E

a

=

XXX V  prąd wzbudzenia  

Y,Y A 

 

=

 

I

f

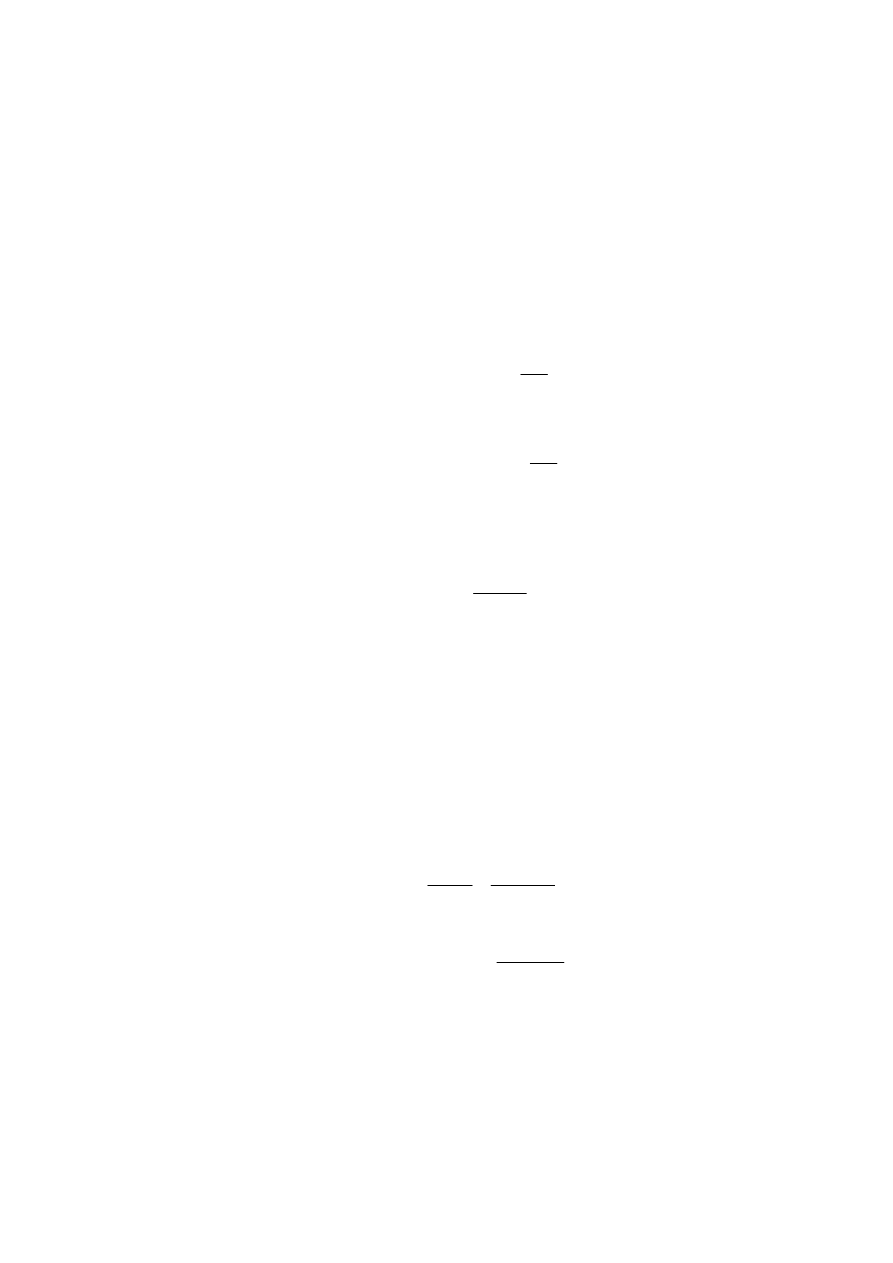
II iteracja  -  przyjmujemy dokładniejszą wartość prądu twornika 
 

   

 

 

f

N

a

aN

I

I

I

I

+

=

≅

 

sprawdzamy siłę elektromotoryczną w tworniku prądnicy 
 

   

 

tc

a

aN

N

N

aN

u

2

R

I

U

E

E

Δ

+

⋅

+

=

′

=

∑

 

sprawdzamy na charakterystyce czy należy skorygować prąd wzbudzenia – 
odczytujemy wartość znamionowego prądu wzbudzenia 

 

Znamionowy prąd twornika 
 

   

 

 

 

I

fN

fN

N

aN

I

I

I

+

=

 

 

2.  Postępujemy jak wyżej aby wyznaczyć znamionowy prąd wzbudzenia, a następnie 

obliczamy znamionową wartość obwodu wzbudzenia 

 

   

 

fN

N

ad

2

E

1

E

fN

I

U

R

R

R

=

+

=

 

stąd wartość opornika dodatkowego – włączonego szeregowo w obwodzie 
wzbudzenia 

 

   

 

2

E

1

E

fN

N

2

E

1

E

fN

ad

R

I

U

R

R

R

−

==

−

=

 

 

3.  Rezystancja krytyczna wynika z nachylenia charakterystyki stanu jałowego E

0

 = f(I

f

)  

w jej początkowym, prostoliniowym odcinku – przy takiej rezystancji obwodu 
wzbudzenia prądnica nie wzbudzi się przy prędkości znamionowej 

 

   

 

 

.)

pocz

(

f

.)

pocz

(

0

fcr

I

E

R

=

 

 
UWAGA: najlepiej przyjąć pierwsze wartości z tabelki 

 

4.  Prędkość krytyczna to taka, przy której charakterystyka stanu jałowego E

0

 = f(I

f

) jest 

styczna, w jej początkowym, prostoliniowym odcinku, do prostej obrazującej spadek 
napięcia na rezystancji obwodu wzbudzenia. 
Przy biegu jałowym i rezystancji obwodu wzbudzenia  R

f

 = R

E1E2

   siła 

elektromotoryczna dla prędkości krytycznej w początkowym, prostoliniowym odcinku 
charakterystyki jest równa spadkowi napięcia na rezystancji  R

E1E2

 

 

   

 

 

2

E

1

E

.)

pocz

(

f

)

ncr

(

0

R

I

E

⋅

=

 

Pamiętamy, że siła elektromotoryczna w tych samych warunkach magnetycznych  
w maszynie (np. w stanie jałowym) zależy od prędkości obrotowej 

 

   

 

 

N

cr

)

n

(

0

)

ncr

(

0

n

c

n

c

E

E

N

⋅

Φ

⋅

⋅

Φ

⋅

=

 

stąd 

 

   

 

 

)

n

.

pocz

(

0

)

ncr

(

0

N

cr

N

E

E

n

n

⋅

=

 

 
UWAGA: jako początkowe wartości SEM i prądu wzbudzenia dla prędkości 
 

nominalnej odczytujemy pierwsze wartości z tabelki 

 

5. BIEG JAŁOWY  -  U 

≅ E

0

 

 
odczytujemy z charakterystyki  E

0

 = f(I

f

)  wartość napięcia dla danego prądu  I

f

 

 
OBCIĄŻENIE PRĄDNICY PRĄDEM ZNAMIONOWYM -  U = E

a

 – I

aN

 · 

ΣR

a

 – 2Δu

tc

   

 
odczytujemy z charakterystyki  E

a

 = f(I

f

)  wartość SEM dla danego prądu  I

f

  

obliczamy napięcie na zaciskach przy obciążeniu prądem twornika  I

aN

  

 

   

 

tc

a

aN

a

u

2

R

I

E

U

Δ

−

⋅

−

=

∑

 

 
UWAGA: w przypadku idealnej kompensacji charakterystyka   
 

E

a(I

a

=I

aN

)

 = E’

(I

a

=I

aN

)

 = E

0

 = f(I

f

)  (przy n = n

N

) 

 

6. BIEG JAŁOWY  -  U 

≅ E

0

 

 
Punkt pracy będzie odpowiadał przecięciu się charakterystyki  E

0

 = f(I

f

)  z prostą 

obrazującą spadek napięcia na rezystancji obwodu wzbudzenia 
 

   

 

 

f

f

0

R

I

U

E

⋅

=

≅

 

 
na charakterystyce kreślimy prostą  U = (I

f

) = I

f

 ·R

f

  

 
z punktu przecięcia z charakterystyką  E

0

 = f(I

f

)  odczytujemy wartość SEM (napięcia) 

oraz prąd wzbudzenia  I

f

 

 

7. BIEG JAŁOWY  -  U 

≅ E

0

 

 
odczytujemy z charakterystyki  E

0

 = f(I

f

)  wartość prądu wzbudzenia  I

f

  dla danego 

napięcia  
 
Dla prędkości   n 

≠ n

N

 

 

   

 

 

N

)

n

(

0

)

n

(

0

n

n

E

E

N

=

 

 
OBCIĄŻENIE PRĄDNICY PRĄDEM ZNAMIONOWYM -  U = E

a

 – I

aN

 · 

ΣR

a

 – 2Δu

tc

   

 
obliczamy SEM pod obciążeniem 
 

   

 

tc

a

aN

a

u

2

R

I

U

E

E

Δ

+

⋅

+

=

′

=

∑

 

odczytujemy z charakterystyki  E

a

 = f(I

f

)  wartość prądu wzbudzenia  I

f

  dla danej 

wartość SEM 
 
Dla prędkości   n 

≠ n

N

  przed odczytem z charakterystyki obliczamy SEM dla 

znamionowych obrotów 

 

   

 

 

n

n

E

E

N

)

n

(

a

)

n

(

a

N

=

 

 
UWAGA: w przypadku idealnej kompensacji charakterystyka   
 

E

a(I

a

=I

aN

)

 = E’

(I

a

=I

aN

)

 = E

0

 = f(I

f

)  (przy n = n

N

) 

 
 
Podpowiedź:  przed przystąpieniem do zadań z silnikiem polecam wykonanie szkicu 

schematu połączenia silnika bocznikowego z zaznaczeniem prądów, siły 
elektromotorycznej i napięcia 

8.  W pierwszej chwili rozruchu prędkość jest równa zero, a więc i SEM równa się zero 

 

 

0

n

=

   

czyli        

0

n

c

E

=

⋅

Φ

⋅

=

 

stąd popłynie maksymalny prąd rozruchowy, a napięcie sieci będzie zrównoważone 
tylko spadkami napięć w obwodzie twornika 
 

   

 

tc

a

max

as

u

2

R

I

U

Δ

+

⋅

=

∑

 

 
maksymalny prąd rozruchowy twornika 

 

   

 

 

∑

Δ

−

=

a

tc

max

as

R

u

2

U

I

 

 
równolegle do obwodu twornika włączony jest obwód wzbudzenia –  
maksymalny prąd wzbudzenia 

 

   

 

 

2

E

1

E

max

f

R

U

I

=

 

 
stąd maksymalny prąd rozruchowy silnika 
 

   

 

 

max

f

max

as

max

s

I

I

I

+

=

 

 

9.  W pierwszej chwili rozruchu prędkość jest równa zero, a więc i SEM równa się zero 

 

 

0

n

=

   

czyli        

0

n

c

E

=

⋅

Φ

⋅

=

 

stąd popłynie maksymalny prąd rozruchowy, a napięcie sieci będzie zrównoważone 
tylko spadkami napięć w obwodzie twornika, w przypadku dodatkowego opornika 
włączonego szeregowo w obwodzie twornika 
 

   

 

(

)

tc

s

a

max

as

u

2

R

R

I

U

Δ

+

+

⋅

=

∑

 

 
jeżeli chcemy ograniczyć prąd twornika do wartości  I

a

 = 1,5 I

aN

 , to musimy włączyć 

szeregowo w obwód twornika opornik o wartości 

 

   

∑

∑

−

⋅

Δ

−

=

−

Δ

−

=

a

aN

tc

a

a

tc

s

R

I

5

,

1

u

2

U

R

I

u

2

U

R

 

 
UWAGA:  prąd rozruchowy silnika bocznikowego jest większy od prądu samego 
 

twornika o prąd wzbudzenia 

 
 
 

Maszyny Asynchroniczne 

Trójfazowy silnik indukcyjny ma następujące dane znamionowe: 
 

P

N

 =     kW 

f

N

 = 50 Hz 

 

U

N

 =     V (poł. uzw. stojana) 

n

N

 =    obr/min 

 cosφ

N

 =     

m

bN

 =     

 

η

N

 =    lub    I

N

 =    A 

 
 
Przykładowe zadania: 
 

1. Obliczyć znamionowy prąd fazowy i przewodowy stojana 
2. Obliczyć znamionową sprawność silnika 
3. Obliczyć znamionowy poślizg 
4. Obliczyć znamionowy poślizg krytyczny i znamionowa prędkość krytyczną 
5. Obliczyć moment znamionowy  
6. Obliczyć znamionowy moment krytyczny 
7. Obliczyć znamionowy moment rozruchowy 
8. Obliczyć moment obciążenia dla silnika wirującego z prędkością  n 

≠ n

N

 

9. Obliczyć prędkość dla silnika obciążonego momentem  M 

≠ M

N

 

 
 
Rozwiązania: 
 
Podpowiedź:  przed przystąpieniem do zadań z silnikiem asynchronicznym polecam 

wyznaczenie prędkości synchronicznej i liczby par biegunów 

 

 

 

p

60

f

n

N

s

⋅

=

  obr/min 

 

1. Znamionowy prąd silnika jest prądem przewodowym  

 
UWAGA: silnik jest znamionowany mocą mechaniczna na wale stad moc wejściowa 
 (elektryczna) 

 

 

 

 

N

N

N

N

N

N

N

el

cos

S

cos

I

U

3

P

P

ϕ

⋅

=

ϕ

⋅

⋅

⋅

=

η

=

 

stąd znamionowy (przewodowy) prąd stojana 

 

 

 

N

N

N

N

N

N

el

N

N

N

cos

U

3

P

cos

U

3

P

U

3

S

I

η

⋅

ϕ

⋅

⋅

=

ϕ

⋅

⋅

=

⋅

=

 

 
Prąd fazowy zależy od skojarzenia uzwojeń !!! 
dla połączenia w GWIAZDĘ –  Y  -  y   prąd fazowy 
 

 

 

 

 

N

phN

I

I

=

 

 
dla połączenia w TRÓJKĄT –  Δ  -  D  -  d   prąd fazowy 

 

 

 

 

 

3

I

I

N

phN

=

 

 

2.  Znamionowa sprawność - uwagi j.w. 

 

 

 

N

N

N

N

N

N

N

.

el

N

N

cos

I

U

3

P

cos

S

P

P

P

ϕ

⋅

⋅

⋅

=

ϕ

⋅

=

=

η

 

 

3.  Znamionowy poślizg 

 

 

 

 

 

s

N

s

N

n

n

n

s

−

=

 

 

4.  Znamionowy poślizg krytyczny 

 

 

 

 

⎟

⎠

⎞

⎜

⎝

⎛

−

+

⋅

=

1

m

m

s

s

2

bN

bN

N

bN

 

 
UWAGA: jeśli w zadaniu na kolokwium nie podano znamionowego poślizgu s

N

 , to 

 

trzeba go wyliczyć ze znamionowej prędkości (zgodnie z p. 3) 

 
Znamionowa prędkość krytyczna 
 

 

 

 

 

(

)

bN

s

bN

s

1

n

n

−

⋅

=

 

 

5.  Moment znamionowy 

 

 

 

 

 

N

N

N

n

2

60

P

M

⋅

π

⋅

⋅

=

 

 
UWAGA: wzór słuszny przy prędkości podanej w obrotach na minutę 

 

6.  Znamionowy moment krytyczny 

 

 

 

 

 

N

bN

bN

M

m

M

⋅

=

 

 
UWAGA: jeśli w zadaniu na kolokwium nie podano momentu znamionowego M

N

 , to 

 

trzeba go wyliczyć (zgodnie z p. 5) 

 
Jeśli nie mamy podanej przeciążalności momentem  m

bN

 , to moment krytyczny 

możemy obliczyć ze wzoru Kloss’a i wartości poślizgów  s

N

  i  s

bN

 (podany lub podana 

prędkość krytyczna) 

 

 

N

bN

bN

N

bN

N

s

s

s

s

M

2

M

+

⋅

=

 stąd     

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

⋅

=

N

bN

bN

N

N

bN

s

s

s

s

2

M

M

 

 

7.  Znamionowy moment rozruchowy wyliczamy dla prędkości równej zero czyli poślizgu 

równego 1 

 

 

 

 

 

bN

bN

bN

N

1

s

s

1

M

2

M

+

⋅

=

 

 
UWAGA: jeśli w zadaniu na kolokwium nie podano znamionowego momentu 
 krytycznego 

M

bN

 , to  

trzeba go wyliczyć (zgodnie z p. 6) 

 
 

8.  Obliczamy poślizg przy prędkości  n 

≠ n 

 

 

 

 

 

s

s

n

n

n

s

−

=

 

moment elektromagnetyczny, w przybliżeniu równy momentowi obciążenia przy tym 
poślizgu obliczamy ze wzoru Kloss’a 

 

 

 

 

 

s

s

s

s

M

2

M

bN

bN

bN

+

⋅

=

 

 
UWAGA: jeśli w zadaniu na kolokwium nie podano znamionowego momentu 
 krytycznego 

M

bN

  i znamionowego poślizgu krytycznego  s

bN

 , to 

 

trzeba je wyliczyć zgodnie z poprzednimi punktami 

 

9.  Obliczamy poślizg przy obciążeniu momentem  M 

≠ M

N

  

 

 

 

 

⎟

⎟
⎠

⎞

⎜

⎜
⎝

⎛

−

⎟

⎠

⎞

⎜

⎝

⎛

−

⋅

=

1

M

M

M

M

s

s

2

bN

bN

bN

 

stąd prędkość 
 

 

 

 

 

( )

s

1

n

n

s

−

⋅

=

 

 
UWAGA: jeśli w zadaniu na kolokwium nie podano znamionowego momentu 
 krytycznego 

M

bN

  i znamionowego poślizgu krytycznego  s

bN

 , to 

 

trzeba je wyliczyć zgodnie z poprzednimi punktami