2013-04-03

1

1

Metody probabilistyczne

Estymacja podstawowych parametrów populacji

Estymacja przedziałowa

2

Estymacja przedziałowa



Estymacja przedziałowa

polega na budowaniu przedziału liczbowego,

który z określonym prawdopodobieństwem będzie zawierał nieznaną
wartość szacowanego parametru θ.



Przedział ten nosi nazwę

przedziału ufności

:

P{g

1

(

θ

n

) <

θ < g

2

(

θ

n

)} = 1-

α

gdzie:

θ

n

– estymator parametru θ,

g

1

(θ

n

) – dolny kres przedziału ufności,

g

2

(θ

n

) – górny kres przedziału ufności,

1-

α - prawdopodobieństwo tzw. współczynnik ufności

2013-04-03

2

3

Estymacja przedziałowa



Przedziałem ufności

nazywa się taki przedział liczbowy,



który z zadanym z góry prawdopodobieństwem (1-



), zwanym

poziomem (współczynnikiem) ufności

, pokrywa nieznaną wartość

parametru w populacji generalnej.



Typowe wartości poziomu ufności: 0,95; rzadziej 0,90 lub 0,98; 0,99



Interpretacja współczynnika ufności (1-



):



Przy wielokrotnym pobieraniu n-

elementowych prób prostych

i wyznaczeniu na ich podstawie granic przedziałów ufności, średnio
w (1-



)*100% przypadkach otrzymujemy przedziały pokrywające

nieznaną wartość parametru.



Długość przedziału ufności:

g

2

(θ

n

) - g

1

(θ

n

) => im długość przedziału

mniejsza tym szacowanie bardziej precyzyjne,



Maksymalny błąd szacunku

( g

2

(θ

n

) - g

1

(θ

n

) )/2.

4

Przedział ufności dla średniej

(wartości przeciętnej) μ – model 1

Model 1



Cecha X w populacji generalnej ma rozkład N(μ,σ),



Średnia μ – nieznana, odchylenie standardowe σ - znane

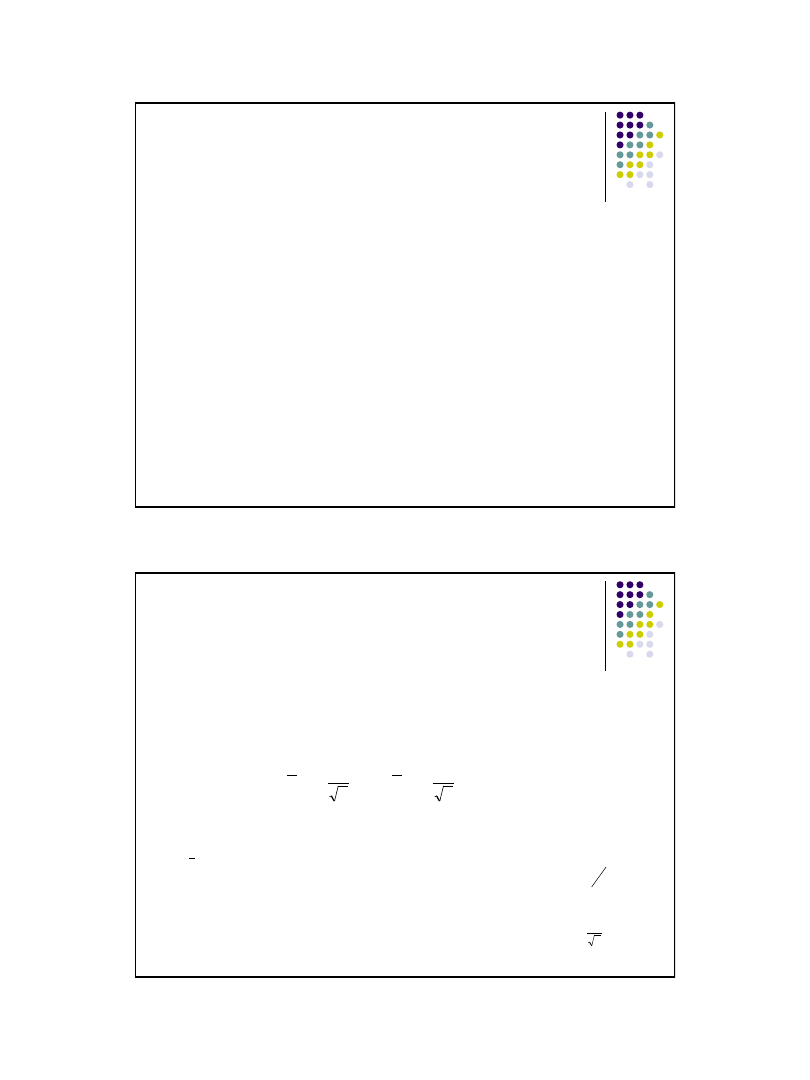
Przedział ufności dla średniej ma postać:

gdzie:



n

– liczebność próby



średnia wyznaczona dla wartości z próby



u

α

-

wartość zmiennej losowej U o rozkładzie N(0,1), dla którego





































1

n

u

X

n

u

X

P





2











u





















1

u

U

u

P















n

N







,

X

2013-04-03

3

5

Przedział ufności dla średniej

(wartości przeciętnej) μ – model 2

Model 2



Cecha X w populacji generalnej ma rozkład N(μ,σ),



Średnia μ – nieznana, odchylenie standardowe σ – nieznane,



Próba mała (n≤30).

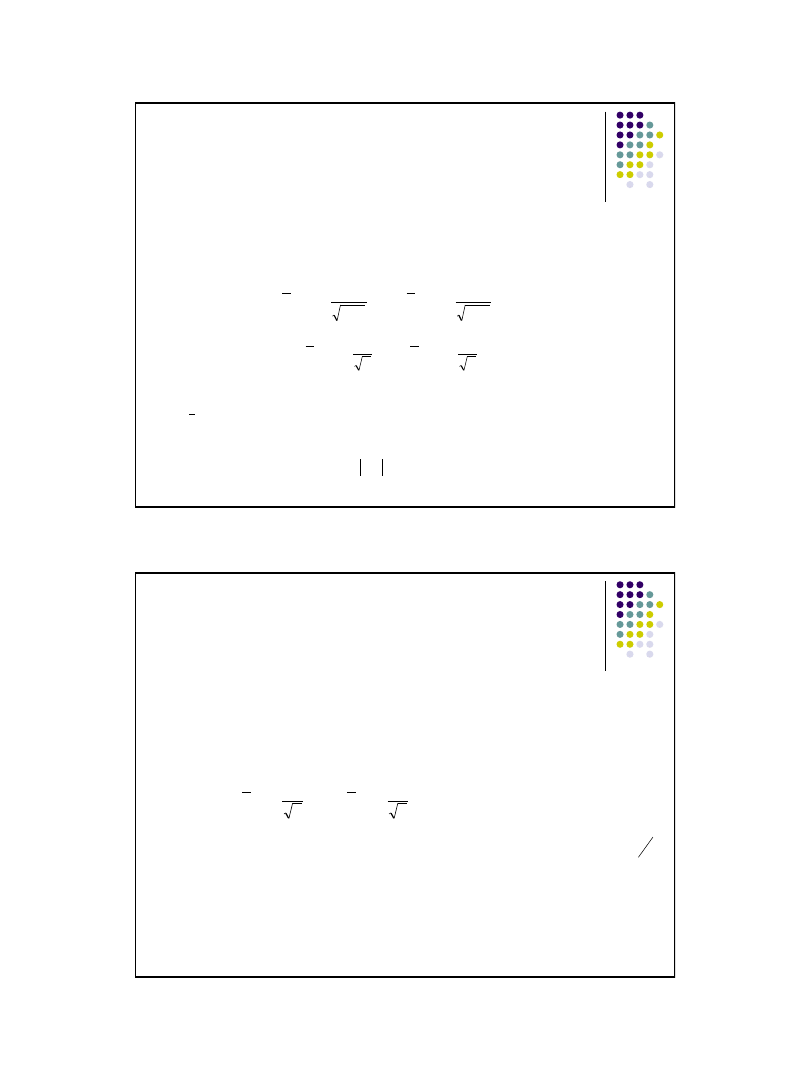
Przedział ufności dla średniej ma postać



lub

gdzie:



n

– liczebność próby,



, S, S

*

średnia i odchylenie standardowe wyznaczone dla wartości z próby,



t

α,n-1

-

wartość zmiennej losowej T o rozkładzie t-Studenta dla n-1 stopni swobody,

dla którego









































1

1

1

1

,

1

,

n

S

t

X

n

S

t

X

P

n

n





































1

*

1

,

*

1

,

n

S

t

X

n

S

t

X

P

n

n

















1

,

1

n

n

t

T

P

X

6

Przedział ufności dla średniej

(wartości przeciętnej) μ – model 3

Model 3



Cecha X w populacji generalnej ma rozkład N(μ,σ),



Średnia μ – nieznana, odchylenie standardowe σ – nieznane,



Próba duża (n>30),

Przedział ufności dla średniej ma postać



u

α

-

wartość zmiennej losowej U o rozkładzie N(0,1), dla którego





2











u

































1

n

S

u

X

n

S

u

X

P





















1

u

U

u

P

2013-04-03

4

7

Przedział ufności dla średniej

(wartości przeciętnej) μ – przykład 1



W 100 losowo wybranych gospodarstwach domowych średnia miesięczna opłata za
energię elektryczną wyniosła 68 złotych, a odchylenie standardowe s=14 złotych.
Oszacuj za pomocą przedziału ufności średnie miesięczne wydatki na energię
elektryczną w całej populacji przyjmując poziom ufności 1-α=0,96.



Dane: n=100, s=14, 1-

α=0,96



Model 3: σ ≈ s,



Odczyt -u

α

:

α = 0,04 =>

α/2 = 0,02



Z tablic dystrybuanty rozkładu normalnego odczytujemy wartość u

0,02

=-2,05, dla

której Φ(-2,05)=0,02



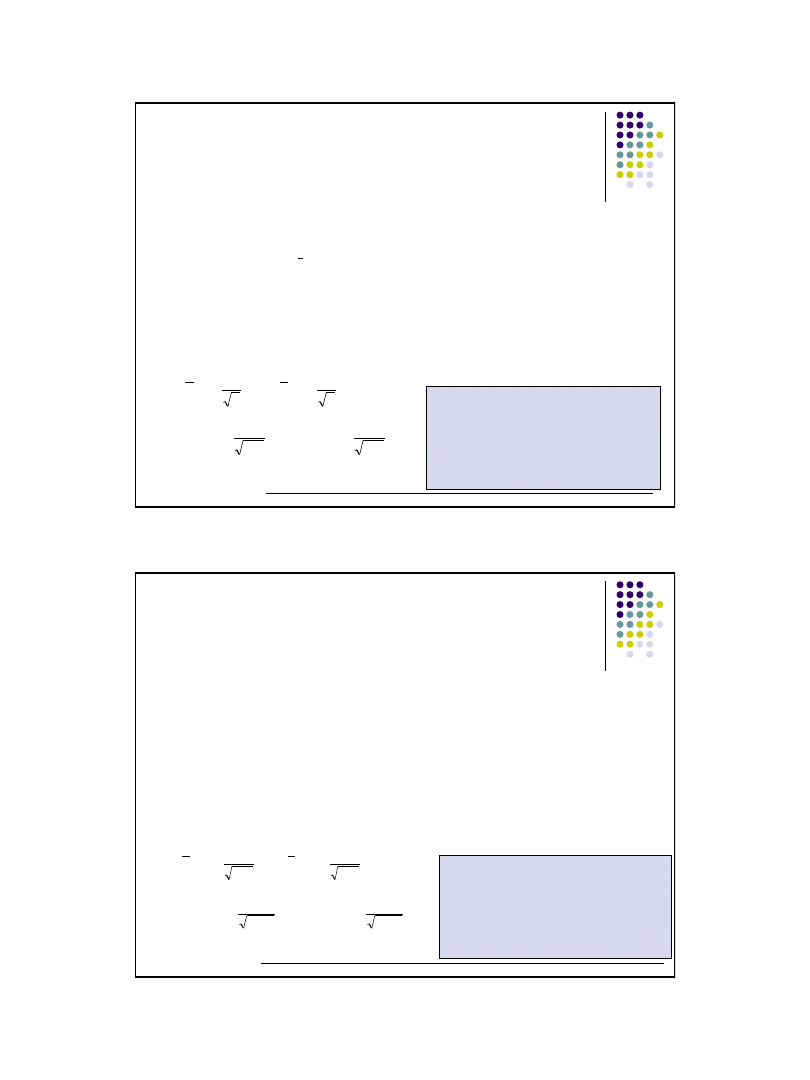
Przedział ufności wyliczymy następująco:

n

u

X

n

u

X



















100

14

05

,

2

68

100

14

05

,

2

68











9

,

70

1

,

65







Wniosek:
Przedział (65,1 zł ; 70,9 zł)
z prawdopodobieństwem 0,96
(z ufnością 96%) pokrywa nieznane
przeciętne wydatki na energię
elektryczną w całej populacji.

68



x

8

Przedział ufności dla średniej

(wartości przeciętnej) μ – przykład 2



Dla 17 losowo wybranych pracowników firmy A otrzymano średni czas dojazdu 26
minut, a odchylenie standardowe s=6 minut. Oszacuj za pomocą przedziału
ufności przeciętny czas dojazdu (μ) w całej populacji pracowników firmy A
przyjmując poziom ufności 0,95.



Dane: n=17, ‾x=26, s=6, 1-α=0,95



Założenie: Cecha ma w populacji rozkład normalny N(μ;



).



Model 2: σ ≈ s,



Odczyt -t

α

:

α = 0,05;



Z tablic rozkładu t-Studenta, dla liczby stopni swobody n-1=17-1=16
wartość –t

0,05,16

=2,1199;



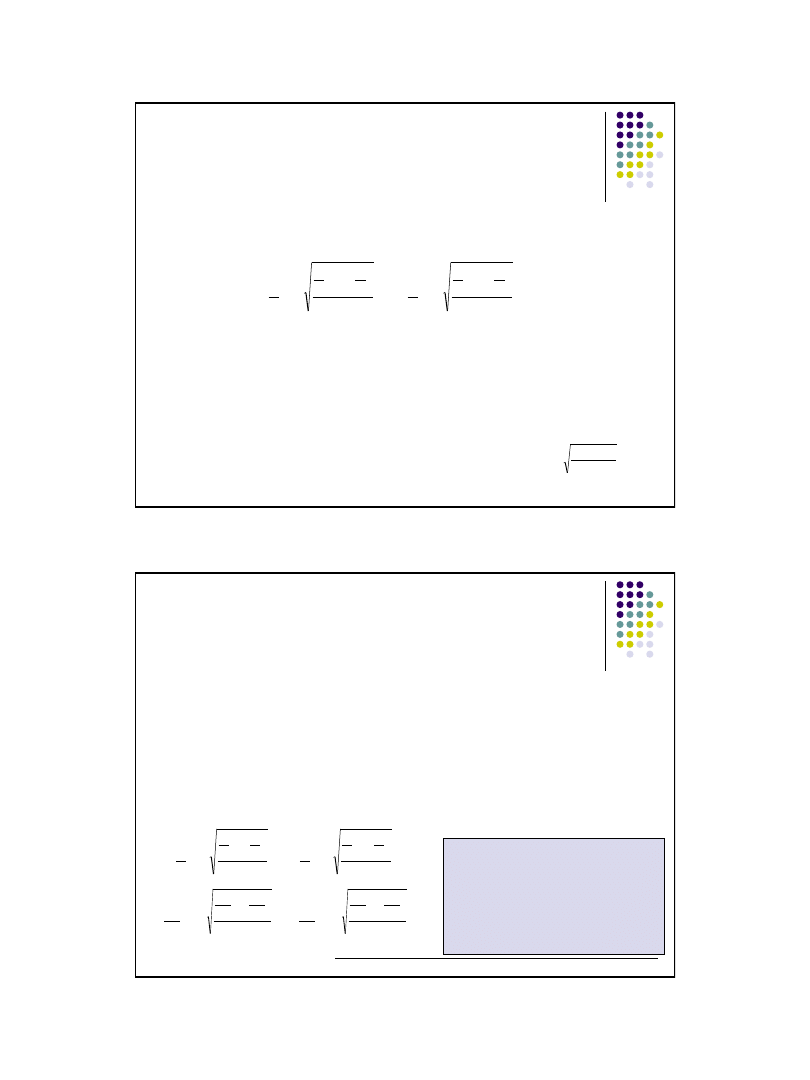
Przedział ufności wyliczymy następująco:

Wniosek:
Przedział (22,8 min; 29,2 min)
z prawdopodobieństwem 0,95
(z ufnością 95%) pokrywa nieznany
przeciętny czas dojazdu w całej
populacji pracowników firmy A

1

1

1

,

1

,

















n

S

t

X

n

S

t

X

n

n







1

17

6

1199

,

2

26

1

17

6

1199

,

2

26















2

,

29

8

,

22







2013-04-03

5

9

Przedział ufności dla wskaźnika struktury p

Model



Przedział taki konstruujemy tylko dla dużych prób (n>100),



Populacja generalna ma rozkład dwupunktowy z parametrem p oraz p > 0,05.

Przedział ufności dla wskaźnika struktury ma postać:

gdzie:



n

– liczebność próby,



m

– liczba elementów wyróżnionych w próbie,



u

α

-

wartość zmiennej losowej U o rozkładzie N(0,1),

dla której P{- u



< U < u



} = 1-















































 

















 



1

1

1

n

n

m

n

m

u

n

m

p

n

n

m

n

m

u

n

m

P

*

*





















n

p

p

p

N

1

*

,

pˆ

10

Przedział ufności wskaźnika struktury p

– przykład



Zapytano 200 losowo wybranych pracowników :
„Kto w codziennych dojazdach do pracy korzysta z prywatnego samochodu?”
W 72 przypadkach otrzymano odpowiedź, że ankietowany korzysta z samochodu.
Zbuduj przedział ufności dla pracowników (p), w którzy dojeżdżają prywatnym
samochodem, przyjmując poziom ufności 0,99,



Dane: n=200, m=72, 1-

α=0,99



Założenie: Cecha ma w populacji rozkład dwupunktowy.



Odczyt -u

α

:

α = 0,01 =>

α/2 = 0,005;



Z tablic dystrybuanty rozkładu normalnego odczytujemy wartość –u

0,005

=2,58;

Φ(-2,58)=0,005



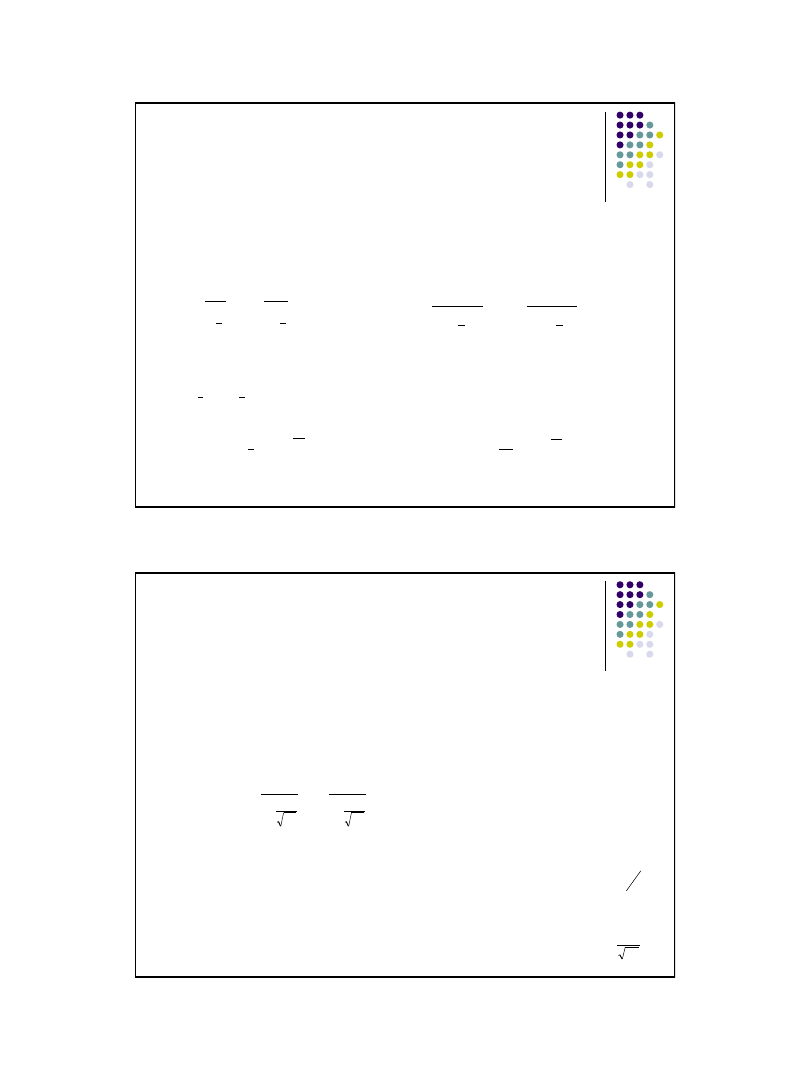
Przedział ufności wyliczymy następująco:

Wniosek:
Przedział (27,2% ; 44,8%) z
prawdopodobieństwem 0,99 (z
ufnością 99%) pokrywa nieznany
(dla całej populacji) odsetek
pracowników dojeżdżających do
pracy prywatnym samochodem.

n

n

m

n

m

u

n

m

p

n

n

m

n

m

u

n

m











 

















 



1

1





200

200

72

1

200

72

58

,

2

200

72

200

200

72

1

200

72

58

,

2

200

72











 

















 



p

448

,

0

272

,

0





p

2013-04-03

6

11

Przedział ufności dla wariancji σ

2

–

model 1

Model 1



Cecha X w populacji generalnej ma rozkład N(μ,σ),



Średnia μ – nieznana, odchylenie standardowe σ – nieznane,



Próba mała (n≤30),

Przedział ufności dla wariancji ma postać:

gdzie:



S

2

lub S*

2

– wariancja z próby,













































1

2

2

1

2

2

2

2

2

nS

nS

P























































1

1

1

2

2

1

2

*

2

2

2

2

*

S

n

S

n

P

2

2





2

2

1







wartości zmiennej losowej χ

2

o n-

1 stopniach swobody, dla której

2

2

1

,

2

2



























n

P

2

2

1

,

2

1

2





























n

P

lub

12

Przedział ufności dla odchylenia standardowego σ

–

model 2

Model 2



Cecha X w populacji generalnej ma rozkład N(μ,σ) lub zbliżony do
normalnego,



Średnia μ – nieznana, odchylenie standardowe σ – nieznane,



Próba duża (n>>30)

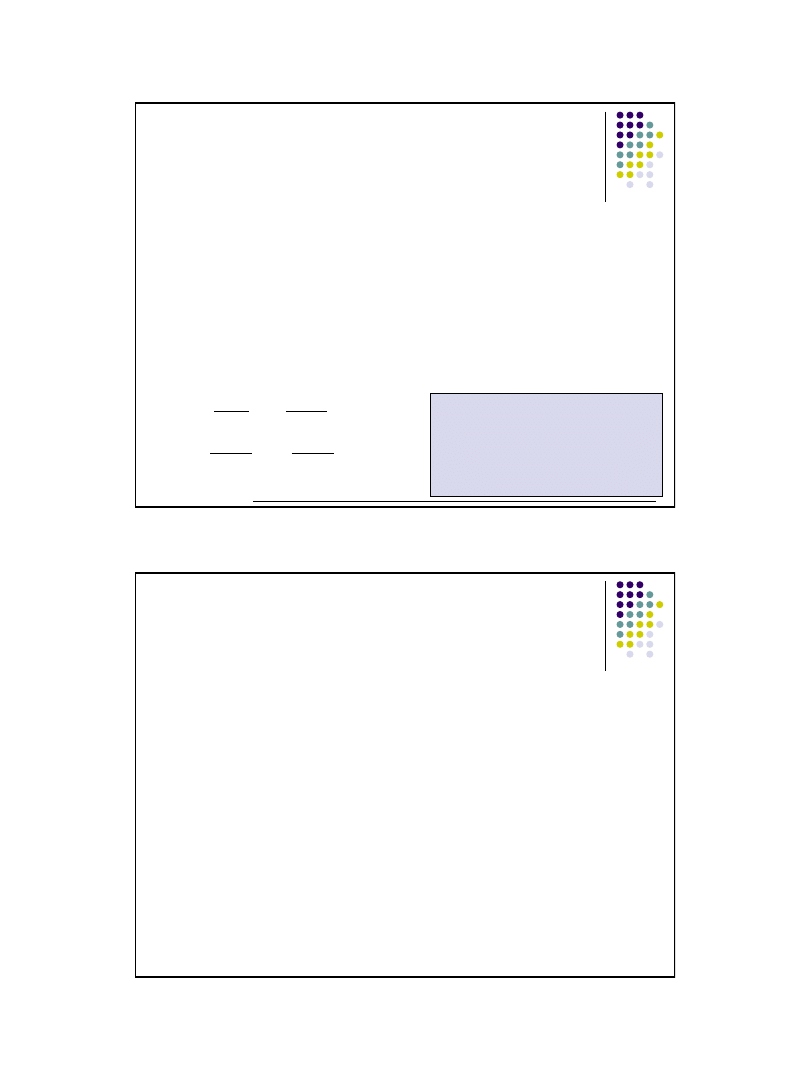
Przedział ufności dla odchylenia standardowego ma postać:

gdzie:



S

– odchylenie standardowe z próby,



u

α

-

wartość zmiennej losowej U o rozkładzie N(0,1), dla której



Estymator s parametru

σ ma asymptotyczny rozkład normalny

 

2

1











u





















1

u

U

u

P













































1

2

1

2

1

n

u

S

n

u

S

P













n

N

2

,





2013-04-03

7

13

Przedział ufności dla wariancji σ

2

– przykład 1



Badając wytrzymałość elementu konstrukcyjnego pewnego urządzenia
dokonano 8 pomiarów wytrzymałości. Wariancja obliczona na podstawie próby
s

2

wynosi 139,5. Zbuduj przedział ufności dla wariancji σ

2

wytrzymałości

elementu przyjmując współczynnik ufności 0,96.



Dane: n=8, s

2

=139,5, 1-

α=0,96,

α = 0,04

; α/2=0,02



Założenie: cecha ma w populacji rozkład normalny N(μ;



).



Model 1: σ ≈ s,



Odczyt

χ

2

1-

α/2,7

i

χ

2

α/2,7



Z tablic rozkładu χ

2

, dla liczby stopni swobody n-1=8-1=7

wartość χ

2

0,02,7

=16,622 i ;

χ

2

0,98,7

=1,564



Przedział ufności wyliczymy następująco:

Wniosek:
Przedział (7,7 ; 25,0)
z prawdopodobieństwem 0,96
(z ufnością 96%) pokrywa nieznane
odchylenie standardowe dla
wytrzymałości elementu

2

1

,

2

/

1

2

2

2

1

,

2

/

2











n

n

nS

nS











564

1

5

139

7

622

16

5

139

7

2

,

,

*

,

,

*











0

25

7

7

4

624

7

58

2

,

;

,

σ









,

,



14

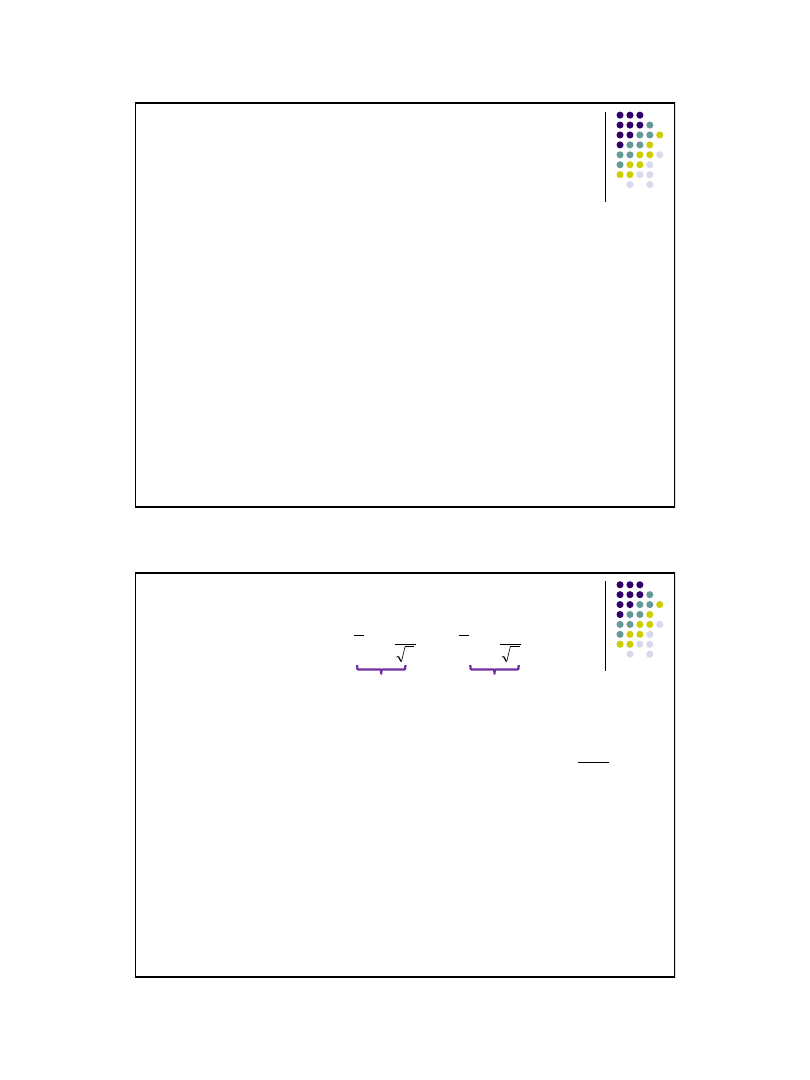
Ustalenie minimalnej liczebności próby

z zadanym z góry

błędem szacunku d

2013-04-03

8

15

Zagadnienie minimalnej liczebności próby

Z reguły z populacji pobiera się tylko jedną n-elementową próbę



Zbyt duża próba

=> zbyt duże koszty, opóźnienia czasu analizy

wyników,



Zbyt mała próba

=> nie zapewnia żądanej dokładności i

wiarygodności wnioskowania.

Aby wyznaczyć

minimalną liczebność próby

należy ustalić:



Poziom współczynnika ufności (1 - α ),



Maksymalny błąd szacunku (długość przedziału ufności).

16

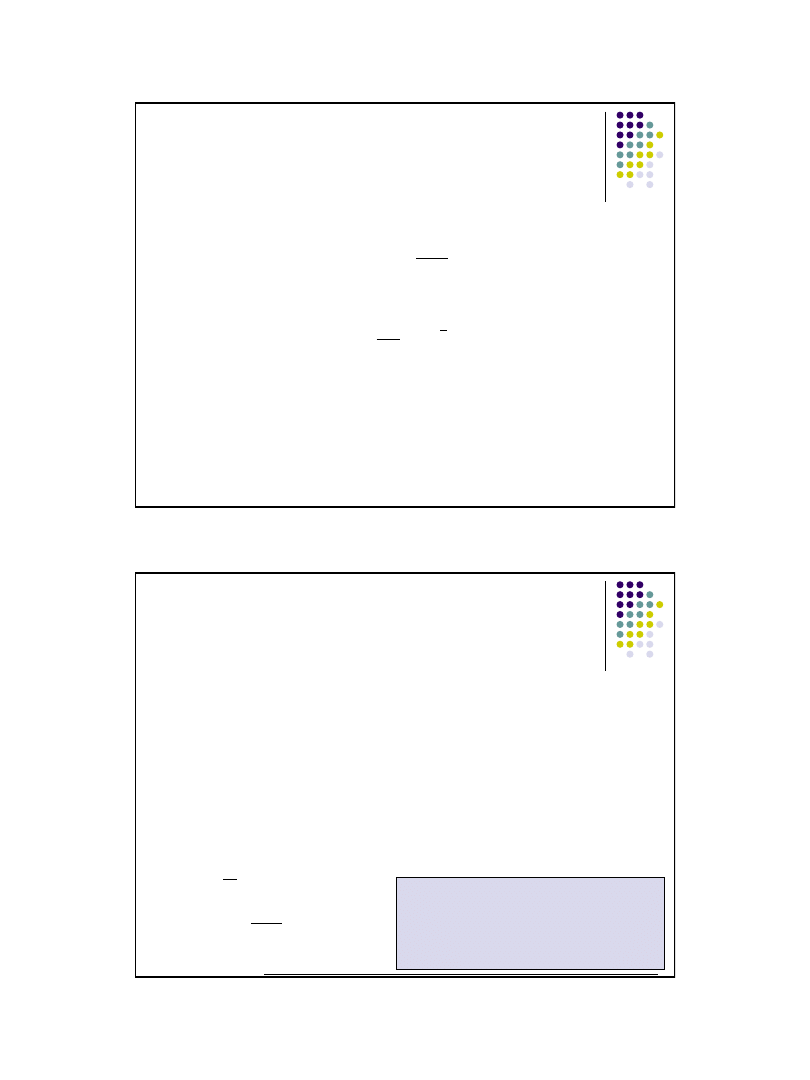
Ustalenie minimalnej liczebności próby dla

oszacowania wartości średniej

Dla szacowania

średniej μ

na poziomie ufności 1-α



gdy znane odchylenie standardowe σ – (model 1)
minimalna liczebność próby wynosi:

gdzie: d

– zakładana dokładność (maksymalny błąd szacunku),

u

α

-

wartość zmiennej losowej U o rozkładzie N(0,1), dla którego,



gdy

n nie jest całkowite – zaokrąglamy n w górę



Większa dokładność wymaga większej liczebności próby

2

2

2

d

u

n



























1

u

U

u

P





































1

n

u

X

n

u

X

P

d d

2013-04-03

9

17

Ustalenie minimalnej liczebności próby dla

oszacowania wartości średniej

Dla szacowania

średniej μ

na poziomie ufności 1-α



gdy σ

2

– nieznane (model 2)

gdzie:



wartość wariancji S

*

2

szacujemy na podstawie n

o

elementowej próby

wstępnej



t

α

-

wartość zmiennej losowej T o rozkładzie t-Studenta o n

0

-1 stopniach

swobody, dla której



Następnie, gdy n>n

0

należy zwiększyć próbę wstępną o n-n

0

elementów.

2

2

*

2

d

S

t

n



















0

1

2

0

2

*

1

1

n

i

i

X

X

n

S





















1

t

T

t

P

18

Wyznaczanie niezbędnej liczby pomiarów do próby –

przykład



Ile niezależnych doświadczeń należy przeprowadzić, aby przy współczynniku
ufności 0,95 oszacować metodą przedziałową średni czas dojazdu
pracowników firmy A z dokładnością do 2 minut. Próba wstępna - 17 losowo
wybranych pracowników firmy A dała średni czas dojazdu 26 minut,
a odchylenie standardowe s* = 6,18 minut.



Dane: n

0

=17, ‾x=26, s*=6,18, d=2, 1-α=0,95



Założenie: Cecha ma w populacji rozkład normalny N(μ;



).



Model 2: σ ≈ s,



Odczyt -t

α

:

α = 0,05;



Z tablic rozkładu t-Studenta, dla liczby stopni swobody n-1=17-1=16
wartość –t

0,05,16

=2,1199;



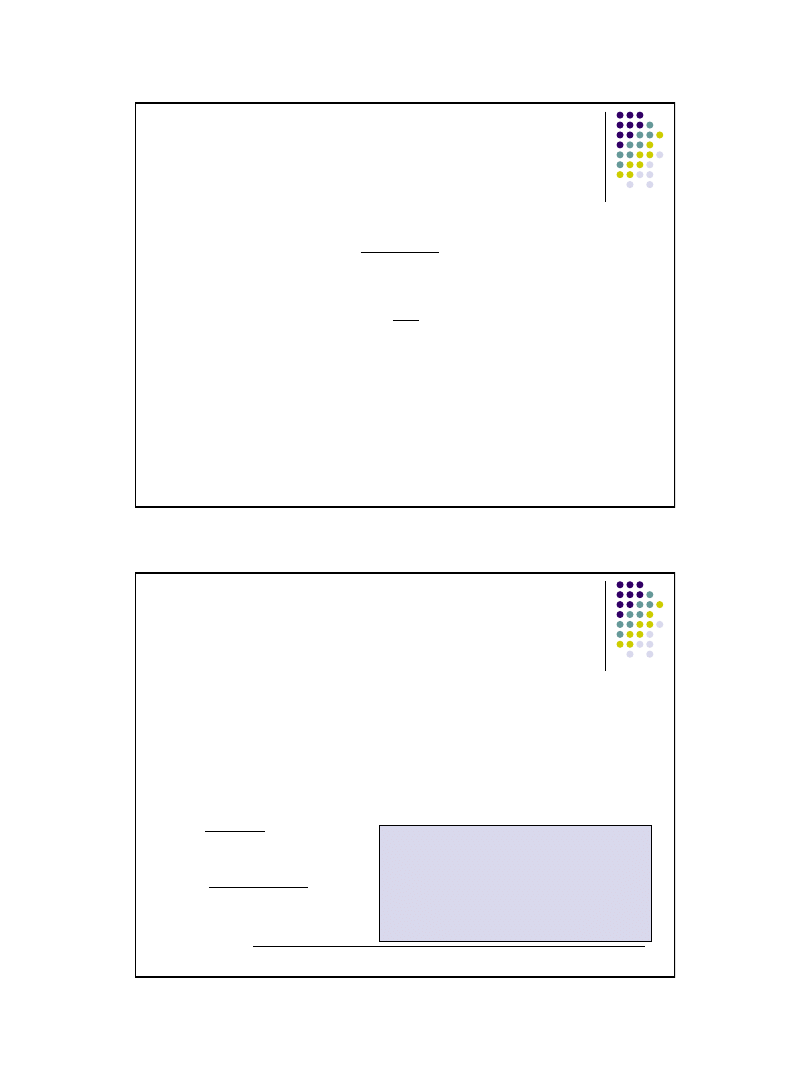
Liczbę elementów w próbie wyliczymy następująco:

Wniosek:
Niezbędna liczba pomiarów dla
oszacowania średniego czasu dojazdu z
dokładnością do 2 minut wynosi 43.
Należy dolosować 43-17=26 elementów

2

2

2

1

d

S

t

n

n

*

,







2

2

2

2

18

,

6

1199

,

2



n

9

,

42



n

2013-04-03

10

19

Ustalenie minimalnej liczebności próby

dla wskaźnika struktury

Dla szacowania

wskaźnika struktury p

na poziomie ufności 1-α

z zadanym z góry błędem szacunku d (połowa długości przedziału ufności)



p

0

– wstępne oszacowane p,



lub za p

0

podstawiamy 0,5



u

α

-

wartość zmiennej losowej U o rozkładzie N(0,1), dla którego,



gdy n nie jest całkowite – zaokrąglamy n w górę



Większa dokładność wymaga większej liczebności próby.





















1

u

U

u

P





2

0

0

2

1

d

p

p

u

n







2

2

4d

u

n





20

Niezbędna liczba pomiarów dla wskaźnika struktury p

– przykład



O ile należy zwiększyć liczbę pomiarów, aby błąd oszacowania wskaźnika
struktury nie przekroczył 4%. Zapytano 200 losowo wybranych pracowników
i w 72 przypadkach otrzymano odpowiedź, że dojeżdżają do pracy prywatnym
samochodem. Współczynnik ufności wynosi 0,99.



Dane: n=200, m=72, p

o

=72/200=0,36; 1-

α=0,99



Założenie: cecha ma w populacji rozkład dwupunktowy.



Odczyt -u

α

:

α = 0,01;

α/2 = 0,005; u

0,995

=2,58;



Niezbędną liczbę pomiarów wyliczymy następująco:

Wniosek:
Niezbędna liczba pomiarów dla
oszacowania odsetka pracowników, którzy
dojeżdżają do pracy prywatnym
samochodem z dokładnością 4%, wynosi
959.
Należy dolosować 959-200 elementów.





2

0

0

2

1

d

p

p

u

n











2

2

04

,

0

36

,

0

1

*

36

,

0

*

58

,

2





n

52

,

958



n