Chuck Norris

ET-DI 2

Gr. Lab. 1

Sprawozdanie

z

ćwiczenia

„ Estymacja przedziałowa cz.1”

1. Cel ćwiczenia

Celem ćwiczenia jest zapoznanie się ze sposobami określania przedziałów ufności dla średniej arytmetycznej oraz wariancji danych o typowych rozkładach prawdopodobieństwa.

2. Przebieg ćwiczenia.

• Dla rozkładu normalnego N(3,5), określić prawdopodobieństwo Pr(X=5)

W tym celu należy do komórki A1 wprowadzamy wartość odpowiadającą prawdopodobieństwu, zaś do B1 wprowadzamy funkcje ROZKŁAD.NORMALNEGO o zadanych parametrach.

Wiadomości dotyczące funkcji ROZKŁAD.NORMALNY:

Zwraca rozkład normalny dla określonej średniej i odchylenia standardowego. Funkcja ta ma bardzo szeroki zakres zastosowań w statystyce, łącznie z badaniem hipotez.

Składnia

ROZKŁAD.NORMALNY(x;średnia;odchylenie_std;skumulowany)

X - to wartość, dla której należy obliczyć rozkład.

Średnia - to średnia arytmetyczna rozkładu.

Odchylenie_std - to odchylenie standardowe rozkładu.

Skumulowany - to wartość logiczna, która określa format funkcji. Jeśli argument skumulowany ma wartość PRAWDA (1), wówczas funkcja ROZKŁAD.NORMALNY zwraca skumulowaną funkcję rozkładu; a jeśli ma wartość FAŁSZ (0), wówczas funkcja ROZKŁAD.NORMALNY zwraca funkcję gęstości prawdopodobieństwa.

2.2. Dla zmiennej losowej X o rozkładzie N(1,2) wyznaczyć prawdopodobieństwa:

a) Pr(X<2.5)

b) Pr (X>-0.5)

c) Pr(2<X<3)

d) Pr (|X|>0.5)

e) Pr (|X-3|<2)

Przydatne zależności:

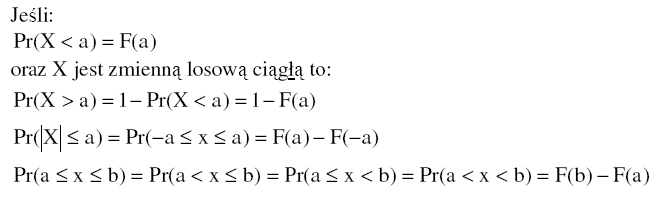
(1)

(2)

(3)

(4)

Ad a) Pr(X<2.5)

W tym przykładzie należy zastosować pierwsza z podanych zależności.

Przechodząc do realizacji należy umieści wartość odpowiadającą wielkości X do komórki A2, zaś do B2 funkcję ROZKŁADU.NORMALNEGO, która zwraca wartość skumulowaną.

Ad b) Pr (X>-0.5)

W tym przypadku trzeba skorzystać z zależności drugiej. Przechodząc do realizacji należy umieści wartość odpowiadającą wielkości X do komórki A3, zaś do B3 funkcję ROZKŁADU.NORMALNEGO, która zwraca wartość skumulowaną. Następnie zgodnie z zastosowaną zależnością wartość 1 pomniejszamy o wartość otrzymanego rozkładu normalnego.

Ad c) Pr(2<X<3)

W tym przypadku trzeba skorzystać z zależności czwartej. Przechodząc do realizacji należy umieści wartość odpowiadającą wielkości X do komórki A4 oraz A5, zaś do B4 i B5 funkcję ROZKŁADU.NORMALNEGO, która zwraca wartość skumulowaną. Następnie zgodnie z zastosowaną zależnością wartość rozkładu normalnego dla X=3 pomniejszamy o wartość otrzymanego rozkładu normalnego dla X=2.

Ad d) Pr (|X|>0.5)

W tym przypadku trzeba skorzystać z zależności trzeciej. Przechodząc do realizacji należy umieści wartość odpowiadającą wielkości X do komórki A6 oraz -X do A7, zaś do B6 i B7 funkcję ROZKŁADU.NORMALNEGO, która zwraca wartość skumulowaną dla zadanych X. Następnie zgodnie z zastosowaną zależnością wartość rozkładu normalnego dla Y= X pomniejszamy o wartość otrzymanego rozkładu normalnego dla Y= -X, gdzie X=0,5.

Ad e) Pr (|X-3|<2)

W tym przypadku trzeba skorzystać z poniższej zależności.

Przechodząc do realizacji należy umieści wartość odpowiadającą wielkości X do komórki A8 oraz A9, zaś do B8 i B59 funkcję ROZKŁADU.NORMALNEGO, która zwraca wartość skumulowaną. Następnie zgodnie z zastosowaną zależnością wartość rozkładu normalnego dla X=5 pomniejszamy o wartość otrzymanego rozkładu normalnego dla X=1.

1. Dla zmiennej X o rozkładzie N(0,1) określ prawdopodobieństwo Pr(|X|<1) i Pr(|X|<3), wykorzystując zależność trzecią i dystrybuantę rozkładu normalnego standaryzowanego - funkcja ROZKŁAD.NORMALNY.S.

ROZKŁAD.NORMALNY.S

Zwraca funkcję skumulowanego rozkładu normalnego. Rozkład ten ma średnią zero i odchylenie standardowe równe jeden. Funkcję tę należy stosować zamiast tabeli obszarów standardowych krzywych normalnych.

Składnia

ROZKŁAD.NORMALNY.S(z)

Z    to wartość, dla której należy obliczyć wartość funkcji.

2.4. Dla zmiennej X o rozkładzie N(0,1) określić prawdopodobieństwo Pr(|X|>2).

Zadanie rozwiązać dwoma sposobami stosując funkcje ROZKŁAD.NORMALNY.S

1. Zaleźć wartość parametru b dla którego Pr(X=b)=0.975 jeśli X ma rozkład N(0,1) Należy zastosować funkcje ROZKŁAD.NORMALNY.S.ODW
   

ROZKŁAD.NORMALNY.S.ODW

Zwraca funkcję odwrotną skumulowanego, standardowego rozkładu normalnego. Rozkład ten ma średnią równą zero i standardowe odchylenie równe jeden.

Składnia

ROZKŁAD.NORMALNY.S.ODW(prawdopodobieństwo)

Prawdopodobieństwo    to prawdopodobieństwo odpowiadające rozkładowi normalnemu.

2. Znaleźć wartość parametru b dla którego prawdziwa jest zależności Pr(|X|>b)=0.3, jeśli rozkład zmiennej X to N(0,2)

Należy wykorzystać zależność

Następnie zastosować funkcje ROZKŁAD.NORMALNY.ODW

3. Należy wyznaczyć prawdopodobieństwo Pr(X>0.95) wykorzystując funkcje ROZKŁAD.T dla rozkładu jednostronnego (ślady=1) o liczbach stopni swobodnych:5, 13, 28, 500

4. 2.8. Należy wyznaczyć prawdopodobieństwo Pr(|X|>0.95) wykorzystując funkcje ROZKŁAD.T dla rozkładu jednostronnego (ślady=2) o liczbach stopni swobodnych:5, 13, 28, 500

ROZKŁAD.T

Zwraca Punkty procentowe (prawdopodobieństwo) dla rozkładu t Studenta, gdzie wartość numeryczna (x) jest obliczoną wartością t, dla której należy obliczyć Punkty procentowe. Rozkład t jest stosowany przy testowaniu hipotez dla małych próbek zbiorów danych. Funkcję tę należy stosować zamiast tabeli wartości krytycznych dla rozkładu t.

Składnia

ROZKŁAD.T(x;stopnie_swobody;ślady)

X    to wartość numeryczna, przy której należy oszacować rozkład.

Stopnie_swobody    to liczba całkowita oznaczająca liczbę stopni swobody.

Ślady    określa, ilu stronny rozkład powinien być zwrócony. Jeśli ślady = 1, funkcja ROZKŁAD.T zwraca rozkład jednostronny. Jeśli ślady = 2, funkcja ROZKŁAD.T zwraca rozkład dwustronny.

5. Znaleźć wartość t taką że prawdopodobieństwo Pr(|X| > t) przyjmuje wartości 0,95 i 0,1 dla liczby stopni swobodnych n= 9, 14,28

Należy wykorzystać funkcje ROZKŁAD.T.ODW dla rozkładu dwustronnego

ROZKŁAD.T.ODW

Zwraca wartość t rozkładu t Studenta jako funkcję prawdopodobieństwa i liczby stopni swobody.

Składnia

ROZKŁAD.T.ODW(prawdopodobieństwo;stopnie_swobody)

Prawdopodobieństwo    to prawdopodobieństwo skojarzone z rozkładem dwustronnym t Studenta.

Stopnie_swobody    to liczba stopni swobody, dla których należy określić rozkład.

6. Średni czas świecenia żarówki wynosi 1 rok a odchylenie standardowe wynosi trzy miesiące (rozkład normalny). Jakie jest prawdopodobieństwo, że wybrana losowo żarówka będzie świeciła 18 miesięcy? Zadanie rozwiązać wykorzystując dystrybuanty rozkładu normalnego oraz normalnego standaryzowanego

Nasza zmienna ma rozkład N(12,3), należy znaleźć Pr(X>18) stosując funkcje ROZKŁAD NORMALNY

Stosując rozkład normalny standaryzowany musi stworzyć zmienną standaryzowaną o rozkładzie N(0,1)

Pr(Z>2)

7. Worki pakowane automatycznie mają średnią wagę 114kg. Wykazano ze 10% worków ma 116kg lub więcej. Określić odchylenie standardowe (rozkład normalny).

Należy wykorzystać zmienną standaryzowaną Z wiemy ze Pr(Z>116)=0,1 stad

Pr(Z<116)=1-Pr(Z<116)=0.9

Należy określić wartość zmiennej standaryzowanej stosując funkcje ROZKŁAD.NORMALNY.S.ODW

Odchylenie standardowe obliczamy ze wzoru :

3. Wnioski

Po przeprowadzeniu ćwiczenia wywnioskowałem iż znając sposób posługiwania się funkcjami typu ROZKŁAD NORMALNY tu dzież ROZKŁAD NORMATNY ODW.

Możemy zaoszczędzić dużo czasu i zyskać w wygodny dla siebie sposób oczekiwane rezultaty, nie trudząc się z obliczaniem „na piechotę” korzystając z zależności matematycznych.

---