Wykład 7

Pomiary zmian pracy wyjścia

F. Gołek

Uniwersytet Wrocławski

Instytut Fizyki Doświadczalnej

[e-mail]

www.pe.ifd.uni.wroc.pl

Wstęp

Pojawienie się pojęcia pracy wyjścia

wiąże się z wczesnymi badaniami
fotoemisji.

Praca wyjścia to energia potrzebna do

przeniesienia elektronu z poziomu
Fermiego na poziom próżni.

Praca wyjścia to wielkość makroskopowa
zwykle wynosząca kilka eV.

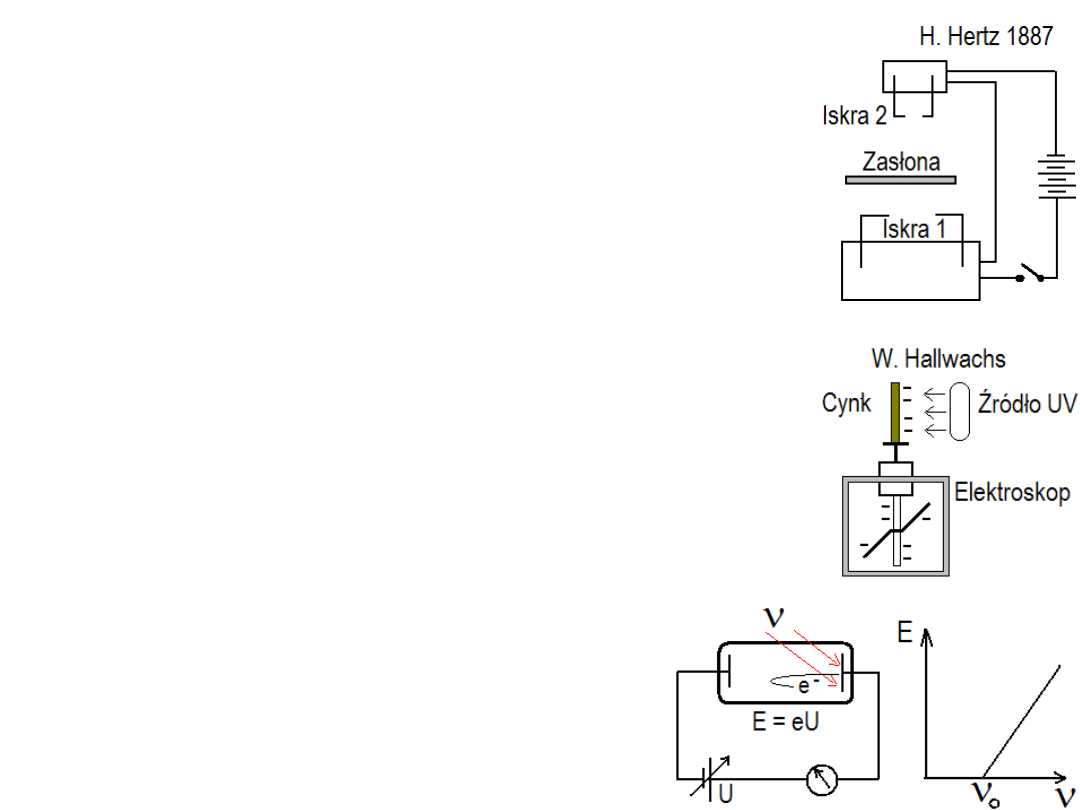
Początki fotoemisji

Fotoefekt odkryli: Hertz w 1887 r. oraz
Hallwachs w 1888 r.
Hertz badał zachowanie się iskry wtórnej
(iskry 2) w obecności promieniowania z
iskry pierwotnej (iskry 1) przy różnych
materiałach zasłony i stwierdził, że to
ultrafiolet z iskry 1 stymuluje iskrę 2.
Obecnie wiemy, że czynią to fotoelektrony
z elektrod iskrownika 2. Hallwachs
zauważył, że ujemnie naładowana płytka
cynku połączona z elektroskopem szybko
ulega rozładowaniu gdy jest oświetlana
ultrafioletem. Dokładniejsze badania
fotoemisji niespodziewanie pokazały, że
energia kinetyczna fotoelektronów nie
zależy od natężenia światła lecz od jej
częstotliwości (barwy).

Początek rozważań nad pracą wyjścia
znajdujemy w publikacji A. Einsteina :

On the

production and transformation of light according to a
heuristic point of view. Ann. d. Physik 17, (1905) 132.

W tej pracy fotoefekt wyjaśniony jest przy pomocy bilansu energetycznego:

E

e

= hν – I

(1)

gdzie: I jest minimalną energią konieczną do wyemitowania elektronu (- pracą
wyjścia zwykle wyrażaną symbolem Ф lub W). E

e

jest maksymalną energią

kinetyczną wyemitowanego elektronu. hν jest energią „cząstki” światła E

v

= hν.

Fotoefekt zachodzi gdy hv

≥

I. Praca ta dała początek rozważaniom nad

dualizmem falowo-cząstkowym i przyczyniła się do uzyskania przez Einsteina
nagrody Nobla w 1921 r.

Jest to jedna z pięciu publikacji napisanych przez Einsteina w 1905 r. Pozostałe cztery prace to:
1) A new determination of the molecular dimensions, Ann. d. Physik 19, 289 (1906) - za tą pracę
Einstein otrzymał doktorat (było to jego drugie podejście do doktoratu).
2) On the motion of particles suspended in a liquid at rest, as required by the molecular-kinetic
theory of heat. Ann. d. Physik 17, 549 (1905).
3) On the electrodynamics of moving bodies Ann. d. Physik 17, 891 (1905)
4) Does the inertial mass of a body depend on its energy content? Ann. d. Physik 18, 639 (1905).

Wigner i Bardeen zaproponowali definicję pracy wyjścia
jako różnicę między energią neutralnego metalu E

N

z N

elektronami w stanie podstawowym (czyli w temp. 0K i o
potencjale V = 0V) a energią E

N-1

tego układu po

usunięciu jednego elektronu do obszaru o potencjale V

0

:

Ф = (E

N-1

+ eV

0

) - E

N

Pracę wyjścia Ф można też definiować poprzez różnicę
między elektrochemicznym potencjałem elektronu w
metalu µ, a energią elektronu Ф

0

w elektrostatycznym

potencjale na zewnątrz metalu:
Ф = Ф

0

- µ

Przy stałych: ciśnieniu p i temperaturze T, µ = (

∂

G/

∂

n)

T,P

G – entalpia swobodna (energia Gibbsa)
Praca wyjścia jest jednym z fundamentalnych
parametrów metali.

Bywa tak, że pomimo iż z definicji praca wyjścia jest energią potrzebną do
przeniesienia elektronu z poziomu Fermiego na poziom próżni to niektórzy
autorzy wyrażają tę wielkość w V (a nie w eV) i piszą równania w postaci:
eФ = - eФ

0

- µ

(np.: D.P. Woodruff, T.A. Delcher Modern techniques of surface science, str.
356). Pewnym usprawiedliwieniem może być fakt, że przy wyznaczaniu pracy
wyjścia mierzone są właśnie napięcia stosowanych w eksperymencie
zasilaczy. Ponadto do zmian pracy wyjścia przyczyniają się liczne efekty natury
elektrostatycznej (np. moment dipolowy adsorbatu), gdyż praca przeniesienia
elektronu to praca przeniesienia jego ładunku elektrycznego (masa nie gra roli).

W literaturze zdarza się, że dla wygody pojęcie potencjału używa się jako
energii potencjalnej elektronów i definicję pracy wyjścia Wignera-Bardeena
zapisuje jako:
W = (E

N-1

+ V

0

) - E

N

Od czego zależy praca wyjścia Ф?

I)

Zależy od położenia poziomu Fermiego, zatem

zależy od wnętrza (tj. rodzaju metalu lub

półprzewodnika)

II) Zależy również od stanu i struktury powierzchni.

Dla wybranego metalu praca wyjścia zależy od:
•

temperatury,

•

struktury powierzchni tj. rodzaju ściany, ilości stopni

atomowych, wielkości tarasów itp.,

•

zanieczyszczeń i zdefektowania,

•

rodzaju adsorbatu,

•

grubości adsorbatu.

wszystkiego co zmienia powierzchniowy moment dipolowy.

Czy pomiar pracy wyjścia jest przydatny?

• Jest użyteczny dzięki temu, że stanowi relatywnie prostą

metodę monitorowania stanu powierzchni (czystości, orientacji i

rekonstrukcji powierzchni, zdefektowania, obecności adsorbatu,

fazy adsorbatu, korozji itp.). Często pomiar zmiany pracy

wyjścia ΔФ dla monokryształu metalu może określać stopień

pokrycia (kalibrowany np. przez obraz LEED lub kinetyki TDS).

• Pojawienie się jednej monowarstwy adsorbatu może zmienić

potencjał powierzchni o wartość od 0.1 V do około 1,5 V.

Ponieważ zmiany tego potencjału można mierzyć z

dokładnością 0,001V, to metoda okazuje się bardzo czułą.

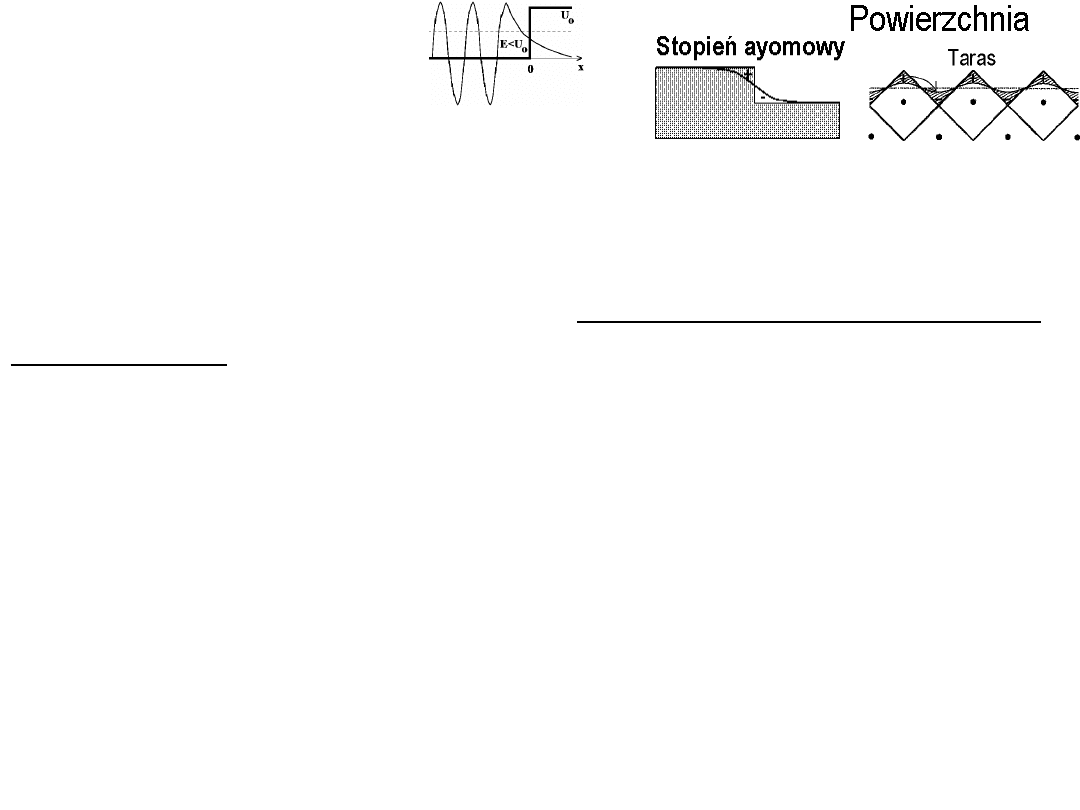
Efekt
Smoluchowskiego

czyli wygładzanie się rozkładu
gęstości elektronowej. Wartość pracy
wyjścia dla danego metalu zależy od typu powierzchni (ściany)
kryształu. Przykładowo dla uszeregowania ścian kryształu
wolframu (bcc): 110, 211, 100, 111 rośnie chropowatość i maleje
praca wyjścia. Efekt ten Smoluchowski wyjaśnia następująco.
Gdyby atomy powierzchni były otoczone identycznym rozkładem
gęstości ładunku ujemnego jak w objętości kryształu to efektu by
nie było. Jednak ze względu na minimalizację energii całkowitej
dochodzi do modyfikacji rozkładu chmur elektronowych na
powierzchni. Mają tu miejsce dwa efekty: pierwszy polega na
pewnym wysunięciu się środka ciężkości ładunku ujemnego do
próżni przypadającego na atom powierzchniowy (wtedy Ф

↑

) i

drugi polegający na wygładzaniu gęstości ładunku ujemnego
na powierzchni (wtedy Ф

↓

). Oba efekty konkurują i wpływają na

wypadkową wartość momentu dipolowego powierzchni metalu.

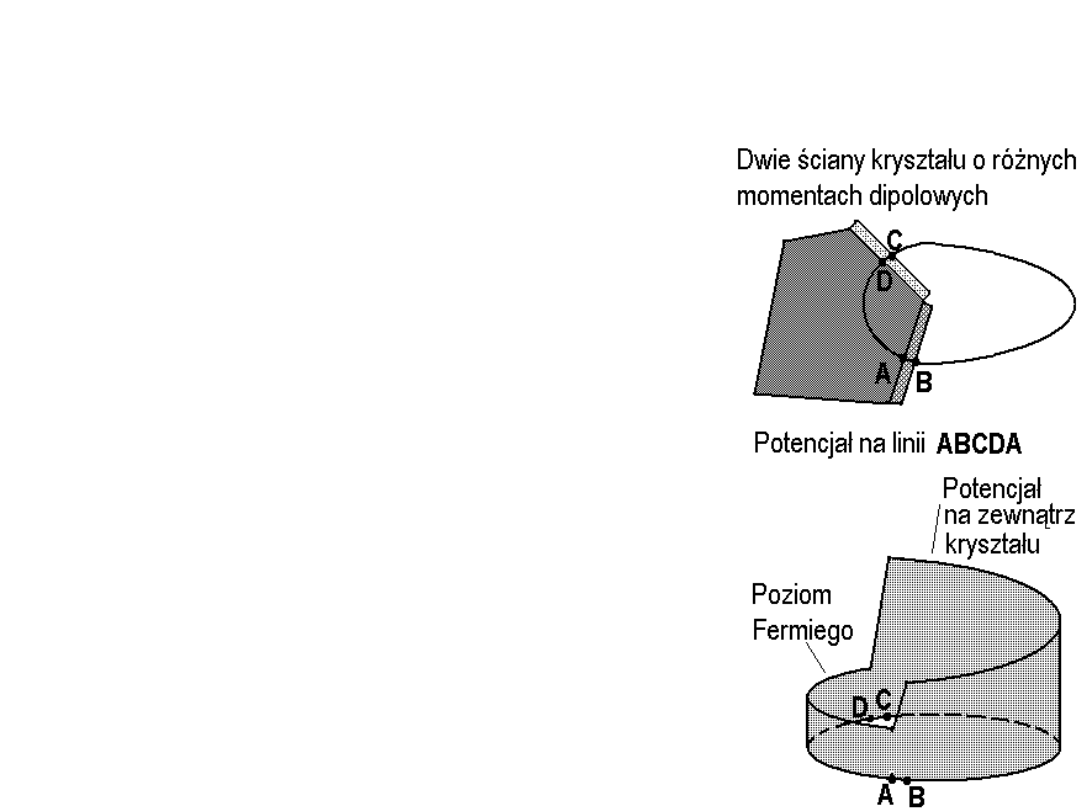
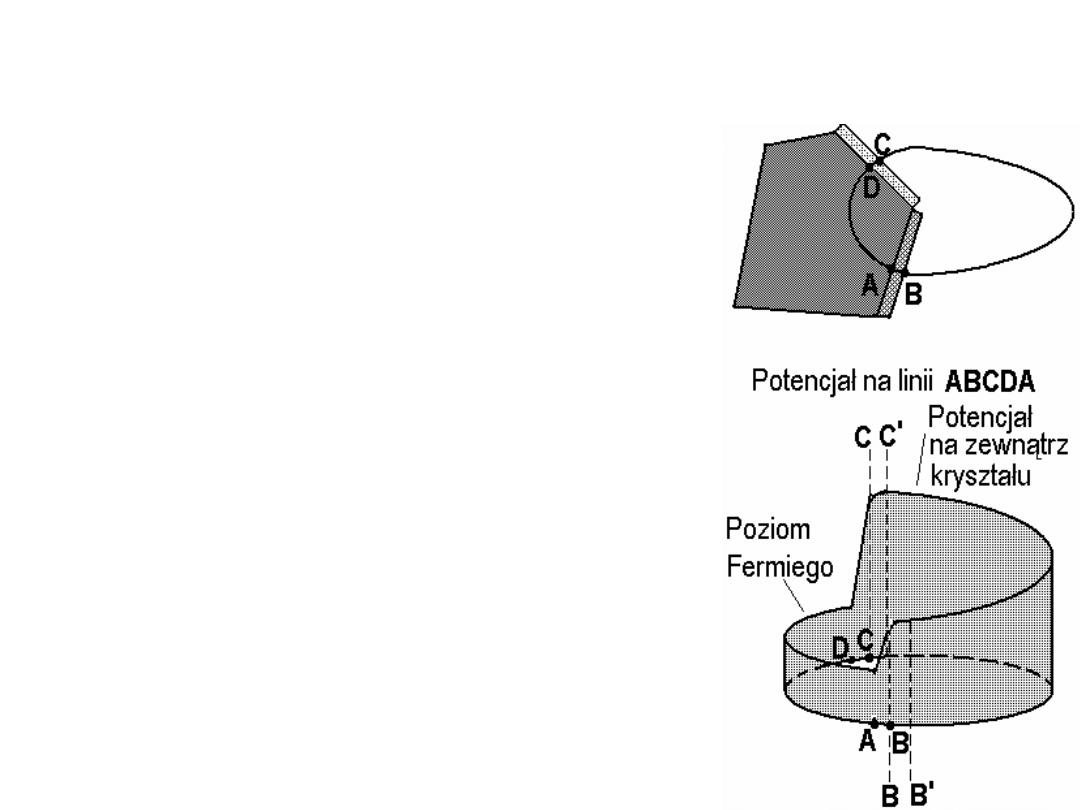
Gdy dwie sąsiednie ściany kryształu

metalu różnią się pracą wyjścia.

Wewnątrz metalu nie ma pola
elektrycznego: mamy „poziom” cieczy
Fermiego. Zatem na rys. obok na odcinku AD
próbny ładunek nie „widzi” zmian potencjału.
Potencjał doznaje skoku na powierzchniach.
Jeżeli momenty dipolowe na ścianach są
różne to skoki potencjału na odcinkach DC i
AB też są różne. Zatem punkty B i C różnią
się potencjałem co oznacza, że na zewnątrz
kryształu mamy pole elektryczne. Widać, że
praca wyjścia w okolicy punktu C jest
większa niż w okolicy punktu B – jest to
oczywiste. Podobno nie-elektrycy mają tu
jakiś problem z wyjaśnieniem sytuacji.

Gdy na zewnątrz kryształu

występuje pole elektryczne.

Gdy na zewnątrz kryształu występuje

pole elektryczne to tzw. poziom próżni

zmienia się z odległością od powierzchni

tego kryształu. Wtedy pracę wyjścia

definiuje się jako: energię potrzebną do

przeniesienia elektronu z poziomu

Fermiego na poziom próżni w

odległości r

o

od powierzchni.

Gdy potencjał maleje z odległością r to

wartość r

o

określa maksimum energii

potencjalnej (dla r = r

o

spełniony jest

warunek: dV/dr = 0).

Gdy potencjał rośnie to za r

o

można przyjąć

wartość makroskopowo małą ale dużą w

skali atomowej np. 1µm, tak by pozostały

wkład energii obrazowej był do

zaniedbania.

Wniosek: na zewnątrz powierzchni
polikryształów występują pola
elektryczne.
Takie pola wpływają na powolne jony i
elektrony w układach UHV.
Dla Mo różnice prac wyjścia między
niskoindeksowymi ścianami nie przekracza
0,4eV natomiast dla Nb i W sięga 0,8 eV.
Dlatego lepiej stosować molibden niż
wolfram w krytycznych miejscach aparatury
pomiarowej w układach UHV.

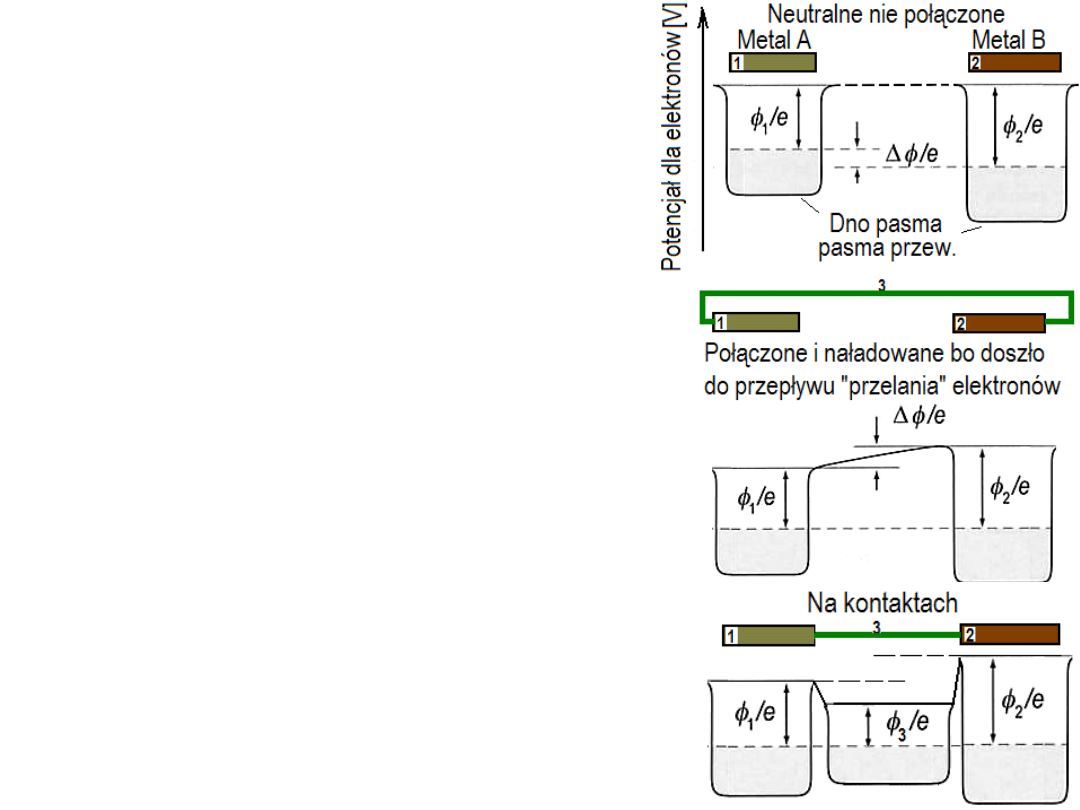
Kontaktowa różnica
potencjału - KRP lub KPD.

Położenie poziomu Fermiego jest cechą
charakterystyczną (i wyróżniającą) każdego
metalu. Dwa kawałki różnych (ale neutralnych
elektrycznie) metali zanim połączymy kontaktem
galwanicznym mają ten sam poziom próżni,
poniżej którego poziomy Fermiego znajdują się
na dwóch różnych głębokościach. Po połączeniu
galwanicznym odrobina elektronów z wyższego
poziomu Fermiego przeleje się do metalu o
początkowo niższym poziomie Fermiego. Dzięki
tak przeniesionemu ładunkowi elektrycznemu
dojdzie do wyrównania poziomów Fermiego ale
pojawią się różne potencjały elektryczne na
różnych metalach. Przeniesiony ładunek
oczywiście rozłoży się tak na powierzchni aby
wewnątrz metali nie było pól elektrycznych.
Ponieważ ta różnica potencjałów powstaje przy
kontakcie galwanicznym umożliwiającym
przelanie się elektronów, nazywamy ją KPD.

Pomiary pracy wyjścia dzielimy na trzy

grupy:

a) Pomiary absolutnej wartości pracy wyjścia
b) Pomiary względnej wartości i zmian pracy

wyjścia (wykorzystanie kontaktowej różnicy
potencjału) – przedmiot tego wykładu.

c) Pomiary mikroskopowe (PEEM, LEEM, STM).

Metody pomiaru absolutnej wartości
pracy wyjścia

a

) Metoda fotoemisyjna,

b

) Metoda termoemisyjna,

c) Metoda emisji polowej,
d) Metoda jonizacji powierzchniowej.

Te metody zapewniają doskonały wynik dla
jednorodnej i czystej powierzchni metalu.

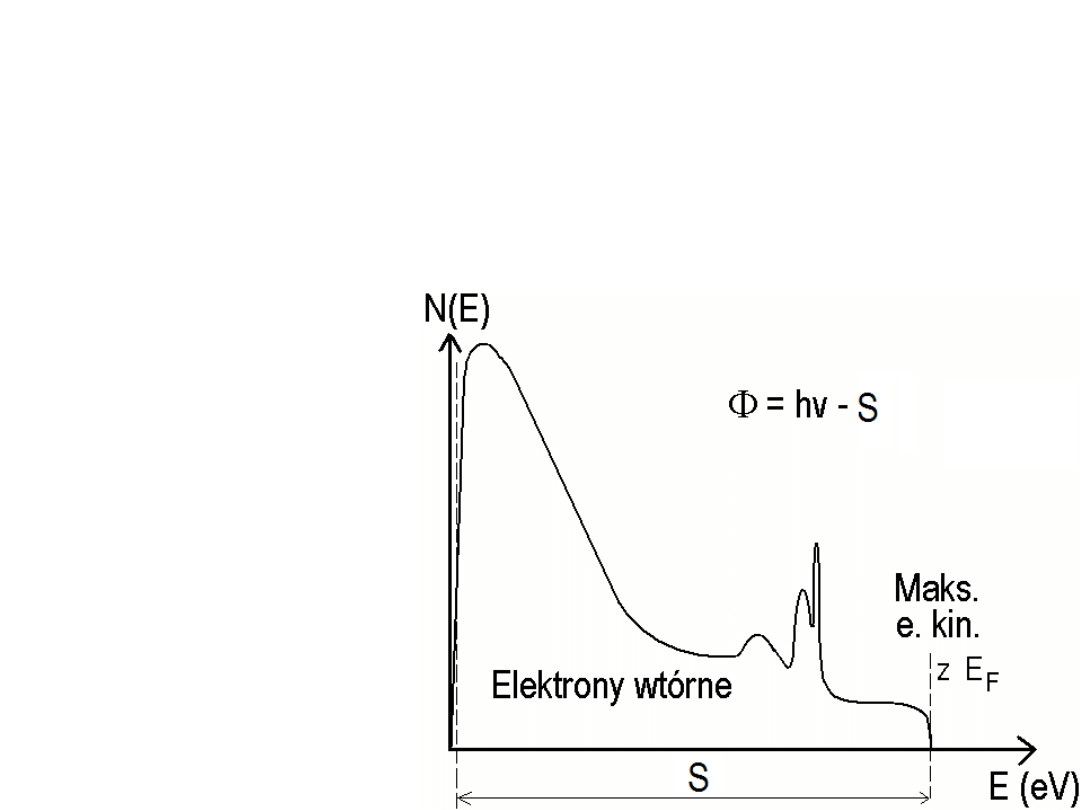
Pomiar pracy wyjścia z zastosowaniem UPS
Polega na pomiarze pełnej szerokości spektrum
fotoelektronów (lub ich energii maksymalnej) S
wzbudzanych monoenergetycznymi fotonami z
zakresu ultrafioletu (np. He 1, hv = 21.22 eV)
i zastosowaniu
relacji: Ф = hv - S

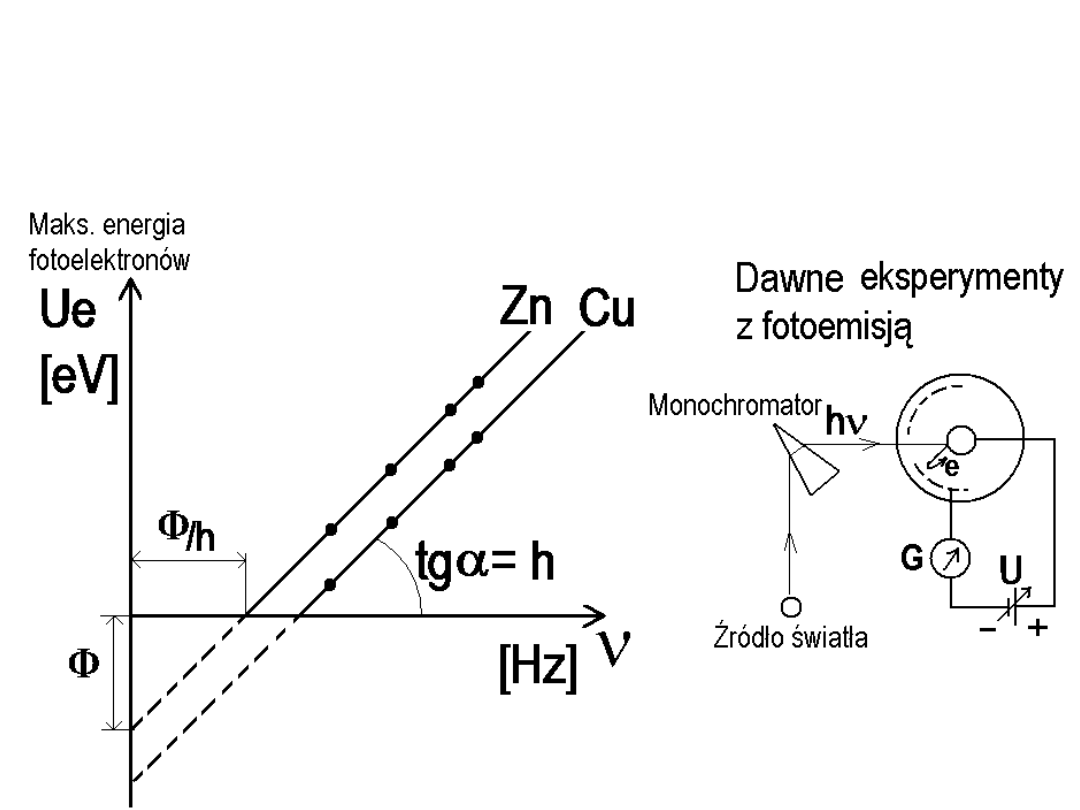
Pomiar progów fotoemisji i praca wyjścia Ф.

E

max

= hv - Ф

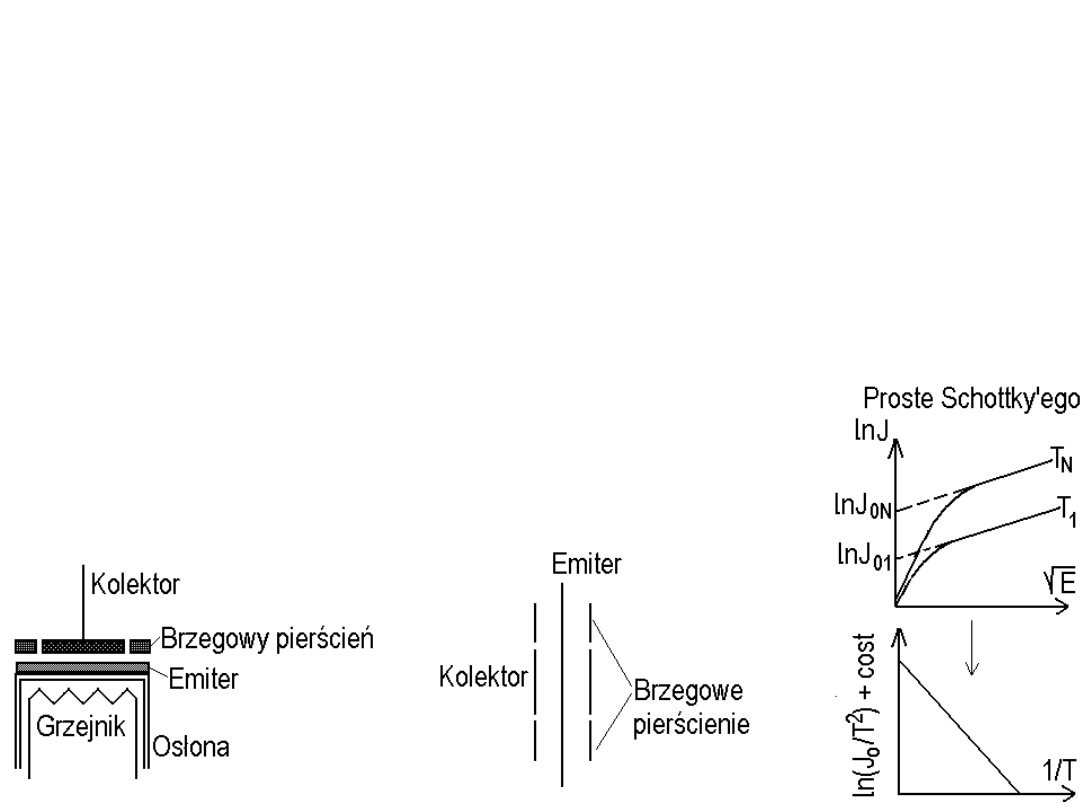
Metoda termoemisyjna dla próbek jednorodnych

Gęstość prądu termoemisji J

o

z powierzchni metalu o

temperaturze T i efektywnej pracy wyjścia Ф wyraża się
równaniem Richardsona-Dushmanna w postaci:
J

o

= C(1-r)T

2

exp(-Ф/k

B

T)

gdzie; C = 120Acm

-2

K

-2

, r – wsp. odbicia

elektronów od powierzchni od wewnątrz, k

B

- stała Boltzmanna.

Mierząc zależność ln(J

o

/T

2

) od 1/T można wyznaczyć Ф

(stosowane są poprawki na: wsp. obicia r, zewn. pole elektryczne E).

Przykładowe układy pomiarowe
planarny cylindryczny

Metoda emisji polowej.

Natężenie emisji polowej (podobnie jak w przypadku termoemisji)
zależy od wartości pracy wyjścia. W praktyce aby uzyskać
znaczne natężenia prądu emisji przy niewielkich napięciach
elektrycznych stosuje się próbki w postaci ostrza o odpowiednio
małym promieniu krzywizny. Gęstość prądu emisji polowej podaje
dość złożone wyrażenie Fowlera-Nordheima. Wyrażenie Fowlera-
Nordheima można uprościć do postaci: J/V

2

= a exp[-bФ

3/2

/cV]

gdzie a, b i c – stałe, V – napięcie elektryczne, cV = E – natężenie
pola elektrycznego. Znając wartości stałych można wyznaczyć
pracę wyjścia Ф.
Wykreślając wyniki pomiaru w postaci zależności
ln(J/V

2

) od 1/V otrzymujemy linie proste z nachyleniem

proporcjonalnym do Ф

3/2

.

Wykonując zatem pomiary dla czystego ostrza oraz dla pokrytego
adsorbatem uzyskujemy możliwość określenia zmiany pracy
wyjścia wywołanej adsorbatami. Stosunek nachyleń wykresów
będzie równy stosunkowi prac wyjścia w potędze 3/2.

Metoda jonizacji powierzchniowej.

Polega na pomiarze wydajności jonizacji neutralnych
atomów odbijanych od badanej powierzchni. Jonizacja
atomów na powierzchni o pracy wyjścia Ф i
temperaturze T opisywana jest przez równanie Saha-
Langmiura:
Y

i

/Y

o

= C exp[(Ф – eU

i

)/kT]

gdzie C – stała, Y

i

/Y

o

stosunek ilości jonów do ilości

neutralnych atomów, Ф praca wyjścia, eU

i

energia

jonizacji atomu, k stała Boltzmana.
Wykreślając eksperymentalną zależność ln(Y

i

/Y

o

) od T

-1

dla wyższych temperatur można znaleźć wielkość pracy
wyjścia.

Metody pomiaru zmian pracy wyjścia

• Metoda pojemnościowa wibracyjna –

metoda Kelvina.

• Metoda diodowa

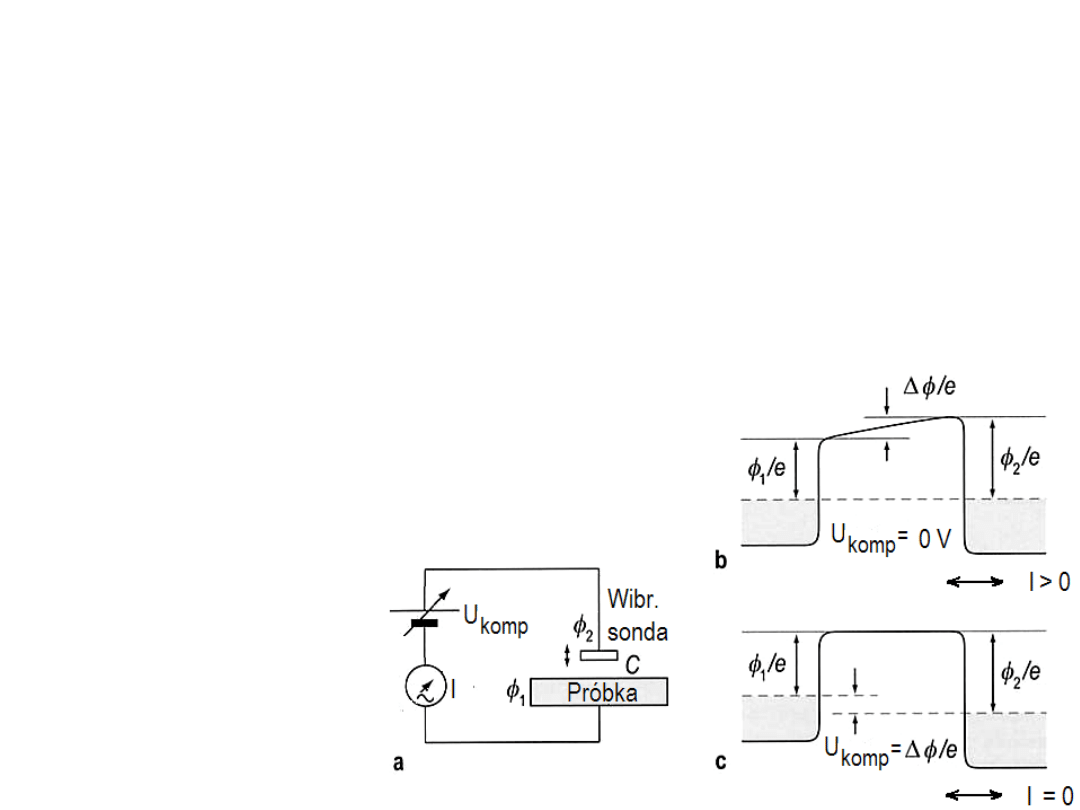
Metoda Kelvina

Wibracje metalowej sondy powodują oscylacje pojemności
kondensatora jaki tworzy układ próbka-sonda. Przy stałej
niezerowej różnicy potencjału na kondensatorze zmiana jego
pojemności wymusza zmianę ładunku na kondensatorze bo
U = Q/C. Zatem wibracje sondy wywołują zmienny prąd dopóki
przy pomocy napięcia kompensacji nie „wyzerujemy” pola
elektrycznego w tym zmiennym kondensatorze. Nastąpi to gdy
U

komp

= ΔФ/e.

Napięcie kompensacji
jest równe kontaktowej
różnicy potencjałów.
Znając pracę wyjścia
sondy można określić
wartość pracy wyjścia
badanego materiału
próbki.

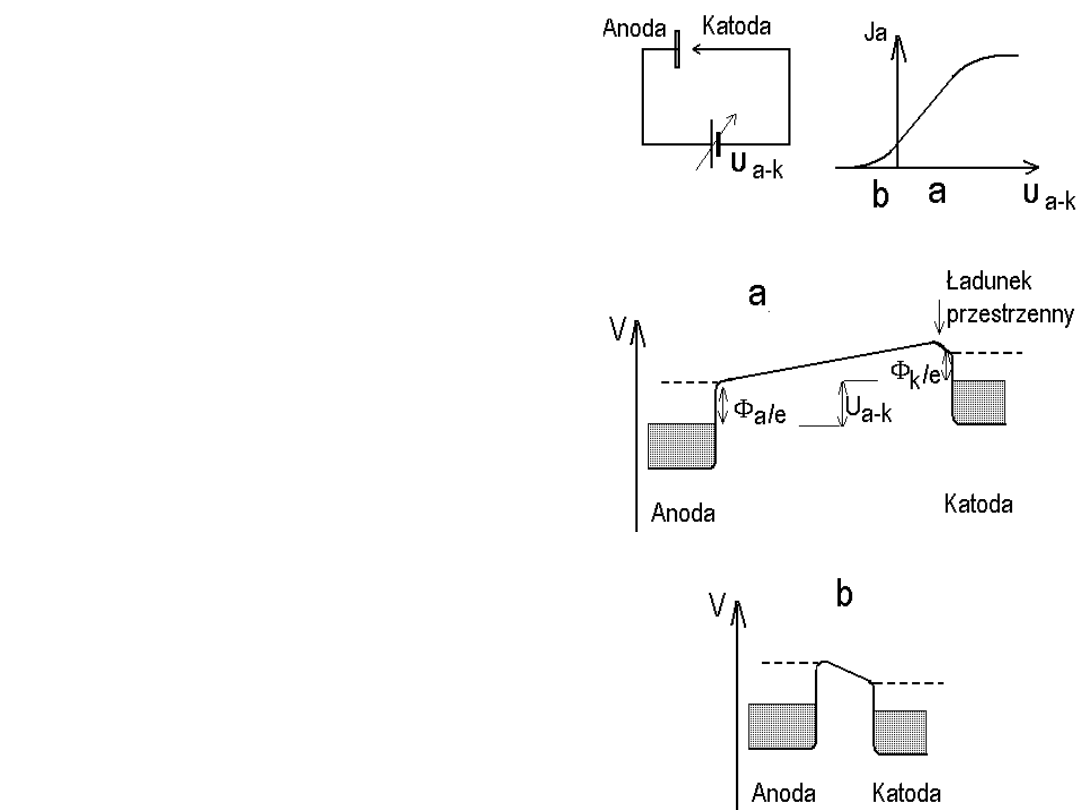
Metoda diodowa

W badaniach zmian pracy wyjścia
w laboratoriach fizyki powierzchni
najczęściej stosowaną jest metoda
diodowa. W metodzie tej układ
diody stanowią: próbka – jako
anoda oraz katoda odpowiedniego
działa elektronowego. Zdarza się,
że do tego celu wykorzystywane
jest działo optyki LEED lub
spektrometru Augera.
Wyróżnia się dwa zakresy napięć w
tej metodzie: a) ograniczanie
ładunku przestrzennego (napięcie
U

a-k

przyspieszające elektrony z

katody) b) pole hamujące (napięcie
U

a-k

jest napięciem hamującym).

Wada: katoda blisko próbki!

Metody diodowe

Metoda diodowa ma wiele odmian:
1) Diody cylindryczne i sferyczne w szklanych układach
pomiarowych (anodą jest wewnętrzna ściana komory).
2) Diody strumieniowe (metoda Andersona).
3) Diody ze skrzyżowanymi włóknami katody i anody.
4) Diody skanujące i układy mikroskopowe.

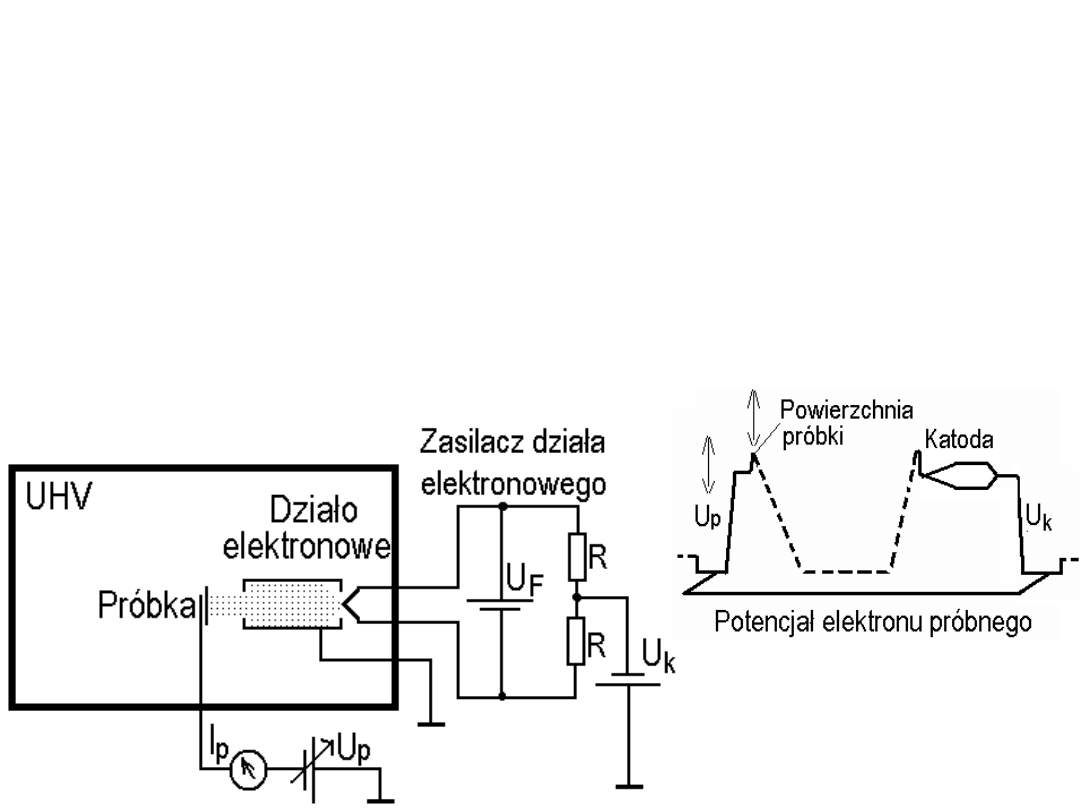
Dioda strumieniowa (metoda Andersona)

W metodzie Andersona formowana jest wąska wiązka elektronów
i kierowana prostopadle do powierzchni próbki (anody). W czasie
eksperymentu zakłada się, że praca wyjścia katody (filamentu) nie
zmienia się a napięcia zasilające działo elektronowe są stabilne.
Założenie uzasadnia bardzo dobra próżnia w komorze pomiarowej
i bardzo wysoka temperatura katody (zwykle około 2000 K).

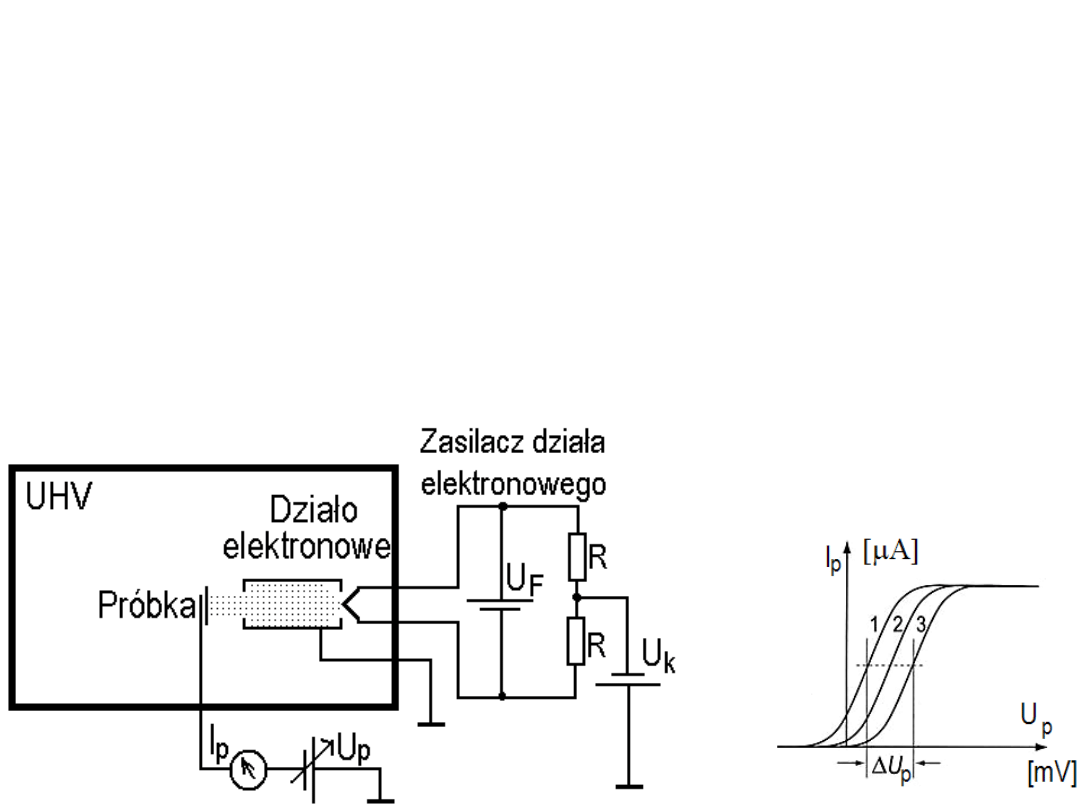
Przy założeniu, że praca wyjścia katody w układzie
pomiarowym się nie zmienia, prąd próbki (anody) jest
monotoniczną funkcją pracy wyjścia próbki Ф

p

i napięcia

elektrycznego U

p

– U

k

między próbką a katodą (w

pomiarowym zakresie kilku Voltów): I

p

= f

o

(U

p

– U

k

– Ф

p

).

Przy ustalonym napięciu katody i ustalonych napięciach
zasilających działo elektronowe możemy napisać:
I

p

= f(U

p

– Ф

p

).

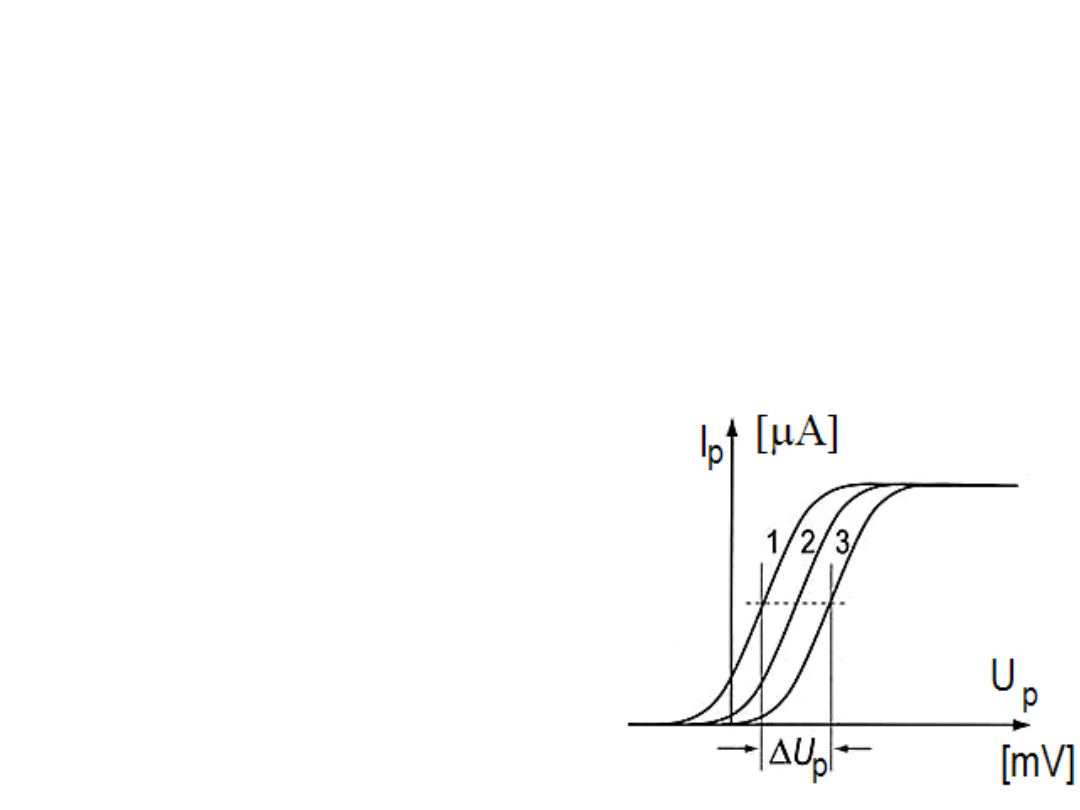
Z wyrażenia I

p

= f(U

p

– Ф

p

) widać, że zmiany Ф

p

można

kompensować zmianami U

p

. Identyczną wartość prądu I

p

po

zmianie Ф

p

o ΔФ

p

uzyskujemy zmieniając U

p

o wartość - ΔФ

p

. (ΔU

p

= - ΔФ

p

). Dawniej pomiar zmian pracy wyjścia polegał na

pomiarze przesunięć krzywych rysujących zależność I

p

od U

p

.

Obserwacji przesunięcia dokonywano oczywiście w obszarze
największej stromości krzywych, zwykle między 10% a 50%
wartości nasycenia I

p

.

Stosując układ sprzężenia
zwrotnego pomiar staje się bardziej
automatyczny bo sam układ
koryguje napięcia anoda-katoda,
tak by utrzymać stałą wartość
prądu anody. Napięcia korekty są
rejestrowane jako ΔФ

p

.

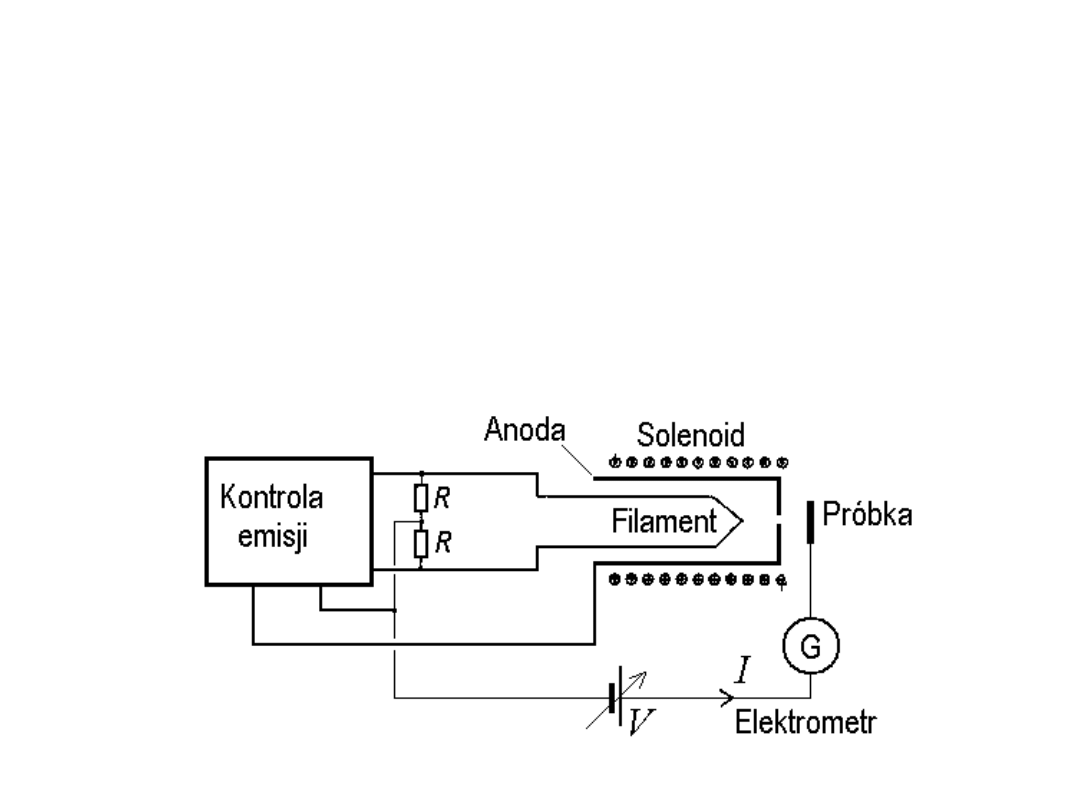
Działo elektronowe z wiązką kolimowaną osiowym
polem magnetycznym (około 10 mT). Solenoid
eliminuje niepożądany wpływ resztkowego pola
magnetycznego w układzie pomiarowym.

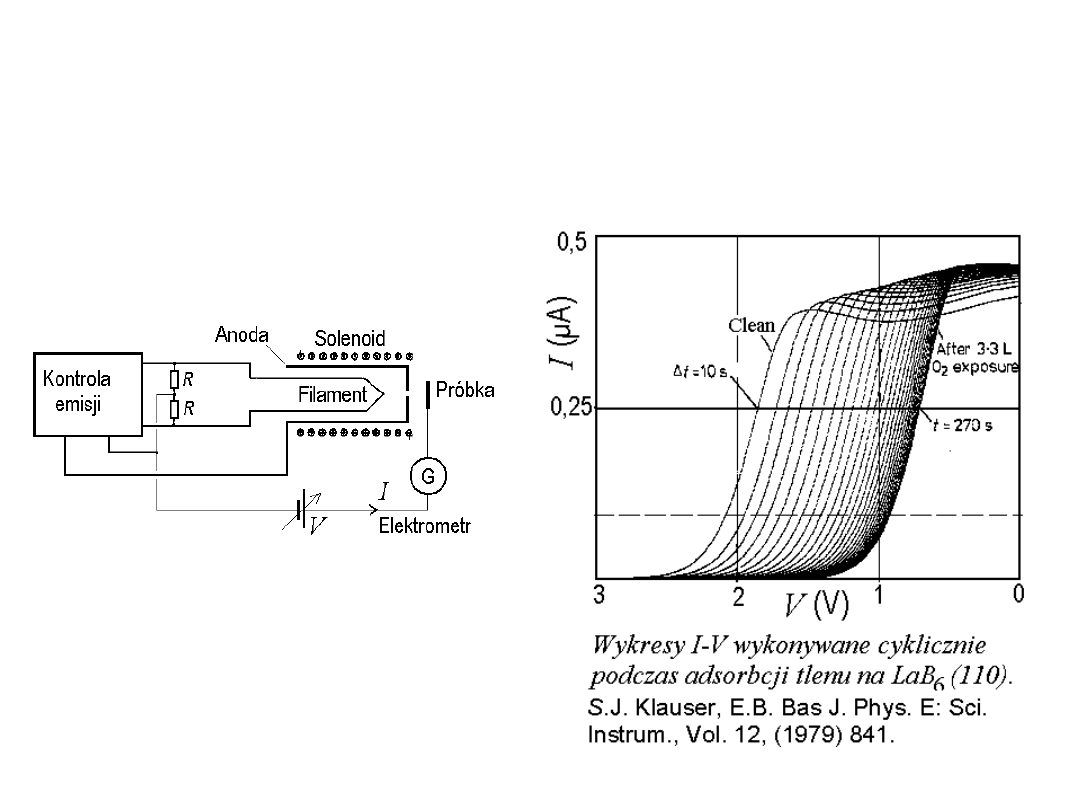
Wybrane wyniki

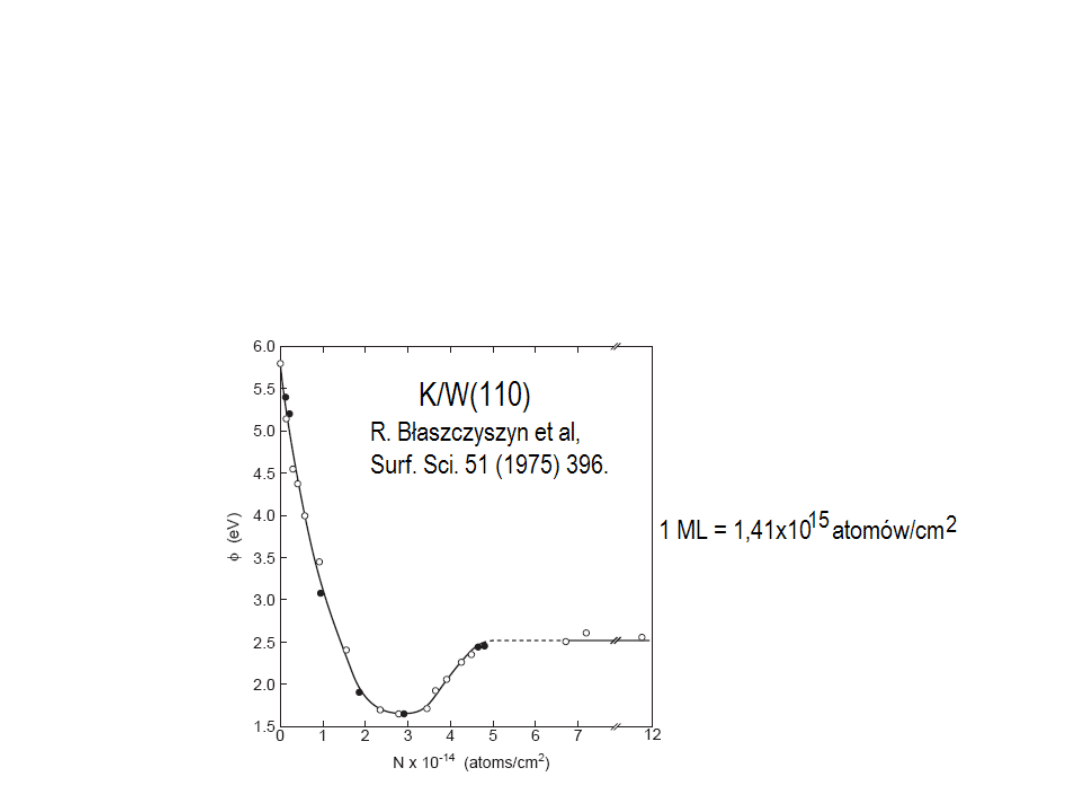
Zależność pracy wyjścia od grubości adsorbatu

Od dawna wiadomo, że gęsto upakowane ściany
monokryształu wykazują większą pracę wyjścia
niż ściany mniej upakowane - bardziej otwarte.
(

R. Smoluchowski, Phys. Rev. 60 (1971) 661

).

Besocke i Wagner wykazali, że adsorpcja
atomów wolframu na powierzchni (110)
monokryształu wolframu znacząco (bo o 0.6 eV)
zmienia pracę wyjścia. Wykazano, że to
pojedyncze atomy dają znaczny moment
dipolowy a nie duże wyspy.

(K. Besocke, H. Wagner, Phys. Rev. 8 (1973) 4597 oraz prace tam

zacytowane).

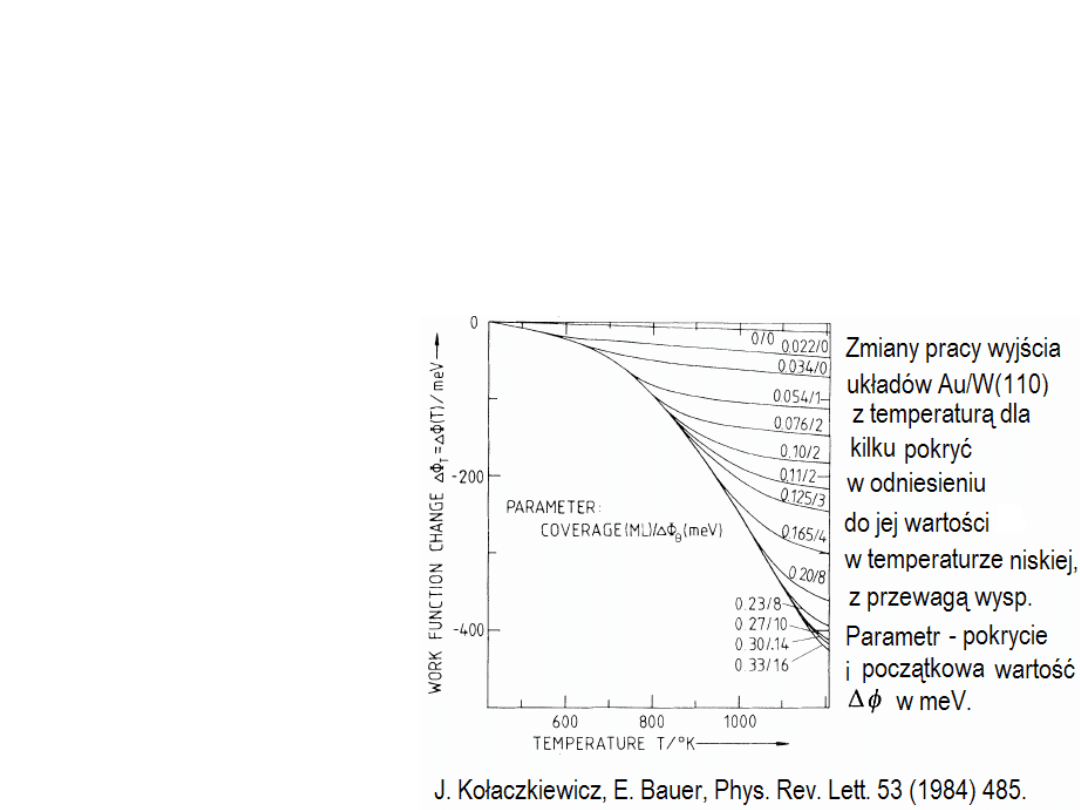
Badanie przejścia fazowego wyspy-
dwuwymiarowy gaz atomów Au na W(110)

Przyjmując N – ilość zaadsorbowanych atomów Au,
n – ilość atomów pojedynczych (odizolowanych) z dużym
momentem dipolowym p, N-n – ilość atomów
w wyspach z małym
momentem dipolowym
p

o

, możemy zapisać:

ΔФ = -4πe[np +(N-n)p

o

]

Wykres ilustruje
przechodzenie wysp
w jednoatomowy gaz
powierzchniowy.

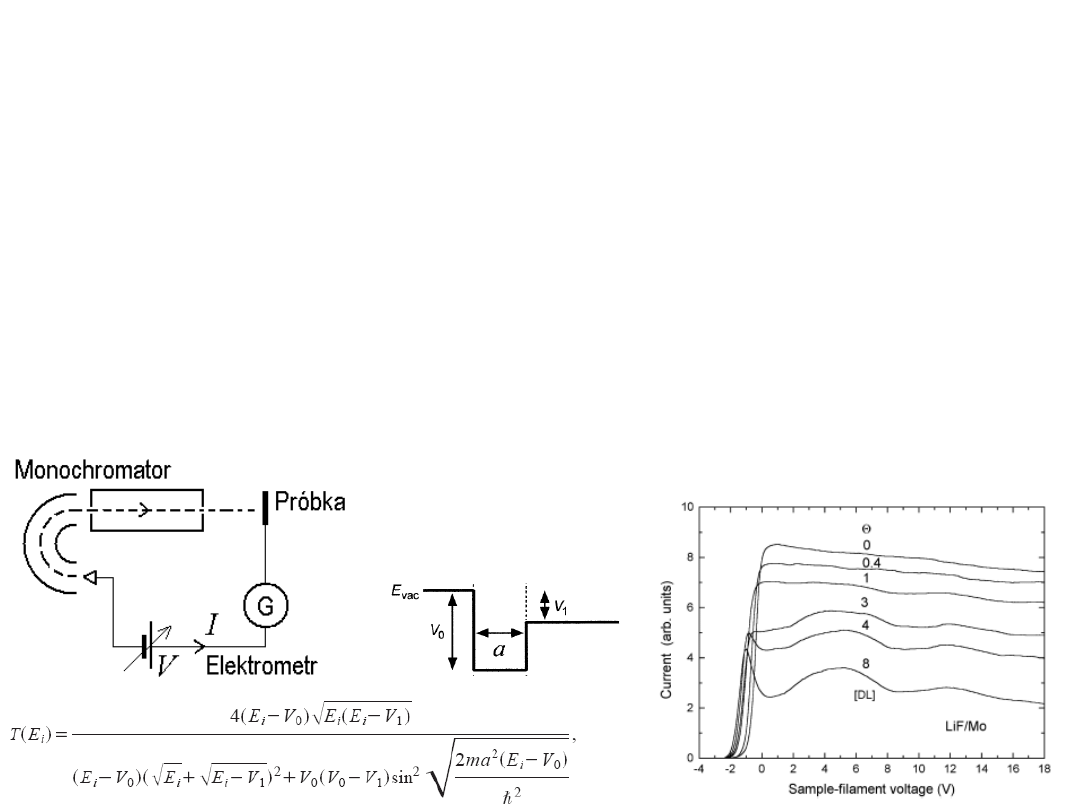
Transmisja powolnych elektronów LEET (low energy
electron transmission) i spektroskopia prądu próbki
TCS (Target current spectroscopy).

Jest to w zasadzie

udoskonalona techniki diody strumieniowej. Udoskonalenie polega na tym, że
prostopadle do próbki kierowana jest zmonochromatyzowana wiązka
elektronów i rejestruje się nie tylko początkowy narost natężenia prądu ale
również obszar powyżej nasycenia. Widać tu obok zmian pracy wyjścia jak
zmienia się współczynnik emisji wtórnej ze zmianą grubości adsorbatu i
energią elektronów pierwotnych.

N. Ueno et al, J. Appl. Phys. 92 (2002) 5203.

F. Gołek, Surf. Sci. 448 (2000) L188.

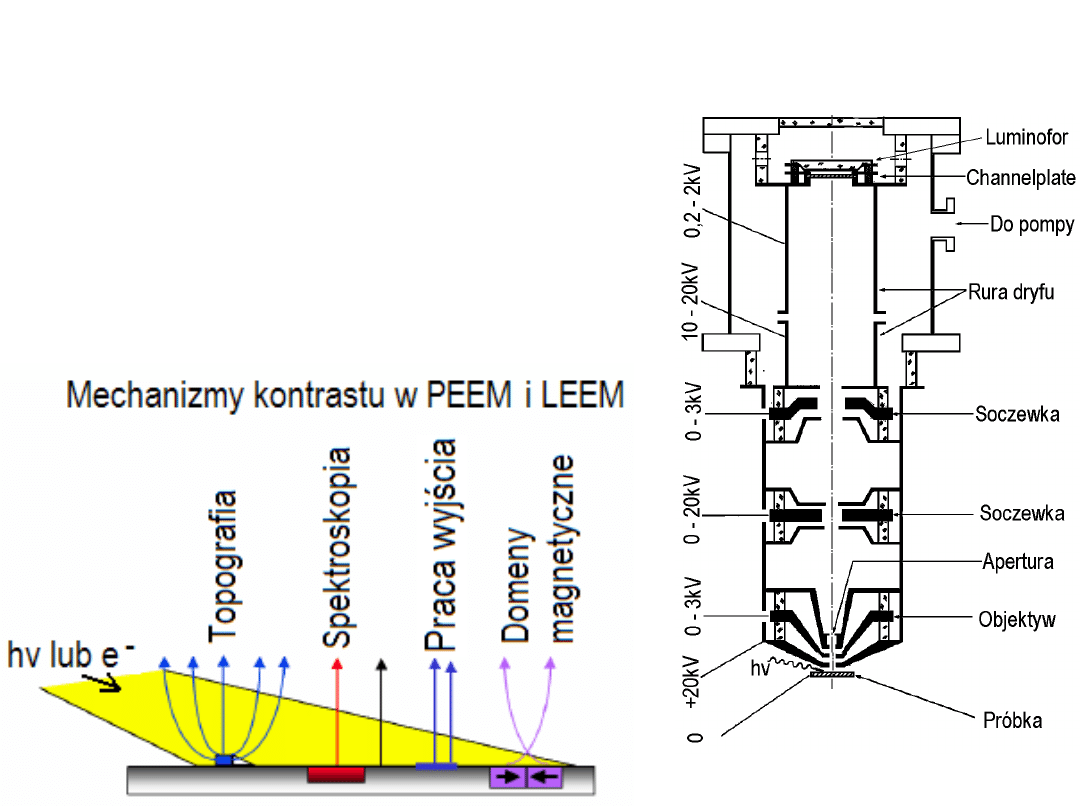
Mikroskopia PEEM i LEEM

H. H. Rotermund, Surf. Sci. Rep. 29,

265 (1997).

Mikroskopie PEEM i LEEM
(

photo-emission electron microscopy i low energy

electon microscopy)

stanowią najbardziej

bezpośrednią metodę badania powierzchniowych
2D (dwuwymiarowych) przejść fazowych.
Pozwalają obserwować nukleację i wzrost
uporządkowanych struktur podczas chłodzenia
oraz ich zanik podczas podgrzewania badanych
próbek.

Wiadomo, że o 2D przejściach fazowych decydują trzy czynniki:

i) oddziaływanie między atomami adsorbatu, ii) niedopasowanie
stałych sieci adsorbatu i podłoża oraz iii) energia aktywacji dla
dyfuzji powierzchniowej.

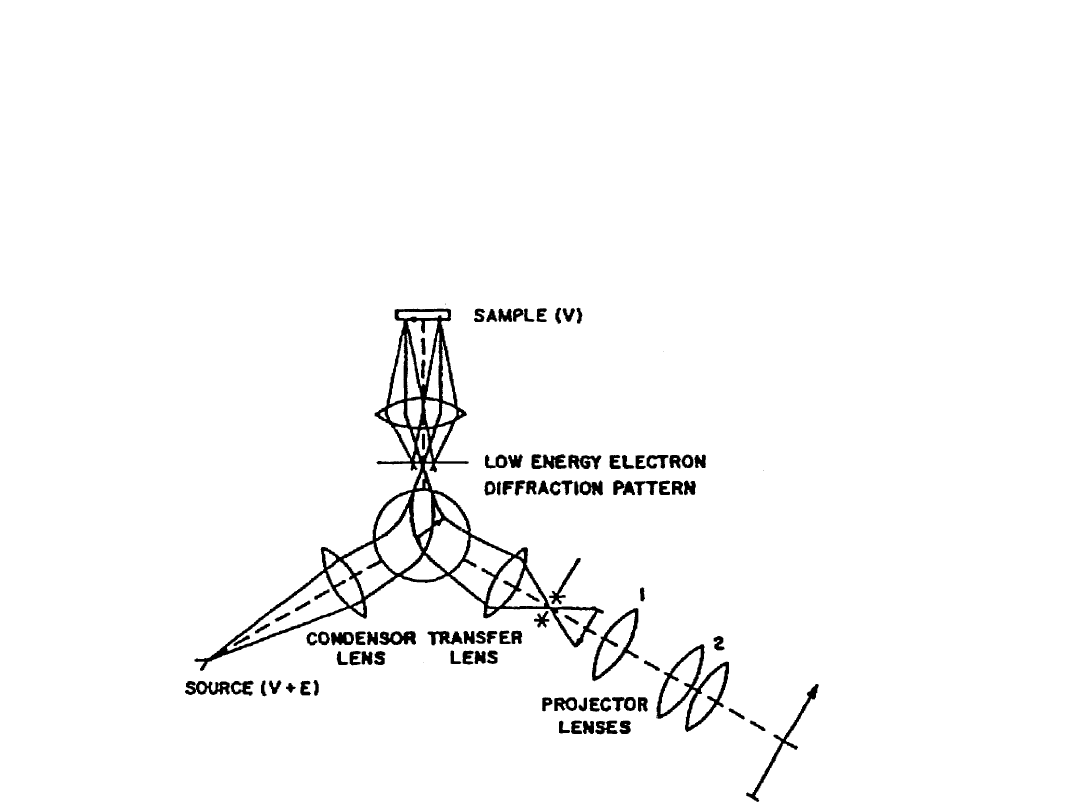
Schemat mikroskopu LEEM

(E. Bauer 1962, pomysł zastosowania powolnych elektronów do

mikroskopowego obrazowania powierzchni)

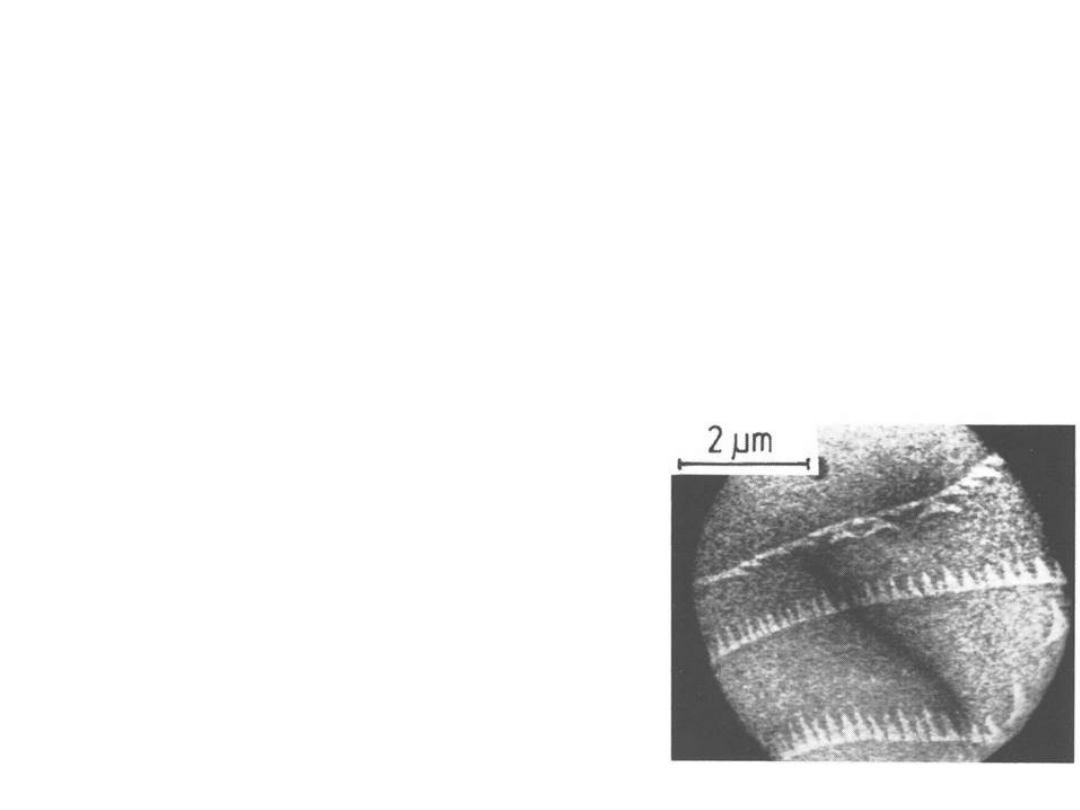
Już pierwsze obrazy Telipsa i Bauera zamieszczone w pracy: W.Telieps
and E. Bauer, Surface Sci.,162 (1985) 163, pokazały współistnienie
dwóch faz (1x1) i (7x7) na ścianie Si(111). Wyniki te wyjaśniły wiele w
toczącej się przez 25 lat dyskusji na temat rekonstrukcji powierzchni
(111) krzemu poniżej temperatury 860

°

C.

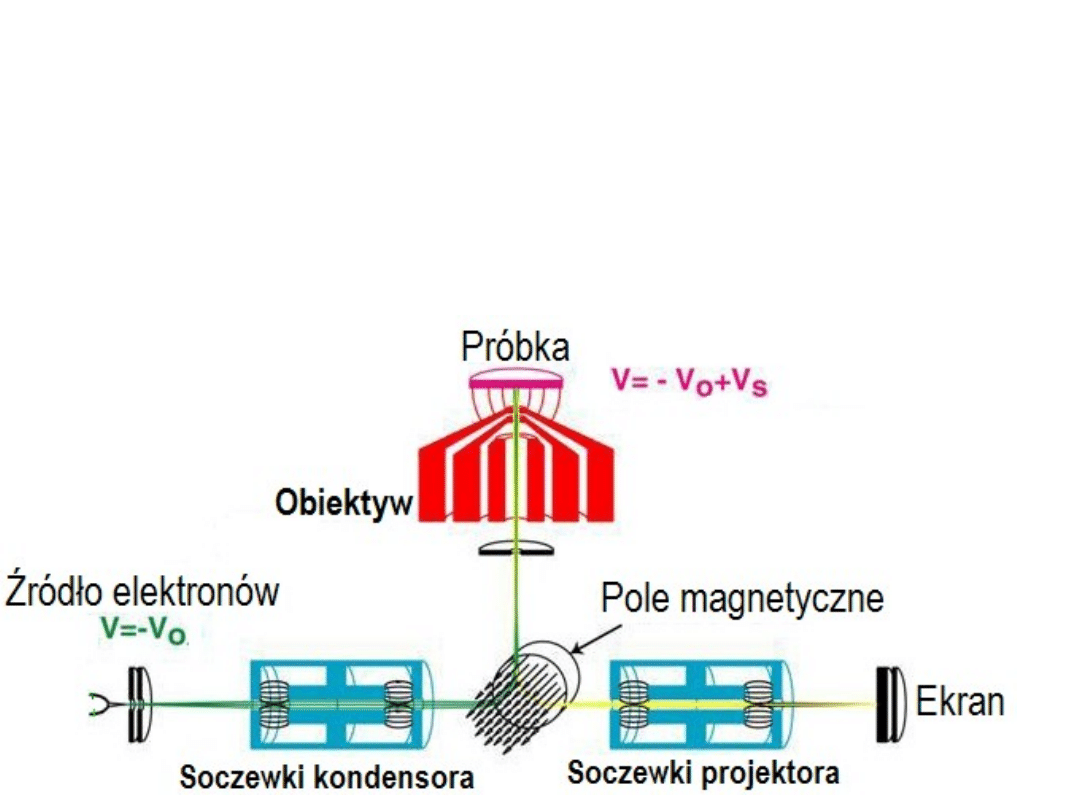
Schemat mikroskopu LEEM

(R. Tromp 2000)

Mikroskopia PEEM i LEEM

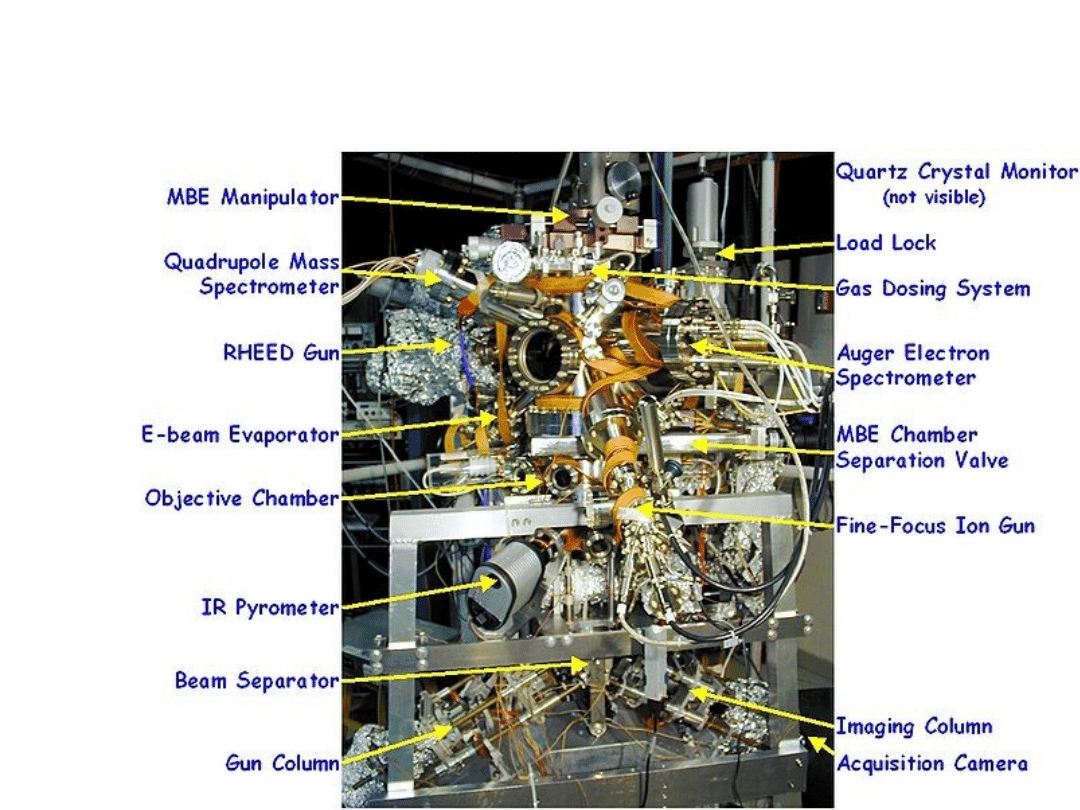
LEEM used for surface science studies at University of
Illinois' Frederick Seitz Materials Research Laboratory in
Urbana, IL, USA.

163

Mikroskopia PEEM
(photoemission electron microscopy).

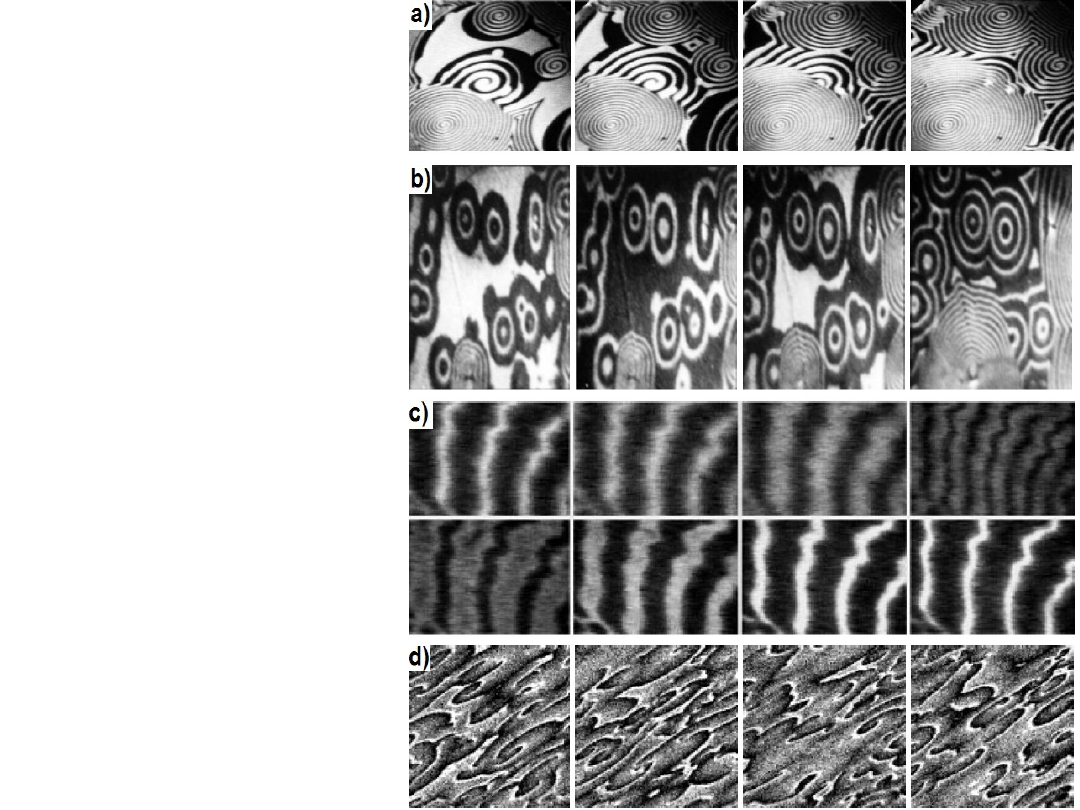
Mikroskopia PEEM

Utlenianie CO na Pt(110)
obserwowane przy pomocy
PEEM. Ciemne obszary –
dominuje tlen, jasne obszary
– dominuje CO. (a) Fale
spiralne, 400

×

400 µm

2

, (b)

fale typu tarcza, 200

×

300

µm

2

, (c) fale stojące,

300

×

200 µm

2

, (d)

chemiczne turbulencje,
360

×

360 µm

2

. (T=536 K,

P

CO

=6,4

×

10

-5

mbar,

P

O

=20

×

10

-5

mbar).

S.Nettesheim, A. von Oertzen, H.
H. Rotermund, and G. Ertl, J.
Chem. Phys. 98 (1993) 9977;
S. Jakubith, H. H. Rotermund,W.
Engel, A. von Oertzen, G. Ertl,
Phys. Rev. Lett. 65 (1990) 3013; S.
Jakubith, PhD, Free University of
Berlin 1991; M. Bertram, PhD,
Tech. University Berlin 2002.

Mikroskopia LEEM

Obserwacja procesu samo-
organizacji, który pojawia się
podczas nanoszenia Pb na Cu(111).
Faza ciemna to stop Pb-Cu nie
uporządkowany, faza jasna to
warstwa samego Pb (jasne i mobilne
punkty to wyspy o średnicy Φ

RMS

=

67 nm). Temperatura próbki = 675
K, pole widzenia wynosi 4 µm.

R. Plass, J.A. Last, N.C. Bartelt, G.L. Kellogg, Nature 412, 875 (2001).

(Pokaz filmu)

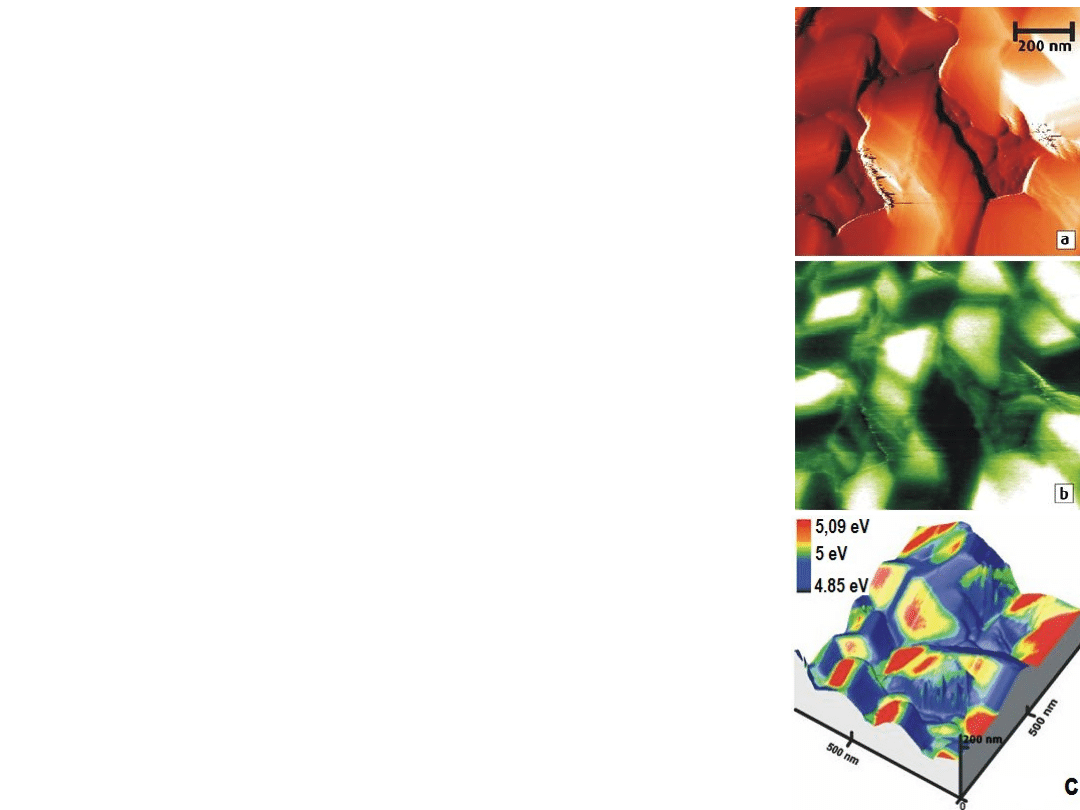
Przykład zastosowania
metody Kelvina: KPFM

(Kelvin probe force microscopy)
z pracy:

S. Sadewasser, Th. Glatzel, M. Rusu, A. Jäger-

Waldau, and M.Ch. Lux-Steiner, Appl. Phys. Lett. 80 (2002)
2979.

a) Topografia warstwy CuGaSe

2

na

powierzchni (110) kryształu ZnSe.
b) Obraz pracy wyjścia.
c) Topografia uwidoczniona jako
efekt 3D, a praca wyjścia jest
nałożona jako skala kolorów.

Mikroskopia KPFM jest bardzo cenna
dla inżynierii materiałowej.

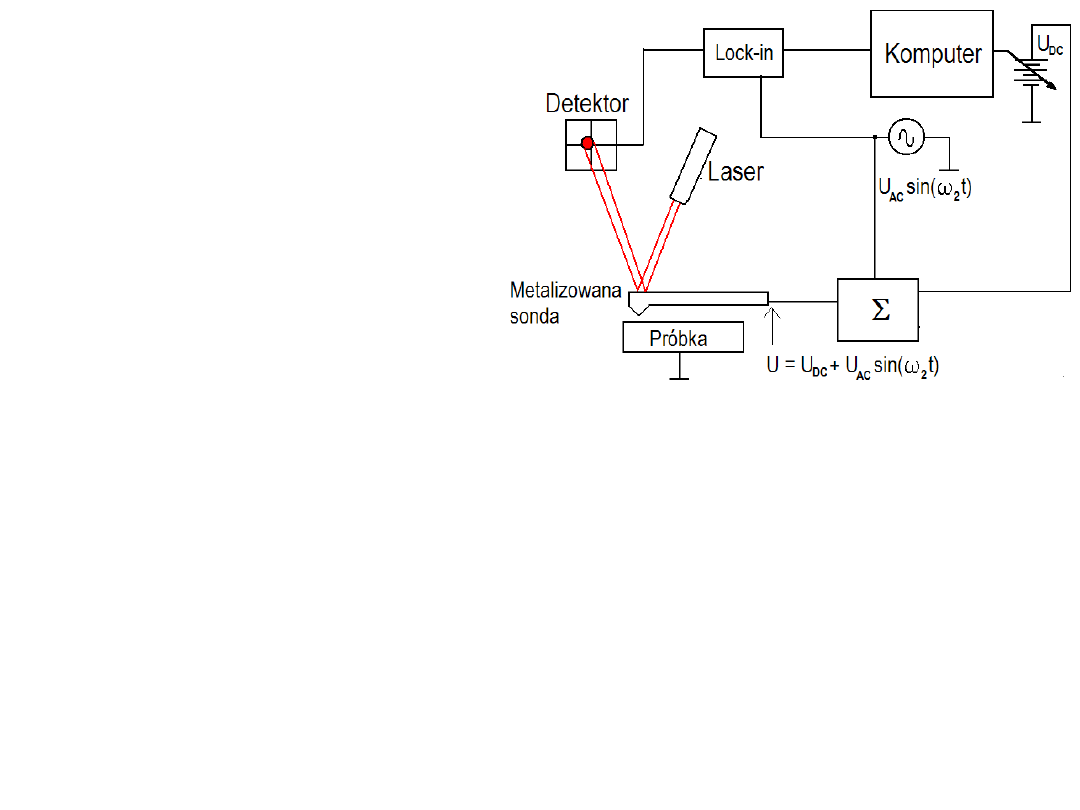
Schemat ideowy KPFM
Energia kondensatora przy
napięciu U

C

wyraża się przez:

E = (U

C

)

2

C/2. Siła przyciągania

między okładkami (tj. między
ostrzem a próbką) jest
pochodną tej energii po
odległości między okładkami:
F = -dE/dz = -(1/2)(U

C

)

2

dC/dz.

Zatem siła jest proporcjonalna do kwadratu aktualnej różnicy potencjałów, która
jest sumą kontaktowej różnicy potencjału U

CPD

i napięcia jakie włączamy w

obwód próbka-ostrze

U= U

DC

+ Vsinωt: F

∝

(U

C

)

2

= (U

CPD

+ U

DC

+

Vsinωt )

2

= [(U

CPD

+ U

DC

)

2

+ 2(U

CPD

+ U

DC

)Vsinωt + (Vsinωt )

2

]; F

∝

[(U

CPD

+ U

DC

)

2

+ V

2

/2 + 2(U

CPD

+ U

DC

)Vsinωt - (V

2

/2)cos2ωt].

Pętla sprzężenia zwrotnego zmieniając wartość U

DC

, minimalizując

siłę F i amplitudę oscylacji utrzymuje równość: (U

CPD

+ U

DC

) = 0

czyli: U

DC

= -U

CPD

.

Literatura

1) R. Smoluchowski, Phys. Rev. 60 (1941) 661.
2) E. Wigner, J. Bardeen Phys. Rev. 48 (1935) 84.
3) P.A. Anderson, Phys. Rev. 88 (1952) 655.
4) N.D. Lang, W. Kohn, Phys. Rev. B 3 (1970) 1215.
5) J. Hölzl, F.K. Schulte, H. Wagner, Springer Tracts in Modern Phys. 85 (1979).
6) E. Bauer, Appl. Phys. A 51 (1990) 71.
7) J. Kołaczkiewicz, E. Bauer: Phys. Rev. Lett. 53 (1984) 485.
8) H. Gollisch: Surf. Sci. 175 (1986) 249.
9) U. Zenweck, et all, Phys. Rev. B 71 (2005) 125424.
10) N.W. Ashcroft, N.D. Mermin, Fizyka ciała stałego.
11) K. Bożek, Acta Phys. Polon. A 109 (2005) 541.
12) L. Kelvin. Phil. Mag., 46 (1898) 82.
13) L. A. Zimmerli, PhD, Basel University 2007.
14) A, Ciszewski, A. Kiejna, Wrocław 1986, Wyd. Uiwersytetu Wrocławskiego.
15) K. Wojciechowski, Wrocław 1993, Wyd. Uiwersytetu Wrocławskiego.
16) J.A. Venables, Introduction to Surface and Thin Film processes, Cambridge 2000.
17) S.J. Klauser, E.B. Bas J. Phys. E: Sci. Instrum., Vol. 12, (1979) 841.
18) L.E. Cheran, H.D. Liess, M. Thompson, Analyst 124 (1999) 961.
19) H. Shelton, Phys. Rev. 107 (1957) 1553.
20) L. Diederich, O.M. Kuttel, P. Aebi, L. Schlapbach, Surf. Sci. 418 (1998) 219.
21) R. Blaszczyszyn et al, Surf. Sci. 51, 396 (1975).
22) R. Plass, J.A. Last, N.C. Bartelt, G.L. Kellogg, Nature 412, 875 (2001).
23) E. Bauer, Rep. Prog. Phys., 57 (1994) 895.
24) E. Bauer, Electron Microscopy, 1 (1962) ed S.S. Breese Jr (New York: Academic).
25) N. Ueno et al, J. Appl. Phys. 92 (2002) 5203.
26) F. Gołek, Surf. Sci. 448 (2000) L188.