NIEPEWNOŚĆ POMIARU ANALITYCZNEGO 

PRZYKŁADY  WYZNACZANIA  NIEPEWNOŚCI 

 
 

Autorzy: 
dr hab. Katarzyna Madej 
dr Andrzej Olech 
dr hab. Jolanta Kochana 
mgr Róża Starczak 

wersja 3.0 (2013 r.) 

1 

PLAN   WYKŁADU 

 
 
1. Wprowadzenie 
 
2.

Wielkości opisujące precyzję i dokładność pomiarów, 
definicja niepewności pomiaru 
 

3.

Rozkłady prawdopodobieństwa – r. Gaussa i r. prostokątny 
 

4.

Prawo przenoszenia (propagacji) niepewności 
 

5.

Dwie szczególne postaci prawa propagacji niepewności 

 

2 

PLAN   WYKŁADU cd. 

 
 
6.  Przykłady obliczeń niepewności 

 

      

6.1 niepewność oznaczenia wagowego substancji 

      

6.2 niepewność stężenia roztworu sporządzanego metodą 

            

wagową w kolbie miarowej 

      

6.3 niepewność wyznaczania pojemności naczyń     

 

 

miarowych oraz ich współmierności 

      

6.4 niepewność wyniku mianowania roztworu na odważki 

            substancji wzorcowej 
      

6.5 niepewność wyniku miareczkowania 

      

6.6 niepewność oznaczenia tlenu w wodzie 

 
7.  Podsumowanie, wnioski 

3 

   

Prezentację opracowano w oparciu o następujące pozycje:  

 
 
1.

Ewa Bulska – „Metrologia chemiczna”, Wydawnictwo Malamut, 2008.  

 
2.  

Barry N. Taylor and Chris E. Kuyatt – „Guidelines for Evaluating and 
Expressing the Uncertainty of  NIST Measurement Results”, 1994 – 
http://physics.nist.gov/Pubs/guidelines/TN1297/tn1297s.pdf 

 
3.  

Henryk Szydłowski – „Niepewności w pomiarach. Międzynarodowe 
standardy w praktyce”, UAM, Wydawnictwo Naukowe, Poznań 2001. 
 

4.  

Anna Kujawska, Paweł Fotowicz – „Obliczanie niepewności metodą 
sumowania niezależnych zmiennych losowych”, Analityka, nr 3, 2003.  
 
 

4 

1. WPROWADZENIE 
 

1995 r. 

– uzgodnienie międzynarodowych norm dotyczących  

„niepewności w pomiarach” 
 
ISO (International Organization for Standardization)  
 
„Guide to Expression of Uncertainty in Measurement” 
 
„Uncertainity of Measurement in Calibration” 
 
„Quantifying Uncertainity in Analytical Measurement” 
 
 

Powyższe dokumenty przetłumaczono w Głównym Urzędzie Miar. 

5 

2. Wielkości opisujące precyzję i dokładność pomiarów 
 

 

•

Niepewność przypadkowa

       dawniej  błąd przypadkowy 

 

 

•

Niepewność systematyczna                   

dawniej 

•

Błąd systematyczny

                       błąd systematyczny 

  
 

•

Błąd gruby 

 

6 

Niepewność pomiaru u(x)  (uncertainty  
in measurement) -  

jest to wielkość wyznaczająca przedział liczbowy,  
w którym wartość prawdziwa leży z określonym, dużym  
prawdopodobieństwem 

 

 
 

 
Na 

u(x)

 składa się: 

• niepewność systematyczna (są to głównie niepewności kalibracji                      
                                                     i rozdzielczości  przyrządu pomiarowego) 
• niepewność przypadkowa   (miara rozrzutu wyników pomiaru)  
 
Rozrzut wyników pomiaru może być wyrażony poprzez odchylenie standardowe  
s(x).  

7 

 
 
 

 
 
 

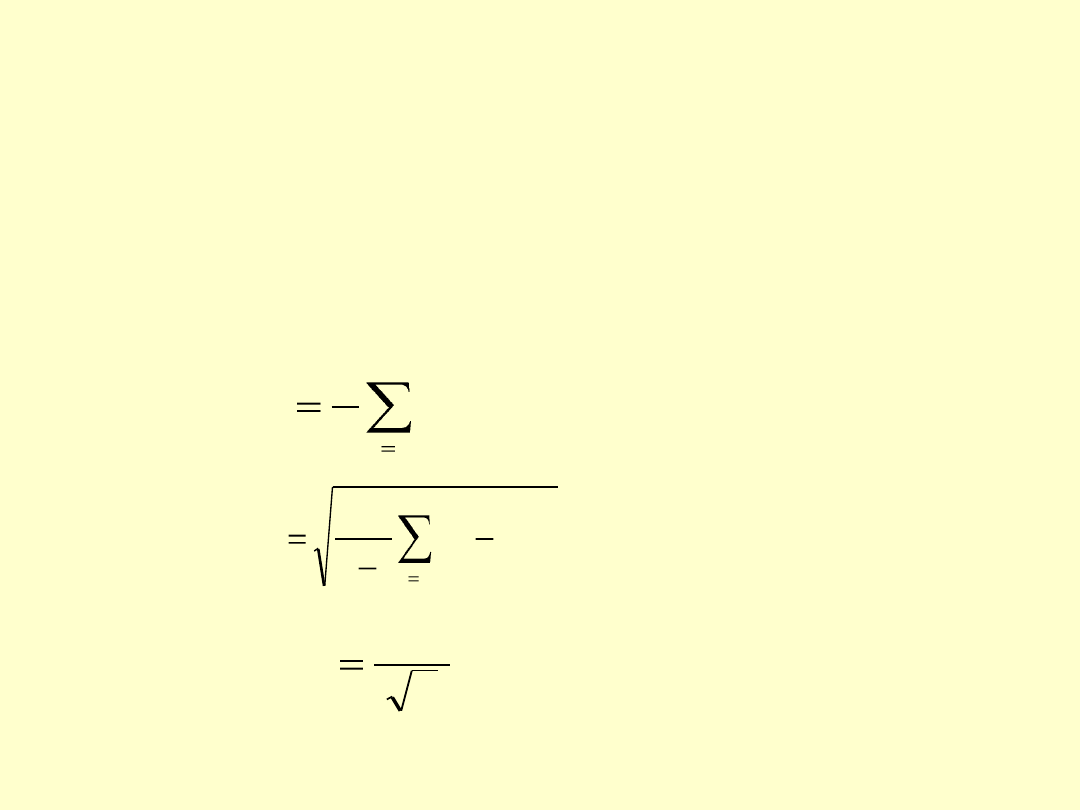
Jeżeli zostało wykonanych n pomiarów: x

1 

, ..., x

n 

 wielkości x,  to  

najprostszym sposobem ich scharakteryzowania jest obliczenie:  

1. średniej arytmetycznej x

śr

 

2. odchylenia standardowego pojedynczego pomiaru s(x) 

3. odchylenia standardowego średniej s(x

śr 

) 

n

i

i

x

n

x

1

śr

1

2

śr

1

)

(

1

1

)

(

x

x

n

x

s

n

i

i

n

x

s

x

s

)

(

)

(

śr

ad 1) 

 

ad 2) 

 

ad 3) 

 

8 

3. Rozkłady prawdopodobieństwa 
rozkład Gaussa i rozkład prostokątny 
 

Rozkład prawdopodobieństwa zmiennej losowej x – 
funkcja przyporządkowująca wartościom zmiennej  
losowej x 

prawdopodobieństwo przyjęcia danej  

wartości przez tę zmienną. 

 
 

9 

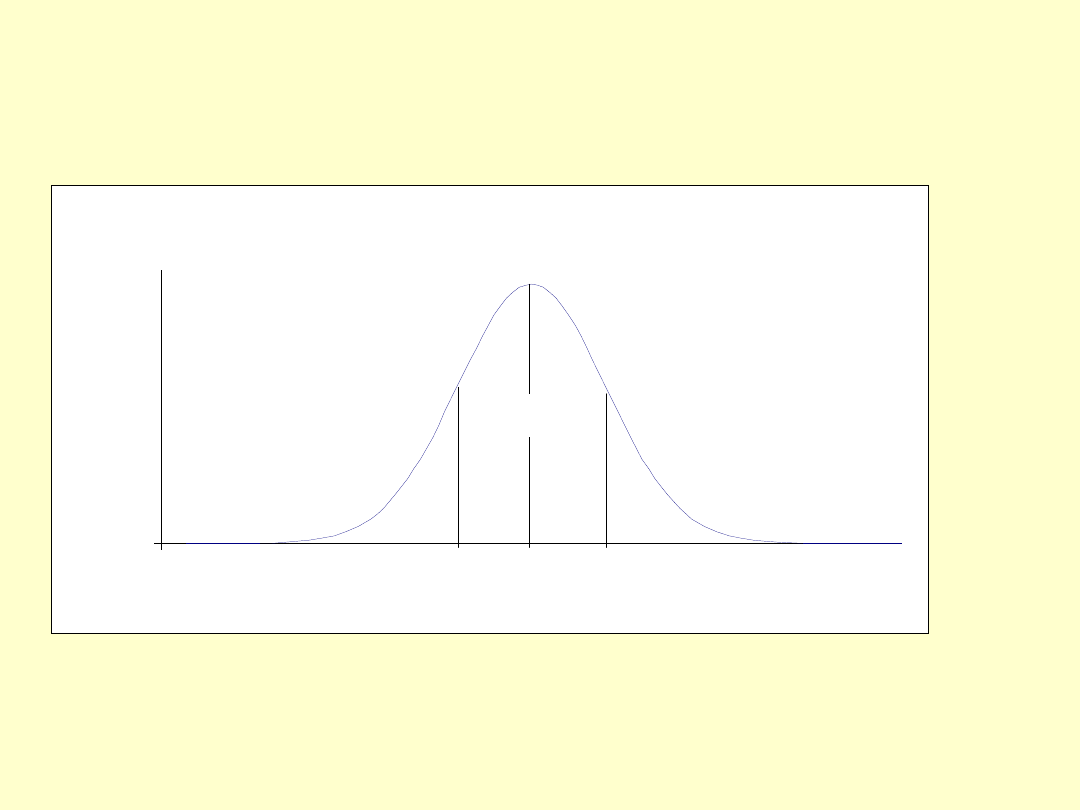
Rozkład Gaussa 

– gdy mierzymy pewną wielkość x (zmienną losową) wiele  
razy, a otrzymane wyniki podlegają rozrzutowi statystycznemu,  
to ten rozrzut najczęściej dobrze opisuje funkcja Gaussa 

 
 

 
 

 

 
 
 
 
 
 
 
 
<x

śr 

– s(x) , x

śr 

+ s(x) >  – przedział ufności, który zawiera 68,3%  

                                              wszystkich wyników pomiarowych  

Krzywa Gaussa

 

0

 

0

 

zmienna losowa   x

 

G

ęs

toś

ć 

praw

do

po

do

bieńs

tw

a 

P

 

x

 

śr

 

– s

 

x

 

śr

 

x

 

śr

 

 + s

 

68,3%

 

10 

 

Niepewność standardowa u(x) 
u(x) = s(x) 
 
np. wyznaczanie pojemności kolby na 100 mL 
101,1 mL    0,8 mL        (  s(x) odpowiada ok. 68 %) 
    

         1,6 mL        (  2 s(x) odpowiada ok. 95 %) 

                   2,4 mL        (  3 s(x) odpowiada ok. 99,7 %) 

 
 

 

 

11 

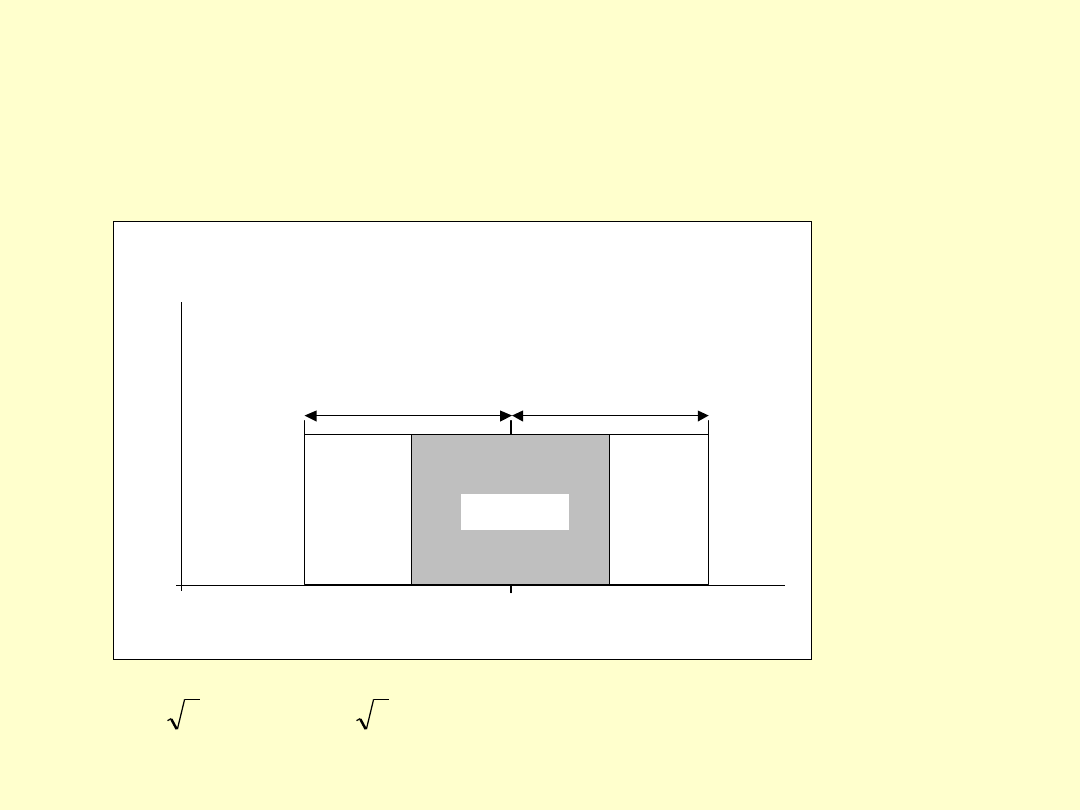
Rozkład prostokątny (jednostajny) 

–  gdy nie występuje rozrzut statystyczny wyników, tzn. kolejne pomiary  
prowadzą do wyniku: x = x

1 

= x

2 

= x

3  

= x

śr

 

, to głównym przyczynkiem  

niepewności jest niepewność wzorcowania a (działka elementarna) 
np. biureta   a = 0,1 mL,  termometr lab. a = 1 C,  waga analit. a = 0,1 mg

 

 

 

 
 
 
 
 

 
 
 
 

< x

śr 

– a/

   

,   x

śr 

+ a/

    

>  –  

przedział ufności, który zawiera 57,7 %  

                                                             wszystkich wyników pomiarowych

  

 

Rozkład prostokątny

0

0

zmienna losowa  x

G

ęs

to

ść

 p

ra

w

d

o

p

o

d

o

b

ie

ń

st

w

a 

P

57,7%

x

śr

 - a/√3

x

śr

x

śr

 + a/√3

a

a

3

3

12 

 

Niepewność standardowa u(x) 
u(x) = s(x) = a/      
 
np. pomiar objętości zużytego titranta w PK  
miareczkowania, a = 0,1 mL  
 
V = 18,75 mL   0,06 mL      (  u(x) odpowiada tu ok. 58%) 
 

 

3

13 

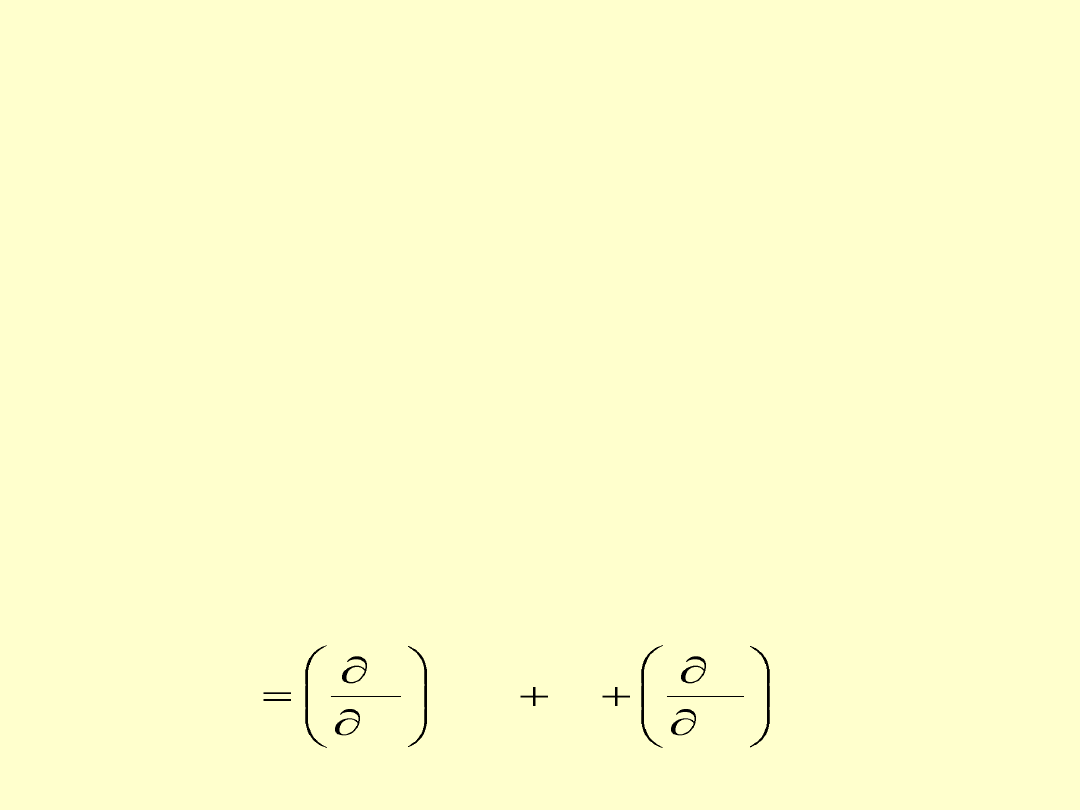
4. Prawo przenoszenia (propagacji) niepewności 

                              

y = f (x

1

 

, … , x

n 

) 

 

gdzie: y 

–  wielkość wyznaczana (pośrednio)  

           x

i

  (i 

= 1,…,n) –  wielkości mierzone bezpośrednio 

 
Jeżeli y jest funkcją n zmiennych niezależnych x

i

 

, to wariancja 

(s

y

2

) funkcji y  

jest sumą wariancji (s

i 

2 

)

  

tych zmiennych 

pomnożonych przez wartości odpowiednich pochodnych 
cząstkowych, podniesione do kwadratu. Określa to prawo 
przenoszenia niepewności wyrażone wzorem: 

2

2

2

1

2

1

2

...

n

n

y

s

x

y

s

x

y

s

14 

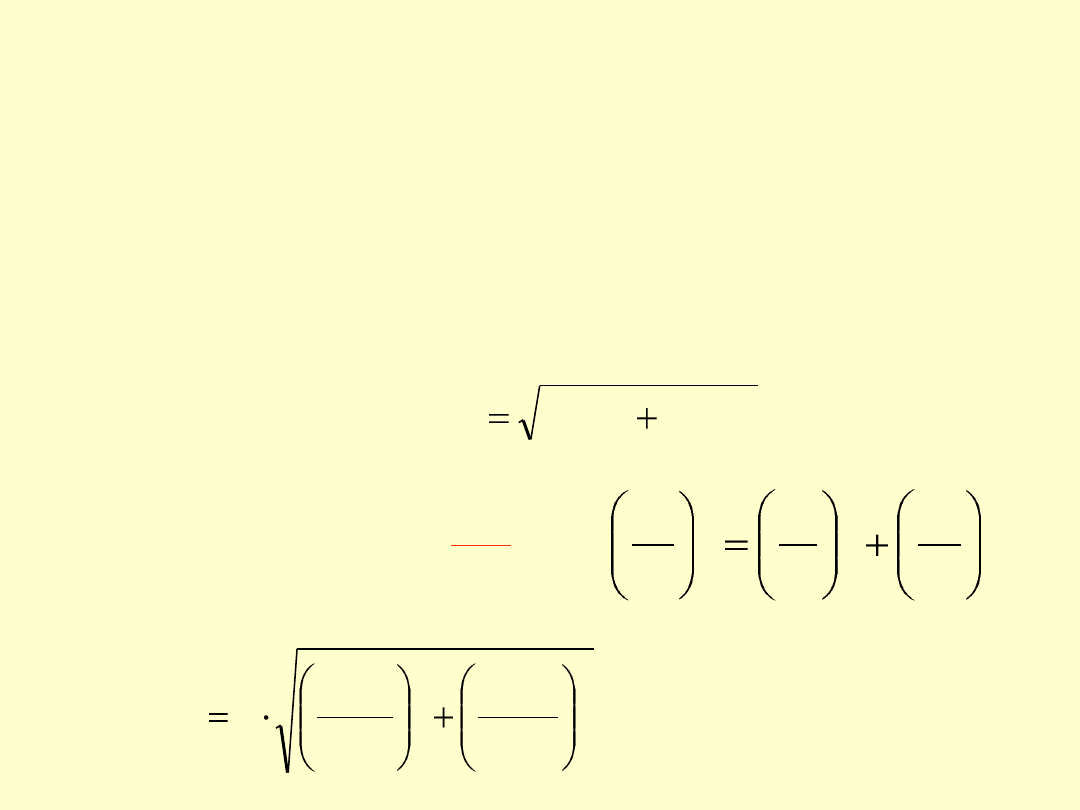
Jako miary wariancji s

i 

2 

przyjmujemy wartości u

2

(x

i

) (gdzie 

u(x

i

) to  

niepewność pomiaru i-tej wielkości x

i

), a obliczoną stąd wartość  

s

y

 nazywamy 

złożoną niepewnością standardową u

c

(y)

 

 

5. W dwóch szczególnych przypadkach prawo propagacji  
niepewności przyjmuje prostszą postać: 
 

A.

Jeśli 

y = x

1 

+ x

2

 

 lub 

y = x

1 

– x

2

 

, to 

 
     s

2

y 

= s

2

1 

+ s

2

2 

 czyli 

 
 
B.

Jeśli 

y = x

1

 

· x

2

  

lub 

y =       

, to 

 
 
 
czyli 
 

)

(

)

(

)

(

2

2

1

2

c

x

u

x

u

y

u

2

1

x

x

2

2

2

2

1

1

2

x

s

x

s

y

s

y

2

2

2

2

1

1

c

)

(

)

(

)

(

x

x

u

x

x

u

y

y

u

15 

Stąd w drugim przypadku (B) wprowadza się pojęcie  

względnych niepewności standardowych. 
 

Są to: 

 

względna niepewność standardowa u(x

i

)/x

i

  

(relative standard uncertainty) 

–  

niepewność wyniku zmiennej x

i

 podzielona przez  

wartość x

i

 

 

 

względna złożona niepewność standardowa u

c

(y)/y  

(relative combined standard uncertainty) 

–  

niepewność wyniku pomiaru y podzielona  przez 

wartość y 

 
 

16 

Wartość y i jej niepewność:    

Wynik = y 

 

u

c

(y)

 (P = 68%) 

 

Jeżeli y jest wynikiem końcowym, to częściej podaje się go  

z prawdopodobieństwem (P) większym, np.  P = 95%  lub   
P = 99% 

 

Wynik końcowy  = y   

U(y) 

 

gdzie:

 

U(y) 

– niepewność rozszerzona (expanded uncertainty) 

           

            

U(y) = 

k

 

· u

c

(y);    

k 

– współczynnik rozszerzenia  

                                            (coverage factor)  

 

                                               k 

=

 2  dla  P 

=

 95% 

                                               k 

=

 3  dla  P 

=

 99% 

 

 

W przypadku gdy wyznaczona wartość y i jej niepewność jest 

wykorzystywana w dalszych obliczeniach,

 bierzemy do 

nich jej niepewność 

nie

rozszerzoną

.  

17 

6. Przykłady obliczania niepewności wyniku dla  
konkretnych przypadków pomiarów 

6.1. Niepewność oznaczenia wagowego substancji 

  I etap: ważenie pustego tygla   
 
 
     II etap: 

operacje analityczne (rozcieńczanie, strącanie,  

                 

sączenie, prażenie lub suszenie osadu) 

 
 III etap: 

ważenie tygla z osadem 

 
 

18 

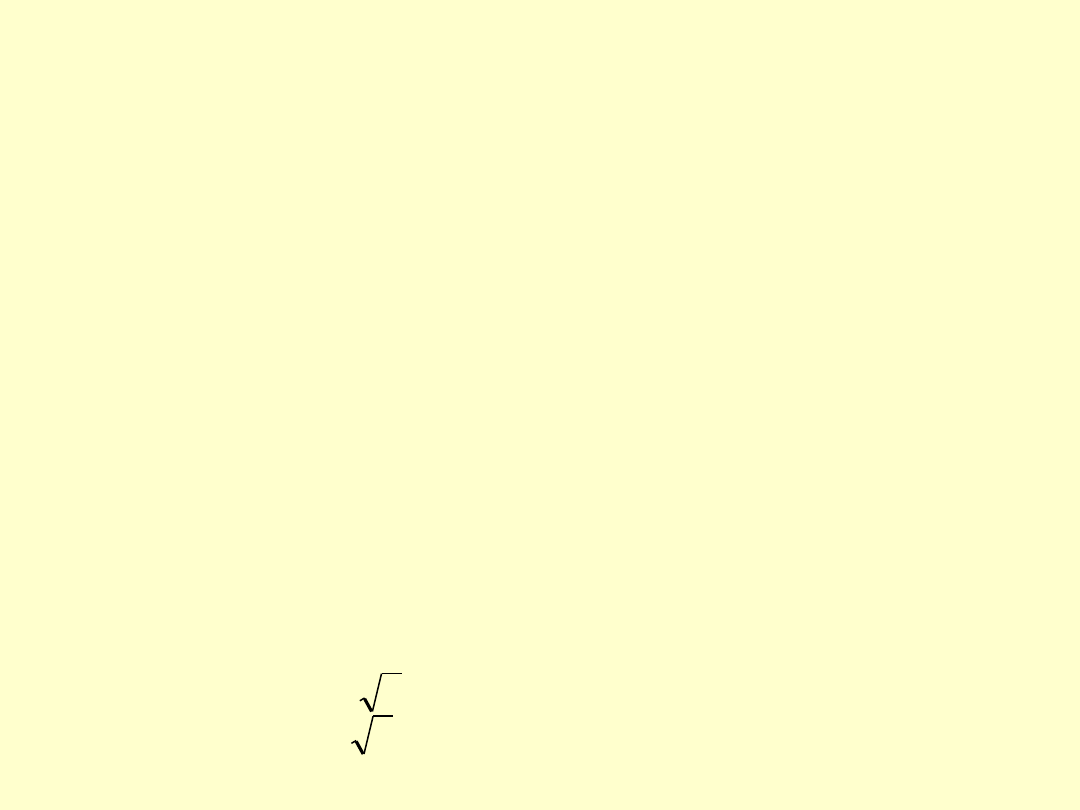
m 

pierw

 

= a · m 

osadu

 

 = a ·(m

 

tygla z os

 – 

m

 

tygla

) 

a – mnożnik analityczny  

np. a = 0,5885 (dla oznaczania Ba w postaci siarczanu) 

 
Pomiar masy na wadze analitycznej 
Na wynik pomiaru masy wpływają: 
- niepewność wskazania wagi dla danej masy (0,2 mg; podane przez  
                                                                           producenta) 
- rozdzielczość wskazania wagi (najmniejsza różnica wskazań: 0,1 mg)               
- rozrzut wskazań wagi (0,1 mg; podane przez producenta, obliczone z 
powtórzeń pomiarów jako odchylenie standardowe pojedynczego 
ważenia) 
 
Po przeliczeniu na niepewności standardowe: 

 

 

 

u

1

(m) = 0,2 mg /       = 0,115 mg (rozkład prostokątny) 

 

u

2

(m) = 0,1 mg /       = 0,058 mg (rozkład prostokątny) 

 

u

3

(m)

 

= 0,1 mg (rozkład normalny)

 

3

3

19 

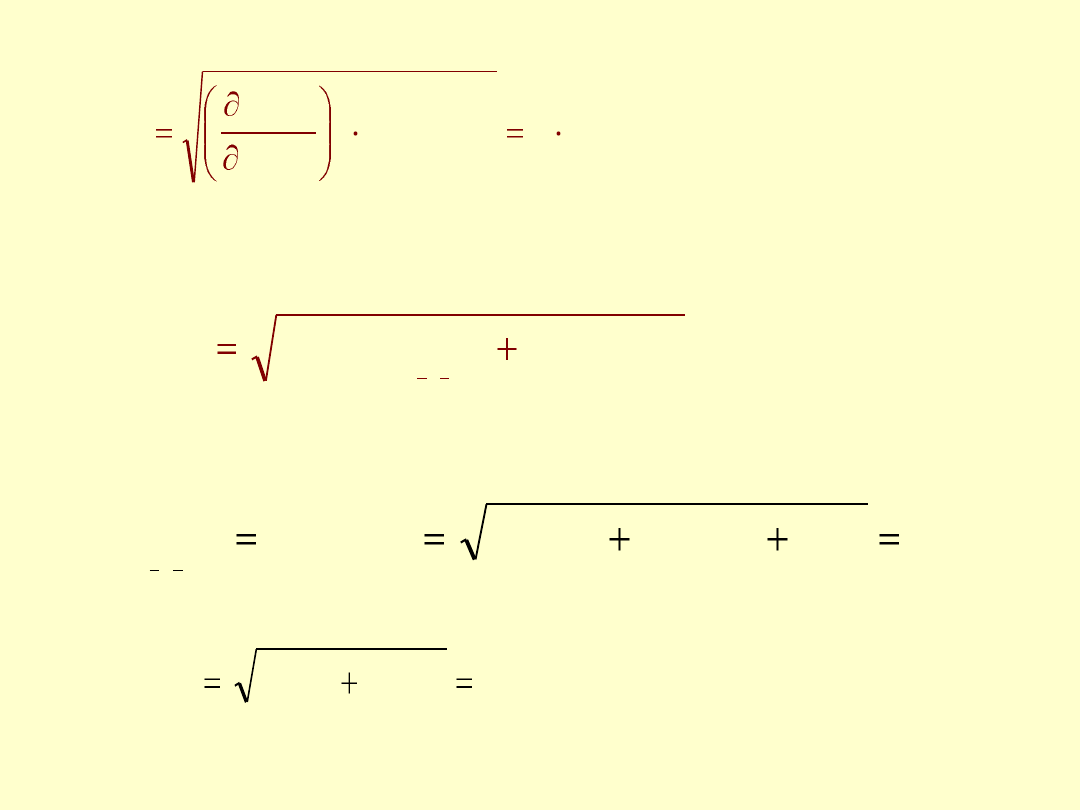
Złożona niepewność standardowa dla m

pierw

: 

 
 

 
 

Niepewność standardowa dla m

osadu

 

= m

tygla z os

 – m

tygla

 

        
 

 

 

Niepewność standardowa ważeń: 
 

 

 

 

 

      

)

(

)

(

)

(

t y g l a

2

o s

z

t y g l a

2

o s ad u

m

u

m

u

m

u

1 6

,

0

1

,

0

0 5 8

,

0

1 1 5

,

0

)

(

)

(

2

2

2

t y g l a

o s

z

t y g l a

m

u

m

u

)

(

)

(

)

(

osadu

osadu

2

2

osadu

pierw

pierw

c

m

u

a

m

u

m

m

m

u

2 3

,

0

1 6

,

0

1 6

,

0

)

(

2

2

o s ad u

m

u

mg 

mg 

20 

Złożona niepewność standardowa dla m

Ba

:  

u

c

 

(m

Ba

 

) = 0,5885 · 0,23 mg = 0,14 mg = 0,00014 g  (P = 68%) 

 

gdy np. masa osadu = 0,3738 g 

m

Ba

 

= a · m

osadu

  

= 0,5885 · 0,3738 g = 0,21998 g  

 
Zazwyczaj podając ostateczny wynik przyjmujemy wyższą wartość 
prawdopodobieństwa P, np. P = 95%,  i wówczas obliczamy  

niepewność rozszerzoną U(y): 
 

U(y) = k · u

c

(y)  (k nazywamy współczynnikiem rozszerzenia) 

 

W przypadku oznaczenia Ba: 

U(m

Ba

) = k · 

 u

c

 

(m

Ba

)

 = 2 · 0,00014 g = 0, 00028 g    

(k = 2 dla P = 95%) 

 

m

Ba 

 

= (0,21998   0,00028) g  

                                                                                       

21 

6.2. Niepewność wyznaczania stężenia roztworu 
sporządzanego metodą wagową  
 
 
 I etap: ważenie pustego naczynia wagowego 
 
 
 II etap: 

ważenie naczynia wagowego z odważką substancji 

 

 
    III etap: 

przeniesienie ilościowe odważki do kolby miarowej,     

                  rozpuszczenie w wodzie   
 
 
 IV etap:  

dopełnienie kolby miarowej wodą do kreski 

                   i wymieszanie  
 
 

 

22 

gdzie: 

m – masa odważki substancji 

             
             p – stopień czystości tej substancji (zakładamy p = 1) 
             
            M – masa molowa związku (np. dla KBrO

3

 równa 167,000 g/mol ) 

 

 

(niepewność u(M) jest do pominięcia) 

             
            V

R

 – objętość roztworu  

 

c = f (m, V

R

) 

 

Niepewność standardowa ważenia dla m

odw 

(analogicznie jak 

w oznaczeniu wagowym): 

 

 
 

23

,

0

)

(

)

(

)

(

n acz

2

o d w

n acz

2

o d w

m

u

m

u

m

u

R

V

M

p

m

c

mg 

23 

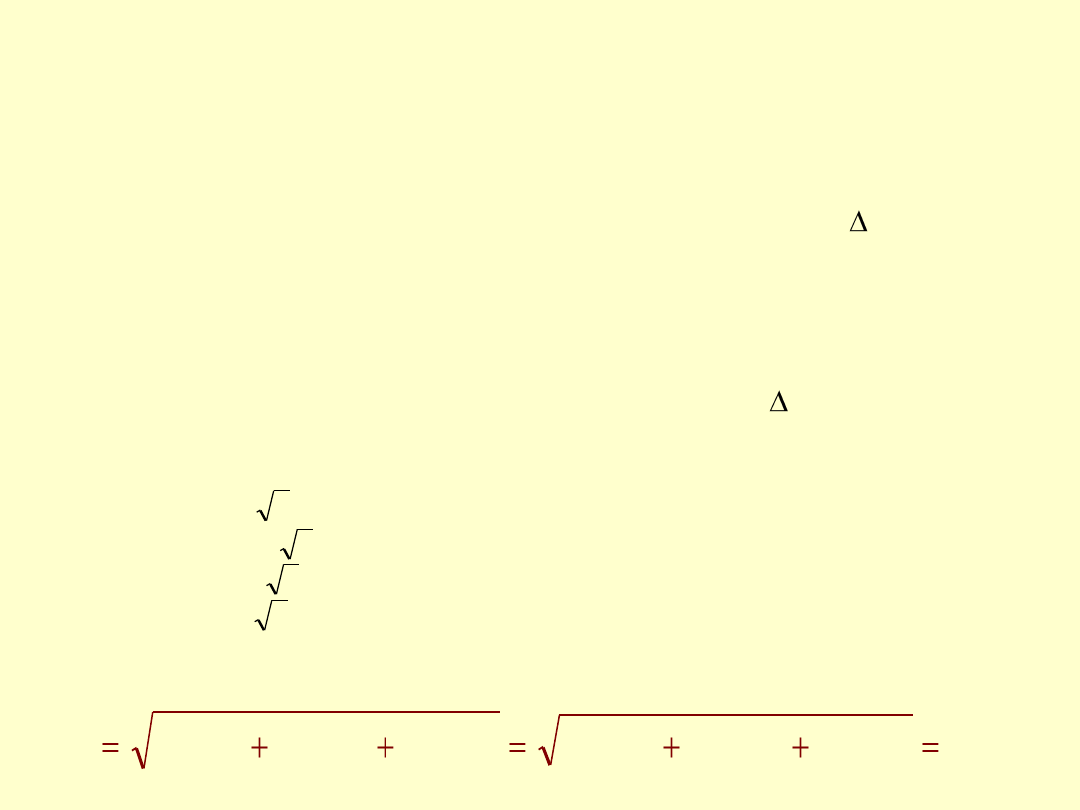
Pomiar objętości roztworu V

R

: 

Na objętość sporządzanego roztworu mogą mieć wpływ: 
–

 

niepewność kalibracji kolby:  

  dla kolby 1 L:  ± 0,8 mL, dla kolby 0,5 L:    0,5 mL;  
  dla kolb o pojemności 0,250 L oraz 0,200 L:   0,3 mL) 
– poprawka temperaturowa dla szkła: 0,013 mL (dla kolby 0,5 L i  T =   2 C, 
zmienia się proporcjonalnie ze zmianą pojemności kolby)  
– niepewność dopełniania kolby do kreski: 
  dla kolby 1 L:  ± 0,5 mL; dla kolby 0,5 L:   0,35 mL,  
  dla kolb o pojemności 0,250 L oraz 0,200 L:   0,2 mL) 
– poprawka temperaturowa :  0,2 mL

 

 (dla 0,5 L roztworu i  T =   2 C, zmienia się 

proporcjonalnie ze zmianą objętości roztworu) 
Po przeliczeniu na niepewności standardowe (przykładowo dla kolby 0,5 L):  
u

1

(V) = 0,5 mL /      = 0,289 mL (rozkład prostokątny) 

u

2

(V) = 0,013 mL /      = 0,008 mL (rozkład prostokątny) 

u

3

(V) = 0,35 mL

 

/     = 0,202 mL

  

(rozkład prostokątny) 

u

4

(V) = 0,2 mL

 

/      = 0,115 mL

 

(rozkład prostokątny) 

 

Niepewność standardowa dla V

R

: 

 
 

 

3

3

3

3

37

,

0

115

,

0

202

,

0

289

,

0

)

(

)

(

)

(

)

(

2

2

2

2

4

2

3

2

1

R

V

u

V

u

V

u

V

u

mL

 

24 

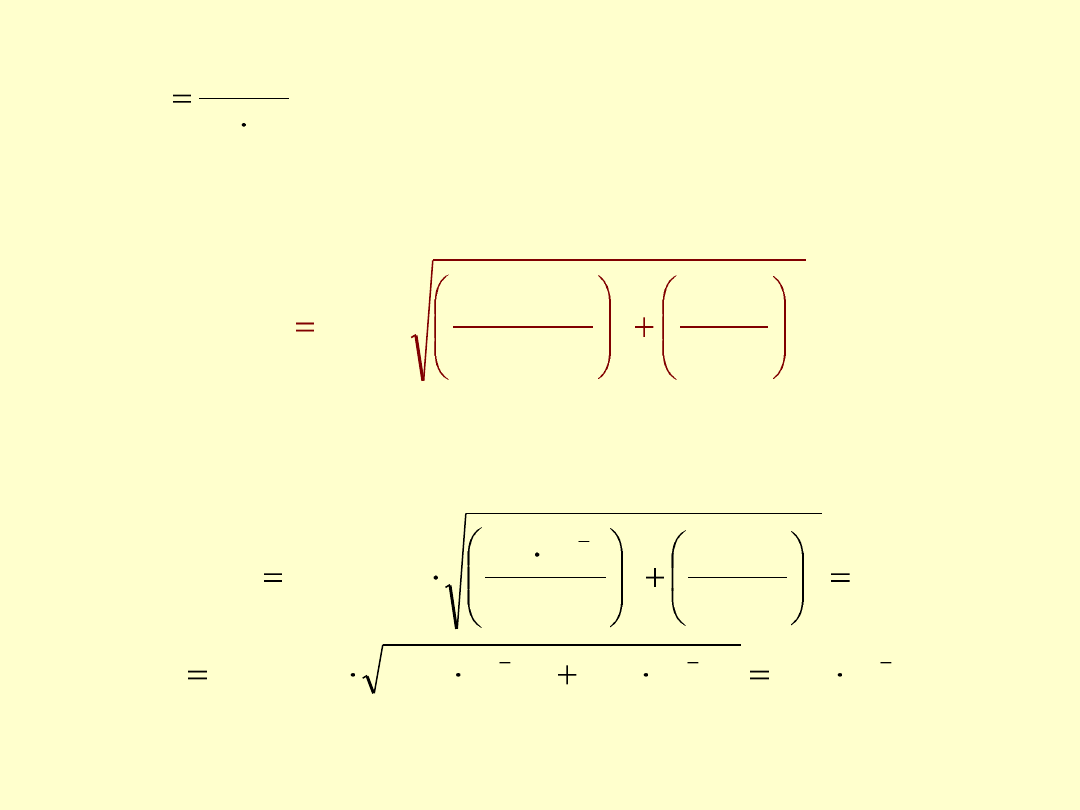
                                                  M = 167,000 g/mol 
 

 

Złożona niepewność standardowa c

KBrO3

:  

 

 

 
 
 

Dla m

KBrO3 

= 1,3900 g   mamy  c

KBrO3 

= 0,016647 mol/L

 

 

stąd: 

 

,

R

KBrO

3

V

M

m

c

2

R

R

2

KBrO

KBrO

KBrO

KBrO

c

)

(

)

(

)

(

3

3

3

3

V

V

u

m

m

u

c

c

u

2

2

4

KBrO

c

00

,

500

37

,

0

3900

,

1

10

3

,

2

016647

,

0

)

(

3

c

u

5

2

4

2

4

10

26

,

1

)

10

4

,

7

(

)

10

65

,

1

(

016647

,

0

mol/L 

25 

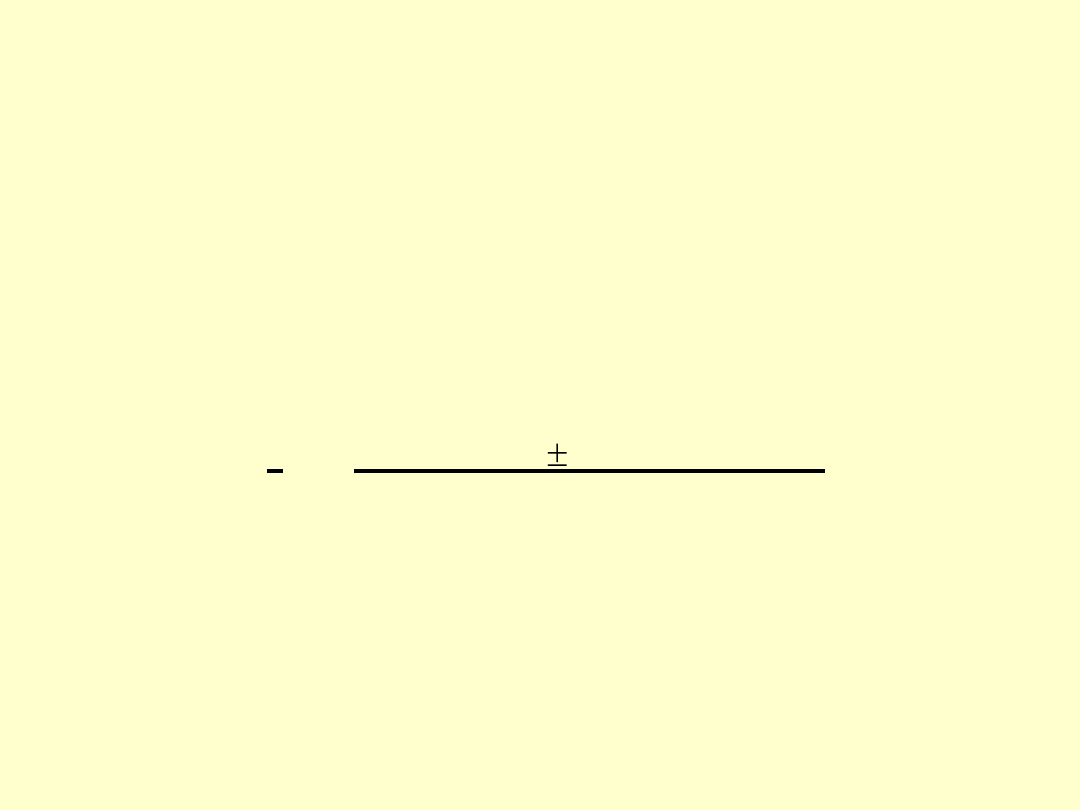
Niepewność rozszerzona dla c

KBrO3

: 

 

U(c

KBrO3

 ) = k · u

c

 

(c

KBrO3

) 

 

dla P = 95%   k = 2 
 
U(c

KBrO3

) = 2 · 0,0000126 mol/L = 0,000025 mol/L   

 
 

c

KBrO3

 = (0,016647   0,000025) mol/L 

26 

6.3. Niepewność wyznaczania pojemności naczyń 

miarowych 

 
 
 Niepewność wyznaczania pojemności kolby miarowej na 100 mL 

 

 
I etap: kilkakrotne (np. 6 razy) zważenie czystej, pustej i suchej  kolby 

 

 

 
II etap: pomiar (np. 8  razy) masy kolby napełnianej do kreski wodą  
             destylowaną o znanej  temperaturze 
 
 

27 

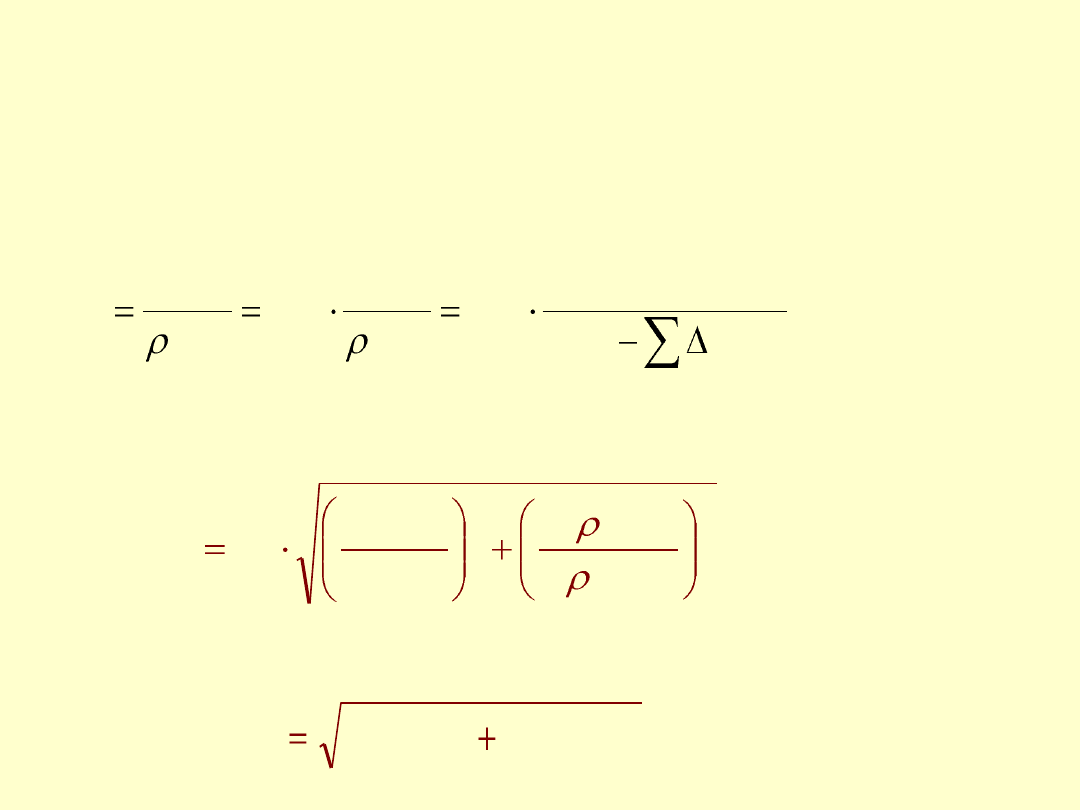
Z pomiarów obliczamy: 
• m

K,śr 

 

• masy wody wypełniającej kolbę  m

Wi 

 = m

K+Wi

 – m

K,śr  

 

W przypadku zmiennej temperatury w czasie pomiarów,   
m

Wi  

przeliczamy na objętości wody V

Wi

, tj.  

 

 
Złożona niepewność standardowa objętości wody  
wypełniającej kolbę V

wi,śr

 = V

K 

: 

 

 

 
Niepewność standardowa masy wody wypełniającej  kolbę m

W 

: 

 

 

 

)

(

1000

1000

)

(

'

1

)

(

'

W

W

W

W

i

i

i

i

i

i

i

T

m

m

T

m

T

m

V

2

2

W

W

K

K

c

)

(

'

))

(

'

(

)

(

)

(

T

T

u

m

m

u

V

V

u

)

(

)

(

)

(

śr

W ,

2

śr

K ,

2

W

m

u

m

u

m

u

28 

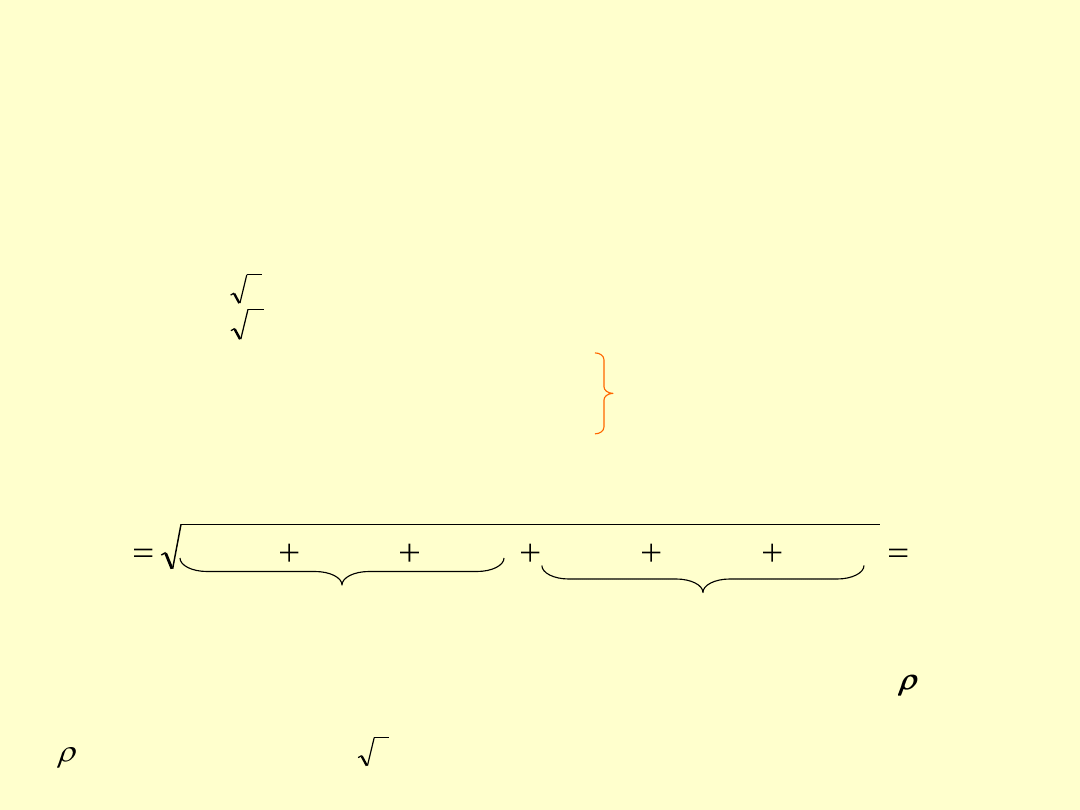
Pomiar masy na  wadze technicznej 
Na pomiar masy na wadze technicznej wpływają: 
• niepewność kalibracji wagi (0,02 g; podane przez producenta)  
• rozdzielczość wskazań wagi (0,01 g)  
• rozrzut wskazań wagi (obliczamy z powtórzeń pomiarów jako odchylenie 

standardowe średniej, czyli s(x

śr

) dla m

K 

oraz dla V

Wi

) 

Po przeliczeniu na niepewności standardowe: 
u

1

(m) = 0,02 g /      = 0,012 g (rozkład prostokątny)  

u

2

(m) = 0,01 g /      = 0,006 g (rozkład prostokątny) 

u

3

(m) = 

0,004 g

 (rozkład normalny) = s(m

Kśr

) 

 

u

4

(m) = 

0,016 g

 (rozkład normalny) = s(m

Wśr

)  

 

 

 

 

      

 

Niepewność standardowa masy wody wypełniającej  kolbę m

w 

: 

 

 

                                            pusta kolba                                        kolba z wodą 

 
Niepewność odczytywania gęstości (zawierającej poprawki) z tablic  ’(T) 

związana z niepewnością pomiaru temperatury termometrem (  1 C) 

u( ’(T)) = (2 ·10

-4 

g/mL ) /       = 1,15·10

-4 

 g/mL

 

(rozkład prostokątny) 

 
 

3

3

025

,

0

016

,

0

006

,

0

012

,

0

004

,

0

006

,

0

012

,

0

)

(

2

2

2

2

2

2

w

m

u

g 

3

Przykładowe wartości 

29 

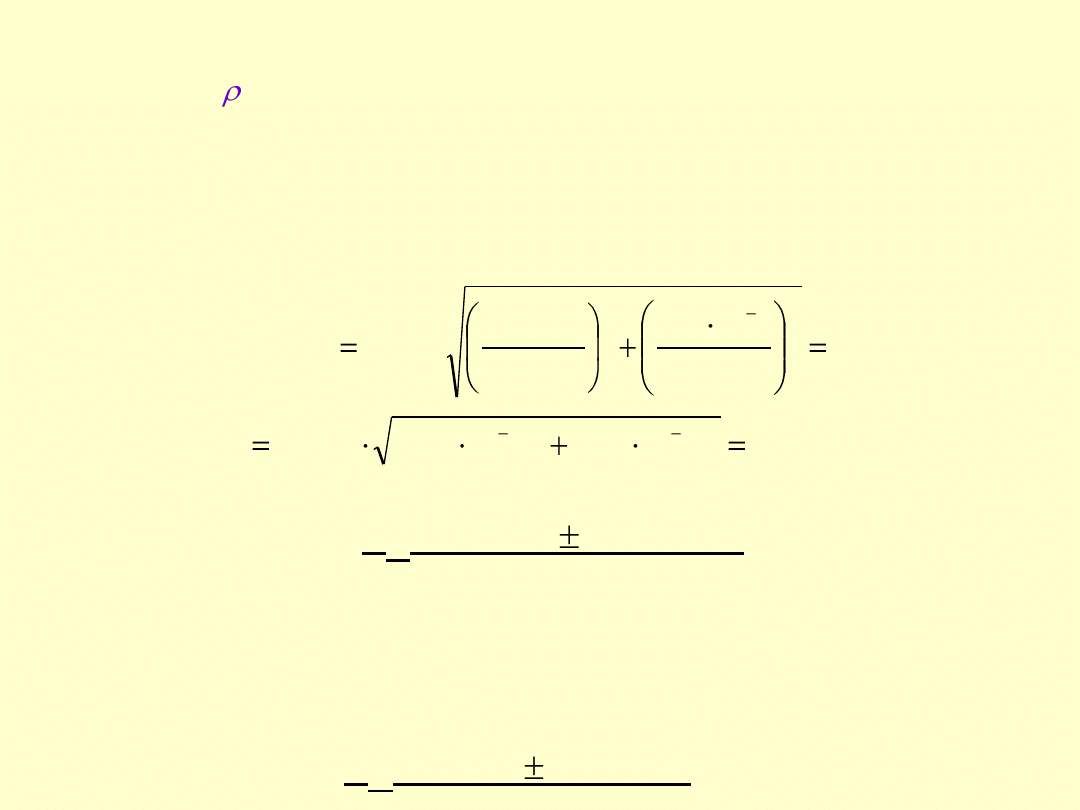
Gdy wyznaczone przez nas wielkości wynoszą przykładowo: 

V

K

 = 99,823 mL,  ’ (24 C) = 0,99616 g/mL 

stąd średnie  m

w 

= V

K

 · 0,99616  g/mL = 99,823 mL · 0,99733 g/mL = 99,4397 g 

 

Złożona niepewność standardowa V

K

: 

 

 

 

 

 

                                       V

K 

= (99,823   0,028) mL 

 

 

 

028

,

0

)

10

15

,

1

(

)

10

51

,

2

(

823

,

99

99733

,

0

10

15

,

1

4397

,

99

025

,

0

823

,

99

)

(

2

4

2

4

2

4

2

K

c

V

u

mL 

Niepewność rozszerzona (k = 2) 

U(V

k

) = 2 · 0,028 mL = 0,056 mL

 

V

K 

= (99,82   0,06) mL 

30 

Niepewność wyznaczania pojemności pipety na 25 mL 

 

 

I 

etap: pomiar masy pustej (może być mokra) kolby na 100 mL 

  

            

II etap: pomiar masy (np. 8 razy) kolby z kolejno dodawanymi porcjami  

              wody destylowanej, spuszczanymi z pipety 

 

 

 

31 

 

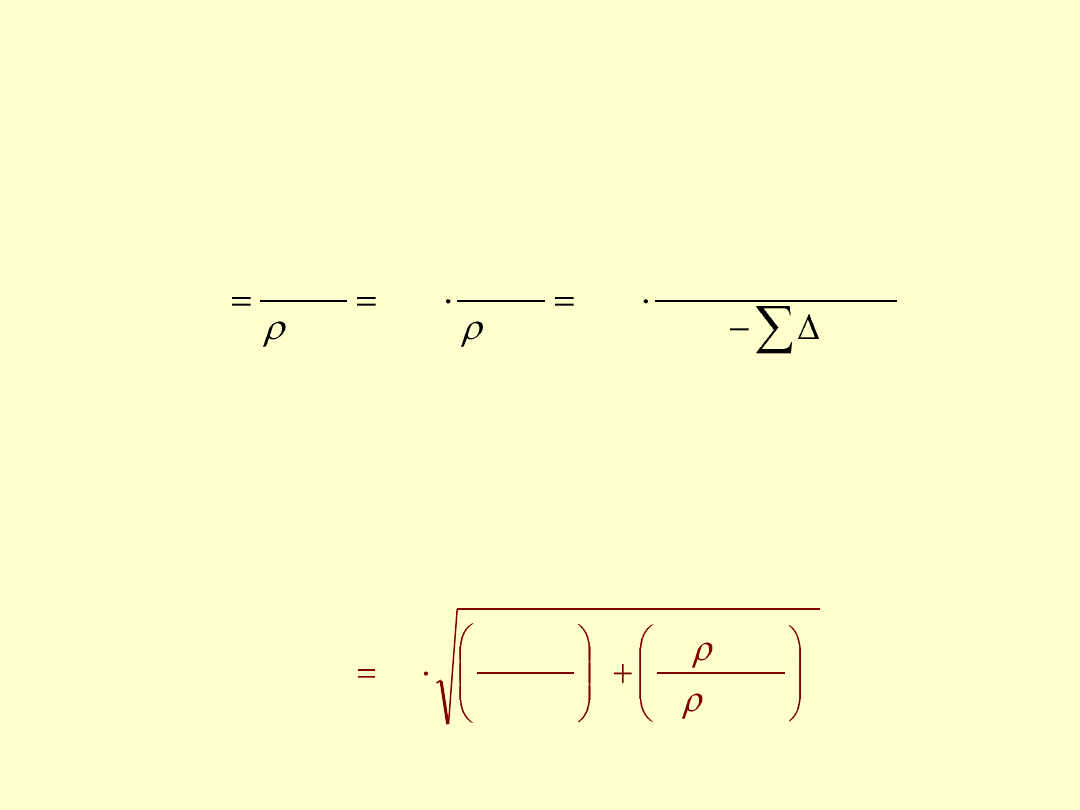
Z pomiarów obliczamy: 
• masy porcji wody wylanych z pipety m

Wi,  

 

m

Wi  

przeliczamy na objętości wody V

Wi

, tj.  

 

 

 

• Obliczamy V

w,śr

 np. V

w,śr

 = V

p

 = 24,923 mL 

 

oraz  s(V

W,śr

) 

Złożona niepewność standardowa objętości wody  
wypełniającej pipetę  V

p 

: 

 

 

 

 

)

(

1000

1000

)

(

'

1

)

(

'

W

W

W

W

i

i

i

i

i

i

i

T

m

m

T

m

T

m

V

2

2

W

W

p

p

c

)

(

'

))

(

'

(

)

(

)

(

T

T

u

m

m

u

V

V

u

32 

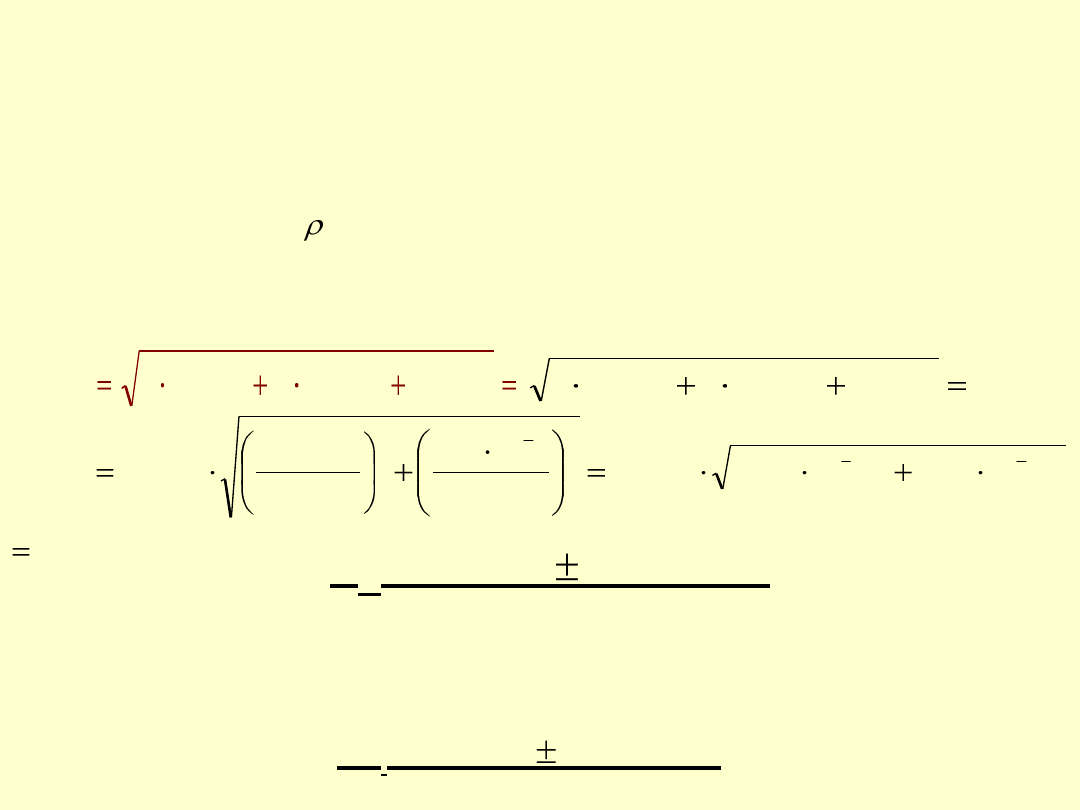
Niepewność standardowa masy wody wypełniającej   
pipetę u(m

w

)

  

u

1

(m), u

2

(m) – są takie same jak w przypadku wyznaczania

 

pojemności kolby 

u

3

(m) = s(m

Wśr

) 

Ponieważ gęstość wody  ’ (24 C) = 0,99616 g/mL, to możemy przyjąć, że: 
jeśli 

np.

 s(V

W,śr

) =  0,004 mL ,  to s(m

W śr 

)  = 0,004 mL · 0,99616 g/mL = 

0,0040 g 

i podobnie  m

w

 = V

p 

· 0,99616 g/mL = 24,7610 g  

 

 
 
                                                      

    V

p 

= (24,923   0,019) mL 

Niepewność rozszerzona (k = 2) 

U(V

p

) = 2 · 0,019 mL = 0,038 mL

 

Vp

 

= (24,923   0,038) mL 

 

)

(

)

(

2

)

(

2

)

(

2

3

2

2

2

1

W

m

u

m

u

m

u

m

u

019

,

0

)

10

15

,

1

(

)

10

64

,

7

(

923

,

24

99733

,

0

10

15

,

1

7610

,

24

019

,

0

923

,

24

)

(

2

4

2

4

2

4

2

p

c

V

u

 mL 

019

,

0

004

,

0

006

,

0

2

012

,

0

2

2

2

2

(przykładowa wartość) 

33 

 g 

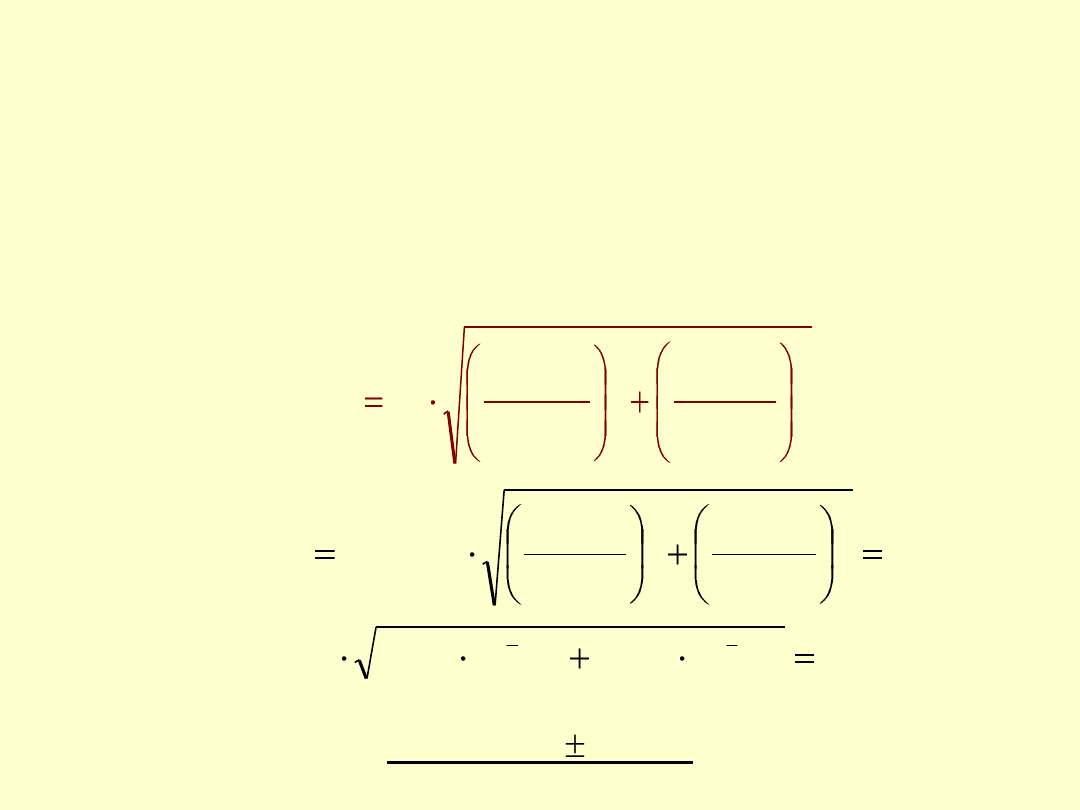
 Niepewność wyznaczania współczynnika współmierności kolby 
     i pipety 

 

W = V

K 

 / V

p 

       np.   W = 99,823 / 24,923 = 4,00526 

 

Złożona niepewność standardowa wartości współczynnika W 
 

 
 
 
 
 
 
                                         
 

W = 4,0053   0,0033 

2

śr

p,

śr

p,

2

śr

K,

śr

K,

c

)

(

)

(

)

(

V

V

u

V

V

u

W

W

u

0033

,

0

)

10

62

,

7

(

)

10

80

,

2

(

00526

,

4

923

,

24

019

,

0

823

,

99

028

,

0

00526

,

4

)

(

2

4

2

4

2

2

c

W

u

34 

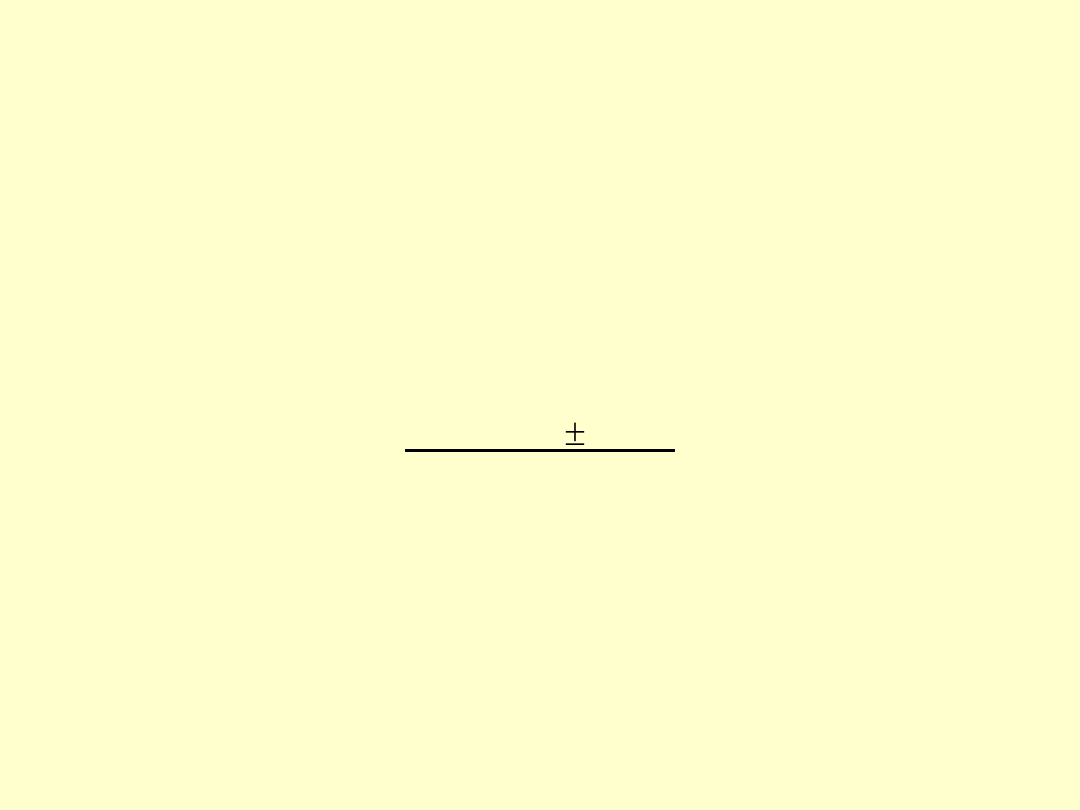
Niepewność rozszerzona 

 

U(W) = k · u

c

 

(W

 

)

   

 

dla  P = 95%    k = 2 

 

U(W) = 2 ·0,0033 = 0,0066 

 

W = 4,005   0,007 

35 

6.4. Niepewność wyniku mianowania roztworu 

 I etap: sporządzenie odważki substancji wzorcowej 

II etap: przeniesienie ilościowe odważki do kolby stożkowej, 
              rozpuszczenie w wodzie destylowanej i dodanie  
              wskaźnika 

III etap: zmiareczkowanie roztworu substancji wzorcowej 
                  roztworem mianowanym  

Etapy I-III muszą być powtórzone minimum 3 razy !  

(zmiareczkowanie przynajmniej 3-ech odważek) 

36 

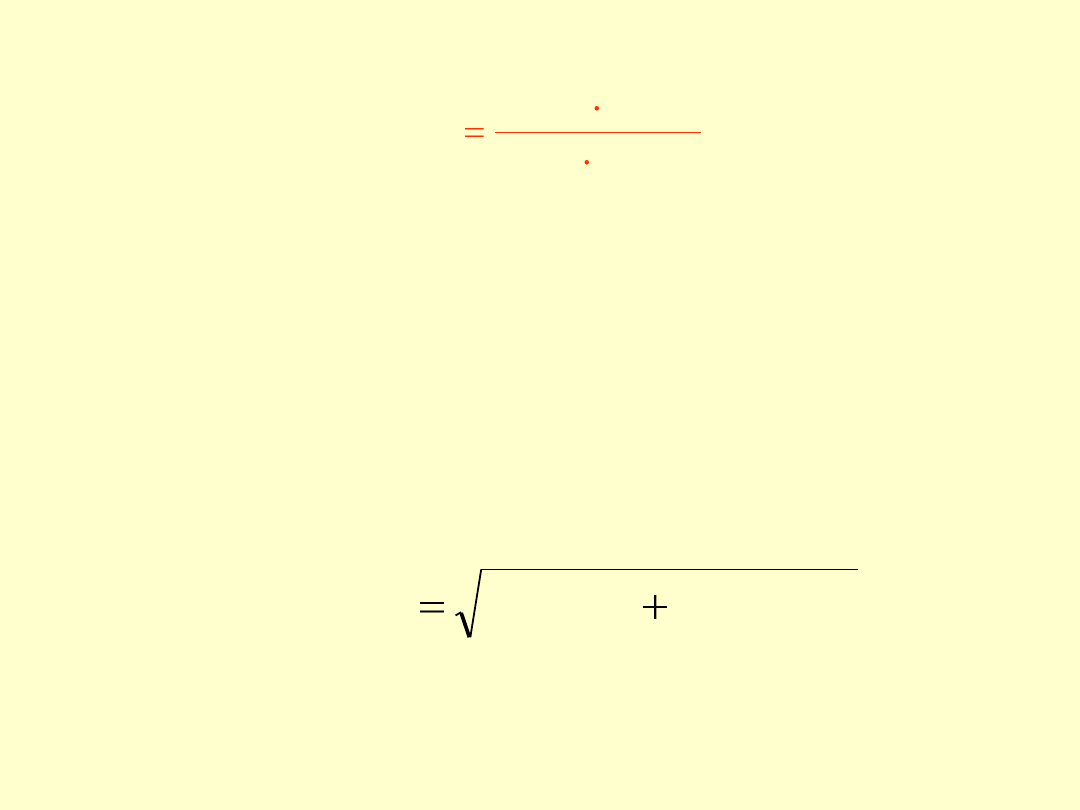
22

,

204

1000

NaOH

odw

NaOH

V

m

c

c

NaOH

 = f (m

odw 

, V

NaOH 

) 

W celu obliczenia 

złożonej niepewności standardowej u

c

(c

NaOH śr

)

 

liczymy oddzielnie niepewność systematyczną, u(c

i

)

syst

 oraz 

niepewność przypadkową, u(c

śr

)

przyp

: 

 

przyp

śr

2

syst

2

śr

NaOH

c

)

(

)

(

)

(

c

u

c

u

c

u

i

37 

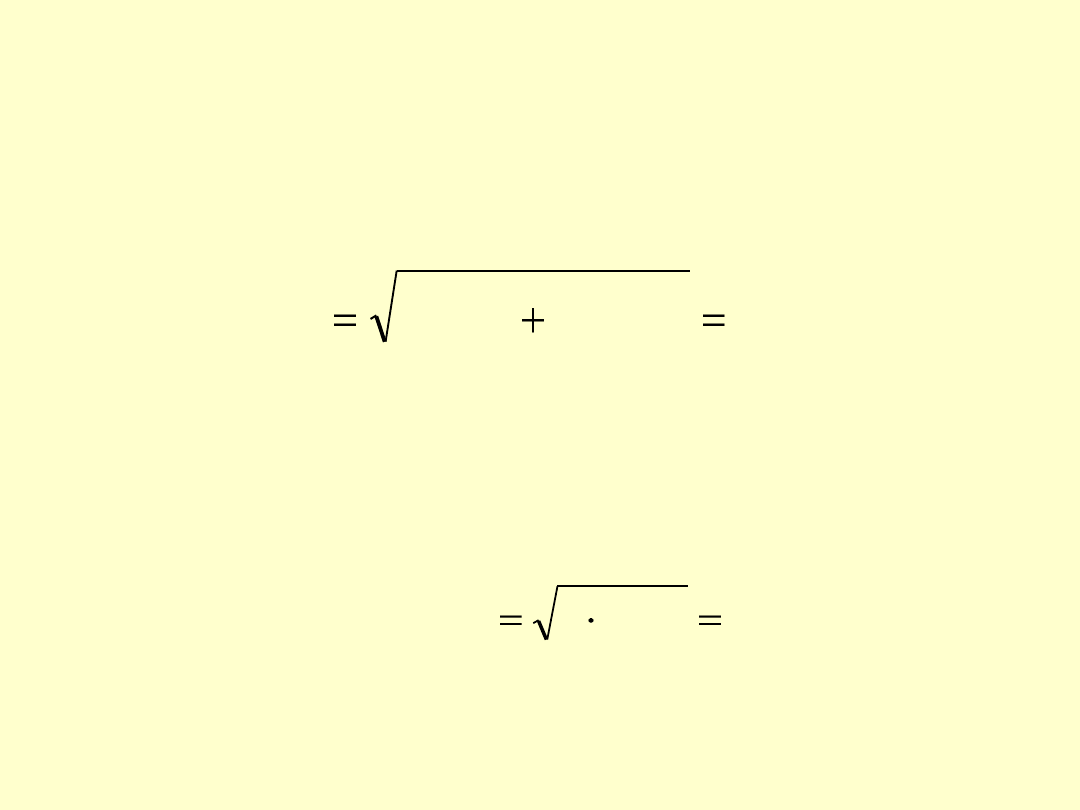
Ponieważ dla każdej odważki należy wykonać dwa ważenia (puste 
naczyńko wagowe i naczyńko z odważką), to:  

18

,

0

13

,

0

2

)

(

2

syst

odw

m

u

Na 

standardową niepewność systematyczną

 składają się te 

udziały niepewności ważenia i miareczkowania, które mają 
charakter systematyczny, czyli u(m)

syst  

i u(V)

syst

 

13

,

0

058

,

0

115

,

0

)

(

2

2

syst

m

u

38 

 mg 

 

mg 

071

,

0

)

029

,

0

(

)

029

,

0

(

)

058

,

0

(

)

(

)

(

)

(

)

(

2

2

2

2

3

2

2

2

1

syst

V

u

V

u

V

u

V

u

Pomiar objętości titranta (roztwór NaOH) 

 

Na pomiar objętości titranta mają wpływ: 
- niepewność kalibracji biurety (dla biurety o poj. 50 mL: 0,1 mL)  
- niepewność kropli (wyznaczona objętość kropli, średnio 0,05 mL) 
- niepewność odczytu (0,05 mL) 
- poprawka temperaturowa objętości szkła (do 0,0025 mL dla   2 C) 

 

Po przeliczeniu na niepewności standardowe: 

 

u

1

(V) = 0,1 mL /       = 0,058 mL (rozkład prostokątny) 

 

u

2

(V) = 0,05 mL /     = 0,029 mL

 

(rozkład prostokątny) 

 

u

3

(V) = 0,05 mL 

 

/      = 0,029 mL

 

(rozkład prostokątny) 

 

u

4

(V) = 0,0025 mL /      = 0,001 mL (rozkład prostokątny) 

 

3

mL 

3

3

3

39 

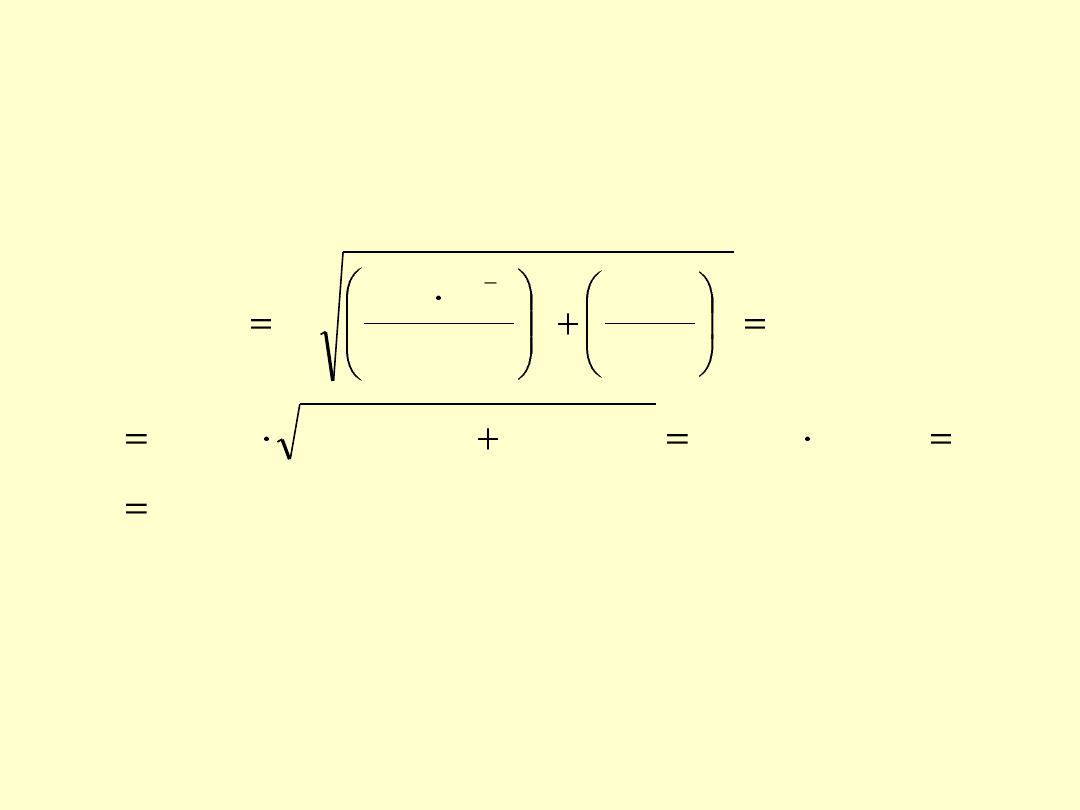
Obliczenia wykonujemy dla średniej masy odważki wodoroftalanu 

(tu przykładowo 0,5000 g)

 i średniej objętości zużytego titranta 

(tu

 

przykładowo 25,00 mL). 
 

00028

,

0

0028

,

0

1013

,

0

)

0028

,

0

(

)

00036

,

0

(

1013

,

0

00

,

25

071

,

0

5000

,

0

10

18

,

0

)

(

2

2

2

2

3

śr

syst

c

c

u

i

mol/L 

40 

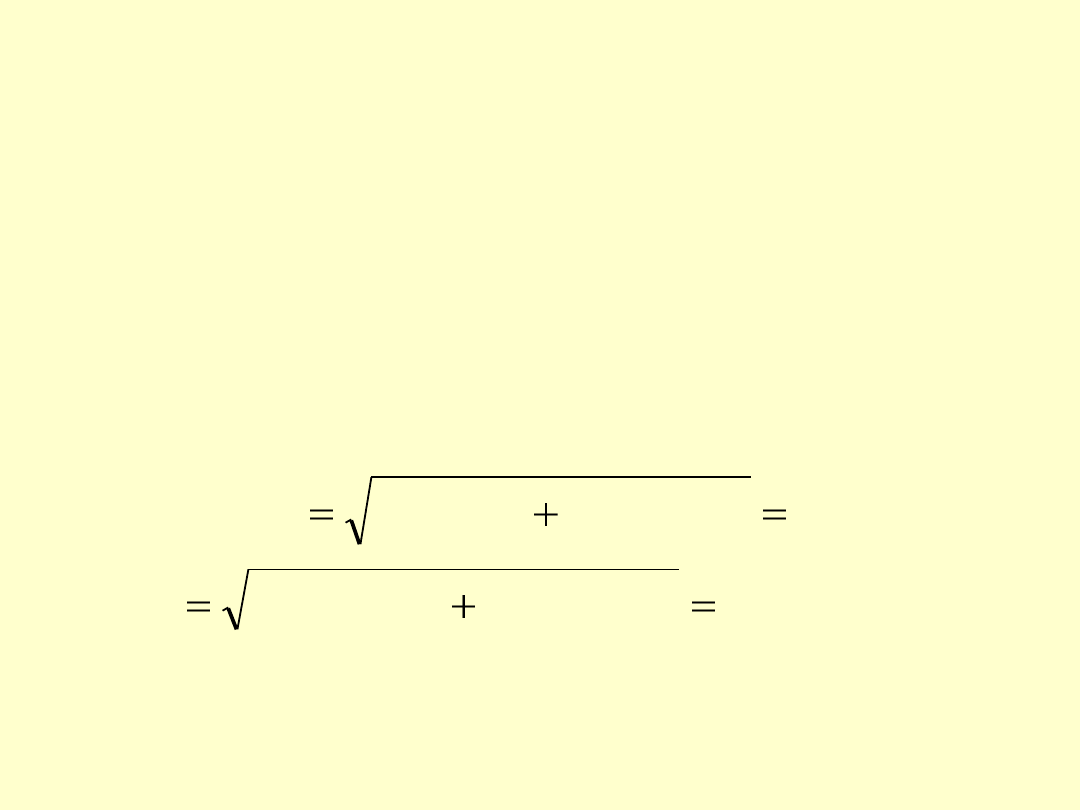
Standardową niepewność przypadkową

 dla c

śr 

obliczamy jako 

odchylenie standardowe średniej z serii wyników c

i

: 

u(c

śr

)

przyp

= s(c

śr

)

 

Stąd,

 przyjmując przykładowo, że s(c

śr

) = 0,00044 mol/L

 

złożona niepewność standardowa u(c

śr

) wynosi: 

00052

,

0

)

00044

,

0

(

)

00028

,

0

(

)

(

)

(

)

(

2

2

przyp

śr

2

syst

2

śr

c

c

u

c

u

c

u

i

mol/L 

41 

Niepewność rozszerzona dla c

NaOH

: 

 

U(c

NaOH

) = k · u

c

 

(c

NaOH 

)

   

 

dla  P = 95%    k = 2 

 

U(c

NaOH

) = 2 ·0,00052 mol/L  = 0,00104 mol/L 

 
 

c

NaOH 

= (0,1013    0,0010) mol/L 

42 

6.5. Niepewność wyniku miareczkowania 

   I etap: ilościowe przeniesienie próbki do kolby na 100 mL,  
               

dopełnienie kolby wodą do kreski i wymieszanie  

 
   II etap:  pobranie do miareczkowania porcji roztworu kwasu  
                

solnego za pomocą pipety na 25 mL, przeniesienie tej 

                

porcji do kolby stożkowej i dodanie wskaźnika 

 
III etap: zmiareczkowanie roztworu kwasu solnego  
                zmianowanym roztworem wodorotlenku sodu 

m = f (V

NaOH

, c

NaOH

, W) 

1000

461

,

36

N aO H

N aO H

H Cl

W

c

V

m

43 

Pomiar objętości titranta (roztwór NaOH) 
Na pomiar objętości titranta mają wpływ: 
- niepewność kalibracji biurety (dla biurety o poj. 50 mL: 0,1 mL) 
- niepewność kropli (wyznaczona objętość kropli, średnio 0,05 mL) 
- niepewność odczytu (0,05 mL) 
- poprawka temperaturowa objętości szkła (do 0,0025 mL dla   2 C) 
- rozrzut wyników miareczkowania – odchylenie standardowe średniej 
(należy wyznaczyć, np. z trzech miareczkowań; uwaga! - może wyjść 
przypadkowo równy zero)

 

 
Po przeliczeniu na niepewności standardowe: 

 

u

1

(V) = 0,1 mL /       = 0,058 mL (rozkład prostokątny) 

 

u

2

(V) = 0,05 mL /     = 0,029 mL

 

(rozkład prostokątny) 

 

u

3

(V) = 0,05 mL 

 

/      = 0,029 mL

 

(rozkład prostokątny) 

 

u

4

 (V) = 0,0025 mL /      = 0,001 mL (rozkład prostokątny) 

 

u

5

 (V) = s(V

NaOH,śr

) (rozkład normalny); 

wartość  

                                             przykładowa

 

0,044 mL

     

3

3

3

3

44 

Niepewność standardowa dla V

NaOH

: 

 

 

 
 
Przyjmując, że 

c

NaOH

 

= (0,1013   0,0005) mol/L , V

NaOH,śr 

= 18,61 mL 

i  

W = 4,0053   0,0033

 

 (współmierność kolby i pipety) 

oraz gdy  m

HCl

  = (

18,61 · 0,1013 · 

36,461

 · 4,0053

) /

 

1000

 = 0,27531 g 

 

Złożona niepewność standardowa dla m

HCl

: 

 
 
 

 

 
 
 

 

)

(

)

(

)

(

)

(

)

(

2

5

2

3

2

2

2

1

N aO H

V

u

V

u

V

u

V

u

V

u

2

2

NaOH

NaOH

2

śr

śr

HCl

HCl

c

)

(

)

(

)

(

)

(

W

W

u

c

c

u

V

V

u

m

m

u

0019

,

0

)

10

2

,

8

(

)

10

9

,

4

(

)

10

5

,

4

(

27531

,

0

0053

,

4

0033

,

0

1013

,

0

0005

,

0

61

,

18

084

,

0

27531

,

0

2

4

2

3

2

3

2

2

2

084

,

0

)

10

4

,

4

(

)

10

9

,

2

(

2

)

10

8

,

5

(

2

2

2

2

2

2

mL 

g 

45 

Niepewność rozszerzona dla m

HCl

: 

 

U(m

HCl

) = k · u

c

 

(m

HCl

)

   

 

dla  P = 95%    k = 2 

 

U(m

HCl

) = 2 ·  0,0019 g = 0,0038 g 

 
 

m

HCl 

= (0,2753    0,0038) g 

46 

'

0

O

S

Na

O

4

1000

998

,

31

3

2

2

2

V

W

c

V

c

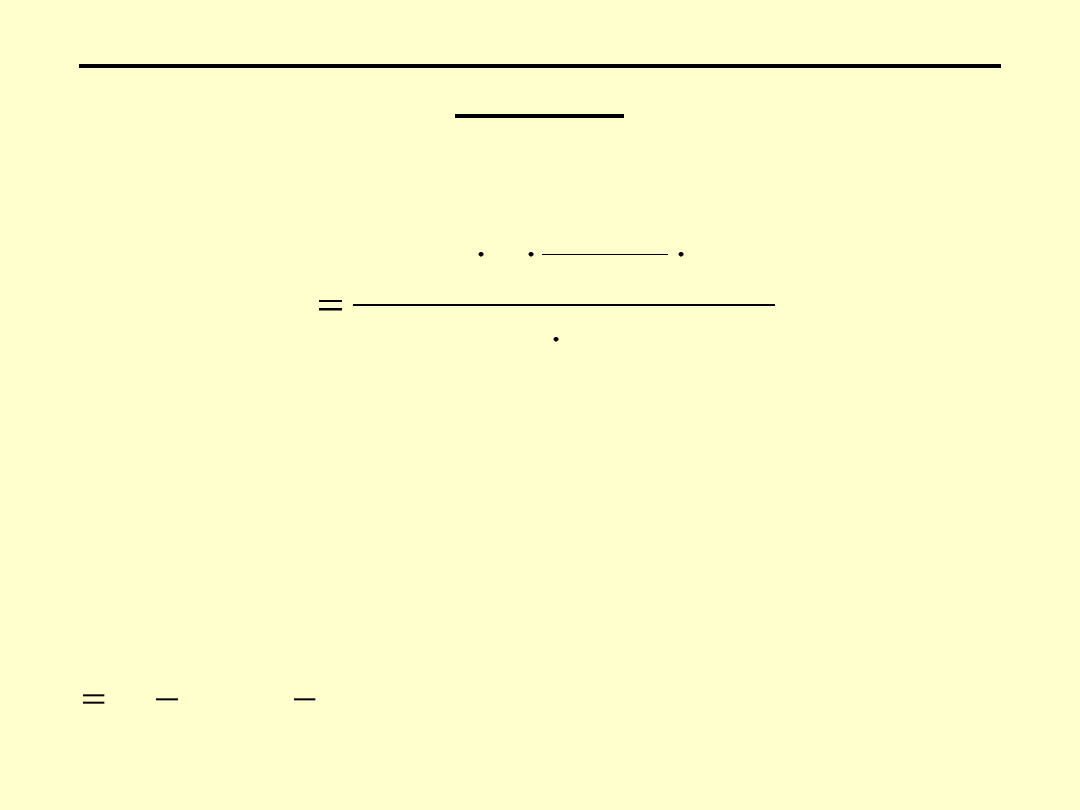
6.6. Niepewność oznaczenia  tlenu w wodzie metodą 

Winklera 

gdzie: 

31,998 – masa molowa tlenu [g/mol], 

c

Na2S2O3

 – stężenie roztworu Na

2

S

2

O

3

 [mol/L],  

W – współczynnik współmierności kolby z pipetą, 

V – objętość roztworu Na

2

S

2

O

3

 zużyta do miareczkowania [ml]       

  

 

 

   – objętość analizowanej  próbki wody [mL]. 

 

 
 

47 

KI

MnSO4

0

'

0

V

V

V

V

[mg/L] 

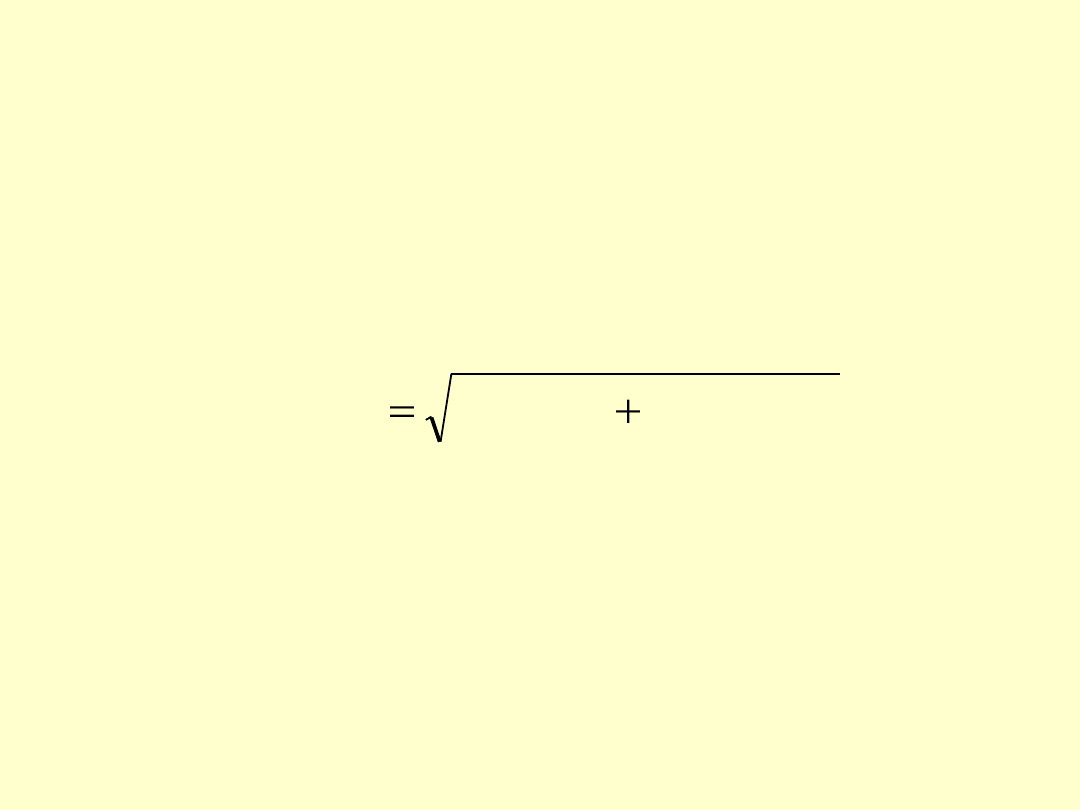
48 

W celu obliczenia 

złożonej niepewności standardowej u

c

(c

O2, śr

)

 

liczymy oddzielnie niepewność systematyczną, u(c

i

)

syst

 oraz 

niepewność przypadkową, u(c

śr

)

przyp

: 

 
 
 
 
 
 
 

przyp

śr

2

syst

2

śr

O2,

c

)

(

)

(

)

(

c

u

c

u

c

u

i

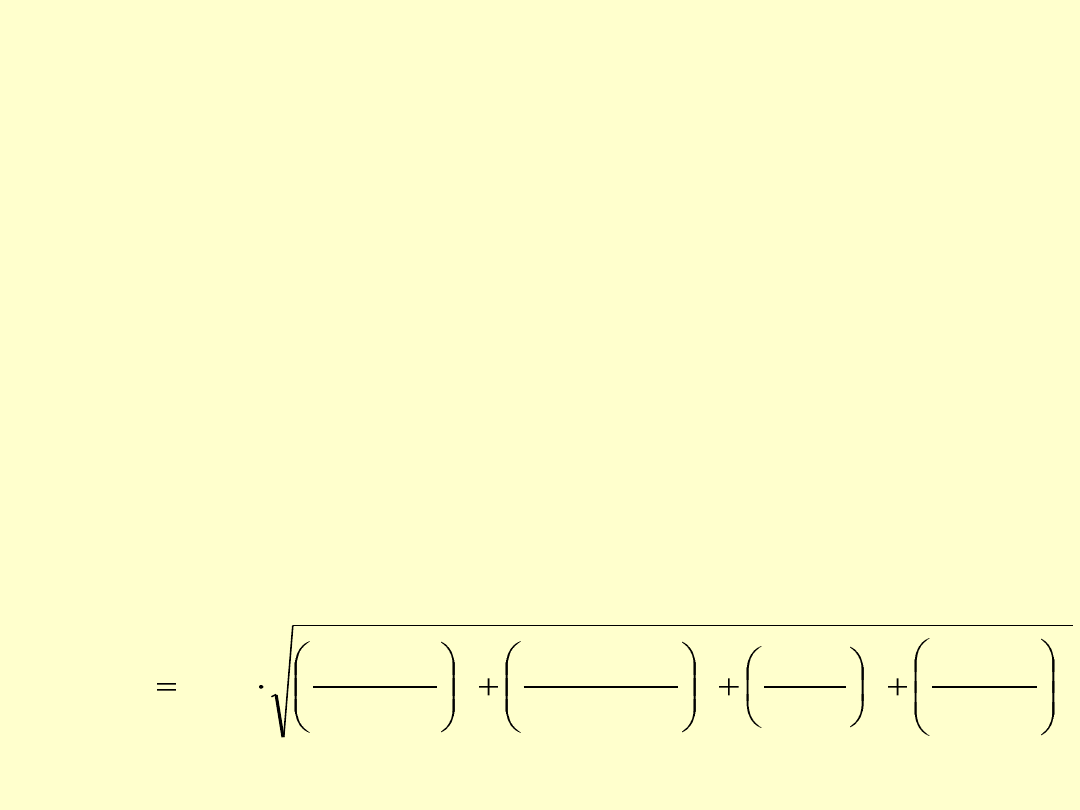
49 

Obliczenia 

standardowej  niepewności  systematycznej

 

u(c

i

)

syst

 

wykonujemy  dla  średniej  objętości  zużytego  titranta,  V

śr 

,  średniej 

pojemności  użytych  kolb  stożkowych  V

0,śr 

,  oraz  średniej  wartości 

c

O2,śr 

. 

Na standardową niepewność systematyczną składają się niepewności: 

 -   u

syst

(V

śr

)  średniej objętości titranta,  

-    u(c

Na2S2O3

) stężenia titranta,  

-    u(W) współczynnika współmierności (tu: rozcieńczenia)  

-                średniej objętości analizowanej próbki. 

Na podstawie prawa przenoszenia niepewności : 

 

                                                                                     

)

(

'

śr

0,

V

u

2

śr

0,

'

śr

0,

2

2

Na2S2O3

Na2S2O3

2

śr

śr

syst

śr

O2,

syst

'

)

(

)

(

)

(

)

(

)

(

V

V

u

W

W

u

c

c

u

V

V

u

c

c

u

i

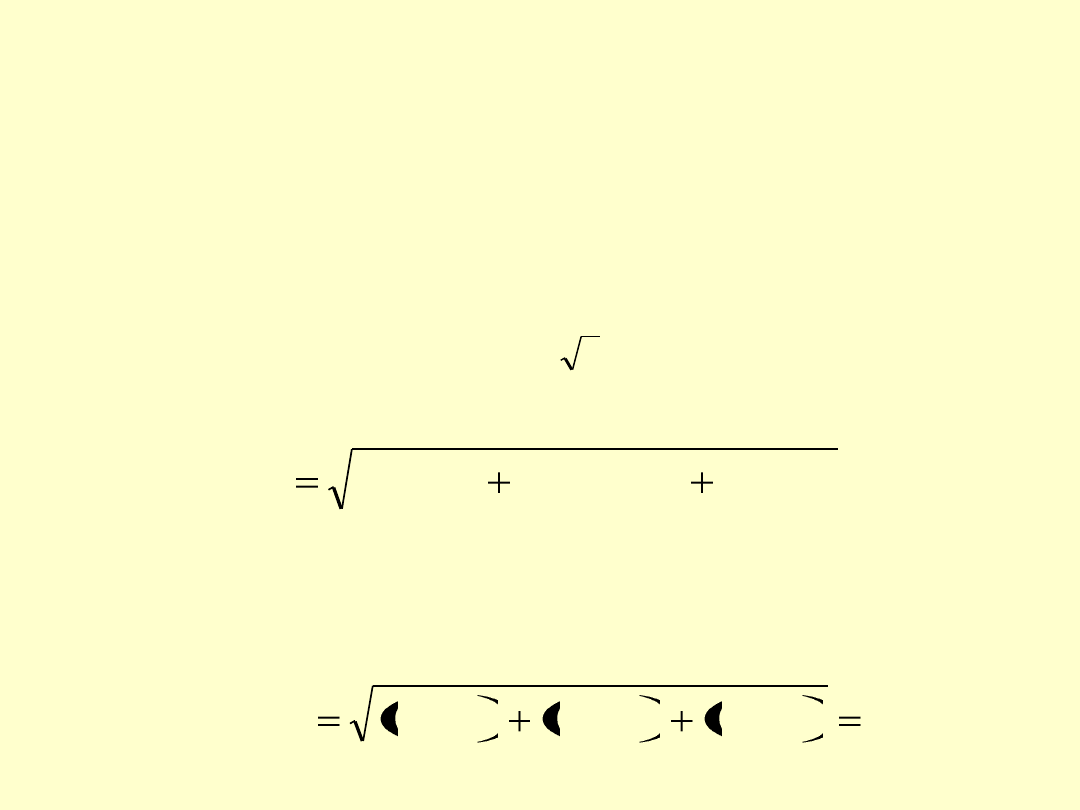
W obliczeniach                przyjmujemy, że: 

– 

niepewność 

pojemności 

każdej 

kolby 

stożkowej 

u(V

0,śr

)  =  0,2  mL  –  rozkład  normalny  –  wielkość  ta  jest 

wyznaczana na etapie kalibracji kolb stożkowych, 

– 

niepewność 

objętości 

dodanych 

roztworów: 

u(V

MnSO4

)  =  u(V

KI

)  =  0,02  mL/        –  rozkład  prostokątny  – 

niepewność odmierzenia pipetą o pojemności 2 mL. 

 

 

Systematyczną niepewność średniej objętości zużytego titranta, 
                  wyznaczamy podobnie, jak przy mianowaniu NaOH: 

 

 

3

50 

)

(

'

śr

0,

V

u

)

(

)

(

)

(

)

(

KI

2

MnSO4

2

śr

0,

2

'

śr

0,

V

u

V

u

V

u

V

u

071

,

0

029

,

0

029

,

0

058

,

0

)

(

2

2

2

śr

syst

V

u

)

(

śr

syst

V

u

 

mL 

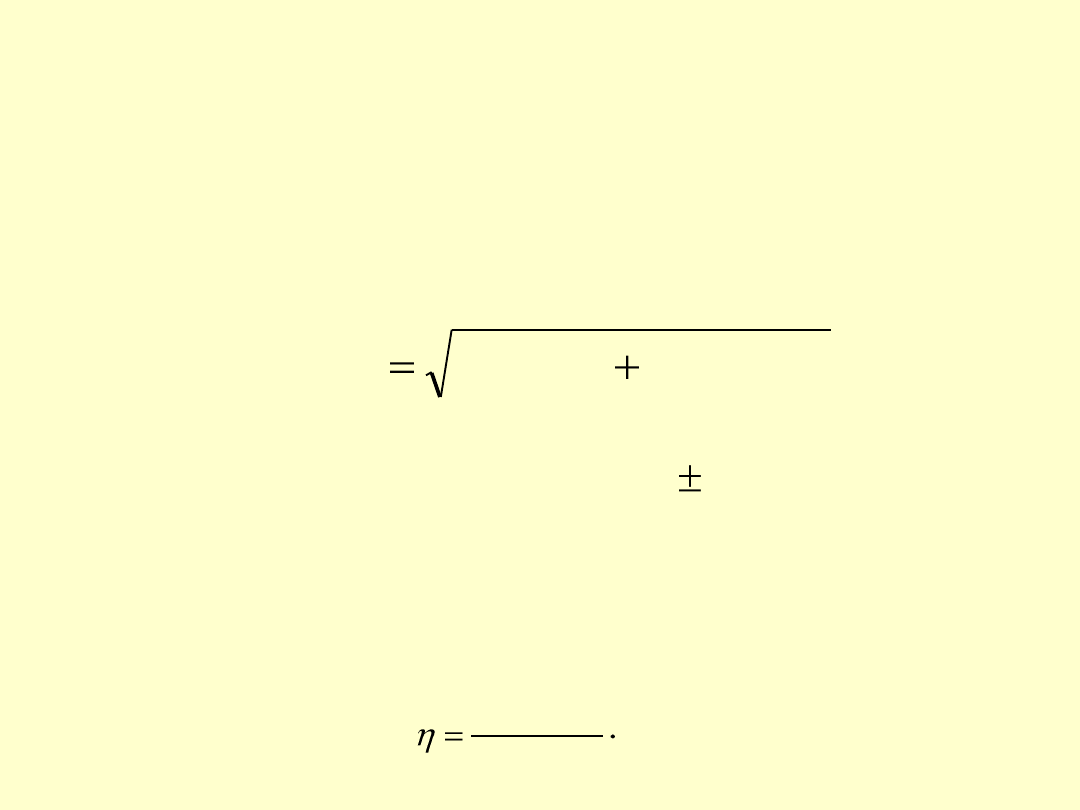
51 

Standardową niepewność przypadkową

 u(c

O2,śr

)

przyp  

obliczamy 

jako odchylenie standardowe średniej z serii wyników c

i

: 

u(c

śr

)

przyp

= s(c

śr

) 

 

Następnie liczymy:  
 
 
 
 

Ostatecznie podajemy wynik  

c

O2

 = c

O2,śr

   2 u

c

(c

O2,śr

) 

 

 

Jeśli znamy temperaturę, T, badanej wody oraz tablicową 

wartość rozpuszczalności tlenu w wodzie w tej temp. c

O2

(T)

tabl.

, to 

możemy obliczyć stopień nasycenia, η, badanej wody tlenem: 

przyp

śr

2

syst

2

śr

 

O2

c

)

(

)

(

)

(

c

u

c

u

c

u

i

%

100

)

(

c

tabl.

O2

śr

O2,

T

c

7. Podsumowanie, wnioski 

 

1.  Każdy wynik pomiaru powinien być podawany wraz z jego  
     niepewnością wyznaczenia. 
 
„Wartość pomiaru bez określenia  
  wartości niepewności  
  nie ma żadnej wartości” 
 
 

WYNIK KOŃCOWY = WYNIK   NIEPEWNOŚĆ

 

(niepewność 

                                                                                      rozszerzona U) 
U(y) = k · u

c

(y)      (np. k   2 dla P = 95%) 

 
 

 
 

52 

 
 
 

 
 
 

 
2.  Wynik końcowy podaje się zwykle do tego miejsca po przecinku, od  
     którego wynik pomiaru jest obarczony niepewnością. Gdy wartość 
     niepewności pomiaru zaczyna się od cyfry 1, 2 albo 3, to  zostawia się  
     dodatkowo kolejną cyfrę zarówno w wyniku pomiaru jak i w wartości 
     niepewności. 
     Przykład:          m

HCl

 

= (0,242   0,006) g 

                      ale   m

HCl

 

= (0,242

3

   0,00

34

) g 

 
       
3. Przy obliczaniu niepewności wypadkowej na wynik końcowy nie mają 
    praktycznie wpływu te z niepewności składowych, które są o rząd lub  
    więcej (czyli 10 lub więcej razy) mniejsze od największej z  
    niepewności składowych  i stąd można je pomijać w rachunkach. 

 

 

53