EAIE	Imię i nazwisko: Dominika Łuszczuk		Rok I	Grupa IV		Zespół 2
Pracownia fizyczna I	Szacowanie niepewności w pomiarach laboratoryjnych					Nr ćwiczenia 0
Data wykonania:	Data oddania:	Zwrot do poprawy:	Data oddania:		Data zaliczenia:	Ocena:

Niepewność i błąd pomiaru

Liczba otrzymana w wyniku procedury pomiaru (wraz z jednostką) nie zawiera pełnej informacji na temat mierzonej wielkości. Niezbędne jest również podanie informacji o dokładności wykonanego pomiaru poprzez oszacowanie niepewności wyniku. Rozróżnia się dwie podstawowe metody szacowania niepewności:

-dla serii pomiarowej, w której dominujący wkład do niepewności mają tzw. niepewności przypadkowe (wymaga to zastosowania przyrządu pomiarowego o odpowiedniej dokładności) jako niepewność przyjmuje się tzw. odchylenie standardowe,

-w przypadku wykonania pojedynczego pomiaru, w sytuacji gdy dominujący jest wkład tzw. niepewności systematycznej związanej z dokładnością przyrządu (np. przy pomiarze długości kartki linijką jest to działka elementarna linijki).

Należy przy tym podkreślić, że - o ile to możliwe - należy starać się tak zaplanować pomiar by dominujący był czynnik niepewności przypadkowych i by można było wykonać serię pomiarów, gdyż pozwala to na uzyskanie większej dokładności.

Warto dodać, że niepewności pomiarowe są nieodłącznym elementem każdego prawidłowo przeprowadzonego pomiaru i - w przeciwieństwie do błędu pomiarowego, który można wyeliminować (jest on zasadniczo wynikiem błędu eksperymentalnego) - nie można ich wyeliminować.

Przyjmuje się, że niepewność wyniku pomiaru zaokrągla się do maksymalnie dwóch cyfr znaczących i wynik pomiaru podaje się z miejscami znaczącymi zgodnymi z niepewnością.

Pomiar jednokrotny

Często spotykamy się z sytuacją, gdy dany pomiar wykonujemy tylko jeden raz. Należy wtedy przyjąć, że dokładność takiego pomiaru równa jest działce elementarnej przyrządu, chyba że producent określił z jaką dokładnością mierzy dany przyrząd (często podawana klasa przyrządu). Nieraz jednak zdarza się, że działka elementarna przyrządu jest mniejsza od rzeczywistej dokładności (np. pomiar czasu spadania przedmiotu przy użyciu stopera z działką 0,01s) i wtedy należy niepewność oszacować kierując się zdrowym rozsądkiem, lub też - co daje lepsze wyniki - wykonać serię pomiarową i obliczyć niepewność standardową.

Rozkład Gaussa, gęstość prawdopodobieństwa.

Definicja (rozkład prawdopodobieństwa)

Rozkładem prawdopodobieństwa na zbiorze liczb rzeczywistych R nazywamy każdą miarę probabilistyczną na B(R) [B(R) to sigma algebra zbiorów borelowskich na R].

Definicja (gęstość rozkładu prawdopodobieństwa)

Jeśli miara μ jest rozkładem prawdopodobieństwa na R i dla pewnej funkcji f:R→R całkowalnej w sensie Lebesquea mamy:

μ (A) = (całka po A z funkcji f(x), gdy A ∈ B(R) )

to funkcję f nazywamy gęstością rozkładu μ.

Z definicji wynika, że gęstość dowolnego rozkładu prawdopodobieństwa jest nieujemna oraz całkowalna do jedynki.

Z drugiej strony: każda funkcja całkowalna do jedynki i nieujemna jest gęstością rozkładu jakiegoś prawdopodobieństwa ( i jest to jeden jedyny rozkład).

Czyli gęstość jednoznacznie wyznacza rozkład.

Rozkład Gaussa (inaczej: rozkład normalny).

Rozkład Gaussa to rozkład prawdopodobieństwa wyznaczony przez gęstość daną wzorem:

Rozkład ten oznaczamy N(μ,σ²), gdzie μ i ,σ² są parametrami rozkładu normalnego.

Pomiary wielokrotne

W przypadku, gdy dominujący na wynik pomiaru jest wpływ różnych czynników przypadkowych najlepszym wyjściem jest wykonanie serii pomiarów, przy czym - ze względu na liczebność próby losowej - dobrze jest powtórzyć pomiar co najmniej 10-krotnie. Można wykazać, że takim przypadku rozkład otrzymanych wyników jest rozkładem Gaussa. Udowadnia się, że w takim przypadku najlepszym estymatorem wartości oczekiwanej wyniku pomiaru jest wartość średnia zmierzonych wielkości:

[1]

najlepszym estymatorem odchylenia standardowego pojedynczego pomiaru jest wielkość:

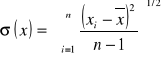
zaś najlepszym estymatorem odchylenia standardowego wartości średniej jest:

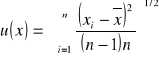
Znaczenie poszczególnych wielkości jest następujące. Wartość średnia uzyskanych rezultatów jest najbardziej prawdopodobną wartością rzeczywistą mierzonej wielkości. Statystyczne znaczenie odchylenia standardowego pojedynczego pomiaru mówi, że z prawdopodobieństwem około 68% wartość kolejnego wykonanego pomiaru będzie zawierała się granicach
, zaś dla odchylenie standardowego wielkości średniej, że wartość średnia kolejnej serii pomiarowej będzie z prawdopodobieństwem około 68% zawierała się w przedziale
.

Pomiary złożone

W sytuacji, gdy wykonujemy pomiary kilku wielkości fizycznych x₁, x₂, ... x_n i na ich podstawie obliczmy inną wielkość y , która jest funkcją wielkości mierzonych, niepewność standardową możemy obliczyć z zależności:

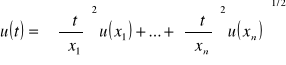
Zależność ta jest poprawna jedynie w przypadku, gdy wielkości x₁...x_n są statystycznie niezależne oraz niepewności względne
są małe.

W przypadku, gdy szacujemy niepewność maksymalną zależność na przenoszenie niepewności ma postać:

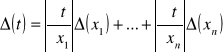
Przedział i poziom ufności

Przedziałem ufności nazywamy taki przedział wartości mierzonej wielkości, że z określonym prawdopodobieństwem (poziom ufności) wynik kolejnej serii pomiarowej zawarty jest w tym przedziale (oznacza to, że z danym prawdopodobieństwem zawarta jest w nim wartość prawdziwa). W przypadku rozkładu normalnego najczęściej stosowane przedziały i poziomy ufności wynoszą:

przedział ufności: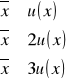
poziom ufności:

Niepewność rozszerzona

Obecnie używana nazwa niepewności rozszerzonej:

gdzie współczynnik k dobiera się do założonego poziomu ufności. Uwzględnia on informacje o rozkładzie odchyłek pomiarowych. Dla przykładu przy małej liczbie pomiarów współczynnik k dobiera się z tablic rozkładu Studenta.

Obliczenia niepewności

Tabela przedstawia wyniki pomiarów z dwóch doświadczeń: obliczania prędkości dźwięku w temperaturze 0˚C na podstawie pomiaru długości fali w zależności od częstotliwości, oraz obliczania przyspieszenia ziemskiego poprzez pomiary okresu drgań wahadła matematycznego.

Nr	Prędkość dźwięku w temperaturze 0˚C vo [m/s]	Przyspieszenie ziemskie g [m/s^2]
1	340,552	9,815925
2	352,865	9,543418
3	361,716	9,868569
4	356,713	9,77601
5	357,868	9,826392
6	333,818	-
7	348,152	-
8	359,253	-
9	344,336	-
10	359,151	-
średnia	351,442	9,766
S(x)	2,958	0,058
uA	2,958	0,058
uB	0,577	0,067
uC	1,765	0,140
x	351,442	9,766
uA	2,958	0,058
x	351,442	9,766
uC	1,765	0,140

Obliczenia współczynnika κ

(wykładnika w równaniu adiabaty oraz stosunku ciepł właściwych)

κ = (v² * μ ) / (R * T)

gdzie: μ = 0,78 * 2 μ_N + 0,21 * 2 μ_o + 0,01 * 2 μ_Ar = 29,36 g/ mol

μ = 0,02936 kg/ mol

R = 8,3143 J/mol*K

κ (wartość tablicowa dla powietrza) = 1,4

Po obliczeniu mamy:

κ = 1,56

Niepewność: u(κ) =0,042616 ≈ 0,04

Odchylenie standardowe σ(κ) = 0,153653 ≈ 0,15

Błąd bezwzględny κ: 0, 16

Błąd względny κ: 11,43%

Regresja liniowa

y = ax + b

Wyznaczamy współczynniki a i b prostej na podstawie wzorów:

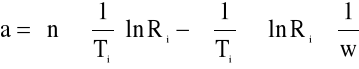
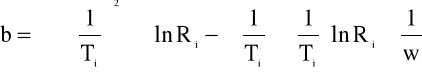
gdzie: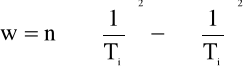

Błędy współczynników a i b zostały wyznaczone na podstawie wzorów:

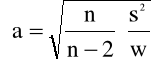
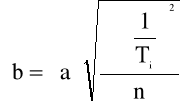
Gdzie: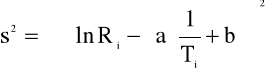

s² = 0,018254806

1. Wyznaczenie współczynnika sprężystości metodą dynamiczną.

Równanie prostej regresji:

Gdzie:

Y= T²

X= M

a = 4п²/k

b= 4п²/k * m/3

Wartość k wyznaczamy ze wzoru otrzymanego po przekształceniu:

A ) Dla sprężyny stalowej

W tabeli podano wartości uśrednione pomiarów (w doświadczeniu zmierzono 3 razy czas 10 okresów).

T [s]	0,982	1,025	1,090	1,281
M [kg]	0,0806	0,0906	0,108	0,1616
T^2 [s^2]	0,964	1,050	1,188	1,641

Niepewność wartości k

- sprężyny stalowej

B ) Dla sprężyny mosiężnej

T [s]	0,371	0,384	0,417	0,504
M [kg]	0,0806	0,0906	0,108	0,1616
T^2 [s^2]	0,138	0,147	0,174	0,254

Niepewność wartości k

[kg/s^2]

- sprężyny mosiężnej

Zależność F(x) dla sprężyny stalowej [metoda statyczna]

Gdzie: g=9,81 [m∙s^-2]

Porównanie metod wyznaczania współczynnika sprężystości

	Metoda statyczna	Metoda dynamiczna
Sprężyna stalowa
Sprężyna mosiężna

Wniosek: wyniki w obu metodach są porównywalne, aczkolwiek metoda statyczna jest dokładniejsza.

2. Wyznaczenie przyspieszenia ziemskiego poprzez pomiary okresu drgań wahadła dla różnych długości wahadła.

Okres drgań wahadła wynosi:

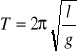
Po przekształceniu otrzymujemy równanie prostej regresji postaci:

Gdzie: x = T²

y = 4 п²Δl

a = g

b = - 4п²lo

Stąd mamy: g = a.

၄l [m]	T1 [s]	T2 [s]	T3 [s]	T4 [s]	T5 [s]	Tśr [s]	u(Tśr) [s]	Tśr^2 [s^s]	u(Tśr^2) [s^2]	y = 4 п^2Δl [m]	x^2 = (T^2)^2 [s^4]	x* y [m * s^s]
0	1,56	1,57	1,69	1,59	1,56	1,593	0,056	2,54	0,18	0,000	6,452	0,000
0,2	1,8	1,81	1,8	1,81	1,8	1,804	0,005	3,25	0,02	7,888	10,563	25,635
0,4	2,03	2,01	2	2,01	2,16	2,043	0,066	4,17	0,27	15,775	17,389	65,783
0,6	2,19	2,2	2,21	2,19	2,2	2,199	0,007	4,84	0,03	23,663	23,426	114,529
0,8	2,4	2,39	2,39	2,38	2,38	2,385	0,008	5,69	0,04	31,551	32,376	179,524
1	2,54	2,55	2,54	2,54	2,54	2,542	0,003	6,46	0,02	39,438	41,732	254,772
1,2	2,79	2,7	2,72	2,69	2,69	2,717	0,042	7,38	0,23	47,326	54,464	349,266
1,22	2,71	2,71	2,83	2,72	2,72	2,74	0,051	7,51	0,28	48,115	56,400	361,343
5,42								41,84		213,756	242,801	1350,852

Po podstawieniu do wzorów otrzymujemy:

a = 9,7135 [m∙s^-2] = g

b = -24,08

Niepewności wynoszą:

δa = δ g = 0,14 [m∙s^-2]

δb = 0,78 [m]

Z równania b = - 4п²lo mżemy obliczyć także lo - długość początkową wahadła.

lo = b / - 4п²

lo = 0,6106 ≈ 0,61 [m]

δ lo = 0,019 [m]

Wartość tablicowa przyspieszenia ziemskiego wynosi g=9,81 [m∙s^-2], więc obliczona wartość g ≈ 9,71 [m∙s^-2] jest porównywalna i mieści się w granicach błędu.

Rozkład Gaussa

Poniższa tabela przedstawia pomiary nieznanego oporu w doświadczeniu dotyczącym mostka Wheatstone'a. Rozkład pomiarów jest rozkładem normalnym (Gaussa), co obrazuje histogram.

Rx2 []	(Rx2 [] - Rx2 ) /σ
28,98	-1,55
32,36	-0,32
32,22	-0,37
33,21	-0,01
33,59	0,12
33,56	0,11
33,73	0,17
33,86	0,22
34	0,27
33,71	0,17
34,03	0,28
34,07	0,30
34	0,27
32,87	-0,14
33,14	-0,04
32,63	-0,23
33	-0,09
33,43	0,07
34,83	0,57
40	2,45
31,5	-0,64
36,67	1,24
34,5	0,45
24	-3,36

Rx_2śr = 33,25

u(Rx₂) = σ = 2,75

Prawdopodobieństwo, z jakim występowały poszczególne wyniki:

- w przedziale (Rx₂ - σ , Rx₂ + σ ) : 83,33 %

- w przedziale (Rx₂ - 2σ , Rx₂ + 2σ ) : 91,66 %

- w przedziale (Rx₂ - 3σ , Rx₂ + 3σ ) : 95,83 %.

---