Autor opracowania: Marek Walesiak

1

PROJEKT B – MODEL NIELINIOWY

Nazwisko i imię studenta 1: ..........................................
Rok i forma studiów studenta 1: ......
Numer grupy lub specjalność studenta 1: .....

Nazwisko i imię studenta 2: ..........................................
Rok i forma studiów studenta 2: ......
Numer grupy lub specjalność studenta 2: .....

Uwagi dla studentów:

1. Program R należy pobrać ze strony: http://cran.r-project.org/
2. Co najmniej jeden projekt (A, B, C) należy przesłać na e-mail prowadzącego laboratoria
3. Projekty można wykonywać osobiście lub w zespołach dwuosobowych (jakość i estetyka wykonania

oraz liczba zrealizowanych projektów będzie decydować o ocenie z laboratorium dla przedmiotu Eko-
nometria)

4. Liczba obserwacji w projekcie A oraz B musi wynosić co najmniej 13 (trzynaście). Dla projektu C

musi być co najmniej pięć cykli. Dla danych statystycznych należy koniecznie podać źródło. Dane
powinny być aktualne

5. Nie wolno w projektach stosować zmiennych użytych w przykładowych projektach prezentowanych

na laboratoriach

6. Wstępnym warunkiem poprawności projektu A i B jest współczynnik determinacji (

Multiple R-

Squared

) nie mniejszy nić 0,50

7. Wraz z każdym projektem opracowanym w edytorze Word (może też być jego odpowiednik z pakietu

OpenOffice) należy przesłać:
a) pliki danych w formacie csv
b) odpowiednie procedury w programie R

8. Termin przesłania projektu (projektów): 03 stycznia 2012 roku
9. Proszę przesyłać projekty z własnych e-maili podając w e-mailu skład zespołu (imię i nazwisko, rok i

forma studiów, numer grupy lub specjalność)

10. Warunkiem przyjęcia projektu (projektów) jest uzyskanie pozytywnej odpowiedzi od prowadzącego

laboratoria

11. Odpowiedzi na e-maile informujące o akceptacji projektu lub projektów będą przesyłane w ciągu

siedmiu dni od ich nadesłania

12. Projekty, które wykonali inni studenci będą odrzucane

Autor opracowania: Marek Walesiak

2

1. Na podstawie danych statystycznych dotyczących zmiennej objaśnianej y i zmiennej objaśniają-

cej x pochodzących z Rocznika Statystycznego sporządzić wykres korelacyjny i metodą oceny
wzrokowej dobrać postać analityczną modelu ekonometrycznego

y – eksport per capita w dolarach USA w wybranych krajach w 1980 r.,
x – udział zatrudnienia w rolnictwie do zatrudnienia ogółem w % w gospodarce narodowej.
Źródło: Rocznik Statystyczny 1982, s. 501 i 552 (zob. Nowak (2002), Zarys metod ekonometrii, PWN,

Warszawa, s. 68).

a) wprowadzić dane statystyczne do programu EXCEL w następującym układzie:

Plik dane_rys5

Plik dane_rys5p

b) zapisać dane w formacie csv na dysku (podać nazwy plików (odpowiednio):

dane_rys5.csv, dane_rys5p.csv)

c) sporządzić wykres korelacyjny dla zmiennych y i x na podstawie danych z pliku np.

dane_rys5.csv (zastosuj w programie R procedurę podaną w pliku Rys_5.r)

Rys. 1. Związek eksportu per capita w dolarach USA
(y) z udziałem zatrudnienia w rolnictwie do zatrudnie-
nia ogółem w % (x) w wybranych krajach w 1980 r.

5

10

15

20

25

30

1000

2000

3000

4000

5000

6000

x

y

Autor opracowania: Marek Walesiak

3

d) na podstawie oceny wzrokowej rys. 1 z punktu c) dobrano do opisu zależności y od x postać potę-

gową:

1

0

ˆ

b

x

b

y





(1)

Transformacja liniowa (w programie R log oznacza logarytm naturalny):

x

b

b

y

log

log

ˆ

log

1

0





Podstawianie:

z

y

ˆ

ˆ

log



,

0

0

log

a

b



,

1

1

a

b





,

v

x



log

v

a

a

z

1

0

ˆ





(2)

2. Wykorzystując w programie R procedurę Estymacja_rys5a.r:

a) oszacować metodą najmniejszych kwadratów parametry strukturalne modelu (2). Zapisać postać

modelu (2) z oszacowanymi parametrami podając w nawiasach pod ocenami estymatorów parame-
trów ich błędy. Podać interpretację parametrów strukturalnych oraz błędów estymatorów parame-
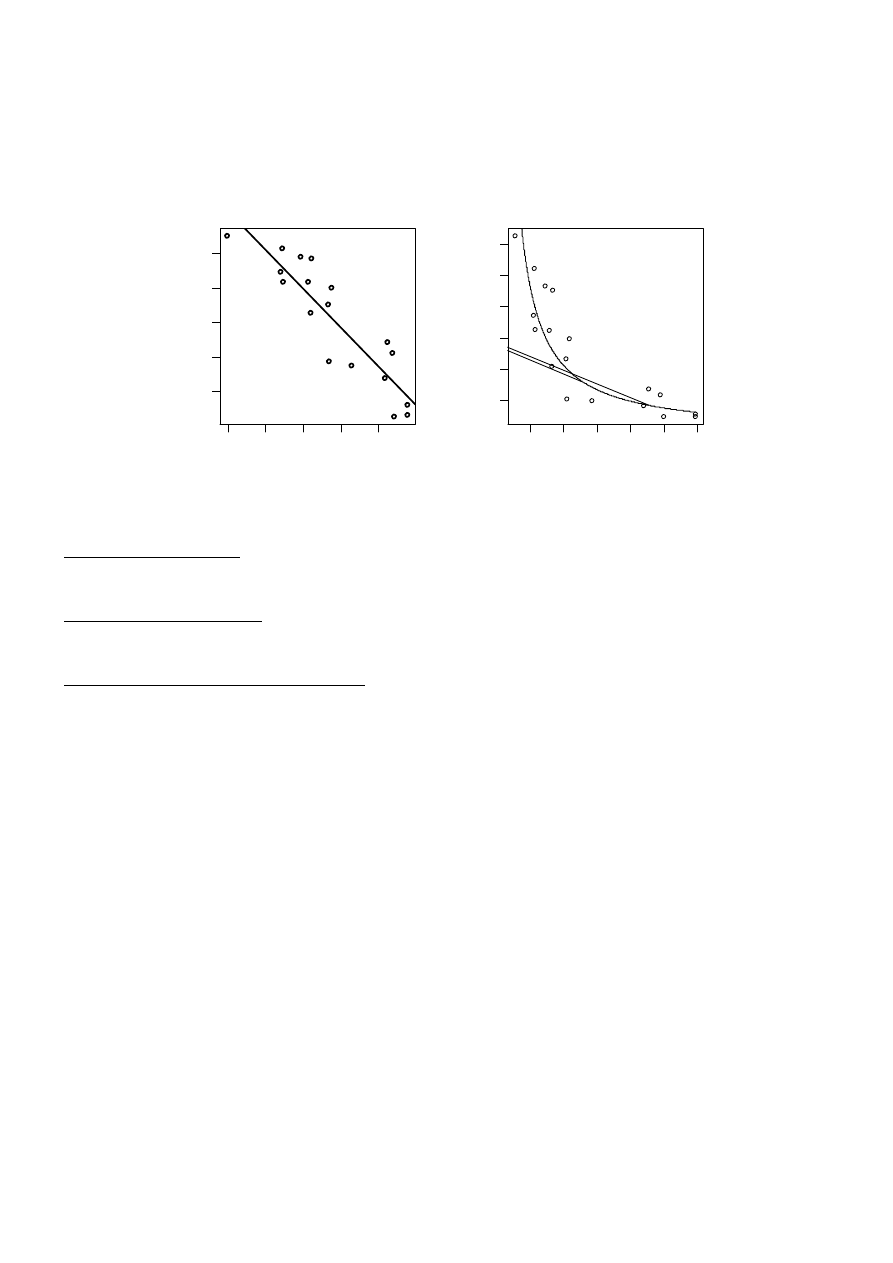
trów strukturalnych dla modelu (2). Zapisać postać modelu (1) z oszacowanymi parametrami.
Przedstawić graficznie obok siebie dopasowane modele (1) i (2) do danych.

b) zinterpretować obliczone parametry struktury stochastycznej dla modelu (2) (standardowy błąd oce-

ny, współczynnik determinacji, skorygowany współczynnik determinacji),

c) wyznaczyć i zinterpretować przedziały ufności dla parametrów strukturalnych dla modelu (2),
d) zbudować tablicę analizy wariancji dla modelu (2),
e) przeprowadzić weryfikację modelu (2) (test Shapiro-Wilka na normalność składnika losowego, te-

sty t i F istotności współczynników regresji),

f) przeprowadzić predykcję oraz zbudować pasma ufności predykcji wewnątrz próby dla modelu po

transformacji liniowej (2) i modelu pierwotnego (1).

ODPOWIEDZI Z WYKORZYSTANIEM obliczeń w programie R

a) oszacować metodą najmniejszych kwadratów parametry strukturalne modelu (2)

Call:
lm(formula = log(y) ~ log(x), data = d, x = TRUE, y = TRUE)

Residuals:
Min 1Q Median 3Q Max
-0,6563 -0,2557 -0,0862 0,3762 0,5555

Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 10,2266 0,3358 30,451 1,36e-15 ***
log(x) -1,1181 0,1337 -8,366 3,09e-07 ***
---
Signif. codes: 0 ‘***’ 0,001 ‘**’ 0,01 ‘*’ 0,05 ‘.’ 0,1 ‘ ’ 1

Residual standard error: 0,3821 on 16 degrees of freedom
Multiple R-Squared: 0.8139, Adjusted R-squared: 0.8023
F-statistic: 69.98 on 1 and 16 DF, p-value: 3,091e-07

a) zapisać postać modelu z oszacowanymi parametrami podając w nawiasach pod ocenami

estymatorów parametrów ich błędy

v

z

)

134

,

0

(

)

336

,

0

(

1181

,

1

2266

,

10

ˆ





(2)

a) podać interpretację parametrów strukturalnych oraz błędów estymatorów parametrów struk-

turalnych dla modelu (2)

1181

,

1

ˆ

1





a

– wzrost (spadek) logarytmu udziału zatrudnienia w rolnictwie do zatrudnienia ogółem w %

w gospodarce narodowej (wartości zmiennej objaśniającej v) o jednostkę spowoduje spadek (wzrost)
logarytmu eksportu per capita w dolarach USA (wartości zmiennej objaśnianej z) średnio o 1,1181
jednostki dla wybranych krajów,

2266

,

10

ˆ

0



a

(wyraz wolny) – nie ma interpretacji.

3358

,

0

)

ˆ

(

0



a

S

– szacując parametr

0

a

, gdybyśmy mogli wiele razy pobrać próbę z tej samej populacji

generalnej, mylimy się średnio in plus i in minus o 0,3358 (

3358

,

0

2266

,

10

0





a

),

Autor opracowania: Marek Walesiak

4

1337

,

0

)

ˆ

(

1



a

S

– szacując parametr

1

a , gdybyśmy mogli wiele razy pobrać próbę z tej samej populacji

generalnej, mylimy się średnio in plus i in minus o 0,1337 (

1337

,

0

1181

,

1

1







a

).

a) zapisać postać modelu (1) z oszacowanymi parametrami.

exp(10.2266)= 27628,41

1181

,

1

41

,

27628

ˆ





x

y

(1)

a) przedstawić graficznie obok siebie dopasowane modele (1) i (2) do danych

1,0

1,5

2,0

2,5

3,0

6

,5

7

,0

7

,5

8

,0

8

,5

log(x)

lo

g

(y)

5

10

15

20

25

30

1000

3000

5000

x

y

b) zinterpretować obliczone parametry struktury stochastycznej dla modelu (2) (standardowy

błąd oceny, współczynnik determinacji, skorygowany współczynnik determinacji)

standardowy błąd oceny (Residual standard error: 0,3821) – wartości empiryczne logaryt-

mu zmiennej objaśnianej (eksport per capita w dolarach USA w wybranych krajach) odchylają się od
wartości teoretycznych przeciętnie o 0,3821.

współczynnik determinacji (Multiple R-Squared: 0.8139) – 81,39% zmienności logarytmu

zmiennej objaśnianej (eksport per capita w dolarach USA w wybranych krajach) zostało wyjaśnionych
przez zbudowany model (2).

skorygowany współczynnik determinacji (Adjusted R-squared: 0.8023) – 80,23% wariancji

logarytmu zmiennej objaśnianej (eksport per capita w dolarach USA w wybranych krajach) zostało wy-
jaśnionych przez zbudowany model (2).

c) wyznaczyć i zinterpretować przedziały ufności dla parametrów strukturalnych dla modelu (2)

[1] Przedziały ufności dla parametrów
5 % 95 %
(Intercept) 9,640247 10,812927
log(x) -1,351463 -0,884768

Z prawdopodobieństwem 0,90 przedział





812927

,

10

640247

,

9

;

pokryje nieznaną wartość parametru

0

a z modelu (2).

Z prawdopodobieństwem 0,90 przedział





884768

,

0

351463

,

1





;

pokryje nieznaną wartość parametru

1

a z modelu (2).

Węższe (szersze) przedziały ufności można uzyskać poprzez zmniejszenie (zwiększenie) poziomu uf-

ności.

d) zbudować tablicę analizy wariancji dla modelu (2),

[1] Analiza wariancji
Analysis of Variance Table
Response: log(y)
Df Sum Sq Mean Sq F value Pr(>F)
log(x) 1 10,2155 10,2155 69,984 3,091e-07 ***
Residuals 16 2,3355 0,1460
---
Signif. codes: 0 ‘***’ 0,001 ‘**’ 0,01 ‘*’ 0,05 ‘.’ 0,1 ‘ ’ 1

Autor opracowania: Marek Walesiak

5

e) przeprowadzić weryfikację modelu (2) (test Shapiro-Wilka)

[1] Test Shapiro-Wilka na normalność składnika losowego
Shapiro-Wilk normality test
data: model$residuals
W = 0,9449, p-value = 0,3513

Z uwagi na to, że

0,3513

value









p

10

,

0



nie ma podstaw do odrzucenia hipotezy o normalności

rozkładu składnika losowego.

e) przeprowadzić weryfikację modelu (2) (testy t i F istotności współczynników regresji),

Test t
t value Pr(>|t|)
30,451 1,36e-15
-8,366 3,09e-07

Z uwagi na to, że dla

0

a

15

36

,

1

10

,

0







e



hipotezę zerową odrzucamy. Oznacza to, że parametr

0

a

istotnie różni się od zera.

Z uwagi na to, że dla

1

a

07

09

,

3

10

,

0







e



hipotezę zerową odrzucamy. Oznacza to, że parametr

1

a istotnie różni się od zera. Zmienna objaśniająca v ma istotny wpływ na zmienną objaśnianą z.

Test F
F-statistic: 69.98 on 1 and 16 DF, p-value: 3,091e-07

Z uwagi na to, że

07

091

,

3

10

,

0







e



hipotezę zerową należy odrzucić. Oznacza to, że parametr

1

a

istotnie różni się od zera. Zmienna objaśniająca v ma istotny wpływ na zmienną objaśnianą z.

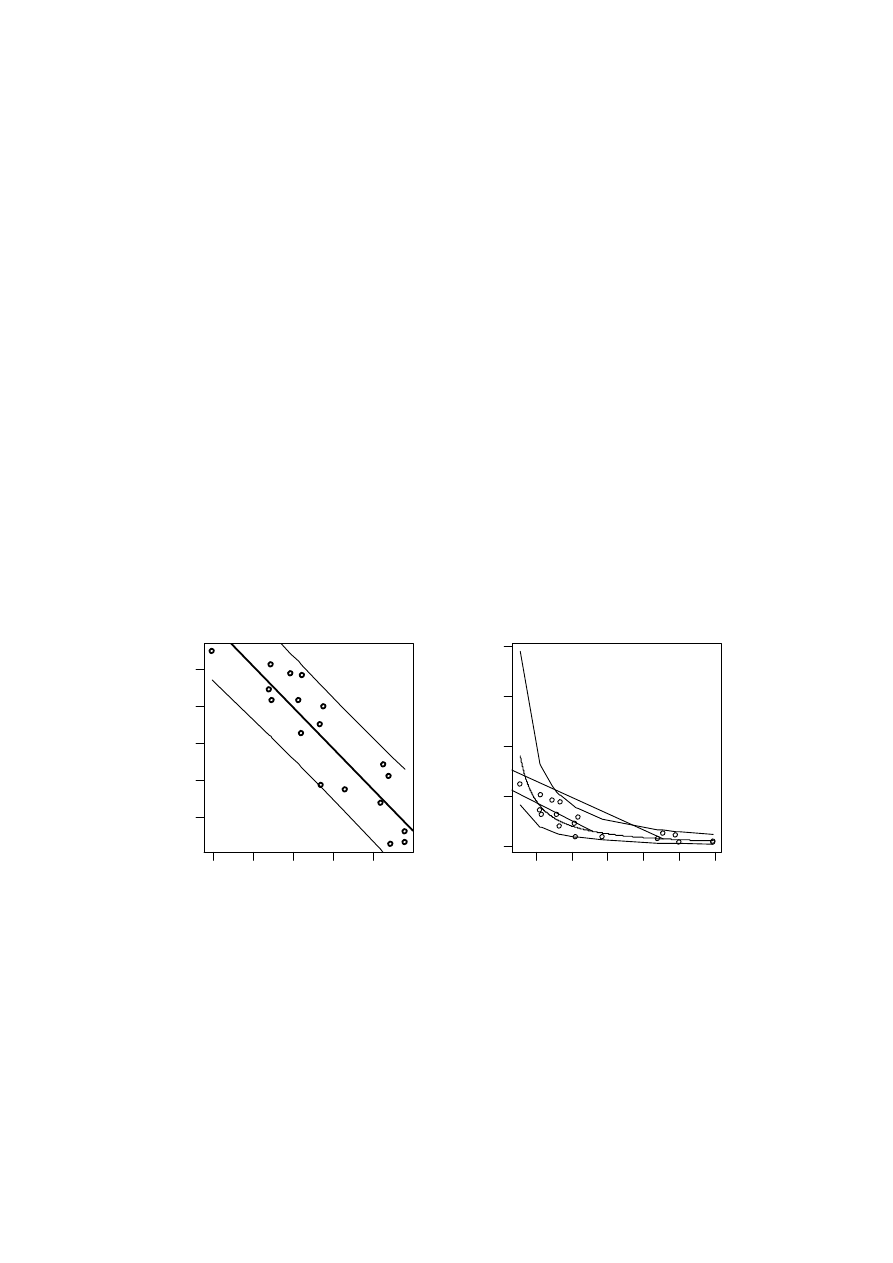
f) przeprowadzić predykcję oraz zbudować pasma ufności predykcji wewnątrz próby dla mode-

lu po transformacji liniowej (2) i modelu pierwotnego (1).

[1] Predykcja w modelu regresji prostej - dla modelu po transformacji linio-
wej

fit lwr upr
Austria 7,608177 6,922620 8,293735
Belgia 9,116017 8,354044 9,877989
Bułgaria 6,650101 5,941155 7,359047
Czechosłowacja 7,259956 6,572501 7,947410
Dania 7,915596 7,225329 8,605862
Finlandia 7,565979 6,880602 8,251357
Francja 7,873922 7,184642 8,563202
Holandia 8,300335 7,595938 9,004732
Norwegia 7,597478 6,911977 8,282979
NRD 7,860369 7,171386 8,549351
Polska 6,431134 5,709134 7,153134
Portugalia 6,627512 5,917344 7,337679
RFN 8,280545 7,577092 8,983998
Rumunia 6,431134 5,709134 7,153134
Szwajcaria 8,019336 7,326147 8,712526
Szwecja 8,320482 7,615101 9,025862
Węgry 6,770444 6,067510 7,473378
Włochy 6,730507 6,025672 7,435343
fit

– prognoza zmiennej z w próbie

lwr – dolna wartość przedziału ufności dla prognozy
upr – górna wartość przedziału ufności dla prognozy

[1] Błąd średni predykcji

SE
Austria 0,3926706
Belgia 0,4364395
Bułgaria 0,4060671
Czechosłowacja 0,3937573
Dania 0,3953679
Finlandia 0,3925675
Francja 0,3948029
Holandia 0,4034614
Norwegia 0,3926383
NRD 0,3946326

Autor opracowania: Marek Walesiak

6

Polska 0,4135441
Portugalia 0,4067669
RFN 0,4029210
Rumunia 0,4135441
Szwajcaria 0,3970422
Szwecja 0,4040250
Węgry 0,4026237
Włochy 0,4037129

[1] Wartość statystyki t
[1] 1,745884

[1] Predykcja w modelu regresji prostej - model pierwotny

fit lwr upr
Austria 2014,6031 1014,9760 3998,740
Belgia 9099,8835 4247,3234 19496,485
Bułgaria 772,8622 380,3739 1570,339
Czechosłowacja 1422,1937 715,1565 2828,241
Dania 2739,6778 1373,7909 5463,593
Finlandia 1931,3595 973,2123 3832,822
Francja 2627,8515 1319,0168 5235,418
Holandia 4025,2203 1990,0963 8141,515
Norwegia 1993,1623 1004,2305 3955,960
NRD 2592,4763 1301,6477 5163,404
Polska 620,8778 301,6098 1278,105
Portugalia 755,5997 371,4239 1537,141
RFN 3946,3436 1952,9407 7974,450
Rumunia 620,8778 301,6098 1278,105
Szwajcaria 3039,1596 1519,5155 6078,577
Szwecja 4107,1379 2028,5997 8315,382
Węgry 871,6991 431,6047 1760,545
Włochy 837,5721 413,9195 1694,839

[1] Pasma ufności predykcji

1,0

1,5

2,0

2,5

3,0

6

,5

7

,0

7

,5

8

,0

8

,5

log(x)

lo

g

(y)

5

10

15

20

25

30

0

5000

10000

20000

x

y

Rys. 2. Pasma ufności predykcji dla modelu po transformacji liniowej (2) oraz dla modelu pierwotnego (1)