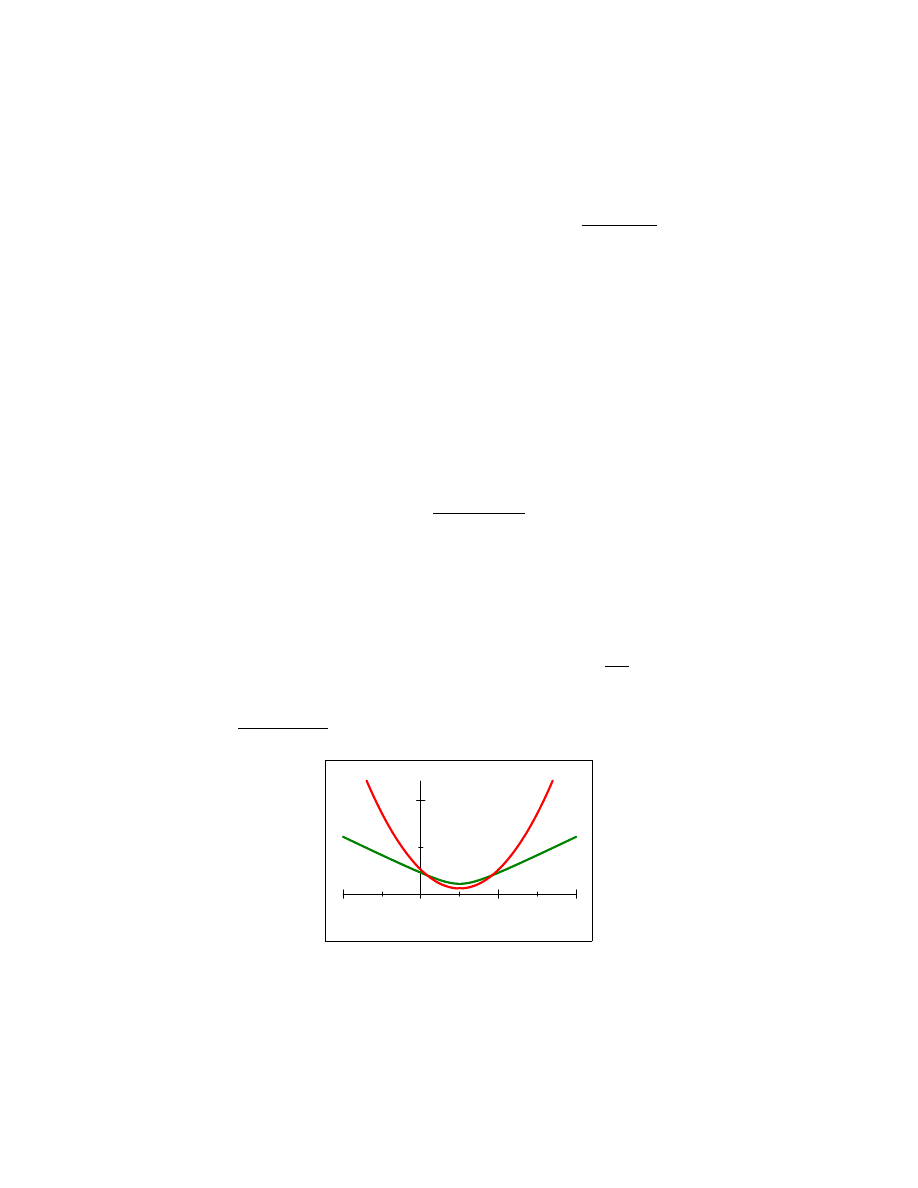
WIT

, Egzamin z Podstaw Matematyki, 20 czerwca 2012

r.

Zadanie 1

.

Okre´slamy funkcj ¾

e wzorem f (x) =

p

x

2

2x + a.

Podaj

warunki konieczne i podaj warunki dostateczne na to, by zbiorem argumen-
tów tej funkcji by÷ca÷

y zbiór liczb rzeczywistych /

R i by jednocze´snie zbiorem

warto´sci by÷zbiór liczb nieujemnych /

R

+

?

Komentarz i rozwi ¾

azanie. Celem zadania by÷

o sprawdzenie rozumienia po-

j ¾

e´c "warunek konieczny" i "warunek dostateczny". Zanim zaczniemy nawet

zastanawia´c si ¾

e nad zadaniem, nale·

zy zastanowi´c si ¾

e, kiedy wyra·

zenie pod pier-

wiastkiem jest nieujemne. Ze szkolnych wiadomo´sci o funkcjach kwadratowych
mamy, ·

ze zachodzi to, gdy wyró·

znik ("delta") tej funkcji kwadratowej jest niedo-

datni (to jest ujemny lub równy zero) - je·

zeli bowiem by÷

by dodatni, to istnia÷

yby

dwa pierwiastki - mi ¾

edzy nimi warto´sc fukcji by÷

aby ujemna. Wyró·

znik ten to

2

2

4a: Jest on niedodatni, gdy a

1:To jest warunek konieczny i dostate-

czny na to, by zbiorem argumentów funkcji f by÷ca÷

y zbiór R: Takie zadanie

omowi÷

em na ostatnim wyk÷

adzie i by÷

o w zestawie zada´n przygotowawczych.

Co z drug ¾

a cze´sci ¾

a zadania? Pozosta´nmy dalej przy analizie funkcji widocznej

pod pierwiastkiem. Spójrz na wykres funkcji g(x) = (x 1)

2

+0; 3 = x

2

2x+1;

3 oraz na wykres funkcji h(x) =

p

x

2

2x + 1; 3: Je·

zeli parabola y = g(x) nie

jest styczna do osi x; to i wykres funkcji h(x) "nie dotyka" osi. Funkcja nie
przekszta÷

ca wtedy ca÷

ej prostej na wszystkie liczby nieujemne.

A zatem warunkiem koniecznym i dostatecznym na to, by zbiorem argumen-

tów tej funkcji by÷ca÷

y zbiór liczb rzeczywistych /

R i by jednocze´snie zbiorem

warto´sci by÷zbiór liczb nieujemnych /

R

+

jest, by parabola by÷

a styczna do osi

x: Jest to zatem warunek a = 1:

Reszta jest ... prosta jak drut. We´zmy np. warunek a

1: Czy jest on

dostateczny? No, nie, bo je·

zeli a

1, to mo·

ze by´c np. a =

17

2012

, a dla takiej

liczby teza zadania nie jest prawdziwa. Ale ten warunek jest konieczny!!! Bo
przecie·

z: a = 1 ) a

1:

p

(x

1)

2

+ 0:3

-2

0

2

4

5

x

y

Zadanie 2

. Podane s ¾

a dwie formu÷

y rachunku zbiorów:

(A[B) n (B\C) = (A n B)[(B n C); A\(B[C) = (A[B)\(A[C)

Jedna z nich jest prawdziwa, druga nie.

1

2.1. Udowodnij prawdziw ¾

a równo´s´c metod ¾

a funkcji charakterystycznych.

2.2. Dla fa÷

szywej podaj kontrprzyk÷

ad zachodz ¾

acy dla podzbiorów zbioru

{1,2,3,4}.

Rozwi ¾

azanie i komentarz. Powinni´smy pami ¾

eta´c regu÷

e rozdzielno´sci mno·

ze-

nia wzgl ¾

edem dodawania: A \ (B [ C) = (A \ B) [ (A \ C): Formu÷a w zadaniu

wygl ¾

ada inaczej: A \ (B [ C) = (A [ B) \ (A [ C) ;"powinna" by´c zatem

fa÷

szywa. To oczywi´scie nie jest powód, ale tylko poszlaka. Na szcz ¾

e´scie prawie

ka·

zdy wybór podzbiorów ze zbioru liczb {1,2,3} czy {1,2,3,4} to potwierdzi.

Pierwsza formu÷

a jest rzeczywi´scie prawdziwa. Dowód jest bardzo prosty -

tak prosty, ·

ze nie b ¾

ed ¾

e go przytacza´c.

Zadanie 3

. Opisz klasy równowa·

zno´sci permutacji czterech liczb przy relacji

s

1

s

2

gdy s

1

i s

2

maj ¾

a ten sam typ rozk÷

adu na cykle, to znaczy ka·

zda z

nich ma tyle samo cykli jedno-, dwu-, trój- , i czteroelementowych. Przyk÷

ad:

permutacja {2,3,4,1} ma jeden cykl czteroelementowy.

Dla u÷

atwienia masz tu wypisane wszystkie permutacje czterech elementów

f1; 2; 3; 4g; f1; 2; 4; 3g; f1; 3; 2; 4g; f1; 3; 4; 2g; f1; 4; 2; 3g; f1; 4; 3; 2g;
f2; 1; 3; 4g; f2; 1; 4; 3g; f2; 3; 1; 4g; f2; 3; 4; 1g; f2; 4; 1; 3g; f2; 4; 3; 1g;
f3; 1; 2; 4g; f3; 1; 4; 2g; f3; 2; 1; 4g; f3; 2; 4; 1g; f3; 4; 1; 2g; f3; 4; 2; 1g;
f4; 1; 2; 3g; f4; 1; 3; 2g; f4; 2; 1; 3g; f4; 2; 3; 1g; f4; 3; 1; 2g; f4; 3; 2; 1g

Rozwi ¾

azanie i komentarz. Zadanie nadzwyczaj ÷

atwe dla kogo´s, kto chocby

jako-tako wie, o co chodzi. Troch ¾

e ·

zmudne.

{{{1}, {2}, {3}, {4}}

- tu mamy cztery cykle jednoelementowe, typ

1; 1; 1; 1.

{{1}, {2}, {4, 3}} - tu mamy dwa cykle jednoelementowe, jeden dwu-. typ

1; 1; 2

{{1}, {3, 2}, {4}}

i tak dalej,

typ 1; 1; 2

{{1}, {3, 4, 2}},

typ 1; 3

{{1}, {4, 3, 2}},

typ 1; 3

{{1}, {4, 2}, {3}},

typ 1; 1; 2

{{2, 1}, {3}, {4}}, typ

1; 1; 2

{{2, 1}, {4, 3}},

typ

2; 2

{{2, 3, 1}, {4}}, typ

1; 3

{{2, 3, 4, 1}},

typ 4

{{2, 4, 3, 1}},

typ

4

{{2, 4, 1}, {3}}, typ

1; 3

{{3, 2, 1}, {4}},

typ 1; 3

{{3, 4, 2, 1}},

typ

4

{{3, 1}, {2}, {4}}, typ 1; 1; 2
{{3, 4, 1}, {2}},

typ 1; 3

{{3, 1}, {4, 2}},

typ 2; 2

{{3, 2, 4, 1}},

typ

4

{{4, 3, 2, 1}},

typ

4

{{4, 2, 1}, {3}},

typ

1; 3

2

{{4, 3, 1}, {2}},

typ

1; 3

{{4, 1}, {2}, {3}}, typ 1; 1; 2
{{4, 2, 3, 1}},

typ

4

{{4, 1}, {3, 2}}}

typ

2; 2

Mamy zatem nastepuj ¾

ace typy (=klasy równowa·

zno´sci) :

{1,1,1,1}, {1,1,2}, {1,3}, {2,2}, {4}

Ich liczebno´sci to odpowiednio: 1; 6; 8; 3; 6:
Przypomn ¾

e, co to jest rozk÷

ad permutacji na cykle. Najlepiej to zrozumie´c na

przyk÷

adzie permutacji o´smiu liczb:

1

2

3

4

5

6

7

8

5

1

8

4

2

3

6

7

: Rozk÷

ada

si ¾

e ona na trzy cykle (1,5,2), (3,8,7,6) oraz (4).

Zadanie 4

.1.

Podaj przyk÷

ad funkcji odwzorowuj ¾

acej zbiór wszystkich

podzbiorów zbioru {1,2,3,4,5} na zbiór dwuelementowych podzbiorów zbioru
{1,2,3,4}. Je·

zeli uwa·

zasz, ·

ze takiej funkcji nie ma, to napisz, dlaczego.

Zadanie 4.2.

Podaj przyk÷

ad funkcji ró·

znowarto´sciowej, odwzorowuj ¾

acej

zbiór wszystkich podzbiorów zbioru {1,2,3,4,5} na zbiór podzbiorów zbioru
{1,2,3,4}. Je·

zeli uwa·

zasz, ·

ze takiej funkcji nie ma, to napisz, dlaczego.

Rozwi ¾

azanie i komentarz. Zadanie tak proste, ·

ze a·

z wstyd. Nale·

za÷

o je tylko

odpowiednio przeczyta´c. Tu (w zadaniu 4.1) nie chodzi o funkcje ze zbioru
{1,2,3,4,5} w zbiór {1,2,3,4}. Tu chodzi o funkcje ze zbioru podzbiorów w zbiór
podzbiorów!!! Ka·

zdemu zbiorowi liczb mi ¾

edzy jeden a pi ¾

e´c nale·

zy przyporz ¾

ad-

kowac dwie liczby!!!! Mo·

zna to zrobi´c na bardzo wiele sposobów, a bodaj·

ze

najprostszy to taki: je·

zeli podzbiór A

f1; 2; 3; 4; 5g ma co najmniej dwa ele-

menty, to przyporz ¾

adkujmy mu dwa najmniejsze, np. f2; 3; 4g > f2; 3g. Je·

zeli

A jest zbiorem o jednym elemencie, albo zbiorem pustym, to przyporz ¾

adkujmy

podzbiór f1; 2g:

Komentarz do 4.2. Zbiór podzbiorów zbioru {1,2,3,4,5} ma 32 elementy, a

zbiór podzbiorów zbioru {1,2,3,4} ma 16 elementów. Nie mo·

ze istnie´c stosowna

funkcja ró·

znowarto´sciowa!!!!!!

3

Zadanie 5

. Okre´slamy relacj ¾

e mi ¾

edzy parami liczb ca÷

kowitych x; y, obie z

przedzia÷

u [ 3; 3] tak:

p

n q; gdy albo p = q albo 0 6= max(p q) 2 q.

Warunek ten rozumiemy jako warunek podwójny: maksimum ró·

znicy sym-

etrycznej nie jest równe 0 i nale·

zy do drugiej pary. Przyk÷

adowo, f 3; 3g n

f 2; 3g, poniewa·

z wi ¾

eksza z liczb

3;

2 pochodzi z drugiej pary.

5.1. Wyznacz elementy maksymalne, mimimalne, najwi ¾

ekszy, najmniejszy

(je´sli s ¾

a).

5.2. Podaj przyk÷

ad maksymalnego ÷

a´ncucha i maksymalnego anty÷

a´ncucha.

5.3. Czy istnieje kres dolny zbioru wszystkich par fx; yg , x

1;

y

1 ?

5.4. Wykorzystuj ¾

ac kwadrat 7 na 7 (np. na kratkowanym papierze, albo ten

obok), zilustruj ten porz ¾

adek gra…cznie.

Komentarz do zadania 5. By÷

o ono trudne. Mozna jednak by÷

o zdoby´c wiele

punktów, czyni ¾

ac kilka ÷

atwych obserwacji. Rozpatrzmy najpierw, co si ¾

e dzieje

dla par z÷

o·

zonych z liczb dodatnich. Wtedy (prawie) nie przeszkadza warunek

max(p; q) = 0:Omówione to by÷

o dok÷

adnie na wyk÷

adzie przed egzaminem. A

zatem mamy w tej cz ¾

e´sci porzadek widoczny na rysunku. Uwaga. Nie ma

relacji mi ¾

edzy 01, 10 mi ¾

edzy 21 i 12 i tak dalej. Podobny porz ¾

adek "panuje"

i w pozosta÷

ych trzech cz ¾

e´sciach. Inaczej dzieje sie z parami zawieraj ¾

acymi

zero. Na przyk÷

ad (0; 0) jest nieporównywalne z ka·

zdym z elementów (i,j), gdzie

i < 0; j < 0:

A zatem na przyk÷

ad (3; 3) jest najwi ¾

ekszy! Niestety, ( 3;

3) nie jest na-

jmniejszy, nie da sie bowiem porównac z (0,0). Jest minimalny, bo mniejszego

4

nie ma. Elementy minimalne sa zaznaczone kó÷

kiem. Tworz ¾

a one maksymalny

anty÷

a´ncuch (·

zadne dwa elementy nie daj ¾

a si ¾

e porówna´c). Zbiór par o wyrazach

nieujemnych ma najwi ¾

eksze ograniczenie dolne (kres dolny), {0,0}, za´s zbiór

par o wyrazach co najmniej 1 ma krs dolny {1,1}. Maksymalny ÷

a´ncuch - to

najd÷

u·

zsza droga od {3,3} do {-3,3}. Na wyk÷

adzie by÷

o jeszcze twierdzenie Dil-

wortha o tym, ·

ze minimalna liczba ÷

a´ncuchów pokrywaj ¾

acych zbiór jest równa

d÷

ugo´sci najwi ¾

ekszego anty÷

a´ncucha. Prosz ¾

e i to powtórzy´c.

5