1
1. Geometria komina
1.1.
Dane wyjściowe
Wysokość od poziomu ±0,00
120,0 m
Głębokość posadowienia
- 3,0 m
Średnica wylotu przewodu
zaprojektować
Średnica zewnętrzna górna
6,26 m
Średnica zewnętrzna dolna
10,42 m
Rodzaj materiału przewodu wewnętrznego
cegła klinkierowa
Rodzaj materiału izolacji
wełna żużlowa
Konstrukcja przewodu
na wspornikach żelbetowych
Sposób posadowienia
bezpośredni
Rodzaj fundamentu
płyta kołowa ∅ 26,0 m
Wyposażenie dodatkowe
–
Lokalizacja
Jaworzno
Temperatura spalin
o Eksploatacyjna
170°𝐶
o Awaryjna
210°𝐶
Wymiary otworów wlotowych dla czopuchów
4,0 x 8,8 m
Otwory dla czopuchów umieszczone na poziomie 9,4 m
Przyjęto charakterystyki materiałowe
Beton w płaszczu nośnym
C 25/30
Beton w fundamencie
C 20/25
Stal zbrojeniowa
A-I
Wełna żużlowa
𝛾 = 1,5 𝑘𝑁 𝑚
3
Cegła czerwona zwykła
𝛾 = 19 𝑘𝑁 𝑚
3
2
1.2.
Wymiary geometryczne – rysunki i tablica 1
1.2.1. Schemat komina wraz z przyjętą numeracją segmentów
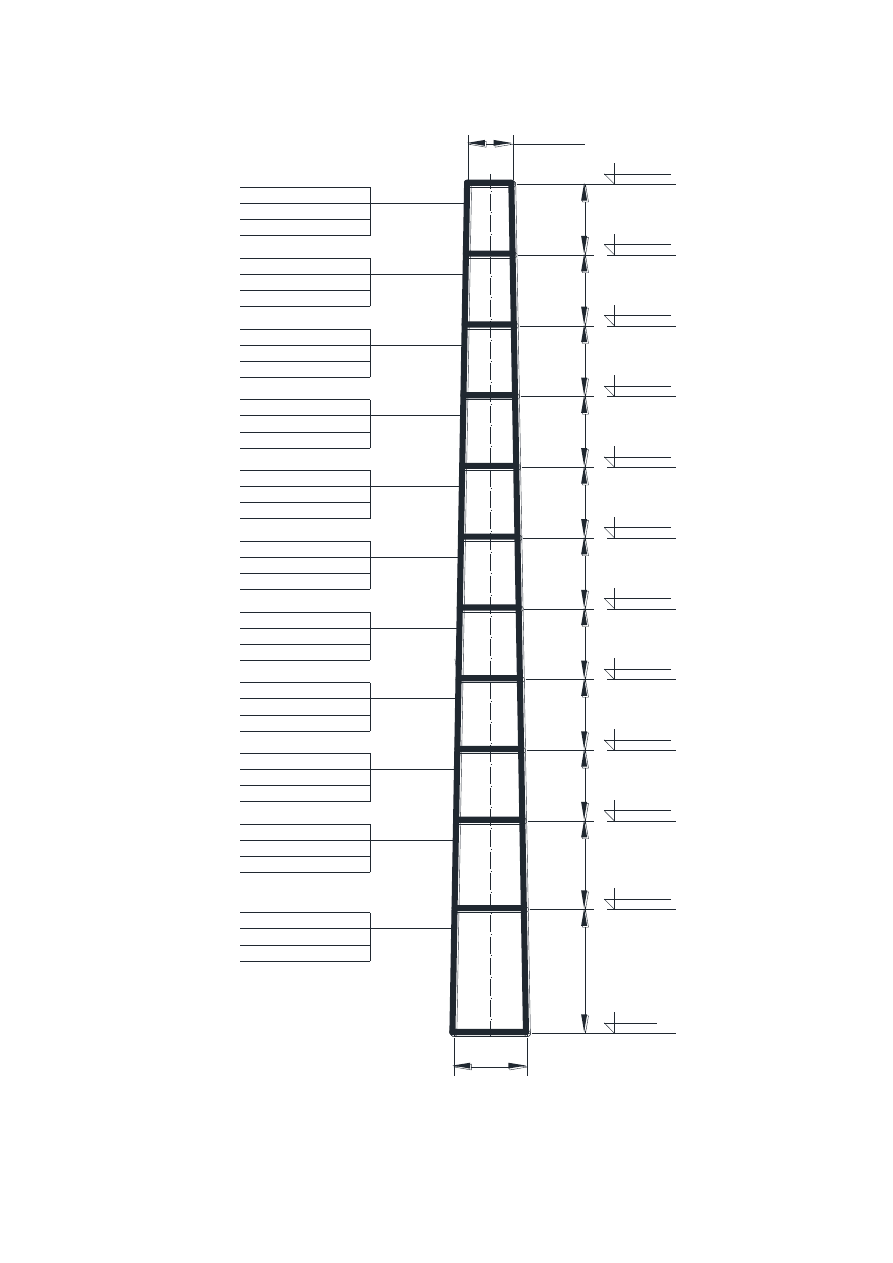
3
I
II
III
IV
V
VI
VII
VIII
IX
X
XI
17
,5
12
,5
10
10
10
10
10
10
10
10
10
6,26
10,42
+120,00
±0,00
płaszcz żelbetowy 20 cm
wełna żużlowa 8 cm
cegła klinkierowa 12 cm
1,7
%
+110,00
+100,00
+90,00
+80,00
+70,00
+60,00
+50,00
+40,00
+30,00
+17,50
płaszcz żelbetowy 22 cm
wełna żużlowa 8 cm
cegła klinkierowa 12 cm
płaszcz żelbetowy 24 cm
wełna żużlowa 8 cm
cegła klinkierowa 12 cm
płaszcz żelbetowy 26 cm
wełna żużlowa 8 cm
cegła klinkierowa 12 cm
płaszcz żelbetowy 28 cm
wełna żużlowa 8 cm
cegła klinkierowa 12 cm
płaszcz żelbetowy 30 cm
wełna żużlowa 8 cm
cegła klinkierowa 12 cm
płaszcz żelbetowy 32 cm
wełna żużlowa 8 cm
cegła klinkierowa 12 cm
płaszcz żelbetowy 34 cm
wełna żużlowa 8 cm
cegła klinkierowa 12 cm
płaszcz żelbetowy 36 cm
wełna żużlowa 8 cm
cegła klinkierowa 12 cm
płaszcz żelbetowy 38 cm
wełna żużlowa 8 cm
cegła klinkierowa 12 cm
płaszcz żelbetowy 40 cm
wełna żużlowa 8 cm
cegła klinkierowa 12 cm
1.2.2. Wymiary geometryczne komina
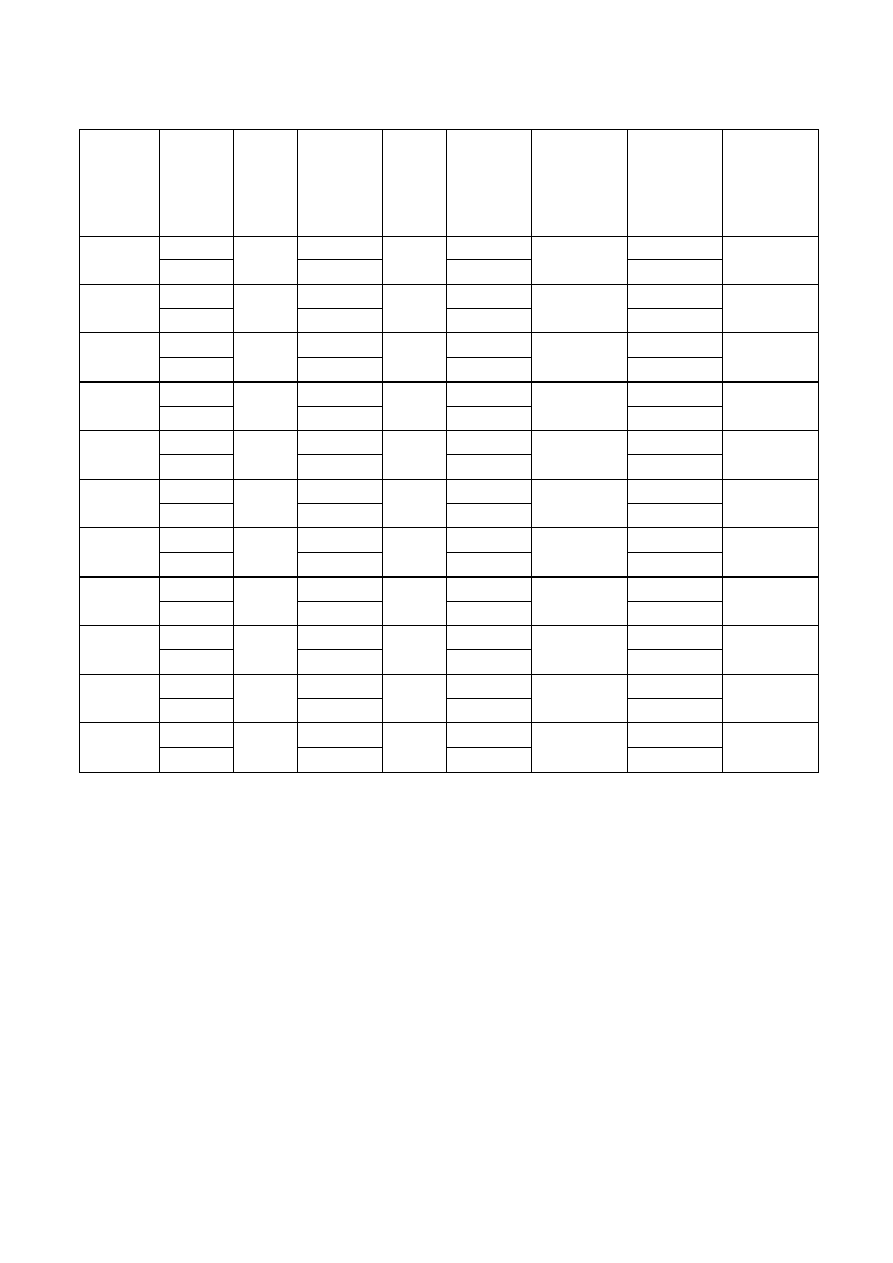
4
Tabela 1 Wymiary geometryczne komina
Nr
segmen
tu
Poziom
przekr
oju [m]
Grubo
ść
trzon
u [cm]
Średnica
zewnętr
zna
trzonu
[m]
Grubo
ść
izolac
ji [cm]
Średnica
zewnętr
zna
izolacji
[m]
Grubość
wymurów
ki [cm]
Średnica
zewnętrz
na
wymurów
ki [m]
Powierzc
hnia
odniesien
ia A
i
[m
2
]
I
120
20
6,26
8
5,86
12
5,7
110
6,61
6,21
6,05
II
110
22
6,61
8
6,17
12
6,01
100
6,95
6,51
6,35
III
100
24
6,95
8
6,47
12
6,31
90
7,3
6,82
6,66
IV
90
26
7,3
8
6,78
12
6,62
80
7,65
7,13
6,97
V
80
28
7,65
8
7,09
12
6,93
70
7,99
7,43
7,27
VI
70
30
7,99
8
7,39
12
7,23
60
8,34
7,74
7,58
VII
60
32
8,34
8
7,7
12
7,54
50
8,69
8,05
7,89
VIII
50
34
8,69
8
8,01
12
7,85
40
9,03
8,35
8,19
IX
40
36
9,03
8
8,31
12
8,15
30
9,38
8,66
8,5
X
30
38
9,38
8
8,62
12
8,46
17,5
9,81
9,05
8,89
XI
17,5
40
9,81
8
9,01
12
8,85
0
10,42
9,62
9,46
5
1.3.
Obliczenia termiczne
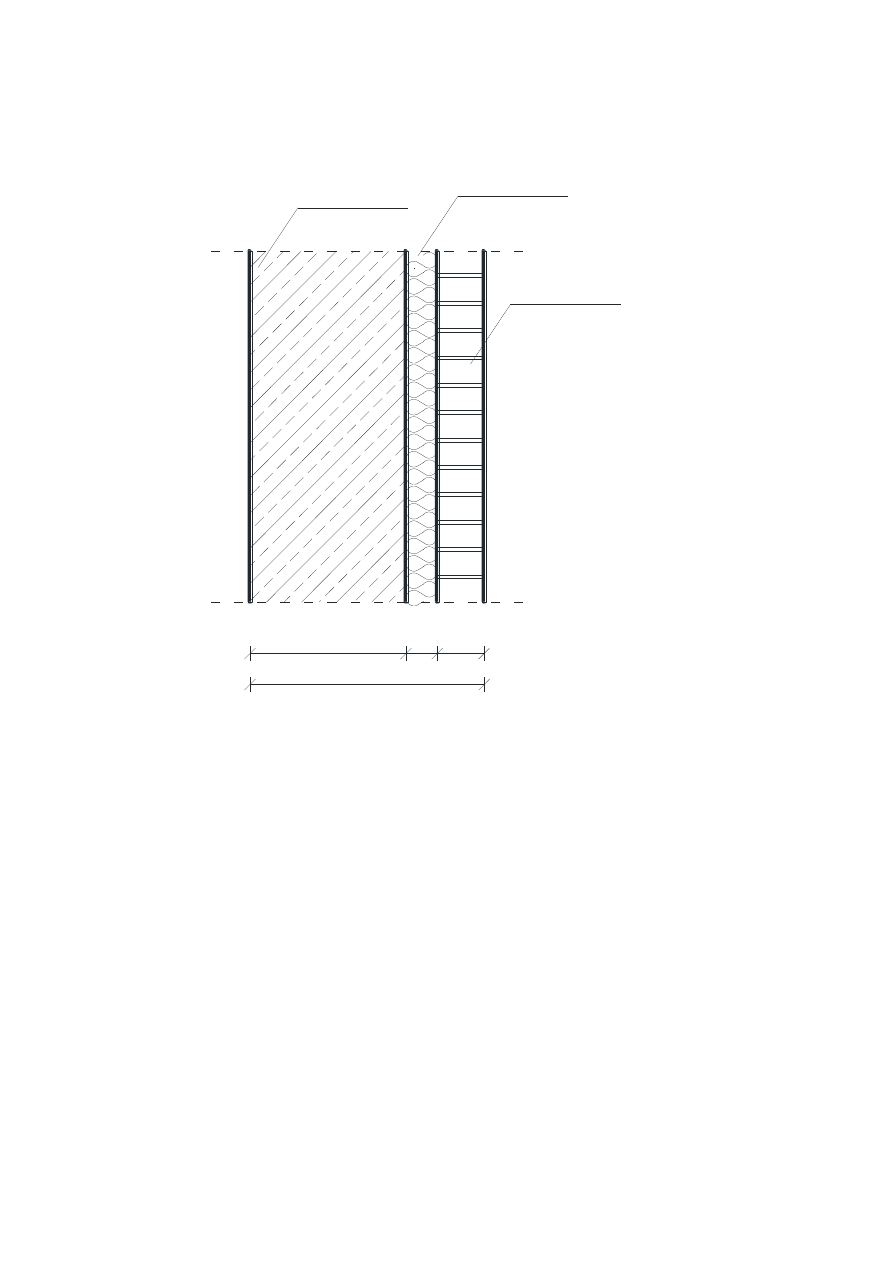
Schemat przegrody wraz z danymi materiałowymi
d
1
d
2
d
3
d
trzon
żelbetowy
izolacja
termiczna
wymurówka
Wartości współczynników przewodności cieplnej
o Trzon żelbetowy
𝜆 = 1,68 [𝑊 𝑚 ∙ 𝐾 ]
o Wełna żużlowa biała
𝜆 = 0,058 [𝑊 𝑚 ∙ 𝐾
]
o Cegła klinkierowa
𝜆 = 1,15 [𝑊 (𝑚 ∙ 𝐾)
]
1.3.1. Wyznaczenie spadku temperatury w ścianie komina przy
temperaturze zewnętrznej +35⁰C
o Prędkość spalin
𝑣
𝑠
= 6 [𝑚/𝑠]
o Współczynnik napływu ciepła
𝛼
𝑛
= 8 + 𝑣
𝑠
= 8 + 6 = 14 [𝑊 (𝑚
2
𝐾)
]
o Współczynnik odpływu ciepła
𝛼
𝑜
= 8 [𝑊 (𝑚
2
𝐾)
]
o Promień zewnętrzny trzonu
𝑟
3
= 𝑅 = 5,21 𝑚
o Promień zewnętrzny izolacji
𝑟
2
= 4,81 𝑚
o Promień zewnętrzny wymurówki
𝑟
1
= 4,73 𝑚
6
o Współczynniki poprawkowe
𝜿
𝒊
=
𝑹
𝒓
𝒊
𝟎,𝟒𝟕
𝜅
1
=
𝑅
𝑟
1
0,47
=
5,21
4,73
0,47
= 1,046
𝜅
2
=
𝑅
𝑟
2
0,47
=
5,21
4,81
0,47
= 1,038
𝜅
3
=
𝑅
𝑟
3
0,47
=
5,21
5,21
0,47
= 1,0
o Współczynnik przenikania ciepła „k” przez warstwową przegrodę cylindryczną
𝟏
𝒌
=
𝟏
𝜶
𝒏
+
𝒅
𝒊
𝝀
𝒊
∙ 𝜿
𝒊
∙
𝑹
𝒓
𝒊
𝒏
𝒊=𝟏
+
𝟏
𝜶
𝒐
1
𝑘
=
1
14
+
0,12
1,15
∙ 1,046 ∙
5,21
4,73
+
0,08
0,058
∙ 1,038 ∙
5,21
4,81
+
0,4
1,68
∙ 1,0 ∙
5,21
5,21
+
1
8
= 2,106
𝑘 =
1
2,13
= 0,475 [𝑊 (𝑚
2
𝐾)
]
o Różnica temperatury
∆𝑇 = 210 − 35 = 175 [𝐾]
o Spadki temperatury w poszczególnych warstwach przegrody
∆𝑻
𝒊
= 𝒌 ∙
𝒅
𝒊
𝝀
𝒊
∙ 𝛋
𝐢
∙
𝐑
𝐫
𝐢
∙ ∆𝐓
∆𝑇
1
= 0,475 ∙
0,12
1,15
∙ 1,046 ∙
5,21
4,73
∙ 175 = 9,99 [𝐾]
∆𝑇
2
= 0,475 ∙
0,08
0,058
∙ 1,038 ∙
5,21
4,81
∙ 175 = 128,90 [𝐾]
∆𝑇
3
= 0,475 ∙
0,4
1,68
∙ 1,0 ∙
5,21
5,21
∙ 175 = 19,78 [𝐾]
7
∆𝑻
𝒏
= 𝒌 ∙
𝟏
𝜶
𝒏
∙ ∆𝑻
∆𝑇
𝑛
= 0,475 ∙
1
14
∙ 175 = 5,94 [𝐾]
∆𝑻
𝒐
= 𝒌 ∙
𝟏
𝜶
𝒐
∙ ∆𝑻
∆𝑇
𝑜
= 0,475 ∙
1
8
∙ 175 = 10,39 [𝐾]
o Sprawdzenie
∆𝑇
𝑛
+ ∆𝑇
1
+ ∆𝑇
2
+ ∆𝑇
3
+ ∆𝑇
𝑜
=
= 5,94 + 9,99 + 128,90 + 19,78 + 10,39 ≅ 175 [𝐾]
1.3.2. Wyznaczenie spadku temperatury w ścianie komina przy
temperaturze zewnętrznej - 25
°
C
o Prędkość spalin
𝑣
𝑠
= 6 [𝑚/𝑠]
o Współczynnik napływu ciepła
𝛼
𝑛
= 8 + 𝑣
𝑠
= 8 + 6 = 14 [𝑊 (𝑚
2
𝐾)
]
o Współczynnik odpływu ciepła
𝛼
𝑜
= 24 [𝑊 (𝑚
2
𝐾)
]
o Współczynnik przenikania ciepła „k” przez warstwową przegrodę cylindryczną
𝟏
𝒌
=
𝟏
𝜶
𝒏
+
𝒅
𝒊
𝝀
𝒊
∙ 𝜿
𝒊
∙
𝑹
𝒓
𝒊
𝒏
𝒊=𝟏
+
𝟏
𝜶
𝒐
1
𝑘
=
1
14
+
0,12
1,15
∙ 1,046 ∙
5,21
4,73
+
0,08
0,058
∙ 1,038 ∙
5,21
4,81
+
0,4
1,68
∙ 1,0 ∙
5,21
5,21
+
1
24
= 2,023
𝑘 =
1
2,02
= 0,494 [𝑊 (𝑚
2
𝐾)
]
o Różnica temperatury
∆𝑇 = 210 − (−25) = 235 [𝐾]
8
o Spadki temperatury w poszczególnych warstwach przegrody
∆𝑻
𝒊
= 𝒌 ∙
𝒅
𝒊
𝝀
𝒊
∙ 𝛋
𝐢
∙
𝐑
𝐫
𝐢
∙ ∆𝐓
∆𝑇
1
= 0,494 ∙
0,12
1,15
∙ 1,046 ∙
5,21
4,73
∙ 235 = 13,79 [𝐾]
∆𝑇
2
= 0,494 ∙
0,08
0,058
∙ 1,038 ∙
5,21
4,81
∙ 235 = 180,22 [𝐾]
∆𝑇
3
= 0,494 ∙
0,4
1,68
∙ 1,0 ∙
5,21
5,21
∙ 235 = 27,66 [𝐾]
∆𝑻
𝒏
= 𝒌 ∙
𝟏
𝜶
𝒏
∙ ∆𝑻
∆𝑇
𝑛
= 0,494 ∙
1
14
∙ 235 = 8,30 [𝐾]
∆𝑻
𝒐
= 𝒌 ∙
𝟏
𝜶
𝒐
∙ ∆𝑻
∆𝑇
𝑜
= 0,494 ∙
1
24
∙ 235 = 4,84 [𝐾]
o Sprawdzenie
∆𝑇
𝑛
+ ∆𝑇
1
+ ∆𝑇
2
+ ∆𝑇
3
+ ∆𝑇
𝑜
=
= 8,30 + 13,79 + 180,22 + 27,66 + 4,84 ≅ 235 [𝐾]
Temperatura wewnętrznej powierzchni żelbetowego trzonu nie przekroczyła 70°𝐶, zaś różnica
temperatur przypadająca na ścianę trzonu nie była większa od 30 K.
9
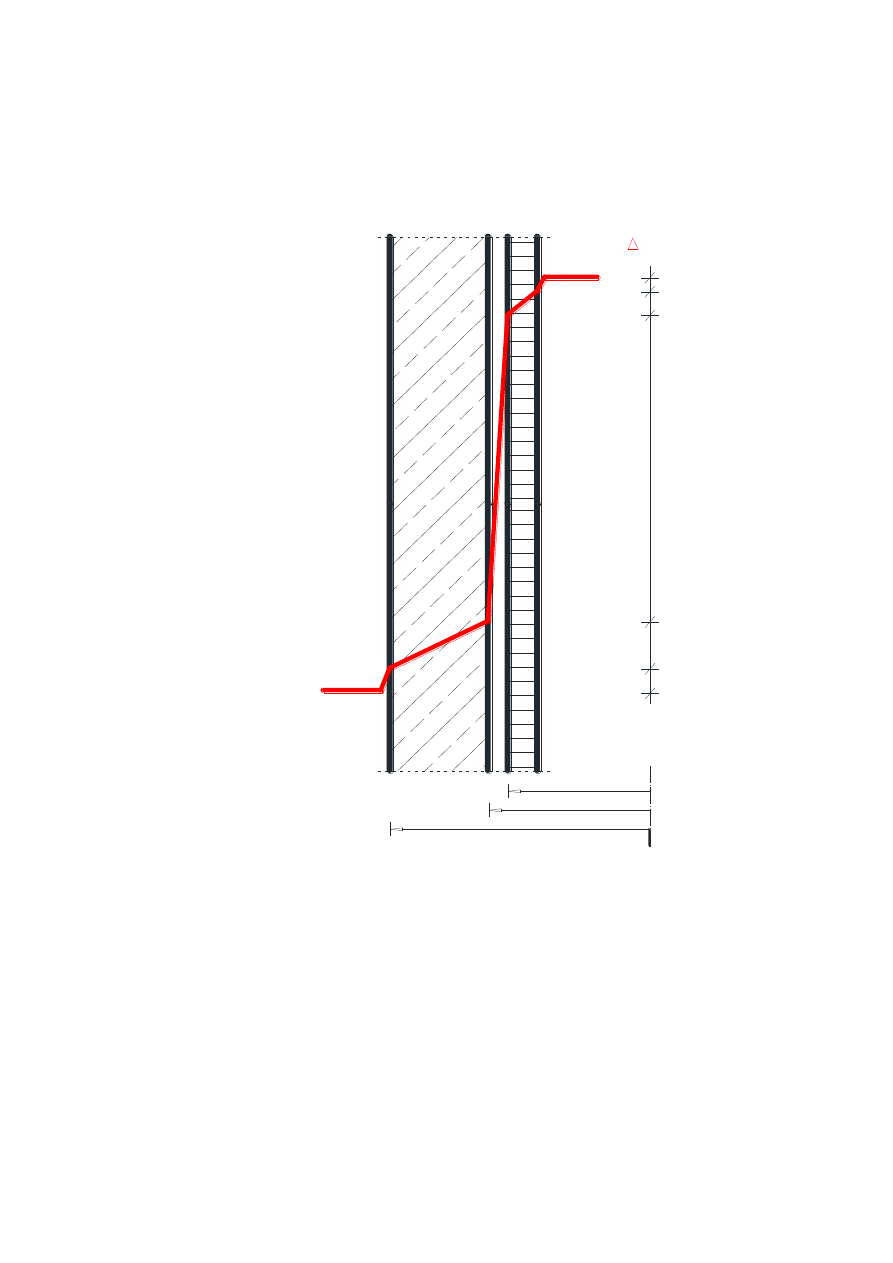
1.3.3. Wykres spadku temperatury w ścianie komina
o Przy temperaturze zewnętrznej +35°C
r =4,73 m
r =4,81 m
r =5,21 m
1
2
3
5,94
9,99
128,9
19,78
10,39
T, K
T, °C
+210,0
+ 204,06
+194,07
+ 65,17
+ 45,39
+ 35,0
10
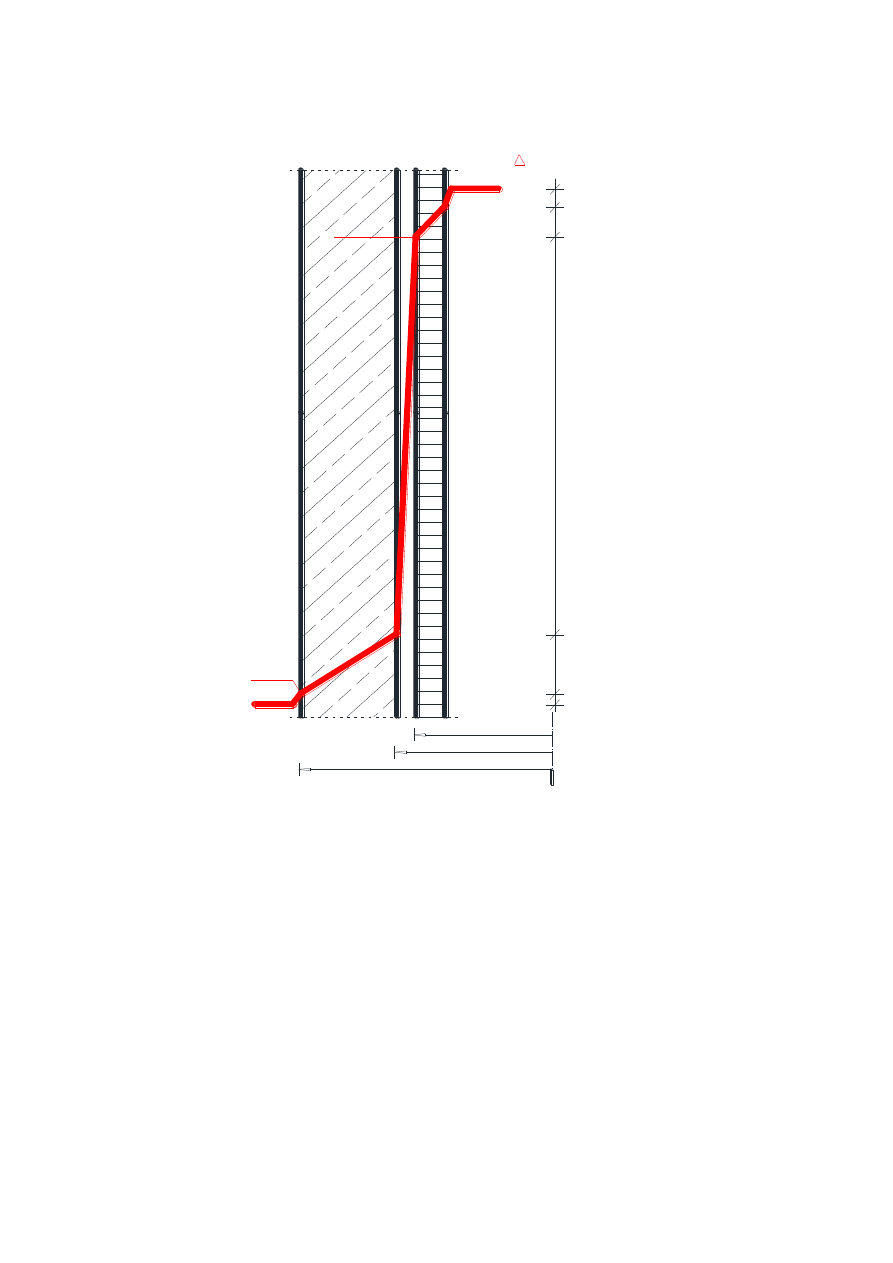
o Przy temperaturze zewnętrznej - 25°𝐂
r =4,73 m
r =4,81 m
r =5,21 m
1
2
3
T, K
T, °C
- 25,0
8,3
13,79
180,22
27,66
4,84
- 19,97
+7,69
+187,91
+201,7
+210,0
11
2. Obliczenia statyczne komina
2.1.
Obciążenie ciężarem własnym
ciężary objętościowe materiałów wykorzystanych do budowy komina
żelbet
γ = 26 kN m
3
wełna żużlowa biała
γ = 1,5 kN m
3
mur z cegły zwykłej
γ = 19 kN m
3
ciężar własny komina
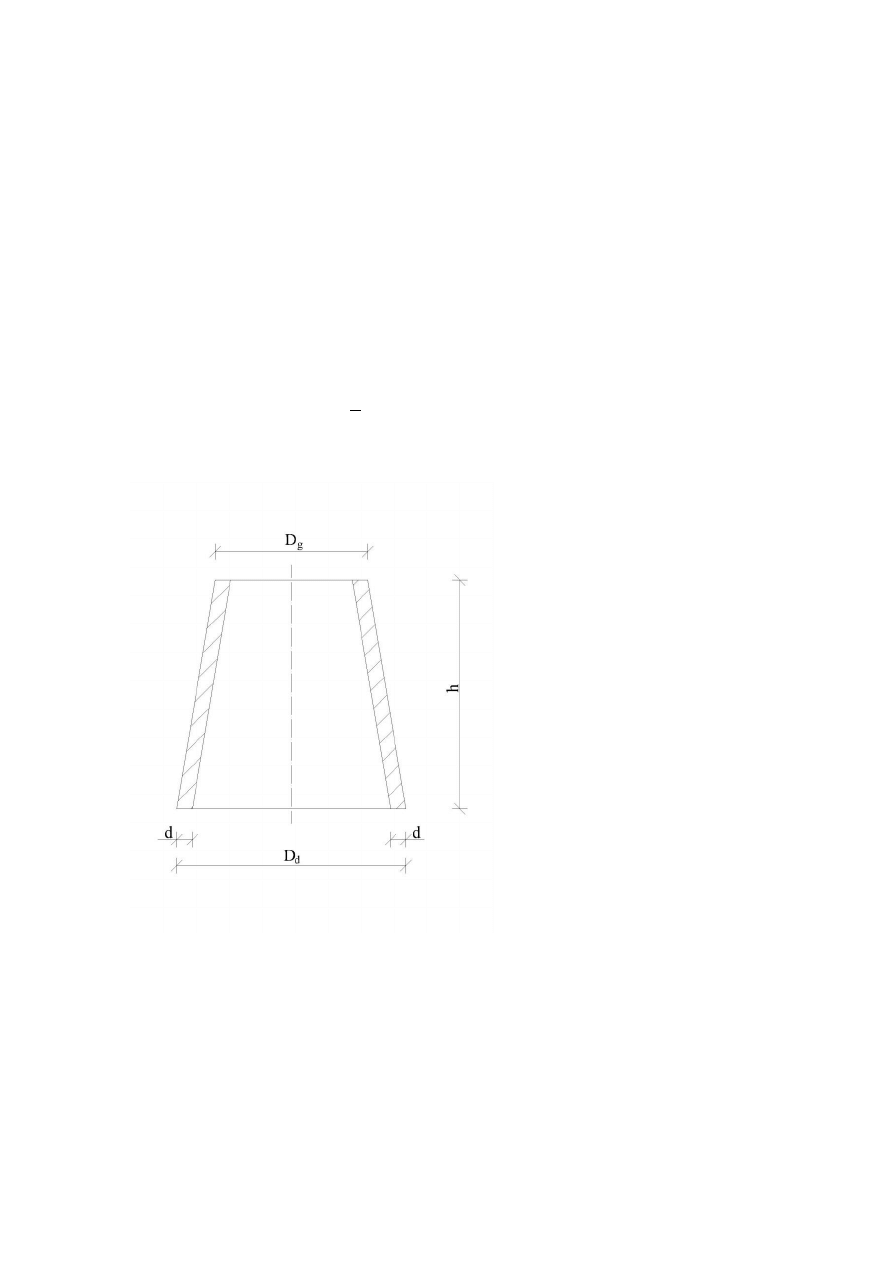
Ciężar własny trzonu, izolacji i wymurówki obliczono ze wzoru
𝐆 =
𝛑
𝟐
∙ 𝐝 ∙ 𝐡 ∙ 𝐃
𝐠
+ 𝐃
𝐝
− 𝟐𝐝 ∙ 𝛄 [𝐤𝐍]
Gdzie
d – grubość warstwy
h – wysokość głowicy
D
g
– górna średnica głowicy
D
d
– dolna średnica głowicy
γ – ciężar objętościowy
materiału
12
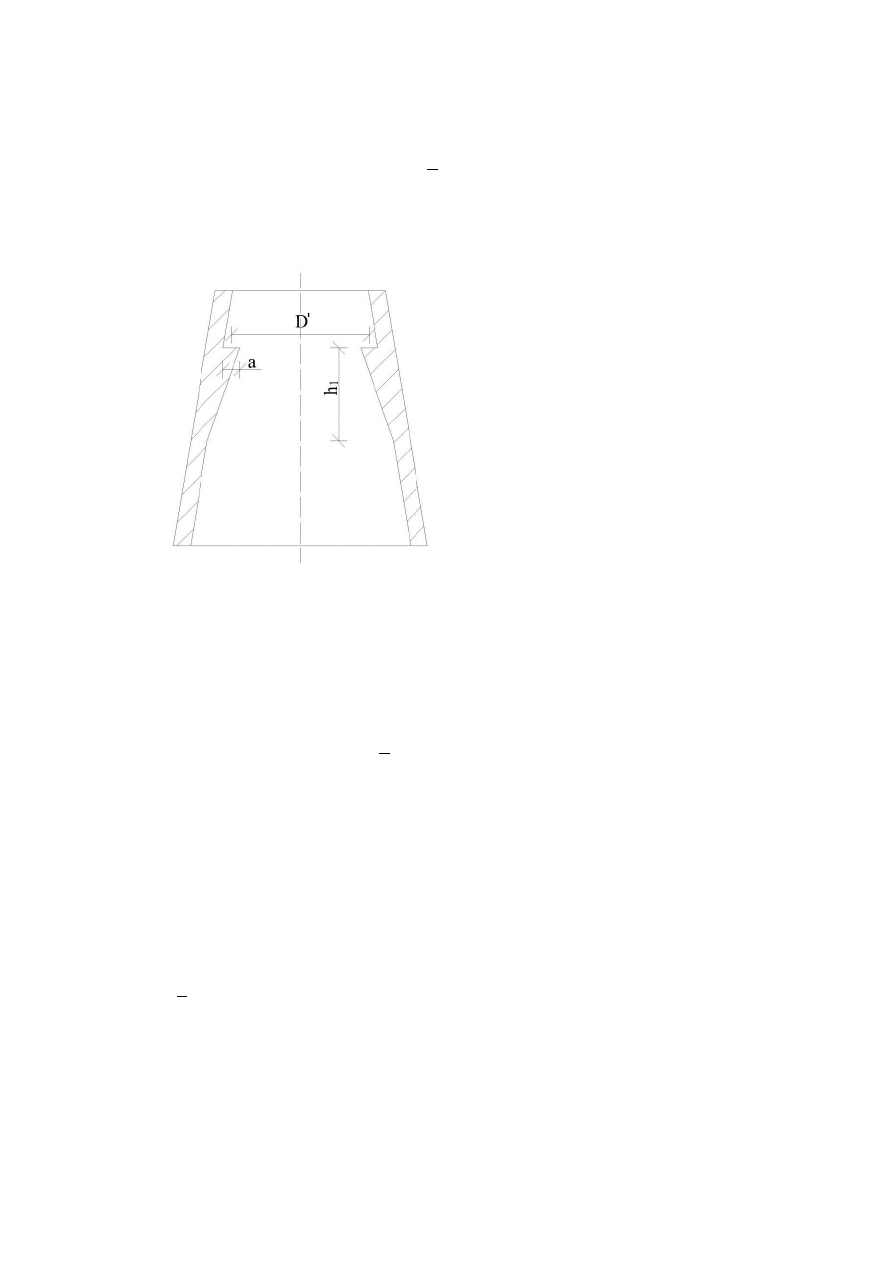
Ciężar wspornika podwykładzinowego obliczono ze wzoru
𝐆
𝐰
=
𝛑
𝟐
∙ 𝐃
′
∙ 𝐚 ∙ 𝐡
𝟏
∙ 𝛄 [𝐤𝐍]
Gdzie
a – szerokość wspornika
h
1
– wysokość wspornika
D’ – odległość między środkami
wsporników
γ – ciężar objętościowy materiału
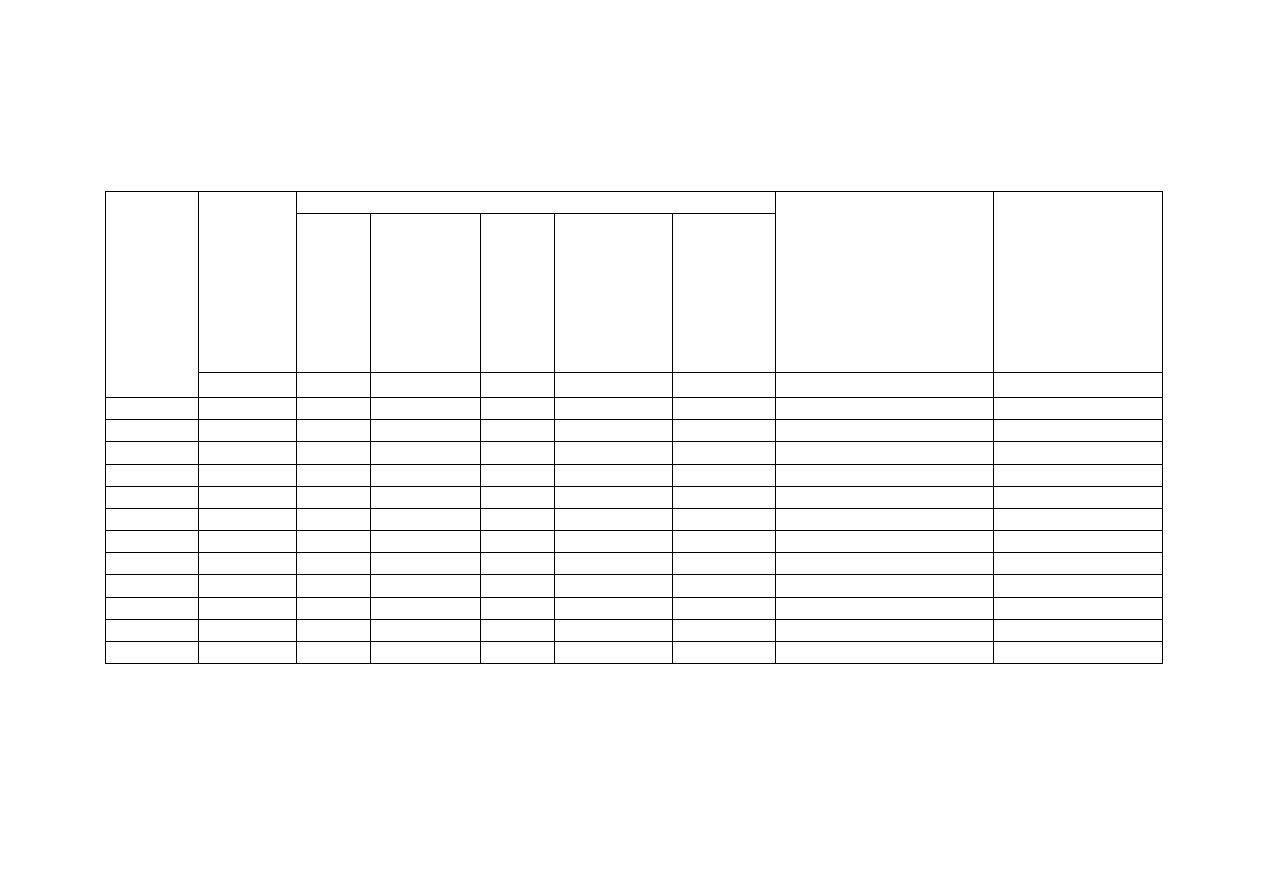
Ciężar głowicy żelbetowej obliczono ze wzoru
𝐆
𝐠
=
𝛑
𝟒
∙ 𝐃
𝐠
𝐳
𝟐
− 𝐃
𝐠
𝐰
𝟐
∙ 𝐡 ∙ 𝛄
Gdzie
D
g
z
− średnica zewnętrzna głowicy [m]
D
g
w
− średnica wewnętrzna głowicy m
h − wysokość głowicy m
γ − ciężar objętościowy [kN m
3
]
G
g
=
π
4
∙ 6,76
2
− 6,26
2
∙ 0,9 ∙ 26 = 119,64 kN
13
Tabela 2 Obciążenie ciężarem własnym
Nr
segmentu
Poziom
przekroju
Ciężar segmentu
Ciężar trzonu i
wsporników
podwykładzinowych
ponad rozpatrywanym
przekrojem
Całkowity ciężar
komina ponad
rozpatrywanym
przekrojem
Trzon
Wspornik
podwykła-
dzinowy
Izolacja Wymurówka
Całkowity
ciężar
segmentu
[m]
[kN]
[kN]
[kN]
[kN]
[kN]
[kN]
[kN]
119,64+
I
110,00
1018,05
-
22,44
412,01
1550
1138
1550
II
100,00
1178,23
64,39
23,59
433,85
1700
2381
3250
III
90,00
1349,02
67,56
24,74
455,68
1897
3797
5147
IV
80,00
1531,48
70,72
25,91
477,88
2106
5399
7253
V
70,00
1723,58
73,78
27,05
499,71
2324
7197
9577
VI
60,00
1926,30
76,95
28,20
521,55
2553
9200
12130
VII
50,00
2140,93
80,11
29,37
543,74
2794
11421
14924
VIII
40,00
2364,95
83,17
30,52
565,58
3044
13869
17969
IX
30,00
2599,58
86,33
31,67
587,41
3305
16555
21274
X
17,50
3573,48
90,31
41,24
765,59
4471
20219
25744
XI
0,00
5551,93
96,13
60,90
1131,96
6841
25867
32585
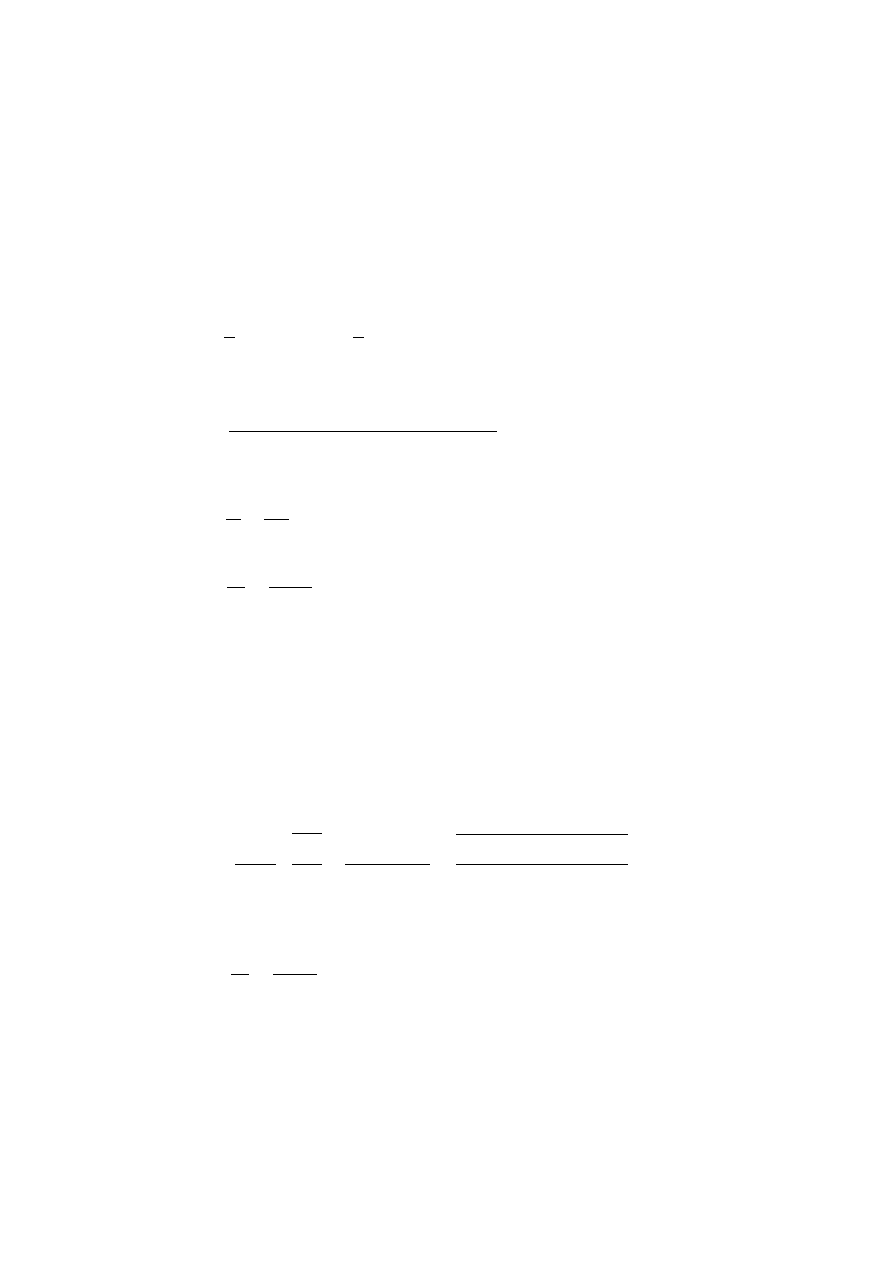
14
2.2.
Obciążenie wiatrem
2.2.1. Podstawowa częstotliwość drgań własnych
Parametry geometryczne przekroju płaszcza nośnego przy fundamencie
Powierzchnia przekroju poprzecznego
𝐹 = 𝜋 ∙ 𝑟
3
2
− 𝑟
2
2
= 𝜋 ∙ 5,21
2
− 4,81
2
= 12,59 𝑚
2
Moment bezwładności przekroju płaszcza
𝐽 =
𝜋
4
∙ 𝑟
3
4
− 𝑟
2
4
=
𝜋
4
∙ 5,21
4
− 4,81
4
= 158,28 𝑚
4
Ciężar trzonu na jednostkę długości
𝐺 =
5551,93 + 96,13 + 60,9 + 1072,38
17,5
= 387,51 𝑘𝑁 𝑚
Uwzględniono następujące wielkości pomocnicze
𝜆 =
𝑔
2
𝑔
1
=
0,20
0,40
= 0,50
𝜇 =
𝑑
2
𝑑
1
=
6,26
10,42
= 0,60 → 𝐾 = 1,35
∆= 0,15
Współczynnik sprężystości podłużnej betonu klasy C25/30 przyjęto jako
𝐸
𝑏
= 3000 𝑘𝑁 𝑐𝑚
2
Częstotliwość drgań własnych komina
𝑛
1
=
1
𝐾𝐻
0
2
𝑔𝐸𝐽
𝐺
=
1
1,35 ∙ 120
2
∙
9,81 ∙ 30 ∙ 10
6
∙ 158,28
387,51
= 0,564 𝐻𝑧
Okres drgań własnych wynosi
𝑇
1
=
1
𝑛
1
=
1
0,564
= 1,773 𝑠
Komin jest budowlą podatną na dynamiczne działanie wiatru
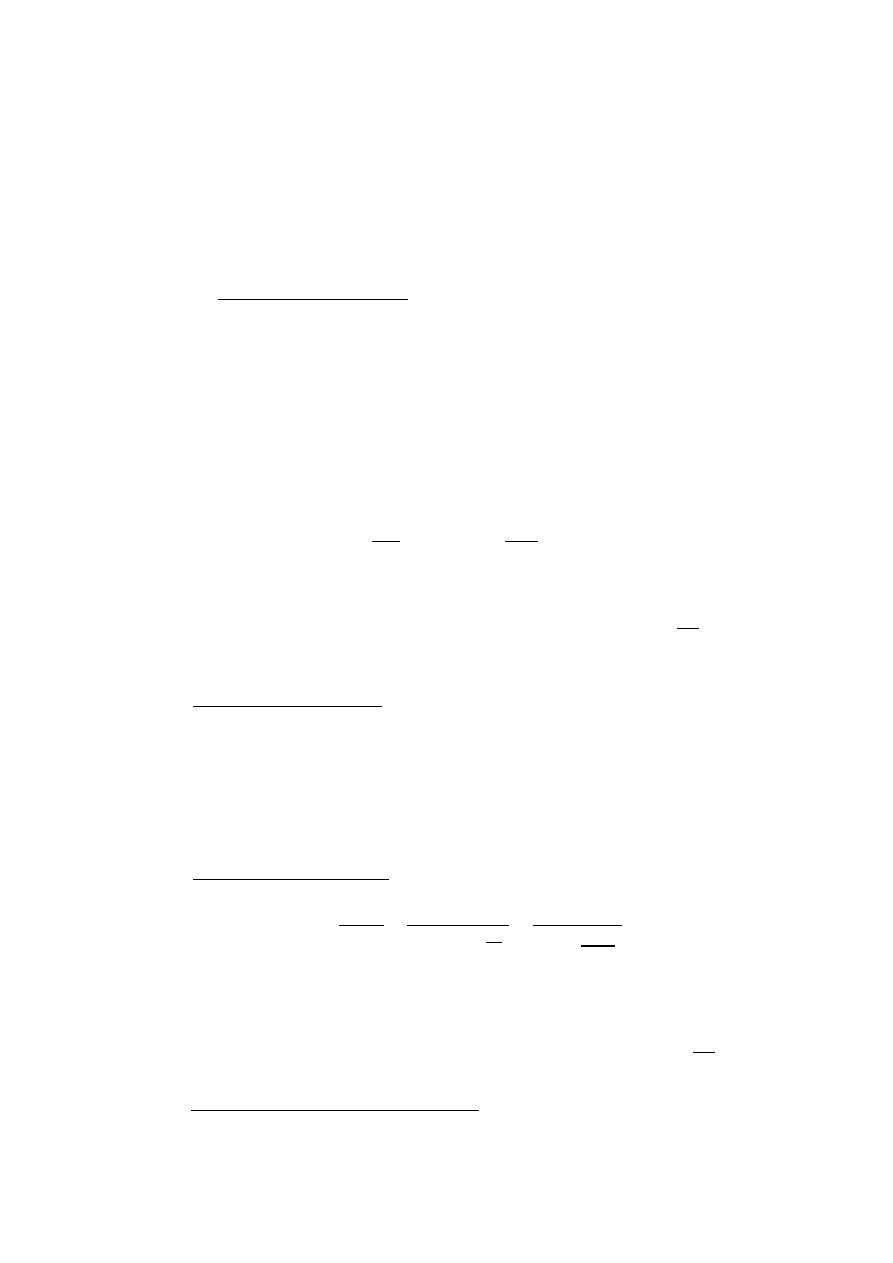
15
2.2.2. Obciążenia charakterystyczne wiatrem
Bazowa prędkość wiatru 𝐯
𝐛
Lokalizacja: Jaworzno
1 strefa, A<300m n.p.m.
Współczynnik sezonowy
c
season
=1,0
Wartość podstawowa bazowej prędkości wiatru
v
b,0
=22,0 m/s
Współczynnik kierunkowy wiatru
c
dir
=1,0
Bazowa prędkość wiatru
v
b
= c
dir
∙ c
season
∙ v
b,0
= 1,0 ∙ 1,0 ∙ 22,0 = 22,0 m/s
Kategoria terenu II
Wymiar chropowatości terenu
z
0
= 0,05 m
z
min
= 2,0 m
Współczynnik terenu k
r
k
r
= 0,19
z
0
z
0,II
0,07
= 0,19
0,05
0,05
0,07
= 0,19
Średnia prędkość wiatru 𝐯
𝐦
(𝐳)
Współczynnik chropowatości
c
r
120 =
120
10
0,17
= 1,526
Współczynnik rzeźby terenu
c
0
120 = 1,0
Średnia prędkość wiatru
v
m
z = c
r
z ∙ c
0
z ∙ v
b
= 1,526 ∙ 1 ∙ 22 = 33,57 m/s
Intensywność turbulencji 𝐈
𝐯
𝐳
Współczynnik turbulencji
k
1
= 1,0
Współczynnik rzeźby terenu
c
0
z = 1,0
Intensywność turbulencji
I
v
z =
ς
z
v
m
z
=
k
1
c
0
z ∙ ln(
z
z
0
)
=
1
1 ∙ ln
(
120
0,05
)
= 0,128
Szczytowe ciśnienie prędkości 𝐪
𝐩
(𝐳)
Gęstość powietrza
ρ = 1,25 kg/m
3
Współczynnik ekspozycji
c
e
z = 2,29
120
10
0,265
= 4,42
Wartość bazowa ciśnienia prędkości
q
b
= 0,5 ∙ ρ ∙ v
b
2
= 0,3 kN/m
2
Szczytowe ciśnienie prędkości wiatru
16
q
p
z = c
r
z ∙ 0,5 ∙ ρ ∙ v
b
2
= 4,42 ∙ 0,5 ∙ 1,25 ∙ 22
2
= 1,337 kN/m
2
Współczynnik oporu dynamicznego c
f
Prędkość wiatru
v =
2q
p
ρ
=
2∙1337
1,25
= 46,25 m/s
Liczbę Reynoldsa
R
e
=
b ∙ v(z
e
)
v
=
6,26 ∙ 46,25
15 ∙ 10
−6
= 2,0 ∙ 10
7
Współczynnik oporu aerodynamicznego walca
c
f,0
= 1,2 +
0,18 log(10 ∙
k
b
)
1 + 0,4 log(
Re
10
3
)
= 1,2 +
0,18 log
(10 ∙
1
6,26
)
1 + 0,4 log(
2,0 ∙ 10
7
10
3
)
= 0,55
Smukłość efektywna
λ = 0,7 ∙
120
6,26
= 13,4
Współczynnik wypełnienia
φ = 1,0
Współczynnik wpływu swobodnego końca
ψ
λ
= 0,7
Współczynnik oporu dynamicznego
c
f
= c
f,0
∙ ψ
λ
= 0,55 ∙ 0,7 = 0,385
Współczynnik konstrukcyjny 𝐜
𝐬
𝐜
𝐝
Skala odniesienia
L
t
= 300 m
Wysokość odniesienia
z
t
= 200 m
Współczynnik
α = 0,67 + 0,05 ln 0,05 = 0,52
Liniowa skala turbulencji
L z = L
t
∙
z
z
t
α
= 300 ∙
72
200
0,52
= 176,36
Współczynnik odpowiedzi pozarezonansowej
𝐵
2
=
1
1 + 0,9 ∙
𝑏 + ℎ
𝐿 𝑧
0,63
=
1
1 + 0,9 ∙
6,26 + 120
176,36
0,63
= 0,59
Intensywność turbulencji
I
v
72 =
1
1 ∙ ln
(
72
0,05
)
= 0,138
Średnia prędkość wiatru
v
m
z = 1,38 ∙ 1 ∙ 22 = 30,40 m/s
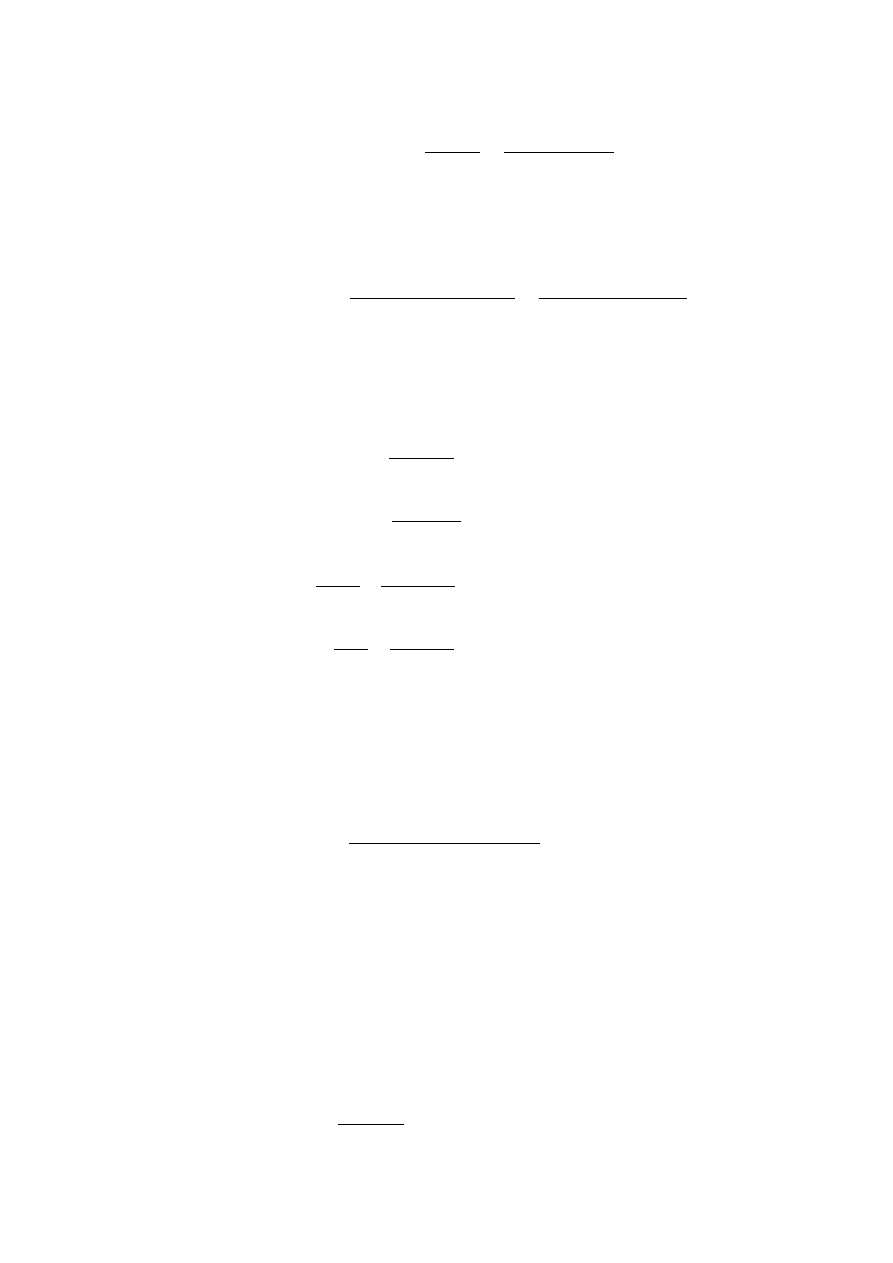
17
Częstotliwość bezwymiarowa
f
l
z, n =
n ∙ L z
v
m
z
=
0,564 ∙ 176,36
30,40
= 3,27
Bezwymiarowa funkcja gęstości spektralnej mocy
S
L
z, n =
6,8 ∙ f
l
z, n
1 + 10,2 ∙ f
l
z, n
5/3
=
6,8 ∙ 3,27
1 + 10,2 ∙ 3,27
5/3
= 0,061
Funkcje admitacji aerodynamicznej
η
h
=
4,6 ∙ 120
176,36
∙ 3,27 = 10,23
η
h
=
4,6 ∙ 6,26
176,36
∙ 3,27 = 0,53
R
h
=
1
10,23
−
1
2 ∙ 10,23
2
∙ 1 − e
−2∙10,23
= 0,093
R
h
=
1
0,53
−
1
2 ∙ 0,53
2
∙ 1 − e
−2∙0,53
= 0,72
Masa równoważna
m
e
= 0,25 ∙ π ∙ 6,26
2
− 4,2
2
∙ 2600 = 77081 kg/m
Logarytmiczny dekrement tłumienia aerodynamicznego
𝛿
𝑎
=
0,385 ∙ 1,25 ∙ 6,26 ∙ 30,40
2 ∙ 0,385 ∙ 77081
= 0,002
Logarytmiczny dekrement tłumienia konstrukcyjnego
𝛿
𝑠
= 0,03
Logarytmiczny dekrement tłumienia
𝛿
= 0,03 + 0,002 = 0,032
Współczynnik odpowiedzi rezonansowej
𝑅
2
=
𝜋
2
2 ∙ 0,032
∙ 0,061 ∙ 0,093 ∙ 0,72 = 0,63
18
Czas uśredniania prędkości średniej wiatru
T=600 s
Częstotliwość przewyższania
𝑣 = 0,564 ∙
0,63
0,59 + 0,63
= 0,41
𝑣𝑇 = 0,41 ∙ 600 = 243,2
Współczynnik wartości szczytowej
k
p
= 2ln 243,2 +
0,6
2ln 243,2
= 3,5
Współczynnik konstrukcyjny
c
s
c
d
=
1 + 2 ∙ 3,5 ∙ 0,138 ∙ 0,59 + 0,63
1 + 7 ∙ 0,138
= 1,05
Wartość jednostkowego obciążenia charakterystycznego wywołanego działaniem
wiatru
𝑝
𝑘
= c
s
c
d
∙ c
f
∙ q
p
z = 1,05 ∙ 1,337 ∙ 0,385 = 0,54 kN/m
2
Wartość jednostkowego obciążenia obliczeniowego wywołanego działaniem wiatru
𝑝
𝑑
= 1,5 ∙ 0,54 = 0,81 kN/m
2
Obciążenie wiatrem Fw
Pole powierzchni odniesienia
Aref = 6,26·10 =62,6 m
2
Obciążenie charakterystyczne
𝐹
𝑤
= 0,54 ∙ 62,6 = 33,8 kN
Obciążenie obliczeniowe
𝐹
𝑤𝑑
= 1,5 ∙ 33,8 = 50,71 kN
19
2.2.3. Siły i momenty zginające pierwszego rzędu od wiatru
Siły poprzeczne T
w
𝐓
𝐰
= 𝐩
𝐤
∙ 𝐀
𝐫𝐞𝐟
Gdzie
p
k
– wartość jednostkowego obciążenia wywołanego wiatrem
A
ref
– pole powierzchni odniesienia
Siła poprzeczna działająca na I segment
T
w
I
= 0,54 ∙ 64,4 = 34,7 kN
Siła poprzeczna działająca na XI segment
T
w
XI
= 0,54 ∙ 177,0 = 95,6 kN
Momenty zginające pierwszego rzędu M
w
𝐌
𝐰
= 𝐓
𝐰
∙ 𝐳
Gdzie
T
w
– wartość siły poprzecznej
z – ramię siły T
w
Moment zginający działający w dolnym przekroju I segmentu
M
w
I
= 34,7 ∙ 5 = 173,5 kNm
Moment zginający działający w dolnym przekroju XI segmentu
M
w
XI
=
8,75 ∙ 95,6 + 21,25 ∙ 64,8 + 31,25 ∙ 49,7 + 41,25 ∙ 47,8 + 51,25 ∙ 46,0 + 61,25 ∙
44,1 + 71,25 ∙ 42,2 + 81,25 ∙ 40,4 + 91,25 ∙ 38,5 + 101,25 ∙ 36,6 + 111,25 ∙ 34,7
=
28168,7 kNm
20
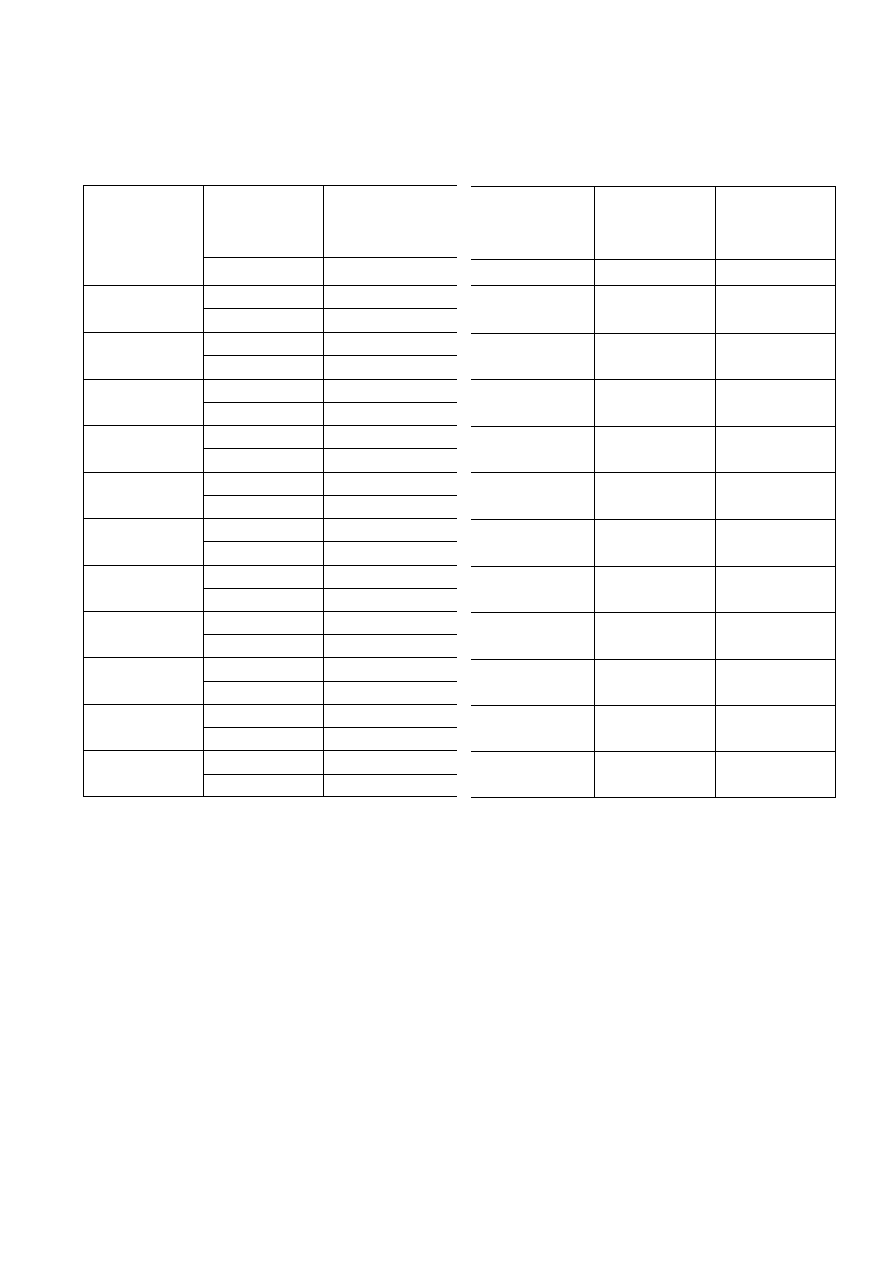
Tabela 3 Siły i momenty zginające pierwszego rzędu od wiatru
Nr segmentu
Poziom
(rzędna)
Obciążenie
wiatrem p
k
[m]
[kN/m
2
]
I
120
0,540
110
0,540
II
110
0,540
100
0,540
III
100
0,540
90
0,540
IV
90
0,540
80
0,540
V
80
0,540
70
0,540
VI
70
0,540
60
0,540
VII
60
0,540
50
0,540
VIII
50
0,540
40
0,540
IX
40
0,540
30
0,540
X
30
0,540
17,5
0,540
XI
17,5
0,540
0
0,540
Powierzchnia
rzutu
bocznego A
ref
Siła pozioma
T
w
Moment
zginający M
w
[m
2
]
[kN]
[kN*m]
64,4
34,7
173,7
67,8
36,6
704,3
71,3
38,5
1610,3
74,8
40,4
2910,5
78,2
42,2
4623,6
81,7
44,1
6768,4
85,2
46,0
9363,5
88,6
47,8
12241,3
92,1
49,7
15979,7
119,9
64,8
20660,1
177,0
95,6
28168,7
21
2.2.4. Sprężyste wychylenie wierzchołka trzonu – metoda Maxwella Mohra
Przyjmując sztywność średnią danego segmentu oraz przyjmując wpływ sił poprzecznych
obliczono sprężyste wychylenie komina ze wzoru Maxwella – Mohra.
y
w
=
MM
p
EI
dx =
1
E
173,7 ∙ 5
2
∙
2
3
∙ 10 +
1
3
∙ 5 ∙
1
19,047
+
+
1
24,4041
∙
173,7 ∙ 10
2
∙
2
3
∙ 10 +
1
3
∙ 20 +
704,3 ∙ 10
2
∙
2
3
∙ 20 +
1
3
∙ 10 +
+
1
30,7815
∙
704,3 ∙ 10
2
∙
2
3
∙ 20 +
1
3
∙ 30 +
1610,3 ∙ 10
2
∙
2
3
∙ 30 +
1
3
∙ 20 +
+
1
38,3783
∙
1610,3 ∙ 10
2
∙
2
3
∙ 30 +
1
3
∙ 40 +
2910,5 ∙ 10
2
∙
2
3
∙ 40 +
1
3
∙ 30 +
+
1
47,1748
∙
2910,5 ∙ 10
2
∙
2
3
∙ 40 +
1
3
∙ 50 +
4623,6 ∙ 10
2
∙
2
3
∙ 50 +
1
3
∙ 40 +
+
1
57,3705
∙
4623,6 ∙ 10
2
∙
2
3
∙ 50 +
1
3
∙ 60 +
6768,4 ∙ 10
2
∙
2
3
∙ 60 +
1
3
∙ 50 +
+
1
69,2306
∙
6768,4 ∙ 10
2
∙
2
3
∙ 60 +
1
3
∙ 70 +
9363,5 ∙ 10
2
∙
2
3
∙ 70 +
1
3
∙ 60 +
+
1
82,6663
∙
9363,5 ∙ 10
2
∙
2
3
∙ 70 +
1
3
∙ 80 +
12241,3 ∙ 10
2
∙
2
3
∙ 80 +
1
3
∙ 70 +
+
1
97,9387
∙
12241,3 ∙ 10
2
∙
2
3
∙ 80 +
1
3
∙ 90 +
15979,7 ∙ 10
2
∙
2
3
∙ 90 +
1
3
∙ 80 +
+
1
116,909
∙
15979,7 ∙ 10
2
∙
2
3
∙ 90 +
1
3
∙ 102,5 +
20660,1 ∙ 12,5
2
∙
2
3
∙ 102,5 +
1
3
∙ 90 +
+
1
144,199
∙
20660,1 ∙ 12,5
2
∙
2
3
∙ 102,5 +
1
3
∙ 120 +
28168,7 ∙ 17,5
2
∙
2
3
∙ 120 +
1
3
∙ 102,5 =
=
1,29 ∙ 10
6
30 ∙ 10
6
= 0,043 m
Dopuszczalne ugięcie wierzchołka komina żelbetowego przyjmuje się
f
dop
=
H
200
=
120
200
= 0,6 m = 60 cm > y
w
= 4,3 cm
Projektowany trzon komina spełnia warunek normowy dotyczący ugięcia wierzchołka.
22
Wykresy momentów zginających
a) wywołanych działaniem wiatru w linii wiatru,
b) od poziomej siły jednostkowej
173,7
704,3
1610,3
2910,5
4623,6
6768,4
9363,5
15979,7
20660,1
28168,7
12241,3
120
110
100
90
80
70
60
50
30
40
17,5
0,0
1
120
102,5
90
80
70
60
50
40
30
20
10
2.2.5. Momenty zginające drugiego rzędu z uwzględnieniem odkształcenia trzonu
Na podstawie tablicy 2 określono
Całkowity ciężar komina od obciążeń w fazie eksploatacji:
N
0
= 32 585 kN
Całkowity ciężar komina od obciążeń w fazie realizacji:
N
0
= 25 867 kN
23
Wpływ ugięcia II rzędu w fazie eksploatacji i realizacji, należy określić w zależności od
współczynników 𝛼
Faza eksploatacji
𝛼
1
= 𝐻
0
𝑁
0
𝐸 𝐽
= 120 ∙
32585
30 ∙ 10
6
∙ 158,196
= 0,31 < 0,35
Faza realizacji:
𝛼
1
= 𝐻
0
𝑁
0
𝐸 𝐽
= 120 ∙
25867
30 ∙ 10
6
∙ 158,196
= 0,28 < 0,35
W obliczeniach nie jest konieczne uwzględnienie wpływu ugięcia drugiego rzędu,
zarówno w fazie obciążeń eksploatacyjnych jak i realizacyjnych.
Tabela 4 Wartości momentów zginających w przekrojach komina
Nr segmentu
Moment
zginający M
i
Faza realizacji
Faza eksploatacji
Moment zginający
całkowity M=0,8*M
I
Moment zginający
całkowity M=M
I
[kN*m]
[kN*m]
[kN*m]
I
173,7
139,0
173,7
II
704,3
563,4
704,3
III
1610,3
1288,2
1610,3
IV
2910,5
2328,4
2910,5
V
4623,6
3698,9
4623,6
VI
6768,4
5414,7
6768,4
VII
9363,5
7490,8
9363,5
VIII
12241,3
9793,0
12241,3
IX
15979,7
12783,8
15979,7
X
20660,1
16528,1
20660,1
XI
28168,7
22535,0
28168,7
3. Sprawdzenie stateczności ogólnej komina
24
W przypadku komina zbieżnego o zmiennym momencie bezwładności siła krytyczna 𝑃
𝑘𝑟
wynosi:
P
kr
=
π
2
EJ
n
4H
0
2
∙ 1 +
J
2
− J
1
J
1
∙
a
1
2
H
0
2
−1
∙ 1 +
J
3
− J
2
J
2
∙
a
2
2
H
0
2
−1
∙ … ∙ 1 +
J
n
− J
n−1
J
n−1
∙
a
n−1
2
H
0
2
−1
=
3,14
2
∙ 30 ∙ 10
6
∙ 144,199
4 ∙ 120
2
∙ 1 +
24,4041 − 19,047
19,047
∙
10
2
120
2
−1
∙ 1 +
30,7815 − 24,4041
24,4041
∙
20
2
120
2
−1
∙ 1 +
38,3783 − 30,7815
30,7815
∙
30
2
120
2
−1
∙ 1 +
47,1748 − 38,3783
38,3783
∙
40
2
120
2
−1
∙ 1 +
57,3705 − 47,1748
47,1748
∙
50
2
120
2
−1
∙ 1 +
69,2306 − 57,3705
57,3705
∙
60
2
120
2
−1
∙ 1 +
82,6663 − 69,2306
69,2306
∙
70
2
120
2
−1
∙ 1 +
97,9387 − 82,6663
82,6663
∙
80
2
120
2
−1
∙ 1 +
116,909 − 97,9387
97,9387
∙
90
2
120
2
−1
∙ 1 +
144,199 − 116,909
116,909
∙
102,5
2
120
2
−1
= 4,313 ∙ 10
5
kN
Maksymalne obciążenie pionowe w fazie eksploatacji wynosi
N
0
= 32 585 kN
Wartość współczynnika stateczności 𝜑
𝑤
φ
w
=
4,313 ∙ 10
5
32 270
= 13,24 > 2,5
Warunek normowy został spełniony
25
4. Wymiarowanie żelbetowego trzonu komina
Naprężenia normalne (pionowe) ściskające w betonie obliczono wg wzoru
ς
C
=
N
Sd
A
C
∙ B [MPa]
gdzie:
N
Sd
− siła ściskająca prostopadła do przekroju MN
A
C
− Powierzchnia przekroju poprzecznego betonu m
2
C − współczynnik
Naprężenia normalne rozciągające w stali obliczono wg wzoru
ς
s
= ς
C
∙ C [MPa]
gdzie:
ς
C
− naprężenia normalne w betonie
C − współczynnik
średni promień trzonu
r
śr
=
R+r
2
gdzie:
R − promień zewnętrzny trzonu żelbetowego [m]
r − promień wewnętrzny trzonu żelbetowego [m]
mimośród siły
e
0
=
M
N
gdzie:
M − moment odpowiednio
dla fazy realizacji lub eksploatacji
N − siła skupiona odpowiednio
dla fazy realizacji lub eksploatacji
26
Dopuszczalne wartości naprężeń normalnych w stadium realizacji
w betonie
ς
c
≤ 0,4 ∙ f
ck
gdzie:
f
ck
− wytrzymałość charakterystyczna
betonu na ściskanie
(dla betonu C25 30
− f
ck
= 25 [MPa])
ς
C
≤ 0,4 ∙ 25 = 10 MPa = 10 000 [kPa]
w stali
ς
s
≤ 0,6 ∙ f
yk
gdzie:
f
yk
− charakterystyczna granica plastyczności stali
dla stali A − I f
yk
= 240 [MPa]
ς
s
≤ 0,6 ∙ 240 = 144 MPa = 144 000 [kPa]
Dopuszczalne wartości naprężeń normalnych w stadium eksploatacji
w betonie
ς
c
≤ 0,65 ∙ f
ck
gdzie:
f
ck
− wytrzymałość charakterystyczna
betonu na ściskanie
dla betonu C25 30
f
ck
= 25 [MPa]
ς
C
≤ 0,65 ∙ 25 = 16,25 MPa = 16 250 [kPa]
w stali
ς
s
≤ 0,7 ∙ f
yk
gdzie:
f
yk
− charakterystyczna granica plastyczności stali
dla stali A − I f
yk
= 240 [MPa]
ς
s
≤ 0,7 ∙ 240 = 168 MPa = 168 000 [kPa]
27
Minimalny procent zbrojenia w kierunku pionowym
ρ
min
=
4,2 ∙ f
ck
100 ∙ f
yk
∙ 100 =
4,2 ∙ 25
100 ∙ 240
∙ 100 = 0,44 %
Minimalny procent zbrojenia w kierunku poziomym
ρ
min
=
2,1 ∙ f
ck
100 ∙ f
yk
∙ 100 =
2,1 ∙ 25
100 ∙ 240
∙ 100 = 0,22 %
o dla segmentów I ÷ X − ρ
min
= 0,35 % ponieważ temp. spalin mieści się w
przedziale 100 − 300°C
o dla segmentu XI − ρ
min
= 0,40 % ponieważ średnica zewnętrzna jest większa od
10 m
28
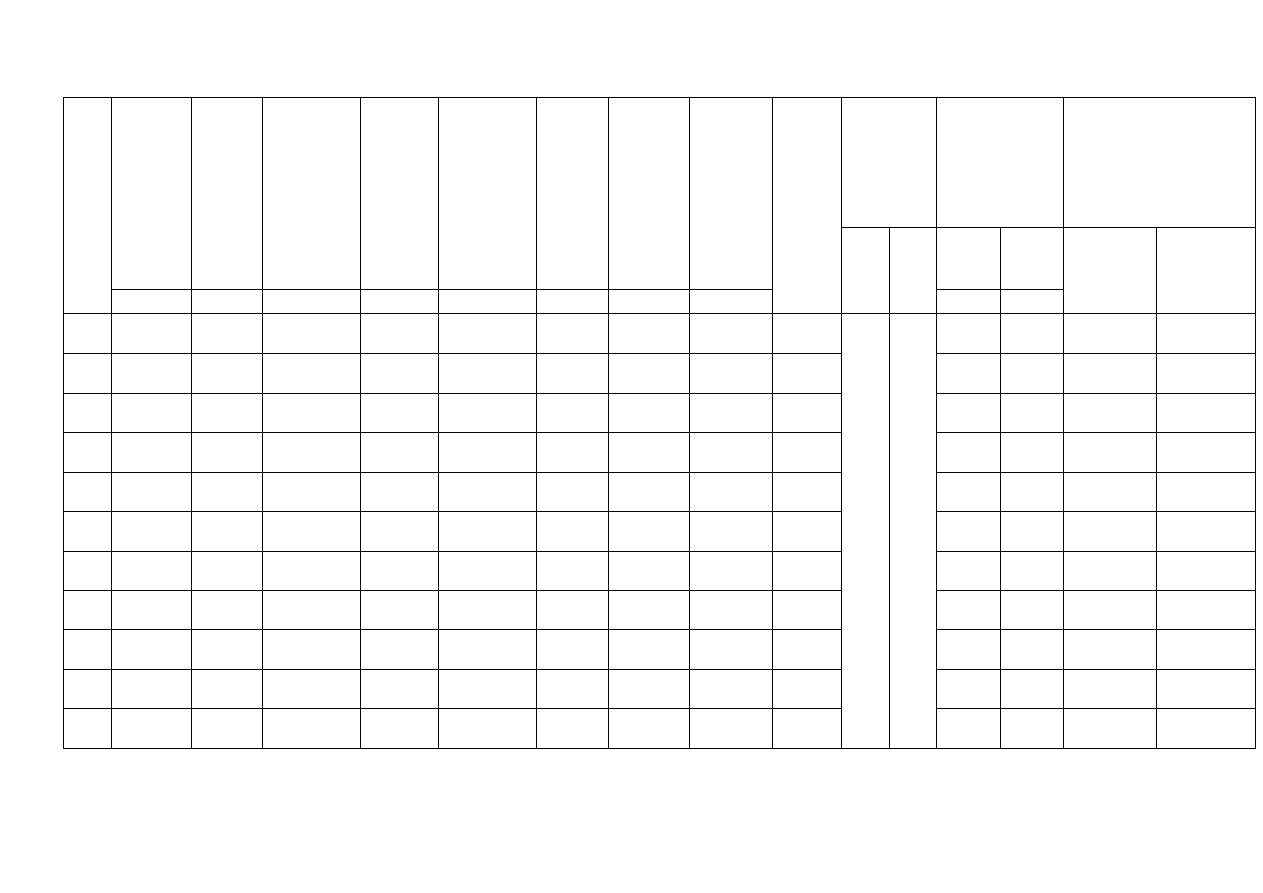
Tabela 5 Wymiarowanie zbrojenia w stadium realizacji
Nr se
gme
n
tu
Poziom
przekroju
Średni
promień
trzonu
r
śr
Pole
powierzchni
betonu A
c
Stopień
zbrojenia
ρ
Pole
powierzchni
zbrojenia A
s
Osiowa
siła
pionowa
N
Moment
zginający
M
Mimośród
siły e
0
Wartość
e
0
/r
s
Wartości
pomocnicze
Naprężenia
Przyjęte zbrojenie w
kierunku pionowym
B
C
w
betonie
σ
c
w stali
σ
s
Zewnętrzne Wewnętrzne
[m]
[m]
[m
2
]
[%]
[cm
2
]
[kN]
[kNm]
[m]
[kPa]
[kPa]
I
110
3,21
4,03
0,44
177,32
1138
139
0,12
0,04
e
0
/r
s
<
0
,5
p
rz
yj
ęt
o
B
=
1
,9
5
9
e
0
/r
s
<
0
,5
p
rz
yj
ęt
o
C
=
0
,0
1
7
553
9
89
𝜙
16 co
23 cm
90
𝜙
16 co
22 cm
II
100
3,37
4,65
0,44
204,6
2381
563,4
0,24
0,07
1003
17
108
𝜙
16 co
20 cm
104
𝜙
16 co
20 cm
III
90
3,53
5,32
0,44
234,08
3797
1288,2
0,34
0,10
1398
24
103
𝜙
18 co
22 cm
103
𝜙
18 co
21 cm
IV
80
3,7
6,03
0,44
265,32
5399
2328,4
0,43
0,12
1754
30
119
𝜙
18 co
20 cm
118
𝜙
18 co
20 cm
V
70
3,86
6,78
0,44
298,32
7197
3698,9
0,51
0,13
2079
35
118
𝜙
18 co
21 cm
118
𝜙
18 co
21 cm
VI
60
4,02
7,57
0,44
333,08
9200
5414,7
0,59
0,15
2381
40
131
𝜙
18 co
20 cm
131
𝜙
18 co
20 cm
VII
50
4,19
8,41
0,44
370,04
11421
7490,8
0,66
0,16
2660
45
128
𝜙
20 co
21 cm
127
𝜙
20 co
20 cm
VIII
40
4,35
9,28
0,44
408,32
13869
9793
0,71
0,16
2928
50
133
𝜙
20 co
21 cm
133
𝜙
20 co
20 cm
IX
30
4,51
10,2
0,44
448,8
16555
12783,8
0,77
0,17
3180
54
127
𝜙
22 co
23 cm
119
𝜙
22 co
23 cm
X
17,5
4,72
11,25
0,44
495
20219
16528,1
0,82
0,17
3521
60
139
𝜙
22 co
22 cm
131
𝜙
22 co
22 cm
XI
0
5,01
12,59
0,44
553,96
25867
22535
0,87
0,17
4025
68
148
𝜙
22 co
22 cm
146
𝜙
22 co
21 cm
29
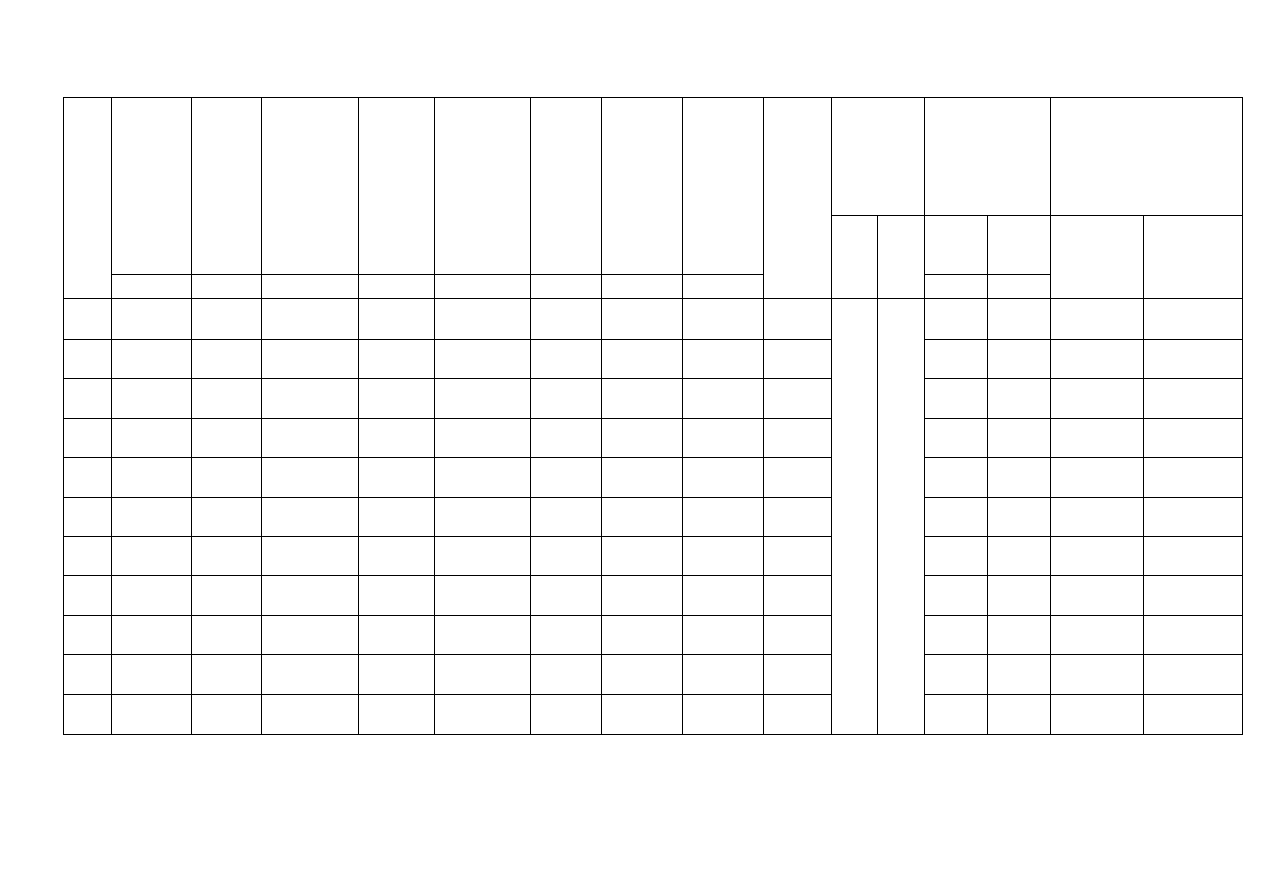
Tabela 6 Wymiarowanie zbrojenia w stadium eksploatacji
Nr se
gme
n
tu
Poziom
przekroju
Średni
promień
trzonu
r
śr
Pole
powierzchni
betonu A
c
Stopień
zbrojenia
ρ
Pole
powierzchni
zbrojenia A
s
Osiowa
siła
pionowa
N
Moment
zginający
0,8*M
Mimośród
siły e
0
Wartość
e
0
/r
s
Wartości
pomocnicze
Naprężenia
Przyjęte zbrojenie w
kierunku pionowym
B
C
w
betonie
σ
c
w stali
σ
s
Zewnętrzne Wewnętrzne
[m]
[m]
[m
2
]
[%]
[cm
2
]
[kN]
[kNm]
[m]
[kPa]
[kPa]
I
110
3,21
4,03
0,44
177,32
1550
173,7
0,11
0,03
e
0
/r
s
<
0
,5
p
rz
yj
ęt
o
B
=
1
,9
5
9
e
0
/r
s
<
0
,5
p
rz
yj
ęt
o
C
=
0
,0
1
7
753
13
89
𝜙
16 co
23 cm
90
𝜙
16 co
22 cm
II
100
3,37
4,65
0,44
204,6
3227
704,3
0,22
0,06
1360
23
108
𝜙
16 co
20 cm
104
𝜙
16 co
20 cm
III
90
3,53
5,32
0,44
234,08
5100
1610,3
0,32
0,09
1878
32
103
𝜙
18 co
22 cm
103
𝜙
18 co
21 cm
IV
80
3,7
6,03
0,44
265,32
7181
2910,5
0,41
0,11
2333
40
119
𝜙
18 co
20 cm
118
𝜙
18 co
20 cm
V
70
3,86
6,78
0,44
298,32
9479
4623,6
0,49
0,13
2739
47
118
𝜙
18 co
21 cm
118
𝜙
18 co
21 cm
VI
60
4,02
7,57
0,44
333,08
12004
6768,4
0,56
0,14
3106
53
131
𝜙
18 co
20 cm
131
𝜙
18 co
20 cm
VII
50
4,19
8,41
0,44
370,04
14770
9363,5
0,63
0,15
3440
58
128
𝜙
20 co
21 cm
127
𝜙
20 co
20 cm
VIII
40
4,35
9,28
0,44
408,32
17784
12241,3
0,69
0,16
3754
64
133
𝜙
20 co
21 cm
133
𝜙
20 co
20 cm
IX
30
4,51
10,2
0,44
448,8
21059
15979,7
0,76
0,17
4045
69
127
𝜙
22 co
23 cm
119
𝜙
22 co
23 cm
X
17,5
4,72
11,25
0,44
495
25489
20660,1
0,81
0,17
4438
75
139
𝜙
22 co
22 cm
131
𝜙
22 co
22 cm
XI
0
5,01
12,59
0,44
553,96
32270
28168,7
0,87
0,17
5021
85
148
𝜙
22 co
22 cm
146
𝜙
22 co
21 cm
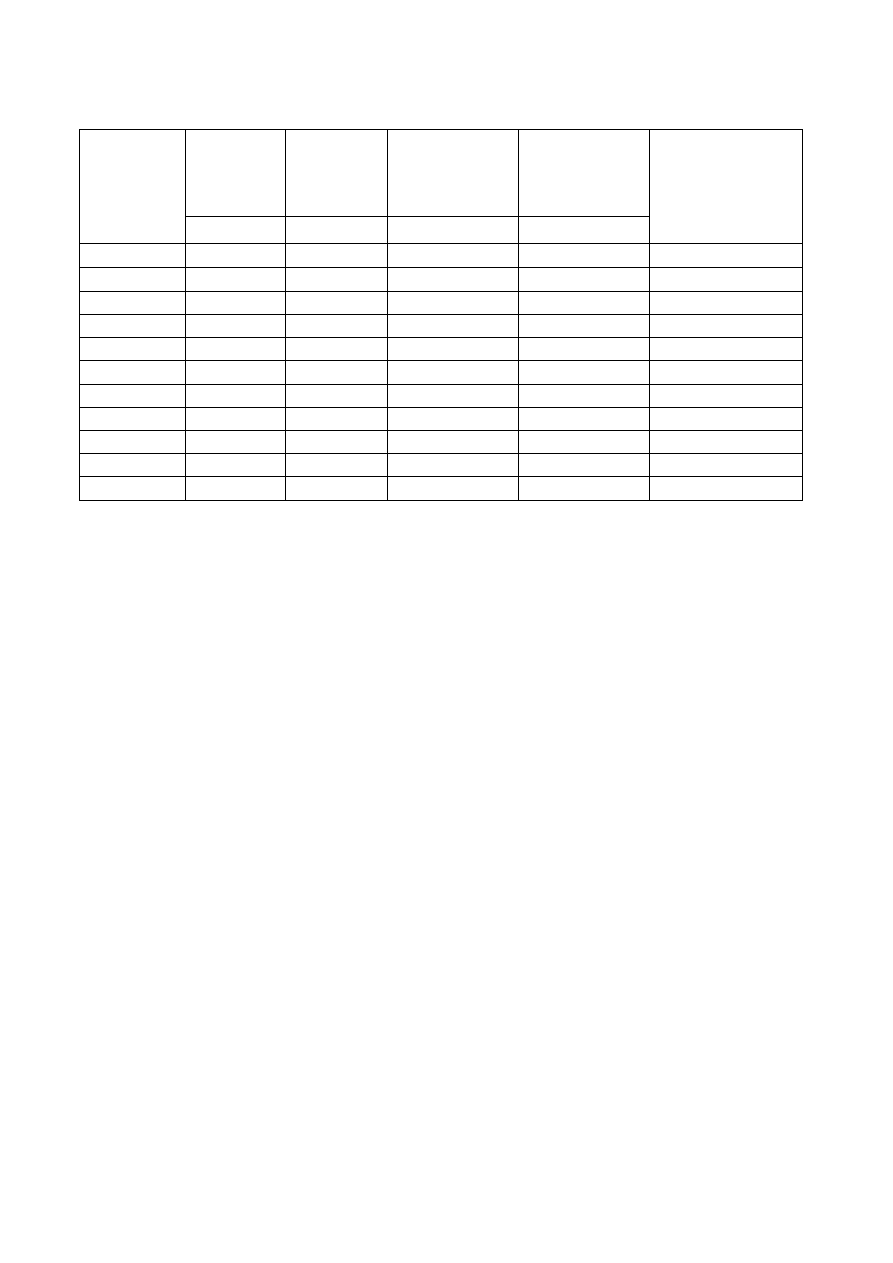
30
Tabela 7 Określenie zbrojenia poziomego
Nr
segmentu
Grubość
trzonu
Stopień
zbrojenia
Pole
powierzchni
betonu
Pole
powierzchni
zbrojenia
Przyjęte zbrojenie
w kierunku
poziomym
[cm]
[%]
[cm
2
]
[cm
2
]
I
20
0,35
2000
7
𝜙14 co 20 cm
II
22
0,35
2200
7,7
𝜙14 co 20 cm
III
24
0,35
2400
8,4
𝜙16 co 20 cm
IV
26
0,35
2600
9,1
𝜙16 co 20 cm
V
28
0,35
2800
9,8
𝜙16 co 20 cm
VI
30
0,35
3000
10,5
𝜙18 co 20 cm
VII
32
0,35
3200
11,2
𝜙18 co 20 cm
VIII
34
0,35
3400
11,9
𝜙18 co 20 cm
IX
36
0,35
3600
12,6
𝜙18 co 20 cm
X
38
0,35
3800
13,3
𝜙20 co 20 cm
XI
40
0,4
4000
16
𝜙22 co 20 cm