DYNAMIKA BUDOWLI
Projekt komina stalowego
DANE OGÓLNE:
Wysoko
ść
komina:
H
140m
:=
Promie
ń
wewn
ę
trzny komina:
rk
2.5m
:=
Ś
rednica zewn
ę
trzna:
dz
2 rk
⋅
:=
dz 5 m
=
Lokalizacja:
Gda
ń
sk
Rodzaj terenu:
C
DANE MATERIAŁOWE:
STAL St3SX:
Wytrzymało
ść
obliczeniowa stali:
fd
205MPa
:=
Moduł spr
ęż
ysto
ś
ci podłu
ż
nej:
E
205GPa
:=
G
ę
sto
ść
stali:
ρ
s
7850
kg
m
3
:=
Ci
ęż
ar jednostkowy:
γ
s
ρ
s g
⋅
:=
γ
s
76.982
kN
m
3
⋅
=
WYKŁADZINA CEGLANA:
Grubo
ść
okładziny:
gc
0.2m
:=
Wysoko
ść
okładziny:
H1
0.6 H
⋅
:=
H1 84m
=
Ci
ęż
ar jednostkowy wykładziny:
ρ
w
1800
kg
m
3
:=
γ
w
ρ
w g
⋅
:=
γ
w
17.652
kN
m
3
⋅
=
ZESTAWIENIE OBCI
Ąś
ENIA WIATREM:
Strefa obci
ąż
enia wiatrem: II (Gda
ń
sk)
Warto
ść
charakterystyczna ci
ś
nienia pr
ę
dko
ś
ci wiatru:
qk
350Pa
:=
Współczynnik oporu aerodynamicznego (przekrój kołowy)
Cz
1.3
:=
Współczynnik ekspozycji (teren C):
dla wysoko
ś
ci 0 - 30m:
•
Ce1
0.7
:=
dla wysoko
ś
ci 30 - 100m:
•
Ce2 z
( )
0.5
0.007 z
⋅
+
:=
Ce2 100
(
)
1.2
=
dla wysoko
ś
ci 100 - 140m:
•
Ce3 z
( )
0.75
0.0045 z
⋅
+
:=
Ce3 140
(
)
1.38
=
Współczynnik działania porywów wiatru:
β
3
:=
Zakładamy:
d
2 rk
⋅
0.4m
+
:=
d
5.4 m
=
Współczynnik bezpiecze
ń
stwa:
γ
fw
1.3
:=
Obci
ąż
enie wiatrem na jednostk
ę
długo
ś
ci komina:
pk1
qk Ce1
⋅
Cz
⋅
β
⋅
d
⋅
:=
pk1 5.16
kN
m
⋅
=
p1
pk1
γ
fw
⋅
:=
p1 6.708
kN
m
⋅
=
pk2
qk Ce2 100
(
)
⋅
Cz
⋅
β
⋅
d
⋅
:=
pk2 8.845
kN
m
⋅
=
p2
pk2
γ
fw
⋅
:=
p2 11.499
kN
m
⋅
=
pk3
qk Ce3 140
(
)
⋅
Cz
⋅
β
⋅
d
⋅
:=
pk3 10.172
kN
m
⋅
=
p3
pk3
γ
fw
⋅
:=
p3 13.224
kN
m
⋅
=
Strona -1-
DYNAMIKA BUDOWLI
Projekt komina stalowego
WST
Ę
PNE PRZYJ
Ę
CIE WYMIARÓW PRZEKROJU KOMINA:
Ś
rednie obci
ąż
enie od obci
ąż
enia trapezowego:
Obci
ąż
enie charakterystyczne:
pksr
0.5 pk2 pk3
+
(
)
⋅
:=
pksr 9.509
kN
m
⋅
=
Obci
ąż
enie obliczeniowe:
psr
γ
fw pksr
⋅
:=
psr 12.361
kN
m
⋅
=
Przyj
ę
cie grubo
ś
ci blachy z warunku no
ś
no
ś
ci:
•
Mmax
psr H
2
⋅
2
:=
Mmax 121139.437 kNm
⋅
=
W
Mmax
fd
:=
W
590924.081 cm
3
⋅
=
tk1
1m
:=
Given
π
64
dz
4
dz 2 tk1
⋅
−
(
)
4
−
⋅
0.5 dz
⋅
W
−
0
=
t1
Find tk1
( )
:=
t1 30.655 mm
⋅
=
Przyj
ę
cie grubo
ś
ci blachy z warunku dopuszczalnego ugi
ę
cia:
•
tk2
1m
:=
Given
pksr H
4
⋅
8 E
⋅
π
64
dz
4
dz 2 tk2
⋅
−
(
)
4
−
⋅
⋅
H
150
−
0
=
t2
Find tk2
( )
:=
t2 50.102 mm
⋅
=
t
max t1 t2
,
( )
:=
t
50.102 mm
⋅
=
Przyj
ę
te wymiary przekroju komina:
•
d
z
t
d
w
t
t
55mm
:=
dz 5 m
=
dw
dz 2 t
⋅
−
:=
dw 4.89 m
⋅
=
Moment bezwładno
ś
ci przekroju komina:
I
π
64
dz
4
dw
4
−
⋅
:=
I
2.612 m
4
⋅
=
Ugi
ę
cie komina:
u
pksr H
4
⋅
8E I
⋅
:=
u
85.273 cm
⋅
=
Ugi
ę
cie dopuszczalne:
H
150
0.933 m
=
Strona -2-
DYNAMIKA BUDOWLI
Projekt komina stalowego
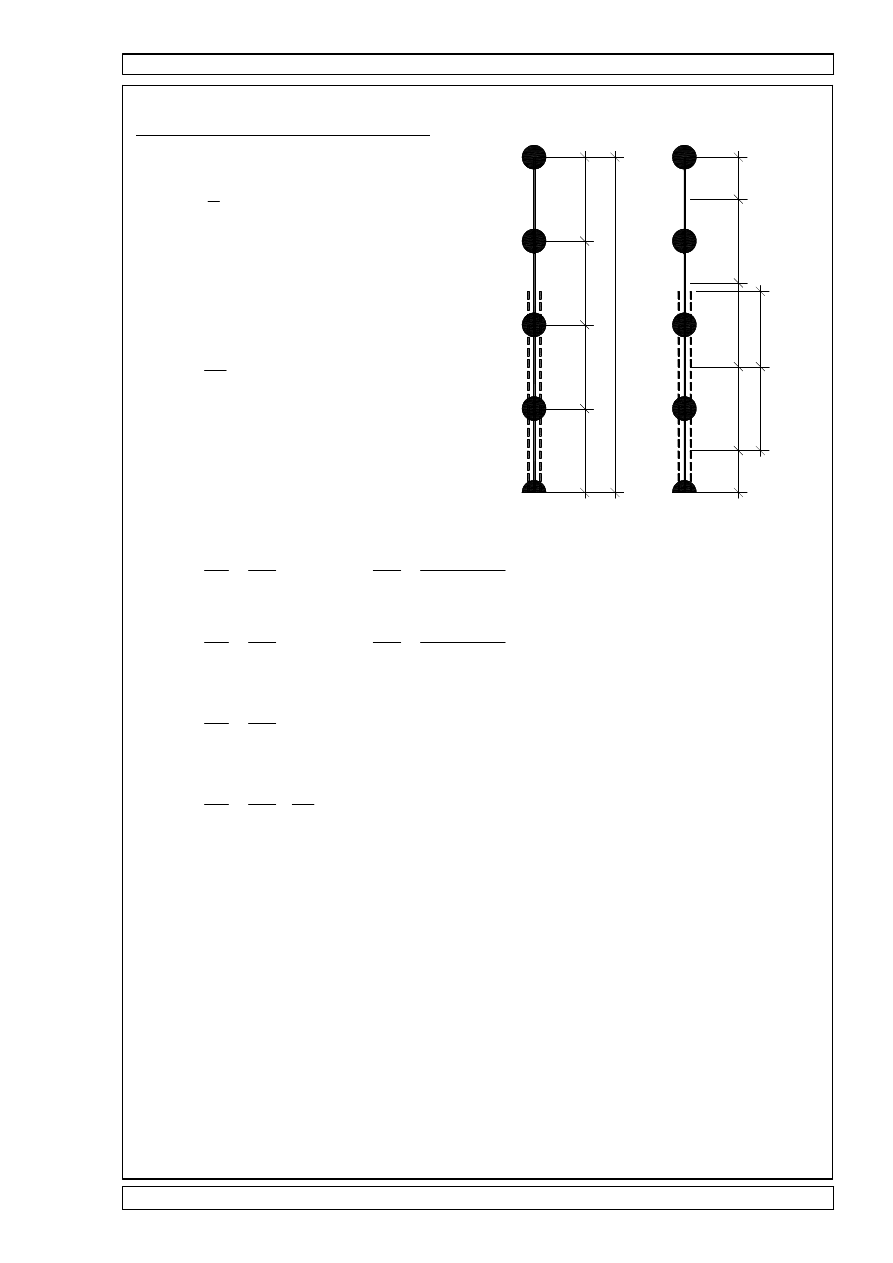
MODEL OBLICZENIOWY KOMINA:
m
0
m
1
m
2
m
3
m
4
3
5
3
5
3
5
3
5
1
7
.5
3
5
3
5
3
5
1
7
.5
1
4
0
m
0
m
3
m
2
m
1
3
1
.5
3
5
m
4
hm
H
4
:=
hm 35m
=
h
hm
hm
hm
hm
2
:=
h
35
35
35
17.5
m
=
hmokl
31.5m
:=
OBLICZENIE MACIERZY MAS:
m1
π
dz
2
4
dw
2
4
−
⋅
hm
⋅
ρ
s
⋅
π
dw
2
4
dw 2 gc
⋅
−
(
)
2
4
−
⋅
hm
⋅
ρ
w
⋅
+
:=
m1 4.204 10
5
×
kg
=
m2
π
dz
2
4
dw
2
4
−
⋅
hm
⋅
ρ
s
⋅
π
dw
2
4
dw 2 gc
⋅
−
(
)
2
4
−
⋅
hmokl
⋅
ρ
w
⋅
+
:=
m2 4.018 10
5
×
kg
=
m3
π
dz
2
4
dw
2
4
−
⋅
hm
⋅
ρ
s
⋅
:=
m3 2.348 10
5
×
kg
=
m4
π
dz
2
4
dw
2
4
−
⋅
hm
2
⋅
ρ
s
⋅
:=
m4 1.174 10
5
×
kg
=
M
m1
0
0
0
0
m2
0
0
0
0
m3
0
0
0
0
m4
:=
M
4.204
10
5
×
0
0
0
0
4.018
10
5
×
0
0
0
0
2.348
10
5
×
0
0
0
0
1.174
10
5
×
kg
=
Strona -3-
DYNAMIKA BUDOWLI
Projekt komina stalowego
OBLICZENIE MACIERZY PODATNO
Ś
CI:
M1
M2
M3
M4
P
P
P
P
P
1
:=
Mu i()
P i
⋅
hm
⋅
:=
M1
Mu 1
( )
:=
M1
35 m
=
M2
Mu 2
( )
:=
M2
70 m
=
M3
Mu 3
( )
:=
M3
105 m
=
M4
Mu 4
( )
:=
M4
140 m
=
Obliczenie współczynników macierzy podatno
ś
ci:
•
δ
1 1
,
1
E I
⋅
1
3
M1
⋅
M1
⋅
hm
⋅
⋅
:=
δ
1 1
,
2.669
10
5
−
×
m
kN
⋅
=
δ
2 2
,
1
E I
⋅
1
3
M2
⋅
M2
⋅
2
⋅
hm
⋅
:=
δ
2 2
,
2.135
10
4
−
×
m
kN
⋅
=
δ
3 3
,
1
E I
⋅
1
3
M3
⋅
M3
⋅
3
⋅
hm
⋅
:=
δ
3 3
,
7.206
10
4
−
×
m
kN
⋅
=
δ
4 4
,
1
E I
⋅
1
3
M4
⋅
M4
⋅
4
⋅
hm
⋅
:=
δ
4 4
,
1.708
10
3
−
×
m
kN
⋅
=
δ
1 2
,
1
E I
⋅
hm
6
2 M1
⋅
M2
⋅
2 0
⋅
M2
2
⋅
+
M1
M2
2
⋅
+
0 M2
⋅
+
⋅
⋅
:=
δ
1 2
,
6.673
10
5
−
×
m
kN
⋅
=
δ
1 3
,
1
E I
⋅
hm
6
2 M1
⋅
M3
⋅
2 0
⋅
2M3
3
⋅
+
M1
2M3
3
⋅
+
0 M3
⋅
+
⋅
⋅
:=
δ
1 3
,
1.068
10
4
−
×
m
kN
⋅
=
δ
1 4
,
1
E I
⋅
hm
6
2 M1
⋅
M4
⋅
2 0
⋅
3M4
4
⋅
+
M1
3M4
4
⋅
+
0 M4
⋅
+
⋅
⋅
:=
δ
1 4
,
1.468
10
4
−
×
m
kN
⋅
=
δ
2 3
,
1
E I
⋅
2hm
6
2 M2
⋅
M3
⋅
2 0
⋅
M3
3
⋅
+
M2
M3
3
⋅
+
0 M3
⋅
+
⋅
⋅
:=
δ
2 3
,
3.737
10
4
−
×
m
kN
⋅
=
δ
2 4
,
1
E I
⋅
2hm
6
2 M2
⋅
M4
⋅
2 0
⋅
M4
2
⋅
+
M2
M4
2
⋅
+
0 M4
⋅
+
⋅
⋅
:=
δ
2 4
,
5.338
10
4
−
×
m
kN
⋅
=
δ
3 4
,
1
E I
⋅
3hm
6
2 M3
⋅
M4
⋅
2 0
⋅
M4
4
⋅
+
M3
M4
4
⋅
+
0 M4
⋅
+
⋅
⋅
:=
δ
3 4
,
1.081
10
3
−
×
m
kN
⋅
=
δ
2 1
,
δ
1 2
,
:=
δ
3 1
,
δ
1 3
,
:=
δ
4 1
,
δ
1 4
,
:=
δ
3 2
,
δ
2 3
,
:=
δ
4 2
,
δ
2 4
,
:=
δ
4 3
,
δ
3 4
,
:=
Strona -4-
DYNAMIKA BUDOWLI
Projekt komina stalowego
δ
2.669
10
5
−
×
6.673
10
5
−
×
1.068
10
4
−
×
1.468
10
4
−
×
6.673
10
5
−
×
2.135
10
4
−
×
3.737
10
4
−
×
5.338
10
4
−
×
1.068
10
4
−
×
3.737
10
4
−
×
7.206
10
4
−
×
1.081
10
3
−
×
1.468
10
4
−
×
5.338
10
4
−
×
1.081
10
3
−
×
1.708
10
3
−
×
m
kN
⋅
=
OBLICZENIE MACIERZY SZTYWNO
Ś
CI:
K
δ
1
−
:=
K
2.348
10
8
×
1.475
−
10
8
×
5.562
10
7
×
9.27
−
10
6
×
1.475
−
10
8
×
1.792
10
8
×
1.197
−
10
8
×
3.245
10
7
×
5.562
10
7
×
1.197
−
10
8
×
1.236
10
8
×
4.558
−
10
7
×
9.27
−
10
6
×
3.245
10
7
×
4.558
−
10
7
×
2.009
10
7
×
kg
s
2
=
OBLICZENIE CZ
Ę
STO
Ś
CI DRGA
Ń
WŁASNYCH:
M
δ
⋅
0.011
0.027
0.025
0.017
0.028
0.086
0.088
0.063
0.045
0.15
0.169
0.127
0.062
0.215
0.254
0.201
s
2
=
ω
eigenvals M
δ
⋅
(
)
:=
ω
0.44667
0.01692
0.00228
0.00083
s
2
=
ω
k
1
1
ω
1
:=
ω
k
1
1.496 Hz
⋅
=
ω
k
2
1
ω
2
:=
ω
k
2
7.688 Hz
⋅
=
ω
k
3
1
ω
3
:=
ω
k
3
20.952 Hz
⋅
=
ω
k
4
1
ω
4
:=
ω
k
4
34.668 Hz
⋅
=
CZ
Ę
STOTLIWO
ŚĆ
I OKRES DRGA
Ń
WŁASNYCH:
fk
ω
k
2
π
⋅
:=
fk
0.238
1.224
3.335
5.518
Hz
⋅
=
Tk
1
fk
:=
Tk
4.199
0.817
0.3
0.181
s
=
Strona -5-

DYNAMIKA BUDOWLI
Projekt komina stalowego
OBLICZENIE WSPÓŁCZYNNIKA DZIAŁANIA PORYWÓW WIATRU:
n
fk
1 1
,
:=
n
0.238 Hz
⋅
=
Współczynnik warto
ś
ci szczytowej:
•
ψ
2 ln 600 n
⋅
(
)
⋅
0.577
2 ln 600 n
⋅
(
)
⋅
+
:=
ψ
3.333
=
Współczynnik oddziaływania turbulentnego o cz
ę
sto
ś
ciach pozarezonansowych:
•
L
dz
:=
ξ
L
H
:=
ξ
0.036
=
Ce
Ce3 140
(
)
:=
Ce 1.38
=
r
0.1
:=
A
0.042
−
28.8
ξ
⋅
1
+
:=
A
0.021
−
=
B
ξ
−
2.65
ξ
⋅
0.24
+
:=
B
0.107
−
=
C
2.29
0.12
ξ
⋅
−
ξ
1.29
−
24.5
ξ
⋅
3.48
+
+
:=
C
1.998
=
kb
A
ln
H
m
2
⋅
B ln
H
m
⋅
+
C
+
:=
kb 0.965
=
Współczynnik oddziaływania turbulentnego o cz
ę
sto
ś
ciach rezonansowych:
•
Charakterystyczna pr
ę
dko
ść
wiatru:
Strefa II
Vk
24
:=
Pr
ę
dko
ść
wiatru na poziomie całkowitej wysoko
ś
ci budowli:
VH
Vk
Ce
⋅
:=
VH 28.194
=
Współczynnik zmniejszaj
ą
cy rezonansowe oddziaływanie porywów:
KL
π
3
1
1
8 n
⋅
H
⋅
3 VH
⋅
m
⋅
+
⋅
1
1
10 n
⋅
L
⋅
VH m
⋅
+
⋅
:=
KL 0.177
=
Współczynnik energii porywów:
x
1200 n
⋅
VH
:=
x
10.136
=
Ko
x
2
1
x
2
+
(
)
4
3
:=
Ko 0.211
=
Logarytmiczny dekrement tłumienia drga
ń
:
∆
0.02
:=
kr
2
π
⋅
KL
⋅
Ko
⋅
∆
:=
kr 11.738
=
β
1
ψ
r
Ce
kb kr
+
(
)
⋅
⋅
+
:=
β
4.198
=
Strona -6-
DYNAMIKA BUDOWLI
Projekt komina stalowego
ZESTAWIENIE OBCI
Ąś
E
Ń
DLA NOWEGO WSPÓŁCZYNNIKA
β
:
Obci
ąż
enie wiatrem na jednostk
ę
długo
ś
ci komina:
pk1
qk Ce1
⋅
Cz
⋅
β
⋅
d
⋅
:=
pk1 7.22
kN
m
⋅
=
p1
pk1
γ
fw
⋅
:=
p1 9.387
kN
m
⋅
=
pk2
qk Ce2 100
(
)
⋅
Cz
⋅
β
⋅
d
⋅
:=
pk2 12.378
kN
m
⋅
=
p2
pk2
γ
fw
⋅
:=
p2 16.091
kN
m
⋅
=
pk3
qk Ce3 140
(
)
⋅
Cz
⋅
β
⋅
d
⋅
:=
pk3 14.235
kN
m
⋅
=
p3
pk3
γ
fw
⋅
:=
p3 18.505
kN
m
⋅
=
Ś
rednie obci
ąż
enie od obci
ąż
enia trapezowego:
Obci
ąż
enie charakterystyczne:
pksr
0.5 pk2 pk3
+
(
)
⋅
:=
pksr 13.306
kN
m
⋅
=
Obci
ąż
enie obliczeniowe:
psr
γ
fw pksr
⋅
:=
psr 17.298
kN
m
⋅
=
SPRAWDZENIE WARUNKÓW:
Sprawdzenie warunku ze wzgl
ę
du na no
ś
no
ść
:
•
Mmax
psr H
2
⋅
2
:=
Mmax 169521.011 kNm
⋅
=
W
Mmax
fd
:=
W
826931.762 cm
3
⋅
=
tk1
1m
:=
Given
π
64
dz
4
dz 2 tk1
⋅
−
(
)
4
−
⋅
0.5 dz
⋅
W
−
0
=
t1
Find tk1
( )
:=
t1 43.223 mm
⋅
=
Sprawdzenie warunku ze wzgl
ę
du na ugi
ę
cie:
•
tk2
1m
:=
Given
pksr H
4
⋅
8 E
⋅
π
64
dz
4
dz 2 tk2
⋅
−
(
)
4
−
⋅
⋅
H
150
−
0
=
t2
Find tk2
( )
:=
t2 71 mm
⋅
=
t
max t1 t2
,
( )
:=
t
71 mm
⋅
=
Przyj
ę
te wymiary przekroju komina:
•
t
72mm
:=
dz 5 m
=
dw
dz 2 t
⋅
−
:=
dw 4.856 m
⋅
=
Strona -7-
DYNAMIKA BUDOWLI
Projekt komina stalowego
Moment bezwładno
ś
ci przekroju komina:
I
π
64
dz
4
dw
4
−
⋅
:=
I
3.385 m
4
⋅
=
Ugi
ę
cie komina:
u
pksr H
4
⋅
8E I
⋅
:=
u
92.093 cm
⋅
=
Ugi
ę
cie dopuszczalne:
H
150
93.333 cm
⋅
=
OBLICZENIE MACIERZY MAS:
m1
π
dz
2
4
dw
2
4
−
⋅
hm
⋅
ρ
s
⋅
π
dw
2
4
dw 2 gc
⋅
−
(
)
2
4
−
⋅
hm
⋅
ρ
w
⋅
+
:=
m1 4.906 10
5
×
kg
=
m2
π
dz
2
4
dw
2
4
−
⋅
hm
⋅
ρ
s
⋅
π
dw
2
4
dw 2 gc
⋅
−
(
)
2
4
−
⋅
hmokl
⋅
ρ
w
⋅
+
:=
m2 4.721 10
5
×
kg
=
m3
π
dz
2
4
dw
2
4
−
⋅
hm
⋅
ρ
s
⋅
:=
m3 3.063 10
5
×
kg
=
m4
π
dz
2
4
dw
2
4
−
⋅
hm
2
⋅
ρ
s
⋅
:=
m4 1.531 10
5
×
kg
=
M
m1
0
0
0
0
m2
0
0
0
0
m3
0
0
0
0
m4
:=
M
4.906
10
5
×
0
0
0
0
4.721
10
5
×
0
0
0
0
3.063
10
5
×
0
0
0
0
1.531
10
5
×
kg
=
OBLICZENIE CZ
Ę
STO
Ś
CI DRGA
Ń
WŁASNYCH:
M
δ
⋅
0.013
0.032
0.033
0.022
0.033
0.101
0.114
0.082
0.052
0.176
0.221
0.166
0.072
0.252
0.331
0.262
s
2
=
ω
eigenvals M
δ
⋅
(
)
:=
ω
0.57178
0.02059
0.0028
0.00102
s
2
=
ω
k
1
1
ω
1
:=
ω
k
1
1.322 Hz
⋅
=
ω
k
2
1
ω
2
:=
ω
k
2
6.97 Hz
⋅
=
Strona -8-

DYNAMIKA BUDOWLI
Projekt komina stalowego
ω
k
3
1
ω
3
:=
ω
k
3
18.908 Hz
⋅
=
ω
k
4
1
ω
4
:=
ω
k
4
31.388 Hz
⋅
=
CZ
Ę
STOTLIWO
ŚĆ
I OKRES DRGA
Ń
WŁASNYCH:
fk
ω
k
2
π
⋅
:=
fk
0.21
1.109
3.009
4.996
Hz
⋅
=
Tk
1
fk
:=
Tk
4.751
0.902
0.332
0.2
s
=
A1
1m
:=
-amplituda masy pierwszej
Id
1
0
0
0
0
1
0
0
0
0
1
0
0
0
0
1
:=
AMPLITUDY W PIERWSZEJ POSTACI DRGA
Ń
WŁASNYCH:
Am1
δ
M
⋅
ω
k
1
2
⋅
Id
−
:=
Am1
0.977
−
0.057
0.092
0.126
0.055
0.824
−
0.309
0.441
0.057
0.2
0.614
−
0.579
0.039
0.143
0.289
0.543
−
=
Z1
Am1
1 2
,
Am1
2 2
,
Am1
3 2
,
Am1
1 3
,
Am1
2 3
,
Am1
3 3
,
Am1
1 4
,
Am1
2 4
,
Am1
3 4
,
1
−
Am1
−
(
)
1 1
,
Am1
−
(
)
2 1
,
Am1
−
(
)
3 1
,
⋅
:=
A1
1
Z1
1
Z1
2
Z1
3
:=
A1
1
3.474
6.713
10.22
=
Strona -9-

DYNAMIKA BUDOWLI
Projekt komina stalowego
AMPLITUDY W DRUGIEJ POSTACI DRGA
Ń
WŁASNYCH:
Am2
δ
M
⋅
ω
k
2
2
⋅
Id
−
:=
Am2
0.364
−
1.59
2.544
3.498
1.53
3.897
8.569
12.242
1.588
5.559
9.721
16.081
1.092
3.971
8.04
11.706
=
Z2
Am2
1 2
,
Am2
2 2
,
Am2
3 2
,
Am2
1 3
,
Am2
2 3
,
Am2
3 3
,
Am2
1 4
,
Am2
2 4
,
Am2
3 4
,
1
−
Am2
−
(
)
1 1
,
Am2
−
(
)
2 1
,
Am2
−
(
)
3 1
,
⋅
:=
A2
1
Z2
1
Z2
2
Z2
3
:=
A2
1
1.706
0.314
2.514
−
=
AMPLITUDY W TRZECIEJ POSTACI DRGA
Ń
WŁASNYCH:
Am3
δ
M
⋅
ω
k
3
2
⋅
Id
−
:=
Am3
3.681
11.703
18.725
25.747
11.263
35.043
63.075
90.107
11.69
40.915
77.908
118.362
8.037
29.225
59.181
92.52
=
Z3
Am3
1 2
,
Am3
2 2
,
Am3
3 2
,
Am3
1 3
,
Am3
2 3
,
Am3
3 3
,
Am3
1 4
,
Am3
2 4
,
Am3
3 4
,
1
−
Am3
−
(
)
1 1
,
Am3
−
(
)
2 1
,
Am3
−
(
)
3 1
,
⋅
:=
A3
1
Z3
1
Z3
2
Z3
3
:=
A3
1
0.024
−
0.968
−
0.983
=
AMPLITUDY W TRZECIEJ POSTACI DRGA
Ń
WŁASNYCH:
Am4
δ
M
⋅
ω
k
4
2
⋅
Id
−
:=
Am4
11.9
32.249
51.599
70.949
31.038
98.321
173.812
248.302
32.213
112.747
216.441
326.161
22.147
80.534
163.08
256.707
=
Z4
Am4
1 2
,
Am4
2 2
,
Am4
3 2
,
Am4
1 3
,
Am4
2 3
,
Am4
3 3
,
Am4
1 4
,
Am4
2 4
,
Am4
3 4
,
1
−
Am4
−
(
)
1 1
,
Am4
−
(
)
2 1
,
Am4
−
(
)
3 1
,
⋅
:=
Strona -10-
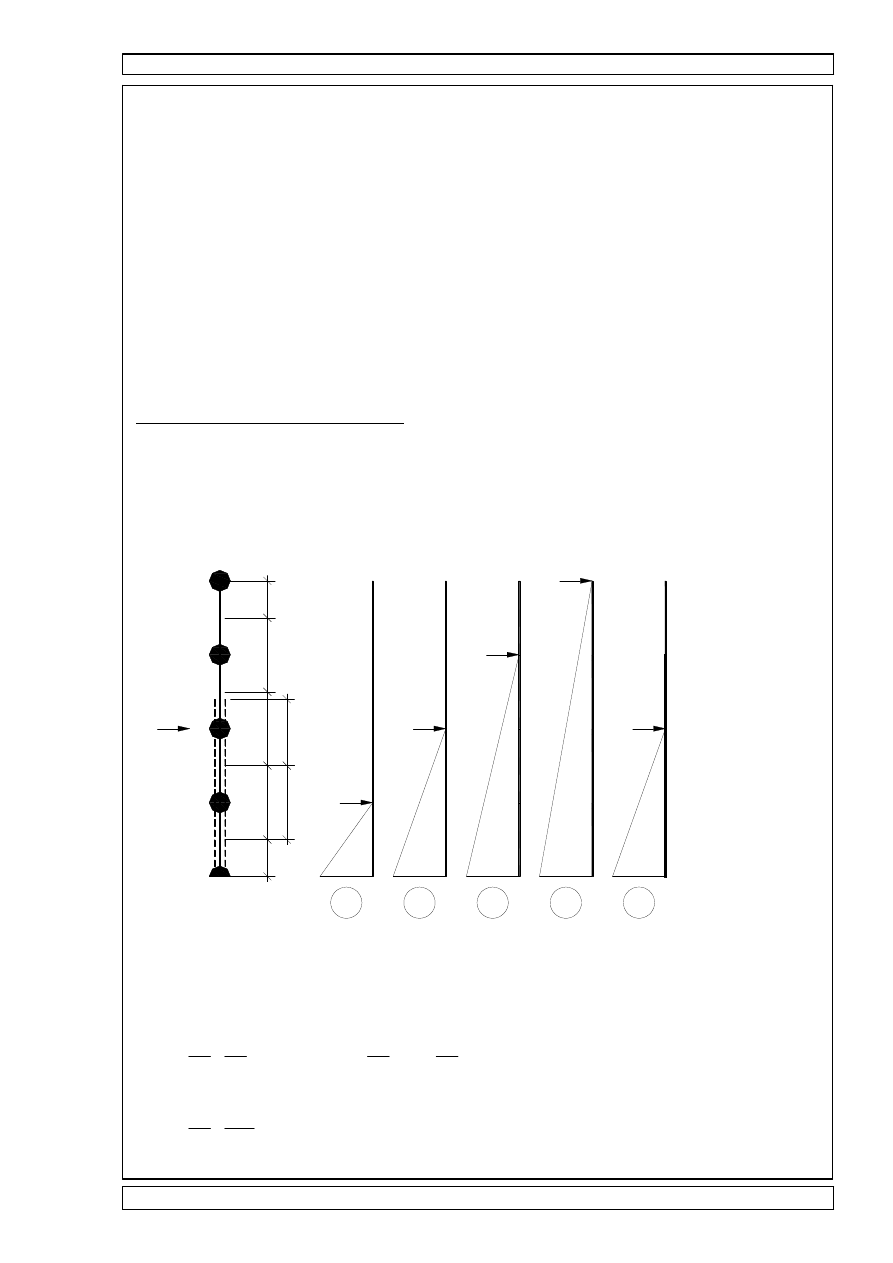
DYNAMIKA BUDOWLI
Projekt komina stalowego
A4
1
Z4
1
Z4
2
Z4
3
:=
A4
1
1.147
−
1.289
0.805
−
=
MACIERZ AMPLITUD:
A
A1
1
A2
1
A3
1
A4
1
A1
2
A2
2
A3
2
A4
2
A1
3
A2
3
A3
3
A4
3
A1
4
A2
4
A3
4
A4
4
:=
A
1
1
1
1
3.474
1.706
0.024
−
1.147
−
6.713
0.314
0.968
−
1.289
10.22
2.514
−
0.983
0.805
−
=
WYMUSZENIE HARMONICZNE:
Siła wymuszaj
ą
ca:
Ya=Pp*sin(wt)
Pp
15kN
:=
w
0.8
ω
k
1
⋅
:=
w
1.058 Hz
⋅
=
tz
1s
:=
P0
Pp sin w tz
⋅
( )
⋅
:=
P0 13.07 kN
⋅
=
hwym
0.5 H
⋅
:=
hwym 70m
=
1
7
.5
3
5
3
5
3
5
1
7
.5
m
0
m
1
m
2
m
3
m
4
3
1
.5
3
5
P
P
P
P
M4
M3
M2
M1
Mp
P
0
P
0
Moment od siły wymuszaj
ą
cej:
Mp
P0 hwym
⋅
:=
Mp
914.931 kNm
⋅
=
Momenty od sił jednostkowych:
M1
35 m
=
M2
70 m
=
M3
105 m
=
M4
140 m
=
∆
1p
1
E I
⋅
hm
6
2 M1
⋅
Mp
⋅
2 0
⋅
Mp
2
⋅
+
M1
Mp
2
⋅
+
0 Mp
⋅
+
⋅
⋅
:=
∆
1p
6.731
10
4
−
×
m
=
∆
2p
1
E I
⋅
2hm
6
2 M2
⋅
Mp
⋅
2 0
⋅
0
⋅
+
M2 0
⋅
+
0 Mp
⋅
+
(
)
⋅
⋅
:=
∆
2p
2.154
10
3
−
×
m
=
Strona -11-
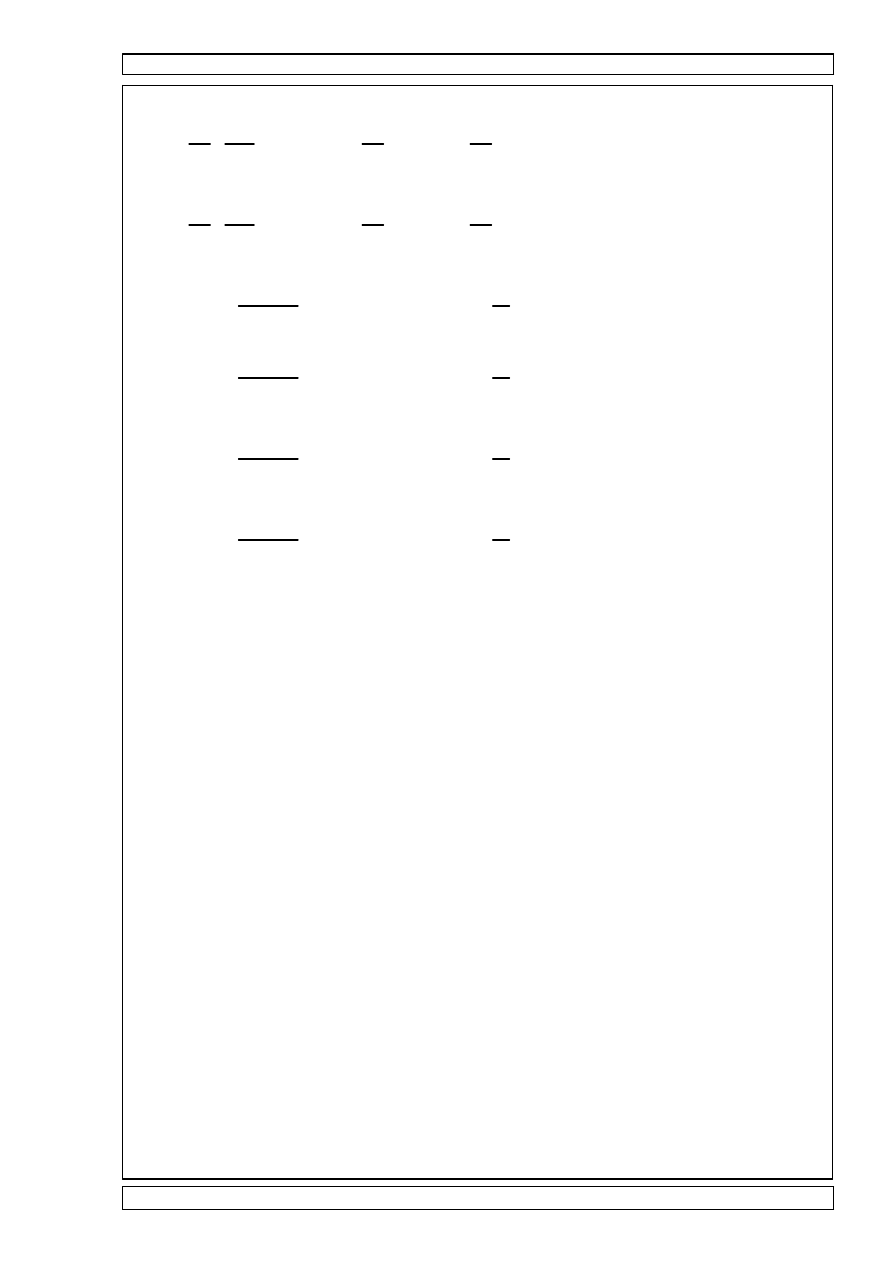
DYNAMIKA BUDOWLI
Projekt komina stalowego
∆
3p
1
E I
⋅
2hm
6
2 M3
⋅
Mp
⋅
2
M3
3
⋅
0
⋅
+
M3 0
⋅
+
M3
3
Mp
⋅
+
⋅
⋅
:=
∆
3p
3.769
10
3
−
×
m
=
∆
4p
1
E I
⋅
2hm
6
2 M4
⋅
Mp
⋅
2
M4
2
⋅
0
⋅
+
M4 0
⋅
+
M4
2
Mp
⋅
+
⋅
⋅
:=
∆
4p
5.385
10
3
−
×
m
=
δ
'
1 1
,
δ
1 1
,
1
M
1 1
,
w
2
⋅
−
:=
δ
'
1 1
,
1.795
−
10
6
−
×
s
2
kg
=
δ
'
2 2
,
δ
2 2
,
1
M
2 2
,
w
2
⋅
−
:=
δ
'
2 2
,
1.679
−
10
6
−
×
s
2
kg
=
δ
'
3 3
,
δ
3 3
,
1
M
3 3
,
w
2
⋅
−
:=
δ
'
3 3
,
2.197
−
10
6
−
×
s
2
kg
=
δ
'
4 4
,
δ
4 4
,
1
M
4 4
,
w
2
⋅
−
:=
δ
'
4 4
,
4.126
−
10
6
−
×
s
2
kg
=
Given
X1
1kN
:=
X2
1kN
:=
X3
1kN
:=
X4
1kN
:=
δ
'
1 1
,
X1
⋅
δ
1 2
,
X2
⋅
+
δ
1 3
,
X3
⋅
+
δ
1 4
,
X4
⋅
+
∆
1p
−
=
δ
2 1
,
X1
⋅
δ
'
2 2
,
X2
⋅
+
δ
2 3
,
X3
⋅
+
δ
2 4
,
X4
⋅
+
∆
2p
−
=
δ
3 1
,
X1
⋅
δ
3 2
,
X2
⋅
+
δ
'
3 3
,
X3
⋅
+
δ
3 4
,
X4
⋅
+
∆
3p
−
=
δ
4 1
,
X1
⋅
δ
4 2
,
X2
⋅
+
δ
4 3
,
X3
⋅
+
δ
'
4 4
,
X4
⋅
+
∆
4p
−
=
SIŁY BEZWŁADNO
Ś
CI:
X1
X2
X3
X4
Find X1 X2
,
X3
,
X4
,
(
)
:=
B
X1
X2
X3
X4
:=
B
0.915
2.959
3.571
2.656
kN
⋅
=
SPECTRUM ODPOWIEDZI:
Wektor sił pionowych:
•
Q
M
1 1
,
M
2 2
,
M
2 2
,
M
2 2
,
g
⋅
:=
Q
4.811
10
3
×
4.63
10
3
×
4.63
10
3
×
4.63
10
3
×
kN
⋅
=
Strona -12-
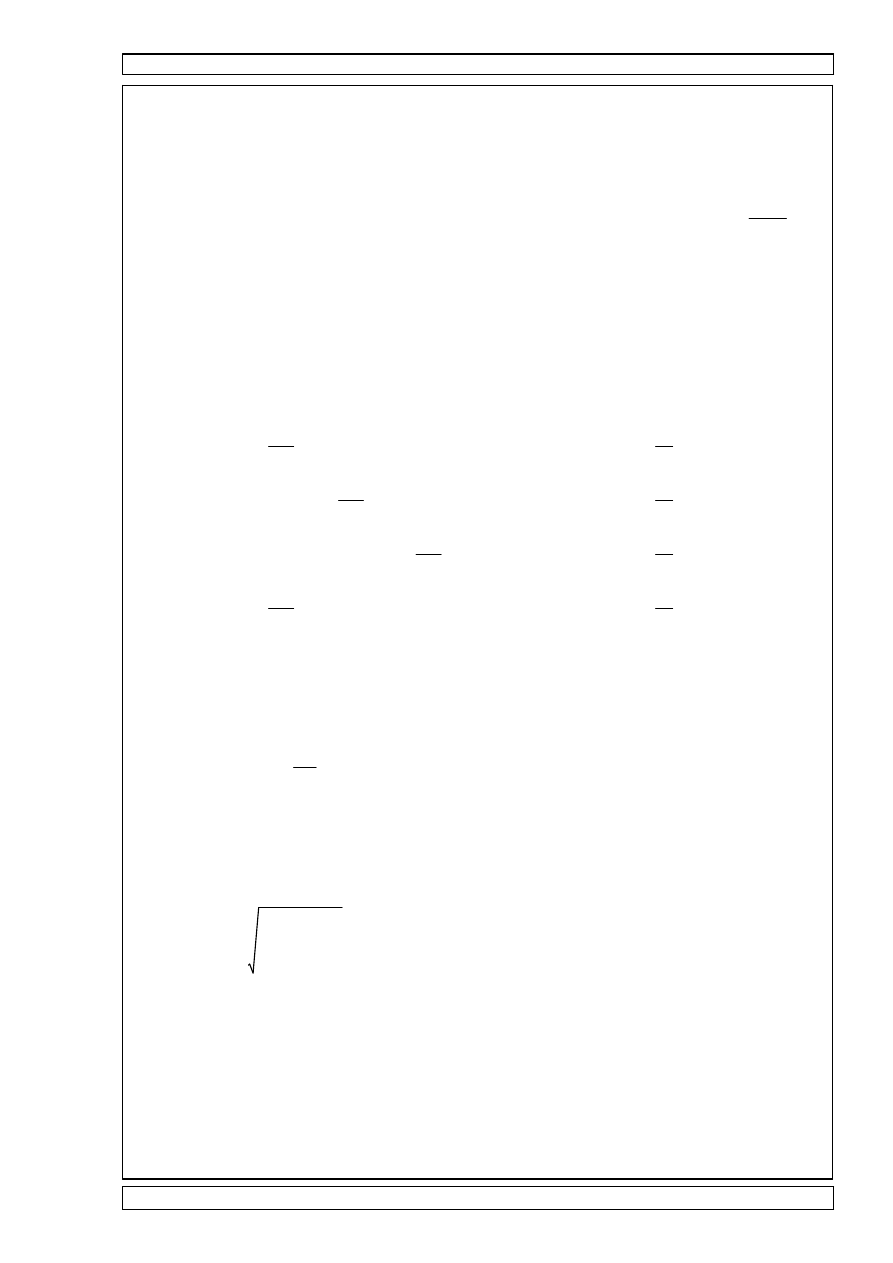
DYNAMIKA BUDOWLI
Projekt komina stalowego
Macierze współczynników drga
ń
:
•
K1
K1
i 1
,
Q
i
A
i j
,
⋅
←
j
1 4
..
∈
for
i
1 4
..
∈
for
:=
K2
K2
i 1
,
Q
i
A
i j
,
⋅
A
T
( )
i j
,
⋅
←
j
1 4
..
∈
for
i
1 4
..
∈
for
:=
η
η
i j
,
A
i j
,
K1
i 1
,
K2
i 1
,
⋅
←
j
1 4
..
∈
for
i
1 4
..
∈
for
:=
K1
4.916
10
4
×
1.164
−
10
4
×
4.552
10
3
×
3.727
−
10
3
×
kN
⋅
=
K2
4.916
10
4
×
1.336
10
4
×
5.869
10
3
×
3
10
3
×
kN
⋅
=
η
1
0.872
−
0.776
1.242
−
3.474
1.487
−
0.018
−
1.425
6.713
0.273
−
0.751
−
1.602
−
10.22
2.191
0.762
1
=
Przyspieszeniowe spectrum odpowiedzi:
•
Sa
1 1
,
0.3
ω
k
1
⋅
mm
s
:=
Sa
1 1
,
3.967
10
4
−
×
m
s
2
=
Sa
2 1
,
0.2
ω
k
1
⋅
0.1
ω
k
2
⋅
+
mm
s
:=
Sa
2 1
,
9.614
10
4
−
×
m
s
2
=
Sa
3 1
,
0.2
ω
k
1
⋅
0.1
ω
k
2
⋅
+
0.03
ω
k
3
⋅
+
mm
s
:=
Sa
3 1
,
1.529
10
3
−
×
m
s
2
=
Sa
4 1
,
0.1
ω
k
1
⋅
mm
s
:=
Sa
4 1
,
1.322
10
4
−
×
m
s
2
=
Wektor obci
ąż
e
ń
:
•
P
P
i j
,
Q
i
η
i j
,
⋅
Sa
i
g
⋅
←
j
1 4
..
∈
for
i
1 4
..
∈
for
:=
P
0.195
0.396
−
0.56
0.078
−
0.676
0.675
−
0.013
−
0.089
1.307
0.124
−
0.542
−
0.1
−
1.989
0.995
0.55
0.062
kN
⋅
=
Suma warto
ś
ci sił bezwładno
ś
ci od postaci drga
ń
na poszczególnych kierunkach mas:
•
B
B
i 1
,
1
4
j
P
i j
,
( )
2
∑
=
←
j
1 4
..
∈
for
i
1 4
..
∈
for
:=
B
2.482
1.272
0.954
0.167
kN
⋅
=
Strona -13-

DYNAMIKA BUDOWLI
Projekt komina stalowego
WYMIARY FUNDAMENTU:
Wysoko
ść
fundamentu:
hf
1.2m
:=
Ci
ęż
ar fundamentu:
γ
z
25
kN
m
3
:=
ρ
z
γ
z
g
:=
ρ
z
2.549
10
3
×
kg
m
3
=
Maksymalne warto
ś
ci sił:
Mmax 1.695 10
5
×
kNm
⋅
=
Tmax
Mmax
H
:=
Tmax 1.211 10
3
×
kN
⋅
=
Moment w podstawie fundamentu:
Mf
Mmax Tmax hf
⋅
+
:=
Mf 1.71 10
5
×
kNm
⋅
=
WARUNEK NA NAPR
Ęś
ENIA EKSTREMALNE:
mp
1500kg
:=
masa siły wymuszaj
ą
cej
a
1m
:=
Given
1
4
i
M
i i
,
∑
=
M
1 1
,
2
+
mp
+
a a
⋅
hf
⋅
ρ
z
⋅
+
g
⋅
a
2
6
Mf
a
3
⋅
−
0
=
Find a
( )
26.92 m
=
Przyj
ę
to wymiar fundamentu:
•
a
27m
:=
Masa fundamentu:
•
mf
a a
⋅
hf
⋅
ρ
z
⋅
:=
mf 2.23 10
6
×
kg
⋅
=
Siła osiowa:
•
N
1
4
i
M
i i
,
∑
=
mp
+
mf
+
g
⋅
:=
N
3.583
10
4
×
kN
⋅
=
Moment obracaj
ą
cy w podstawie fundamentu:
•
Mo
Mf
:=
Mo 1.71 10
5
×
kNm
⋅
=
Moment utrzymuj
ą
cy w podstawie fundamentu:
•
Mu
g a
2
hf
⋅
ρ
z
⋅
⋅
hf
2
⋅
N
a
2
⋅
+
:=
Mu 4.968 10
5
×
kNm
⋅
=
Mo Mu
<
Strona -14-

DYNAMIKA BUDOWLI
Projekt komina stalowego
JEDNOSTKI:
ORIGIN
1
:=
mm
1
10
3
−
×
m
=
kN
1000N
:=
Nm
N m
⋅
:=
MPa
MN
m
2
:=
t
1000kg
:=
Pa
N
m
2
:=
MN
1000kN
:=
kNm
kN m
⋅
:=
GPa
GN
m
2
:=
GN
1000MN
:=
MNn
MN m
⋅
:=
kPa
kN
m
2
:=
GNm
GN m
⋅
:=
Strona -15-

DYNAMIKA BUDOWLI
Projekt komina stalowego
Mmaxk
pksr H
2
⋅
2
:=
Mmaxk 93184.182 kNm
⋅
=
u
1
E I
⋅
1
4
Mmaxk
⋅
140
⋅
m 140
⋅
m
⋅
:=
u
85.273 cm
⋅
=
Strona -16-

DYNAMIKA BUDOWLI
Projekt komina stalowego
ms i
( )
π
dz
2
4
dw
2
4
−
⋅
h
i
( )
⋅
ρ
s
⋅
π
dw
2
4
dw 2 gc
⋅
−
(
)
2
4
−
⋅
h
i
( )
⋅
ρ
w
⋅
+
:=
Strona -17-

DYNAMIKA BUDOWLI
Projekt komina stalowego
n
n
Hz
:=
Strona -18-
Wyszukiwarka
Podobne podstrony:
Projekt komina stalowego 2
Projekt komina stalowego 2
A Biegus projektowanie konctrukcji stalowych wg PN EN 1993 1 1 cz 1
Projekt stropu stalowego wytyczne i wymagania
Projekt komina przemysłowego
Projekt Stropu Stalowego wg Eurocodu 3
EKONOMIKA BUDOWNICTWA, PROCES PROJEKTOWY, Budownictwo stalowe obejmuje zasadniczo budowle i konstruk
Projekt komina zelbetowego
PN EN 1993 1 1 Projektowanie konstrukcji stalowych Reguły ogólne i reguły dla budynków
Projekt Komina, budownictwo, semestr VI, budownictwo przemysłowe, kominy
Praca projektowa Słup stalowy osiowo ściskany, szkola, szkola, sem 5, konstrukcje metalowe
Projektowanie stężeń stalowych
projekt stropu stalowego
Projekt hali stalowej obliczenia
PN EN 1993 1 8 Eurokod 3 Projektowanie konstrukcji stalowych Część 1 8 Projektowanie węzłów
PN EN 1993 1 1 2006 Projekt konstr stalowych
więcej podobnych podstron