2.2 Zestawienie obciążeń stropu.

IPE 300 - eksploatacja
Rodzaj warstwy	ob. charakterystyczne	γf	ob. obliczeniowe
		[kN/m^2]	[-]	[kN/m^2]
płyta g-k gr. 9,5mm	0,07	1,2	0,08
belka stalowa dwuteowa IPE 300	0,41	1,1	0,46
blacha trapezowa TRB-55 h=55mm gr 1mm	0,12	1,1	0,13
płyta betonowa gr. nadbetonu = 50mm [0,068*24]	1,63	1,1	1,80
folia polietylenowa	-	-	-
styropian h=40mm [0,04*0,45]	0,02	1,2	0,02
folia polietylenowa	-	-	-
gładź cementowa h=30mm [0,03*21]	0,63	1,3	0,82
płytki lastrykowe h=20cm na zaprawie cementowej 1:3	0,76	1,3	0,99
obciążenie zmienne	5,50	1,2	6,60
RAZEM:	9,14		10,90

A zatem: g_k=9,14kN/m² oraz g_o=10,90kN/m².

2.3. Obliczenie belki A1.

2.3.1. Przyjęcie wymiarów kształtownika.

Zebranie obciążenia z rozpiętości belek:

.

Długość obliczeniowa belki:

.

Schemat statyczny:

Wówczas moment zginający w środku przęsła wynosi:

.

Przyjęto wstępnie przekrój dwuteowy IPE 300 wykonany ze stali StS3 (f_d=215MPa dla t<16mm). Z „Tablic do projektowania konstrukcji metalowych” autorstwa Władysława Boguckiego i Mikołaja Żyburtowicza [1] odczytać można że:

.

Warunek normowy nośności momentowej ma następującą postać:

(wzór 42 PN-90/B-03200),

a zatem należy sprawdzić, czy:

, gdzie
(dla dwuteowników IPE).

Mamy więc:

.

Ponieważ

,

to warunek nośności nie jest spełniony i należy przyjąć wyższy przekrój.

Przyjęto IPE 330 (
).Wówczas:

IPE 330 - eksploatacja
Rodzaj warstwy	ob. charakterystyczne	γf	ob. obliczeniowe
		[kN/m^2]	[-]	[kN/m^2]
płyta g-k gr. 9,5mm	0,07	1,2	0,08
belka stalowa dwuteowa IPE 330	0,48	1,1	0,53
blacha trapezowa TRB-55 h=55mm gr 1mm	0,12	1,1	0,13
płyta betonowa gr. nadbetonu = 50mm [0,068*24]	1,63	1,1	1,80
folia polietylenowa	-	-	-
styropian h=40mm [0,04*0,45]	0,02	1,2	0,02
folia polietylenowa	-	-	-
gładź cementowa h=30mm [0,03*21]	0,63	1,3	0,82
płytki lastrykowe h=20cm na zaprawie cementowej 1:3	0,76	1,3	0,99
obciążenie zmienne	5,50	1,2	6,60
RAZEM:	9,21		10,97

Wtedy: g_k=9,21kN/m² oraz g_o=10,97kN/m²,

,

,

.

Ponieważ

,

to warunek nośności momentowej jest spełniony.

Dobór wymiarów kształtownika ze względu na sztywność dla obciążenia całkowitego:

.

, gdzie E=205GPa.

Zakładając, że f_gr=f_n=0,02m mamy:

.

Jest to minimalny moment bezwładności jakim powinien się charakteryzować przekrój.

Powyższy warunek spełnia IPE 300 (I_x=8360cm⁴).

Ostatecznie przyjęto IPE 330.

2.3.2. Klasyfikacja przekroju (wg tab. 6 PN-90/B-03200).

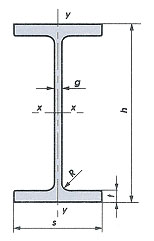
IPE 330

H = 330mm;

s = b_f = 160mm;

g = t_w =7,5mm;

t = t_f = 11,5mm;

R = 18mm.

.

Sprawdzam klasę przekroju dla środnika:

,

wobec tego środnik należy do klasy 1.

Sprawdzam klasę przekroju dla półek:

,

więc półki również należą do klasy 1.

Zatem cały przekrój należy do klasy 1.

2.3.3. Nośność obliczeniowa przekroju na ścinanie (obciążenia eksploatacyjne).

Sprawdzam, czy spełniony jest warunek smukłości:

(tab.7 PN-90/B-03200),

.

Można zatem obliczyć nośność przy ścinaniu wg wzoru:

(wzór 47 PN-90/B-03200),

gdzie
.

Wówczas:

.

Warunek normowy nośności na ścinanie jest następujący:

,

gdzie
. Wówczas:

,

a zatem warunek nośności na ścinanie jest spełniony.

Sprawdzam czy V<0,6V_R:

Ponieważ powyższy warunek jest spełniony, to nośność momentową wyznaczam jako nośność na zginanie bez ścinania.

2.3.4. Nośność obliczeniowa przekroju przy jednokierunkowym zginaniu (obciążenia eksploatacyjne).

Dla przyjętego IPE 330
.

Z wcześniejszych obliczeń mamy: g_o=10,97kN/m²,
.

Wówczas nośność przekroju przy jednokierunkowym zginaniu wynosi:

.

Aby był spełniony warunek nośności prawdziwa musi być zależność:

(wzór 52 PN-90/B-03200),

,

zatem warunek nośności momentowej przy jednokierunkowym zginaniu jest spełniony.

2.3.5. Sprawdzenie stanu granicznego użytkowania (obciążenia eksploatacyjne).

Aby nie został przekroczony stan graniczny użytkowania spełniony musi być warunek:

Określam maksymalne ugięcie:

,

.

Ponieważ:

,

to stan graniczny użytkowania nie jest przekroczony.

2.3.6. Sprawdzenie nośności na ścinanie belki (obciążenie montażowe).

Zestawienie obciążeń dla fazy montażu:

IPE 330 - montaż
Rodzaj warstwy	ob. charakterystyczne	γf	ob. obliczeniowe
		[kN/m^2]	[-]	[kN/m^2]
belka stalowa dwuteowa IPE 330	0,48	1,1	0,53
blacha trapezowa TRB-55 h=55mm gr 1mm	0,12	1,1	0,13
płyta betonowa gr. nadbetonu = 50mm [0,068*24]	1,63	1,1	1,80
deskowanie (deski sosnowe) gr. 50mm [0,05*6,0]	0,30	1,2	0,36
obciążenie człowiekiem z narzędziami	1,50	1,4	2,10
RAZEM:	4,03		4,92

Wtedy: g_k=4,03kN/m² oraz g_o=4,92kN/m²

Spełniony musi być następujący warunek:

,

gdzie
(wyznaczono w pkt 2.3.4.) oraz

Wówczas:

,

a zatem spełniony jest warunek nośności na ścinanie w fazie montażu.

Sprawdzam czy V<0,6V_R:

Ponieważ powyższy warunek jest spełniony, to nośność momentową wyznaczam jako nośność na zginanie bez ścinania.

2.3.6. Sprawdzenie nośności momentowej przekroju przy jednokierunkowym zginaniu (obciążenia montażowe).

(wzór 52 PN-90/B-03200),

gdzie
. Wyznaczam współczynnik zwichrzenia:

Aby wyznaczyć
należy najpierw określić smukłość względną przy zwichrzeniu:

(wzór 51 PN-90/B-03200),

gdzie β=1. Wówczas:

Korzystając z tab. 11 PN-90/B-03200 można odczytać, że:

=0,758,

wtedy:

,

(wyznaczono w pkt 2.3.3.)

Należy sprawdzić, czy:

.

Powyższy warunek jest prawdziwy, a zatem spełniony jest warunek nośności momentowej w fazie montażu.

2.3.8. Sprawdzenie oparcia belki na murze.

Średnie lokalne naprężenia ściskające pod obciążeniem skupionym wywołanym naciskiem belki określone muszą spełniać następujący warunek:

(wzór 39 PN-B-03002:1999).

(wzór 2 PN-B-03002:1999).

Wytrzymałość cegły:

(wzór 1 PN-B-03002:1999).

Dla cegły zwykłej (f_B=15MPa) o wysokości 65mm można zapisać, że:

Wytrzymałość zaprawy:

Współczynnik K=0,5.

Wówczas:

.

Obliczenia wykonane są dla skrajnej belki, dla której:

.

Przyjęto wysokość ścian: H=5m oraz szerokość muru: t=0,51m.

Wtedy:

.

.

.

Ponieważ
, to przyjęto x=1.

,

(wyznaczono w pkt 2.3.3. jako reakcję równą sile tnącej).

Wtedy:

Ponieważ warunek jest spełniony, to nie jest konieczna podkładka.

2.4. Obliczenie belki A2.

2.4.1. Przyjęcie wymiarów kształtownika.

Wstępnie przyjęto przekrój dwuteowy IPE 330. Zestawienie obciążeń:

IPE 330 - eksploatacja
Rodzaj warstwy	ob. charakterystyczne	γf	ob. obliczeniowe
		[kN/m^2]	[-]	[kN/m^2]
płyta g-k gr. 9,5mm	0,07	1,2	0,08
belka stalowa dwuteowa IPE 330	0,48	1,1	0,53
blacha trapezowa TRB-55 h=55mm gr 1mm	0,12	1,1	0,13
płyta betonowa gr. nadbetonu = 50mm [0,068*24]	1,63	1,1	1,80
folia polietylenowa	-	-	-
styropian h=40mm [0,04*0,45]	0,02	1,2	0,02
folia polietylenowa	-	-	-
gładź cementowa h=30mm [0,03*21]	0,63	1,3	0,82
płytki lastrykowe h=20cm na zaprawie cementowej 1:3	0,76	1,3	0,99
obciążenie zmienne	5,50	1,2	6,60
RAZEM:	9,21		10,97

Wtedy: g_k=9,21kN/m² oraz g_o=10,97kN/m²,

Zebranie obciążenia z rozpiętości belek:

.

Długość obliczeniowa belki:

.

Schemat statyczny:

Wówczas moment zginający w środku przęsła wynosi:

.

Przyjęto wstępnie przekrój dwuteowy IPE 330 wykonany ze stali StS3y (f_d=215MPa dla t<16mm). Z „Tablic do projektowania konstrukcji metalowych” autorstwa Władysława Boguckiego i Mikołaja Żyburtowicza [1] odczytać można że:

.

Warunek normowy nośności momentowej ma następującą postać:

(wzór 42 PN-90/B-03200),

a zatem należy sprawdzić, czy:

, gdzie
(dla dwuteowników IPE).

Mamy więc:

.

Ponieważ

,

to warunek nośności nie jest spełniony i należy przyjąć wyższy przekrój.

Przyjęto IPE 400 (
).Wówczas:

IPE 400 - eksploatacja
Rodzaj warstwy	ob. charakterystyczne	γf	ob. obliczeniowe
		[kN/m^2]	[-]	[kN/m^2]
płyta g-k gr. 9,5mm	0,07	1,2	0,08
belka stalowa dwuteowa IPE 400	0,65	1,1	0,72
blacha trapezowa TRB-55 h=55mm gr 1mm	0,12	1,1	0,13
płyta betonowa gr. nadbetonu = 50mm [0,068*24]	1,63	1,1	1,80
folia polietylenowa	-	-	-
styropian h=40mm [0,04*0,45]	0,02	1,2	0,02
folia polietylenowa	-	-	-
gładź cementowa h=30mm [0,03*21]	0,63	1,3	0,82
płytki lastrykowe h=20cm na zaprawie cementowej 1:3	0,76	1,3	0,99
obciążenie zmienne	5,50	1,2	6,60
RAZEM:	9,38		11,16

Wtedy: g_k=9,38kN/m² oraz g_o=11,16kN/m²,

,

,

.

Ponieważ

,

to warunek nośności momentowej jest spełniony.

Dobór wymiarów kształtownika ze względu na sztywność dla obciążenia całkowitego:

.

, gdzie E=205GPa.

Zakładając, że f_gr=f_n=0,028m mamy:

.

Jest to minimalny moment bezwładności jakim powinien się charakteryzować przekrój.

Powyższy warunek spełnia IPE 400 (I_x=23130cm⁴).

Ostatecznie przyjęto IPE 400.

2.4.2. Klasyfikacja przekroju (wg tab. 6 PN-90/B-03200).

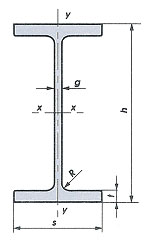
IPE 400

H = 400mm;

s = b_f = 180mm;

g = t_w =8,6mm;

t = t_f = 13,5mm;

R = 21mm.

.

Sprawdzam klasę przekroju dla środnika:

,

wobec tego środnik należy do klasy 1.

Sprawdzam klasę przekroju dla półek:

,

więc półki również należą do klasy 1.

Zatem cały przekrój należy do klasy 1.

2.4.3. Nośność obliczeniowa przekroju na ścinanie (obciążenia eksploatacyjne).

Sprawdzam, czy spełniony jest warunek smukłości:

(tab.7 PN-90/B-03200),

.

Można zatem obliczyć nośność przy ścinaniu wg wzoru:

(wzór 47 PN-90/B-03200),

gdzie
.

Wówczas:

.

Warunek normowy nośności na ścinanie jest następujący:

,

gdzie
. Wówczas:

,

a zatem warunek nośności na ścinanie jest spełniony.

Sprawdzam czy V<0,6V_R:

Ponieważ powyższy warunek jest spełniony, to nośność momentową wyznaczam jako nośność na zginanie bez ścinania.

2.4.4. Nośność obliczeniowa przekroju przy jednokierunkowym zginaniu (obciążenia eksploatacyjne).

Dla przyjętego IPE 400
.

Z wcześniejszych obliczeń mamy: g_o=11,16kN/m²,
.

Wówczas nośność przekroju przy jednokierunkowym zginaniu wynosi:

.

Aby był spełniony warunek nośności prawdziwa musi być zależność:

(wzór 52 PN-90/B-03200),

,

zatem warunek nośności momentowej przy jednokierunkowym zginaniu jest spełniony.

2.4.5. Sprawdzenie stanu granicznego użytkowania (obciążenia eksploatacyjne).

Aby nie został przekroczony stan graniczny użytkowania spełniony musi być warunek:

Określam maksymalne ugięcie:

,

.

Ponieważ:

,

to stan graniczny użytkowania nie jest przekroczony.

2.4.6. Sprawdzenie nośności na ścinanie belki (obciążenie montażowe).

Zestawienie obciążeń dla fazy montażu:

IPE 400 - montaż
Rodzaj warstwy	ob. charakterystyczne	γf	ob. obliczeniowe
		[kN/m^2]	[-]	[kN/m^2]
belka stalowa dwuteowa IPE 400	0,65	1,1	0,72
blacha trapezowa TRB-55 h=55mm gr 1mm	0,12	1,1	0,13
płyta betonowa gr. nadbetonu = 50mm [0,068*24]	1,63	1,1	1,80
deskowanie (deski sosnowe) gr. 50mm [0,05*6,0]	0,30	1,2	0,36
obciążenie człowiekiem z narzędziami	1,50	1,4	2,10
RAZEM:	4,20		5,10

Wtedy: g_k=4,20kN/m² oraz g_o=5,10kN/m²

Spełniony musi być następujący warunek:

,

gdzie
(wyznaczono w pkt 2.4.3.) oraz

Wówczas:

,

a zatem spełniony jest warunek nośności na ścinanie w fazie montażu.

Sprawdzam czy V<0,6V_R:

Ponieważ powyższy warunek jest spełniony, to nośność momentową wyznaczam jako nośność na zginanie bez ścinania.

2.4.7. Sprawdzenie nośności momentowej przekroju przy jednokierunkowym zginaniu (obciążenia montażowe).

(wzór 52 PN-90/B-03200),

gdzie
. Wyznaczam współczynnik zwichrzenia:

Aby wyznaczyć
należy najpierw określić smukłość względną przy zwichrzeniu:

(wzór 51 PN-90/B-03200),

gdzie β=1. Wówczas:

Korzystając z tab. 11 PN-90/B-03200 można odczytać, że:

=0,707,

wtedy:

,

(wyznaczono w pkt 2.4.4.)

Należy sprawdzić, czy:

.

Powyższy warunek jest prawdziwy, a zatem spełniony jest warunek nośności momentowej w fazie montażu.

2.4.8. Sprawdzenie oparcia belki na murze.

Średnie lokalne naprężenia ściskające pod obciążeniem skupionym wywołanym naciskiem belki określone muszą spełniać następujący warunek:

(wzór 39 PN-B-03002:1999).

(wzór 2 PN-B-03002:1999).

Wytrzymałość cegły:

(wzór 1 PN-B-03002:1999).

Dla cegły zwykłej (f_B=15MPa) o wysokości 65mm można zapisać, że:

Wytrzymałość zaprawy:

Współczynnik K=0,5.

Wówczas:

.

Obliczenia wykonane są dla skrajnej belki, dla której:

.

Przyjęto wysokość ścian: H=5m oraz szerokość muru: t=0,51m.

Wtedy:

.

.

.

Ponieważ
, to przyjęto x=1.

,

(wyznaczono w pkt 2.4.3 jako reakcję równą sile tnącej).

Wtedy:

Ponieważ warunek jest spełniony, to nie jest konieczna podkładka.

2.4.9. Sprawdzenie oparcia belki na murze wg PN-87/B-03002.

Aby projektowanie podkładki nie było konieczne spełniony musi być warunek:

(wzór 26 norma PN-87/B-03002)

gdzie m_d - współczynnik korekcyjny
.

Wówczas:

.

Zakładając, że oparcie belki A2 na murze wynosi b=36cm, ściana ma szerokość h=51cm zaś szerokość oparcia dwuteownika IPE 400 jest równa jego szerokości a=s=18cm. Wtedy:

,

oraz
,
. Wówczas:

.

Oraz:

,

gdzie
(reakcja z punktu 2.4.3.). Wtedy:

Odczytano z poprzedniego punktu, że:

.

A zatem:
.

Ostatecznie:

.

Wobec tego nie trzeba projektować podkładki.

2.5. Obliczenie belki A3 - podciąg drugorzędny.

2.5.1. Przyjęcie wymiarów kształtownika.

Wstępnie przyjęto dwuteownik szerokostopowy HEB 300.

BELKA A-3
HEB 300 - eksploatacja
Rodzaj warstwy	ob. charakterystyczne	γf	ob. obliczeniowe
		[kN/m^2]	[-]	[kN/m^2]
płyta g-k gr. 9,5mm	0,07	1,2	0,08
belka stalowa dwuteowa HEB 300	1,15	1,1	1,27
blacha trapezowa TRB-55 h=55mm gr 1mm	0,12	1,1	0,13
płyta betonowa gr. nadbetonu = 50mm [0,068*24]	1,63	1,1	1,80
folia polietylenowa	-	-	-
styropian h=40mm [0,04*0,45]	0,02	1,2	0,02
folia polietylenowa	-	-	-
gładź cementowa h=30mm [0,03*21]	0,63	1,3	0,82
płytki lastrykowe h=20cm na zaprawie cementowej 1:3	0,76	1,3	0,99
obciążenie zmienne	5,50	1,2	6,60
RAZEM:	9,88		11,71
BEZ BELKI:	8,73		10,44

Wtedy: g_k=9,88kN/m² oraz g_o=10,44kN/m²,

Zebranie obciążenia z rozpiętości belek:

.

Długość obliczeniowa belki:

.

Schemat statyczny:

W celu uzyskania wykresów momentów i sił tnących wprowadzono powyższy schemat statyczny do programu RM-WIN. Otrzymano następujące wykresy:

WYKRES MOMENTÓW [kNm]:

WYKRES SIŁ TNĄCYCH [kN]:

Widać, że M_max=238,28kNm oraz V_max= 141,97kN.

2.5.2. Klasyfikacja przekroju (wg tab. 6 PN-90/B-03200).

Przyjęto wstępnie przekrój dwuteowy szerokostopowy HEB 300 wykonany ze stali 18G2A (f_d=295MPa dla 40mm>t=19mm>16mm). Z „Tablic do projektowania konstrukcji metalowych” autorstwa Władysława Boguckiego i Mikołaja Żyburtowicza [1] odczytać można że:

.

Należy sprawdzić, czy przy obliczaniu nośności trzeba uwzględniać ścinanie. W tym celu wyznaczam klasę przekroju:

HEB 300

H = 300mm;

b_f = 300mm;

t_w =11mm;

t_f = 19mm;

r = 27mm

.

Sprawdzam klasę przekroju dla środnika:

,

wobec tego środnik należy do klasy 1.

Sprawdzam klasę przekroju dla półek:

,

więc półki również należą do klasy 1.

Zatem cały przekrój należy do klasy 1.

2.5.3. Nośność obliczeniowa przekroju (obciążenia eksploatacyjne).

Sprawdzam warunek:

gdzie V - siła tnąca odpowiadająca największemu momentowi zginającemu oraz

.

Sprawdzam warunek smukłości dla dwuteownika z tab. 7 PN-90-B-03200:

.

Ponieważ warunek smukłości jest spełniony, to:

Wtedy:

Sprawdzam wobec tego, czy:

Ponieważ:

to nie należy redukować nośności obliczeniowej przekroju do wartości M_R,V.

Wobec tego dla przekroju klasy 1 mamy:

(wzór 42. PN-90-B-03200)

Przyjęto α_P=1 (założono, że nie nastąpi wykorzystanie elementu ponad granicę sprężystości). Wówczas:

Sprawdzić należy warunek nośności elementu jednokierunkowo zginanego:

(wzór 52 PN-90/B-03200),

Zakładam, że w fazie eksploatacji belka jest zabezpieczona przed zwichrzeniem, wobec tego:

=1.

Wówczas:

Ze względu na niewielkie wykorzystanie nośności przekroju zdecydowano przyjąć mniejszy dwuteownik.

Przyjęto: HEB 240 ze stali 18G2A (f_d=295MPa dla 40mm>t=19mm>16mm). Z „Tablic do projektowania konstrukcji metalowych” odczytać można że:

.

Należy sprawdzić, czy przy obliczaniu nośności trzeba uwzględniać ścinanie. W tym celu wyznaczam klasę przekroju:

HEB 240

H = 240mm;

b_f = 240mm;

t_w =10mm;

t_f = 17mm;

r = 21m

.

Sprawdzam klasę przekroju dla środnika:

,

wobec tego środnik należy do klasy 1.

Sprawdzam klasę przekroju dla półek:

,

więc półki również należą do klasy 1.

Zatem cały przekrój należy do klasy 1.

Sprawdzam warunek:

gdzie V - siła tnąca odpowiadająca największemu momentowi zginającemu oraz

.

Sprawdzam warunek smukłości dla dwuteownika z tab. 7 PN-90-B-03200:

.

Ponieważ warunek smukłości jest spełniony, to:

Wtedy:

Sprawdzam wobec tego, czy:

Ponieważ:

to nie należy redukować nośności obliczeniowej przekroju do wartości M_R,V.

Wobec tego dla przekroju klasy 1 mamy:

(wzór 42. PN-90-B-03200)

Przyjęto α_P=1 (założono, że nie nastąpi wykorzystanie elementu ponad granicę sprężystości). Wówczas:

Sprawdzić należy warunek nośności elementu jednokierunkowo zginanego:

(wzór 52 PN-90/B-03200),

Zakładam, że w fazie eksploatacji belka jest zabezpieczona przed zwichrzeniem, wobec tego:

=1.

Wówczas:

2.5.4. Sprawdzenie stanu granicznego użytkowania (obciążenia eksploatacyjne).

Aby nie został przekroczony stan graniczny użytkowania spełniony musi być warunek:

Określam maksymalne ugięcie:

,

.

,

gdzie
:

,

Wtedy:

Ponieważ:

,

to stan graniczny użytkowania nie jest przekroczony.

2.5.5. Sprawdzenie nośności belki (obciążenie montażowe).

HEB 240 - montaż
Rodzaj warstwy	ob. charakterystyczne	γf	ob. obliczeniowe
		[kN/m^2]	[-]	[kN/m^2]
belka stalowa dwuteowa HEB 240	0,82	1,1	0,90
blacha trapezowa TRB-55 h=55mm gr 1mm	0,12	1,1	0,13
płyta betonowa gr. nadbetonu = 50mm [0,068*24]	1,63	1,1	1,80
deskowanie (deski sosnowe) gr. 50mm [0,05*6,0]	0,30	1,2	0,36
obciążenie człowiekiem z narzędziami	1,50	1,4	2,10
RAZEM:	4,37		5,29

Wtedy: g_k=4,37kN/m² oraz g_o=5,29kN/m²

WYKRES MOMENTÓW [kNm]:

WYKRES SIŁ TNĄCYCH [kN]:

Sprawdzam czy V<0,6V_R, gdzie V_R wyznaczono w punkcie 2.5.3. zaś V to maksymalna siła tnąca odpowiadająca maksymalnemu momentowi zginającemu:

Ponieważ powyższy warunek jest spełniony, to nośność momentową wyznaczam jako nośność na zginanie bez ścinania.

2.5.6. Sprawdzenie nośności momentowej przekroju przy jednokierunkowym zginaniu (obciążenia montażowe).

(wzór 52 PN-90/B-03200),

gdzie
. Wyznaczam współczynnik zwichrzenia:

Aby wyznaczyć
należy znaleźć wartość
, która wyraża się wzorem

(wzór 50),

Należy zatem wyznaczyć M_cr. Obliczenia wykonano zgodnie z zaleceniami załącznika 1. do PN-90/B-03200:

(wzór Z1-9)

gdzie
. Z tabeli Z1-2 odczytano dla belki swobodnie podpartej obciążonej obciążeniem równomiernie rozłożonym:

A₁=0,61, A₂=0,53, a_s=0,12m, b_y=0, B=1,14.

Wówczas:

.

Wyznaczam N_y:

(wzór Z1-4)

Gdzie μ_y=1 (z tablicy Z1-2) oraz I_y=3920cm⁴ (z „Tablic do projektowania konstrukcji metalowych”). Wtedy:

Wyznaczam N_z:

Z tablicy Z1-2 odczytano: μ_ω=1. Z „Tablic do projektowania konstrukcji metalowych”:
oraz
, i_x=10,3cm, i_y=6,08cm, G=80GPa.

Wtedy:

Wyznaczam M_cr:

Z punktu 2.5.3. mamy:
. Wówczas:

=0,948 ( z tablicy 11.),

Należy sprawdzić, czy:

.

Powyższy warunek jest prawdziwy, a zatem spełniony jest warunek nośności momentowej w fazie montażu.

2.5.7. Sprawdzenie oparcia belki na murze.

Średnie lokalne naprężenia ściskające pod obciążeniem skupionym wywołanym naciskiem belki określone muszą spełniać następujący warunek:

(wzór 39 PN-B-03002:1999).

Wytrzymałość muru na ściskanie wyznaczono w punkcie 2.4.8.:
, γ_m=1,7.

.

Przyjęto wysokość ścian: H=5m oraz szerokość muru: t=0,51m.

Wtedy:

.

.

.

Ponieważ
, to przyjęto x=1.

,

(maksymalna reakcja podporowa wyznaczona w pkt 2.5.1.)

Wtedy:

Ponieważ warunek jest spełniony, to nie jest konieczna podkładka.

2.6. Obliczenie belki B (podciąg).

2.6.1. Schemat statyczny.

Przybliżona wartość obciążenia ciężarem własnym:

Wartości reakcji belek odczytano z programu RM-WIN:

• charakterystyczne:

R_A-1=86,23kN, 2*R_A-1=172,46kN.

R_A-3=139,54kN, 2*R_A-3=279,08kN.

• obliczeniowe:

R_A-1=103,14kN, 2*R_A-1=206,28kN.

R_A-3=141,97kN, 2*R_A-3=283,94kN.

WYKRES MOMENTÓW [kNm]:

WYKRES SIŁ TNĄCYCH [kN]:

M_max=3449,92kNm; V_Mmax=105,02kN; V_max=544,75kN;

2.6.2. Wstępny dobór przekroju.

Projektowany przekrój ma należeć do klasy czwartej.

Zakładam, że belka będzie wykonana ze stali St3S (f_d=215MPa).

Aby określić optymalną wysokość przekroju, korzystam ze wzoru

.

gdzie: t_w=11mm,
. Wówczas:

.

Przyjęto h=135cm=1,35m; t_f=30mm=0,03m. Wtedy:

Wyznaczam szerokość stopki b_f:

Przyjęto: b_f=0,40m.

Ostatecznie:

h=1,36m

t_w=11mm

t_f=30mm

h_w=1,30m

b_f=0,40m.

2.6.3. Określenie nośności przekroju.

Nośność elementu zginanego:

(wzór 52 PN-B/90-03200).

Przy założeniu, że belka jest zabezpieczona przed zwichrzeniem (φ=1), należy do klasy 4 i jest wykonana ze stali St3S a jej środnik ma grubość
(f_d=215MPa) mamy:

W celu określenia współczynnika ψ określam smukłość względną ścianki:

(wzór 7 PN-B/90-03200),

gdzie b=h_w=1,30m; t=t_w=0,011m; K=0,4 (gdyż stosunek naprężeń średnich do maksymalnych jest równy zeru). Wówczas:

.

Z tablicy 9. można odczytać, że wtedy
.

Zgodnie z punktem 4.2.2.3 mamy:

.

Dla przyjętego przekroju wyznaczono moment bezwładności I_x=1242400cm⁴ oraz wskaźnik na zginanie W_x=18406cm³. Zatem:

Ze względu na dobre wykorzystanie przyjętego przekroju nie wykonuję optymalizacji wymiarów. Ostateczne wymiary, przyjęte do dalszych obliczeń:

h=1,36m

t_w=11mm

t_f=30mm

h_w=1,30m

b_f=0,40m.

2.6.4. Korekta sił wewnętrznych (z uwzględnieniem ciężaru własnego belki).

Wyznaczam pole przekroju:

.

Wtedy masa na 1m belki wynosi:

.

Wówczas:

.

Wartość obliczeniowa obciążenia ciężarem własnym:

2.6.5. Nośność na zginanie.

2.6.5.1. Kształtowanie podłużne blachownicy.

Ponieważ l=22m, to należy podzielić blachownicę na 5 elementów o długości:

• środkowy: 5,00m

• pozostałe: 4,25m

2.6.5.1.1. Nośność odcinka środkowego (nr 1).

(wzór 52 PN-B/90-03200)

gdzie:

, φ_L=1.

Wówczas:

A zatem warunek nośności momentowej odcinka środkowego jest spełniony.

Należy również sprawdzić stateczność pasa. Warunek normowy:

(wzór 9 PN-90/B-03200),

gdzie

.

zaś φ_P jest zależne od:

(wzór 7 PN-90/B-03200),

gdzie
; t=t_f=0,03m;

K=2,2+0,8ν gdzie ν=1 (stały rozkład naprężeń w półce). Wtedy: K=3,0. Wówczas:

Wtedy: φ_P=1.

Można zatem zapisać, że:

.

Oznacza to, że warunek stateczności pasa jest spełniony.

2.6.5.1.2. Nośność odcinka nr 2 i nr 4.

Ze względu na niewielkie różnice momentów zginających na odcinkach 2 i 4 wymiaruję oba odcinki na większy moment:

Przyjęto półkę o grubości t_f=20mm. Wówczas
.

Określam wskaźnik przyjętego przekroju:

Moment bezwładności względem osi X przechodzącej przez środek ciężkości przekroju:

• Połowy środnika:
  

• Jednej półki:
  

Moment bezwładności całego przekroju:

Wtedy:

.

Ponieważ

,

to należy zwiększyć wysokość półki.

Przyjęto półkę o grubości t_f=24mm. Wówczas
.

Wtedy moment bezwładności półki wyniesie:

Wówczas:

Oraz:

Ponieważ

,

to należy zwiększyć wysokość półki.

Ponieważ wówczas różnica wysokości półek na odcinku 1 i odcinkach 2,4 byłaby mniejsza niż 6 mm, postanowiono wydłużyć odcinek 1.

Wówczas:

• Środkowy odcinek: 5,4m

• Pozostałe: 4,15m.

Wtedy:

W takim przypadku również nie jest spełniony warunek:

Ostatecznie zdecydowano pozostać przy poprzednim podziale na elementy (środkowy: 5,00m, pozostałe 4,25m) i zmniejszyć wymiar półki o 5mm. Wówczas:

Moment bezwładności półki:

Wówczas:

Oraz:

Ponieważ

,

to przyjęte wymiary na odcinku 2 oraz 4 są wystarczające.

Ostatecznie przyjęto na odcinkach 2 i 4:

h=1,35m

t_w=11mm

t_f=25mm

h_w=1,30m

b_f=0,40m.

2.6.5.1.3. Nośność odcinka nr 3 i nr 5.

Ze względu na niewielkie różnice momentów zginających na odcinkach 2 i 4 wymiaruję oba odcinki na większy moment:

Przyjęto półkę o grubości t_f=18mm. Wówczas
.

Określam wskaźnik przyjętego przekroju:

Moment bezwładności względem osi X przechodzącej przez środek ciężkości przekroju:

• Połowy środnika:
  

• Jednej półki:
  

Moment bezwładności całego przekroju:

Wtedy:

.

Ponieważ

,

to przyjęte wymiary na odcinku 3 oraz 5 są wystarczające.

Ostatecznie przyjęto na odcinkach 3 i 5:

h=1,336m

t_w=11mm

t_f=18mm

h_w=1,30m

b_f=0,40m.

2.6.5.2. Sprawdzenie warunku nośności momentowej blachownicy.

(wzór 52 PN-B/90-03200)

Dla odcinka 1: punkt 2.6.5.1.1.

Dla odcinka 2,4:

Warunek nośności momentowej jest spełniony.

Dla odcinka 3,5:

2.6.6. Sprawdzenie warunku nośności na ścinanie.

Sprawdzam warunek smukłości środnika wg tab.7:

,

wówczas:

.

Wobec tego:

(wzór 16 PN-90/B-03200).

gdzie
a

(wzór 7 PN-90/B-03200).

gdzie:

Ponieważ:

β=a/b=4,25m/1,3m=3,27, to:

Więc K=0,8.

Wówczas:

Natomiast:

Pole czynne przy ścinaniu:

Ostatecznie:

Sprawdzam nośność na ścinanie dla maksymalnej siły tnącej V_max=553,33kN:

.

Warunek nośności na ścinanie jest spełniony.

Sprawdzam warunek:

.

Ponieważ:

,

to nośność momentowa wyraża się wzorem:

(wzór 46 PN-90/B-03200).

2.6.6. Sprawdzenie zredukowanej nośności momentowej.

2.6.6.1. Dla odcinków 3, 5.

gdzie M_R^3,5=
; I_v=201391,6cm⁴, I=826795,2cm⁴. Wówczas:

Wtedy:

Ze względu na powtarzające się problemy ze spełnieniem warunków nośności postanowiono powtórzyć wstępny dobór przekroju z większym zapasem nośności:

2.7. Obliczenie belki B (podciąg).

2.7.1. Schemat statyczny.

Przybliżona wartość obciążenia ciężarem własnym:

Wtedy:

Wartości reakcji belek odczytano z programu RM-WIN:

• charakterystyczne:

R_A-1=86,23kN, 2*R_A-1=172,46kN.

R_A-3=139,54kN, 2*R_A-3=279,08kN.

• obliczeniowe:

R_A-1=103,14kN, 2*R_A-1=206,28kN.

R_A-3=141,97kN, 2*R_A-3=283,94kN.

WYKRES MOMENTÓW [kNm]:

WYKRES SIŁ TNĄCYCH [kN]:

M_max=3465,04kNm; V_Mmax=105,02kN; V_max=547,50kN;

2.7.2. Wstępny dobór przekroju.

Projektowany przekrój ma należeć do klasy czwartej.

Zakładam, że belka będzie wykonana ze stali St3Sy (f_d=215MPa).

Aby określić optymalną wysokość przekroju, korzystam ze wzoru

.

gdzie: t_w=11mm,
. Wówczas:

.

Przyjęto h=146cm=1,46m; t_f=30mm=0,03m. Wtedy:

Wyznaczam szerokość stopki b_f:

Przyjęto: b_f=0,40m.

Ostatecznie:

h=1,46m

t_w=11mm

t_f=30mm

h_w=1,40m

b_f=0,40m.

2.7.3. Określenie nośności przekroju.

Nośność elementu zginanego:

(wzór 52 PN-B/90-03200).

Przy założeniu, że belka jest zabezpieczona przed zwichrzeniem (φ=1), należy do klasy 4 i jest wykonana ze stali St3Sy a jej środnik ma grubość
(f_d=215MPa) mamy:

W celu określenia współczynnika ψ określam smukłość względną ścianki:

(wzór 7 PN-B/90-03200),

gdzie b=h_w=1,40m; t=t_w=0,011m; K=0,4 (gdyż stosunek naprężeń średnich do maksymalnych jest równy zeru). Wówczas:

.

Z tablicy 9. można odczytać, że wtedy
.

Zgodnie z punktem 4.2.2.3 mamy:

.

Dla przyjętego przekroju wyznaczono moment bezwładności I_x=1478653,4cm⁴ oraz wskaźnik na zginanie W_x=20255,5cm³. Zatem:

Ze względu na na duży wpływ sił tnących nie wykonuję optymalizacji wymiarów. Ostateczne wymiary, przyjęte do dalszych obliczeń:

h=1,46m

t_w=11mm

t_f=30mm

h_w=1,40m

b_f=0,40m.

2.7.4. Korekta sił wewnętrznych (z uwzględnieniem ciężaru własnego belki).

Wyznaczam pole przekroju:

.

Wtedy masa na 1m belki wynosi:

.

Wówczas:

.

Wartość obliczeniowa obciążenia ciężarem własnym:

2.7.5. Nośność na zginanie.

2.7.5.1. Kształtowanie podłużne blachownicy.

Ponieważ l=22m, to należy podzielić blachownicę na 5 elementów o długości:

• środkowy: 5,00m

• pozostałe: 4,25m

2.7.5.1.1. Nośność odcinka środkowego (nr 1).

(wzór 52 PN-B/90-03200)

gdzie:

, φ_L=1.

Wówczas:

A zatem warunek nośności momentowej odcinka środkowego jest spełniony.

2.7.5.1.2. Nośność odcinka nr 2 i nr 4.

Ze względu na niewielkie różnice momentów zginających na odcinkach 2 i 4 wymiaruję oba odcinki na większy moment:

Przyjęto półkę o grubości t_f=24mm. Wówczas
.

Określam wskaźnik przyjętego przekroju:

Moment bezwładności względem osi X przechodzącej przez środek ciężkości przekroju:

• Połowy środnika:
  

• Jednej półki:
  

Moment bezwładności całego przekroju:

Wtedy:

.

Ponieważ

,

to przyjęte wymiary przekroju są wystarczające.

Wymiary przekroju na odcinkach 2,4:

h=1,448m

t_w=11mm

t_f=24mm

h_w=1,40m

b_f=0,40m.

2.7.5.1.3. Nośność odcinka nr 3 i nr 5.

Ze względu na niewielkie różnice momentów zginających na odcinkach 3 i 5 wymiaruję oba odcinki na większy moment:

Przyjęto półkę o grubości t_f=18mm. Wówczas
.

Określam wskaźnik przyjętego przekroju:

Moment bezwładności względem osi X przechodzącej przez środek ciężkości przekroju:

• Połowy środnika: (jak w punkcie 2.6.5.1.2.)

• Jednej półki:
  

Moment bezwładności całego przekroju:

Wtedy:

.

Ponieważ

,

to przyjęte wymiary na odcinku 3 oraz 5 są wystarczające.

Ostatecznie przyjęto na odcinkach 3 i 5:

h=1,436m

t_w=11mm

t_f=18mm

h_w=1,40m

b_f=0,40m.

2.7.5.2. Sprawdzenie warunku nośności momentowej blachownicy.

(wzór 52 PN-B/90-03200)

Dla odcinka 1: punkt 2.6.5.1.1.

Dla odcinka 2,4:

Warunek nośności momentowej jest spełniony.

Dla odcinka 3,5:

2.7.6. Sprawdzenie warunku nośności na ścinanie.

Sprawdzam warunek smukłości środnika wg tab.7:

,

wówczas:

.

A zatem przekrój nie jest odporny na lokalną utratę stateczności.

Wobec tego:

(wzór 16 PN-90/B-03200).

gdzie
a

(wzór 7 PN-90/B-03200).

gdzie:

Ponieważ:

β=a/b=4,25m/1,4m=3,04, to:

Więc K=0,8.

Wówczas:

Natomiast:

Pole czynne przy ścinaniu:

Ostatecznie:

Sprawdzam nośność na ścinanie dla maksymalnej siły tnącej V_max=547,50kN:

.

Warunek nośności na ścinanie jest spełniony.

Sprawdzam warunek:

.

Ponieważ:

,

to nośność momentowa wyraża się wzorem:

(wzór 46 PN-90/B-03200).

2.7.7. Sprawdzenie zredukowanej nośności momentowej.

2.7.7.1. Dla odcinków 3, 5.

gdzie M_R^3,5=
; I_v=251533,3cm⁴, I=975433,0cm⁴.

Wówczas:

Wtedy:

Warunek zredukowanej nośności momentowej odcinków 3 i 5 jest spełniony.

2.7.7.2. Dla odcinków 2,4.

(wzór 16 PN-90/B-03200).

Ponieważ na odcinkach 2, 4 nie zmieniają się wymiary środnika, ani materiał, z którego jest wykonany, to nie zmienia się również nośność przekroju na ścinanie:

Z programu RM-WIN odczytano maksymalną siłę tnącą na odcinkach 2, 4: V_max=329,66kN:

.

Warunek nośności na ścinanie jest spełniony.

Sprawdzam warunek:

.

Ponieważ:

,

to nośność momentowa wyraża się wzorem:

(wzór 46 PN-90/B-03200).

gdzie M_R^2,4=
; I_v=251533,3cm⁴, I=975433,0cm⁴.

Wówczas:

Wtedy:

Warunek zredukowanej nośności momentowej odcinków 2 i 4 jest spełniony.

2.7.7.3. Dla odcinka środkowego (nr 1).

(wzór 16 PN-90/B-03200).

Ponieważ odcinek środkowy jest dłuższy, to:

β=a/b=5,0m/1,4m=3,57, to:

Więc K=0,8 (pozostałe współczynniki pozostają zatem bez zmian).

Ostatecznie:

Z programu RM-WIN odczytano maksymalną siłę tnącą na odcinku 1: V_max=111,82kN:

.

Warunek nośności na ścinanie jest spełniony.

Sprawdzam warunek:

.

Ponieważ:

,

to na odcinku 1 nie należy liczyć nośności zredukowanej.

A zatem warunek stanu granicznego nośności momentowej został spełniony w każdym przekroju.

2.7.8. Wymiarowanie żeber poprzecznych.

2.7.8.1. Dobór wymiarów.

Przyjęto szerokość żebra: t_z=12mm (>t_w=11m), stal na żebra: St3Sy (f_d=215MPa). Żebro projektuję na przekrój klasy 3, a zatem zgodnie z tab. 6 PN-90/B-03200 mamy:

.

Wtedy:

A zatem:

Przyjęto: b_z=0,16m.

Szerokość współpracującą środnika
.

Przyjęto rozmieszczenie żeber w odległości:

• na skróconych zewnętrznych odcinkach belki 3 i 5 co a=1,7m zaczynając od podpory

• na pozostałych co a=1,9m.

Rozstaw żeber powinien spełniać warunek:

Ponieważ:

to warunek ten jest spełniony.

Dodatkowo spełniony powinien być również warunek:

,

gdzie:
. Wówczas:

Moment bezwładności przekroju względem osi środnika:

Wtedy:

A zatem warunek sztywności jest spełniony.

2.7.8.2. Sprawdzenie warunku nośności żebra.

Nośność na jednoosiowe ściskanie:

(wzór 39 PN-90/B-03200).

gdzie

(wzór 33),

Dla przekroju klasy 3 ψ=1,

Wówczas:

Współczynnik wyboczeniowy
zależy od smukłości względnej pręta:

(wzór 35),

gdzie

(wzór 37)

Dla powyższego wzoru: μ=0,8; l₀=h_w=1,4m oraz

.

Wtedy:

.

Smukłość porównawcza wyraża się wzorem:

(wzór 38).

Wówczas:

.

A zatem:

Z tablicy 11 odczytano: φ=1.

Ostatecznie dla:

• żebra podporowego:

Siłę osiową na podporze odczytano z programu RM-WIN:

N= Rb=827,69kN. Wtedy:

Warunek nośności żebra podporowego jest spełniony.

• żebra pośrednie:

N= R_A-1=103,14kN.

Warunek nośności żebra pośredniego jest spełniony.

2.7.8.3. Sprawdzenie warunku nośności żebra na docisk.

Warunek nośności na docisk:

,

gdzie
(przy uwzględnieniu wycięcia na spoinę w żebrze c=4cm);
.

Ostatecznie dla:

• żebra podporowego:

Warunek nośności żebra podporowego na docisk nie jest spełniony.

Należy wobec tego uciąć żebro 10 cm nad półką blachownicy.

• żebra pośredniego:

Warunek nośności żebra pośredniego na docisk jest spełniony.

2.7.8.4. Dobór grubości spoiny połączenia żeber z blachownicą.

Warunek nośności połączenia zakładkowego przy obciążeniu osiowym:

(wzór 94. PN-90/B-03200),

gdzie:
, współczynnik α_II=0,8 (odczytano z tablicy 18. dla stali St3Sy o Re<255MPa i spoiny pachwinowej), f_d=215MPa.

Wówczas dla:

• żebra podporowego:

F= Rb=827,69kN. Po przekształceniach mamy:

Ze względu na warunki konstrukcyjne:

gdzie t₁=11mm, t₂=13mm. Wtedy:

Ostatecznie przyjęto a=4mm.

Wtedy:
.

• żebra pośredniego:

F=R_A-1=103,14kN. Po przekształceniach mamy:

Ze względu na warunki konstrukcyjne:

gdzie t₁=11mm, t₂=12mm. Wtedy:

Ostatecznie przyjęto a=2,0mm.

Wtedy:
.

2.7.9. Dobór grubości spoiny połączenia środnika z pasami blachownicy.

Nośność połączenia pasa ze środnikiem:

(wzór 96 PN-90/B-03200).

gdzie V=Rb=827,69kN,
,
(z punktu 2.7.5.1.3.), α_II=0,85,
. Wtedy po przekształceniach mamy:

Warunki konstrukcyjne:

gdzie t₁=11mm, t₂¹=30mm, t₂^2,4=24mm, t₂^3,5=18mm. Powstają zatem 3 warunki:

Aby nie różnicować grubości spoiny na długości blachownicy przyjęto:

a=5mm.

Wówczas:

.

2.7.10. Wymiarowanie styku montażowego blachownicy.

Sprawdzam naprężenia w miejscu styku w pasie dolnym:

.

Dla styku części 1 i 2(4) mamy:

M_max^2,4=3203,34kNm, W_x^2,4=16919,3cm³,
. Wówczas:

Warunek maksymalnych naprężeń dla styku odcinków 1 i 2(4) jest spełniony.

Dla styku części 2(4) i 3(5) mamy:

M_max^3,5=2381,14kNm, W_x^3,5=13585,4cm³,
. Wówczas:

Warunek maksymalnych naprężeń w pasie dolnym dla styku odcinków 2(4) i 3(5) jest spełniony.

Sprawdzam warunek wytrzymałościowy dla środnika:

,

gdzie
zaś:

_,

_.

Wtedy:

Warunek maksymalnych naprężeń w środniku dla styku odcinków 2(4) i 3(5) jest spełniony.

Ze względów konstrukcyjnych przyjęto przesunięcie styków montażowych w pasie dolnym o 0,3m w stronę mniejszych momentów.

2.7.11. Stan graniczny użytkowania blachownicy.

2.7.11.1. Ugięcie.

Warunek SGU:

Zgodnie z tablicą 4:
.

Ugięcie blachownicy wyraża się wzorem:

gdzie: q_K=3,03kN/m, E=205GPa, I₂=1478653,4cm⁴ (z punktu 2.7.3.), l₀=22m,

,
.

Wtedy:

Ponieważ:

to spełniony jest warunek stanu granicznego użytkowania dotyczący ugięcia.

2.7.11.2. Drgania własne.

Wg punktu 3.3.5. normy PN-90/B-03200 dla belek o rozpiętości powyżej l>12m spełniony musi być następujący warunek:

,

gdzie
natomiast:

.

W powyższym wzorze:
oraz

.

Ponieważ nie znamy wartości p, to przyjęto, że
, co w konsekwencji stanowi zapas bezpieczeństwa przy obliczeniach. Wówczas:

.

Wtedy:

.

A zatem spełniony jest warunek normowy drgań własnych.

2.7.12. Wymiarowanie łożyska podporowego blachownicy.

Dla blachy podłożyskowej przyjęto:
; stal 18G2A (f_d=285MPa).

Szerokość blachy wyznaczam z warunku wytrzymałości muru:

,

gdzie f_dm=2,65MPa (z punktu 2.4.9), R_B=827,69kN. Wówczas:

.

Postanowiono zwiększyć wymiar b: b=0,8m. Wtedy:

.

Przyjęto zatem a=0,4m>0,39m.

Wtedy moment zginający „skrzydełka” blachy wynosi:

Grubość blachy t wyznaczam z warunku:

,

gdzie
. Po przekształceniu mamy:

.

Dodatkowo blacha podłożyskowa powinna spełnić warunek maksymalnego ugięcia:

.

Po przekształceniach otrzymano:

,

gdzie
. Wtedy:

A zatem:
. Przyjęto: t=0,065m.

Ostatecznie wymiary blachy podłożyskowej:

a=0,4m

b=0,8m

t=0,065m.

Wstępne przyjęcie wymiarów łożyska stalowego wykonanego ze stali 18G2A (f_d=285MPa):

a=20cm, r=75cm, l=b_f+2*5cm=40cm+10cm=50cm; (wówczas: h=8,94cm).

Maksymalne naprężenia w łożysku wyrażone są wzorem:

,

gdzie
, E=205GPa, zgodnie z tablica 3:
Więc:

.

A zatem wymiary łożyska są wystarczające. Ze względów konstrukcyjnych zwiększono długość łożyska do l=0,55m.

Ostateczne wymiary łożyska:

a=0,20m

r=0,75m

l=0,55m

3. Połączenia belek.

3.1. Połączenia belki A-1 z blachownicą.

Przyjęto połączenie śrubami M16, klasy 5.6. Jako kategorię połączenia przyjęto kategorię A. Połączono za pomocą żeber pośrednich o grubości t=12mm.

Założono wstępnie połączenie trzema śrubami. Wówczas zgodnie z tablicą 15 PN-90/B-03200 mamy następujące warunki:

• Odległości od czoła blachy w kierunku obciążenia (a₁):

A zatem:
.

Przyjęto: a₁=40mm.

• Odległość od krawędzi bocznej blachy (a₂):

(Analogicznie jak a₁)

A zatem:
.

Przyjęto: a₂=40mm.

• Rozstaw łączników w szeregu (a):

Maksymalny rozstaw łączników w szeregu determinują warunki konstrukcyjne (wysokość blachy łączącej).

Przyjęto: a=50mm.

Wtedy odległość między środkiem ciężkości śrub a osią pionową podciągu wynosi:

A zatem obciążenie momentem wynosi:

Wtedy siła H przypadająca na jedną śrubę ma wartość:

Natomiast siła tnąca:

.

Wypadkowa działająca na pojedynczą śrubę:

.

Warunek nośności śruby dla połączenia kategorii A:

,

gdzie

,

ponieważ R_m=500MPa,
(ścięcie nastąpi w części nienagwintowanej). Wówczas:

.

Ponieważ
, to postanowiono zwiększyć średnicę śrub i ich wytrzymałość jednocześnie przesuwając cały szereg bliżej osi podciągu:

Przyjęto śruby M24 klasy 6.6. Wtedy:

.

Wypadkowa działająca na pojedynczą śrubę:

.

Warunek nośności śruby dla połączenia kategorii A:

,

gdzie

,

ponieważ R_m=600MPa,
(ścięcie nastąpi w części nienagwintowanej). Wówczas:

.

Nośność na docisk:

,

gdzie:

d`=d=24mm (docisk następuje w części nienagwintowanej;
(grubość środnika belki A1).

,

gdzie: R_e=0,6R_m=360MPa oraz γ_s=1,20. Wtedy:

Ostatecznie:

.

Ponieważ:

,

to warunek nośności połączenia belki A1 z blachownicą jest spełniony.

Ostateczne do wykonania połączenia belki A1 z blachownicą przyjęto śruby:

M24 klasy 6.6.

3.2. Połączenia podciągu A-3 z blachownicą.

Przyjęto połączenie śrubami M16, klasy 6.6. Jako kategorię połączenia przyjęto kategorię A. Połączono za pomocą żeber pośrednich o grubości t=12mm.

• Odległości od czoła blachy w kierunku obciążenia (a₁):

A zatem:
.

Przyjęto: a₁=25mm.

• Odległość od krawędzi bocznej blachy (a₂):

(Analogicznie jak a₁)

A zatem:
.

Przyjęto: a₂=25mm.

• Rozstaw łączników w szeregu (a):

Maksymalny rozstaw łączników w szeregu determinują warunki konstrukcyjne (wysokość blachy łączącej).

Przyjęto: a=40mm.

Wówczas:

.

.

Warunek nośności śruby dla połączenia kategorii A:

,

gdzie

,

ponieważ R_m=600MPa,
(ścięcie nastąpi w części nienagwintowanej). Wówczas:

.

Ze względu na brak możliwości zmian konstrukcyjnych połączenia postanowiono zwiększyć klasę śrub do 12.9.

Wtedy:

Nośność na docisk:

,

gdzie:

d`=d=16mm (docisk następuje w części nienagwintowanej;
(grubość środnika belki A3).

,

gdzie: R_e=0,9R_m=1080MPa oraz γ_s=1,20. Wtedy:

Ostatecznie:

.

Ponieważ:

,

to warunek nośności połączenia belki A3 z blachownicą jest spełniony.

Ostateczne do wykonania połączenia belki A3 z blachownicą przyjęto śruby:

M16 klasy 12.9 (nie jest to połączenie sprężone).

3.3. Połączenia belki A-2 z podciągiem A-3.

Do połączenia belek A-2 i A-3 należy wykonać w odpowiednich miejscach żebra:

Przyjęto szerokość żebra: t_z=11mm (>t_w=10m), stal na żebra: St3Sy (f_d=215MPa). Żebro projektuję na przekrój klasy 3, a zatem zgodnie z tab. 6 PN-90/B-03200 mamy:

.

Wtedy:

A zatem:

Przyjęto: b_z=0,115m.

Szerokość współpracującą środnika
.

Ponieważ żebro służy jedynie połączeniu dwóch belek nie sprawdzam warunków minimalnego rozstawu, ani sztywności.

Ze względu na podobną geometrię żebra projektowanego i żeber blachownicy i jednocześnie mniejszą siłę tnącą nie sprawdzam nośności żebra uznając ją za wystarczającą.

Warunek nośności połączenia zakładkowego przy obciążeniu osiowym:

(wzór 94. PN-90/B-03200),

gdzie:
, współczynnik α_II=0,8 (odczytano z tablicy 18. dla stali St3Sy o Re<255MPa i spoiny pachwinowej), f_d=215MPa.

Wówczas dla F= 105,59kN. Po przekształceniach mamy:

Ze względu na warunki konstrukcyjne:

gdzie t₁=10mm, t₂=11mm. Wtedy:

Ostatecznie przyjęto a=5mm.

Wtedy:
.

Postanowiono wykonać połączenie doczołowe za pomocą dwóch dospawanych blach w kategorii D. Wstępnie założono grubość blach t=20mm i połączenie na śruby M20 6.6.

Wówczas nośność trzpienia śruby wynosi:

,

gdzie R_m=600MPa, R_e=360MPa, A_S=12,57cm². Wobec tego:

Sprawdzam, czy grubość blachy spełnia warunek normowy grubości:

Ponieważ t=0,02m>0,017m, to przyjęta grubość blachy jest wystarczająca.

Wyznaczam nośność momentową połączenia:

,

gdzie m_i=2; y₁=0,207m; y₂=0,137m;y₃=0,067m;

Ponieważ
, to sumowanie ogranicza się do pierwszego szeregu śrub. Wtedy:

.

Moment w połączeniu:

Ponieważ M=20,97kNm<M_Rj=106,69kNm oraz S=149,81kN<S_Rt=384,64kN, to spełniony jest warunek nośności połączenia doczołowego.

Sprawdzam nośność spoin w połączeniu blach z kształtownikami:

Ponieważ w przypadku blachy łączonej z A2 obciążenie musi przenieść mniejsza ilość spoin niż w przypadku blachy łączonej z A3, to postanowiono sprawdzić tylko nośność blachy z połączenia z A2:

Kład powierzchni obliczeniowych spoin na płaszczyznę pionową:

Założono grubość spoin a=5mm.

Siła poprzeczna R_A-2=149,81kN jest przenoszona w całości przez spoiny pionowe, których pole przekroju obliczeniowego wynosi:

Naprężenia normalne w spoinie:

,

gdzie
. Wówczas:

Ponieważ płaszczyzna obliczeniowa spoin pionowych jest nachylona pod kątem 45°, to należy rozłożyć naprężenia normalne powstałe od sił na kierunek prostopadły i równoległy do powierzchni obliczeniowej (złożony stan naprężenia). Tak powstałe naprężenia muszą spełniać warunek:

.

Dodatkowo w spoinie pionowej powstają naprężenia styczne od siły R_A-2, które muszą spełniać warunek:

.

A zatem wytrzymałość spoiny w punkcie 1 musi spełniać warunek:

,

gdzie f_d=215MPa (wytrzymałość obliczeniowa słabszej części łączonej) oraz κ=0,85 (dla R_m=258MPa). Wtedy:

Wobec tego warunek nośności spoin pionowych jest spełniony.

Dla spoin poziomych należy sprawdzić warunek:

,

gdzie
. Wtedy:

A zatem warunek nośności spoin poziomych jest spełniony.

20

68

---