Politechnika Lubelska
Ćwiczenia projektowe z
Budownictwa Przemysłowego

Komina żelbetowy przemysłowy
Prowadzący: Wykonał:
Dr inż. Marta Słowik
SPIS TREŚCI
1. Określenie charakterystyk geometrycznych komina.
1.1. Dane do projektowania.
H = 75m - wysokość komina nad poziomem terenu
D = 3,8m - średnica zewnętrzna wylotu komina
i = 1…7 - ilość segmentów
Ts = 300ºC - temperatura odprowadzanych spalin
Klasa Betonu - B37
Klasa Stali - A III
Izolacja - Wełna żużlowa, zbita, szara
Wykładzina - Cegła zwykła
Usytuowanie komina: II strefa obciążenia wiatrem
Rys. 1.1. Schemat podziału komina na segmenty.
1.2. Charakterystyki wytrzymałościowe materiałów.
STAL - klasa A-III
fyk= 395 MPa - charakterystyczna granica plastyczności stali
fyd = 350 MPa - obliczeniowa granica plastyczności stali
Es = 200 · 103 MPa - moduł sprężystości stali
BETON - klasa B 30
fck = 30 MPa - wytrzymałość charakterystyczna na ściskanie
fcd = 20 MPa - wytrzymałość obliczeniowa na ściskanie
Ecm = 32 · 103 MPa - moduł sprężystości betonu
Ciężary objętościowe oraz współczynniki bezpieczeństwa do ciężarów obliczeniowych:
trzon- żelbet γż = 26![]()
wymurówka- cegłą szamotowa γc = 18![]()
,
izolacja- wełna żużlowa szara γi = 3![]()
,
1.3. Geometria komina
![]()
- wysokość ponad teren górnej krawędzi segmentu „i” w [m]
gp,i - grubość płaszcza betonowego segmentu „i” w [m]
giz = 0.08 · m - grubość izolacji z wełny żużlowej szarej w [m]
gw = 0.12 · m - grubość wykładziny z cegły szamotowej w [m]
hi - wysokość pojedynczego segmentu [m]
1.4. Obliczenie promieni.
Płaszcz- zewnętrzny
![]()
= ![]()
![]()
/ 2 - średnica zewnętrzna segmentu płaszcza betonowego [m]
Płaszcz- wewnętrzny
![]()
= ![]()
![]()
-![]()
- średnica wewnętrzna segmentu płaszcza betonowego [m]
Izolacji- wewnętrzna
![]()
= ![]()
-giz - średnica wewnętrzna izolacji z wełny mineralnej [m]
Wykładziny
![]()
= ![]()
- gw - średnica wewnętrzna wykładziny z cegły górna [m]
Dane geometryczne komina obliczone z powyższych wzorów zestawiono w tablicy 1
1.5. Zestawienie wymiarów geometrycznych komina.
Tabela 1.1.
Zestawienie wymiarów geometrycznych komina.
Nr segmentu |
Wysokość segmentu hi |
Grubość trzonu |
Grubość izolacji |
Grubość wymurówki |
Promień zewnętrzny trzonu |
Promień wewnętrzny trzonu |
Promień wewnętrzny izolacji |
Promień wewnętrzny wymurówki |
|
[m] |
[cm] |
[cm] |
[cm] |
[m] |
[m] |
[m] |
[m] |
1 |
11 |
18 |
10 |
12 |
1,9 |
1,72 |
1,62 |
1,5 |
2 |
11 |
18 |
10 |
12 |
1,9 |
1,72 |
1,62 |
1,5 |
3 |
11 |
18 |
10 |
12 |
1,9 |
1,72 |
1,62 |
1,5 |
4 |
11 |
20 |
10 |
12 |
1,9 |
1,7 |
1,6 |
1,48 |
5 |
11 |
20 |
10 |
12 |
1,9 |
1,7 |
1,6 |
1,48 |
6 |
10 |
20 |
10 |
12 |
1,9 |
1,7 |
1,6 |
1,48 |
7 |
10 |
22 |
10 |
12 |
1,9 |
1,68 |
1,58 |
1.46 |
2. Zestawienie obliczeniowych obciążeń pionowych.
2.1. Obliczeniowy ciężar poszczególnych segmentów komina (bez wsporników).
Ciężary poszczególnych segmentów trzonu żelbetowego wyznaczono wg wzoru:
![]()
= ![]()
· (rpz,i2 - rpw,i2) · hi · γż
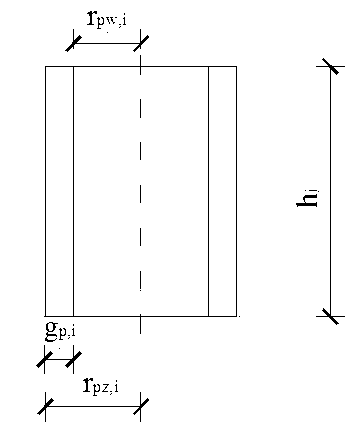
Rys. 1.2. Oznaczenia wielkości do obliczania ciężaru segmentu trzonu żelbetowego.
2.2. Obliczeniowy ciężar wsporników.
Ciężary wsporników wyznaczano wg wzoru :
![]()
= ![]()
· hw · ![]()
· γż
gdzie:
hw = 1.25m - wysokość wspornika
sw = giz + gw sw = 0.22m - szerokość wspornika
sw = giz + gw - 2cm sw = 0.20m - szerokość wspornika gdy segment ma zwiększona
grubość ścianki płaszcza w stosunku do poprzedniego
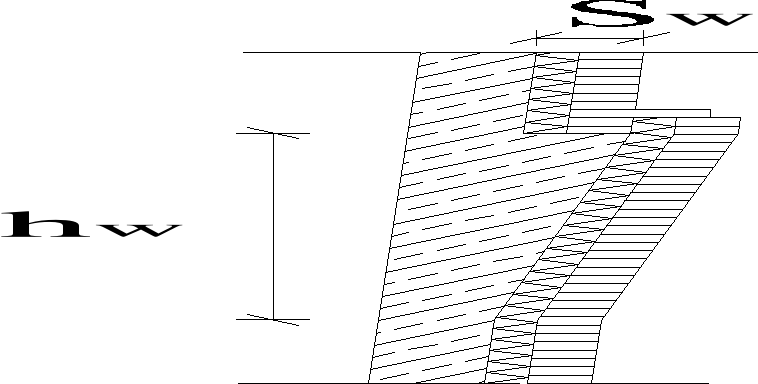
Rys.1.3. Oznaczenia wielkości do obliczania ciężaru wspornik podwykładzinowego.
3.3. Obliczeniowy ciężar głowicy komina.
Gg = ![]()
gdzie:
rgz = 2.1m - promień zewnętrzny głowicy
rgw = 1,9m - promień wewnętrzny głowicy
hg = 0.7m - wysokość głowicy
Gg = 45.741 kN - ciężar głowicy zostanie doliczony do ciężaru segmentu nr 1
3.4. Obliczeniowy ciężar izolacji.
Ciężary izolacji w poszczególnych segmentach obliczono ze wzoru:
![]()
= ![]()
· (rpw,i2 - ri,i2) · hi · γi
3.5. Obliczeniowy ciężar wykładziny (cegła zwykła).
Ciężary wykładziny w poszczególnych segmentach obliczano ze wzoru:
![]()
= ![]()
· (ri,i2 - rw,i2) · hi · γw
3.7. Zestawienie charakterystycznych obciążeń pionowych komina.
Tabela 1.2.
Zestawienie obciążeń pionowych komina.
Poziom przekroju |
Ciężar Płaszcza |
Ciężar wsporników lub głowicy |
Ciężar płaszcza ze wspornikami |
Ciężar izolacji |
Ciężar wykładziny |
Ciężar całkowity segmentu |
Ciężar komina ponad rozpatrywanym przekrojem |
[m] |
[kN] |
[kN] |
[kN] |
[kN] |
[kN] |
[kN] |
[kN] |
75 |
- |
|
- |
- |
- |
- |
- |
64 |
585,460 |
45,741 |
631,201 |
34,627 |
232,890 |
898,717 |
898,717 |
53 |
585,460 |
33,081 |
618,541 |
34,627 |
232,890 |
886,057 |
1784,775 |
42 |
585,460 |
33,081 |
618,541 |
34,627 |
232,890 |
886,057 |
2670,832 |
31 |
711,608 |
29,589 |
741,198 |
34,212 |
229,904 |
1005,314 |
3676,146 |
20 |
646,917 |
32,673 |
679,589 |
34,212 |
229,904 |
943,706 |
4619,851 |
10 |
588,106 |
32,673 |
620,779 |
34,212 |
229,904 |
884,895 |
5504,746 |
0 |
643,323 |
29,222 |
672,544 |
33,797 |
226,918 |
933,260 |
6438,006 |
4. Obciążenie wiatrem.
Obciążenie charakterystyczne wywołane działaniem wiatru zostanie obliczone wg wzoru :
pk = 1,2qk · Ce · Cx · β ·γd
gdzie:
qk - charakterystyczne ciśnienie prędkości wiatru
qk = 0,35kN/m2 dla II strefy obciążeń wiatrem
Ce - współczynnik ekspozycji
Cx - współczynnik oporu aerodynamicznego
β - współczynnik działania porywów wiatru
β = 2,0 dla kominów o wysokości do 100m
γd = 1.3 - współczynnik ujmujący konsekwencje założeń modelowych
4.1. Wyznaczenie współczynnika ekspozycji.
Zgodnie z zaleceniem PN-77/B-02011 przyjęto że komin znajduje się w terenie typu A.
Współczynnik ekspozycji wyznaczono na podstawie tablicy nr 4 PN-77/B-02011
z1 = 69,5m C e,1 = 1.23 + 0.0067 · 69.5 C e,1 = 1,696
z2 = 58,5m C e,2 = 1.23 + 0.0067 · 58.5 C e,2 = 1.622
z3 = 47,5m C e,3 = 1.23 + 0.0067 · 47.5 C e,3 = 1.548
z4 = 36,5m C e,4 = 0.9 + 0.015 · 36.5 C e,4 = 1.448
z5 = 25.5m C e,5 = 0.9 + 0.015 · 25.5 C e,5 = 1.283
z6 = 15m C e,6 = 0.8 + 0.02 · 15 C e,6 = 1.1
z7 = 5m C e,7 = 1 C e,7 = 1,000
4.2. Wyznaczenie współczynnika aerodynamicznego.
Cx = 0,7 · ![]()
gdy ![]()
Cx = 0,7 gdy ![]()
![]()
więc: Cx = 0,7 · ![]()
Cx = 0,687 wg PN-88/B-03004
4.3. Zestawienie obciążeń od wiatru oraz przeliczenie tych obciążeń na siły skupione.
Charakterystyczna siła skupiona od obciążeń wiatrem na poszczególny segment:
Pk = pk • A10 v 11
Obliczeniowa siła skupiona od obciążeń wiatrem na poszczególny segment:
P = Pk • γf
Gdzie: γf = 1,3
Pola powierzchni odniesienia działania obciążeń od wiatru na segmenty komina:
- dla segmentów o wysokości 11 metrów.
A11 = h3-7 • D = 11m • 3,8m
A11 = 41,8m2
- dla segmentów o wysokości 10 metrów.
A10 = h1-2 • D = 10m • 3,8m
A10 = 38m2
Tabela 1.3.
Zestawienie obciążeń od wiatru.
Nr segmentu |
Poziom przekroju |
Wsp. Ekspozycji Cx |
pk |
Powierzchnia odniesienia |
Obciążenie charakterystyczne wiatrem danego segmentu |
Obciążenie obliczeniowe |
l.p. |
[m] |
|
[kPa] |
[m2] |
[kN] |
[kN] |
1 |
69,5 |
1,696 |
1,272 |
41,8 |
53,184 |
69,139 |
2 |
58,6 |
1.622 |
1,217 |
41,8 |
50,864 |
66,123 |
3 |
47,5 |
1.548 |
1,161 |
41,8 |
48,543 |
63,106 |
4 |
36,5 |
1.448 |
1,086 |
41,8 |
45,407 |
59,029 |
5 |
25,5 |
1.283 |
0,963 |
41,8 |
40,233 |
52,303 |
6 |
15 |
1,100 |
0,825 |
38 |
31,359 |
40,766 |
7 |
5 |
1,000 |
0,750 |
38 |
28,508 |
37,060 |
5. Obciążenie termiczne.
5.1. Dane do obliczeń.
ts = (300 + 275) = 573 K - temperatura odprowadzanych spalin
tw = (1,2 • 300 + 273) = 633 K - temperatura wewnętrzna (temp. spalin pow. o 20%)
tzl = 35 +273 = 308 K - temperatura zewnętrzna dla lata
tzz = -25 + 273 = 248 K - temperatura zewnętrzna dla zimy
αn = 17,5 ![]()
- współczynnik napływu ciepła
αo = 8.7 ![]()
- współczynnik odpływu ciepła
Obliczenia termiczne przeprowadzono dla ostatniego segmentu 7
R = 1,9 m - promień zewnętrzny trzonu w ostatnim segmencie
Warstwa I - Beton zbrojony
g1 = 0,22 m λ1 = 1,75 ![]()
rz1 = 1,9 m ![]()
κ1 = 1
Warstwa I - Wełna żużlowa
g2 = 0,10 m λ2 = 0,07 ![]()
rz2 = 1,68 m ![]()
,131 κ 2 = 1,07
Warstwa I - Cegła zwykła
g3 = 0,12 m λ2 = 0,75![]()
rz2 = 1,58 m ![]()
,2 κ 3 = 1,1
gdzie:
gi - grubość danej warstwy
λi - współczynnik przewodności cieplnej danej warstwy (wg tab. Z-1 PN-88/B-03004)
χi - współczynnik uwzględniający zakrzywienie ściany ( wg rys. 4-b PN-88/B-03004)
ri - promień zewnętrzny danej warstwy
5.2. Obliczenia współczynnika przedoności cieplnej „k”.
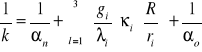
k = 0,45
5.3. Obliczenie termiczne dla warunków letnich.
5.3.1. Określenie całkowitej różnicy temperatur.
Δt = tw - tzl = 633 K - 308 K = 325 K
5.3.2. Określenie różnicy temperatur. na brzegach i między warstwami.
Δtαn = k • 1/αn • Δt = 8,29 K
Δtαo = k • 1/αo • Δt = 16,69 K
Δt1-2 = k • ![]()
κ1 • ![]()
• Δt = 18,35 K
Δt2-3 = k • ![]()
κ2 • ![]()
• Δt = 250,94 K
Δt3-4 = k • ![]()
κ3 • ![]()
• Δt = 30,72 K
5.3.3. Określenie temperatur. na brzegach i między warstwami.
tw = 633 K
tzl = 308 K
t1 = tw - Δtαn = 624,71K
t2 = t1 - Δt1-2 = 606,35 K
t3 = t2 - Δt2-3 = 355,41 K
t2 = tzl + Δtαo = 324,69 K
Sprawdzenie:
t4 = t3 - Δt3-4 = 324,69 K
Wykres:
5.3.4. Określenie max temperatury w płaszczu i max. różnicy temperatur w
płaszczu.
tmax-l = t3 = 355,41 K - 273 K = 82,41 ○C
Δtmax-l = t3 - t4 = 30,72 ○C
5.4. Obliczenie termiczne dla warunków zimowych.
5.4.1. Określenie całkowitej różnicy temperatur.
Δt = tw - tzl = 633 K - 248 K = 385 K
5.4.2. Określenie różnicy temperatur. na brzegach i między warstwami.
Δtαn = k • 1/αn • Δt = 9,83 K
Δtαo = k • 1/αo • Δt = 19,77 K
Δt1-2 = k • ![]()
κ1 • ![]()
• Δt = 21,74 K
Δt2-3 = k • ![]()
κ2 • ![]()
• Δt = 297,27 K
Δt3-4 = k • ![]()
κ3 • ![]()
• Δt = 36,39 K
5.4.3. Określenie temperatur. na brzegach i między warstwami.
tw = 633 K
tzl = 348 K
t1 = tw - Δtαn = 623,17 K
t2 = t1 - Δt1-2 = 601,43 K
t3 = t2 - Δt2-3 = 304,16 K
t4 = tzl + Δtαo = 267,77 K
Sprawdzenie:
t4 = t3 - Δt3-4 = 267,77 K
Wykres:
5.4.4. Określenie max temperatury w płaszczu i max. różnicy temperatur w
płaszczu.
tmax-z = t3 = 304,16 K - 273K = 31,16○C
Δtmax-z = t3 - t4 = 36,39○C
5.5. Sprawdzenie z warunkami normowymi.
Obliczone:
tmax = max(tmax-z, tmax-l) tmax = 82,41○C
Δtmax = max(Δtmax-z, Δtmax-l) Δtmax = 36,39○C
Dopuszczalne:
tmax,dop = 150○C ≥ tmax = 82,41○C Warunek spełniony
Δtmax,dop = 30○C ≤ Δtmax = 36,39○C Warunek nie spełniony
Wniosek: Można w obliczeniach uwzględnić wpływ temperatury przez zmniejszenie nieprzekraczalnych wartości naprężeń w betonie o 25% w stosunku do podanych w pkt 5.5.2. PN-88/B-03004
6. Obliczenie sił wewnętrznych w płaszczu komina
6.1. Wyznaczenie wartości momentów zginających od parcia wiatru (I rzędu)
Obliczone obciążenie od wiatru zostało zamienione na siły skupione przyłożone w połowie wysokości każdego segmentu, zaś moment od tego obciążenia został obliczony u podstawy każdego segmentu. Działanie momentów I rzędu zostało obliczone w stadium eksploatacji i zestawione w tabeli.
Wzór do wyznaczenia momentu I rzędu w stadium eksploatacji w podstawie i-tego segmentu :
MI= ![]()
[kNm]
Tabela 1.4.
Wartości charakterystyczne momentów I rzędu w stadium eksploatacji.
Nr segmentu |
Poziom przekroju [m] |
Moment zginający [kNm] |
1 |
64 |
292,512 |
2 |
53 |
1157,286 |
3 |
42 |
2568,796 |
4 |
31 |
4497,032 |
5 |
20 |
6896,289 |
6 |
10 |
9435,389 |
7 |
0 |
12273,820 |
6.2 Momenty II rzędu
Współczynnik:
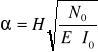
Gdzie:
N0 = 6848,539 KN - całkowity ciężar komina
E = 32 GPa - moduł sprężystości betonu
I0 = 3,98cm4 - moment bezwładności przekroju płaszcza betonowego u
podstawy komina
α = 0,55 > 0,35 Warunek został spełniony więc musimy uwzględnić wpływ
momentów II rzędu
Wartość momentów zginających II rzędu w poszczególnych przekrojach komina
obliczono ze wzoru:
MII = ![]()
Gdzie: MI_0 - moment I rzędu dla poziomu H = 0m,
fi = ![]()
- uśredniona funkcja wpływu drugiego rzędu
gdzie: z - odległość podstawy i-tego
segmentu do poziomu terenu
Tabela 1.5.
Wartości momentów dodatkowych (II rzędu).
Nr segmentu |
Poziom przekroju [m] |
fi |
Moment zginający [kNm] |
1 |
64 |
0,03 |
118,90 |
2 |
53 |
0,11 |
424,04 |
3 |
42 |
0,23 |
838,13 |
4 |
31 |
0,35 |
1283,84 |
5 |
20 |
0,45 |
1683,86 |
6 |
10 |
0,52 |
1942,83 |
7 |
0 |
0,55 |
2042,06 |
6.3. Łączne wartości momentów I i II rzędu:
Tabela 1.6.
Łączna wartość momentów M = MI + MII.
Nr segmentu |
Poziom Przekroju [m] |
Moment Zginający [kNm] |
1 |
64 |
411,41 |
2 |
53 |
1581,33 |
3 |
42 |
3406,92 |
4 |
31 |
5780,87 |
5 |
20 |
8580,15 |
6 |
10 |
11378,22 |
7 |
0 |
14315,88 |
7. Obliczenie największego sprężystego wychylenia wierzchołka
komina
δw
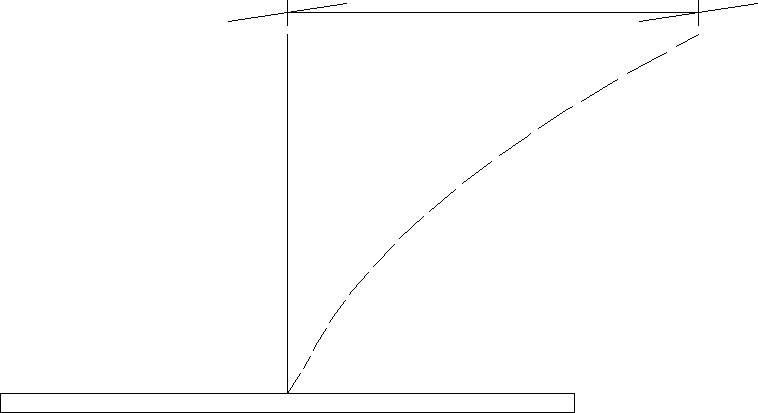
Rys. 1.4. Schemat odkształcenia trzonu komina (wychylenie sprężyste).
![]()
= 298,097 kN (suma wartości poszczególnych sił wg punktu 4.3 )
H = 75m - wysokość komina
Io = 3,979m4 - moment bezwładności płaszcza w poziomie połączenia terenu
Ecm = 32000 MPa - moduł sprężystości betonu B-37 w płaszczu komina
a= δw = 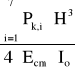
- ugięcie trzonu komina pod wpływem wiatru
a = 0.247m
a = 0.247m <![]()
· H = 0.375m
Komin jest dostatecznie sztywny
8. Wymiarowanie płaszcza komina
D = 3,8 m - średnica zewnętrzna płaszcza komina
fck = 30 MPa - wytrzymałość charakterystyczna na ściskanie
fyk = 395 MPa - charakterystyczna granica plastyczności stali
8.1. Minimalny stopień zbrojenia poziomego
ρmin_poz = 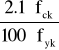
ρmin_poz = 0.159 %
Warunek temperatury spalin: Ts = 300ºC
Ts ≥ 300ºC więc przyjęto: ρpoz_min = 0.4%
8.2. Minimalny stopień zbrojenia pionowego
ρmin_pion = 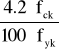
ρmin_pion = 0.319%
Przyjęto dla segmentów 1-6: ρpion_min = 0.4%
Ponieważ w ostatnim segmencie naprężenie w stali zostały przekroczone zwiększono minimalny stopień zbrojenia dla tego segmentu
Przyjęto dla 7 segmentu: ρpion_min = 0.6%
8.3. Sprawdzenie naprężeń w trzonie komina
Stosunek współczynników sprężystości podłużnej betonu i stali :
ne = ![]()
zgodnie z zaleceniami normy PN-88/B-03004 przyjęto ne = 8
8.3.1. Przyjęcie współczynników B i C
Współczynniki przyjęto dla ne = 8
![]()
- promień zewnętrzny trzonu komina
![]()
- promień wewnętrzny trzonu komina
![]()
=![]()
- pole przekroju poprzecznego komina
![]()
-promień okręgu środkowego przekroju pierścieniowego![]()
M - moment zginający w stadium eksploatacji
Neki - siła ściskająca pionowa w stadium eksploatacji
eeoi = ![]()
- mimośród siły ściskającej w stadium eksploatacji
Tabela 1.7.
Zestawienie obliczeń do wyznaczania współczynników B i C na podstawie tab. Z6-1.
Nr Segm. |
Rzędna [m] |
rpz,i [m] |
rpw,i [m] |
rsi [m] |
M [kNm] |
Neki [kN] |
eeo [m] |
eeo/rsi
|
B |
C |
0 |
75 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
1 |
64 |
1,9 |
1,72 |
1,81 |
411,41 |
898,717 |
0,458 |
0,253 |
1,927 |
0,019 |
2 |
53 |
1,9 |
1,72 |
1,81 |
1581,33 |
1784,775 |
0,886 |
0,490 |
1,927 |
0,019 |
3 |
42 |
1,9 |
1,72 |
1,81 |
3406,92 |
2670,832 |
1,276 |
0,705 |
2,528 |
3,534 |
4 |
31 |
1,9 |
1,7 |
1,8 |
5780,87 |
3676,146 |
1,573 |
0,874 |
3,341 |
9,53 |
5 |
20 |
1,9 |
1,7 |
1,8 |
8580,15 |
4619,851 |
1,857 |
1,032 |
4,292 |
16,689 |
6 |
10 |
1,9 |
1,7 |
1,8 |
11378,22 |
5504,746 |
2,067 |
1,148 |
4,952 |
21,284 |
7 |
0 |
1,9 |
1,68 |
1,79 |
14315,88 |
6438,006 |
2,224 |
1,242 |
5,199 |
19,742 |
Nieprzekraczalne wartości naprężeń normalnych w stadium eksploatacji :
a) beton : 0.65 · fck = 19,5 MPa
b) stal : 0.7 · fyk = 276.5 MPa
Sprawdzenie naprężeń w betonie i stali :
σci = 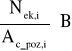
σsi = σci · C
Tabela 1.8.
Zestawienie naprężeń w betonie i stali w stadium eksploatacji.
Nr Segm. |
Rzędna [m] |
Neki [kN] |
Ac_poz [m2] |
B |
C |
σci [MPa] |
σsi [MPa] |
0 |
75 |
- |
- |
- |
- |
- |
- |
1 |
64 |
898,717 |
2,047 |
1,927 |
0,019 |
0,846 |
0,016 |
2 |
53 |
1784,775 |
2,047 |
1,927 |
0,019 |
1,680 |
0,032 |
3 |
42 |
2670,832 |
2,047 |
2,528 |
3,534 |
3,298 |
11,656 |
4 |
31 |
3676,146 |
2,262 |
3,341 |
9,53 |
5,430 |
51,746 |
5 |
20 |
4619,851 |
2,262 |
4,292 |
16,689 |
8,766 |
146,297 |
56 |
10 |
5504,746 |
2,262 |
4,952 |
21,284 |
12,051 |
256,501 |
7 |
0 |
6438,006 |
2,474 |
5,199 |
19,742 |
13,527 |
267,059 |
Warunki nieprzekraczalności naprężeń normalnych zostały spełnione we wszystkich segmentach.
8.4. Zbrojenie pionowe
Ac_poz,i = ![]()
- pole przekroju poziomego komina
As_pion.i = ρpion • Ac - pole powierzchni zbrojenia pionowego
We wszystkich segmentach komina przyjęto że: ρpion= ρpion_min
Zgodnie z zaleceniami PN-88/B- 03004 stopień zbrojenia zewnętrznego powinien wynosić nie mniej niż 0,2%, więc przyjęto po stronie zewnętrznej minimalny stopień zbrojenia As_pion.i_1 = 0.002 • Ac
, a od strony wewnętrznej pozostała ilość zbrojenia
As_pion.i_2 = As_pion.i - As_pion.i_1 = (ρpion_min - 0,002) • Ac
z wyjątkiem ostatniego segmentu w którym:
As_pion.7_1 = 0.003 • Ac
As_pion.7_2 = 0.003 • Ac
8.4.1. Wyznaczenie długości obwodu w osiach zbrojenia pionowego dla poszczególnych segmentów
Przyjęto zbrojenie dwustronne na całej wysokości komina. Na całej wysokości komina przyjęto otulinę zbrojenia o grubości 3 cm ponieważ przyjęto że średnica prętów zbrojeniowych nie przekroczy 16 mm. Zgodnie z PN-88/B-03004 maksymalny odstęp między prętami pionowymi przyjęto równy 30 mm
promień do osi zbrojenia dla danego segmentu
Rf,i_1 = ![]()
- c - 0,5 ϕ - zbrojenia zewnętrznego
Rf,i_2 = ![]()
+ c + 0,5 ϕ - zbrojenia wewnętrznego
gdzie: ϕ = 12mm - przyjęta średnica zbrojenia pionowego
c = 3cm - przyjęta grubość otuliny
![]()
- promień zewnętrzny trzonu komina
![]()
- promień wewnętrzny trzonu komina
obwód w osiach zbrojenia dla danego segmentu
Li_1 = 2 · π · Rf,i_1 - zbrojenia zewnętrzne
Li_2 = 2 · π · Rf,i_2 - zbrojenia wewnętrzne
wymagana minimalna liczba prętów zbrojeniowych
ni_1 =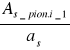
- zbrojenia zewnętrzne
ni_2 =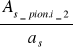
- zbrojenia wewnętrzne
gdzie: as = 1,131 cm2 pole przekroju przyjętego zbrojenia pionowego
Wymagany rozstaw prętów w zbrojeniu
Si_1 = ![]()
- zbrojenia zewnętrzne
Si_2 = ![]()
- zbrojenia wewnętrz
Tabela 1.9.
Zestawienie obliczeniowych niezbędnych przekrojów zbrojenia w poszczególnych segmentach.
Segment |
Ac _poz [m2] |
Stopień Zbr. „ρ” |
Rf,i_1 [m] |
Rf,i_2 [m] |
Li_1 [m] |
Li_2 [m] |
As_pion.i_1 [cm2] |
As_pion.i_2 [cm2] |
ni_1 [szt] |
ni_2 |
1 |
2,047 |
0,4% |
1,848 |
1,772 |
11,611 |
11,134 |
40,94 |
40,94 |
36,199 |
36,199 |
2 |
2,047 |
0,4% |
1,848 |
1,772 |
11,611 |
11,134 |
40,94 |
40,94 |
36,199 |
36,199 |
3 |
2,047 |
0,4% |
1,848 |
1,772 |
11,611 |
11,134 |
40,94 |
40,94 |
36,199 |
36,199 |
4 |
2,262 |
0,4% |
1,848 |
1,752 |
11,611 |
11,008 |
45,24 |
45,24 |
39,999 |
39,999 |
5 |
2,262 |
0,4% |
1,848 |
1,752 |
11,611 |
11,008 |
45,24 |
45,24 |
39,999 |
39,999 |
6 |
2,262 |
0,4% |
1,848 |
1,752 |
11,611 |
11,008 |
45,24 |
45,24 |
39,999 |
39,999 |
7 |
2,474 |
0,6% |
1,848 |
1,732 |
11,611 |
10,882 |
74,23 |
74,23 |
65,632 |
65,632 |
Tabela 1.10.
Zestawienie przyjętych przekrojów zbrojenia w poszczególnych segmentach.
Segment |
Obliczeniowe pole zbrojenia |
Przyjęte zbrojenie |
Pole przyjętego zbrojenia |
Obliczony rozstaw prętów |
||||
|
As_pion.i_1 [cm2] |
As_pion.i_2 [cm2] |
Zewnętrzne |
Wewnętrzne |
As_pion.i_1 [cm2] |
As_pion.i_2 [cm2] |
Si_1 [m] |
Si_2 [m] |
1 |
40,94 |
40,94 |
40 x ϕ 12 |
40 x ϕ 12 |
45,24 |
45,24 |
0,290 |
0,278 |
2 |
40,94 |
40,94 |
40 x ϕ 12 |
40 x ϕ 12 |
45,24 |
45,24 |
0,290 |
0,278 |
3 |
40,94 |
40,94 |
40 x ϕ 12 |
40 x ϕ 12 |
45,24 |
45,24 |
0,290 |
0,278 |
4 |
45,24 |
45,24 |
40 x ϕ 12 |
40 x ϕ 12 |
45,24 |
45,24 |
0,290 |
0,275 |
5 |
45,24 |
45,24 |
40 x ϕ 12 |
40 x ϕ 12 |
45,24 |
45,24 |
0,290 |
0,275 |
6 |
45,24 |
45,24 |
40 x ϕ 12 |
40 x ϕ 12 |
45,24 |
45,24 |
0,290 |
0,275 |
7 |
74,23 |
74,23 |
80 x ϕ 12 |
80 x ϕ 12 |
90,48 |
90,48 |
0,145 |
0,136 |
8.4.2. Obliczenia dotyczące zakotwienia i łączenia prętów dla segmentu 7
Beton: B37
Stal: A-III
fbd = 3,0MPa - przyczepność obliczeniowa wg tab. 26 PN-B-03264
fyd = 350MPa - obliczeniowa granica plastyczności stali wg tab. 5 PN-B-03264
ϕ = 12mm - średnica prętów zbrojenia równoleżnikowego
● podstawowa długość zakotwień
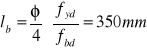
● minimalna długość zakotwienia dla prętów rozciąganych :
10 • ϕ = 120 mm
lb.min ≥max 100 mm więc: lb.min =210 mm
0,6 • lb = 210mm
● minimalna długość zakotwienia dla prętów rozciąganych :
10 • ϕ = 120 mm
lb.min ≥max 100 mm więc: lb.min =120 mm
0,3 • lb = 105mm
● obliczeniowa długość zakotwień prętów dla 6-ego segmentu
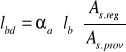
As.reg - pole przekroju zbrojenia wymaganego zgodnie z obliczeniami
As.prof - pole przekroju zbrojenia zastosowanego
αa = 1,0 - wsp. efektywności zakotwienia dla prętów prostych
As.reg = 74,23 cm2
As.prov = 90,48 cm2
![]()
> lb.min
Przyjęto: lbd = 350mm
● minimalna długość zakładu:
ls.min = 0,3 • αa • α1 • lb = 0,3 • 1,0 •1,0 • 35cm = 10,5cm
● wymagana długość zakładu:
ls = lbd • α1 = 350 mm >ls.min = 105 mm
Przyjęto długośc zakładu we wszystkich segmentach: ls = 350mm
Zakłady sąsiednich prętów należy sytuować względem siebie w przemieszczeniu o długości zakładu czyli: 350 mm
8.4. Zbrojenie poziome
Ac_pion,i = gp.i • 100cm - pole przekroju pionowego komina
As_poz.i = ρpoz • Ac - pole powierzchni zbrojenia poziomego
Gdzie: gp.i - grubośc ściany trzonu komina dla danego segmentu
We wszystkich segmentach komina przyjęto że: ρpoz= ρpoz_min = 0,4%
Przyjęto obustronne zbrojenie poziome na calej wysokości komina. Zgodnie z zaleceniami PN-88/B- 03004 przyjęto równą, symetryczną ilość zbrojenia po na obu krawędziach trzonu więc dla strony zewnętrznej:
As_poz.i_1 = 0,5 • ρpoz Ac
, a od strony wewnętrznej pozostała ilość zbrojenia
As_poz.i_2 = 0,5 • ρpoz Ac
Na całej wysokości komina przyjęto otulinę zbrojenia o grubości 3 cm ponieważ przyjęto że średnica prętów zbrojeniowych nie przekroczy 16 mm. Zgodnie z PN-88/B-03004 maksymalny odstęp między prętami poziomych wynosi 20 mm
Tabela 1.11.
Zestawienie przyjętych przekrojów zbrojenia poziomego w poszczególnych segmentach.
Segment |
Grub. Płaszcz gp.i [cm] |
Pole betonu Ac Na 1m [m2] |
Obliczeniowe pole zbrojenia |
Przyjęte zbrojenie |
Pole przyjętego zbrojenia |
|||
|
|
|
As_poz.i_1 [cm2] |
As_poz.i_2 [cm2] |
Zewnętrzne |
Wewnętrzne |
As_poz.i_1 [cm2] |
As_poz.i_2 [cm2] |
1 |
18 |
1,80 |
3,6 |
3,6 |
ϕ 10 co 20cm |
ϕ 10 co 20cm |
3,93 |
3,93 |
2 |
18 |
1,80 |
3,6 |
3,6 |
ϕ 10 co 20cm |
ϕ 10 co 20cm |
3,93 |
3,93 |
3 |
18 |
1,80 |
3,6 |
3,6 |
ϕ 10 co 20cm |
ϕ 10 co 20cm |
3,93 |
3,93 |
4 |
20 |
2,00 |
4 |
4 |
ϕ 12 co 20cm |
ϕ 12 co 20cm |
5,66 |
5,66 |
5 |
20 |
2,00 |
4 |
4 |
ϕ 12 co 20cm |
ϕ 12 co 20cm |
5,66 |
5,66 |
6 |
20 |
2,00 |
4 |
4 |
ϕ 12 co 20cm |
ϕ 12 co 20cm |
5,66 |
5,66 |
7 |
22 |
2,20 |
4,4 |
4,4 |
ϕ 12 co 20cm |
ϕ 12 co 20cm |
5,66 |
5,66 |
BIBLIOGRAFIA
1. Wykaż literatury:
1. Praca zbiorowa : Budownictwo betonowe, tom XIII. Arkady, Warszawa 1966
2. Kobiak J. , Stachurski W. : Konstrukcje żelbetowe, tom II. Arkady, Warszawa 1987.
2. Wykaz Norm:
1. PN-88/B-03004. Kominy murowane i żelbetowe. Obliczenia statyczne i
projektowanie.
2. PN-B-03264:1999 Konstrukcje betonowe żelbetowe i sprężone. Obliczenia statyczne
i projektowanie.
3. PN-77/B-02011 Obciążenia w obliczeniach statycznych. Obciążenie wiatrem.
.
3
Wyszukiwarka
Podobne podstrony:
4.1 Opis techniczny komina 09.09.10, budownictwo, semestr VI, budownictwo przemysłowe, kominy
PROJEKT 1 KS, AGH, Semestr VI, Konstrukcje stalowe [Matachowski], projekt 1
METODY PROJEKCYJNE, Psychologia UŚ, Semestr VI, Diagnoza psychologiczna
Projekt-tomek, m.szpaner, Semestr VI, OBSER, Projekt, zadziory
TS - projekt, Edukacja, studia, Semestr VI, Teoria Sterowania, Projekt
PROJEKT PRZEMYSŁOWEGO KOMINA ŻELBETOWEGO, Żelbetowe budownictwo przemysłowe, komin żelbetowy
TEST 01 z cwiczen projektowych, Politechnika Krakowska, V Semestr, Budownictwo przemysłowe, maerial
żelbet-Płyta zginana dwukierunkowo, budownictwo, semestr VI, konstrukcje betonowe, projekt
projekt betonowe, Budownictwo AGH 1, Propsy na V i VI semestr, Kaśka, konstrukcje betonowe, mój proj
wymiennik projekt, Inżynieria Chemiczna i Procesowa, Semestr VI, od Pani Doktorantki, aparatura prze
PROJEKT 3 prefabrykacja, Budownictwo PWr, SEMESTR 9
projekt obwiednia, Budownictwo, Inżynierka, Budownictwo, Semestr 3, Mechanika budowli, projekt z obw
STR TYTUŁ, Semestr 7, Budownictwo Przemysłowe
Projekt stalowe, budownictwo, semestr5, Konstrukcje stalowe, Projekt, PROJEKT, Przodek
infra+kolos, STUDIA budownictwo, SEMESTR VI, instalacje budowlane
Opis techniczny, NAUKA, Politechnika Bialostocka - budownictwo, Semestr III od Karola, Budownictwo
Mechanika gruntów - 2 projekt, Studia Budownictwo Zielona Góra Uz, semestr 3, mechanika gruntow, Mec
projekt 2 wytyczne, Budownictwo, Inżynierka, Budownictwo, Semestr 3, Mechanika budowli
Druki do koszorysowania, budownictwo, semestr VI, ekonomika budownictwa
więcej podobnych podstron