1

Teoria podobienstwa

Wyniki rozwiazania analitycznego, numerycznego lub analogowego

równania rózniczkowego opisujacego zjawisko fizyczne, mozna uogólnic
przedstawiajac je w postaci bezwymiarowej jezeli zastosuje sie teorie
podobienstwa.
Podstawa teorii podobienstwa sa trzy twierdzenia:
* Podobne do siebie zjawiska maja jednakowe wartosci liczb
podobienstwa - twierdzenie Newtona.
* Rozwiazanie ogólne (calke ogólna) ukladu równan rózniczkowych
mozna przedstawic w postaci funkcji liczb podobienstwa okreslonych na
podstawie tych równan - twierdzenie Buckinghama.
* Warunkiem koniecznym i dostatecznym podobienstwa zjawisk
fizycznych jest równosc liczb podobienstwa wynikajacych z równan
rózniczkowych opisujacych zjawisko i warunków jednoznacznosci (tj.
geometrycznych, fizycznych, czasowych i brzegowych) ich rozwiazania -
twierdzenie Kirpiczowa - Guchmana.

Zjawiska podobne musza nalezec do tego samego rodzaju zjawisk

fizycznych i byc opisywane tymi samymi równaniami rózniczkowymi.
Podobnymi nazywa sie sie te zjawiska, w których wartosci
jednoimiennych wielkosci charakteryzujacych rozpatrywane zjawisko
maja sie do siebie jak odpowiednie stale liczby bezwymiarowe, zwane
stalymi podobienstwa. Podobienstwo zjawisk fizycznych uwarunkowane
jest przede wszystkim podobienstwem geometrycznym rozpatrywanego
ukladu.
Bezwymiarowe stale podobienstwa powiazane sa ze soba zaleznosciami
wynikajacymi z równan matematycznych opisujacych dane zjawisko
fizyczne. Zaleznosci te uzyskane z równan algebraicznych lub
rózniczkowych, pozwalaja grupowac wielkosci fizyczne w bezwymiarowe
(kryterialne) liczby podobienstwa.

Jezeli skala czasu dla liczb podobienstwa jest identyczna,

podobienstwo cieplne w warunkach przeplywu nieustalonego mozna
zapisac ogólna funkcja:

Nu = f(Fo, Ho, Gr, Re, Pr); [1]

W warunkach przeplywu ustalonego, dla których liczby Fouriera i Herona
maja wartosc zerowa (Fo = 0, Ho = 0) podobienstwo cieplne mozna
mozna zapisac jako funkcje:

Nu = f(Gr, Re ,Pr); [2]

lub ogólnym wzorem:

Nu = C

⋅

Gra

⋅

Reb

⋅

Prc;

[3]

gdzie:

•

Nu - liczba Nusselta, opisujaca podobienstwo warunków
przysciennych dla przeplywu ciepla:

h

l

Nu

⋅⋅⋅⋅

α

αα

α

====

[4]

•

Pr - liczba Prandtla, opisujaca podobienstwo rodzaju plynu, a
stanowiaca kombinacje parametrów charakteryzujacych fizyczne
wlasciwosci czynnika:

a

Pr

νννν

====

[5]

•

Gr - liczba Grashofa, opisujaca ruch plynu spowodowany róznica
gestosci:

t

l

g

Gr

2
f

3

f

∆∆∆∆

⋅⋅⋅⋅

νννν

⋅⋅⋅⋅

⋅⋅⋅⋅

ββββ

====

[6]

•

Re - liczba Reynoldsa, opisujaca podobienstwo hydrodynamiczne
ruchu poprzez stosunek sily bezwladnosci do sily tarcia:

νννν

⋅⋅⋅⋅

====

l

w

Re

[7]

•

Fo - liczba Fouriera, opisujaca nieustalony przeplyw ciepla:

2

l

a

Fo

ττττ

⋅⋅⋅⋅

====

[8]

•

Ho - liczba Herona, opisujaca nieustalony przeplyw:

l

w

Ho

ττττ

⋅⋅⋅⋅

====

[9]

•

C, a, b, c - stale, ustalane w oparciu o dane pomiarowe;

Pozostale oznaczenia we wzorach to:

•

h - wspólczynnik przejmowania ciepla, W/(m2

⋅

K);

•

l - wymiar liniowy, m;

•

λ

- wspólczynnik przewodnosci cieplnej, W/(m2

⋅

K);

•

ν

` - lepkosc m

2

/s;

•

a - dyfuzyjnosc cieplna (wspólczynnik wyrównywania

temperatury), m /s;

•

β

- wspólczynnik rozszerzalnosci objetosciowej, 1/K;

•

t - ró¿nica temperatur, K;

•

w - predkosc, m/s;

•

τ

- czas, s;

•

g - przyspieszenie grawitacyjne, m /s.

Liczbe Nusselta mozna zapisac ogólnym wzorem:

d

w

f

c

b

a

Pr

Pr

Gr

Re

Pr

C

Nu













⋅⋅⋅⋅

⋅⋅⋅⋅

⋅⋅⋅⋅

⋅⋅⋅⋅

====

[10]

W przypadku konwekcji naturalnej i liczbe Nusselta mozna opisac
wzorem:

d

w

f

A

Pr

Pr

)

Gr

(Pr

C

Nu













⋅⋅⋅⋅

⋅⋅⋅⋅

⋅⋅⋅⋅

====

[11]

Natomiast w przypadku ruchu burzliwego, liczba Grashofa, Gr = 0, stad:

d

w

f

b

a

Pr

Pr

Pr

Re

C

Nu













⋅⋅⋅⋅

⋅⋅⋅⋅

⋅⋅⋅⋅

====

[12]

gdzie:

•

A,a, b, c, d, e - stale, ustalane w oparciu o dane pomiarowe;

•

µ

- lepkosc dynamiczna, Pa

⋅

s;

•

w - indeks dla temperatury sciany;

•

f - indeks dla temperatury plynu.

2

Przejmowanie ciepla w ukladzie

nieograniczonym na drodze konwekcji

Przestrzen nieograniczona wystepuje wówczas, gdy stosunek

otaczajacego plynu do powierzchni wymiany ciepla jest bardzo duzy
(przestrzen nie wplywa na wymiane ciepla). Wielkosc wspólczynnika
przejmowania ciepla zalezy od rodzaju plynu. Jego wartosc jest
najwieksza przy ruchu laminarnym, nastepnie przy ruchu przejsciowym
maleje, aby wzrosnac i osiagnac stala wartosc przy ruchu
burzliwym.Charakter oplywu jest uzalezniony od róznicy temperatur ciala
i plynu, i tak dla

∆

t < 15 K przewaza ruch laminarny, zas dla

∆

t > 15 K,

ruch burzliwy.

∆

∆∆

∆

α

αα

α

t

δδδδ

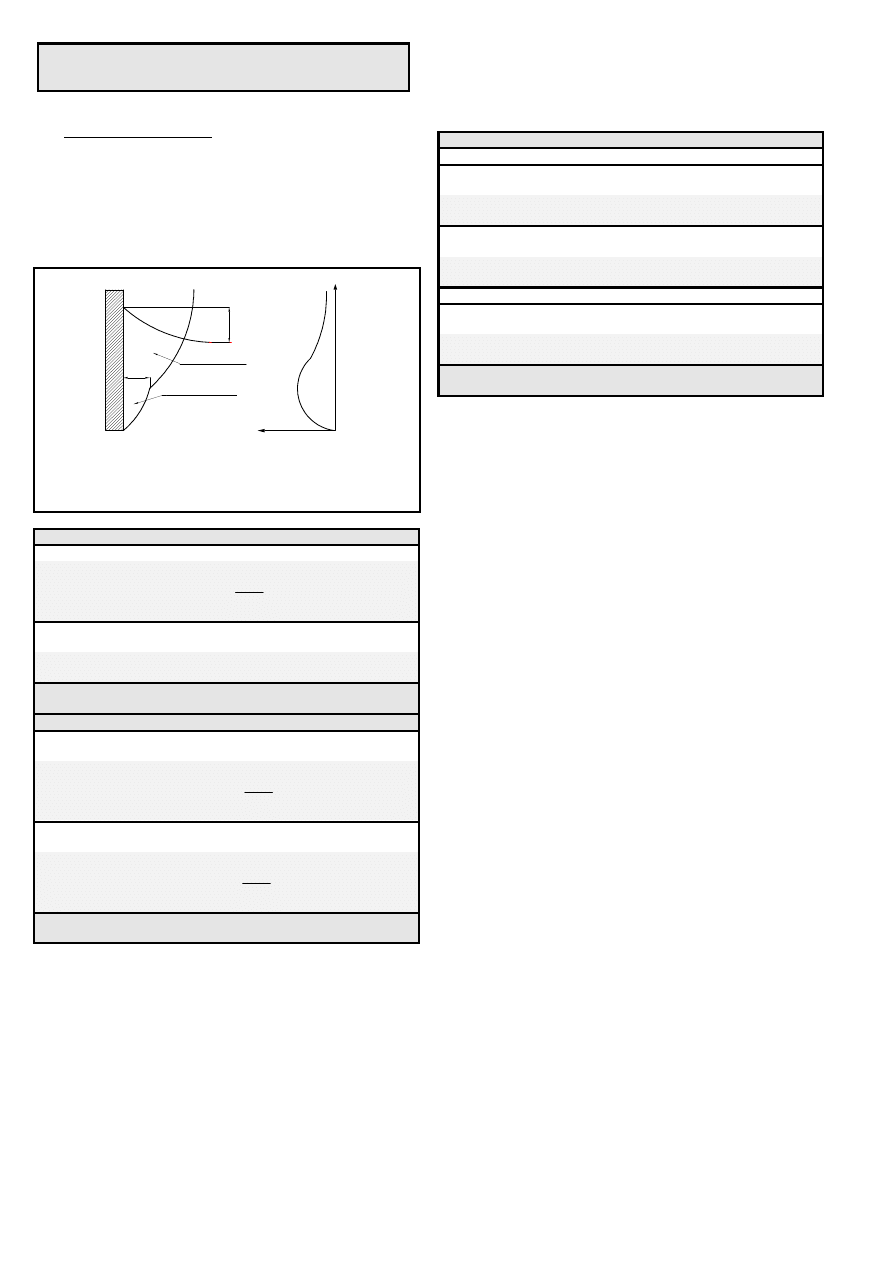
Ruch laminarny

Ruch burzliwy

t

H

t

f

w

Rys.1. Przejmowanie ciepla w przestrzeni nieograniczonej na drodze

konwekcji

Objasnienia indeksów:
w - indeks dla temperatury sciany;

f - indeks dla temperatury plynu w duzej odleglosci od sciany.

1. Przejmowanie od rur poziomych

dla 103 < Gr

⋅

Pr < 108

25

,

0

25

,

0

Pr

Pr

)

Pr

(

5

,

0













⋅

⋅

⋅

=

w

f

f

f

Gr

Nu

[13]

dla Gr

⋅

Pr > 108

3

/

1

)

Pr

(

1

,

0

f

f

Gr

Nu

⋅

⋅

=

[16]

Charakterystycznym wymiarem liniowym (l) dla rur poziomych i kul jest
ich srednica.

2. Przejmowanie od plyt i rur pionowych

dla 103 < Gr

⋅

Pr < 109

25

,

0

25

,

0

Pr

Pr

)

Pr

(

75

,

0













⋅

⋅

⋅

=

w

f

f

f

Gr

Nu

[14]

dla Gr

⋅

Pr > 109

25

,

0

33

,

0

Pr

Pr

)

Pr

(

15

,

0













⋅

⋅

⋅

=

w

f

f

f

Gr

Nu

[18]

Charakterystycznym wymiarem liniowym dla plyt i rur pionowych jest ich
wysokosc.

3. Plyty poziome

Plyta goraca zwrócona do góry, lub plyta zimna zwrócona na dól

dla 105 < Gr

⋅

Pr < 2

⋅

107

25

,

0

)

Pr

(

54

,

0

f

f

Gr

Nu

⋅

⋅

=

[15]

dla 2

⋅

107 < Gr QPr < 3

⋅

1010

3

/

1

)

Pr

(

14

,

0

f

f

Gr

Nu

⋅

⋅

=

[16]

Plyta goraca zwrócona do dolu

dla 3

⋅

105 < Gr QPr < 3

⋅

1010

25

,

0

)

Pr

(

27

,

0

f

f

Gr

Nu

⋅

⋅

=

[17]

Charakterystycznym wymiarem liniowym (l) dla plyt poziomych jest ich
krótszy bok.

gdzie:

•

Nuf - liczba Nusselta dla temperatury plynu;

•

Prf

- liczba Prandtla dla temperatury plynu;

•

Prw - liczba Prandtla dla temperatury scianki;

•

Grf - liczba Grashofa dla temperatury plynu.