WM

4. Ćwiczenie projektowe numer 4 – przykład 11

1

4. Ćwiczenie projektowe numer 4 – przykład 11

4.1. Ćwiczenie projektowe numer 4

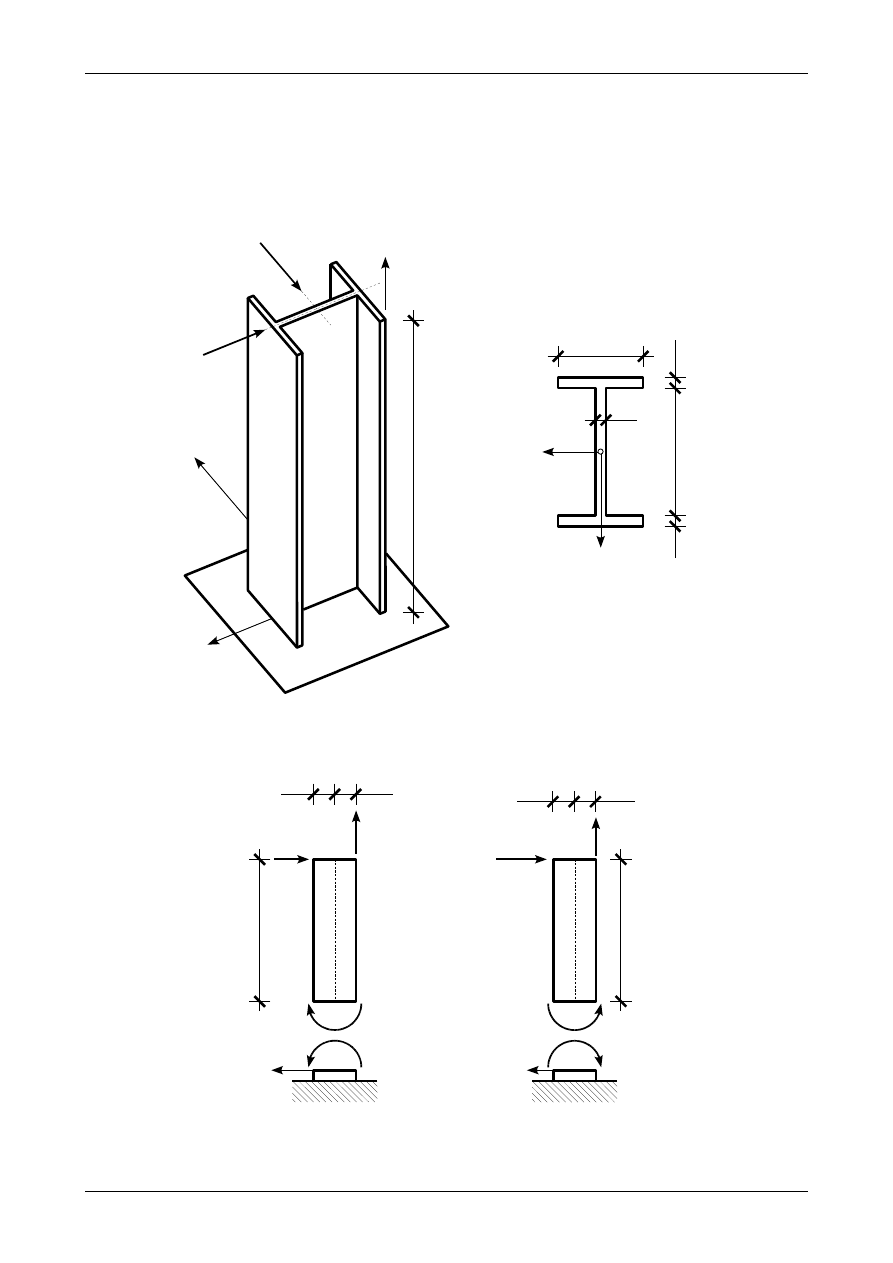
Dany jest pręt wspornikowy o przekroju dwuteowym przedstawiony na rysunku 4.1. W przekroju przy

utwierdzeniu

α−α

wyznaczyć wykres naprężenia normalnego

σ

X

.

α −

α

2,

3

Z=Z

gl

Y=

Y

gl

α − α

8,0

1,5

2,

0

Y=Y

gl

Z=Z

gl

sc

2,

0

[cm]

10

,0

[m]

108,0 kN

1,7

kN

4,1

kN

Rys. 4.1. Pręt wspornikowy

[m]

Y=Y

gl

Z=Z

gl

M

Y

M

Z

2,

3

0,04

0,07

a)

1,7 kN

108,0 kN

b)

M

Y

M

Z

2,

3

108,0 kN

4,1 kN

0,04

0,07

Rys. 4.2. Widoki pręta wspornikowego

Dr inż. Justyna Grzymisławska

BS-I

WM

4. Ćwiczenie projektowe numer 4 – przykład 11

2

4.2. Określenie sił przekrojowych

Siła normalna w przekroju

α−α

wynosi

N =108,0 kN

.

Momenty zginające zgodnie z rysunkiem 4.2 wynoszą

M

Y

=

4,1⋅2,3−108,0⋅0,07=1,870 kN⋅m=187,0 kN⋅cm

.

M

Z

=−

1,7⋅2,3108,0⋅0,04=0,410 kN⋅m=41,00 kN⋅cm

.

4.3. Wykres naprężenia normalnego

Charakterystyki geometryczne przekroju pręta wspornikowego wynoszą

A=2⋅8,0⋅2,010,0⋅1,5=47,0 cm

2

,

J

Y

=

8,0⋅14,0

3

12

−

6,5⋅10,0

3

12

=

1288cm

4

,

J

Z

=

2⋅

2,0⋅8,0

3

12



10,0⋅1,5

3

12

=

173,5 cm

4

.

Funkcja naprężenia normalnego

σ

X

ma postać



X

=

108,0

47,0

−

41,0

173,5

⋅

y 

187,0

1288

⋅

z

,



X

=

2,298−0,2363⋅y 0,1452⋅z

.

Oś obojętna ma postać

−

0,2363⋅y0,1452⋅z=−2,298

,

0,1028⋅y−0,06319⋅z =1

,

y

9,728



z

−

15,83

=

1

.

Współrzędne odcinkowe osi obojętnej wynoszą więc

Dr inż. Justyna Grzymisławska

BS-I

WM

4. Ćwiczenie projektowe numer 4 – przykład 11

3

[cm]

Y=Y

gl

Z=Z

gl

9,728

1

5,

8

3

sc

2

1

σ

X

[MP

a]

3,

36

4

42

,6

0

22

,9

8

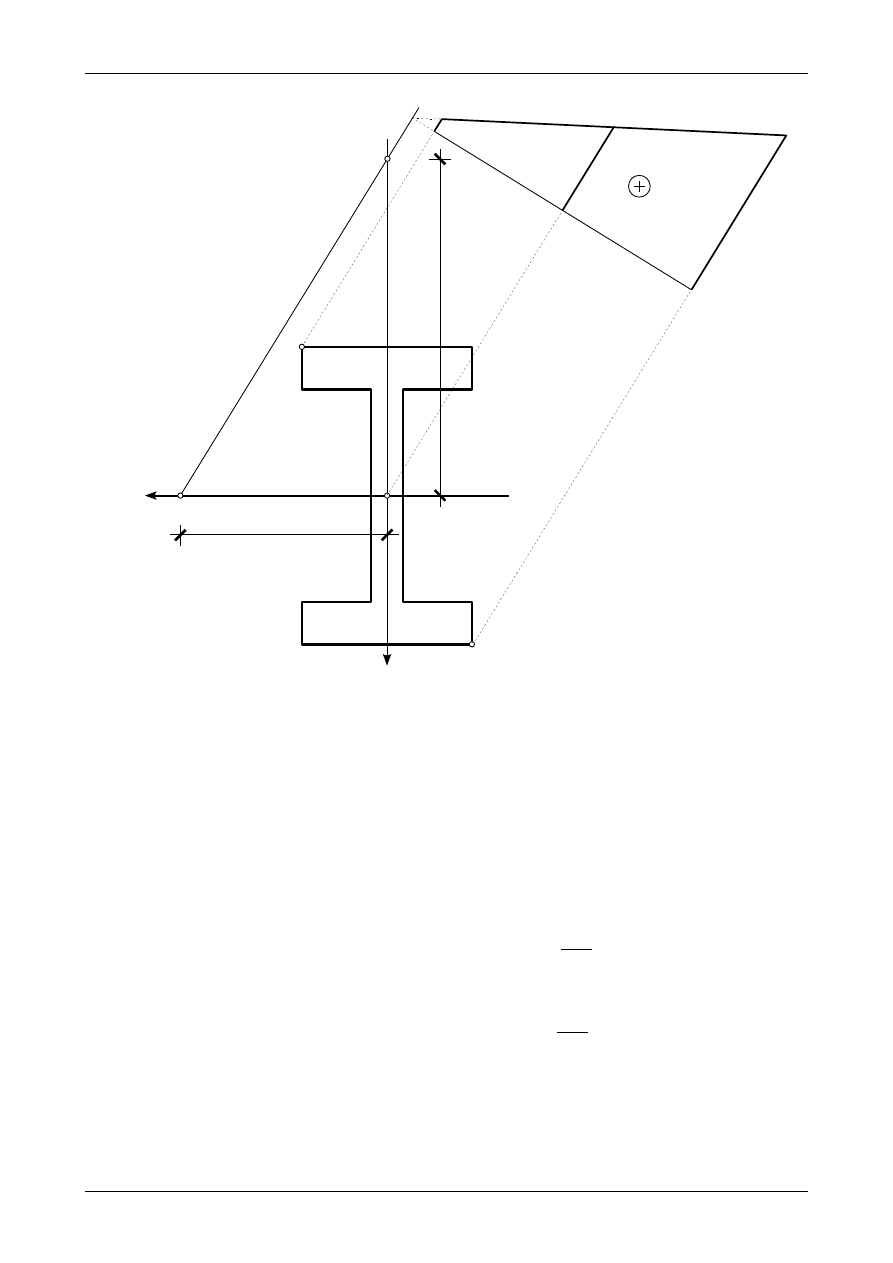
Rys. 4.3. Wykres naprężenia normalnego w przekroju pręta wspornikowego

y

0

=

9,728 cm

,

z

0

=−

15,83 cm

.

Naprężenia normalne

σ

X

w najdalej oddalonych od osi obojętnej punktach wynoszą



X



1 

=

2,298−0,2363⋅4,00,1452⋅



−

7,0



=

0,3364

kN

cm

2

=

3,364 MPa

,



X



2

=

2,298−0,2363⋅



−

4,0





0,1452⋅7,0=4,260

kN

cm

2

=

42,60 MPa

.

Wykres naprężenia normalnego

σ

X

w przekroju pręta wspornikowego przedstawia rysunek 4.3.

Dr inż. Justyna Grzymisławska

BS-I