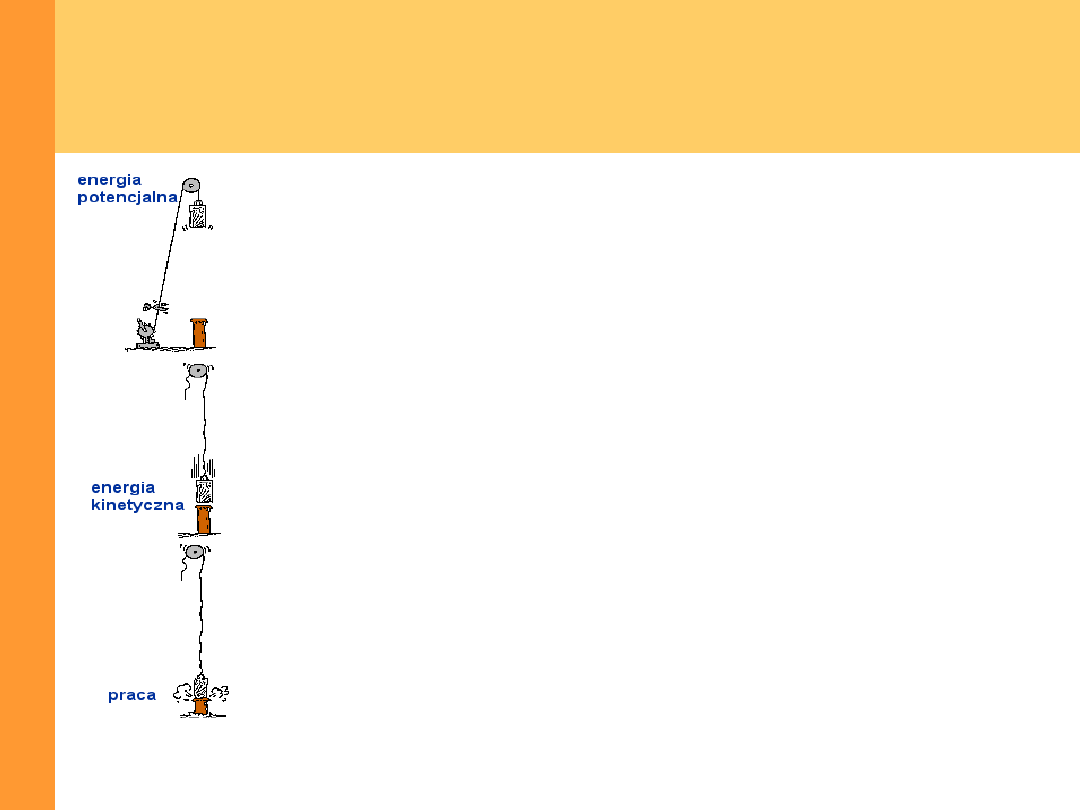


Zasada zachowania energii



Środek masy:



definicja,



ruch środka masy,



Zasada zachowania pędu



Zderzenia:



sprężyste, niesprężyste,



centralne, niecentralne,



Podstawy dynamiki

Zasada zachowania energii

Układ odosobniony:

jest to układ, na który nie działają żadne

siły zewnętrzne.

Układ zachowawczy:

jest to układ, w którym działające siły

wewnętrzne są siłami zachowawczymi



praca wykonana przez

te siły nie zależy od drogi przemieszczenia.

Energią potencjalną

ciała w punkcie

A

względem punktu

O

nazywamy pracę, jaką wykonuje siła zachowawcza przy
przesunięciu ciała od punktu

A

do punktu

O

:

AO

p

W

A

E



)

(

A

O

1

Jeżeli ciało o masie

m

ulega przesunięciu z punktu

A

do

B

,

to różnica energii potencjalnej w tych punktach, względem
punktu

O

wynosi:

BA

AO

BO

p

p

W

W

W

A

E

B

E









)

(

)

(

2

O

A

B

Zasada zachowania energii

Zasada zachowania energii

Zasada zachowania energii mechanicznej mówi, że dla

ciała podlegającego działaniu siły zachowawczej,

suma energii kinetycznej i potencjalnej jest stała.

Energia mechaniczna układu odosobnionego
i zachowawczego jest stała.

const

E

E

P

K





Zasada ta obowiązuje dla pojedynczego ciała, ale jest też bardziej ogólna
i obowiązuje dla wszystkich odosobnionych układów ciał. W takich
układach suma energii kinetycznych i potencjalnych wszystkich ciał
pozostaje stała bez względu na oddziaływania w nich zachodzące.
Energia może być przekształcana z jednej formy w inną, ale nie może być
wytworzona ani niszczona.

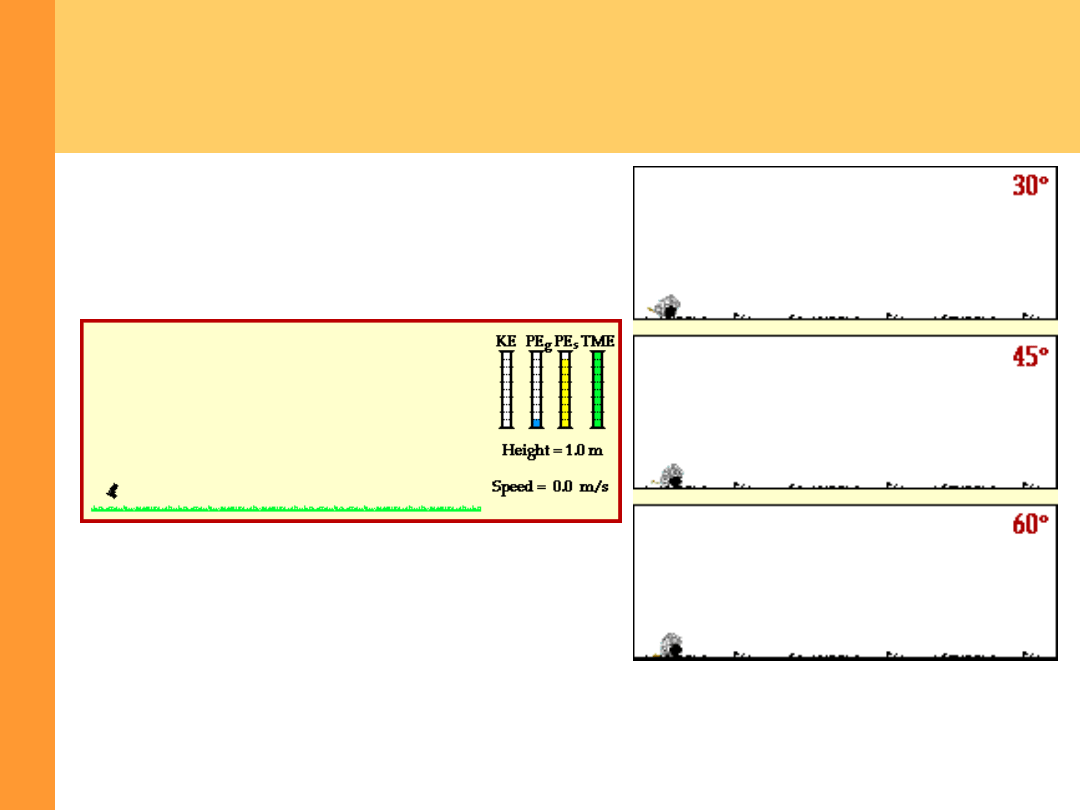
Zasada zachowania energii -

przykład

Rzut ukośny:

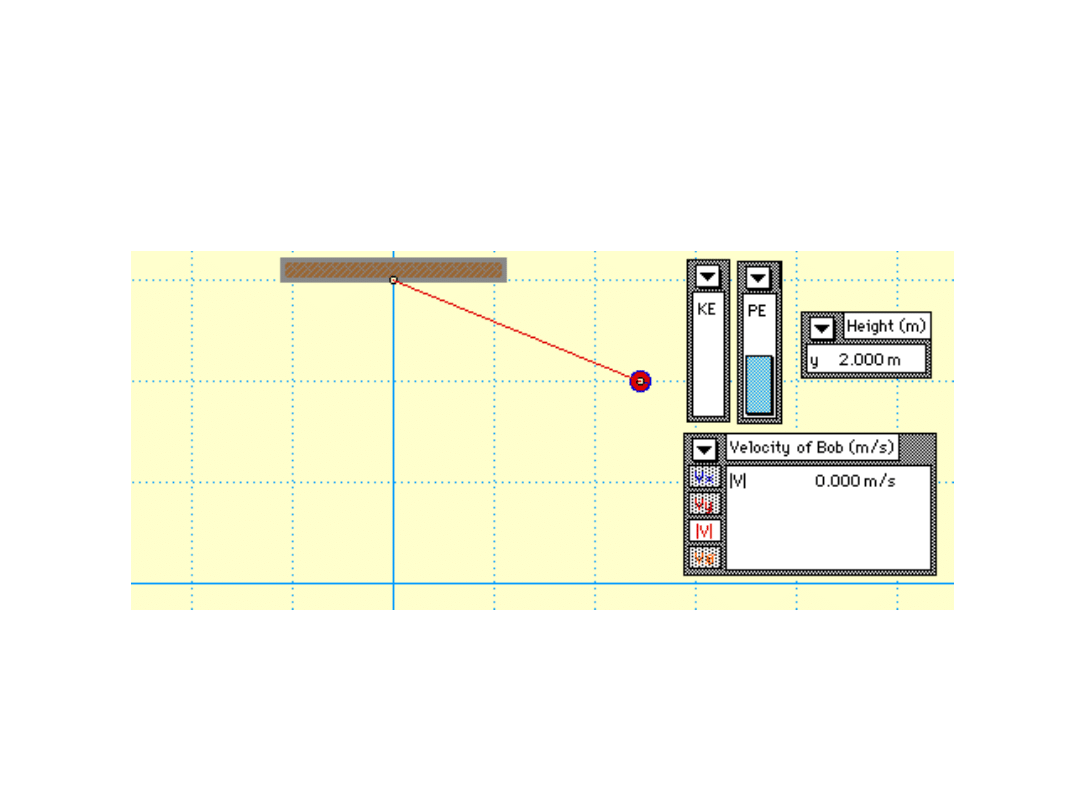
Wahadło:

Środek masy

























n

i

i

n

i

i

i

n

n

n

s

m

x

m

m

m

m

x

m

x

m

x

m

x

1

1

2

1

2

2

1

1

.....

.....



Dotychczas przedmioty traktowaliśmy jako punkty materialne.



W rzeczywistości ciała są układami ogromnej liczby atomów.



Rozważmy ruch złożony ciała (obrotowo – postępowy).







n

i

i

i

s

x

m

M

x

1

1



Istnieje w tym układzie jeden punkt, który porusza się po linii prostej ze

stałą prędkością -

środek masy.

2

1

2

2

1

1

m

m

x

m

x

m

x

s









Dla mas rozłożonych wzdłuż jednej prostej:

x

s

m

1

m

2

x

1

x

2

x

0

O

Środek masy







n

i

i

i

s

m

M

1

1

r

r







Ogólnie możemy napisać:

i

i

i

i

z

y

x















r

s

s

s

s

z

y

x















r



Środek masy układu punktów materialnych zależy tylko od mas tych

punktów i od wzajemnego ich rozmieszczenia, a nie zależy od wyboru

układu odniesienia



Aby obliczyć położenie środka masy ciała rozciągłego dzielimy je (w myśli)

na

n

małych części o masach

D

m

1

,

D

m

2

, …,

D

m

n









D

D



n

i

i

n

i

i

i

s

m

r

m

r

1

1







Dla brył o regularnym kształcie środek masy pokrywa się ze środkiem symetrii

Ruch środka masy

zew

s

F

a

M









Środek masy układu

punktów materialnych

porusza się w taki sposób,

jakby cała masa układu

była skupiona w

środku

masy

i jakby wszystkie

siły zewnętrzne nań

działały

Zasada zachowania pędu



Pęd punktu materialnego:



Jeżeli mamy do czynienia z układem punktów materialnych, to:

i

i

i

m

p

v

















n

1

i

i

v





i

m

p



Całkowity pęd układu punktów materialnych jest równy iloczynowi

całkowitej masy układu i prędkości jego środka masy.











n

i

i

i

s

m

1

v

v

M





Ponieważ

s

v









M

p

to:

dt

p

d

dt

M

d

dt

d

M

a

M

F

s

zew

























)

v

(

v

s

s

II zasada dynamiki :

Zasada zachowania pędu



II zasada dynamiki :

dt

p

d

F

zew









Jeżeli nie działają siły zewnętrzne (lub wypadkowa jest równa zero):

dt

p

d

F

zew









0

const

p







Jeżeli wypadkowa sił zewnętrznych
działających na układ jest równa zeru, to
całkowity wektor pędu układu jest stały.

Jeżeli wypadkowa sił zewnętrznych
działających na układ jest równa zeru, to
pęd układu w stanie początkowym jest
równy

pędowi

układu

w

stanie

końcowym.

Zasada zachowania pędu



Popęd siły

:

dt

p

d

F

zew









Wyrażenie po lewej stronie jest popędem siły

p

d

dt

F

zew









Przyrost

pędu ciała równa się popędowi

działającej na nie siły.

p

t

F





D



D

Zasada zachowania pędu

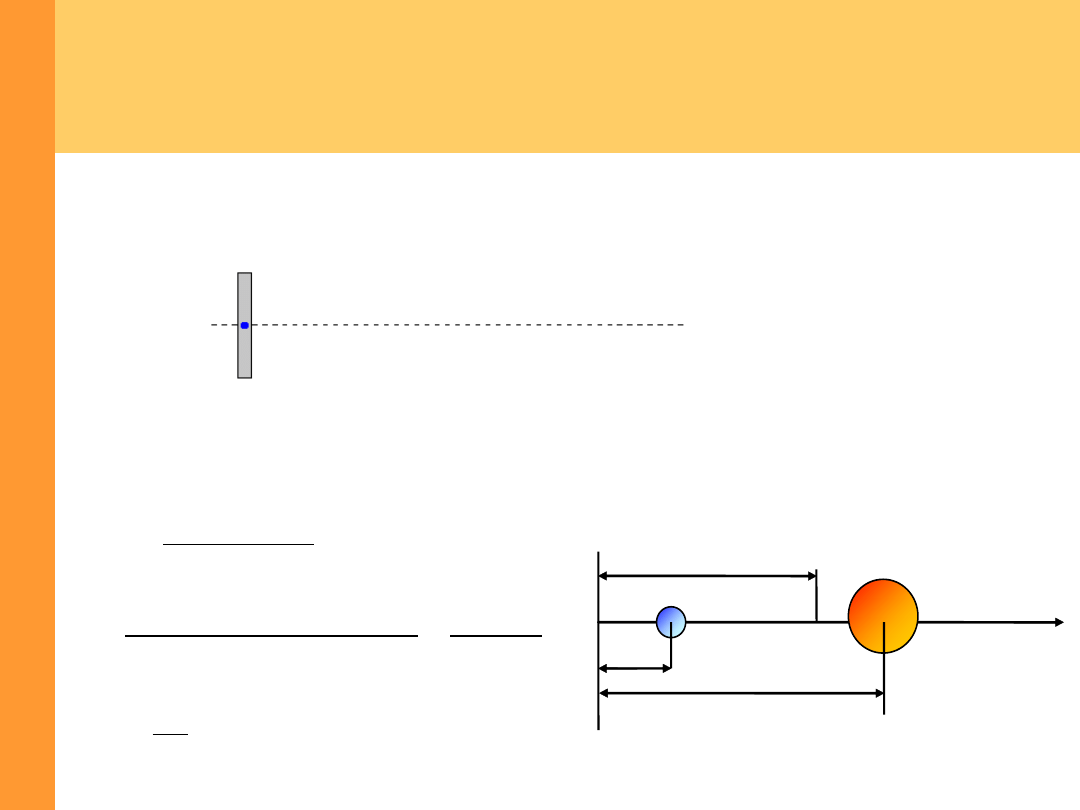
- przykład

m

1

m

2

2

2

1

1

v

v

0

















m

m

p

x

Zderzenia



Zderzenie

– krótkotrwałe oddziaływanie dwóch ciał.

Podział:



zderzenia bezpośrednie – (mechaniczne)



zderzenia „bezstykowe” (rozproszenie) –

za pośrednictwem wszelkiego rodzaju pól



zderzenia sprężyste (elastyczne) – spełniona jest

zasada zachowania pędu i energii kinetycznej



zderzenia niesprężyste (nieelastyczne) –

spełniona jest zasada zachowania pędu:



idealnie niesprężyste – ciała łączą się



zderzenia centralne

– ciała poruszają się

wzdłuż linii łączącej środki



zderzenia niecentralne

– ukośne

Zderzenia sprężyste













































2

2

1

1

2

2

1

1

2

2

2

2

1

1

2

2

2

2

1

1

2

1

2

1

2

1

2

1

u

m

u

m

v

m

v

m

u

m

u

m

v

m

v

m

Centralne zderzenia sprężyste dla kul o masach

m

1

i

m

2

oraz ich prędkości

przed zderzeniem

v

1

i

v

2

.

Szukamy prędkości

u

1

i

u

2

obu kul po zderzeniu.

W zderzeniu sprężystym – zasada zachowania energii kinetycznej oraz
pędu.



























)

(

)

(

)

(

)

(

2

2

2

1

1

1

2

2

2

2

2

2

1

2

1

1

v

u

m

u

v

m

v

u

m

u

v

m

/

:

)

(

)

(

)

(

)

(

)

(

)

(

2

2

2

1

1

1

2

2

2

2

2

1

1

1

1

1



































v

u

m

u

v

m

v

u

v

u

m

u

v

u

v

m

0



D

E

0



D

p



Zderzenia sprężyste

2

1

1

2

2

2

1

1

)

(

)

(

v

u

v

u

v

u

u

v













2

2

1

2

1

2

1

1

1

1

2

1

1

2

1

1

1

2

)

2

(

)

(

v

m

u

m

v

m

u

m

v

m

v

u

v

m

u

v

m

































2

1

1

2

1

2

2

1

1

1

1

2

1

2

1

1

2

2

)

(

2

2

m

m

v

m

m

v

m

u

u

m

u

m

v

m

v

m

v

m































2

1

2

1

2

1

1

2

2

1

1

2

1

2

2

2

1

2

1

2

)

(

2

)

(

2

)

(

)

(

m

m

v

m

m

v

m

u

m

m

v

m

m

v

m

m

m

v

v

u



































Zderzenia sprężyste




































2

1

2

1

2

1

1

2

2

1

1

2

1

2

2

1

)

(

2

)

(

2

m

m

v

m

m

v

m

u

m

m

v

m

m

v

m

u

i ostatecznie:

Zbadajmy zachowanie się prędkości końcowych w zależności od mas

i prędkości początkowych:



Niech

m

1

=

m

2











1

2

2

1

v

u

v

u

wtedy:

czyli kule o jednakowych masach wymieniają wzajemne swe prędkości

Zderzenia sprężyste




































2

1

2

1

2

1

1

2

2

1

1

2

1

2

2

1

)

(

2

)

(

2

m

m

v

m

m

v

m

u

m

m

v

m

m

v

m

u



niech

v

2

= 0

wtedy:


























2

1

1

1

2

2

1

1

2

1

1

2

)

(

m

m

v

m

u

m

m

v

m

m

u

jeśli dodatkowo

m

1

=

m

2











1

2

1

0

v

u

u

Zderzenia sprężyste




































2

1

2

1

2

1

1

2

2

1

1

2

1

2

2

1

)

(

2

)

(

2

m

m

v

m

m

v

m

u

m

m

v

m

m

v

m

u



gdy druga kula ma masę znacznie większą od pierwszej i jest nieruchoma

jeśli dodatkowo
(odbicie od ściany)

0

2

2

1





v

i

m

m

1

2

1

2

1

2

1

2

1

2

1

1

1

2

1

1

v

m

m

m

m

u

v

m

m

m

m

u





















2

m

0

lim

2

1

2







m

m

m













0

2

1

1

u

v

u

Zderzenia niesprężyste

Zmiana energii kinetycznej

D

E

:

Zderzenia niesprężyste kul o masach

m

1

i

m

2

o prędkościach przed

zderzeniem

v

1

i

v

2

.

Niech obie prędkości mają te same kierunki i niech

v

1

>

v

2

. Po zderzeniu następuje trwałe odkształcenie i ciała poruszają się razem.

Obliczyć wspólną prędkości

u

.

2

1

2

2

1

1

2

1

2

2

1

1

)

(

m

m

v

m

v

m

u

u

m

m

v

m

v

m























2

)

(

2

2

2

2

1

2

2

2

2

2

1

1

1

u

m

m

E

v

m

E

v

m

E

kk

k

k











0

)

(

)

(

2

)

(

2

2

1

2

1

2

1

2

1























D

v

v

m

m

m

m

E

E

E

E

k

k

kk

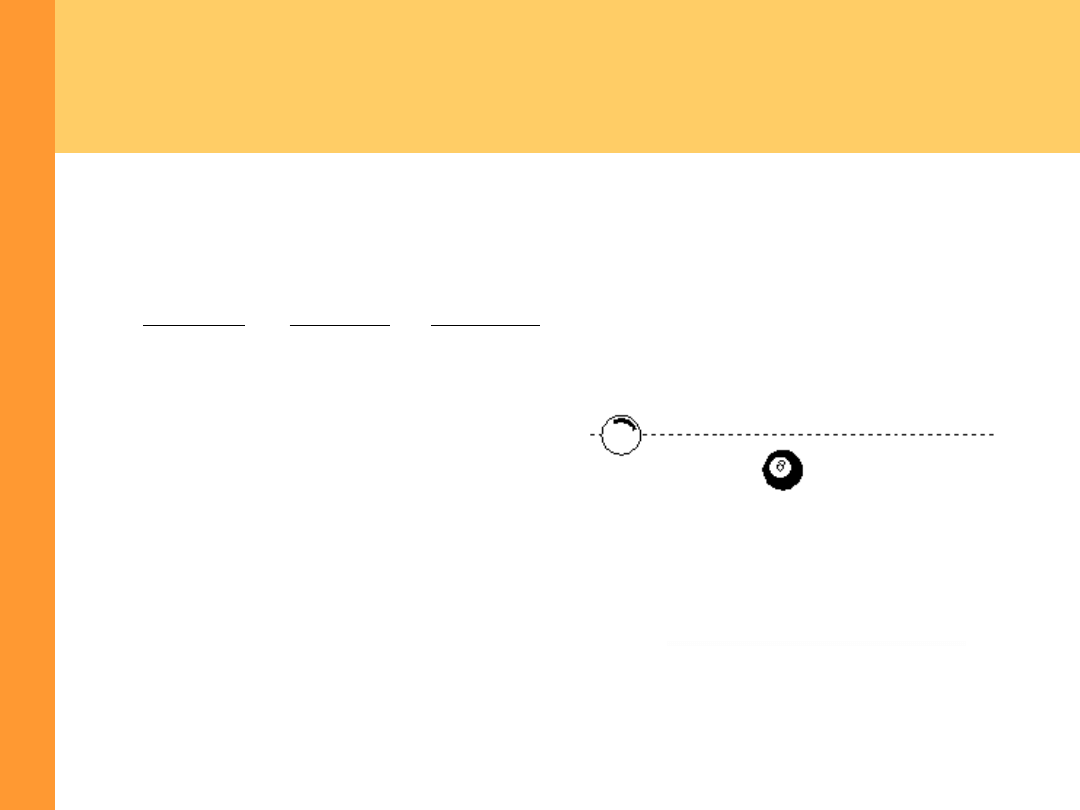
Zderzenia ukośne

Rozpatrzymy ukośne zderzenie sprężyste kuli o masie

m

z

identyczną

spoczywającą kulą.





























2

1

1

2

2

2

1

2

1

2

2

2

u

m

u

m

v

m

u

m

u

m

v

m





















2

1

1

2

2

2

1

2

1

u

u

v

u

u

v







Po zderzeniu wektory prędkości

u

1

i

u

2

są do siebie prostopadłe.

Zderzenia -

przykłady