ZESZYTY NAUKOWE AKADEMII MARYNARKI WOJENNEJ
ROK LII NR 1 (184) 2011
67
J a n u s z K o l e n d a
A k a d e m i a M a r y n a r k i W o j e n n e j
W S P Ó Ł C Z Y N N I K B E Z P I E C Z E Ń S T W A
Z M Ę C Z E N I O W E G O W A Ł Ó W
P R Z Y L O S O W Y M Z G I N A N I U I S K R Ę C A N I U
STRESZCZENIE
Artykuł dotyczy bezpieczeństwa zmęczeniowego wałów poddanych równoczesnemu
działaniu momentów gnących i skręcających o losowym charakterze i stacjonarnych w szerszym
sensie. Zakłada się, że wynikające stąd naprężenia normalne i tnące są nieskorelowane oraz że
mają znane wartości średnie i gęstości widmowe mocy. Pozwala to oba te naprężenia rozpatry-
wać oddzielnie i wykorzystywać znany wzór na współczynnik bezpieczeństwa zmęczeniowego
wałów na podstawie obliczeń cząstkowych współczynników bezpieczeństwa zmęczeniowego przy
zginaniu i skręcaniu. W tym celu wyznaczono ekwiwalentne naprężenia normalne i tnące jako
procesy Gaussa oraz wartości oczekiwane cząstkowych współczynników bezpieczeństwa. Prze-
prowadzono obliczenia przykładowe.
Słowa kluczowe:
wały, obciążenia losowe, wytrzymałość zmęczeniowa.
WSTĘP
Na skutek obciążeń zewnętrznych w poprzecznych przekrojach wałów po-
wstają naprężenia:
⎯ normalne
x
σ
od momentów gnących;
⎯ tnące
xy
σ
od momentów skręcających;
⎯ tnące
xy
σ
od sił poprzecznych;
⎯ normalne
x
σ
od sił wzdłużnych (ściskających bądź rozciągających).
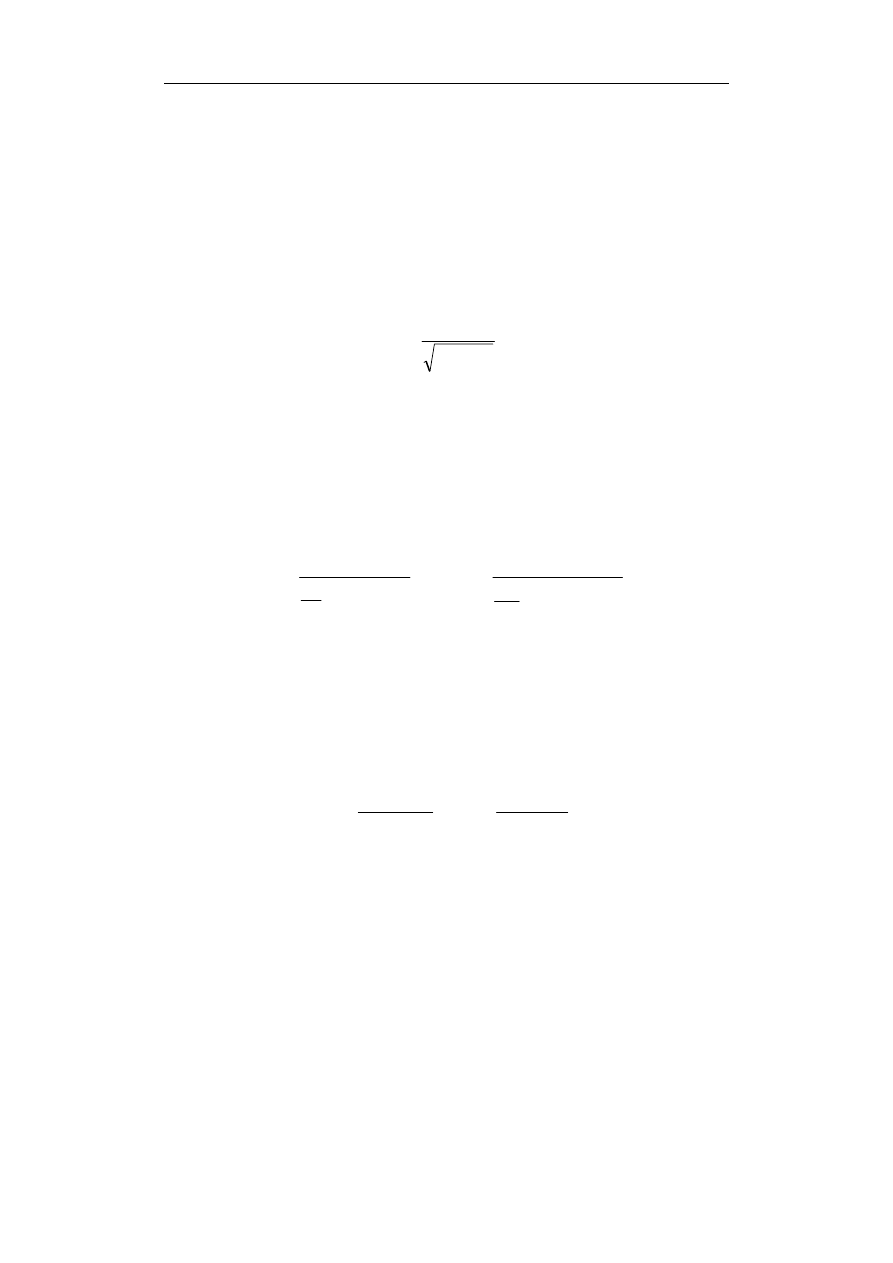
Janusz Kolenda
68
Zeszyty
Naukowe
AMW
Zazwyczaj naprężenia tnące od sił poprzecznych nie są uwzględniane w ob-
liczeniach wytrzymałościowych wałów z powodu ich małej wartości w porównaniu
do naprężeń wywołanych zginaniem i skręcaniem. Również obciążenia wzdłużne
wałów poddanych znacznym momentom skręcającym i gnącym są zwykle pomijane
w tego typu obliczeniach [5]. To samo dotyczy obliczeń zmęczeniowych, przy czym
w najbardziej „zgrubnym” algorytmie rzeczywiste współczynniki bezpieczeństwa
zmęczeniowego na zginanie
x
δ
i na skręcanie
xy
δ
liczy się dla każdego rodzaju
naprężeń osobno, a następnie określa łączny rzeczywisty współczynnik bezpieczeń-
stwa zmęczeniowego
δ
ze wzoru [1, 2, 5]:
2
2
xy
x
xy
x
δ
δ
δ
δ
δ
+
=
. (1)
Wzór (1) jest ważny dla ogólnego przypadku płaskiego stanu naprężenia ze
składowymi
xy
x
σ
σ
i
, a zatem również dla cykli niesymetrycznych. Nie zachodzi
przy tym konieczność spełnienia założenia o zgodności faz i częstości naprężeń
składowych [2].
Z uwzględnieniem takich czynników wpływających na wytrzymałość zmę-
czeniową, jak działanie karbu, wielkość przedmiotu i wrażliwość materiału na asy-
metrię cyklu, występujące w (1) współczynniki wyznaczane są za pomocą wzorów:
xym
xy
xya
xy
xy
so
xy
xm
x
xa
x
x
go
x
Z
,
Z
σ
ψ
σ
ε
β
δ
σ
ψ
σ
ε
β
δ
+
=
+
=
, (2)
gdzie:
xya
xa
σ
σ
,
— nominalne amplitudy naprężeń składowych;
xym
xm
σ
σ
,
— wartości średnie naprężeń składowych;
ε
β
,
—
współczynniki działania karbu i wielkości przedmiotu, których wartości
określone są w literaturze specjalistycznej [2, 5];
ψ
—
współczynniki wrażliwości materiału na asymetrię cyklu definiowane jako
sj
sj
so
xy
gj
gj
go
x
Z
Z
Z
Z
Z
Z
−
=
−
=
2
,
2
ψ
ψ
, (3)
gdzie:
so
go
Z
Z
,
— granice zmęczenia przy cyklach wahadłowych;
sj
gj
Z
Z
,
— granice zmęczenia przy cyklach odzerowo tętniących.
Współczynnik bezpieczeństwa zmęczeniowego wałów przy losowym zginaniu i skręcaniu
1 (184) 2011
69
W przypadku gdy naprężenia składowe
xy
xy
x
x
σ
σ
σ
σ
~
i
~
=
=
mają charakter
procesów losowych z amplitudami o rozkładach normalnych, prawdopodobieństwo
zniszczenia zmęczeniowego można odczytać z wykresów, korzystając z algorytmu
obliczeń opisanego w [2]. W niniejszej pracy przedstawiono możliwość wykorzysta-
nia wzorów (1) — (3) do oszacowania wartości oczekiwanej współczynnika bezpie-
czeństwa zmęczeniowego przy łącznym występowaniu losowego zginania i skręcania.
Założono przy tym, że naprężenia składowe
xy
x
σ
σ
~
i
~
są nieskorelowanymi procesami
stacjonarnymi (w szerszym sensie) o znanych wartościach średnich i gęstościach
widmowych mocy, które zamodelowano równoważnymi w sensie wytrzymałości
zmęczeniowej naprężeniami ekwiwalentnymi
xye
xe
σ
σ
~
i
~
.
EKWIWALENTNE
NAPRĘŻENIA
SKŁADOWE
Rozpatrywane naprężenia normalne
( )
~ t
x
σ
i tnące
( )
t
xy
σ
~
można zapisać jako:
( )
( )
( )
( )
t
t
t
t
xy
xym
xy
x
xm
x
σ
σ
σ
σ
σ
σ
+
=
+
=
~
~
, (4)
gdzie:
xym
xm
σ
σ
i
—
naprężenia średnie;
( )
( )
t
t
xy
x
σ
σ
i
— procesy stochastyczne.
Przy założeniu stacjonarności tych procesów oraz znajomości wartości
oczekiwanych naprężeń średnich
{ }
{ }
xym
xm
E
σ
σ
E
i
poszukiwać będziemy ekwiwa-
lentnych naprężeń składowych w postaci dogodnej do obliczeń zmęczeniowych [3]:
( ) { }
( )
( )
{ }
( )
t
E
t
t
E
t
xye
xym
xye
xe
xm
xe
σ
σ
σ
σ
σ
σ
+
=
+
=
~
~
, (5)
gdzie
( )
(
)
(
)
(
)
( )
(
)
(
)
(
)
t
j
b
t
j
b
t
b
t
t
j
a
t
j
a
t
a
t
xy
xy
xy
xy
xye
x
x
x
x
xe
ω
ω
α
ω
σ
ω
ω
α
ω
σ
−
+
=
+
=
−
+
=
+
=
−
−
exp
exp
sin
exp
exp
sin
1
1
1
1
(6)
to procesy Gaussa spełniające warunki:
Janusz Kolenda
70
Zeszyty
Naukowe
AMW
( )
( )
( )
( )
τ
τ
τ
τ
xy
xye
x
xe
K
K
K
K
=
=
. (7)
W zależnościach (6) i (7) oznaczono:
b
a
,
— amplitudy ekwiwalentnych naprężeń składowych (zmienne losowe);
xy
x
α
α
,
— kąty fazowe ekwiwalentnych naprężeń składowych (zmienne losowe);
xy
x
ω
ω
,
— częstości ekwiwalentnych naprężeń składowych;
( )
( )
*
1
1
1
*
1
1
1
,
exp
2
,
exp
2
b
b
j
j
b
b
a
a
j
j
a
a
xy
x
=
=
=
=
−
−
α
α
; (8)
j
—
jedność urojona;
( )
*
⋅
—
wielkość zespolona sprzężona;
( )
( )
τ
τ
xye
xe
K
K
,
— funkcje autokorelacji procesów
( )
( )
t
t
xye
xe
σ
σ
i
;
( )
( )
τ
τ
xy
x
K
K
,
— funkcje autokorelacji procesów
( )
( )
t
t
xy
x
σ
σ
i
;
τ
—
odstęp czasu,
przy czym
{ } { }
{ } { }
{ } { }
{ } { }
0
0
1
*
1
1
*
1
1
1
1
*
1
1
*
1
1
1
=
=
=
=
=
=
=
=
−
−
−
−
−
−
b
b
E
b
b
E
b
E
b
E
a
a
E
a
a
E
a
E
a
E
; (9)
{}
⋅
E
— wartość oczekiwana.
Warunki (7) prowadzą do relacji:
(
)
(
)
[
]
(
)
(
)
[
]
{
}
( ) ( )
{
}
(
)
(
)
[
]
(
)
(
)
[
]
{
}
( ) ( )
{
}
2
1
*
2
1
2
1
1
*
1
1
*
1
2
1
*
2
1
2
1
1
*
1
1
*
1
exp
exp
exp
exp
exp
exp
exp
exp
t
t
E
t
j
b
t
j
b
t
j
b
t
j
b
E
t
t
E
t
j
a
t
j
a
t
j
a
t
j
a
E
xy
xy
xy
xy
xy
xy
x
x
x
x
x
x
σ
σ
ω
ω
ω
ω
σ
σ
ω
ω
ω
ω
=
−
+
+
−
=
=
−
+
+
−
−
−
−
−
, (10)
czyli z uwzględnieniem (8) i (9):
Współczynnik bezpieczeństwa zmęczeniowego wałów przy losowym zginaniu i skręcaniu
1 (184) 2011
71
{ }
(
)
(
)
[
]
( )
{ } (
)
(
)
[
]
( )
τ
τ
ω
τ
ω
τ
τ
ω
τ
ω
xy
xy
xy
x
x
x
K
j
j
b
E
K
j
j
a
E
=
−
+
=
−
+
exp
exp
4
1
exp
exp
4
1
2
2
. (11)
Oznaczono tu:
{ } { }
2
2
,
b
E
a
E
— wartości średniokwadratowe amplitud ekwiwalentnych naprężeń
składowych;
1
2
t
t
−
=
τ
.
W wyniku transformacji Fouriera równań (11) otrzymuje się:
{ }
(
) (
)
[
]
( )
{ } (
) (
)
[
]
( )
ω
ω
ω
δ
ω
ω
δ
ω
ω
ω
δ
ω
ω
δ
xy
xy
xy
x
x
x
S
b
E
S
a
E
=
+
+
−
=
+
+
−
2
2
4
1
4
1
, (12)
gdzie:
( ) ( )
ω
ω
xy
x
S
S
,
— gęstości widmowe mocy procesów
( )
( )
t
t
xy
x
σ
σ
i
;
δ
— funkcja delta Diraca.
Na podstawie równań (12) można sformułować następujące warunki rów-
noważności naprężeń
( )
t
xe
σ
i
( )
t
x
σ
oraz
( )
t
xye
σ
i
( )
t
xy
σ
[3, 4]:
{ }
(
) (
)
[
]
( )
{ } (
) (
)
[
]
( )
∫
∫
∫
∫
∞
∞
−
∞
∞
−
∞
∞
−
∞
∞
−
=
+
+
−
=
+
+
−
ω
ω
ω
ω
ω
δ
ω
ω
δ
ω
ω
ω
ω
ω
δ
ω
ω
δ
d
S
d
b
E
d
S
d
a
E
xy
xy
xy
x
x
x
2
2
4
1
4
1
. (13)
Zatem
{ }
( )
{ }
( )
∫
∫
∞
∞
−
∞
∞
−
=
=
ω
ω
ω
ω
d
S
b
E
d
S
a
E
xy
x
2
2
2
2
. (14)
Janusz Kolenda
72
Zeszyty
Naukowe
AMW
Zważywszy, że amplitudy a i b procesów (6) jako wąskopasmowych proce-
sów Gaussa mają rozkład Rayleigha, ich momenty statystyczne wynoszą [6]:
{ }
{ }
k
xy
k
k
k
x
k
k
s
k
b
E
k
s
k
a
E
⎟
⎠
⎞
⎜
⎝
⎛ +
Γ
=
=
⎟
⎠
⎞
⎜
⎝
⎛ +
Γ
=
2
1
2
,...
2
,
1
,
2
1
2
2
/
2
/
, (15)
gdzie:
Γ
— funkcja gamma;
xy
x
s
s ,
— odchylenia standardowe amplitud a i b.
Stąd
{ } (
)
{ } (
)
xy
x
s
b
E
s
a
E
2
/
1
2
/
1
5
,
0
,
5
,
0
π
π
=
=
; (16)
{ }
{ }
2
2
2
2
2
,
2
xy
x
s
b
E
s
a
E
=
=
. (17)
Porównując prawe strony wyrażeń (14) i (17), otrzymuje się:
( )
( )
2
/
1
2
/
1
,
⎥
⎦
⎤
⎢
⎣
⎡
=
⎥
⎦
⎤
⎢
⎣
⎡
=
∫
∫
∞
∞
−
∞
∞
−
ω
ω
ω
ω
d
S
s
d
S
s
xy
xy
x
x
. (18)
WARTOŚCI
OCZEKIWANE
WSPÓŁCZYNNIKÓW
BEZPIECZEŃSTWA
Na podstawie wzorów (2) wartości oczekiwane cząstkowych współczynni-
ków bezpieczeństwa zmęczeniowego wałów poddanych działaniu ekwiwalentnych
naprężeń składowych (5) wynoszą:
{ }
{ }
{ }
{ }
{ }
{ }
xym
xy
xy
xy
so
xy
xm
x
x
x
go
x
E
b
E
Z
E
E
a
E
Z
E
σ
ψ
ε
β
δ
σ
ψ
ε
β
δ
+
=
+
=
, (19)
Współczynnik bezpieczeństwa zmęczeniowego wałów przy losowym zginaniu i skręcaniu
1 (184) 2011
73
czyli z uwzględnieniem (16) i (18):
{ }
( )
{ }
{ }
( )
{ }
xym
xy
xy
xy
xy
so
xy
xm
x
x
x
x
go
x
E
d
S
Z
E
E
d
S
Z
E
σ
ψ
ω
ω
π
ε
β
δ
σ
ψ
ω
ω
π
ε
β
δ
+
⎥
⎦
⎤
⎢
⎣
⎡
=
+
⎥
⎦
⎤
⎢
⎣
⎡
=
∫
∫
∞
∞
−
∞
∞
−
2
/
1
2
/
1
5
,
0
5
,
0
. (20)
Wyrażenia (1) i (20) umożliwiają wyznaczenie wartości oczekiwanej łącz-
nego współczynnika bezpieczeństwa zmęczeniowego wałów w przypadku równo-
czesnego działania momentów gnących i momentów skręcających o losowym
charakterze ze wzoru:
{ }
{ }
{ }
{ }
[
]
{ }
[
]
2
2
xy
x
xy
x
E
E
E
E
E
δ
δ
δ
δ
δ
+
=
. (21)
P r z y k ł a d
Wał poddany jest równoczesnemu działaniu stacjonarnych momentów gną-
cych i skręcających. W analizowanym przekroju wywołują one naprężenia
( )
( )
( )
( )
t
t
t
t
xy
mxy
xy
x
mx
x
σ
σ
σ
σ
σ
σ
+
=
+
=
~
~
,
gdzie
mxy
mx
σ
σ
i
to wartości średnie o charakterze losowym oraz
( )
(
)
( )
(
)
∑
∑
=
=
+
=
+
=
r
l
xyl
xyl
xyl
xyl
xy
p
k
xk
xk
xk
xk
x
t
B
t
A
t
t
B
t
A
t
1
1
sin
cos
sin
cos
ω
ω
σ
ω
ω
σ
. (22)
W wyrażeniach (22)
xyl
xyl
xk
xk
B
A
B
A
i
,
,
są zmiennymi losowymi o zero-
wych wartościach średnich, statystycznie niezależnymi od siebie. Wyznaczyć war-
tość oczekiwaną łącznego współczynnika bezpieczeństwa zmęczeniowego przy
założeniu, że znane są wartości oczekiwane
{ }
{ }
xym
xm
E
E
σ
σ
i
oraz wartości śred-
niokwadratowe
{ } { } { } { }
.
i
,
,
2
2
2
2
xyl
xyl
xk
xk
B
E
A
E
B
E
A
E
Janusz Kolenda
74
Zeszyty
Naukowe
AMW
R o z w i ą z a n i e
Formuły Eulera
(
)
(
)
[
]
(
)
(
)
[
]
t
j
t
j
t
t
j
t
j
t
ω
ω
ω
ω
ω
ω
−
−
=
−
+
=
exp
exp
2
1
sin
exp
exp
2
1
cos
pozwalają zapisać wyrażenia (22) w postaci:
( )
(
)
(
)
[
]
( )
(
)
(
)
[
]
∑
∑
=
=
−
+
=
−
+
=
r
l
xyl
xyl
xyl
xyl
xy
p
k
xk
xk
xk
xk
x
t
j
D
t
j
C
t
t
j
D
t
j
C
t
1
1
exp
exp
exp
exp
ω
ω
σ
ω
ω
σ
, (23)
gdzie:
*
*
,
2
1
2
1
,
2
1
2
1
xyl
xyl
xyl
xyl
xyl
xk
xk
xk
xk
xk
C
D
B
j
A
C
C
D
B
j
A
C
=
+
=
=
+
=
. (24)
Oznaczając
xyl
xyl
xk
xk
−
−
=
−
=
−
ω
ω
ω
ω
,
,
otrzymuje się z (23)
( )
(
)
( )
(
)
∑
∑
−
=
−
=
=
=
r
r
l
xyl
xyl
xy
p
p
k
xk
xk
x
t
j
G
t
t
j
G
t
ω
σ
ω
σ
exp
exp
, (25)
gdzie:
r
l
D
G
r
l
C
G
p
k
D
G
p
k
C
G
xyl
xyl
xyl
xyl
xk
xk
xk
xk
−
−
−
=
=
=
=
−
−
−
=
=
=
=
,...,
2
,
1
dla
,...,
2
,
1
dla
,...,
2
,
1
dla
,...,
2
,
1
dla
Współczynnik bezpieczeństwa zmęczeniowego wałów przy losowym zginaniu i skręcaniu
1 (184) 2011
75
Funkcje autokorelacji naprężeń (25) wyrażają się następująco:
(
)
(
)
(
)
{
}
(
)
[
]
(
)
(
)
(
)
{
}
(
)
[
]
∑ ∑
∑
∑
∑ ∑
∑
∑
−
=
−
=
−
=
−
=
−
=
−
=
−
=
−
=
−
=
=
⎭
⎬
⎫
⎩
⎨
⎧
−
=
−
=
=
⎭
⎬
⎫
⎩
⎨
⎧
−
=
r
r
l
r
r
n
xyl
xyn
xyn
xyl
r
r
l
r
r
n
xyn
xyn
xyl
xyl
xy
p
p
k
p
p
m
xk
xm
xm
xk
p
p
k
p
p
m
xm
xm
xk
xk
x
t
t
j
G
G
E
t
j
G
t
j
G
E
t
t
K
t
t
j
G
G
E
t
j
G
t
j
G
E
t
t
K
1
2
*
2
1
*
2
1
1
2
*
2
1
*
2
1
exp
exp
exp
,
exp
exp
exp
,
ω
ω
ω
ω
ω
ω
ω
ω
. (26)
Na podstawie założeń i relacji (24) zachodzą związki:
{
}
{ } { }
(
)
{
}
{ } { }
(
)
⎪⎩
⎪
⎨
⎧
≠
+
=
=
=
⎪⎩
⎪
⎨
⎧
≠
+
=
=
=
n
l
B
E
A
E
H
n
l
H
G
G
E
m
k
B
E
A
E
H
m
k
H
G
G
E
xyl
xyl
xyl
xyl
xyn
xyl
xk
xk
xk
xk
xm
xk
dla
0
4
1
,
dla
dla
0
4
1
,
dla
2
2
*
2
2
*
. (27)
Stąd
( )
(
)
( )
(
)
∑
∑
−
=
−
=
=
=
r
r
l
xyl
xyl
xy
p
p
k
xk
xk
x
j
H
K
j
H
K
τ
ω
τ
τ
ω
τ
exp
exp
. (28)
Poddając funkcje (28) transformacji Fouriera, otrzymuje się gęstości wid-
mowe mocy naprężeń składowych:
( )
(
)
( )
(
)
∑
∑
−
=
−
=
−
=
−
=
r
r
l
xyl
xyl
xy
p
p
k
xk
xk
x
H
S
H
S
ω
ω
δ
ω
ω
ω
δ
ω
. (29)
Janusz Kolenda
76
Zeszyty
Naukowe
AMW
Zatem
( )
( )
∫
∑
∑
∫
∑
∑
∞
∞
−
−
=
=
∞
∞
−
−
=
=
=
=
=
=
r
r
l
r
l
xyl
xyl
xy
p
p
k
p
k
xk
xk
x
H
H
d
S
H
H
d
S
1
1
4
2
4
2
ω
ω
ω
ω
, (30)
czyli z uwzględnieniem oznaczeń
xyl
xk
H
H
i
w (27)
( )
{ } { }
(
)
( )
{ } { }
(
)
∫
∑
∫
∑
∞
∞
−
=
∞
∞
−
=
+
=
+
=
r
l
xyl
xyl
xy
p
k
xk
xk
x
B
E
A
E
d
S
B
E
A
E
d
S
1
2
2
1
2
2
ω
ω
ω
ω
. (31)
Oznacza to, że rozwiązanie postawionego zadania sprowadza się do pod-
stawienia do wzoru (21) następujących wartości oczekiwanych cząstkowych współ-
czynników bezpieczeństwa zmęczeniowego wału:
{ }
{ } { }
(
)
{ }
{ }
{ } { }
(
)
{ }
xym
xy
r
l
xyl
xyl
xy
xy
so
xy
xm
x
p
k
xk
xk
x
x
go
x
E
B
E
A
E
B
Z
E
E
B
E
A
E
B
Z
E
σ
ψ
π
ε
δ
σ
ψ
π
ε
δ
+
⎥
⎦
⎤
⎢
⎣
⎡
+
=
+
⎥
⎦
⎤
⎢
⎣
⎡
+
=
∑
∑
=
=
2
/
1
1
2
2
2
/
1
1
2
2
5
,
0
5
,
0
. (32)
WNIOSKI
Projektowanie wałów napędowych i pośrednich w układach maszynowych
jest zadaniem odpowiedzialnym, mającym istotny wpływ na trwałość i niezawod-
ność układu. Stąd wynika duże znaczenie obliczeń mających na celu ocenę wartości
współczynnika bezpieczeństwa zmęczeniowego wałów. Podobnie jak ocena współ-
czynnika bezpieczeństwa zmęczeniowego w najbardziej obciążonych elementach
czy węzłach układu powinna ona wchodzić w zakres obliczeń sprawdzających
układ. W odniesieniu do elementów pracujących w złożonym stanie naprężenia
Współczynnik bezpieczeństwa zmęczeniowego wałów przy losowym zginaniu i skręcaniu
1 (184) 2011
77
o zdeterminowanych składowych normalnych i tnących służy temu wzór (1). Niniej-
szy artykuł jest próbą rozszerzenia zakresu zastosowań tego wzoru na stacjonarne
obciążenia losowe. Jak ukazano w przykładzie, może on w szczególności służyć do
oceny bezpieczeństwa zmęczeniowego wałów w stosunkowo obszernej klasie ukła-
dów maszynowych, gdzie obciążenia wykazują losowe fluktuacje i naprężenia są
okresowe w sensie średniokwadratowym.
BIBLIOGRAFIA
[1]
Dąbrowski Z., Maksymiuk M., Wały i osie, PWN, Warszawa 1984.
[2]
Kocańda S., Szala J., Podstawy obliczeń zmęczeniowych, PWN, Warszawa
1997.
[3]
Kolenda J., On fatigue safety of metallic elements under static and dynamic
loads, Politechnika Gdańska, Gdańsk 2004.
[4]
Kolenda J., O wyznaczaniu warstwic bezpieczeństwa zmęczeniowego elementów
konstrukcyjnych przy jednoosiowych obciążeniach stochastycznych, „Zeszyty
Naukowe” AMW, 2010, nr 1.
[5]
Kyzioł L., Podstawy konstrukcji maszyn, cz. II, AMW, Gdynia 2008.
[6]
Pacut A., Prawdopodobieństwo. Teoria. Probabilistyczne modelowanie w tech-
nice, PWN, Warszawa 1985.
C O E F F I C I E N T O F F A T I G U E S A F E T Y
O F S H A F T S U N D E R R A N D O M B E N D I N G
A N D T O R S I O N
ABSTRACT
The paper deals with fatigue safety of shafts subjected to simultaneous bending and tor-
sional loads of random character, stationary in the wide sense. It is assumed that the resulting
normal and shear stresses are not correlated with each other, and that their mean values and power
spectral densities are known. Consequently, both these stresses can be considered separately
and the known formula for the coefficient of fatigue safety of shafts based on the calculations
Janusz Kolenda
78
Zeszyty
Naukowe
AMW
of partial coefficients of fatigue safety under bending and torsion can be applied. For this purpose
equivalent normal and shear stresses as Gaussian processes and expected values of the partial
coefficients of fatigue safety are determined. Exemplary calculations are carried out.
Keywords:
shafts, random loads, fatigue strength.
Recenzent dr hab. inż. Janusz Kozak