DSP-MATLAB,

Ć

wiczenie 4,









P.Korohoda, KE AGH

1

Próbkowanie i transformacje Fouriera

Zawartość instrukcji:

1 Materiał z zakresu DSP

1.1 Próbkowanie sygnału

e

j

v t

⋅ ⋅ ⋅ ⋅

2

π

1.1.2 Częstotliwość cyfrowa i pulsacja cyfrowa

1.2 Odpowiedź częstotliwościowa systemu

1.2.1 Odpowiedź częstotliwościowa jako fragment transformaty “Z” odpowiedzi

impulsowej

1.3 Transformacja Fouriera z “czasem” dyskretnym

1.3.1 Porównanie Transformacji Fouriera z czasem dyskretnym z Transformacją Fouriera

dla sygnałów z czasem ciągłym

1.4 Dyskretna Transformacja Fouriera
1.5 Transformata DFT jako próbkowanie transformaty D-TFT

2 Korzystanie z pakietu MATLAB

2.1 Opis wybranych funkcji
2.2 Przykłady realizacji wybranych zadań

2.2.1 Demonstracja okresowości sygnału kosinusoidalnego względem “czasu” i

częstotliwości

2.2.2 Wyznaczanie odpowiedzi częstotliwościowej filtru FIR rzędu N-1 dla pojedynczej

wartości częstotliwości cyfrowej

2.2.3 Wyznaczanie transmitancji “Z” filtru typu FIR o zadanej odpowiedzi impulsowej dla

pojedynczej wartości z

2.2.4 Wyznaczanie przybliżenia transformaty D-TFT ze wzoru definicyjnego (27):
2.2.5 Wyznaczanie transformaty DFT ze wzoru definicyjnego (33):
2.2.6 Wyznaczanie przybliżenia transformaty D-TFT za pomocą funkcji fft:
2.2.7 Wykres fazy - efekt ograniczania do zakresu od minus pi do pi

3 Dodatek teoretyczny nr 2 - Relacja pomiędzy Transformacją Fouriera z Czasem

Dyskretnym (ang. D-TFT) i Transformacją Fouriera z Czasem Ciągłym (ang.
C-TFT)

4 Dodatek teoretyczny nr 3 - Relacja pomiędzy Transformacją Fouriera z Czasem

Dyskretnym (ang. D-TFT) i Dyskretną Transformacją Fouriera (ang. DFT);
Relacja pomiędzy DFT i C-TFT

1 Materiał z zakresu DSP

1.1 Próbkowanie sygnału

e

j

v t

⋅ ⋅ ⋅ ⋅

2

π

DSP-MATLAB,

Ć

wiczenie 4,









P.Korohoda, KE AGH

2

W podrozdziale tym będzie mowa o próbkowaniu rozumianym jako tworzenie ciągu wartości
chwilowych funkcji pobranych w równych odstępach “czasu”:

s n

s n

t

[ ]

(

)

=

⋅ ∆

, gdzie przez

n

oznaczono dowolną liczbę całkowitą. Odstęp ten będzie dalej oznaczany jako

∆

t

T

=

.

Sygnał

e

j

v t

⋅ ⋅ ⋅ ⋅

2

π

jest zespoloną funkcją określoną na ciągłej zmiennej

t

. Zmienną

v

można

traktować jako parametr, określający częstotliwość sygnału, analogicznie jak w przypadku funkcji
trygonometrycznych, ponieważ:

(

)

(

)

s t

e

v t

j

v t

C

j

v t

( )

cos

sin

=

=

⋅ ⋅ ⋅ + ⋅

⋅ ⋅ ⋅

⋅ ⋅ ⋅ ⋅

2

2

2

π

π

π

(1)

Sygnał cyfrowy pochodzący z próbkowania powyższego sygnału można zapisać w następujący sposób:

s n

e

j

v n T

[ ]

=

⋅ ⋅ ⋅ ⋅ ⋅

2

π

(2)

Interpretując (1) można odwrócić role i zmienną

t

przyjąć jako parametr, natomiast (1) określić jako

funkcję zmiennej

v

. Łatwo zauważyć, że właściwości funkcji będą identyczne, gdyż od

t

zależy ona

w identyczny sposób jak od

v

. Można zatem stwierdzić, że jest to funkcja dwóch zmiennych (

t

oraz

v

) i jest to funkcja symetryczna względem tych zmiennych. Zatem, jeżeli założy się ustaloną wartość

t

, co z kolei daje

n T

const

⋅ =

, to widać natychmiast, że funkcja (1) jest okresowa względem

zmiennej

v

.

Funkcja

( )

( )

e

j

j

⋅

=

+ ⋅

ϕ

ϕ

ϕ

cos

sin

(3)

jest okresowa, przy czym okres podstawowy wynosi

∆

ϕ

π

0

2

= ⋅

, z czego wynika, że każda wartość

∆

ϕ

π

= ⋅ ⋅

n 2

jest także okresem funkcji (3). Z porównania (3) oraz (1) wynika, że dla każdej

ustalonej wartości

t

n T

n

= ⋅

wyrażenie okresu sygnału (1) w odniesieniu do zmiennej

v

daje:

∆

v

T

=

1

(4)

W analogiczny sposób można wyobrazić sobie, iż ciąg próbek (2) jest funkcją zmiennej całkowitej

n

oraz częstotliwości

v

. Ustalając

n

n

ust

=

otrzymuje się wartość próbki

s n

s v

ust

[

]

( )

=

jako funkcję

ciągłej zmiennej

v

.

Ponieważ ciąg

s n

[ ]

powstaje z wartości (1) pobranych właśnie w chwilach

t

n

, więc ciąg ten

wykazuje okresowość względem zmiennej

v

, z okresem (4).

Oznacza to, że przy ustalonym

T

dla każdej wartości

n

wartość odpowiedniej próbki sygnału

rozpatrywana w funkcji

v

jest okresowa. Okres (4) jest taki sam dla wszystkich wartości

n

. Zatem po

spróbkowaniu (1) i otrzymaniu ciągu w postaci (2) nie da się już w oparciu o ten ciąg rozróżnić, czy

sygnał sprzed próbkowania (czyli (1)) miał częstotliwość

v

, czy też

v

T

k

+ ⋅

1

(dla dowolnej liczby

całkowitej

k

). Efekt ten jest nazywany

aliasingiem. Jak łatwo zauważyć, identyczny efekt powstaje

także w przypadku próbkowania funkcji sinus lub też kosinus (dla każdej z osobna).
Ponieważ każdy sygnał z czasem ciągłym posiadający transformatę Fouriera można zinterpretować jako
kombinację liniową nieskończonej ilości sygnałów typu (1), więc efekt aliasingu dotyczy w taki sam
sposób każdego takiego sygnału. Rozważanie efektu aliasingu powstającego w wyniku próbkowania
prowadzi do opisanego w dodatku teoretycznym nr 1 (patrz instrukcja do ćwiczenia 1) twierdzenia o
próbkowaniu.

DSP-MATLAB,

Ć

wiczenie 4,









P.Korohoda, KE AGH

3

1.1.2 Częstotliwość cyfrowa i pulsacja cyfrowa

W dalszych rozważaniach przydatne będzie pojęcie częstotliwości dla sygnałów cyfrowych. Ponieważ
okres próbkowania

T

jest wartością stałą, więc opis sygnału w postaci (2) można nieco uprościć

podstawiając:

f

v T

= ⋅

(5)

Pozwala to na przepisanie (2) do postaci:

s n

e

e

j

v n T

j

f n

[ ]

=

=

⋅ ⋅ ⋅ ⋅ ⋅

⋅ ⋅ ⋅ ⋅

2

2

π

π

(6)

Bezwymiarowa wielkość

f

jest w tym przypadku wielkością ciągłą, jednak ze względu na powiązanie

z sygnałami cyfrowymi będzie dla uproszczenia nazywana skrótowo częstotliwością cyfrową.
Zależność (5) jest dość istotna, ponieważ przedstawia, jaka jest zależność pomiędzy częstotliwością dla
sygnałów z czasem ciągłym

v

, wyrażoną w Hz, oraz bezwymiarową częstotliwością cyfrową.

Niekiedy spotyka się opis sygnału ciągłego (1) zawierający zamiast częstotliwości

v

wyrażanej w Hz

pulsację

Ω

w radianach na sekundę:

s

t

e

C

j

t

( )

=

⋅Ω⋅

(7)

Postępując podobnie jak w przypadku częstotliwości, można zatem wprowadzić pojęcie pulsacji
cyfrowej, wyrażanej w radianach:

ω

π

=

⋅

=

⋅ ⋅

Ω

T

f

2

(8)

Sygnał cyfrowy (2) można zatem zapisać również tak:

s n

e

j

n

[ ]

=

⋅ ⋅

ω

(9)

Warto zauważyć, że w literaturze anglo-języcznej spotyka się słowo frequency w odniesieniu do:
a) częstotliwości w Hz, b) pulsacji w radianach na sekundę, c) bezwymiarowej częstotliwości cyfrowej
oraz d) pulsacji cyfrowej w radianach. Należy pamiętać, że wielkości te są wprawdzie powiązane
wzajemnie (zależności (5) i (8)), jednak mimo wszystko są to cztery różne wielkości, wyrażane za
pomocą różnych jednostek. Dlatego warto się upewnić jakiego znaczenia słowa frequency używa w
danym przypadku autor.

Efekt aliasingu powoduje, że sygnał cyfrowy (2) jest okresowy z punktu widzenia parametru

v

i okres

podstawowy wynosi

1

T

. Z zależności (5) oraz (8) wynika, że sygnał cyfrowy jest okresowy również ze

względu na

f

oraz

ω

, przy czym w każdym przypadku okres podstawowy jest równy odpowiednio

1

oraz

2

⋅

π

. Okresowość ciągu

s n

[ ]

wyrażoną względem

f

lub

ω

można zapisać następująco (

k

to dowolna liczba całkowita):

(

)

s n

e

e

f

j

f n

j

f

k n

[ ]

=

=

⋅ ⋅ ⋅ ⋅

⋅ ⋅ ⋅ + ⋅

2

2

π

π

(10)

lub też

(

)

s n

e

e

j

n

j

k

n

ω

ω

ω

π

[ ]

=

=

⋅ ⋅

⋅ + ⋅ ⋅ ⋅

2

(11)

DSP-MATLAB,

Ć

wiczenie 4,









P.Korohoda, KE AGH

4

We wzorach (10) i (11) zaznaczono dodatkowo, że sygnały są uzależnione od wartości parametru, który
może przyjmować dowolne wartości rzeczywiste - odpowiednio:

f

dla (10) oraz

ω

dla (11).

Warto tu wspomnieć o pewnej ciekawostce, iż nie zawsze ciąg pochodzący z próbkowania sygnału
okresowego musi być też okresowy. W celu wykazania, że jest to możliwe sformułujemy warunek, jaki
musi być spełniony, by w takim przypadku ciąg próbek był okresowy. Jeżeli warunek ten nie będzie
spełniony, to ciąg próbek nie będzie okresowy.
Rozpatrujemy sygnał jako funkcję czasu ciągłego. W konsekwencji ciąg próbek jest funkcją zmiennej

n

. Niech sygnał z czasem ciągłym

x t

( )

będzie okresowy z okresem

P

:

x t

x t

P

( )

(

)

=

+

(12)

Przyjmując, że ciąg próbek tego sygnału

x n

x n T

[ ]

(

)

=

⋅

jest także okresowy, otrzymujemy:

x n

x n

N

[ ]

[

]

=

+

(13)

przy czym oczywiście wartość okresu

N

musi być liczbą naturalną. Z porównania (12) i (13) oraz

zależności

t

n T

n

= ⋅

wynika, że aby zachodziły obie równości ((12) i (13)) muszą istnieć dwie liczby

naturalne

k

oraz

m

, takie że:

k P

m N T

⋅ = ⋅ ⋅

(14)

Równość (14) można opisać tak, że musi istnieć taka całkowita wielokrotność okresu

P

, by takiemu

odcinkowi czasu odpowiadała całkowita ilość okresów ciągu (czyli

N T

⋅

).

Z (14) wynika wprost poszukiwany warunek:

P

T

m N

k

=

⋅

(15)

Prawa strona warunku (15) oznacza liczbę wymierną, ponieważ wszystkie występujące w niej liczby są
naturalne. Zatem, aby w wyniku próbkowania sygnału okresowego powstał ciąg nieokresowy,
wystarczy by iloraz okresu

P

sygnału do okresu próbkowania

T

był liczbą niewymierną. Nie jest to

takie trudne do spełnienia, przykładowo: dla sygnału sinusoidalnego o częstotliwości

v

=

100

π

Hz

próbkowanego z okresem

T

=

0 01

.

s otrzymuje się, że:

P

T

T v

=

⋅

=

1

π

(16)

1.2 Odpowiedź częstotliwościowa systemu

Sygnał cyfrowy (2) nie może być naturalnie rezultatem próbkowania sygnału pochodzącego ze świata
rzeczywistego. Jest to sygnał o charakterze teoretycznym, jednak jest on dość ważny, ponieważ
umożliwia wygodną interpretację pewnych powszechnie stosowanych pojęć. Przyjmijmy, że na wejście
systemu cyfrowego, liniowego i stacjonarnego, czyli opisanego przez odpowiedź impulsową

h n

[ ]

(odpowiedź ta może być skończona lub nieskończona), zostanie podany sygnał w postaci ciągu (2).
Okazuje się, że odpowiedź systemu na ten sygnał będzie takim samym sygnałem, jedynie pomnożonym
przez pewną stałą liczbę zespoloną, zależną jedynie od wartości

f

, a niezależnej od indeksu

n

. Jeżeli

odpowiedź systemu

swy

n

f

[ ]

na sygnał typu (10) zapiszemy w postaci splotu tego sygnału

wejściowego i odpowiedzi impulsowej systemu

h n

[ ]

, to:

DSP-MATLAB,

Ć

wiczenie 4,









P.Korohoda, KE AGH

5

swy n

e

H f

h n

e

H f

swy n

s n

f

j

f n

j

f n

f

f

[ ]

( )

[ ]

( )

[ ]

[ ]

=

⋅

=

∗

⇓

=

⋅ ⋅ ⋅ ⋅

⋅ ⋅ ⋅ ⋅

2

2

π

π

(17)

gdzie

H f

( )

jest dla ustalonej wartości

f

wielkością stałą, niezależną od

n

, natomiast ogólnie jest

to zespolona funkcja zmiennej

f

.

Słuszność (17) można wykazać podstawiając do tej zależności pełny wzór na splot:

(

)

h n

e

h k e

e

h k e

j

f n

j

f n k

k

j

f n

j

f k

k

[ ]

[ ]

[ ]

∗

=

⋅

=

⋅

⋅

⋅ ⋅ ⋅ ⋅

⋅ ⋅ ⋅ ⋅ −

=−∞

∞

⋅ ⋅ ⋅ ⋅

− ⋅ ⋅ ⋅ ⋅

=−∞

∞

∑

∑

2

2

2

2

π

π

π

π

(18)

Z porównania (17) i (18) wynika, że:

H f

h k

e

j

f k

k

( )

[ ]

=

⋅

− ⋅ ⋅ ⋅ ⋅

=−∞

∞

∑

2

π

(19)

Określona przez (19) funkcja zmiennej

f

jest nazywana odpowiedzią częstotliwościową systemu. Jak

wynika z przeprowadzonych rozważań,

H f

( )

jest zespoloną funkcją częstotliwości cyfrowej

i przedstawia zależność pomiędzy sygnałem wyjściowym i wejściowym systemu liniowego
stacjonarnego, gdy sygnał wejściowy jest w postaci (2) (lub też (6)). Odpowiedź częstotliwościowa
może być wyrażona także jako funkcja pulsacji cyfrowej:

H

h k

e

j

k

k

( )

[ ]

ω

ω

=

⋅

− ⋅ ⋅

=−∞

∞

∑

(20)

Ze wzorów (19) oraz (20) widać, iż wszystkie składniki odpowiednich sum posiadają pewien wspólny
okres. Dla (19) jest to

∆

f

=

1

, dla (20)

∆

ω

π

= ⋅

2

. Zatem odpowiedź częstotliwościowa jako

kombinacja liniowa takich składników posiada taki sam okres. Można to wyjaśnić również w oparciu
o zależność (17) - ponieważ sygnał wejściowy jest okresowy ze względu na częstotliwość

f

, zatem

odpowiedź częstotliwościowa jest także okresowa.
Ponieważ okresowość odpowiedzi częstotliwościowej wynika z okresowości (względem parametru

f

lub

ω

) sygnału wejściowego, więc dla zaznaczenia tego faktu stosuje się często także następujące

oznaczenie:

H e

h k

e

j

f

j

f k

k

(

)

[ ]

⋅ ⋅ ⋅

− ⋅ ⋅ ⋅ ⋅

=−∞

∞

=

⋅

∑

2

2

π

π

(21)

lub

H e

h k

e

j

j

k

k

(

)

[ ]

⋅

− ⋅ ⋅

=−∞

∞

=

⋅

∑

ω

ω

(22)

1.2.1 Odpowiedź częstotliwościowa jako fragment transformaty “Z” odpowiedzi impulsowej

Jeżeli podstawimy:

e

z

j

f

⋅ ⋅ ⋅

=

2

π

(23)

to wzór (21) przyjmie postać transformaty “Z” odpowiedzi impulsowej

h n

[ ]

:

DSP-MATLAB,

Ć

wiczenie 4,









P.Korohoda, KE AGH

6

H z

h n z

n

n

( )

[ ]

=

⋅

−

=−∞

∞

∑

(24)

Oznacza to, że odpowiedź częstotliwościowa to fragment transformaty “Z” odpowiedzi impulsowej,
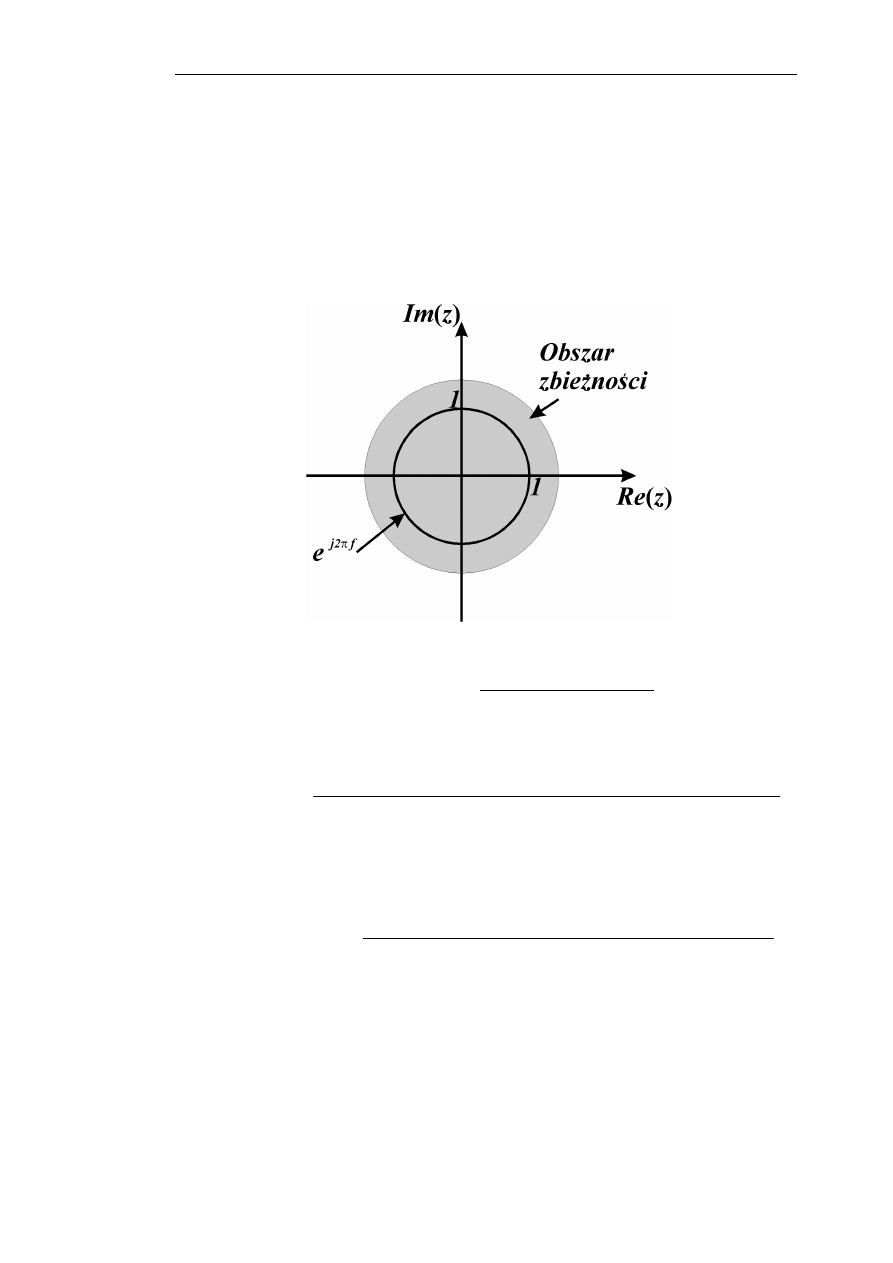
określony dla wartości “z” spełniających zależność (23). Zależność ta wyznacza na płaszczyźnie
zespolonej “z” okrąg jednostkowy o środku w punkcie (0,0). Warto pamiętać, że gdyby okrąg ten nie
zawierał się w obszarze zbieżności transformaty “Z”, to dla takiego systemu nie dałoby się wyznaczyć
odpowiedzi częstotliwościowej.

Rys.1. Płaszczyzna zespolona zmiennej “z” z zaznaczonym przykładowym obszarem zbieżności

transformaty oraz okręgiem określającym fragment, którego dotyczy odpowiedź częstotliwościowa

Ponieważ odpowiedź częstotliwościowa jest dla okręgu jednostkowego na płaszczyźnie “z”
równoznaczna z transformatą “Z” odpowiedzi impulsowej, więc dla tego samego okręgu jest ona także
równoznaczna z transmitancją danego systemu. Można zatem, dla tak ograniczonego zbioru wartości
“z”, odpowiedni wzór wielomianowy na transmitancję przepisać do następującej postaci:

H e

b

b

e

b

e

b

e

a

e

a

e

a

e

j

f

j

f

j

f

M

j

f

M

j

f

j

f

K

j

f

K

(

)

(

)

(

)

⋅ ⋅ ⋅

− ⋅ ⋅ ⋅

− ⋅ ⋅ ⋅

− ⋅ ⋅ ⋅ ⋅

−

− ⋅ ⋅ ⋅

− ⋅ ⋅ ⋅

− ⋅ ⋅ ⋅ ⋅ −

=

+ ⋅

+ ⋅

+

+

⋅

+

⋅

+

⋅

+

+

⋅

2

1

2

2

3

4

2

1

2

2

3

4

2

1

1

π

π

π

π

π

π

π

⋯

⋯

(25)

lub też do postaci iloczynowej z zapisanymi wprost zerami i biegunami:

(

) (

) (

)

(

) (

) (

)

H e

K

e

z

e

z

e

z

e

p

e

p

e

p

j

f

m

j

f

j

f

j

f

M

j

f

j

f

j

f

K

(

)

⋅ ⋅ ⋅

⋅ ⋅ ⋅

⋅ ⋅ ⋅

⋅ ⋅ ⋅

−

⋅ ⋅ ⋅

⋅ ⋅ ⋅

⋅ ⋅ ⋅

−

=

⋅

−

⋅

−

⋅ ⋅

−

−

⋅

−

⋅ ⋅

−

2

2

1

2

2

2

1

2

1

2

2

2

1

π

π

π

π

π

π

π

⋯

⋯

(26)

DSP-MATLAB,

Ć

wiczenie 4,









P.Korohoda, KE AGH

7

1.3 Transformacja Fouriera z “czasem” dyskretnym

Odpowiedź impulsowa jest sygnałem cyfrowym opisującym system liniowy i stacjonarny. Każdy sygnał
cyfrowy można więc zinterpretować jako odpowiedź impulsową odpowiedniego systemu. Dla takiego
systemu możliwe jest wyznaczenie - o ile odpowiedni tylko zachodzi zbieżność transformaty “Z” dla
odpowiedzi impulsowej na okręgu jednostkowym - odpowiedzi częstotliwościowej. Można więc
przyjąć, że dla niemal dowolnego sygnału cyfrowego

x n

[ ]

- sygnał ten ma umożliwiać zbieżność

transformaty “Z” dla okręgu jednostkowego (23) - określa się funkcję

X e

j

f

(

)

⋅ ⋅ ⋅

2

π

w analogiczny

sposób, jak w poprzednich podrozdziałach wyznaczano odpowiedź częstotliwościową. Zależność

określająca związek pomiędzy

x n

[ ]

oraz

X e

j

f

(

)

⋅ ⋅ ⋅

2

π

nosi nazwę Transformacji Fouriera z Czasem

Dyskretnym i jest często oznaczana skrótowo jako D-TFT (ang. Discrete-Time Fourier Transform).
Nazwa ta bierze się stąd, że transformacja wykazuje istotne podobieństwo do Transformacji Fouriera
znanej z teorii sygnałów, jednak w tym przypadku czas (umowny) jest reprezentowany w postaci
indeksów

n

, a tylko częstotliwość jest wielkością ciągłą. Wzór definiujący D-TFT jest następujący:

(

)

X f

x n

j

f n

n

( )

[ ] exp

=

⋅

− ⋅ ⋅ ⋅ ⋅

=−∞

∞

∑

2

π

(27)

lub w zapisie bazującym na pulsacji cyfrowej:

(

)

X

x n

j

n

n

( )

[ ] exp

ω

ω

=

⋅

− ⋅ ⋅

=−∞

∞

∑

(28)

W zależnościach (27) i (28) powrócono do zapisu wskazującego na

f

lub

ω

jako na zmienną

niezależną, ponieważ transformatę

X f

( )

(lub

X ( )

ω

) przedstawia się zazwyczaj w postaci pary

wykresów amplitudy i fazy lub też części rzeczywistej i urojonej, gdy oś pozioma opisana jest za
pomocą zmiennej

f

(lub odpowiednio

ω

).

Transformacja odwrotna do (27) określona jest wzorem:

(

)

x n

X f

j

f n df

[ ]

( ) exp

=

⋅

⋅ ⋅ ⋅ ⋅ ⋅

−

∫

2

1

2

1

2

π

(29)

natomiast transformacja odwrotna do (28), to:

(

)

x n

X

j

n d

[ ]

( ) exp

=

⋅

⋅

⋅ ⋅ ⋅

−

∫

1

2

π

ω

ω

ω

π

π

(30)

Transformacja odwrotna polega na wyznaczaniu całki w ramach jednego okresu transformaty, który - ze
względu na jej okresowość - zawiera kompletną informację o ciągu pierwotnym

x n

[ ]

. Wyprowadzenie

wzoru (29) można znaleźć w dodatku teoretycznym nr 2.

DSP-MATLAB,

Ć

wiczenie 4,









P.Korohoda, KE AGH

8

1.3.1 Porównanie Transformacji Fouriera z czasem dyskretnym z Transformacją Fouriera dla
sygnałów z czasem ciągłym

W dodatku teoretycznym można również znaleźć obszerną dyskusję na temat związków D-TFT z
Transformacją Fouriera dla sygnałów z czasem ciągłym, czyli C-TFT (ang. Continuous-Time Fourier
Transform). W skrócie związki te można opisać następująco.
Rozważając dany ciąg

x n

[ ]

zawsze można założyć, że jest to sygnał cyfrowy pochodzący

z próbkowania z okresem

T

odpowiedniego sygnału ciągłego

x t

( )

. Próbkowaniem nazywa się tutaj

pobieranie wartości chwilowych

x t

( )

w odstępach

∆

t

T

=

. Określa się w ten sposób parę - sygnał

x t

( )

oraz ciąg

x n

[ ]

. Można również założyć, że sygnał

x t

( )

został spróbkowany funkcją

grzebieniową o takim samym okresie

T

i w wyniku tego powstał sygnał

x t

T

( )

, będący funkcją

grzebieniową zmodulowaną sygnałem

x t

( )

. Zagadnienie takiego próbkowania było obszernie opisane

w dodatku teoretycznym nr 1. Po sporządzeniu wykresów transformat można stwierdzić, że
Transformata Fouriera typu C-TFT dla sygnału

x

t

T

( )

oraz Transformata Furiera typu D-TFT dla ciągu

x n

[ ]

mają identyczny kształt, pod warunkiem, że dopasuje się odpowiednio skale częstotliwości:

v

(wyrażanej w Hz) dla C-TFT i częstotliwości

f

(bezwymiarowej) dla D-TFT. Dopasowanie polega na

tym, że odcinkowi

v

o długości

v

T

T

=

1

odpowiada odcinek

f

o długości 1. Przez

v

T

oznaczono

częstotliwość próbkowania. Rys. 2 stanowi ilustrację opisanej zależności dla wykresów amplitud
odpowiednich transformat. Warto pamiętać, że delta Diraca jest pseudo-funkcją określoną dla czasu
ciągłego, zatem i funkcja grzebieniowa, a także sygnał spróbkowany taką funkcją - czyli

x

t

T

( )

- też

są określone dla czasu ciągłego. Ciąg

x n

[ ]

natomiast jest określony wyłącznie dla całkowitych

wartości

n

.

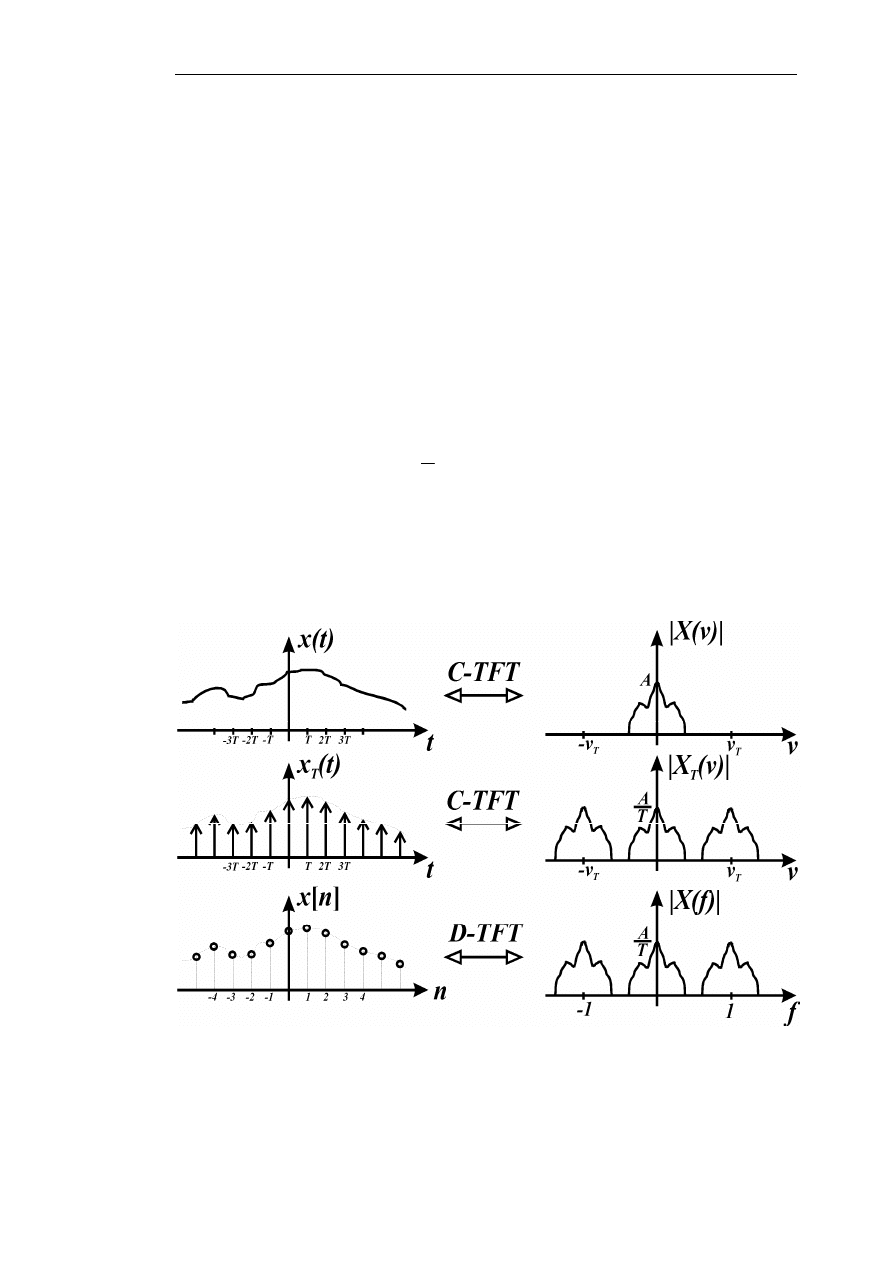
Rys.2. Ilustracja zależności pomiędzy odpowiednimi transformatami - wykresy przedstawiają tylko

amplitudę - dla (kolejno od góry):

a)

x t

( )

- czyli sygnału z czasem ciągłym,

b)

x

t

T

( )

- tego samego sygnału, ale po spróbkowaniu funkcją grzebieniową,

c)

x n

[ ]

- sygnału cyfrowego pochodzącego z pobrania wartości chwilowych sygnału

x t

( )

DSP-MATLAB,

Ć

wiczenie 4,









P.Korohoda, KE AGH

9

Przykładowo, jeżeli częstotliwość próbkowania wynosi

v

T

=

44

kHz, to wartość transformaty D-TFT

dla częstotliwości cyfrowej

f

=

0 25

,

jest taka sama, jak wartość transformaty C-TFT sygnału

x

t

T

( )

wyznaczona dla częstotliwości

v

=

11

kHz wyznaczona. Z kolei, jeżeli zostały spełnione

warunki twierdzenia o próbkowaniu, to wartość transfomaty C-TFT od

x

t

T

( )

dla tej częstotliwości jest

T

kHz

=

1

44

mniejsza niż wartość transformaty C-TFT od

x t

( )

. Zgodność ta wynika to z faktu, że

wartość

v

=

11

kHz mieści się w odcinku od

− ⋅

1

2

v

T

do

+ ⋅

1

2

v

T

.

1.4 Dyskretna Transformacja Fouriera

W przypadku D-TFT czas jest reprezentowany przez indeksy przebiegające wartości od minus do plus
nieskończoności. Jednak w zagadnieniach praktycznych zakres indeksów czasowych jest ograniczony
do pewnego skończonego przedziału wartości. W takiej sytuacji możliwe jest stosowanie Dyskretnej
Transformacji Fouriera, wskrócie DFT (ang. Discrete Fourier Transform). Wprowadza się w tym celu
nowe indeksy, tak by pierwszy z nich posiadał wartość zero. Nie ogranicza to w żadnej mierze
interpretacji otrzymanych wyników w odniesieniu do oryginalnego zakresu indeksów. Jeżeli,
przykładowo, rozważany jest ciąg

x n

0

[ ]

dla

n

=< −

>

10

100

,

, to dla potrzeb DFT można

wprowadzić przesunięcie indeksów o 10 i otrzymać ciąg

x n

[ ]

dla

n

=<

>

0

110

,

. Związek

pomiędzy

x n

0

[ ]

oraz

x n

[ ]

jest oczywisty, bowiem:

x n

x n

0

10

[

]

[ ]

−

=

dla

n

=<

>

0

110

,

.

DFT wykazuje szereg podobieństw do D-TFT. Jeżeli założymy, że w ciągu nieskończonym z wyjątkiem

N

kolejnych elementów wszystkie pozostałe mają wartość zero, to po wprowadzeniu nowych

indeksów zakres sumowania we wzorze na D-TFT (22) można następująco ograniczyć:

(

)

X f

x n

j

f n

n

N

( )

[ ] exp

=

⋅

− ⋅ ⋅ ⋅ ⋅

=

−

∑

2

0

1

π

(31)

Jeżeli z otrzymanej według (31) transformaty zostanie pozostawiony tylko jeden okres - na przedziale

f

od zera do 1 - i na tym odcinku zostanie pobranych

N

próbek, w oddalonych o

∆

f

N

=

1

punktach, poczynając od punktu

f

=

0

, to otrzyma się

N

wartości. Punkty próbkowania

f

k

są

rozłożone na osi

f

równomiernie, można je więc we wzorze (31) zastąpić ich numerami,

wprowadzając indeksy częstotliwościowe:

k

f

N

k

=

⋅

(32)

Otrzymany według powyższego opisu ciąg

N

próbek transformaty D-TFT można zatem zapisać

następująco:

X k

x n

j

k n

N

k

N

n

N

[ ]

[ ] exp

:

, ,...,

=

⋅

− ⋅ ⋅ ⋅ ⋅











=

−

=

−

∑

2

0 1

1

0

1

π

(33)

Zależność (33) jest wzorem Dyskretnej Transformacji Fouriera, czyli DFT. Wzór na odwrotną DFT jest
do (33) bardzo podobny:

x n

N

X k

j

k n

N

n

N

k

N

[ ]

[ ] exp

:

, ,...,

=

⋅

⋅

⋅ ⋅ ⋅ ⋅











=

−

=

−

∑

1

2

0 1

1

0

1

π

(34)

Para wzorów (33) i (34) stanowi przykład wzoru na DFT zaimplementowany w Matlab’ie. Ze względu
na różne zastosowania parę zależności na DFT oraz na odwrotną DFT można ogólnie zapisać z
użyciem stałej

c

DFT

:

DSP-MATLAB,

Ć

wiczenie 4,









P.Korohoda, KE AGH

10

X k

c

x n

j

k n

N

k

N

DFT

n

N

[ ]

[ ] exp

:

, ,...,

=

⋅

⋅

− ⋅ ⋅ ⋅ ⋅











=

−

=

−

∑

2

0 1

1

0

1

π

(35)

x n

N c

X k

j

k n

N

n

N

DFT k

N

[ ]

[ ] exp

:

, ,...,

=

⋅

⋅

⋅ ⋅ ⋅ ⋅











=

−

=

−

∑

1

2

0 1

1

0

1

π

(36)

Najczęściej stosuje się wartość

c

DFT

ze zbioru

1

1

1

N

N

,

,













. W pierwszym przypadku

X[ ]

0

jest

wartością średnią wszystkich elementów ciągu

x n

[ ]

. W drugim, w wyniku transformacji nie zmienia

się całkowita energia ciągu. Właściwość tą, zwaną równością Parsevala, można zapisać tak:

x n

X k

n

N

k

N

[ ]

[ ]

2

0

1

2

0

1

=

−

=

−

∑

∑

=

(37)

Natomiast, gdy

c

DFT

=

1

, to

X[ ]

0

jest sumą wszystkich elementów ciągu pierwotnego.

Równość Parsevala można zapisać bardziej ogólnie, uwzględniając stałą

c

DFT

:

(

)

c

N

x n

X k

DFT

n

N

k

N

⋅

⋅

=

=

−

=

−

∑

∑

2

2

0

1

2

0

1

[ ]

[ ]

(38)

Transformacja DFT przekształca pierwotny ciąg

N

elementów (zwykle jest to ciąg rzeczywisty)

w ciąg transformaty (zazwyczaj zespolony) składający się również z

N

elementów. Warto zaznaczyć,

ż

e z punktu widzenia definicji DFT ciąg pierwotny może być także zespolony, co zostało uwzględnione

w zapisie (37) i (38).

1.5 Transformata DFT jako próbkowanie transformaty D-TFT

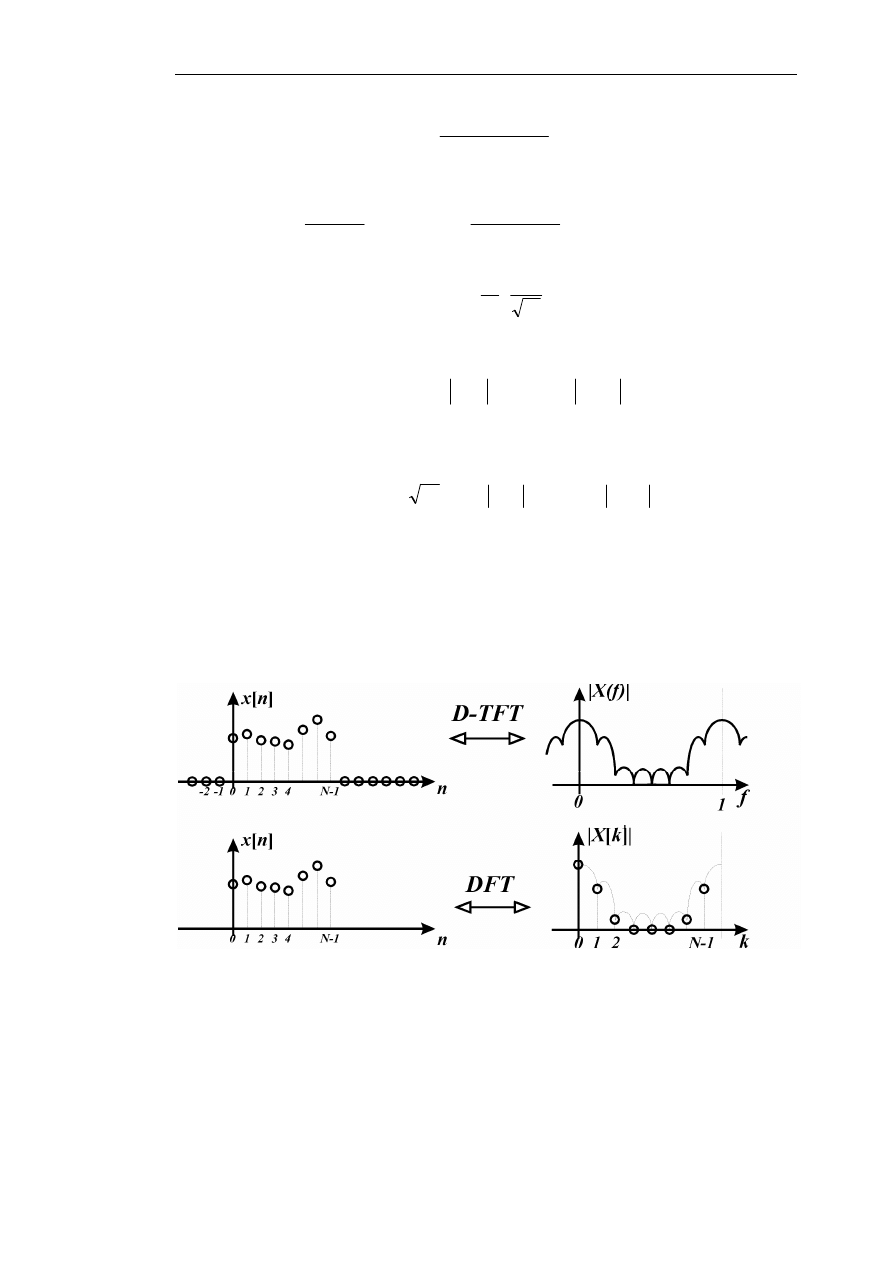
Jak wynika z poprzedniego podrozdziału, pomiędzy DFT i D-TFT istnieje bezpośredni związek. Rys.3
przedstawia ilustrację tej zależności.

Rys.3. Ilustracja faktu, że transformata DFT może być interpretowana jako efekt próbkowania jednego

okresu transformaty D-TFT, gdy transformata D-TFT jest wyznaczona dla tego samego skończonego

ciągu jednak przedłużonego do nieskończoności elementami zerowymi

Korzystając z relacji między transformatą C-TFT dla sygnału z czasem ciągłym i D-TFT ciągu
pochodzącego z próbkowania tego sygnału oraz informacji podanych powyżej można określić związek
pomiędzy widmem Fouriera sygnału z czasem ciągłym i DFT odpowiedniego fragmentu ciągu
cyfrowego pochodzącego z próbkowania tego sygnału. W ramach przygotowywania się do ćwiczeń
należy przygotować się do określania, jaka częstotliwość w Hz odpowiada określonemu indeksowi
częstotliwościowemu

k

i na odwrót.

DSP-MATLAB,

Ć

wiczenie 4,









P.Korohoda, KE AGH

11

2 Korzystanie z pakietu MATLAB

2.1 Opis wybranych funkcji

Wybrane polecenia programu MATLAB:
fft( dane wejściowe )

wyznaczenie dyskretnej transformaty Fouriera zadanego
ciągu za pomocą algorytmu szybkiej transformaty
Fouriera

ifft( dane wejściowe )

operacja odwrotna do fft

fftshift( dane wejściowe )

przesunięcie w dziedzinie Fouriera, tak by składowa
stała znalazła się (prawie) w środku ciągu

sum( wektor lub macierz )

wyznaczanie sumy elementów wektora lub, gdy zostanie
podana macierz, wektora sum kolejnych kolumn tej
macierzy

flops

wyświetlenie stanu licznika operacji
zmiennoprzecinkowych, flops(0) zeruje ten licznik

mesh

wykreślanie w aktywnym oknie graficznym wykresu
funkcji dwóch zmiennych podanej w postaci
zdyskretyzowanej jako macierz (wykres trójwymiarowy)

colormap

zmiana palety kolorów używanej do wykreślania
wykresów

view

obrót wykresu trójwymiarowego wokół osi pionowej i
poziomej do pozycji podanej w postaci kątów azymutu i
elewacji

Szczegóły dotyczące formatu danych wejściowych należy odczytać za pomocą polecenia „help”.

W przypadku funkcji fft oraz ifft możliwe jest wyznaczanie transformaty DFT dla ilości elementów
innej niż długość ciągu podanego jako dane wejściowe. Wystarczy w tym celu podać drugą zmienną,
określającą ilość punktów. Przykładowo dla 8-punktowego ciągu

x n

[ ]

można wyliczyć 32-punktową

transformatę DFT przez podanie polecenia:

>>X=fft(x,32);

W przypadku, gdy ilość punktów transformaty jest większa niż długość ciągu pierwotnego, to ciąg ten
jest przedłużany do odpowiedniej długości wartościami zerowymi. Jeżeli ilość punktów transformaty
jest mniejsza niż długość ciągu, to ciąg ten jest przy wyznaczaniu transformaty obcinany do wskazanej
długości.

Uwaga: jeżeli zamieniamy zespolony wektor wierszowy na kolumnowy (lub odwrotnie) stosując
operator transpozycji macierzy, należy pamiętać, że otrzymane wartości będą miały odwrócony znak
części urojonej - wynika to z definicji transpozycji dla macierzy zespolonych. Można to łatwo
„poprawić” stosując polecenie „conj”.

2.2 Przykłady realizacji wybranych zadań

Poniżej pokazano przykładowe sekwencje poleceń realizujące zadania podobne do tych, które będą
realizowane w ramach laboratorium - w większości poniższych przykładów pominięto końcowy etap
wykreślania odpowiednich wykresów.

2.2.1 Demonstracja okresowości sygnału kosinusoidalnego względem “czasu” i częstotliwości:

>> t=0:0.02:3;
>> v=0:0.02:2:
>> s=cos(2*pi*v’*t);
>> mesh(t,v,s);
>> colormap([0,0,0]);
>> axis([min(t),max(t),min(v),max(v),-1,1]);
>> grid
>> view([75,65]);

DSP-MATLAB,

Ć

wiczenie 4,









P.Korohoda, KE AGH

12

2.2.2 Wyznaczanie odpowiedzi częstotliwościowej filtru FIR rzędu N-1 dla pojedynczej wartości
częstotliwości cyfrowej:

>> N=8;
>> h=rand(1,N);
>> f=0.25;
>> n=0:N-1;
>> s_we=exp(j*2*pi*f*n);
>> s_wy=filter(h,1,s_we);
>> H=s_wy/s_we;

W przykładzie wyznaczono odpowiedź systemu tylko dla ciągów 8-punktowych, ponieważ w 8.
punkcie odpowiedzi zanika różnica pomiędzy odpowiedzią na odpowiedni nieskończony ciąg i na ciąg
skończony zastosowany w przykładzie. Wynika to z faktu, iż odpowiedź impulsowa jest właśnie 8-
elementowa.

2.2.3 Wyznaczanie transmitancji “Z” filtru typu FIR o zadanej odpowiedzi impulsowej dla
pojedynczej wartości z:

>> f=0.5;
>> z=exp(j*2*pi*f)
>> h=rand(1,8);
>> p=0:length(h)-1;
>> H=sum(h.*(z.^p));

2.2.4 Wyznaczanie przybliżenia transformaty D-TFT ze wzoru definicyjnego (27):

>> f=-30:0.01:30;
>> T=1/20;
>> x=rand(1,32);
>> n=-10:21;

i następnie:

>> k=0; for ff=f, k=k+1; X(k)=sum(x.*exp(-j*2*pi*f*n*T)); end;

albo:

>> k=(1:length(f))’;
>> X(k)=exp(-j*2*pi*f’*n*T)*x’;

2.2.5 Wyznaczanie transformaty DFT ze wzoru definicyjnego (33):

>> N=32;
>> n=0:31;
>> x=rand(1,N);

i następnie:

>> for k=n; X(k+1)=sum(x.*exp(-j*2*pi*k*n/N)); end;

albo:

>> k=n’;
>> X(k+1)=exp(-j*2*pi*k*n/N)*x’;

2.2.6 Wyznaczanie przybliżenia transformaty D-TFT za pomocą funkcji fft:

>> N=8;
>> Nmax=1024;
>> x=rand(1,N);
>> X=fft(x,Nmax);

2.2.7 Wykres fazy - efekt ograniczania do zakresu od minus pi do pi:

>> fi=(-10:0.1:10)*pi;
>> X=exp(j*fi);
>> stem( fi, angle(X));
>> stem(fi, unwrap(angle(X)));

Jak uzasadnić wprowadzenie demonstrowanego powyżej ograniczenia na zakres wartości fazy?

DSP-MATLAB,

Ć

wiczenie 4,









P.Korohoda, KE AGH

13

D

odatek teoretyczny nr 2

Relacja pomiędzy Transformacją Fouriera z Czasem Dyskretnym (ang.

D-TFT) i Transformacją Fouriera z Czasem Ciągłym (ang. C-TFT)

Definicja D-TFT dla ciągu

x n

[ ]

:

X f

x n e

f

j

f n

n

( )

[ ]

:

=

⋅

∈ℜ

− ⋅ ⋅ ⋅ ⋅

=−∞

∞

∑

2

π

(1)

Definicja C-TFT dla sygnału

x t

( )

(dotyczy takich sygnałów, dla których poniższa całka jest zbieżna -

dla sygnałów okresowych stosuje się pewne poszerzenie definicji, do znaku trzech gwiazdek ***
rozważania dotyczyć będą wyłącznie sygnałów gwarantujących zbieżność wzoru definicyjnego):

Ψ

( )

( )

:

v

x t

e

dt

v

j

v t

=

⋅

∈ℜ

− ⋅ ⋅ ⋅ ⋅

−∞

∞

∫

2

π

(2)

Definicja transformacji odwrotnej do C-TFT (z uwagami odnośnie zbieżności analogicznymi do wzoru
(2)):

x t

v

e

dv

t

j

v t

( )

( )

:

=

⋅

∈ℜ

⋅ ⋅ ⋅ ⋅

−∞

∞

∫

Ψ

2

π

(2a)

Załóżmy, że wartości ciągu

x n

[ ]

są równe amplitudom delt Diraca po próbkowaniu sygnału

x t

( )

w

równych odstępach czasu T, czyli po prostu chwilowym wartościom sygnału w równo oddalonych
punktach czasu:

x n

x n T

[ ]

(

)

=

⋅

(3)

Dla przypomnienia, funkcja grzebieniowa to ciąg równo oddalonych delt Diraca (w tym przypadku
oddalonych o T):

g

t

t

n T

T

n

( )

(

)

=

− ⋅

=−∞

∞

∑

δ

(4)

Zatem spróbkowany funkcją grzebieniową sygnał

x t

( )

można zapisać następująco (inaczej jest to

funkcja grzebieniowa zmodulowana amplitudowo sygnałem

x t

( )

):

x

t

x t

g

t

T

T

( )

( )

( )

=

⋅

(5)

Wynik C-TFT dla sygnału (5) określony jest wzorem:

Ψ

T

T

j

v t

v

x t

g t

e

dt

( )

( )

( )

=

⋅

⋅

− ⋅ ⋅ ⋅ ⋅

−∞

∞

∫

2

π

(6)

Skorzystajmy z (4) i podstawmy za funkcję grzebieniową do (6):

DSP-MATLAB,

Ć

wiczenie 4,









P.Korohoda, KE AGH

14

Ψ

T

n

j

v t

v

x t

t

n T

e

dt

( )

( )

(

)

=

⋅

− ⋅











⋅

=−∞

∞

− ⋅ ⋅ ⋅ ⋅

−∞

∞

∑

∫

δ

π

2

(7)

Ponieważ w wyrażeniu podcałkowym występuje iloczyn wyrażeń, skorzystamy z przemienności
mnożenia oraz rozdzielności mnożenia względem dodawania i przepiszemy (7) do postaci:

[

]

Ψ

T

j

v t

n

v

x t

e

t

n T

dt

( )

( )

(

)

=

⋅

⋅

− ⋅











− ⋅ ⋅ ⋅ ⋅

=−∞

∞

−∞

∞

∑

∫

2

π

δ

(8)

Zakładając, że całka (7) jest zbieżna dla każdego składnika sumy możemy całkę sumy wyrażeń zastąpić
sumą całek:

Ψ

T

j

v t

n

v

x t

e

t

n T dt

( )

( )

(

)

=

⋅

⋅

− ⋅













− ⋅ ⋅ ⋅ ⋅

−∞

∞

=−∞

∞

∫

∑

2

π

δ

(9)

Warto teraz przypomnieć, że całka z funkcji pomnożonej przez deltę Diraca przesuniętą o

∆

T

jest

równa wartości tej funkcji w punkcie

∆

T

(dowód w tym miejscu pomijamy), czyli przykładowo:

p t

t

T dt

p

T

( )

(

)

(

)

−∞

∞

∫

⋅

−

=

δ

∆

∆

(10)

Traktując iloczyn

x t

e

j

v t

( )

⋅

− ⋅ ⋅ ⋅ ⋅

2

π

jako powyższą funkcję ciągłą możemy przepisać (9) do postaci:

Ψ

T

j

v n T

n

v

x n T

e

( )

(

)

=

⋅ ⋅

− ⋅ ⋅ ⋅ ⋅ ⋅

=−∞

∞

∑

2

π

(11)

Wyrażenie (11) jest już bardzo podobne do (1), należy jeszcze wykonać podstawienie (3) oraz:

v

f

T

=

(12)

Po powyższych podstawieniach otrzymujemy, że:

X f

f

T

T

( )

=











Ψ

(13)

Oznacza to, że funkcja ciągła częstotliwości f (D-TFT ciągu

x n

[ ]

) jest identyczna (z dokładnością do

skali T określonej zależnością (12) dla zmiennej niezależnej) z funkcją ciągłą zmiennej v (C-TFT
sygnału ciągłego ).

DSP-MATLAB,

Ć

wiczenie 4,









P.Korohoda, KE AGH

15

Wynika z tego szereg wniosków, np. taki:

Ψ

T

v

( )

jest transformatą C-TFT sygnału spróbkowanego z okresem T, zatem ta transformata jest

okresowa względem zmiennej v z okresem

v

T

0

1

=

, z (13) wynika więc, że transformata D-TFT,

X f

( )

, jest także okresowa względem zmiennej

f

z okresem

f

0

1

=

.

Spotykane są także definicje obu transformat oparte na pulsacji. Otrzymuje się je przez następujące
podstawienia.
Dla D-TFT:

ω

π

= ⋅ ⋅

2

f

(14)

oraz dla C-TFT:

Ω = ⋅ ⋅

2

π

v

(15)

Pomiędzy pulsacjami (14) i (15) zachodzi naturalnie analogiczny do (12) związek:

Ω =

ω

T

(16)

Przy podstawieniach (14) i (15) można wykazać, że zachodzi także odpowiedni związek pomiędzy
transformatą D-TFT (czyli w tym przypadku:

X ( )

ω

) oraz transformatą C-TFT (czyli teraz:

X

T

( )

Ω

)

:

X

T

T

( )

ω

ω

=











Ψ

(17)

Funkcja

X ( )

ω

jest okresowa względem zmiennej

ω

i jak łatwo z (14) zauważyć okres ten wynosi

2

⋅

π

.

Warto także wskazać inną możliwość przejścia od (8) do (11).

[

]

Ψ

T

j

v t

n

v

x t

e

t

n T

dt

( )

( )

(

)

=

⋅

⋅

− ⋅











− ⋅ ⋅ ⋅ ⋅

=−∞

∞

−∞

∞

∑

∫

2

π

δ

(8 - powtórzone)

Zakładamy, że całka (8) jest zbieżna w każdym podprzedziale całkowania i następnie dzielimy cały
przedział całkowania na odcinki o długości T i środkach w punktach określonych dla całkowitych k
następująco:

t

k T

k

= ⋅

(18)

Ponieważ suma całek na wszystkich podprzedziałach jest równa całce na pełnym przedziale
całkowania, więc (8) można przepisać do postaci:

[

]

Ψ

T

j

v t

n

t

T

t

T

k

v

x t

e

t

n T

dt

k

k

( )

( )

(

)

=

⋅

⋅

− ⋅































− ⋅ ⋅ ⋅ ⋅

=−∞

∞

−

+

=−∞

∞

∑

∫

∑

2

2

2

π

δ

(19)

W danym podprzedziale całkowania mieści się tylko jedna odpowiednio przesunięta delta Diraca,
zatem suma pod całką może być zastąpiona przez pojedynczy składnik:

DSP-MATLAB,

Ć

wiczenie 4,









P.Korohoda, KE AGH

16

Ψ

T

j

v t

t

T

t

T

k

v

x t

e

t

k T dt

k

k

( )

( )

(

)

=

⋅

⋅

− ⋅





















− ⋅ ⋅ ⋅ ⋅

−

+

=−∞

∞

∫

∑

2

2

2

π

δ

(20)

Teraz korzystając z (10) i podstawiając n za k można łatwo dokończyć wykazanie równoważności (13).

Opierając się na wykazanej zależności pomiędzy D-TFT i C-TFT można wywnioskować, że
transformacja odwrotna do (1) będzie dana wzorem wynikającym z (2a). Ponieważ D-TFT jest
powiązane ściśle z C-TFT sygnału ciągłego w czasie spróbkowanego funkcją grzebieniową, zatem
wypiszemy wzór na transformację odwrotną do C-TFT dla tego właśnie przypadku:

x t

v

e

dv

t

T

T

j

v t

( )

( )

:

=

⋅

∈ℜ

⋅ ⋅ ⋅ ⋅

−∞

∞

∫

Ψ

2

π

(21)

Dla przypomnienia - ogólny wzór na odwrotną transformację jest następujący:

x t

v

e

dv

t

j

v t

( )

( )

:

=

⋅

∈ℜ

⋅ ⋅ ⋅ ⋅

−∞

∞

∫

Ψ

2

π

(2a - powtórzone)

Z transformaty odwrotnej wyznaczonej według (21) wybieramy teraz jedynie te wartości

x t

( )

, które

odpowiadają elementom ciągu

x n

[ ]

, zatem (21) przybiera postać:

x n T

v

e

dv

n

I

T

T

j

v n T

(

)

( )

:

⋅

=

⋅

∈

⋅ ⋅ ⋅ ⋅ ⋅

−∞

∞

∫

Ψ

2

π

(22)

Z kolei transformata odwrotna dla sygnału niespróbkowanego wyznaczona jedynie w tych samych,
wybranych punktach czasu opisana jest w sposób następujący:

x n T

v

e

dv

n

I

j

v n T

(

)

( )

:

⋅

=

⋅

∈

⋅ ⋅ ⋅ ⋅ ⋅

−∞

∞

∫

Ψ

2

π

(23)

Pomiędzy wynikami obu transformat odwrotnych (22) i (23) w tych wybranych punktach czasu
zachodzi następujący związek (wynikający ze sposobu próbkowania):

x

n T

x n T

t

n T

T

(

)

(

)

(

)

⋅

=

⋅

⋅

− ⋅

δ

(24)

Dążymy zatem do tego, by w oparciu o

Ψ

T

v

( )

(będące w ścisłym związku z

X f

( )

) wyznaczyć

wartości

x n

[ ]

(które są z kolei odpowiednio równe wartościom

x n T

(

)

⋅

). W tym celu należy

doprowadzić do równości zmodyfikowanej odpowiednio prawej strony (22) i lewej strony (23).
Natępnie wystarczy wykorzystać (12) oraz (13) i zastąpić po prawej stronie

Ψ

T

v

( )

przez

X f

( )

.

Przyjmijmy, że sygnał ciągły przed próbkowaniem ma taką transformatę, że jego częstotliwość
maksymalna i częstotliwość próbkowania spełniają warunek o próbkowaniu umożliwiający wierne
odtworzenie. Zauważmy, że możemy to zawsze założyć, ponieważ nie interesuje nas w zasadzie jak
wyglądał sygnał ciągły

x t

( )

- wykonujemy różne operacje jedynie na sygnale spróbkowanym

x

t

T

( )

oraz na wybranych wartościach chwilowych

x t

( )

. To jak wygląda sygnał

x t

( )

pomiędzy tymi

DSP-MATLAB,

Ć

wiczenie 4,









P.Korohoda, KE AGH

17

wybranymi punktami nie ma żadnego znaczenia z punktu widzenia przedstawionej dyskusji. W każdym
razie, gdybyśmy chcieli później wyciągnąć w oparciu o odwrotną transformację D-TFT jakieś wnioski
odnośnie całego

x t

( )

, to sygnałów takich może być dla konkretnego ciągu

x n

[ ]

nieskończenie wiele.

Zawsze jednak można zastosować interpolację prowadzącą do takiego

x t

( )

, który spełnia warunek o

próbkowaniu.
Jeżeli zatem

x t

( )

spełnia warunek o próbkowaniu, to jego transformata

Ψ

( )

v

jest związana z

transformatą sygnału spróbkowanego ,

Ψ

T

v

( )

, następująco:

Ψ

Ψ

( )

( )

,

.

v

T

v

dla

v

v

v

dla

pozost v

T

=

⋅

∈ −








0

0

2

2

0

(25)

W celu wyznaczenia wartości

x t

( )

w wybranych punktach

t

n T

= ⋅

wystarczy zatem wyznaczyć

transformatę odwrotną do C-TFT dla

T

v

T

⋅ Ψ

( )

na przedziale zawierającym pojedynczy okres - od

−

v

0

2

do

v

0

2

:

x n T

T

v

e

dv

n

I

T

j

v n T

v

v

(

)

( )

:

⋅

= ⋅

⋅

∈

⋅ ⋅ ⋅ ⋅ ⋅

−

∫

Ψ

2

2

2

0

0

π

(26)

Podstawiając według (12) i (13) oraz (3), doprowadzając między innymi do zmiany zmiennej po której
wyznaczana jest całka a zatem i do zmiany granic całkowania, otrzymujemy:

x n T

T

e

d

f

T

n

I

T

f

T

j

f

T

n T

f

T

f

T

(

)

( )

:

⋅

= ⋅

⋅

∈

⋅ ⋅ ⋅ ⋅ ⋅

−

⋅

⋅

∫

Ψ

2

2

2

0

0

π

(27)

czyli (warto przypomnieć, że zawsze

f

0

1

=

):

x n

X f

e

df

n

I

j

f n

[ ]

( )

:

=

⋅

∈

⋅ ⋅ ⋅ ⋅

−

∫

2

1

2

1

2

π

(28)

Wzór (28) stanowi więc przepis na transformację odwrotną do D-TFT.

Jak łatwo zauważyć, dla sygnałów o których była dotychczas mowa (czyli spróbkowanych funkcją
grzebieniową) całka (2a) nie będzie zbieżna dla żadnej wartości

t

ponieważ funkcja

Ψ

T

v

( )

jest

okresowa. Podobny problem pojawia się także w przypadku transformacji w przód dla funkcji
okresowej - zarówno C-TFT jak i D-TFT. Konieczne jest zatem poszerzenie definicji (1) i (2) - oraz
automatycznie (2a) i (28).

***

DSP-MATLAB,

Ć

wiczenie 4,









P.Korohoda, KE AGH

18

Uzupełnienie dyskusji o przypadek dla sygnałów okresowych (czy to w dziedzinie
czasu, czy częstotliwości).

Poszerzenie definicji transformacji polega na przyjęciu, że jeżeli para funkcji

x t

( )

oraz

Ψ

( )

v

jest

powiązana jednym z dwóch wzorów całkowych (albo na transformatę w przód albo odwrotną), to
zachodzi również transformacja w drugą stronę, nawet, gdy całka w odpowiadającym wzorze nie jest
zbieżna. Przykładowo, jeżeli odwrotna transformata C-TFT (wzór całkowy (2a)) z przesuniętej delty
Diraca jest zbieżna i daje zespoloną eksponentę, to także transformata C-TFT z zespolonej eksponenty
(będącej sygnałem okresowym) istnieje i jest równa tej delcie Diraca:

[

]

[

]

F

v

v

e

F

e

v

v

C T

j

v t

C T

j

v t

−

−

⋅ ⋅ ⋅ ⋅

−

⋅ ⋅ ⋅ ⋅

−

=

⇔

=

−

1

2

2

δ

δ

π

π

(

)

(

)

∆

∆

∆

∆

(29)

Rozpoczniemy od okresowego sygnału ciągłego w dziedzinie czasu (podstawowy okres sygnału wynosi
P). Sygnał okresowy można rozwinąć w szereg Fouriera, zatem:

x

t

c

e

P

k

j

k

P

t

k

( )

=

⋅

⋅ ⋅ ⋅ ⋅

=−∞

∞

∑

2

π

(30)

Z liniowości transformacji C-TFT (2) oraz (29) wynika, że transformata sygnału (30) jest ciągiem
poprzesuwanych delt Diraca, skalowanych amplitudowo współczynnikami rozwinięcia w szereg:

[

]

F

x

t

X

v

c

v

k v

C T

P

P

k

P

k

−

=−∞

∞

=

=

⋅

− ⋅

∑

( )

( )

(

)

δ

(31)

gdzie

v

P

P

=

1

(32)

Zatem transformata ta jest funkcją prążkową.
Określony powyżej sygnał o okresie P po spróbkowaniu z krokiem próbkowania T oznaczymy
następująco:

x

t

x

t

g

t

P T

P

T

,

( )

( )

( )

=

⋅

(33)

Ze względu na rozdzielność dodawania względem mnożenia wzór (33) można rozpisać na sumę
próbkowanych z osobna wyrazów szeregu (30). Pojedynczy, przykładowo k-ty, wyraz szeregu (30) po
spróbkowaniu opisany jest następująco:

x

t

x

t

g

t

c

e

g

t

P T k

P k

T

k

j

k t

P

T

, ,

,

( )

( )

( )

( )

=

⋅

=

⋅

⋅

⋅

⋅ ⋅ ⋅

2

π

(34)

Korzystając z tego, że mnożenie w dziedzinie czasu odpowiada splotowi w dziedzinie częstotliwości,
można opisać transformatę C-TFT sygnału (34) jako:

[

]

(

)

F

x

t

c

v

k v

T

g

v

C T

P T k

k

P

v

−

=

⋅

− ⋅

∗

⋅











, ,

( )

(

)

( )

δ

1

0

(35)

Ponieważ splot z przesuniętą deltą Diraca daje przesunięcie funkcji o tyle samo o ile przesunięta jest
delta (a funkcja grzebieniowa jest sumą poprzesuwanych delt Diraca), więc (35) opisuje deltę Diraca w

dziedzinie częstotliwości

v

, przesuniętą o

k v

P

⋅

w prawo, o amplitudzie

c

T

k

i powielonej co

v

0

wzdłuż całej osi częstotliwości.

DSP-MATLAB,

Ć

wiczenie 4,









P.Korohoda, KE AGH

19

Porównując powyższe wzory można zatem zauważyć, że transformata C-TFT sygnału okresowego i
próbkowanego funkcją grzebieniową jest okresową funkcją prążkową. Prążkowa transformata sygnału
okresowego nie próbkowanego jest tym razem pomnożona przez współczynnik 1/T i powielona wzdłuż
osi częstotliwości co

v

0

. Jest to dokładna analogia do transformaty spróbkowanego sygnału

nieokresowego, tyle że tym razem transformata jest prążkowa (suma poprzesuwanych delt Diraca).
Warto zauważyć, że zazwyczaj powinno się zapewnić warunek:

v

v

P

<<

0

. Również i tego przypadku

dotyczy związek pomiędzy częstotliwością próbkowania i maksymalną częstotliwością sygnału (to, że
transformata jest prążkowa nie oznacza, iż sygnał nie może mieć częstotliwości maksymalnej).
Okazuje się, że w takim przypadku (gdy sygnał jest okresowy), to D-TFT wiąże się z C-TFT w
identyczny sposób jak w (13) (lub (17)). Suma (1) nie jest skończona i dlatego do wyznaczenia
transformaty należy posłużyć się poszerzoną definicją i wiedzą o tym, że według odwrotnej D-TFT (28)
z odpowiedniego ciągu delt Diraca w dziedzinie częstotliwości otrzyma się ciąg wartości
odpowiadający wartościom chwilowym ciągłego sygnału okresowego.

DSP-MATLAB,

Ć

wiczenie 4,









P.Korohoda, KE AGH

20

D

odatek teoretyczny nr 3

Relacja pomiędzy Transformacją Fouriera z Czasem Dyskretnym (ang.

D-TFT) i Dyskretną Transformacją Fouriera (ang. DFT)

Relacja pomiędzy DFT i C-TFT

Definicja D-TFT dla ciągu

x n

[ ]

:

X f

x n e

f

j

f n

n

( )

[ ]

:

=

⋅

∈ℜ

− ⋅ ⋅ ⋅ ⋅

=−∞

∞

∑

2

π

(1)

Definicja DFT dla ciągu

x n

[ ]

:

X k

x n e

k

N

j

k n

N

n

N

[ ]

[ ]

:

, ,...,

=

⋅

=

−

− ⋅⋅ ⋅ ⋅ ⋅

=

−

∑

2

0

1

0 1

1

π

(2)

Z definicji od razu wynika, że transformata D-TFT jest funkcją ciągła ze względu na

f

, natomiast

transformata DFT jest ciągiem o tej samej ilości elementów, co ciąg pierwotny - dyskretny jest i czas i
częstotliwość, a ponieważ określony jest odstęp pomiędzy kolejnymi punktami w obu dziedzinach, więc
do określenia zmiennej niezależnej pozostawia się jedynie indeks (czasowy lub częstotliwościowy).
Ponadto transformata D-TFT określona jest dla nieskończonego ciągu

x n

[ ]

, natomiast DFT dla ciągu

skończonego.
Jaka jest zatem relacja pomiędzy obiema powyższymi transformatami?
Wartości elementów ciągu z indeksami czasowymi mogą być traktowane jako chwilowe wartości
odpowiedniej funkcji czasu wybrane w chwilach czasu oddalonych o T sekund (patrz relacja pomiędzy
D-TFT i C-TFT):

x n

x n T

[ ]

(

)

=

⋅

(3)

Taka interpretacja umożliwia powiązanie Transformacji Fouriera z Czasem Dyskretnym (ang. D-TFT) i
Transformacji Fouriera z Czasem Ciągłym (and. C-TFT). Wykażemy teraz, że jeżeli założymy
analogiczną do (3) zależność w dziedzinie częstotliwości, to transformata DFT stanowi ciąg N
wartości chwilowych ciągłej transformaty D-TFT wybranych z jednego okresu tej transformaty

(a jest ona, jak wiadomo, okresowa), oddalonych na osi częstotliwości

f

o

1

N

. Przepiszmy zatem

(2) wstawiając okres próbkowania w dziedzinie częstotliwości

f

N

N

=

1

(dla przypomnienia: okres

transformaty D-TFT wynosi

f

0

1

=

):

X k

x n e

k

N

j

k f

n

N f

n

N

N

N

[ ]

[ ]

:

, ,...,

=

⋅

=

−

− ⋅⋅ ⋅ ⋅ ⋅ ⋅

⋅

=

−

∑

2

0

1

0 1

1

π

(4)

W (4) można zauważyć, że:

N f

f

N

⋅

=

=

0

1

(5)

oraz, oznaczając przez

f

k

k-ty punkt na osi częstotliwości, że:

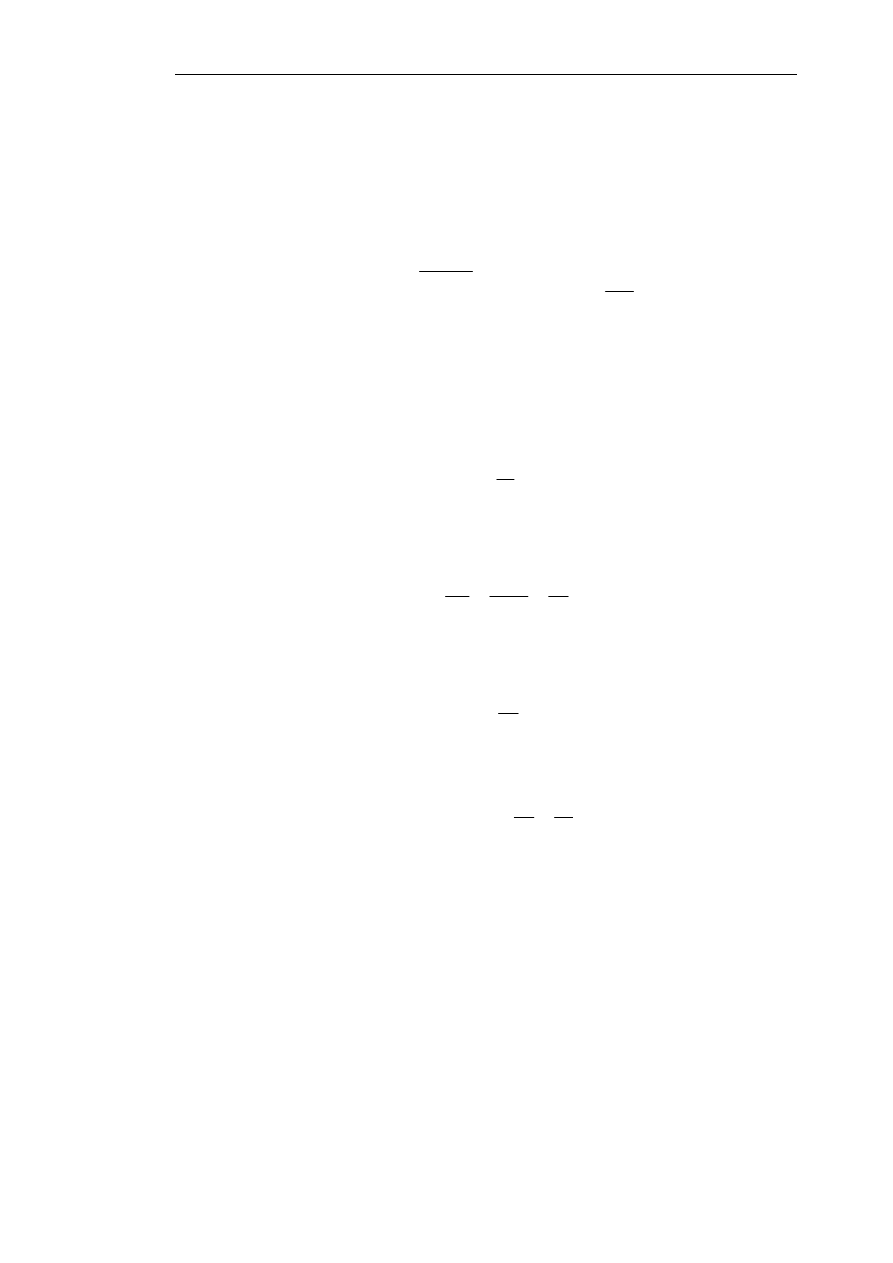
DSP-MATLAB,

Ć

wiczenie 4,









P.Korohoda, KE AGH

21

k f

f

N

k

⋅

=

(6)

Podstawiając (5) i (6) do (4) oraz zakładając, że ciąg

x n

[ ]

przyjmuje dla nie uwzględnionych

indeksów czasowych wartości zerowe, można wykazać, że wzór (4) określa D-TFT (wzór (1)) dla
wybranych wartości

f

:

X k

x n e

X k

f

f

X k f

j

f n

f

n

N

k

k

k

[ ]

[ ]

(

)

=

⋅

=

⋅











=

⋅

− ⋅⋅ ⋅ ⋅ ⋅

=

−

∑

2

0

1

0

0

π

(7)

Prawa strona (7) oznacza wybrane wartości transformaty D-TFT. Pamiętając, że

k przyjmuje jedynie

całkowite wartości od 0 do

N-1, widzimy, że faktycznie DFT dotyczy tylko jednego okresu D-TFT.

Dotatkowo krok próbkowania w dziedzinie częstotliwości związany jest z długością interesującego nas
odcinka w dziedzinie czasu (dyskretnego) następująco:

f

N

N

=

1

(8)

lub dzieląc obie strony przez krok próbkowania

T w dziedzinie czasu (otrzymując w ten sposób wymiar

czasu w sekundach, a częstotliwości w Hz):

v

f

T

N T

t

N

N

=

=

⋅

=

1

1

∆

(8a)

Analogiczny związek zachodzi pomiędzy krokiem próbkowania w dziedzinie czasu i okresem w
dziedzinie częstotliwości. Dla czasu dyskretnego krok próbkowania wynosi po prostu „1”:

1

1

0

=

f

(9)

Mnożąc obie strony (9) przez

T otrzymujemy:

T

T

T

f

v

= ⋅ =

=

1

1

0

0

(9a)

gdzie

T jest krokiem próbkowania osi czasu wyrażonym w sekundach, a

v

0

okresem transformaty

C-TFT wyrażonym w Hz.

Można więc teraz także odnieść DFT do C-TFT.
Jeżeli założymy, że:

x n

dla

n

n

N

[ ]

lub

(

)

=

<

>

−

0

0

1

(10)

to można zastosować następującą interpretację:

x n

x n T

X k

X k f

N

[ ]

(

)

[ ]

(

)

=

⋅

∧

=

⋅

(11)

Oznacza to, że wartości ciągu

x n

[ ]

są chwilowymi wartościami ciągłego sygnału

x t

( )

, dla chwil

czasu określonych przez zależność:

DSP-MATLAB,

Ć

wiczenie 4,









P.Korohoda, KE AGH

22

t

n T

n

= ⋅

(12)

Natomiast wartości ciągu

X k

[ ]

(czyli w dziedzinie indeksów częstotliwościowych) stanowią wartości

chwilowe ciągłej funkcji

X f

( )

(wyniku D-TFT), a więc zarazem funkcji

Ψ

T

v

( )

(tj. wyniku C-TFT

dla spróbkowanej funkcją grzebieniową - z krokiem próbkowania T - funkcji

x t

( )

):

X k

X k f

k f

T

v

N

T

N

T

k

[ ]

(

)

(

)

=

⋅

=

⋅











=

Ψ

Ψ

(13)

Zatem

X k

[ ]

jest jednocześnie wartością

Ψ

T

v

( )

(czyli wyniku C-TFT) dla:

v

v

k f

T

k v

k

N

N

=

=

⋅

= ⋅

(14)

gdzie

v

t

N

=

1

∆

i oznacza odwrotność przedziału czasu, z którego pochodzą próbki czasowe, czyli

przedziału, w którym badamy funkcję czasu zakładając, że poza nim jest ona zerowa (a ściślej, że
próbki są zerowe poza tym przedziałem czasu).