T

R

A

N

S

F

O

R

M

A

C

J

E

T

R

A

N

S

F

O

R

M

A

C

J

E

W

S

P

W

S

P

Ó

Ó

Ł

Ł

R

Z

R

Z

Ę

Ę

D

N

Y

C

H

D

N

Y

C

H

Ja

n

u

sz

W

a

lo

Ja

n

u

sz

W

a

lo

Ja

n

u

sz

W

a

lo

x

”

z”

y

”

z’

y’

x’

(C

)

jw

(C

)

jw

2

2

/5

4

/5

4

T

ra

n

s

fo

rm

a

c

je

w

s

p

T

ra

n

s

fo

rm

a

c

je

w

s

p

ó

ó

ł

ł

rz

rz

ę

ę

d

n

y

c

h

d

n

y

c

h

(1

)

(1

)

Z

a

d

a

n

ie

t

ra

n

sf

o

rm

a

cj

i

w

sp

ó

łrz

ę

d

n

y

ch

p

o

m

ię

d

zy

d

w

o

m

a

u

k

ła

d

a

m

i

g

e

o

d

e

zy

jn

y

m

i,

z

w

a

n

y

m

i

zw

y

k

le

u

k

ła

d

a

m

i

p

ie

rw

o

tn

y

m

i

w

tó

rn

y

m

,

p

o

le

g

a

n

a

o

b

lic

ze

n

iu

w

sp

ó

łrz

ę

d

n

y

ch

w

u

k

ła

d

zi

e

w

tó

rn

y

m

n

a

p

o

d

st

a

w

ie

z

n

a

jo

m

o

ś

ci

w

sp

ó

łrz

ę

d

n

y

ch

w

u

k

ła

d

zi

e

p

ie

rw

o

tn

y

m

o

ra

z

zn

a

n

e

g

o

m

o

d

e

lu

t

ra

n

sf

o

rm

a

cj

i

(p

ra

w

a

tra

n

sf

o

rm

a

cj

i)

.

M

o

d

e

l

tra

n

sf

o

rm

a

cj

i

m

o

ż

e

b

y

ć

zn

a

n

y

(

w

cz

e

ś

n

ie

j

zd

e

fi

n

io

w

a

n

y

)

lu

b

w

y

zn

a

cz

a

s

ię

g

o

w

o

p

a

rc

iu

o

p

u

n

k

ty

ł

ą

cz

n

e

,

k

tó

ry

ch

w

sp

ó

łr

zę

d

n

e

z

n

a

n

e

s

ą

w

o

b

y

d

w

u

u

k

ła

d

a

ch

.

In

a

cz

e

j

p

u

n

k

ty

u

k

ła

d

u

p

ie

rw

o

tn

e

g

o

i

w

tó

rn

e

g

o

t

o

d

w

a

z

b

io

ry

,

k

tó

ry

ch

c

zę

ś

ci

ą

w

sp

ó

ln

ą

je

st

z

b

ió

r

p

u

n

k

tó

w

ł

ą

cz

n

y

ch

.

(C

)

jw

(C

)

jw

3

3

/5

4

/5

4

T

ra

n

s

fo

rm

a

c

je

w

s

p

T

ra

n

s

fo

rm

a

c

je

w

s

p

ó

ó

ł

ł

rz

rz

ę

ę

d

n

y

c

h

d

n

y

c

h

(2

)

(2

)

W

p

rz

y

p

a

d

k

u

z

a

d

a

n

e

g

o

(

zn

a

n

e

g

o

)

m

o

d

e

lu

t

ra

n

sf

o

rm

a

cj

i

p

u

n

k

ty

ł

ą

cz

n

e

s

łu

ż

ą

w

y

zn

a

cz

e

n

iu

p

a

ra

m

e

tró

w

(w

sp

ó

łc

zy

n

n

ik

ó

w

w

f

u

n

k

cj

a

ch

t

ra

n

sf

o

rm

a

cy

jn

y

ch

).

T

ra

n

sf

o

rm

a

cj

a

w

sp

ó

łrz

ę

d

n

y

ch

m

o

ż

e

b

y

ć

„u

k

ry

ta

”

w

p

ro

ce

si

e

w

y

ró

w

n

a

n

ia

w

sp

ó

łr

zę

d

n

y

ch

m

e

to

d

ą

p

o

ś

re

d

n

ic

zą

cą

,

k

ie

d

y

w

si

e

ci

g

e

o

d

e

zy

jn

e

j

n

a

d

a

je

m

y

w

sp

ó

łrz

ę

d

n

e

p

u

n

k

to

m

n

a

w

ią

za

n

ia

.

T

ra

n

sf

o

rm

u

je

s

ię

w

sp

ó

łr

zę

d

n

e

o

rt

o

k

a

rt

e

zj

a

ń

sk

ie

p

rz

e

st

rz

e

n

n

e

,

w

sp

ó

łr

zę

d

n

e

g

e

o

d

e

zy

jn

e

i

p

ła

sk

ie

,

zw

y

k

le

w

y

ra

ż

o

n

e

w

j

a

k

im

ś

o

d

w

zo

ro

w

a

n

iu

.

(C

)

jw

(C

)

jw

4

4

/5

4

/5

4

T

ra

n

s

fo

rm

a

c

je

w

s

p

T

ra

n

s

fo

rm

a

c

je

w

s

p

ó

ó

ł

ł

rz

rz

ę

ę

d

n

y

c

h

d

n

y

c

h

(3

)

(3

)

W

sp

ó

łr

zę

d

n

e

p

u

n

kt

ó

w

p

o

tr

an

sf

o

rm

ac

ji

(u

kł

ad

w

tó

rn

y)

W

sp

ó

łr

zę

d

n

e

p

u

n

kt

ó

w

ł

ą

cz

n

yc

h

(u

kł

ad

p

ie

rw

o

tn

y)

W

sp

ó

łr

zę

d

n

e

p

u

n

kt

ó

w

ł

ą

cz

n

yc

h

(u

kł

ad

w

tó

rn

y)

W

sp

ó

łr

zę

d

n

e

p

u

n

kt

ó

w

d

o

t

ra

n

sf

o

rm

ac

ji

(u

kł

ad

p

ie

rw

o

tn

y)

M

o

d

e

l

(p

ra

w

o

)

tr

a

n

s

fo

rm

a

c

ji

(C

)

jw

(C

)

jw

5

5

/5

4

/5

4

T

ra

n

s

fo

rm

a

c

je

w

s

p

T

ra

n

s

fo

rm

a

c

je

w

s

p

ó

ó

ł

ł

rz

rz

ę

ę

d

n

y

c

h

d

n

y

c

h

(4

)

(4

)

(C

)

jw

(C

)

jw

6

6

/5

4

/5

4

T

ra

n

s

fo

rm

a

c

ja

T

ra

n

s

fo

rm

a

c

ja

H

e

lm

e

rt

a

H

e

lm

e

rt

a

-

-

H

ri

s

to

w

a

H

ri

s

to

w

a

(1

)

(1

)

M

e

to

d

a

t

ra

n

sf

o

rm

a

cj

i

w

sp

ó

łrz

ę

d

n

y

ch

k

rz

y

w

o

lin

io

w

y

ch

(g

e

o

g

ra

fi

cz

n

y

ch

g

e

o

d

e

zy

jn

y

ch

)

d

la

o

b

sz

a

ró

w

o

p

ro

m

ie

n

iu

d

o

1

0

0

0

k

m

.

O

p

ra

co

w

a

n

a

p

rz

e

z

H

e

lm

e

rt

a

i

u

le

p

sz

o

n

a

w

l

a

ta

ch

4

0

-

ty

ch

p

rz

e

z

H

ri

st

o

w

a

.

T

ra

n

sf

o

rm

a

cj

a

p

o

zw

a

la

p

rz

e

lic

za

ć

w

sp

ó

łrz

ę

d

n

e

p

o

m

ię

d

zy

u

k

ła

d

a

m

i

o

d

n

ie

si

e

n

ia

z

e

z

m

ia

n

ą

p

a

ra

m

e

tr

ó

w

e

lip

so

id

y

.

M

e

to

d

a

st

o

so

w

a

n

a

w

sp

ó

łc

ze

ś

n

ie

d

o

ś

ć

rz

a

d

k

o

.

(C

)

jw

(C

)

jw

7

7

/5

4

/5

4

T

ra

n

s

fo

rm

a

c

ja

T

ra

n

s

fo

rm

a

c

ja

H

e

lm

e

rt

a

H

e

lm

e

rt

a

-

-

H

ri

s

to

w

a

H

ri

s

to

w

a

(2

)

(2

)

O

g

ó

ln

e

z

a

le

ż

n

o

ś

ci

d

e

fi

n

iu

ją

ce

p

ra

w

o

t

ra

n

sf

o

rm

a

cj

i:

(

)

(

)

f
a
A

s

B
f

L

l

L

L

f
a
A

s

B
f

B

b

B

B

o

o

o

o

o

o

,

,
,

,

,

,
,

,

2

1

+
=

+
=

+
=
+
=

,

1

1

1

1

1

1

df

df

f

da

da

f

dA

dA

f

ds

ds

f

dB

dB

f

db

dB

dB

o

o

o

∂

∂

∂

∂

∂

+

+

+

+

 



 



+
=

+

=

.

2

2

2

2

2

df

df

f

da

da

f

dA

dA

f

ds

ds

f

dB

dB

f

dL

dl

dL

dL

o

o

o

∂

∂

∂

∂

∂

+

+

+

+

+

=
+

=

Z

m

ia

n

y

p

u

n

k

tu

p

o

cz

ą

tk

o

w

e

g

o

o

d

B

o

,

d

L

o

,

d

łu

g

o

ś

ci

l

in

ii

g

e

o

d

e

zy

jn

e

j

o

d

s,

a

zy

m

u

tu

o

d

A

i

p

a

ra

m

e

tr

ó

w

e

lip

so

id

y

o

da

i

d

f

p

o

ci

ą

g

a

ją

za

s

o

b

ą

zm

ia

n

y

w

sp

ó

łr

zę

d

n

y

ch

p

u

n

k

tu

k

o

ń

co

w

e

g

o

o

d

B

i

d

L

co

w

yr

c

żc

ją

ró

żn

icn

ki

nu

p

n

łn

n

w

p

o

nt

c

ci

p

o

d

c

n

n

j

p

rnn

n

H

n

lm

n

rt

c

:

(C

)

jw

(C

)

jw

8

8

/5

4

/5

4

T

ra

n

s

fo

rm

a

c

ja

T

ra

n

s

fo

rm

a

c

ja

H

e

lm

e

rt

a

H

e

lm

e

rt

a

-

-

H

ri

s

to

w

a

H

ri

s

to

w

a

(3

)

(3

)

H

ri

st

o

w

d

o

w

y

zn

a

cz

e

n

ia

ró

ż

n

ic

ze

k

w

y

k

o

rz

y

st

a

ł

sz

e

re

g

i

p

o

tę

g

o

w

e

L

e

g

e

n

d

re

’a

i

w

e

fe

k

ci

e

o

trz

y

m

a

ł

w

zo

ry

,

k

tó

re

d

la

p

rz

y

p

a

d

k

u

k

ie

d

y

e

lip

so

id

y

o

b

y

d

w

u

u

k

ła

d

ó

w

s

ą

to

ż

sa

m

e

m

a

ją

p

o

st

a

ć

:

.

,

dA
D

dp
C

dB

B

dL

A

dL

dA
D

dp
C

dB

B

dL

A

dB

i

i

o

i

o

i

i

i

i

o

i

o

i

i

′′

+

′′

+

′′

+

′′

=

′

+

′

+

′

+

′

=

0
=′

i

A

′=

−

−

−

B

b

b

l

i

i

i

i

1

1

3

6

2

2

(

)

(

)

(

)

,

,

)

8(

)

7(

)

4(

2

2

2

i

i

i

i

i

i

l

b

l

b

b

C

−

−

−
=′

′=

−

+

+

D

l

b

l

l

i

i

i

i

i

(

)

(5

)

(

)

,

2

9

3

′′=

A

i

1

,

′′=

+

+

−

B

l

b

l

b

l

l

i

i

i

i

i

i

i

(

)

(

)

(

)

(

)

,

1

2

1

4

1

8

2

1

2

3

,
)
22(

)
19(

)
15(

3

2

i

i
i

i

i

i

i

l

l

b

l

b

l

C

−

+

+
=′′

′′=

+

−

+

−

D

b

b

l

b

b

l

i

i

i

i

i

i

i

(

)

(

)

(

)

(

)

(

)

,

1

1

1

3

1

6

1

7

2

0

2

2

3

2

(*

)

(C

)

jw

(C

)

jw

9

9

/5

4

/5

4

T

ra

n

s

fo

rm

a

c

ja

T

ra

n

s

fo

rm

a

c

ja

H

e

lm

e

rt

a

H

e

lm

e

rt

a

-

-

H

ri

s

to

w

a

H

ri

s

to

w

a

(4

)

(4

)

,)

(

3
)1

(

4

2

η
η

−

=

t

,)

1(

cos
)

2(

2

η+

=

B

,

2

)

(

3

)

3(

2

2

2

η

η

t

−

=

,

2

3

)

4(

2

ηt

=

,

cos

3
)

5(

2

ηt

B

=

,

2

)

1(

cos

)

6(

2

2

2

η+
+

=

t

B

,

2

)

1(

cos

)

7(

2

2

η+

=

t

B

,

3

cos

)

8(

2

B

=

,

6

)

1(

cos

)

9(

2

3

t

B

+

=

,

cos

1

)
11(

4

2

B

η
η

+
−

=

,)

1(

)
12(

4

2

2

η
η

+
−

=

t

,

cos

)

2

1(

)
13(

2

B

t

η

−

=

,

2

1
)
14(

2

2

2

2

η

η

t

t

−
−
+

=

,)

1(

)
15(

2

η

−

=

t

,

2

cos

)
16(

t

B

=

,

cos

3

3
1

)
17(

2

B

t

+

=

,)

1(

)
18(

2

t

t

+
=

,

3

3
2

)
19(

2

t

+

=

,

2

)

1(

cos

)
20(

2

t

B

+

=

,

6

)

1(

cos

)
21(

2

2

t

t

B

+

=

.

6

cos

)
22(

2

2

t

B

=

(C

)

jw

(C

)

jw

1

0

1

0

/5

4

/5

4

T

ra

n

s

fo

rm

a

c

ja

T

ra

n

s

fo

rm

a

c

ja

H

el

m

er

ta

H

el

m

er

ta

-

-

H

ri

st

o

w

a

H

ri

st

o

w

a

(5

)

(5

)

(C

)

jw

(C

)

jw

1

1

1

1

/5

4

/5

4

T

ra

n

s

fo

rm

a

c

ja

T

ra

n

s

fo

rm

a

c

ja

H

el

m

er

ta

H

el

m

er

ta

-

-

H

ri

st

o

w

a

H

ri

st

o

w

a

(6

)

(6

)

(P

rn

n

b

in

g

t

rc

n

n

fo

rm

c

c

ji)

(P

rn

n

b

in

g

t

rc

n

n

fo

rm

c

c

ji)

1

.

D

la

p

u

n

k

tó

w

ł

ą

cz

n

y

ch

o

b

lic

za

m

y

w

y

ra

zy

w

o

ln

e

d

B

i

,d

L

i

(r

ó

ż

n

ic

e

w

sp

ó

łr

zę

d

n

y

ch

p

u

n

k

tó

w

ł

ą

cz

n

y

ch

w

u

k

ła

d

a

ch

p

ie

rw

o

tn

y

m

i

w

tó

rn

y

m

)

i

w

sp

ó

łc

zy

n

n

ik

i

p

rz

y

n

ie

w

ia

d

o

m

y

ch

w

ró

w

n

a

n

ia

ch

(*

),

p

rz

y

c

zy

m

b

i

=

B

i

-B

o

i

l

i

=

L

i

-L

o

,

a

B

o

i

L

o

to

w

sp

ó

łr

zę

d

n

e

b

ie

g

u

n

a

t

ra

n

sf

o

rm

a

cj

i

w

u

k

ła

d

zi

e

p

ie

rw

o

tn

y

m

2

.

Z

ro

zw

ią

za

n

ia

u

k

ła

d

u

ró

w

n

a

ń

(*

)

o

b

lic

za

m

y

n

ie

w

ia

d

o

m

e

d

B

o

,

d

L

o

,

d

p

=

d

s/

s,

d

A

3

.

O

b

lic

za

m

y

b

j

,l

j

–

ró

ż

n

ic

e

w

sp

ó

łr

zę

d

n

y

ch

p

u

n

k

tó

w

d

o

tra

n

sf

o

rm

a

cj

i

i

b

ie

g

u

n

a

t

ra

n

sf

o

rm

a

cj

i

4

.

O

b

lic

za

m

y

w

sp

ó

łc

zy

n

n

ik

i

A

’…

D

”

d

la

k

a

ż

d

e

g

o

„

j”

5

.

W

y

zn

a

cz

a

m

y

d

B

j

,d

L

j

z

ró

w

n

a

ń

(*

)

(C

)

jw

(C

)

jw

1

2

1

2

/5

4

/5

4

T

ra

n

sf

o

rm

ac

je

T

ra

n

sf

o

rm

ac

je

w

sp

w

sp

. p

ro

st

o

k

. p

ro

st

o

k

ą

ą

tn

yc

h

tn

yc

h

(1

)

(1

)

(O

g

(O

g

ó

ó

ln

n

m

o

d

n

ln

t

rc

n

n

fo

rm

c

c

ji)

ln

n

m

o

d

n

ln

t

rc

n

n

fo

rm

c

c

ji)

T

ra

n

s

fo

rm

a

c

ja

i

z

o

m

e

tr

y

c

z

n

a

(a

n

g

.

ri

g

id

b

o

d

y

tr

a

n

sf

o

rm

a

ti

o

n

)

re

a

liz

u

je

sz

ty

w

n

e

r

u

ch

y

:

o

b

ró

t

i

p

rz

e

su

n

ię

ci

e

.

N

ie

p

o

w

o

d

u

je

z

n

ie

k

sz

ta

łc

e

ń

k

ą

tó

w

i

sk

a

li

u

k

ła

d

u

p

ie

rw

o

tn

e

g

o

.

W

ła

ś

ci

w

o

ś

ci

t

ra

n

sfo

rm

a

cj

i

iz

o

m

e

tr

y

cz

n

e

j

b

y

w

a

ją

w

a

ż

n

e

w

z

a

st

o

so

w

a

n

ia

ch

g

e

o

d

e

zy

jn

y

ch

.

P

o

zw

a

la

ją

n

a

w

p

a

so

w

a

n

ie

j

a

k

o

ś

ci

o

w

o

l

e

p

sz

e

j

si

e

ci

(

n

p

.

G

P

S

)

w

s

ta

ry

u

k

ła

d

l

o

k

a

ln

y

,

k

tó

re

g

o

s

k

a

lę

o

k

re

ś

la

n

o

z

a

p

o

m

o

cą

p

o

m

ia

ró

w

lin

io

w

y

ch

.

Z

a

ch

o

w

a

n

ie

n

ie

zm

ie

n

io

n

e

j

sk

a

li

p

o

w

o

d

u

je

j

e

d

n

a

k

w

zr

o

st

o

d

ch

y

łe

k

n

a

p

u

n

k

ta

ch

ł

ą

cz

n

y

ch

i

w

r

e

zu

lt

a

ci

e

r

e

la

ty

w

n

ie

w

ię

k

sz

y

b

łą

d

t

ra

n

sfo

rm

a

cj

i.

O

g

ra

n

ic

za

t

o

s

to

so

w

a

n

ie

t

ra

n

sfo

rm

a

cj

i

iz

o

m

e

tr

y

cz

n

e

j

d

o

n

ie

w

ie

lk

ic

h

o

b

sz

a

ró

w

g

d

zi

e

w

y

m

a

g

a

n

a

j

e

st

b

a

rd

zo

w

y

so

k

a

d

o

k

ła

d

n

o

ś

ć

i

w

y

ra

ż

e

n

ie

w

sp

ó

łr

zę

d

n

y

ch

s

ie

ci

w

i

n

n

y

m

n

iż

ic

h

m

a

ci

e

rz

y

st

y

u

k

ła

d

zi

e

w

sp

ó

łr

zę

d

n

y

ch

.

W

ła

ś

ci

w

o

ś

ci

t

ra

n

sfo

rm

a

cj

i

iz

o

m

e

tr

y

cz

n

e

j

za

w

ę

ż

a

ją

je

j

st

o

so

w

a

n

ie

g

łó

w

n

ie

d

o

p

o

m

ia

ró

w

r

e

a

liz

a

cy

jn

y

ch

i

k

o

n

tr

o

ln

y

ch

o

b

ie

k

tó

w

i

n

ż

y

n

ie

rs

k

ic

h

t

a

k

ic

h

j

a

k

za

p

o

ry

w

o

d

n

e

,

o

b

ie

k

ty

p

rz

e

m

y

sł

o

w

e

,

m

o

st

y

i

tp

.

(C

)

jw

(C

)

jw

1

3

1

3

/5

4

/5

4

T

ra

n

sf

o

rm

ac

je

T

ra

n

sf

o

rm

ac

je

w

sp

w

sp

. p

ro

st

o

k

. p

ro

st

o

k

ą

ą

tn

yc

h

tn

yc

h

(2

)

(2

)

(O

g

(O

g

ó

ó

ln

n

m

o

d

n

ln

t

rc

n

n

fo

rm

c

c

ji)

ln

n

m

o

d

n

ln

t

rc

n

n

fo

rm

c

c

ji)

T

ra

n

s

fo

rm

a

c

ja

p

rz

e

z

p

o

d

o

b

ie

ń

s

tw

o

(l

in

io

w

a

t

ra

n

sf

o

rm

a

cj

a

k

o

n

fo

re

m

n

a

;

a

n

g

.

si

m

ila

ri

ty

tr

a

n

sf

o

rm

a

ti

o

n

)

-

re

a

liz

u

je

p

o

d

o

b

n

ie

j

a

k

t

ra

n

sfo

rm

a

cj

a

iz

o

m

e

tr

y

cz

n

a

s

zt

y

w

n

e

r

u

ch

y

,

o

b

ró

t,

p

rz

e

su

n

ię

ci

e

i

d

o

d

a

tk

o

w

o

p

rz

e

sk

a

lo

w

u

je

(h

o

m

o

te

ti

a

)

w

sp

ó

łr

zę

d

n

e

u

k

ła

d

u

p

ie

rw

o

tn

e

g

o

.

Je

st

t

o

n

a

jb

a

rd

zi

e

j

zn

a

n

a

i

p

o

w

sz

e

ch

n

ie

u

ż

y

w

a

n

a

tr

a

n

sfo

rm

a

cj

a

w

p

ra

k

ty

ce

g

e

o

d

e

zy

jn

e

j.

W

y

n

ik

a

t

o

z

w

ie

rn

o

k

ą

tn

o

ś

ci

t

ra

n

sfo

rm

a

cj

i,

c

o

p

o

w

o

d

o

w

a

ło

st

o

so

w

a

n

ie

j

e

j

w

c

za

sa

ch

k

ie

d

y

p

o

m

ia

ry

k

ą

tó

w

i

k

ie

ru

n

k

ó

w

b

y

ły

n

a

jw

a

ż

n

ie

js

zą

z

m

e

to

d

w

y

zn

a

cz

a

n

ia

p

o

zy

cj

i.

Z

a

st

o

so

w

a

n

ia

t

ra

n

sfo

rm

a

cj

i

w

ie

rn

o

k

ą

tn

e

j

to

p

rz

e

lic

za

n

ie

w

sp

ó

łr

zę

d

n

y

ch

p

ro

st

o

k

ą

tn

y

ch

n

a

n

ie

w

ie

lk

ic

h

o

b

sz

a

ra

ch

i

r

e

la

ty

w

n

ie

n

is

k

ic

h

w

y

m

a

g

a

n

ia

ch

d

o

k

ła

d

n

o

ś

ci

o

w

y

ch

,

k

a

lib

ra

cj

a

z

e

sk

a

n

o

w

a

n

y

ch

o

b

ra

zó

w

m

a

p

i

z

d

ję

ć

lo

tn

ic

zy

ch

,

a

t

a

k

ż

e

b

a

d

a

n

ia

g

e

o

m

e

tr

y

cz

n

y

ch

w

ła

ś

ci

w

o

ś

ci

o

b

ie

k

tó

w

p

rz

e

m

y

sł

o

w

y

ch

i

i

n

ż

y

n

ie

rs

k

ic

h

.

(C

)

jw

(C

)

jw

1

4

1

4

/5

4

/5

4

T

ra

n

sf

o

rm

ac

je

T

ra

n

sf

o

rm

ac

je

w

sp

w

sp

. p

ro

st

o

k

. p

ro

st

o

k

ą

ą

tn

yc

h

tn

yc

h

(3

)

(3

)

(O

g

(O

g

ó

ó

ln

n

m

o

d

n

ln

t

rc

n

n

fo

rm

c

c

ji)

ln

n

m

o

d

n

ln

t

rc

n

n

fo

rm

c

c

ji)

T

ra

n

s

fo

rm

a

c

ja

a

fi

n

ic

z

n

a

(a

n

g

.

g

e

n

e

ra

l

a

ff

in

e

tr

a

n

sf

o

rm

a

ti

o

n

)

w

y

w

o

d

zą

ca

si

ę

z

o

d

w

zo

ro

w

a

ń

rz

u

to

w

y

ch

,

za

ch

o

w

u

je

r

ó

w

n

o

le

g

ło

ś

ć

p

ro

st

y

ch

,

n

ie

za

ch

o

w

u

je

r

ó

w

n

o

ś

ci

k

ą

tó

w

i

z

m

ie

n

ia

s

k

a

lę

k

a

ż

d

e

j

z

o

si

w

sp

ó

łr

zę

d

n

y

ch

.

P

rz

e

k

sz

ta

łc

e

n

ia

a

fi

n

ic

zn

e

p

rz

e

k

sz

ta

łc

a

ją

p

ro

st

e

i

p

ła

sz

cz

y

zn

y

n

a

p

ro

st

e

i

p

ła

sz

cz

y

zn

y

.

N

a

jc

zę

ś

ci

e

j

w

y

k

o

rz

y

st

y

w

a

n

a

p

rz

y

k

a

lib

ra

cj

i

zd

ję

ć

lo

tn

ic

zy

ch

(

o

ri

e

n

ta

cj

a

w

e

w

n

ę

tr

zn

a

)

i

ze

sk

a

n

o

w

a

n

y

ch

a

rk

u

sz

y

m

a

p

.

Ja

k

o

t

ra

n

sfo

rm

a

cj

ę

w

sp

ó

łr

zę

d

n

y

ch

g

e

o

d

e

zy

jn

y

ch

s

to

su

ję

si

ę

m

e

to

d

ę

a

fi

n

ic

zn

ą

d

la

u

k

ła

d

ó

w

o

re

la

ty

w

n

ie

d

u

ż

y

ch

z

n

ie

k

sz

ta

łc

e

n

ia

ch

i

z

m

ie

n

n

y

ch

s

k

a

la

ch

w

o

b

u

k

ie

ru

n

k

a

ch

o

si

w

sp

ó

łr

zę

d

n

y

ch

(

ta

k

i

p

rz

y

p

a

d

e

k

m

o

ż

e

m

y

z

a

o

b

se

rw

o

w

a

ć

n

p

.

w

o

d

w

zo

ro

w

a

n

iu

G

a

u

ss

a

–

K

rü

g

e

ra

).

(C

)

jw

(C

)

jw

1

5

1

5

/5

4

/5

4

T

ra

n

sf

o

rm

ac

je

T

ra

n

sf

o

rm

ac

je

w

sp

w

sp

. p

ro

st

o

k

. p

ro

st

o

k

ą

ą

tn

yc

h

tn

yc

h

(4

)

(4

)

(O

g

(O

g

ó

ó

ln

n

m

o

d

n

ln

t

rc

n

n

fo

rm

c

c

ji)

ln

n

m

o

d

n

ln

t

rc

n

n

fo

rm

c

c

ji)

T

ra

n

s

fo

rm

a

c

ja

p

rz

e

z

p

o

w

in

o

w

a

c

tw

o

(a

n

g

.

o

rt

h

o

g

o

n

a

l

a

ff

in

e

tr

a

n

sf

o

rm

a

ti

o

n

)

-

tr

a

n

sfo

rm

a

cj

a

p

rz

e

z

p

o

w

in

o

w

a

ct

w

o

j

e

st

o

d

m

ia

n

ą

tr

a

n

sfo

rm

a

cj

i

a

fi

n

ic

zn

e

j

i

cz

ę

st

o

b

y

w

a

z

n

ią

m

y

lo

n

a

.

R

ó

ż

n

ic

ą

m

ię

d

zy

tr

a

n

sfo

rm

a

cj

a

m

i

a

fi

n

ic

zn

ą

i

p

rz

e

z

p

o

w

in

o

w

a

ct

w

o

j

e

st

n

ie

zm

ie

n

n

o

ś

ć

k

ą

ta

m

ię

d

zy

o

si

a

m

i

u

k

ła

d

u

p

ie

rw

o

tn

e

g

o

p

o

w

y

k

o

n

a

n

iu

t

ra

n

sf

o

rm

a

cj

i.

W

z

a

st

o

so

w

a

n

iu

d

o

u

k

ła

d

ó

w

p

ro

st

o

k

ą

tn

y

ch

m

o

ż

n

a

w

ię

c

st

w

ie

rd

zi

ć

ż

e

p

rz

e

k

sz

ta

łc

e

n

ie

p

rz

e

z

p

o

w

in

o

w

a

ct

w

o

z

a

ch

o

w

u

je

p

ro

st

o

k

ą

tn

o

ś

ć

u

k

ła

d

u

w

sp

ó

łr

zę

d

n

y

ch

,

p

rz

e

k

sz

ta

łc

e

n

ie

a

fi

n

ic

zn

e

z

a

ś

w

o

g

ó

ln

o

ś

ci

n

ie

z

a

ch

o

w

u

je

te

g

o

w

a

ru

n

k

u

.

T

ra

n

sfo

rm

a

cj

a

p

rz

e

z

p

o

w

in

o

w

a

ct

w

o

r

e

a

liz

u

ję

tr

a

n

sl

a

cj

ę

,

o

b

ró

t

o

b

u

o

si

w

sp

ó

łr

zę

d

n

y

ch

o

t

e

n

s

a

m

k

ą

t

i

ró

ż

n

e

s

k

a

lo

w

a

n

ie

k

a

ż

d

e

j

z

o

si

u

k

ła

d

u

.

(C

)

jw

(C

)

jw

1

6

1

6

/5

4

/5

4

T

ra

n

sf

o

rm

ac

je

T

ra

n

sf

o

rm

ac

je

w

sp

w

sp

. p

ro

st

o

k

. p

ro

st

o

k

ą

ą

tn

yc

h

tn

yc

h

(5

)

(5

)

(K

(K

ą

ą

ty

E

u

ln

rc

i

m

c

c

in

rn

o

b

ro

t

ty

E

u

ln

rc

i

m

c

c

in

rn

o

b

ro

t

ó

ó

w

)

w

)

W

y

ja

ś

n

ie

n

ie

i

st

o

ty

tz

w

.

o

b

ro

tó

w

e

u

le

ro

w

sk

ic

h

(C

)

jw

(C

)

jw

1

7

1

7

/5

4

/5

4

T

ra

n

sf

o

rm

ac

je

T

ra

n

sf

o

rm

ac

je

w

sp

w

sp

. p

ro

st

o

k

. p

ro

st

o

k

ą

ą

tn

yc

h

tn

yc

h

(6

)

(6

)

(K

(K

ą

ą

ty

E

u

ln

rc

i

m

c

c

in

rn

o

b

ro

t

ty

E

u

ln

rc

i

m

c

c

in

rn

o

b

ro

t

ó

ó

w

)

w

)

K

ą

ty

E

u

le

ra

c

h

a

ra

k

te

ry

zu

ją

w

za

je

m

n

e

n

a

ch

y

le

n

ie

u

k

ła

d

ó

w

g

e

o

d

e

zy

jn

y

ch

re

p

re

ze

n

to

w

a

n

y

ch

p

rz

e

z

o

si

e

e

lip

so

id

o

d

n

ie

si

e

n

ia

o

ri

e

n

to

w

a

n

y

ch

k

la

sy

cz

n

ie

a

lb

o

w

zg

lę

d

e

m

ś

re

d

n

ie

g

o

u

k

ła

d

u

z

ie

m

sk

ie

g

o

.

K

ą

ty

E

u

le

ra

o

zn

a

cz

a

ją

k

o

le

jn

e

o

b

ro

ty

j

a

k

ie

t

rz

e

b

a

w

y

k

o

n

a

ć

,

a

b

y

d

o

p

ro

w

a

d

zi

ć

d

o

r

ó

w

n

o

le

g

ło

ś

ci

(

p

o

k

ry

w

a

n

ia

s

ię

)

o

si

d

w

ó

ch

u

k

ła

d

ó

w

.

P

rz

y

jm

u

je

s

ię

zw

y

k

le

k

o

le

jn

o

ść

o

b

ro

tó

w

:

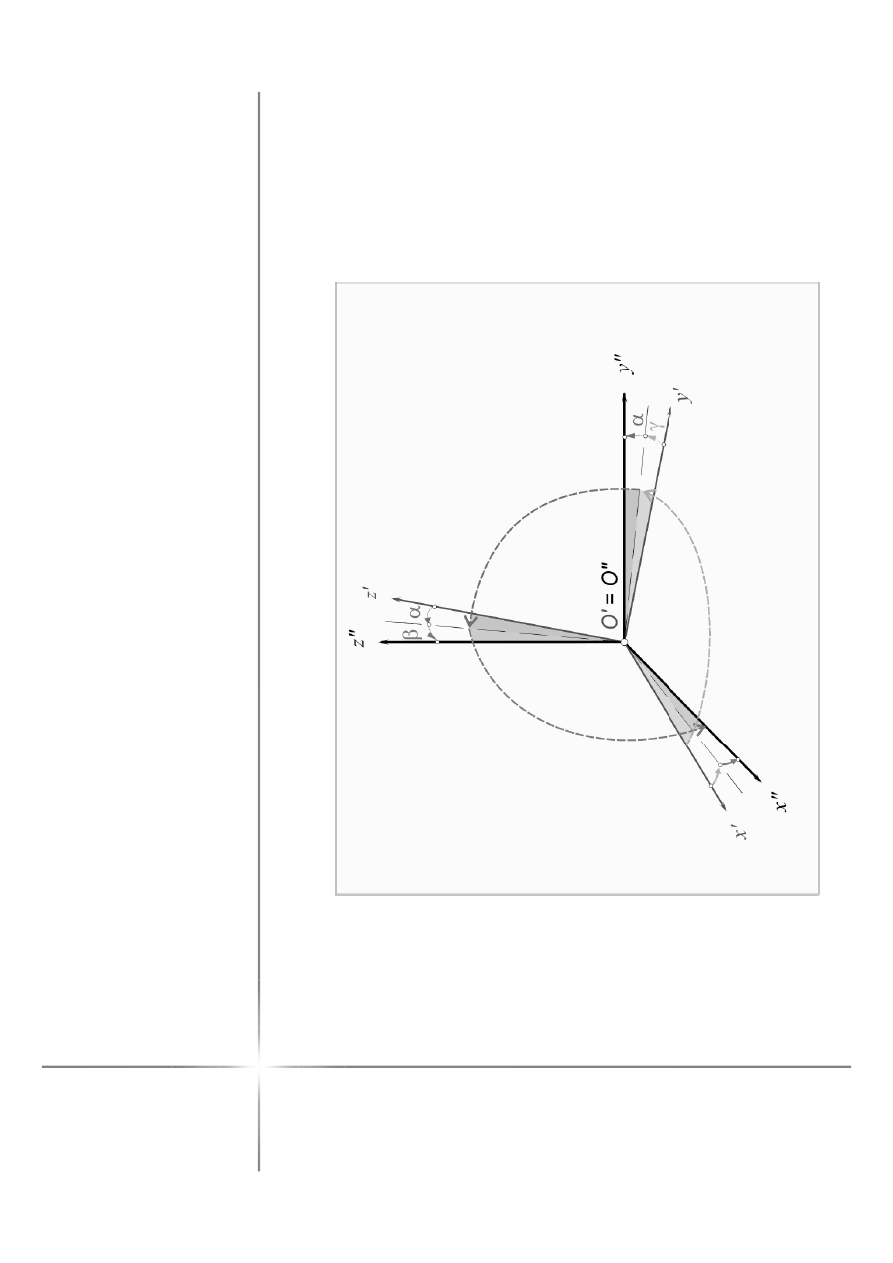
1

)

w

o

k

ó

ł

o

si

z

o

k

ą

t

γ

,

2

)

w

o

k

ó

ł

o

si

x

o

k

ą

t

α

,

3

)

w

o

k

ó

ł

o

si

y

o

k

ą

t

–

β

(-

β

o

zn

a

cz

a

o

b

ró

t

w

l

e

w

o

).

K

ą

ty

t

e

s

ą

n

ie

w

ie

lk

ie

i

r

za

d

k

o

p

rz

e

k

ra

cz

a

ją

1

-2

”

(o

ri

e

n

ta

cj

a

k

la

sy

cz

n

y

ch

u

k

ła

d

ó

w

n

a

p

u

n

k

ta

ch

L

a

p

la

ce

’a

o

d

b

y

w

a

ła

s

ię

m

e

to

d

a

m

i

a

st

ro

n

o

m

ic

zn

y

m

i

p

o

p

rz

e

z

w

y

zn

a

cz

e

n

ie

s

ze

ro

k

o

ś

ci

g

e

o

g

ra

fi

cz

n

e

j-a

st

ro

n

o

m

ic

zn

e

j

i

a

zy

m

u

tu

a

st

ro

n

o

m

ic

zn

e

g

o

)

(C

)

jw

(C

)

jw

1

8

1

8

/5

4

/5

4

T

ra

n

sf

o

rm

ac

je

T

ra

n

sf

o

rm

ac

je

w

sp

w

sp

. p

ro

st

o

k

. p

ro

st

o

k

ą

ą

tn

yc

h

tn

yc

h

(7

)

(7

)

(K

(K

ą

ą

ty

E

u

ln

rc

i

m

c

c

in

rn

o

b

ro

t

ty

E

u

ln

rc

i

m

c

c

in

rn

o

b

ro

t

ó

ó

w

)

w

)

M

a

ci

e

rz

o

b

ro

tó

w

B

m

o

ż

n

a

z

lin

e

a

ry

zo

w

a

ć

z

u

w

a

g

i

n

a

m

a

łe

k

ą

ty

o

b

ro

tu

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)





















=

"

,'

co

s

"

,'

co

s

"

,'

co

s

"

,'

co

s

"

,'

co

s

"

,'

co

s

"

,'

co

s

"

,'

co

s

"

,'

co

s

z
z

y
z

x
z

z
y

y
y

x
y

z
x

y
x

x
x

B

E

le

m

e

n

ta

m

i

m

a

ci

e

rz

y

s

ą

co

si

n

u

sy

k

ą

tó

w

,

ja

k

ie

t

w

o

rz

ą

o

si

e

u

k

ła

d

ó

w

p

ie

rw

o

tn

e

g

o

i

w

tó

rn

e

g

o

.

Je

st

t

o

m

a

ci

e

rz

o

rt

o

g

o

n

a

ln

a

,

a

w

ię

c

B

=

B

T

lu

b

B

x

B

-1

=

E

,

co

m

o

ż

n

a

z

a

p

is

a

ć

w

y

ra

ź

n

ie

w

p

o

st

a

ci

:

∑

=







≠

=







=

=

3

1

,

0

1

,

i

jk

jk

ik

ij

k
j

k
j

gdy

b

b

δ

δ

(C

)

jw

(C

)

jw

1

9

1

9

/5

4

/5

4

T

ra

n

sf

o

rm

ac

je

T

ra

n

sf

o

rm

ac

je

w

sp

w

sp

. p

ro

st

o

k

. p

ro

st

o

k

ą

ą

tn

yc

h

tn

yc

h

(8

)

(8

)

(K

(K

ą

ą

ty

E

u

ln

rc

i

m

c

c

in

rn

o

b

ro

t

ty

E

u

ln

rc

i

m

c

c

in

rn

o

b

ro

t

ó

ó

w

)

w

)

R

o

zp

a

tr

u

ją

c

o

d

p

o

w

ie

d

n

ie

t

ró

jk

ą

ty

n

a

s

fe

rz

e

j

e

d

n

o

st

k

o

w

e

j

w

g

r

y

su

n

k

ó

w

:

S

k

ą

d

z

t

w

ie

rd

ze

n

ia

c

o

si

n

u

só

w

d

o

st

a

je

m

y

n

a

p

rz

e

k

ą

tn

e

j:

1

co

s

co

s

)
,

co

s(

1

co

s

co

s

)
,

co

s(

1

co

s

co

s

)
,

co

s(

≈

=

′′

′

≈

=

′′

′

≈

=

′′

′

β

α

γ

α

γ

β

z
z

y
y

x
x

(C

)

jw

(C

)

jw

2

0

2

0

/5

4

/5

4

T

ra

n

sf

o

rm

ac

je

T

ra

n

sf

o

rm

ac

je

w

sp

w

sp

. p

ro

st

o

k

. p

ro

st

o

k

ą

ą

tn

yc

h

tn

yc

h

(9

)

(9

)

(K

(K

ą

ą

ty

E

u

ln

rc

i

m

c

c

in

rn

o

b

ro

t

ty

E

u

ln

rc

i

m

c

c

in

rn

o

b

ro

t

ó

ó

w

)

w

)

P

o

zo

st

a

łe

w

y

ra

zy

m

a

ci

e

rz

y

d

o

st

a

je

m

y

w

o

p

a

rc

iu

o

r

y

su

n

e

k

:

(

)

(

)

(

)

(

)

(

)

(

)

α
α

α

β

β

β

α

α

α

γ
γ

γ

β
β

β

γ
γ

γ

≅

=
−

=

′′

′

−

≅

−

=
+

=

′′

′

−

≅

−

=
+

=

′′

′

≅

=
−

=

′′

′

≅

=
−

=

′′

′

−

≅

−

=
+

=

′′

′

sin

90

cos
)
,

cos(

sin

90

cos
)
,

cos(

sin

90

cos
)
,

cos(

sin

90

cos
)
,

cos(

sin

90

cos
)
,

cos(

sin

90

cos
)
,

cos(

o

o

o

o

o

o

y
z

x
z

z
y

x
y

z
x

y
x

δ

B

E

B

+
=





















−

−

−

+ 



















=





















−

−

−

=′

0

0

0

1

0

0

0

1

0

0

0

1

1

1

1

α

β

α

γ

β

γ

α

β

α

γ

β

γ

O

st

a

te

cz

n

ie

d

o

st

a

je

m

y

z

lin

e

a

ry

zo

w

a

n

ą

sk

o

ś

n

o

sy

m

e

tr

y

cz

n

ą

i

q

u

a

si

-o

rt

o

g

o

n

a

ln

ą

m

a

ci

e

rz

o

b

ro

tó

w

B

’

p

o

st

a

ci

:

(C

)

jw

(C

)

jw

2

1

2

1

/5

4

/5

4

T

ra

n

sf

o

rm

ac

je

T

ra

n

sf

o

rm

ac

je

w

sp

w

sp

. p

ro

st

o

k

. p

ro

st

o

k

ą

ą

tn

yc

h

tn

yc

h

(1

0

)

(1

0

)

(K

(K

ą

ą

ty

E

u

ln

rc

i

m

c

c

in

rn

o

b

ro

t

ty

E

u

ln

rc

i

m

c

c

in

rn

o

b

ro

t

ó

ó

w

)

w

)

.

10

9.

5

,

10

2.

1
1

10

9

k
j

dla

k
j

dla

jk

jk

≠

⋅

=

=

⋅
+

=

−

−

δ

δ

Z

a

k

ła

d

a

ją

c,

ż

e

α

=β

=γ

<

5

”

n

ie

o

rt

o

g

o

n

a

ln

o

ść

m

a

ci

e

rz

y

B

’

w

y

n

ie

si

e

:

δ

r

r

'

r

'

δ

B

)

(E

r

'

B

'

r

"

+
=

⋅

+
=

⋅
=

T

ra

n

sf

o

rm

a

cj

ę

w

e

k

to

ra

r

’

(w

sp

ó

łr

zę

d

n

y

ch

w

u

k

ła

d

zi

e

p

ie

rw

o

tn

y

m

)

w

y

n

ik

a

ją

cą

je

d

y

n

ie

z

o

b

ro

tó

w

e

u

le

ro

w

sk

ic

h

m

o

ż

n

a

z

a

p

is

a

ć

ja

g

o

s

u

m

ę

w

e

k

to

ra

r

’

i

n

ie

w

ie

lk

ie

g

o

w

e

k

to

ra

δδδδr

t

zn

.:

(C

)

jw

(C

)

jw

2

2

2

2

/5

4

/5

4

Je

ś

li

zn

ie

k

sz

ta

łc

e

n

ia

s

ie

ci

s

ą

ró

ż

n

e

w

k

ie

ru

n

k

a

ch

k

a

ż

d

e

j

z

o

si

,

to

m

a

m

y

d

o

c

zy

n

ie

n

ia

z

p

o

w

in

o

w

a

ct

w

e

m

(

ta

k

a

z

n

ie

k

sz

ta

łc

e

n

ie

s

ie

ci

c

zę

st

o

n

a

zy

w

a

n

e

j

e

st

z

n

ie

k

sz

ta

łc

e

n

ie

m

a

fi

n

ic

zn

y

m

).

M

a

ci

e

rz

s

k

a

li

m

o

ż

n

a

z

a

p

is

a

ć

ja

k

o

s

u

m

ę

m

a

ci

e

rz

y

j

e

d

n

o

st

k

o

w

e

j

E

i

m

a

ci

e

rz

y

z

n

ie

k

sz

ta

łc

e

ń

δδδδM

:

T

ra

n

sf

o

rm

ac

je

T

ra

n

sf

o

rm

ac

je

w

sp

w

sp

. p

ro

st

o

k

. p

ro

st

o

k

ą

ą

tn

yc

h

tn

yc

h

(1

1

)

(1

1

)

(M

c

c

in

rn

n

n

in

k

n

n

tc

(M

c

c

in

rn

n

n

in

k

n

n

tc

ł

ł

c

n

c

n

ń

ń

)

)

ij

ij

ij

s

s

m

κ
+

=

=

1

)
,

,
(

)

,

,

(

z

y

x

z

y

x

diag

gdzie

m

m

m

diag

κ
κ
κ

=

+
=

=

δ

M

δ

M

E

M

S

k

a

la

s

ie

ci

w

y

ra

ż

a

s

to

su

n

e

k

b

o

k

u

s

ie

ci

s

ij

d

o

t

e

g

o

s

a

m

e

g

o

b

o

k

u

w

y

ra

ż

o

n

e

g

o

w

j

e

d

n

o

st

k

a

ch

w

zo

rc

o

w

y

ch

s

ij

,

a

z

n

ie

k

sz

ta

łc

e

n

ie

κ

ij

to

ró

ż

n

ic

a

s

k

a

li

o

d

j

e

d

n

o

ś

ci

:

(C

)

jw

(C

)

jw

2

3

2

3

/5

4

/5

4

T

ra

n

sf

o

rm

ac

je

T

ra

n

sf

o

rm

ac

je

w

sp

w

sp

. p

ro

st

o

k

. p

ro

st

o

k

ą

ą

tn

yc

h

tn

yc

h

(1

2

)

(1

2

)

(M

c

c

in

rn

n

n

in

k

n

n

tc

(M

c

c

in

rn

n

n

in

k

n

n

tc

ł

ł

c

n

c

n

ń

ń

)

)

δ

r

r

'

r

'

δ

M

)

(E

r

'

M

r

"

+
=

⋅

+
=

⋅
=

D

la

t

e

j

sa

m

e

j

sk

a

li

w

zd

łu

ż

w

sz

y

st

k

ic

h

o

si

d

o

st

a

je

m

y

u

p

ro

sz

cz

o

n

ą

p

o

st

a

ć

ró

w

n

a

n

ia

:

O

st

a

te

cz

n

ie

z

m

ia

n

ę

sk

a

li

w

e

k

to

ra

r

’

m

o

ż

n

a

z

a

p

is

a

ć

w

p

o

st

a

ci

:

z

y

x

g

d

zi

e

κ

κ

κ
κ

κ

κ

=
=
=

⋅

+
=

⋅
+
=

'

1

r

r

'

r

'
)

(

r

"

(C

)

jw

(C

)

jw

2

4

2

4

/5

4

/5

4

T

ra

n

sf

o

rm

ac

je

T

ra

n

sf

o

rm

ac

je

w

sp

w

sp

. p

ro

st

o

k

. p

ro

st

o

k

ą

ą

tn

yc

h

tn

yc

h

(1

3

)

(1

3

)

(T

rc

n

n

fo

rm

c

c

jc

c

fi

n

ic

n

n

c

)

(T

rc

n

n

fo

rm

c

c

jc

c

fi

n

ic

n

n

c

)





















=





















=

+

⋅
=

o

o

o

o

o

z

y

x

oraz

a

a

a

a

a

a

a

a

a

gdzie

r

A

r
r

'

A

r

"

33

32

31

23

22

21

13

12

11

O

g

ó

ln

y

p

rz

y

p

a

d

e

k

t

ra

n

sf

o

rm

a

cj

i

a

fi

n

ic

zn

e

j

m

o

ż

n

a

z

a

p

is

a

ć

w

p

o

st

a

ci

:

δ

B

δ

M

δ

B

δ

M

E

δ

B

)

(E

δ

M

)

(E

B

M

A

⋅

+
+

+
=

+
⋅

+
=

⋅
=

(C

)

jw

(C

)

jw

2

5

2

5

/5

4

/5

4

T

ra

n

sf

o

rm

ac

je

T

ra

n

sf

o

rm

ac

je

w

sp

w

sp

. p

ro

st

o

k

. p

ro

st

o

k

ą

ą

tn

yc

h

tn

yc

h

(1

4

)

(1

4

)

(T

rc

n

n

fo

rm

c

c

jc

q

u

c

n

i

(T

rc

n

n

fo

rm

c

c

jc

q

u

c

n

i

-

-

c

fi

n

ic

n

n

c

)

c

fi

n

ic

n

n

c

)

δ

B

δ

M

δ

B

δ

M

E

δ

B

)

(E

δ

M

)

(E

B

M

A

⋅

+
+

+
=

+
⋅

+
=′

⋅
=

P

rz

y

jm

u

ją

c,

ż

e

m

a

ci

e

rz

A

je

st

i

lo

cz

y

n

e

m

m

a

ci

e

rz

y

s

k

a

li

M

i

o

b

ro

tó

w

B

’

d

o

st

a

n

ie

m

y

:

D

la

m

a

ły

ch

k

ą

tó

w

o

b

ro

tu

i

m

a

ły

ch

z

n

ie

k

sz

ta

łc

e

ń

w

i

lo

cz

y

n

ie

m

a

ci

e

rz

y

δδδδM

δδδδB

’

w

y

st

ę

p

u

ją

m

a

łe

I

I-

rz

ę

d

u

κ

ακακακα

, , , , κ

βκβκβκβ

, κ

γ

, κ

γ

, κ

γ

, κ

γ

co

p

o

zw

a

la

p

o

m

in

ą

ć

te

n

sk

ła

d

n

ik

s

u

m

y

i

z

a

p

is

a

ć

za

le

ż

n

o

ść

d

la

t

zw

.

tr

a

n

sf

o

rm

a

cj

i

q

u

a

si

-a

fi

n

ic

zn

e

j:

δ

r

r

'

r

'

δ

A

)

(E

r

"

δ

B

δ

M

A

+
=

⋅

+
=

+

=
δ

(C

)

jw

(C

)

jw

2

6

2

6

/5

4

/5

4

T

ra

n

sf

o

rm

ac

je

T

ra

n

sf

o

rm

ac

je

w

sp

w

sp

. p

ro

st

o

k

. p

ro

st

o

k

ą

ą

tn

yc

h

tn

yc

h

(1

5

)

(1

5

)

(T

rc

n

n

fo

rm

c

c

jc

q

u

c

n

i

(T

rc

n

n

fo

rm

c

c

jc

q

u

c

n

i

-

-

c

fi

n

ic

n

n

c

)

c

fi

n

ic

n

n

c

)

(

)

T

o

r

r

δ

A

T

'

r
T
r

'

r

"

1

'

'

'

'

:

z

y

x

z

y

x

gdzie

o

o

o

z

y

x

=





















−

−

−

=

=

⋅
+
=

κ
α

β

α

κ
γ

β

γ

κ

„P

o

sz

e

rz

e

n

ie

”

m

a

ci

e

rz

y

δδδδA

o

w

e

k

to

r

tr

a

n

sl

a

cj

i

r

o

i

fo

rm

a

ln

e

z

a

p

is

a

n

ie

ta

k

ie

j

m

a

ci

e

rz

y

T

p

o

zw

a

la

n

a

z

w

a

rt

y

z

a

p

is

m

o

d

e

lu

t

ra

n

sf

o

rm

a

cj

i

q

u

a

si

-

a

fi

n

ic

zn

e

j

w

p

o

st

a

ci

:

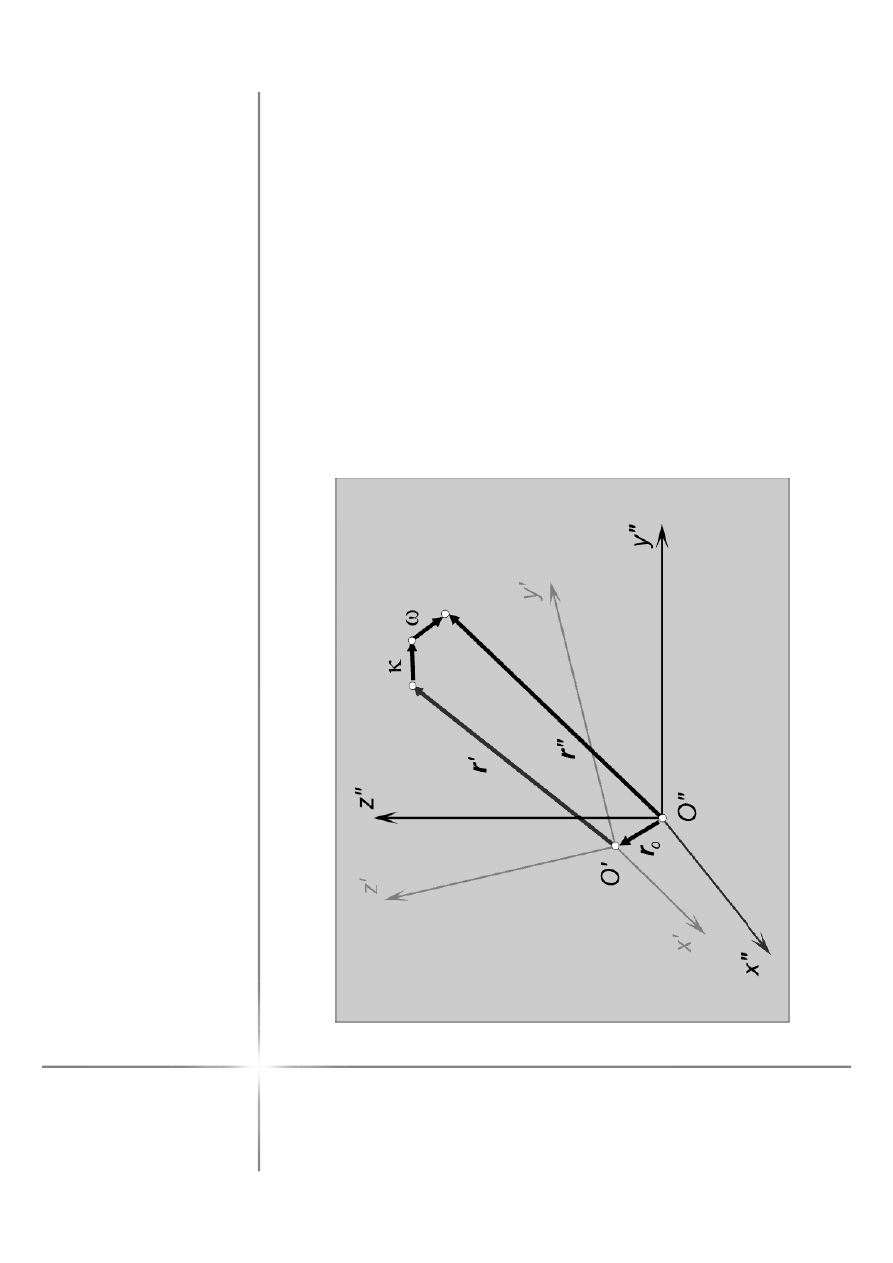
(C

)

jw

(C

)

jw

2

7

2

7

/5

4

/5

4

T

ra

n

sf

o

rm

ac

je

T

ra

n

sf

o

rm

ac

je

w

sp

w

sp

. p

ro

st

o

k

. p

ro

st

o

k

ą

ą

tn

yc

h

tn

yc

h

(1

6

)

(1

6

)

T

ra

n

sf

o

rm

a

cj

a

w

e

k

to

ra

r

’

n

a

w

e

k

to

r

r”

–

p

rz

y

p

a

d

e

k

o

g

ó

ln

y

r

–

w

e

k

to

r

tr

a

n

sl

a

cj

i

κκκκ

–

w

e

k

to

r

„z

n

ie

k

sz

ta

łc

e

ń

”

ωωωω

–

w

e

k

to

r

„o

b

ro

tó

w

”

(C

)

jw

(C

)

jw

2

8

2

8

/5

4

/5

4

T

ra

n

sf

o

rm

ac

je

T

ra

n

sf

o

rm

ac

je

w

sp

w

sp

. p

ro

st

o

k

. p

ro

st

o

k

ą

ą

tn

yc

h

tn

yc

h

(1

7

)

(1

7

)

(T

rc

n

n

fo

rm

c

c

jc

q

u

c

n

i

(T

rc

n

n

fo

rm

c

c

jc

q

u

c

n

i

-

-

c

fi

n

ic

n

n

c

)

c

fi

n

ic

n

n

c

)

)

"
'
(

i

i

i

i

r

r
'

r
T

v

−
+

⋅
=

W

c

e

lu

w

y

zn

a

cz

e

n

ia

p

a

ra

m

e

tr

ó

w

t

ra

n

sf

o

rm

a

cj

i

m

o

ż

n

a

z

a

p

is

a

ć

ró

w

n

a

n

ia

p

o

p

ra

w

e

k

w

p

o

st

a

ci

:

Z

e

w

zg

lę

d

ó

w

p

ra

k

ty

cz

n

y

ch

ł

a

tw

ie

j

ro

zd

zi

e

lić

p

a

ra

m

e

tr

y

t

ra

n

sf

o

rm

a

cj

i

i

w

sp

ó

łc

zy

n

n

ik

i

n

a

d

w

ie

m

a

ci

e

rz

e

R

’

i

t

ta

k

,

ż

e

:

(

)

T

o

z

y

x

i

i

i

i

i

i

i

i

i

i

z

y

x

x

y

z

x

z

y

y

z

x

0

0

'

1

0

0

0

0

0

0

1

0

0

0

0

0

0

1

0

0

0

γ
β
α
κ
κ
κ

=





















−

−

−

=

t

R

)

"
'
(

'

i

i

i

i

r

r

t

R

v

−
+

⋅
=

S

k

ą

d

o

st

a

te

cz

n

ie

:

t
R

r

T

'

i

'

i

=

(C

)

jw

(C

)

jw

2

9

2

9

/5

4

/5

4

T

ra

n

sf

o

rm

ac

je

T

ra

n

sf

o

rm

ac

je

w

sp

w

sp

. p

ro

st

o

k

. p

ro

st

o

k

ą

ą

tn

yc

h

tn

yc

h

(1

8

)

(1

8

)

(T

rc

n

n

fo

rm

c

c

jc

p

rn

n

n

p

o

d

o

b

in

(T

rc

n

n

fo

rm

c

c

jc

p

rn

n

n

p

o

d

o

b

in

ń

ń

n

tw

o

)

n

tw

o

)

(

)

T

r

T

'

r

T
r

'

r

"

1

'

'

'

'

0

0

0

:

)

1(

z

y

x

z

y

x

gdzie

o

o

o

P

P

=





















−

−

−

=

⋅
+

⋅
+
=

α

β

α

γ

β

γ

κ

P

rz

y

jm

u

ją

c

je

d

n

a

k

o

w

ą

sk

a

lę

w

zd

łu

ż

w

sz

y

st

k

ic

h

o

si

κ

x

=

κ

y

=

κ

z

=

κ

d

o

st

a

je

m

y

o

cz

y

w

is

tą

za

le

ż

n

o

ść

o

p

is

u

ją

cą

tr

a

n

sf

o

rm

a

cj

ę

p

rz

e

z

p

o

d

o

b

ie

ń

st

w

o

:

(C

)

jw

(C

)

jw

3

0

3

0

/5

4

/5

4

T

ra

n

sf

o

rm

ac

je

w

sp

T

ra

n

sf

o

rm

ac

je

w

sp

ó

ó

ł

ł

rz

rz

ę

ę

d

n

yc

h

p

d

n

yc

h

p

ł

ł

as

ki

ch

as

ki

ch

(1

)

(1

)

(T

rc

n

n

fo

rm

c

c

jc

c

fi

n

ic

n

n

c

)

(T

rc

n

n

fo

rm

c

c

jc

c

fi

n

ic

n

n

c

)

S

k

re

ś

la

ją

c

tr

ze

ci

w

ie

rs

z

i

tr

ze

ci

ą

k

o

lu

m

n

ę

w

m

a

ci

e

rz

T

tr

a

n

sf

o

rm

a

cj

i

w

sp

ó

łr

zę

d

n

y

ch

p

ro

st

o

k

ą

tn

y

ch

p

rz

e

st

rz

e

n

n

y

ch

(

3

D

)

d

o

st

a

je

m

y

z

a

le

ż

n

o

ś

ci

d

la

t

ra

n

sf

o

rm

a

cj

i

a

fi

n

ic

zn

e

j

n

a

p

ła

sz

cz

y

ź

n

ie

(

2

D

):

(

)

T

r

T

T

'

r
T
r

'

r

"

1

'

'

'

lu

b

:

y

x

y

x

d

c

b

a

y

x

gdzie

o

o

o

o

y

x

=

 



 



=

















−

=

⋅
+
=

κ
γ

γ

κ

D

la

m

ał

yc

h

k

ą

tó

w

γγγγ

D

la

d

o

w

o

ln

yc

h

γγγγ

(C

)

jw

(C

)

jw

3

1

3

1

/5

4

/5

4

T

ra

n

sf

o

rm

ac

je

w

sp

T

ra

n

sf

o

rm

ac

je

w

sp

ó

ó

ł

ł

rz

rz

ę

ę

d

n

yc

h

p

d

n

yc

h

p

ł

ł

as

ki

ch

as

ki

ch

(2

)

(2

)

(T

rc

n

n

fo

rm

c

c

jc

H

n

lm

n

rt

c

)

(T

rc

n

n

fo

rm

c

c

jc

H

n

lm

n

rt

c

)

P

rz

y

jm

u

ją

c

je

d

n

a

k

o

w

ą

sk

a

lę

w

zd

łu

ż

o

si

κ

x

=

κ

y

=

κ

d

o

st

a

je

m

y

z

a

le

ż

n

o

ś

ć

o

p

is

u

ją

cą

tr

a

n

sf

o

rm

a

cj

ę

H

e

lm

e

rt

a

(

p

rz

e

z

p

o

d

o

b

ie

ń

st

w

o

):

(

)

T

r

T

'

r

T

r

'

'

r

T
r

'

r

"

1

'

'

'

co

s

si

n

si

n

co

s

:

)

1(

y

x

y

x

gdzie

o

o

H

H

=

 



 



−

=

⋅
⋅
+
=

⋅

+

⋅
+
=

γ

γ

γ

γ

κ

κ

U

w

a

g

a

!

M

a

ci

e

rz

T

m

o

ż

n

a

w

y

p

ro

w

a

d

zi

ć

z

p

ro

st

y

ch

z

a

le

ż

n

o

ś

ci

g

e

o

m

e

tr

y

cz

n

y

ch

l

u

b

k

o

rz

y

st

a

ją

c

z

m

a

ci

e

rz

y

o

b

ro

tó

w

,

k

tó

re

j

e

le

m

e

n

ta

m

i

są

co

si

n

u

sy

k

ie

ru

n

k

o

w

e

p

o

m

ię

d

zy

o

si

a

m

i

u

k

ła

d

u

p

ie

rw

o

tn

e

g

o

i

w

tó

rn

e

g

o

…

JW1

Slajd 31

JW1

Korzystając z macierzy obrotów trzeba pamiętać, że kąty określene są względem układu pierwotnego!!! W transformacji potrzebujemy relacji

odwrotnej, więc albo należy zmienić znak kątów obrotu, albo przekształcić wyjściowe zależności.

Janusz; 2007-11-04

(C

)

jw

(C

)

jw

3

2

3

2

/5

4

/5

4

S

to

so

w

an

e

m

o

d

el

e

tr

an

sf

o

rm

ac

ji

S

to

so

w

an

e

m

o

d

el

e

tr

an

sf

o

rm

ac

ji

(1

)

(1

)

(7

(7

-

-

p

c

rc

m

n

tr

o

w

c

t

rc

n

n

fo

rm

c

c

jc

p

c

rc

m

n

tr

o

w

c

t

rc

n

n

fo

rm

c

c

jc

B

y

r

B

y

r

š

š

y

y

-

-

W

o

lf

c

W

o

lf

c

)

)

W

o

ry

g

in

a

ln

y

m

p

o

d

e

jś

ci

u

B

u

rš

a

i

W

o

lf

(1

9

6

3

-7

)

za

p

u

n

k

t

w

y

jś

ci

a

d

o

w

y

p

ro

w

a

d

ze

n

ia

m

a

ci

e

rz

y

o

b

ro

tó

w

p

rz

y

ję

li

3

m

a

ci

e

rz

e

o

b

ro

tó

w

e

le

m

e

n

ta

rn

y

ch

k

o

le

jn

o

w

o

k

ó

ł

o

si

z,

x

i

y

:





















−

=





















−

=





















−
=

β

β

β

β

α

α

α

α

γ

γ

γ

γ

cos

0

sin

0

1

0

sin

0

cos

cos

sin

0

sin

cos

0

0

0

1

1

0

0

0

cos

sin

0

sin

cos

y

x

z

R

R

R

(C

)

jw

(C

)

jw

3

3

3

3

/5

4

/5

4

S

to

so

w

an

e

m

o

d

el

e

tr

an

sf

o

rm

ac

ji

S

to

so

w

an

e

m

o

d

el

e

tr

an

sf

o

rm

ac

ji

(2

)

(2

)

(7

(7

-

-

p

c

rc

m

n

tr

o

w

c

t

rc

n

n

fo

rm

c

c

jc

p

c

rc

m

n

tr

o

w

c

t

rc

n

n

fo

rm

c

c

jc

B

y

r

B

y

r

š

š

y

y

-

-

W

o

lf

c

W

o

lf

c

)

)

(

)

z

x

y

R

R

R

R

⋅

⋅

=

γ

β

α

,
,

W

y

n

ik

o

w

ą

m

a

ci

e

rz

o

b

ro

tu

u

zy

sk

u

je

s

ię

p

o

p

rz

e

z

su

p

e

rp

o

zy

cj

ę

(z

ło

ż

e

n

ie

)

o

b

ro

tó

w

e

le

m

e

n

ta

rn

y

ch

:

(

)

o

r
r

R

r

+

⋅

⋅
+
=

'

)

1(
"

,
,

γ

β

α

κ

P

rz

y

jm

u

ją

c

je

d

n

a

k

o

w

ą

sk

a

lę

w

zd

łu

ż

w

sz

y

st

k

ic

h

o

si

κ

x

=

κ

y

=

κ

z

=

κ

d

o

st

a

je

m

y

z

a

le

ż

n

o

ść

o

p

is

u

ją

cą

tr

a

n

sf

o

rm

a

cj

ę

p

rz

e

z

p

o

d

o

b

ie

ń

st

w

o

o

si

e

d

m

iu

p

a

ra

m

e

tr

a

ch

:

T

ra

n

sf

o

rm

a

cj

a

z

w

a

n

a

j

e

st

c

zę

st

o

t

ra

n

sf

o

rm

a

cj

ą

H

e

lm

e

rt

a

w

p

rz

e

st

rz

e

n

i

p

o

p

rz

e

z

a

n

a

lo

g

ię

d

o

t

ra

n

sf

o

rm

a

cj

i

w

sp

ó

łr

zę

d

n

y

ch

p

ła

sk

ic

h

p

o

m

im

o

t

e

g

o

,

ż

e

H

e

lm

e

rt

n

ie

z

a

jm

o

w

a

ł

si

ę

tr

a

n

sf

o

rm

a

cj

a

m

i

3

D

!

L

in

e

a

ry

za

cj

a

m

a

ci

e

rz

y

o

b

ro

tó

w

p

ro

w

a

d

zi

d

o

w

cz

e

ś

n

ie

js

ze

j

fo

rm

y

t

ra

n

sf

o

rm

a

cj

i

p

rz

e

z

p

o

d

o

b

ie

ń

st

w

o

.

(C

)

jw

(C

)

jw

3

4

3

4

/5

4

/5

4

S

to

so

w

an

e

m

o

d

el

e

tr

an

sf

o

rm

ac

ji

S

to

so

w

an

e

m

o

d

el

e

tr

an

sf

o

rm

ac

ji

(3

)

(3

)

R

y

su

n

k

i

p

o

m

o

cn

ic

ze

☺

x”

z”

y”

z’

y’

x’

α

β

γ

z’

y’

x’

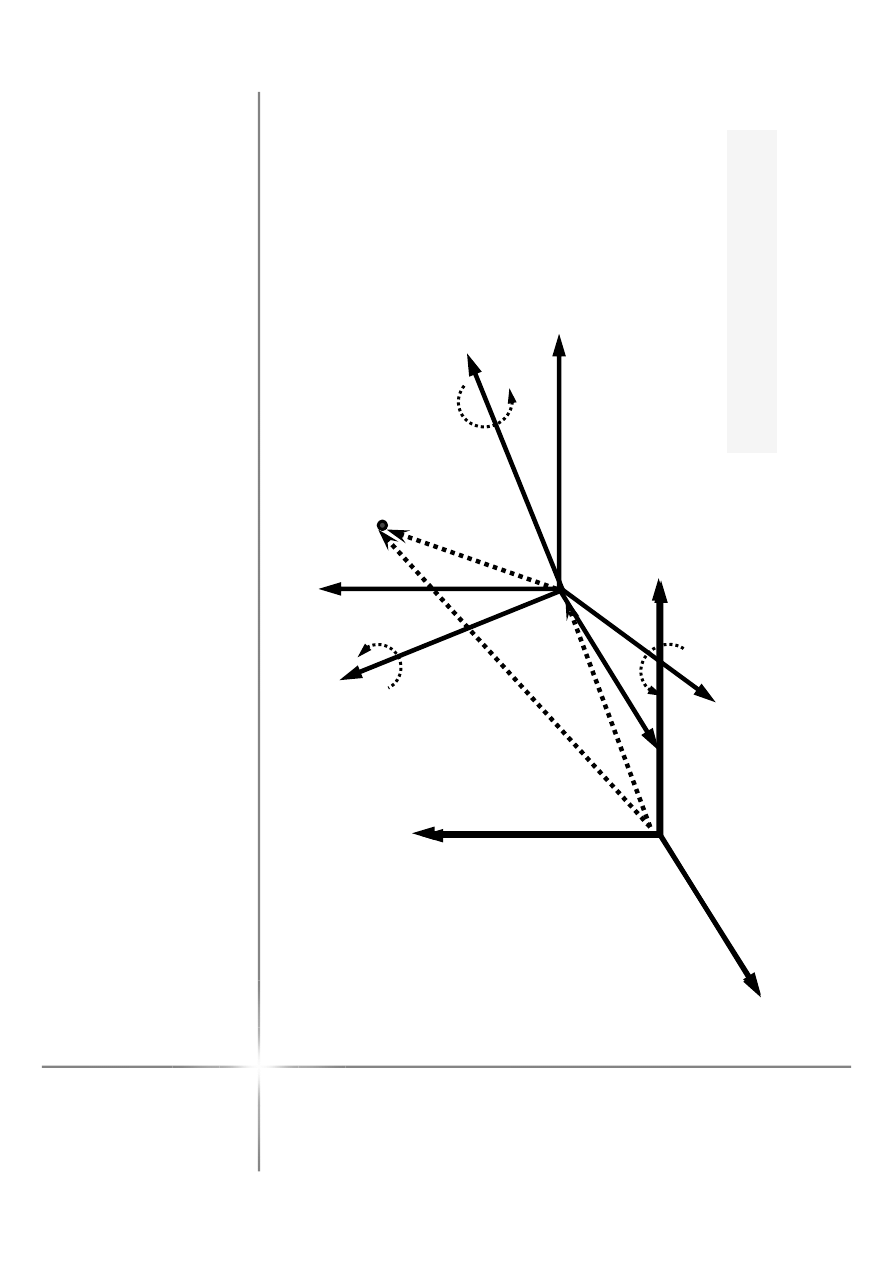
(C

)

jw

(C

)

jw

3

5

3

5

/5

4

/5

4

S

to

so

w

an

e

m

o

d

el

e

tr

an

sf

o

rm

ac

ji

S

to

so

w

an

e

m

o

d

el

e

tr

an

sf

o

rm

ac

ji

(3

)

(3

)

(7

(7

-

-

p

c

rc

m

n

tr

o

w

c

t

rc

n

n

fo

rm

c

c

jc

p

c

rc

m

n

tr

o

w

c

t

rc

n

n

fo

rm

c

c

jc

B

y

r

B

y

r

š

š

y

y

-

-

W

o

lf

c

W

o

lf

c

)

)

x”

z”

y”

z’

y

’

x

’

α

β

γ

P

P

r”

r

o

r’

(

)

o

r
r

R

r

+

⋅

⋅
+
=

'

)

1(
"

,
,

γ

β

α

κ

z’

y’

x’

z’

y’

x’

(C

)

jw

(C

)

jw

3

6

3

6

/5

4

/5

4

S

to

so

w

an

e

m

o

d

el

e

tr

an

sf

o

rm

ac

ji

S

to

so

w

an

e

m

o

d

el

e

tr

an

sf

o

rm

ac

ji

(4

)

(4

)

(T

rc

n

n

fo

rm

c

c

jc

M

o

(T

rc

n

n

fo

rm

c

c

jc

M

o

ł

ł

o

d

n

o

d

n

ń

ń

n

k

in

g

o

)

n

k

in

g

o

)

(

)

o

r
r

R

r

+

∆⋅

⋅
+
=

'

)

1(
"

,
,

γ

β

α

κ

T

ra

n

sf

o

rm

a

cj

a

w

g

i

d

e

i

M

o

ło

d

e

ń

sk

ie

g

o

p

o

le

g

a

n

a

p

rz

e

n

ie

si

e

n

iu

ś

ro

d

k

a

o

b

ro

tó

w

d

o

ś

ro

d

k

a

c

ię

ż

k

o

ś

ci

s

ie

ci

u

k

ła

d

u

w

tó

rn

e

g

o

.

T

a

k

i

za

b

ie

g

p

o

zw

a

la

zw

ię

k

sz

y

ć

d

o

k

ła

d

n

o

ść

w

y

zn

a

cz

e

n

ia

p

a

ra

m

e

tr

ó

w

t

ra

n

sf

o

rm

a

cj

i

w

p

rz

y

p

a

d

k

u

m

a

ły

ch

s

ie

ci

(k

o

rz

y

st

n

ie

js

zy

k

sz

ta

łt

r

o

zw

ią

zy

w

a

n

y

ch

fi

g

u

r

i

st

o

su

n

e

k

w

ie

lk

o

ś

ci

n

ie

w

ia

d

o

m

y

ch

).

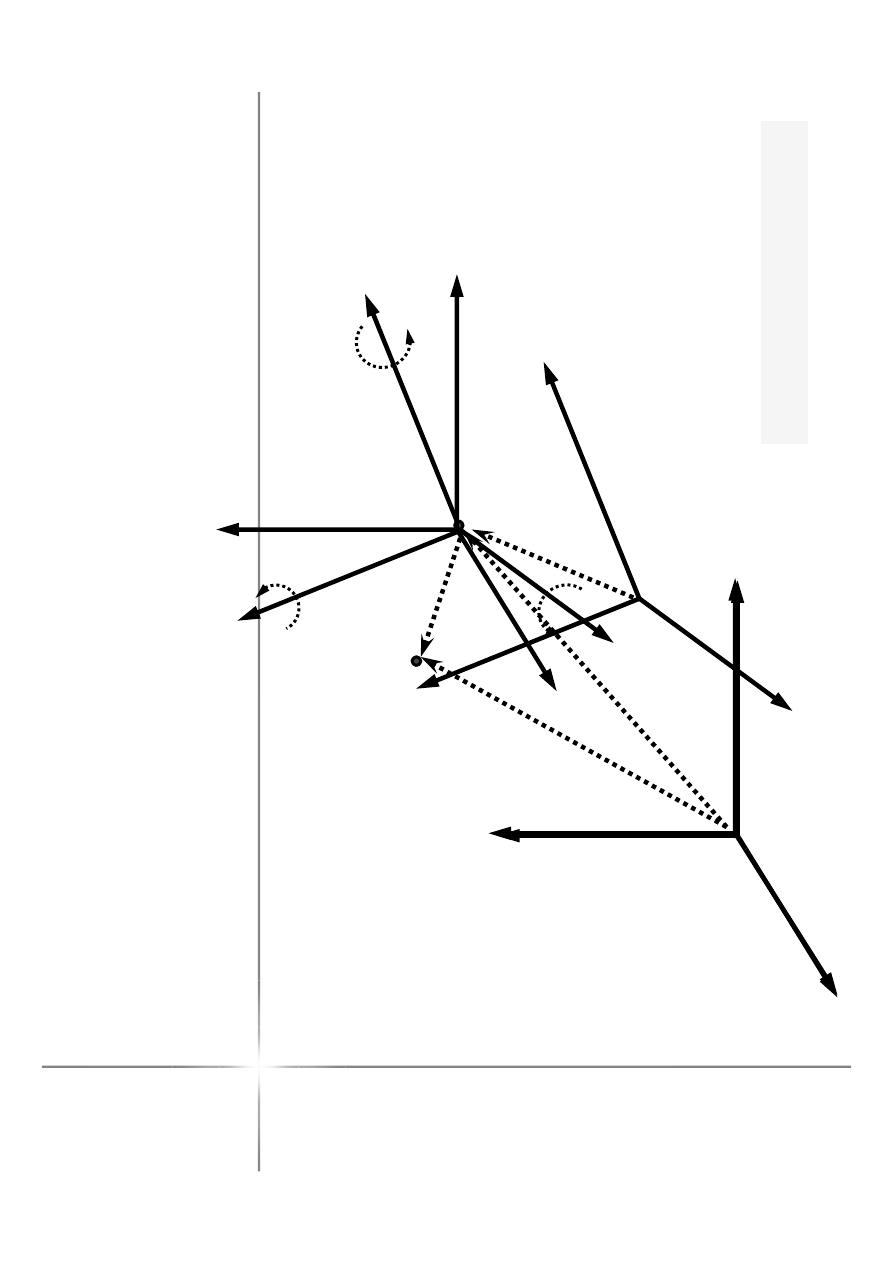
(C

)

jw

(C

)

jw

3

7

3

7

/5

4

/5

4

S

to

so

w

an

e

m

o

d

el

e

tr

an

sf

o

rm

ac

ji

S

to

so

w

an

e

m

o

d

el

e

tr

an

sf

o

rm

ac

ji

(5

)

(5

)

(T

rc

n

n

fo

rm

c

c

jc

M

o

(T

rc

n

n

fo

rm

c

c

jc

M

o

ł

ł

o

d

n

o

d

n

ń

ń

n

k

in

g

o

)

n

k

in

g

o

)

x”

z”

y”

z’

y

’

x

’

α

β

γ

P

P

o

o

r”

r

o

r’

(

)

o

r
r

R

r

+

∆⋅

⋅
+
=

'

)

1(
"

,
,

γ

β

α

κ

z’

y’

x’

z’

y’

x’

∆∆∆∆r

’

P

P

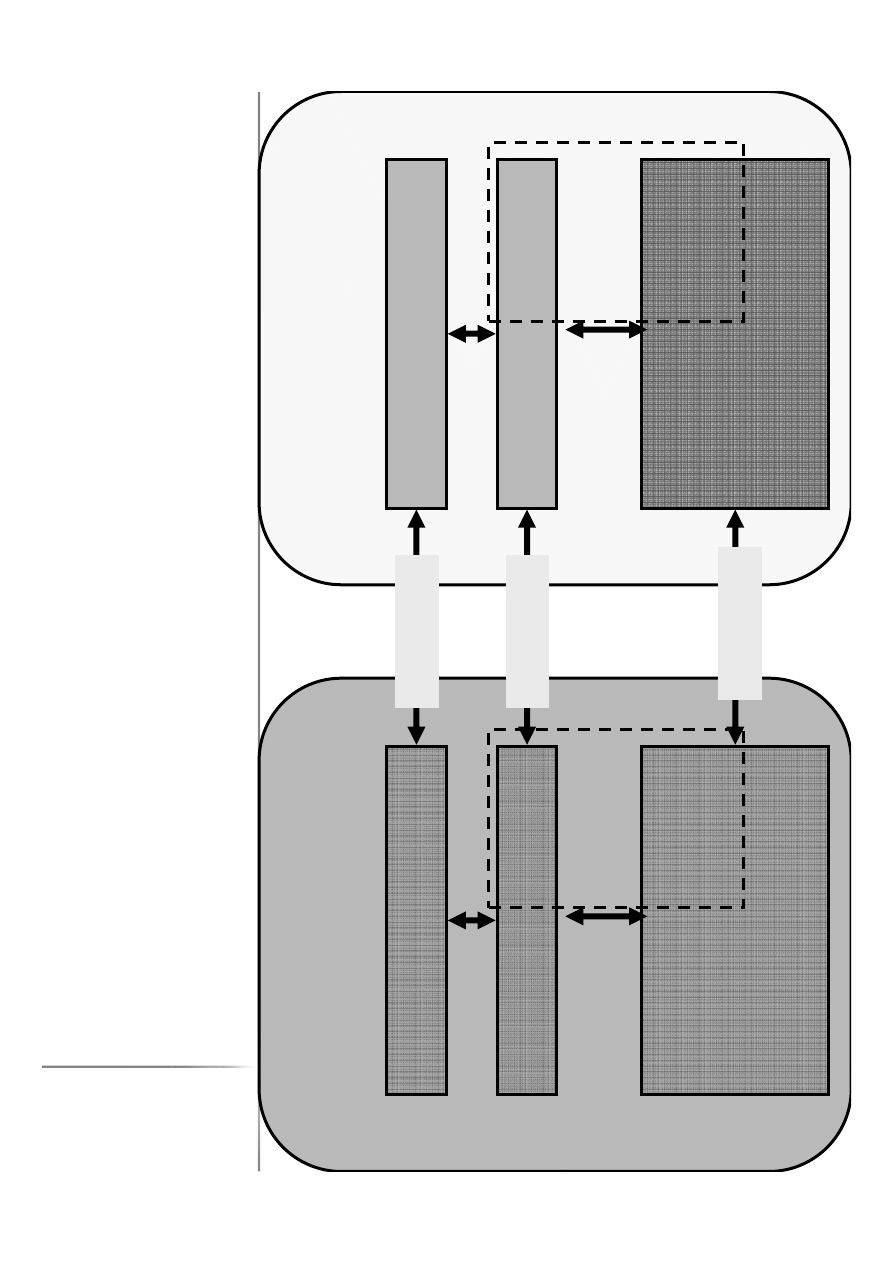
(C

)

jw

(C

)

jw

3

8

3

8

/5

4

/5

4

T

ra

n

sf

o

rm

ac

je

w

sp

T

ra

n

sf

o

rm

ac

je

w

sp

ó

ó

ł

ł

rz

rz

ę

ę

d

n

yc

h

d

n

yc

h

(M

o

(M

o

ż

ż

liw

n

liw

n

„

„

p

rn

n

j

p

rn

n

j

ś

ś

c

ic

c

ic

”

”

tr

c

n

n

fo

rm

c

c

y

jn

n

)

tr

c

n

n

fo

rm

c

c

y

jn

n

)

(x

y

z

)

(B

L

|

H

)

(x

y

|

h

)

(n

p

.

u

k

ła

d

y

2

0

0

0

,

1

9

9

2

,

U

T

M

)

U

K

Ł

A

D

P

I

E

R

W

OT

N

Y

(n

p

. u

kł

ad

E

T

R

F

’8

9,

el

ip

so

id

a

G

R

S

80

/W

G

S

84

)

M

o

d

el

g

eo

id

y

F

o

rm

u

ły

o

d

w

zo

ro

w

aw

cz

e

(x

y

z

)

(B

L

|

H

)

(x

y

|

h

)

(n

p

.

u

k

ła

d

y

1

9

4

2

,

1

9

6

5

,

1

9

8

0

)

U

K

Ł

A

D

W

T

ÓR

N

Y

(n

p

. u

kł

ad

P

u

łk

o

w

o

’4

2,

el

ip

so

id

a

K

ra

so

w

sk

ie

g

o

)

M

o

d

el

g

eo

id

y

F

o

rm

u

ły

o

d

w

zo

ro

w

aw

cz

e

n

p

. m

et

o

d

a

H

ir

vo

n

en

a

n

p

. m

et

o

d

a

H

ir

vo

n

en

a

T

ra

n

sf

T

ra

n

sf

.

3

D

.

3

D

T

ra

n

sf

T

ra

n

sf

.

2

D

.

2

D

T

ra

n

.

H

T

ra

n

.

H

-

-

H

H

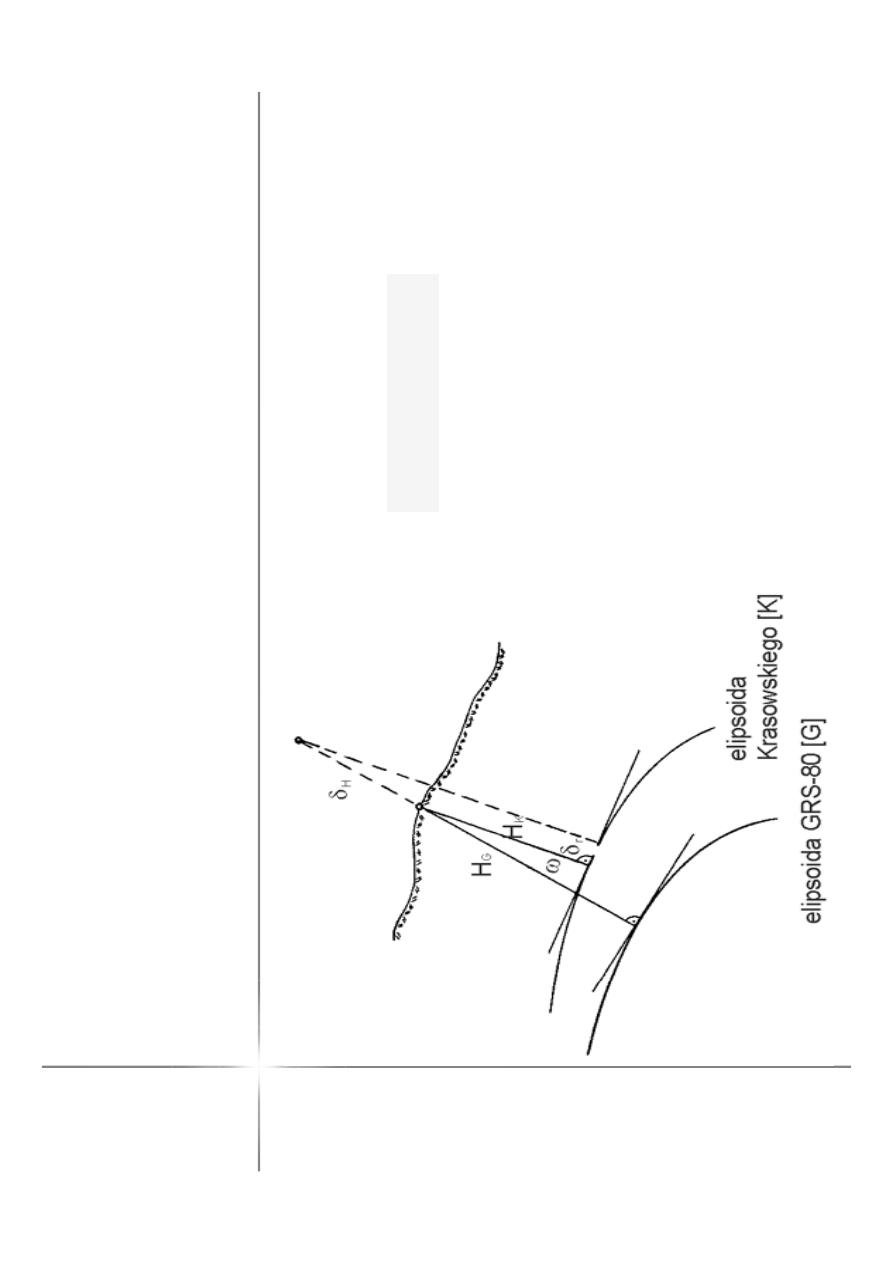
(C

)

jw

(C

)

jw

3

9

3

9

/5

4

/5

4

T

ra

n

sf

o

rm

ac

je

w

sp

T

ra

n

sf

o

rm

ac

je

w

sp

ó

ó

ł

ł

rz

rz

ę

ę

d

n

yc

h

d

n

yc

h

(W

p

(W

p

ł

ł

y

w

b

y

w

b

łę

łę

d

u

w

y

n

o

k

o

d

u

w

y

n

o

k

o

ś

ś

c

i

n

c

w

n

p

c

i

n

c

w

n

p

ó

ó

ł

ł

rn

rn

ę

ę

d

n

n

h

o

ry

n

o

n

tc

ln

n

)

d

n

n

h

o

ry

n

o

n

tc

ln

n

)

W

p

ły

w

b

łę

d

u

o

k

re

ś

le

n

ia

w

y

so

k

o

ś

ci

n

a

w

sp

ó

łr

zę

d

n

e

B

L

m

o

ż

n

a

z

a

p

is

a

ć

:

z

cz

e

g

o

w

y

n

ik

a

,

ż

e

d

la

ω

=

5

”

(m

a

k

sy

m

a

ln

a

r

ó

ż

n

ic

a

o

ri

e

n

ta

cj

i

e

lip

so

id

w

u

k

ła

d

a

ch

1

9

4

2

i

E

T

R

F

8

9

)

b

łą

d

p

o

zi

o

m

y

w

y

n

o

si

2

.4

m

m

n

a

1

0

0

m

!

M

a

o

n

c

h

a

ra

k

te

r

sy

st

e

m

a

ty

cz

n

y

;

w

p

ra

k

ty

cz

n

y

ch

z

a

st

o

so

w

a

n

ia

ch

zw

y

k

le

z

a

n

ie

d

b

y

w

a

ln

y

.

"
/

"

ρ
ω
δ
δ

⋅

≈

H

r

(C

)

jw

(C

)

jw

4

0

4

0

/5

4

/5

4

T

ra

n

sf

o

rm

ac

je

w

sp

T

ra

n

sf

o

rm

ac

je

w

sp

ó

ó

ł

ł

rz

rz

ę

ę

d

n

yc

h

d

n

yc

h

(P

ro

b

ln

m

(P

ro

b

ln

m

„

„

n

u

b

n

ty

tu

c

ji

n

u

b

n

ty

tu

c

ji

”

”

p

c

rc

m

n

tr

p

c

rc

m

n

tr

ó

ó

w

t

rc

n

n

fo

rm

c

c

ji)

w

t

rc

n

n

fo

rm

c

c

ji)

W

o

g

ó

ln

y

m

p

rz

y

p

a

d

k

u

n

ie

j

e

st

z

n

a

n

y

m

o

d

e

l

tr

a

n

sf

o

rm

a

cj

i,

s

tą

d

w

y

zn

a

cz

o

n

e

p

a

ra

m

e

tr

y

(

g

łó

w

n

ie

k

ą

ty

o

b

ro

tó

w

i

z

n

ie

k

sz

ta

łc

e

n

ia

)

n

ie

o

d

p

o

w

ia

d

a

ją

w

a

rt

o

ś

ci

ą

rz

e

cz

y

w

is

ty

m

.

W

y

st

ę

p

u

je

t

zw

.

Z

ja

w

is

k

o

su

b

st

y

tu

cj

i

p

a

ra

m

e

tr

ó

w

t

ra

n

sf

o

rm

a

cj

i.

R

ó

ż

n

y

w

za

je

m

n

y

u

k

ła

d

z

n

ie

k

sz

ta

łc

e

ń

i

o

b

ro

tó

w

d

a

je

t

e

n

s

a

m

su

m

a

ry

cz

n

y

e

fe

k

t

tz

n

.

su

m

a

m

a

ci

e

rz

y

δδδδM

+

δδδδB

je

st

t

a

k

a

s

a

m

a

d

la

ró

ż

n

y

ch

s

k

ła

d

n

ik

ó

w

.

S

u

b

st

y

tu

cj

a

p

a

ra

m

e

tr

ó

w

o

b

n

iż

a

„

w

a

rt

o

ść

p

o

zn

a

w

cz

ą

”

tr

a

n

sf

o

rm

a

cj

i.

D

la

s

ie

ci

l

o

k

a

ln

y

ch

m

a

t

o

z

w

y

k

le

m

a

łe

z

n

a

cz

e

n

ie

;

w

p

rz

y

p

a

d

k

u

s

ie

ci

k

ra

jo

w

y

ch

c

zy

k

o

n

ty

n

e

n

ta

ln

y

ch

m

o

ż

e

j

u

ż

b

y

ć

is

to

tn

e

.

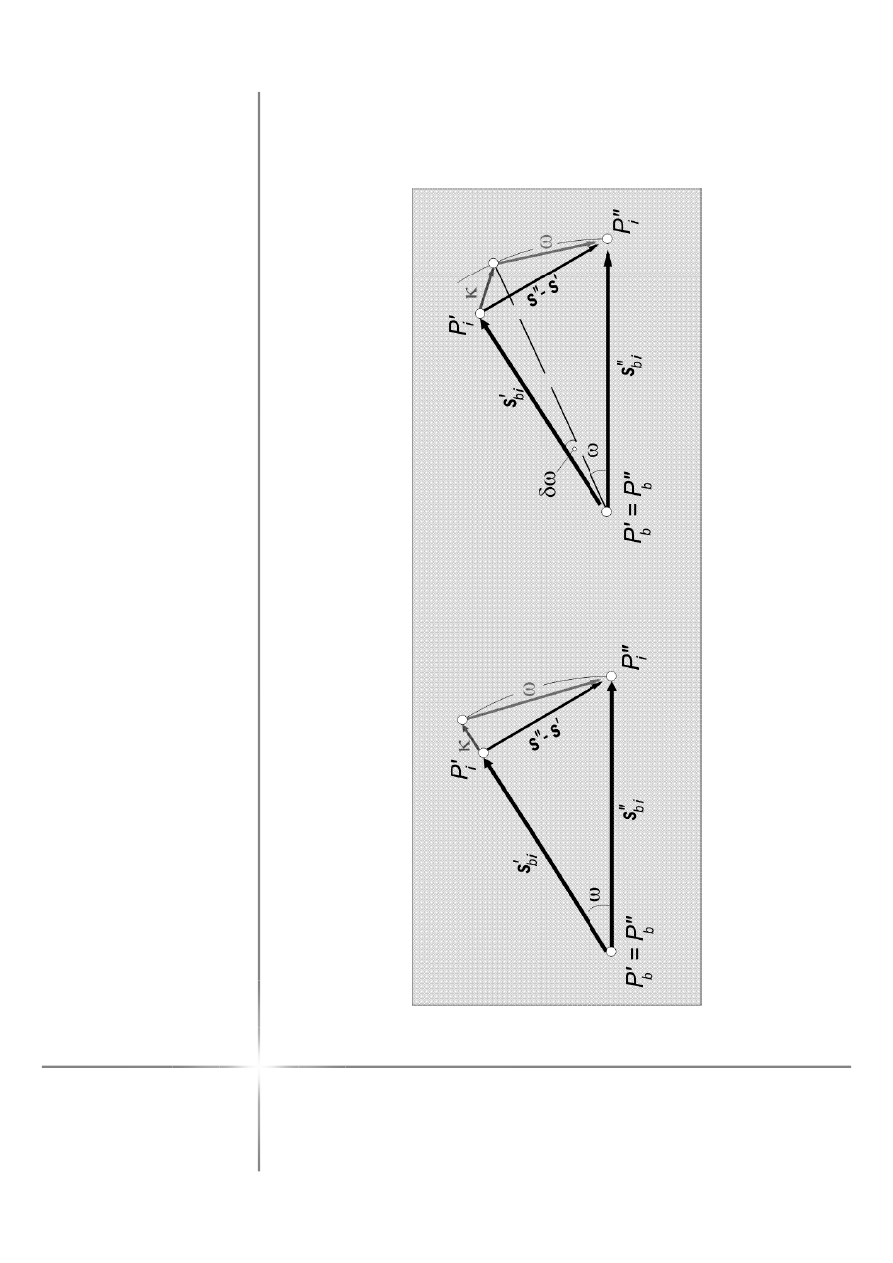
(C

)

jw

(C

)

jw

4

1

4

1

/5

4

/5

4

T

ra

n

sf

o

rm

ac

je

w

sp

T

ra

n

sf

o

rm

ac

je

w

sp

ó

ó

ł

ł

rz

rz

ę

ę

d

n

yc

h

d

n

yc

h

(P

ro

b

ln

m

(P

ro

b

ln

m

„

„

n

u

b

n

ty

tu

c

ji

n

u

b

n

ty

tu

c

ji

”

”

p

c

rc

m

n

tr

p

c

rc

m

n

tr

ó

ó

w

t

rc

n

n

fo

rm

c

c

ji)

w

t

rc

n

n

fo

rm

c

c

ji)

Il

u

st

ra

cj

a

g

ra

fi

cz

n

a

p

ro

b

le

m

u

s

u

b

st

y

tu

cj

i

p

a

ra

m

e

tr

ó

w

t

ra

n

sf

o

rm

a

cj

i

(C

)

jw

(C

)

jw

4

2

4

2

/5

4

/5

4

T

ra

n

sf

o

rm

ac

je

w

sp

T

ra

n

sf

o

rm

ac

je

w

sp

ó

ó

ł

ł

rz

rz

ę

ę

d

n

yc

h

d

n

yc

h

(P

ro

b

ln

m

(P

ro

b

ln

m

„

„

n

u

b

n

ty

tu

c

ji

n

u

b

n

ty

tu

c

ji

”

”

p

c

rc

m

n

tr

p

c

rc

m

n

tr

ó

ó

w

t

rc

n

n

fo

rm

c

c

ji)

w

t

rc

n

n

fo

rm

c

c

ji)

W

c

e

lu

w

y

zn

a

cz

e

n

ia

„

p

ra

w

d

zi

w

y

ch

w

a

rt

o

ś

ci

”

p

a

ra

m

e

tr

ó

w

tr

a

n

sf

o

rm

a

cj

i

(w

r

ze

cz

y

w

is

to

ś

ci

d

o

b

re

g

o

i

ch

p

rz

y

b

liż

e

n

ia

)

n

a

le

ż

y

p

ro

ce

s

e

st

y

m

a

cj

i

p

a

ra

m

e

tr

ó

w

r

o

zb

ić

n

a

t

rz

y

e

ta

p

y

:

1

.

W

y

zn

a

cz

e

n

ie

m

a

ci

e

rz

y

o

b

ro

tó

w

n

a

p

o

d

st

a

w

ie

w

e

k

to

ró

w

je

d

n

o

st

k

o

w

y

ch

w

e

k

to

ró

w

w

o

d

zą

cy

ch

p

u

n

k

tó

w

(

)

"

'

'

,

"

"

"

,

'

'

'

i

i

i

i

i

i

i

i

i

i

e

e

e

δ

B

v

r

r

e

r

r

e

−
+

⋅
=

=

=

(C

)

jw

(C

)

jw

4

3

4

3

/5

4

/5

4

T

ra

n

sf

o

rm

ac

je

w

sp

T

ra

n

sf

o

rm

ac

je

w

sp

ó

ó

ł

ł

rz

rz

ę

ę

d

n

yc

h

d

n

yc

h

(P

ro

b

ln

m

(P

ro

b

ln

m

„

„

n

u

b

n

ty

tu

c

ji

n

u

b

n

ty

tu

c

ji

”

”

p

c

rc

m

n

tr

p

c

rc

m

n

tr

ó

ó

w

t

rc

n

n

fo

rm

c

c

ji)

w

t

rc

n

n

fo

rm

c

c

ji)

i

i

i

bi

bi

bi

1

1

l

s

δ

M

v

s

s

l

+

′

⋅

=

′′

−

′

=

2

.

W

y

zn

a

cz

e

n

ie

m

a

ci

e

rz

y

z

n

ie

k

sz

ta

łc

e

ń

p

rz

y

w

y

k

o

rz

y

st

a

n

iu

w

e

k

to

ró

w

sw

o

b

o

d

n

y

ch

s

b

i

(p

o

w

st

a

ły

ch

p

o

p

o

łą

cz

e

n

iu

p

u

n

k

tó

w

z

t

zw

.

b

ie

g

u

n

e

m

tr

a

n

sfo

rm

a

cj

i)

3

.

W

y

zn

a

cz

e

n

ie

t

ra

n

sl

a

cj

i

(

)

(

)

(

)

i

i

i

o

i

r

r

r

δ

M

δ

B

r

v

′′

−′
+′

⋅

+

+
=

(C

)

jw

(C

)

jw

4

4

4

4

/5

4

/5

4

T

ra

n

sf

o

rm

ac

je

w

sp

T

ra

n

sf

o

rm

ac

je

w

sp

ó

ó

ł

ł

rz

rz

ę

ę

d

n

yc

h

d

n

yc

h

(P

ro

b

ln

m

k

o

rn

k

t

p

o

n

t

(P

ro

b

ln

m

k

o

rn

k

t

p

o

n

t

-

-

tr

c

n

n

fo

rm

c

c

y

jn

y

c

h

)

tr

c

n

n

fo

rm

c

c

y

jn

y

c

h

)

U

w

a

g

i

w

st

ę

p

n

e

z

w

ią

za

n

e

z

p

ro

b

le

m

e

m

k

o

re

k

t:

1

.

M

o

d

e

le

t

ra

n

sfo

rm

a

cj

i

p

o

m

ię

d

zy

d

w

o

m

a

u

k

ła

d

a

m

i

o

d

n

ie

si

e

n

ia

w

y

zn

a

cz

a

n

e

są

w

o

p

a

rc

iu

o

d

w

a

z

b

io

ry

w

sp

ó

łr

zę

d

n

y

ch

p

u

n

k

tó

w

d

o

st

o

so

w

a

n

ia

,

k

tó

re

re

a

liz

u

ją

(p

rz

e

n

o

sz

ą

)

u

k

ła

d

o

d

n

ie

si

e

n

ia

w

t

e

re

n

ie

.

2

.

R

e

a

liz

a

cj

a

e

m

p

ir

y

cz

n

e

g

o

u

k

ła

d

u

o

d

n

ie

si

e

n

ia

(

u

k

ła

d

u

w

sp

ó

łr

zę

d

n

y

ch

)

n

a

d

ro

d

ze

p

ro

ce

su

p

o

m

ia

ro

w

o

-o

b

lic

ze

n

io

w

e

g

o

g

e

n

e

ru

je

m

n

ie

js

ze

l

u

b

w

ię

k

sz

e

ro

zb

ie

ż

n

o

ś

ci

w

s

to

su

n

k

u

d

o

m

o

d

e

lu

m

a

te

m

a

ty

cz

n

e

g

o

(

„i

d

e

a

ln

e

g

o

”)

.

3

.

W

w

ie

lu

p

rz

y

p

a

d

k

a

ch

b

ę

d

zi

e

i

st

n

ia

ła

k

o

n

ie

cz

n

o

ś

ć

je

d

n

o

zn

a

cz

n

y

ch

ro

zs

tr

zy

g

n

ię

ć

(z

a

ch

o

w

a

n

ia

n

ie

zm

ie

n

n

o

ś

ci

w

sp

ó

łr

zę

d

n

y

ch

p

u

n

k

tó

w

w

je

d

n

y

m

z

u

k

ła

d

ó

w

),

k

tó

ra

w

y

m

u

sz

a

s

to

so

w

a

n

ie

p

e

w

n

y

ch

o

p

e

ra

cj

i

k

o

ry

g

u

ją

cy

ch

(

tz

w

.

k

o

re

k

t

p

o

st

-t

ra

n

sfo

rm

a

cy

jn

y

ch

).

(C

)

jw

(C

)

jw

4

5

4

5

/5

4

/5

4

T

ra

n

sf

o

rm

ac

je

w

sp

T

ra

n

sf

o

rm

ac

je

w

sp

ó

ó

ł

ł

rz

rz

ę

ę

d

n

yc

h

d

n

yc

h

(P

ro

b

ln

m

k

o

rn

k

t

p

o

n

t

(P

ro

b

ln

m

k

o

rn

k

t

p

o

n

t

-

-

tr

c

n

n

fo

rm

c

c

y

jn

y

c

h

)

tr

c

n

n

fo

rm

c

c

y

jn

y

c

h

)

P

rz

y

k

ła

d

o

w

y

p

ro

b

le

m

t

o

p

rz

e

lic

ze

n

ie

w

sp

ó

łr

zę

d

n

y

ch

z

u

k

ła

d

u

„

2

0

0

0

”

d

o

u

k

ła

d

u

„

1

9

6

5

”.

M

o

ż

n

a

t

u

w

y

ró

ż

n

ić

2

e

ta

p

y

:

„

2

0

0

0

”

„

1

9

6

5

”

P

rz

e

k

s

z

ta

łc

e

n

ie

m

a

te

m

a

ty

c

z

n

e

P

P

’

P

”

Od

c

h

y

łk

a

(p

u

n

k

t

z

z

a

s

o

b

u

,

a

rc

h

iw

a

ln

y

)

(x

y

|

h

)

2

0

0

0

=

>

(B

L

H

)

G

R

S

8

0

=

>

(x

y

z)

G

R

S

8

0

=

>

(x

y

z)

K

ra

s

=

>

(B

L

H

)

K

ra

s

=

>

(x

y

|

h

)

1

9

6

5

2

.

E

m

p

ir

y

cz

n

y

(e

ta

p

„

w

p

a

so

w

a

n

ia

”

u

zy

sk

a

n

y

ch

w

1

e

ta

p

ie

w

sp

ó

łr

zę

d

n

y

ch

w

u

k

ła

d

e

m

p

ir

y

cz

n

y

)

(x

,y

)

1

9

6

5

=

>

(x

,~

y

)

1

9

6

5

1

.

M

a

te

m

a

ty

cz

n

y

(w

y

k

o

rz

y

st

u

ją

cy

z

n

a

n

e

ś

ci

sł

e

f

o

rm

u

ły

p

rz

e

lic

ze

n

io

w

e

,

tr

a

n

sf

o

rm

a

cy

jn

e

i

o

d

w

zo

ro

w

a

w

cz

e

)

(C

)

jw

(C

)

jw

4

6

4

6

/5

4

/5

4

T

ra

n

sf

o

rm

ac

je

w

sp

T

ra

n

sf

o

rm

ac

je

w

sp

ó

ó

ł

ł

rz

rz

ę

ę

d

n

yc

h

d

n

yc

h

(P

ro

b

ln

m

k

o

rn

k

t

p

o

n

t

(P

ro

b

ln

m

k

o

rn

k

t

p

o

n

t

-

-

tr

c

n

n

fo

rm

c

c

y

jn

y

c

h

)

tr

c

n

n

fo

rm

c

c

y

jn

y

c

h

)

K

o

re

k

ta

l

o

k

a

ln

a

n

ie

j

e

st

k

o

n

ie

cz

n

a

w

p

rz

y

p

a

d

k

u

,

k

ie

d

y

o

d

ch

y

łk

i

n

a

p

u

n

k

ta

ch

ł

ą

cz

n

y

ch

s

ą

n

a

p

o

zi

o

m

ie

b

łę

d

ó

w

i

ch

w

y

zn

a

cz

e

n

ia

.

W

p

rz

e

ci

w

n

y

m

w

y

p

a

d

k

u

w

y

ró

ż

n

ia

s

ię

3

r

o

d

za

je

k

o

re

k

t:

1

.

K

o

re

k

ty

g

lo

b

a

ln

e

o

c

h

a

ra

k

te

rz

e

w

ie

rn

o

k

ą

tn

y

m

(d

la

c

a

łe

j

st

re

fy

,

p

rz

y

d

a

tn

e

p

rz

y

t

ra

n

sf

o

rm

a

cj

i

d

o

b

re

j

ja

k

o

ś

ci

o

w

o

s

ie

ci

n

p

.

G

P

S

d

o

u

k

ła

d

u

l

o

k

a

ln

e

g

o

;

w

p

rz

y

p

a

d

k

u

p

rz

e

jś

ci

a

z

u

k

ła

d

u

2

0

0

0

d

o

1

9

6

5

z

m

n

ie

js

za

o

d

ch

y

łk

i

o

b

lis

k

o

7

0

%

;

w

ie

lo

m

ia

n

y

z

e

sp

o

lo

n

e

d

o

5

s

to

p

n

ia

)

2

.

K

o

re

k

ty

g

lo

b

a

ln

e

o

c

h

a

ra

k

te

rz

e

a

fi

n

ic

zn

y

m

(d

la

c

a

łe

j

st

re

fy

,

re

a

liz

o

w

a

n

e

zw

y

k

le

z

a

p

o

m

o

cą

w

ie

lo

m

ia

n

ó

w

5

-6

s

to

p

n

ia

,

w

p

rz

y

p

a

d

k

u

p

rz

e

jś

ci

a

z

u

k

ła

d

u

2

0

0

0

d

o

1

9

6

5

z

m

n

ie

js

za

o

d

ch

y

łk

i

d

o

p

o

zi

o

m

u

2

-5

c

m

)

3

.

K

o

re

k

ty

l

o

k

a

ln

e

(o

g

ra

n

ic

zo

n

e

d

o

n

ie

w

ie

lk

ie

g

o

o

b

sz

a

ru

o

p

a

rt

e

n

a

z

a

st

o

so

w

a

n

iu

p

ła

sk

ie

j

tr

a

n

sf

o

rm

a

cj

i

H

e

lm

e

rt

a

o

ra

z

k

o

re

k

ty

p

o

st

-t

ra

n

sf

o

rm

a

cy

jn

e

j

H

a

u

sb

ra

n

d

ta

)

(C

)

jw

(C

)

jw

4

7

4

7

/5

4

/5

4

T

ra

n

sf

o

rm

ac

je

w

sp

T

ra

n

sf

o

rm

ac

je

w

sp

ó

ó

ł

ł

rz

rz

ę

ę

d

n

yc

h

d

n

yc

h

(P

ro

b

ln

m

k

o

rn

k

t

p

o

n

t

(P

ro

b

ln

m

k

o

rn

k

t

p

o

n

t

-

-

tr

c

n

n

fo

rm

c

c

y

jn

y

c

h

)

tr

c

n

n

fo

rm

c

c

y

jn

y

c

h

)

P

o

d

su

m

o

w

a

n

ie

s

ta

ty

st

y

cz

n

e

d

o

ty

cz

ą

ce

o

d

ch

y

łe

k

p

o

m

ię

d

zy

m

a

te

m

a

ty

cz

n

y

m

a

e

m

p

ir

y

cz

n

y

m

u

k

ła

d

e

m

„

1

9

6

5

”

(w

g

p

ro

f.

R

.

K

a

d

a

ja

)

0

,5

0

,5

0

,5

0

,5

0

,8

0

,8

0

,0

2

0

,0

2

0

,0

4

0

,0

4

0

,0

4

0

,0

4

0

,0

5

0

,0

5

0

,0

7

0

,0

7

0

,4

5

0

,4

5

5

5

0

,2

0

,2

0

,2

0

,2

0

,5

0

,5

0

,0

3

0

,0

3

0

,0

3

0

,0

3

0

,0

5

0

,0

5

0

,0

3

0

,0

3

0

,1

2

0

,1

2

0

,1

0

0

,1

0

4

4

0

,2

0

,2

0

,3

0

,3

1

,0

1

,0

0

,0

3

0

,0

3

0

,0

4

0

,0

4

0

,0

4

0

,0

4

0

,0

4

0

,0

4

0

,1

8

0

,1

8

0

,2

0

0

,2

0

3

3

0

,2

0

,2

0

,2

0

,2

0

,6

0

,6

0

,0

4

0

,0

4

0

,0

3

0

,0

3

0

,0

5

0

,0

5

0

,0

4

0

,0

4

0

,1

0

0

,1

0

0

,1

9

0

,1

9

2

2

0

,3

0

,3

0

,4

0

,4

0

,6

0

,6

0

,0

5

0

,0

5

0

,0

5

0

,0

5

0

,1

2

0

,1

2

0

,0

9

0

,0

9

0

,1

7

0

,1

7

0

,1

5

0

,1

5

1

1

∆

∆

p

p

∆

∆

p

p

∆

∆

p

p

∆

∆

y

y

∆

∆

x

x

∆

∆

y

y

∆

∆

x

x

∆

∆

y

y

∆

∆

x

x

(A

)

(A

)

(K

)

(K

)

(B

)

(B

)

A

fi

n

ic

zn

a

A

fi

n

ic

zn

a

(A

)

(A

)

K

o

n

fo

re

m

n

a

(

K

)

K

o

n

fo

re

m

n

a

(

K

)

B

e

z

k

o

re

k

ty

(

B

)

B

e

z

k

o

re

k

ty

(

B

)

M

a

k

sy

m

a

ln

e

[

m

]

M

a

k

sy

m

a

ln

e

[

m

]

P

rz

e

ci

P

rz

e

ci

ę

ę

tn

e

[

m

]

tn

e

[

m

]

S

tr

e

fa

S

tr

e

fa

(C

)

jw

(C

)

jw

4

8

4

8

/5

4

/5

4

T

ra

n

sf

o

rm

ac

je

w

sp

T

ra

n

sf

o

rm

ac

je

w

sp

ó

ó

ł

ł

rz

rz

ę

ę

d

n

yc

h

d

n

yc

h

(K

o

rn

k

ty

p

o

n

t

(K

o

rn

k

ty

p

o

n

t

-

-

tr

c

n

n

fo

rm

c

c

y

jn

n

H

c

u

n

b

rc

n

d

tc

)

tr

c

n

n

fo

rm

c

c

y

jn

n

H

c

u

n

b

rc

n

d

tc

)

Z

w

y

k

le

w

w

y

n

ik

u

t

ra

n

sf

o

rm

a

cj

i

w

sp

ó

łr

zę

d

n

e

p

u

n

k

tó

w

ł

ą

cz

n

y

ch

w

u

k

ła

d

zi

e

w

tó

rn

y

m

o

tr

zy

m

u

ją

w

a

rt

o

ś

ci

r

ó

ż

n

ią

ce

s

ię

o

d

w

sp

ó

łr

zę

d

n

y

ch

k

a

ta

lo

g

o

w

y

ch

(a

rc

h

iw

a

ln

y

ch

).

W

c

e

lu

u

n

ik

n

ię

ci

a

t

a

k

ie

j

„d

w

o

is

to

ś

ci

”

w

p

ro

w

a

d

za

s

ię

cz

a

se

m

k

o

re

k

ty

p

o

st

-t

ra

n

sf

o

rm

a

cy

jn

e

H

a

u

sb

ra

n

d

ta

„z

e

ru

ją

ce

”

ró

ż

n

ic

e

w

sp

ó

łr

zę

d

n

y

ch

n

a

p

u

n

k

ta

ch

ł

ą

cz

n

y

ch

,

a

d

la

p

u

n

k

tó

w

tr

a

n

sf

o

rm

o

w

a

n

y

ch

w

p

ro

w

a

d

za

ją

ce

p

o

p

ra

w

k

i

p

o

st

a

ci

:

(

)

(

)

(

)

(

)

∑

∑

∑

∑

=

=

=

=

=

=

n

i

ij

n

i

ij

yi

yj

n

i

ij

n

i

ij

xi

xj

d

d

v

v

d

d

v

v

1

2

1

2

1

2

1

2

/

1

/

/

1

/

g

d

zi

e

:

i=

1

…

n

to

w

sk

a

ź

n

ik

p

u

n

k

tó

w

ł

ą

cz

n

y

ch

a

j

–

w

sk

a

ź

n

ik

p

u

n

k

tó

w

d

o

t

ra

n

sfo

rm

a

cj

i.

(C

)

jw

(C

)

jw

4

9

4

9

/5

4

/5

4

T

ra

n

sf

o

rm

ac

je

w

sp

T

ra

n

sf

o

rm

ac

je

w

sp

ó

ó

ł

ł

rz

rz

ę

ę

d

n

yc

h

d

n

yc

h

(K

o

rn

k

ty

p

o

n

t

(K

o

rn

k

ty

p

o

n

t

-

-

tr

c

n

n

fo

rm

c

c

y

jn

n

H

c

u

n

b

rc

n

d

tc

)

tr

c

n

n

fo

rm

c

c

y

jn

n

H

c

u

n

b

rc

n

d

tc

)

Il

u

st

ra

cj

a

g

ra

fi

cz

n

a

k

o

re

k

t

H

a

u

sb

ra

n

d

ta

…

P

u

n

k

t

d

o

st

o

so

w

a

n

ia

P

u

n

k

t

tr

a

n

sf

o

rm

o

w

a

n

y

W

e

k

to

r

p

o

p

ra

w

e

k

O

d

le

g

ło

ś

ć

o

d

p

u

n

k

tó

w

łą

cz

n

y

ch

(C

)

jw

(C

)

jw

5

0

5

0

/5

4

/5

4

T

ra

n

sf

o

rm

ac

je

w

sp

T

ra

n

sf

o

rm

ac

je

w

sp

ó

ó

ł

ł

rz

rz

ę

ę

d

n

yc

h

d

n

yc

h

(T

rc

n

n

fo

rm

c

c

jn

w

in

lo

m

ic

n

o

w

n

(T

rc

n

n

fo

rm

c

c

jn

w

in

lo

m

ic

n

o

w

n

…

…

)

)

W

p

ra

k

ty

ce

s

to

su

je

s

ię

ta

k

ż

e

t

ra

n

sf

o

rm

a

cj

e

w

y

k

o

rz

y

st

u

ją

ce

w

ie

lo

m

ia

n

y

a

lg

e

b

ra

ic

zn

e

(p

rz

e

k

sz

ta

łc

e

n

ie

a

fi

n

ic

zn

e

)

lu

b

w

ie

lo

m

ia

n

y

z

e

sp

o

lo

n

e

(p

rz

e

k

sz

ta

łc

e

n

ie

w

ie

rn

o

k

ą

tn

e

u

k

ła

d

ó

w

).

D

la

w

ie

lo

m

ia

n

u

a

lg

e

b

ra

ic

zn

e

g

o

m

a

m

y

z

a

le

ż

n

o

ś

ci

p

o

st

a

ci

:

j

n

i

m

j

i

ij

j

n

i

m

j

i

ij

y

x

b

Y

y

x

a

X

⋅
⋅

=

⋅
⋅

=

∑

∑

∑

∑

=

=

=

=

0

0

0

0

g

d

zi

e

:

X

,Y

-

w

sp

ó

łr

zę

d

n

e

p

u

n

k

tó

w

w

u

k

ła

d

zi

e

w

tó

rn

y

m

,

x,

y

-

u

n

o

rm

o

w

a

n

e

w

sp

ó

łr

zę

d

n

e

p

u

n

k

tó

w

w

u

k

ła

d

zi

e

p

ie

rw

o

tn

y

m

t

zn

.

x=

(

x

-

x

o

)*

C

o

ra

z

y=

(

y

–

y

o

)*

C

C

–

p

a

ra

m

e

tr

s

k

a

lu

ją

cy

(

n

p

.

1

/d

m

a

x

),

x

o

,y

o

–

ś

ro

d

e

k

c

ię

ż

k

o

ś

ci

o

b

sz

a

ru

.

(C

)

jw

(C

)

jw

5

1

5

1

/5

4

/5

4

T

ra

n

sf

o

rm

ac

je

w

sp

T

ra

n

sf

o

rm

ac

je

w

sp

ó

ó

ł

ł

rz

rz

ę

ę

d

n

yc

h

d

n

yc

h

(T

rc

n

n

fo

rm

c

c

jn

w

in

lo

m

ic

n

o

w

n

(T

rc

n

n

fo

rm

c

c

jn

w

in

lo

m

ic

n

o

w

n

…

…

)

)

D

la

w

ie

lo

m

ia

n

u

z

e

sp

o

lo

n

e

g

o

za

le

ż

n

o

ś

ci

p

o

st

a

ci

:

)

(

)

(

)

(

)

..

.

(

(

(

..

.

3

2

1

0

2

2

1

0

0

j

j

j

n

n

n

n

n

j

j

c

i

b

yi
x

iY

X

gdzie

⋅

+

=

+
=

+

=

+

⋅

+
⋅

+
⋅

+
=

+
+

+

+
=

=

∑

=

a

z

Z

z
a

a

z

a

z

a

z

a

z
a

z
a

z
a

a

z

Z

g

d

zi

e

:

X

,Y

-

w

sp

ó

łr

zę

d

n

e

p

u

n

k

tó

w

w

u

k

ła

d

zi

e

w

tó

rn

y

m

,

x,

y

-

u

n

o

rm

o

w

a

n

e

w

sp

ó

łr

zę

d

n

e

p

u

n

k

tó

w

w

u

k

ła

d

zi

e

p

ie

rw

o

tn

y

m

t

zn

.

x=

(

x

-

x

o

)*

C

o

ra

z

y=

(

y

–

y

o

)*

C

C

–

p

a

ra

m

e

tr

s

k

a

lu

ją

cy

(

n

p

.

1

/d

m

a

x

),

x

o

,y

o

–

ś

ro

d

e

k

c

ię

ż

k

o

ś

ci

o

b

sz

a

ru

.

(C

)

jw

(C

)

jw

5

2

5

2

/5

4

/5

4

T

ra

n

sf

o

rm

ac

je

w

sp

T

ra

n

sf

o

rm

ac

je

w

sp

ó

ó

ł

ł

rz

rz

ę

ę

d

n

yc

h

d

n

yc

h

(T

rc

n

n

fo

rm

c

c

jn

w

in

lo

m

ic

n

o

w

n

(T

rc

n

n

fo

rm

c

c

jn

w

in

lo

m

ic

n

o

w

n

…

…

)

)

S

to

p

ie

ń

w

ie

lo

m

ia

n

u

z

a

le

ż

y

o

d

w

ie

lk

o

ś

ci

„

ró

ż

n

ic

o

w

y

ch

”

zn

ie

k

sz

ta

łc

e

ń

w

u

k

ła

d

zi

e

p

ie

rw

o

tn

y

m

i

w

tó

rn

y

m

.

W

c

e

lu

o

k

re

ś

le

n

ia

s

to

p

n

ia

w

ie

lo

m

ia

n

u

b

a

d

a

s

ię

zw

y

k

le

i

st

o

tn

o

ść

k

o

le

jn

y

ch

w

sp

ó

łc

zy

n

n

ik

ó

w

w

s

to

su

n

k

u

d

o

ic

h

b

łę

d

ó

w

w

y

zn

a

cz

e

n

ia

,

b

ą

d

ź

st

o

su

ją

c

p

e

w

n

e

t

e

st

y

s

ta

ty

st

y

cz

n

e

(n

p

.

F

-t

e

st

).

O

st

a

te

cz

n

ie

p

rz

y

jm

u

je

s

ię

n

a

jn

iż

sz

y

z

m

o

ż

liw

y

ch

(w

s

e

n

si

e

o

cz

e

k

iw

a

n

e

j

d

o

k

ła

d

n

o

ś

ci

t

ra

n

sf

o

rm

a

cj

i

i/

lu

b

d

o

k

ła

d

n

o

ś

ci

p

u

n

k

tó

w

łą

cz

n

y

ch

)

st

o

p

ie

ń

w

ie

lo

m

ia

n

u

.

C

o

c

ie

k

a

w

e

w

ie

lo

m

ia

n

z

e

sp

o

lo

n

y

I

-g

o

s

to

p

n

ia

o

d

p

o

w

ia

d

a

m

o

d

e

lo

w

i

tr

a

n

sf

o

rm

a

cj

i

p

ła

sk

ie

j

H

e

lm

e

rt

a

!

☺

(C

)

jw

(C

)

jw

5

3

5

3

/5

4

/5

4

C

za

se

m

p

o

tr

ze

b

n

e

s

ą

m

o

d

e

le

t

ra

n

sf

o

rm

a

cj

i

p

o

m

ię

d

zy

u

k

ła

d

a

m

i

w

„o

b

ie

s

tr

o

n

y

”.

P

a

ra

m

e

tr

y

t

ra

n

sf

o

rm

a

cj

i

o

d

w

ro

tn

e

j

m

o

ż

n

a

o

tr

zy

m

a

ć

w

y

zn

a

cz

a

ją

c

je

n

a

n

o

w

o

w

p

ro

ce

d

u

rz

e

e

st

y

m

a

cj

i

p

a

ra

m

e

tr

ó

w

tr

a

n

sf

o

rm

a

cj

i

p

o

z

a

m

ia

n

ie

u

k

ła

d

ó

w

p

ie

rw

o

tn

e

g

o

i

w

tó

rn

e

g

o

(c

za

se

m

ja

k

d

la

t

ra

n

sfo

rm

a

cj

i

M

o

ło

d

e

ń

sk

ie

g

o

c

zy

w

ie

lo

m

ia

n

o

w

y

ch

t

o

j

e

d

y

n

y

s

p

o

só

b

).

M

o

ż

n

a

t

e

ż

„o

d

w

ró

ci

ć

”

ró

w

n

a

n

ie

p

ie

rw

o

tn

e

ta

k

,

a

b

y

w

y

ra

zi

ć

w

e

k

to

r

w

sp

ó

łr

zę

d

n

y

ch

w

u

k

ła

d

zi

e

p

ie

rw

o

tn

y

m

w

f

u

n

k

cj

i

w

e

k

to

ra

w

u

k

ła

d

zi

e

w

tó

rn

y

m

(t

a

k

i

sp

o

só

b

m

o

ż

liw

y

j

e

st

n

p

.

w

p

rz

y

p

a

d

k

u

t

ra

n

sfo

rm

a

cj

i

a

fi

n

ic

zn

e

j

cz

y

B

u

rs

y

-W

o

lfa

).

T

ra

n

sf

o

rm

ac

je

w

sp

T

ra

n

sf

o

rm

ac

je

w

sp

ó

ó

ł

ł

rz

rz

ę

ę

d

n

yc

h

d

n

yc

h

(T

rc

n

n

fo

rm

c

c

jc

(T

rc

n

n

fo

rm

c

c

jc

„

„

o

d

w

ro

tn

c

o

d

w

ro

tn

c

”…

”…

)

)

(

)

o

r
r

R

r

+

⋅

⋅
+
=

'

)

1(
"

,
,

γ

β

α

κ

(

)

)

"

(

)

1(

1

'

1

,
,

o

r

r

R

r

−
⋅

⋅

+

=

−

γ

β

α

κ

o

r
r

'

A

r

"

+

⋅
=

)

(

'

1

o

r
r

'

A

r

−
⋅

=

−

(C

)

jw

(C

)

jw

5

4

5

4

/5

4

/5

4

T

ra

n

sf

o

rm

ac

je

w

sp

T

ra

n

sf

o

rm

ac

je

w

sp

ó

ó

ł

ł

rz

rz

ę

ę

d

n

yc

h

d

n

yc

h

()

()

O

t

ra

n

sf

o

rm

a

cj

a

ch

t

o

n

a

r

a

zi

e

t

y

le

…

☺