1
08-06-04
Konstrukcje metalowe - Wykład 11
1
Belki jedno- i dwukierunkowo zginane
KONSTRUKCJE METALOWE
08-06-04
Konstrukcje metalowe - Wykład 11
2
PLAN WYKŁADU
PRZYKŁADY BELEK
PRZEKROJE
OBCIĄŻENIA
SCHEMATY STATYCZNE
ROZPIĘTOŚĆ OBLICZENIOWA
SIŁY I MOMENTY PRZEKROJOWE
SGN - NOŚNOŚCI PRZEKROJOWE
ZWICHRZENIE
SGN - NOŚNOŚCI ELEMENTÓW
SGU - UGIĘCIA
SGU - DRGANIA
08-06-04
Konstrukcje metalowe - Wykład 11
3
PRZYKŁADY BELEK
Źródło [8]
08-06-04
Konstrukcje metalowe - Wykład 11
4
PRZYKŁADY BELEK
08-06-04
Konstrukcje metalowe - Wykład 11
5
PRZYKŁADY BELEK
Źródło [8]
08-06-04
Konstrukcje metalowe - Wykład 11
6
PRZYKŁADY BELEK
Źródło [8]
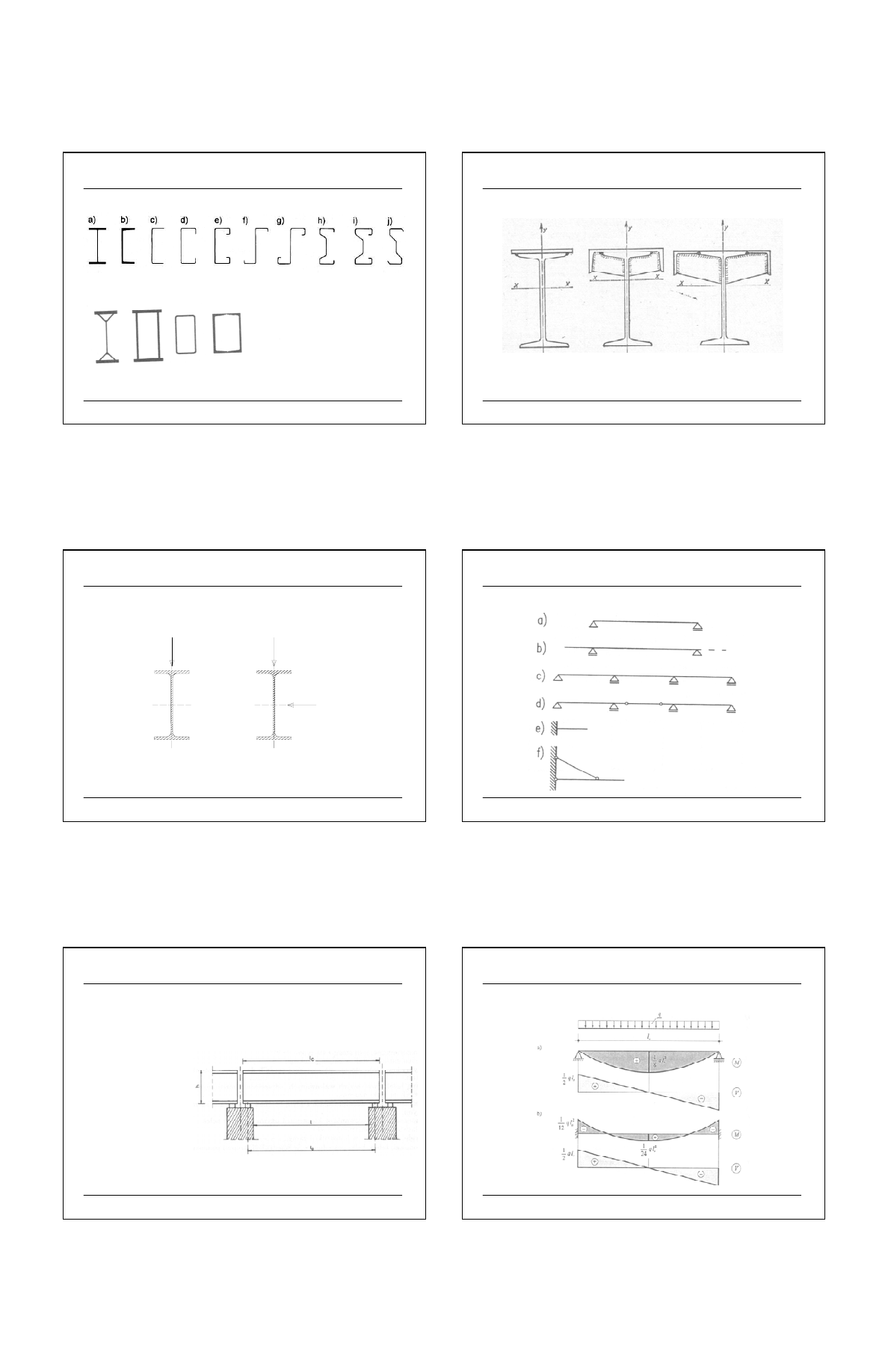
2
08-06-04
Konstrukcje metalowe - Wykład 11
7
PRZEKROJE
Źródło [4]
Źródło [5]
08-06-04
Konstrukcje metalowe - Wykład 11
8
Źródło [6]
PRZEKROJE
08-06-04
Konstrukcje metalowe - Wykład 11
9
OBCIĄŻENIA
BELKI JEDNO- I DWUKIERUNKOWO ZGINANE
q
q
q
y
x
08-06-04
Konstrukcje metalowe - Wykład 11
10
SCHEMATY STATYCZNE
SCHEMATY STATYCZNE BELEK
Źródło [5]
08-06-04
Konstrukcje metalowe - Wykład 11
11
ROZPIĘTOŚĆ OBLICZENIOWA
Rozpiętość obliczeniową belek l
0
należy przyjmować równą osiowemu
rozstawowi podpór (łożysk), a przy oparciu powierzchniowym lub
zamocowaniu w ścianie równą:
- belki obustronnie podparte lub
zamocowane
- belki wspornikowe lub skrajne
belki ciągłe
0
1,05
l
l
=
⋅
0
1,025
l
l
=
⋅
przy czym
0
0,5
l
l
h
≥ +
⋅
Źródło [4]
08-06-04
Konstrukcje metalowe - Wykład 11
12
SIŁY I MOMENTY PRZEKROJOWE
BELKI JEDNOPRZĘSŁOWE
Źródło [1]
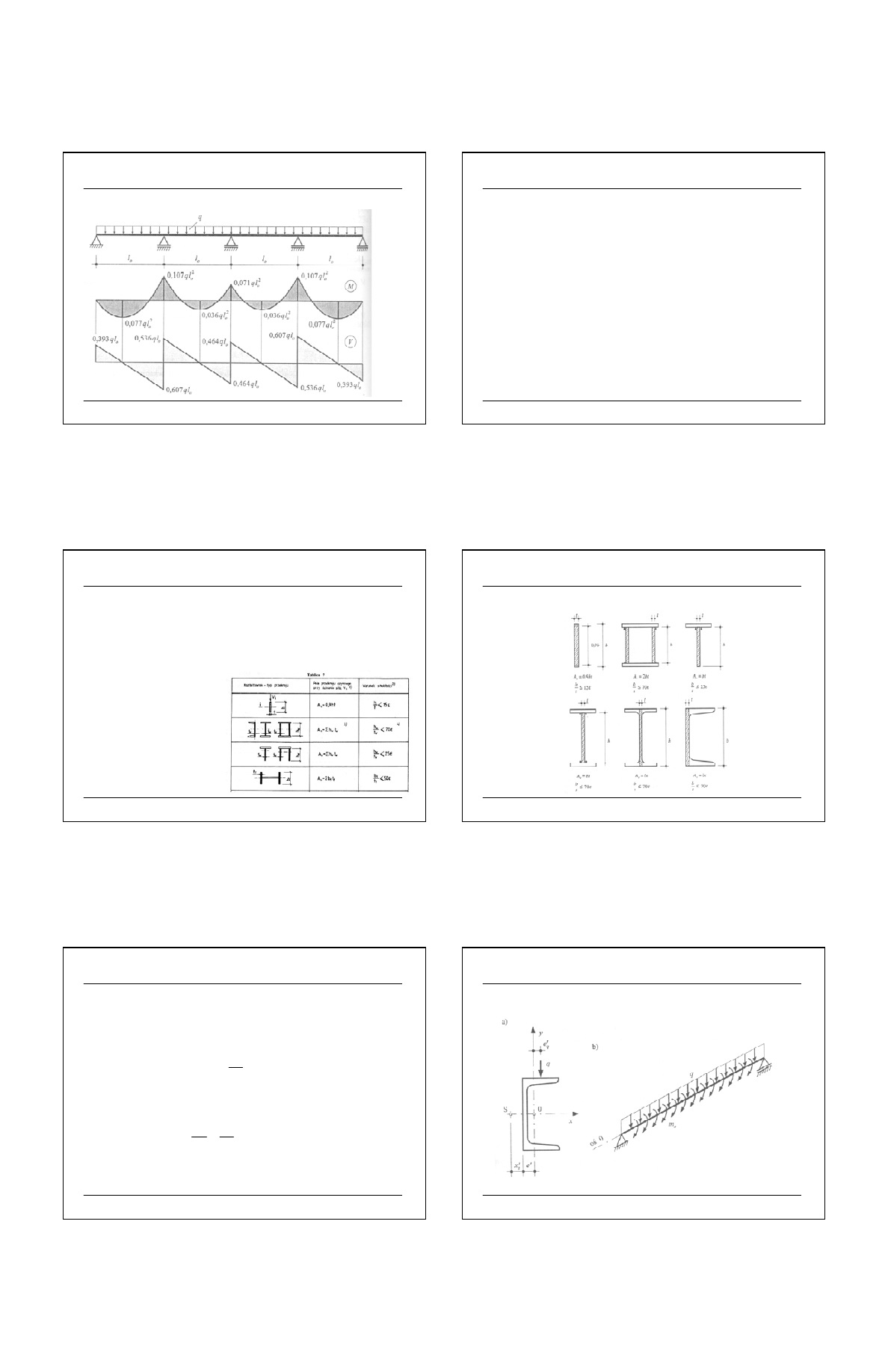
3
08-06-04
Konstrukcje metalowe - Wykład 11
13
SIŁY I MOMENTY PRZEKROJOWE
BELKI WIELOPRZĘSŁOWE
Źródło [1]
08-06-04
Konstrukcje metalowe - Wykład 11
14
SGN - NOŚNOŚCI PRZEKROJOWE
NOŚNOŚĆ PRZEKROJU ZGINANEGO
R
p
d
M
W f
α
=
⋅ ⋅
(42)
R
c
d
M
W
f
ψ
= ⋅
⋅
,
[1
(
1)]
c
t
R
d
p
W
W
W
M
W f
ψ α
>
=
=
⋅
⋅ + ⋅
−
(43)
gdy
Klasa 1 i 2
Klasa 3 i 4
gdzie:
α
p
- obliczeniowy współczynnik rezerwy plastycznej przekroju wg zał. 4
ψ
- współczynnik redukcyjny
W (W
c
, W
t
) - wskaźnik wytrzymałości (krawędzi ściskanej, rozciąganej)
08-06-04
Konstrukcje metalowe - Wykład 11
15
NOŚNOŚĆ PRZEKROJU ŚCINANEGO
0,58
R
pV
V
d
V
A
f
ϕ
=
⋅
⋅
⋅
(16)
gdzie:
ϕ
pV
- współczynnik niestateczności przy ścinaniu
A
V
- pole przekroju czynnego
przy ścinaniu wg Tabl. 7
SGN - NOŚNOŚCI PRZEKROJOWE
Źródło [7]
08-06-04
Konstrukcje metalowe - Wykład 11
16
SGN - NOŚNOŚCI PRZEKROJOWE
POLE PRZEKROJU CZYNNEGO PRZY ŚCINANIU (A
V
)
Źródło [1]
08-06-04
Konstrukcje metalowe - Wykład 11
17
NOŚNOŚĆ PRZEKROJU ZGINANEGO Z UWZGLĘDNIENIEM
ŚCINANIA
2
,
1,1 0,3
R V
R
R
V
M
M
V
⎡
⎤
⎛
⎞
⎢
⎥
=
⋅
−
⋅⎜ ⎟
⎢
⎥
⎝
⎠
⎣
⎦
(45)
Przekroje bisymetryczne dwuteowe klasy 1 i 2 zginane względem osi
największej wytrzymałości, V > V
0
= 0,6 V
R
2
,
1
R V
R
V
R
J
V
M
M
J
V
⎡
⎤
⎛
⎞
⎢
⎥
=
⋅ −
⋅⎜ ⎟
⎢
⎥
⎝
⎠
⎣
⎦
(46)
Pozostałe przypadki, V > V
0
= 0,3 V
R
gdzie:
J
V
- moment bezwładności części przekroju czynnej przy ścinaniu (wg Tabl. 7) względem
osi obojętnej,
J - moment bezwładności całego przekroju
SGN - NOŚNOŚCI PRZEKROJOWE
08-06-04
Konstrukcje metalowe - Wykład 11
18
NOŚNOŚĆ PRZEKROJU ZGINANEGO CEOWEGO
SGN - NOŚNOŚCI PRZEKROJOWE
Źródło [1]
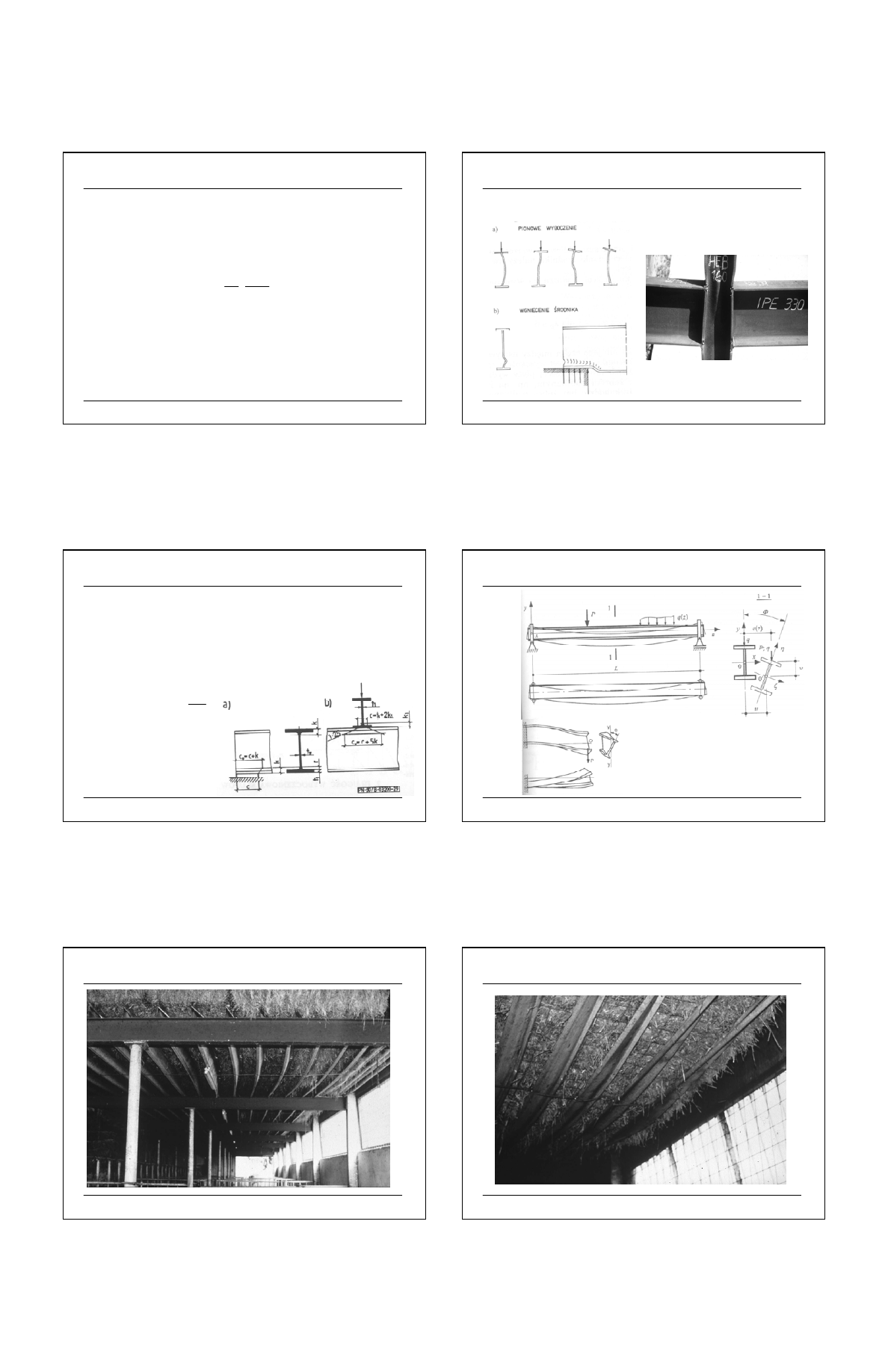
4
08-06-04
Konstrukcje metalowe - Wykład 11
19
NOŚNOŚĆ PRZEKROJU ZGINANEGO CEOWEGO
W przypadku pojedynczych ceowników walcowanych, zginanych
w płaszczyźnie środnika lub do niej równoległej, wpływ drugorzędnego
skręcania można uwzględnić w sposób przybliżony przyjmując M
R, red
.
2
,
0,85
w
R red
d
R
f
e t
V
M
W f
V
b t
⎡
⎤
⎛
⎞
⋅
⎢
⎥
=
⋅
⋅
−
⋅
⎜
⎟
⎜
⎟
⋅
⎢
⎥
⎝
⎠
⎣
⎦
(44)
gdzie:
V - siła poprzeczna w rozpatrywanym przekroju,
V
R
- nośność obliczeniowa przekroju przy ścinaniu,
e - mimośród obciążenia poprzecznego (płaszczyzny zginania),
względem środka ścinania przekroju, przy czym e < b ,
t
w
- grubość środnika,
b, t
f
- szerokość i średnia grubość półki.
SGN - NOŚNOŚCI PRZEKROJOWE
08-06-04
Konstrukcje metalowe - Wykład 11
20
NOŚNOŚĆ ŚRODNIKA BELKI WALCOWANEJ POD OBCIĄŻENIEM
SKUPIONYM
SGN - NOŚNOŚCI PRZEKROJOWE
Źródło [8]
Źródło [4]
08-06-04
Konstrukcje metalowe - Wykład 11
21
NOŚNOŚĆ ŚRODNIKA BELKI WALCOWANEJ POD OBCIĄŻENIEM
SKUPIONYM
,
0
R w
w
c
d
P
P
c t
f
η
≤
= ⋅ ⋅ ⋅
(98)
gdzie:
η
c
- współczynnik redukcyjny, który dla wynosi:
1, 25 0,5
c
c
d
f
σ
η
=
−
⋅
0,5
d
c
d
f
f
σ
⋅
<
≤
(23)
σ
c
- naprężenia ściskające
w środniku skierowane
wzdłuż styku z pasem
SGN - NOŚNOŚCI PRZEKROJOWE
Źródło [7]
08-06-04
Konstrukcje metalowe - Wykład 11
22
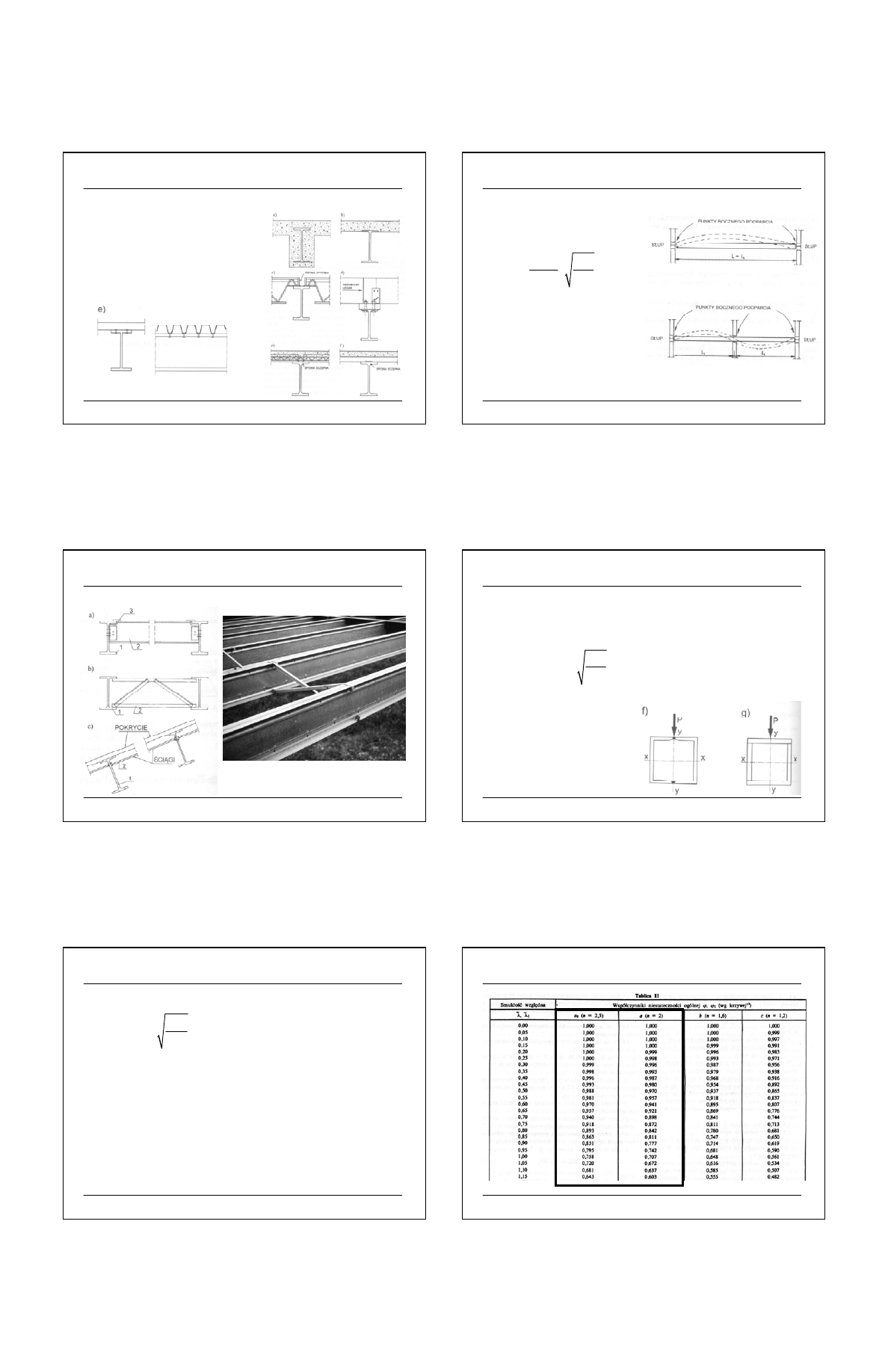
ZWICHRZENIE
Źródło [2]
Źródło [1]
08-06-04
Konstrukcje metalowe - Wykład 11
23
ZWICHRZENIE
Ź
ród
ło [8]
08-06-04
Konstrukcje metalowe - Wykład 11
24
ZWICHRZENIE
Ź
ród
ło [8]
5
08-06-04
Konstrukcje metalowe - Wykład 11
25
ZWICHRZENIE
KONSTRUKCYJNE ZABEZPIECZENIE BELEK PRZED ZWICHRZENIEM
Można przyjąć, że są konstrukcyjnie
zabezpieczone przed zwichrzeniem:
- elementy których pas ściskany jest
stężony sztywną tarcza,
Źródło [4]
Źródło [2]
08-06-04
Konstrukcje metalowe - Wykład 11
26
ZWICHRZENIE
KONSTRUKCYJNE ZABEZPIECZENIE BELEK PRZED ZWICHRZENIEM
- dwuteowniki walcowane gdy
spełniony jest warunek:
1
35
215
y
d
i
l
f
β
⋅
≤
⋅
(40)
gdzie:
l
1
- rozstaw bocznych stężeń pasa ściskanego lub
odległość między przekrojami zabezpieczonymi
przed obrotem i przemieszczeniem bocznym
(tzw. podparcie widełkowe)
i
y
- promień bezwładności przekroju względem
osi Y
β
- współczynnik momentu zginającego wg Tabl. 12
poz. a) jak dla elementu o długości l
0
=l
1
Źródło [4]
08-06-04
Konstrukcje metalowe - Wykład 11
27
ZWICHRZENIE
KONSTRUKCYJNE ZABEZPIECZENIE BELEK PRZED ZWICHRZENIEM
Źródło [8]
Źródło [4]
08-06-04
Konstrukcje metalowe - Wykład 11
28
ZWICHRZENIE
KONSTRUKCYJNE ZABEZPIECZENIE BELEK PRZED ZWICHRZENIEM
- elementy skrzynkowe lub rurowe
gdy spełniony jest warunek:
1
0
215
100
d
l
b
f
≤
⋅ ⋅
(41)
gdzie:
l
1
- jak we wzorze (40),
b
0
- osiowy rozstaw środników
Źródło [2]
08-06-04
Konstrukcje metalowe - Wykład 11
29
SMUKŁOŚĆ BELKI I WSPÓŁCZYNNIK ZWICHRZENIA
1,15
R
L
cr
M
M
λ
=
⋅
(50)
gdzie:
M
R
- nośność przekroju zginanego,
M
cr
- moment krytyczny wg klasycznej teorii stateczności;
odpowiednie wzory do obliczeń M
cr
podano w zał. 1
ZWICHRZENIE
Na podstawie
λ
L
określa się współczynnik zwichrzenia
ϕ
L
wg Tabl. 11.
Dla elementów walcowanych i spawanych w sposób zmechanizowany
korzysta się z krzywej „a
0
”, natomiast w pozostałych przypadkach z
krzywej „a”.
Dla elementów zabezpieczonych przed zwichrzeniem oraz zginanych
względem osi o mniejszej bezwładności przekroju przyjmuje się
ϕ
L
=1.
08-06-04
Konstrukcje metalowe - Wykład 11
30
ZWICHRZENIE
Źródło [7]
6
08-06-04
Konstrukcje metalowe - Wykład 11
31
SGN - NOŚNOŚCI ELEMENTÓW
NOŚNOŚĆ ELEMENTU JEDNOKIERUNKOWO ZGINANEGO
1
L
R
M
M
ϕ
≤
⋅
(52)
NOŚNOŚĆ ELEMENTU ŚCINANEGO
R
V
V
≤
gdzie:
M - moment zginający w przekroju,
ϕ
L
- współczynnik zwichrzenia
gdzie:
V - siła poprzeczna w przekroju
08-06-04
Konstrukcje metalowe - Wykład 11
32
SGN - NOŚNOŚCI ELEMENTÓW
NOŚNOŚĆ ELEMENTU ROZCIĄGANEGO I ZGINANEGO
1
y
x
Rt
L
Rx
Ry
M
M
N
N
M
M
ϕ
+
+
≤
⋅
(54)
gdzie:
N, M
x
, M
y
- siła rozciągająca i momenty zginające w przekroju
N
Rt
, M
Rx
, M
Ry
- nośności przekrojowe
ϕ
L
- współczynnik zwichrzenia
08-06-04
Konstrukcje metalowe - Wykład 11
33
SGN - NOŚNOŚCI ELEMENTÓW
NOŚNOŚĆ ELEMENTU ŚCISKANEGO I ZGINANEGO
1
y
y
x
x
i
i
Rc
L
Rx
Ry
M
M
N
N
M
M
β
β
ϕ
ϕ
⋅
⋅
+
+
≤ − ∆
⋅
⋅
(58)
gdzie:
N, M
x
, M
y
- siła ściskająca i momenty zginające w przekroju
N
RC
, M
Rx
, M
Ry
- nośności przekrojowe
β
x
,
β
y
- współczynniki momentów zginających (wg Tabl. 12)
ϕ
i
- współczynniki wyboczeniowe i=x, y
ϕ
L
- współczynnik zwichrzenia
∆
i
- składnik poprawkowy określony wzorem:
2
1, 25
0,1
i
i
i
i
i
Ri
RC
M
N
M
N
β
ϕ λ
⋅
∆ =
⋅ ⋅
⋅
⋅
≤
(57)
08-06-04
Konstrukcje metalowe - Wykład 11
34
SGU - UGIĘCIA
UGIĘCIE BELKI JEDNOKIERUNKOWO ZGINANEJ
max
dop
f
f
≤
4
0
max
5
384
k
q l
f
E J
⋅
=
⋅
⋅
np. dla belki obciążonej obciążeniem
ciągłym równomiernie rozłożonym:
gdzie:
f
dop
- ugięcie dopuszczalne
np. z Tabl. 4
Źródło [7]
08-06-04
Konstrukcje metalowe - Wykład 11
35
4
0
5
384
kx
x
x
x
q
l
f
E J
⋅
=
⋅
⋅
4
0
5
384
ky
y
y
y
q
l
f
E J
⋅
=
⋅
⋅
2
2
max
x
y
dop
f
f
f
f
=
+
≤
SGU - UGIĘCIA
UGIĘCIE BELKI DWUKIERUNKOWO ZGINANEJ
np. dla belki obciążonej obciążeniem
ciągłym równomiernie rozłożonym:
q
q
y
x
08-06-04
Konstrukcje metalowe - Wykład 11
36
SGU - UGIĘCIA
UGIĘCIE BELKI OBETONOWANEJ
W przypadku belek obetonowanych, a także belek monolitycznie
zespolonych z płytami stropowymi można uwzględnić w obliczeniach
współpracę belki stalowej z betonem. Jeśli nie przeprowadza się
dokładnej analizy, to ugięcie belki stropowej można zmniejszyć o
20%.
Źródło [4]
7
08-06-04
Konstrukcje metalowe - Wykład 11
37
SGU - DRGANIA
DRGANIA BELEK
Częstotliwość drgań własnych konstrukcji stropu w pomieszczeniach
użyteczności publicznej (wolnych od ścian działowych) o rozpiętości
l > 12 m powinna wynosić co najmniej 5 Hz.
Warunku tego można nie spełniać, gdy ugięcie konstrukcji od
kombinacji obciążeń długotrwałych nie przekracza 10 mm.
Różnica częstości drgań wzbudzonych i drgań własnych konstrukcji
narażonych na oddziaływania typu harmonicznego, powinna wynosić
co najmniej 25% częstości drgań własnych.
08-06-04
Konstrukcje metalowe - Wykład 11
38
BIBLIOGRAFIA
1. Rykaluk K. „Konstrukcje stalowe. Podstawy i elementy” Wydawnictwo DWE, Wrocław
2001
2. Łubiński M., Filipowicz A., Żółtowski W. „Konstrukcje metalowe. Część I” Wydawnictwo
Arkady, Warszawa 2006
3. Bogucki W., Żyburtowicz M. „Tablice do projektowania konstrukcji metalowych”
Wydawnictwo Arkady, Warszawa 2007
4. Żmuda J. „Podstawy projektowania konstrukcji metalowych” Wydawnictwo Arkady,
Warszawa 1997
5. Bródka J., Broniewicz M. „Projektowanie konstrukcji stalowych zgodnie z Eurokodem
3-1-1 wraz z przykładami obliczeń” Wydawnictwo Politechniki Białostockiej, Białystok
2001
6. Medwadowski J. et al. „Stalowe konstrukcje budowlane” Wydawnictwo PWN, Warszawa
1980
7. PN-90/B-03200 „Konstrukcje stalowe. Obliczenia statyczne i projektowanie”
8. Materiały dydaktyczne ESDEP