1

6. PODSTAWY PLANOWANIA EKSPERYMENTU

6.1. Pojęcie i rola badań doświadczalnych

Przez eksperyment rozumiemy badanie jakiegoś zjawiska, polegające na celowym

wywoływaniu tego zjawiska lub jego zmian oraz obserwacji i pomiarach, umożliwiających
wnioskowanie o jego właściwościach. Eksperyment przeprowadza się na drodze badań
doświadczalnych mających na celu poznanie informacji o faktach, obiektach, zjawiskach
bądź procesach. Na podstawie zgromadzonych informacji określa się model zjawiska, który
stanowi jego reprezentację w postaci użytkowej wyrażającej istotne jego cechy. Istnieją
modele lingwistyczne, fizyczne, matematyczne. Najczęściej stosowany model
matematyczny jest opisem zjawiska za pomocą liczb, zmiennych, zbiorów, funkcji, relacji
itd. Znajomość modelu matematycznego umożliwia przewidywanie przebiegu zjawiska lub
zachowania obiektu w różnych warunkach. Podstawy teoretyczne badań doświadczalnych
ujmuje dziedzina wiedzy nazywana teorią eksperymentu. Obejmuje ona następujące
zagadnienia:
1. planowanie eksperymentów,
2. metodykę modelowania matematycznego,
3. technikę przeprowadzania pomiarów,
4. analizę wyników pomiarów.

Zanim powstała teoria eksperymentu badania doświadczalne dotyczyły prostych

obiektów o jednej wielkości wejściowej. Eksperyment polegał na przeprowadzeniu
pomiarów wielkości wyjściowej y dla L arbitralnie wybranych wartości wielkości
wejściowej x oraz wyznaczeniu funkcji aproksymującej y = f(x). Wraz ze wzrostem
złożoności analizowanych obiektów, spowodowanym zwiększeniem liczby wielkości
wejściowych, badania doświadczalne realizowano w oparciu o dwie metody: metodę badań
kompletnych i monoselekcyjnych.

W metodzie badań kompletnych doświadczenie odbywało się w następujący sposób:

a) dla każdej zmiennej x

k

, k = 1, 2, ..., s wybierano L wartości równomiernie

rozmieszczonych w przedziale [x

k min

, x

k max

],

b) dla każdej kombinacji wartości wielkości wejściowych wykonywano pojedynczy

pomiar,

c) na podstawie przeprowadzonych pomiarów wyznaczano funkcję aproksymującą f(

⋅

).

Graficzna interpretacja tej metody na przykładzie poszukiwania ekstremum obiektu o

dwóch zmiennych wejściowych przedstawiona została na rys. 6.1.

Metoda badań kompletnych była skuteczną metodą identyfikacji funkcji obiektu badań

dla jednej lub dwóch zmiennych wejściowych. Adoptowanie tej metody do obiektów o
większej liczbie zmiennych prowadziło do eksplozji kombinatorycznej wynikającej z liczby
koniecznych do wykonania pomiarów:

n = L

S

(6.1)

Przykładowo dla s = 10, L = 10, oraz przyjmując czas trwania jednego pomiaru równy

1s uzyskujemy całkowity czas badań kompletnych wynoszący ponad 317lat!

W celu ograniczenia liczby wykonywanych pomiarów opracowano metodę badań

monoselekcyjnych, w której zastosowano procedurę właściwą obiektowi badań o jednym
wejściu w odniesieniu do obiektu o wielu wejściach. W metodzie tej dla każdej zmiennej x

k

wybierano L wartości równomiernie rozmieszczonych w przedziale [x

k min

, x

k max

]. Następnie

2

dokonywano pojedynczego wyboru (monoselekcji) kolejnych wartości x

k

i badano wpływ

tej wielkości na wielkość wyjściową y.

x

2

x

1

y

= f(

x

1

, x

2

)

y

max

Rys. 6.1. Plan kompletny dla dwóch zmiennych wejściowych

Równocześnie przyjmowano, iż wartości pozostałych wielkości wejściowych są stałe:
x

q

= const, q = 1, 2, ..., s ; q ≠ k. W ten sposób całkowicie ignorowano współzależności

między wielkościami wejściowymi i zamiast funkcji wielu zmiennych y = f(x

1

, x

2

, ..., x

k

, ..., x

s

)

uzyskiwano jedynie zbiór wielu funkcji jednej zmiennej y = f

k

(x

k

) dla arbitralnych wartości

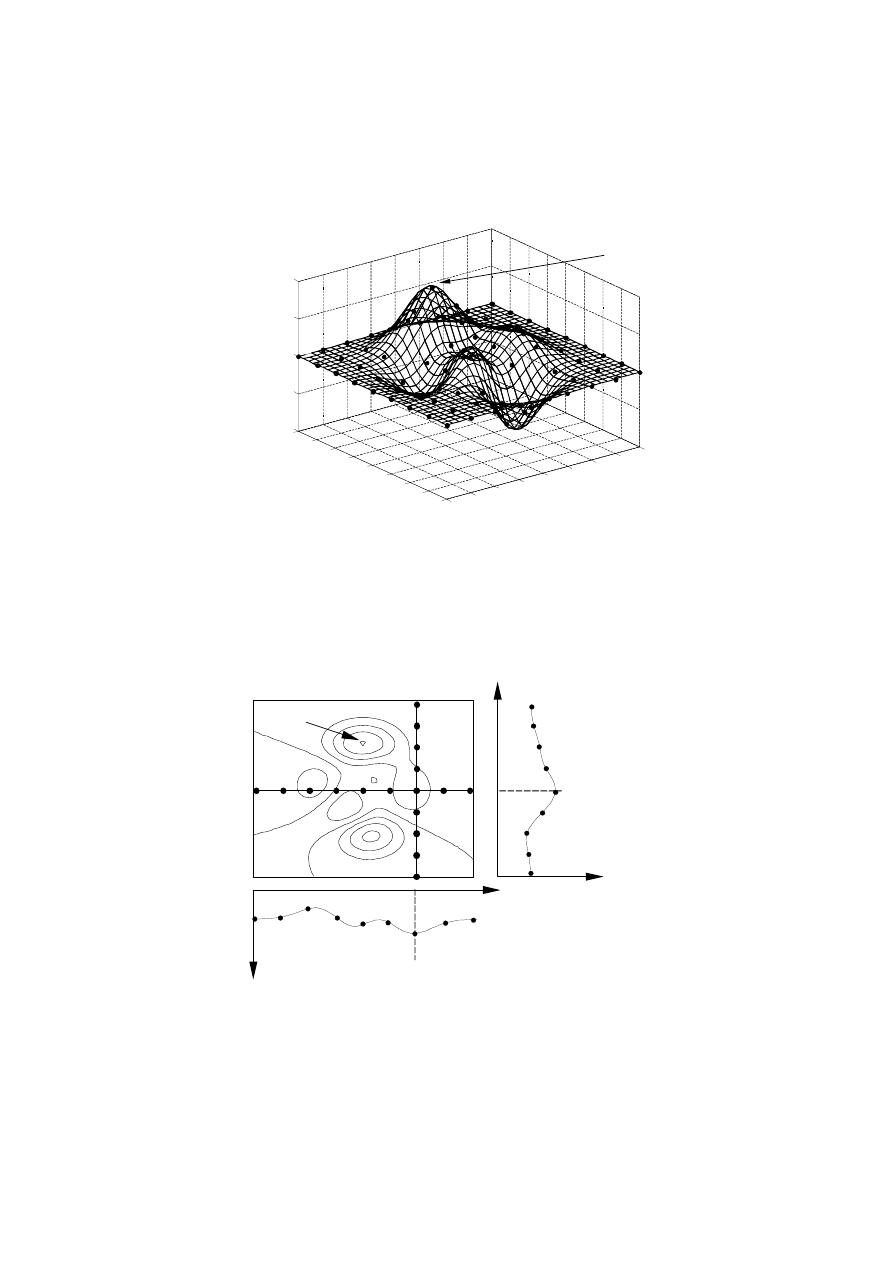
pozostałych zmiennych (rys. 6.2).

x

1

x

2

y

x

1 opt

y

y = f( x

1

, x

2

)

y = f

1

( x

1

)

x

2

= const

y = f

2

(x

2

)

x

1

= x

1 opt

= const

x

2

x

1

x

2 opt

y

max

Rys. 6.2. Badania monoselekcyjne dla dwóch zmiennych wejściowych.

Poszukiwane ekstremum funkcji nie zostaje wyznaczone

3

W porównaniu do metody badań kompletnych osiągnięto znaczną redukcję liczby

koniecznych do przeprowadzenia pomiarów:

(

)

∑

=

−

+

=

s

k

L

L

n

2

1

(6.2)

Dla s = 10, L = 10, oraz przyjmując czas trwania jednego pomiaru równy 1s całkowity

czas badań monoselekcyjnych uległ skróceniu do zaledwie 91s.

Ze względu na ograniczenia metody kompletnej i monoselekcyjnej przy analizie

złożonych obiektów zaistniała potrzeba opracowania nowych metod badawczych. Nastąpił
rozwój teorii eksperymentu. Powstały metody planowania badań doświadczalnych, które
umożliwiły zwiększenie ilości i jakości uzyskiwanej informacji naukowej. Zmniejszeniu
uległa liczba koniecznych do przeprowadzenia pomiarów, a więc zredukowano koszty i
czas trwania badań.

Badania kompletne i monoselekcyjne pozostawiały swobodę wyboru wartości wielkości

wejściowych (punktów pomiarowych) dla których realizowano eksperyment, natomiast
wyniki pomiarów analizowano matematycznie dopiero po przeprowadzeniu doświadczenia.

Wykorzystując zasady teorii eksperymentu ustala się wstępnie cel i metodę analizy

wyników pomiarów, natomiast punkty pomiarowe generowane są na podstawie
określonych procedur matematycznych. Pojedynczy punkt pomiarowy, będący
s–wymiarowym wektorem wartości wielkości wejściowych, nazywany jest układem planu
eksperymentu, natomiast zbiór wszystkich punktów pomiarowych stanowi plan
eksperymentu. W zależności od celu badań i stosowanych metod analizy uzyskuje się
rozmieszczenie punktów, które pozwala na:
- uwypuklenie poszukiwanych cech obiektu np. liniowości, współzależności zmiennych

wejściowych, niezależności wielkości wyjściowej od wielkości wejściowych,

- wyznaczenie ekstremum globalnego funkcji obiektu badań,
- zmniejszenie

nakładu obliczeniowego przy identyfikacji modelu obiektu.

Jak wspomnieliśmy celem badań doświadczalnych jest zwykle wyznaczenie modelu

obiektu badań. W ogólności rozróżnia się identyfikację strukturalną polegającą na ustalaniu
struktury modelu i wyznaczeniu wartości jego parametrów, oraz identyfikację
parametryczną polegającą na ustaleniu wartości parametrów modelu przy a priori danej
strukturze modelu. Wyznaczenie dokładnego modelu badanego obiektu jest bardzo trudne
ze względu na oddziaływanie na rzeczywisty obiekt wielu trudnych lub niemożliwych do
zmierzenia zakłóceń losowych. Z tego względu w teorii eksperymentu stosuje się
identyfikację parametryczną, w której przy założonej strukturze modelu i określonych
danych wejściowych wyznacza się takie wartości parametrów, które zminimalizują
niedokładność modelu. Przyjmuje się postać funkcji aproksymującej model obiektu
(najczęściej wielomian algebraiczny) i wyznacza się wartości współczynników tego
wielomianu korzystając z metody regresji.

Planowanie eksperymentu odbywa się zatem według następującego scenariusza:

a) charakterystyka obiektu badań polegająca na sformułowaniu zagadnienia

wymagającego rozwiązania na drodze doświadczalnej, ustaleniu wielkości
charakteryzujących obiekt badań (wielkości wejściowe, wyjściowe, stałe i zakłócające),
oraz przyjęciu liczby poziomów zmiennych wejściowych, czyli wybranie wartości, które
mogą przyjmować zmienne wejściowe,

b) ustalenie celu badań doświadczalnych, którym może być:

- identyfikacja modelu obiektu badań,
- optymalizacja empiryczna – wyznaczenie ekstremum globalnego modelu obiektu,

4

- badania eliminacyjne – eliminacja wielkości wejściowych o nieistotnym znaczeniu,

c) generacja lub wybór planu eksperymentu najlepiej dostosowanego do obiektu badań

i przyjętego celu badań doświadczalnych,

d) realizacja pomiarów w oparciu o wybrany plan doświadczenia,
e) analiza danych empirycznych zmierzająca do osiągnięcia założonego celu badań

doświadczalnych,

f) analiza merytoryczna rezultatów przeprowadzonych badań polegająca na logicznej

ocenie zjawisk związanych z badanym obiektem,

g) sformułowanie wniosków poznawczych, praktycznych i rozwojowych z

przeprowadzonych badań.

W dalszej części niniejszego rozdziału omówione zostały podstawowe zagadnienia z

zakresu planowania i analizy eksperymentu. Przedstawione wiadomości zaczerpnięto ze
specjalistycznej literatury poświęconej metodologii prowadzenia badań empirycznych [1-5],
adresowanej do inżynierów różnych specjalności, zajmujących się doświadczalnictwem
oraz identyfikacją modeli matematycznych obiektów.

6.2. Charakterystyka obiektu badań

Metody planowania eksperymentu mają charakter uniwersalny, niezależny od

merytorycznego obszaru, w którym realizowany jest eksperyment. Uzyskano to dzięki
wprowadzeniu uniwersalnego, przyczynowo-skutkowego modelu obiektu badań (rys. 6.3),
który opisują następujące wielkości modelujące:
a) niezależne wielkości wejściowe: {x

1

, x

2

, ..., x

k

, ..., x

s

}, k = 1, 2, ..., s,

b) zależne wielkości wyjściowe: {y

1

, y

2

, ..., y

p

, ..., y

w

}, p = 1, 2, ..., w,

c) wielkości stałe {c}, które mają wpływ

na działanie układu, ale ich wartości są
ustalone i niezmienne w czasie, przez
co mogą zostać pominięte w analizie
statystycznej,

d) wielkości zakłócające {h}, których

istnienie spowodowane jest oddziały-
waniem losowych czynników w
obiekcie badań na wielkości
wyjściowe oraz niedoskonałościami
metod i środków pomiarowych.

Do wielkości wejściowych wlicza się te, których wpływ na wielkości wyjściowe

interesuje realizatora badań. Mogą to być wielkości: fizyczne, chemiczne, techniczne,
ekonomiczne i inne. W odniesieniu do każdej wielkości wejściowej określa się zakresy
wartości x

k min

≤ x

k

≤ x

k max

, k = 1, 2, ..., s zakładając, iż eksperyment jest fizycznie

realizowalny jeżeli wartości mieszczą się w wyznaczonych przedziałach.

W celu uniezależnienia się od fizycznej interpretacji oraz zmniejszenia błędów

numerycznych podczas analizy danych empirycznych wielkości wejściowe normuje się do
bezwymiarowego przedziału [-

α, α]. Wielkość α jest nazywana ramieniem gwiezdnym i

stanowi jeden z elementów charakteryzujących plan eksperymentu.

Normowanie wielkości wejściowej x

k

realizowane jest zgodnie ze wzorem:

(

)

α

α

−

−

−

=

min

max

min

2

k

k

k

k

k

x

x

x

x

x(

(6.3)

OBIEKT

BADAŃ

x

1

x

2

:

x

k

:

x

s

y

1

y

2

:

y

p

:

y

w

Rys. 6.3. Uniwersalny, statyczny

model obiektu badań

5

Rzeczywistą wartość wielkości wejściowej uzyskuje się przez zastosowanie

przekształcenia odwrotnego zwanego denormowaniem:

(

)(

)

min

min

max

2

k

k

k

k

k

x

x

x

x

x

+

−

+

=

α

α

(

(6.4)

Jeżeli wszystkie wielkości modelujące są niezależne od czasu wówczas mamy do

czynienia z obiektem statycznym. W przeciwnym razie, jeżeli przynajmniej jeden z
parametrów jest funkcją czasu, wówczas operujemy pojęciem obiekt dynamiczny. Metody
identyfikacji obiektów dynamicznych są dużo bardziej złożone bowiem wymagają
rozwiązywania równań różniczkowych i w związku z tym nie będą omawiane w tym
podręczniku.

Analizę obiektu badań opisanego liczbą w > 1 wielkości wyjściowych sprowadza się

przez dekompozycję do analizy w obiektów o jednym wyjściu. Dalsze rozważania będą
dotyczyły obiektu zawierającego i-wejść x

k

, k = 1, 2, ..., s oraz jedno wyjście y.

6.3. Metody planowania eksperymentu

Kolejnym etapem badań doświadczalnych (po charakterystyce obiektu i ustaleniu celu

badań) jest wyznaczenie zbioru punktów pomiarowych czyli generacja lub wybór planu
eksperymentu. Algorytmy generacji planów ustala teoria eksperymentu na podstawie
określonych reguł matematycznych. Prowadząc badania doświadczalne najczęściej
wybieramy jeden plan z bazy planów eksperymentów dedykowany określonemu celowi
badawczemu np. identyfikacji modelu liniowego, optymalizacji modelu liniowo-
kwadratowego, badaniu wpływu poszczególnych składników na właściwości mieszaniny
chemicznej.

W zapisie matematycznym plan eksperymentu stanowi macierz









































=

ns

nk

n

n

us

uk

u

u

s

k

s

k

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

...,

,

...,

,

,

...

...,

...,

...,

...,

...,

...,

,

...,

,

,

...

...,

...,

...,

...,

...,

...,

,

...,

,

,

...,

,

...,

,

,

2

1

2

1

2

2

22

21

1

1

12

11

X

(6.5)

gdzie: n – liczba układów planu eksperymentu; s – liczba zmiennych wejściowych.
Wiersz x

u

= [x

u1

, x

u2

, ..., x

uk

, ..., x

us

] macierzy X stanowi układ planu eksperymentu.

Istnieją różne klasyfikacje planów w zależności od struktury modelu identyfikowanego

obiektu, parametrów wielkości modelujących oraz celu badań doświadczalnych.

Liczba poziomów L zmiennych wejściowych x

k

determinuje plan L-poziomowy

(dwupoziomowy, trójpoziomowy, wielopoziomowy).

W zależności od proporcji liczby punktów pomiarowych n oraz liczby parametrów P

identyfikowanego modelu wyróżnia się:
a) plany nienasycone, w których n > P,
b) plany nasycone, w których n = P.

Rząd planu doświadczenia uzależniony jest natomiast od stopnia wielomianu

aproksymującego model obiektu. Aproksymacja wielomianem algebraicznym stopnia i
wymaga zastosowania planu i-tego rzędu.

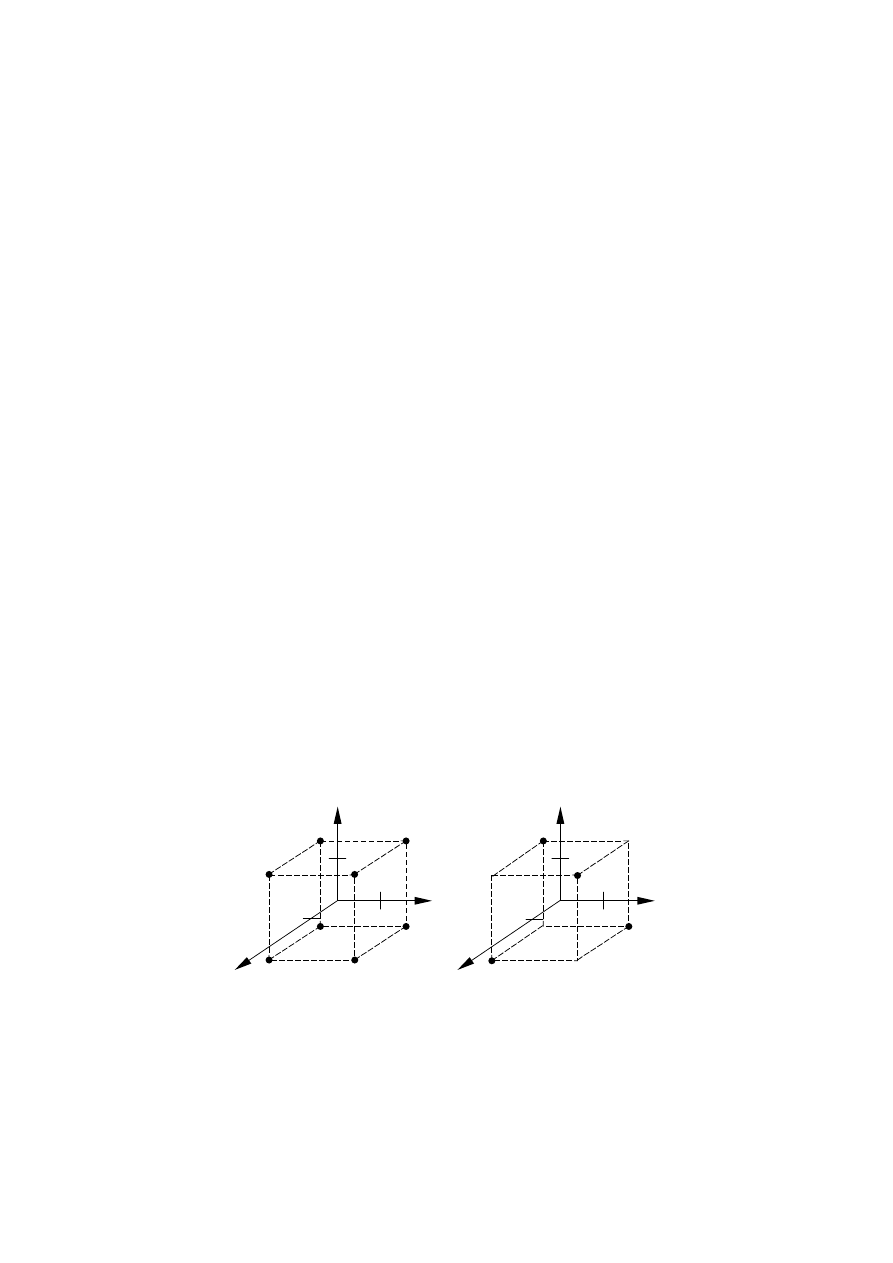
6

W zależności od wpływu czasu na wartości zmiennych wejściowych wyróżniamy dwa

rodzaje planów:
a) statyczne – wszystkie wielkości modelujące są niezależne od czasu,
b) dynamiczne – przynajmniej jedna z wielkości modelujących jest funkcją czasu.

Najistotniejszym kryterium podziału jest przyjęty cel badań doświadczalnych.

a) Weryfikację istotności wpływu wielkości wejściowych na wielkość wyjściową

przeprowadza się w oparciu o plan randomizowany, który wprowadza element
losowości do zbioru punktów pomiarowych.

b) Identyfikację modelu obiektu badań najlepiej zrealizować w oparciu o plan

zdeterminowany, którego układy determinują ustalone założenia teoretyczne.

c) Przy wyznaczaniu ekstremum funkcji korzystamy z planu optymalizacyjnego.

Największe praktyczne zastosowanie mają plany zdeterminowane, a wśród nich plany

nazywane ułamkowymi lub poliselekcyjnymi.

Zdeterminowane metody planowania opisane zostały w dalszej części tego rozdziału.

Dokonano przy tym podziału w zależności od liczby poziomów zmiennych wejściowych.
Jako szczególny przypadek planów zdeterminowanych, mających zastosowanie w badaniu
zjawisk chemicznych, opisana została metoda planowania sympleksowego. Omówiono
także technikę planowania optymalnego.

6.3.1. Planowanie dwupoziomowe

Metoda planowania dwupoziomowego wykorzystywana jest do identyfikacji liniowych

modeli obiektów. W metodzie tej każda zmienna wejściowa przyjmuje tylko dwie wartości
(poziomy). Łączna liczba układów planu eksperymentu w planie dwupoziomowym wynosi
2

S

, gdzie s jest liczbą zmiennych wejściowych. Taki plan nosi nazwę dwupoziomowego

całkowitego lub kompletnego i oznaczany jest symbolem 2

S

. Dla większej liczby

zmiennych wejściowych przeprowadzenie eksperymentu całkowitego jest praktycznie
niemożliwe ze względu na dużą liczbę koniecznych do przeprowadzenia pomiarów.
W takim przypadku stosowane są plany ułamkowe (oznaczane symbolem 2

S-P

) zawierające

pewną liczbę układów z planu eksperymentu całkowitego. Istnieją zatem plany połówkowe,
ćwiartkowe, ósemkowe itd.

Unormowane zmienne wejściowe w planie dwupoziomowym przyjmują wartości

k

x(

={ -1, 1}. Rozmieszczenie układów planu całkowitego i ułamkowego (połówkowego)

dla trzech zmiennych wejściowych we współrzędnych unormowanych podano na rys. 6.4.

1

1

1

1

x(

2

x(

3

x(

1

1

1

1

x(

2

x(

3

x(

0

0

a) b)

Rys. 6.4. Rozmieszczenie we współrzędnych unormowanych układów planu dwupoziomowego:

a) całkowitego, b) ułamkowego (połówkowego)

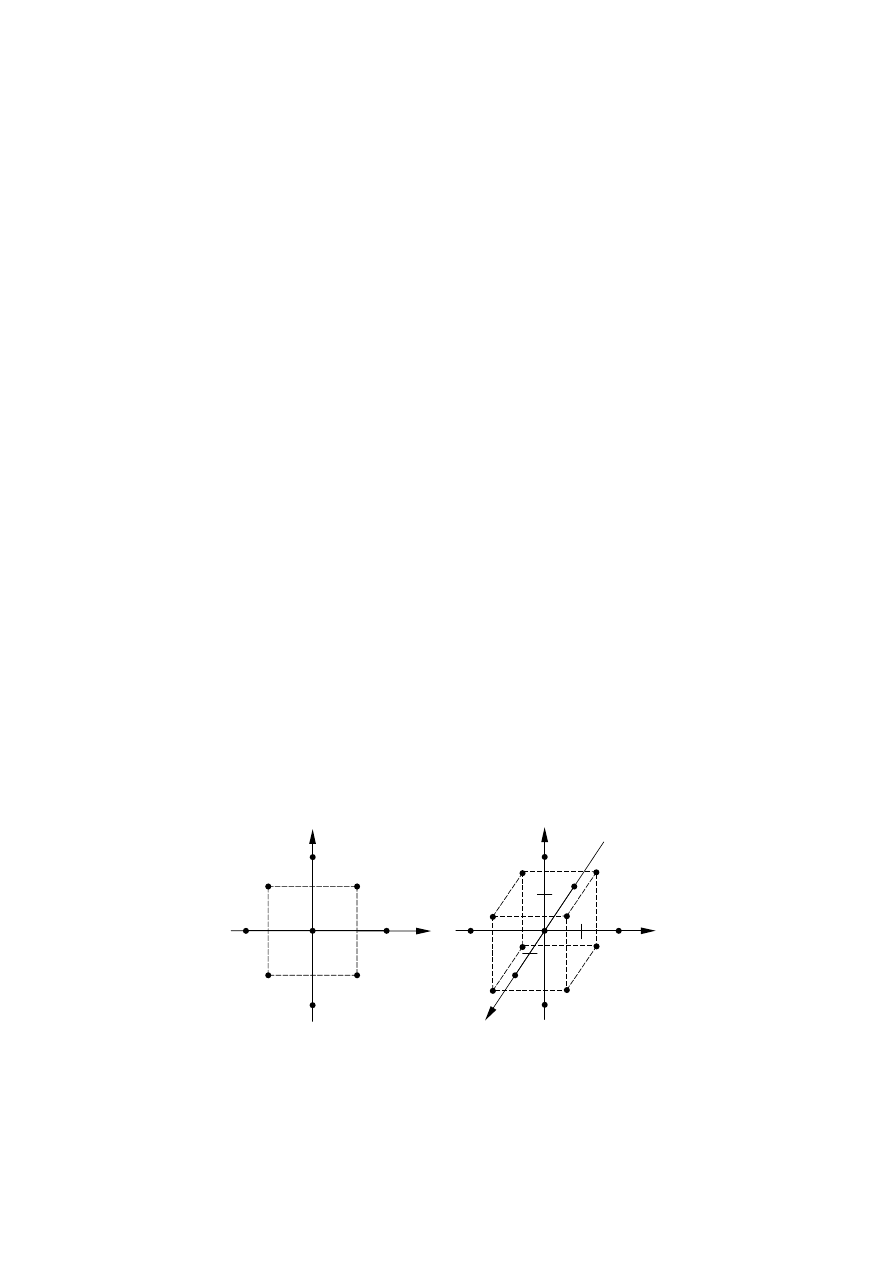
7

Wybór konkretnych układów nie może być przypadkowy, gdyż plan ułamkowy dla
standaryzowanych zmiennych wejściowych powinien spełniać warunki:
a) symetrii układów względem środka eksperymentu,
b) ortogonalności, polegającej na zerowaniu wszystkich iloczynów skalarnych wektorów

kolumnowych unormowanej macierzy X,

c) równości sum kwadratów we wszystkich kolumnach unormowanej macierzy X.

6.3.2. Planowanie trójpoziomowe

Metoda planowania trójpoziomowego umożliwia identyfikację kwadratowego modelu

obiektu. W metodzie tej unormowane zmienne wejściowe przyjmują wartości

k

x(

={ -1, 0, 1}.

W planie trójpoziomowym całkowitym (oznaczenie 3

S

) występuje bardzo gwałtowny

wzrost liczby układów wraz ze wzrostem liczby wejść obiektu, stąd planowanie
trójpoziomowe ma bardzo małe możliwości praktyczne. Identyfikacja modelu na podstawie
planu trójpoziomowego jest bardziej skomplikowana niż na podstawie planu
dwupoziomowego. Z tego powodu nie zostały opracowane plany eksperymentów
trójpoziomowych ułamkowych.

6.3.3. Planowanie wielopoziomowe

Planowanie wielopoziomowe zapewnia identyfikację modeli liniowo-kwadratowych.

Szczególny przypadek planowania wielopoziomowego – planowanie pięciopoziomowe –
stanowi rozszerzenie planowania dwupoziomowego i jest najczęściej wykorzystywane w
praktyce.

Wyróżniamy trzy zasadnicze typy planowania wielopoziomowego:

1) planowanie kompozycyjne,
2) planowanie ortogonalne,
3) planowanie rotabilne.

Planowanie kompozycyjne jest rozwinięciem planowania dwupoziomowego typu 2

S

lub

2

S-P

o dwa rodzaje układów (dla zmiennych unormowanych):

a) gwiezdne typu (0, ..., 0,

±α, 0, ..., 0), w których zmieniane są kolejno wartości

zmiennych wejściowych między poziomami

±α dla pozostałych zmiennych na

poziomie 0, przy czym wielkość

α stanowi ramię gwiezdne planu,

b) centralne typu (0, 0, ..., 0) stanowiące centrum planu eksperymentu.

Przykłady planów kompozycyjnych dla unormowanych zmiennych wejściowych

przedstawia rys. 6.5.

1

1

1

1

x(

2

x(

3

x(

0

α

α

α

1

1

1

x(

2

x(

0

α

α

a)

b)

Rys. 6.5. Plany wielopoziomowe (kompozycyjne) we współrzędnych unormowanych dla różnej

liczby zmiennych wejściowych: a) dwóch, b) trzech

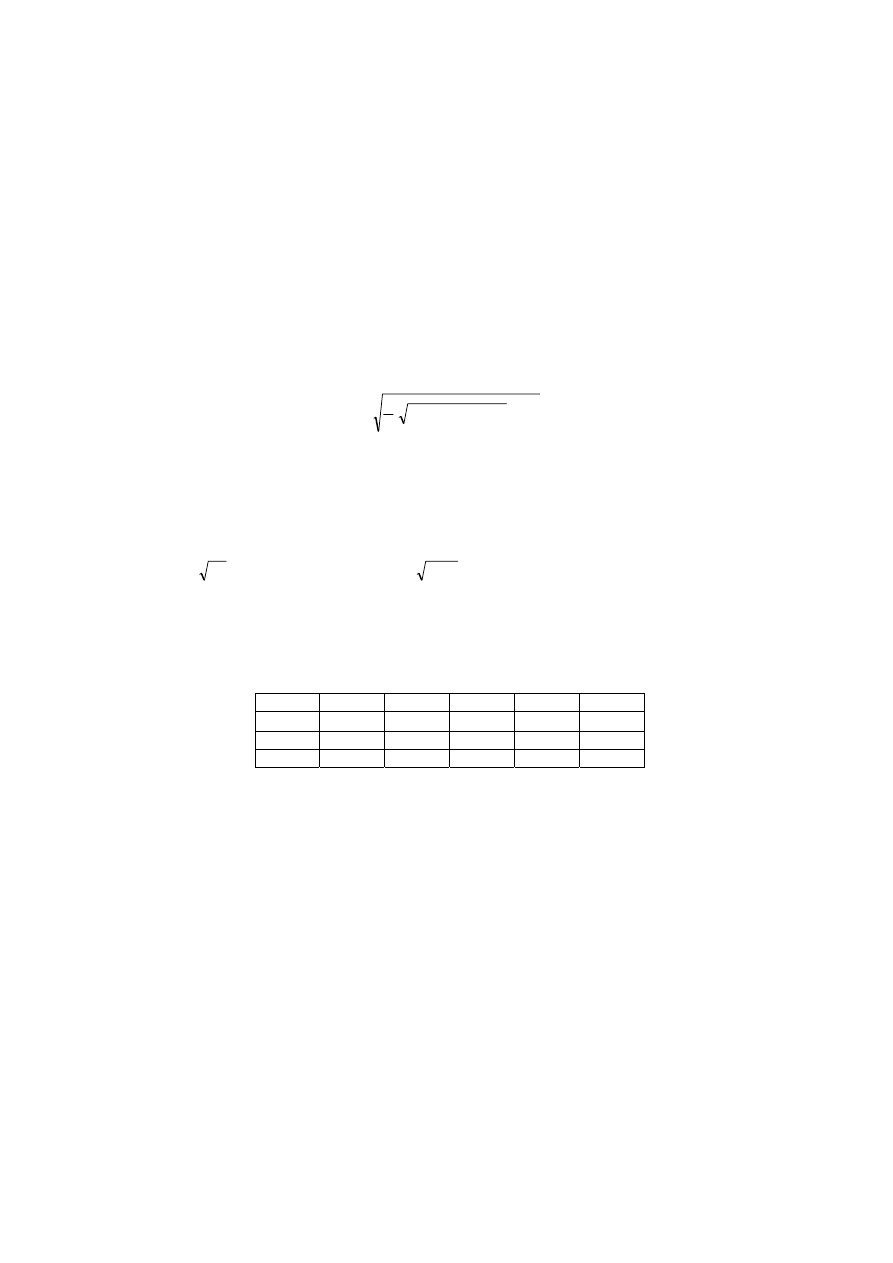
8

Liczba układów planu kompozycyjnego wynosi n = 2

S

+ 2s + 1 (2

S

układów planu

dwupoziomowego, 2s układów gwiezdnych i jeden układ centralny). Stąd podstawową
zaletą tego planu jest znaczne ograniczenie liczby układów w porównaniu do planu
trójpoziomowego, w szczególności dla większych wartości s.

Dobierając odpowiednią wartość ramienia gwiezdnego

α w planie kompozycyjnym

oraz zwiększając do n

o

liczbę układów w centrum planu można spełnić postulat

ortogonalności planu doświadczenia. Uzyskujemy w ten sposób znaczne uproszczenie
obliczeń przy wyznaczaniu parametrów modelu identyfikowanego obiektu oraz ocenie
statystycznej otrzymanych współczynników. Plan spełniający postulat ortogonalności
nazywany jest planem ortogonalnym.

Wartość ramienia gwiezdnego planu ortogonalnego dla określonych wartości s i n

o

wyznaczamy ze wzoru

(

)

[

]

d

d

d

n

n

S

n

n

−

+

+

=

0

2

2

1

α

(6.6)

gdzie: n

d

= 2

S

dla panu całkowitego lub n

d

= 2

S-P

dla planu ułamkowego.

Planowanie rotabilne ma na celu spełnienie postulatu niezależności planu od obrotu

układu współrzędnych w przestrzeni wielkości wejściowych. Zastosowanie planu
rotabilnego umożliwia identyfikację modelu o wariancjach zależnych tylko od odległości
od punktu centralnego eksperymentu.

Warunek rotabilności planu jest spełniony, jeżeli wartość ramienia gwiezdnego wynosi

4

2

S

=

α

dla panu całkowitego lub

4

2

P

S

−

=

α

dla panu ułamkowego.

W tablicy 6.1. podano zestawienie wartości ramienia gwiezdnego, zalecaną liczbę

układów w centrum planu n

o

oraz łączną liczbę układów n planu rotabilnego dla liczby

zmiennych wejściowych od 2 do 6.

Tablica 6.1.

Zestawienie optymalnych wartości parametrów dla planu rotabilnego

s

2 3 4 5 6

α

1,414 1,682 2,000 2,378 2,828

n

o

5 6 7 10 15

n

13 20 31 52 91

6.3.4. Planowanie sympleksowe

Specyficzny sposób planowania eksperymentu stosowany jest w przypadku badania

właściwości mieszaniny zależnej od jej składu.

Skład mieszaniny możemy opisać za pomocą wektora zmiennych x = [x

1

, x

2

, ..., x

s

],

przy czym na zmienne te są narzucone następujące ograniczenia fizykalne:

a) objętość mieszaniny jest stała, niezależna od jej składu:

∑

=

=

s

k

k

x

1

const (6.7)

b) zawartość każdego składnika w mieszaninie jest niezerowa:

x

k

≥ 0 , k = 1, 2, ..., s (6.8)

9

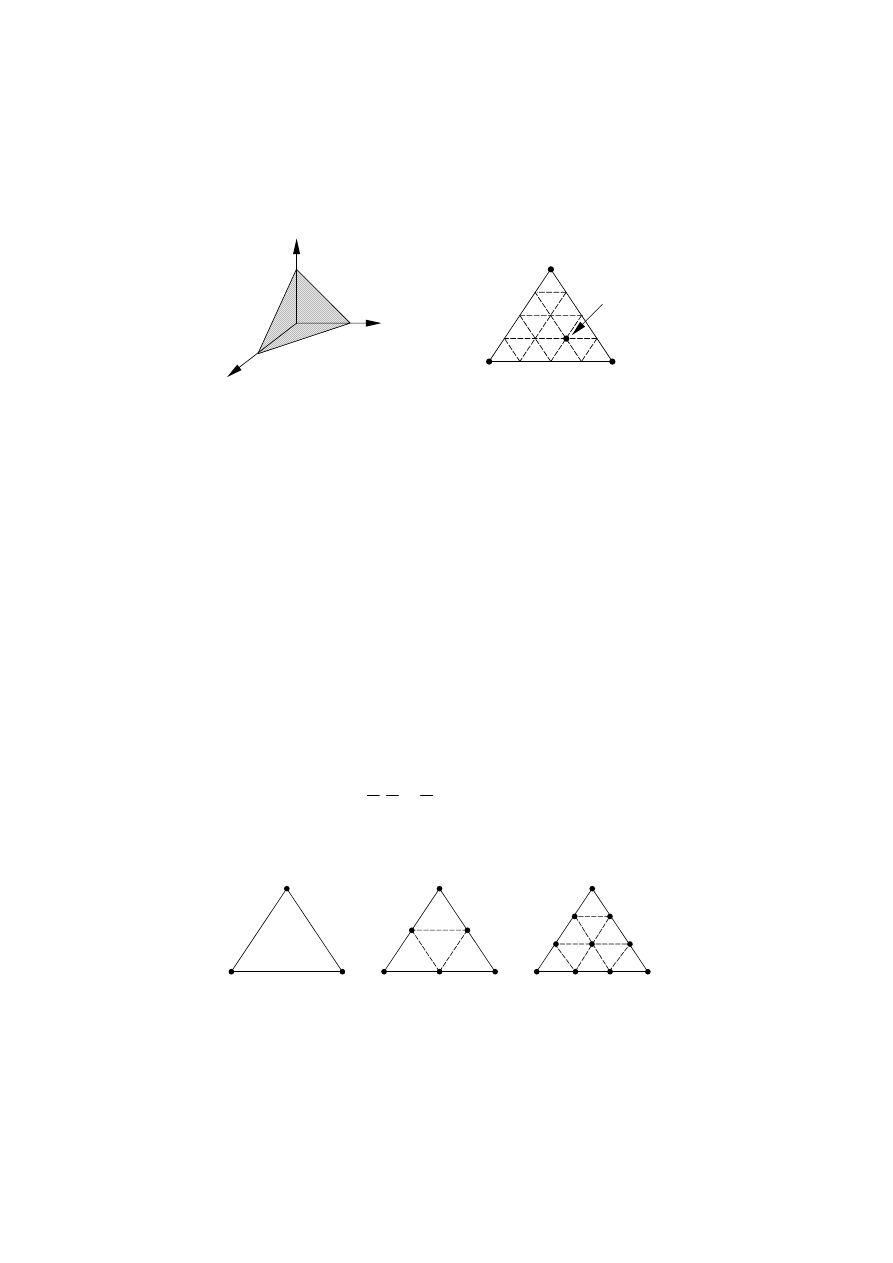
Przykładowo dla mieszaniny zawierającej trzy składniki wszystkie możliwe składy

mieszaniny leżą w przestrzeni trójwymiarowej na płaszczyźnie (warunek 6.7), ograniczonej
trójkątem (warunek 6.8). Sytuacja taka została zilustrowana na rys. 6.6.

x

1

x

2

x

3

a) b)

x

1

=1

x

2

=0

x

3

=0

x

1

=0

x

2

=1

x

3

=0

x

1

=0

x

2

=0

x

3

=1

x

1

=1/2

x

2

=1/4

x

3

=1/4

Rys. 6.6. Płaszczyzna składów mieszaniny o trzech składnikach:

a) w przestrzeni trójwymiarowej, b) w przestrzeni dwuwymiarowej

W ogólnym przypadku przestrzeń dopuszczalnych wartości s składników mieszaniny

jest sympleksem o s wierzchołkach na (s – 1)–wymiarowej hiperpłaszczyźnie.

W omawianych dotąd metodach planowania wartość wyjściową obiektu opisanego s

zmiennymi wejściowymi traktowano jako funkcję s zmiennych niezależnych
aproksymowaną za pomocą wielomianu algebraicznego stopnia R. W metodzie planowania
sympleksowego natomiast zmienne wejściowe związane są zależnością sumacyjną (6.7),
która zmniejsza liczę zmiennych niezależnych do s–1. Do opisu obiektu na który nałożone
są ograniczenia (6.7) i (6.8) stosuje się wielomian zredukowany stopnia R–1, który uzyskuje
się drogą odpowiednich przekształceń wielomianu algebraicznego stopnia R. Często
zachodzi potrzeba ograniczenia dużej liczby współczynników wielomianów
zredukowanych. Usuwając część z nich uzyskuje się uproszczone wielomiany
zredukowane.

Z uwagi na konieczność spełnienia warunków (6.7) i (6.8) sympleksowy plan

eksperymentu może zawierać wyłącznie układy stanowiące punkty leżące na sympleksie
s –wymiarowym.

Do wyznaczenia K współczynników wielomianu zredukowanego stopnia R dla s

zmiennych stosowane są plany siatkowe całkowite typu {s, R}. Plan siatkowy całkowity
{s, R} jest zbiorem układów określonych wzorami:

R

R

R

R

x

k

,...,

2

,

1

,

0

=

oraz

1

1

∑

=

=

s

k

k

x

(6.9)

Na rys. 6.7 podano przykładowe plany typu {3, R} mieszanin trójskładnikowych

s = 3 stopnia R = 1, 2, 3, 4.

x

1

=1

a) b)

c)

x

2

=1

x

3

=1

x

1

=1

x

2

=1

x

3

=1

x

1

=1

x

2

=1

x

3

=1

{3,1} {3,2}

{3,3}

Rys. 6.7. Całkowity plan sympleksowy dla trzech zmiennych stopnia:

a) pierwszego, b) drugiego, c) trzeciego

10

x

1

=1

x

2

=1

x

4

=1

{4,3}

x

3

=1

Rys. 6.8. Całkowity plan sympleksowy

trzeciego stopnia dla czterech zmiennych

Liczba układów planu całkowitego

siatkowego wynosi:













−

+

=

R

s

R

n

1

(6.10)

Rys. 6.8 przedstawia rozmieszczenie

układów planu typu {4, 3} mieszaniny
czteroskładnikowej.

Zasadniczą wadą planów siatkowych

całkowitych typu {s, R} jest badanie
właściwości mieszaniny przede wszystkim
na granicy sympleksu.

Wadę tę usuwa się stosując plany siatkowe ułamkowe typu {s}, stanowiące zbiór

układów określonych wzorami:

(1, 0, ..., 0), (

0

,...,

0

,

2

1

,

2

1

), (

s

s

s

s

1

,...,

1

,

1

,

1

) (6.11)

Przykład planu siatkowego ułamkowego przedstawia rys. 6.9.

x

1

=1

x

2

=1

x

4

=1

{4}

x

3

=1

x

1

=1

x

2

=1

x

3

=1

{3}

a) b)

Rys. 6.9. Ułamkowy plan sympleksowy dla trzech (a) i czterech zmiennych (b)

Liczba układów planu siatkowego ułamkowego wynosi:

1

2

−

=

s

n

(6.12)

Plany siatkowe typu {s} stosowane są dla liczby składników s ≥ 5 ze względu na

znacznie mniejszą liczbę współczynników wielomianów zredukowanych w odróżnieniu od
planów typu {s, R}.

6.3.5. Planowanie optymalne

Wraz z rozwojem technik obliczeniowych wymagania stawiane planom eksperymentu

polegające na ułatwianiu obliczeń związanych z wyznaczaniem współczynników modelu
stały się mało istotne. Postulowano natomiast opracowanie metod planowania
zapewniających niezależne szacowanie współczynników modelu, ogólniejsze stawianie
zadań planowania eksperymentu oraz zastosowanie do rozwiązywania tych zadań aparatu
analizy matematycznej w postaci teorii miary.

Nastąpił rozwój metod planowania optymalnego, w których analizując właściwości

macierzy informacyjnej Fishera M (patrz punkt 6.5.1 – Identyfikacja modelu obiektu

11

badań, wzór 6.33) optymalizowano wartości wariancji określonych parametrów w analizie
modelu metodą regresji. Najpopularniejsze plany optymalne to plany: D-, E-, A-, G- oraz V-
optymalne.

Plan D-optymalny minimalizuje wartość uogólnionej wariancji parametrów modelu.

Zadanie to sprowadza się do maksymalizacji wyznacznika macierzy informacyjnej M.

Plan E-optymalny minimalizuje wartość największej wariancji parametrów modelu,

poprzez maksymalizację najmniejszej wartości własnej macierzy M.

Plan A-optymalny minimalizuje średnią wariancję parametrów modelu. Zadanie to

polega na minimalizacji śladu macierzy kowariancyjnej C, będącej odwrotnością macierzy M.

Plany G-(V-) optymalne polegają natomiast na minimalizacji największej (średniej)

wartości wariancji prognozowanej wartości funkcji modelu (wzór 6.15) w punktach
stanowiących plan eksperymentu.

Z uwagi na szczególny charakter każdego przeprowadzanego eksperymentu wybór

konkretnego planu pozostaje zawsze w gestii badacza, który często kieruje się własnymi
kryteriami lub intuicją. Plan doświadczenia musi jednak spełniać podstawowe kryteria:
informatywności, realizowalności i efektywności.

Kryterium informatywności planu polega na jego zdolności do dostarczenia wymaganej

ilości informacji potrzebnej do osiągnięcia założonego celu badań.

Jeżeli np. celem badań jest wyznaczenie wielomianu aproksymującego stopnia i, o

liczbie współczynników niewiadomych P, wówczas powinny być spełnione zależności:

n ≥ P (6.13)

L ≥ i + 1 (6.14)

gdzie: n – liczba układów planu; L – liczba poziomów każdej wielkości wejściowej.
Zastosowanie tego kryterium do wyboru planu doświadczenia spowoduje odrzucenie

planów nie spełniających warunków (6.13) i (6.14).

Kryterium realizowalności planu polega na sprawdzeniu, czy analizowany plan jest

możliwy do fizycznej realizacji na stanowisku badawczym, w szczególności czy badany
obiekt będzie funkcjonował dla zadanego zbioru punktów pomiarowych. Plany nie
możliwe do realizacji są odrzucane, a o ostatecznym wyborze decyduje kryterium
efektywności.

Kryterium efektywności dotyczy ograniczenia kosztów i czasu badań poprzez

zmniejszenie liczby wykonywanych pomiarów. Ograniczenie liczby pomiarów zmniejsza
jednak możliwość dokładnego wyznaczenia funkcji obiektu badań. Trzeba zatem pójść na
kompromis między wzrostem dokładności identyfikacji funkcji obiektu uzyskiwanej przy
zwiększaniu liczby pomiarów, a redukcją kosztów badań uzyskiwaną z kolei przy
zmniejszaniu liczby pomiarów.

6.4. Realizacja pomiarów

Dla każdego układu x

u

zawartego w macierzy planu eksperymentu X wykonywany jest

pomiar, którego wynik stanowi u-element wektora kolumnowego wielkości wyjściowych
y = [y

1

, y

2

, ..., y

u

, ..., y

n

]

T

.

W rzeczywistym obiekcie badań na wielkość wyjściową y oprócz wielkości

wejściowych x

k

wpływają również wielkości zakłócające {h} mające charakter losowy.

Wielkość wyjściowa y jest zatem zmienną losową, do której opisu stosuje się dwie miary:

12

a) położenia (np. wartość oczekiwana),
b) rozproszenia (np. odchylenie standardowe).

Wyznaczenie wartości parametrów statystycznych zmiennej losowej wymaga

przeprowadzenia dodatkowych pomiarów (powtórzeń) w celu uzyskania próby z populacji
generalnej.

Przyjmuje się następujące warianty realizacji powtórzeń:

1. Dla każdego układu planu doświadczenia wykonuje się jednakową liczbę r powtórzeń.

Wariant ten stosuje się wówczas, gdy na podstawie analizy obiektu badań można
przypuszczać, że zakłócenia losowe zależą od wartości x

k

.

2. Jeżeli w planie doświadczenia występują jednakowe układy (np. plan ortogonalny,

rotalny) wówczas dla każdego układu wykonuje się jeden pomiar, a powtórzenia
uzyskuje się dzięki pomiarom wartości wielkości wyjściowej dla jednakowych
układów.

3. Powtórzenia realizuje się niezależnie od planu doświadczenia dla arbitralnie wybranych

wartości x

k

.

6.5. Analiza danych empirycznych

6.5.1. Identyfikacja modelu obiektu badań

Model obiektu badań przedstawia się w postaci zależności matematycznej nazywanej

funkcją modelu, opisującej związek między wielkościami wejściowymi x, a wielkością
wyjściową modelu

yˆ

:

yˆ

= f (x ; a) (6.15)

gdzie

a = [a

1

, a

2

, ...a

P

]

T

(6.16)

jest wektorem P parametrów.

Istotną kwestią jest ustalenie struktury modelu, a więc odpowiedni wybór funkcji

modelu. Przy złym wyborze nie uzyskamy dostatecznego dopasowania wyników pomiarów
do wartości wyjściowych modelu dla punktów pomiarowych nie wchodzących w skład
planu doświadczenia. Przyjęty model nie będzie wówczas adekwatny do obiektu badań i
uniemożliwi przewidywanie przebiegu zjawiska lub zachowania obiektu w różnych
warunkach.

Najczęściej stosowaną funkcją modelu jest liniowa kombinacja funkcji bazowych

yˆ

= a

0

f

0

(x) + a

1

f

1

(x) + … + a

P

f

P

(x), (6.17)

którą można zapisać w postaci wektorowej

yˆ

= [f(x)]a (6.18)

gdzie: f(x) = [f

0

(x), f

1

(x), ..., f

P

(x)] jest wektorem funkcji bazowych.

Jeżeli liczba pomiarów n wykonywanych w trakcie eksperymentu jest równa liczbie

parametrów P (plan nasycony) wówczas identyfikacja parametryczna modelu opisanego
funkcją (6.15) polega na rozwiązaniu układu P równań

f [x

1

(u), x

2

(u), ..., x

i

(u); a

1

, a

2

, ..., a

P

] = y(u), u = 1, 2, ..., n (6.19)

względem parametrów a

1

, a

2

, ..., a

P

.

13

Jeżeli liczba pomiarów n jest większa od liczby parametrów P (plan nienasycony)

wówczas identyfikację parametryczną przeprowadza się metodą regresji polegającą na
znalezieniu takich wartości parametrów a

1

, a

2

, ..., a

P

, dla których funkcja modelu

aproksymuje, najlepiej w sensie przyjętego kryterium, wyniki pomiarów y
przeprowadzonych dla ustalonego planu doświadczenia X.

Najbardziej rozpowszechnioną metodą aproksymacji jest metoda najmniejszych

kwadratów. W metodzie tej funkcjonałem podlegającym minimalizacji jest suma
kwadratów błędów aproksymacji

( )

[

]

( ) ( )

[

] (

) (

)

)

(

ˆ

ˆ

ˆ

T

2

2

a

y

y

y

y

ϕ

=

−

−

=

−

=

∆

=

∑

∑

u

y

u

y

u

S

(6.20)

gdzie:

y

ˆ jest wektorem kolumnowym wyjść modelu obliczonym ze wzoru (6.15), a

sumowanie wykonuje się względem numeru pomiaru u = 1, 2, ..., n.

Minimalizacja funkcjonału (6.20) sprowadza się do poszukiwania minimum funkcji

ϕ

zależnej od P zmiennych rzeczywistych a

1

, a

2

, ..., a

P

. Warunkiem koniecznym uzyskania

minimum funkcji

ϕ jest minimalizacja pochodnych cząstkowych

0

=

∂

∂

p

a

ϕ

; p = 1, 2, ..., P (6.21)

Warunek ten dla modelu liniowego względem funkcji bazy (6.17) jest również
wystarczający.

Dominującą postacią funkcji aproksymującej utworzonej na bazie modelu liniowego

względem funkcji bazy jest wielomian algebraiczny drugiego stopnia, z podwójnymi
iloczynami stanowiącymi tzw. interakcje, o ogólnej postaci:

...

...

...

ˆ

2

1

12

2

2

1

11

1

1

0

+

+

+

+

+

+

+

+

=

x

x

a

x

a

x

a

x

a

x

a

a

y

i

ii

i

i

(6.22)

Przykładowo dla dwóch zmiennych wejściowych x

1

i x

2

wielomian drugiego stopnia

przedstawia się następująco:

2

2

22

2

1

11

2

1

12

2

2

1

1

0

ˆ

x

a

x

a

x

x

a

x

a

x

a

a

y

+

+

+

+

+

=

(6.23)

Wielomian ten można zapisać w postaci wektorowej (6.18) przyjmując następujące

postacie funkcji bazowych:

f

1

(x) = 1 ; f

2

(x) = x

1

; f

3

(x) = x

2

; f

4

(x) = x

1

x

2

; f

5

(x) = x

1

2

; f

6

(x) = x

2

2

(6.24)

oraz zapisując wektor funkcji bazowych oraz wektor parametrów w postaci:

f(x) = [1 x

1

x

2

x

1

x

2

x

1

2

x

2

2

] , a = [a

0

a

1

a

2

a

12

a

11

a

22

]

T

(6.25)

W oparciu o macierz planu doświadczenia X oraz na podstawie zdefiniowanych funkcji

bazowych (6.24) tworzona jest macierz F o wymiarze n

× N

b

, która odgrywa rolę macierzy

obserwacji nowych zmiennych wejściowych. Liczba tych zmiennych jest równa liczbie
identyfikowanych parametrów N

b

. Tworzenie macierzy F polega na wykonaniu na

argumentach x

ku

macierzy X operacji określonych przez poszczególne funkcje bazowe. Dla

wielomianu drugiego stopnia macierz F ma postać:

14









































=

2

2

2

1

2

1

2

1

2

2

2

1

2

1

2

1

2

22

2

21

22

21

22

21

2

12

2

11

12

11

12

11

,

,

,

,

,

1

...

...,

...,

...,

...,

,

1

,

,

,

,

,

1

...

...,

...,

...,

...,

,

1

,

,

,

,

,

1

,

,

,

,

,

1

n

n

n

n

n

n

u

u

u

u

u

u

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

F

(6.26)

Identyfikacja parametryczna modelu dla planu nasyconego sprowadza się do

rozwiązania układu równań

Fa = y (6.27)

Dla planu nienasyconego układ ten jest sprzeczny ze względu na błędy pomiarów

wielkości wyjściowej y i/lub nieodpowiedni dobór struktury modelu. W takiej sytuacji
wykorzystując warunek minimalizacji funkcjonału danego wzorem (6.20) rozwiązuje się
tzw. równania normalne określone wzorem

F

T

Fa = F

T

y (6.28)

Jeżeli w trakcie wykonywania pomiarów przyjęto liczbę powtórzeń u-tego układu planu

doświadczenia równą r

u

wówczas równania normalne zapisuje się w postaci

F

T

RFa = F

T

R

y

(6.29)

gdzie R jest macierzą diagonalną powtórzeń pomiarów o wymiarze n

× n:

R = diag (r

1

, r

2

, ..., r

n

) (6.30)

Wektor

y

jest natomiast wektorem wartości średnich wielkości wyjściowej dla

kolejnych układów planu doświadczenia

[

]

T

2

1

,...,

,...,

,

n

u

y

y

y

y

=

y

(6.31)

∑

=

=

u

r

j

j

u

u

u

y

r

y

1

)

(

1

(6.32)

Rozwiązanie układu równań (6.28) wymaga w pierwszej kolejności wyznaczenia

macierzy informacyjnej Fishera o postaci:

M = F

T

RF (6.33)

Następnie oblicza się wyznacznik macierzy informacyjnej i sprawdza warunek

det (M) ≠ 0 (6.34)

Jeżeli warunek ten nie jest spełniony wówczas macierz M jest osobliwa i należy

zmodyfikować plan doświadczenia. W przeciwnym razie oblicza się macierz odwrotną
(kowariancyjną) C = M

-1

i rozwiązuje układ równań normalnych ze wzoru

a = CF

T

R

y

(6.35)

15

Metoda najmniejszych kwadratów rozwiązywania układu równań normalnych jest

szczególnie przydatna do aproksymacji wyników pomiarów wielomianami liniowymi oraz
wielomianami drugiego stopnia. Dla wielomianów wyższych rzędów mogą wystąpić
trudności w ocenie zgodności funkcji modelu z zachowaniem się obiektu badań w pełnym
zakresie wartości wejściowych.

Do identyfikacji modeli obiektów, oprócz wielomianów algebraicznych, można

stosować również inne postacie funkcji aproksymujących:

- funkcje

eksponencjalne, np.

x

a

e

a

y

1

0

=

- funkcje

potęgowe, np.

1

0

a

x

a

y

=

Warunkiem zastosowania metody najmniejszych kwadratów jest wówczas

przeprowadzenie „linearyzacji” funkcji poprzez zastosowanie nowych zmiennych
pomocniczych.

Zaleca się przeprowadzanie aproksymacji dla unormowanych wartości wielkości

wejściowych. Zmniejszeniu ulegają wówczas błędy obliczeń numerycznych spowodowane
zaokrągleniami przy wielokrotnym wykonywaniu operacji matematycznych. Możliwa jest
również weryfikacja istotności współczynników funkcji testem t-Studenta.

Przedstawiona metoda rozwiązywania układu równań normalnych wymaga obliczenia

macierzy odwrotnej. Operacja odwracania macierzy jest jednak złożona obliczeniowo i
podatna na błędy numeryczne wynikające z zaokrągleń pośrednich wyników obliczeń. Z
tego względu opracowano szereg metod rozwiązywania układów równań nie
wymagających przeprowadzania operacji odwracania macierzy np. metoda eliminacji
Gaussa-Jordana, rozkład względem wartości szczególnych SVD, metody dekompozycji
LU, Choleskiego i QR. Każda z wymienionych metod odznacza się pewnymi
właściwościami, które predestynują ją do rozwiązania układu równań normalnych (6.28),
utworzonego na podstawie wybranego planu doświadczenia i z którym związana jest
określona struktura macierzy informacyjnej M.

Identyfikację modelu można zrealizować poprzez interpolację wyników pomiarów

funkcjami sklejanymi – splajnami (ang. spline). Metoda ta polega na interpolowaniu
kolejnych par danych {x

u

, y

u

} wielomianami algebraicznymi stopnia m w taki sposób, aby

uzyskać funkcję gładką tzn. ciągłą i mającą ciągłe pochodne do rzędu m – 1 włącznie na
całym przedziale [x

k min

, x

k max

]. Konieczne jest również spełnienie twierdzenia o

jednoznaczności funkcji sklejanej, orzekające że m – 1 pochodne dla argumentów x

k min

i x

k max

powinny wynosić zero. Zastosowanie metody interpolacji funkcjami sklejanymi jest

uzasadnione dla małych wartości błędów pomiarów wielkości wyjściowej y.

6.5.2. Weryfikacja adekwatności modelu obiektu

Model obiektu opisuje jego właściwości i zachowanie tylko w przybliżeniu.

Spowodowane jest to niedokładnością wyznaczenia parametrów modelu oraz
nieadekwatnością struktury modelu.
Na niedokładność wyznaczenia parametrów modelu mają wpływ następujące czynniki:
- błędy przyjętej metody identyfikacji parametrów modelu,
- błędy obliczeń numerycznych,
- błędy danych użytych do identyfikacji parametrów modelu.

Nieadekwatność struktury modelu wynika natomiast z trzech czynników:
- pominięcia wśród wielkości modelujących obiekt, czynników istotnych dla przebiegu

zjawisk w obiekcie,

- niewłaściwą specyfikacją wielkości modelujących obiekt,

16

- przyjęciem niewłaściwego typu równania modelu.

Oceny adekwatności modelu dokonuje się na dwa sposoby.
Pierwsza metoda polega obliczeniu wartości błędu aproksymacji wybraną funkcją f(

⋅)

i porównaniu jej z pewną arbitralnie wybraną wartością dopuszczalną e

d

. Jeśli obliczona

wartość błędu e

max

jest mniejsza od e

d

wówczas uznaje się wyznaczony model za

adekwatny.

Najczęściej stosuje się następujące definicje błędów aproksymacji:

a) maksymalny bezwzględny błąd aproksymacji

u

u

y

y

ˆ

max

max

−

=

ε

(6.36)

b) maksymalny błąd względny

%

100

ˆ

max

max

⋅













−

=

u

u

u

y

y

y

δ

(6.37)

c) błąd średniokwadratowy

(

)

n

y

y

n

u

u

u

∑

=

−

=

1

max

ˆ

δ

(6.38)

gdzie:
y

u

– wartość wielkości wyjściowej w u-układzie planu doświadczenia,

u

yˆ

– wartość wielkości wyjściowej obliczonej z wyznaczonej funkcji aproksymującej,

n – liczba układów planu doświadczenia.

Innym sposobem jest zastosowanie statystycznego testu istotności – testu F

(Snedecora), w którym weryfikuje się statystycznie hipotezę:

H:

σ

a

2

⇔ σ

2

, (6.39)

porównując wariancję błędów aproksymacji (wariancję adekwatności)

σ

a

2

z wariancją

niedokładności pomiarów wielkości wyjściowej

σ

2

.

Przyjmuje się następujące hipotezy:

1) hipoteza zerowa H

0

:

σ

a

2

=

σ

2

oznaczająca, iż model jest adekwatny,

2) hipoteza alternatywna: H

1

:

σ

a

2

>

σ

2

oznaczająca, iż model nie jest adekwatny.

Procedura weryfikacji statystycznej dla jednakowej liczby powtórzeń r we wszystkich

układach planu eksperymentu jest następująca:
a) Oblicza się wartość funkcji testowej

2

2

σ

σ

a

F

=

, (6.40)

przy czym:

(

)

∑

=

−

=

n

u

u

u

a

y

y

f

r

1

2

2

2

ˆ

σ

(6.41)

17

∑

=

−

=

n

u

u

f

r

1

2

1

2

1

σ

σ

,

(

)

1

1

2

)

(

2

−

−

=

∑

=

r

y

y

r

j

u

j

u

u

σ

(6.42)

W powyższych wzorach f

1

= n(r–1) jest liczbą stopni swobody wariancji

σ

2

, natomiast

f

2

= n – N

b

jest liczbą stopni swobody wariancji

σ

a

2

.

b) Na podstawie rozkładu F (Snedecora) odczytuje się z tablicy statystycznej wartość

krytyczną

1

2

,

,

f

f

F

α

odpowiadającą założonemu poziomowi ufności

α.

c) Sprawdza się warunek F ≤

1

2

,

,

f

f

F

α

. Jeśli warunek jest spełniony wówczas nie ma

podstaw do odrzucenia hipotezy zerowej i przyjmuje się, że model jest adekwatny. W
przeciwnym razie prawdziwa jest hipoteza alternatywna, czyli model nie jest
adekwatny.
Stwierdzenie na podstawie jednej z wymienionych metod nieadekwatności modelu

obiektu oznacza konieczność ponownego przeprowadzenia aproksymacji funkcją o innej
postaci lub zwiększenie liczby pomiarów dla każdego układu planu doświadczenia.

6.5.3. Weryfikacja istotności współczynników funkcji aproksymującej

Charakteryzując obiekt badań przyjmuje się określoną liczbę zmiennych wejściowych.

Nie ma jednak pewności czy wszystkie zdefiniowane zmienne wejściowe mają wpływ na
działanie obiektu. Stwierdzenie braku skorelowania określonej zmiennej wejściowej x

k

ze

zmienną wyjściową y umożliwia uproszczenie modelu badań poprzez usunięcie zmiennej
x

k

. Działanie takie jest uzasadnione głównie ze względów ekonomicznych, gdyż prostszy

model oznacza mniejszą ilość sprzętu technicznego nie-zbędnego do przeprowadzenia
pomiarów oraz uproszczenie obliczeń matematycznych.

Informacja o wpływie kolejnych wielkości wejściowych x

k

na wielkość wyjściową y jest

ukryta w wartościach współczynników funkcji aproksymującej. Przykładowo jeśli
wszystkie współczynniki przy x

2

wynoszą zero tzn. a

2

= a

22

= a

12

= 0 wówczas można

stwierdzić, że wielkość wyjściowa y nie zależy od wielkości wejściowej x

2

. Gdyby

natomiast współczynniki przy x

2

wynosiły: a

22

= a

12

= 0 oraz a

2

≠ 0 wówczas można

wyciągnąć wniosek, że wielkość x

2

wpływa na wielkość wyjściową, ale tylko liniowo. Jak

widać analiza współczynników funkcji aproksymującej jest bardzo istotna dla realizatora
badań, który uzyskuje w ten sposób istotne informacje o sposobie działania obiektu.
Analiza ta nosi nazwę weryfikacji istotności współczynników funkcji aproksymującej.
Realizowana jest w oparciu o test t-Studenta oraz ocenę wartości kowariancji wszystkich
par współczynników {a

i

, a

j

} funkcji aproksymującej f(

⋅). Kowariancję współczynników a

i

oraz a

j

oblicza się ze wzoru:

cov(a

i

, a

j

) = c

ij

⋅

σ

2

(6.43)

gdzie c

ij

jest elementem macierzy kowariancyjnej C stanowiącej odwrotność macierzy

informacyjnej M (wzór 6.31). Wykrycie nieistotnych współczynników funkcji
aproksymującej na podstawie testu t-Studenta lub ich wzajemnego skorelowania
(niezerowej wartości kowariancji) wskazuje na konieczność uproszczenia modelu. Po
wyznaczeniu funkcji aproksymującej należy ponownie przeprowadzić weryfikację jej
adekwatności. Dopiero pozytywne przejście tej weryfikacji jest podstawą eliminacji
nieistotnych współczynników.

18

6.5.4. Optymalizacja funkcji aproksymującej

Optymalizacja wyznaczonej funkcji aproksymującej f(

⋅

) polega na znalezieniu

ekstremum globalnego (maksimum lub minimum) w zadanych przedziałach wartości
wielkości wejściowych [x

k min

, x

k max

]. Istnieje wiele metod optymalizacji dedykowanych

określonym rodzajom funkcji, jednak żadna z metod nie ma charakteru uniwersalnego
gwarantującego uzyskanie ekstremum globalnego dowolnej funkcji wielu zmiennych.

Metody gradientowe optymalizacji bazują na obliczeniach wartości pochodnych

(cząstkowych, kierunkowych) optymalizowanej funkcji i wymagają spełnienia warunku
różniczkowalności funkcji w całym zakresie zmienności wartości wielkości wejściowych,
co przy pewnych postaciach funkcji aproksymujących nie jest spełnione. Ponadto
algorytmy te cechuje skłonność do utykania w ekstremach lokalnych bez gwarancji
osiągnięcia ekstremum globalnego. Z tego względu opracowano szereg algorytmów
bezgradientowych (np. metoda Monte Carlo, metoda symulowanego wyżarzania, metoda
wg Gaussa-Seidela), które w obliczeniach nie wykorzystują pochodnych optymalizowanej
funkcji. Algorytmy te są mniej efektywne od algorytmów gradientowych pod względem
dokładności wyznaczania ekstremum i cechuje je także znaczne wydłużenie procesu
obliczeniowego. W przeciwieństwie do metod gradientowych są jednak skuteczniejsze w
wyznaczaniu ekstremów globalnych.

Z uwagi na wady każdej z dostępnych metod optymalizacji zaleca się równoczesne

wykonywanie obliczeń z zastosowaniem dwóch lub trzech algorytmów oraz wybór
najlepszego wyniku.

6.6. Analiza merytoryczna wyników badań doświadczalnych

Istotnym krokiem realizacji eksperymentu jest analiza merytoryczna wyników

przeprowadzonych badań. Sposób jej realizacji jest uzależniony od natury obiektu badań.
Obiekt fizyczny wymaga na przykład odrębnej analizy niż obiekt chemiczny, a jeszcze
innej niż obiekt ekonomiczny. Niezależnie jednak od natury obiektu należy poddać ocenie
poprawność realizacji badań i skuteczność zastosowanych metod analizy danych
empirycznych.

Wyznaczenie funkcji aproksymującej modelu obiektu oraz przeprowadzenie jej

optymalizacji powinno być uzupełnione sporządzeniem odpowiednich wykresów, które
pozwolą zweryfikować stopień osiągnięcia założonych na wstępie celów eksperymentu
naukowego. Wykres funkcji aproksymującej można przedstawić na płaszczyźnie lub w
przestrzeni tylko dla jednej lub dwóch zmiennych wejściowych. Dla większej liczby
zmiennych sporządza się wykresy zależności zmiennej wyjściowej od każdej zmiennej
wejściowej z osobna, przy ustalonych wartościach pozostałych wielkości wejściowych.
Wartości te można wybrać arbitralnie lub przyjąć wartości optymalne, dla których funkcja
aproksymująca osiąga ekstremum. Uzyskujemy wówczas tzw. cięcia przestrzeni
wielowymiarowej w ekstremum globalnym.

Ostatecznie można sformułować wnioski poznawcze, praktyczne i rozwojowe z

przeprowadzonych badań, które mogą dotyczyć poznania nowych zjawisk, wdrożenia
nowych technologii oraz wskazać zagadnienia wymagające dalszego rozpoznania na drodze
doświadczalnej.

19

6.7. Inteligentne systemy planowania eksperymentu

Kluczową rolę w rozwoju nowoczesnych metod planowania eksperymentu zaczynają

odgrywać systemy inteligentne wywodzące się z obszaru inżynierii systemów
inteligentnych (ang. Intelligent Systems Engineering). Powstała koncepcja drugiej
generacji planów eksperymentu (2GD), tzw. planów inteligentnych eksperymentu (akronim:
InDE). Konieczność wprowadzania nowych metod planowania wynika z istotnych
ograniczeń dotychczasowych metod, określanych jako pierwsza generacja planów
eksperymentu (1GD).

Metodologia teorii eksperymentu w pierwszej generacji planowania eksperymentów

wymagała dopasowania przeprowadzanego eksperymentu do jednego z istniejących
planów. Plany drugiej generacji są natomiast generowane poprzez inteligentne
dostosowywanie do warunków realizacji eksperymentu.

Na gruncie nowych metod planowania dominujące dotychczas procedury weryfikacji

postawionych hipotez są wypierane przez metody eksploracyjne (Data Mining). Wśród
nich można wymienić metodę rekurencyjnego podziału (analizę dyskryminacyjną), metody
wizualne, sztuczne sieci neuronowe i algorytmy genetyczne.

Metody eksploracyjne oparte na sztucznych sieciach neuronowych stosowane do

aproksymacji funkcji badanego obiektu marginalizują aproksymację numeryczną. Metody
numeryczne wymagają bowiem dokonania wielu założeń, które często nie mają fizycznego
odzwierciedlenia w rzeczywistych obiektach. Można tu wymienić następujące
ograniczenia:
1. Konieczność realizacji eksperymentu dla ściśle określonego zbioru wartości

wejściowych występujących w wybranym planie eksperymentu, pomimo iż wartości te
mogą znacznie różnić się od obowiązujących standardów lub też nie być realizowalne w
praktyce,

2. Zachowanie stałej dla wszystkich wielkości wejściowych liczby wartości wielkości

wejściowych, co może odbiegać od fizycznych możliwości generacji poszczególnych
sygnałów wejściowych obiektu,

3. Rozmieszczenie układów planu eksperymentu zwykle z zachowaniem określonej

symetrii tworzącej regularny obszar wielkości wejściowych, co nie jest skutecznym
mechanizmem identyfikacji funkcji rzeczywistych obiektów.

Warunki te można odrzucić, jeżeli wyniki pomiarów uzyskane w oparciu o inteligentny

plan eksperymentu będą stanowiły dane do aproksymacji neuronowej. W ten sposób można
indywidualnie generować plan eksperymentu do założonych z góry cech właściwych
konkretnemu obiektowi badań i warunków realizacji eksperymentu. Istotna zaleta planu
inteligentnego polega na możliwości jego wielokrotnego generowania, aż do uzyskania
rezultatu spełniającego postulaty badacza.

6.8. Komputerowe wspomaganie badań doświadczalnych

Jeszcze do niedawna złożoność obliczeniowa stosowanych algorytmów

matematycznych stanowiła istotną przeszkodę w rozwoju teorii eksperymentu. Żmudne i
czasochłonne obliczenia wymuszały opracowywanie specjalnych planów eksperymentu
ułatwiających obliczenia oraz ograniczenie liczby przeprowadzanych analiz.

Obecnie dysponujemy znacznymi mocami obliczeniowymi jakie oferują nam

komputery osobiste i problem złożoności obliczeniowej algorytmów nie ma już istotnego
znaczenia. Szeroko rozpowszechnione jest oprogramowanie CADEX/DOE (akronim:
Computer Aided Design and Analysis of Experiments / Design of Experiments)
wspomagające prowadzenie badań doświadczalnych (tablica 6.2).

20

Tablica 6.2.

Najbardziej znane o

programowanie CADEX/DOE

nazwa programu

firma lub uczelnia oferująca program

Design Expert

Stat-Ease

DAX-Expert – System ekspertowy

planowanie i analiza eksperymentu

Politechnika Krakowska

STATISTICA – moduł Planowanie

Doświadczeń

StatSoft

STATGRAPHICS PLUS

Manugistics

Matlab – Statistics Toolbox

MathWorks

JMP – The Statistical Discovery Software

SAS Institute

Oferowane oprogramowanie CADEX/DOE zawiera obszerną pomoc elektroniczną

wyjaśniającą wiele spraw związanych z planowaniem eksperymentu i podającą wskazówki
ułatwiające realizację badań doświadczalnych. Obsługa programów wymaga jednak od
użytkownika gruntownego przygotowania merytorycznego oraz umiejętności interpretacji
prezentowanych wyników analiz.

Przykład 1

Rozważmy eksperyment polegający na identyfikacji modelu zjawiska ruchu pocisku

balistycznego wystrzelonego z wyrzutni z prędkością początkową v

0

i ustawionej pod

kątem

ϕ do powierzchni Ziemi. Analizujemy wpływ dwóch wielkości wejściowych:

x

1

= v

0

i x

2

=

ϕ na zasięg pocisku y = s, tj. dystans pomiędzy wyrzutnią a miejscem

zetknięcia się pocisku z Ziemią.

Wprowadzamy następujące ograniczenia na wartości zmiennych wejściowych:

1) zakres wysokości ustawienia działa: v

0min

= 100 m/s, v

0max

= 200 m/s,

2) zakres kąta ustawienia działa:

ϕ

min

= 0,175rad = 10

°,

ϕ

max

= 1,396rad = 80

°.

Celem badań jest wyznaczenie funkcji modelu procesu w postaci wielomianu

algebraicznego drugiego stopnia o postaci:

5

2

2

1

3

3

2

2

1

2

2

2

1

1

ˆ

x

x

a

x

x

a

x

x

a

y

+

+

=

(6.44)

oraz przeprowadzenie optymalizacji funkcji modelu polegającej na znalezieniu ekstremum
globalnego w zadanych przedziałach wartości. Na podstawie charakterystyki obiektu badań
i założonego celu badań wybrano kompozycyjny, centralny plan doświadczenia o wartości
ramienia gwiezdnego

α = 1,414 zawierający n = 9 układów (tablica 6.3). Dla każdego

układu wykonano r = 10 pomiarów zasięgu pocisku i wyznaczono wartości parametrów
statystycznych: wartość oczekiwaną

u

y

i wariancję

σ

u

2

(tablica 6.3).

Identyfikację funkcji modelu przeprowadzono rozwiązując układ równań normalnych

(6.35). Uzyskano w ten sposób następujące wartości parametrów:

a

1

= 0,203 a

2

= -0,130 a

3

= -0,020

Adekwatność przyjętej struktury modelu weryfikujemy za pomocą testu F – Snedecora,

przyjmując hipotezy:
1) zerową H

0

:

σ

a

2

=

σ

2

oznaczająca, iż model jest adekwatny,

2) alternatywną: H

1

:

σ

a

2

>

σ

2

oznaczająca, iż model nie jest adekwatny.

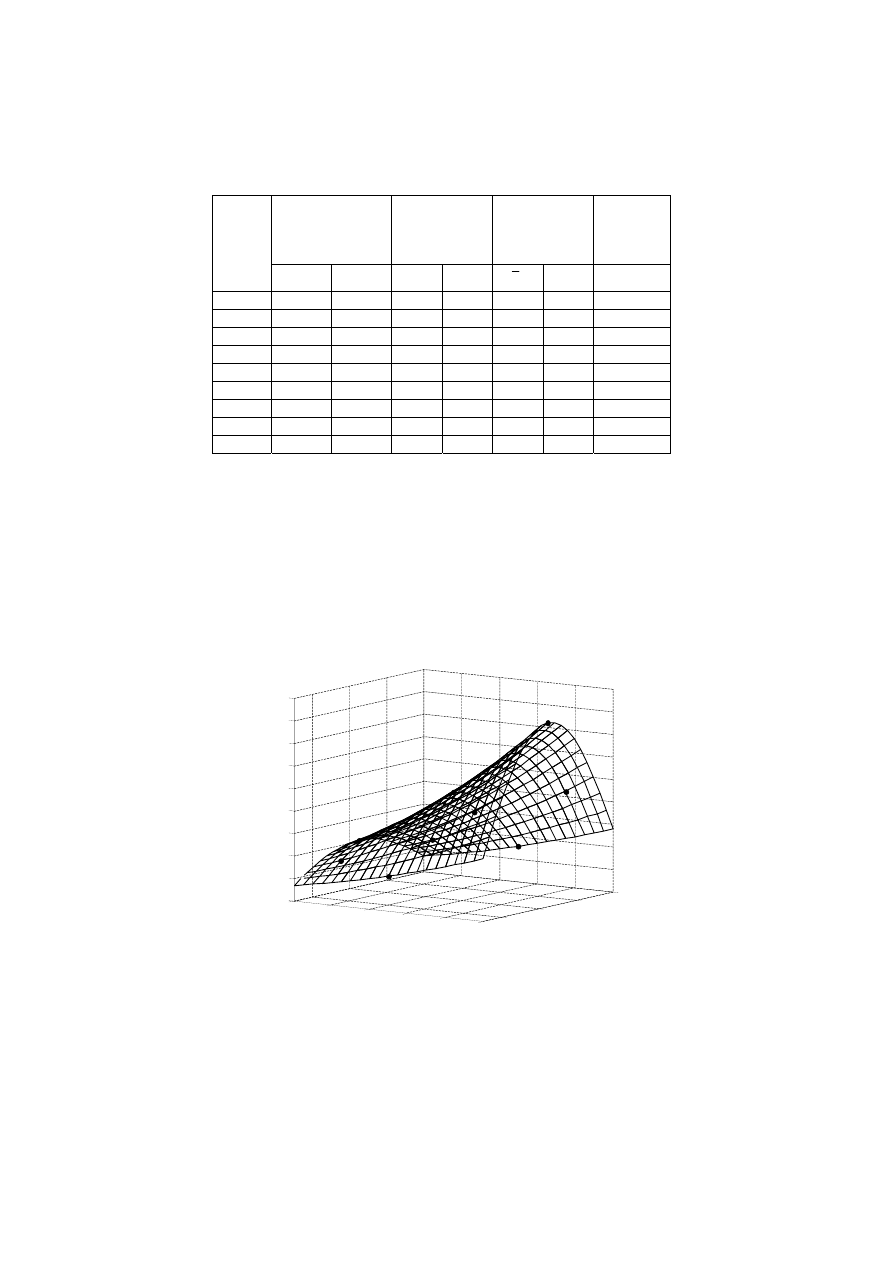
21

Tablica 6.3.

unormowane

wartości

zmiennych

wejściowych

rzeczywiste

wartości

zmiennych

wejściowych

wielkość

wyjściowa

wartość

obliczona

z funkcji

modelu

numer

układu

u

1

u

x(

2

u

x(

x

u1

x

u2

u

y

2

u

σ

yˆ

1 -1 -1

114,6 20,25

866

260

868

2 -1 1

114,6 69,75

869

197

864

3 1 -1

185,4 20,25 2266

1404

2268

4 1 1

185,4 69,75 2253

2011

2258

5 -1.414 0 100 45

1020

405 1023

6 1.414 0 200 45

4086

4858 4090

7 0

-1.414

150

10

776

121

780

8 0

1.414

150

80

790

423

789

9 0 0

150

45

2316

1406

2301

Na podstawie danych zgromadzonych w tablicy 6.3 obliczamy:

1) wariancję błędów aproksymacji (ze wzoru 6.41):

σ

a

2

= 536,7

2) wariancję wyników pomiarów (ze wzorów 6.42):

σ

2

= 1232

3) wartość funkcji testowej (ze wzoru 6.40): F = 0,4358

Dla rozkładu F – Snedecora odczytujemy z tablicy statystycznej wartość krytyczną dla

poziomu ufności

α = 0,9 i liczby stopni swobody f

1

= n(r - 1) = 81 oraz f

2

= n – N

b

= 6.

Wartość ta wynosi

1

2

,

,

f

f

F

α

= 1,8482.

Wobec spełnienia warunku F ≤

1

2

,

,

f

f

F

α

nie mamy podstaw do odrzucenia hipotezy

zerowej i przyjmujemy, że model obiektu jest adekwatny.

100

120

140

160

180

200

20

40

60

80

0

500

1000

1500

2000

2500

3000

3500

4000

4500

kąt ustawienia działa [deg]

prędkość początkowa [m/s]

zasięg
[m]

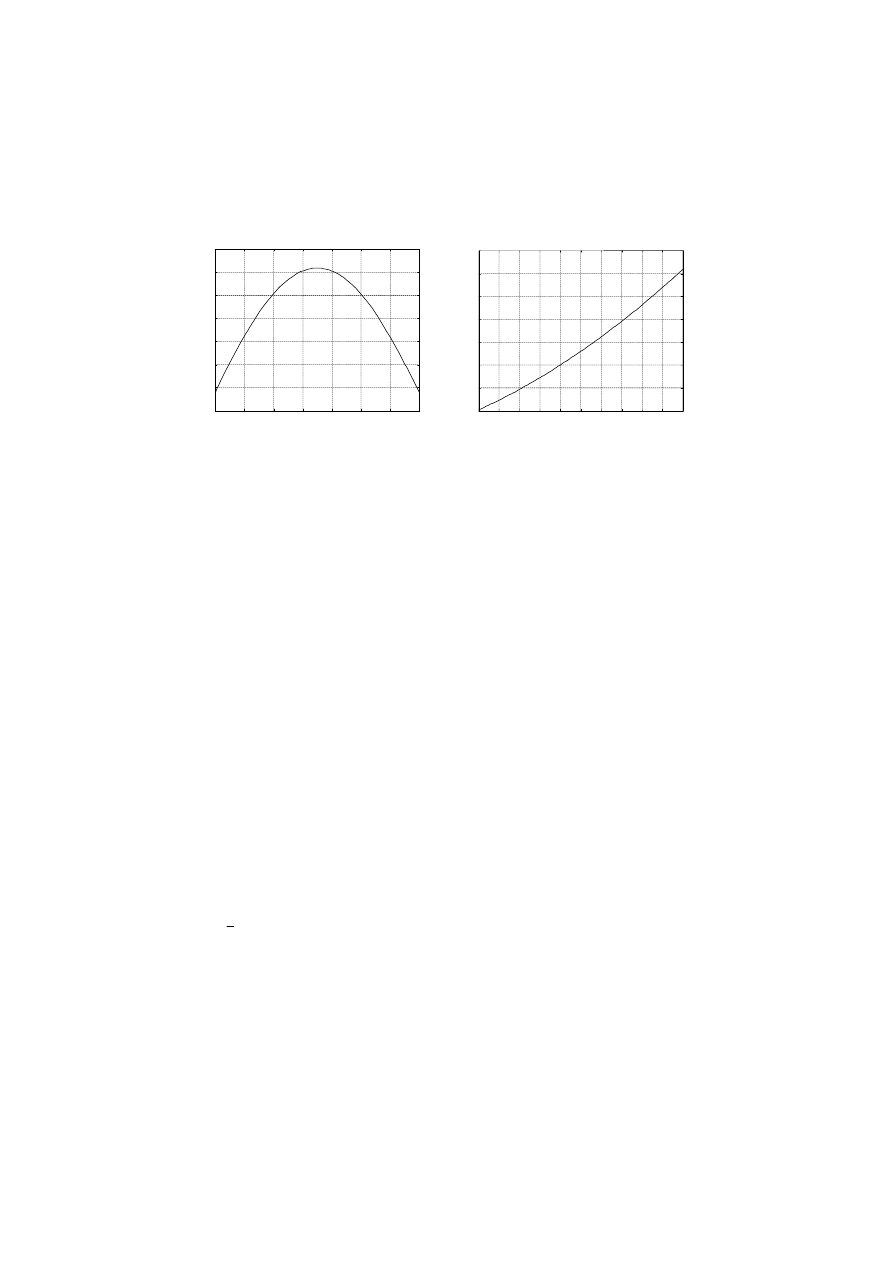
Rys. 6.10. Identyfikacja modelu zjawiska ruchu pocisku balistycznego

Optymalizację funkcji modelu przeprowadzono w oparciu o metodę gradientową

i uzyskano następujące wartości zmiennych wejściowych v

0opt

= 200m/s i

ϕ

opt

= 45

°.

22

Maksymalny zasięg pocisku balistycznego obliczony z funkcji modelu wynosi zatem
s

max

= 4090m. Rysunki 6.11a i 6.11b przedstawiają cięcia dwuwymiarowej przestrzeni

zmiennych wejściowych v

0

i

ϕ w ekstremum globalnym.

Przykład 2

Rozważmy eksperyment polegający na identyfikacji modelu procesu chemicznego

osadzania warstw półprzewodnikowych z fazy gazowej podczas produkcji układów
scalonych. Analizujemy wpływ dwóch wielkości wejściowych x

1

i x

2

na jednorodność

warstwy półprzewodnikowej (zmienna wyjściowa y), obliczonej na podstawie pomiarów
rezystancji warstwy za pomocą sondy czteroostrzowej w 49 punktach rozmieszczonych na
powierzchni płytki półprzewodnikowej.

Wielkościami wejściowymi są:

1) ciśnienie w jednostkach [torr] (1 torr oznacza ciśnienie 1 mm słupa rtęci) – zmienna x

1

,

2) iloraz objętości dwóch związków chemicznych wchodzących w skład mieszaniny

gazowej (H

2

i WF

6

) – zmienna x

2

.

Przyjęto następujące granice zmiennych wejściowych:

1) x

1min

= 4 torr, x

1max

= 80 torr,

2) x

2min

= 2, x

2max

= 10.

Celem badań jest wyznaczenie funkcji modelu procesu w postaci wielomianu

algebraicznego drugiego stopnia o postaci:

2

2

22

2

1

11

2

1

12

2

2

1

1

0

ˆ

x

a

x

a

x

x

a

x

a

x

a

a

y

+

+

+

+

+

=

(6.45)

Na podstawie charakterystyki obiektu badań i założonego celu badań wybrano

kompozycyjny, centralny plan doświadczenia o wartości ramienia gwiezdnego

α = 0,71

zawierający n = 11 układów (tablica 6.4). Dla każdego układu wykonano pomiary
rezystancji w 49 punktach i wyznaczono wartości parametrów statystycznych: wartość
średnią

u

y

i odchylenie standardowe

σ

u

. W tablicy 6.4 podano wartości odchylenia

standardowego podzielone przez wartość średnią i wyrażone w procentach.

Rozwiązując układ równań normalnych (6.35) uzyskano następujące wartości

parametrów modelu dla unormowanych zmiennych wejściowych:

a

0

= 6,198 a

1

= -1,910 a

2

= -0,224 a

12

= 1,686 a

11

= -0,197 a

22

= -0,297

10

20

30

40

50

60

70

80

1000

1500

2000

2500

3000

3500

4000

4500

kąt ustawienia działa [deg]

zasięg
[m]

100

110

120

130

140

150

160

170

180

190

200

1000

1500

2000

2500

3000

3500

4000

4500

prędkość początkowa [m/s]

zasięg
[m]

Rys. 6.11. C

ięcia dwuwymiarowej przestrzeni zmiennych wejściowych

w ekstremum globalnym

: a) s = f(

ϕ

) dla

v

0

= v

0opt

, b) s = f(

v

0

) dla

ϕ =ϕ

opt

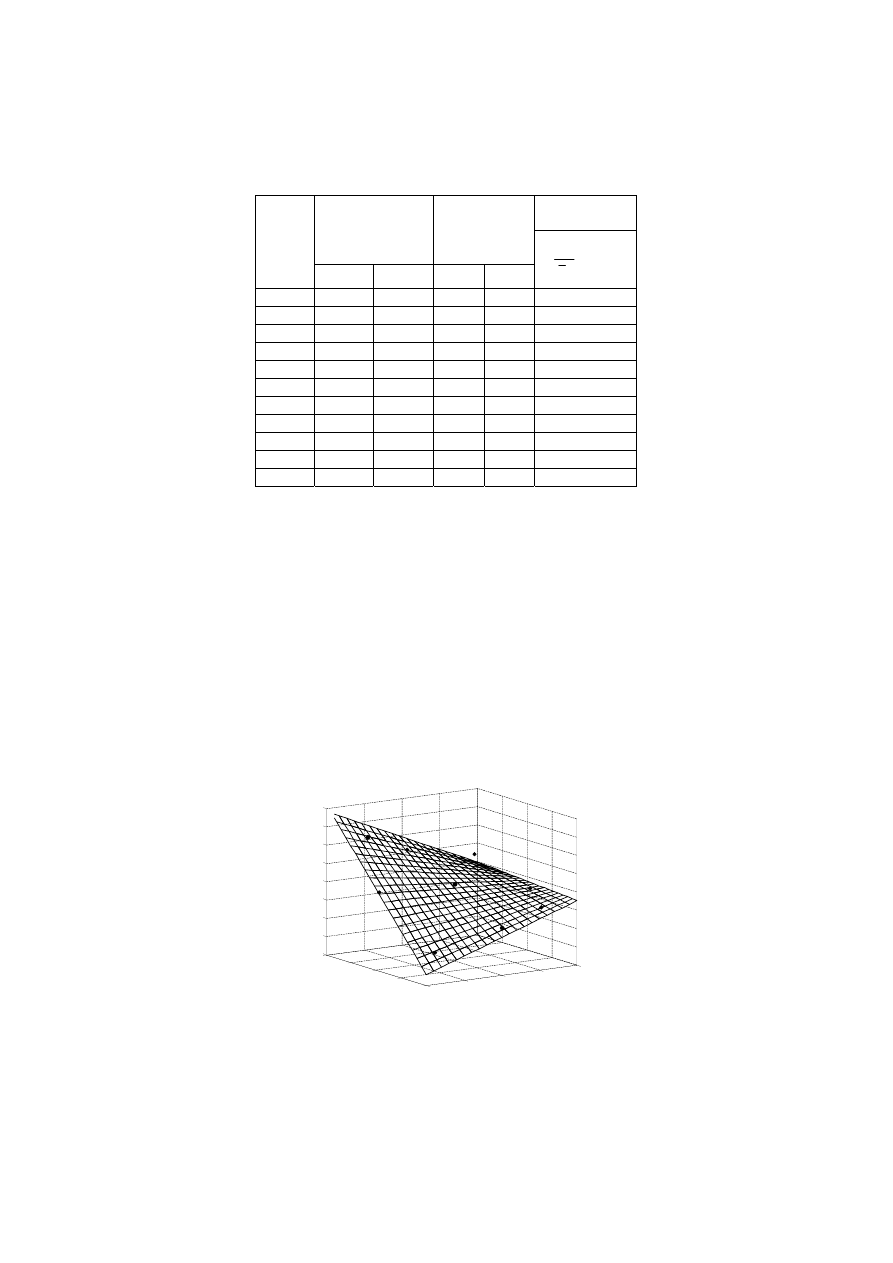
23

Tablica 6.4.

wielkość

wyjściowa

unormowane

wartości

zmiennych

wejściowych

rzeczywiste

wartości

zmiennych

wejściowych

numer

układu

u

1

u

x(

2

u

x(

x

u1

x

u2

%

100

2

⋅

u

u

y

σ

1 -0,71

-0,71

15,13

3,17 8,6

2 -0,71

0,71

15,13

8,83 6,9

3 0,71

-0,71

68,87

3,17 3,4

4 0,71

0,71

68,87

8,83 5,1

5 -1 0 4 6 7,3
6 1 0 80

6 4,6

7 0 -1

42

2 6,3

8 0 1 42

10 5,4

9 0 0 42

6 6,2

10 0 0 42

6 6,4

11 0 0 42

6 5,0

Następnie przeprowadzono analizę istotności współczynników funkcji aproksymującej

testem t-Studenta. Współczynniki a

11

i a

22

okazały się nieistotne więc dokonano

identyfikacji modelu o uproszczonej postaci:

2

1

12

2

2

1

1

0

ˆ

x

x

a

x

a

x

a

a

y

+

+

+

=

(6.46)

uzyskując następujące wartości parametrów:

a

0

= 5,978 a

1

= -1,910 a

2

= -0,224 a

12

= 1,686

Adekwatność przyjętej struktury modelu zweryfikowano testem F-Snedecora.

Pozytywne przejście tego testu umożliwiło eliminację współczynników a

11

i a

22

z funkcji

modelu.

Ostatecznie korzystając z operacji denormowania uzyskano następujące wartości

współczynników dla rzeczywistych zmiennych wejściowych:

a

0

= 11,246 a

1

= -0,117 a

2

= -0,526 a

12

= 0,011

0

20

40

60

80

2

4

6

8

10

2

3

4

5

6

7

8

9

10

iloraz objętości H

2

/WF

6

ciśnienie [torr]

jednorodność

Rys. 6.12.

Identyfikacja modelu procesu

osadzania warstw półprzewodnikowych