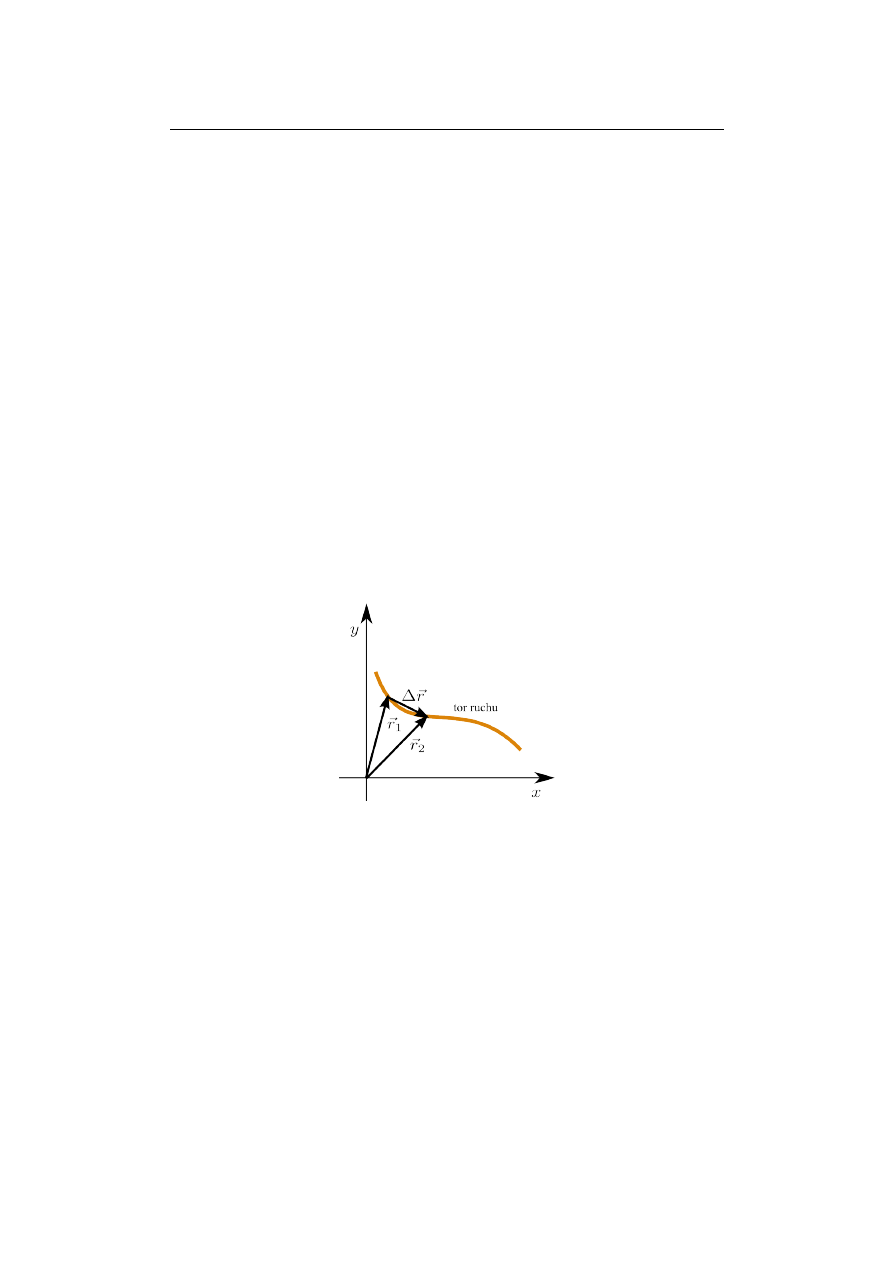
Prędkość jako wielkość wektorowa

1

Położenie w przestrzeni

Do opisu położenia w przestrzeni nie wystarcza podanie jednej liczby np. odległości.
Zauważmy, że w takim wypadku:

• odległość od punktu wyznacza jednoznacznie jedynie sferę,

• odległość od prostej wyznacza jedynie powierzchnię walcową,

• a odległość od płaszczyzny wyznacza jedynie płaszczyznę.

Dochodzimy w końcu do wniosku, że do jednoznacznego podania położenia punk-

tu w przestrzeni potrzebne są przynajmniej trzy liczby. Na przykład odległości od
płaszczyzn wyznaczonych przez osie kartezjańskiego układu współrzędnych czy też
odległości i kąty w innego rodzaju układach (współrzędne walcowe lub sferyczne).

Taka trójka liczb stanowi wektor, na których zdefiniowanych jest wiele działań

matematycznych upraszczających zapis jak i obliczenia.

Oprócz graficznego przestawiania wektora w postaci narysowanej strzałki, stoso-

wać będziemy współrzędne kartezjańskie xyz i wektory przy ich użyciu zapisane. Jest
kilka sposobów zapisu wektora położenia:

r = ~

r = [r

x

, r

y

, r

z

] = [x, y, z]

Dwa pierwsze sposoby (fontem pogrubionym i ze znakiem strzałki) są ogólniejsze

bo niekoniecznie oznaczają wektor w zapisie współrzędnych kartezjańskich. Wektor
położenia jest najłatwiejszy do wyobrażenia bo bezpośrednio odnosi się do przestrzeni
geometrycznej (rys.

1

).

Rys. 1. Położenie jako wektor ~

r

1

i ~

r

2

w uładzie odniesienia xy. Zmiana położenia

(przemieszczenie) reprezentowana jest przez wektor ∆~

r.

Wektorami jest też wiele innych wielkości a współrzędne tych wektorów wyrażo-

ne są w stosownych jednostkach. Rysowanie ich wiąże się z obraniem pewnej skali,
przelicznika pomiędzy odległością na papierze a wartością wielkości.

1

Prędkość jako wielkość wektorowa

Wektor prędkości jest zdefiniowany jako stosunek wektora przemieszczenia do czasu
w jakim to przemieszczenie nastąpiło. Wektor prędkości ma więc taki sam kierunek
jak wektor przemieszczenia.

Długości wektora prędkości (czyli wartości prędkości) nie można jednak porów-

nywać do długości wektora przemieszczenia bo po pierwsze są wyrażone w innych
jednostkach a po drugie im krótszy weźmiemy pod uwagę odcinek czasu to prze-
mieszczenie się zmniejsza a prędkość nie (niekoniecznie). O ile wektor przemieszczenia
(rys.

2

) ma naturalną skalę odległości to dla wektora prędkości skalę tę trzeba obrać.

Wektor prędkości średniej zdefiniowany jest jako

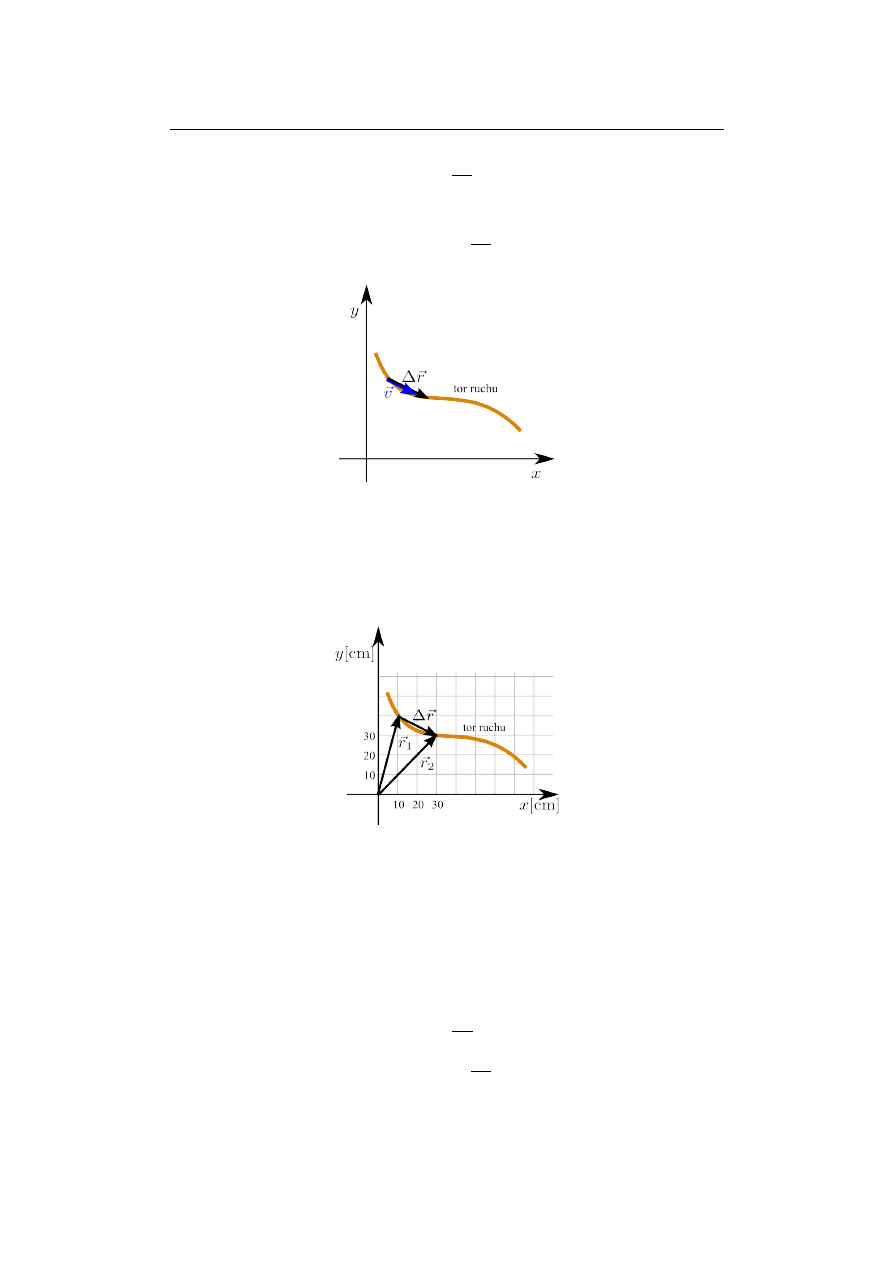
Przyspieszenie styczne i przyspieszenie dośrodkowe

2

v

sr

=

∆~

r

∆t

,

a wektor prędkości chwilowej jako

v

ch

= lim

∆t→0

∆~

r

∆t

.

Rys. 2. Wektor prędkości (~

v) jest równoległy do wektora przemieszczenia ( ~

∆t)

Przykład. 1. Na rys.

3

zaznaczone są dwa położenia ~

r

1

i ~

r

2

poruszającego się punktu.

Wiedząc, że zaznaczona zmiana położenia nastąpiła w czasie ∆t = 0,2 s wyznacz
wektor prędkości (wartość, kierunek, składową x, składową y).

Rys. 3. Ilustracja do przykładu

1

2

Przyspieszenie styczne i przyspieszenie dośrodko-
we

Podobnie zdefiniowany jest wektor przyspieszenia (rys.

4

):

a

sr

=

∆~

v

∆t

,

a

ch

= lim

∆t→0

∆~

v

∆t

.

Bardzo przydatnym jest rozdzielenie wektora przyspieszenia na dwie składowe ale

nie kartezjańskie xy lecz na przyspieszenia styczne i przyspieszenie dośrodkowe
(inaczej: normalne lub radialne). Pierwsza składowa odnosi się do zmian wartości
prędkości a druga do zmian kierunku prędkości.

Przyspieszenie styczne i przyspieszenie dośrodkowe

3

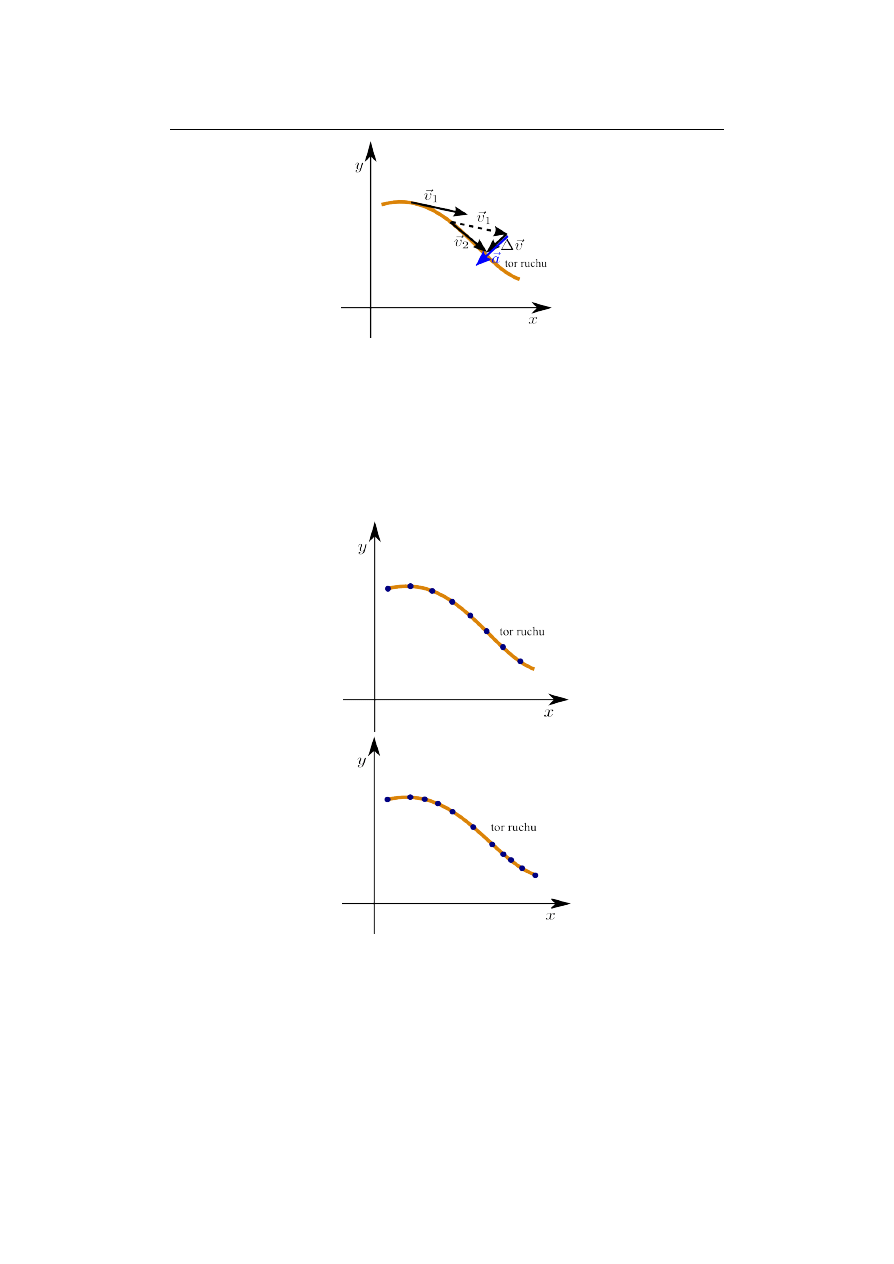
Rys. 4. Wektor przyspieszenia (~a) jest równoległy do wektora zmiany prędkości ( ~

∆v)

Zwróćmy uwagę na rys. gdzie przedstawiony jest schemat poruszania się jakiegoś

ciała w układzie odniesienia xy (z lewa na prawo). Zaznaczone punkty odpowiadają
położeniu ciała w jednakowych odstępach czasu. Zwróćmy uwagę, że przypadek a)
moglibyśmy uznać za ruch bez przyspieszenia bo obiekt pokonuje takie same odległości
w każdym odcinku czasu (w odróżnieniu od sytuacji na rys. b).

a)

b)

Rys. 5. Schemat poruszania się pewnego ciała w układzie xy. Kropkami oznaczono

położenia w jednakowych odstępach czasu

To stwierdzenie jest do pewnego stopnia uzasadnione bo faktycznie nie zmie-

nia się wartość prędkości lub też inaczej przyspieszenie styczne wynosi zero.
Zmienia się jednak kierunek prędkości a to oznacza, że w sensie wektorowym mamy
do czynienia z pewną zmianą prędkości ∆~

v.

Jako, że matematycznie każdą krzywą można lokalnie czyli w danym miejscu przy-

bliżyć fragmentem okręgu o pewnym promieniu to zastanawiając się nad wartością
przyspieszenia dośrodkowego uznajmy, że mamy do czynienia z ruchem jednostajnym
po okręgu (rys.

6

).

Przyspieszenie styczne i przyspieszenie dośrodkowe

4

Rys. 6. Układ wektorów prędkości i położenia w ruchu jednostajnym po okręgu o pro-

mieniu r

Zwróćmy uwagę, że z geometrii układu wektorów ~

r i ~

v – podobieństwa trójkątów

o tym samym kącie θ wynika proporcja

∆v

v

=

∆r

r

.

Która po wstawieniu do wzoru na wartość przyspieszenia kątowego

a

d

=

∆v

∆t

,

daje nam

a

d

=

v

∆r

r

∆t

=

v

r

∆r

∆t

=

v

r

v =

v

2

r

Tak więc nawet jeśli obiekt porusza się ze stałą prędkością a zmienia się kierunek

jego ruchu to posiada on przyspieszenie – przyspieszenie dośrodkowe.

W przypadku ruchu po okręgu zagadnienie nie jest skomplikowane ale gdy tor

ruchu jest złożony pamiętać należy, że nie tylko zmienia się promień krzywizny toru
(czyli okręgu, którego częścią jest dany, mały fragment toru) ale także położenie środka
tej krzywizny.

Zagadnienie wyznaczanie promienia i środka krzywizny pominiemy bo jest ono

zasadniczo zadaniem geometrycznym a ponadto ograniczymy się zwykle do sytuacji
najłatwiejszej a więc ruchu po okręgu gdzie promień krzywizny (okręgu) jest dany lub
łatwy do zmierzenia.

Ćwiczenie. 2. Dwa jachty opuściły port o tym samym czasie. Jacht A popłynął
kursem NW z prędkością 14 węzłów, a jacht B kursem 280

◦

z prędkością 10 węzłów.

• Z prędkością o jakiej wartości poruszał się jacht A względem B?

• Po jakim czasie były odległe o 12 mil?

• Jaki namiar będzie miał jacht B względem A po tym czasie?

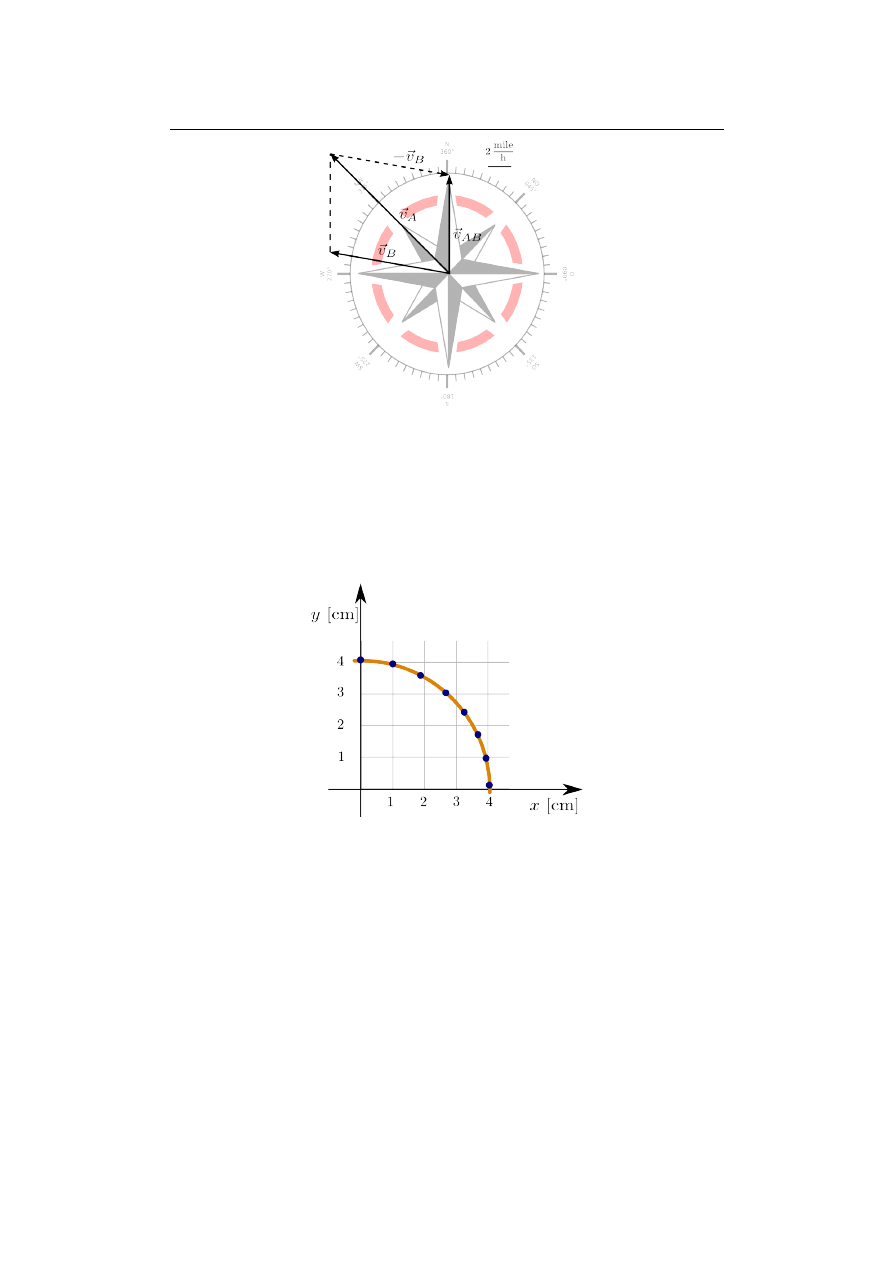
Rozw: Na rysunek róży wiatrów wektory prędkości obydwu jachtów przyjmując

zaznaczoną skalę. Prędkość z jaką poruszał się jacht A względem B otrzymamy jeśli
jacht B potraktujemy jako nieruchomy a więc dodamy do wektorów prędkości wektor
−~v

B

.

Otrzymany wektor prędkości ~

v

AB

jest właśnie poszukiwaną prędkością. Mierząc

jego długość otrzymujemy wartość 8,3 mile/h. Jest ona na tyle dokładna na ile do-
kładnie wykonaliśmy rysunek.

Przyspieszenie styczne i przyspieszenie dośrodkowe

5

Odległość między jachtami będzie rosła w tempie 8,3 mile/h tak więc jak łatwo

policzyć po około 1,5 h będzie wynosiła 12 mil.

Jachty będą ciągle w linii północ-południe tak więc jacht B będzie miał namiar

180

◦

.

Ćwiczenie. 3. Na rysunkuprzedstawiono położenia ciała w kolejnych chwilach czasu
w odstępie 0,01 s. Na podstawie analizy rysunku oszacuj przyspieszenie dośrodkowe
ciała.

Odp: Ok. 22 m/s

2

.

Ćwiczenie. 4. W niedalekiej (?) przyszłości pociągi na polskich torach będą mogły
osiągać prędkość 220 km/h. Załóżmy, że dla wygody pasażerów ogranicza się od-
czuwalne przyspieszenie do 0,06 wartości przyspieszenia ziemskiego. Zakręty o jakich
promieniach mogłyby być dopuszczalne na tych torach?

Odp: 6,3 km.

Ćwiczenie. 5. Przy użyciu arkusza kalkulacyjnego lub innego programu obliczenio-
wego wykreśl położenie kamienia rzuconego z prędkością początkową 5 m/s i kątem
30

◦

do poziomu w kolejnych chwilach czasu odległych o 0,1 s.

Rozw.: Przykład rozwiązania przedstawiony jest na rysunku poniżej. Do kolumn

tabeli wpisano wyrażenia na położenie od czasu w ruchu jednostajnym (x) oraz jed-
nostajnie zmiennym (y)

x = v

0x

t = v

0

cos(α)t = 5 cos(30

◦

) t

Przyspieszenie styczne i przyspieszenie dośrodkowe

6

y = v

0y

t −

gt

2

2

= v

0

sin(α)t −

gt

2

2

=

= v

0

sin(30

◦

) t −

9,81 t

2

2

Ćwiczenie. 6. Wykonaj podobne ćwiczenie jak poprzednieale wprowadź możliwość
łatwego dobierania prędkości początkowej i kąta rzutu.

Ćwiczenie. 7. Oblicz zasięg rzutu i maksymalną wysokość na jaką wzniesie się ka-
mień rzucony z prędkością 50 m/s pod różnymi kątami: 15, 30, 45, 60, 75

◦

.

Uwaga: Zamiast korzystać z algebraicznego rozwiązania i żmudnego przekształca-

nia wzorów można wykorzystać arkusz kalkulacyjny sporządzony dla dwóch poprzed-
nich zadań i potrzebne wielkości odczytać z wykresów lub z tabeli.

Ćwiczenie. 8. Pod jakim kątem do poziomu należy wyrzucić pocisk o prędkości
początkowej 25 m/s aby dotarł do celu odległego o 20 m? Czy rozwiązanie jest jed-
noznaczne?

Rozw. W większości podręczników można znaleźć wyprowadzenie wzoru na zasięg

w rzucie ukośnym. Skorzystajmy z niego.

z =

v

2

0

sin(2α)

g

Jak widać, w równaniu powyższym jedyną niewiadomą jest kąt α,

sin(α) =

2z

v

2

0

,

przy czym α zawierać się musi w przedziale (0, 90

◦

). Oznacza to też, że argument

funkcji sinus zawiera się w przedziale (0, 180

◦

) a co z kolei oznacza, że są dwa kąty

o tej samej wartości sinusa.

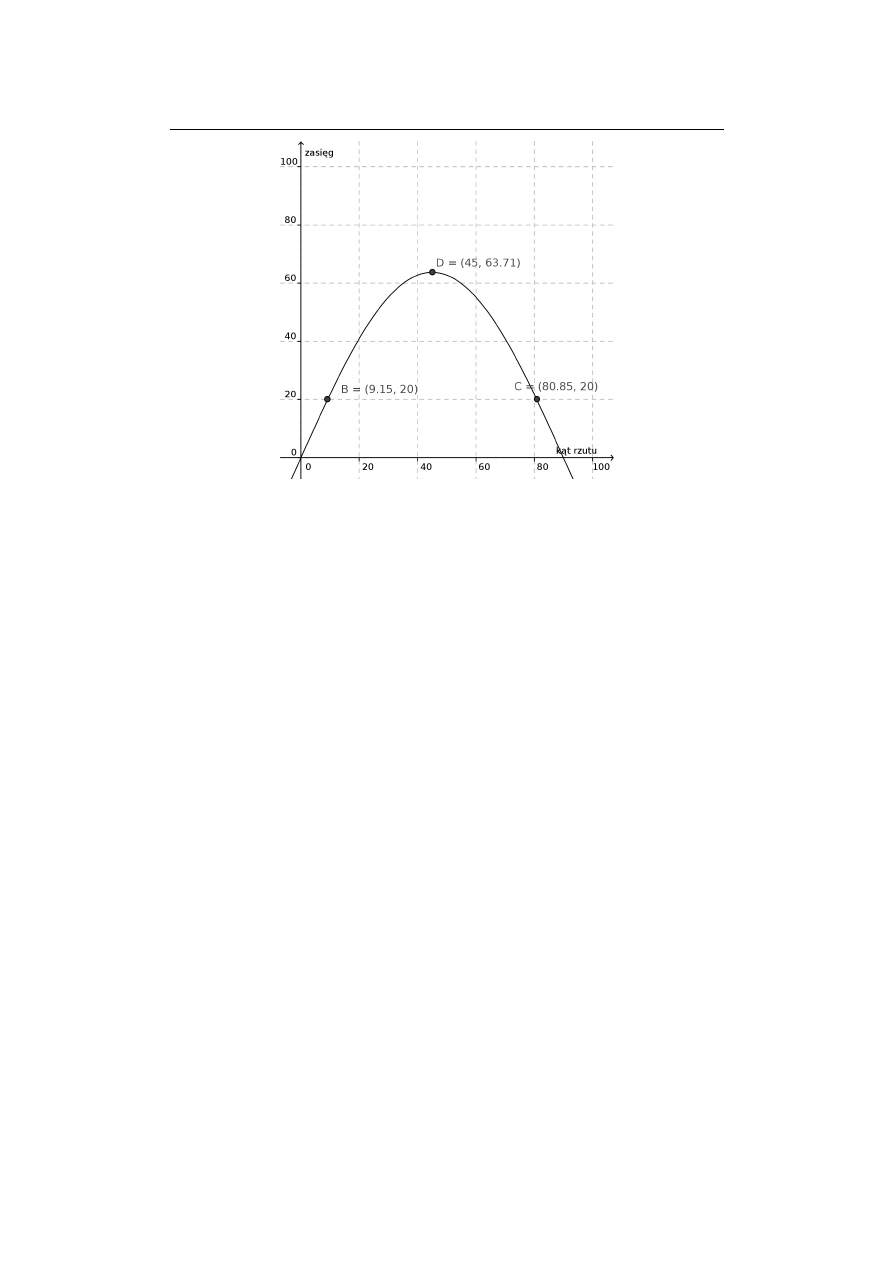
Nie rozwiązujmy jednak dalej tego zadania algebraicznie ale za pomocą stosownego

programu (tu GeoGebra) wykonajmy wykres zależności zasięgu z (oś y) od kąta α (oś
x)

y =

25

2

sin(x

◦

)

9,81

Przyspieszenie styczne i przyspieszenie dośrodkowe

7

Widać, że zgodnie z oczekiwaniami zasięg jest niewielki dla małego kąta rzutu

(rzut poziomy) oraz dla kąta bliskiego 90

◦

(rzut pionowy) osiągając maksimum przy

kącie 45

◦

.

Z wykresu możemy odczytać także kąty dla jakich zasięg wynosi 20 m, a mianowicie

9,15

◦

oraz 80,85

◦

i inne informacje jak na przykład zasięg maksymalny.

Ćwiczenie. 9. Pewien astronauta na pewnej planecie może przy odbiciu z prędko-
ścią 3 m/s doskoczyć na maksymalną odległość 15 m. Oblicz z jakim tamtejszym
„przyspieszeniem ziemskim” ma ów astronauta do czynienia.

Odp: 0,3 m/s

2

.

Ćwiczenie. 10. Pocisk został wystrzelony tak, że jego zasięg poziomy równy jest
trzykrotnej maksymalnej wysokości. Oblicz pod jakim kątem do poziomu pocisk został
wystrzelony. Podaj wynik z dokładnością do trzech miejsc znaczących.

Uwaga. Najprościej skorzystać z wykonanego wcześniej wykresu zależności za-

sięgu od kąta rzutu. Otrzymujemy kąty: 9,52

◦

oraz 77,6

◦

. Oczywiście bezpośrednio

z wykresu taką dokładność trudno osiągnąć.