...wielkie umysły,
my l podobnie...
ROZDZIAŁ IV
DRGANIA UKŁADÓW
O SKO CZONEJ LICZBIE STOPNI SWOBODY
1. WST P
2. ZAŁO ENIA DO BADA MODELI
3. DRGANIA UKŁADÓW O JEDNYM STOPNIU SWOBODY
4. DRGANIA UKŁADÓW O DWÓCH STOPNIACH SWOBODY
5. DRGANIA UKŁADÓW O SKO CZONEJ LICZBIE STOPNI SWOBODY
1. WST P
Głównym celem dynamicznego badania konstrukcji jest pomiar jej rzeczywistej
odpowiedzi dla oceny poprawno ci wyników rozwi zania teoretycznego, czyli weryfikacja
modelu matematycznego dla uzyskania informacji o obci eniach oraz innych parametrach,
które s wymagane w analizie dynamicznej. Badania dynamiczne pozwalaj na
wprowadzanie uzasadnionych zmian projektowych konstrukcji w celu podniesienia jej
warto ci u ytkowych i niezawodno ci działania.
W tym rozdziale przedstawiono podstawy teoretyczne opisu i analizy układów
mechanicznych o ró nym stopniu skomplikowania. Dotyczy to ró nej liczby stopni swobody,
decyduj cej o skomplikowaniu modelu maszyny, a tym samym o zło ono ci analizy
matematycznej.
Z punktu widzenia liczby stopni swobody wprowadza si podział układów
mechanicznych na:
-
układy o jednym stopniu swobody,
-
układy o sko czonej liczbie swobody (układy dyskretne),
-
układy o niesko czonej liczbie stopni swobody.
Układ, który mo e gromadzi tylko jedn posta energii i lokalizowa j tylko w
jednym elemencie, jest nazywany układem dynamicznym pierwszego rz du, gdy równania
opisuj ce jego ruch s funkcj tylko jednej zmiennej i jej pierwszej pochodnej. Inne zasady
przedstawiono podczas opisu zachowania si modeli układów, w ró nych warunkach
wymusze .
2. ZAŁO ENIA DO BADA MODELI
Rzeczywiste układy mechaniczne to układy masowo – dyssypacyjno - spr yste
opisywane za pomoc przemieszcze , ich pochodnych zwi zanych z odkształceniami oraz
wywołuj cymi je siłami. Wielko ci opisuj ce s ze sob sprz one, s zmienne w czasie i
nazywane s w dynamice maszyn sygnałami. Sygnały przemieszcze , pr dko ci i
przyspiesze oraz działaj cych sił maj charakter uogólniony, tzn. przemieszczenia s
zarówno translacyjne jak i rotacyjne, a siły s skupione i pary sił s reprezentowane przez ich
momenty.
Równania ruchu, opisuj ce drgania dyskretnego modelu fizycznego, maj w ogólnym
przypadku posta [33,64]:
0
)
,
,...
,...,
,
,
,...,
,...,
,
,
,...,
,...,
,
,
,...,
,
(
2
1
..
..
2
..
1
..
.
2
.
1
.
2
1
=
t
R
R
R
R
q
q
q
q
q
q
q
q
q
q
q
F
w
i
n
i
n
i
n
k
gdzie: n - liczba stopni swobody, w – liczba wi zów, t – czas, R
j
– j-ta nieznana siła
uogólniona (reakcja), q
i
– i-te przemieszczenie,
i
q
.
- i-ta pr dko uogólniona,
i
q
..
- i-te
przy pieszenie uogólnione.
Przy modelowaniu dynamicznych własno ci układów mechanicznych stosuje si
szereg uproszcze w zakresie opisu i zasad budowy modeli fenomenologicznych.
W celu modyfikacji własno ci dynamicznych układów mechanicznych buduje si
modele strukturalne, które odzwierciedlaj organizacj wewn trzn i zachowuj własno ci
transformacyjne układu.
Ka dy układ mechaniczny zło ony jest z elementów: masowych (punkty materialne,
nieodkształcalne lub odkształcalne bryły), spr ystych (spr yny) i tłumi cych (np. tłumiki).
Mówi si wi c o układach m, k, c (masowo – dyssypacyjno - spr ystych). Tylko w
uproszczeniu mo na mówi o modelu masowym, masowo-spr ystym lub masowo-
dyssypacyjnym. Ka dy układ (model), posiadaj cy własno ci spr yste wytr cony z
poło enia równowagi, b dzie realizował ruch przemienny wokół poło enia równowagi. Taki
ruch nazywamy drganiami mechanicznymi.
Drgania mechaniczne w zale no ci od: liczby stopni swobody układu, równania
(równa ) opisuj cego ruch, sposobu wytr cenia z poło enia równowagi (sposobu
wymuszenia), modelu układu, charakteru sygnału przemieszcze i kierunku ruchu dzielimy
na [14,33,71]:
- drgania układów o jednym stopniu swobody, o wielu stopniach swobody - drgania układów
dyskretnych: o niesko czonej liczbie stopni swobody - drgania układów ci głych;
- drgania liniowe; nieliniowe;
- drgania autonomiczne (swobodne); nieautonomiczne (wymuszone: zewn trznie lub
wewn trznie);
- drgania zachowawcze (bez tłumienia); niezachowawcze (z dyssypacj energii; lub z
tłumieniem);
- drgania zdeterminowane; stochastyczne;
- drgania wzdłu ne, poprzeczne, translacyjne, rotacyjne (gi tne, skr tne), itp.
Kluczem do okre lenia dynamiki obiektów czyli drga obiektów mechanicznych jest
zatem znajomo mo liwych odpowiedzi układu dynamicznego, do którego mo na
zredukowa badany obiekt.
2.1 Drgania translacyjne i skr tne
W praktycznych zastosowaniach na pocz tku rozwa a modelowane obiekty bada
przedstawiane s jako elementarne modele drgaj ce o jednym stopniu swobody. Przykłady
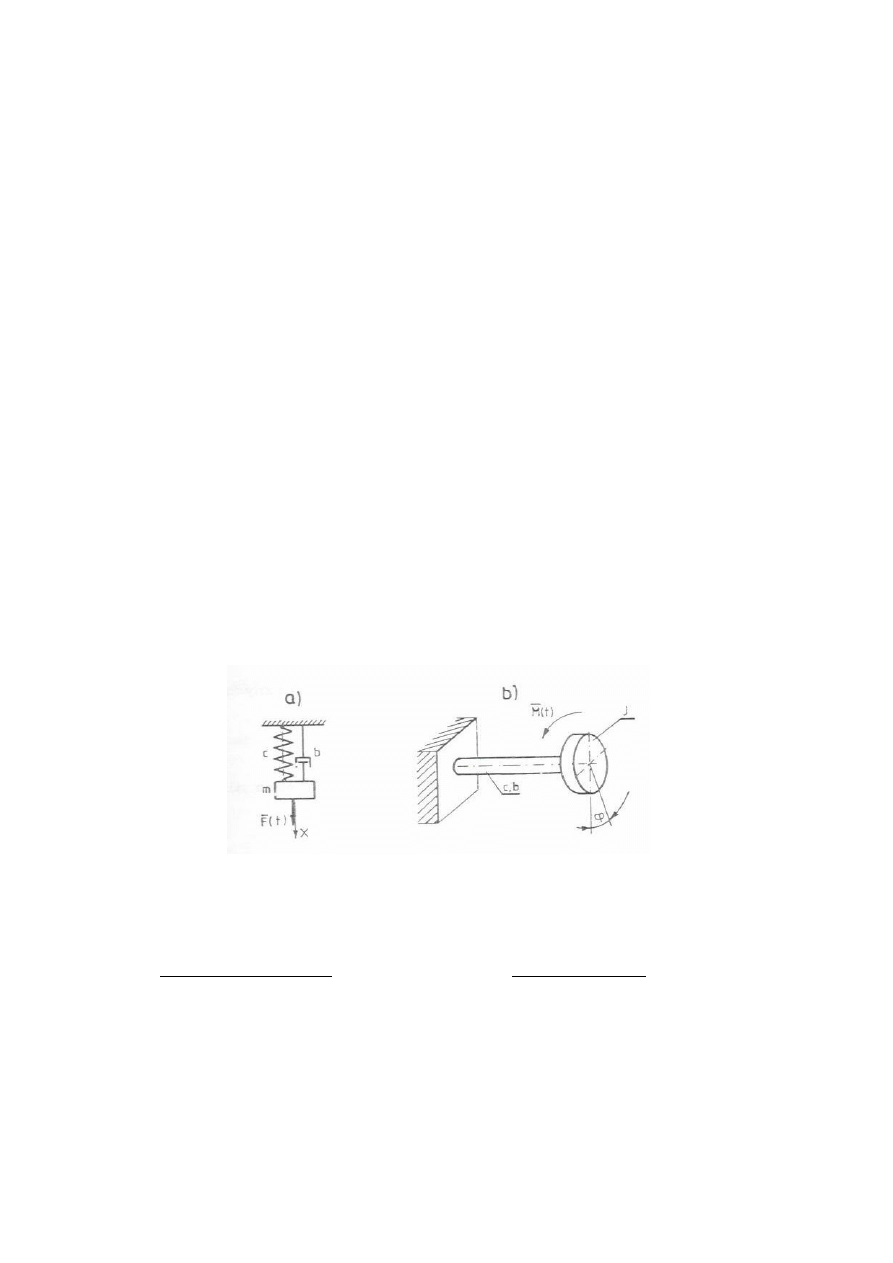
takich układów z wymuszeniem siłowym lub momentowym przedstawiono na rys. 4.1
[a).model o wymuszeniu siłowym, b). model o wymuszeniu momentowym].
Czy wnioski płyn ce z analizy drga typu skr tnego s takie same jak dla drga typu
translacyjnego?
Rys.4.1 Schematy modeli fizycznych o jednym stopniu swobody dla drga translacyjnych a).
oraz dla drga skr tnych b).
Stosuj c zasad d’Alemberta dla ka dego z modeli otrzymuje si równania:
model translacyjny a). model skr tny b).
=
+
0
bezwl
i
F
F
=
+
0
bezwl
sil
i
M
M
.
..
0
)
(
=
−
−
−
x
m
x
c
kx
t
F
0
)
(
..
.
=
−
−
−
ϕ
ϕ
ϕ
I
C
K
t
M
ostatecznie za :
)
(
.
..
t
F
kx
x
c
x
m
=
+
+
)
(
.
..
t
M
K
C
I
=
+
+
ϕ
ϕ
ϕ
(4.1)
Otrzymane równania, słuszne nie tylko dla układu o jednym stopniu swobody, s
identyczne, a wi c wnioski płyn ce z analizy ich rozwi za b d równie identyczne.
2.2 Wymuszenie siłowe i kinematyczne
Dla tej samej ogólno ci rozwa a rozpatrzmy wymuszenia siłowe i kinematyczne
przedstawione na rys.4.2. W pierwszym przypadku wymuszenie pochodzi od zadanej
zewn trznej siły b d momentu, za w drugim przypadku mamy zadany ruch na torze
(wymuszenie kinematyczne) [14].
Oba przypadki wymuszenia s modelowo równowa ne, a zadane przemieszczenie z(t)
działaj c poprzez spr yn k i tłumik c jest ródłem siły równowa nej F(t), przy czym
.
)
(
z
c
kz
t
F
+
=
. Wiedz c o tym mo na dalsze rozwa ania ograniczy do drga translacyjnych
z wymuszeniem siłowym, a wnioski przenosi na dowolny ruch z dowolnym typem
wymuszenia.
Rys.4.2 Ilustracja równowa no ci wymuszenia siłowego a). i kinematycznego b) [14].
2.3 Wyznaczanie parametrów zast pczych
Podstawowe metody wyznaczania parametrów (cech) strukturalnych modeli układów
mechanicznych to metody identyfikacji; prostej dla układów prostych i zło onej dla układów o
wielu stopniach swobody.
W przypadku prostych układów mechanicznych, niekoniecznie o małej liczbie stopni
swobody, ale z łatwym podziałem na dyskretne elementy masowe, spr yste i tłumi ce
najbardziej efektywna jest metoda analityczna oparta na znajomo ci geometrii i własno ci
materiałowych elementów konstrukcyjnych układu.
Metoda analityczna zawiera si w kilku etapach. Najpierw dokonuje si my lowej
dyskretyzacji rzeczywistego układu mechanicznego. Ł czy si elementy w grupy o
zbli onych cechach dominuj cych, np. o wyra nie przewa aj cych cechach masowych nad
spr ystymi lub tłumi cymi. Elementy masowe traktuje si wi c jako nieodkształcalne bryły
lub punkty materialne. Elementy bezmasowe ((spr yste i tłumi ce) najcz ciej traktowane
jednocze nie jako spr ysto-tłumi ce s ujmowane jako odkształcalne. Tak poł czone
elementy w grupy przedstawia si tylko jednym elementem zwanym zast pczym lub
zredukowanym. Jest on reprezentowany tylko jednym parametrem zredukowanym, b d cym
albo wprost parametrem strukturalnym, albo elementem pewnej kombinacji parametrów
zredukowanych.
Parametry zast pcze wyznacza si dla potrzeb analizy dynamiki układu, najcz ciej
przy zało eniu równowa no ci dynamicznej grupy elementów konstrukcyjnych i elementu
zast pczego. Równowa no dynamiczna oznacza równowa no energii ruchu elementów
układu rzeczywistego i elementów zast pczych, co oznacza ich równowa no energii
kinetycznej, potencjalnej i funkcji dyssypacji energii.
2.4 Wyznaczanie mas zast pczych
Rzeczywiste elementy masowe s w ogólno ci bryłami nieodkształcalnymi, wi c ich
energia kinetyczna jest sum energii kinetycznej ruchu post powego z pr dko ci V
s
rodka
masy oraz energii kinetycznej ruchu obrotowego dookoła osi chwilowego obrotu,
przechodz cej przez rodek masy.
2
2
2
1
2
1
i
i
i
i
kz
J
V
m
E
ω
+
=
(4.2)
Zast pczymi elementami masowymi mog by albo punkty materialne, albo bryły
doskonale sztywne. Zakłada si najcz ciej, e punkty materialne wykonuj ruch
prostoliniowy, a bryły ruch obrotowy dookoła stałej osi.
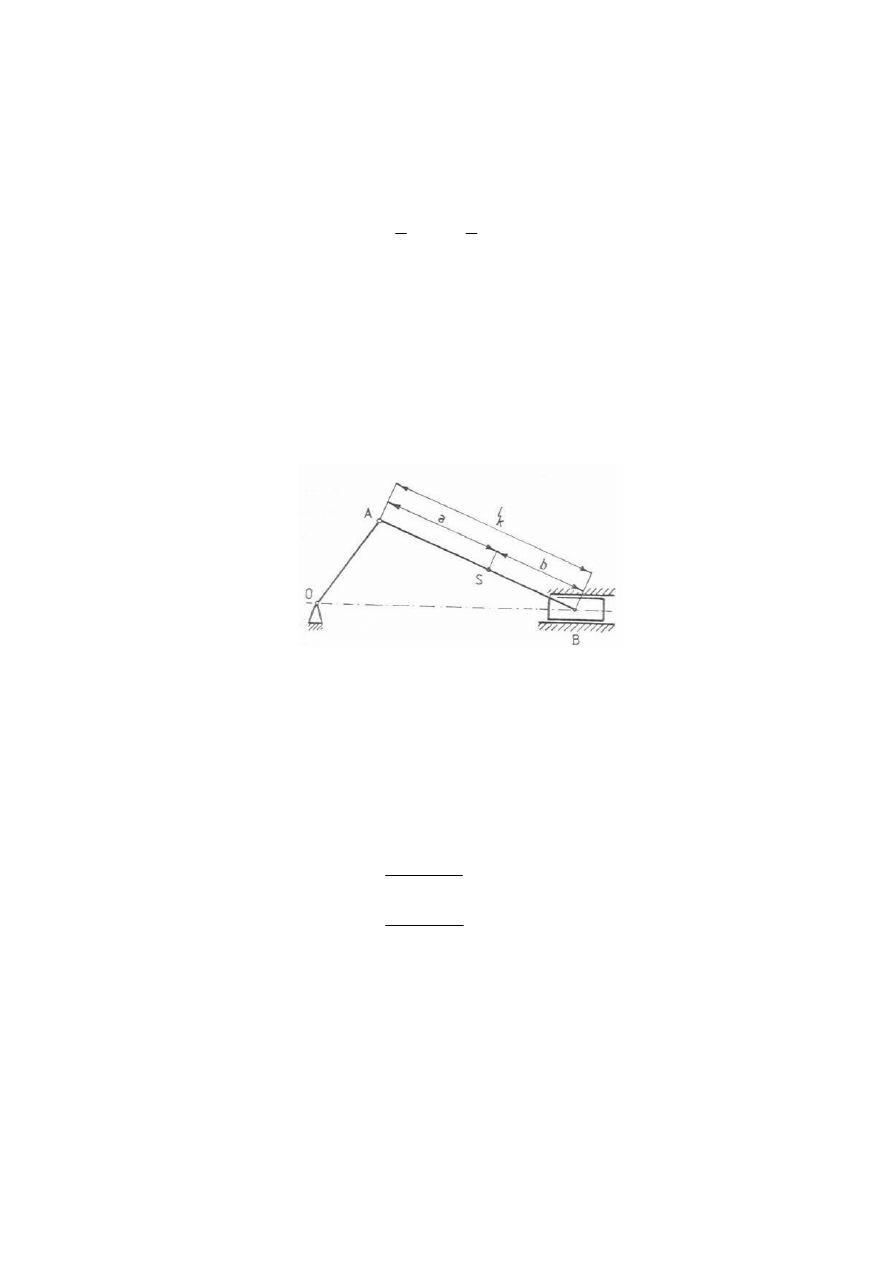
Dokonuj c redukcji masy korbowodu mechanizmu korbowo-tłokowego (rys.4.3) do
dwóch punktów A i B pokrywaj cych si z osi sworznia wału korbowego O oraz z osi
sworznia tłokowego przyjmuje si oznaczenia:
-
masa korbowodu m
k
,
-
długo korbowodu l
k
,
-
moment bezwładno ci J
s
wzgl dem osi przechodz cej przez rodek masy S odległy od osi
A o a = A S oraz od osi B o b = B S, przy czym a + b = l
k
.
Rys.4.3 Schemat mechanizmu korbowo - tłokowego.
Równowa no dynamiczna energii zachodzi musi dla dowolnych warto ci V
s
ruchu
post powego oraz
ω
ruchu obrotowego, a wi c równie dla ich szczególnych warto ci
równych niejednocze nie zeru. Wynikaj st d równania równowa no ci mas oraz
równowa no ci momentów bezwładno ci wzgl dem osi przechodz cej przez rodek masy S:
B
A
k
m
m
m
+
=
dla
ω
= 0 (4.3)
2
2
b
m
a
m
J
B
A
S
+
=
dla V
S
= 0
(4.4)
a st d warto ci mas zast pczych m
A
i m
B
:
2
2
2
b
a
b
m
J
m
k
S
A
−
−
=
(4.5)
2
2
2
a
b
a
m
J
m
k
S
B
−
−
=
(4.6)
Warunek równowa no ci statycznej oznacza równowa no momentów statycznych
układu rzeczywistego i zast pczego:
0
=
−
b
m
a
m
B
A
(4.7)
Spełnienie jednocze nie trzech warunków równowa no ci statycznej i dynamicznej
wymaga zast pienia korbowodu trzema punktami materialnymi (A,S,B) i wówczas równania
równowagi s nast puj ce:
S
B
A
k
m
m
m
m
+
+
=
2
2
b
m
a
m
J
B
A
S
+
=
(4.8)
0
=
−
b
m
a
m
B
A
Masy zast pcze w układzie tym przyjmuj posta :
;
k
S
A
al
J
m
=
;
k
S
B
bl
J
m
=
ab
J
m
m
S
k
S
−
=
(4.9)
2.5 Zast pcze sztywno ci modelowanych układów
Je eli w układzie wyst puj ró ne elementy spr yste, nale y wówczas wyznaczy
zast pczy współczynnik spr ysto ci. Mo na tu rozwa y dwa przypadki poł cze
spr ystych – poł czenie równoległe i szeregowe. Zast pczy współczynnik spr ysto ci
wyznacza si z warunku równowagi energii potencjalnych.
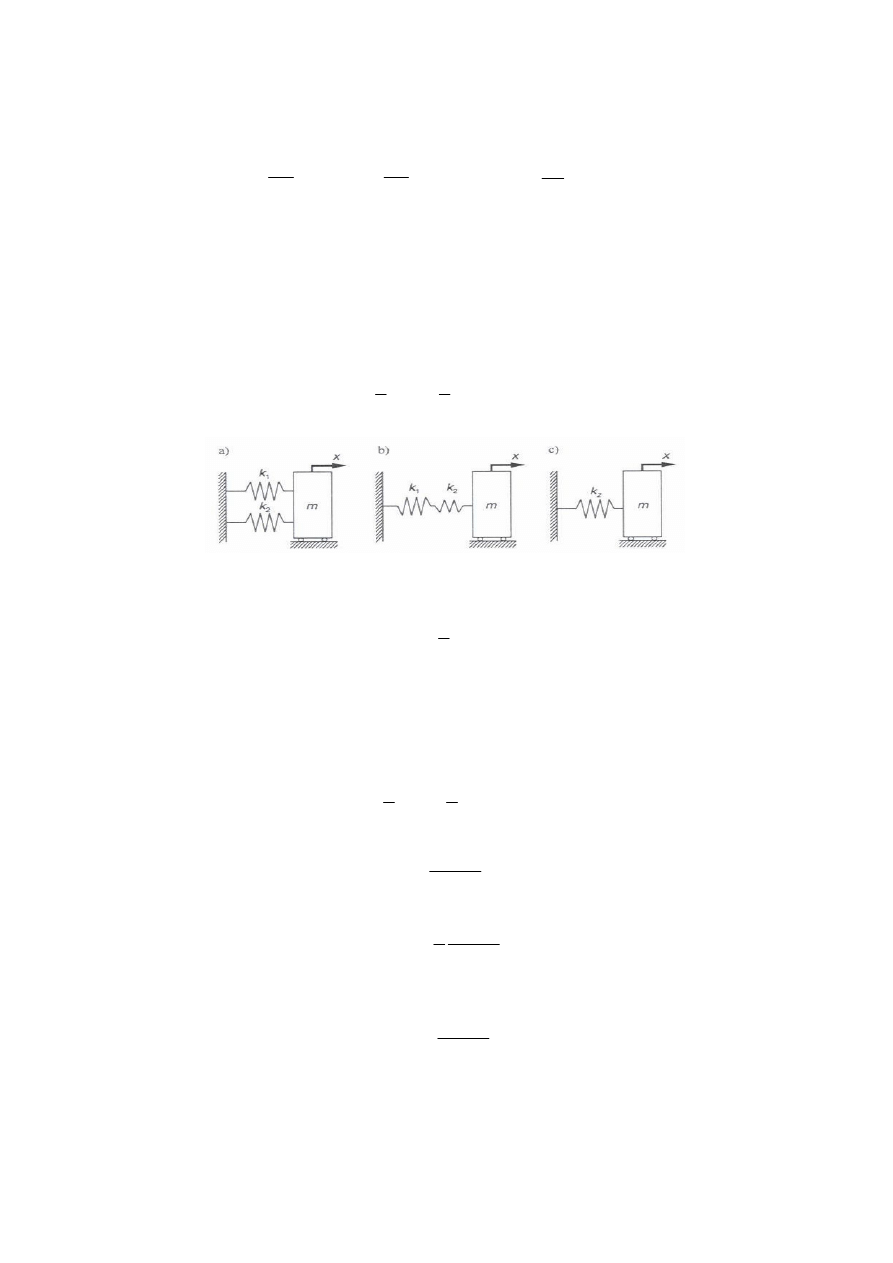
Jak wynika z rys.4.4 energia potencjalna poł czenia równoległego przy przesuni ciu o
x
wynosi:
2
2
2
1
2
1
2
1
x
k
x
k
E
P
+
=
(4.10)
Rys.4.4 Poł czenia spr yste: równoległe a). i szeregowe b). oraz sztywno zast pcza.
Energia potencjalna układu zast pczego przy tym samym przesuni ciu wynosi:
2
2
1
x
k
E
z
P
=
(4.11)
Po porównaniu tak opisanych energii otrzymuje si dla poł czenia równoległego:
2
1 k
k
z
k
+
=
(4.12)
Dla poł cze szeregowych nadajemy przesuni cie x na ko cu spr yny o
współczynniku k
2
. Spr yna o współczynniku spr ysto ci k
1
zostanie odkształcona o z i
energia potencjalna obu spr yn wynosi:
2
2
2
1
)
(
2
1
2
1
z
x
k
z
k
E
P
−
+
=
(4.13)
Poniewa w punkcie A jest równowaga dwóch sił: k
1
z = k
2
(x-z)
, mo na wyznaczy :
x
k
k
k
z
2
1
2
+
=
(4.14)
Po podstawieniu (4.14) do (4.13) i przekształceniu otrzymuje si :
2
2
1
2
1
2
1
x
k
k
k
k
E
P
+
=
(4.15)
Porównuj c dalej (4.10) i (4.15) otrzymuje si zast pczy współczynnik spr ysto ci dla
poł czenia szeregowego:
2
1
2
1
k
k
k
k
k
z
+
=
(4.16)
2.6 Oszacowanie zast pczego tłumienia obiektu
Parametr ten jest niezb dny przy oszacowaniu amplitudy odpowiedzi rezonansowej
modelu b d szybko ci zaniku drga . Do jego wyznaczenia nale y z eksperymentu
wyznaczy logarytmiczny dekrement tłumienia
∆, b d stopie tłumienia ξ oraz cz sto
własn
ω
0
, co cz sto wykorzystuje si do weryfikacji modelu.
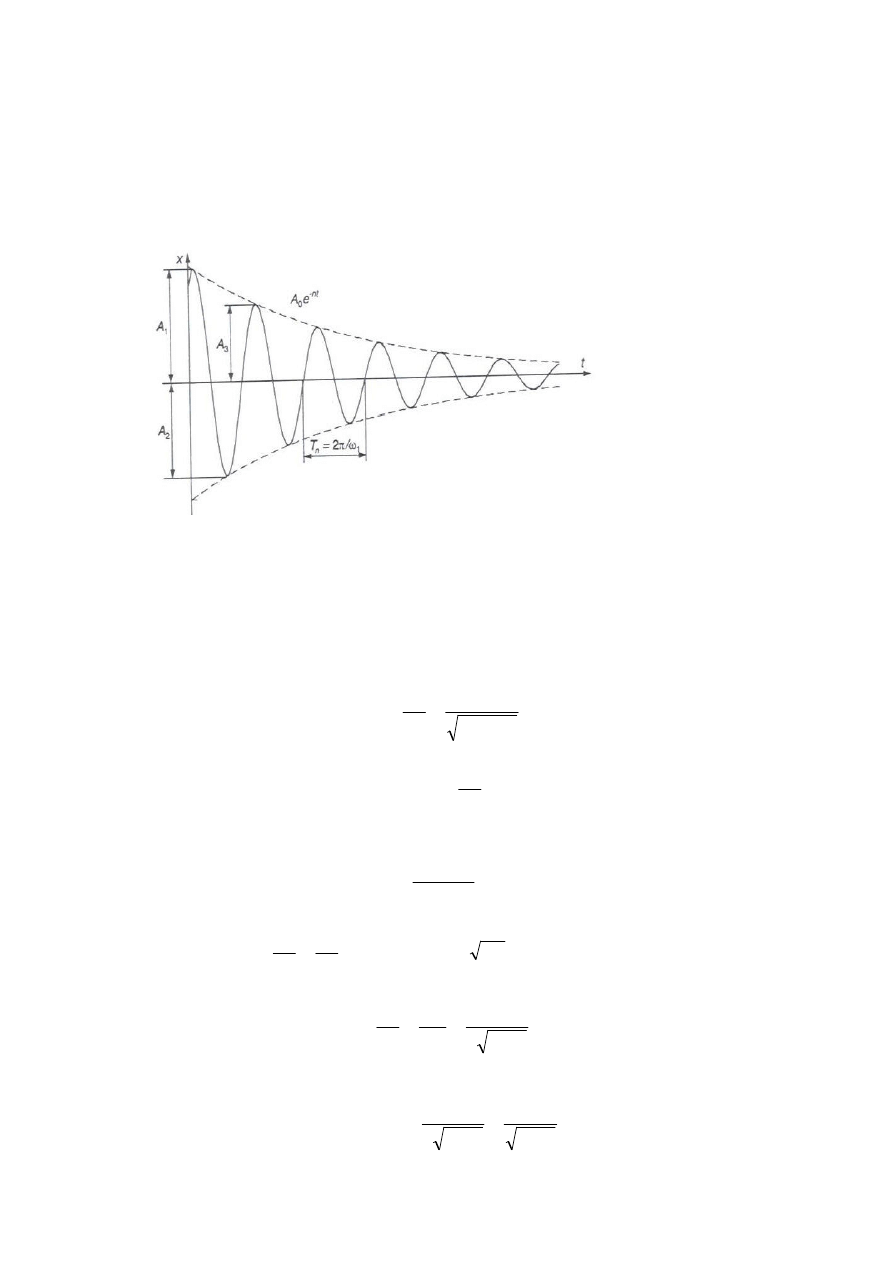
Realizacja eksperymentu testem impulsowym, polegaj cym na uderzeniowym
wymuszeniu obiektu w punkcie spodziewanego działania wymuszenia i odbiorze odpowiedzi
w punkcie redukcji R. Jako wynik uzyskuje si obraz drga zanikaj cych, przedstawiony na
rys.4.5.
ξ
Π
=
=
∆
2
ln
3
1
A
A
∆
=lnA
1
/A
3
=2
Πξ
Rys.4.5 Ilustracja do wyznaczenia logarytmicznego dekrementu tłumienia
∆ i zast pczego
tłumienia c
z
.
Wynikiem eksperymentu jest tu logarytmiczny dekrement tłumienia
∆, b d stopie
tłumienia
ξ
oraz cz sto własna
ω
0
, co słu y do weryfikacji oblicze i badanego modelu.
Drgania tłumione przedstawione na rys.4.5 s nieokresowe, jednak kolejne poło enia
rodkowe i kolejne wychylenia s osi gane po jednakowych odst pach czasu. Zatem, okres
drga tłumionych mo na wyznaczy z zale no ci:
2
2
0
1
2
2
n
T
−
=
=
ω
π
ω
π
(4.17)
który jest wi kszy od okresu drga tłumionych:
0
0
1
2
ω
π
=
T
T
(4.18)
Dekrement logarytmiczny tłumienia, definiowany jako stosunek warto ci dwóch
kolejnych maksymalnych amplitud, przyj to za miar tłumienia drga :
1
1
)
(
)
(
ln
nT
T
t
x
t
x
=
+
=
∆
(4.19)
Stopie tłumienia dla ułatwienia dalszej analizy mo na zapisa w postaci:
0
ω
ξ
h
c
c
kr
=
=
oraz
1
,
2
=
=
=
ξ
gdy
mk
c
c
kr
(4.20)
Dla rys. 4.5 mo na napisa :
z
z
z
zkr
z
kr
k
m
c
c
c
c
c
2
=
=
=
ξ
(4.21)
W takim razie dekrement logarytmiczny tłumienia wynosi:
z
z
z
z
z
z
k
m
c
k
m
c
π
π
πξ
=
=
=
∆
2
2
2
(4.22)
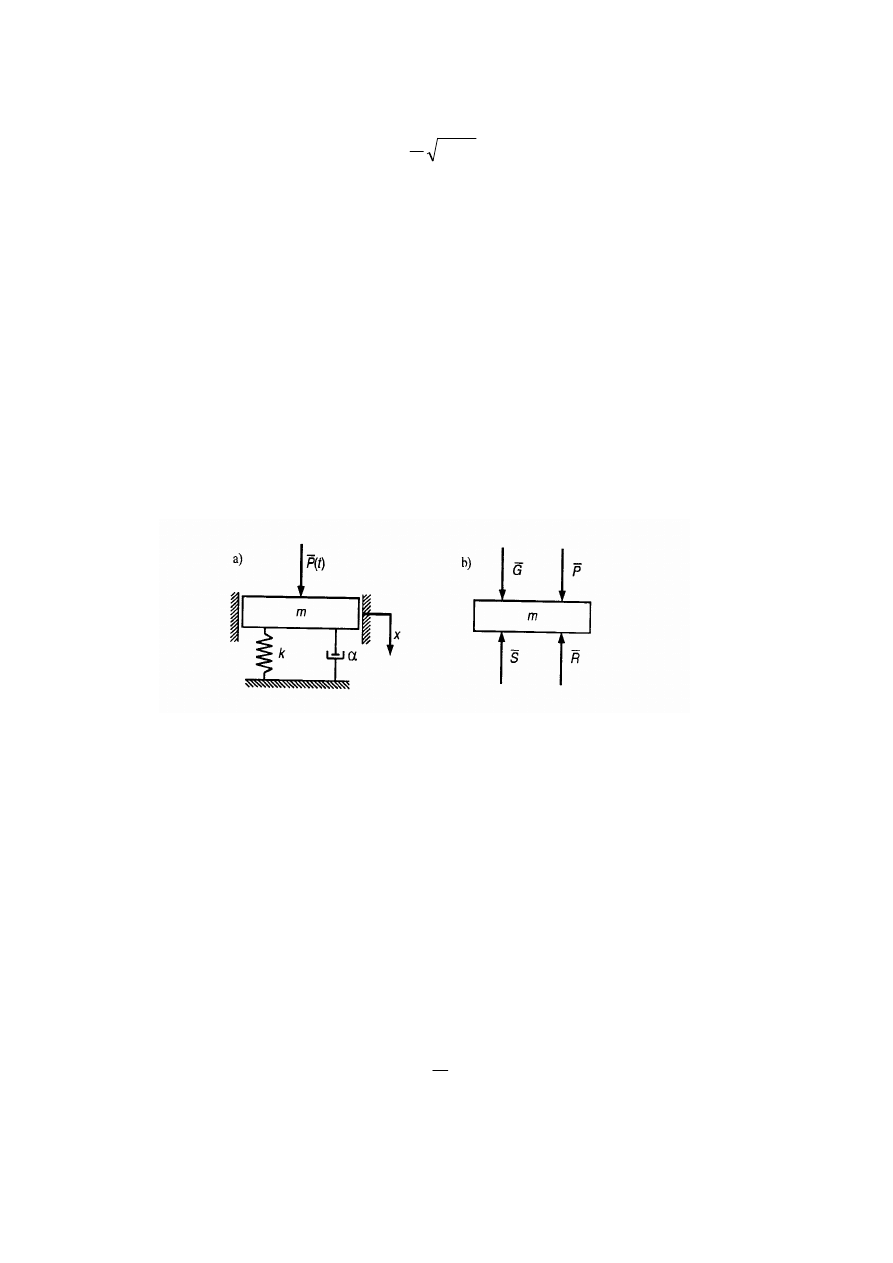
a z tego tłumienie zast pcze:
z
z
z
k
m
c
π
∆
=
(4.23)
Znaj c zatem z eksperymentu dekrement logarytmiczny tłumienia
∆ oraz z dalszych oblicze
zast pcz mas i sztywno (m
z
, k
z
) mo na wyznaczy warto zast pczego tłumienia c
z
w
badanym modelu.
3. DRGANIA UKŁADÓW O JEDNYM STOPNIU SWOBODY
Drgania układu powstaj ce na skutek naruszenia poło enia równowagi układu
mechanicznego, który nast pnie porusza si pod działaniem sił spr ystych, ci ko ci lub
tarcia nazywa si drganiami swobodnymi. W układach o jednym stopniu swobody naruszenie
poło enia równowagi charakteryzuje si warunkami pocz tkowymi: pocz tkowym
poło eniem x
0
i pocz tkow pr dko ci
0
*
x
.
3.1 DRGANIA SWOBODNE
Drgania swobodne układu o jednym stopniu swobody mo na przedstawi modelem
jak na rys.4.6, bez uwzgl dnienia siły zewn trznej P(t).
c =
α
Rys.4.6 Model układu o jednym stopniu swobody
Jako współrz dn uogólnion przyjmuje si przemieszczenie x masy
m
odniesione do
poło enia równowagi statycznej układu [8,13,17].
Drganiami wymuszonymi układu mechanicznego nazywa si takie drgania, które
zachodz wskutek działania sił zewn trznych P(t) na układ.
Równanie dynamiczne ruchu masy m otrzymuje si korzystaj c z II zasady Newtona:
P
G
R
S
x
m
+
+
−
−
=
*
*
(4.24)
gdzie: P – siła wymuszaj ca, G – ci ar masy układu, S – siła reakcji spr yny,
R – siła oporu tłumika.
Przy zało eniu, e odkształcenia spr yny s niewielkie, mo na przyj , e siła S jest liniow
funkcj x:
]
[
st
x
k
S
δ
+
=
(4.25)
Współczynnik k nazywa si współczynnikiem spr ysto ci obci enia spr yny do
wywołanego przez nie ugi cia [N/m]. Natomiast:
k
G
st
=
δ
(4.26)
oznacza ugi cie statyczne spr yny, wywołane ci arem G.
Siła R mo e przedstawia nie tylko opór tłumika specjalnie wprowadzonego układu,
ale równie siły tarcia w prowadnicach, opór o rodka, w którym drga ciało, itp. Pozostaj c na
gruncie układów liniowych, przyjmuje si , e
siła oporu jest proporcjonalna do pr dko ci
ruchu ciała o masie m:
*
x
c
R
=
(4.27)
Ten typ oporu nazywamy liniowym tłumieniem wiskotycznym (lepkim), współczynnik c
nazywa si współczynnikiem tłumienia lepkiego i ma wymiar [kg/s] .
Za pomoc (4.27) mo na wyrazi siły oporu tłumików olejowych lub sił tarcia w
przypadku lizgania si po sobie cz ci dobrze smarowanych, czy te w czasie ruchu ciała w
cieczy lub gazie przy zało eniu, e pr dko v jest dostatecznie mała. Po podstawieniu (4.25)
i (4.27) do (4.24) otrzymuje si :
k
G
t
P
kx
x
c
x
m
st
δ
−
+
=
+
+
)
(
*
*
*
(4.28)
Je eli teraz uwzgl dnimy zale no (4.26), otrzymamy poszukiwane równanie drga w
postaci:
)
(
*
*
*
t
P
kx
x
c
x
m
=
+
+
(4.29)
Drgania swobodne nie tłumione
Przyczyna ruchu obiektu, a wi c i modelu wynika tu z zadanych warunków
pocz tkowych. Przyjmuj c w (4.29) c = 0 i P(t) = 0, otrzymuje si
równanie drga
swobodnych układu zachowawczego (układu, w którym obowi zuje zasada zachowania
energii) w postaci:
0
*
*
=
+ kx
x
m
(4.30)
Dziel c obie strony (4.30) przez m, otrzymuje si :
0
2
0
*
*
=
+
x
x
ω
(4.31)
gdzie:
m
k
=
0
ω
nazywane jest
cz sto ci drga własnych.
Rozwi zanie ogólne równania (4.31) ma posta :
t
C
t
C
x
0
2
0
1
sin
cos
ω
ω
+
=
(4.32)
Równanie to zawiera dwie stałe dowolne C
1
, C
2
, które wyznacza si z warunków
pocz tkowych. Przyjmuj c, e w chwili t = 0, x = x
0
oraz
0
*
*
x
x
= , wówczas:
0
1
x
C
= ,
0
0
*
2
ω
x
C
=
(4.33)
oraz
t
x
t
x
x
0
0
0
*
0
0
sin
sin
ω
ω
ω
+
=
(4.34)
Drgania swobodne (4.34) mo na równie zapisa w postaci
przemieszczenia drga :
)
sin(
0
ϕ
ω
+
=
t
A
x
(4.35)
gdzie:
2
0
0
*
2
0
+
=
ω
x
x
A
,
0
*
0
0
tg
x
x
ω
ϕ
=
(4.36)
Ze wzorów (4.35) i (4.36) wynika, e drgania swobodne liniowego układu zachowawczego
maj posta drga harmonicznych o amplitudzie A i k cie przesuni cia fazowego
ϕ
,
zale nego od warunków pocz tkowych. Cz sto ci za drga własnych
0
ω
i okres drga
0
0
2
ω
π
=
T
zale wył cznie od masy i spr ysto ci układu.
Ró niczkuj c równanie (4.35) otrzymuje si
pr dko drga :
)
cos(
0
0
*
ϕ
ω
ω
+
=
t
A
x
(4.37)
b d c równie okresow funkcj czasu o tym samym okresie co przesuni cie. Z kolei
ró niczkuj c pr dko otrzymuje si warto
przyspieszenia drga :
x
t
A
x
2
0
0
2
0
*
*
)
sin(
ω
ϕ
ω
ω
−
=
+
−
=
(4.38)
Jest ono okresow funkcj czasu o tym samym okresie co przesuni cie i pr dko .
Przy pieszenie jest proporcjonalne do przesuni cia i jest skierowane przeciwnie do
przesuni cia (4.38), czyli jest stale skierowane do poło enia równowagi [33,71].
Równanie (4.38) mo na napisa w postaci:
0
2
0
*
*
=
+
x
x
ω
(4.39)
i jest ono
równaniem drga harmonicznych albo równaniem drga oscylatora
harmonicznego. Wynika z niego, e drgania własne układu o jednym stopniu swobody s w
zupełno ci okre lone przez cz sto drga własnych. Amplituda drga zale y od warunków
pocz tkowych (patrz 4.36), natomiast cz sto ci własne i okres drga od nich nie zale .
Drgania swobodne tłumione
Równanie drga swobodnych tłumionych otrzymuje si , przyjmuj c we wzorze (4.29)
P(t)=0:
0
*
*
*
=
+
+
kx
x
c
x
m
(4.40)
lub po podzieleniu przez mas w postaci:
0
2
2
0
*
*
*
=
+
+
x
x
h
x
ω
(4.41)
gdzie:
,
2
m
c
h
=
m
k
=
2
0
ω
.
Rozwi zaniem tego równania jest posta :
rt
Ae
x
=
, a
równanie charakterystyczne dla (4.41) ma
posta :
0
2
2
0
2
=
+
+
ω
hr
r
(4.42)
Ogólne rozwi zanie tego równania zale y od warto ci i znaku wyró nika, który ma znan
posta :
)
(
4
2
0
2
ω
−
=
∆
h
St d:
2
0
2
2
,
1
ω
−
+
−
=
h
h
r
t
r
t
r
e
A
e
A
t
x
2
1
2
1
)
(
+
=
(4.43)
Analizuj c pierwiastki charakterystyczne r
1,2
zauwa a si , e wyznaczaj one trzy obszary
zachowania si modelu, zale nie od warto ci współczynnika tłumienia h:
0
ω
h
;
0
ω
=
h
;
0
ω
h
. (4.44)
Wprowadzaj c bezwymiarowy stopie tłumienia
ξ
, który spełnia relacje:
0
ω
ξ
h
c
c
kr
=
=
;
mk
c
c
kr
2
=
=
; gdy
1
=
ξ
(4.45)
wida , e krytyczna warto tłumienia zale y od masy i spr ysto ci. Wskazane trzy warto ci
tłumienia (4.44) charakteryzuj
tłumienie nadkrytyczne, krytyczne i podkrytyczne, dla
których mo na przypisa nast puj ce rozwi zania:
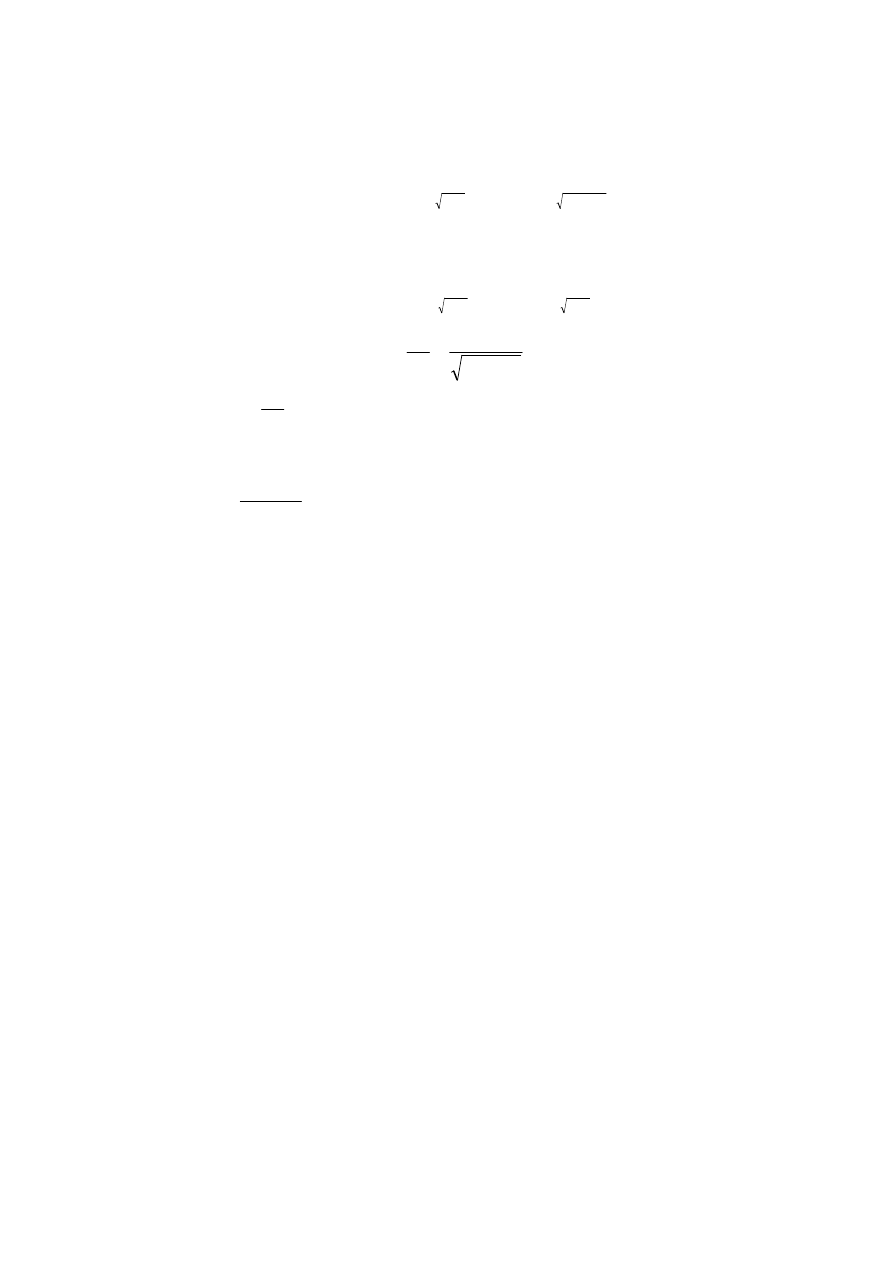
- tłumienie nadkrytyczne:
kr
c
c
,
)
1
(
ξ
;
t
t
e
A
e
A
x
0
2
0
2
)
1
(
2
)
1
(
1
ω
ξ
ξ
ω
ξ
ξ
−
−
−
−
+
−
+
=
-
tłumienie krytyczne:
kr
c
c
=
,
)
1
(
=
ξ
;
t
e
t
A
A
x
0
)
(
2
1
ξω
−
+
=
(4.46)
-
tłumienie podkrytyczne:
kr
c
c
,
)
1
(
ξ
;
t
i
i
e
A
e
A
x
0
2
0
2
)
1
(
2
)
1
(
1
ω
ξ
ξ
ω
ξ
ξ
−
−
−
−
−
−
+
=
- okres drga tłumionych:
2
2
0
0
1
2
2
h
T
−
=
=
ω
π
ω
π
jest wi kszy od okresu drga nie
tłumionych:
0
0
1
2
ω
π
=
T
T
;
- logarytmiczny dekrement tłumienia (jako stosunek dwu kolejnych amplitud)
umo liwiaj cy eksperymentalne okre lanie współczynnika tłumienia wyznacza si z
zale no ci:
1
1
)
(
)
(
ln
hT
T
t
x
t
x
=
+
=
δ
.
W zastosowaniach technicznych z tłumieniem nadkrytycznym mamy do czynienia w
konstrukcji ró nego rodzaju indykatorów wskazówkowych, za z tłumieniem podkrytycznym
w układach amortyzacji. Materiały konstrukcyjne cechuj si bardzo małym stopniem
tłumienia
1
ξ
co objawia si słabym zanikiem drga w konstruowanych układach.
3.2 DRGANIA WYMUSZONE
Mo liwy charakter wymusze w funkcji czasu, które mog wyst powa w realnych
przypadkach obci e dynamicznych układów spr ystych mo na podzieli na:
procesy
zdeterminowane, gdzie nast pstwo warto ci siły w czasie jest ci le okre lone jedn funkcj
p(t) = f(t) oraz
procesy przypadkowe, gdzie opis wymuszenia ujmuje cały zbiór oddzielnych
realizacji p(t) = {f
i
(t)}. Dokładniejszy podział na klasy zwi zane z rodzajem opisu procesów
wymuszaj cych i wskazaniem mo liwo ci ich zastosowa przedstawiono w rozdziale VII.
Drgania wymuszone to drgania powstaj ce wtedy, gdy punkt drgaj cy w o rodku o
stałej tłumienia poddany jest dodatkowo działaniu siły sinusoidalnie zmiennej z biegiem
czasu. Drgania odbywane w warunkach rzeczywistych, w dowolnym o rodku materialnym,
zawsze s poł czone z przekazywaniem energii otoczeniu w zwi zku z pokonywaniem sił
oporu. W wyniku wykonywanej pracy energia ciała drgaj cego maleje, zmniejsza si te
amplituda drga .
Drgania nie podtrzymywane sił zewn trzn ulegaj tłumieniu, gasn , zanikaj — st d
ich nazwy: drgania tłumione, gasn ce, zanikaj ce.
W o rodkach o wi kszych stałych tłumieniach (o wi kszych dekrementach
logarytmicznych tłumienia) wygaszanie drga jest gwałtowniejsze. Teoretycznie spadek
amplitudy A do zera powinien nast pi dopiero po czasie t = to w praktyce ju po czasie
sko czonym obserwuje si faktyczny zanik drga . Warto podkre li , e badanie drga
tłumionych w okre lonym o rodku pozwala wyznaczy jego współczynnik oporu.
3.2.1 Drgania wymuszone nietłumione
Opis drga wymuszonych nietłumionych uzyskuje si , przyjmuj c w (4.29) c=0 i
P(t)=cos
ω
t, w postaci:
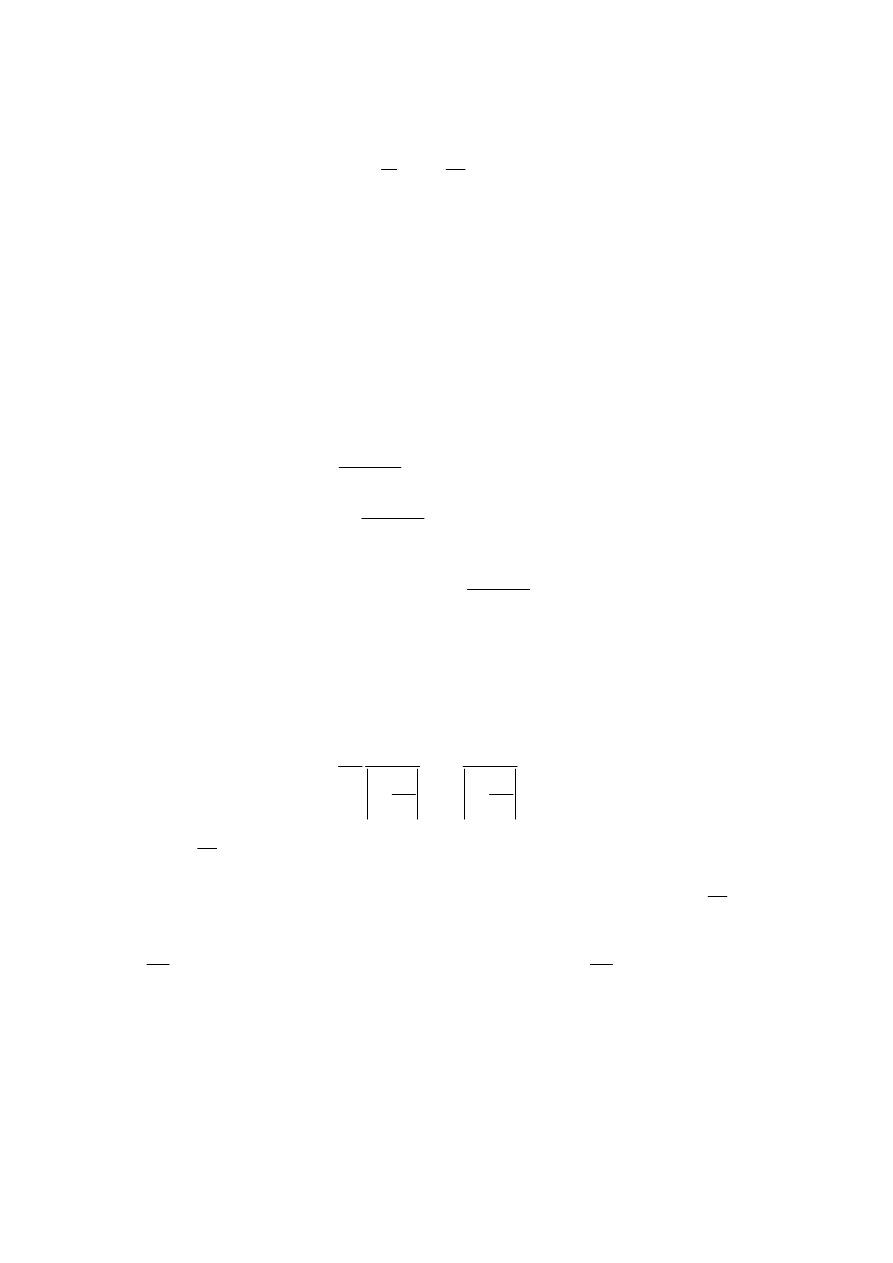
t
P
kx
x
m
ω
cos
0
*
*
=
+
(4.47)
albo:
t
q
x
x
ω
ω
cos
2
*
*
=
+
, gdzie:
m
k
=
2
ω
,
m
P
q
0
=
.
Równanie to jest równaniem ró niczkowym liniowym niejednorodnym. Jego rozwi zanie
ogólne jest równe sumie rozwi zania ogólnego x
1
odpowiedniego równania jednorodnego
(4.30) oraz rozwi zania szczególnego x
2
:
2
1
x
x
x
+
=
(4.48)
przy czym:
t
C
t
C
x
0
2
0
1
1
sin
cos
ω
ω
+
=
.
Rozwi zania szczególnego równania (4.47) szukamy w postaci:
t
A
x
ω
cos
2
=
(4.49)
gdzie A jest stałym współczynnikiem, którego warto nale y wyznaczy . Podstawiaj c do
wyra enia (4.47) wyra enie (4.49) otrzymuje si :
0
cos
]
)
(
[
2
2
0
=
−
−
t
q
A
ω
ω
ω
(4.50)
Aby powy sze równanie było spełnione, winno by :
0
)
(
2
2
0
=
−
−
q
A
ω
ω
, czyli
2
2
0
ω
ω
−
=
q
A
, co po podstawieniu do (4.49) daje:
t
q
x
ω
ω
ω
cos
2
2
0
2
−
=
(4.51)
Uwzgl dniaj c zale no ci (4.51) i (4.48) otrzymujemy zatem:
t
q
t
C
t
C
x
ω
ω
ω
ω
ω
cos
sin
cos
2
2
0
0
2
0
1
−
+
+
=
(4.52)
Ruch punktu materialnego stanowi wi c wynik superpozycji dwóch rodzajów ruchu drga
harmonicznych. Pierwsze z nich pokrywaj si z badanymi wcze niej drganiami
swobodnymi, drugie za odpowiadaj szczególnemu rozwi zaniu (4.51). Te ostatnie drgania
nosz nazw drga wymuszonych, a ich okres jest taki sam jak okres siły P wywołuj cej te
drgania: T=2
π/ω.
Amplituda drga wymuszonych wynosi wi c [33]:
2
0
2
2
0
2
2
0
1
1
1
1
ω
ω
δ
ω
ω
ω
−
=
−
=
st
q
A
(4.53)
gdzie:
k
P
st
0
=
δ
jest wychyleniem statycznym.
Gdy
0
=
ω
, czyli gdy siła wymuszaj ca jest stała, otrzymujemy:
k
P
x
st
0
2
=
=
δ
, układ
wykonuje drgania swobodne, których rodkiem jest poło enie równowagi układu.
Gdy
∞
→
0
ω
ω
, to amplituda drga wymuszonych
∞
→
A
. Gdy
1
0
→
ω
ω
, tzn. gdy cz sto
siły wymuszonej zbli a si do cz sto ci własnej, amplituda
∞
→
A
. Przypadek ten nosi
nazw rezonansu i polega na zwielokrotnieniu amplitudy drga w porównaniu z ugi ciem
statycznym.
Rezonans jest zjawiskiem zachodz cym w układach drganiowych, gdy cz stotliwo
drga wymuszaj cych
ω jest równa lub bliska cz stotliwo ci drga własnych ω
0
. Rezonans
polega na szybkim wzro cie amplitudy drga układu fizycznego, tym wi kszym im mniejsze
jest tłumienie drga w układzie. Charakterystyk rezonansow układu przedstawia krzywa
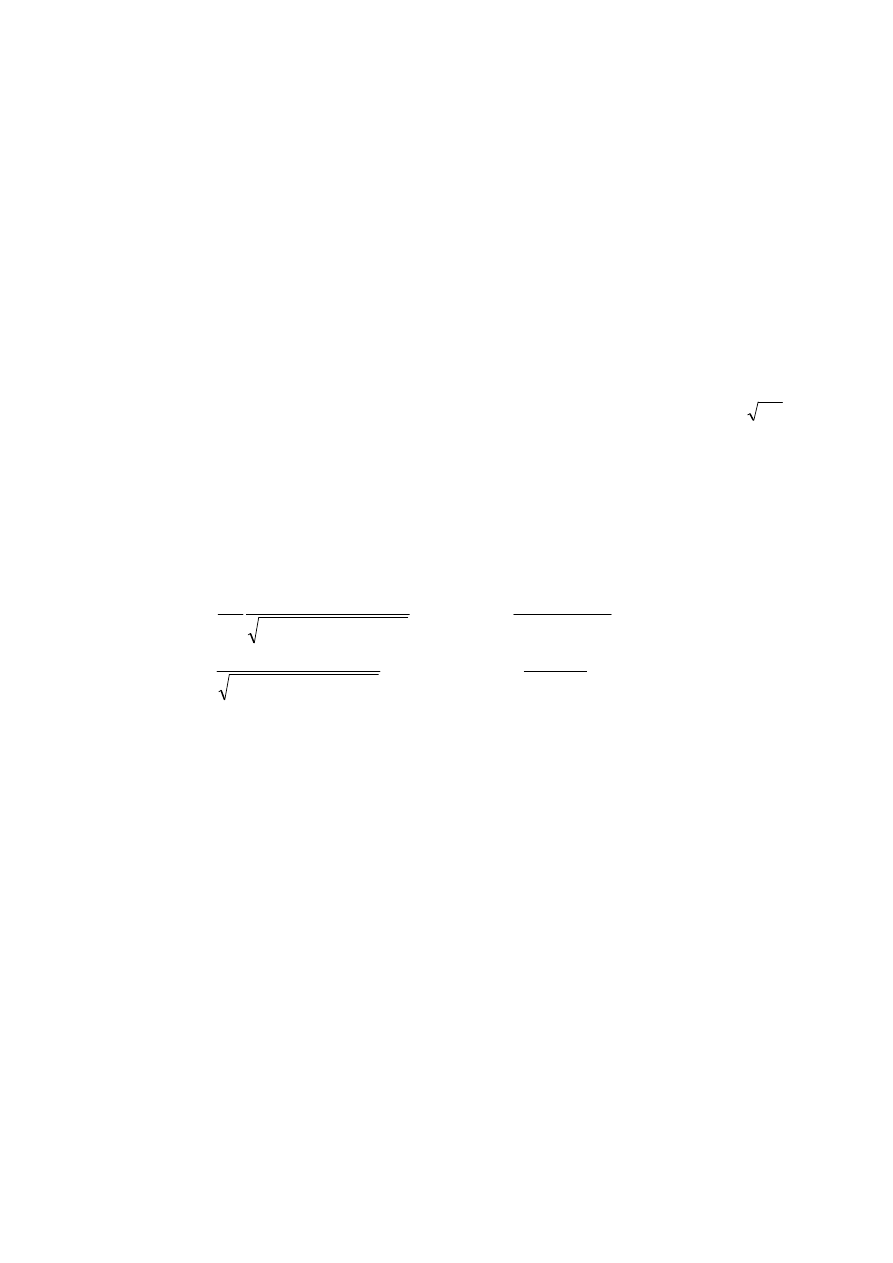
rezonansowa. Im szersza jest krzywa rezonansowa, tym łatwiej jest pobudzi układ
drganiowy do drga wymuszonych - układ jest mniej selektywny. Powstaj w nim drgania ju
przy cz stotliwo ciach drga wymuszaj cych, znacznie ró ni cych si od cz stotliwo ci
rezonansowej. W miar zbli ania si cz stotliwo ci drga wymuszaj cych do cz stotliwo ci
drga własnych układu, amplituda drga wymuszonych ro nie i osi ga maksymaln warto ,
gdy:
ω
=
ω
r
.
Sko czona warto amplitudy drga rezonansowych wynika st d, e w układach
rzeczywistych cz
energii zostaje stracona - układ jest dyssypatywny [14,33,71].
Drgania wymuszone tłumione
Rozwa aj c drgania układu mechanicznego z rys.1 w przypadku gdy
t
P
t
P
ω
sin
)
(
0
=
, mo na
napisa równanie drga wymuszonych tłumionych:
t
P
kx
x
c
x
m
ω
sin
0
*
*
*
=
+
+
(4.54)
Przyjmuj c, e tłumienie jest podkrytyczne [
)
1
ξ
zastosowania praktyczne] albo
mk
c
równanie powy sze po podzieleniu przez mas mo na przedstawi w postaci:
t
q
x
x
h
x
ω
ω
sin
2
2
0
*
*
*
=
+
+
(4.55)
Rozwi zanie tego równania przy warunkach pocz tkowych:
0
,
0
,
0
*
=
=
=
x
x
t
mo na
przedstawi w postaci:
)
sin(
)
sin(
1
1
ϕ
ω
ω
−
+
−
−
=
−
t
A
v
t
e
A
x
ht
(4.56)
gdzie:
2
2
2
2
2
0
1
4
)
(
1
1
ω
ω
ω
ω
h
q
A
+
−
=
,
2
2
2
1
1
2
tg
ω
ω
ω
−
−
=
h
h
v
(4.57)
2
2
2
2
2
0
4
)
(
ω
ω
ω
h
q
A
+
−
=
,
2
2
0
2
tg
ω
ω
ω
ϕ
−
=
h
(4.58)
We wzorze (4.56) pierwszy składnik przedstawia drgania swobodne tłumione, powstałe na
skutek przyło enia siły wymuszaj cej przy zerowych warunkach pocz tkowych. Drugi
składnik przedstawia natomiast drgania ustalone wymuszone. Po pewnym czasie drgania
swobodne zostaj wytłumione i mo na je pomin . Pozostaj drgania wymuszone maj ce
posta drga harmonicznych o cz sto ci siły wymuszaj cej :
)
sin(
ϕ
ω
−
=
t
A
x
. Drgania te s
opó nione w fazie w stosunku do obci enia o k t
ϕ
wyznaczony z drugiego wzoru (4.58).
Drgania liniowe układu (o jss) przy wymuszeniu harmonicznym
Je eli układ mechaniczny posiada tylko jeden stopie swobody i posiada liniowe
charakterystyki spr ysto ci i tłumienia (rys.4.7), a działa na niego harmoniczna siła
wymuszaj ca, to równanie jego ruchu jest:
)
t
(
H
Cq
q
B
q
A
=
+
+
,
(4.59)
q – współrz dna uogólniona (przemieszczenie translacyjne x[m], rotacyjne ),
A – { m – masa [kg]; I masowy moment bezwładno ci [kgm
2
]},
B – {b - współczynnik tłumienia translacyjnego [Ns/m];
b
0
- współczynnik tłumienia rotacyjnego Nms/rad]},
C – {c – współczynnik sztywno ci translacyjnej [N/m];
c
0
– współczynnik sztywno ci rotacyjnej [Nm/rad]},
H(t) – {F(t) – siła wymuszaj ca [N];
M(t) – moment wymuszaj cy [Nm]}.
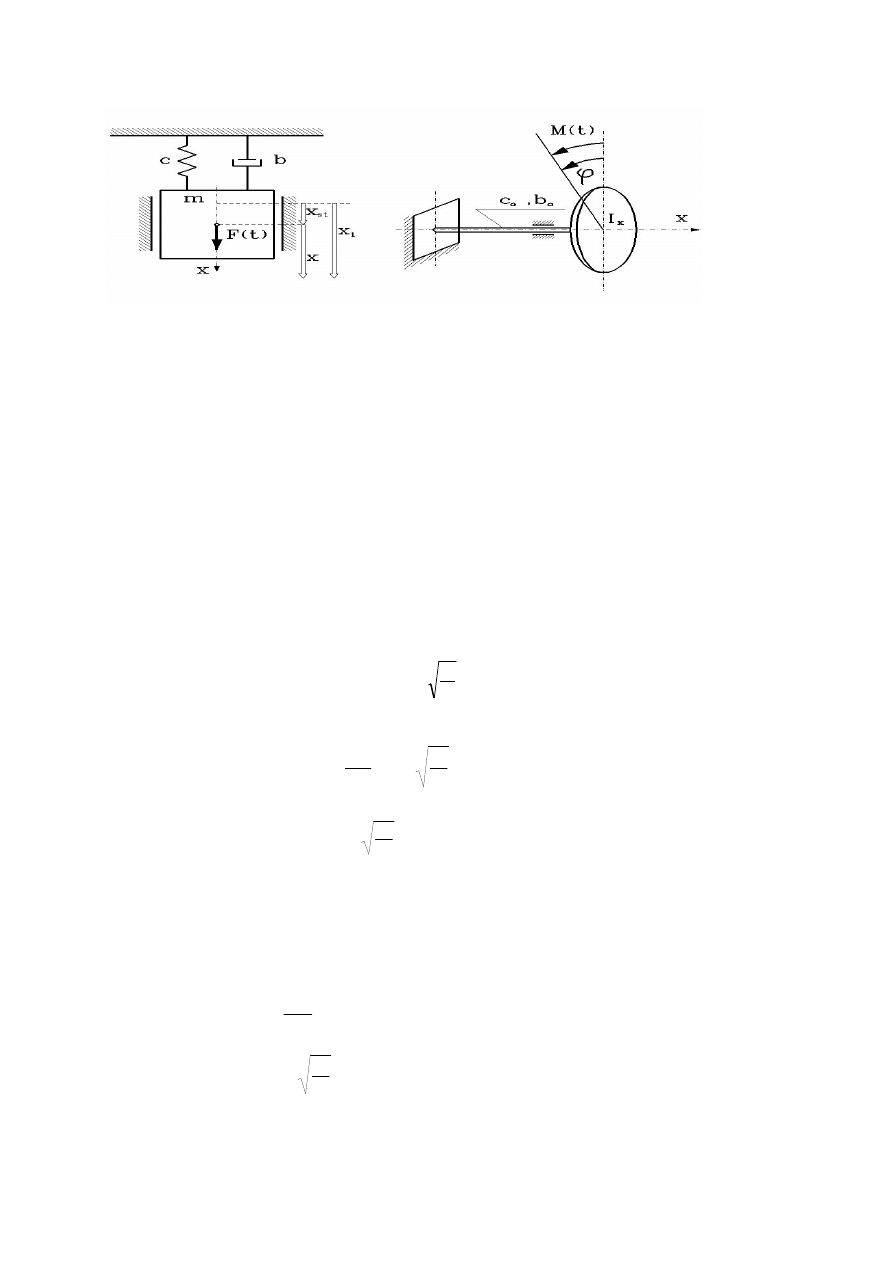
Rys.4.7 Modele układów o jednym stopniu swobody
Drgania autonomiczne (swobodne)
Je eli na układ wst pnie wyprowadzony z poło enia równowagi nie działaj adne
wymuszenia [H(t)=0], to otrzymujemy nast puj ce równanie:
0
Cq
q
B
q
A
=
+
+
,
(4.60)
Jest to równanie drga swobodnych tłumionych. Je eli pominiemy tłumienie , to
równanie ulegnie dalszemu uproszczeniu:
0
Cq
q
A
=
+
+
,
(4.61)
Rozwi zaniem ogólnym powy szego równania jest funkcja sygnału harmonicznego:
( )
(
)
ϕ
+
ω
=
t
sin
q
t
q
0
0
(4.62)
0
– cz sto kołowa sygnału [rad/s];
- faza sygnału harmonicznego [rad].
Po podstawieniu otrzymamy:
(
)
(
)
0
t
sin
q
A
C
0
0
2
0
=
ϕ
+
ω
ω
−
(4.63)
która to zale no , jest spełniona dla dowolnej chwili czasowej t tylko wtedy, gdy:
A
C
A
C
=
=
−
0
2
0
st t
0
ω
ω
(4.64)
Jest to cz sto kołowa nie tłumionych drga własnych, nazywana cz sto ci własn układu.
Okres drga własnych jest równy:
A
C
2
2
T
0
0
π
=
ω
π
=
(4.65)
Ogólne rozwi zanie ma posta :
( )
ϕ
+
=
t
C
A
sin
q
t
q
0
(4.66)
gdzie amplituda drga q
0
i faza , s stałymi całkowania, zale nymi od warunków
pocz tkowych ruchu.
Je eli wyst puje tłumienie wiskotyczne (B 0), to równanie drga (4.60) w wyniku
podzielenia obustronnie przez współczynnik bezwładno ci A przyjmie nast puj c posta :
0
q
q
h
2
q
2
0
=
ω
+
+
(4.67)
gdzie:
[
]
rad/s
A
2
B
h
=
(4.68)
jest jednostkowym współczynnikiem tłumienia wiskotycznego, natomiast
[
]
rad/s
A
C
0
=
ω
(4.69)
jest cz sto ci własn układu.
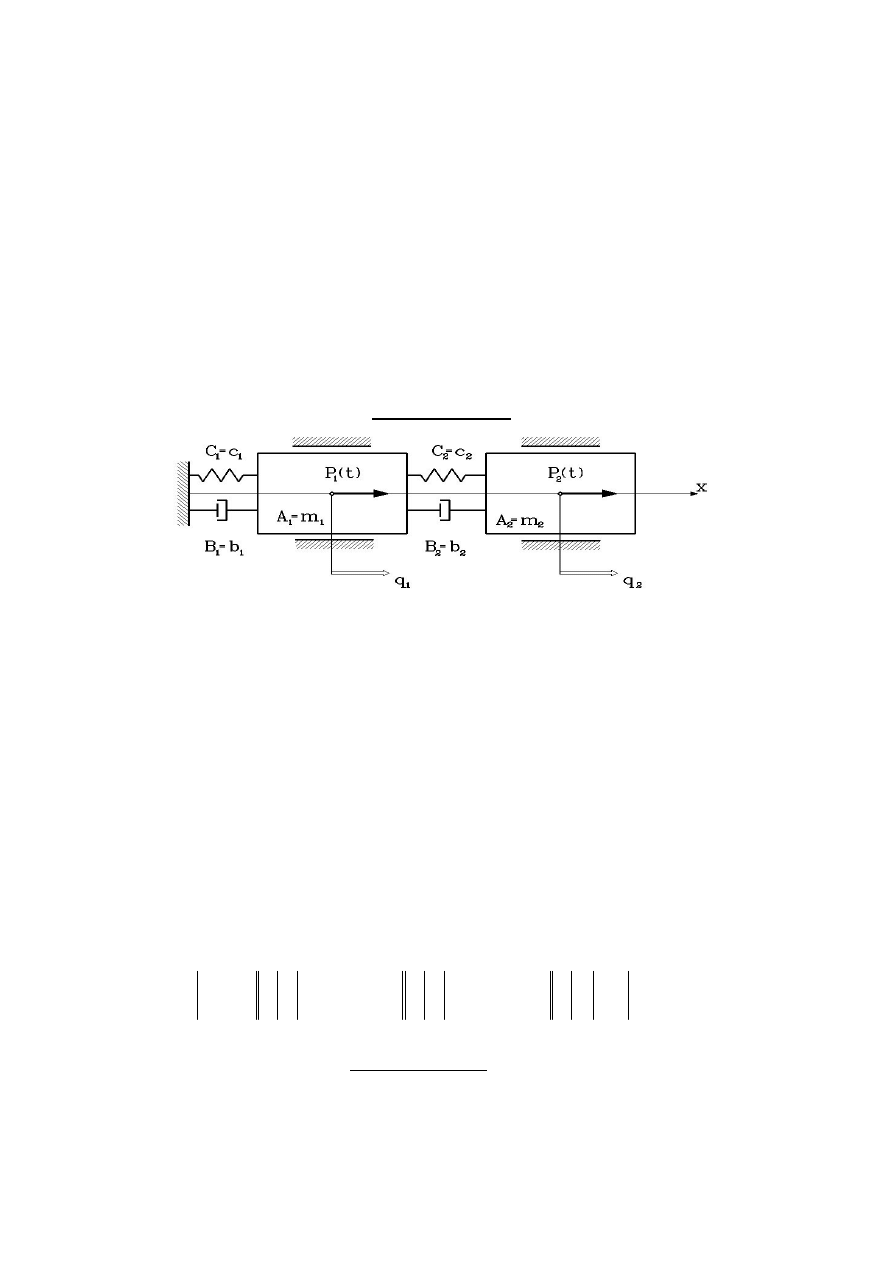
4. DRGANIA UKŁADÓW O DWÓCH STOPNIACH SWOBODY
W wielu przypadkach analizy dynamicznej obiektów mechanicznych zamiast jednego
stopnia swobody trzeba uwzgl dni kilka stopni swobody ruchu drgaj cego. Dotyczy to
szczególnie obiektów o konstrukcji niejednorodnej z gwałtown zmian własno ci masowo –
spr ysto – dyssypacyjnych, np. podwieszenie do belki ci aru na linie, wstawienie
podatnego sprz gła w linii nap dowej agregatu maszynowego czy podparcie bryły sztywnej
spr ynami i tłumikami w wielu płaszczyznach. Najmniejsz komplikacj wyró nia si tu
model o dwóch stopniach swobody, na którego przykładzie mo na wyja ni wi kszo cech
szczególnych układów o wielu stopniach swobody [14,33,57].
Opis obiektu o dwóch stopniach swobody (rys.4.8) jest nieco trudniejszy, chocia
efekt ko cowy jest podobny [64].
UKŁAD O 2 SSW
Rys.4.8 Model układu o dwóch stopniach swobody
Po uwolnieniu z wi zów ka dego elementu, otrzymuje si nast puj ce układy sił
działaj cych na te elementy:
( ) (
) (
)
( ) (
) (
)
.
,
,
:
;
c
-
,
b
-
,
,
,
:
1
2
2
1
2
2
2
1
1
1
1
1
2
2
1
2
2
1
q
q
c
q
q
b
t
P
II
q
q
q
q
c
q
q
b
t
P
I
−
−
−
−
(4.70)
Stosuj c zasad d’Alemberta dla ka dego z tych elementów, mo emy zapisa dwa
równania:
(
)
(
) ( )
(
) (
)
( )
t
P
q
q
c
q
q
b
q
m
t
P
q
q
c
q
q
b
q
c
q
b
q
m
2
1
2
2
1
2
2
2
2
1
1
2
2
1
2
2
1
1
1
1
1
1
+
−
−
−
−
=
+
−
+
−
+
−
−
=
(4.71)
Wprowadzaj c pewne uporz dkowanie powy szych równa , otrzymamy układ
ró niczkowy równa ruchu:
(
)
(
)
( )
( )
t
P
q
c
q
c
q
b
q
b
q
m
t
P
q
c
q
c
c
q
b
q
b
b
q
m
2
1
2
2
2
1
2
2
2
2
2
1
2
2
1
2
1
2
2
1
2
1
1
1
=
−
+
−
+
=
−
+
+
−
+
+
(4.72)
Stosuj c prawa rachunku macierzowego, równanie ruchu (4.70) mo na zapisa :
(
)
(
)
( )
( )
t
P
t
P
q
q
c
c
c
c
c
q
q
b
b
b
b
b
q
q
m
m
2
1
2
1
2
2
2
2
1
2
1
2
2
2
2
1
2
1
2
1
0
0
=
−
−
+
+
−
−
+
+
(4.73)
lub ogólnie:
Q
Cq
q
B
q
A
=
+
+
(4.74)
Jak wida , mimo wielu zało e w czasie modelowania układu wyst puj ce tu
równania ruchu układu s nieliniowe i ich rozwi zanie nie jest proste. Mo na to wykona
analitycznie, poprzez ró nego typu linearyzacj członów nieliniowych, numerycznie całkuj c
krok po kroku metod ró nic sko czonych, albo numerycznie na modelu analogowym.
Charakterystyczne warto ci opisu układu: cz sto ci własne i postacie drga , cz sto
trudne do wyznaczenia analitycznego mo na okre li w drodze identyfikacji zło onej w
czasie eksperymentu, co zostanie omówione w dalszej cz ci opracowania.
5. DRGANIA UKŁADÓW O SKO CZONEJ LICZBIE STOPNI
SWOBODY
Układy drgaj ce mo na umownie podzieli na dwa podzbiory: układy dyskretne i
układy ci głe. Umowno podziału wynika z tego, e układy drgaj ce s przestrzennymi
elementami zbudowanymi z materiałów odkształcalnych, s wi c układami ci głymi o
niesko czonej liczbie stopni swobody. Dla celów praktycznych wiele układów fizycznych
mo na jednak uwa a za dyskretne. W praktyce decyzja, czy dany układ potraktowa jako
dyskretny, czy jako ci gły zale y od argumentów uzasadniaj cych z jednej strony dokładno
wyników oblicze , a z drugiej korzy uzyskania wyników oblicze wynikaj ca z
dyskretyzacji rozpatrywanego układu [33,57].
Układ dyskretny jest takim układem, którego równania ruchu mo na wyrazi za
pomoc zbioru równa ró niczkowych zwyczajnych dla sko czonej liczby poszukiwanych
funkcji jednej zmiennej rzeczywistej - czasu.
W analizie dynamicznej układów dyskretnych dla przypadku małych drga
posługujemy si trzema rodzajami współrz dnych. Współrz dne zewn trzne (np.
kartezja skie) słu ce do opisu konfiguracji układu drgaj cego w poło eniu równowagi
statycznej. Współrz dne lokalne, które s funkcjami czasu i opisuj przemieszczenia
elementów masowych układu drgaj cego z poło enia równowagi statycznej. Współrz dne
uogólnione Lagrange’a, które s tak e funkcjami czasu, s zbiorem niezale nych wielko ci
geometrycznych, za pomoc których mo na okre li wszystkie przemieszczenia lokalne.
Liczba współrz dnych uogólnionych nie mo e by mniejsza od liczby dynamicznych
stopni swobody. Cz sto liczb współrz dnych uogólnionych przyjmuje si równ liczbie
dynamicznych stopni swobody. Jest to przypadek tzw. bazy minimalnej [8,14,33,57,71].
W przypadku małych drga współrz dne lokalne s liniow transformacj współ-
rz dnych uogólnionych, przy czym współczynniki transformacji zale wył cznie od
konfiguracji układu dynamicznego.
Układ o sko czonej liczbie stopni swobody przedstawiany jest jako zbiór punktów
materialnych poł czonych bezmasowymi spr ynami i tłumikami. Rozwa ane układy liniowe
w praktyce in ynierskiej to najcz ciej takie, w których siły spr yste i tłumienia s
liniowymi funkcjami przemieszcze i pr dko ci punktów materialnych. S to układy
holonomiczne, a liczba stopni swobody równa si liczbie współrz dnych uogólnionych.
Współrz dne uogólnione s przesuni ciami lub k tami obrotu mas.
Drgania swobodne nietłumione
Najbardziej ogóln postaci równa ró niczkowych ruchu s równania Lagrange'a
drugiego rodzaju. Ruch układu holonomicznego, skleronomicznego o n stopniach swobody,
opisany we współrz dnych uogólnionych za pomoc tych równa , ma posta :
j
j
j
Q
q
E
q
E
dt
d
=
∂
∂
−
∂
∂
*
(4.75)
gdzie: E - energia kinetyczna układu, Qj - zewn trzna siła uogólniona odpowiadaj ca
współrz dnej q
j
, skierowana zgodnie z dodatnim zwrotem tej współrz dnej.
Energia kinetyczna rozpatrywanego układu ma posta kwadratowej formy pr dko ci
uogólnionych:
=
=
n
j
i
j
i
ij
q
q
a
E
1
,
*
*
2
1
)
,...,
2
,
1
,
(
n
j
i
=
(4.76)
Liczby a
ij
= a
ji
nazywaj si w s p ó ł c z y n n i k a m i b e z w ł a d n o c i układu.
W przypadku drga swobodnych układów spr ystych bez tłumienia siły uogólnione Q
j
wyra aj si poprzez energi potencjaln układu:
j
j
q
V
Q
∂
∂
−
=
)
,...,
2
,
1
(
n
j
=
(4.77)
przy czym energia potencjalna układu jest dodatnio okre lon form kwadratow
współrz dnych uogólnionych ze stałymi współczynnikami:
=
=
n
j
i
j
i
ij
q
q
c
V
1
,
2
1
)
,...,
2
,
1
,
(
n
j
i
=
(4.78)
gdzie liczby c
ij
= c
ji
nazywaj si współczynnikami spr ysto ci:
ji
j
i
ij
c
q
q
V
c
=
∂
∂
=
2
(4.79)
Energia potencjalna jest funkcj współrz dnych uogólnionych, ale mo na przyj , e w
poło eniu równowagi jest równa zeru. Podobnie w poło eniu równowagi s równe zeru
uogólnione siły spr ysto ci, co pozwala po podstawieniach (4.77) i (4.78) do (4.75) uzyska
równania ró niczkowe ruchu w postaci:
n
n
n
n
q
c
q
c
q
c
q
a
q
a
q
a
1
2
12
1
11
*
*
1
2
*
*
12
1
*
*
11
...
...
−
−
−
−
=
+
+
+
n
n
n
n
q
c
q
c
q
c
q
a
q
a
q
a
2
2
22
1
21
*
*
2
2
*
*
22
1
*
*
21
...
...
−
−
−
−
=
+
+
+
(4.80)
......................................................................................
n
nn
n
n
n
nn
n
n
q
c
q
c
q
c
q
a
q
a
q
a
−
−
−
−
=
+
+
+
...
...
2
2
1
1
*
*
2
*
*
2
1
*
*
1
Wprowadzaj c dalej zdefiniowane energie w postaci :
=
=
n
j
j
j
q
a
E
1
2
*
2
1
oraz
=
=
n
j
i
j
i
ij
q
q
c
V
1
,
2
1
(4.81)
to układ przechodzi w układ równa ró niczkowych rozprz onych wzgl dem uogólnionych
przyspiesze :
n
n
q
c
q
c
q
c
q
a
1
2
12
1
11
1
*
*
1
...
−
−
−
−
=
n
n
q
c
q
c
q
c
q
a
2
2
22
1
21
2
*
*
2
...
−
−
−
−
=
(4.82)
....................................................
n
nn
n
n
n
n
q
c
q
c
q
c
q
a
−
−
−
−
=
...
2
2
1
1
*
*
Jest to prosta posta równa ró niczkowych ruchu. Z kolei je eli do sumy kwadratów
doprowadzi si energi potencjaln :
=
=
n
j
i
j
i
ij
q
q
a
E
1
,
*
*
2
1
oraz
=
=
n
j
j
j
q
c
V
1
2
2
1
(4.83)
wówczas układ przechodzi w układ równa ró niczkowych rozprz onych wzgl dem
współrz dnych uogólnionych:
n
n
q
a
q
a
q
a
q
c
*
*
1
2
*
*
12
1
*
*
11
1
1
...
−
−
−
−
=
n
n
q
a
q
a
q
a
q
c
*
*
2
2
*
*
22
1
*
*
21
2
2
...
−
−
−
−
=
(4.84)
.......................................................
n
nn
n
n
n
n
q
a
q
a
q
a
q
c
*
*
2
*
*
2
1
*
*
1
...
−
−
−
−
=
i nazywa si odwrotn postaci równa ruchu.
Do prostej postaci równa ruchu mo na doj , korzystaj c bezpo rednio z drugiego
prawa Newtona dla wydzielonych z układu punktów materialnych, wyra aj c siły
spr ysto ci przez przemieszczenia:
0
1
*
*
=
+
=
n
j
i
ij
i
i
y
r
y
m
(4.85)
gdzie:
i
m - i-ta skupiona masa;
i
y - przemieszczenie masy;
ij
r - jednostkowa reakcja układu.
Je li oprócz mas skupionych układ mechaniczny ma tak e ciała sztywne, to k ty
obrotu tych ciał mo na oznaczy przez y
i
, a przez m
i
rozumie si momenty bezwładno ci
wzgl dem osi, wokół których zachodz obroty. Sumy znajduj ce si w ka dym z równa
(4.85) przedstawiaj wzi te z przeciwnym znakiem siły działaj ce na ka d z mas [8,13].
5.1 Drgania własne nietłumione (Zagadnienie własne)
Zagadnienie własne, dotycz ce drga swobodnych nietłumionych, opisuje ruch układu
dynamicznego bez sił wymuszaj cych i bez uwzgl dnienia tłumienia. Ruch jest
spowodowany warunkami pocz tkowymi, tj. nadaniem układowi pocz tkowego
przemieszczenia lub pocz tkowej pr dko ci.
Problematyk zagadnienia własnego podzielono nast puj ce cz ci:
a). analiz cz sto ci własnych i wektorów własnych - te wielko ci graj główn rol w
okre laniu reakcji dynamicznej liniowych układów poddanych działaniu sił wymuszaj cych,
b). okre lenie wła ciwo ci powy szych poj ,
c). rozwi zania zagadnienia własnego.
Analiza cz sto ci własnych i wektorów własnych
Równanie ruchu drga własnych otrzymuje si z równania ruchu (4.74) po pomini ciu członu
zawieraj cego macierz tłumienia oraz wektor obci e zewn trznych. Wówczas otrzymuje
si :
0
*
*
=
+ Kq
q
B
(4.86)
gdzie: 0 jest wektorem zerowym. Warunki pocz tkowe, po których nast puje ruch układu, s
nast puj ce:
0
)
0
(
q
q
= oraz
0
*
*
)
0
(
q
q
=
(4.87)
Rozwi zanie dla zadanego zagadnienia pocz tkowego (4.86) i (4.87) polega na
podaniu warunków, dla których jest mo liwy ruch rozpatrywanego układu. Przez analogi z
układem o jednym stopniu swobody zało ymy, e drgania własne s ruchem harmonicznym i
rozwi zania równania (4.86) poszukujemy w postaci funkcji harmonicznych o cz sto ci
ω
i
fazie pocz tkowej
ϕ
, czyli:
)
sin(
)
(
ϕ
ω
+
=
→
t
q
t
q
(4.88)
gdzie:
→
q jest wektorem amplitud drga własnych, który reprezentuje kształt przemieszcze
elementów masowych układu w kierunku współrz dnych uogólnionych, czyli kształt postaci
drga .
Po podstawieniu wyra enia (4.88) i jego drugiej pochodnej do równania ruchu (4.86)
otrzymuje si :
0
)
sin(
)
(
2
=
+
+
−
→
ϕ
ω
ω
t
q
K
B
(4.89)
Poniewa równanie to powinno by spełnione dla dowolnej chwili t, otrzymamy nast puj cy
układ równa algebraicznych, w którym wyst puje nieznany wektor
→
q oraz nieznana cz sto
kołowa
ω
:
0
)
(
2
=
−
→
q
B
K
ω
(4.90)
Jest to układ liniowych jednorodnych równa algebraicznych, który ma rozwi zania
niezerowe tylko wówczas, gdy:
0
)
det(
2
=
−
B
K
ω
(4.91)
Po rozwini ciu tego wyznacznika otrzymuje si wielomian n-tego stopnia wzgl dem
2
ω
(dla
układu maj cego n dynamicznych stopni swobody). Równanie to nazywa si
równaniem
charakterystycznym zagadnienia własnego lub równaniem cz sto ci. Pierwiastkami
równania (4.91) s cz sto ci kołowe drga własnych:
n
ω
ω
ω
,...,
,
2
1
, (n=d).
W ród pierwiastków mog wyst pi pierwiastki wielokrotne, wektor utworzony ze
zbioru cz sto ci uporz dkowanych w kolejno ci warto ci rosn cych nazywa si wektorem
cz sto ci, a pierwsz cz sto
ω
1
nazywa si
cz sto ci podstawow :
]
,...,
,
[
2
1
n
ω
ω
ω
ω
=
.
Mo na dowie , e dla symetrycznych i dodatnio okre lonych macierzy bezwładno ci
i macierzy sztywno ci o warto ciach rzeczywistych, warto ci liczbowe wektora
ω
s
rzeczywiste i dodatnie.
Ka dej cz sto ci
ω
i
odpowiada takie rozwi zanie
i
w
q
=
→
, e :
0
)
(
2
=
−
i
i
w
B
K
ω
(4.92)
Wektor w
i
nazywa si i-tym
wektorem własnym lub i-t postaci drga własnych. Okre la on
z dokładno ci do stałego czynnika rozkład przemieszcze na kierunkach współrz dnych
uogólnionych podczas drga z cz sto ci
ω
i
. Opisuje wi c odkształcon posta układu
dynamicznego drgaj cego z dan cz sto ci drga własnych. Zbiór wektorów własnych
ω
i
tworzy macierz własn
W:
=
=
nn
n
n
n
n
n
w
w
w
w
w
w
w
w
w
w
w
w
W
,
...
,
,
....
..........
..........
,
...
,
,
,
...
,
,
]
,...,
,
[
2
1
2
22
21
1
12
11
2
1
(4.93)
Rozwi zanie drga własnych układu dyskretnego opisanego równaniem ruchu (4.86)
lub (4.92) jest kombinacj liniow drga harmonicznych o cz sto ciach kołowych
ω
i
i
amplitudach proporcjonalnych do wektorów w
i
, czyli:
{
}
{
}
+
=
+
=
i
c
s
i
ci
i
si
i
q
t
q
t
W
t
q
t
q
w
t
q
ω
ω
ω
ω
cos
sin
)
cos
sin
(
)
(
(4.94)
gdzie:
{
}
)
(cos
sin
t
diag
t
i
ω
ω
=
;
T
cn
c
c
i
q
q
q
q
]
,...,
,
[
2
1
=
.
Elementy wektorów
q
s
oraz
q
c
s dowolnym stałymi, które mo na wyznaczy warunków
pocz tkowych (4.87).
Nale y podkre li , e głównymi zagadnieniami analizy drga własnych dla danego
układu dynamicznego s [8,13]:
- obliczenia wektora cz sto ci drga własnych;
- obliczenia macierzy własnej W (zbioru wektorów własnych);
- analiza ruchu mas układu dla zadanych warunków pocz tkowych.
Macierz własna
W została zdefiniowana jako uporz dkowany zbiór wektorów
własnych i zapisana została zale no ci (4.93). Macierz widmow
Ω
Ω
Ω
Ω
definiuje si jako
macierz diagonaln , gdzie na głównej przek tnej znajduj si kwadraty cz sto ci własnych:
=
=
Ω
n
n
w
diag
2
2
2
1
2
2
2
2
1
2
.....
..........
..........
....
..........
..........
..........
,
]
,...,
,
(
ω
ω
ω
ω
ω
(4.94)
Ka da cz sto własna i ka dy wektor własny spełniaj nast puj c zale no (uogólnion do
poj macierzy własnej
W i macierzy widmowej
Ω
Ω
Ω
Ω
macierzow :
Ω
= BW
KW
(4.95)
która w zwartej formie przedstawia relacj wszystkich warto ci i wektorów własnych.
Mo na stwierdzi , e wektory własne s nie tylko ortogonalne, ale tak e
normalizowane z wag macierzy bezwładno ci.
Rozwi zanie zagadnienia własnego
Okre lenie wła ciwo ci układu drgaj cego, tj. macierzy widmowej
Ω
Ω
Ω
Ω
i macierzy
własnej
W lub tylko ograniczonej liczby ich pierwszych elementów, wymaga rozwi zania
zagadnienia własnego (4.90), które dla wygody dalszych rozwa a mo na napisa w
nast puj cej postaci:
Bw
Kw
λ
=
(4.96)
gdzie:
K - jest macierz sztywno ci; B - macierz bezwładno ci układu drgaj cego o n
dynamicznych stopniach swobody; za
2
ω
λ
=
. Istnieje n warto ci własnych
i
λ
(rad
2
/ s
2
) i
odpowiada im n wektorów własnych
w spełniaj cych równanie (4.96). Wielko ci
i
λ
i
w
i
tworz n par własnych (
i
λ
,
w
i
), i = 1, 2,...,n, gdzie warto ci własne mog by uporz dkowane
w nast puj cy sposób:
n
n
λ
λ
λ
λ
≤
≤
≤
≤
≤
−1
2
1
...
0
(4.97)
Warto ci własne
i
λ
s pierwiastkami równania charakterystycznego (4.91), tj.:
0
)
det(
)
(
=
−
=
B
K
f
λ
λ
(4.98)
gdzie: f(
λ
) jest wielomianem n-tego stopnia. Je li n jest du liczb (np. kilka tysi cy lub
wi cej), to d ymy do okre lenia pierwszych (najni szych) p cz sto ci własnych i
odpowiadaj cych im p wektorów własnych.
W dynamice maszyn macierz sztywno ci
K jest zawsze dodatnio okre lona, a w
sformułowaniach metody elementów sko czonych jest cz sto macierz pasmow . Natomiast
macierz
B mo e mie ró ne wła ciwo ci - mo e by macierz pełn lub pasmow i wówczas
jest zawsze dodatnio okre lona. Mo e by jednak równie macierz diagonaln , której
niektóre elementy mog by równe zeru. Wówczas macierz
B jest macierz pół dodatnio
okre lon . Je li elementy na jej głównej przek tnej s wi ksze od zera, to macierz
B jest
dodatnio okre lona.
Tworzenie niezawodnych i efektywnych metod rozwi zania zagadnienia własnego
było przedmiotem wielu prac naukowych - szczególnie po upowszechnieniu komputerów. S
to głównie metody numeryczne - iteracyjne, których obliczenia s zako czone wówczas, gdy
uzyska si rozwi zanie z zadan dokładno ci . Metody te mo na podzieli na główne trzy
grupy: metody iteracji wektora, metody transformacyjne, techniki iteracyjne wielomianu
równania charakterystycznego.
Uzasadnienie, e metody rozwi zywania zagadnienia własnego maj charakter
iteracyjny wynika st d,
e nale y znale pierwiastki wielomianu równania
charakterystycznego f(
λ
), (4.98). Nie istniej jednak jawne zale no ci na obliczenie tych
pierwiastków w przypadkach, kiedy stopie wielomianu jest wi kszy ni 4, czyli dla n > 4
konieczne jest zastosowanie procesu iteracyjnego. Dla okre lenia pary własnej (
i
λ
,
w
i
), je li
jeden człon jest obliczony iteracyjnie, drugi mo e by obliczony bez iteracji.
Dotychczas przedstawiono wiele algorytmów, kombinacji dwóch lub wi cej metod do
rozwi zania zagadnienia własnego du ych systemów. Szczegółowe omówienie tych metod
podaj specjalistyczne opracowania [8,13,17].
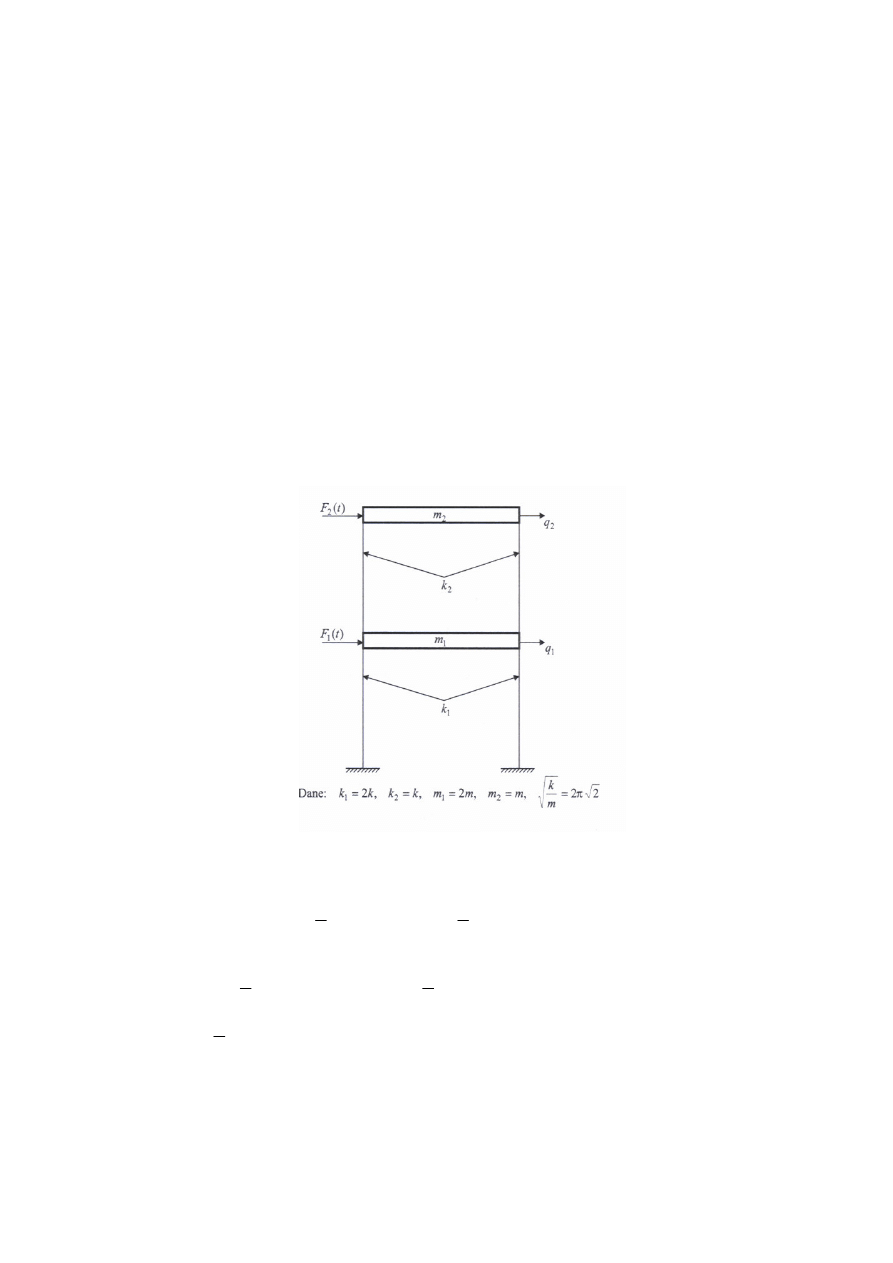
Przykład [8,13]. Wyznaczy macierzowe równanie ruchu i rozwi za zagadnienie własne
modelu obliczeniowego przedstawionego na rys.4.9. Elementy pionowe s osiowo
nieodkształcalne, mo liwy jest wi c tylko ruch poziomy obu mas.
Rozwi zanie. Układ ma dwa stopnie swobody. Do opisu ruchu przyj to dwie współrz dne
uogólnione q
1
i q
2
. Bilans energetyczny prowadzi do nast puj cych wyników:
Rys.4.9 Model układu dynamicznego o dwóch stopniach swobody
-
energia kinetyczna:
)
2
(
2
1
)
(
2
1
2
2
*
2
1
*
2
2
*
2
2
1
*
1
q
m
q
m
q
m
q
m
E
k
+
=
+
=
-
energia potencjalna:
]
2
3
[
2
1
]
2
)
[(
2
1
]
)
(
[
2
1
2
2
2
1
2
1
2
2
2
2
1
2
2
1
2
1
2
1
2
2
2
1
1
kq
q
kq
kq
q
k
q
q
k
q
k
k
q
q
k
q
k
E
p
+
−
=
=
+
−
+
=
−
+
=
-
praca sił wymuszaj cych:
2
2
1
1
)
(
)
(
q
t
F
q
t
F
L
+
=
Wstawiaj c powy sze wyra enia do równa Lagrange’a otrzymuje si macierzowe równanie
ruchu w postaci:
=
−
−
+
)
(
)
(
3
0
0
2
2
1
2
1
2
*
*
*
*
1
t
F
t
F
q
q
k
k
k
k
q
q
m
m
Równanie charakterystyczne zagadnienia własnego przyjmuje wi c posta :
0
3
5
2
)
(
2
2
2
=
+
−
=
k
km
m
f
λ
λ
λ
którego rozwi zanie s dwa pierwiastki:
m
k /
5
,
0
1
=
λ
oraz
m
k /
0
,
2
2
=
λ
. Wektor cz sto ci
ma nast puj ce warto ci:
s
rad
m
k
m
k
/
4
2
/
0
,
2
/
5
,
0
2
1
=
=
=
π
π
ω
ω
ω
Okresy drga własnych dla poszczególnych cz sto ci s równe:
s
T
0
,
1
/
2
1
1
=
=
ω
π
,
s
T
5
,
0
/
2
2
2
=
ω
π
.
Po okre leniu cz sto ci własnych w celu wyznaczenia wektorów własnych korzysta si z
równania ruchu (4.92). Dla pierwszej cz sto ci mamy:
[
]
0
1
2
1
=
−
w
B
K
ω
co dalej w jawnej postaci daje:
=
−
−
−
−
0
0
2
3
22
11
2
1
2
1
ω
ω
ω
ω
m
k
k
k
m
k
które po wstawieniu warto ci
m
k /
5
,
0
2
1
=
ω
jest równowa ne układowi równa
algebraicznych jednorodnych:
0
5
,
0
0
2
22
11
21
11
=
+
−
=
−
kw
kw
kw
kw
Układ ten ma niesko czenie wiele rozwi za , co nie pozwala na wyznaczenie
amplitudy drga swobodnych, lecz jedynie umo liwia wyznaczenie kształtu drga układu z
dokładno ci do stałej. Mamy wi c, po skre leniu drugiego równania:
11
21
2
ω
ω
=
To umo liwia po przyj ciu dowolnej warto ci
11
ω
obliczy warto
21
ω
. W praktyce
post pujemy tak, aby maksymalna warto wektora
w
1
była równa jedno ci:
=
0
,
1
5
,
0
1
w
Druga cz sto umo liwia okre lenie drugiego wektora własnego, czyli:
[
]
0
2
2
2
=
−
w
B
K
ω
Po wstawieniu warto ci
m
k
w
/
0
,
2
22
=
otrzymuje si układ równa :
0
0
22
12
22
12
=
−
−
=
−
−
kw
kw
kw
kw
z którego wynika:
22
12
w
w
−
=
. Wektor własny w
2
korzystnie jest przyj w postaci:
−
=
0
,
1
0
,
1
2
w
Macierz własna rozpatrywanego przykładu jest wi c nast puj ca:
−
=
0
,
1
0
,
1
0
,
1
5
,
0
W
, a
wektory własne pokazano na rys. 4.10.
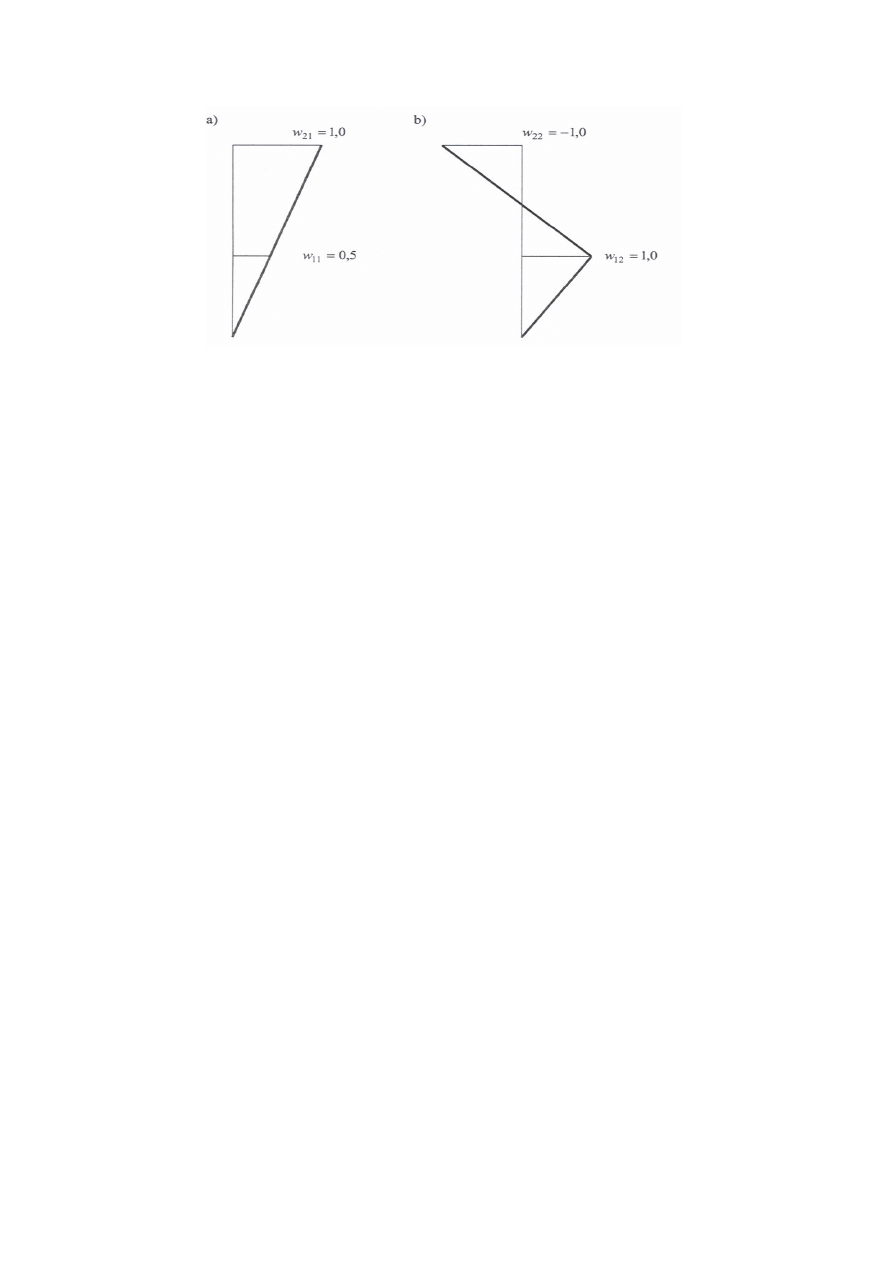
Rys.4.10 Pierwsza i druga posta drga własnych układu.
5.2 Drgania swobodne tłumione
Je eli układ mechaniczny zawiera oprócz sił spr ystych a elementów tarcia
wiskotycznego (siły tłumienia zale ne liniowo od pr dko ci), to równania ró niczkowe ruchu
układu
w prostej postaci s nast puj ce:
=
=
=
+
+
n
j
n
j
j
ij
j
ij
i
q
c
q
q
a
1
1
*
*
*
1
0
α
)
,...,
2
,
1
(
n
i
=
(4.99)
lub
w postaci odwrotnej:
=
=
=
+
+
n
j
n
k
ji
k
k
ij
j
j
i
y
y
m
y
1
1
*
*
*
0
δ
α
δ
(4.100)
gdzie:
k
α
- współczynnik tłumienia wiskotycznego.
Je eli ka dy z kierunków k pokrywa si z ka dym z kierunków j (tj. je li wszystkie
elementy tarcia s przyło one do mas układu), to liczba powy szych równa jest równa n.
Je eli s tak e elementy tarcia, które daj siły oporu nie przyło one bezpo rednio do jednej z
mas układu, to równanie (4.100) mo na uło y tak e dla kierunku działania tych sił, przy
czym ka dy z takich elementów tarcia zwi ksza liczb stopni swobody układu o 1/2.
Rozwi zanie układu równa (4.99) opisuj
drgania swobodne tłumione, tj. drgania,
jakie wykonuje układ mechaniczny wyprowadzony z poło enia równowagi, przy warunkach
pocz tkowych ruchu ró nych od zera. Warunki te zapisujemy w nast puj cy sposób:
0
=
t
,
0
i
i
q
q
=
,
0
*
*
i
i
q
q
=
,
)
,...,
2
,
1
(
n
i
=
(4.101)
Przy tych warunkach pocz tkowych nale y zbada przebieg rozwi za układu, np.
(4.99). Rozwi zania układu tych równa szukamy w postaci funkcji:
t
i
i
e
A
q
λ
=
(4.102)
gdzie: A
i
-pewne stałe rzeczywiste,
λ
- liczba rzeczywista lub zespolona.
Po podstawieniu (4.102) do (4.99) i uproszczeniu przez e
λ
t otrzymamy:
=
=
=
+
+
n
j
n
j
j
ij
i
ij
i
i
A
c
A
A
a
1
1
2
0
α
λ
λ
(4.103)
Jest to liniowy układ równa algebraicznych o niewiadomych A
i
. Układ ten posiada
niezerowe rozwi zania, je li współczynnik przy niewiadomych jest równy zeru.
Współczynnik ten piszemy w nast puj cej postaci:
(4.104)
Równanie (4.104) nazywa si
równaniem charakterystycznym, a jego rozwi zanie
pierwiastkami charakterystycznymi. Równanie charakterystyczne mo e posiada pierwiastki
rzeczywiste lub zespolone. W przypadku pierwiastków rzeczywistych ogólne rozwi zanie
mo emy napisa w postaci:
=
=
n
j
t
ij
i
j
e
A
y
1
λ
(4.105)
Je eli pierwiastki charakterystyczne s zespolone, ogólne rozwi zanie ma posta :
=
−
=
n
j
j
t
v
ij
i
j
e
A
y
1
)
sin(
ϕ
ω
(4.106)
gdzie:
ij
A - rozwi zanie układu (4.103),
j
ϕ
- stałe zale ne do warunków pocz tkowych,
j
j
v
ω
,
- odpowiednie cz ci rzeczywiste i urojone pierwiastka charakterystycznego
j
λ
.
Poniewa
j
λ
w rozwi zaniach (4.102) i ,
j
v w (4.103) s ujemne, rozwi zania układu
(4.99) d
do zera. Rozwi zania (4.102) d
do zera asymptotycznie, nie wykonuj c
oscylacji, a rozwi zania (4.103) d
do zera w sposób oscylacyjny [8,13].
5.3 Drgania wymuszone nietłumione
Nieraz na układ n punktów materialnych działaj siły spr yste oraz siły zewn trzne
zale ne od czasu P(t), działaj ce w kierunku i = l, 2, ..., n. Równanie ró niczkowe ruchu
mo emy
w prostej postaci zapisa nast puj co:
)
(
1
*
*
t
P
y
r
y
m
i
n
j
i
ij
i
i
=
+
=
(4.107)
lub
w postaci odwrotnej:
)
(
1
*
*
1
1
t
P
y
m
y
j
n
j
ij
j
i
n
j
ij
=
=
=
+
δ
δ
(4.108)
Rozwi zanie ogólne układu (4.107) lub (4.108) składa si z rozwi zania ogólnego
układu jednorodnego i rozwi zania szczególnego układu niejednorodnego. Rozwi zania
ogólnego układu jednorodnego opisuj drgania swobodne nietłumione, które pominiemy w
dalszych rozwa aniach (
w układach rzeczywistych wyst puje pewne tłumienie i drgania
swobodne zanikaj , z tego wzgl du mo emy rozwi zanie drga swobodnych pomin ), a
zajmiemy si - rozwi zaniem szczególnym układu niejednorodnego. Rozwi zania te opisuj
drgania, które nazywamy
drganiami wymuszonymi.
Poniewa do układów liniowych stosuje si zasad superpozycji, mo na rozwa a
drgania wymuszone kolejno siłami przyło onymi do poszczególnych punktów materialnych,
a nast pnie otrzymane rozwi zania dodawa . Rozwi zania równa ró niczkowych (4.107) lub
(4.108) mo na przedstawi w postaci rozło enia na postacie własne:
=
=
n
j
j
j
t
q
a
y
1
1
1
)
(
=
=
n
j
j
j
t
q
a
y
1
2
2
)
(
(4.109)
..........................
=
=
n
j
j
nj
n
t
q
a
y
1
)
(
gdzie: a
ij
- amplitudy znormowanych postaci własnych drga , a funkcje q
j
(t) wyznacza si z
układu równa ró niczkowych ruchu :
=
=
+
n
j
j
j
t
P
a
q
q
1
1
1
2
1
1
*
*
)
(
ω
=
=
+
n
j
j
j
t
P
a
q
q
1
2
2
2
2
2
*
*
)
(
ω
(4.110)
.....................................
=
=
+
n
j
j
jn
n
n
n
t
P
a
q
q
1
2
*
*
)
(
ω
gdzie:
n
ω
ω
,...,
1
- cz sto ci drga własnych.
Je eli siły P
j
(t) maj posta wymusze harmonicznych w postaci:
,
sin
01
1
t
P
P
ω
=
,
sin
02
2
t
P
P
ω
=
...,
,
sin
0
t
P
P
n
n
ω
=
(4.111)
to rozwi zaniem dowolnego z równa (4.110) jest suma:
t
a
P
q
i
n
j
ji
j
i
ω
ω
ω
sin
2
2
1
0
−
=
=
(4.112)
Zamiast (4.112) mo na napisa :
t
a
P
a
y
i
n
j
ji
j
n
s
is
i
ω
ω
ω
sin
2
2
1
0
1
−
=
=
=
(4.113)
W tym przypadku amplitudy drga mog by tak e otrzymane nie bezpo rednio, je eli
podstawi si w (4.107) lub (4.108):
t
A
y
i
i
ω
sin
=
(4.114)
Amplitudy drga A
i
wyznaczamy z układu równa algebraicznych otrzymanych po
podstawieniu (4.114) do (4.107) lub (4.108) i uproszczeniu przez
ω
t w
prostej postaci:
=
=
+
−
n
j
i
i
ij
i
i
P
A
r
A
m
1
0
2
ω
(4.115)
lub w
postaci odwrotnej:
=
=
=
−
n
j
j
n
j
ij
ij
i
j
P
A
m
A
1
0
1
2
δ
δ
ω
(4.116)
Po rozwi zaniu tych równa otrzymamy amplitudy drga układu. W przeciwie stwie
do drga swobodnych tłumionych, które opisuj stan przej ciowy, drgania wymuszone
okre laj stan ustalony. Stanem ustalonym jest równie stan spoczynku w poło eniu
równowagi układu mechanicznego. Drgania wymuszone układów z tłumieniem dodatnim
opisuj stan ustalony stacjonarny, gdy siła wymuszaj ca jest funkcj okresow . Drgania
wymuszone nietłumione opisuj stan ustalony niestacjonarny, gdy cz sto siły wymuszaj cej
jest równa jednej z cz sto ci własnej układu, tzn. gdy mamy do czynienia ze zjawiskiem
rezonansu [14,33,71].
5.4 Drgania wymuszone tłumione
Przy harmonicznych siłach wymuszaj cych (4.111) wpływ sił tarcia wiskotycznego
wyra a si w dwóch podstawowych efektach:
- fazy drga ró nych punktów układu nie pokrywaj si ze sob i ró ni si od fazy sił
wymuszaj cych,
- amplitudy drga punktów układu s mniejsze od odpowiadaj cych im amplitud układu bez
tarcia i wsz dzie s sko czone.
Dynamiczne równania ruchu w
prostej postaci maj zapis:
)
(
1
1
*
*
*
t
P
y
r
y
y
m
i
n
j
n
j
i
ij
i
ij
i
i
=
+
+
=
=
α
(4.117)
lub
w postaci odwrotnej:
)
(
1
1
*
*
*
1
1
t
P
y
y
m
y
j
n
j
ij
n
j
ij
j
j
j
j
n
j
ij
=
=
=
=
+
+
δ
δ
α
δ
(4.118)
Amplitudy drga wymuszonych wyznacza si drog podstawienia rozwi zania:
t
b
t
a
y
i
i
i
ω
ω
cos
sin
+
=
,
)
,...,
2
,
1
(
n
i
=
(4.119)
do równa ró niczkowych ruchu. W miejsce wyra enia (4.119) mo na tak e przyj :
)
sin(
ϕ
ω
−
=
t
A
y
i
i
,
)
,...,
2
,
1
(
n
i
=
(4.120)
gdzie:
2
2
i
i
i
b
a
A
+
=
,
i
i
i
a
b
=
ϕ
tg
(4.121)
K t
ϕ
i
nazywa si k tem przesuni cia fazowego, za A
i
- amplitud drga .
Rozwa ania przedstawione w tym punkcie znajduj zastosowanie podczas analizy
stanu dynamicznego układów mechanicznych o dwóch i wi cej stopniach swobody. Wiele z
informacji tu przedstawionych stanowi podstaw wprowadzanej do bada dynamiki maszyn
analizy modalnej.