Zarz

ą

dzanie projektem

c.d.

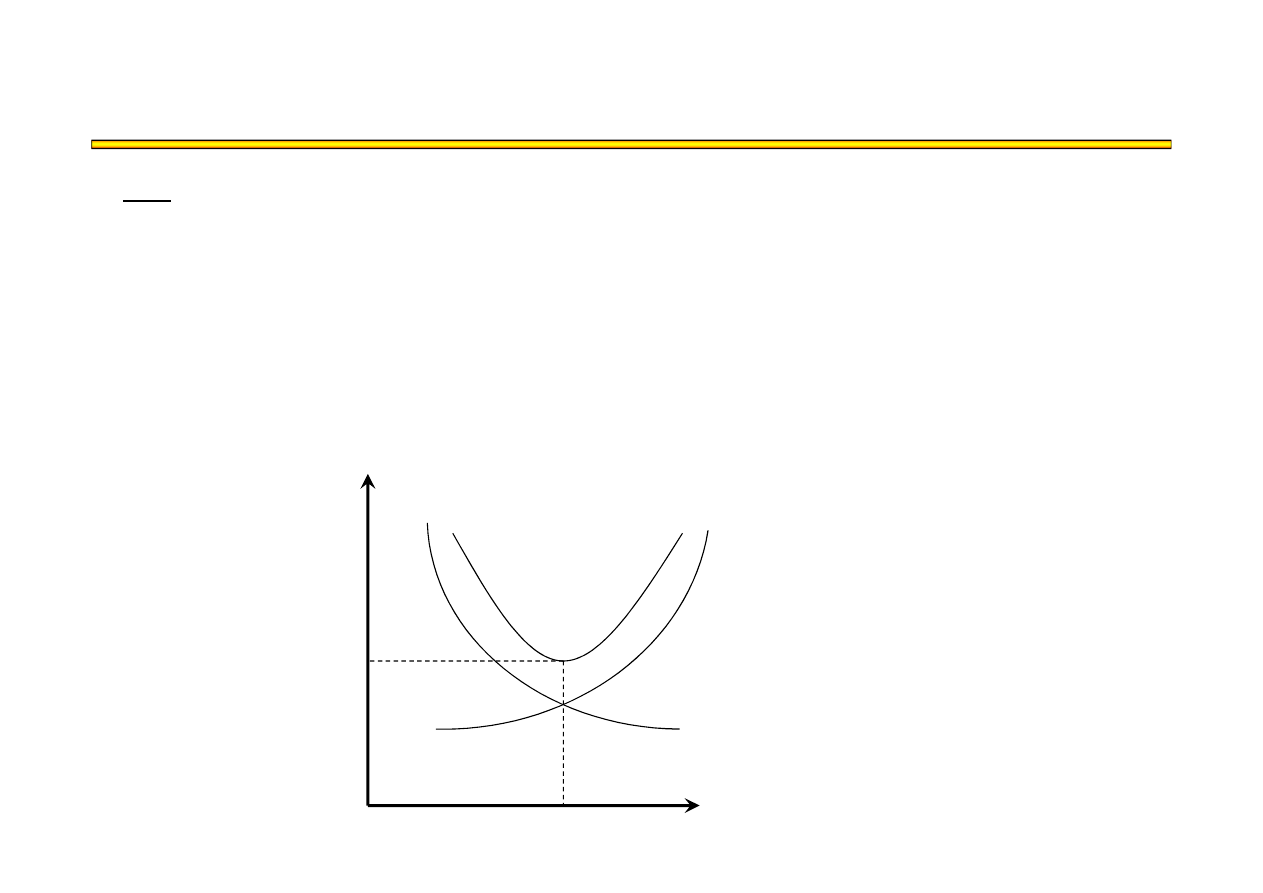
Analiza kosztowo-czasowa LESS (1)

Cel:

Wyznaczenie takiego terminu ko

ń

cowego przedsi

ę

wzi

ę

cia, dla którego koszt

całkowity (KC) osi

ą

gnie warto

ść

najmniejsz

ą

.

KC = KB + KP

KB

– koszty bezpo

ś

rednie zwi

ą

zane z poszczególnymi czynno

ś

ciami

KP

– koszty po

ś

rednie zwi

ą

zane z całym przedsi

ę

wzi

ę

ciem (czasem jego trwania)

`

KC

KB

KP

t

K

KC*

t*

Analiza kosztowo-czasowa LESS (2)

Zało

ż

enia:

n

– liczba zdarze

ń

w sieci

(i,j)

– czynno

ść

o zdarzeniu pocz

ą

tkowym i oraz ko

ń

cowym j

i = 1,2…n;

j = 1,2,…,n

t

ij

n

– normalny czas trwania czynno

ś

ci (i,j) – (wyj

ś

ciowy)

t

ij

g

– graniczny czas trwania czynno

ś

ci (i,j) – (najkrótszy)

K

ij

n

– normalny koszt bezpo

ś

redni wykonania czynno

ś

ci (i,j) w czasie t

ij

n

K

ij

g

– graniczny koszt bezpo

ś

redni wykonania czynno

ś

ci (i,j) w czasie

t

ij

g

t

ij

– czas trwania czynno

ś

ci (i,j) t

ij

g

≤

t

ij

≤

t

ij

n

K

ij

– koszt trwania czynno

ś

ci (i,j) w czasie t

ij

s

ij

– koszt przy

ś

pieszenia wykonania czynno

ś

ci (i,j) o jednostk

ę

czasu

(jednostkowy koszt akceleracji czynno

ś

ci (i,j)

g

ij

n

ij

n

ij

g

ij

ij

ij

ij

t

t

K

K

t

K

s

−

−

=

∆

∆

=

Analiza kosztowo-czasowa LESS (3)

Iteracyjna analiza kosztowo czasowa:

1. Analiza rozpoczynana jest od przyj

ę

cia: t

ij

= t

ij

n

2. W ka

ż

dej iteracji przyspieszana jest o jednostk

ę

czasu odpowiednio

wybrana czynno

ść

krytyczna

3. W ka

ż

dej iteracji liczone s

ą

koszty całkowite przedsi

ę

wzi

ę

cia

4. Kryterium zako

ń

czenia post

ę

powania: koszty całkowite zaczynaj

ą

rosn

ąć

Zasady wyboru przyspieszanej czynno

ś

ci:

1. Przyspiesza

ć

mo

ż

na wył

ą

cznie czynno

ś

ci krytyczne

2. Spo

ś

ród czynno

ś

ci krytycznych nale

żą

cych do jednej

ś

cie

ż

ki krytycznej,

nale

ż

y wybra

ć

czynno

ść

o najni

ż

szym koszcie akceleracji

3. Je

ż

eli istnieje kilka

ś

cie

ż

ek krytycznych, to nale

ż

y przyspieszy

ć

po jednej

czynno

ś

ci krytycznej z ka

ż

dej

ś

cie

ż

ki.

Analiza kosztowo-czasowa LESS (4) – przykład

Czynno

ść

Czas trwania

normalny

t

ij

Czas trwania

graniczny

t

ij

Koszt

normalny

K

ij

n

Koszt

graniczny

K

ij

g

Koszt

akceleracji

s

ij

A (1,2)

6

4

200

270

35

B (1,3)

2

1

10

20

10

C (2,5)

4

3

250

300

50

D (2,4)

6

4

300

460

80

E (2,3)

3

2

10

20

10

F (5,7)

2

1

20

30

10

G (4,7)

5

4

100

130

30

H (3,6)

3

2

80

110

30

I (6,7)

2

2

30

30

0

J (7,8)

2

1

10

20

10

Razem

××××

××××

1010

××××

××××

Funkcja kosztów po

ś

rednich:

KP = 40t

8

+ 50

0

0

1

6

6

2

12

12

4

12

15

5

17

17

7

9

12

3

12

15

6

19

19

8

A

B

C

D

E

F

H

G

I

J

(2, 1, 10)

(6, 4, 35)

(3, 2, 10)

(6, 4, 80)

(4, 3, 50)

(5, 4, 30)

(3, 2, 30)

(2, 1, 10)

(2, 2, 0)

(2, 1, 10)

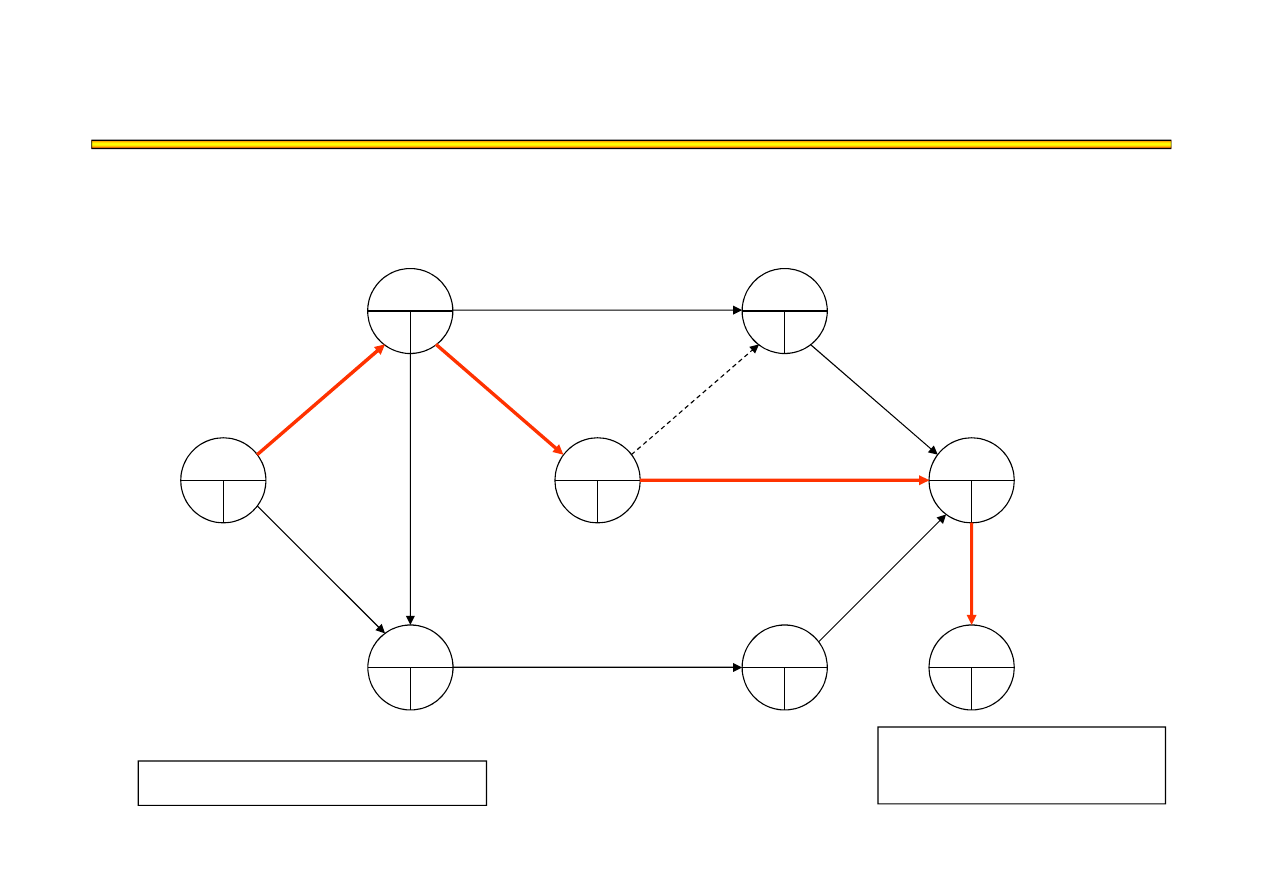
Analiza kosztowo-czasowa LESS (5) – przykład

t

8

= 19

KP = 40

●

19+50 = 810

Ś

cie

ż

ka krytyczna:

A,D,G,J

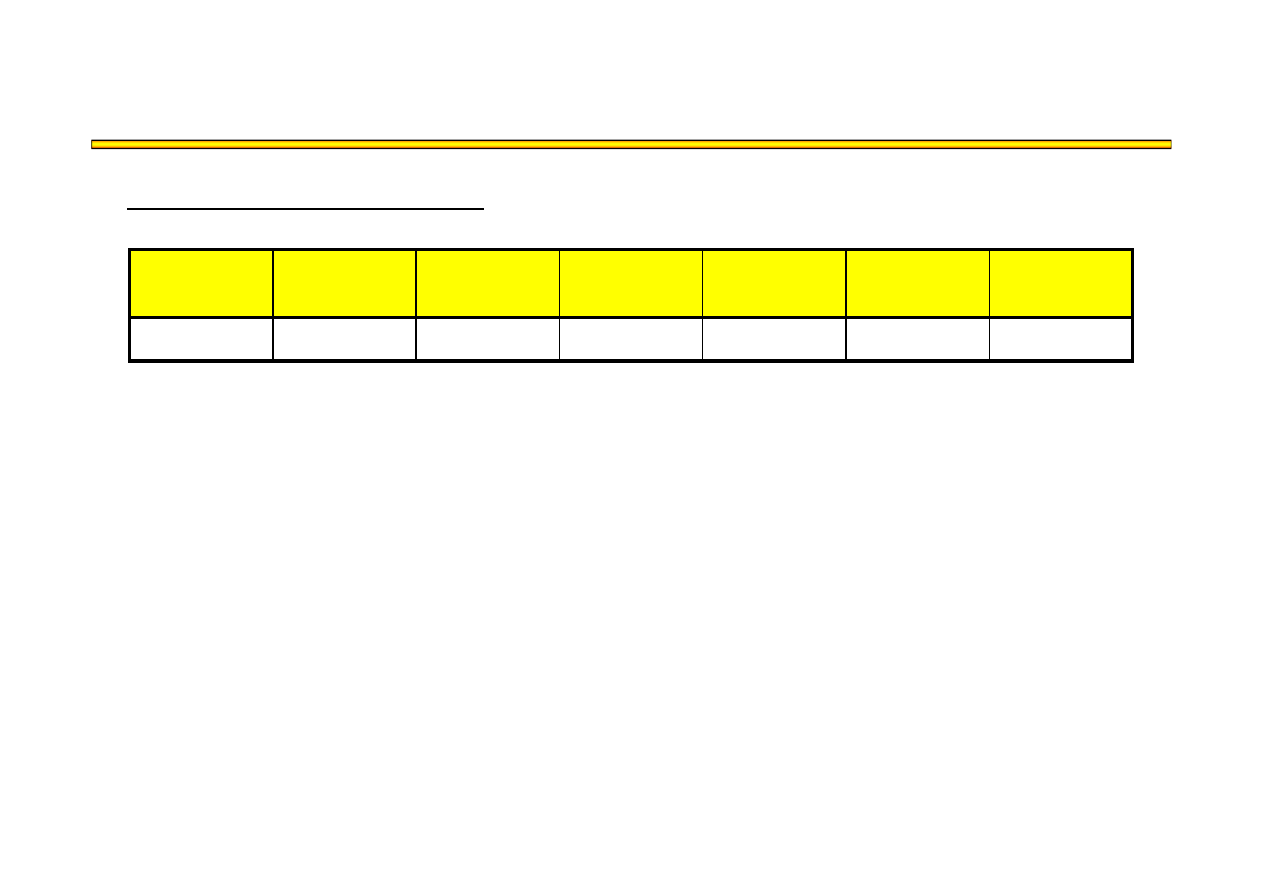
Analiza kosztowo-czasowa LESS (6) – przykład

t

8

KB

KP

KC

Czynno

ś

ci

przy

ś

p.

Koszt

przy

ś

p.

Ś

cie

ż

ka

krytyczna

19

1010

810

1820





A,D,G,J

Zestawienie kolejnych iteracji:

0

0

1

6

6

2

12

12

4

12

15

5

17

17

7

9

12

3

12

15

6

18

18

8

A

B

C

D

E

F

H

G

I

J

(2, 1, 10)

(6, 4, 35)

(3, 2, 10)

(6, 4, 80)

(4, 3, 50)

(5, 4, 30)

(3, 2, 30)

(2, 1, 10)

(2, 2, 0)

(2, 1, 10)

1

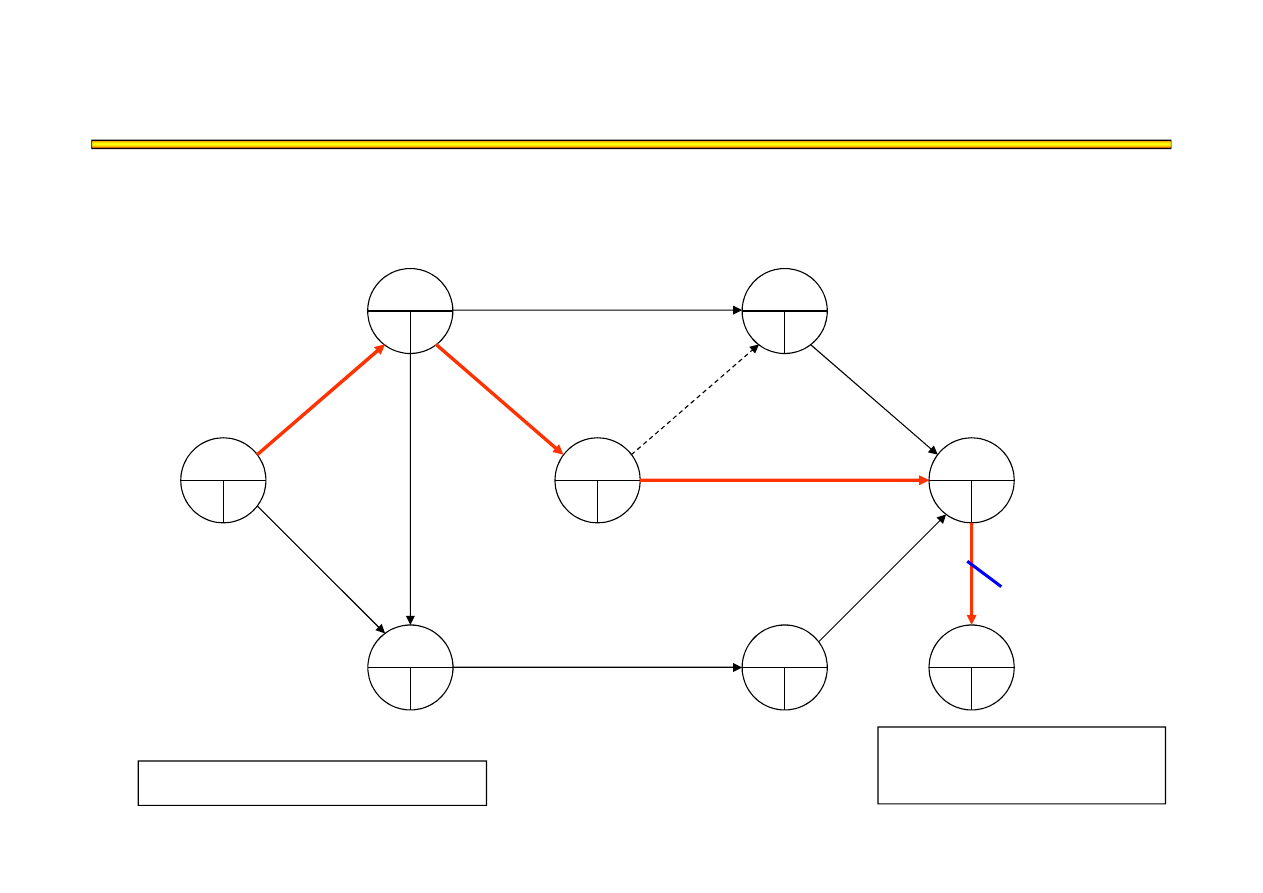
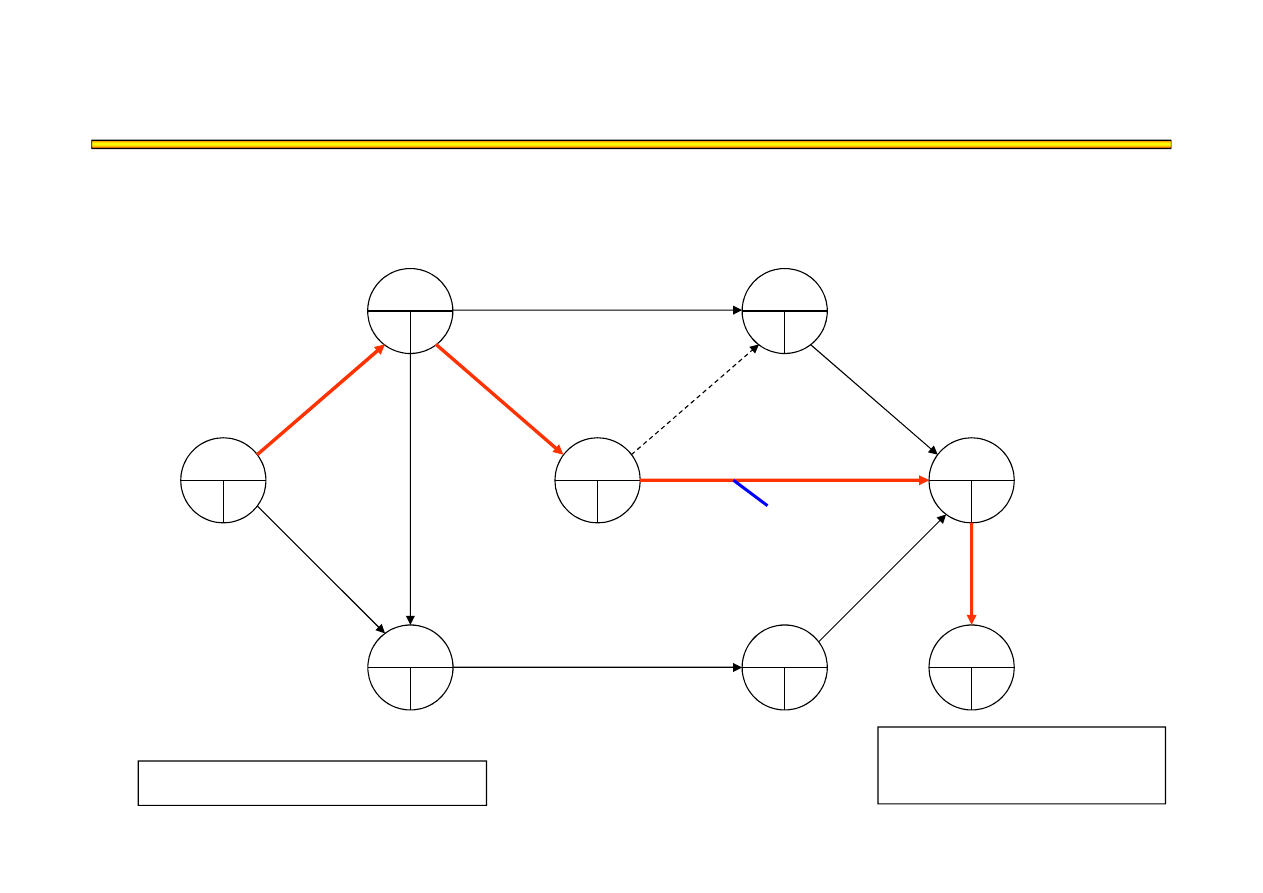
Analiza kosztowo-czasowa LESS (7) – przykład

t

8

= 18

KP = 40

●

18+50 = 770

Ś

cie

ż

ka krytyczna:

A,D,G,J

Analiza kosztowo-czasowa LESS (8) – przykład

t

8

KB

KP

KC

Czynno

ś

ci

przy

ś

p.

Koszt

przy

ś

p.

Ś

cie

ż

ka

krytyczna

19

1010

810

1820





A,D,G,J

18

1020

770

1790

J

10

A,D,G,J

Zestawienie kolejnych iteracji:

0

0

1

6

6

2

12

12

4

12

14

5

16

16

7

9

11

3

12

14

6

17

17

8

A

B

C

D

E

F

H

G

I

J

(2, 1, 10)

(6, 4, 35)

(3, 2, 10)

(6, 4, 80)

(4, 3, 50)

(5, 4, 30)

4

(3, 2, 30)

(2, 1, 10)

(2, 2, 0)

(1, 1, 10)

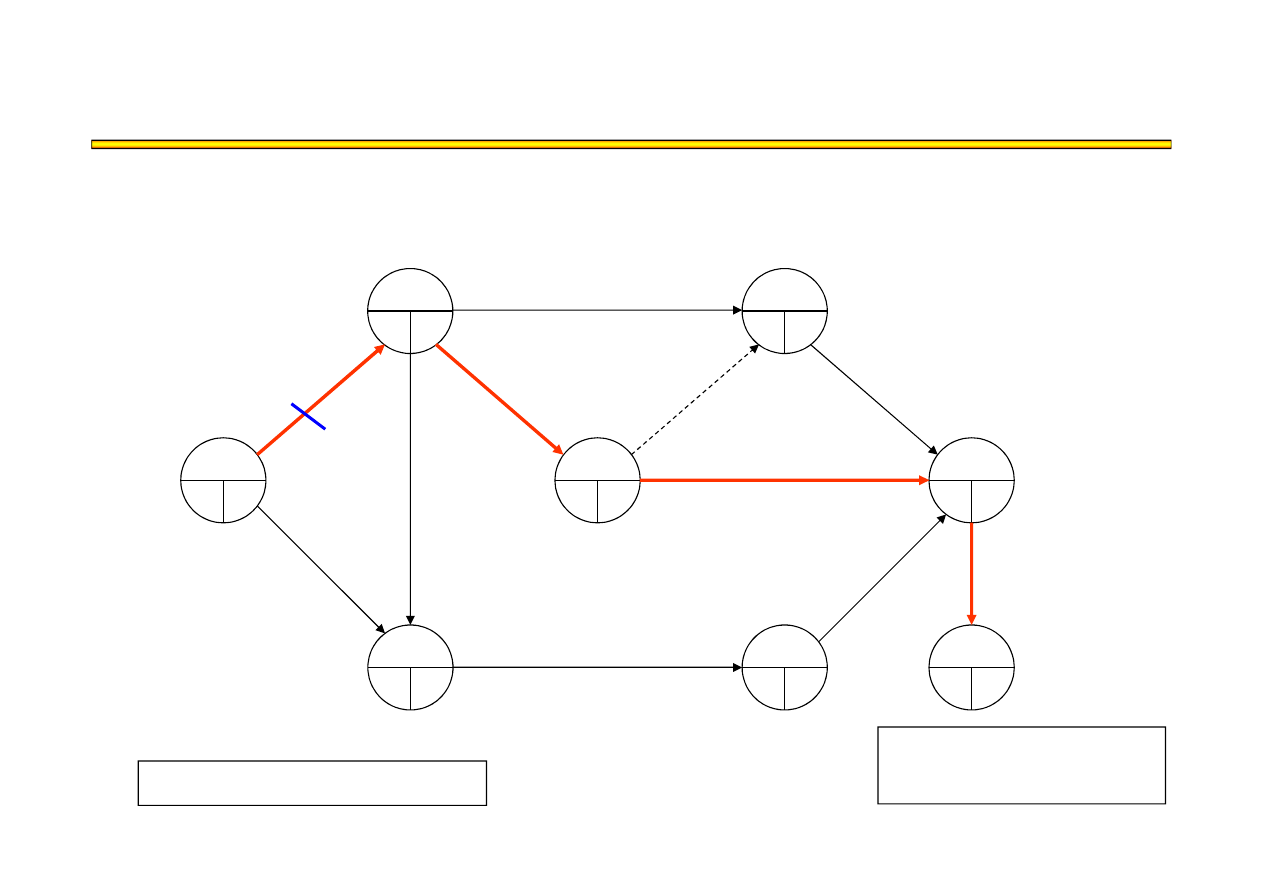
Analiza kosztowo-czasowa LESS (9) – przykład

t

8

= 17

KP = 40

●

17+50 = 730

Ś

cie

ż

ka krytyczna:

A,D,G,J

Analiza kosztowo-czasowa LESS (10) – przykład

t

8

KB

KP

KC

Czynno

ś

ci

przy

ś

p.

Koszt

przy

ś

p.

Ś

cie

ż

ka

krytyczna

19

1010

810

1820





A,D,G,J

18

1020

770

1790

J

10

A,D,G,J

17

1050

730

1780

G

30

A,D,G,J

Zestawienie kolejnych iteracji:

0

0

1

5

5

2

11

11

4

11

13

5

15

15

7

8

10

3

11

13

6

16

16

8

A

B

C

D

E

F

H

G

I

J

(2, 1, 10)

(6, 4, 35)

5

(3, 2, 10)

(6, 4, 80)

(4, 3, 50)

(4, 4, 30)

(3, 2, 30)

(2, 1, 10)

(2, 2, 0)

(1, 1, 10)

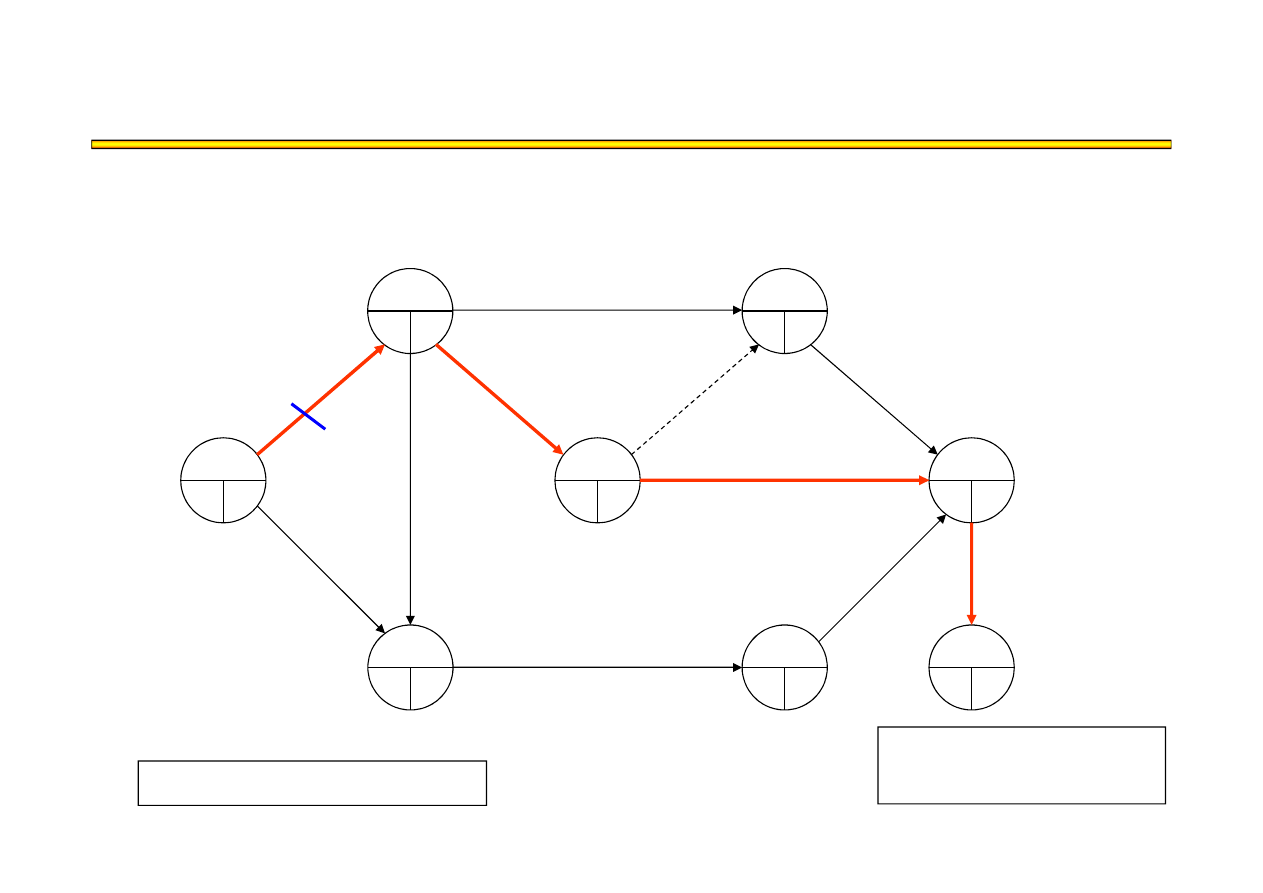
Analiza kosztowo-czasowa LESS (11) – przykład

t

8

= 16

KP = 40

●

16+50 = 690

Ś

cie

ż

ka krytyczna:

A,D,G,J

Analiza kosztowo-czasowa LESS (12) – przykład

t

8

KB

KP

KC

Czynno

ś

ci

przy

ś

p.

Koszt

przy

ś

p.

Ś

cie

ż

ka

krytyczna

19

1010

810

1820





A,D,G,J

18

1020

770

1790

J

10

A,D,G,J

17

1050

730

1780

G

30

A,D,G,J

16

1085

690

1775

A

35

A,D,G,J

Zestawienie kolejnych iteracji:

0

0

1

4

4

2

10

10

4

10

12

5

14

14

7

7

9

3

10

12

6

15

15

8

A

B

C

D

E

F

H

G

I

J

(2, 1, 10)

(5, 4, 35)

4

(3, 2, 10)

(6, 4, 80)

(4, 3, 50)

(4, 4, 30)

(3, 2, 30)

(2, 1, 10)

(2, 2, 0)

(1, 1, 10)

Analiza kosztowo-czasowa LESS (13) – przykład

t

8

= 15

KP = 40

●

15+50 = 650

Ś

cie

ż

ka krytyczna:

A,D,G,J

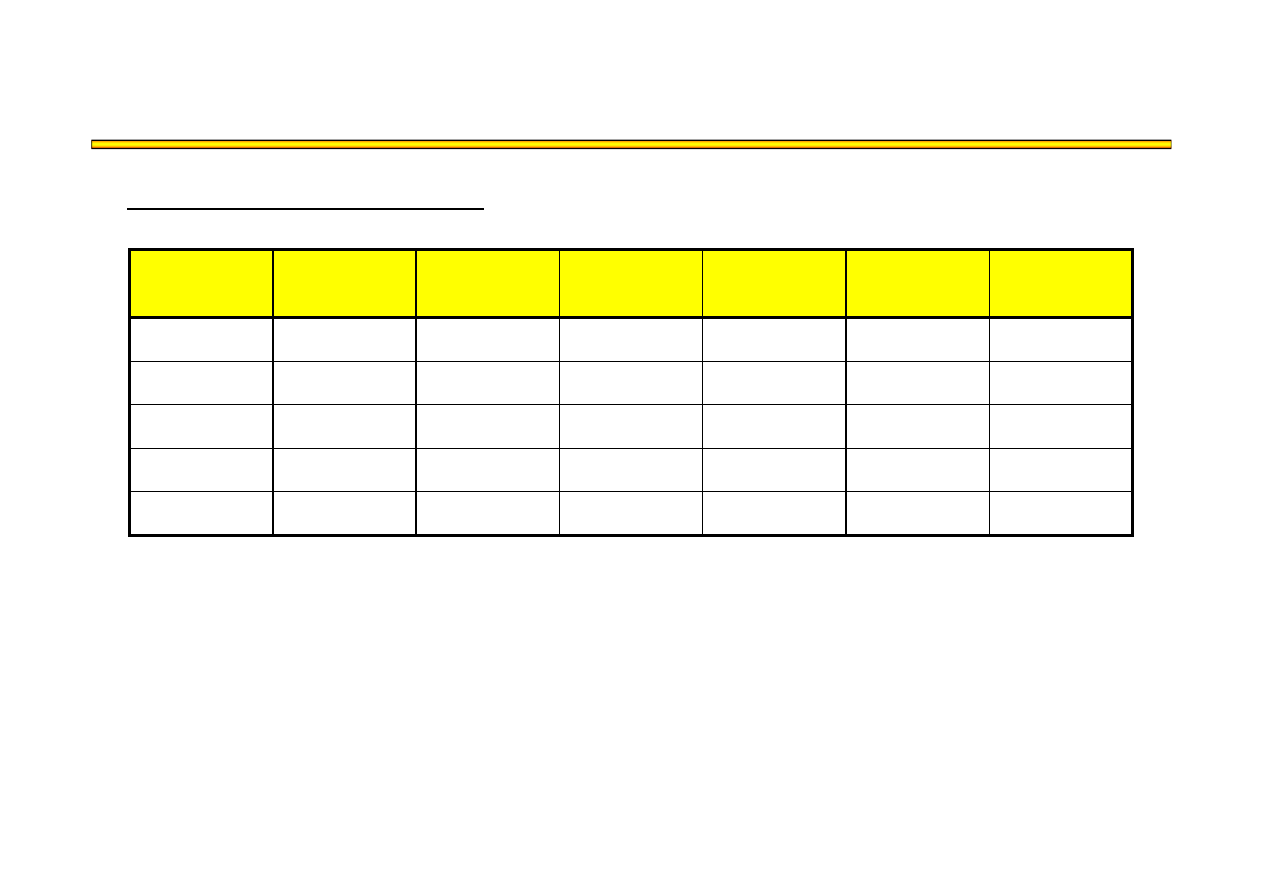
Analiza kosztowo-czasowa LESS (14) – przykład

t

8

KB

KP

KC

Czynno

ś

ci

przy

ś

p.

Koszt

przy

ś

p.

Ś

cie

ż

ka

krytyczna

19

1010

810

1820





A,D,G,J

18

1020

770

1790

J

10

A,D,G,J

17

1050

730

1780

G

30

A,D,G,J

16

1085

690

1775

A

35

A,D,G,J

15

1120

650

1770

A

35

A,D,G,J

Zestawienie kolejnych iteracji:

0

0

1

4

4

2

9

9

4

9

11

5

13

13

7

7

8

3

10

11

6

14

14

8

A

B

C

D

E

F

H

G

I

J

(2, 1, 10)

(4, 4, 35)

(3, 2, 10)

(6, 4, 80)

5

(4, 3, 50)

(4, 4, 30)

(3, 2, 30)

(2, 1, 10)

(2, 2, 0)

(1, 1, 10)

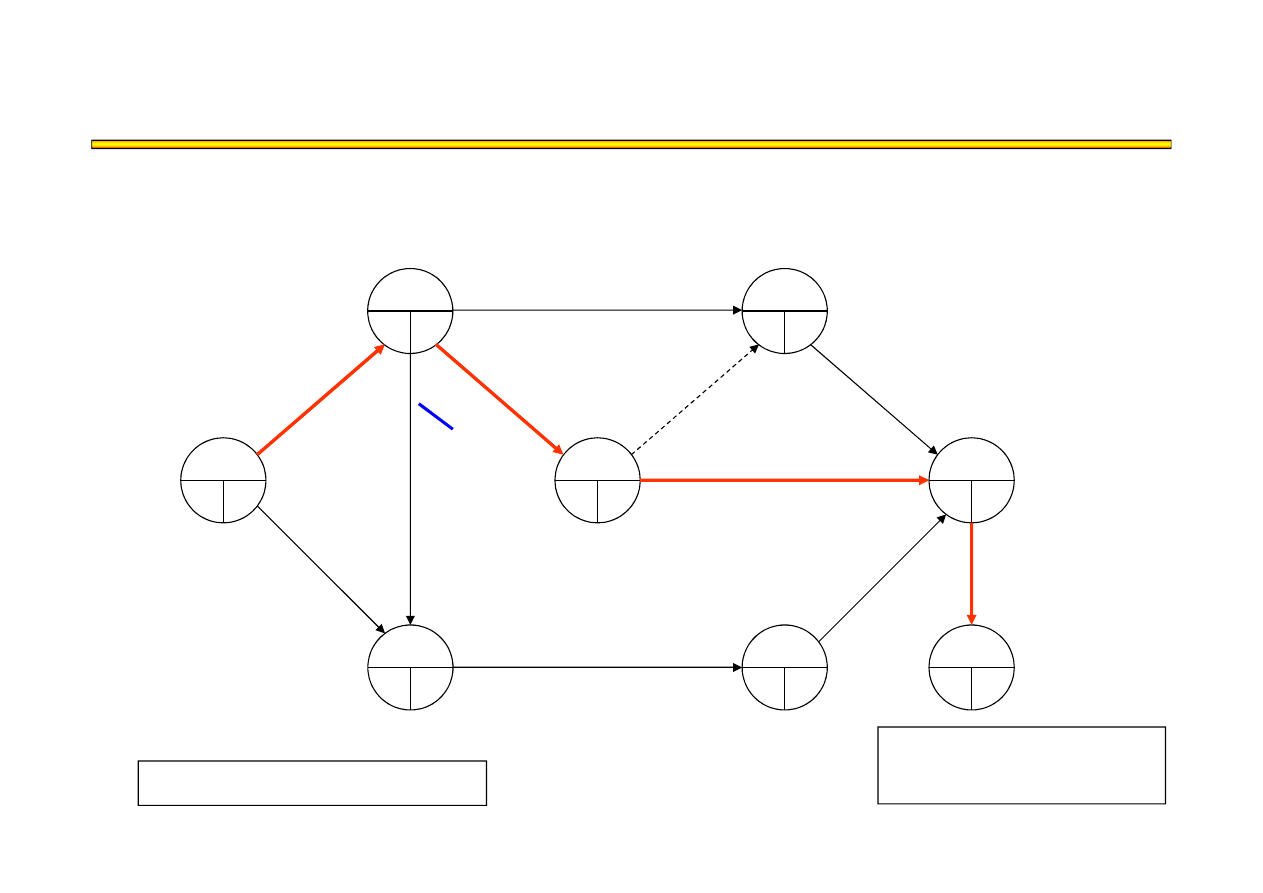
Analiza kosztowo-czasowa LESS (15) – przykład

t

8

= 14

KP = 40

●

14+50 = 610

Ś

cie

ż

ka krytyczna:

A,D,G,J

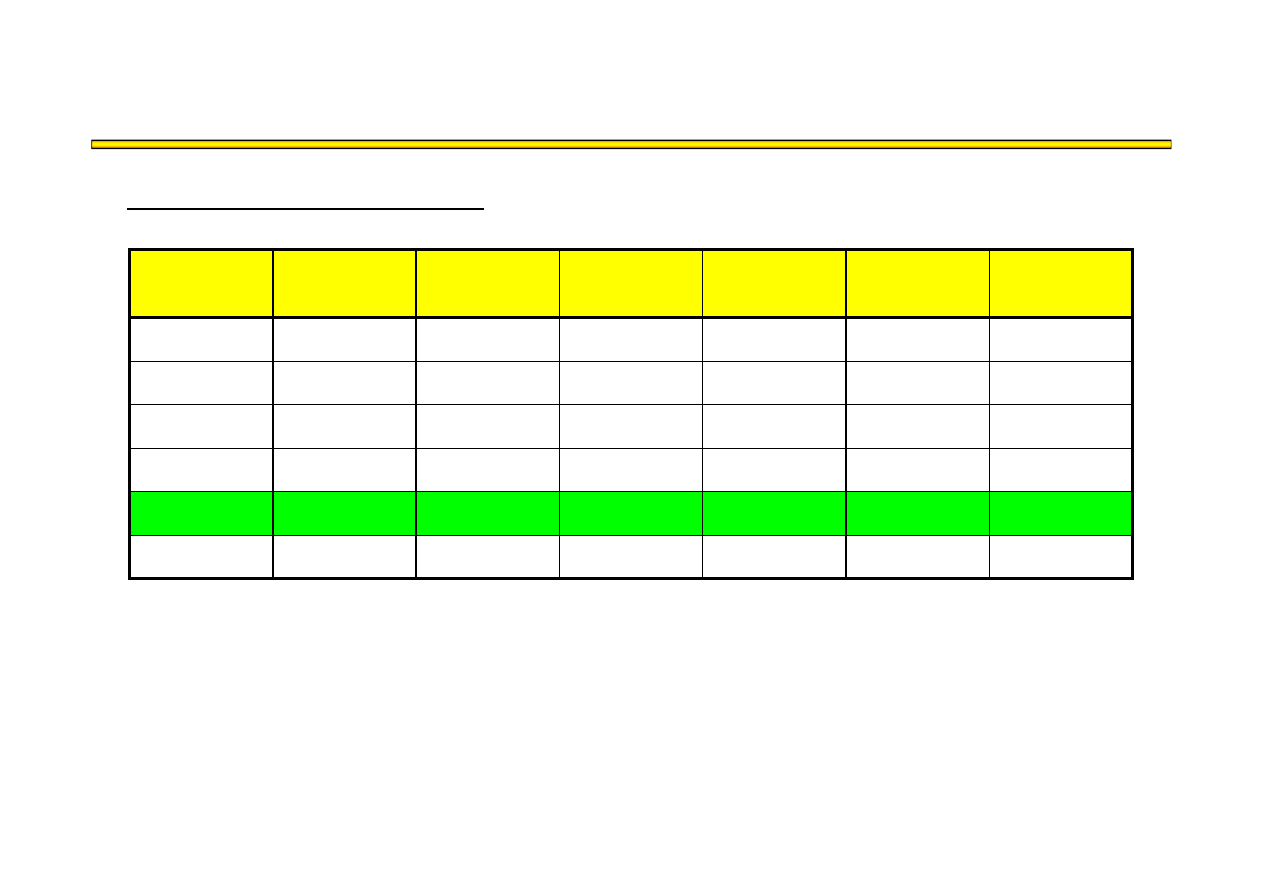
Analiza kosztowo-czasowa LESS (16) – przykład

t

8

KB

KP

KC

Czynno

ś

ci

przy

ś

p.

Koszt

przy

ś

p.

Ś

cie

ż

ka

krytyczna

19

1010

810

1820





A,D,G,J

18

1020

770

1790

J

10

A,D,G,J

17

1050

730

1780

G

30

A,D,G,J

16

1085

690

1775

A

35

A,D,G,J

15

1120

650

1770

A

35

A,D,G,J

14

1200

610

1810

D

80

A,D,G,J

Zestawienie kolejnych iteracji:

0

0

1

4

4

2

8

8

4

8

10

5

12

12

7

7

7

3

10

10

6

13

13

8

A

B

C

D

E

F

H

G

I

J

(2, 1, 10)

(4, 4, 35)

(3, 2, 10)

(5, 4, 80)

4

(4, 3, 50)

(4, 4, 30)

(3, 2, 30)

(2, 1, 10)

(2, 2, 0)

(1, 1, 10)

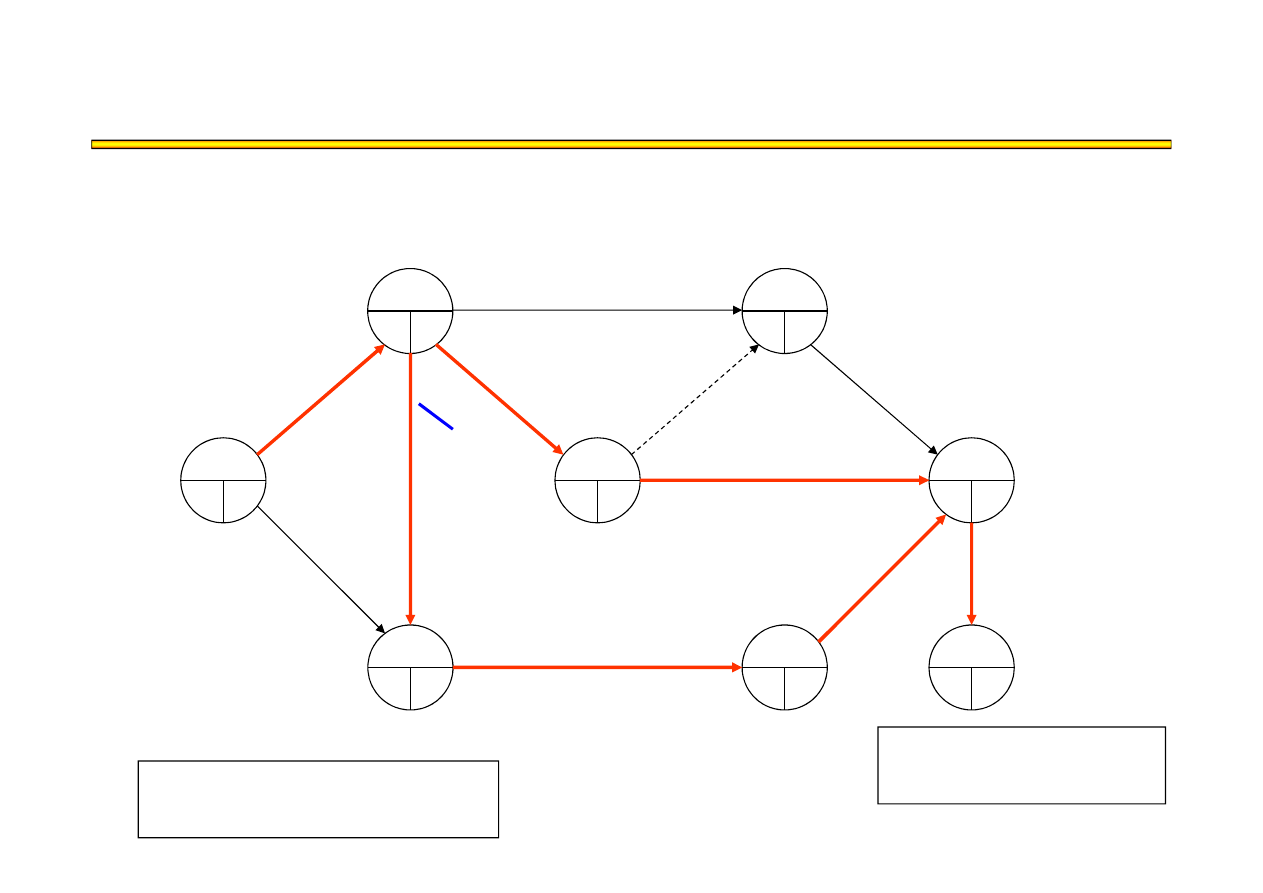
Analiza kosztowo-czasowa LESS (17) – przykład

t

8

= 13

KP = 40

●

13+50 = 570

Ś

cie

ż

ka krytyczna:

A,D,G,J
A,E,H,I,J

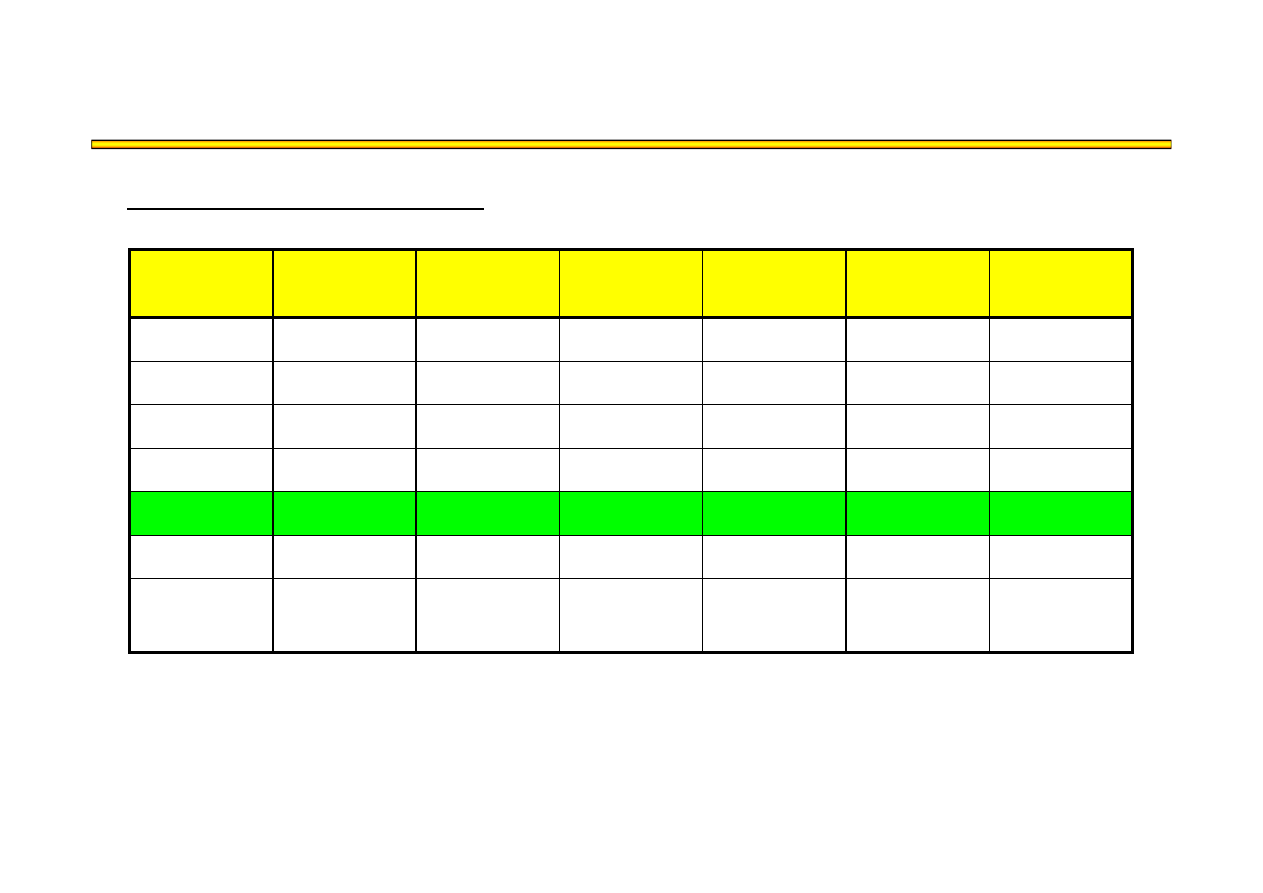
Analiza kosztowo-czasowa LESS (18) – przykład

t

8

KB

KP

KC

Czynno

ś

ci

przy

ś

p.

Koszt

przy

ś

p.

Ś

cie

ż

ka

krytyczna

19

1010

810

1820





A,D,G,J

18

1020

770

1790

J

10

A,D,G,J

17

1050

730

1780

G

30

A,D,G,J

16

1085

690

1775

A

35

A,D,G,J

15

1120

650

1770

A

35

A,D,G,J

14

1200

610

1810

D

80

A,D,G,J

13

1280

570

1850

D

80

A,D,G,J

A,E,H,I,J

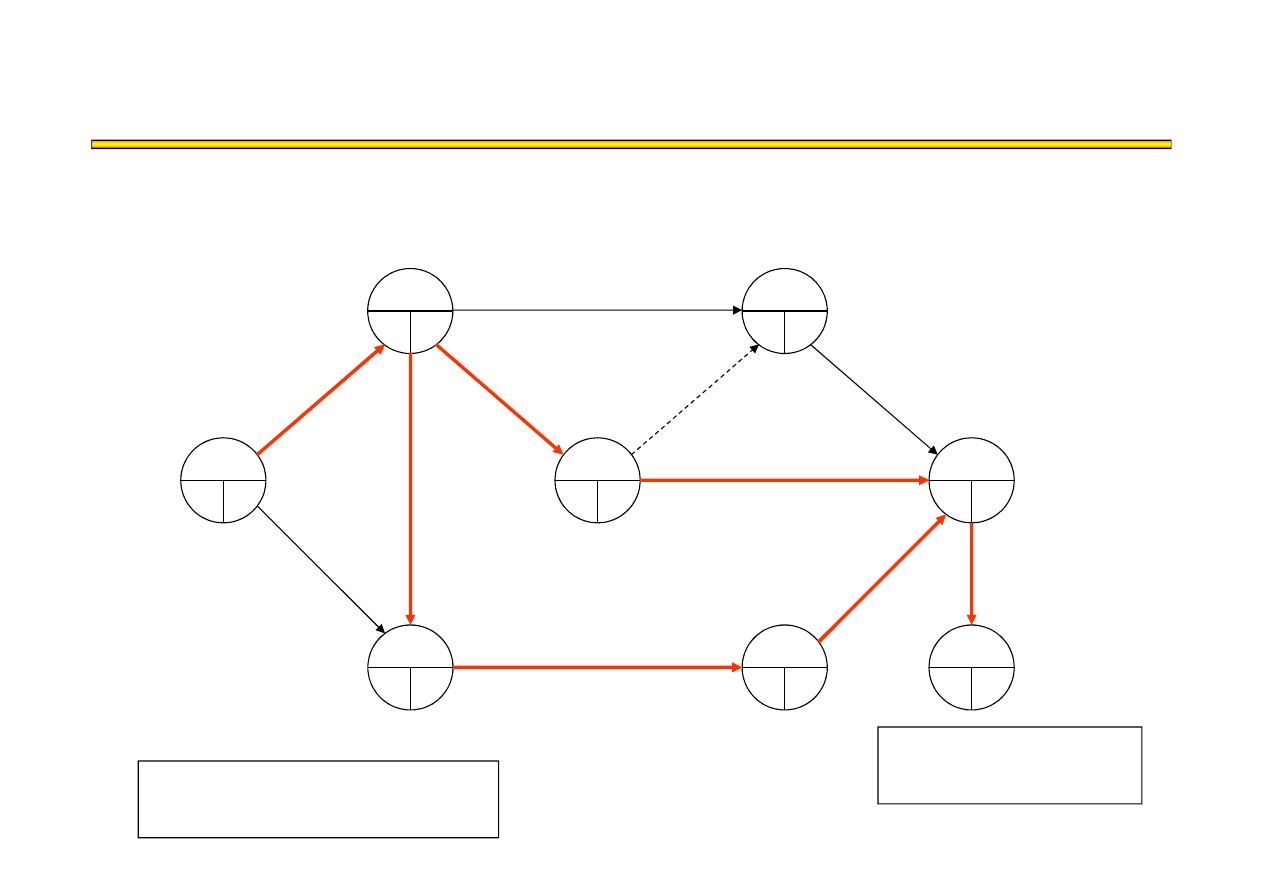
Zestawienie kolejnych iteracji:

0

0

1

4

4

2

8

8

4

8

10

5

12

12

7

7

7

3

10

10

6

13

13

8

A

B

C

D

E

F

H

G

I

J

(2, 1, 10)

(4, 4, 35)

(3, 2, 10)

(4, 4, 80)

(4, 3, 50)

(4, 4, 30)

(3, 2, 30)

(2, 1, 10)

(2, 2, 0)

(1, 1, 10)

Analiza kosztowo-czasowa LESS (17) – przykład

t

8

= 12

→

nierealne

Ś

cie

ż

ka krytyczna:

A,D,G,J
A,E,H,I,J

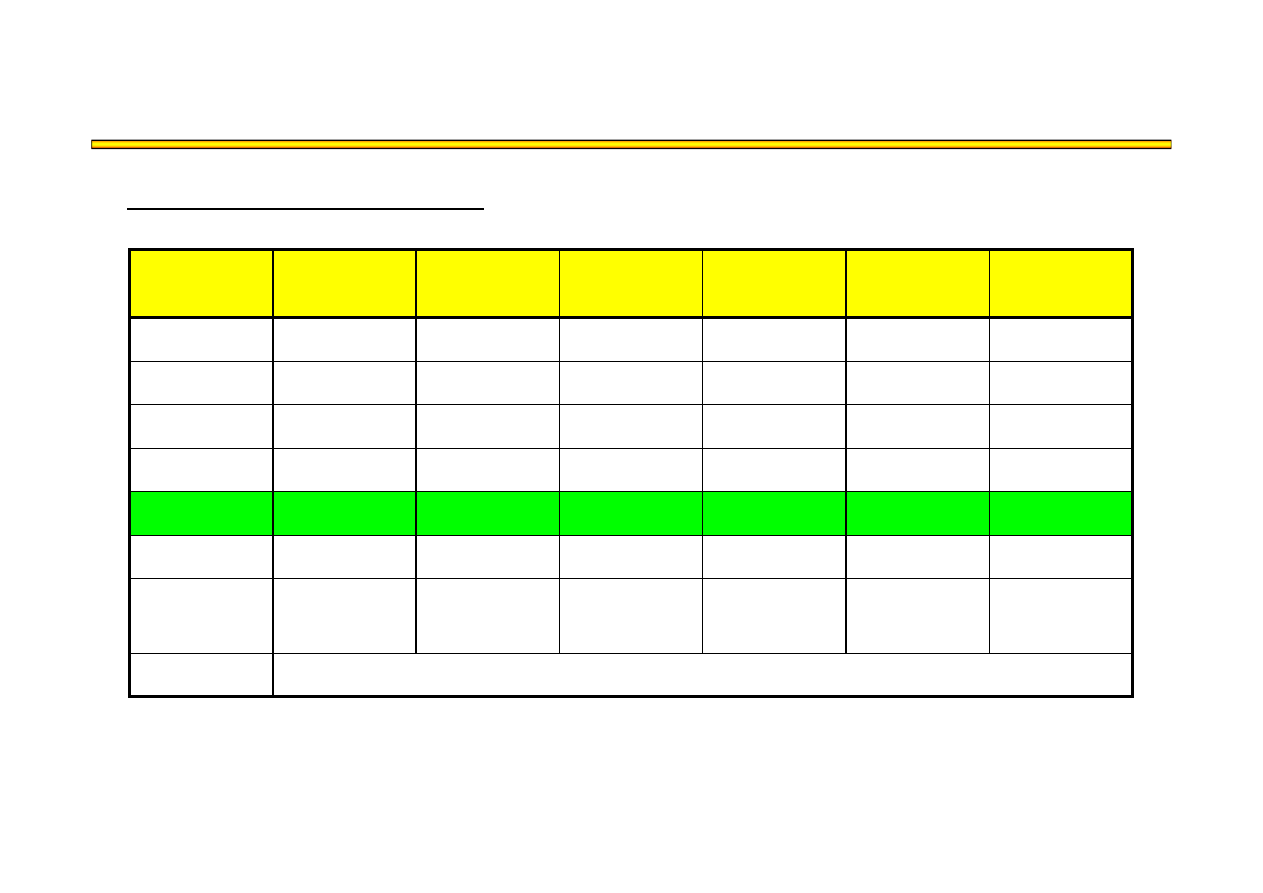
Analiza kosztowo-czasowa LESS (18) – przykład

t

8

KB

KP

KC

Czynno

ś

ci

przy

ś

p.

Koszt

przy

ś

p.

Ś

cie

ż

ka

krytyczna

19

1010

810

1820





A,D,G,J

18

1020

770

1790

J

10

A,D,G,J

17

1050

730

1780

G

30

A,D,G,J

16

1085

690

1775

A

35

A,D,G,J

15

1120

650

1770

A

35

A,D,G,J

14

1200

610

1810

D

80

A,D,G,J

13

1280

570

1850

D

80

A,D,G,J

A,E,H,I,J

12

nierealne

Zestawienie kolejnych iteracji: