OPTYMALIZACJA W

LOGISTYCE

BUDOWA RANKINGU

OBIEKTÓW W

Ś

WIETLE OCEN

WIELOKRYTERIALNYCH

Opracowano na podstawie: Z.J

ę

drzejczyk, K. Kukuła, J. Skrzypek, A. Walkosz, Badania

operacyjne w przykładach i zadaniach, PWN, Warszawa 2002

Zjawisko zło

ż

one

W ró

ż

nych sferach ludzkiej aktywno

ś

ci wyst

ę

puje du

ż

a liczba zjawisk, które

mo

ż

na okre

ś

li

ć

mianem zło

ż

one. Przez zjawisko zło

ż

one rozumie

ć

nale

ż

y

pewien abstrakcyjny twór zwi

ą

zany ze stanem jako

ś

ciowym (bezpo

ś

rednio

nie mierzalnym)

rzeczywistych obiektów opisywany przez co najmniej dwie cechy.

Porównania ró

ż

nych obiektów poło

ż

onych w przestrzeni w zakresie zjawisk

zło

ż

onych stwarzaj

ą

konieczno

ść

sporz

ą

dzania ich ocen, a w dalszej

kolejno

ś

ci konstrukcji rankingu. Zjawiska zło

ż

one s

ą

zwykle

charakteryzowane wieloma ró

ż

norodnymi cechami, które maj

ą

ró

ż

ne miana

i wykazuj

ą

ró

ż

ne rz

ę

dy wielko

ś

ci. Wielokryterialna ocena zjawiska w

ró

ż

nych obiektach staje si

ę

mo

ż

liwa, gdy dokonamy przekształcenia

warto

ś

ci cech oryginalnych celem ich ujednolicenia. Przekształcone

zmienne s

ą

pozbawione mian i przybieraj

ą

warto

ś

ci zbli

ż

onego rz

ę

du

wielko

ś

ci. Sposoby transformacji warto

ś

ci oryginalnych cech

diagnostycznych nazywamy metodami normowania. Unormowane warto

ś

ci

zmiennych diagnostycznych mog

ą

by

ć

poddane procesowi agregacji, co

prowadzi do uzyskania zmiennej syntetycznej (agregatowej)
charakteryzuj

ą

cej ka

ż

dy obiekt ze wzgl

ę

du na oceniane zjawisko zło

ż

one.

Znajomo

ść

ocen obiektów pozwala na konstrukcj

ę

ich rankingu, tzn. układu,

w którym obiekty s

ą

uporz

ą

dkowane w kolejno

ś

ci od najlepszego do

najgorszego ze wzgl

ę

du na warto

ść

zmiennej syntetycznej.

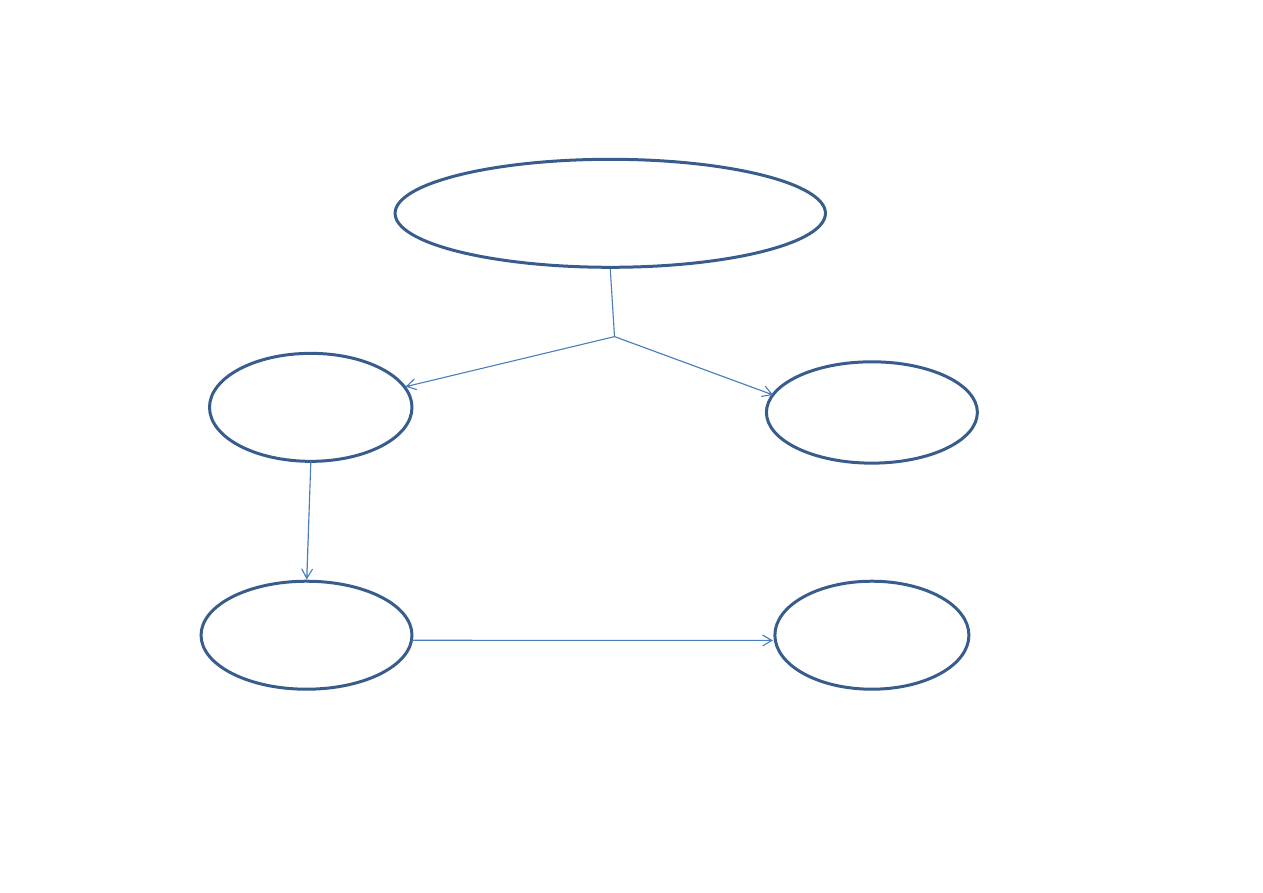
Schemat powstawania zmiennej syntetycznej

Proces wyboru

W

Wyj

ś

ciowy zbiór zmiennych

opisuj

ą

cych zjawisko zło

ż

one

X

Zbiór

zmiennych

diagnostycznyc

h

przyj

ę

cie

Y

Zbiór zmiennych

opisuj

ą

cych

zredukowany

odrzucenie

Z

Zbiór zmiennych

unormowanych

normalizacj
a

Q

Zbiór

zmiennych

syntetycznych

agregacj
a

Oznaczenia

Istot

ą

bada

ń

wielokryterialnych jest ich uj

ę

cie porównawcze, co oznacza,

ż

e

poziom zjawiska zło

ż

onego rozpatruje si

ę

w ró

ż

nych obiektach. Po

dokonaniu redukcji zbioru wyj

ś

ciowego cech

W

pozostaj

ą

zmienne

zaliczane do zbioru cech diagnostycznych

X

. Niech

O

oznacza zbiór

obiektów

O = { O

1

,

O

2

,…,O

r

}

Gdzie

r

jest liczb

ą

badanych obiektów. Ka

ż

dy obiekt jest charakteryzowany

przez zbiór zmiennych diagnostycznych

X = { X

1

,X

2

,…,Xs )

Gdzie

s

jest liczb

ą

zmiennych diagnostycznych, wykorzystywanych do opisu

zjawiska zło

ż

onego w obiektach.

Ze wzgl

ę

du na zró

ż

nicowanie potrzeb u

ż

ytkowników bada

ń

oraz stopie

ń

dyspozycyjno

ś

ci bazy danych, analiz

ę

zjawiska mo

ż

emy przeprowadzi

ć

,

wykorzystuj

ą

c:

– podej

ś

cie statyczne

,

– podej

ś

cie dynamiczne.

W podej

ś

ciu statycznym rozpatrujemy zjawisko zło

ż

one w jednym z wybranych

okresów, gwarantuj

ą

cym zebranie kompletnych danych

Niezb

ę

dne w badaniach statystycznych dane tworz

ą

macierz dwuwymiarow

ą

o

postaci:

Gdzie

x

ij

oznacza realizacj

ę

zmiennej

X

j

w obiekcie

O

i

. Zatem i-ty obiekt

opisuje wektor zmiennych

Wektor

[x

i

]

jest

s

-wymiarow

ą

obserwacj

ą

charakteryzuj

ą

c

ą

obiekt

O

i

.

Ka

ż

demu obiektowi odpowiada punkt w przestrzeni

s

-wymiarowej.

[ ]

























=

rs

r

r

s

s

ij

x

x

x

x

x

x

x

x

x

x

...

...

...

...

...

...

...

2

1

2

22

21

1

12

11

[ ] [

]

)

r

1,2,...,

i

(

...

2

1

=

=

is

i

i

i

x

x

x

x

Problemy rozpoznania i ujednolicania charakteru

zmiennych.

U podstaw porz

ą

dkowania liniowego prowadz

ą

cego do konstrukcji rankingu

obiektów le

ż

y konieczno

ść

podziału zbioru zmiennych diagnostycznych na

trzy podzbiory:

S

,

D

i

N

. podział te spełnia warunek zupełno

ś

ci

I warunek rozł

ą

czno

ś

ci

Gdzie:

S – podzbiór zmiennych diagnostycznych zwanych stymulantami

D - podzbiór zmiennych diagnostycznych zwanych destymulantami

N - podzbiór zmiennych diagnostycznych zwanych nominantami

N

D

S

X

∪

∪

=

Θ

=

∩

=

∩

N

D

D

S

Stymulant

ą

nazywamy tak

ą

zmienn

ą

diagnostyczn

ą

, której wzrost

kojarzy

ć

nale

ż

y ze wzrostem, a spadek ze spadkiem oceny zjawiska

zło

ż

onego.

Destymulant

ą

nazywamy tak

ą

zmienn

ą

diagnostyczn

ą

, której wzrost

kojarzy

ć

nale

ż

y ze spadkiem, a spadek ze wzrostem oceny zjawiska

zło

ż

onego.

Nominant

ą

nazywamy tak

ą

zmienn

ą

diagnostyczn

ą

, która ma

okre

ś

lon

ą

, najkorzystniejsz

ą

( z punktu widzenia oceny zjawiska

zło

ż

onego ) warto

ść

nominaln

ą

. Gdy nominanta przyjmuje warto

ś

ci

wi

ę

ksze lub mniejsze od warto

ś

ci nominalnej to powoduje spadek

oceny zjawiska zło

ż

onego.

Metoda unitaryzacji zerowanej

Metody unitaryzacyjne charakteryzuj

ą

si

ę

przyj

ę

ciem stałego punktu

odniesienia, który stanowi rozst

ę

p zmiennej normowanej:

Takie podej

ś

cie sprawia,

ż

e rozst

ę

p cechy unormowanej

Z

j

jest stały i wynosi

jeden. W

metodzie unitaryzacji zerowanej

( MUZ )

wykorzystujemy

nast

ę

puj

ą

cy sposób transformacji :

• Dla stymulant

( )

ij

i

ij

j

x

x

X

R

min

max

i

−

=

ij

i

ij

i

ij

i

ij

ij

x

x

x

x

z

min

max

min

−

−

=

•

Dla destymulant

•

Dla nominant – w przypadku wyst

ę

powania jednej warto

ś

ci nominalnej

ij

i

ij

i

ij

ij

i

x

x

x

x

ij

z

min

max

max

−

−

=













































〉

−

−

=

〈

−

−

=

oj

ij

i

oj

ij

i

oj

oj

ij

i

oj

ij

i

ij

ij

c

x

c

x

c

c

x

c

x

x

z

ij

ij

ij

ij

gdy x

max

max

x

gdy x

1

gdy x

min

min

•

Dla nominant w przypadku wyst

ę

powania przedziału warto

ś

ci nominalnych

j

j

c

c

2

1

,













































〉

−

−

≤

≤

〈

−

−

=

j

ij

i

j

ij

i

j

j

ij

i

j

ij

i

ij

ij

c

x

c

x

c

c

x

c

x

x

z

2

ij

2

ij

2

ij

1j

1

ij

1

gdy x

max

max

x

x

c

gdy

1

gdy x

min

min

Unormowanie cech diagnostycznych jest etapem wst

ę

pnym pozwalaj

ą

cym

doprowadzi

ć

do uzyskania ł

ą

cznej oceny wielokryterialnej ka

ż

dego z

branych pod uwag

ę

obiektów. Ł

ą

czn

ą

ocen

ę

ka

ż

dego z nich mo

ż

emy

uzyska

ć

drog

ą

agregacji na wiele sposobów. Dwa najprostsze sposoby u

zyskanie zmiennej syntetycznej s

ą

nast

ę

puj

ą

ce:

)

,...,

2

,

1

(

1

r

i

z

Q

s

j

ij

i

=

=

∑

=

)

,...,

2

,

1

(

1

1

r

i

z

s

Q

s

j

ij

i

=

=

∑

=

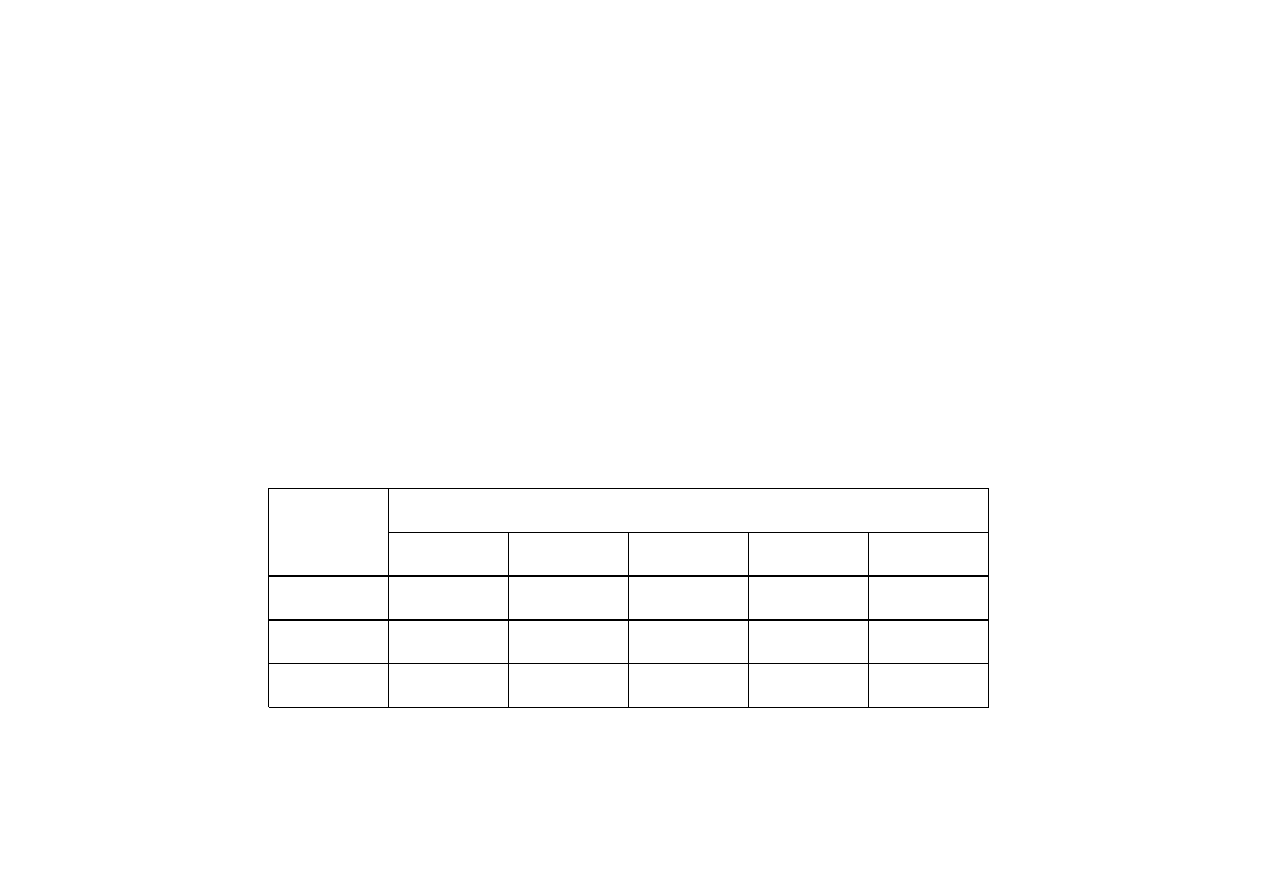
Przykład

Nale

ż

y wybra

ć

najlepszego dostawc

ę

leków na podstawie nast

ę

puj

ą

cych

zmiennych

diagnostycznych:

X

1

- cena zamawianych leków (EURO),

X

2

- koszty transportu kolejowego (EURO),

X

3

- koszty transportu lotniczego (EURO),

X

4

-

koszty transportu samochodowego (EURO),

X

5

- termin płatno

ś

ci ( dni).

Dostawca

Zmienne diagnostyczne

x

i1

x

i2

x

i3

x

i4

X

i5

A

5000

300

570

380

7

B

4670

310

680

440

14

C

4250

350

750

470

10

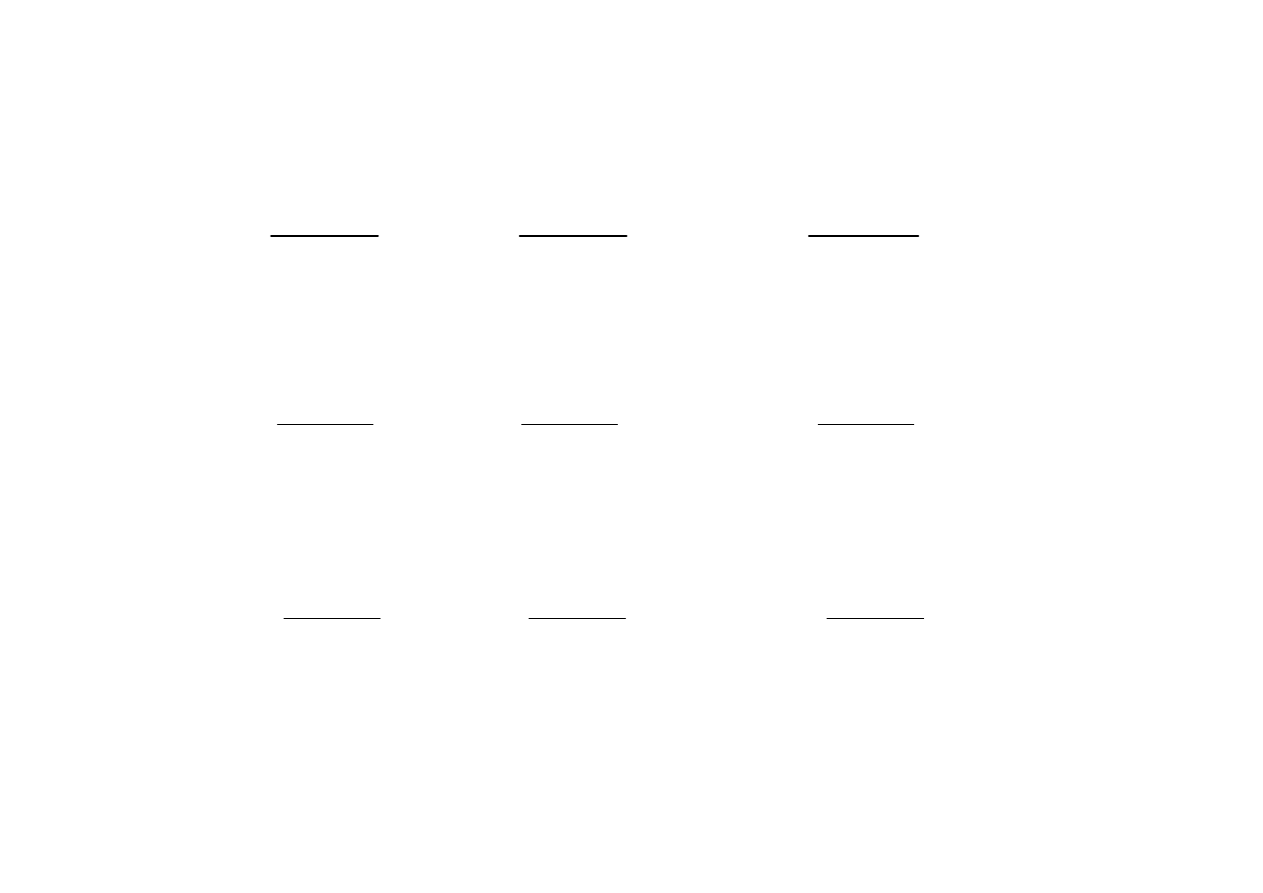
1

4 4

.

0

0

5 0 0 0

m a x

4 25 0

m i n

4 2 5 0

5 0 0 0

4 2 5 0

5 0 0 0

3 1

4 2 50

5 0 0 0

4 6 70

5 0 0 0

2 1

42 5 0

5 0 0 0

5 0 0 0

5 0 0 0

1 1

1

1

=

=

=

=

=

=

=

=

−

−

−

−

−

−

z

z

z

x

x

i

i

i

i

0

25

.

0

1

350

max

300

min

300

350

350

350

32

300

350

310

350

22

300

350

300

350

12

2

2

=

=

=

=

=

=

=

=

−

−

−

−

−

−

z

z

z

x

x

i

i

i

i

0

39

.

0

1

750

max

570

min

570

750

750

750

33

570

750

680

750

23

570

750

570

750

13

3

3

=

=

=

=

=

=

=

=

−

−

−

−

−

−

z

z

z

x

x

i

i

i

i

0

3 3

.

0

1

4 7 0

m a x

3 8 0

m i n

3 8 0

4 7 0

4 7 0

4 70

3 4

3 8 0

4 7 0

44 0

4 7 0

2 4

3 8 0

4 7 0

3 8 0

4 7 0

1 4

4

4

=

=

=

=

=

=

=

=

−

−

−

−

−

−

z

z

z

x

x

i

i

i

i

4 3

.

0

1

0

1 4

m a x

7

m i n

7

1 4

7

1 0

3 4

7

1 4

7

1 4

2 4

7

1 4

7

7

1 5

5

5

=

=

=

=

=

=

=

=

−

−

−

−

−

−

z

z

z

x

x

i

i

i

i

Najlepszy dostawca zgodnie z przyj

ę

tymi kryteriami to dostawca A

Dostawc
a

Zmienne unormowane

z

i1

z

i2

z

i3

z

i4

z

i5

Q

i

A

0

1

1

1

0

3

B

0.44

0.25

0.39

0.33

1

2.41

C

1

0

0

0

0.43

1.43