Numeryczne rozwiązywanie równań różniczkowych zwyczajnych

(ściślej równań stanu) - przypomnienie i inercje w Matlabie

Najważniejszym dla każdego inżyniera opisem matematycznym są
równania różniczkowe zwyczajne z czasem jako zmienną niezależną.
Ogólnie mają postać:

;

)

(

),

,

,

(

dt

d

0

0

t

t

x

x

P

u

x,

f

x

=

=

;

)

(

),

,

,

(

0

0

t

t

x

x

P

u

x,

f

x

.

=

=

inna forma zapisu

gdzie:

n

R

∈

x

m

R

∈

u

r

R

∈

P

0

C

∈

f

]

,

[

0

∞

∈ t

t

Ten, dla wielu odstraszający, zapis matematyczny jest potrzebny dla uogólnień, czyli
analizy cech charakterysycznych dla pewnych klas obiektów technicznych. Konkretne
przykłady są związane z konkretnymi obiektami i najczęsciej zamiast zmiennych
stanu x (czyli x

1

, x

2

itd do x

n

), wymuszeń u (u

1

, ... u

m

) oraz parametrów P (P

1

, ... P

r

)

są konkretne zmienne fizykalne. Tym niemniej najprostszą metodę numerycznego
rozwiązywania takich równań przedstawimy na początku w zapisie ogólnym.

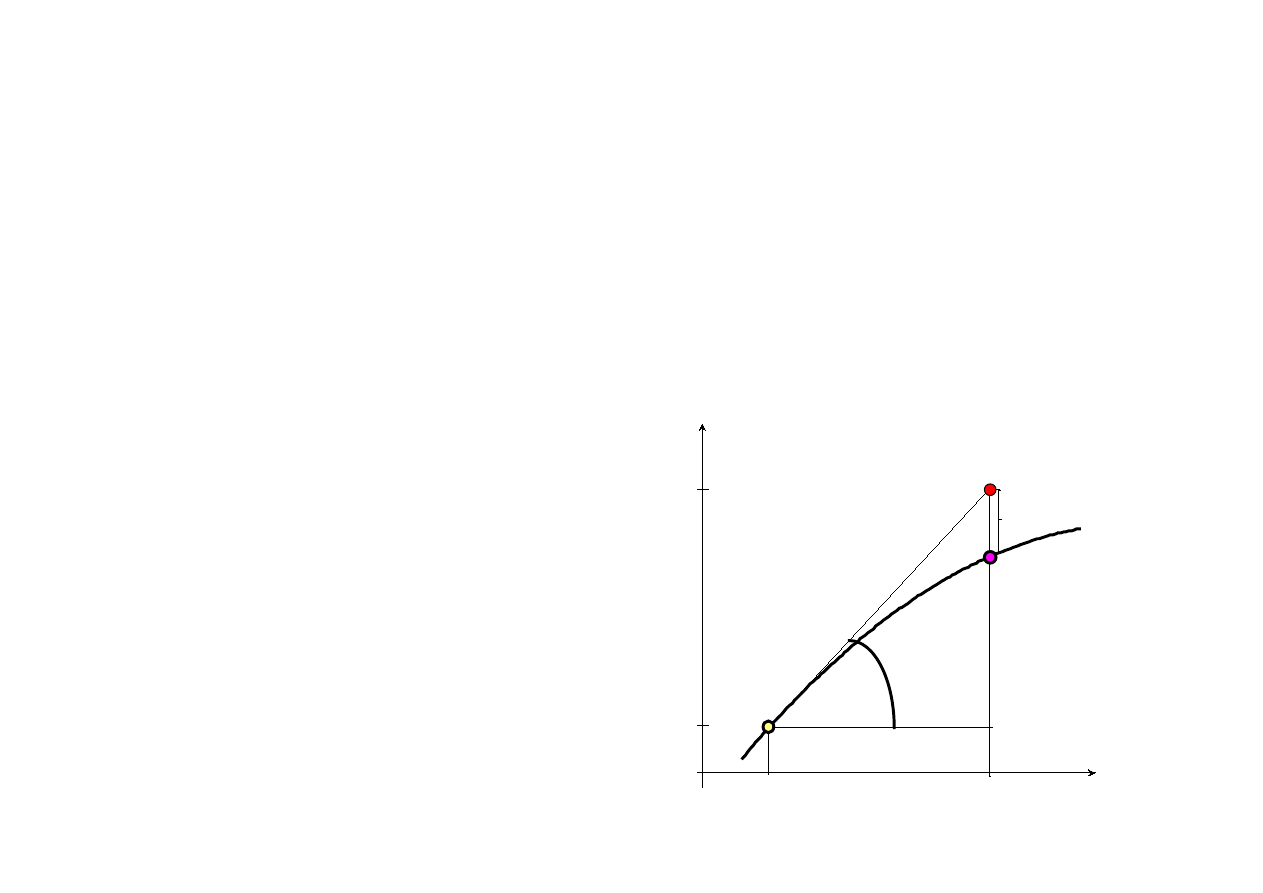
I tak, tzw. metoda Eulera ma następującą postać:

h

k

k

k

f

x

x

+

=

+1

gdzie

h krok całkowania dobierany przez eksperymentatora h = t

k+1

- t

k

k kolejne chwile czasu począwszy od k= 0 dla t

0

f

k

– prawe strony równań w chwili t

k

Algorytm jest wyjątkowo prosty:

wszystkie

nasze x w chwili następnej

to

wszystkie

x w chwili poprzedniej

plus prawe strony RR razy krok h.
Dla jednej zmiennej x algorytm ma
oczywistą interpretację
(lub wyprowadzenie) patrz rysunek.
Trzeba też pamietać, że:

x(t)

h

t

x

t

t

k+1

k

k+1

x

k

α

ε

x(t )

k+1

x(t )

k+1

obliczone

szukane

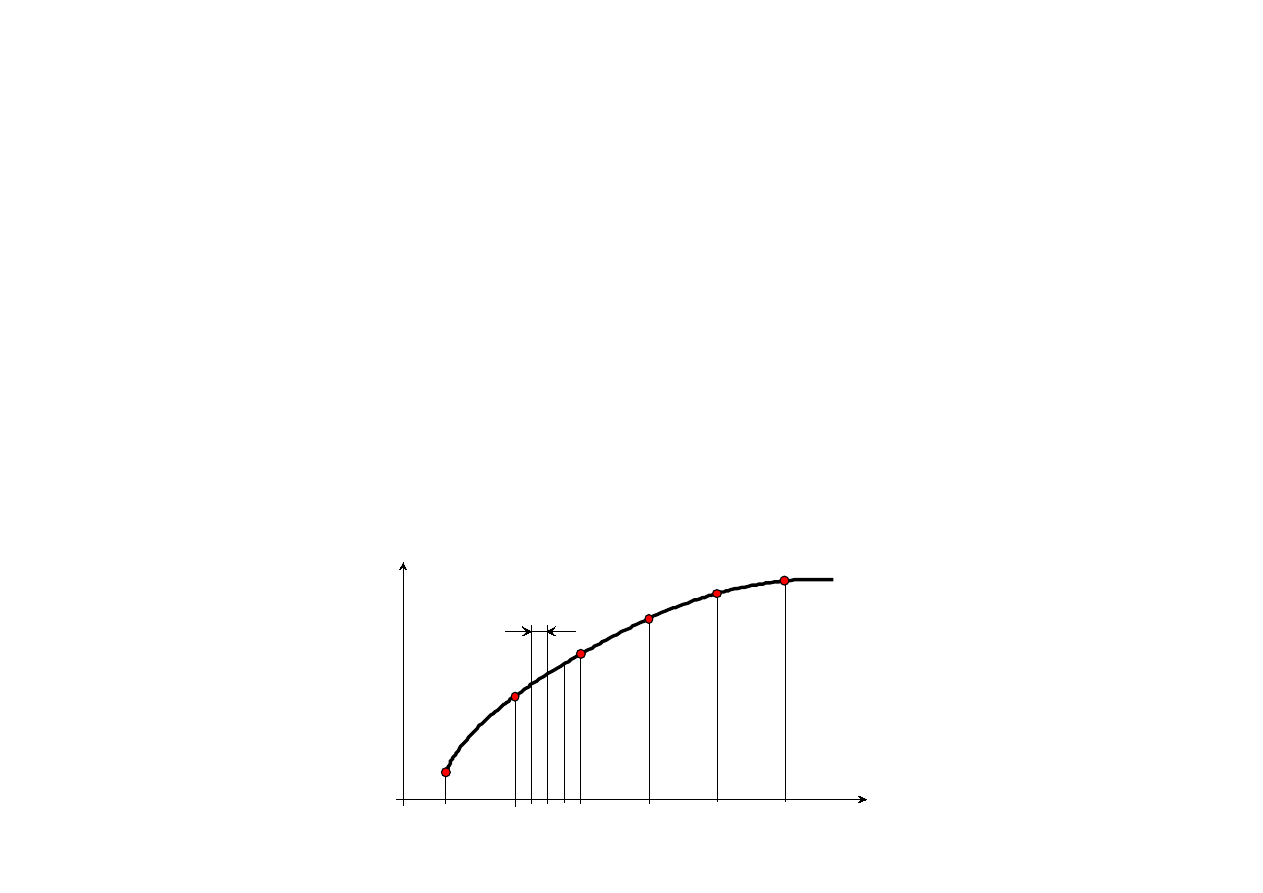
Aby otrzymać dobre wyniki (mały błąd obliczeń) należy całkować jak najmniejszym
krokiem h. Z drugiej strony duża liczba punktów na wykresie x(t) może być nieczytelna.
Bardzo wygodne jest prowadzenie obliczeń przy użyciu dwóch kroków:

a) krok obserwacji (pomiędzy punktami do wykresu, lub innych celów),
krok jest zależny od czytelności przebiegu, lub narzucony;

b) krok całkowania h = Dt/NIS ; gdzie NIS (integer) liczba kroków h w kroku Dt.

Zmieniając NIS powinniśmy dostać te same przebiegi ale o coraz lepszej dokładności
(przy wzroście NIS).
W programie realizujemy to za pomocą dwóch pętli zewnętrznej z krokiem Dt
i wewnętznej z krokiem NIS.
Jeśli na pewno liczymy krokiem h = Dt to wystarczy jedna pętla.

t

x

Dt

h

Przykład: (układ 2 równań RRZ)

dx1/dt = -5x1 + x2 +u
dx2/dt = x1 – 3x2 +sin(t)

fragment kodu:

x1 = x1 + (-5*x1+x2 +u)*h;
x2 = x2 + (x1 – 3*x2 + sin(t))*h;

Czy to jest dobrze napisane?

To jest źle!! w drugim równaniu jest już nowe x1!!!

Ma być (patrz algorytm!):

Najpierw wszystkie prawe strony na podstawie poprzednich x-ów !!!

F1 = -5*x1 + x2 + u;
F2 = x1 – 3*x2 + sin(t);
x1 = x1 + F1*h;
x2 = x2 + F2*h;

Dla jednego równiania lub rownan niezależnych
(choć to niekonieczne) też najpierw policzmy
prawą stronę, aby mieć nawyk.

Jak ocenić czy mamy dobre wyniki i ewentualnie bład obliczeń.
Wszystkie (rozsądne) metody numerycznego całkowania RRZ są konwergencyjne
– to znaczy przy zmniejszeniu h maleje na pewno błąd.
Sprawdzenie jest oczywiste. Należy przeprowadzic obliczenia jakims krokiem h.
Jesli obliczenia krokiem 0.5h (czyli NIS = 2NIS) dają taki sam przebieg to jest OK.
Ewentualne różnice to w przybliżeniu rząd błędu.

Program symulacyjny UDYN_simplest. (gotowiec do wpisywania równań)

Najprostsze równanie obiektu inercyjnego (np skok stężenia substratu na wejściu
mieszalnika): dx/dt = (u-x)/T; T stala czasowa.

include <stdlib.h>
#include<stdio.h>
#include<math.h>
int i,m,NIS;
double t,Dt,tmax,h,x[101],f[101],T,u;
FILE *wy;
int main() {
wy =
fopen("c:\\mmmat4\\plotfile\\OUT2m", "wt");
t=0.0; tmax=100; //poczatek i koniec obliczen
Dt = 1.0; NIS = 10; // kroki obserwacji i calk.
x[1]=0; u=1; T=20; // dane

do
{
for(m=1;m<=NIS;m++)
{
h = Dt/NIS;
f[1] = (u-x[1])/T;
x[1] = x[1] + f[1]*h ;
t = t + h;
}
fprintf(wy,"%lf %lf %lf \n",
t,x[1],f[1]);
}
while (t <= tmax);
fclose(wy);
system("PAUSE");
return 0; }

Program: UDYN1RRZ.m - w Matlabie

clear all
t=0.0; tmax=100; % poczatek i koniec obliczen
Dt = 1.0; NIS = 10; % kroki obserwacji i calk
x1 = 0; u = 1; T = 20; % dane
tp = 0; xp = 0;
while t <= tmax
for m=1:1:NIS,
h = Dt/NIS;
f1 = (u-x1)/T;
x1 = x1 + f1*h ;
t = t + h;
end; % for
tp = [tp,t]; xp = [xp,x1];
end; % while
plot (tp,xp);

Można też wykorzystać procedurę biblioteczną z automatycznym doborem kroku
całkowania i z narzuconym dupuszczalnym błędem obliczeń.

ODE45
Solve differential equations, higher order method. ODE45 integrates a system of ordinary
differential equations using 4th and 5th order Runge-Kutta formulas.
[T,Y] = ODE45('yprime', T0, Tfinal, Y0) integrates the system of ordinary differential equations
described by the M-file YPRIME.M, over the interval T0 to Tfinal, with initial conditions Y0.
[T, Y] = ODE45(F, T0, Tfinal, Y0, TOL, 1) uses tolerance TOL and displays status while the
integration proceeds.
INPUT:
F - String containing name of user-supplied problem description.
Call: yprime = fun(t,y) where F = 'fun'.
t - Time (scalar).
y - Solution column-vector.
yprime - Returned derivative column-vector; yprime(i) = dy(i)/dt.
t0 - Initial value of t.
tfinal- Final value of t.
y0 - Initial value column-vector.
tol - The desired accuracy. (Default: tol = 1.e-6).
trace - If nonzero, each step is printed. (Default: trace = 0).
OUTPUT:
T - Returned integration time points (column-vector).
Y - Returned solution, one solution column-vector per tout-value.
The result can be displayed by: plot(tout, yout).

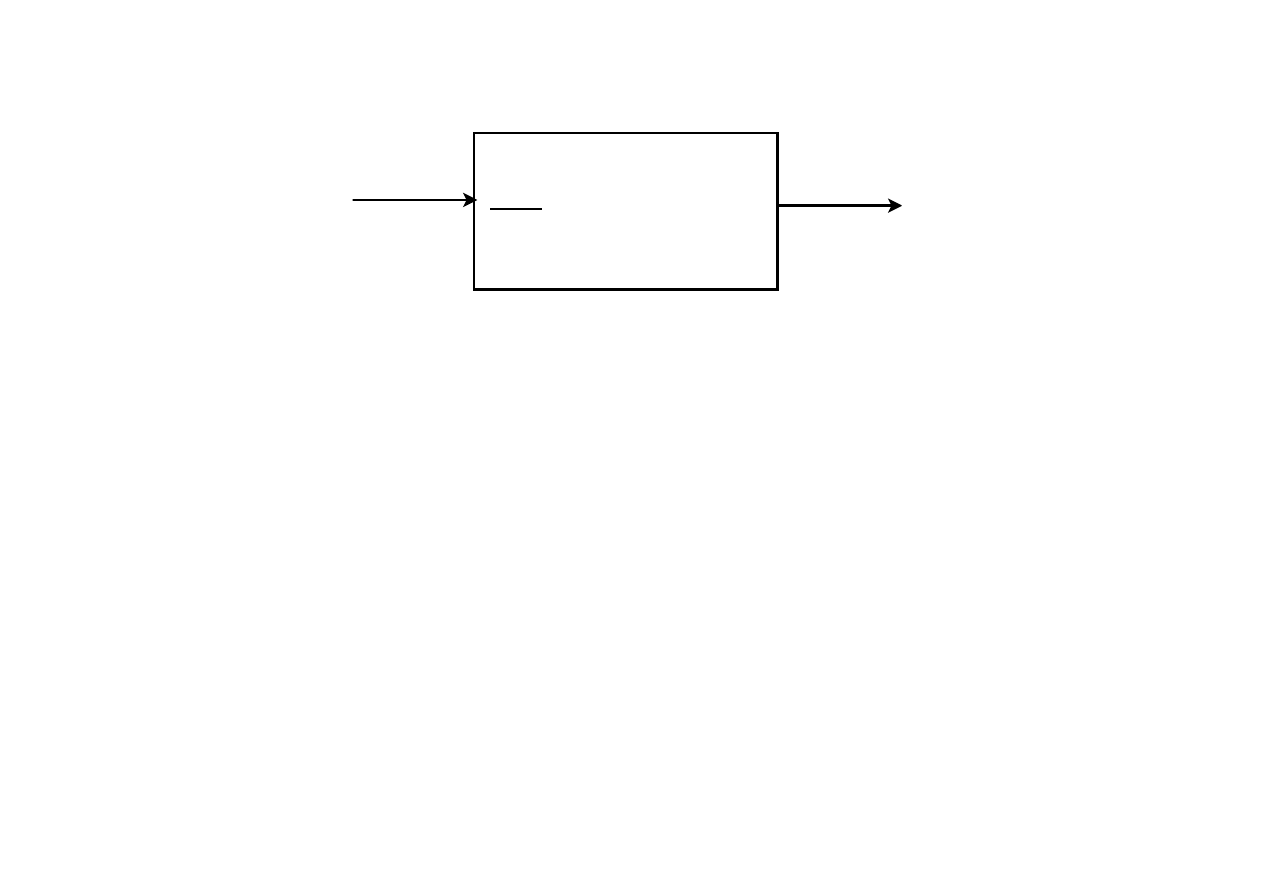
u1

x1

1

1

1

1

1

/

)

(

T

x

u

k

dt

dx

−

=

schemat obiektu dynamicznego inercyjnego

Program inerc1.m

clear all; global P:
P(1) = 1; % Sterowanie k*u
P(2) = 20; % Stala czasowa T
t0 = 0; tmax = 100; x0 = 0;
[t,x] = ode45('Inerc1f',t0, tmax, x0, 1.0E-6);
plot (t, x);

Plik Inerc1f.m

function d = inercja1 (t,x)
global P;
d(1) = (P(1) – x(1))/P(2);

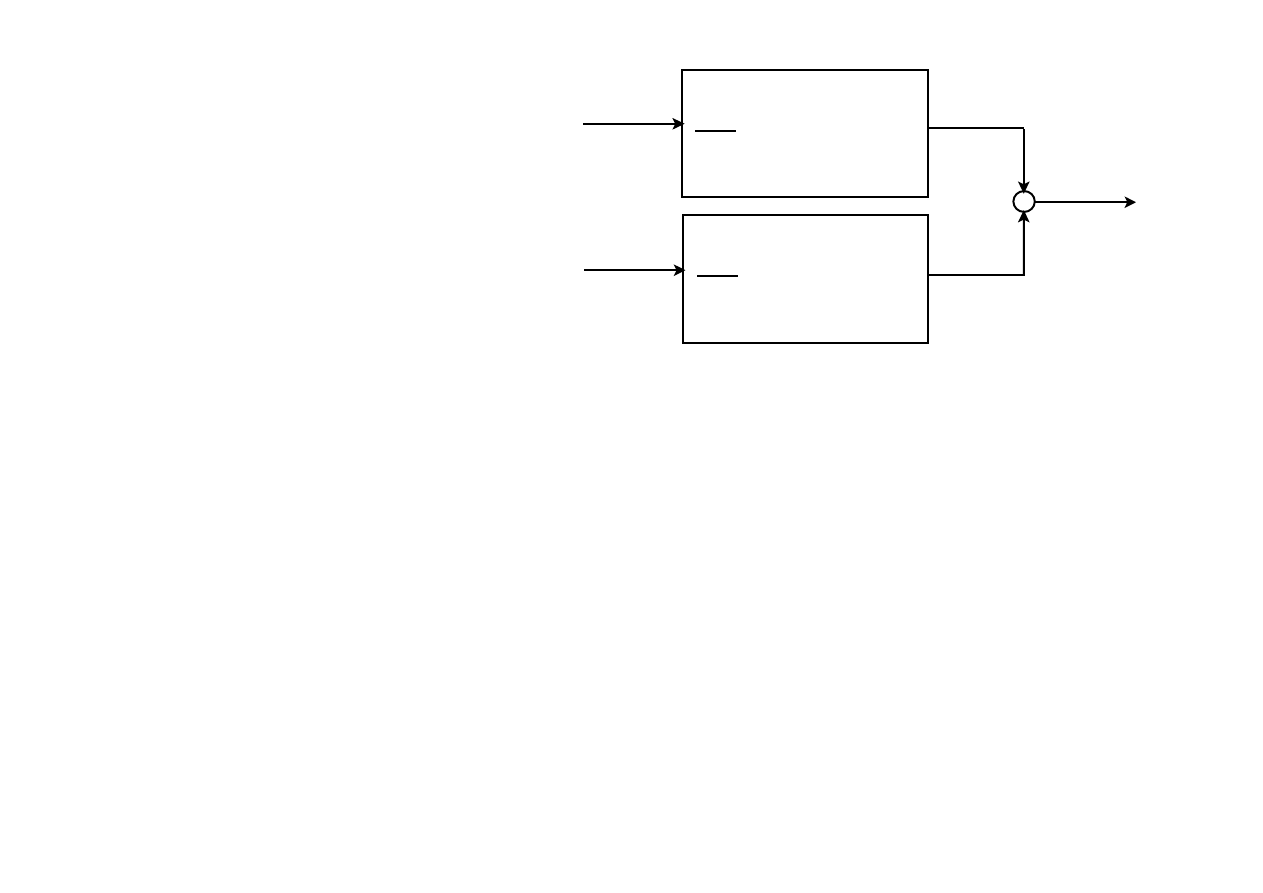
u1

x1

1

1

1

1

1

/

)

(

T

x

u

k

dt

dx

−

=

u2

x2

2

2

2

2

2

/

)

(

T

x

u

k

dt

dx

−

=

u1 = u2= 1

+

−

y

Bardzo ciekawy obiekt

Program inerc2.m
clear all; global P;
P(1) = 1; % sterowanie k1*u1
P(2) = 20; % Stala czasowa T1
P(3) = 10; % sterowanie k2*u2
P(4) = 2; % stala czasowa T2
t0 = 0; tmax = 100; x0(1) = 0; x0(2) = 0;
[t,x] = ode45('Inerc2f',t0, tmax, x0, 1.0E-6);
y = x(:,1) - x(:,2);
plot (t, x(:,1)); pause;
plot (t, x(:,2)); pause;
plot (t, y); pause;

Plik inerc2f.m
function d = RRZw(t,x)
global P;
d(1) = (P(1) - x(1))/P(2);
d(2) = (P(3) - x(2))/P(4);

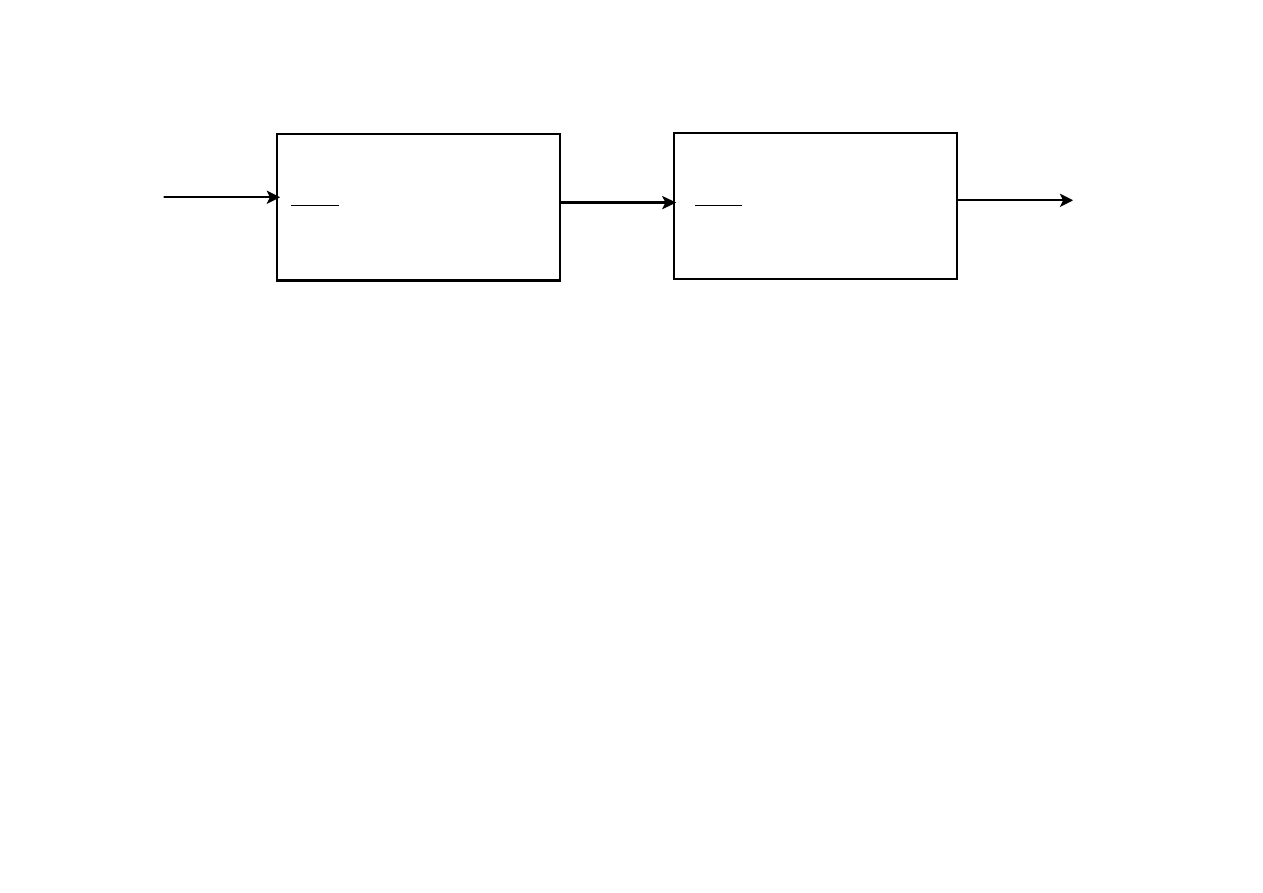
u1

x1

1

1

1

1

1

/

)

(

T

x

u

k

dt

dx

−

=

x2

2

2

1

2

2

/

)

(

T

x

x

k

dt

dx

−

=

Kaskada 2 inercji

Program kask1.m

clear all; global P;
P(1) = 1; % sterowanie u1
P(2) = 20; % Stala czasowa T1
P(3) = 10; % k2
P(4) = 20; % stala czasowa T2

t0 = 0; tmax = 100; x0(1) = 0; x0(2) = 0;
[t,x] = ode45('kask1f',t0, tmax, x0, 1.0E-6);
plot (t, x(:,1)); pause;
plot (t, x(:,2)); pause;

Plik kask1f.m

function d = RRZw(t,x)
global P;
d(1) = (P(1) - x(1))/P(2);
d(2) = (P(3)*x(1) - x(2))/P(4);