METODY NUMERYCZNE I
OPTYMALIZACJA
Wydział Elektroniki
Kier. Automatyka i Robotyka III r.
dr inż. Ewa Szlachcic
Zakład Sterowania i Optymalizacji
Instytut Informatyki, Automatyki i Robotyki
Politechnika Wrocławska
pok. 219 C-3
Materiały: ewa.szlachcic.staff.iiar.pwr.wroc.pl
Wydział Elektroniki
AiR III r.
Program wykładu
Wprowadzenie do metod numerycznych i zadań optymalizacji
Definicja zadania optymalizacji i jego klasyfikacja
Przykłady praktycznych zadań optymalizacji
Metody rozwiązywania układów równań liniowych
Metody rozwiązywania równania nieliniowego
Metody rozwiązywania układu równań nieliniowych
Metody aproksymacji funkcji
Metody interpolacji funkcji
Metody programowania liniowego PL
Metody programowania nieliniowego PN:
Metody optymalizacji bez ograniczeń
Metody optymalizacji z ograniczeniami
Przegląd metod optymalizacji lokalnej i globalnej
Techniki meta-heurystyczne optymalizacji – oparte nie tylko na biologii (algorytmy
genetyczne, ewolucyjne, immunologiczne, mrówkowe, algorytmy optymalizacji
rojem cząstek, poszukiwania harmonii)
Wydział Elektroniki
AiR III r.
Literatura cz. 1 Metody numeryczne
Klamka J., Ogonowski Z., Jamicki M., Stasik M., Metody
numeryczne, Wyd. Pol Śląskiej Gliwice 2004
Majchrzak E., Mochnacki B., Metody numeryczne, Podstawy
teoretyczne, aspekty praktyczne i algorytmy, Wyd. Pol Śląskiej
Gliwice 2004
Povstenko J., Wprowadzenie do metod numerycznych, Wyd. Akad.
Ofic. Wyd. EXIT, Warszawa 2002
Fortuna Z., Macukow B., Wąsowski J., Metody numeryczne, WNT
Warszawa 1998
Wanat K., Algorytmy numeryczne, Wyd. Dir, Gliwice, 1993
Bjorck A., Dahlquist G., Metody numeryczne, PWN 1987
Ralston A., Wstęp do analizy numerycznej, PWN, Warszawa, 1983
Dryja M., Jankowscy J. i M., Przegląd metod i algorytmów
numerycznych, WNT, Warszawa 1982
Wydział Elektroniki
AiR III r.
Stachurski A., Wierzbicki A.P., Podstawy optymalizacji, PWN
Warszawa 1999
Cegielski A. Programowanie matematyczne, Wyd. Uniw. Zielonog.
2004
Findeisen S., Szymanowski W., Wierzbicki A., Teoria i metody
obliczeniowe optymalizacji, PWN, 1987
Garfinkel R.S, Nemhauser G.L., Programowanie całkowitoliczbowe,
PWN, Warszawa, 1978
Michalewicz Z., Algorytmy genetyczne+struktury danych= programy
ewolucyjne, WNT Warszawa, 1999
Arabas J., Wykłady z algorytmów ewolucyjnych, WNT Warszawa,
2001
Wierzchoń S.T., Sztuczne systemy immunologiczne, Teoria i
zastosowania, EXIT Warszawa, 2002.
Literatura cz.2 Metody optymalizacji
Wydział Elektroniki
AiR III r.
Układy równań liniowych
Należy rozwiązać układ m równań liniowych z n niewiadomymi:
T
n
x
x
x
x
]
,...,
,
[
2
1
n
j
i
j
ij
b
x
a
1
(i=1,2,3,…,m)
lub w zapisie macierzowym:
b
Ax
gdzie: A = [a
ij
] jest macierzą współczynników stopnia [m*n]
x-wektor niewiadomych,
b- wektor wyrazów wolnych.
T
m
b
b
b
b
]
,...,
,
[
2
1
Wydział Elektroniki
AiR III r.
Układy równań nieliniowych
0
)
,...,
,...,
,
(
........
..........
..........
..........
0
)
,...,
,...,
,
(
0
)
,...,
,...,
,
(
2
1
2
1
2
2
1
1
n
i
n
n
i
n
i
x
x
x
x
f
x
x
x
x
f
x
x
x
x
f
0
)
(x
F
x
f
x
f
x
f
x
f
x
F
n
i
...
...
)
(
2
1
Układ n równań nieliniowych zawierający n niewiadomych:
lub w postaci macierzowej
gdzie:
n
i
x
x
x
x
x
...
...
2
1
Wydział Elektroniki
AiR III r.
Wektor zmiennych decyzyjnych x:
gdzie: n – ilość zmiennych decyzyjnych.
Funkcja celu (funkcja kryterialna) f(x) :
oraz m funkcji ograniczeń g
i
(x):
T
n
x
x
x
,...,
,
2
1
x
1
:
R
R
f
n
x
m
i
dla
R
R
g
n
i
,...,
1
:
1
x
Sformułowanie zadania optymalizacji
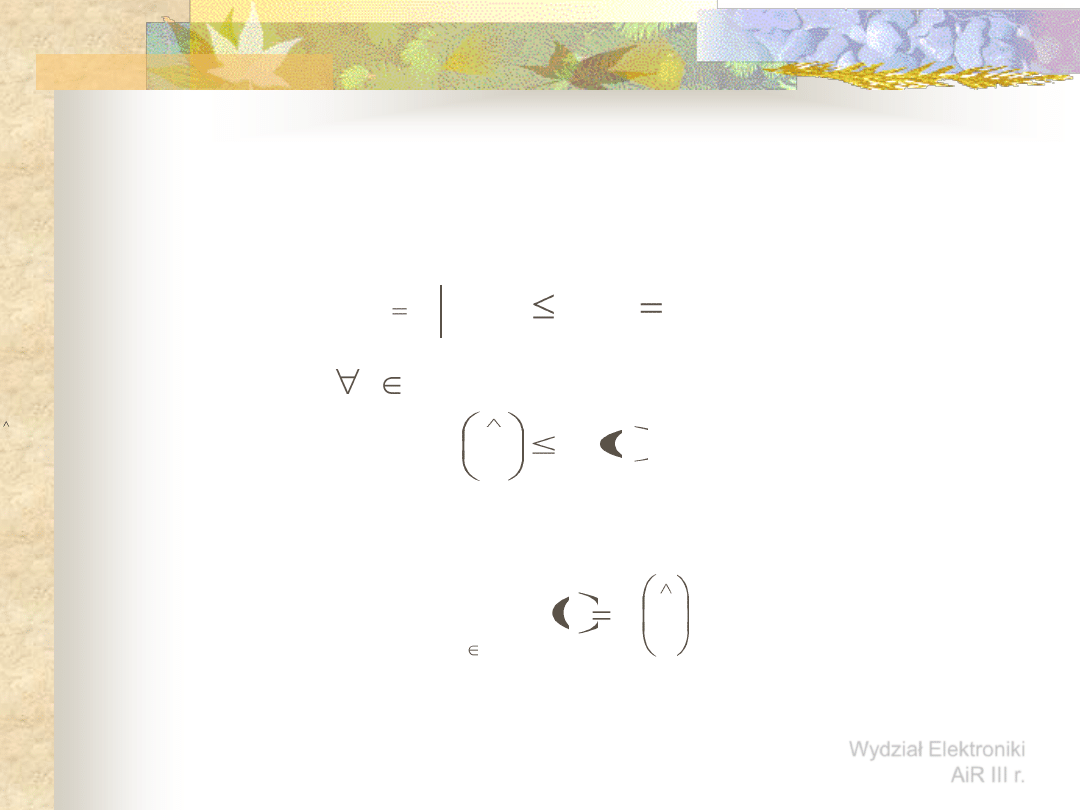
Wydział Elektroniki
AiR III r.
Zadanie optymalizacji polega na znalezieniu wektora zmiennych
decyzyjnych x, należącego do zbioru rozwiązań dopuszczalnych X w
postaci:
takiego, że dla
}
,...,
1
,
0
)
(
{
m
i
g
i
X
x
x
X
x
Co jest równoznaczne zapisowi
:
x
x
x
f
f
x
x
x
f
f
X
min
Wydział Elektroniki
AiR III r.
Programowanie liniowe. Podstawy teoretyczne PL. Warunki
konieczne i dostateczne optymalizacji liniowej. Metody simpleks,
dwufazowy simpleks, dualny simpleks. Inne algorytmy liniowe.
Programowanie liniowe ze zmiennymi rzeczywistymi,
programowanie liniowe ze zmiennymi dyskretnymi.
w tym:
Programowanie całkowitoliczbowe liniowe
Metody odcięć. Metody podziału i ograniczeń. Klasyczne zadania
optymalizacji dyskretnej (problem plecakowy, przydziału,
komiwojażera, problemy szeregowania zadań.), przepływy w sieciach
i zadania transportowe.
Programowanie nieliniowe. Podstawy teoretyczne PN. Warunki
konieczne i wystarczające optymalności. Metody dokładne i
heurystyczne (m.in.. genetyczne i ewolucyjne) poszukiwania
ekstremum bez ograniczeń i z ograniczeniami
.
Wydział Elektroniki
AiR III r.
Optymalne projektowanie procesów technologicznych
Identyfikacja procesów technologicznych
Optymalne zarządzanie przedsiębiorstwem - minimalizacja kosztów,
maksymalizacja zysków w przedsiębiorstwie
Polioptymalne zadanie dla modelu gospodarki narodowej (np.:
maksymalizacja konsumpcji i środków trwałych oraz minimalizacja
poziomu zadłużenia zagranicznego gospodarki)
Sterowanie procesem technologicznym
Projektowanie efektywnej struktury systemu (np. sieci komputerowej)
Projektowanie optymalnego przepływu w sieciach ( sieci dystrybucji wody,
sieci dystrybucji gazu, sieci komputerowej)
Zadania optymalnego przydziału, zadania dystrybucji produktów
Zadania optymalnego rozmieszczenia ( minimalizacja strat czy odpadów-
optymalny rozkrój , optymalne cięcie, optymalny kształt)
Przykłady praktycznych zastosowań
:
Wydział Elektroniki
AiR III r.
Zadanie programowania liniowego PL
przy ograniczeniach
:
x
c
x
T
f
max
0
2
2
1
1
x
b
x
A
b
x
A
dim x=n, dim c=n
Macierze A
1
, A
2
odpowiadają za współczynniki w m
1
i m
2
ograniczeniach
dim A
1
=[m
1
x n], dim A
2
=[m
2
x n]
Wektory b
1
, b
2
odpowiadają za prawe strony ograniczeń
dim b
1
=m
1
, dim b
2
=m
2
Wydział Elektroniki
AiR III r.
Zadanie programowania kwadratowego
2
2
2
1
1
2
)
(
min
x
x
f x
x
b
Ax
x
x
x
T
T
X
f
5
.
0
max
gdzie:
:
0
,
:
x
e
x
D
x
T
X
Przykład zadania programowania nieliniowego
przy ograniczeniach:
2
2
1
2
2
1
x
x
x
x