
Grzegorz Nikiel
Akademia Techniczno-Humanistyczna w Bielsku-Białej
Wydział Budowy Maszyn i Informatyki
Katedra Technologii Maszyn i Automatyzacji
Zakład Komputerowego Projektowania Wytwarzania
Laboratorium Automatyzacji Projektowania i Wytwarzania
Optymalizacja wielokryterialna
w projektowaniu procesów
wytwarzania – wybrane zagadnienia
Raport z bada własnych
_____________________________________________________________
Bielsko-Biała 2004

Spis tre ci
1. Wst p................................................................................................................................... 3
2. Polioptymalizacja z wykorzystaniem ocen rozmytych – metoda Baasa i Kwakernaaka.... 7
3. Polioptymalizacja z wykorzystaniem metody Baasa i Kwakernaaka – przykład ............. 16
4. Polioptymalizacja z wykorzystaniem ocen rozmytych – metoda Yagera......................... 28
5. Polioptymalizacja z wykorzystaniem metody Yagera – przykład .................................... 30
6. Optymalizacja wielokryterialna z wykorzystaniem ocen rozmytych – metoda
zmodyfikowana ................................................................................................................. 33
7. Polioptymalizacja z wykorzystaniem metody zmodyfikowanej – przykład..................... 37
8. Pakiet programów do optymalizacji wielokryterialnej ..................................................... 42
8.1. PoliOpt1 – polioptymalizacja z wykorzystaniem ocen rozmytych – metoda Baasa
i Kwakernaaka...................................................................................................................... 42
8.2. PoliOpt2 – polioptymalizacja z wykorzystaniem ocen rozmytych – metoda
zmodyfikowana.................................................................................................................... 46
8.3. Yager – polioptymalizacja metod Yagera ................................................................. 51
9. Literatura ........................................................................................................................... 54
Niniejszego opracowania nie wolno w cało ci ani w cz ciach rozpowszechnia
ani powiela za pomoc urz dze elektronicznych, mechanicznych, optycznych
i innych, wprowadza do systemów umo liwiaj cych jego odtworzenie w cało ci lub
cz ci – Internet, sieci lokalne.
(C) Copyright by Grzegorz Nikiel, Bielsko-Biała 2004

1. Wst p
Optymalizacja jest rozumiana jako d enie do osi gni cia pewnego stanu
idealnego, spełniaj cego pewne okre lone wymagania. Ogólnie optymalizacj dzieli
si na:
–
jednokryterialn , kiedy osi gni cie stanu idealnego wymagane jest wobec jednego
kryterium oceny tego stanu;
–
wielokryterialn (wektorow , polioptymalizacj ), kiedy osi gni cie stanu
idealnego jest zale ne od wielu kryteriów oceny tego stanu.
Przy du ej liczbie kryteriów oceny stanu idealnego dochodzi cz sto do
sprzeczno ci mi dzy kryteriami, co oznacza, e poszukiwane rozwi zanie nie
ekstremalizuje wszystkich kryteriów, rozwa anych osobno, lecz stanowi pewnego
rodzaju kompromis pomi dzy nimi. Problem polioptymalizacji polega wi c w głównej
mierze na zdefiniowaniu tego kompromisu. W wielu przypadkach mo liwe jest na
podstawie heurystycznej wiedzy o optymalizowanym procesie sformułowanie innego,
zast pczego
kryterium, wzgl dem którego poszukuje
si
rozwi zania
kompromisowego.
Formalnie polioptymalizacj mo na sformułowa nast puj co [2]:
Niech
X = {x
l
}, l = 1, 2,...., N jest wektorem zmiennych decyzyjnych, traktowanych
jako niezale ne. Niech
F = {f
i
}, i = 1, 2,....,M jest zbiorem kryteriów (funkcji)
wzgl dem których oceniane s rozwi zania w poszukiwaniu kompromisu. Niech dane
s ograniczenia nało one na warto ci rozwi za :
–
nierówno ciowe
G = {g
k
}, k = 1, 2, ...,K, gdzie:
0
)
(
≤
X
k
g
;
–
równo ciowe
H = {h
j
}, j = 1, 2,...,J, gdzie:
0
)
(
=
X
j
h
Celem polioptymalizacji jest osi gni cie rozwi zania, dla którego spełniony b dzie
warunek:
)}
(
),....,
(
),
(
{
)
(
min
2
1
X
X
X
X
F
l
f
f
f
=
(1)
Je eli wymagane jest maksymalizowanie pewnej funkcji
*
l
f , wtedy mo na
wprowadzi kryterium pomocnicze wg zale no ci:
)
(
max
)
(
min
*
X
X
−
−
=
l
l
f
f
(2)
Historycznie pierwsze próby poszukiwania minimum poczynili G.W. Leibniz
(1646-1716) i L. Euler (1707-1783) daj c podwaliny do optymalizacji
wykorzystywanych przez I. Newtona (1643-1727), J. Bernoulliego (1655-1705)
i D. Bernoulliego (1700-1782). Podstawy matematyczne optymalizacji stworzone
zostały przez J.L. Lagrange’a (1736-1813) i W.R. Hamiltona (1805-1865).
Wykorzystanie aproksymacji do wyznaczania optimum pewnych skomplikowanych
funkcji zostało opracowane przez L. Rayleigha (1842-1919), W. Ritza (1878-1909)
i B.G. Galerkina (1871-1945). W ko cu francusko-włoski ekonomista V. Pareto
(1848-1923) sformułował zasad optymalizacji wielokryterialnej w zagadnieniach
ekonomicznych, któr pó niej nazwano optymalizacj w sensie Pareto.
W najprostszym uj ciu rozwi zanie jest optymalne w sensie Pareto, je eli nie jest
mo liwe znalezienie rozwi zania lepszego z uwagi na co najmniej jedno kryterium bez
pogorszenia z uwagi na pozostałe. Graficznie zasada ta została przedstawiona na Rys.
1.
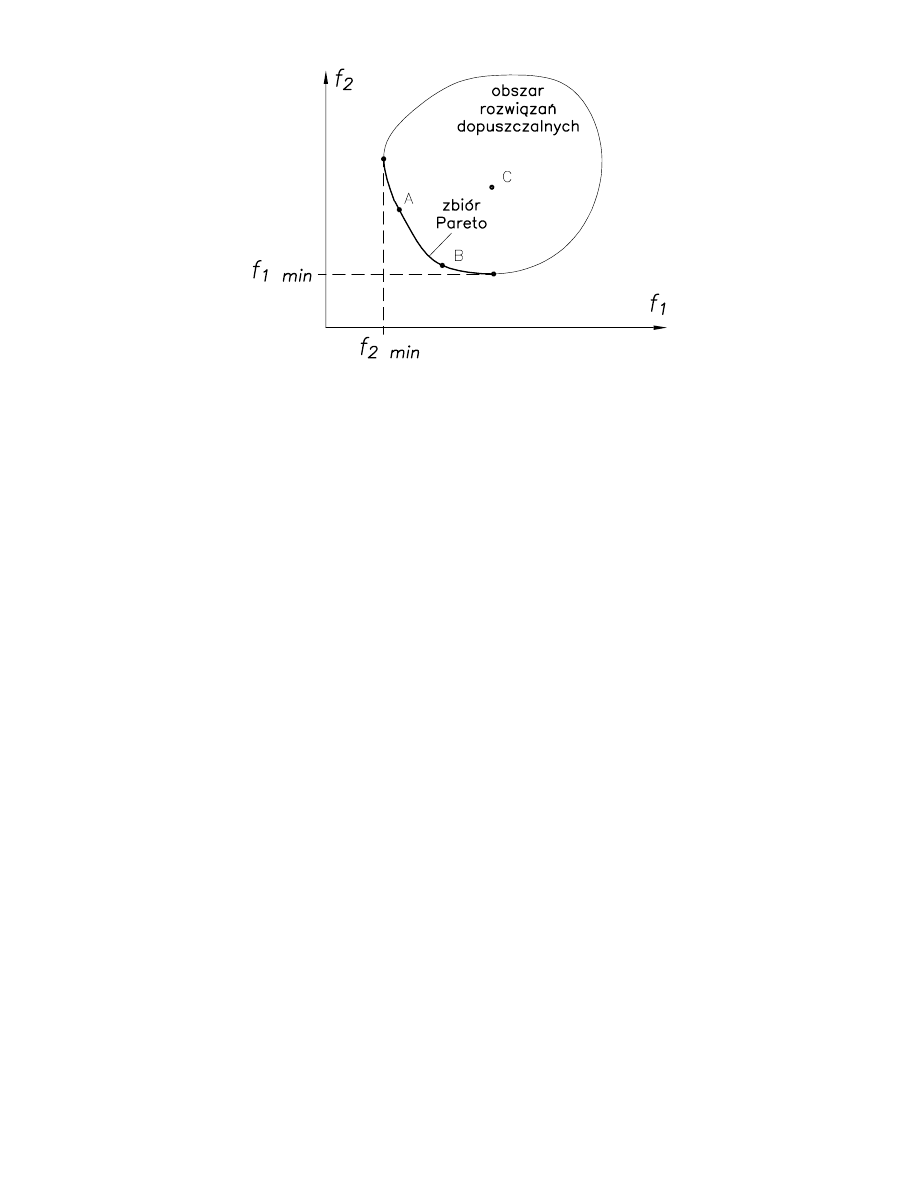
Rys. 1. Definicja optimum w sensie Pareto
Rozwi zanie C mo e zosta polepszone zarówno wobec kryterium f
1
, jak i f
2
. Dla
rozwi za A i B taka mo liwo nie istnieje – poprawa wzgl dem jednego kryterium
powoduje pogorszenie z uwagi na drugie – nale one zatem do zbioru rozwi za
optymalnych w sensie Pareto.
Spo ród innych metod optymalizacji wielokryterialnej wymieni nale y:
1.
Metoda wa onych kryteriów (ang. Weighted Objectives Method) – polega ona na
sprowadzeniu optymalizacji wielokryterialnej do jednokryterialnej przez
wprowadzenie kryterium zast pczego, b d cego sum wa on kryteriów:
(
)
MIN
)
(
1
→
⋅
=
=
M
q
q
q
f
w
Z
X
(3)
gdzie:
=
=
≤
≤
M
q
q
q
w
w
1
1
1
0
(4)
Graficznie rozwi zanie mo na przedstawi jako punkt przeci cia obszaru
rozwi za dopuszczalnych z hiperprost P, zale n od warto ci wa no ci
kryteriów w
q
(Rys. 2). Ze wzgl du na zrównowa enie wpływu poszczególnych
kryteriów mo na wprowadzi normowanie kryteriów. Problemem w tej metodzie
jest wybór a priori warto ci wag kryteriów, co w oczywisty sposób mo e
prowadzi do ró nych rozwi za .
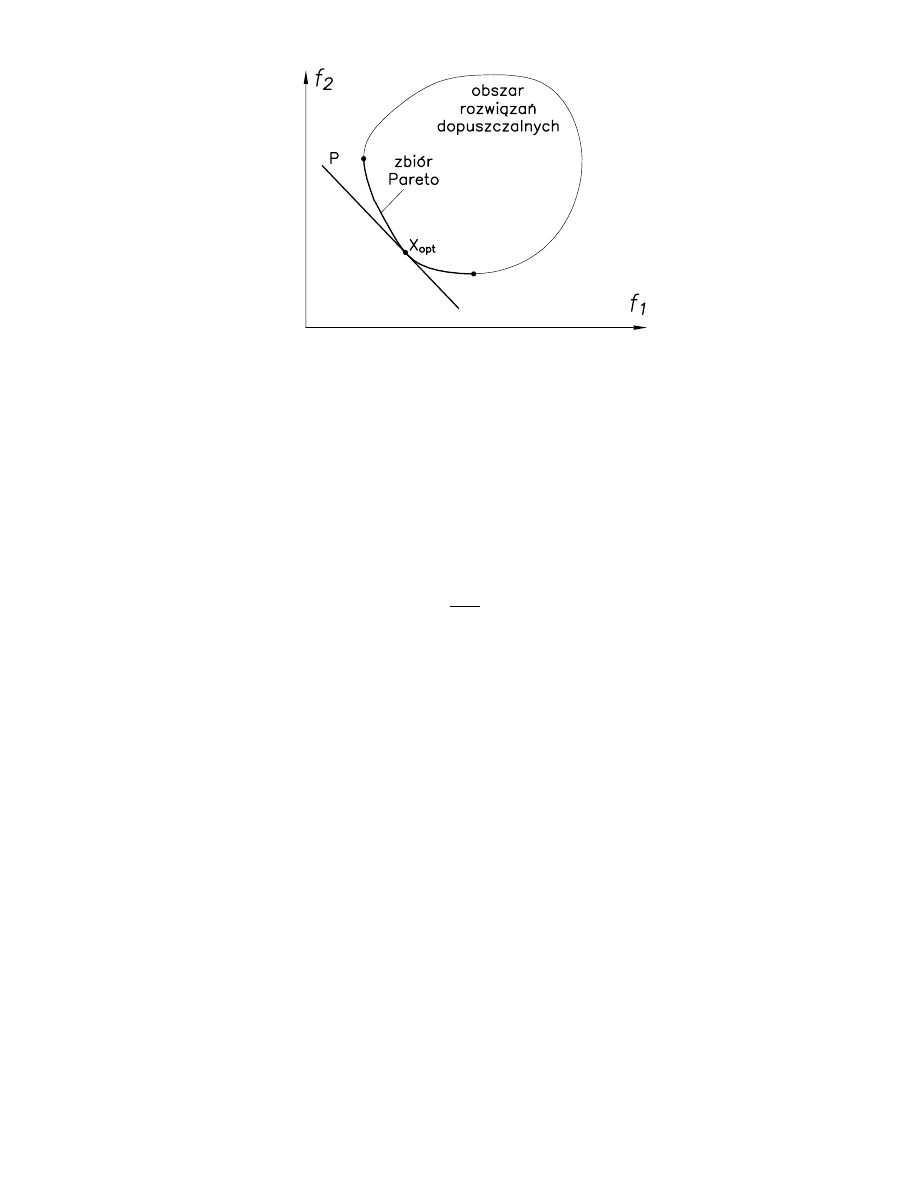
Rys. 2. Optimum wg metody wa onych kryteriów
2.
Metoda optymalizacji hierarchicznej (ang. Hierarchical Optimization Method) –
równie polega na sprowadzeniu polioptymalizacji do optymalizacji kolejno
wykonywanej wzgl dem wszystkich kryteriów. W tym celu nale y wykona
nast puj ce procedur :
–
Uszeregowa kryteria od najwa niejszego (f
1
) do najmniej wa nego (f
M
).
–
Znale rozwi zanie optymalne
X
1
wzgl dem kryterium f
1
i pierwotnych
ograniczeniach.
–
Poszukiwa rozwi za optymalnych
X
i
, i = 2, 3, ...,M wzgl dem pozostałych
kryteriów przy wprowadzaniu dodatkowych ogranicze :
)
(
100
1
)
(
1
1
1
1
−
−
−
−
⋅
±
≤
i
i
i
i
f
f
X
X
ε
(5)
gdzie
i
ε
jest procentow warto ci wariancji dozwolon dla funkcji
kryterialnej f
i
. Warto ta jest swoist wa no ci obliczonego w poprzednim
kroku post powania optimum. Warto wariancji mo e równie przyjmowa
warto równ zero, wtedy tak metod polioptymalizacji nazywa si
metod leksykograficzn (ang. Lexicographic Method).
3.
Metoda ograniczonych kryteriów (ang. Trade-Off Method,
ε
-constraint Method)
– w tej metodzie a priori s ustalane poziomy warto ci, jakie mog przyjmowa
poszczególne kryteria co prowadzi do ograniczenia przestrzeni rozwi za
dopuszczalnych. Problem polioptymalizacji jest sprowadzany do problemu
optymalizacji wzgl dem wybranego kryterium f
r
przy zwi kszonej o (M-1) liczbie
ogranicze wynikaj cych z pozostałych kryteriów, co matematycznie mo na
zapisa nast puj co:
J
j
h
K
k
g
r
i
M
i
f
f
j
k
i
i
r
,...,
1
;
0
)
(
,...,
1
;
0
)
(
;
,...,
1
;
)
(
MIN
)
(
=
=
=
≤
≠
=
≤
→
X
X
X
X
ε
(6)
gdzie
i
ε
jest warto ci limituj c kryterium
i
f , ustalon a priori.

4.
Metoda kryterium globalnego (ang. Global Criterion Method) – w metodzie tej
poszukuje si rozwi zania przybli onego
F(X
*
) (mo e nim by rozwi zanie
stanowi ce ekstremum dla poszczególnych kryteriów rozpatrywanych osobno) dla
sformułowania kryterium dla optymalizacji jednokryterialnej o postaci:
MIN
)
(
)
(
)
(
1
*
*
→
−
=
M
i
P
i
i
i
f
f
f
X
X
X
(7)
przy zachowaniu ogranicze równo ciowych i nierówno ciowych. Warto
wykładnika P jest przyjmowana a priori, najcz ciej przyjmuje warto ci
z przedziału (1; 2).
5.
Metody funkcji odległo ci i Mini-Maxu (ang. Method of Distance Functions,
Min-Max Method) – metody te s zbli one do metody kryterium globalnego, gdzie
równie na pocz tku post powania poszukuje si pewnego rozwi zana
przybli onego (lub idealnego), minimalizuj c w drugiej fazie funkcj o postaci:
MIN
)
(
)
(
)
(
1
1
*
*
→
−
=
M
i
P
P
i
i
i
f
f
f
X
X
X
(8)
Je eli P = 2 wtedy minimalizujemy odległo mi dzy rozwi zaniem przybli onym
a optymalnym (
Metoda funkcji odległo ci).
Warto P =
∞ prowadzi do metody Min-Max – minimalizacji maksymalnych
odchyle rozwi zania optymalnego od przybli onego:
MIN
)
(
)
(
)
(
MAX
*
*
,..,
1
→
−
=
X
X
X
i
i
i
M
i
f
f
f
(9)
Stosuje si równie metod Min-Max z wagami, przypisanymi do poszczególnych
kryteriów:
MIN
)
(
)
(
)
(
MAX
*
*
,..,
1
→
−
⋅
=
X
X
X
i
i
i
j
M
i
f
f
f
w
(10)
6.
Metoda programowania celów (ang. Goal Programming Method) – jest pewn
ogóln technik polioptymalizacji. W tym podej ciu kryteria s traktowane jako
cele które nale y osi gn lub jako warto ci progowe których warto ci kryteriów
nie mog przekroczy . Na warto ci kryteriów mog zosta zatem narzucone
warunki: wi kszy lub równy; mniejszy lub równy; równy. Rozwa my problem
polioptymalizacji z uwagi na dwie funkcje f
1
i f
2
. Przyjmijmy pierwszy cel –
kryterium f
1
b dzie mniejsze lub równe z
1
, oraz drugi – niech f
2
b dzie równe z
2
.
Wtedy zapis metody programowania celów b dzie nast puj cy:
2
2
2
2
1
1
1
2
2
2
2
1
1
)
(
)
(
MIN
)
(
z
d
d
f
z
d
f
d
w
d
w
d
w
=
+
−
≤
−
→
+
+
−
+
+
−
−
+
+
+
+
X
X
(11)

z
uwzgl dnieniem
ogranicze
równo ciowych
i
nierówno ciowych.
W powy szym wzorze w
i
s współczynnikami kary odpowiadaj cymi ka dej
odchyłce warto ci kryterium d
i
które wyznaczaj niepo dane odchylenia
osi gni tego celu.
7.
Metoda funkcji u yteczno ci (ang. Utility Function Method) – metoda ta, znana
z nauk ekonomicznych [9], wykorzystuje funkcj u yteczno ci o postaci:
(MAX)
MIN
)
(
→
F
U
(12)
okre lon w sposób heurystyczny. Najcz ciej jest ona addytywna wzgl dem
kryterium:
)
(
...
)
(
)
(
)
(
2
2
1
1
M
M
f
U
f
U
f
U
U
+
+
+
=
F
(13)
8.
Metoda algorytmów ewolucyjnych (ang. Evolutionary Algorithms) – jest to grupa
metod, zaliczaj cych si do technik sztucznej inteligencji. Ich przydatno jest
widoczna dopiero w przypadku problemów, gdzie potencjalna liczba rozwi za
optymalnych w sensie Pareto mo e si ga znacznych warto ci (rz du milionów lub
wi cej). Wtedy tradycyjne metody nie cechuj si tak skuteczno ci , jak
algorytmy ewolucyjne. W przypadku małej liczby rozwi za dopuszczalnych
lepiej sprawdzaj si tradycyjne metody optymalizacji.
2. Polioptymalizacja z wykorzystaniem ocen rozmytych – metoda Baasa
i Kwakernaaka
Zaprezentowane w poprzednim rozdziale metody s realizowane przy wa nym
zało eniu – warto ci ocen kryteriów optymalizacji s ci le okre lone, maj charakter
deterministyczny. W praktyce to zało enie nie zawsze jest prawdziwe. Cz sto
informacje o ocenach z zało enia maj charakter przybli ony, subiektywny, nieostry.
St d powstało szereg metod wykorzystuj cych inn posta ocen ni deterministyczn .
Wi kszo tych metod bazuje na metodzie wa onych kryteriów – zale no (3).
Jedn z nich jest metoda zaproponowana przez S.M. Baasa i H. Kwakernaaka [1],
w której wykorzystali zarówno oceny kryteriów K
i
, jak i wa no ci kryteriów w
i
w postaci rozmytej:
(
)
MAX
)
(
~
~
~
1
→
⋅
=
=
M
i
i
i
K
w
Z
X
(14)
Metoda ta jest wykorzystywana przy wyborze rozwi zania optymalnego ze
sko czonego zbioru
A rozwi za dopuszczalnych (np. wariantów procesu
wytwarzania, postaci półfabrykatu, narz dzi, obrabiarek itp.):
N
k
A
A
A
A
N
k
,...,
2
,
1
};
,...,
,...,
,
{
2
1
=
=
A
(15)
przy pomocy zbioru kryteriów
K:
{
}
M
i
K
K
K
K
M
i
,...,
2
,
1
;
)
(
),..,
(
),..,
(
),
(
)
(
2
1
=
=
A
A
A
A
A
K
(16)
przy czym wa no ka dego kryterium jest dana w postaci rozmytej (dokładniej liczby
rozmytej) o funkcji przynale no ci:
1
;
0
);
(
~
∈
=
i
i
Vi
i
v
v
w
µ
(17)
Ka de z rozwi za ze zbioru
A jest oceniane wzgl dem ka dego kryterium ze zbioru
K, przy czym ocena ta jest w postaci liczby rozmytej o funkcji przynale no ci:
1
;
0
);
(
)
(
~
∈
=
ki
ki
Rki
k
i
r
r
A
K
µ
(18)
Zakłada si , e warto ci ocen rozwi za , jak i wa no ci kryteriów s okre lone na
przedziale
1
0; co zwi zane jest m.in. z warunkiem (4).
Przy takich zało eniach warto kryterium zast pczego dla ka dego rozwi zania
ze zbioru
A jest równie liczb rozmyt o funkcji przynale no ci danej wyra eniem
(por. (14)):
1
;
0
);
(
)
(
....
)
(
)
(
)
(
)
(
)
(
)
(
~
2
2
2
2
1
1
1
1
∈
⋅
+
+
⋅
+
⋅
=
=
k
kM
VkM
M
RM
k
Vk
R
k
k
R
k
Zk
k
k
z
r
v
r
v
r
v
z
A
Z
µ
µ
µ
µ
µ
µ
µ
(19)
co zgodnie z ogólnymi zasadami działa na liczbach rozmytych prowadzi do
zale no ci:
(
)
=
=
=
⋅
=
=
M
i
ki
i
k
ki
Rki
M
i
i
Vi
M
i
k
Zk
r
v
z
r
v
z
1
,..,
1
,..,
1
)
(
min
),
(
min
min
sup
)
(
µ
µ
µ
(20)
Takie post powanie ka demu rozwi zaniu ze zbioru
A przyporz dkowuje ocen
rozmyt kryterium zast pczego. Zgodnie z zale no ci (14) nale y poszukiwa
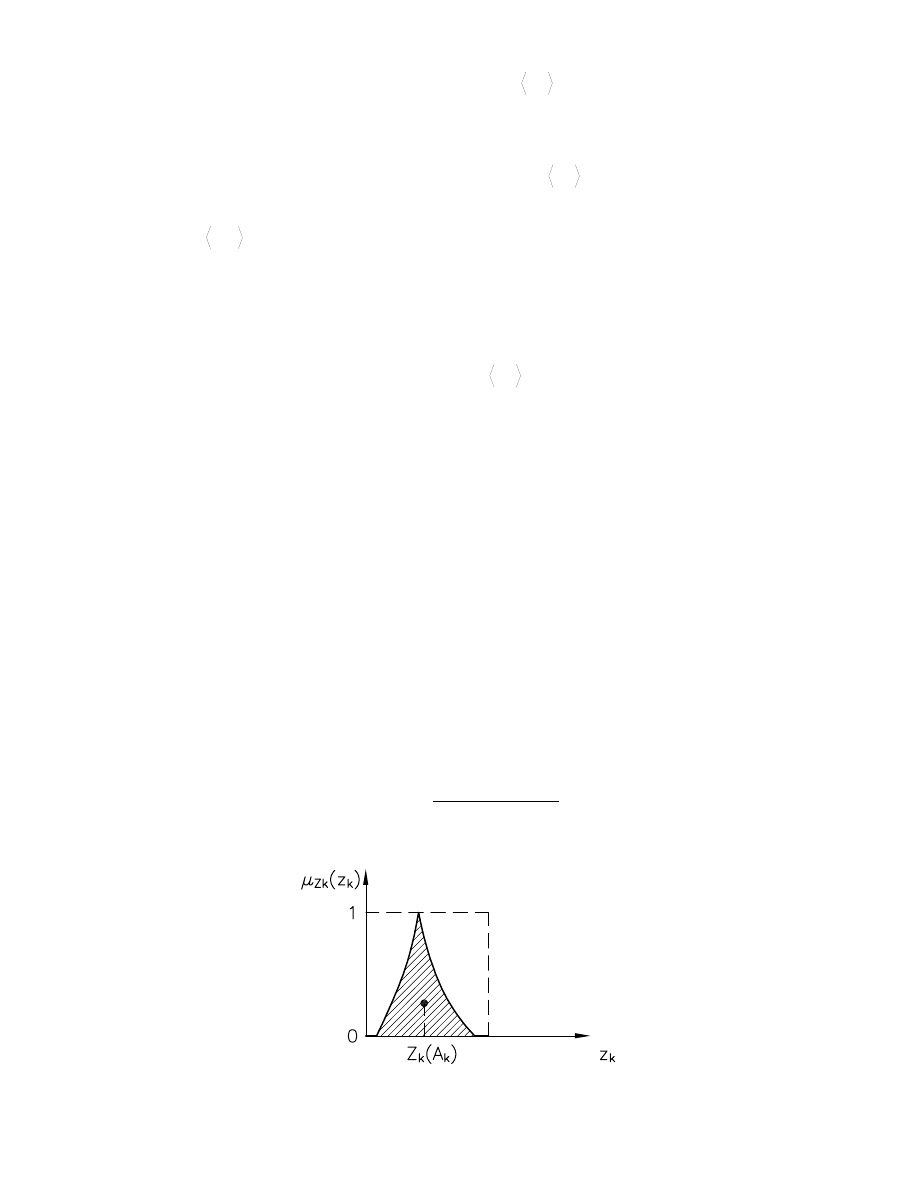
maksymalnej warto ci tej oceny. Poniewa jest ona liczb rozmyt nale y dokona jej
defuzyfikacji (wyostrzenia). Spo ród wielu metod najbardziej wiarygodn w tym
zagadnieniu jest metoda rodka ci ko ci, przypisuj ca funkcji przynale no ci (liczbie
rozmytej) liczb rzeczywist , okre laj c współrz dn rodka ci ko ci pola pod
wykresem tej funkcji (Rys. 3):
)
(
)
(
)
(
1
0
1
0
⋅
⋅
⋅
=
dz
z
dz
z
z
A
Z
k
Zk
k
Zk
k
k
µ
µ
(21)
Rys. 3. Zasada defuzyfikacji funkcji rozmytej metod rodka ci ko ci

Polioptymalizacja sprowadza si zatem do zadania poszukiwania rozwi zania,
dla którego warto oceny kryterium zast pczego jest maksymalna
(
MAX
)
(
→
k
k
A
Z
).
Aby uzyska wa no ci kryteriów, jak i oceny rozwi za ze zbioru
A wzgl dem
wszystkich kryteriów wykorzystuje si ocen porównawcz ekspertów – metoda
Saaty’ego (AHP, ang. Analitical Hierarchy Process) [12]. W ocenie uczestniczy P
ekspertów. Ka dy z nich dokonuje:
–
subiektywnej oceny wzgl dnej wa no ci kryteriów;
–
subiektywnej oceny wzgl dnej rozwi za wzgl dem wszystkich kryteriów;
zestawionych w postaci macierzy Saaty’ego, odpowiednio:
,...,
2
,
1
;
,...,
2
,
1
,
;
]
[
tj
sj
Vstj
j
Vst
V
w
w
U
P
j
M
t
s
U
=
=
=
=
U
(22)
co daje ł cznie P macierzy M
×
M, oraz:
)
(
)
(
,...,
2
,
1
;
,...,
2
,
1
;
,...,
2
,
1
,
;
]
[
t
ij
s
ij
Rstij
ij
Rst
R
A
K
A
K
U
P
j
M
i
N
t
s
U
=
=
=
=
=
U
(23)
co daje ł cznie M*P macierzy N
×
N. j-ty ekspert porównuj c s-te i t-te kryterium
(ocena U
Vstj
) lub s-te i t-te rozwi zanie wzgl dem i-tegi kryterium (ocena U
Rstij
)
przyjmuje nast puj c skal ocen, b d cych liczbami rzeczywistymi:
–
1 je eli s-ty i t-ty element s traktowane równowa nie;
–
3 je eli s-ty element jest nieco wa niejszy ni t-ty;
–
5 je eli s-ty element jest du o wa niejszy ni t-ty;
–
7 je eli s-ty element jest istotnie wa niejszy ni t-ty;
–
9 je eli s-ty element jest absolutnie wa niejszy ni t-ty;
–
2, 4, 6, 8 dla sytuacji po rednich;
–
U
Vstj
= 1/U
Vtsj
; U
Rstij
= 1/ U
Rtsij
;
–
1 je eli s = t.
Oceniaj c parami wa no ci kryteriów ekspert uzyskuje M niezale nych
porówna dla j-tego kryterium. Wtedy przyj te zało enie:
Vtsj
Vstj
U
U
1
=
(24)
jest prawdziwe, je eli oceny wa no ci spełniaj nast puj c zale no :
Vitj
Vsij
Vstj
U
U
U
⋅
=
(25)
nazywan warunkiem zgodno ci (oceny musz tworzy spójn cało ). Z warunku
(22) otrzymuje si nast puj c zale no dla j-tego eksperta:
M
t
s
w
w
U
w
w
U
sj
tj
j
Vst
tj
sj
j
Vst
,...,
2
,
1
,
;
1
=
=
⋅
→
=
(26)

Je eli ustalimy indeks s i posumujemy równania (26) wzgl dem indeksu t to
otrzymamy [7]:
=
=
=
⋅
M
t
sj
tj
j
Vst
M
s
M
w
w
U
1
,...,
2
,
1
;
(27)
Mno c równania (27) stronami przez w
sj
otrzymujemy układ równa :
=
=
⋅
=
⋅
M
t
sj
tj
Vstj
M
s
w
M
w
U
1
,...,
2
,
1
;
(28)
Grupuj c składniki układu otrzymujemy jego nast puj c posta wektorow :
P
j
M
j
j
Vj
,...,
2
,
1
;
=
⋅
=
⋅
w
w
U
(29)
Rozpatrzmy nast puj cy układ równa :
j
j
Vj
w
w
U
⋅
=
⋅
λ
(30)
lub jego równowa n posta :
(
)
0
=
⋅
−
j
Vj
w
1
U
λ
(31)
Układ równa (31) ma nietrywialne rozwi zanie, je eli wyznacznik:
(
)
0
det
=
− 1
U
λ
Vj
(32)
Wektor
w
j
nazywa si wektorem własnym macierzy
U
Vj
, a
λ
– warto ci własn
tej e macierzy. Układ M równa ma M warto ci własnych. Ich suma jest równa
ladowi macierzy, czyli sumie elementów na jej przek tnej głównej.
W rozpatrywanym problemie na przek tnej le same jedynki, st d lad macierzy jest
równy M. Je eli układ równa ma jedn niezerow warto własn , to jest ona równa
dokładnie M i wektor własny, odpowiadaj cy tej warto ci jest jednocze nie wektorem
w
j
wa no ci kryteriów, ustalonym przez j-tego eksperta. Je eli nie s spełnione
warunki zgodno ci, to za wektor
w
j
wa no ci kryteriów przyjmuje si wektor własny,
odpowiadaj cy maksymalnej warto ci własnej
λ
max
, która jednak nie mo e zbyt
odbiega od warto ci idealnej, równej M. Aby sprawdzi , czy warto własna ma
odpowiednio warto wyznacza si wska nik rozbie no ci CI:
1
max
−
−
=
M
M
CI
λ
(33)
oraz wska nik zgodno ci CR:
R
CI
CR
=
(34)
gdzie R jest warto ci zale n od rozmiaru macierzy M wg Tabl. 1. Zaleca si , aby
warto wska nika zgodno ci CR była mniejsza lub równa 0,1. Je eli warto ta jest
wi ksza – nale y powtórzy post powanie oceny wa no ci kryteriów przez j-tego
eksperta. W analogiczny sposób s wyznaczane oceny rozwi za – K
ij
(
A) – dla
wszystkich ekspertów.

Tabl. 1. Warto ci współczynnika R
M
R
M
R
1
2
3
4
5
6
7
8
0,00
0,00
0,58
0,90
1,12
1,24
1,32
1,41
9
10
11
12
13
14
15
1,45
1,49
1,51
1,53
1,56
1,57
1,59
Aby zapewni odpowiednio du warto własn
λ
max
wykorzystuje si cz sto
nast puj ce post powanie przy tworzeniu macierzy Saaty’ego [12]:
1.
Przy pomocy ekspertów wypełnia si pierwszy wiersz i pierwsz kolumn
macierzy ocen kryteriów lub rozwi za , korzystaj c z zale no ci (24).
2.
Na przek tnej głównej macierzy przyjmuje si warto ci równe 1.
3.
Pozostałe warto ci w macierzy wyznacza si korzystaj c z zasady konsystencji (dla
ocen kryteriów):
P
j
M
t
s
U
U
U
sj
Vs
tj
Vs
Vstj
,...,
2
,
1
;
,...,
2
,
1
,
;
,
1
,
1
=
=
=
−
−
(35)
oraz warunku (24). Podobna zale no obowi zuje dla ocen rozwi za . Dla tak
skonstruowanej macierzy istnieje jedna niezerowa warto własna, równa rozmiarowi
macierzy.
Po okre leniu wa no ci kryteriów i ocen rozwi za przez poszczególnych
ekspertów wyznacza si ł czne oceny wa no ci kryteriów (w postaci liczb rozmytych)
oraz oceny rozwi za (równie w postaci liczb rozmytych), przy czym wcze niej
dokonuje si normowania ocen ekspertów wg zale no ci [1]:
N
k
P
j
M
i
A
K
A
K
A
K
P
j
M
i
w
w
w
k
ij
j
i
k
ij
k
ij
ij
j
i
ij
ij
,...,
2
,
1
;
,...,
2
,
1
;
,...,
2
,
1
;
)
(
max
)
(
)
(
ˆ
,...,
2
,
1
;
,..,
2
,
1
;
max
ˆ
,
,
=
=
=
=
=
=
=
(36)
Ł czne wa no ci kryteriów (
Vi
µ
) i oceny rozwi za (
Rki
µ
), podane przez P
ekspertów, s modelowane za pomoc trójk tnych funkcji przynale no ci (Rys. 4).
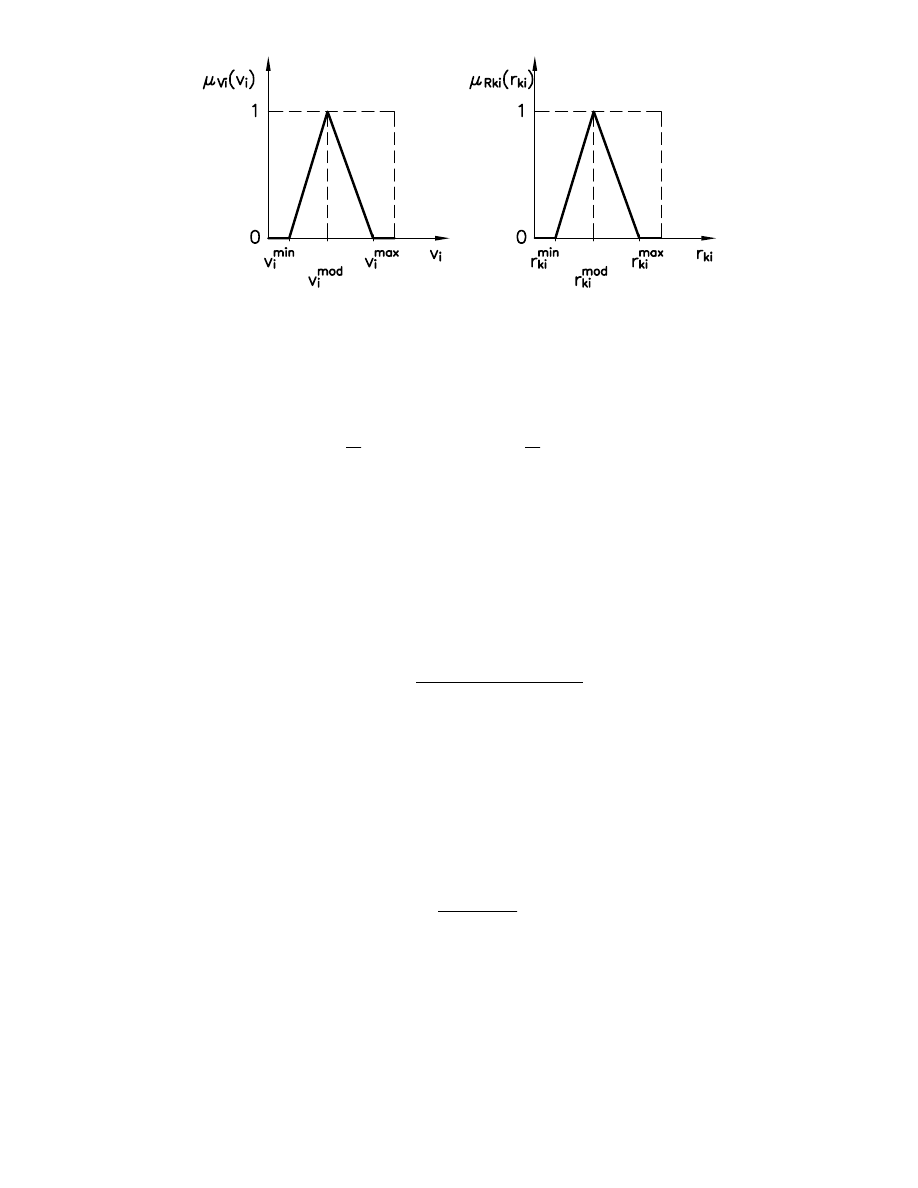
Rys. 4. Modelowanie wa no ci kryteriów i ocen rozwi za za pomoc liczb rozmytych
o trójk tnej funkcji przynale no ci
Współrz dne charakterystyczne funkcji przynale no ci s obliczane z zale no ci:
)
(
ˆ
max
ˆ
max
)
(
ˆ
1
ˆ
1
)
(
ˆ
min
ˆ
min
max
max
1
mod
1
mod
min
min
k
ij
j
ki
ij
j
i
P
j
k
ij
ki
P
j
ij
i
k
ij
j
ki
ij
j
i
A
K
r
w
v
A
K
P
r
w
P
v
A
K
r
w
v
=
=
=
=
=
=
=
=
(37)
W nast pnym etapie, zgodnie z zale no ci (19) mo na okre li posta funkcji
przynale no ci kryterium zast pczego dla poszczególnych rozwi za ze zbioru
A.
W toku powy szego post powania ze wzgl du na dokonane unormowanie ocen –
wzór (36) – zale no (19) nale y jednak zmodyfikowa do postaci:
(
)
=
=
⋅
=
M
i
i
Vi
M
i
ki
Rki
i
Vi
k
Zk
v
r
v
z
1
1
)
(
)
(
)
(
)
(
µ
µ
µ
µ
(38)
co zgodnie z ogólnymi zasadami działa na liczbach rozmytych prowadzi do
zale no ci:
(
)
=
=
=
=
⋅
=
=
M
i
i
M
i
ki
i
k
ki
Rki
M
i
i
Vi
M
i
k
Zk
v
r
v
z
r
v
z
1
1
,..,
1
,..,
1
)
(
min
),
(
min
min
sup
)
(
µ
µ
µ
(39)
Skorzystanie bezpo rednio z zale no ci (39) nie jest proste, st d w praktyce korzysta
si z uproszczonych metod działa na liczbach rozmytych, wykorzystuj cych
α-przekroje zbiorów rozmytych. α-przekrojem zbioru rozmytego B ⊆ X, oznaczanym
B
α
, nazywamy nast puj cy zbiór nierozmyty:
{
}
α
µ
α
≥
∈
=
)
(
:
x
x
B
B
X
(40)
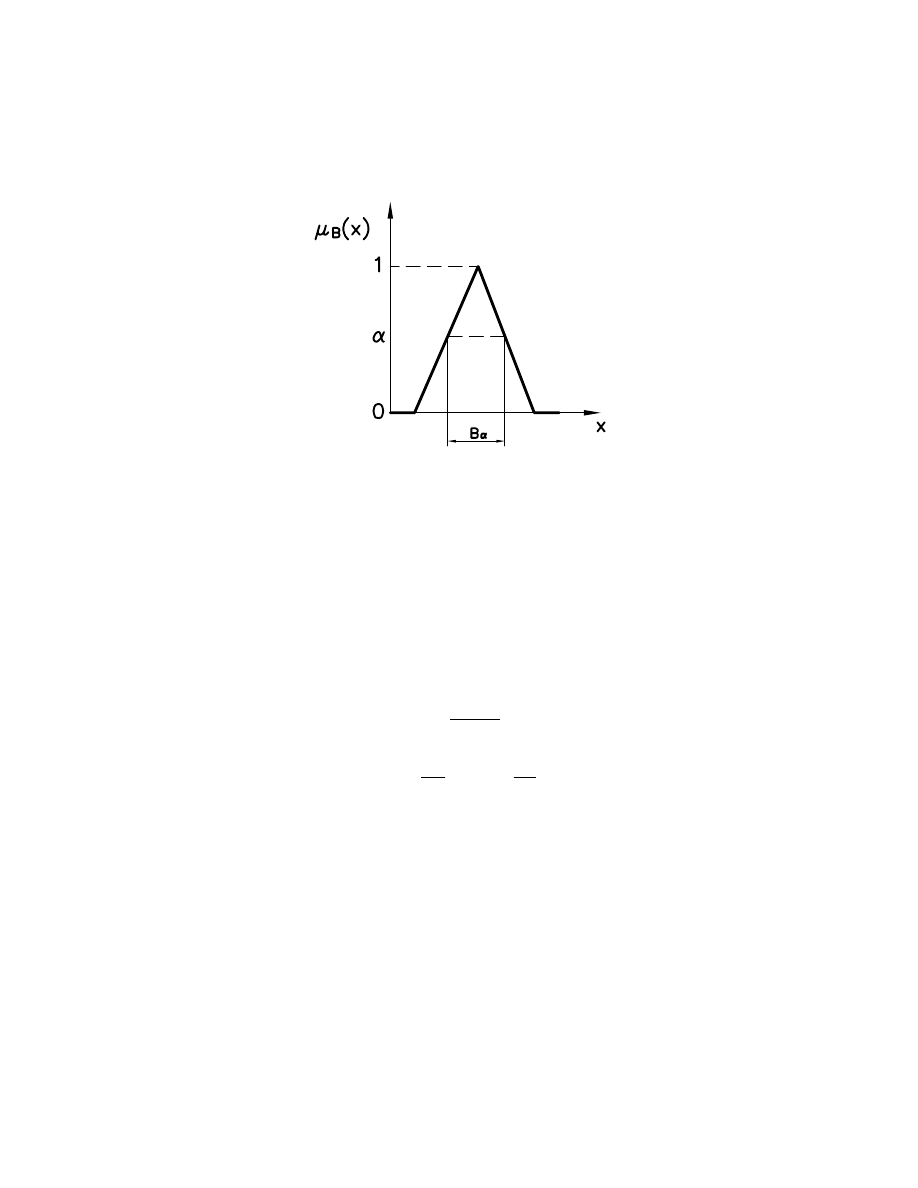
okre lony przez funkcj :
<
≥
=
α
µ
α
µ
χ
α
)
(
dla
0
)
(
dla
1
x
x
B
B
(41)
Ilustracj
α-przekroju zbioru rozmytego przedstawiono na Rys. 5.
Rys. 5.
α-przekrój zbioru rozmytego
Przy takie definicji
α-przekroju operacje na liczbach rozmytych mog zosta
zdefiniowane w nast puj cej postaci (Rys. 6):
α
α
α
α
α
α
µ
µ
µ
d
b
f
c
a
e
x
x
x
B
A
C
+
=
+
=
+
=
;
)
(
)
(
)
(
(42)
α
α
α
α
α
α
µ
µ
µ
d
b
f
c
a
e
x
x
x
B
A
C
⋅
=
⋅
=
⋅
=
;
)
(
)
(
)
(
(43)
α
α
α
α
α
α
µ
µ
µ
c
b
f
d
a
e
x
x
x
B
A
C
=
=
=
;
)
(
)
(
)
(
(44)
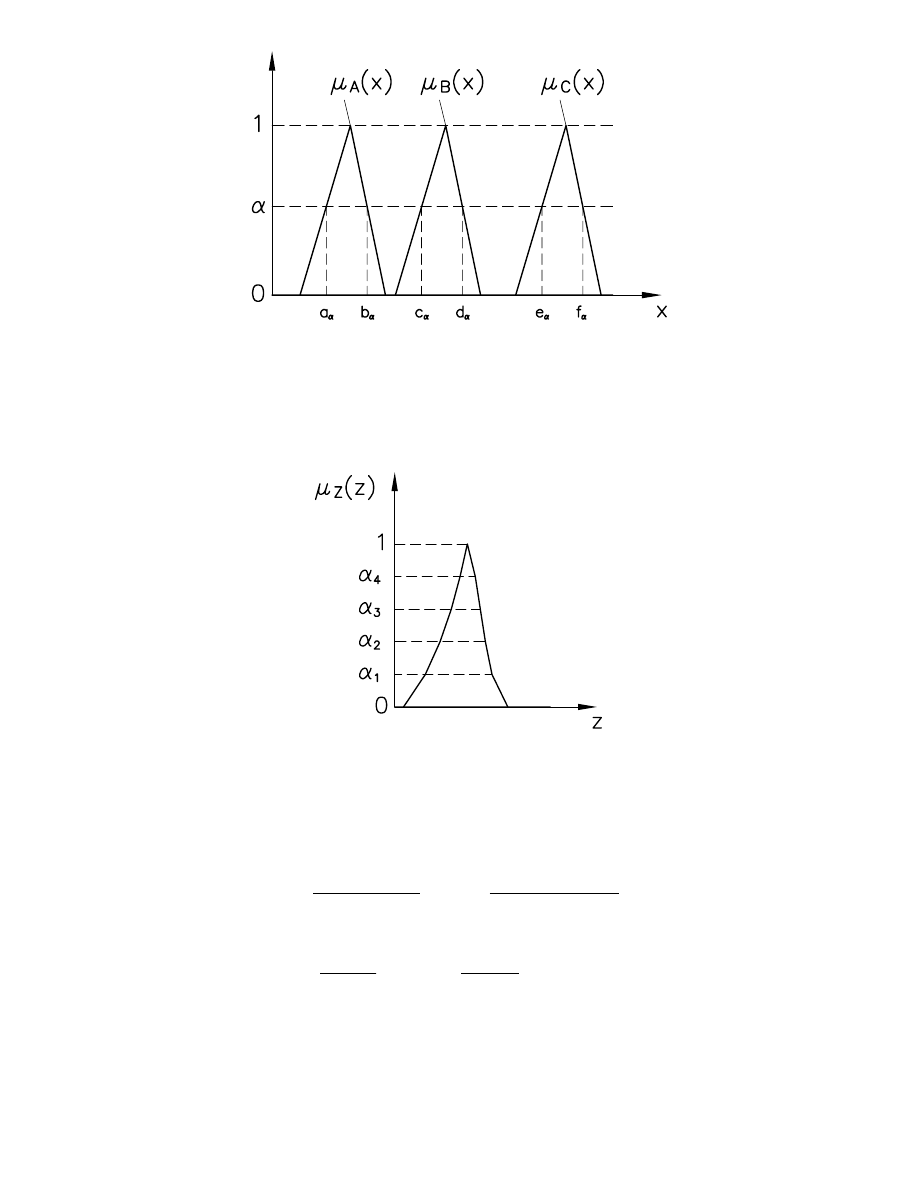
Rys. 6. Dane do definicji operacji arytmetycznych na liczbach rozmytych
Przeprowadzaj c dla zale no ci (38) obliczenia dla odpowiednio du ej liczby
α-przekrojów wg powy szych zasad uzyskuje si wzgl dnie dokładne przybli enie
postaci funkcji przynale no ci dla ocen kryteriów zast pczych. W takim przypadku
pole pod wykresem tej funkcji (zgodnie z (21)) b dzie sum pól trapezów (Rys. 7).
Rys. 7. Kształt funkcji przynale no ci oceny kryterium zast pczego przybli ony za pomoc
α-przekrojów
Przyst puj c zatem do wyznaczenia poło enia rodka ci ko ci pola pod
wykresem tej funkcji – wzór (21) – wyprowadzono zale no na poło enie rodka
ci ko ci pola trapezu oraz warto ci siły ci ko ci (Rys. 8) [oprac. własne]:
2
2
2
;
4
3
2
1
1
2
4
3
4
1
4
3
1
2
x
x
S
x
x
R
x
x
x
Q
x
x
x
P
H
x
x
x
x
F
P
Q
R
S
Q
R
S
P
x
C
C
+
=
+
=
−
+
=
+
−
=
⋅
+
−
−
=
+
−
−
⋅
−
⋅
=
(45)
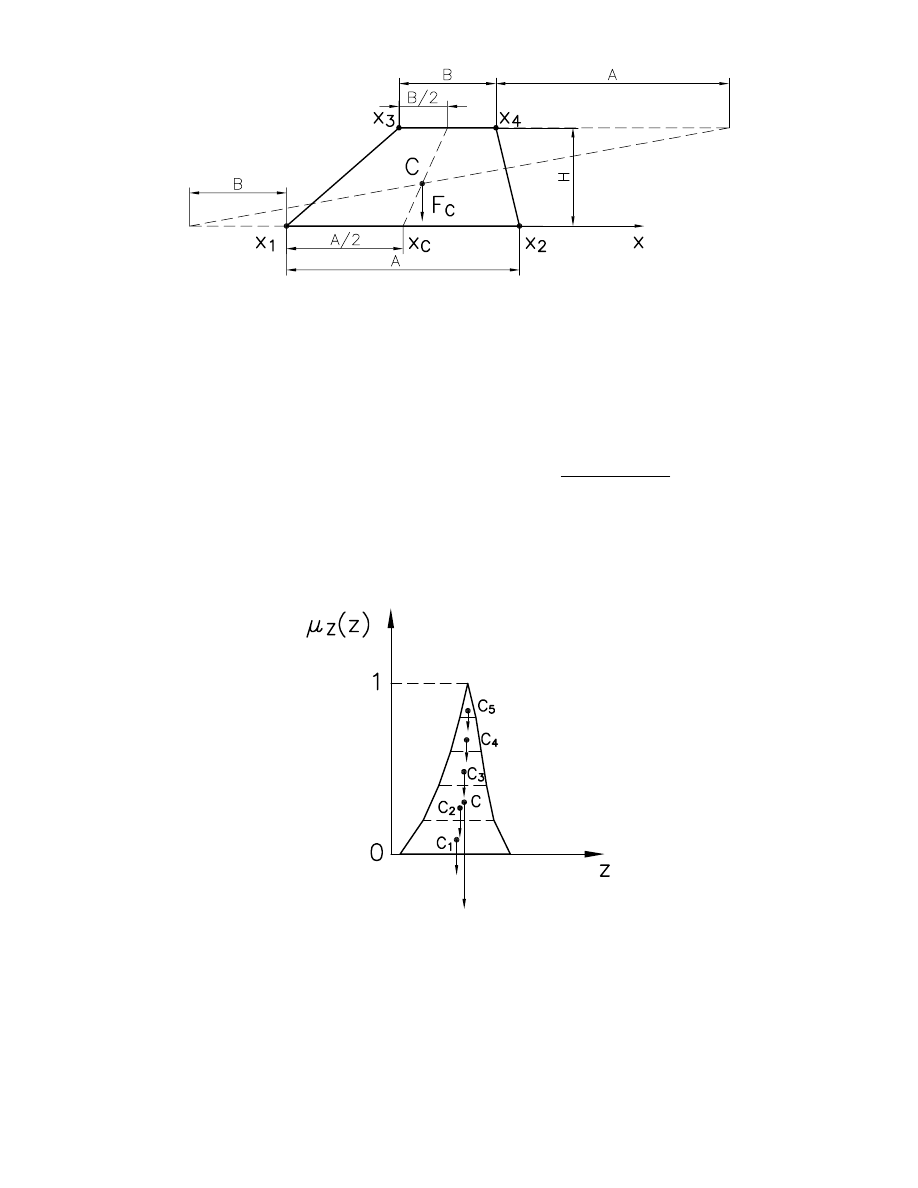
Rys. 8. Wyznaczanie poło enia rodka ci ko ci pola trapezu
Je eli poło enie rodka ci ko ci i warto siły ci ko ci wyznaczy dla
wszystkich pól składowych całego pola pod wykresem funkcji przynale no ci, to
mo liwe jest wyznaczenie wypadkowego poło enia rodka ci ko ci korzystaj c
z równania momentów sił ci ko ci pól (Rys. 9):
(
)
(
)
=
=
=
=
⋅
=
→
⋅
=
⋅
u
i
Ci
u
i
Ci
Ci
C
u
i
u
i
Ci
C
Ci
Ci
F
x
F
x
F
x
x
F
1
1
1
1
(46)
gdzie: u – liczba składowych trapezów, na jakie podzielono pole pod wykresem
funkcji przynale no ci.
Rys. 9. Okre lanie poło enia rodka ci ko ci całego pola pod wykresem funkcji
przynale no ci kryterium zast pczego
Zale no (46) pozwala ju wyznaczy warto ci wzgl dne ocen kryteriów
zast pczych dla wszystkich rozwi za ze zbioru
A (21), a tym samym wybra
rozwi zanie optymalne, o maksymalnej warto ci tej oceny.
Nale y zaznaczy , i otrzymane w wyniku opisanego post powania wzgl dne
warto ci ocen kryteriów zast pczych powinny by
interpretowane w takiej skali,
w jakiej były
okre lane oceny poszczególnych ekspertów.
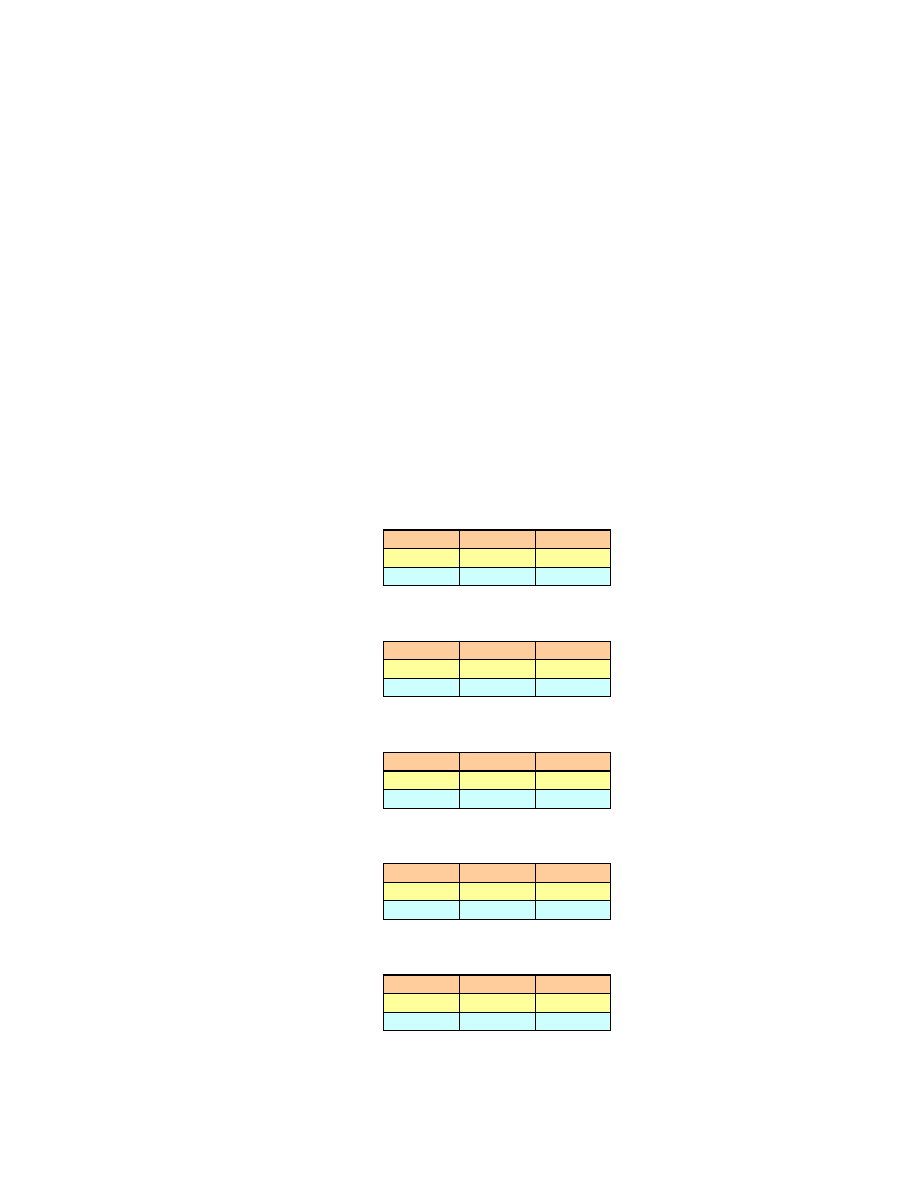
3. Polioptymalizacja z wykorzystaniem metody Baasa i Kwakernaaka –
przykład
W pracach [11] i [4] zaprezentowano przykład wyboru najlepszego samochodu
osobowego. Analizowano zbiór trzech rozwi za dopuszczalnych (zbiór
A):
1.
A1
– Fiat Punto;
2.
A2
– Peugeot 206;
3.
A3
– Volkswagen Polo;
przy przyj ciu nast puj cych kryteriów:
1.
K1(
A) – cena samochodu;
2.
K2(
A) – koszty eksploatacji po 5-ciu latach u ytkowania;
3.
K3(
A) – komfort jazdy;
4.
K4(
A) – stylistyka nadwozia;
5.
K5(
A) – bezpiecze stwo jazdy.
W ocenie wa no ci kryteriów oraz ocenie rozwi za uczestniczyło trzech
ekspertów (E1, E2, E3). Ka dy z nich dokonał oceny rozwi za wzgl dem
rozpatrywanych kryteriów przyjmuj c skal punktow 1
÷5 (im wy sza warto
punktowa tym lepsza ocena) – Rys. 10 – oraz wa no ci kryteriów, przyjmuj c skal
1
÷7 – Rys. 11.
K1
A1
A2
A3
E1
4
3
1
E2
5
3
1
E3
4
3
1
K2
A1
A2
A3
E1
4
2
5
E2
4
2
5
E3
4
2
4
K3
A1
A2
A3
E1
3
5
2
E2
2
5
1
E3
3
5
2
K4
A1
A2
A3
E1
4
5
2
E2
3
5
1
E3
2
5
3
K5
A1
A2
A3
E1
2
3
4
E2
3
2
4
E3
2
2
4
Rys. 10. Oceny punktowe rozwi za dopuszczalnych wzgl dem poszczególnych kryteriów
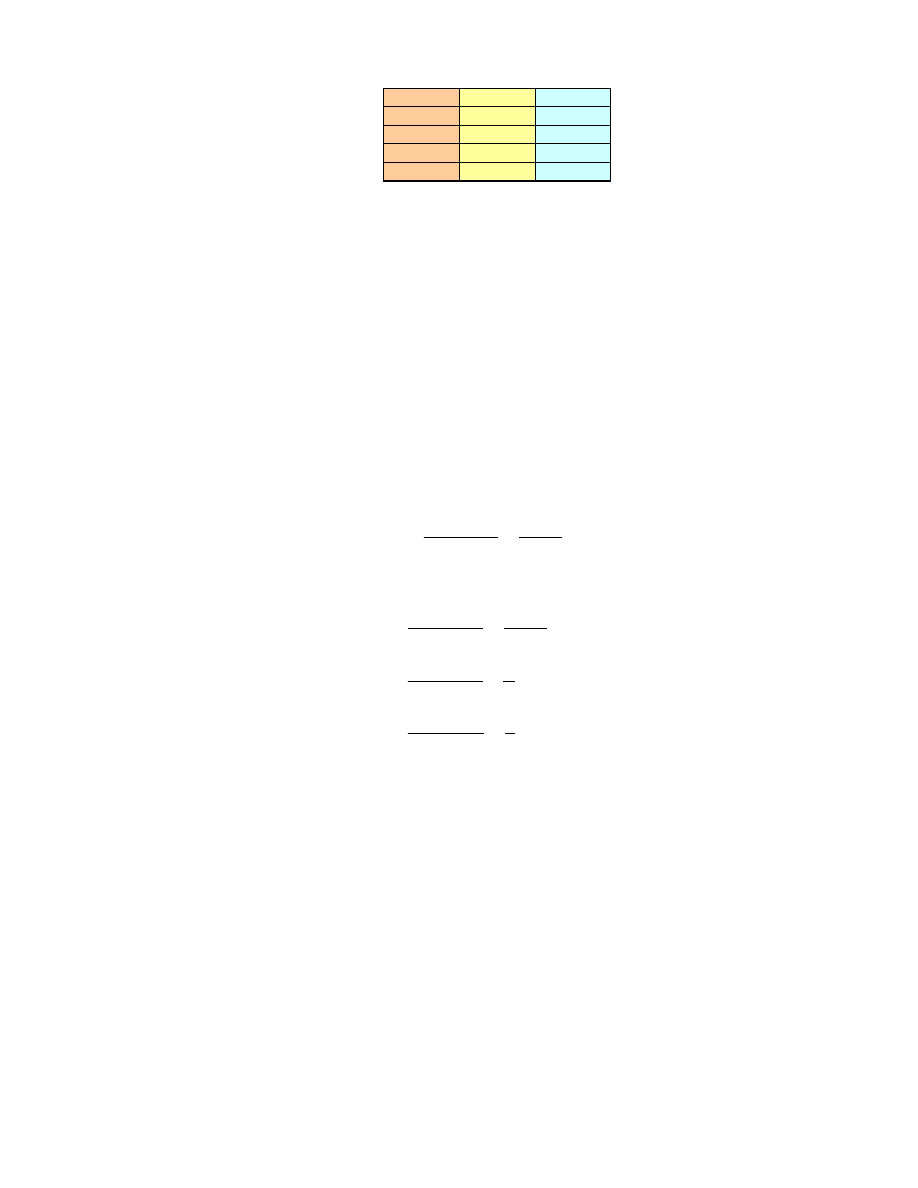
E1
E2
E3
K1
2
3
2
K2
7
6
6
K3
3
2
3
K4
2
3
1
K5
6
4
5
Rys. 11. Oceny punktowe wa no ci kryteriów
Na podstawie ocen punktowych utworzono macierze Saaty’ego (Rys. 12, Rys.
13, Rys. 14 i Rys. 15). Przyj to nast puj ce post powanie (na przykładzie macierzy
E1/K1 – ocena eksperta E1 rozwi za wzgl dem kryterium K1):
–
Na przek tnej głównej macierzy wpisano warto ci 1;
–
Ocen wariantu pierwszego (A1) przyj to jako bazow – warto 1 w komórce
″A1-A1″;
–
Oceny pozostałych wariantów (A2, A3) obliczano dziel c liczb punktów
przydzielonych wariantowi A1 (4) przez liczb punktów przydzielonych
pozostałym wariantom: A2 (3) i A3 (1), uzyskuj c warto ci w pierwszym wierszu
macierzy: 4/3 (
″A1-A2″) oraz 4 (″A1-A3″);
–
Pozostałe komórki nad przek tn główn obliczono korzystaj c z zasady
konsystencji macierzy Saaty’ego – zale no (35):
3
333
.
1
4
A2"
-
A1
"
A3"
-
A1
"
A1"
A2
"
=
=
=
−
(47)
–
Komórki pod przek tn główn obliczono z zale no ci (24):
33
.
0
3
1
A3"
-
A2
"
1
A2"
-
A3
"
25
.
0
4
1
A3"
-
A1
"
1
A1"
-
A3
"
75
.
0
333
.
1
1
A2"
-
A1
"
1
A1"
-
A2
"
=
=
=
=
=
=
=
=
=
(48)
W podobny sposób obliczono macierze dla wa no ci kryteriów.
A1
A2
A3
A1
1.0000
1.3333
4.0000
A2
0.7500
1.0000
3.0000
A3
0.2500
0.3333
1.0000
E1/K2
A1
A2
A3
A1
1.0000
2.0000
0.8000
A2
0.5000
1.0000
0.4000
A3
1.2500
2.5000
1.0000
E1/K3
A1
A2
A3
A1
1.0000
0.6000
1.5000
A2
1.6667
1.0000
2.5000
A3
0.6667
0.4000
1.0000
E1/K4
A1
A2
A3
A1
1.0000
0.8000
2.0000
A2
1.2500
1.0000
2.5000
A3
0.5000
0.4000
1.0000
E1/K5
A1
A2
A3
A1
1.0000
0.6667
0.5000
A2
1.5000
1.0000
0.7500
A3
2.0000
1.3333
1.0000
E2/K1
A1
A2
A3
A1
1.0000
1.6667
5.0000
A2
0.6000
1.0000
3.0000
A3
0.2000
0.3333
1.0000
E2/K2
A1
A2
A3
A1
1.0000
2.0000
0.8000
A2
0.5000
1.0000
0.4000
A3
1.2500
2.5000
1.0000
E2/K3
A1
A2
A3
A1
1.0000
0.4000
2.0000
A2
2.5000
1.0000
5.0000
A3
0.5000
0.2000
1.0000
E2/K4
A1
A2
A3
A1
1.0000
0.6000
3.0000
A2
1.6667
1.0000
5.0000
A3
0.3333
0.2000
1.0000
E2/K5
A1
A2
A3
A1
1.0000
1.5000
0.7500
A2
0.6667
1.0000
0.5000
A3
1.3333
2.0000
1.0000
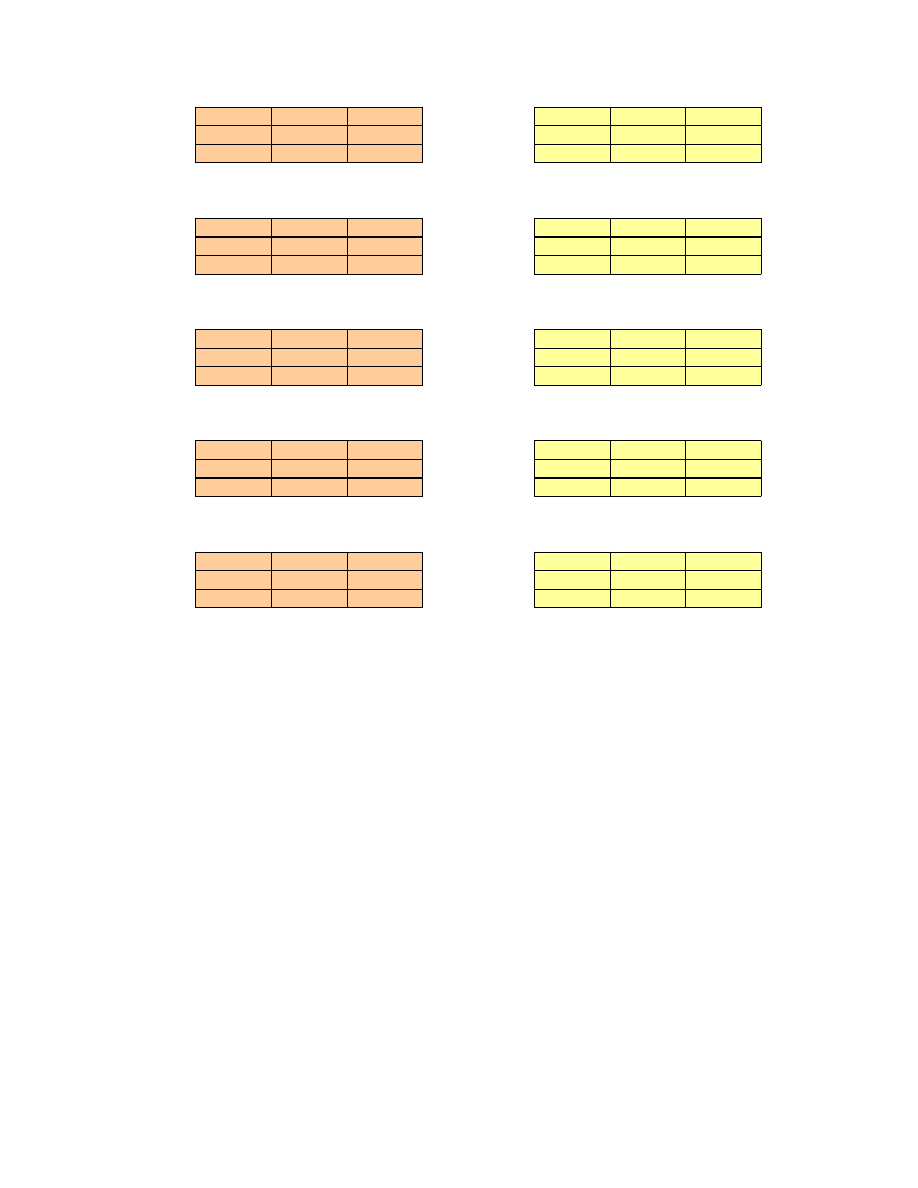
Rys. 12. Macierze Saaty’ego ocen
rozwi za dla eksperta E1
Rys. 13. Macierze Saaty’ego ocen
rozwi za dla eksperta E2
E3/K1
A1
A2
A3
A1
1.0000
1.3333
4.0000
A2
0.7500
1.0000
3.0000
A3
0.2500
0.3333
1.0000
E3/K2
A1
A2
A3
A1
1.0000
2.0000
1.0000
A2
0.5000
1.0000
0.5000
A3
1.0000
2.0000
1.0000
E3/K3
A1
A2
A3
A1
1.0000
0.6000
1.5000
A2
1.6667
1.0000
2.5000
A3
0.6667
0.4000
1.0000
E3/K4
A1
A2
A3
A1
1.0000
0.4000
0.6667
A2
2.5000
1.0000
1.6667
A3
1.5000
0.6000
1.0000
E3/K5
A1
A2
A3
A1
1.0000
1.0000
0.5000
A2
1.0000
1.0000
0.5000
A3
2.0000
2.0000
1.0000
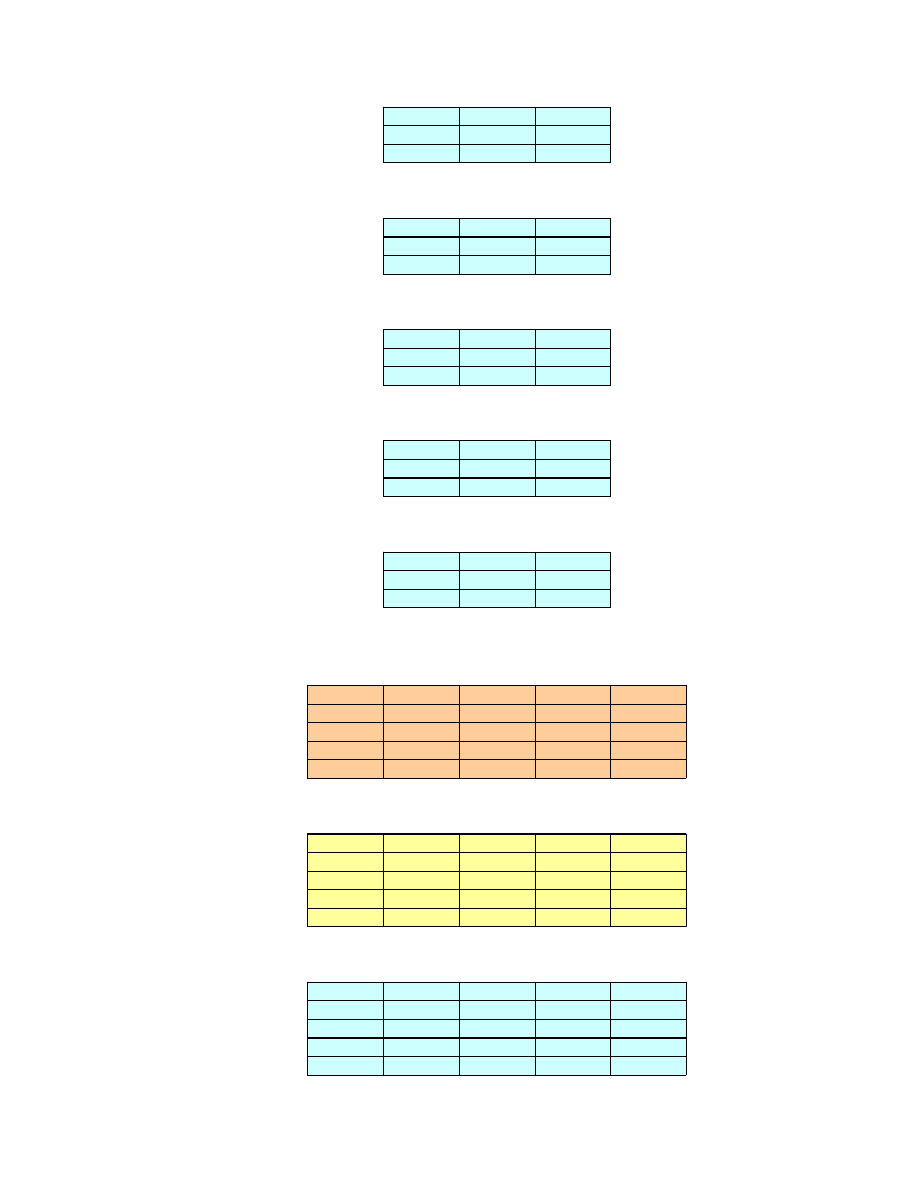
Rys. 14. Macierze Saaty’ego ocen rozwi za dla eksperta E3
E1
K1
K2
K3
K4
K5
K1
1.0000
0.2857
0.6667
1.0000
0.3333
K2
3.5000
1.0000
2.3333
3.5000
1.1667
K3
1.5000
0.4286
1.0000
1.5000
0.5000
K4
1.0000
0.2857
0.6667
1.0000
0.3333
K5
3.0000
0.8571
2.0000
3.0000
1.0000
E2
K1
K2
K3
K4
K5
K1
1.0000
0.5000
1.5000
1.0000
0.7500
K2
2.0000
1.0000
3.0000
2.0000
1.5000
K3
0.6667
0.3333
1.0000
0.6667
0.5000
K4
1.0000
0.5000
1.5000
1.0000
0.7500
K5
1.3333
0.6667
2.0000
1.3333
1.0000
E3
K1
K2
K3
K4
K5
K1
1.0000
0.3333
0.6667
2.0000
0.4000
K2
3.0000
1.0000
2.0000
6.0000
1.2000
K3
1.5000
0.5000
1.0000
3.0000
0.6000
K4
0.5000
0.1667
0.3333
1.0000
0.2000
K5
2.5000
0.8333
1.6667
5.0000
1.0000
Rys. 15. Macierze Saaty’ego wa no ci kryteriów dla wszystkich ekspertów
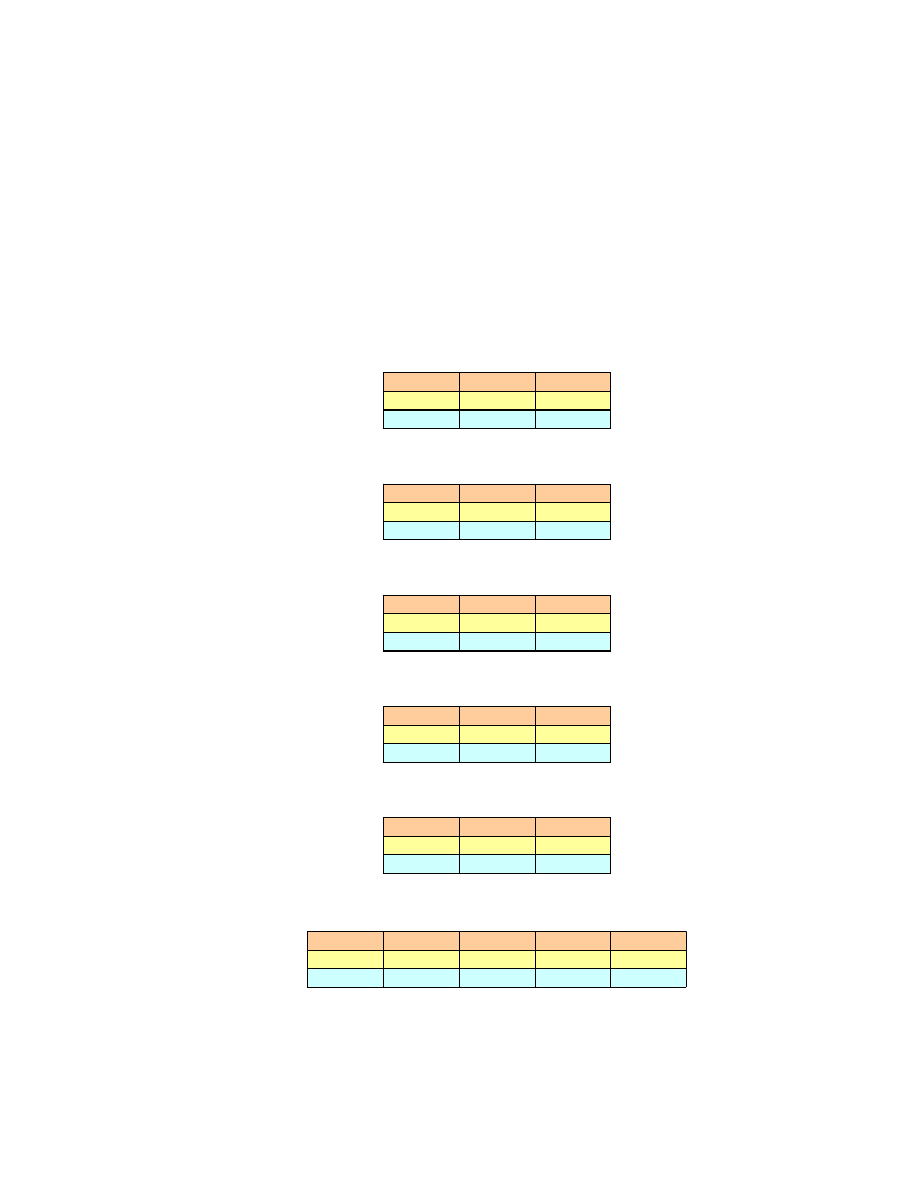
Kolejnym etapem jest obliczenie dla ka dej macierzy Saaty’ego wektora
własnego odpowiadaj cego najwi kszej warto ci własnej. Z uwagi na przyj cie zasady
konsystencji przy tworzeniu macierzy wektor ten de facto jest zawarty w pierwszej
kolumnie macierzy. Przyjmuje si jednak zasad normowania współrz dnych wektora
własnego tak, aby suma ich kwadratów była równa 1:
( )
(
)
P
j
N
k
A
K
w
M
i
k
ij
M
i
ij
,...,
2
,
1
;
,....,
2
,
1
;
1
)
(
;
1
1
2
1
2
=
=
=
=
=
=
(49)
Obliczone na podstawie zale no ci (49) wektory własne poszczególnych macierzy
przedstawiono na Rys. 16 i Rys. 17.
K1
A1
A2
A3
E1
0.7845
0.5883
0.1961
E2
0.8452
0.5071
0.1690
E3
0.7845
0.5883
0.1961
K2
A1
A2
A3
E1
0.5963
0.2981
0.7454
E2
0.5963
0.2981
0.7454
E3
0.6667
0.3333
0.6667
K3
A1
A2
A3
E1
0.4867
0.8111
0.3245
E2
0.3651
0.9129
0.1826
E3
0.4867
0.8111
0.3245
K4
A1
A2
A3
E1
0.5963
0.7454
0.2981
E2
0.5071
0.8452
0.1690
E3
0.3244
0.8111
0.4867
K5
A1
A2
A3
E1
0.3714
0.5571
0.7428
E2
0.5571
0.3714
0.7428
E3
0.4082
0.4082
0.8165
Rys. 16. Współrz dne wektorów własnych dla macierzy ocen rozwi za
K1
K2
K3
K4
K5
E1
0.1902
0.7217
0.2853
0.1902
0.5705
E2
0.3487
0.6975
0.2325
0.3487
0.4650
E3
0.2309
0.6928
0.3464
0.1155
0.5774
Rys. 17. Współrz dne wektorów własnych dla macierzy wa no ci kryteriów
Kolejnym krokiem jest normowanie współrz dnych wektorów własnych wg
zale no ci (36). Unormowane wektory własne przedstawiono na Rys. 18 i Rys. 19.
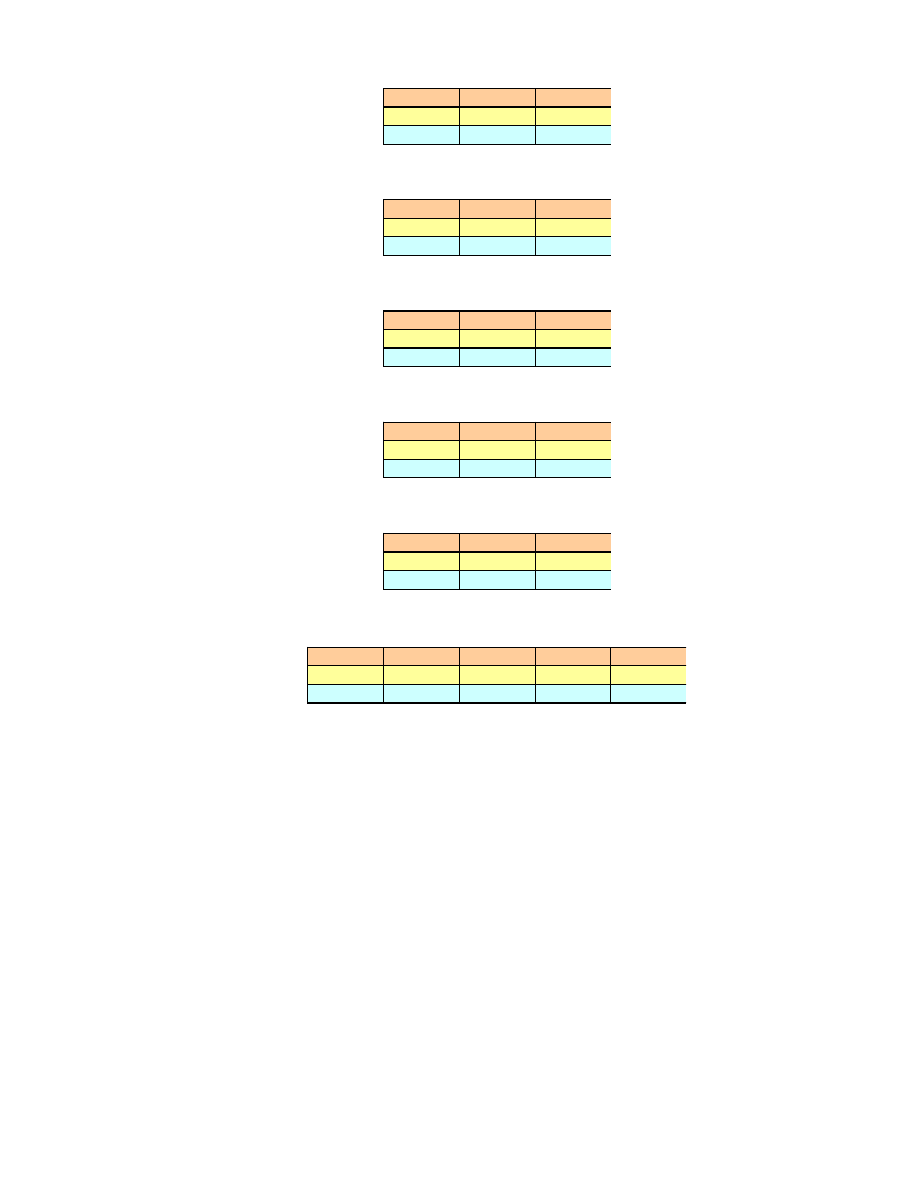
K1
A1
A2
A3
E1
0.9282
0.6961
0.2320
E2
1.0000
0.6000
0.2000
E3
0.9282
0.6961
0.2320
K2
A1
A2
A3
E1
0.8000
0.4000
1.0000
E2
0.8000
0.4000
1.0000
E3
0.8944
0.4472
0.8944
K3
A1
A2
A3
E1
0.5331
0.8885
0.3554
E2
0.4000
1.0000
0.2000
E3
0.5331
0.8885
0.3554
K4
A1
A2
A3
E1
0.7055
0.8819
0.3528
E2
0.6000
1.0000
0.2000
E3
0.3839
0.9597
0.5758
K5
A1
A2
A3
E1
0.4549
0.6823
0.9097
E2
0.6823
0.4549
0.9097
E3
0.5000
0.5000
1.0000
Rys. 18. Współrz dne unormowane wektorów własnych dla macierzy ocen rozwi za
K1
K2
K3
K4
K5
E1
0.2635
1.0000
0.3953
0.2635
0.7905
E2
0.4832
0.9665
0.3222
0.4832
0.6443
E3
0.3200
0.9600
0.4800
0.1600
0.8000
Rys. 19. Współrz dne unormowane wektorów własnych dla macierzy wa no ci kryteriów
Kolejnym krokiem jest wyznaczenie współrz dnych charakterystycznych funkcji
przynale no ci dla rozmytych wa no ci kryteriów i ocen rozwi za – zale no (37).
Ich warto ci przedstawiono na Rys. 20 i Rys. 21. Na podstawie tych danych
sporz dzono wykresy funkcji przynale no ci ocen rozwi za – Rys. 22
÷ Rys. 26 –
oraz wa no ci kryteriów – Rys. 27.
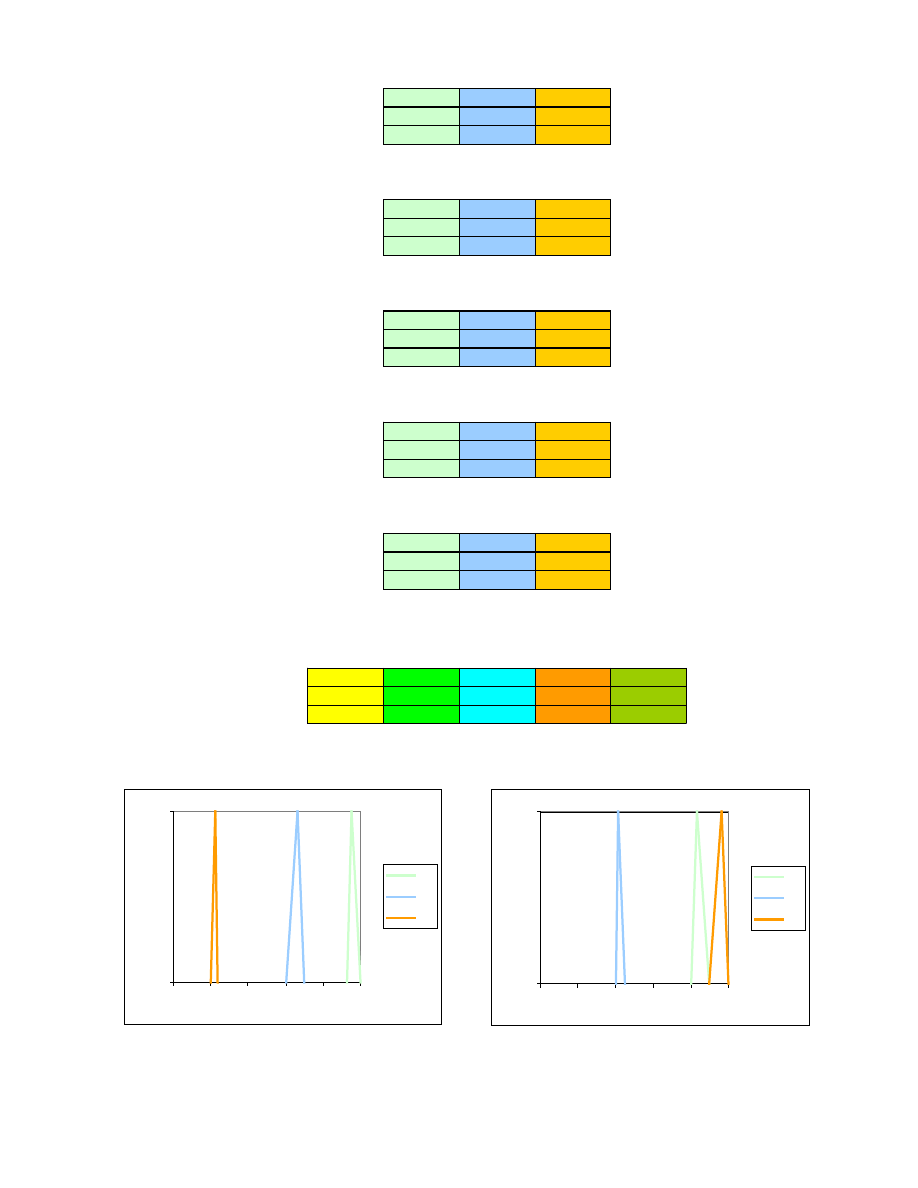
K1
A1
A2
A3
r_min
0.9282
0.6000
0.2000
r_mod
0.9521
0.6641
0.2214
r_max
1.0000
0.6961
0.2320
K2
A1
A2
A3
r_min
0.8000
0.4000
0.8944
r_mod
0.8315
0.4157
0.9648
r_max
0.8944
0.4472
1.0000
K3
A1
A2
A3
r_min
0.4000
0.8885
0.2000
r_mod
0.4887
0.9257
0.3036
r_max
0.5331
1.0000
0.3554
K4
A1
A2
A3
r_min
0.3839
0.8819
0.2000
r_mod
0.5631
0.9472
0.3762
r_max
0.7055
1.0000
0.5758
K5
A1
A2
A3
r_min
0.4549
0.4549
0.9097
r_mod
0.5457
0.5457
0.9398
r_max
0.6823
0.6823
1.0000
Rys. 20. Współrz dne charakterystyczne wykresów funkcji przynale no ci rozmytych ocen
rozwi za
K1
K2
K3
K4
K5
v_min
0.2635
0.9600
0.3222
0.1600
0.6443
v_mod
0.3556
0.9755
0.3992
0.3023
0.7449
v_max
0.4832
1.0000
0.4800
0.4832
0.8000
Rys. 21. Współrz dne charakterystyczne wykresów funkcji przynale no ci wa no ci
kryteriów
0
1
0.0
0.2
0.4
0.6
0.8
1.0
K1
A1
A2
A3
Rys. 22. Oceny rozmyte rozwi za
wzgl dem kryterium K1
0
1
0.0
0.2
0.4
0.6
0.8
1.0
K2
A1
A2
A3
Rys. 23. Oceny rozmyte rozwi za
wzgl dem kryterium K2
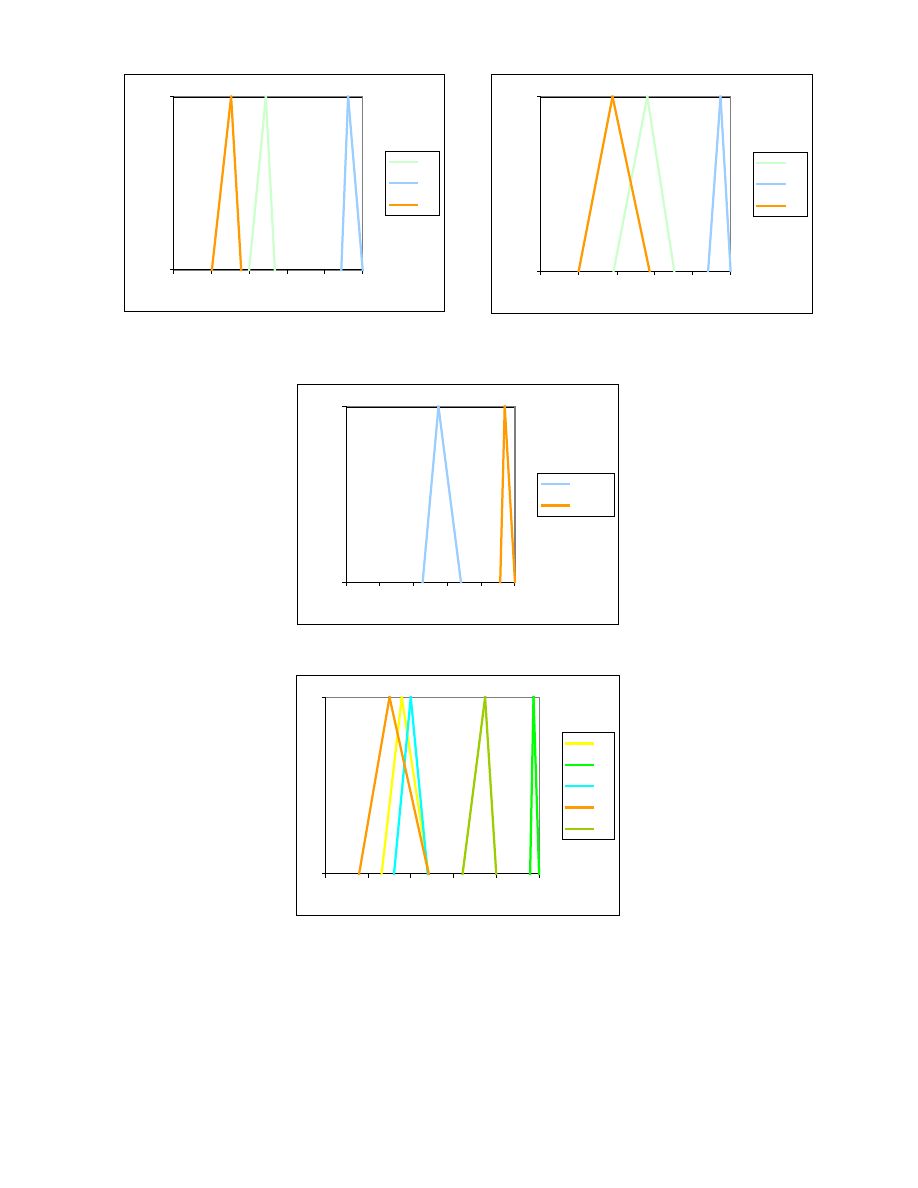
0
1
0.0
0.2
0.4
0.6
0.8
1.0
K3
A1
A2
A3
Rys. 24. Oceny rozmyte rozwi za
wzgl dem kryterium K3
0
1
0.0
0.2
0.4
0.6
0.8
1.0
K4
A1
A2
A3
Rys. 25. Oceny rozmyte rozwi za
wzgl dem kryterium K4
0
1
0.0
0.2
0.4
0.6
0.8
1.0
K5
A1=A2
A3
Rys. 26. Oceny rozmyte rozwi za wzgl dem kryterium K5
0
1
0.0
0.2
0.4
0.6
0.8
1.0
K1
K2
K3
K4
K5
Rys. 27. Oceny rozmyte wa no ci kryteriów
Po ustaleniu ł cznych wa no ci kryteriów i ocen rozwi za wyznacza si posta
funkcji przynale no ci kryteriów zast pczych poszczególnych rozwi za korzystaj c
z zale no ci (38), (42), (43) i (44). Obliczenia wykonywano dla 11
α-przekrojów
(
α = 0,0; 0,1; 0,2;....; 0,9; 1,0). Warto ci graniczne α-przekrojów wyznaczano
z zale no ci (Rys. 28):
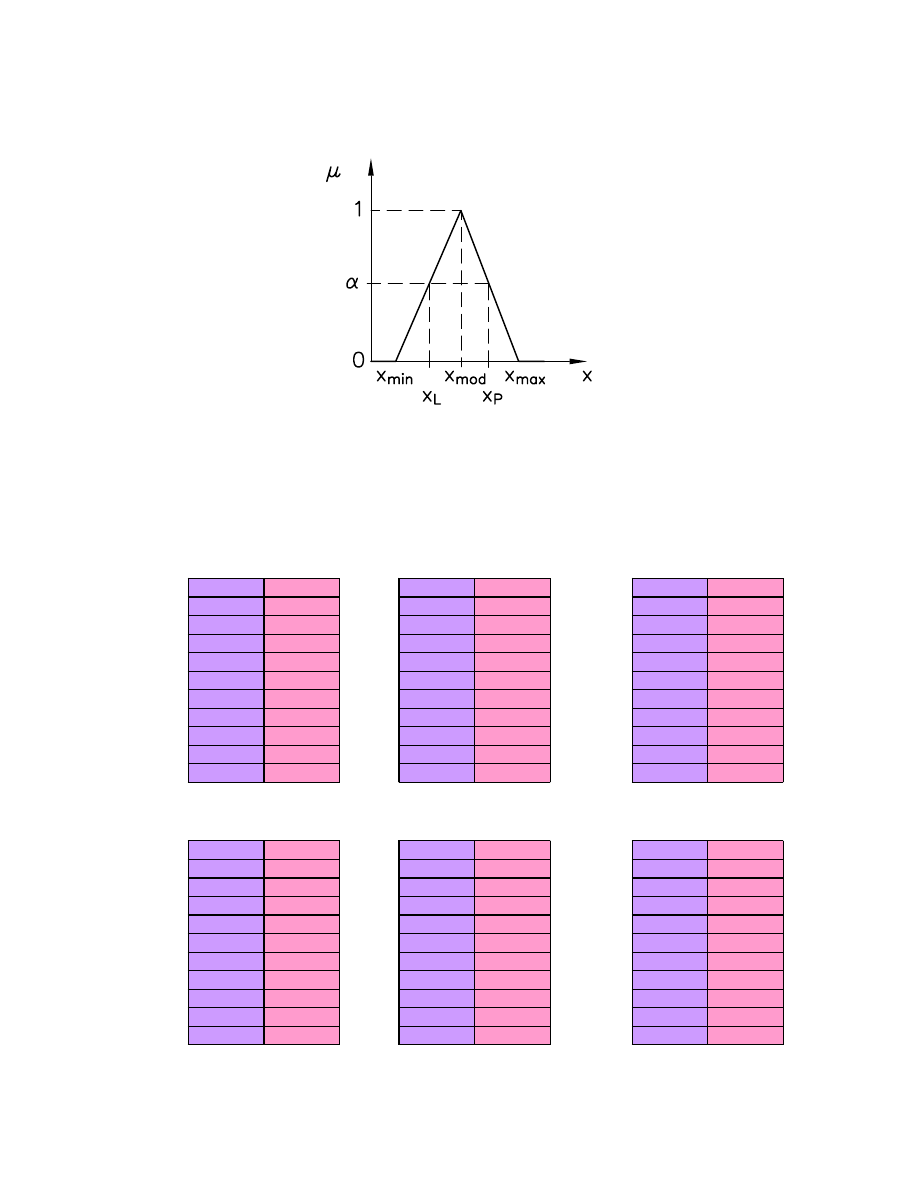
α
α
α
α
⋅
−
−
=
⋅
−
+
=
)
(
)
(
mod
max
max
min
mod
min
x
x
x
x
x
x
x
x
P
L
(50)
Rys. 28. Schemat obliczania granic
α-przekrojów
Dla zilustrowania omówionej metody oblicze na Rys. 29
÷ Rys. 33
zamieszczono arkusz wyników mno e rozmytych wa no ci kryteriów przez rozmyte
oceny rozwi zania A1 wzgl dem kolejnych kryteriów (38), ich sum oraz sum
wa no ci kryteriów (Rys. 34) – zale no (38).
K1(A1)
xL
xP
w1
xL
xP
w1*K1(A1)
xL
xP
0.0
0.9282
1.0000
0.0
0.2635
0.4832
0.0
0.2446
0.4832
0.1
0.9306
0.9952
0.1
0.2727
0.4704
0.1
0.2538
0.4682
0.2
0.9330
0.9904
0.2
0.2819
0.4577
0.2
0.2630
0.4533
0.3
0.9354
0.9856
0.3
0.2911
0.4449
0.3
0.2723
0.4385
0.4
0.9378
0.9808
0.4
0.3003
0.4322
0.4
0.2816
0.4239
0.5
0.9402
0.9761
0.5
0.3096
0.4194
0.5
0.2910
0.4094
0.6
0.9425
0.9713
0.6
0.3188
0.4066
0.6
0.3004
0.3950
0.7
0.9449
0.9665
0.7
0.3280
0.3939
0.7
0.3099
0.3807
0.8
0.9473
0.9617
0.8
0.3372
0.3811
0.8
0.3194
0.3665
0.9
0.9497
0.9569
0.9
0.3464
0.3684
0.9
0.3290
0.3525
1.0
0.9521
0.9521
1.0
0.3556
0.3556
1.0
0.3386
0.3386
Rys. 29. Mno enie rozmytej wa no ci kryterium K1 i rozmytej oceny rozwi zania A1
K2(A1)
xL
xP
w2
xL
xP
w2*K2(A1)
xL
xP
0.0
0.8000
0.8944
0.0
0.9600
1.0000
0.0
0.7680
0.8944
0.1
0.8032
0.8881
0.1
0.9616
0.9976
0.1
0.7723
0.8859
0.2
0.8063
0.8818
0.2
0.9631
0.9951
0.2
0.7765
0.8775
0.3
0.8095
0.8755
0.3
0.9647
0.9927
0.3
0.7808
0.8691
0.4
0.8126
0.8692
0.4
0.9662
0.9902
0.4
0.7851
0.8607
0.5
0.8158
0.8630
0.5
0.9678
0.9878
0.5
0.7894
0.8524
0.6
0.8189
0.8567
0.6
0.9693
0.9853
0.6
0.7938
0.8441
0.7
0.8221
0.8504
0.7
0.9709
0.9829
0.7
0.7981
0.8358
0.8
0.8252
0.8441
0.8
0.9724
0.9804
0.8
0.8024
0.8275
0.9
0.8284
0.8378
0.9
0.9740
0.9780
0.9
0.8068
0.8193
1.0
0.8315
0.8315
1.0
0.9755
0.9755
1.0
0.8111
0.8111
Rys. 30. Mno enie rozmytej wa no ci kryterium K2 i rozmytej oceny rozwi zania A1
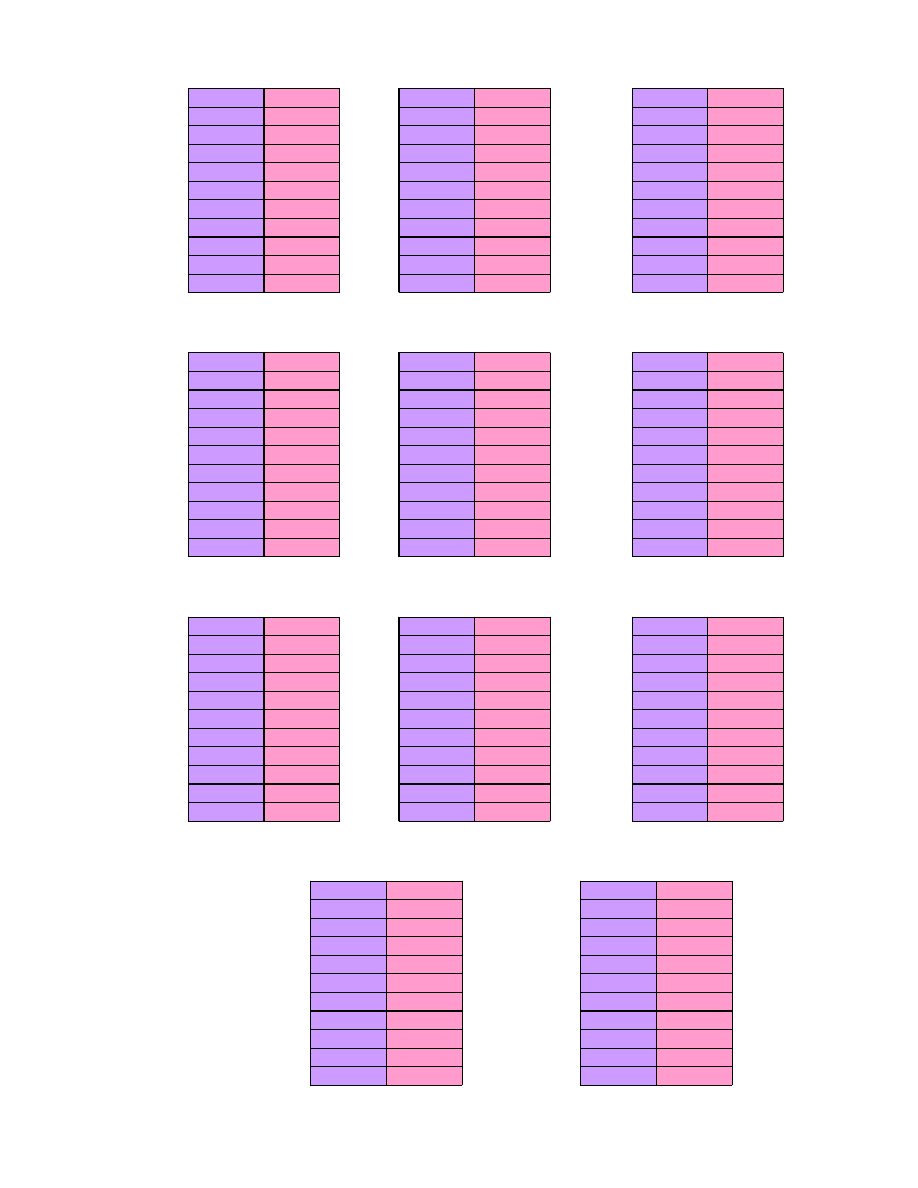
K3(A1)
xL
xP
w3
xL
xP
w3*K3(A1)
xL
xP
0.0
0.4000
0.5331
0.0
0.3222
0.4800
0.0
0.1289
0.2559
0.1
0.4089
0.5287
0.1
0.3299
0.4719
0.1
0.1349
0.2495
0.2
0.4177
0.5242
0.2
0.3376
0.4638
0.2
0.1410
0.2432
0.3
0.4266
0.5198
0.3
0.3453
0.4558
0.3
0.1473
0.2369
0.4
0.4355
0.5153
0.4
0.3530
0.4477
0.4
0.1537
0.2307
0.5
0.4444
0.5109
0.5
0.3607
0.4396
0.5
0.1603
0.2246
0.6
0.4532
0.5065
0.6
0.3684
0.4315
0.6
0.1670
0.2185
0.7
0.4621
0.5020
0.7
0.3761
0.4234
0.7
0.1738
0.2126
0.8
0.4710
0.4976
0.8
0.3838
0.4154
0.8
0.1808
0.2067
0.9
0.4798
0.4931
0.9
0.3915
0.4073
0.9
0.1879
0.2008
1.0
0.4887
0.4887
1.0
0.3992
0.3992
1.0
0.1951
0.1951
Rys. 31. Mno enie rozmytej wa no ci kryterium K3 i rozmytej oceny rozwi zania A1
K4(A1)
xL
xP
w4
xL
xP
w4*K4(A1)
xL
xP
0.0
0.3839
0.7055
0.0
0.1600
0.4832
0.0
0.0614
0.3409
0.1
0.4018
0.6913
0.1
0.1742
0.4651
0.1
0.0700
0.3215
0.2
0.4197
0.6770
0.2
0.1885
0.4470
0.2
0.0791
0.3026
0.3
0.4377
0.6628
0.3
0.2027
0.4289
0.3
0.0887
0.2843
0.4
0.4556
0.6485
0.4
0.2169
0.4108
0.4
0.0988
0.2664
0.5
0.4735
0.6343
0.5
0.2312
0.3928
0.5
0.1094
0.2491
0.6
0.4914
0.6201
0.6
0.2454
0.3747
0.6
0.1206
0.2323
0.7
0.5093
0.6058
0.7
0.2596
0.3566
0.7
0.1322
0.2160
0.8
0.5273
0.5916
0.8
0.2738
0.3385
0.8
0.1444
0.2002
0.9
0.5452
0.5773
0.9
0.2881
0.3204
0.9
0.1571
0.1850
1.0
0.5631
0.5631
1.0
0.3023
0.3023
1.0
0.1702
0.1702
Rys. 32. Mno enie rozmytej wa no ci kryterium K4 i rozmytej oceny rozwi zania A1
K5(A1)
xL
xP
w5
xL
xP
w5*K5(A1)
xL
xP
0.0
0.4549
0.6823
0.0
0.6443
0.8000
0.0
0.2931
0.5458
0.1
0.4640
0.6686
0.1
0.6544
0.7945
0.1
0.3036
0.5312
0.2
0.4731
0.6550
0.2
0.6644
0.7890
0.2
0.3143
0.5168
0.3
0.4821
0.6413
0.3
0.6745
0.7835
0.3
0.3252
0.5025
0.4
0.4912
0.6277
0.4
0.6845
0.7780
0.4
0.3363
0.4883
0.5
0.5003
0.6140
0.5
0.6946
0.7725
0.5
0.3475
0.4743
0.6
0.5094
0.6003
0.6
0.7047
0.7669
0.6
0.3589
0.4604
0.7
0.5185
0.5867
0.7
0.7147
0.7614
0.7
0.3706
0.4467
0.8
0.5275
0.5730
0.8
0.7248
0.7559
0.8
0.3824
0.4332
0.9
0.5366
0.5594
0.9
0.7348
0.7504
0.9
0.3943
0.4197
1.0
0.5457
0.5457
1.0
0.7449
0.7449
1.0
0.4065
0.4065
Rys. 33. Mno enie rozmytej wa no ci kryterium K5 i rozmytej oceny rozwi zania A1
Suma(wi*Ki(A1))
xL
xP
Suma(wi)
xL
xP
0.0
1.4960
2.5202
0.0
2.3500
3.2464
0.1
1.5346
2.4563
0.1
2.3928
3.1995
0.2
1.5740
2.3934
0.2
2.4355
3.1526
0.3
1.6144
2.3313
0.3
2.4783
3.1057
0.4
1.6556
2.2700
0.4
2.5210
3.0588
0.5
1.6977
2.2097
0.5
2.5638
3.0120
0.6
1.7407
2.1503
0.6
2.6065
2.9651
0.7
1.7846
2.0918
0.7
2.6493
2.9182
0.8
1.8293
2.0341
0.8
2.6920
2.8713
0.9
1.8750
1.9774
0.9
2.7348
2.8244
1.0
1.9215
1.9215
1.0
2.7775
2.7775
Rys. 34. Sumy rozmyte ocen rozwi za oraz wa no ci kryteriów
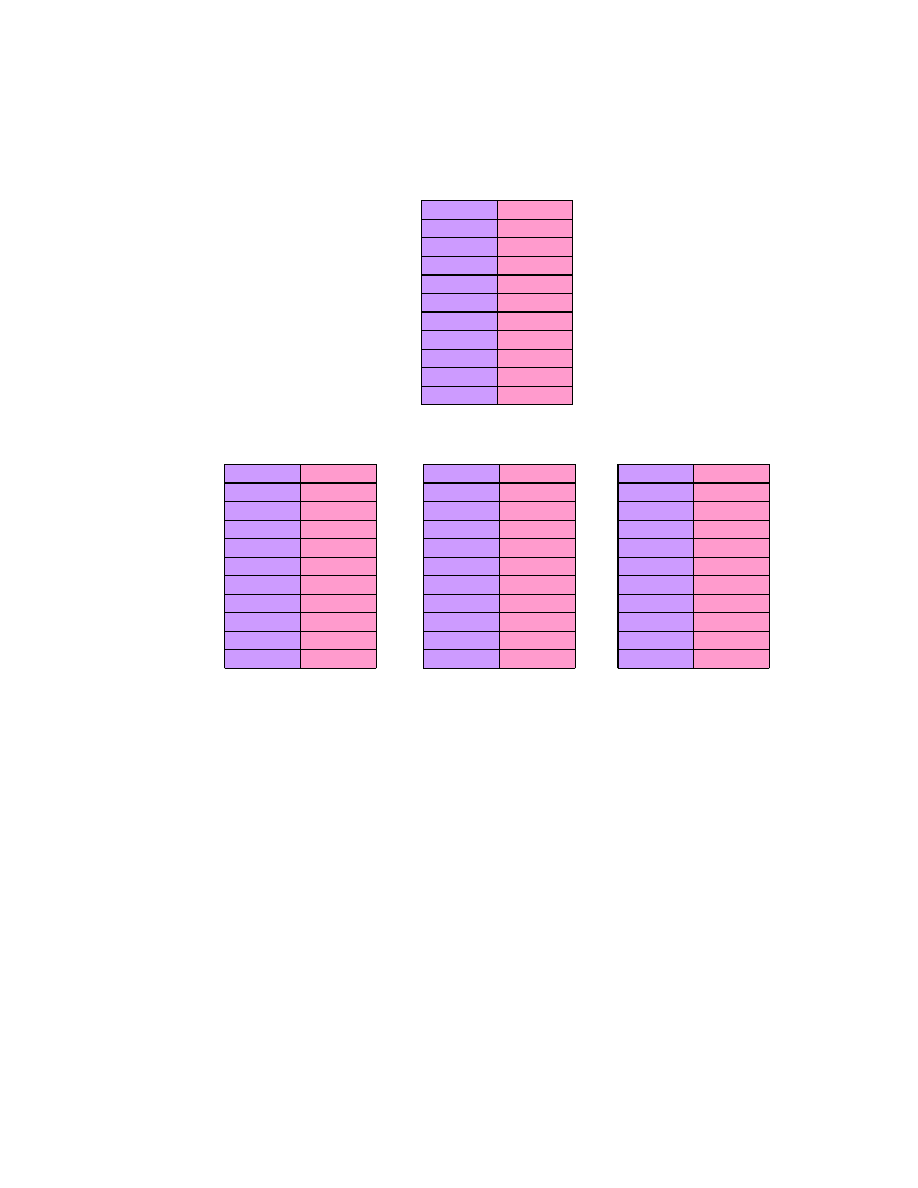
Ostatecznie, na Rys. 35 zamieszczono obliczenia oceny kryterium zast pczego
dla rozwi zania A1, za na Rys. 36 unormowane postacie funkcji przynale no ci ocen
kryterium zast pczego dla wszystkich analizowanych rozwi za . Na ich podstawie
sporz dzono wykresy funkcji przynale no ci – Rys. 37.
Z(A1)
xL
xP
0.0
0.4608
1.0724
0.1
0.4796
1.0266
0.2
0.4993
0.9827
0.3
0.5198
0.9407
0.4
0.5412
0.9005
0.5
0.5637
0.8619
0.6
0.5871
0.8250
0.7
0.6115
0.7896
0.8
0.6371
0.7556
0.9
0.6639
0.7231
1.0
0.6918
0.6918
Rys. 35.
α-przekroje funkcji przynale no ci ocen kryterium zast pczego dla rozwi zania A1
α
Z(A1)
Z(A2)
Z(A3)
0.0
0.4296
1.0000
0.3626
0.9097
0.4578
0.9368
0.1
0.4472
0.9572
0.3801
0.8695
0.4740
0.9026
0.2
0.4655
0.9163
0.3982
0.8310
0.4909
0.8700
0.3
0.4847
0.8771
0.4171
0.7940
0.5086
0.8388
0.4
0.5047
0.8396
0.4367
0.7584
0.5270
0.8091
0.5
0.5256
0.8037
0.4571
0.7243
0.5463
0.7807
0.6
0.5474
0.7692
0.4783
0.6914
0.5664
0.7535
0.7
0.5702
0.7362
0.5003
0.6598
0.5874
0.7275
0.8
0.5941
0.7046
0.5233
0.6295
0.6094
0.7027
0.9
0.6190
0.6742
0.5472
0.6002
0.6323
0.6790
1.0
0.6451
0.6451
0.5721
0.5721
0.6563
0.6563
Rys. 36.
α-przekroje funkcji przynale no ci ocen kryterium zast pczego dla wszystkich
rozwi za
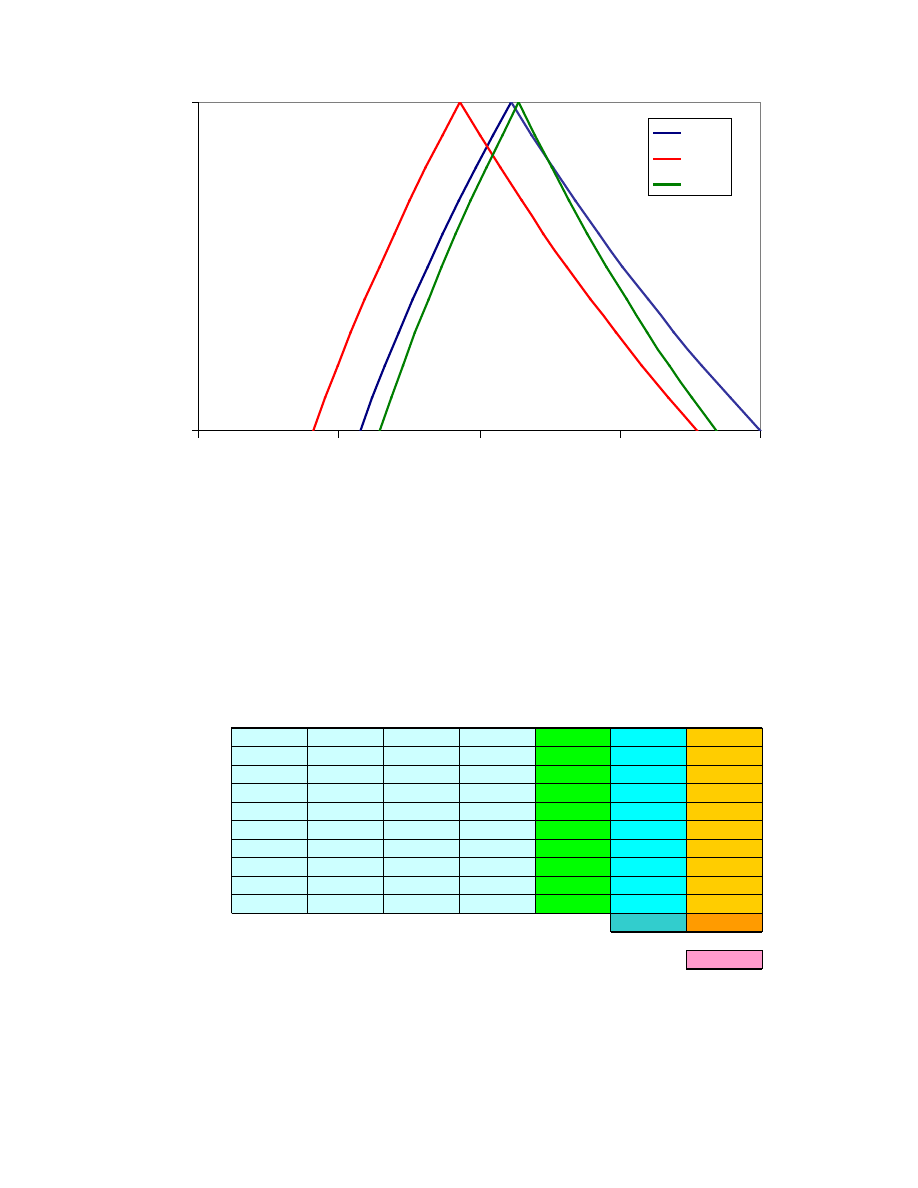
0.0
1.0
0.2
0.4
0.6
0.8
1.0
µ
Z(A1)
Z(A2)
Z(A3)
Rys. 37. Wykresy funkcji przynale no ci ocen rozwi za wzgl dem kryterium zast pczego
Ostatnim krokiem jest defuzyfikacja (wyostrzenie) rozmytych ocen kryterium
zast pczego metod wyznaczania poło enia rodka ci ko ci pól pod wykresami
funkcji przynale no ci – zale no ci (45) i (46). Na Rys. 38 zamieszczono przebieg
oblicze dla rozwi zania A1, natomiast w Tabl. 2 zestawiono deterministyczne
warto ci ocen kryterium zast pczego dla wszystkich rozwa anych rozwi za oraz ich
warto ci unormowane.
Z(A1)
α
P
Q
R
S
xCi
FCi
xCi*FCi
0.1 -0.0804
1.5276
0.7148
0.7022
0.7086
0.0540
0.0383
0.2 -0.0036
1.4264
0.7022
0.6909
0.6967
0.0480
0.0335
0.3
0.0730
1.3280
0.6909
0.6809
0.6860
0.0422
0.0289
0.4
0.1497
1.2321
0.6809
0.6721
0.6766
0.0364
0.0246
0.5
0.2265
1.1387
0.6721
0.6646
0.6685
0.0307
0.0205
0.6
0.3037
1.0474
0.6646
0.6583
0.6616
0.0250
0.0165
0.7
0.3814
0.9581
0.6583
0.6532
0.6559
0.0194
0.0127
0.8
0.4597
0.8706
0.6532
0.6493
0.6514
0.0138
0.0090
0.9
0.5389
0.7847
0.6493
0.6466
0.6481
0.0083
0.0054
1.0
0.6190
0.7003
0.6466
0.6451
0.6461
0.0028
0.0018
Suma=
0.2805
0.1912
xC=
0.6816
Rys. 38. Obliczenia poło enia rodka ci ko ci pola pod wykresem funkcji przynale no ci
oceny kryterium zast pczego dla rozwi zania A1
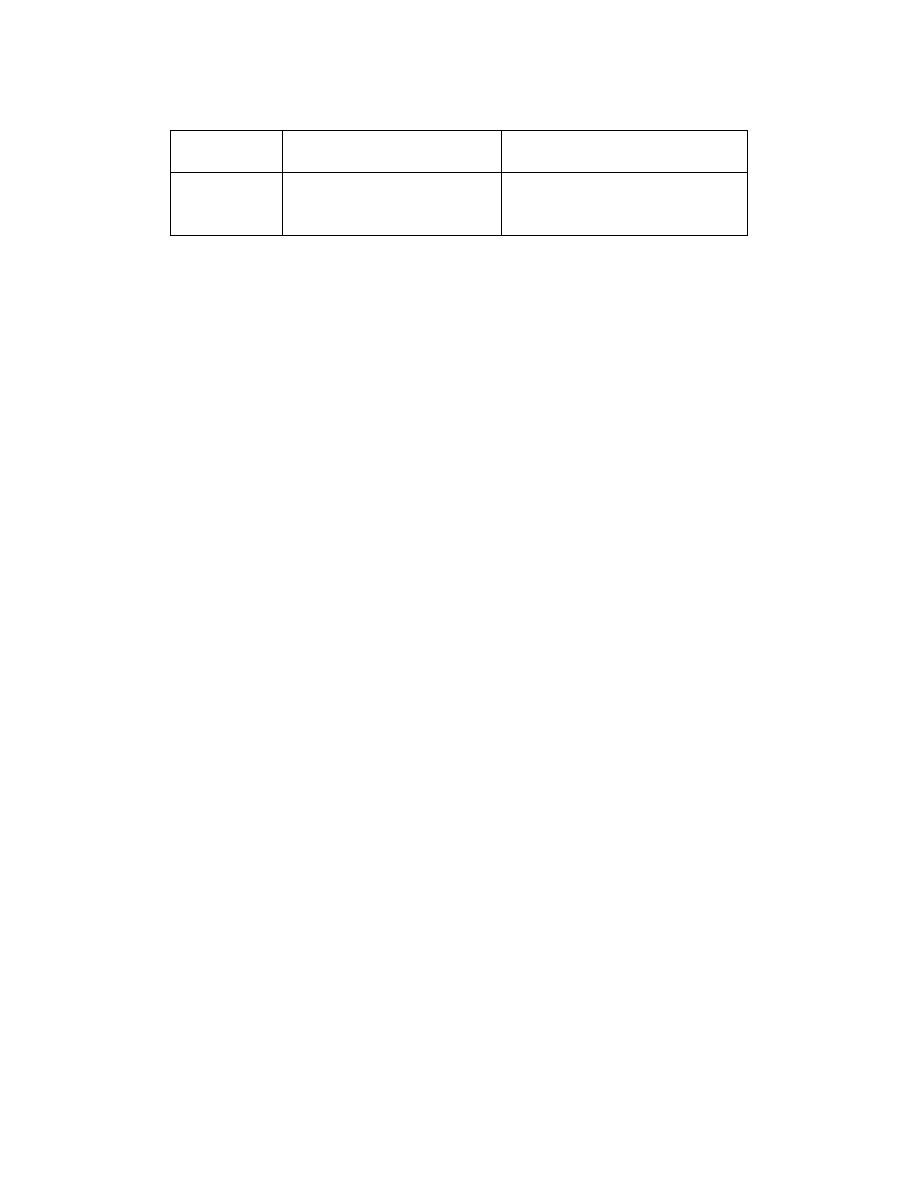
Tabl. 2. Warto ci ocen kryterium zast pczego dla analizowanych rozwi za dopuszczalnych
Rozwi zanie Ocena wzgl dem kryterium
Zast pczego
Unormowana ocena wzgl dem
kryterium zast pczego
A1
A2
A3
0.6816
0.6060
0.6749
1.125
1.000
1.114
Na podstawie zarówno postaci wykresów funkcji przynale no ci, jak i warto ci
ocen kryterium zast pczego mo na stwierdzi , e najgorszym jest rozwi zanie A2
(Peugot 206). Rozwi zania A1 (Fiat Punto) i A3 (Volkswagen Polo) s do siebie
bardzo zbli one, cho niewielk przewag posiada A1. To rozwi zanie nale y uzna
za optymalne w wietle przeprowadzonego post powania polioptymalizacyjnego.
4. Polioptymalizacja z wykorzystaniem ocen rozmytych – metoda Yagera
W metodzie Yagera [5], [13] wybór rozwi zania optymalnego traktowany jest
jako decyzja rozmyta D, której składnikami s rozpatrywane rozwi zania ze zbioru
A
(15), a ci lej ich przynale no ci do decyzji optymalnej:
N
N
A
D
A
D
A
D
D
/
....
/
/
2
2
1
1
+
+
+
=
(51)
Składnik o najwi kszej warto ci funkcji przynale no ci do decyzji optymalnej jest
traktowany jako rozwi zanie optymalne w zagadnieniu polioptymalizacji – por.
metoda Jaina [5]. Z uwagi na wielokryterialn ocen rozwi za funkcja
przynale no ci do decyzji optymalnej dla danego rozwi zania musi by zale na od
ocen wzgl dem wszystkich kryteriów. Wyznacza si j w kategoriach rozmytych,
agreguj c funkcje przynale no ci rozwi zania do decyzji optymalnej, rozpatrywanych
osobno wzgl dem poszczególnych kryteriów. Stosuje si nast puj ce sposoby
agregowania [5]:
1.
Iloczyn logiczny funkcji przynale no ci (decyzja typu minimum):
N
k
A
A
A
A
k
K
k
K
k
K
k
D
M
k
,...,
2
,
1
);
(
...
)
(
)
(
)
(
2
1
=
∧
∧
∧
=
µ
µ
µ
µ
(52)
co praktycznie sprowadza si do:
))
(
(
min
)
(
,..,
1
k
K
M
i
k
D
A
A
i
k
µ
µ
=
=
(53)
2.
Iloczyn algebraiczny funkcji przynale no ci:
)
(
...
)
(
)
(
)
(
2
1
k
K
k
K
k
K
k
D
A
A
A
A
M
k
µ
µ
µ
µ
⋅
⋅
⋅
=
(54)
3.
Suma logiczna funkcji przynale no ci (decyzja typu maksimum):
)
(
...
)
(
)
(
)
(
2
1
k
K
k
K
k
K
k
D
A
A
A
A
M
k
µ
µ
µ
µ
∨
∨
∨
=
(55)
co praktycznie sprowadza si do:
))
(
(
max
)
(
,..,
1
k
K
M
i
k
D
A
A
i
k
µ
µ
=
=
(56)

Ponadto uwzgl dnia si wa no poszczególnych kryteriów, wprowadzaj c
współczynniki wagowe w
i
, co w konsekwencji prowadzi do nast puj cych postaci
funkcji agreguj cych oceny rozwi za (52), (54), (55):
(
) (
)
(
)
(
) (
)
(
)
(
) (
)
(
)
M
M
k
M
M
k
M
M
k
w
k
K
w
k
K
w
k
K
k
D
w
k
K
w
k
K
w
k
K
k
D
w
k
K
w
k
K
w
k
K
k
D
A
A
A
A
A
A
A
A
A
A
A
A
)
(
...
)
(
)
(
)
(
)
(
...
)
(
)
(
)
(
)
(
...
)
(
)
(
)
(
2
2
1
1
2
2
1
1
2
2
1
1
µ
µ
µ
µ
µ
µ
µ
µ
µ
µ
µ
µ
∨
∨
∨
=
⋅
⋅
⋅
=
∧
∧
∧
=
(57)
Wa no ci kryteriów w
i
wyznacza si podobnie jak w post powaniu Baasa
i Kwakernaaka, korzystaj c z metody Saaty’ego. Ka dy z P ekspertów buduje macierz
porówna kryteriów parami
U
Vj
, j = 1, 2, ..., P (22). Na ich podstawie tworzy si
ł czn macierz Saaty’ego wa no ci kryteriów jako redni z macierzy ekspertów wg
zale no ci:
=
⋅
=
=
=
P
j
Vstj
st
st
U
P
B
M
t
s
B
1
1
,..,
2
,
1
,
];
[
B
(58)
Wa no ci w
i
kryteriów s wyznaczane na podstawie współrz dnych wektora
własnego
]
[
i
Y
=
Y
macierzy B, odpowiadaj cej najwi kszej warto ci własnej,
korzystaj c z zale no ci:
M
i
Y
Y
w
M
i
i
i
i
,...,
2
,
1
;
1
=
=
=
(59)
W drugim kroku eksperci oceniaj ka dy z wariantów wzgl dem ka dego
kryterium. Stosowane s dwie metody oceny:
Punktowa [1]– przyjmuj c skal punktow 0; L przy czym im wy sza warto
liczbowa tym wy sza ocena eksperta danego wariantu. Zakres skali ocen L nie jest
ci le sprecyzowany, wynika z subiektywnej oceny rozpi to ci jako ci ocenianych
wariantów (zaleca si jako warto maksymaln przyj 10). Oceny punktowe
ekspertów s zebrane w tablicy
S = [S
kij
], gdzie S
kij
oznacza ocen punktow k-tego
rozwi zania wzgl dem i-tego kryterium dla j-tego eksperta. Oceny te poddaje si
unormowaniu wg zale no ci:
L
S
S
S
kij
kij
kij
=
=
ˆ
]
ˆ
[
ˆS
(60)
Bazowa [10] – jedno z rozwi za przyjmuje si za rozwi zanie bazowe
(odniesienia), wzgl dem którego oceniane s pozostałe. Oceny rozwi za maj
charakter rozmyty, przy czym wyra aj one stopie przynale no ci g
kijl
ocenianego
k-tego rozwi zania do pewnej klasy l rozwi za lepszych b d gorszych od
rozwi zania bazowego:

L
L
l
P
j
M
i
N
k
g
g
g
L
L
l
kijl
kijl
kijl
,...,
0
,...,
;
,...,
2
,
1
;
,...,
2
,
1
;
,..,
2
,
1
1
)
1
;
0
(
];
[
−
=
=
=
=
=
∈
=
−
=
G
(61)
Liczba wszystkich klas (2L+1) przyjmowana jest w granicach 3
÷7. Przynale no
do klas ujemnych oznacza, e rozwi zanie oceniono jako gorsze od bazowego,
dodatnich za – jako lepsze. Przynale no do klasy 0 oznacza równowa no
z rozwi zaniem bazowym. Z ka d klas wi e si pewn procentow warto ,
wyra aj c o ile rozwi zanie przynale ce do tej klasy jest lepsze b d gorsze od
bazowego. Przyjmuje si stały przyrost tej warto ci dla kolejnych klas.
Na podstawie ocen rozmytych
G wyznacza si unormowane oceny rozwi za ,
korzystaj c z zale no ci:
(
)
L
l
g
L
S
S
L
L
l
kijl
kij
kij
2
ˆ
]
ˆ
[
ˆ
−
=
⋅
+
=
=
S
(62)
Z unormowanych ocen ekspertów wyznacza si ł czn ocen rozwi za przez
ich u rednienie (zało enie o równej wa no ci ekspertów):
M
i
N
k
S
P
C
C
P
j
kij
ki
ki
,...,
2
,
1
;
,...,
2
,
1
;
ˆ
1
]
[
1
=
=
⋅
=
=
=
C
(63)
Unormowane, deterministyczne oceny punktowe rozwi za C
ki
uto samia si
warto ciami rozmytymi funkcji przynale no ci rozwi za do decyzji optymalnej
z uwagi na poszczególne kryteria, czyli:
ki
k
i
C
A
=
)
(
µ
(64)
Dalsze post powanie jest prowadzone wg zale no ci (57), co ostatecznie
prowadzi do wyboru rozwi zania optymalnego:
MAX
)
(
→
k
D
A
k
µ
(65)
5. Polioptymalizacja z wykorzystaniem metody Yagera – przykład
Ocenie poddano k = 5 rozwi za :
A = {A
1
, A
2
, A
3
, A
4
, A
5
} wzgl dem M = 3
kryteriów:
K(A) = {K
1
, K
2
, K
3
}. Oceny dokonał P = 1 ekspert.
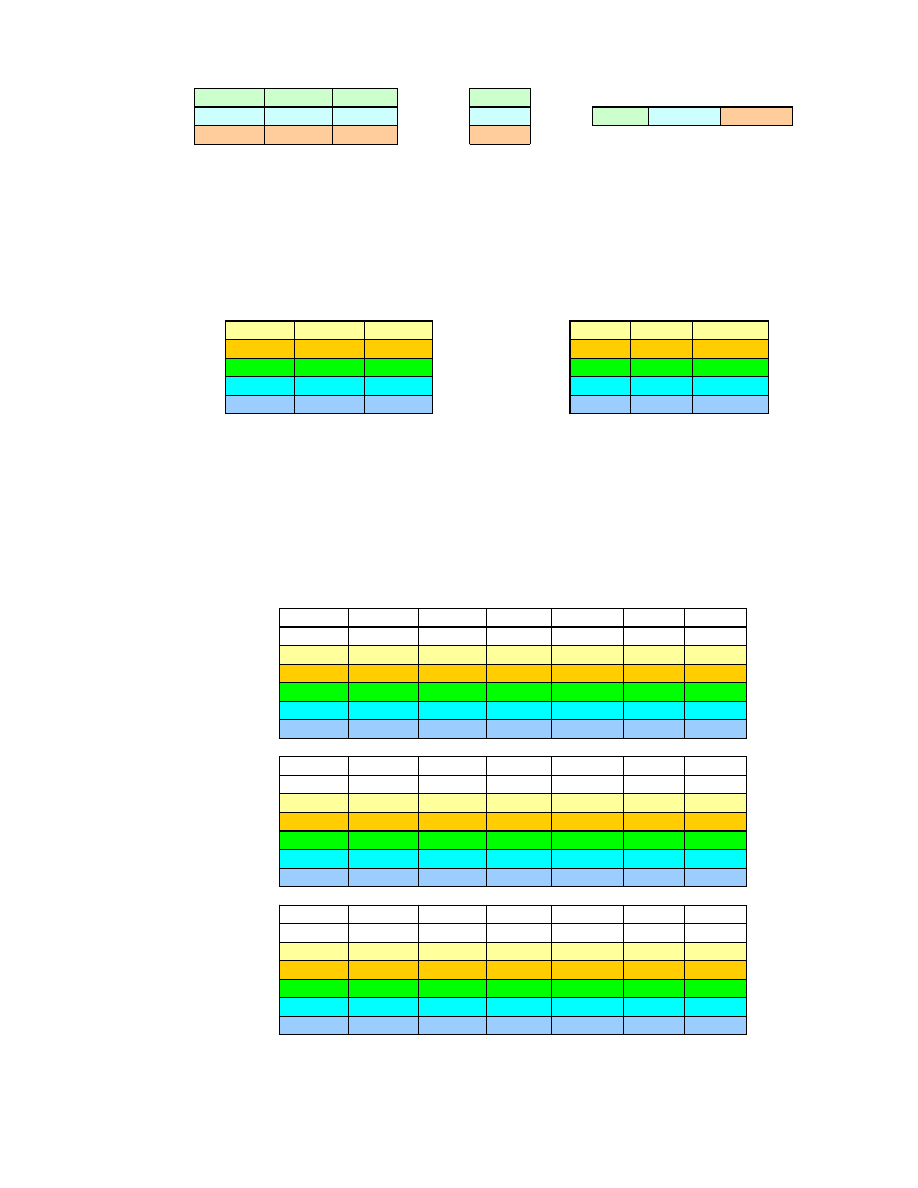
W pierwszym etapie dokonano oceny wa no ci kryteriów (macierz
B (57)),
obliczenia wektora własnego
Y dla najwi kszej warto ci własnej oraz warto ci
współczynników wagowych w
i
(57) – Rys. 39.
K1
K2
K3
Y
1.0000
1.5000
5.0000
K1
0.821
K1
K2
K3
B =
0.6667
1.0000
3.3333
K2
0.547
0.5359 0.3570
0.1070
0.2000
0.3000
1.0000
K3
0.164
i
w
Rys. 39. Dane i obliczenia wa no ci kryteriów
W drugim etapie wyznaczono:
1.
Oceny punktowe
S rozwi za wzgl dem poszczególnych kryteriów przy
rozpi to ci skali L = 7. Warto ci ocen oraz ich warto ci unormowane
Sˆ (60)
przedstawiono na Rys. 40. Dla jednego eksperta
S
C ˆ
= (61).
K1
K2
K3
K1
K2
K3
A1
2
1
1
A1
0.2857 0.1429
0.1429
A2
2
1
2
A2
0.2857 0.1429
0.2857
A3
1
7
7
A3
0.1429 1.0000
1.0000
A4
2
1
7
A4
0.2857 0.1429
1.0000
A5
1
1
7
A5
0.1429 0.1429
1.0000
ki
S
ki
ki
C
S
=
ˆ
Rys. 40. Oceny punktowe rozwi za wzgl dem poszczególnych kryteriów i ich warto ci
unormowane oraz oceny ł czne (wersja punktowa)
2.
Warto ci rozmyte
G ocen przy przyj ciu liczby klas (2L+1) równej 7 i warto ci
przyrostu procentowego oceny jako ci rozwi za równego 15%. Zostały one
przedstawione na Rys. 41. Na ich podstawie obliczono warto ci ocen
unormowanych
Sˆ (62) oraz ł cznych C (63), gdzie dla jednego eksperta
S
C ˆ
= –
Rys. 42.
Klasy
-3
-2
-1
0
1
2
3
45%
30%
15%
15%
30%
45%
A1
0.00
0.00
0.00
1.00
0.00
0.00
0.00
A2
0.00
0.00
0.10
0.90
0.00
0.00
0.00
A3
0.00
0.40
0.60
0.00
0.00
0.00
0.00
A4
0.00
0.00
0.20
0.80
0.00
0.00
0.00
A5
0.00
0.50
0.50
0.00
0.00
0.00
0.00
-3
-2
-1
0
1
2
3
45%
30%
15%
15%
30%
45%
A1
0.00
0.00
0.00
1.00
0.00
0.00
0.00
A2
0.00
0.00
0.00
0.90
0.10
0.00
0.00
A3
0.00
0.00
0.00
0.00
0.00
0.10
0.90
A4
0.00
0.00
0.20
0.80
0.00
0.00
0.00
A5
0.00
0.00
0.10
0.90
0.00
0.00
0.00
-3
-2
-1
0
1
2
3
45%
30%
15%
15%
30%
45%
A1
0.00
0.00
0.00
1.00
0.00
0.00
0.00
A2
0.00
0.00
0.00
0.30
0.70
0.00
0.00
A3
0.00
0.00
0.00
0.00
0.00
0.05
0.95
A4
0.00
0.00
0.00
0.00
0.00
0.10
0.90
A5
0.00
0.00
0.00
0.00
0.00
0.20
0.80
1
k
G
2
k
G
3
k
G
Rys. 41. Warto ci ocen rozmytych rozwi za wzgl dem poszczególnych kryteriów (wersja
bazowa)
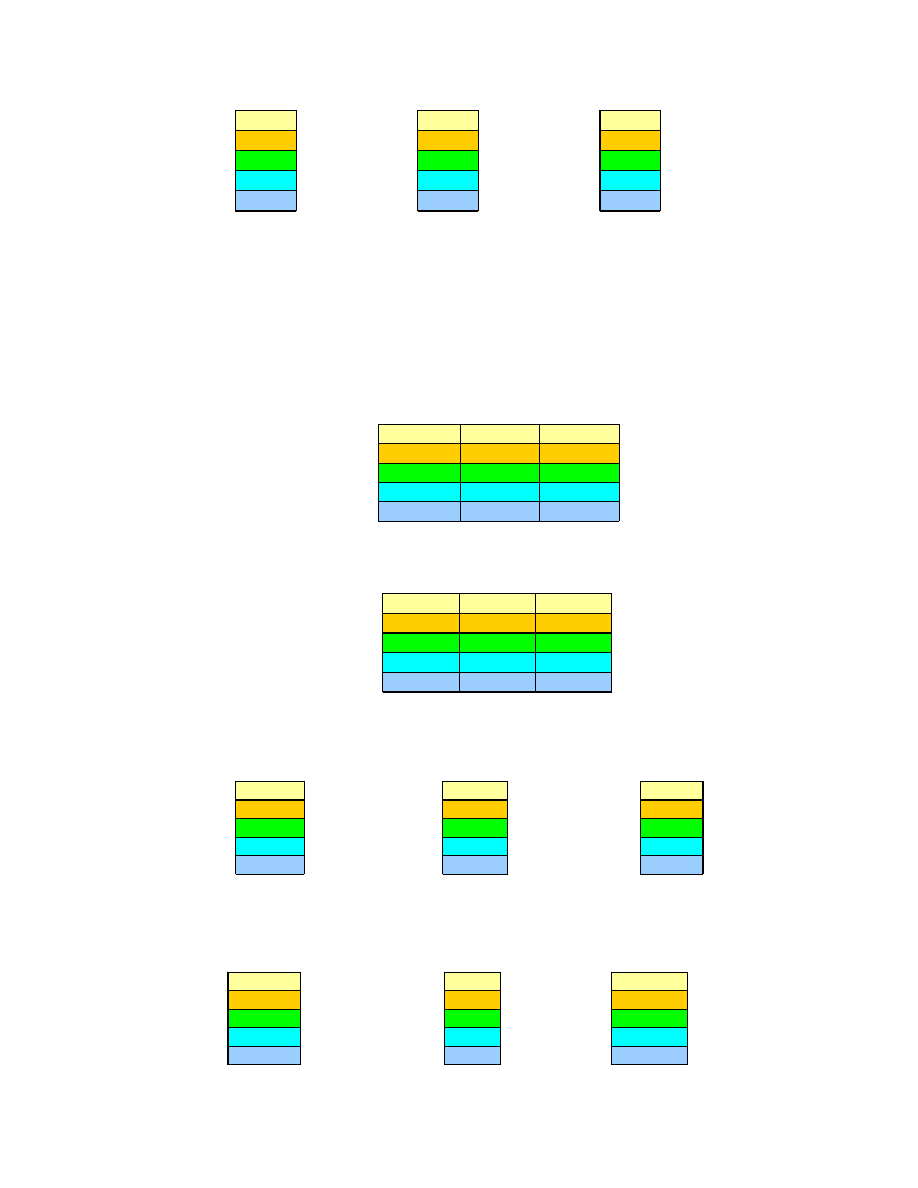
A1
0.5000
A1
0.5000
A1
0.5000
A2
0.4833
A2
0.5167
A2
0.6167
A3
0.2667
A3
0.9833
A3
0.9917
A4
0.4667
A4
0.4667
A4
0.9833
A5
0.2500
A5
0.4833
A5
0.9667
1
1
ˆ
k
k
C
S
=
2
2
ˆ
k
k
C
S
=
3
3
ˆ
k
k
C
S
=
Rys. 42. Oceny unormowane oraz ł czne rozwi za (wersja bazowa)
W trzecim etapie post powania na podstawie ł cznych ocen unormowanych
korzystaj c z zale no ci (57) wyznaczono warto ci funkcji przynale no ci rozwi za
do decyzji optymalnej korzystaj c z wszystkich trzech opisanych sposobów
agregowania – Rys. 45 i Rys. 46, przy czym na Rys. 43 i Rys. 44 przedstawiono
warto ci funkcji przynale no ci rozwi za do decyzji optymalnej z uwagi na
poszczególne kryteria, podniesione do pot gi równej wa no ci w
i
kryterium.
K1
K2
K3
A1
0.5110
0.4992
0.8120
A2
0.5110
0.4992
0.8745
A3
0.3525
1.0000
1.0000
A4
0.5110
0.4992
1.0000
A5
0.3525
0.4992
1.0000
(
)
i
w
k
Ki
A )
(
µ
Rys. 43. Warto ci funkcji przynale no ci
(
)
i
w
k
Ki
A )
(
µ
(wersja punktowa)
K1
K2
K3
A1
0.6897
0.7808
0.9285
A2
0.6773
0.7900
0.9496
A3
0.4925
0.9940
0.9991
A4
0.6647
0.7618
0.9982
A5
0.4757
0.7714
0.9964
(
)
i
w
k
Ki
A )
(
µ
Rys. 44. Warto ci funkcji przynale no ci
(
)
i
w
k
Ki
A )
(
µ
(wersja bazowa)
Minimum
Iloczyn
Maksimum
A1
0.4992 MAX
A1
0.2071
A1
0.8120
A2
0.4992 MAX
A2
0.2231
A2
0.8745
A3
0.3525
A3
0.3525 MAX
A3
1.0000 MAX
A4
0.4992 MAX
A4
0.2551
A4
1.0000 MAX
A5
0.3525
A5
0.1759
A5
1.0000 MAX
Dk
µ
Dk
µ
Dk
µ
Rys. 45. Warto ci funkcji przynale no ci rozwi za do decyzji optymalnej wg trzech metod
agregowania ocen (wersja punktowa)
Minimum
Iloczyn
Maksimum
A1
0.6897 MAX
A1
0.5000
A1
0.9285
A2
0.6773
A2
0.5081
A2
0.9496
A3
0.4925
A3
0.4891
A3
0.9991 MAX
A4
0.6647
A4
0.5054 MAX
A4
0.9982
A5
0.4757
A5
0.3656
A5
0.9964
Dk
µ
Dk
µ
Dk
µ
Rys. 46. Warto ci funkcji przynale no ci rozwi za do decyzji optymalnej wg trzech metod
agregowania ocen (wersja bazowa)

Jak wynika z przedstawionych rozwi za w zale no ci od przyj tej metody
agregowania ocen rozmytych otrzymano ró ne rozwi zania rozwi zana optymalnego.
Najbardziej wiarygodn wydaje si by metoda iloczynu, uwzgl dniaj ca oceny
wzgl dem wszystkich kryteriów.
6. Optymalizacja wielokryterialna z wykorzystaniem ocen rozmytych –
metoda zmodyfikowana
Przedstawione w poprzednich rozdziałach post powania polioptymalizacyjne
Baasa i Kwakernaaka oraz Yagera cechuj si nast puj cymi wadami:
1.
Ocena rozmyta jest wynikiem rozbie no ci w ocenach deterministycznych wielu
ekspertów. Je eli ich oceny b d zgodne to nie b d one miały charakteru
rozmytego.
2.
Eksperci dokonuj oceny wg niejasnej, przyj tej w metodzie Saaty’ego skali ocen
wzgl dnych, nie oddaj cych w pełni rzeczywistych proporcji pomi dzy
ocenianymi rozwi zaniami.
3.
Oceny ekspertów maj w rzeczywisto ci charakter deterministyczny, nie
pozwalaj c im na wyra enie swoich w tpliwo ci i subiektywnych odczu
w stosunku do wyra anych ocen.
4.
Ocena rozwi za dopuszczalnych przez eksperta jest dokonywana na ogół przy
przyj ciu przez niego pewnych subiektywnych wa no ci kryteriów, wzgl dem
których ta ocena jest dokonywana. W opisanym post powaniu wa no kryteriów
jest w pewien sposób u redniana, co mo e prowadzi do zafałszowania
rzeczywistych preferencji eksperta.
Aby te wady wyeliminowa , przyj to nast puj ce zało enia do modyfikacji
przedstawionego post powania:
1.
Oceny ekspertów powinny mie charakter rozmyty.
2.
Na podstawie ocen rozwi za i wa no ci kryteriów podanych przez
poszczególnych ekspertów wyznaczana jest rozmyta posta oceny kryterium
zast pczego. W dalszym post powaniu oceny ekspertów s agregowane w ł czn
posta oceny kryterium zast pczego z mo liwo ci uwzgl dnienia wa no ci
ekspertów.
3.
Sposób oceny rozwi za i wa no ci kryteriów powinien w bardziej naturalny
sposób oddawa rzeczywisty przebieg oceny wielokryterialnej, stosowanej
w praktyce nie tylko przemysłowej.
Wobec
przyj tych
zało e
sformułowano
nast puj c
procedur
polioptymalizacji. W post powaniu bierze udział P ekspertów, oceniaj cych N
rozwi za dopuszczalnych ze zbioru
A (15) wzgl dem M kryteriów (16). Poszukiwane
jest rozwi zanie, osi gaj ce maksimum oceny kryterium zast pczego, b d cego
wa on sum ocen rozwi za wzgl dem przyj tych M kryteriów (14). Zarówno oceny
rozwi za jak i wa no ci kryteriów maj charakter rozmyty. Przyj to tu nast puj ce
rozwi zanie:
1.
Ocena wa no ci
ij
w~ i-tego kryterium przez j-tego eksperta jest modelowana za
pomoc liczby rozmytej o trójk tnej funkcji przynale no ci (Rys. 47):
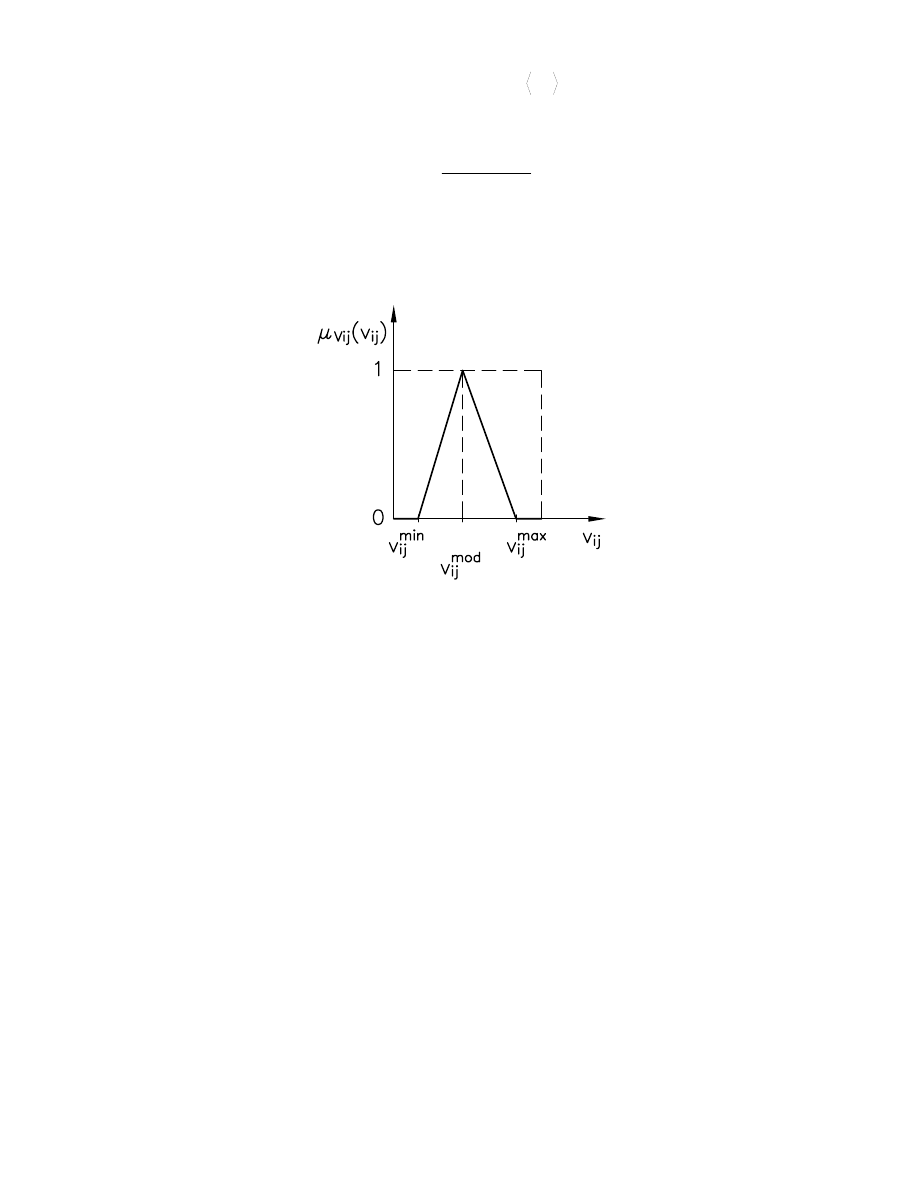
1
;
0
);
(
~
∈
=
ij
ij
Vij
ij
v
v
w
µ
(66)
przy czym:
2
max
min
mod
ij
ij
ij
v
v
v
+
=
(67)
Ekspert dokonuj c oceny wa no ci kryterium traktuje j jako „około
mod
ij
v
”, przy
czym swoj niepewno co do precyzji tego okre lenia wyra a w postaci wielko ci
przedziału (
max
min
,
ij
ij
v
v
).(66)
Rys. 47. Ocena rozmyta wa no ci i-tego kryterium przez j-tego eksperta
Z uwagi na powszechnie stosowane zało enie (4) dla j-tego eksperta musi by
prawdziwy warunek:
=
=
M
i
ij
w
1
1
~
(68)
W
najprostszym
podej ciu
mo na
wykorzysta
zale no
(21),
przyporz dkowuj c liczbie rozmytej liczb rzeczywist , okre laj c poło enie
rodka ci ko ci pola pod wykresem funkcji. Z uwagi na symetri wykresu funkcji
przynale no ci oceny wa no ci kryteriów uzyskujemy warunek dla j-tego
eksperta:
=
=
M
i
ij
v
1
mod
1
(69)
Zale no (69) pozwala na zapisanie wzoru na normowanie warto ci
współrz dnych charakterystycznych funkcji przynale no ci:
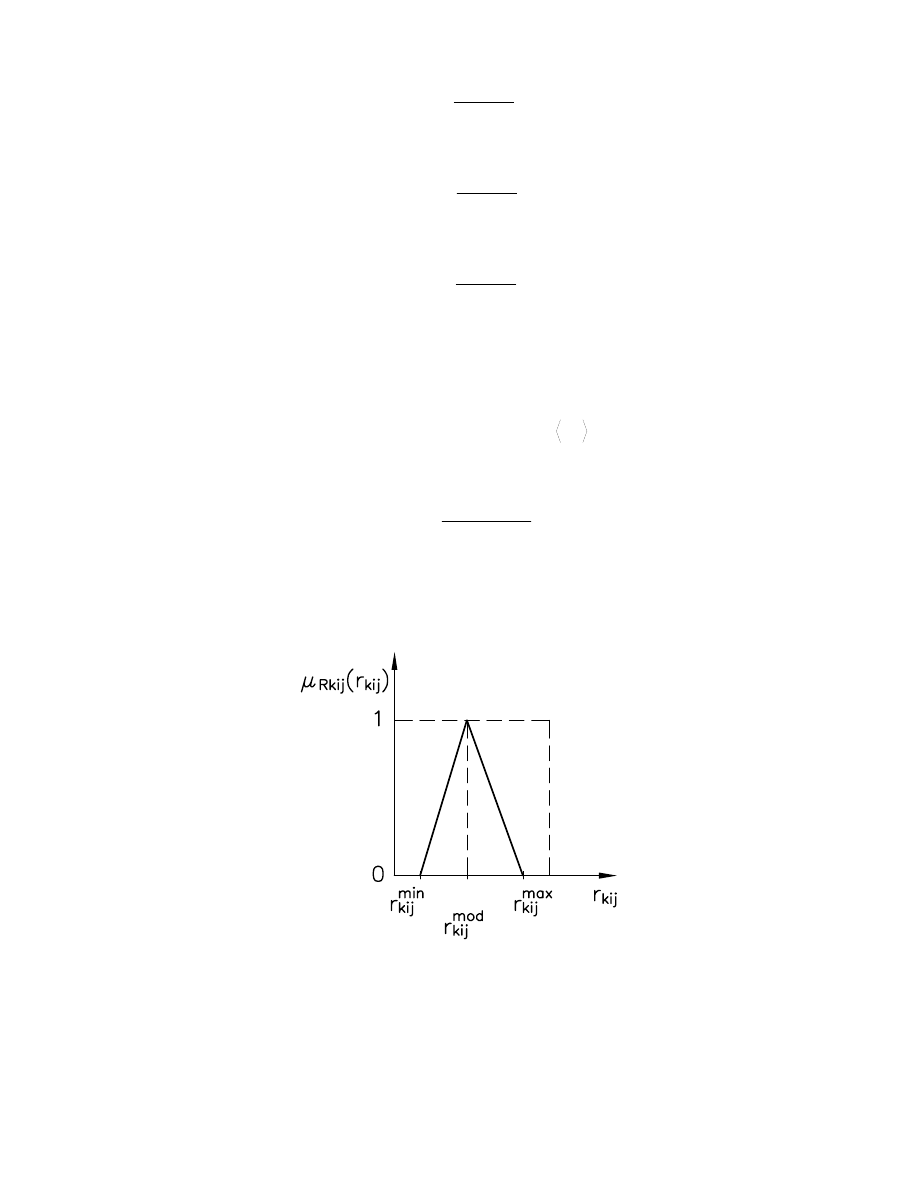
=
=
=
=
=
=
M
i
ij
ij
ij
M
i
ij
ij
ij
M
i
ij
ij
ij
v
v
v
v
v
v
v
v
v
1
mod
max
max
1
mod
mod
mod
1
mod
min
min
ˆ
ˆ
ˆ
(70)
2.
Ocena k-tego rozwi zania wzgl dem i-tego kryterium przez j-tego eksperta jest
modelowana za pomoc liczby rozmytej o trójk tnej funkcji przynale no ci (Rys.
48):
1
;
0
);
(
)
(
~
∈
=
kij
kij
Rkij
k
ij
r
r
A
K
µ
(71)
przy czym:
2
max
min
mod
kij
kij
kij
r
r
r
+
=
(72)
Ekspert dokonuj c oceny kryterium traktuje j jako „około
mod
kij
r
”, przy czym
swoj niepewno co do precyzji tego okre lenia wyra a w postaci wielko ci
przedziału (
max
min
,
kij
kij
r
r
).
Rys. 48. Ocena rozmyta k-tego rozwi zania przez j-tego eksperta w wietle i-tego
kryterium
Ocena
)
(
~
k
ij
A
K
j-tego eksperta jest traktowana jako subiektywny stopie
spełnienia przez k-te rozwi zanie pewnego stanu idealnego w wietle i-tego
kryterium (analogia do metody Mini-Maxu). Warto tej oceny powinna zatem

mie ci si w przedziale 0;1 . Poniewa ma ona charakter rozmyty, podobnie jak
dla wa no ci kryterium mo na wi c zapisa warunek:
1
mod
;
1
≤
∈
∧
kij
r
M
i
(73)
Je eli warunek ten nie jest spełniony konieczne jest normowanie współrz dnych
charakterystycznych funkcji przynale no ci wg wzoru:
=
=
=
=
=
=
M
i
kij
kij
kij
M
i
kij
kij
kij
M
i
kij
kij
kij
r
r
r
r
r
r
r
r
r
1
mod
max
max
1
mod
mod
mod
1
mod
min
min
ˆ
ˆ
ˆ
(74)
W przeciwnym przypadku:
max
max
mod
mod
min
min
ˆ
ˆ
ˆ
kij
kij
kij
kij
kij
kij
r
r
r
r
r
r
=
=
=
(75)
W nast pnym kroku dla ka dego z ekspertów dokonuje si wyznaczenia ocen
rozmytych kryterium zast pczego (por. (38), (39)):
(
)
(
)
=
=
=
⋅
=
=
⋅
=
M
i
ij
Vij
M
i
kij
Rkij
ij
Vij
kj
Zk
M
i
k
ij
ij
j
k
k
v
r
v
z
A
K
w
A
Z
1
1
1
)
(
)
(
)
(
)
(
)
(
~
~
)
(
~
µ
µ
µ
µ
(76)
co zgodnie z ogólnymi zasadami działa na liczbach rozmytych prowadzi do
zale no ci:
(
)
=
=
=
=
⋅
=
=
M
i
ij
M
i
kij
ij
kj
kij
Rkij
M
i
ij
Vij
M
i
kj
Zk
v
r
v
z
r
v
z
1
1
,..,
1
,..,
1
)
(
min
),
(
min
min
sup
)
(
µ
µ
µ
(77)

Praktyczny aspekt wyznaczania funkcji przynale no ci danej wzorem (77) jest
dokładnie taki sam, jak to opisano w rozdz. 2 (zale no ci (42), (43) i (44)).
Kolejnym etapem jest wyznaczenie oceny ł cznej rozwi za wzgl dem
kryterium zast pczego dla wszystkich ekspertów wg zale no ci:
P
A
Z
A
Z
P
j
j
k
k
k
k
=
=
1
)
(
~
)
(
~
(78)
równie przy wykorzystaniu zale no ci (42), (43) i (44). W liczniku wzoru (78) mo na
wprowadzi wa on sum ocen kryterium zast pczego z uwagi na wa no ci
ekspertów, w opisanym post powaniu przyj to jednak równ wa no ekspertów.
Ostatnim krokiem post powania jest wyostrzenie ocen rozmytych kryteriów
zast pczych przy wykorzystanej w rozdz. 2 metody rodka ci ko ci (46) oraz wybór
rozwi zania optymalnego, dla którego uzyskano maksimum oceny kryterium
zast pczego.
7. Polioptymalizacja z wykorzystaniem metody zmodyfikowanej –
przykład
Dla zilustrowania post powania polioptymalizacyjnego przy u yciu opisanej
metody zanalizowany został nast puj cy problem: dokona wyboru optymalnego
procesu wytwarzania wałka z uz bieniem sto kowym (Rys. 49) przy wielko ci serii
produkcyjnej ok. 1000 szt. Rozpatrzono cztery warianty procesów:
A1 Koło z bate i wałek wykonywane oddzielnie z pr ta, nast pnie koło jest
wtłaczane na wałek.
A2 Koło z bate i wałek wykonywane oddzielnie z pr ta, koło osadzone na wpu cie.
A3 Wałek jednolity, wykonywany z odkuwki matrycowej.
A4 Wałek jednolity, wykonywany z pr ta.
Do wyboru optymalnego procesu wykorzystano trzy kryteria:
K1 Technologiczno procesu wytwarzania.
K2 Koszt wytwarzania.
K3 Jako u ytkowa wyrobu.
Ocen wykonało trzech niezale nych technologów (E1, E2 i E3). W Tabl. 3
zamieszczono warto ci ocen wa no ci kryteriów, natomiast w Tabl. 4 oceny
wariantów procesu wzgl dem poszczególnych kryteriów podane przez tych ekspertów.
Na podstawie tych ocen dla ka dego z ekspertów wyznaczono z zale no ci (76), (77)
oceny rozmyte kryteriów zast pczych. Wykresy funkcji przynale no ci ocen
rozmytych przedstawiono na Rys. 50, Rys. 51 i Rys. 52. W ostatnim kroku
wyznaczono posta rozmyt oceny kryterium zast pczego w odniesieniu do
wszystkich ekspertów (78). Wykresy funkcji przynale no ci ocen rozmytych
zamieszczono na Rys. 53. Wykorzystuj c metod rodka ci ko ci dokonano
wyostrzenia ocen rozmytych (45), (46), które przedstawiono w Tabl. 5. Na podstawie
wyników post powania polioptymalizacyjnego stwierdzono,
e najlepszym
rozwi zaniem jest wariant A1 (wałek składany z kołem wtłaczanym).
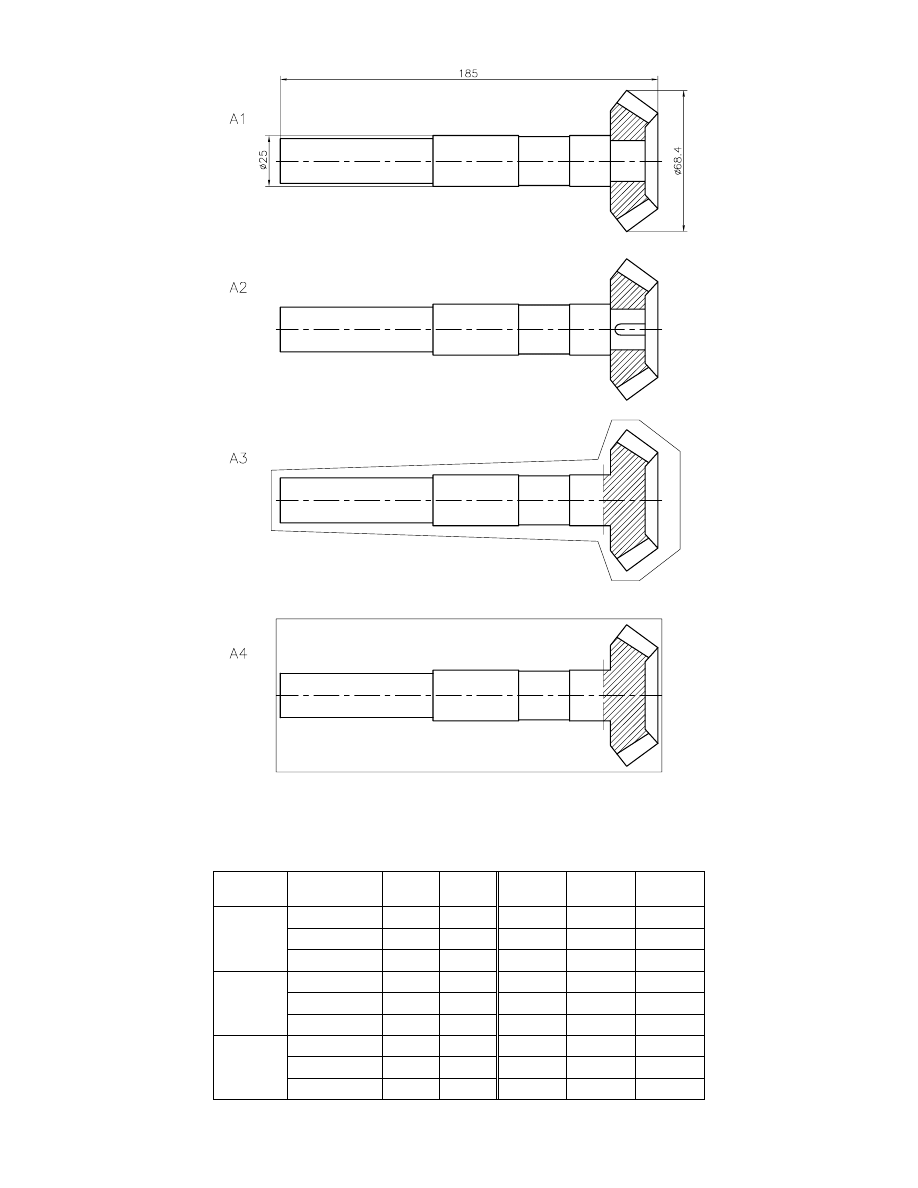
Rys. 49. Warianty technologiczne wałka z uz bieniem sto kowym
Tabl. 3. Warto ci ocen wa no ci kryteriów podane przez ekspertów oraz ich warto ci
unormowane (70)
Ekspert Kryterium
min
ij
v
max
ij
v
min
ˆ
ij
v
mod
ˆ
ij
v
max
ˆ
ij
v
K1
0,20
0,30
0,2667 0,3333 0,4000
K2
0,35
0,40
0,4667 0,5000 0,5333
E1
K3
0,10
0,15
0,1333 0,1667 0,2000
K1
0,30
0,40
0,2667 0,3111 0,3556
K2
0,40
0,60
0,3556 0,4444 0,5333
E2
K3
0,20
0,35
0,1778 0,2444 0,3111
K1
0,35
0,45
0,3182 0,3636 0,4091
K2
0,35
0,50
0,3182 0,3864 0,4545
E3
K3
0,20
0,35
0,1818 0,2500 0,3182

Tabl. 4. Warto ci ocen wariantów podane przez ekspertów oraz ich warto ci unormowane
(74), (75)
Ekspert Kryterium Wariant
min
kij
r
max
kij
r
min
ˆ
kij
r
mod
ˆ
kij
r
max
ˆ
kij
r
A1
0,60
0,70
0,60
0,65
0,70
A2
0,50
0,70
0,50
0,60
0,70
A3
0,20
0,40
0,20
0,30
0,40
K1
A4
0,70
0,90
0,70
0,80
0,90
A1
0,70
0,80
0,70
0,75
0,80
A2
0,60
0,80
0,60
0,70
0,80
A3
0,10
0,20
0,10
0,15
0,20
K2
A4
0,30
0,40
0,30
0,35
0,40
A1
0,70
0,90
0,70
0,80
0,90
A2
0,60
0,70
0,60
0,65
0,70
A3
0,70
0,80
0,70
0,75
0,80
E1
K3
A4
0,70
0,80
0,70
0,75
0,80
A1
0,30
0,60
0,30
0,45
0,60
A2
0,20
0,50
0,20
0,35
0,50
A3
0,30
0,50
0,30
0,40
0,50
K1
A4
0,50
0,70
0,50
0,60
0,70
A1
0,60
0,80
0,60
0,70
0,80
A2
0,50
0,70
0,50
0,60
0,70
A3
0,20
0,40
0,20
0,30
0,40
K2
A4
0,30
0,50
0,30
0,40
0,50
A1
0,40
0,50
0,40
0,45
0,50
A2
0,30
0,50
0,30
0,40
0,50
A3
0,50
0,70
0,50
0,60
0,70
E2
K3
A4
0,50
0,70
0,50
0,60
0,70
A1
0,20
0,50
0,20
0,35
0,50
A2
0,30
0,60
0,30
0,45
0,60
A3
0,70
0,90
0,70
0,80
0,90
K1
A4
0,50
0,80
0,50
0,65
0,80
A1
0,70
0,90
0,70
0,80
0,90
A2
0,60
0,70
0,60
0,65
0,70
A3
0,10
0,30
0,10
0,20
0,30
K2
A4
0,20
0,40
0,20
0,30
0,40
A1
0,20
0,40
0,20
0,30
0,40
A2
0,20
0,50
0,20
0,35
0,50
A3
0,60
0,80
0,60
0,70
0,80
E3
K3
A4
0,60
0,80
0,60
0,70
0,80
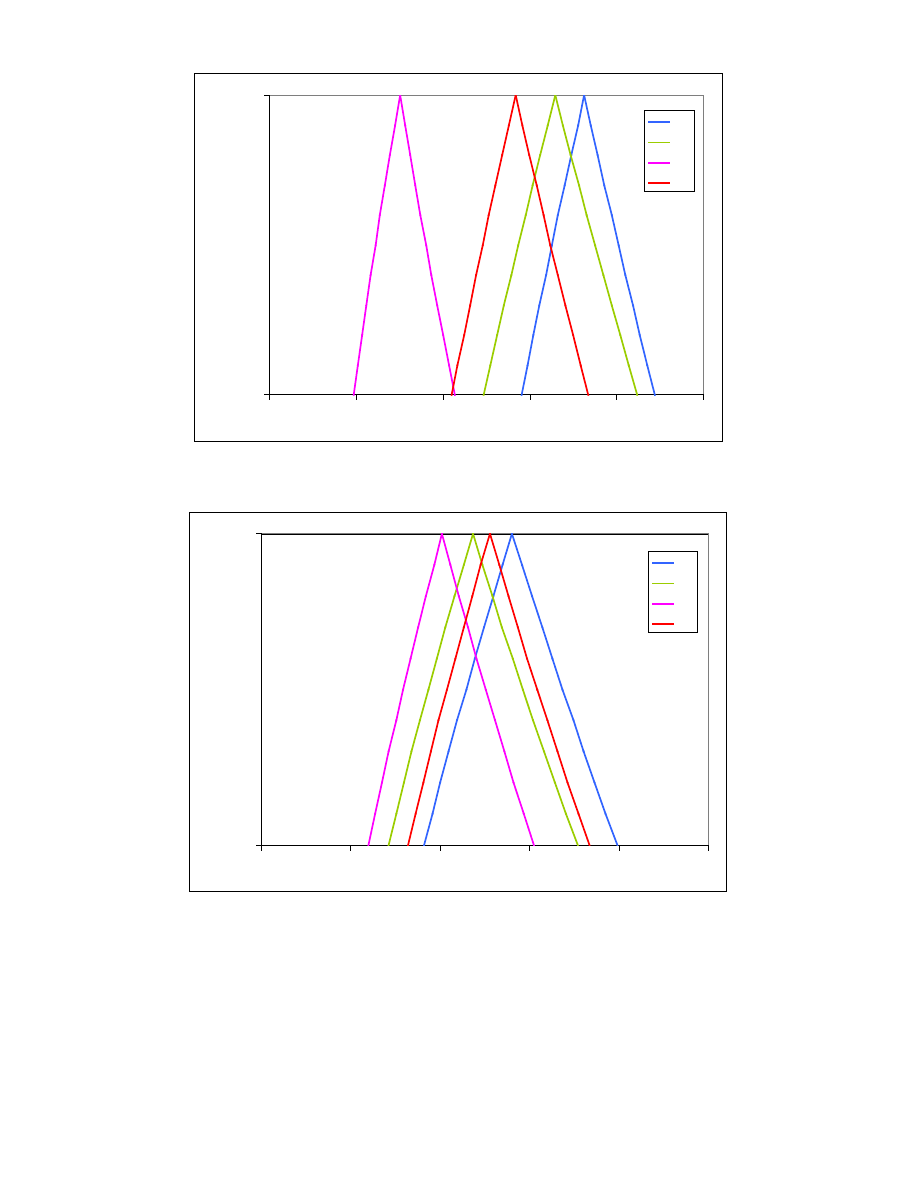
0.0
1.0
0
0.2
0.4
0.6
0.8
1
µ(Z)
E1
A1
A2
A3
A4
Rys. 50. Funkcje przynale no ci ocen rozmytych kryterium zast pczego dla eksperta E1
0.0
1.0
0
0.2
0.4
0.6
0.8
1
µ(Z)
E2
A1
A2
A3
A4
Rys. 51. Funkcje przynale no ci ocen rozmytych kryterium zast pczego dla eksperta E2
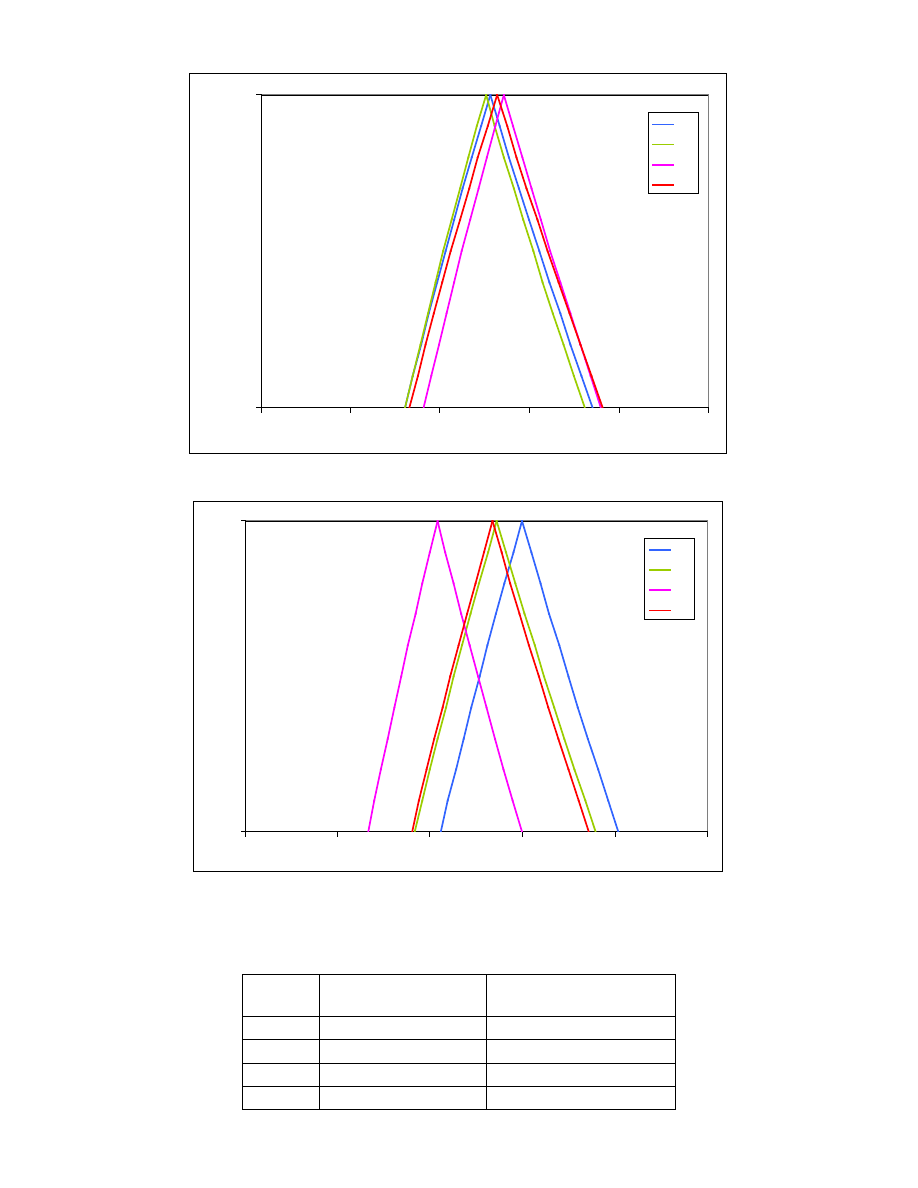
0.0
1.0
0
0.2
0.4
0.6
0.8
1
µ(Z)
E3
A1
A2
A3
A4
Rys. 52. Funkcje przynale no ci ocen rozmytych kryterium zast pczego dla eksperta E3
0
1
0
0.2
0.4
0.6
0.8
1
µ(Z)
A1
A2
A3
A4
Rys. 53. Funkcje przynale no ci ocen rozmytych kryterium zast pczego
Tabl. 5. Warto ci ocen kryterium zast pczego dla analizowanych rozwi za wariantów
procesu technologicznego
Wariant Ocena wg kryterium
zast pczego
Unormowana ocena wg
kryterium zast pczego
A1
0.6071
1,000
A2
0.5537
0,912
A3
0.4239
0,698
A4
0.5435
0,895
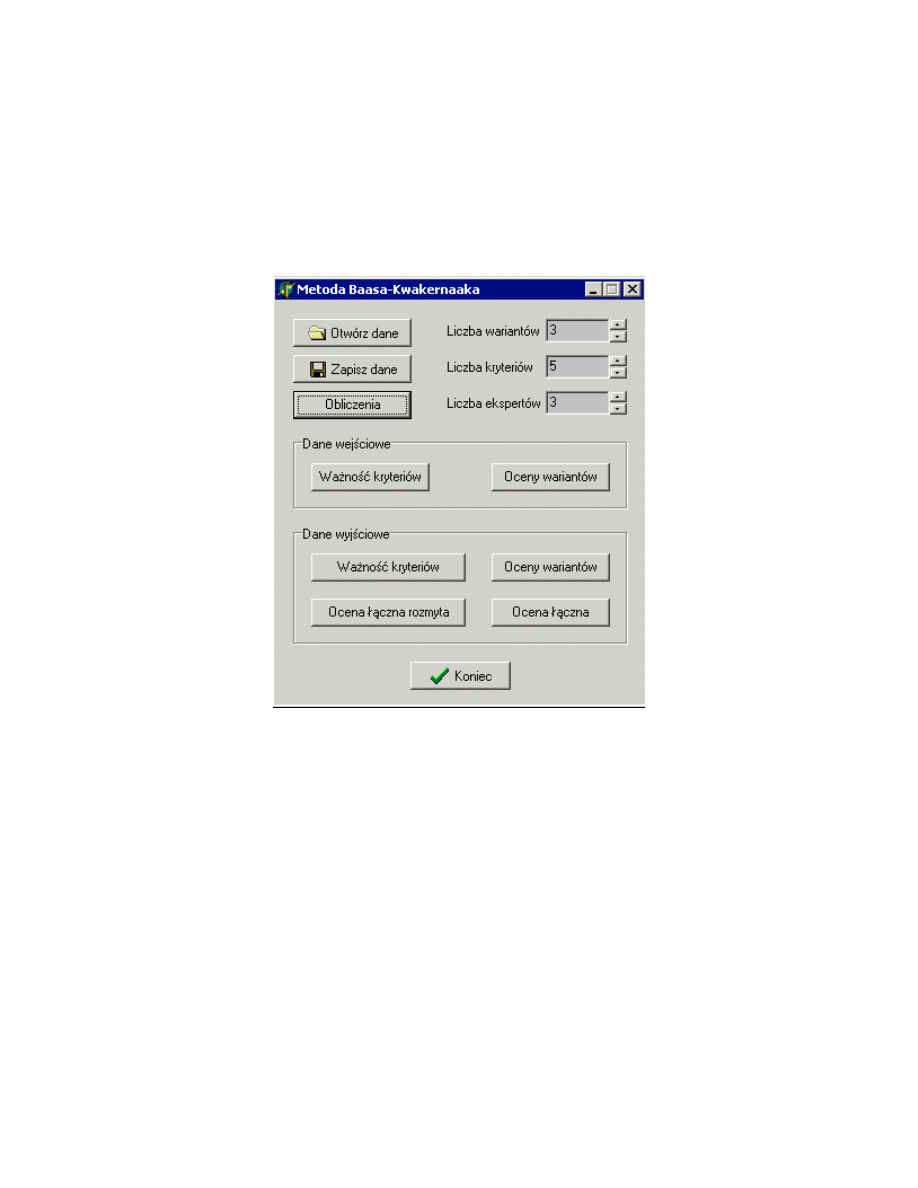
8. Pakiet programów do optymalizacji wielokryterialnej
W ramach analizy zagadnienia optymalizacji wielokryterialnej z wykorzystaniem
ocen rozmytych przygotowano pakiet programów wykorzystuj cych przedstawione
metody.
8.1. PoliOpt1 – polioptymalizacja z wykorzystaniem ocen rozmytych – metoda
Baasa i Kwakernaaka
Plansza główna programu (Rys. 54) zawiera nast puj ce funkcje:
Rys. 54. Plansza główna programu PoliOpt1
Otwórz dane – odczyt danych z pliku dyskowego.
Zapisz dane – zapis danych do pliku dyskowego.
Obliczenia – wykonanie oblicze zwi zanych z wyznaczeniem ocen kryterium
zast pczego.
Liczba wariantów – zmiana liczby analizowanych wariantów dopuszczalnych.
Liczba kryteriów – zmiana liczby kryteriów wzgl dem których dokonywana jest
ocena.
Liczba ekspertów – zmiana liczby ekspertów, którzy dokonuj oceny.
Dane wej ciowe
Wa no kryteriów – oceny wa no ci kryteriów, wprowadzane przez ekspertów
(Rys. 55).
Oceny wariantów – oceny wariantów wzgl dem wszystkich kryteriów,
wprowadzane przez ekspertów (Rys. 56).
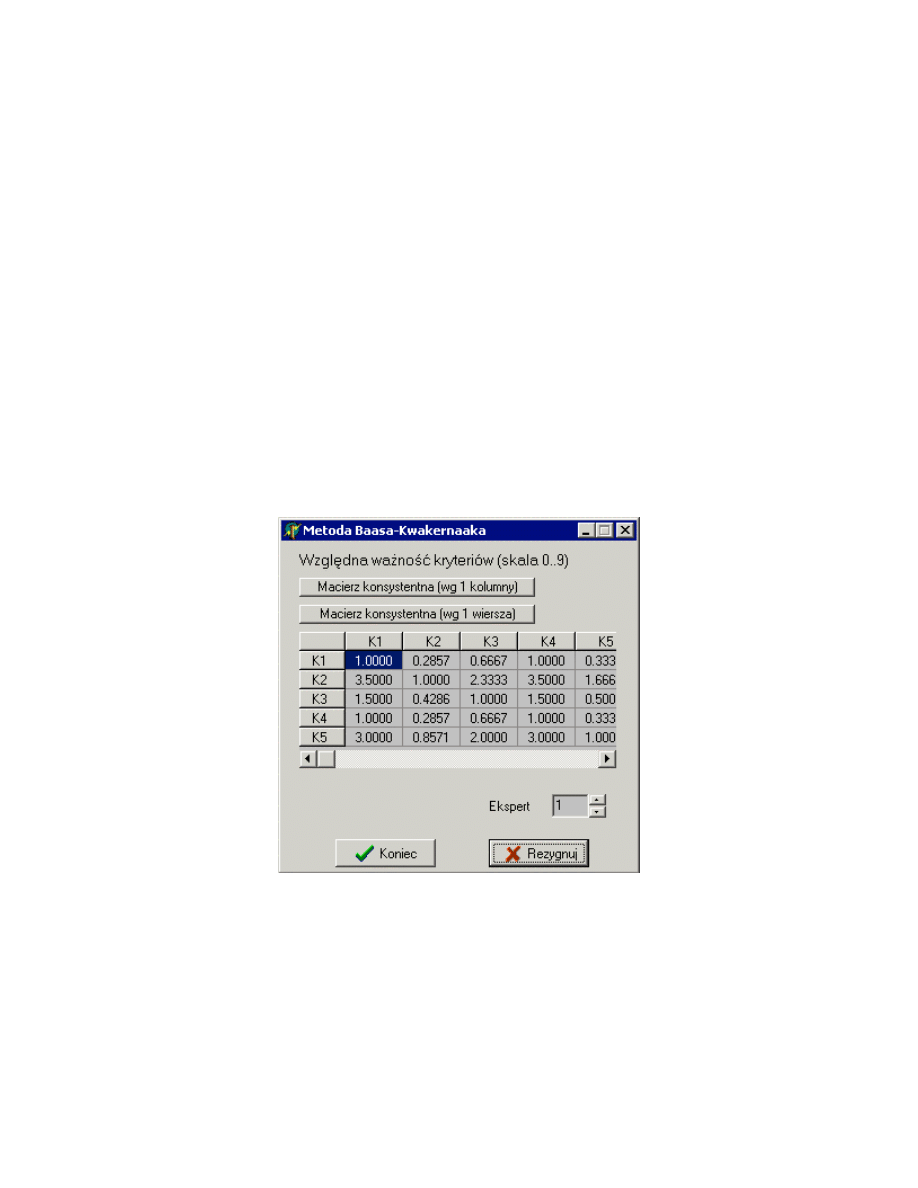
Dane wyj ciowe
Wa no kryteriów – wykresy funkcji przynale no ci ocen rozmytych wa no ci
kryteriów, wyznaczonych na podstawie ocen ekspertów (Rys. 57).
Oceny wariantów – wykresy funkcji przynale no ci ocen rozmytych wariantów
wzgl dem poszczególnych kryteriów, wyznaczonych na podstawie ocen
ekspertów (Rys. 58).
Ocena ł czna rozmyta – wykresy funkcji przynale no ci ocen rozmytych
wariantów wzgl dem kryterium zast pczego (Rys. 59).
Ocena ł czna – warto ci deterministyczne ocen wariantów wzgl dem kryterium
zast pczego (Rys. 60).
Dane wej ciowe -> Wa no kryteriów (Rys. 55).
Wa no kryteriów jest oceniania przez wszystkich ekspertów przez ocenianie
parami wszystkich kryteriów i zestawienie ocen w macierzy Saaty’ego. Mo liwe
jest wykorzystanie warunków konsystencji macierzy Saaty’ego, wtedy wystarczy
wprowadzi oceny tylko w pierwszym wierszu lub pierszej kolumnie macierzy,
pozostałe komórki mog zosta obliczone automatycznie. Skala warto ci ocen
mo e zosta przyj ta w sposób dowolny, zaleca si proponowan przez
Saaty’ego skal (0,..,9).
Rys. 55. Panel wprowadzania ocen wa no ci kryteriów, podanych przez ekspertów
Dane wej ciowe -> Oceny wariantów (Rys. 56).
Oceny wariantów eksperci równie przeprowadzaj przez porównania parami
i zestawianie ocen w macierzy Saaty’ego. Sposób post powania identyczny jak
dla wa no ci kryteriów.
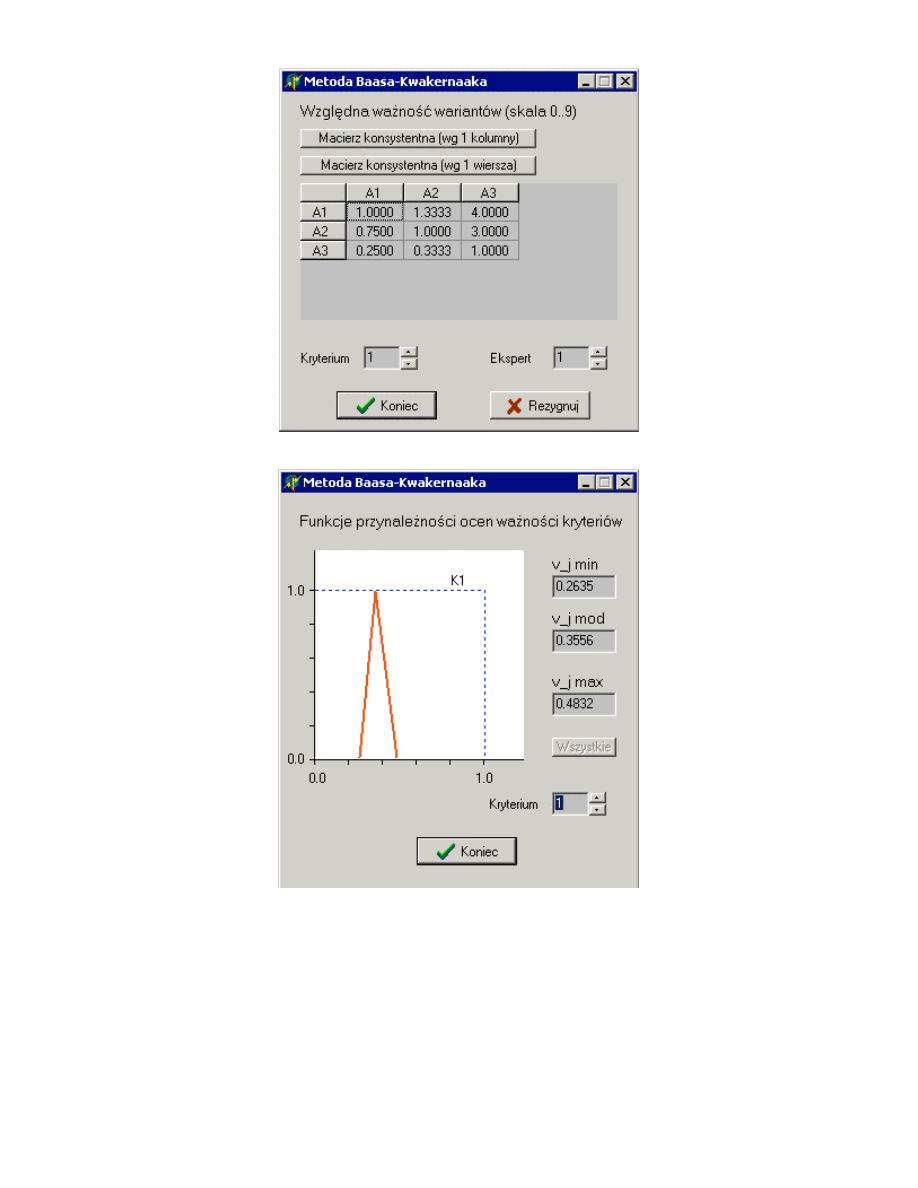
Rys. 56. Panel wprowadzania ocen wariantów, podanych przez ekspertów
Rys. 57. Wykresy funkcji przynale no ci ocen rozmytych wa no ci kryteriów
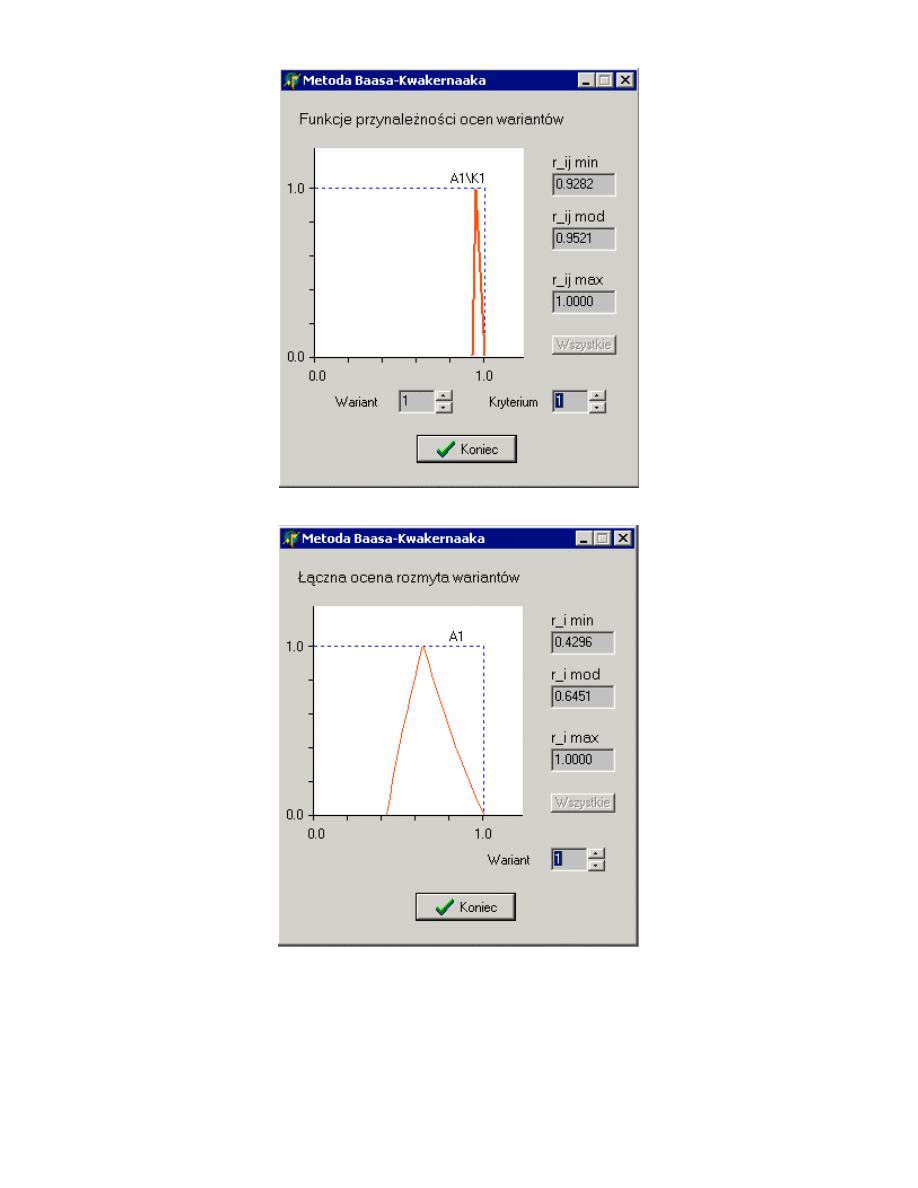
Rys. 58. Wykresy funkcji przynale no ci ocen rozmytych wariantów
Rys. 59. Wykresy rozmytych ocen ł cznych wariantów, wyznaczone na podstawie ocen
poszczególnych ekspertów
Dane wyj ciowe -> Ocena ł czna (Rys. 60).
Panel ocen ł cznych zawiera wyznaczone dla wszystkich wariantów oceny
deterministyczne, wyznaczone metod rodka ci ko ci dla wykresów funkcji
przynale no ci (Rys. 59). Nale y pami ta , i oceny te s wyra one w takiej
samej skali, w jakiej eksperci wyra ali oceny porównawcze wariantów
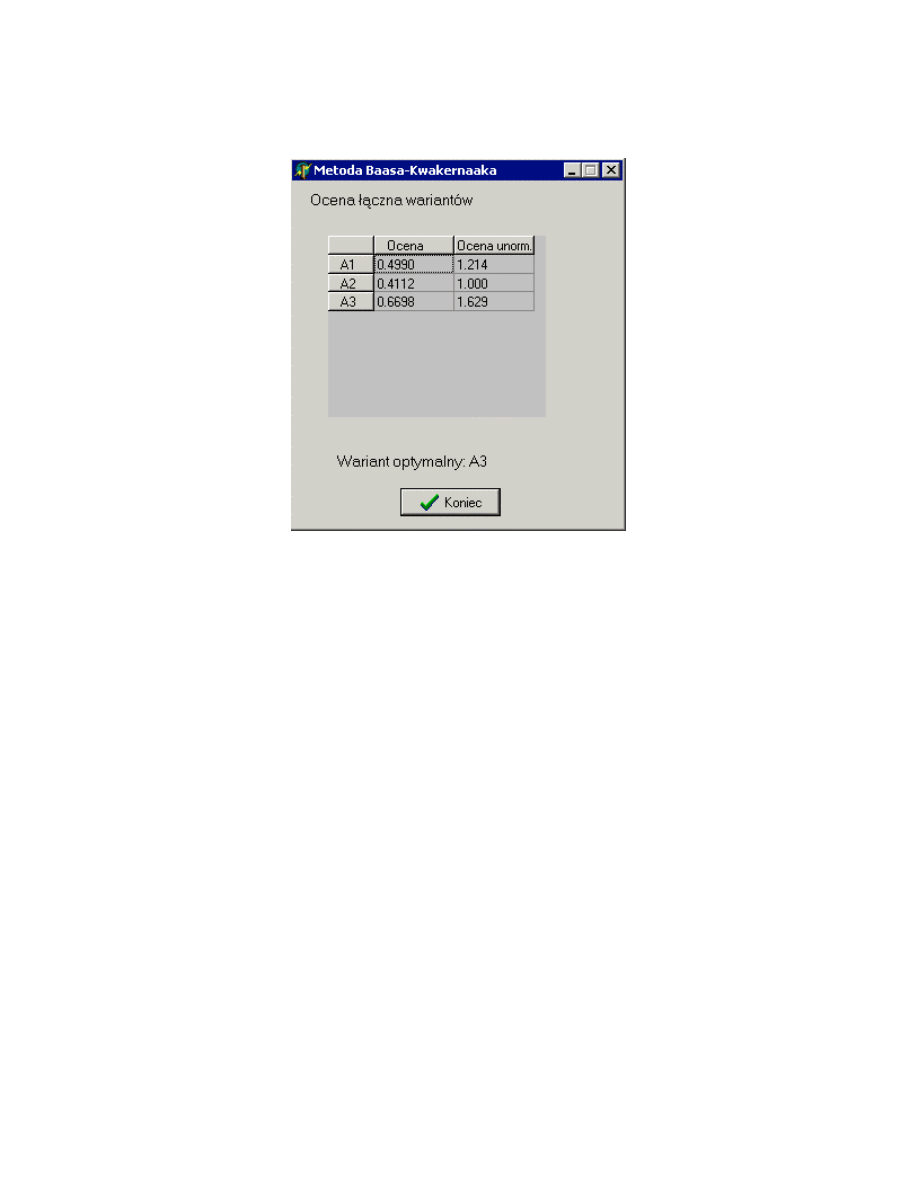
i wa no ci kryteriów – s traktowane jako oceny wzgl dne. Dlatego w tabeli
podano równie warto ci unormowane wzgl dem wariantu o najmniejszej
warto ci oceny kryterium zast pczego.
Rys. 60. Oceny ł czne wariantów wzgl dem kryterium zast pczego
8.2. PoliOpt2 – polioptymalizacja z wykorzystaniem ocen rozmytych – metoda
zmodyfikowana
Plansza główna programu (Rys. 61) zawiera nast puj ce funkcje:
Otwórz dane – odczyt danych z pliku dyskowego.
Zapisz dane – zapis danych do pliku dyskowego.
Obliczenia – wykonanie oblicze zwi zanych z wyznaczeniem ocen kryterium
zast pczego.
Liczba wariantów – zmiana liczby analizowanych wariantów dopuszczalnych.
Liczba kryteriów – zmiana liczby kryteriów wzgl dem których dokonywana jest
ocena.
Liczba ekspertów – zmiana liczby ekspertów, którzy dokonuj oceny.
Dane wej ciowe
Kryteria – oceny wa no ci kryteriów, wprowadzane przez ekspertów (Rys. 62).
Warianty – oceny wariantów wzgl dem poszczególnych kryteriów,
wprowadzane przez ekspertów (Rys. 63).
Wa no kryteriów – wykresy funkcji przynale no ci ocen wa no ci kryteriów,
opracowane na podstawie danych wprowadzonych przez ekspertów (Rys. 64).
Oceny wariantów – wykresy funkcji przynale no ci ocen wariantów,
opracowane na podstawie danych wprowadzonych przez ekspertów (Rys. 65).
Dane wyj ciowe
Rozmyte oceny ekspertów – wykresy funkcji przynale no ci ocen rozmytych
wszystkich wariantów wzgl dem kryterium zast pczego, wyznaczone dla
poszczególnych ekspertów (Rys. 66).
Rozmyta ocena ł czna – wykresy ł cznyh funkcji przynale no ci ocen
rozmytych wszystkich wariantów wzgl dem kryterium zast pczego, wyznaczone
na podstawie ocen wszystkich ekspertów (Rys. 67).
Unormowana ocen ł czna – deterministyczne warto ci ocen wariantów
wzgl dem kryterium zast pczego (Rys. 68).
Rys. 61. Plasza główna programu PoliOpt2
Dane wej ciowe -> Kryteria (Rys. 62).
Zgodnie z zale no ciami (51) i (52) oceny wa no ci kryteriów eksperci podaj
jako graniczne warto ci przedziału jako „około
mod
ij
v
” (
max
min
,
ij
ij
v
v
). Dla ułatwienia
przyj to skal (0,...,100) zamiast (0,..,1). Na etapie dalszych oblicze
automatycznie oceny s dzielone przez 100. Przycisk
Normuj pozwala na
unormowanie ocen zgodnie z zale no ci (70).
Rys. 62. Panel wprowadzania ocen wa no ci kryteriów
Dane wej ciowe -> Warianty (Rys. 63).
Wprowadzanie ocen wariantów przebiega podobnie jak dla ocen wa no ci
kryteriów – zale no (71) i (72). Ocena ekspertów obejmuje graniczne warto ci
przedziału „około
mod
kij
r
” (
max
min
,
kij
kij
r
r
). Przycisk
Normuj pozwala na normowanie
ocen zgodnie z zale no ciami (74) i (75).
Rys. 63. Panel wprowadzania ocen wariantów
Rys. 64. Wykresy funkcji przynale no ci ocen wa no ci kryteriów dla poszczególnych
ekspertów
Rys. 65. Wykresy funkcji przynale no ci ocen wariantów wzgl dem poszczególnych
kryteriów dla poszczególnych ekspertów
Rys. 66. Wykresy funkcji przynale no ci ocen rozmytych wariantów wzgl dem kryterium
zast pczego, podanych przez poszczególnych ekspertów
Rys. 67. Wykresy funkcji przynale no ci rozmytych ocen ł cznych wariantów wzgl dem
kryterium zast pczego
Dane wyj ciowe -> Unormowana ocena ł czna (Rys. 68).
Na podstawie rozmytych ocen ł cznych wariantów wzgl dem kryterium
zast pczego (Rys. 67) metod rodka ci ko ci wyznaczana s oceny
deterministyczne wariantów. W przeciwie stwie do tradycyjnego podej cia
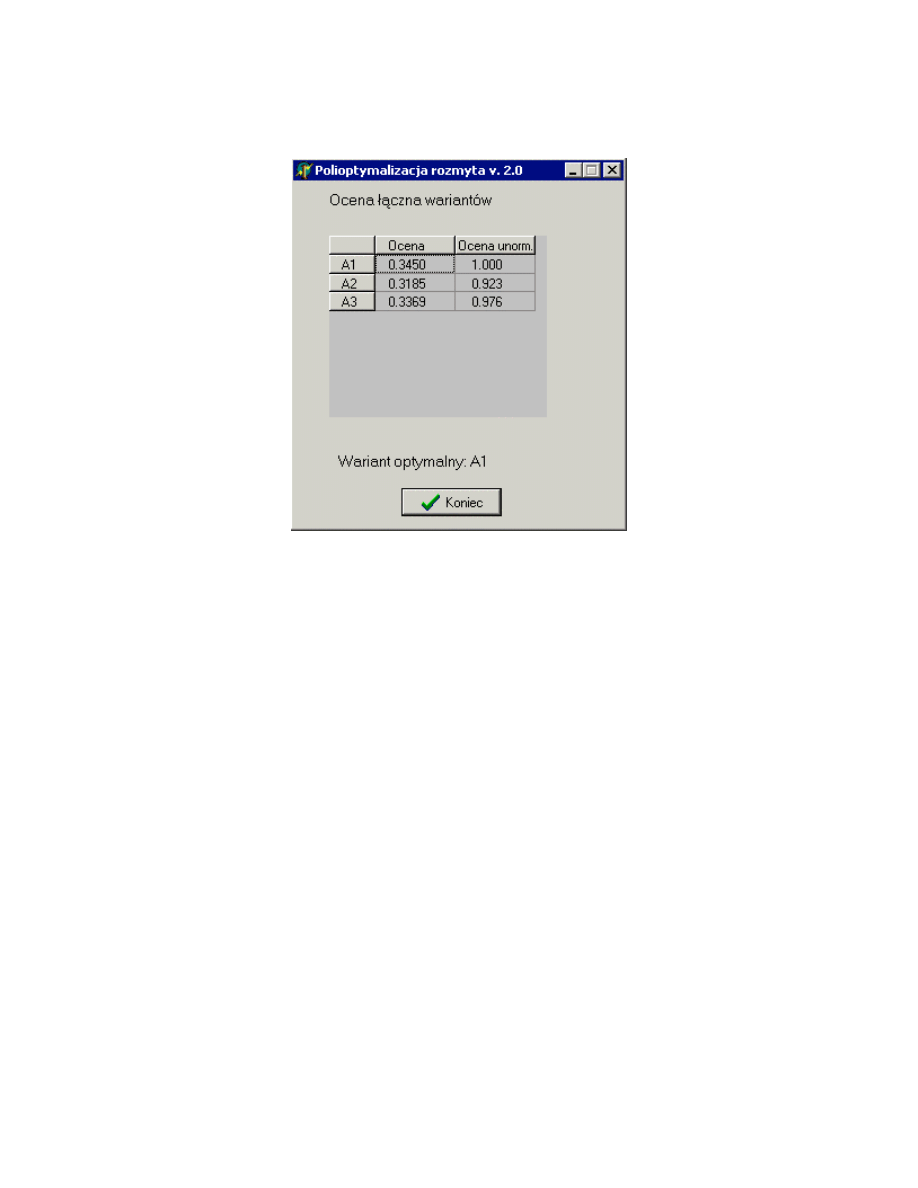
w metodzie Baasa i Kwakernaaka oceny te przedstawiaj rzeczywiste warto ci
wariantów jako stopie osi gni cia przez nie pewnego stanu idealnego. Dla
ułatwienia oceny s normowane wzgl dem wariantu o najwy szej ocenie.
Rys. 68. Oceny ł czne wariantów wzgl dem kryterium zast pczego
8.3. Yager – polioptymalizacja metod Yagera
Plansza główna programu zawiera pi zakładek. Kolejne z nich zawieraj :
Dane ogólne (Rys. 69):
Liczba wariantów (N);
Liczba kryteriów (M);
Liczba ekspertów (P);
Skala ocen punktowych (L – dla wersji punktowej);
Liczba klas L (L – dla wersji bazowej);
Metoda – wybór metody polioptymalizacji;
Decyzja – wybór metody agregacji ocen ł cznych wariantów.
Kryteria (Rys. 70) – warto ci ocen porównawczych (macierze Saaty’ego) wa no ci
kryteriów. Dla ułatwienia mo na wykorzysta automatyczne tworzenie macierzy
z warunku konsystencji, przyjmuj c jako dane wej ciowe pierwszy wiersz lub
pierwsz kolumn macierzy.
Bazowa (Rys. 71) – warto ci ocen rozwi za podawane wg metody bazowej.
Punktowa (Rys. 72) – warto ci ocen rozwi za podawane wg metody punktowej.
Wyniki (Rys. 73) – wyniki poliotymalizacji, obejmuj ce: ł czne wa no ci kryteriów
w
i
oraz warto ci funkcji przynale no ci rozwi za do decyzji optymalnej
µ
Dk
. Dla
ułatwienia wyrózniane s rozwi zania o najwi kszej warto ci funkcji przynale no ci
(b d ce ostatecznym wynikiem post powania poliotymalizacyjnego).
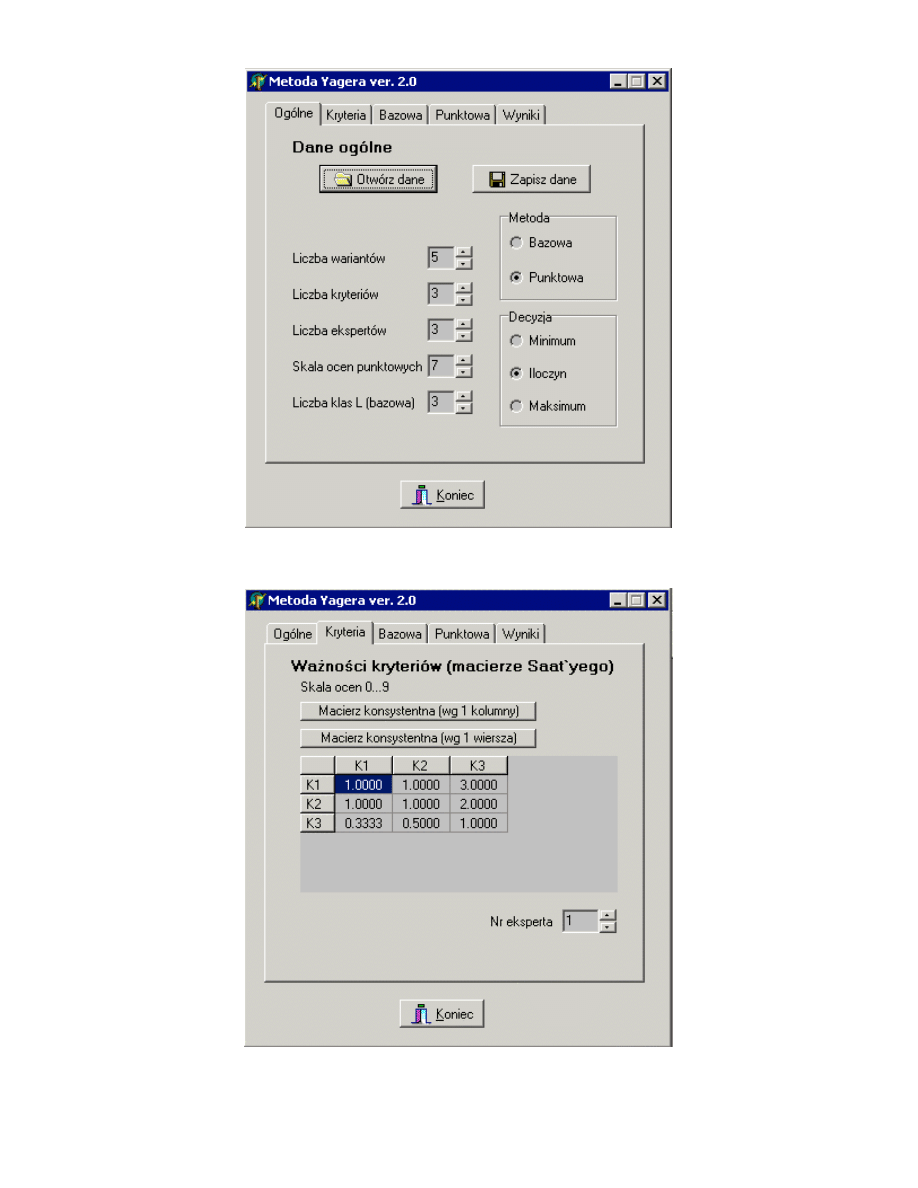
Rys. 69. Dane ogólne
Rys. 70. Warto ci ocen wa no ci kryteriów
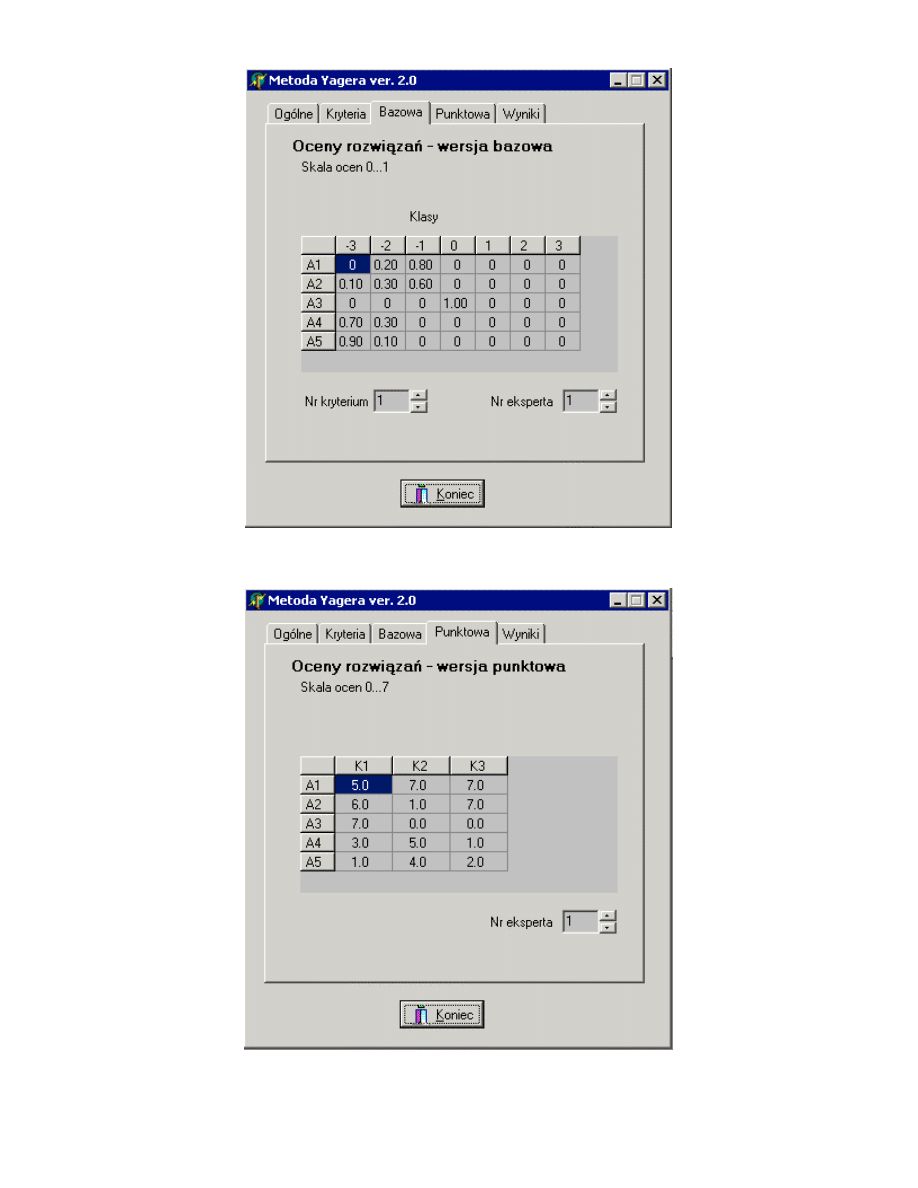
Rys. 71. Oceny rozwi za wg metody bazowej
Rys. 72. Oceny rozwi za mg metody punktowej
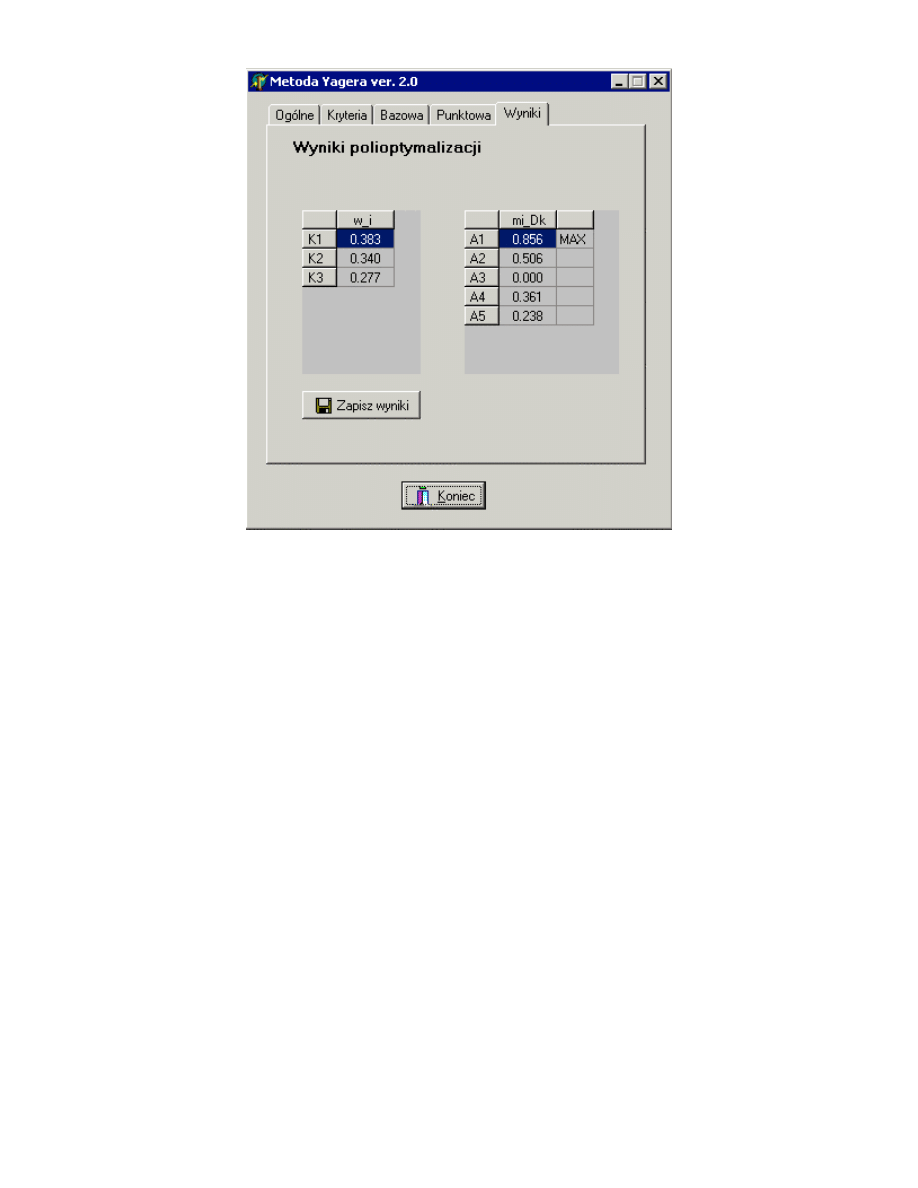
Rys. 73. Wyniki polioptymalizacji metod Yagera
9. Literatura
[1]
Baas S.M., Kwakernaak H. „Rating and Raking of Multiple-Aspects Alternatives
Using Fuzzy Sets”, Automatica, vol. 13 (1977), pp. 47-58.
[2]
Eschenauer H., Koski J., Osyczka A., „Multicriteria Design Optimization”.
Springer-Verlag, Berlin 1990.
[3]
Fuller R., Carlsson C., „Fuzzy Multiple Criteria Decision Making”. Fuzzy Sets
and Systems
, 78(1996), pp. 139-153.
[4]
Gajczak R., „Wielokryterialne metody oceny i wyboru procesów wytwarzania”.
Praca niepublikowana, ATH Bielsko-Biała 2002.
[5]
Kacprzyk J., „Zbiory rozmyte w analizie systemowej”. PWN Warszawa 1986.
[6]
Knosala R., Pedrycz W., „Komputerowy system wspomagaj cy proces oceny
rozwi za konstrukcyjnych”. Zeszyty Naukowe Politechniki
l skiej,
Mechanika Nr 86, Gliwice 1987.
[7]
Krawczyk
S.,
„Metody
ilo ciowe
w
planowaniu
(działalno ci
przedsi biorstwa)”. Academia Oeconomica, Wydaw. C.H. Beck, Warszawa
2001.
[8]
M. Detyniecki, R. R. Yager, „Ranking fuzzy numbers using alpha-weighted
valuations”. International Journal of Uncertainty, Fuzziness and Knowledge-
Based Systems, vol. 8 (2001) 5, pp. 573-592.
[9]
Panek E., „Ekonomia matematyczna”. Akademia Ekonomiczna w Poznaniu,
Pozna 2000.

[10]
Płonka S., „Metody oceny i wyboru optymalnej struktury procesu
technologicznego”. Zesz. Nauk. Politechniki Łódzkiej Filii w Bielsku-Białej
nr 48, Budowa i Eksploatacja Maszyn z. 31, Bielsko-Biała 1998.
[11]
Płonka S., Pytlak B., Gajczak R. „Ocena rozwi za konstrukcyjnych
z zastosowaniem logiki rozmytej”. XXI Symp. Podstaw Konstrukcji Maszyn,
WNT Warszawa 2003, str. 137-144.
[12]
Saaty T.L., „The Analytic Hierarchy Processes”. McGraw-Hill, New York
1980.
[13]
Yager, R.R., „Fuzzy Decision Making Including Unequal Objectives”. Fuzzy
Sets and Systems, vol. 1 (1978), pp. 87-95.
Wyszukiwarka
Podobne podstrony:
optymal id 338894 Nieznany
Optymalizacja 2 id 338903 Nieznany
Optymalizacja w2 pdf id 338946 Nieznany
Optymalizacja w1 pdf id 338945 Nieznany
Optymalizacja w4 pdf id 338947 Nieznany
Optymalizacja w2 pdf id 338946 Nieznany
Abolicja podatkowa id 50334 Nieznany (2)
4 LIDER MENEDZER id 37733 Nieznany (2)
katechezy MB id 233498 Nieznany
metro sciaga id 296943 Nieznany
perf id 354744 Nieznany
interbase id 92028 Nieznany
Mbaku id 289860 Nieznany
Probiotyki antybiotyki id 66316 Nieznany
miedziowanie cz 2 id 113259 Nieznany
LTC1729 id 273494 Nieznany
D11B7AOver0400 id 130434 Nieznany
analiza ryzyka bio id 61320 Nieznany
więcej podobnych podstron