3. Analiza regresji.

a) Gęstośd prawdopodobieostwa

Łączny rozkład gęstości prawdopodobieostwa :

y

x

y

y

Y

y

x

x

X

x

P

y

x

P

y

x

































]

,

[

lim

)

,

(

0

;

0

Definiujemy również rozkłady brzegowe











dy

y

x

p

x

p

)

,

(

)

(











dx

y

x

p

y

p

)

,

(

)

(

oraz











1

)

,

(

)

,

(

dxdy

y

x

p

y

x

p

Zmienne X i Y są niezależne tylko wtedy gdy

)

(

)

(

)

,

(

y

p

x

p

y

x

p





Wartośd średnia rozkładu dwuwymiarowego wartości x i y

 

















dxdy

y

x

p

x

x

)

,

(



 

















dxdy

y

x

p

y

y

)

,

(



Wartośd wariancji rozkładu dwuwymiarowego wartości x i y

 



















dxdy

y

x

p

x

x

x

)

,

(

)

(

2

2





 



















dxdy

y

x

p

y

y

y

)

,

(

)

(

2

2





Wartośd kowariancji – zależności liniowej między X i Y























)

(

,

x

y

x

x

C



dxdy

y

x

p

y

y

)

,

(

)

(







-- nie jestem pewien czy ma byd całka podwójna

Rozkład normalny 2 zmiennych losowych- funkcja gęstości

2

2

2

2

1

2

]}

)

(

)

(

)

(

2

)

[(

]

)

1

(

2

1

exp{[

)

,

(

xy

y

x

y

y

y

y

x

x

xy

x

x

xy

y

y

x

x

y

x

p





























































Gdzie

y

x

xy

xy

C





 

- współczynnik korelacji.

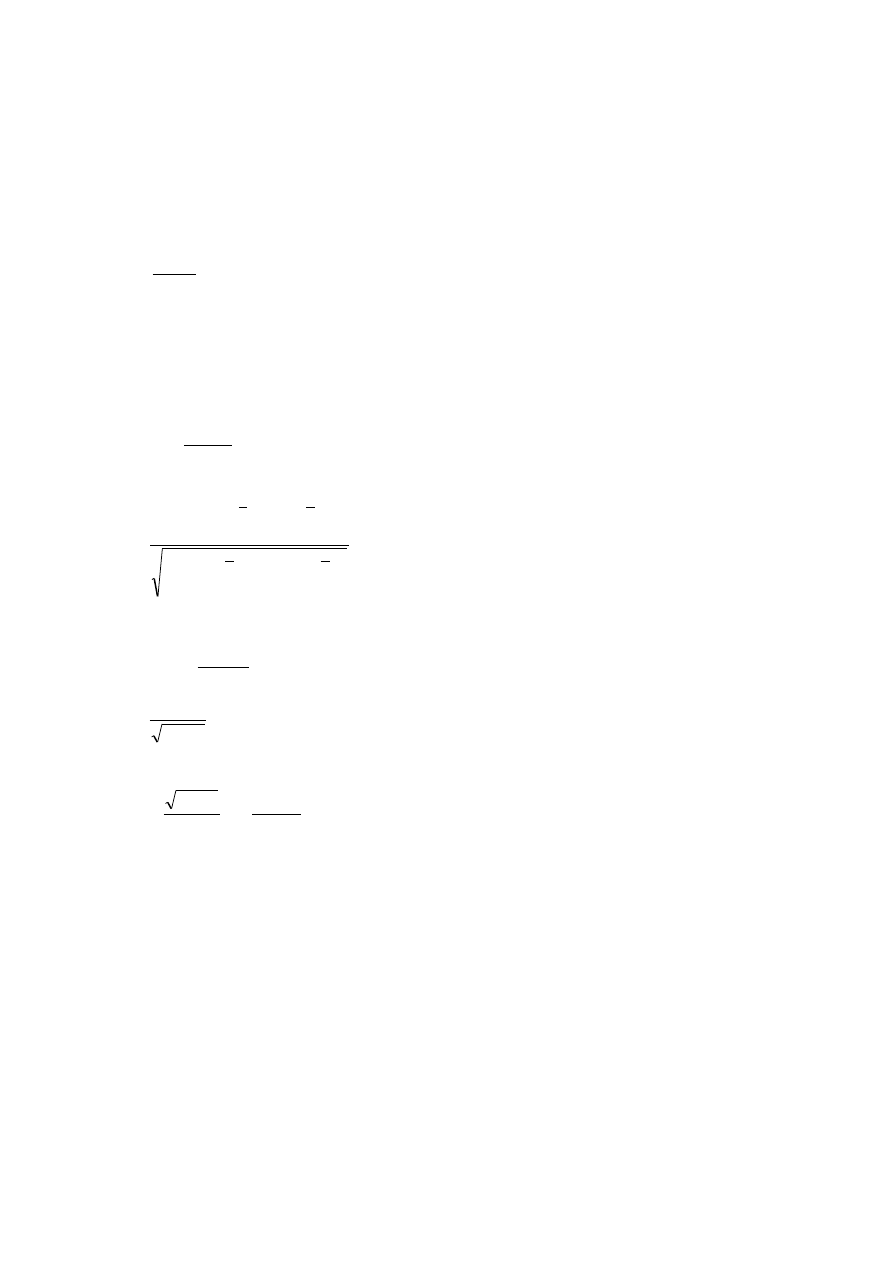
Jeżeli

,

0



xy



to znaczy że zmienne są nieskorelowane (są niezależne od siebie),

wtedy wzór na gęstośd prawdopodobieostwa przyjmuje postad

)

(

)

(

)

,

(

y

p

x

p

y

x

p





Współczynnik korelacji

,

xy



y

x

xy

xy

C





 

W celu wyznaczenia korelacji można posłużyd się testem statystycznym (sprawdza czy
istnieje korelacja)

Definiujemy

)

1

ln(

5

.

0

xy

xy

w











Przy czym



























N

i

i

N

i

i

N

i

i

i

xy

y

y

x

x

y

y

x

x

1

2

1

2

1

)

(

)

(

)

(

)

(



Zmienna losowa w ma rozkład normalny przy czym

)

1

1

ln(

5

.

0

xy

xy

w













3

1





N

w



N- liczba pomiarów

Sprawdzamy czy

C

xy

xy

C

Z

N

Z















)

1

ln(

2

3





Z-odczytujemy z tablic dla podanego poziomu istotności

Jeżeli ten warunek jest spełniony to korelacja wynosi 0