1

1

Analiza regresji

2

Podstawowe pojęcia:

analiza regresji –badanie zależności funkcyjnej między

zmiennymi losowymi X i Y

regresja – odzwierciedlenie zależności między zmiennymi

losowymi w postaci funkcyjnej

korelacja – stopień zależności między zmiennymi losowymi.

Miarą jest współczynnik korelacji, który pokazuje w jakim

stopniu wartości zmiennej losowej skupiają się dookoła linii

regresji.

3

Wyniki pomiarów s

ą najczęściej powiązane ze sobą pewną teorią,

podaj

ącą zależności między różnymi wielkościami.

Je

żeli znamy te zależności to można na podstawie pomiarów

wyznaczy

ć oceny statystyczne parametrów równania.

Przy okre

ślaniu parametrów równania

pos

ługujemy się najczęściej

metod

ąąąą najmniejszych kwadratów.

Oznaczmy zale

żność funkcyjną

y=f(x: a

0

, a

1

, ….a

n

)

gdzie a

0

, a

1

, ….a

n

– parametry funkcji

Ta zale

żność może mieć postać:

y=ax+b, y=ae

b

x

+c, y=ax

b

e

c

x

itp.

i okre

śla się ją jako funkcję regresji

2

4

Mając dane uzyskane z pomiarów: y

1

, x

1

; y

2

, x

2

……. y

n

, x

n

ocen

ę parametrów

a

0

, a

1

, ….a

n

okre

ślamy z warunku:

suma kwadratów odchyle

ń mierzonych wartości y

k

od warto

ści obliczonej f(x

k

: a

0

, a

1

, … a

n

)

ma przyjmowa

ć wartość najmniejszą.

[

]

∑

=

=

−

=

n

k

n

k

k

a

a

a

x

f

y

S

1

2

1

0

min

)

,...

,

:

(

Ró

żniczkując cząstkowo zależność

S

otrzymujemy uk

ład równań jednorodnych

0

....

0

0

1

0

=

∂

∂

=

∂

∂

=

∂

∂

n

a

S

a

S

a

S

po rozwiązaniu, którego znajdujemy a

0

, a

1

, … a

n

.

Są to współczynniki regresji

5

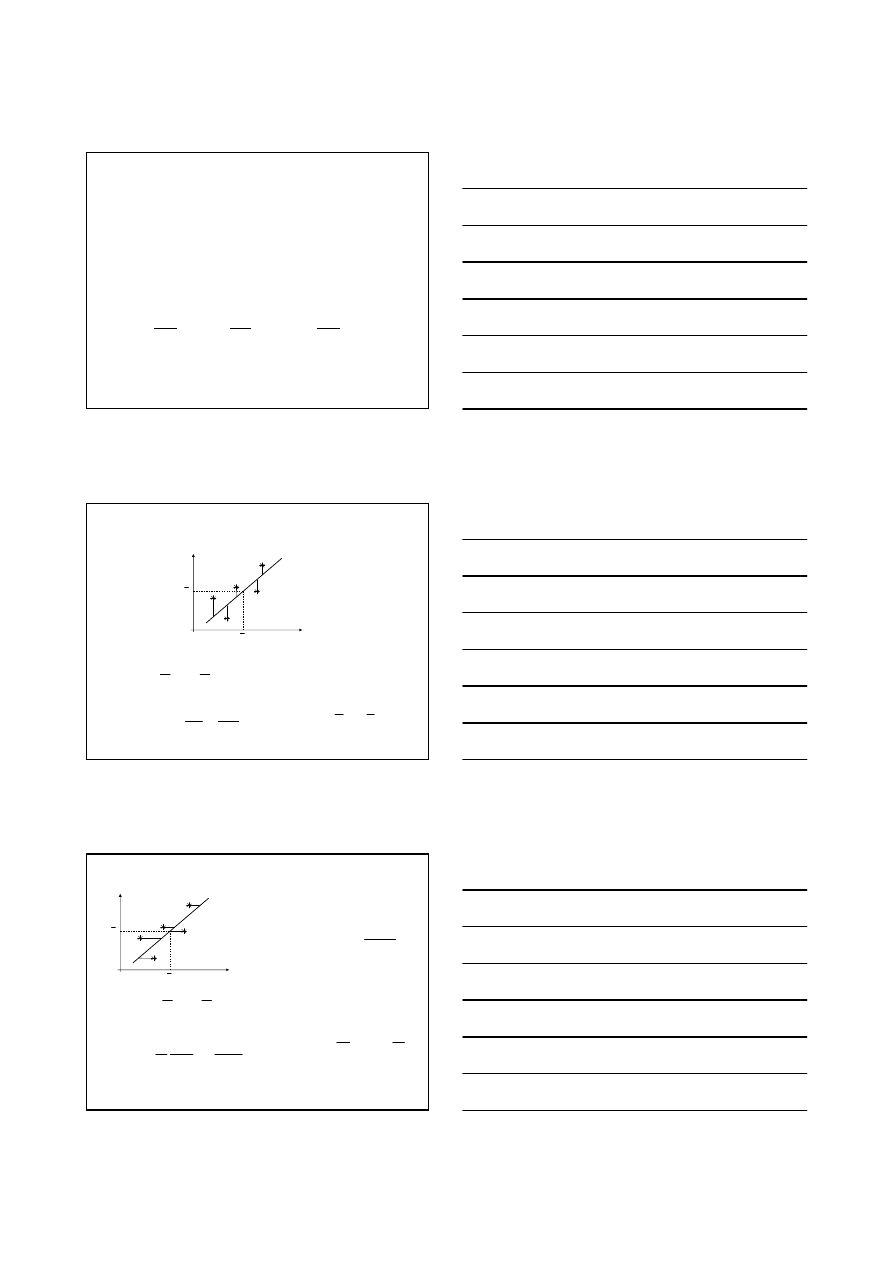
REGRESJA PROSTOLINIOWA

Oszacowanie prostej regresji:

cechy Y wzgl

ędem X

y=ax+b

Tworzymy funkcje F(a,b)=Σd

i

2

=min

d

i

y

x

y

x

[

]

∑

+

−

=

2

)

(

)

,

(

b

ax

y

b

a

F

i

i

Z równań

0

;

0

=

∂

∂

=

∂

∂

b

F

a

F

wyznacza się współczynniki regresji:

2

x

xy

x

y

S

S

S

S

r

a

=

=

x

a

y

b

−

=

6

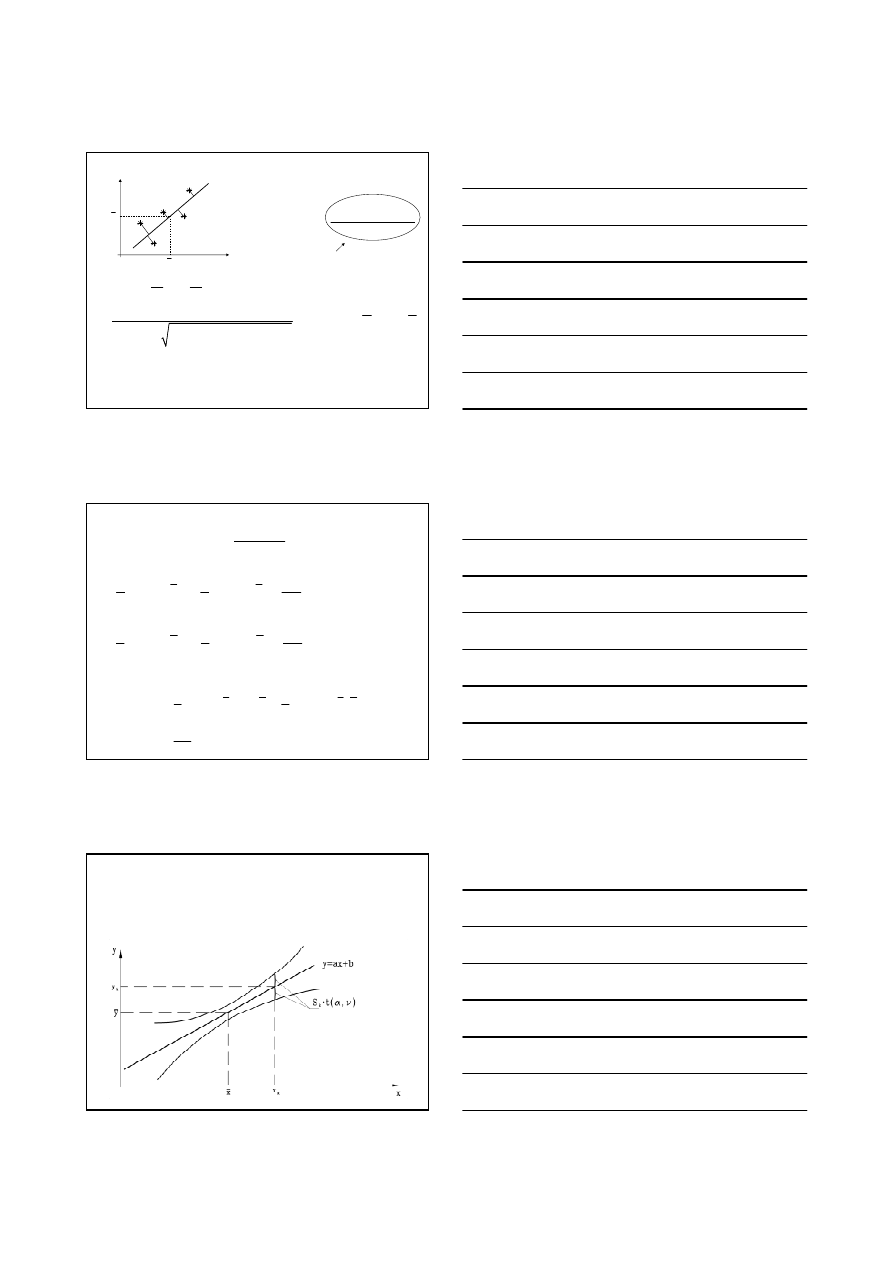
Oszacowanie prostej regresji:

cechy X wzgl

ędem Y

y=a’x+b’

Z równań

0

'

;

0

'

=

∂

∂

=

∂

∂

b

F

a

F

wyznacza się współczynniki regresji:

y

x

y

x

d’

i

∑

























−

−

=

2

'

'

)

'

,

'

(

a

b

y

x

b

a

F

i

i

xy

y

x

y

S

S

S

S

r

a

2

1

'

=

=

x

a

y

b

'

'

−

=

3

7

Oszacowanie prostej regresji ortogonalnej

y

x

y

x

d*

i

y=a*x+b*

Z równań

0

*

;

0

*

=

∂

∂

=

∂

∂

b

F

a

F

wyznacza się współczynniki regresji:

(

)

∑

+

−

+

=

1

*

*

*

*)

*,

(

2

2

a

y

b

x

a

b

a

F

i

i

to jest kwadrat odległości punktu od prostej

(

)

2

2

2

2

2

2

2 cov( , )

*

4 cov ( , )

x

y

x

y

x y

a

S

S

S

S

x y

=

−

+

−

+

x

a

y

b

*

*

−

=

(wg: Poradnik Matematyczny cz.2, Dziubi

ński, Świątkowski, PWN 1982)

8

y

x

S

S

y

x

r

⋅

=

)

,

cov(

(

)



























−

=

−

=

−

=

∑

∑

∑

∑

=

=

=

=

2

1

1

2

2

1

2

2

1

1

2

1

2

1

N

i

i

N

i

i

N

i

i

N

N

i

i

N

x

x

x

N

N

x

x

x

x

S

(

)



























−

=

−

=

−

=

∑

∑

∑

∑

=

=

=

=

2

1

1

2

2

1

2

2

1

1

2

1

2

1

N

i

i

N

i

i

N

i

i

N

N

i

i

N

y

y

y

N

N

y

y

y

y

S

współczynnik korelacji liniowej |r|≤1

Kowariancja:

(

)(

)













⋅

−

=

=

⋅

−

=

−

−

=

=

∑

∑

∑

∑

∑

=

=

=

=

=

N

i

i

N

i

i

N

i

i

i

N

i

i

i

N

N

i

i

i

N

xy

y

x

y

x

N

N

y

x

y

x

y

y

x

x

S

y

x

1

1

1

2

1

1

1

1

1

)

,

cov(

Wariancje:

9

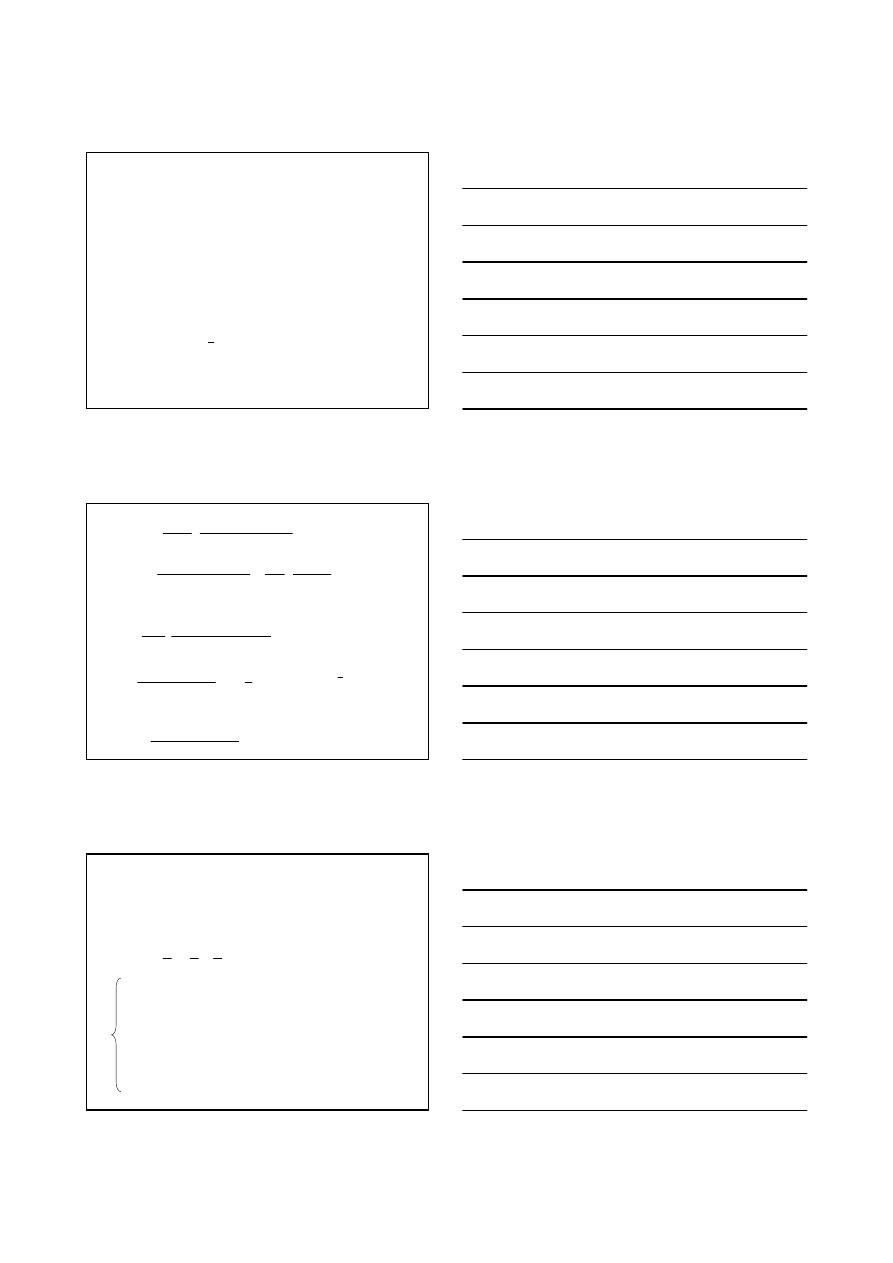
Przedział ufności dla prostej regresji f(x)=y=ax+b na
poziomie ufności 1-α

Obszar ten wyznacza si

ę wg wzoru:

P{y

k

-S

k

·

t(α,ν) <Y(X)< y

k

-S

k

·

t(α,ν)}= 1-α

4

10

gdzie

y

k

=a·x

k

+b

x

k

– dowolna wartość zmiennej losowej X

t(α,ν) – kwantyl rozkładu t-Studenta rzędu α o ν=n-2

stopniach swobody

Y(X) –

hipotetyczna średnia wartość cechy Y dla danej cechy X

[[[[

]]]]

2

2

2

2

)

(

x

x

S

S

S

k

x

a

k

−

−

−

−

+

+

+

+

=

=

=

=

- wariancja dla k-tego punktu

11

wariancja wyrazu wolnego prostej regresji

wariancja wspó

łczynnika kierunkowego prostej regresji

((((

))))

((((

))))

((((

))))

((((

))))

)

2

(

1

)

(

2

2

2

2

2

2

2

2

2

2

2

−

−

−

−

−

−

−

−

⋅⋅⋅⋅

=

=

=

=

−

−

−

−

=

=

=

=

=

=

=

=

−

−

−

−

−

−

−

−

⋅⋅⋅⋅

−

−

−

−

=

=

=

=

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

n

r

S

S

x

x

n

n

S

x

x

n

x

f

y

n

n

S

x

y

i

i

i

i

i

i

a

((((

))))

((((

))))

((((

))))

((((

))))

2

2

2

2

2

2

2

2

2

2

2

2

2

2

1

)

(

2

1

x

S

S

x

n

S

x

x

n

x

S

x

x

n

x

f

y

x

n

S

x

a

i

a

i

i

i

i

i

i

i

i

b

+

+

+

+

=

=

=

=

=

=

=

=

−

−

−

−

=

=

=

=

=

=

=

=

−

−

−

−

−

−

−

−

⋅⋅⋅⋅

−

−

−

−

=

=

=

=

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

((((

))))

)

2

(

)

(

2

2

−

−

−

−

−

−

−

−

=

=

=

=

∑

∑

∑

∑

n

x

f

y

S

i

i

12

REGRESJA KRZYWOLINIOWA

Wyznaczanie paraboli regresji:

[

]

∑

+

+

−

=

2

2

)

(

)

,

,

(

c

bx

ax

y

c

b

a

F

i

i

i

∑

∑

∑

∑

=

+

+

i

i

i

i

i

y

x

x

c

x

b

x

a

2

3

∑

∑

∑

∑

=

+

+

i

i

i

i

i

y

x

x

c

x

b

x

a

2

2

3

4

Tworzymy funkcje F(a,b,c)=Σd

i

2

=min

Z równań

0

;

0

;

0

=

∂

∂

=

∂

∂

=

∂

∂

c

F

b

F

a

F

wyznacza się współczynniki regresji:

∑

∑

∑

=

⋅

+

+

i

i

i

y

n

c

x

b

x

a

2

5

13

(

)(

)

;

1

∑

∑

∑

−

=

i

i

i

i

y

x

n

y

x

δ

(

)

(

)

;

1

2

2

∑

∑

∑

−

=

i

i

i

i

y

x

n

y

x

β

(

)

;

1

2

2

∑

∑

−

=

i

i

x

n

x

α

(

)

(

)

;

1

2

3

∑

∑

∑

−

=

i

i

i

x

x

n

x

γ

(

)

;

1

2

2

4

∑

∑

−

=

i

i

x

n

x

ε

Wprowadzamy zmienne pomocnicze:

14

parametry paraboli regresji:

;

2

γ

αε

γδ

αβ

−

−

=

a

Wspó

łczynnik zgodności (im mniejszy tym lepsza zgodność)

[

]

(

)

1

0

;

)

(

2

2

2

2

≤

≤

−

−

=

∑

∑

ϕ

ϕ

gdzie

y

y

x

f

y

i

i

i

;

2

γ

αε

βγ

δε

−

−

=

b

(

)

(

)

(

)

;

1

1

1

2

∑

∑

∑

−

−

=

i

i

i

x

n

a

x

n

b

y

n

c

Wspó

łczynnik korelacji krzywoliniowej

2

1

ϕ

−

=

R

15

Wyznaczanie hiperboli regresji dla funkcji homograficznej:

;

)

1

(

B

Ax

x

By

x

Ay

y

B

x

A

y

y

x

x

k

k

k

k

k

+

−

+

+

=

⇒

+

⋅

=

−

−

k

k

y

y

x

x

Y

x

X

−

−

=

= ;

⇒

)

,

(

k

k

y

x

;

)

(

b

ax

d

cx

x

f

y

+

+

=

=

Stosuj

ąc podstawienie:

B

X

A

Y

+

⋅

=

dowolny punkt ze zbioru punktów (x

i

, y

i

)

gdzie

otrzymujemy nowy zbiór punktów (X

i

, Y

i

),

dla którego oszacujemy parametry prostej regresji

b

a

d

c

6

16

(

)

X

A

Y

B

X

X

n

Y

X

Y

X

n

A

i

i

i

i

i

i

⋅

−

=

−

⋅

−

=

∑

∑

∑

∑

∑

;

2

2

parametry hiperboli regresji

k

k

k

x

By

d

Ay

c

B

b

A

a

−

=

+

=

=

=

;

1

;

[

]

(

)

1

0

;

)

(

2

2

2

2

≤

≤

−

−

=

∑

∑

ϕ

ϕ

gdzie

y

y

x

f

y

i

i

i

Wspó

łczynnik zgodności (im mniejszy tym lepsza zgodność)

b

ax

d

cx

x

f

i

i

i

+

+

=

)

(