Czyli jak
‘przewidzieć’
wynik?

Analiza regresji prostej

05.05.2010

Troche teorii



Regresja to

w statystyce metoda,

pozwalająca na zbadanie związku
pomiędzy

różnymi

wielkościami

występującymi

w

danych

i

wykorzystanie

tej

wiedzy

do

przewidywania nieznanych wartości
jednych wielkości na podstawie
znanych wartości innych.

regresja prosta

2

analiza regresji

Jednozmiennowa

Wielozmiennowa

prosta

wieloraka

regresja prosta

3

Rodzaje analizy regresji

Logika analizy regresji



Dokonujac analizy regresji budujemy
model zaleznosci liniowej pomiedzy
zmienna niezalezna a zmienna
zalezna.



W modelu wartosci jakie przyjmuje
zmienna zalezna, zaleza glownie od
wartosci zmiennej niezaleznej
(predyktora).

regresja prosta

4

Dokładniej
o predyktorze



Zarówno analiza regresji,
jak i korelacji nie pokazują zależności

przyczynowo – skutkowej wśród zmiennych.



Dlatego określenia: zmienna zależna i

niezależna nie mają tu uzasadnienia.



W związku z tym do analizy regresji

wprowadzono określenia:
dla zmiennej niezależnej:

PREDYKTOR

,

natomiast zmienna zależna to ta, której

wartość przewidujemy na podstawie

predyktora.

5

regresja prosta

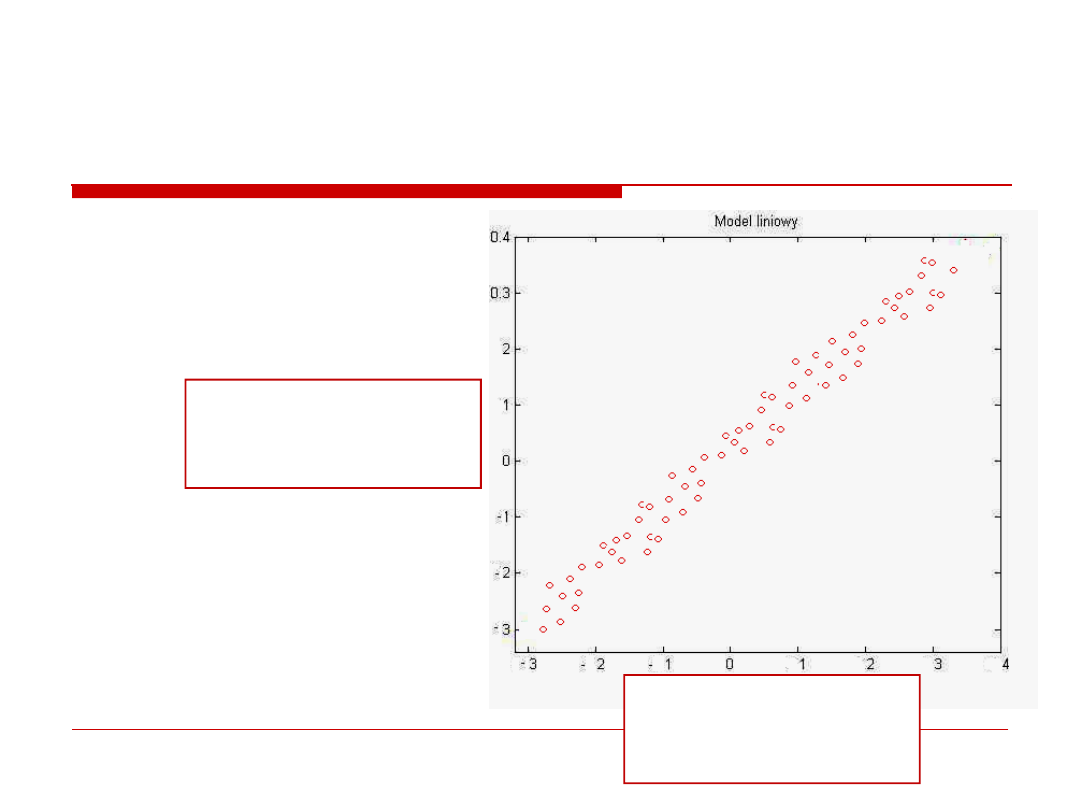
Dlaczego model liniowy?

Czy apetyt rosnie
w miare jedzenia?

6

regresja prosta

JEDZENIE

zm. wyjasniajaca

PREDYKTOR

X

X

Y

Y

APETYT

zm. wyjasniana

ZM. ZALEZNA

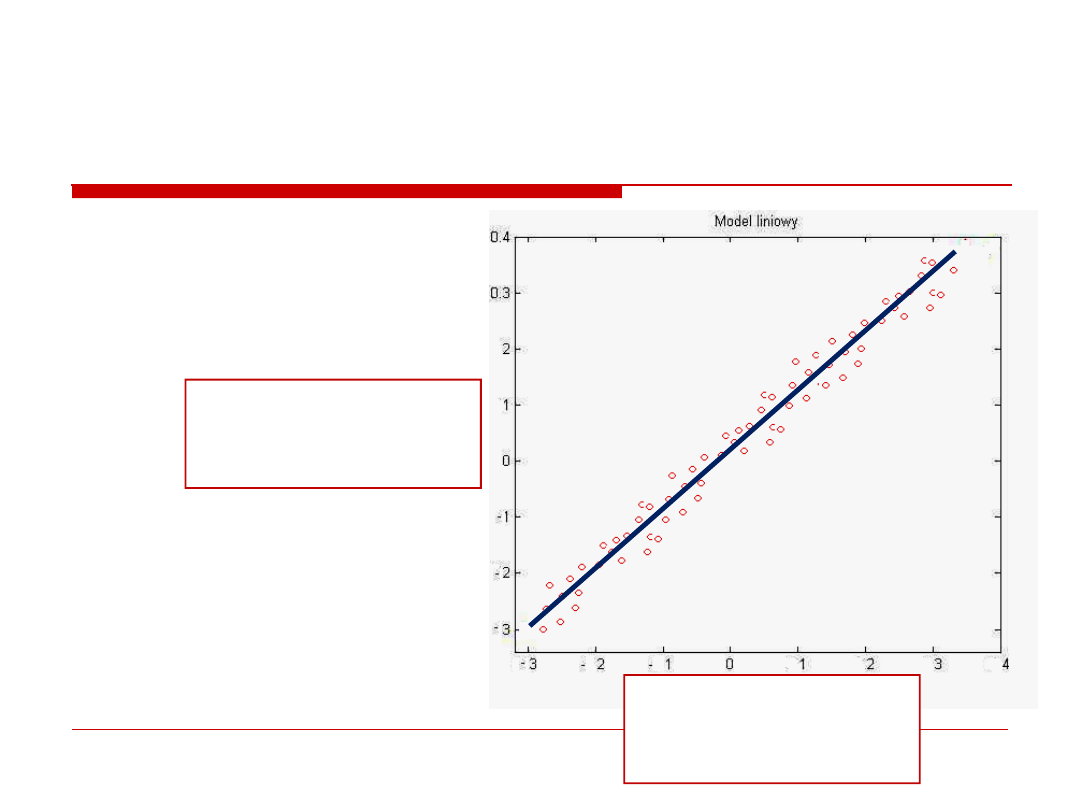
Czy apetyt rosnie w miare jedzenia?

7

regresja prosta

JEDZENIE

zm. wyjasniajaca

PREDYKTOR

X

X

Y

Y

APETYT

zm. wyjasniana

ZM. ZALEZNA

Jak znalezc linie?



Pierwszym krokiem analizy regresji jest
najdokladniejsze dopasowanie linii do
danych.



Linia musi byc najblizej wszystkich
punktow jednoczesnie.



Umozliwia to metoda najmniejszych
kwadratow.

regresja prosta

8

Metoda najmniejszych kwadratow



Pozwala na wykreslenie linii regresji
(dopasowania), poprzez odnalezienie
takich wspolczynnikow regresji, aby
suma podniesionych do kwadratu
odleglosci punktow od prostej byla jak
najmniejsza.

regresja prosta

9

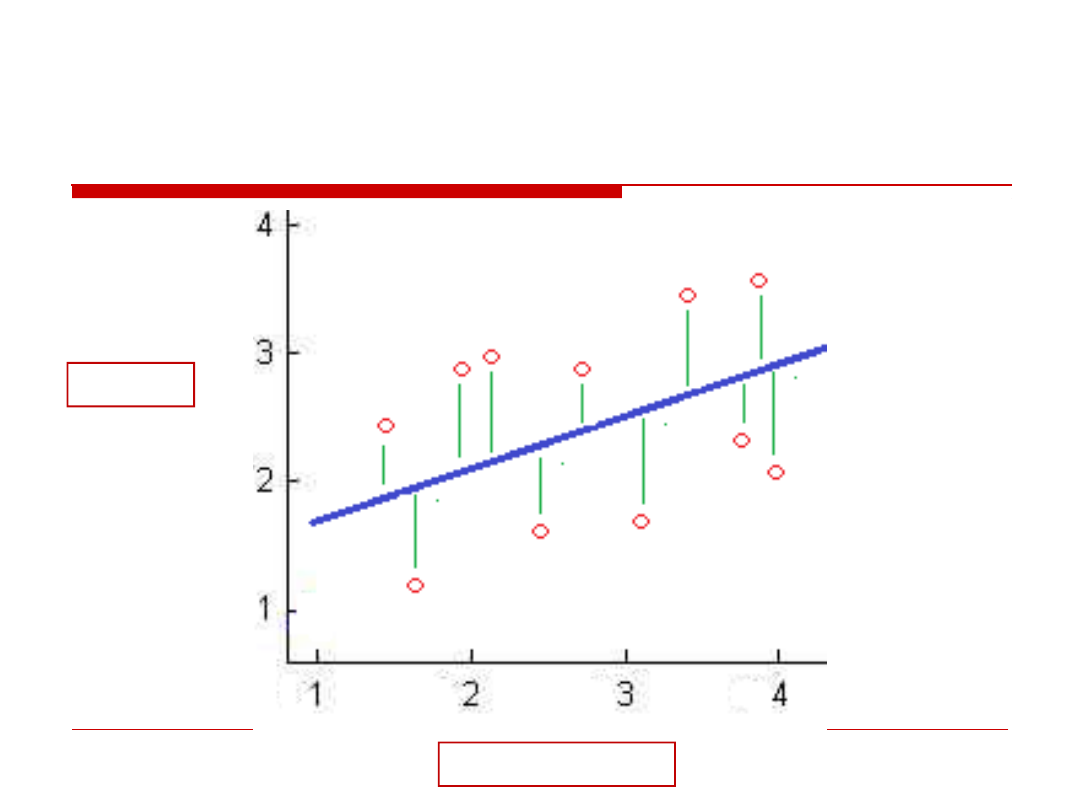
Metoda najmniejszych kwadratow

10

regresja prosta

JEDZENIE

X

X

Y

Y

APETYT

Linia dopasowania
moze sie wznosic lub opadac

regresja prosta

11

Im wieksza wartosc

predyktora (X), tym

wieksza wartosc

zmiennej Y

ZWIAZEK DODATNI,

ZWIAZEK DODATNI,

POZYTYWNY

POZYTYWNY

Im wieksza wartosc

predyktora (X), tym

mniejsza wartosc

zmiennej Y

ZWIAZEK UJEMNY,

ZWIAZEK UJEMNY,

NEGATYWNY

NEGATYWNY

+

-

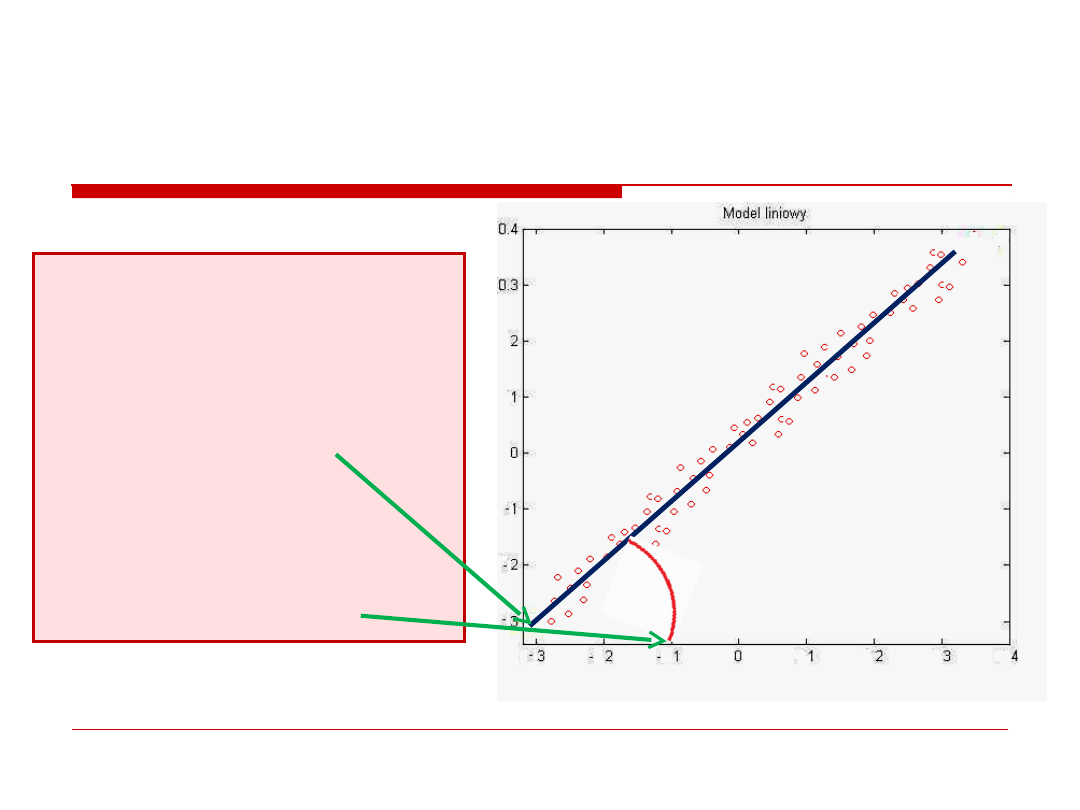
Cechy modelu

Cechy liniii regresji
okreslane sa przez
dwie charakterystyki:



Punkt przeciecia
z osia Y.



Nachylenie
wzgledem osi X.

12

regresja prosta

X

X

Y

Y

Bardziej formalnie



Model to rownanie opisujace
linie prosta zawierajace dwa
wspolczynniki: stala okreslajaca
punkt przeciecia (b) i wspolczynnik
kierunkowy, opisujacy nachylenie linii
(a). Oraz przewidywana wartosc
zmiennej zaleznej (y) i wartosc
predyktora (x).

y = ax + b

y = ax + b

regresja prosta

13

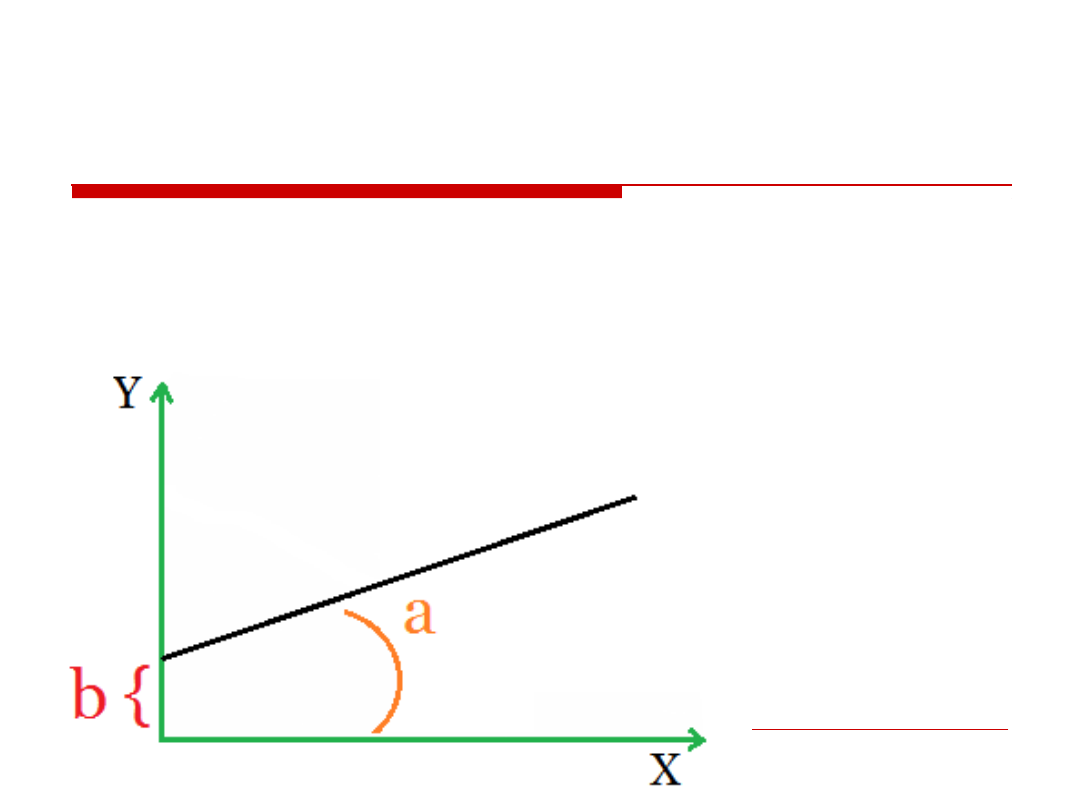
y = ax + b

y = ax + b

regresja prosta

14

Y – przewidywane wartosci zm. zaleznej

X – wartosci predyktora
a – nachylenie linii
(o ile zmieni sie y, gdy x zmieni sie o jednostke).
b – stala (wyraz wolny, punkt przecieca linii regresji),
ile wynosi y, gdy x = 0.

Współczynnik korelacji r Pearsona



Opierają się na nim metody:
analiza regresji, analiza czynnikowa, analiza rzetelności,



Przybiera wartości od <-1;1>



Wartosci ujemne informuja o spadku (Y maleje ze
wzrostem X).



Wartosci dodatnie informuja o wzroscie (Y rosnie ze
wzrostem X).



Jesli r = 0, to znaczy, ze dane na wykresie nie tworza
zaleznosci liniowej.



Jesli r = 1, lub r = -1, to znaczy, ze dane ukladaja sie w
idealna zaleznosc.



Ocena jakościowa: umowna

regresja prosta

15

Współczynnik determinacji



Pokazuje w jakim stopniu model regresji
odzwierciedla relacje miedzy danymi.



Miara sily zwiazku jest R² (wspolczynnik
determinacji).



Wynik R² mozna rozumiec jako proporcje
zmiennosci ZZ wyjasnianej przez rownanie
regresji w stosunku do calej zmiennosci ZZ.
Gdy R² = 0.53, mozna stwierdzic, ze apetyt da
sie w 53% przewidziec na podstawie ilosci
spozytego jedzenia.

regresja prosta

16

R²



Wielkosc tego wspolczynnika jest
zawsze dodatnia i przyjmuje wartosci
od 0 do 1.



Po wyciagnieciu pierwiastka
otrzymujemy informacje na temat
kierunku, wzrostu i spadku jednej
zmiennej w stosunku do drugiej.

regresja prosta

17

Zalozenia analizy regresji

(jako testu parametrycznego)



Zm. zalezna i predyktory

pochodza z populacji o rozkladzie normalnym (Test

Kolmogorowa-Smirnowa).



Obie zmienne mierzone na skali ilosciowej
(ewentualnie nominalnej, ale tylko
dwukategorialnej)!



Liczba przypadków równa 10 x liczba zmiennych:
dwie zmienne to konieczność przebadania min. 20
osób.



W regresji wielozmiennowej, predyktory nie powinny
ze soba korelowac, a wiec musza byc niezalezne.

regresja prosta

18

Zadanie 1

Badacze chcieli sprawdzic, czy zdolnosci
matematyczne

wsrod

studentow

maja

zwiazek z wynikami osiaganymi na zajeciach
ze statystyki. Sprawdzali czy na podstawie
testu umiejetnosci matematycznych mozna
przewidziec wyniki ze statystyki?
Przeanalizowano wyniki 30 studentow.

osiagniecia.sav

regresja prosta

19

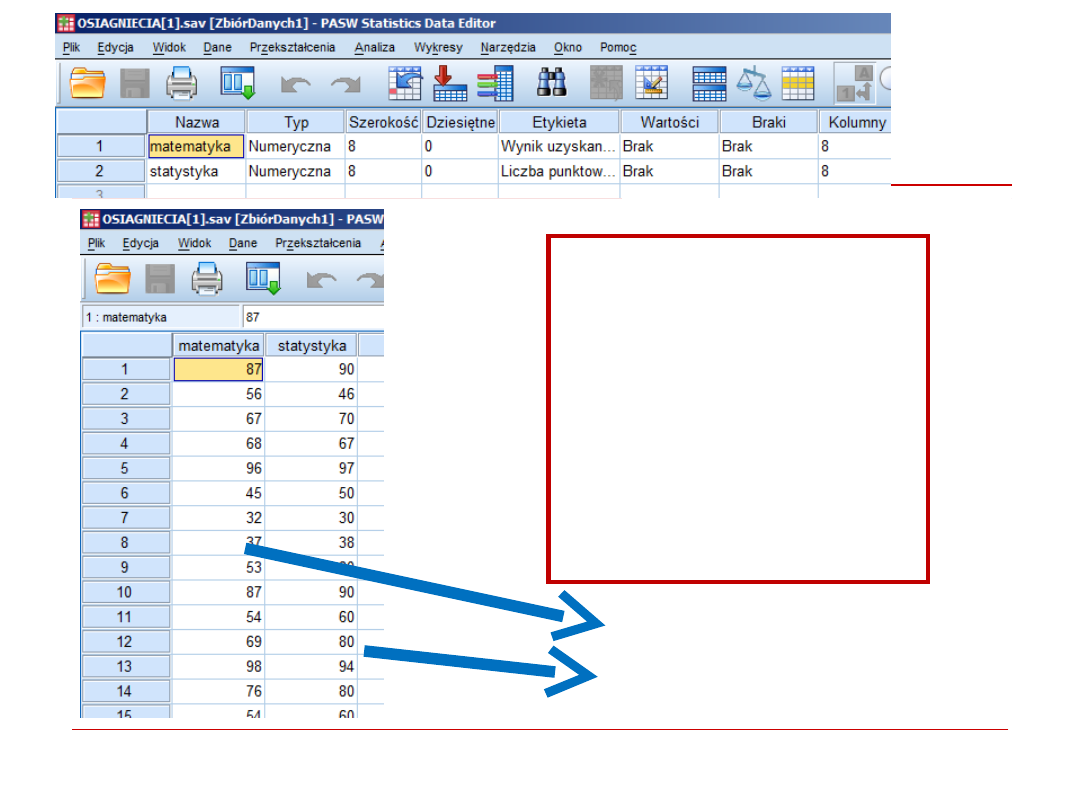
regresja prosta

20

LICZBA PUNKTOW

ZDOBYTYCH W TESCIE

MATEMATYCZNYM I

LICZBA

PUNKTOW

UZYSKANYCH NA

STATYSTYCE

DANE DLA 30

STUDENTOW

PREDYKTOR

PREDYKTOR (matematyka)

ZM. WYJASNIANA

ZM. WYJASNIANA
(staystyka)

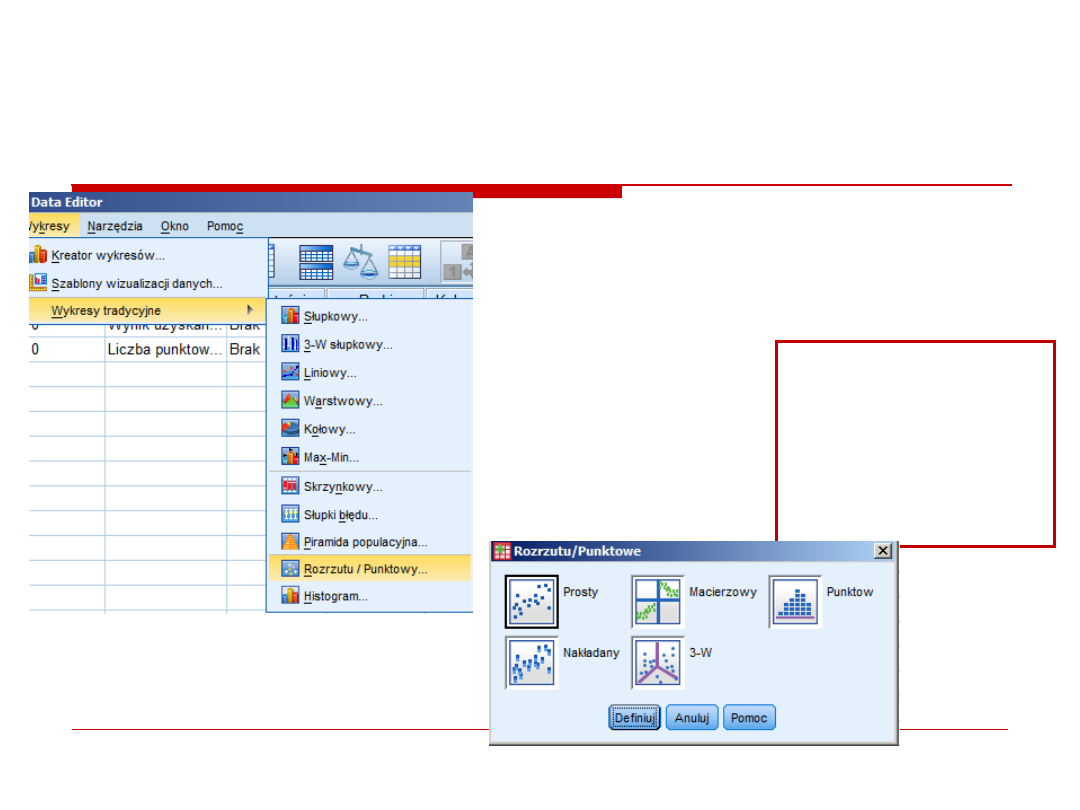
Na poczatek wykres rozrzutu

regresja prosta

21

Os X:
PREDYKTOR

Os Y:
ZM. WYJASNIANA,
WYNIKOWA

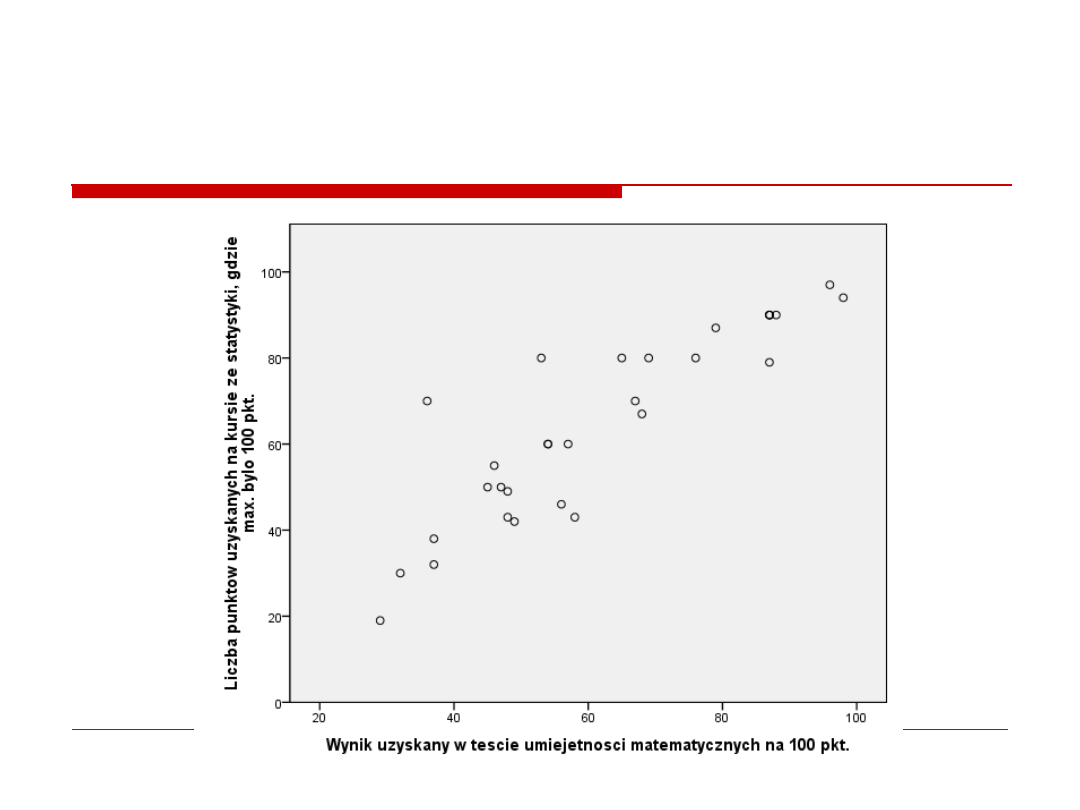
Dane ukladaja sie w zw. linowy dodatni

regresja prosta

22

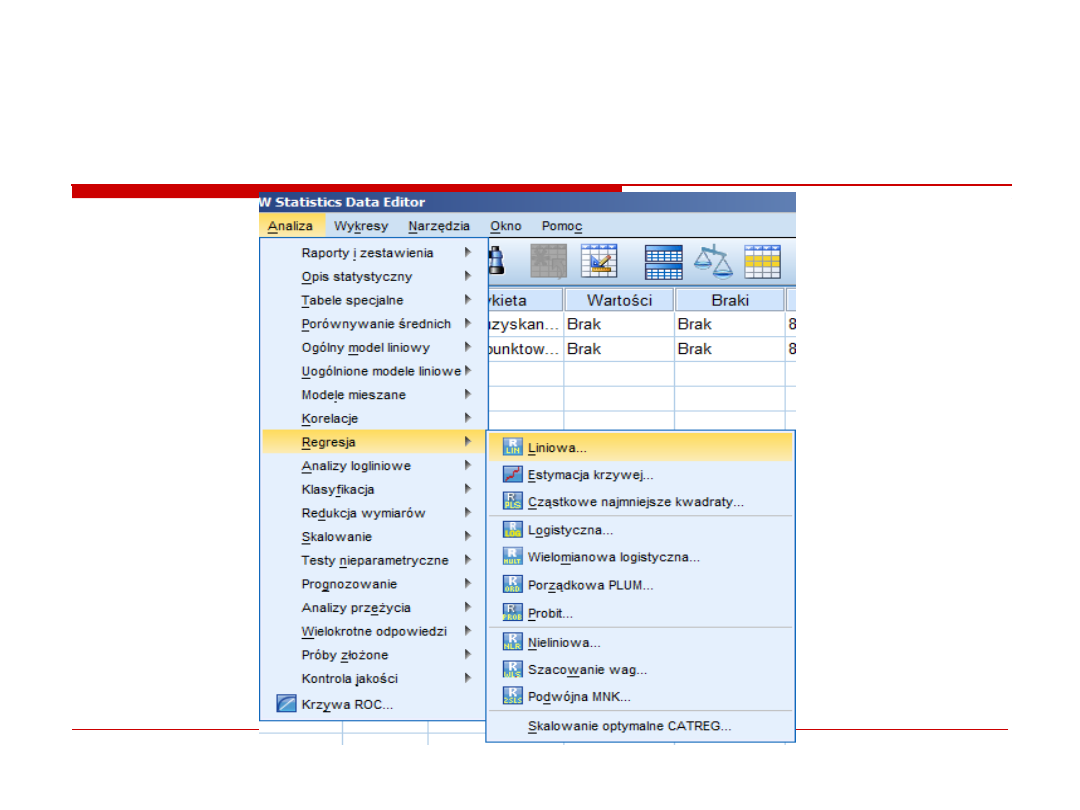
A teraz analiza...

regresja prosta

23

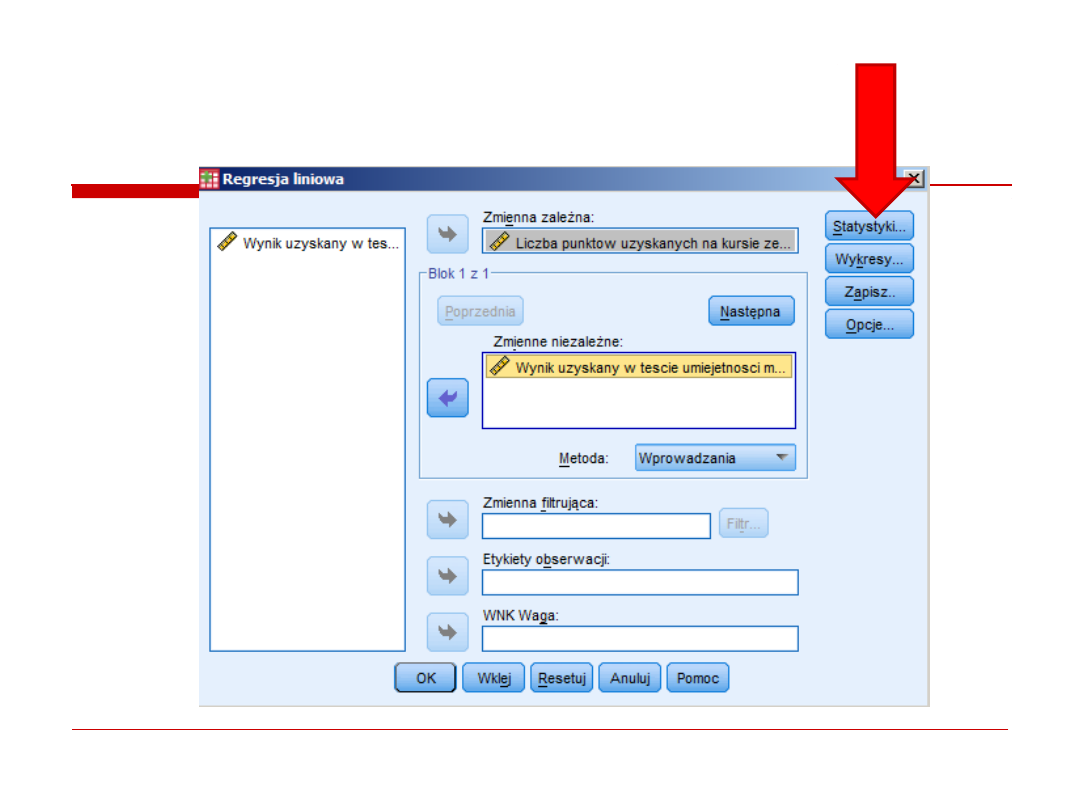
regresja prosta

24

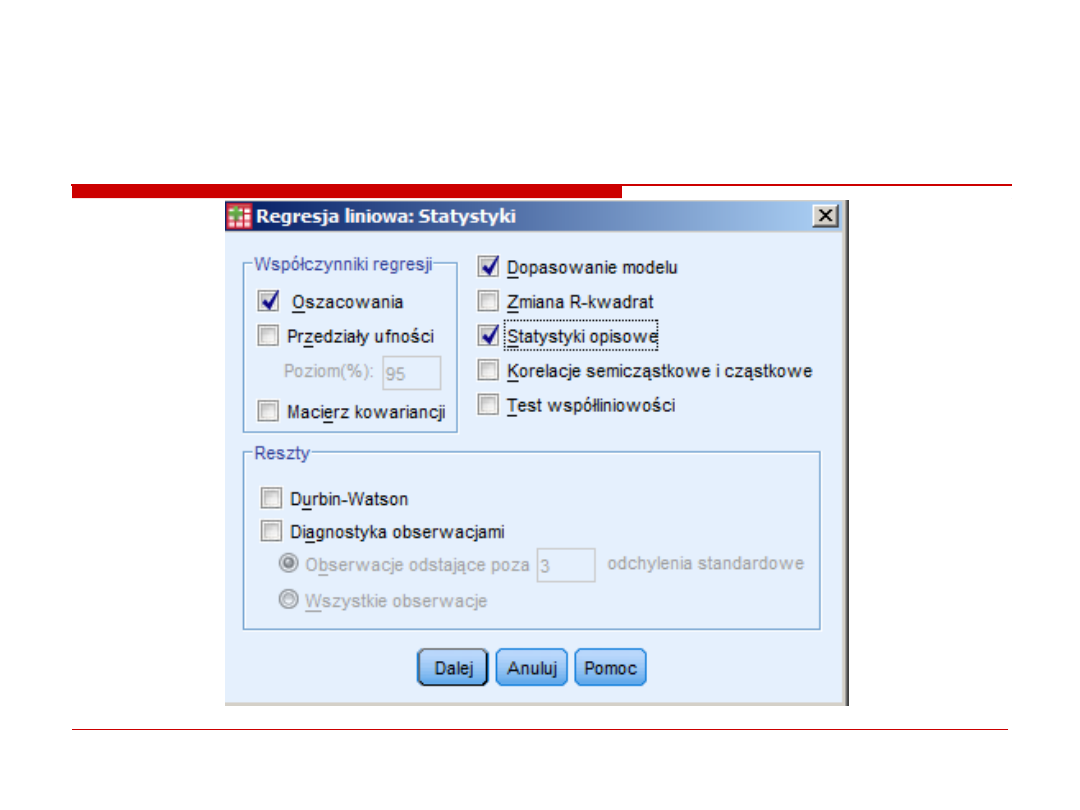
Opcje:

regresja prosta

25

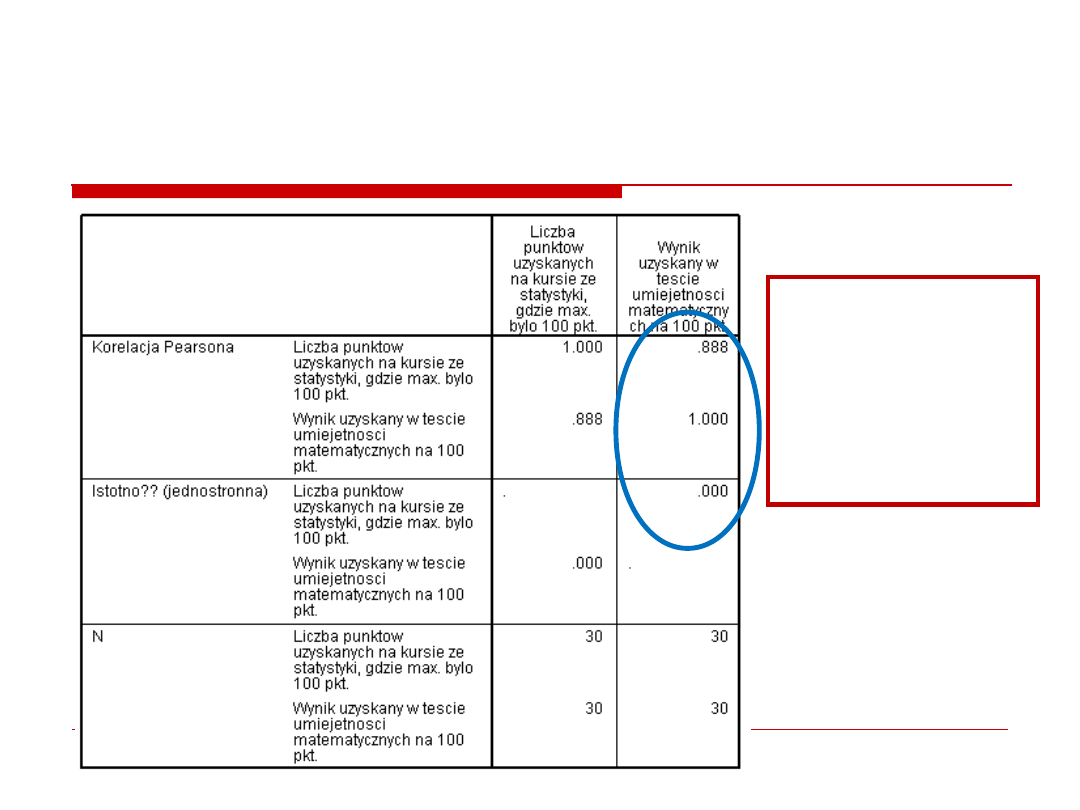
Wyniki:

regresja prosta

26

r (30) = .89
SILNA
DODATNIA
KORELACJA
p < . 001

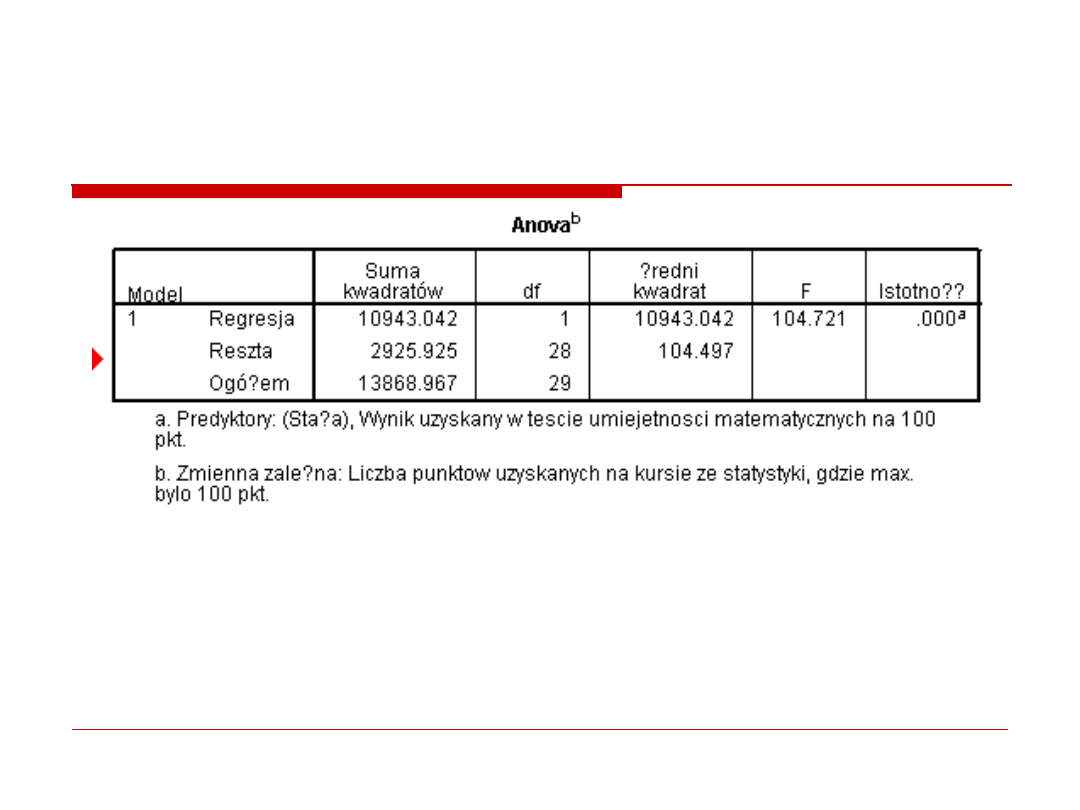
Wyniki cd.

regresja prosta

27

F (1, 28) = 104.72, p < .001

Istotnosc testu F informuje nas o tym,

czy model jest dobrze dopasowany.

Jesli jest istotny, to znaczy, ze tak.

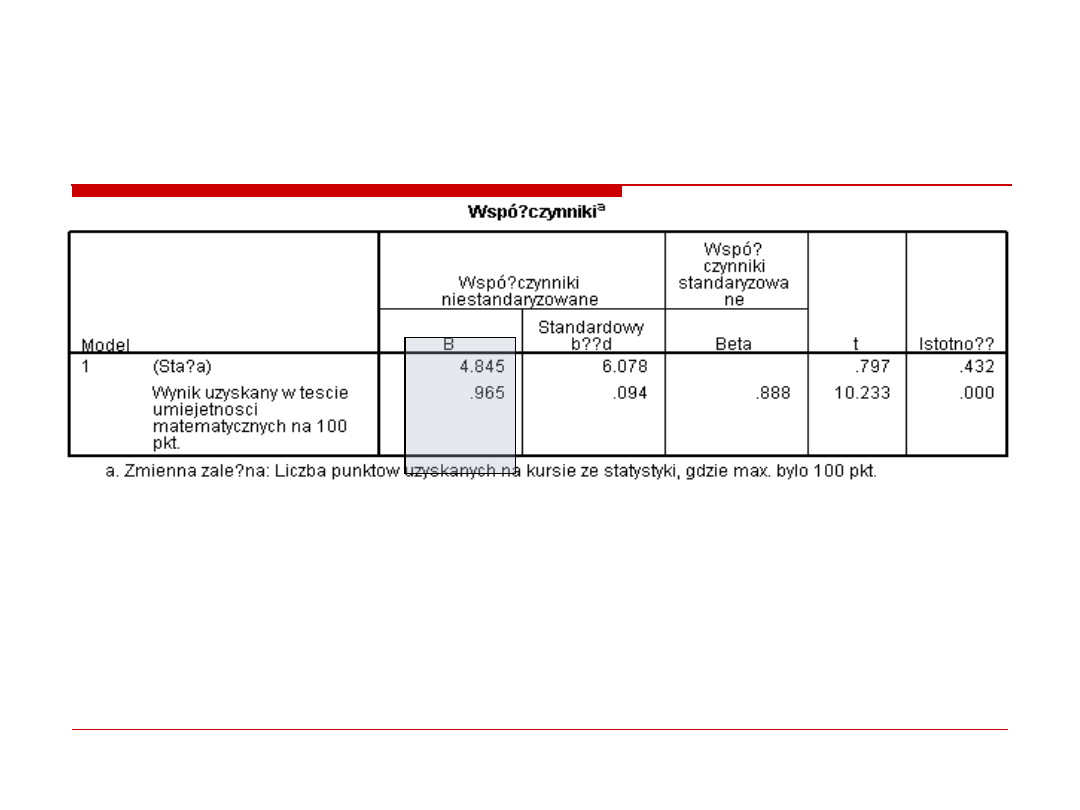
Wyniki cd.

Przewidywanie wartosci zmiennej wyjasnianej

regresja prosta

28

βo = 4.845 oznacza, że gdy w tescie matematycznym student
otrzyma 0 pkt., to ze statystyki otrzyma 0 pkt! Ten efekt jest
nieistotny!

β1 = .965 oznacza wielkość zmiany zmiennej Y, gdy zmienna X
wzrośnie o jedną jednostkę (1 pkt.)

Wzrost wyniku w tescie matematycznym o 1 pkt., powoduje wzrost
liczby punktow na statystyce o .97 pkt.

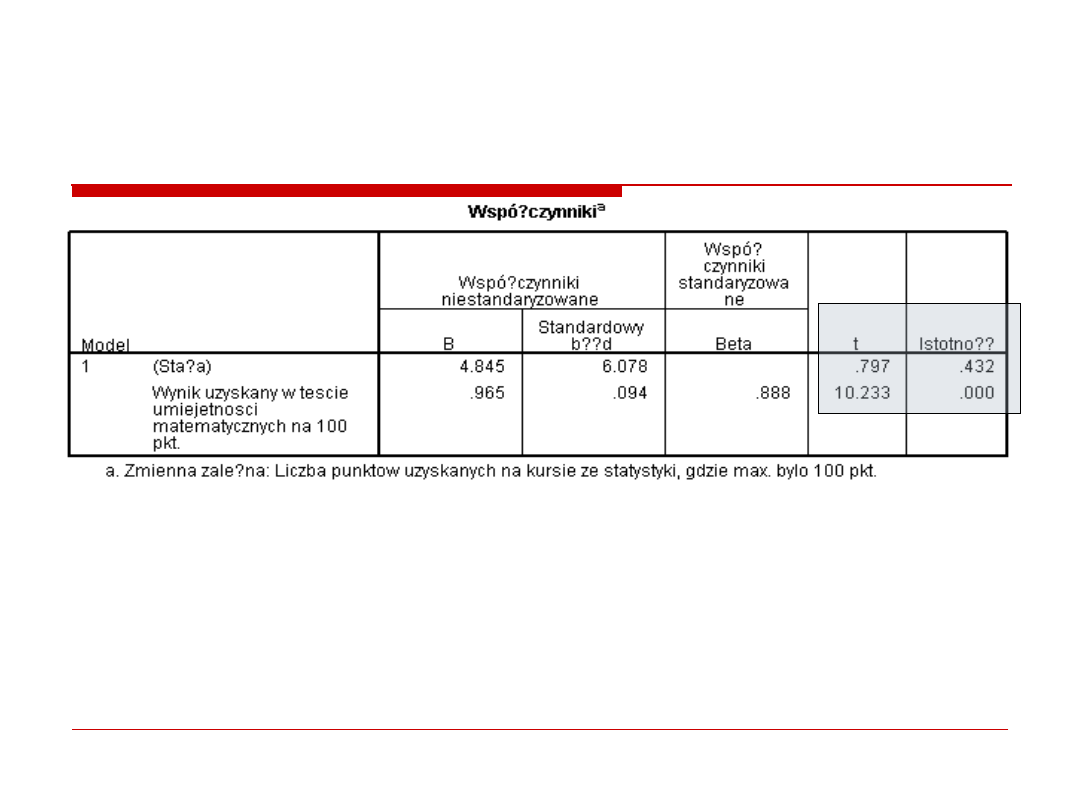
O czym informuje test t?

regresja prosta

29

Istotność testu t wskazuje tu, czy wartość różni się istotnie od zera.
Jeśli test t nie jest istotny, oznacza, że Beta nie różni się istotnie od
zera – zmiana wartości predyktora nie powoduje zmiany zmiennej Y.

Efektywnosc modelu:

regresja prosta

30

r = .89 korelacja pomiędzy liczba punktow uzyskanych w tescie
matematycznym a wynikiem ze statystyki.

R

2

= .79 Wynik w tescie matematycznym wyjasnia 78,9% wariancji

wyniku ze statystyki (mnożymy tę wartość x 100).

BŁĄD STANDARDOWY OSZACOWANIA - mówi nam jakim błędem
obarczone jest nasze przewidywanie wynikow ze statystyki – o 10.22
pkt. w górę i w dół.

interpretacja

regresja prosta

31

Badano możliwość przewidywania wynikow z kursu ze
statystyki na podstawie liczby punktow z testu
matematycznego. Model regresji okazał się być dobrze
dopasowany: F (1, 28) = 104.72, p < .001. Zmienna
wynik testu matematycznego wyjaśnia 79% wariancji
wynikow ze statystyki. Zależność między predyktorem a
zmienną wyjaśnianą była silna i dodatnia (Beta=.89). Im
więcej punktow z matematyki, tym wieksze osiagniecia
na statystyce. Wartość współczynnika kierunkowego
wyniosła .97, t (28) = 10.23, p < .001, a wartość stałej
wyniosła 0, t (28) = .78, p = .432. Oznacza to, że z
każdym kolejnym punktem w tescie matematycznym,
liczba punktow ze statystyki ma szanse wzrosnac o .97.

Zadanie 2

Badacze chcieli sprawdzic czy na podstawie
czasu spedzanego na korzystaniu z mediów
(TV, internet) da sie przewidziec wyniki w
tescie tworczosci.
W tym celu przeanalizowali deklaracje 60
osob na temat dziennego czasu jaki spedzaja
z mediami (w godzinach), oraz wynikow jakie
osiagneli na skali tworczosci.

tworczosc.sav

regresja prosta

32

ANALIZA KROK PO KROKU 

regresja prosta

33

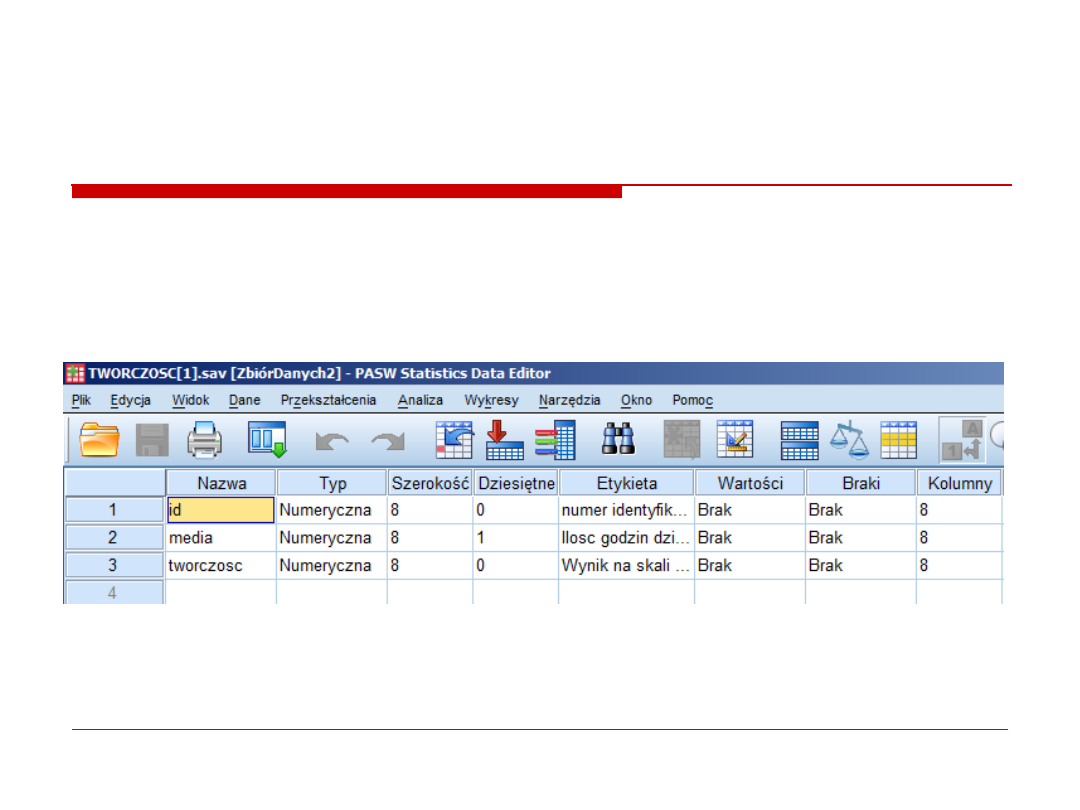
0. przedbiegi

regresja prosta

34

Zapoznanie sie ze zmiennymi.

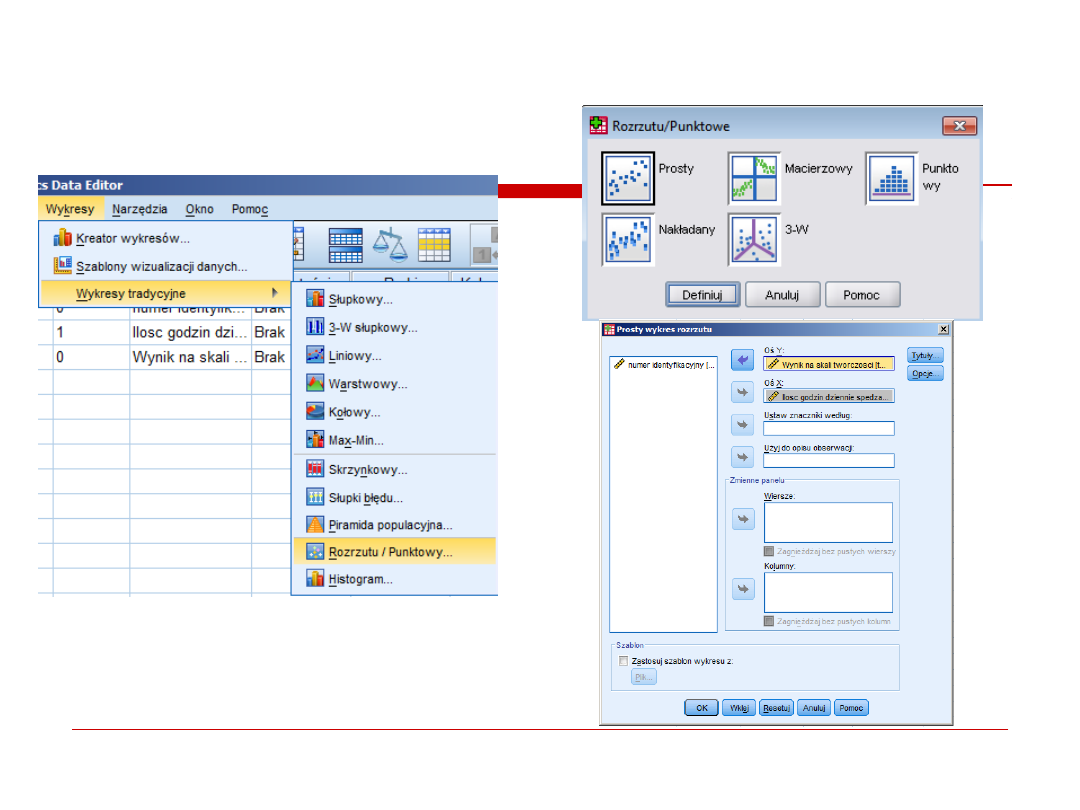
1. wykres

regresja prosta

35

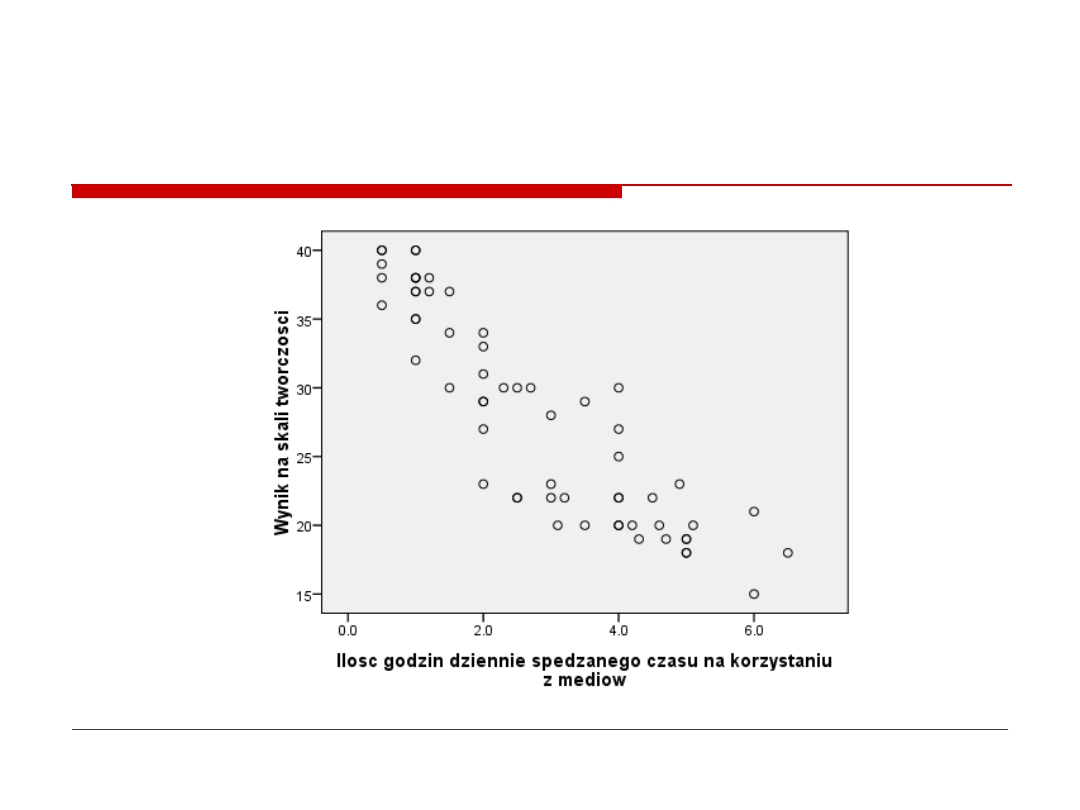
Jak widac zaleznosc miedzy zmiennymi
jest odwrotnie proporcjonalna

regresja prosta

36

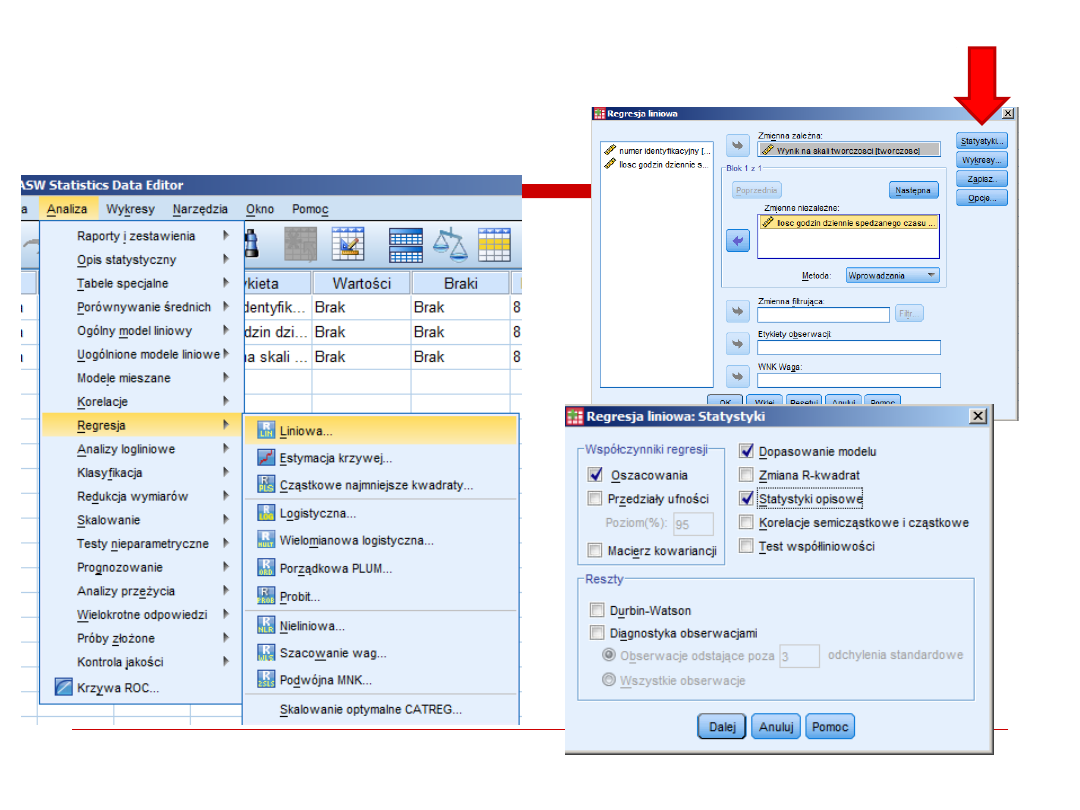
2. analiza

regresja prosta

37

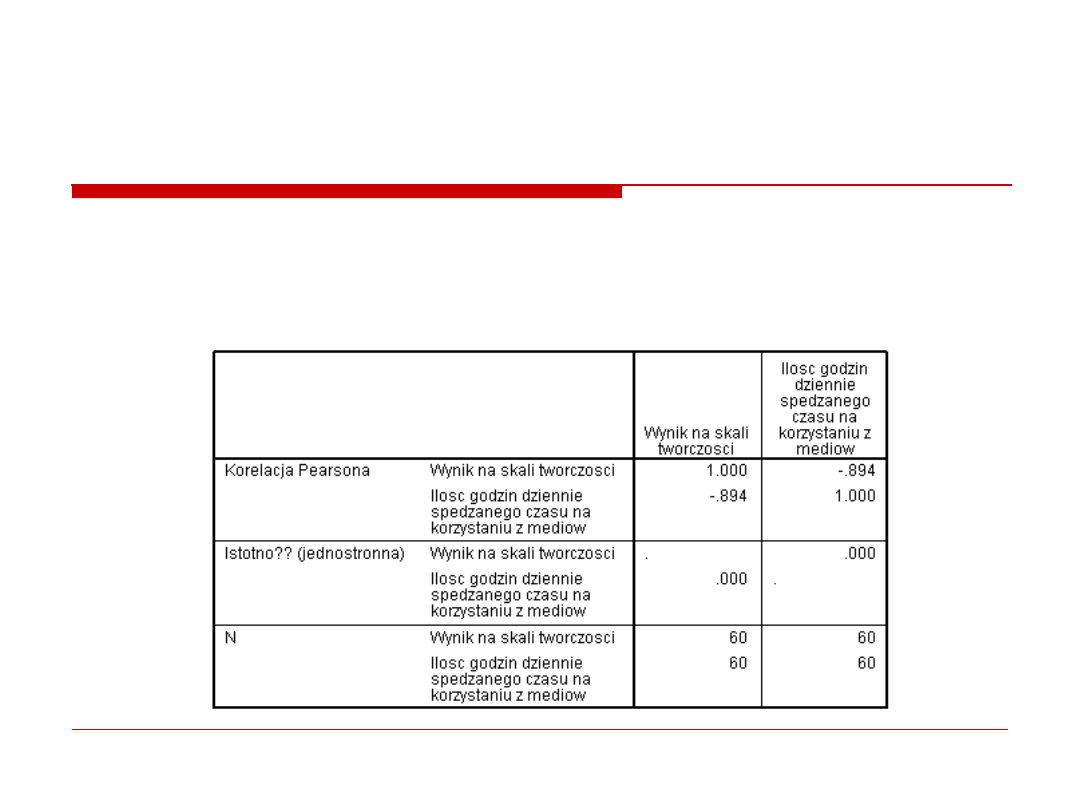
3. korelacje



Istnieje silna negatywna zaleznosc pomiedzy dzienna liczba
godzin korzystania z mediow a wynikiem na skali tworczosci.



r (60) = -.89, p < .001

regresja prosta

38

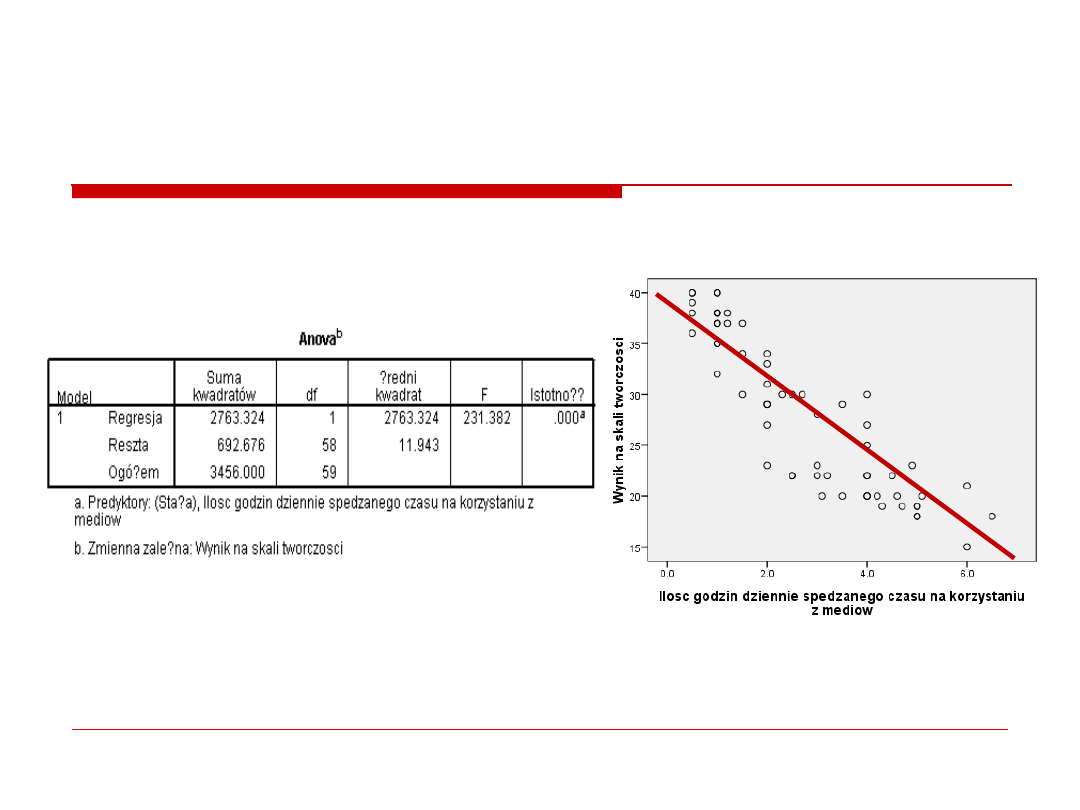
4. Analiza wariancji



Czyli czy model jest dopasowany?

regresja prosta

39

F

F

(1, 58) = 231.38,

(1, 58) = 231.38,

p

p

< .001

< .001

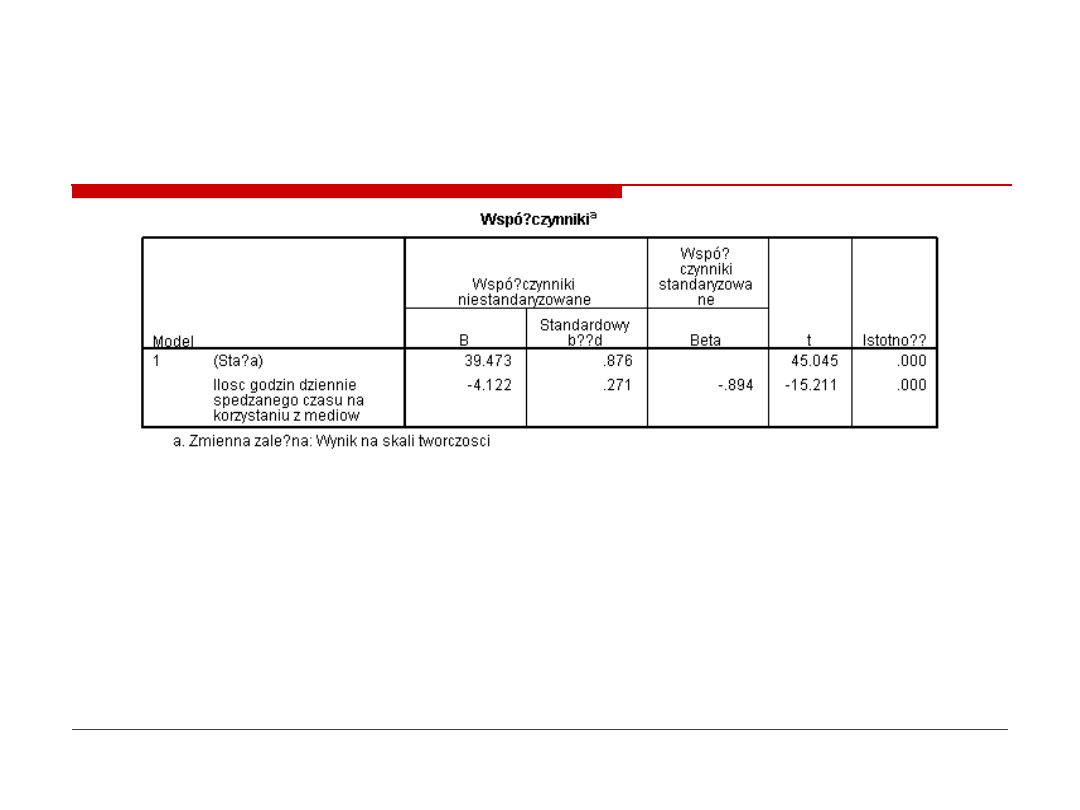
5. Predykcja

Przewidywanie wartosci zmiennej wyjasnianej.



βo = 39.47 oznacza, że gdy osoba badana w ogole nie
korzysta z mediow (X = 0), to na skali tworczosci otrzyma
39.47 pkt.



β1 = -4.12 oznacza, ze wzrost czasu poswieconego na
korzystnie z mediow o 1h, powoduje spadek liczby punktow na
skali tworczosci o 4.12.



Czy zmiana wartosci predyktora powoduje zmiane zm. Y?

regresja prosta

40

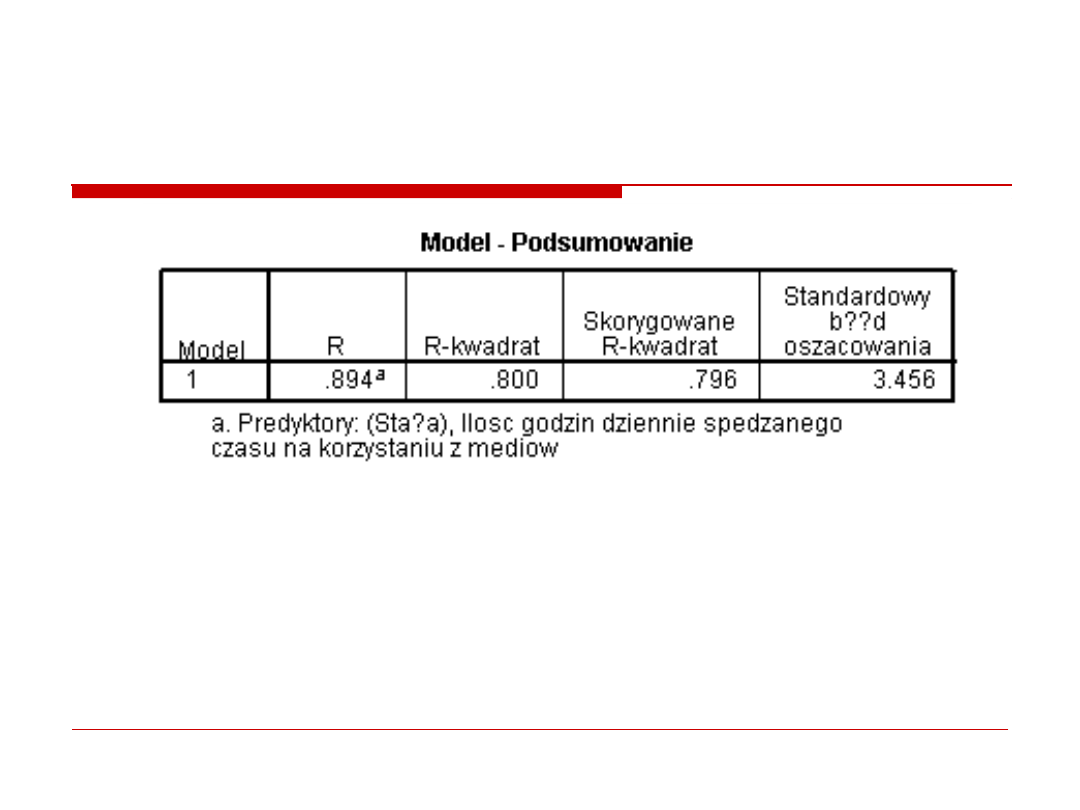
6. Efektywnosc modelu



r = -.89 (zaleznosc miedzy zmiennymi)



R

2

= .80 Liczba h spedzonych z mediami wyjasnia 80%

wariancji wyniku na skali tworczosci.



BŁĄD STANDARDOWY OSZACOWANIA – przewidywania
wynikow na skali tworczosci obarczone sa błędem 3.46 pkt. w
górę i w dół.

regresja prosta

41

7

. Interpretacja



regresja prosta

42

Badano możliwość przewidywania wynikow w tescie
tworczosci na podstawie ilosci godzin dziennie
spedzanych na korzystaniu z mediow. Model regresji
okazał się być dobrze dopasowany: F(1, 58) = 231.38, p
< .001. Zmienna liczba godzin z mediami wyjaśnia 80%
wariancji wynikow na skali tworczosci. Zależność między
predyktorem a zmienną wyjaśnianą była silna i ujemna
(Beta=.89). Im więcej godzin dziennie z mediami, tym
mniejsze osiagniecia w tescie tworczosci. Wartość
współczynnika kierunkowego wyniosła 4.12, t(58) =
15.21, p < .001, a wartość stałej 38.47, t(58) = 45.05, p
< .001. Oznacza to, że z każda kolejna godzina
dziennego korzystania z mediow, liczba punktow na skali
tworczosci moze zmalec o 4.12.

Zadanie 3

regresja prosta

43

Badacze chcieli sprawdzic czy reaktywnosc
emocjonalna (RE) osoby badanej ma zwiazek i
wyjasnia syndrom wypalenia zawodowego.
Przebadanych zostalo 50 pracownikow duzej
korporacji. Na podstawie kwestionariusza
temperamentu FCZ_KT otrzymano wskaznik
RE, a na podstawie Kwestionariusza
wypalenia zawodowego ogolny wskaznik
wypalenia.

wypalenie.sav

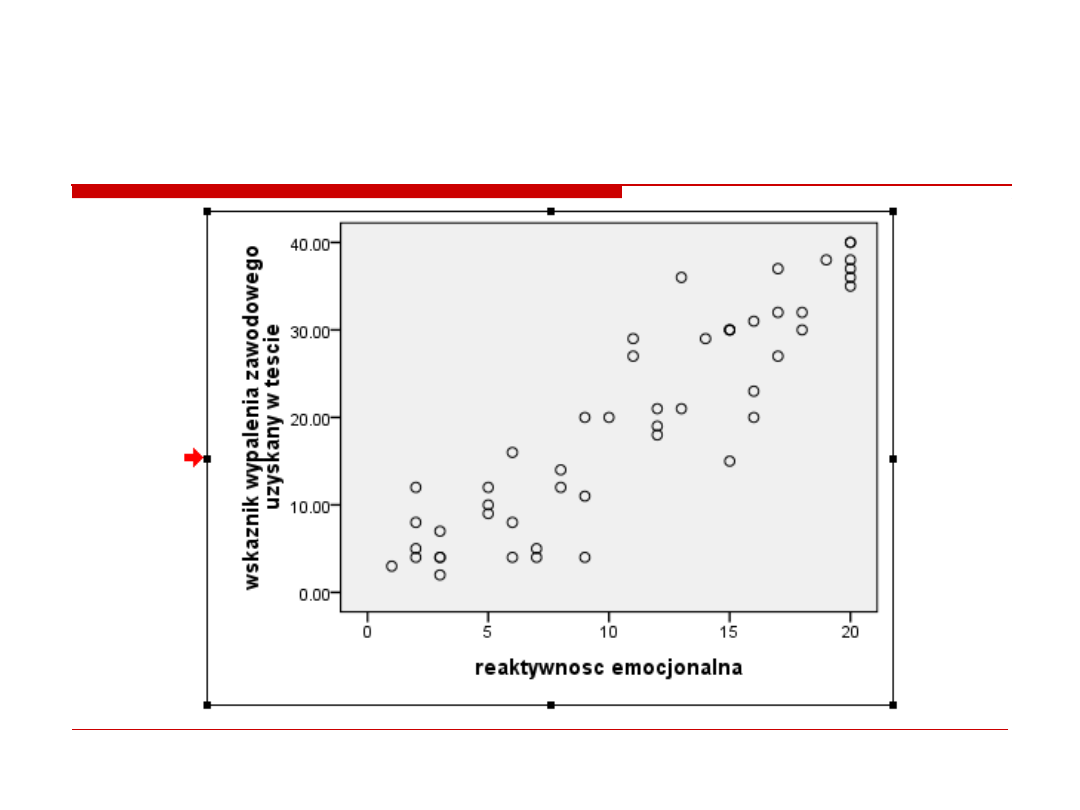
1. wykres

regresja prosta

44

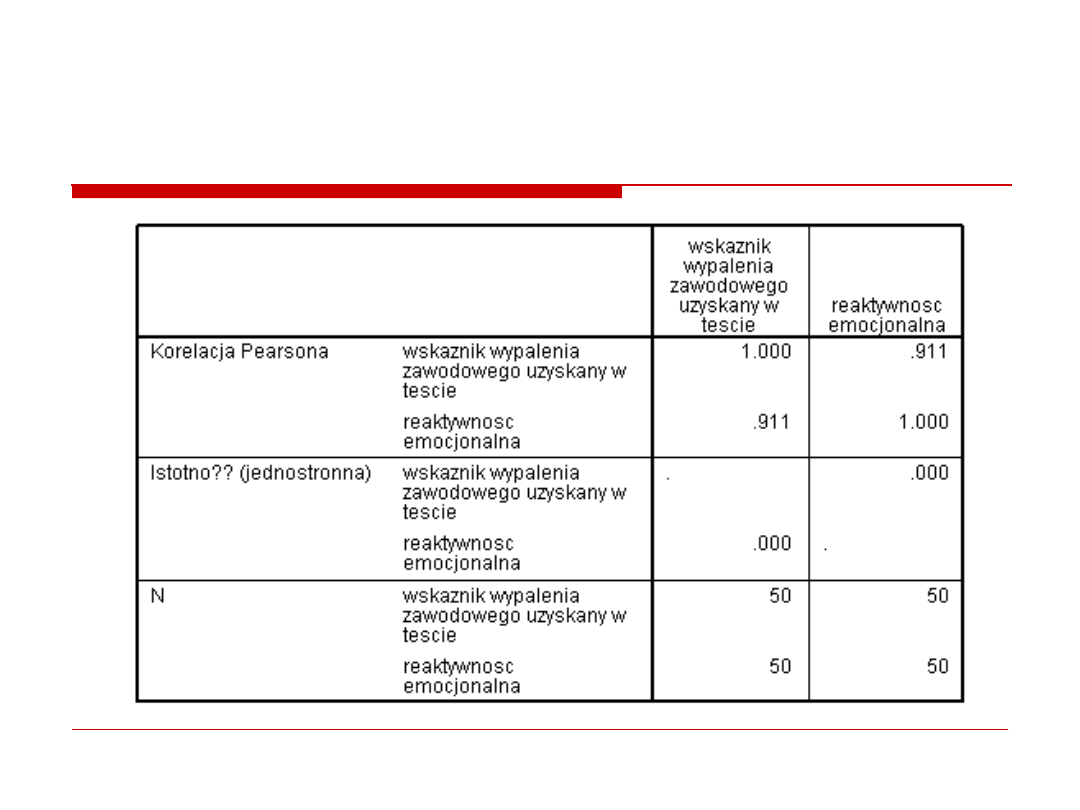
2. korelacje

regresja prosta

45

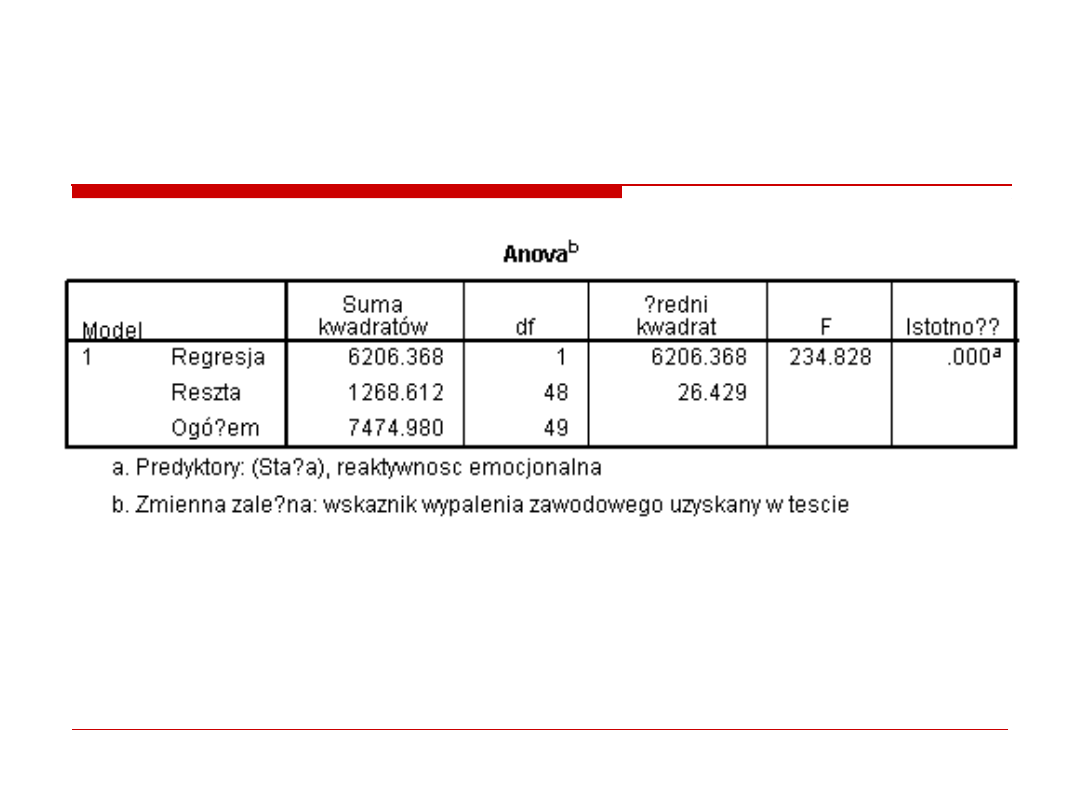
3. Analiza wariancji

regresja prosta

46

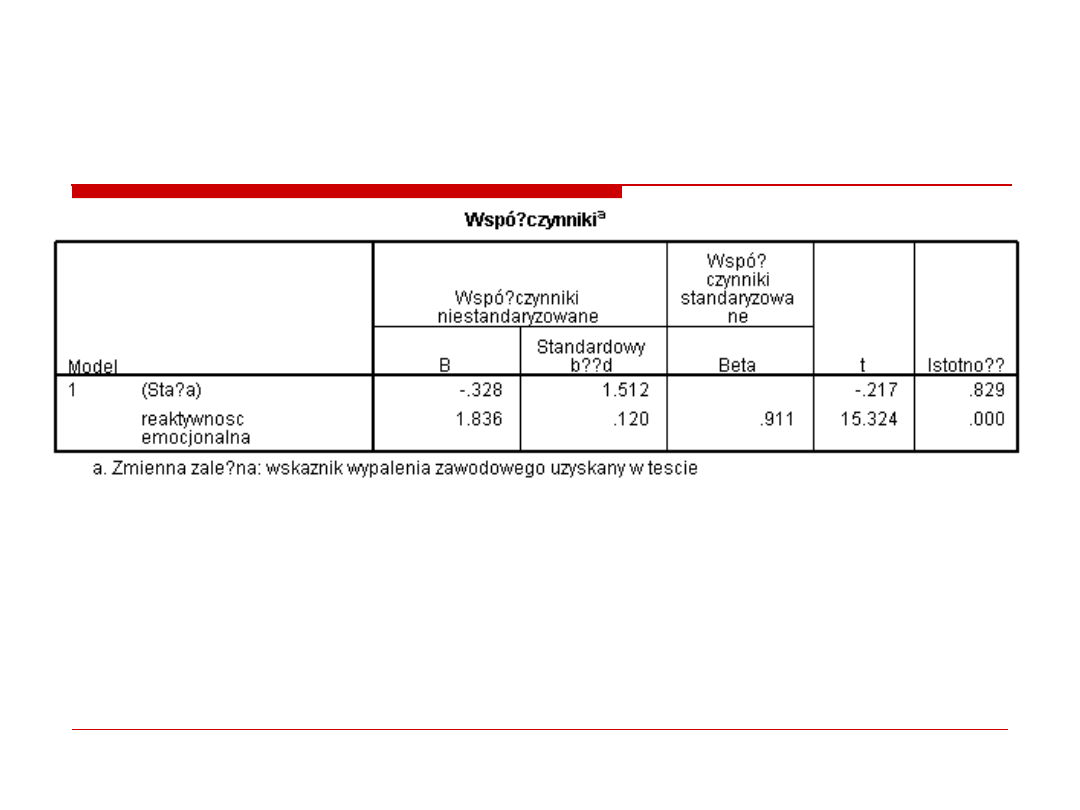
3. Predykcja



βo = .33 Gdy RE wynosi 0, to wynik na skali
wypalenia wynosi 0.



β1 = 1.84 Jesli predyktor (RE) wzrosnie o 1, to
poziom wypalenia zawodowego zwiekszy sie o 1.84.

regresja prosta

47

4. Efektywnosc modelu

regresja prosta

48

Zadanie 4

Studenci

zastanawiali

sie

czy

na

podstawie wynikow Memory Brain Test da
sie przewidziec ilosc zapamietanych liczb
podawanych w 20 elementowym ciagu. W
tym celu zbadano 30 osob stosujac Brain
Test i pozniej sprawdzajac pojemnosc ich
pamieci roboczej.

pamiec.sav

regresja prosta

49

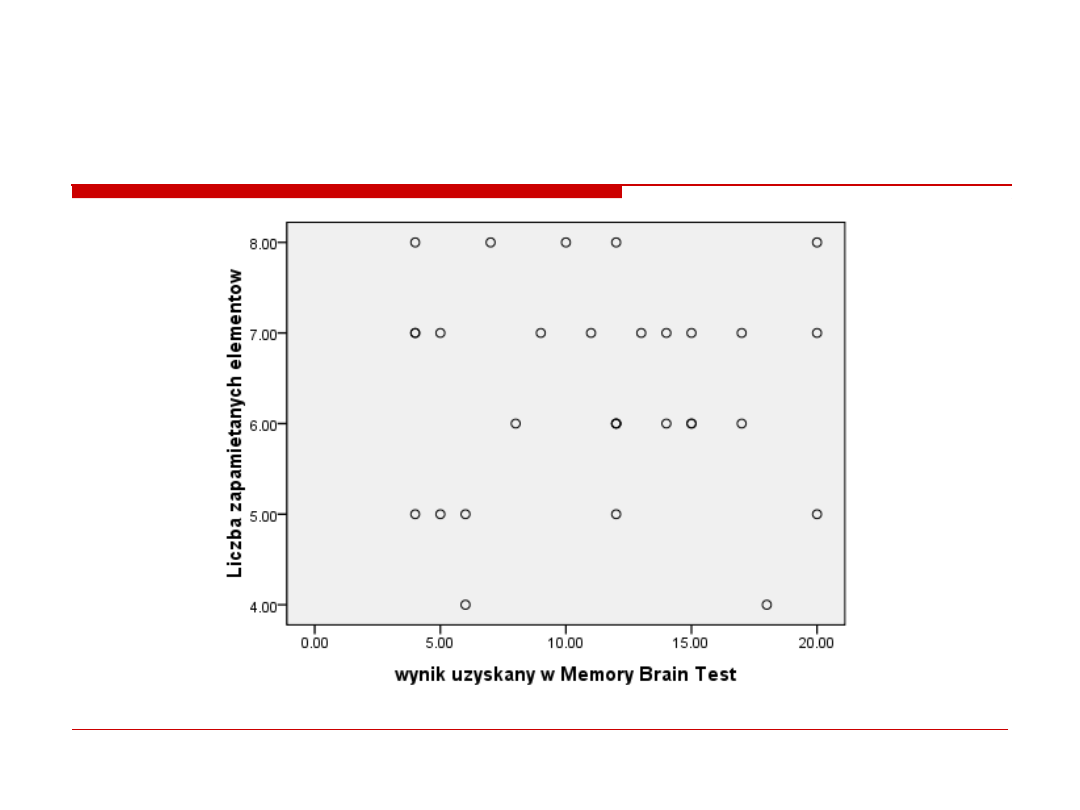
1. Wykres

regresja prosta

50

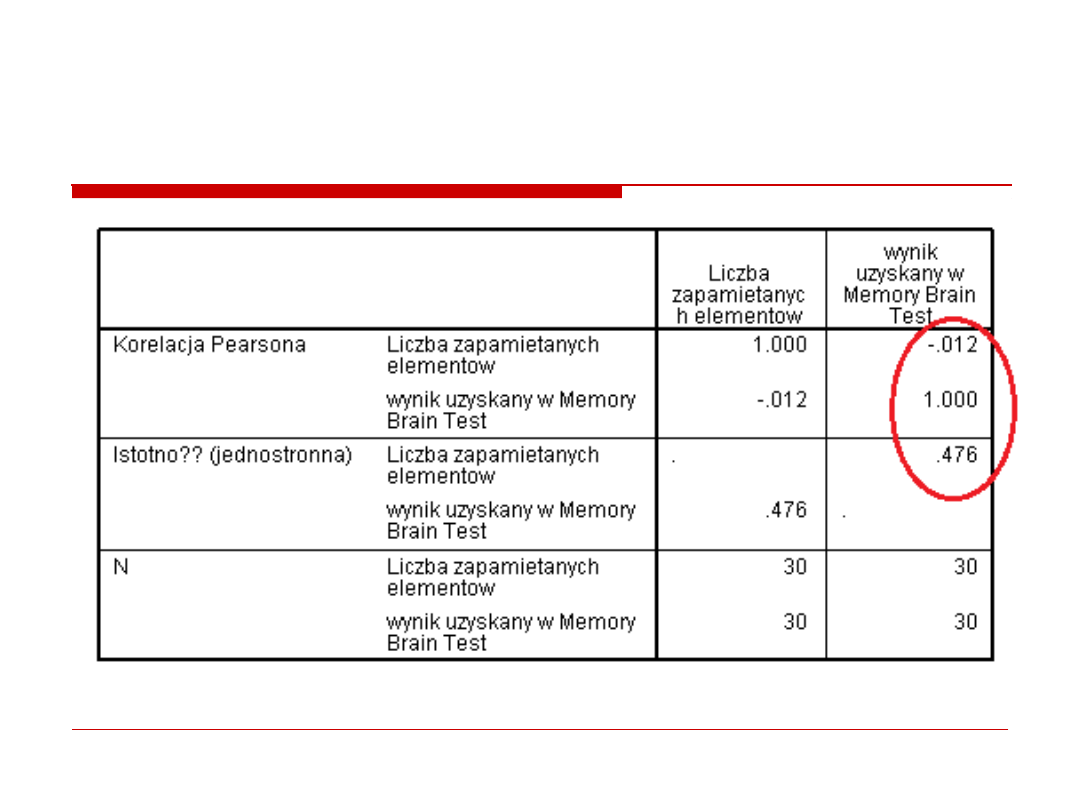
2. korelacje

regresja prosta

51

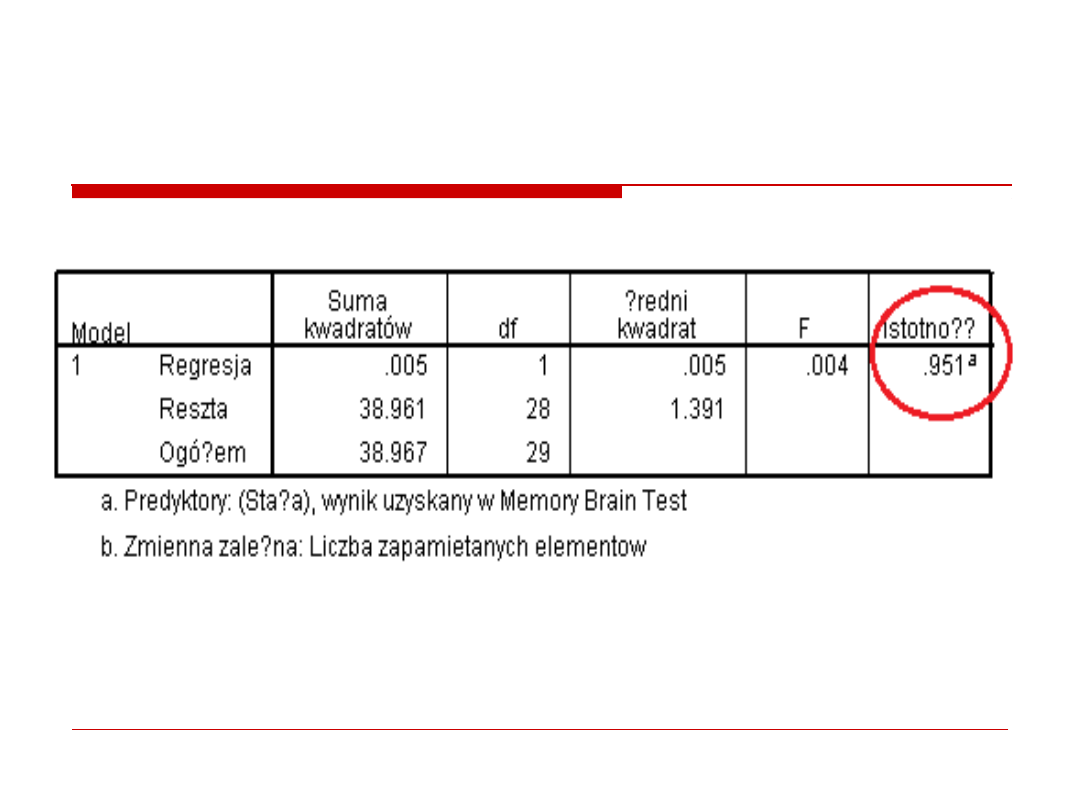
3. Analiza wariancji

regresja prosta

52

Zadanie 5

Komisja antykorupcyjna chciala sprawdzic
czy w pewnym szpitalu lapowki zaleza od
poziomu placy lekarza. Sprawdzali czy ilosc
kopert przyjmowanych przez lekarzy moze
byc przewidywana na podstawie wysokosci
ich wynagrodzenia (w tys.). Analizowano
przypadki 20 lekarzy.

korupcja.sav

regresja prosta

53

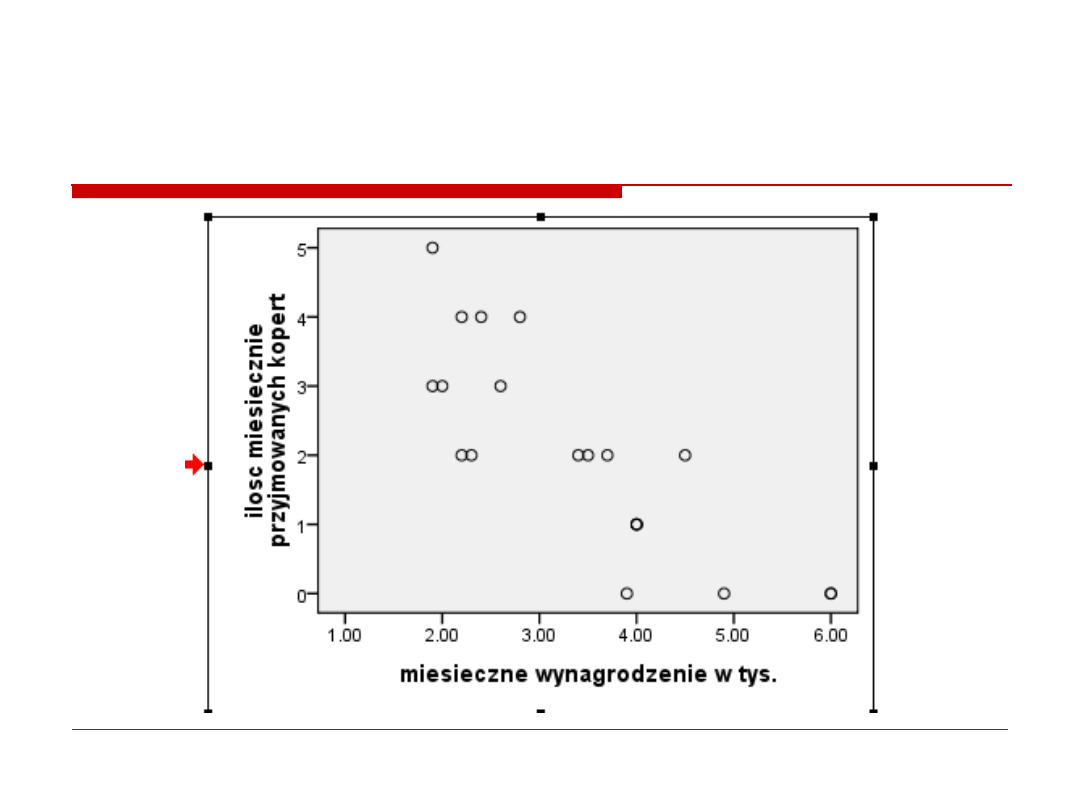
1. Wykres

regresja prosta

54

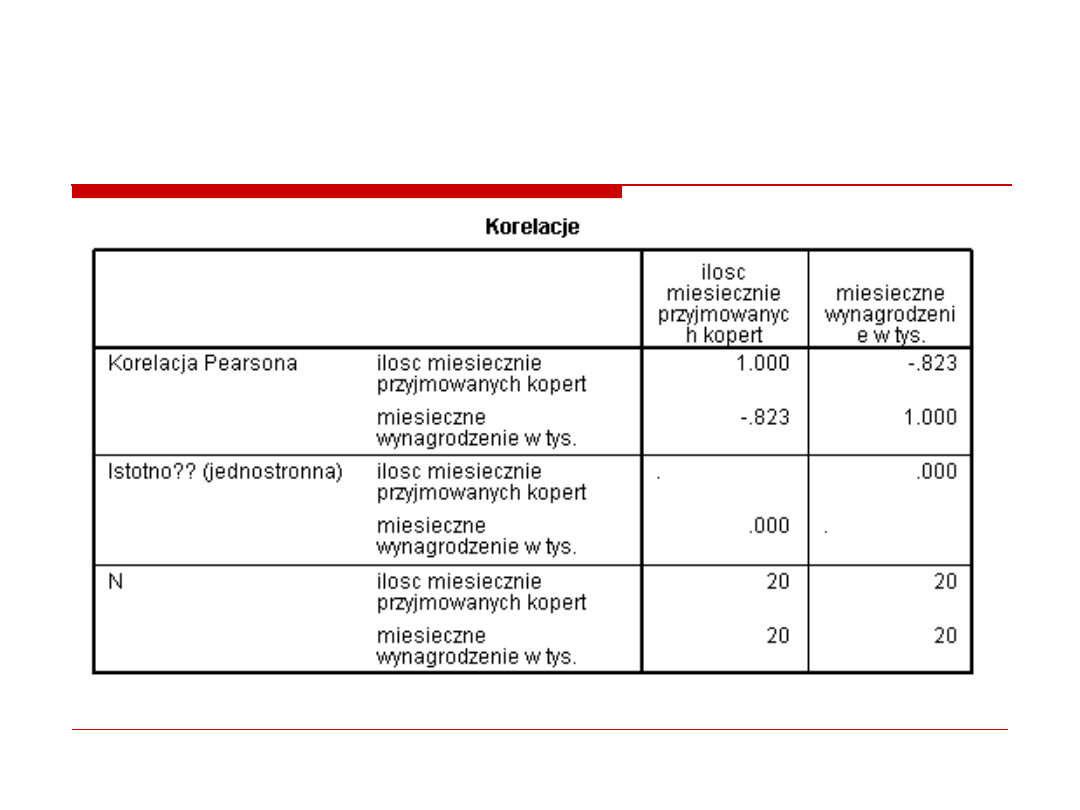
2. korelacje

regresja prosta

55

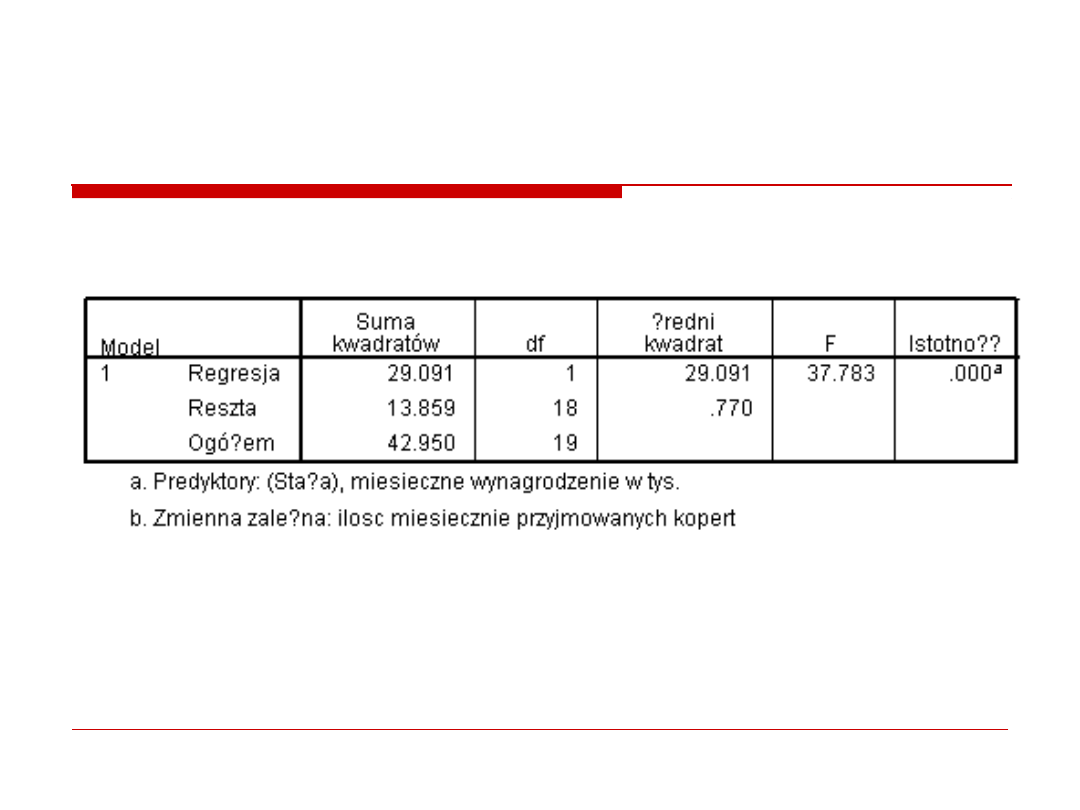
3. Analiza wariancji

regresja prosta

56

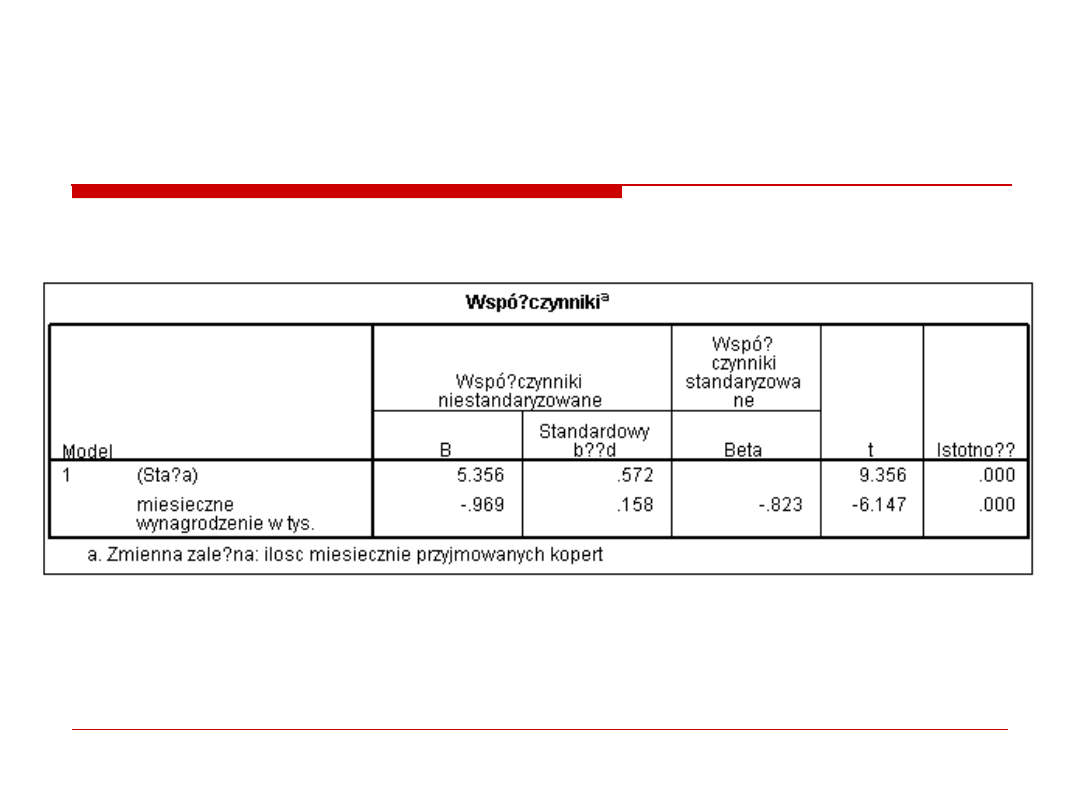
4. Predykcja

regresja prosta

57

5. Efektywnosc modelu

regresja prosta

58

regresja prosta

59

Podsumowanie tego, co najwazniejsze.

Analiza regresji



Służy

do

opisania

relacji

między

zmiennymi, a także do przewidywania
wartości kryterium (zmiennej zależnej) na
podstawie wartości predyktora (zmienna
niezależna).



Przeprowadzając tę analizę, posługujemy
się szeregiem statystyk (współczynników)
w celu określenia siły korelacji i kształtu
związku między badanymi zmiennymi.

regresja prosta

60

Wspolczynniki raz jeszcze



R:

współczynnik

korelacji

Pearsona

(R

regresyjne); służy do oszacowania korelacji
między zmiennymi, wartości R interpretujemy
tak samo, jak r Pearsona (korelacja mała,
średnia i duża).



R2: służy do określenia w jakim stopniu
zmienna niezależna pozwala na przewidzenie
zmienności kryterium, czyli jak dobrym
predyktorem jest dana zmienna niezależna; im
bliżej R2 do 1 (100%), tym lepszym
predyktorem jest dana zmienna.

regresja prosta

61

Wspolczynniki raz jeszcze



F i wartość p: określają, czy R jest istotne
czy nie, wartości te interpretujemy w
klasyczny sposób (jeśli p < .05, to R jest
istotne)



Beta: służy do oszacowania wpływu
predyktora na kształt linii regresji, czyli
stopnia wpływu zmiennej niezależnej na
zależną

(przydatny

szczególnie

w

analizie regresji wielokrotnej)



t :określa, czy wsp. Beta jest istotny.

regresja prosta

62