Analiza regresji

Regresja jednozmiennowa

• Jeden predyktor, jedna zmienna zależna

(obie zmienne ilościowe)

• Założenia:

– odpowiednia liczba osób badanych (formuła 50

+ 8),

– prostoliniowa zależność (oceniana na oko),
– normalność rozkładu zmiennych (przy małych

liczebnościach test Shapiro-Wilka, przy małych
K-S),

– usunięte przypadki odstające i skrajne

Podsumowanie

• Za pomocą metody najmniejszych kwadratów

dopasowywana jest linia prosta spełniająca

taki warunek, że suma odległości wyników od

linii jest minimalna (wyniki badanych leżą jak

najbliżej tej linii analiza wariancji)

• Dowiadujemy się jak silny jest związek i jaki

jest jego kierunek (współczynnik beta)

• Uzyskujemy informacje o parametrach

prostej. Dzięki temu możemy zapisać

zależnośc między zmiennymi w postaci wzoru

matematycznego i precyzyjnie przewidywać

wielkość zmiennej przewidywanej znając tylko

wielkość predyktora.

Przykład – Pokaż mi, ile masz

książek…

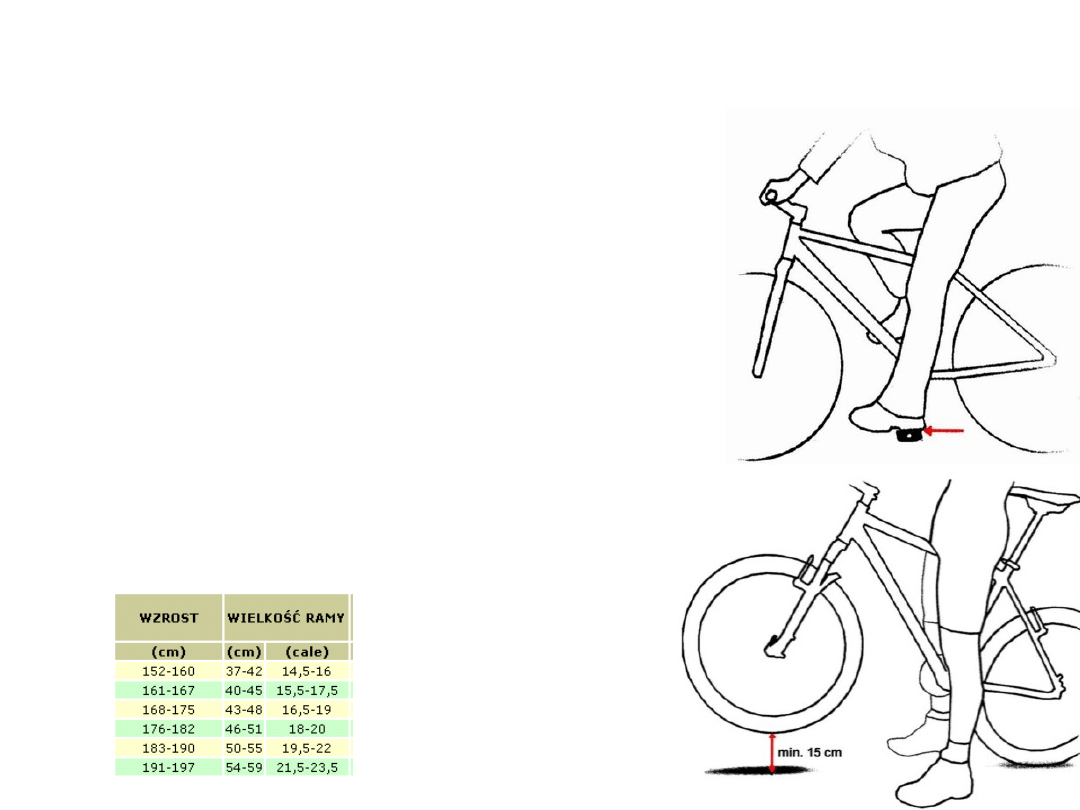
• Jak dobra rozmiar ramy
• Wysokość ramy musi zapewniać

dostateczny dystans pomiędzy
górną rurą ramy a kroczem. Ma on
pozwolić na bezpieczne zeskoczenie
z pedałów bez przykrych
konsekwencji. W rowerze górskim
rowerzysta, kiedy stoi okrakiem nad
ramą, musi mieć możliwość
uniesienia przedniego koła co
najmniej 15 cm nad ziemię.

Oglądamy wykres

• Wykres wygląda

mało
zachęcająco, ale
nie widać
żadnych
dewiantów ani
zależności
krzywoliniowej

0

1

2

3

4

5

6

7

L.KSIAZEK W DOM BIBLIOTECE R (OBECNIE)

0

20

40

60

80

100

W

Y

N

IK

W

T

E

S

C

IE

A

L

F

A

B

E

T

F

U

N

K

C

/1

99

9/

0-

10

0

Czy model jest dobrze dopasowany?

Analiza wariancji

b

188548,096

1 188548,1

234,958

,000

a

768772,778

958

802,477

957320,874

959

Regresja
Reszta
Ogółem

Model
1

Suma

kwadratów

df

Średni

kwadrat

F

Istotność

Predyktory: (Stała), q163 L.KSIAZEK W DOM BIBLIOTECE R (OBECNIE)

a.

Zmienna zależna: alfa WYNIK W TESCIE ALFABET FUNKC/1999/0-100

b.

Analiza wariancji testująca dopasowanie modelu
regresji jest istotna F(1, 958)=234,9; p<0,001.
Oznacza to, że model regresji jest bardziej
precyzyjny niż opis danych za pomocą średniej
grupowej

Współczynniki

Standaryzowany współczynnik regresji wynosi beta=0,44 i jest istotnie

różny od zera (p<0,001), co oznacza, że zależność między

analizowanymi zmiennymi jest dość silna i dodatnia. Osoba posiadająca

dużo książek ma wysoki wynik w teście rozumienia tekstu.

Rozbieżność współczynnika beta jest weryfikowana testem t-Studenta dla

jednej próby (H0: beta=0).

Tą samą metodą jest testowana wartość stałej.

Współczynniki

a

25,851

1,591

16,247

,000

7,847

,512

,444

15,328

,000

(Stała)
q163 L.KSIAZEK W
DOM BIBLIOTECE
R (OBECNIE)

Model
1

B

Błąd

standardowy

Współczynniki

niestandaryzowane

Beta

Współczynniki

standaryzowa

ne

t

Istotność

Zmienna zależna: alfa WYNIK W TESCIE ALFABET FUNKC/1999/0-100

a.

Wartość statystyki t

Wartość statystyki t testu sprawdzającego

rozbieżność parametrów od zera to wartość

parametru dzielona przez błąd standardowy, a

zatem:

t=25,851 / 1,591 = 16,247

Współczynniki

a

25,851

1,591

16,247

,000

7,847

,512

,444

15,328

,000

(Stała)
q163 L.KSIAZEK W
DOM BIBLIOTECE
R (OBECNIE)

Model
1

B

Błąd

standardowy

Współczynniki

niestandaryzowane

Beta

Współczynniki

standaryzowa

ne

t

Istotność

Zmienna zależna: alfa WYNIK W TESCIE ALFABET FUNKC/1999/0-100

a.

Statystyka t a statystyka F

Analiza wariancji

b

188548,096

1 188548,1

234,958

,000

a

768772,778

958

802,477

957320,874

959

Regresja
Reszta
Ogółem

Model
1

Suma

kwadratów

df

Średni

kwadrat

F

Istotność

Predyktory: (Stała), q163 L.KSIAZEK W DOM BIBLIOTECE R (OBECNIE)

a.

Zmienna zależna: alfa WYNIK W TESCIE ALFABET FUNKC/1999/0-100

b.

Współczynniki

a

25,851

1,591

16,247

,000

7,847

,512

,444

15,328

,000

(Stała)
q163 L.KSIAZEK W
DOM BIBLIOTECE
R (OBECNIE)

Model
1

B

Błąd

standardowy

Współczynniki

niestandaryzowane

Beta

Współczynniki

standaryzowa

ne

t

Istotność

Zmienna zależna: alfa WYNIK W TESCIE ALFABET FUNKC/1999/0-100

a.

F=
t

2

Współczynniki

Współczynniki niestandaryzowane wynoszą: stała=25,85 i współczynnik

kierunkowy=7,85. Zapis równania, które posłużyć może do przewidywania wyników

wyglądać będzie następująco:

Y=7,85*X+25,85
Co to oznacza?
Osoba, która w ogóle nie ma żadnej książki uzyskała…..punktów w teście rozumienia

tekstu.

Wraz z zakupem jednej książki wynik w teście rośnie o……… punktów.

Współczynniki

a

25,851

1,591

16,247

,000

7,847

,512

,444

15,328

,000

(Stała)
q163 L.KSIAZEK W
DOM BIBLIOTECE
R (OBECNIE)

Model
1

B

Błąd

standardowy

Współczynniki

niestandaryzowane

Beta

Współczynniki

standaryzowa

ne

t

Istotność

Zmienna zależna: alfa WYNIK W TESCIE ALFABET FUNKC/1999/0-100

a.

Współczynniki

Równanie opisujące zależność między zmiennymi

Y=7,85*X+25,85

Jeśli Andrzej ma 5 książek to jego wynik w teście będzie

wynosił 7,85*5+25,85= 65 punktów w teście.

Jak bardzo się mylimy? Jaki jest błąd naszego

wnioskowania?

Współczynniki

a

25,851

1,591

16,247

,000

7,847

,512

,444

15,328

,000

(Stała)
q163 L.KSIAZEK W
DOM BIBLIOTECE
R (OBECNIE)

Model
1

B

Błąd

standardowy

Współczynniki

niestandaryzowane

Beta

Współczynniki

standaryzowa

ne

t

Istotność

Zmienna zależna: alfa WYNIK W TESCIE ALFABET FUNKC/1999/0-100

a.

Błąd wnioskowania

Jak bardzo się mylimy? Jaki jest błąd naszego

wnioskowania?

O błędzie wnioskowania można się wypowiadać na

podstawie błędów standardowych obu parametrów.

Błąd standardowy określa o ile przeciętnie się mylimy w

szacowaniu obu parametrów równania regresji

Jeśli chodzi o stałą to błąd wynosi 1,59 dla współczynnika

kierunkowego 0,512. Można zapytać, czy to dużo, czy

mało? Zależy od wielkości parametru. Można obliczyć

procentową wartość błędu względem współczynnika: dla

stałej to 6% dla współczynnika kierunkowego to 6,5%

Współczynniki

a

25,851

1,591

16,247

,000

7,847

,512

,444

15,328

,000

(Stała)
q163 L.KSIAZEK W
DOM BIBLIOTECE
R (OBECNIE)

Model
1

B

Błąd

standardowy

Współczynniki

niestandaryzowane

Beta

Współczynniki

standaryzowa

ne

t

Istotność

Zmienna zależna: alfa WYNIK W TESCIE ALFABET FUNKC/1999/0-100

a.

Błąd wnioskowania

Niektórzy autorzy zamiast procentowej wartości błędu

podają proporcję wartość parametru/błąd. Jeśli

wartość tej proporcji jest bardzo mała to nasze

oszacowania nie są precyzyjne.

Współczynniki

a

25,851

1,591

16,247

,000

7,847

,512

,444

15,328

,000

(Stała)
q163 L.KSIAZEK W
DOM BIBLIOTECE
R (OBECNIE)

Model
1

B

Błąd

standardowy

Współczynniki

niestandaryzowane

Beta

Współczynniki

standaryzowa

ne

t

Istotność

Zmienna zależna: alfa WYNIK W TESCIE ALFABET FUNKC/1999/0-100

a.

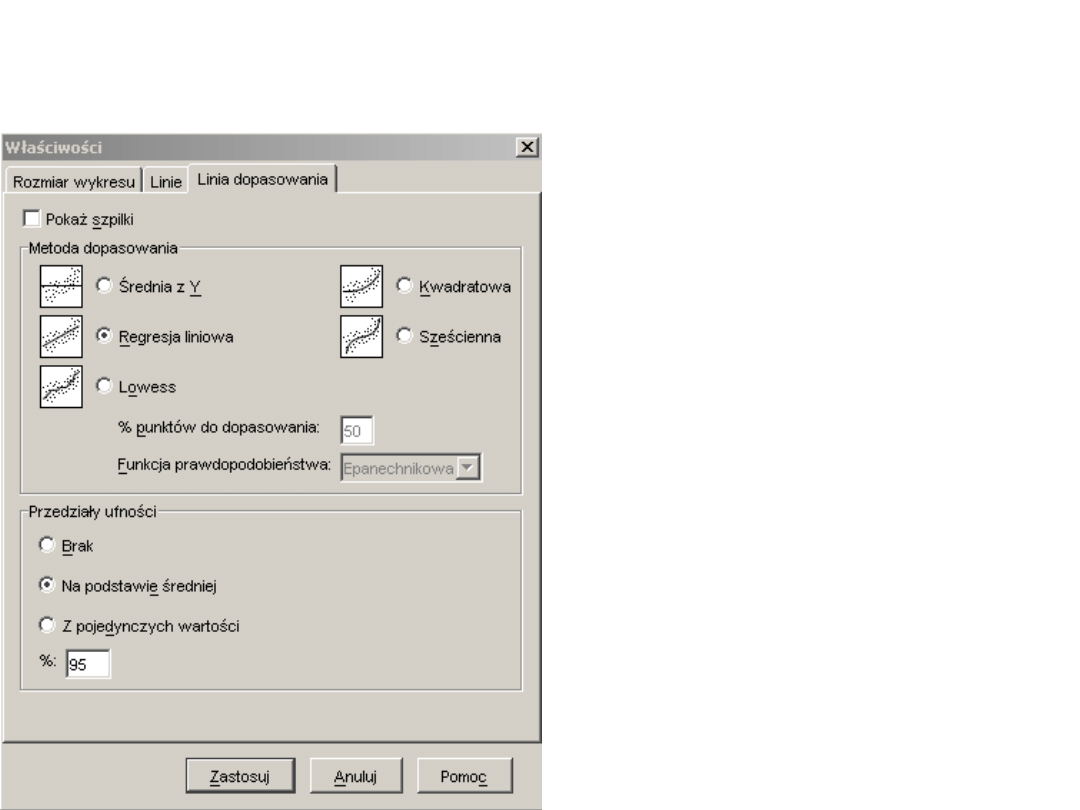
Precyzja wnioskowania -

graficznie

• Precyzje

wnioskowania można

także przedstawić

graficznie w postaci

przedziału ufności

wokół linii regresji.

Przedział ufności

określa gdzie z 95%

prawdopodobieństwe

m może przechodzić

linia regresji.

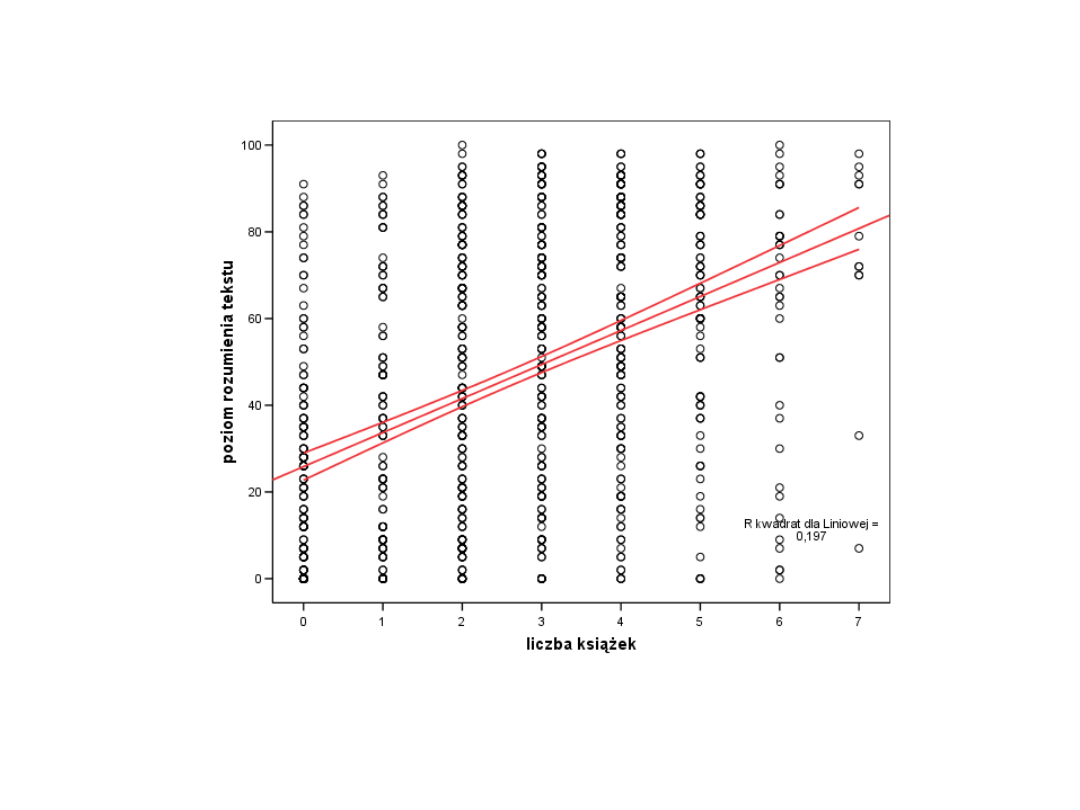
Precyzja przewidywania - graficznie

• Przewidywanie jest precyzyjne bo przedział

ufności jest wąski

Procent wyjaśnionej wariancji

• Zmienna liczba książek pozwala wyjaśnić

prawie 20% (mnożymy R –kwadrat przez
100%) zmienności zmiennej analfabetyzm
funkcjonalny

Model - Podsumowanie

,444

a

,197

,196

28,328

Model
1

R

R-kwadrat

Skorygowane

R-kwadrat

Błąd

standardowy

oszacowania

Predyktory: (Stała), q163 L.KSIAZEK W DOM BIBLIOTECE R
(OBECNIE)

a.

Procent wyjaśnionej

wariancji

• R-kwadrat to wyjaśniona suma kwadratów

(suma kwadratów dla regresji) dzielona
przez całkowitą sumę kwadratów (sumę
kwadratów ogółem).

Model - Podsumowanie

,444

a

,197

,196

28,328

Model
1

R

R-kwadrat

Skorygowane

R-kwadrat

Błąd

standardowy

oszacowania

Predyktory: (Stała), q163 L.KSIAZEK W DOM BIBLIOTECE R
(OBECNIE)

a.

Analiza wariancji

b

188548,096

1 188548,1

234,958

,000

a

768772,778

958

802,477

957320,874

959

Regresja
Reszta
Ogółem

Model
1

Suma

kwadratów

df

Średni

kwadrat

F

Istotność

Predyktory: (Stała), q163 L.KSIAZEK W DOM BIBLIOTECE R (OBECNIE)

a.

Zmienna zależna: alfa WYNIK W TESCIE ALFABET FUNKC/1999/0-100

b.

Predykcja zmiennej zależnej w

oparciu o wiele predyktorów

(2 i więcej)

Regresja

wielokrotna

Multiple

Regression

Regresja wielokrotna

• Kilka predyktorów ilościowych, jedna zmienna

przewidywana ilościowa

• Założenia jak w regresji jednozmiennowej

Kolejne kroki analizy regresji wielokrotnej

(wielozmiennowej) identyczne jak w

jednozmiennowej:

Testowanie dopasowania modelu
Określenie siły i kierunku zależności między

predyktorami a zmienną przewidywaną

Określenie łącznej efektywności modelu (R-kwadrat)

Medyczny przykład

• Przewidujemy umieralność na chorobę

wieńcową (CW) w zależności od ilości

wypalanych papierosów i poziomu stresu

pacjenta.

• Rzeczywiste dane
• Przy dwóch predyktorach i jednej zmiennej

zależnej nie dopasowujemy linii prostej a

płaszczyznę do punktów umieszczonych w

przestrzeni trójwymiarowej. Każdy punkt

(osoba badana) może zostać opisana przez

trzy właściwości.

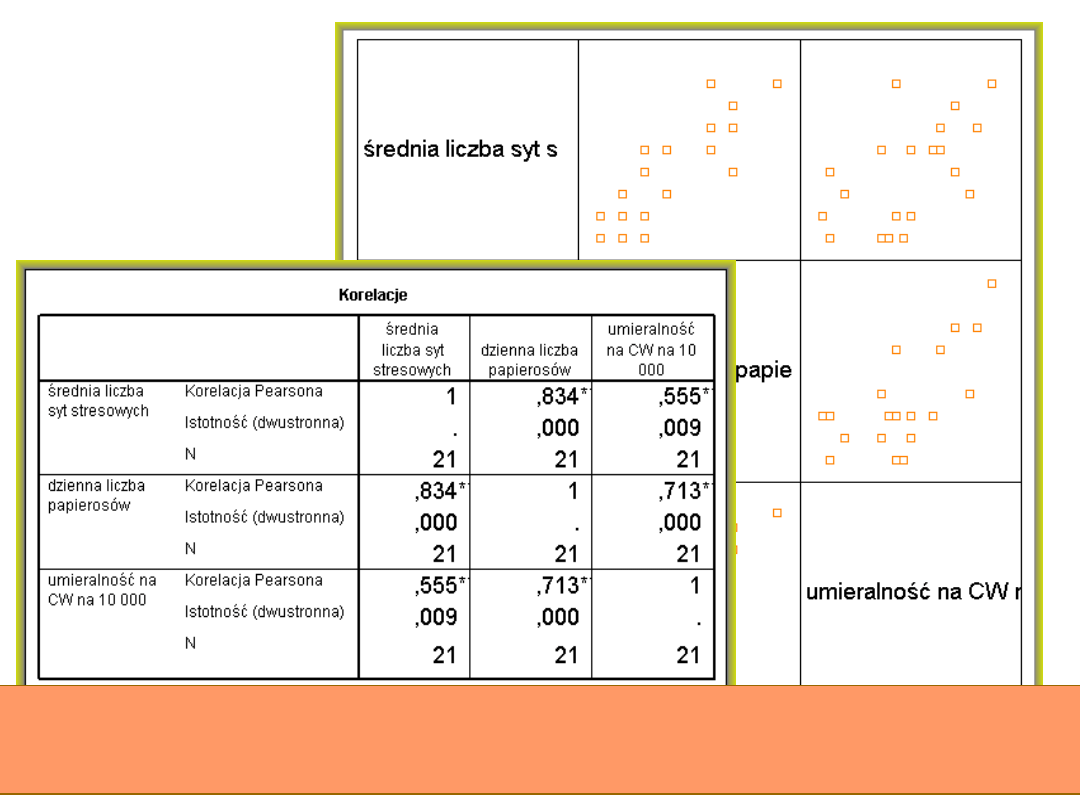
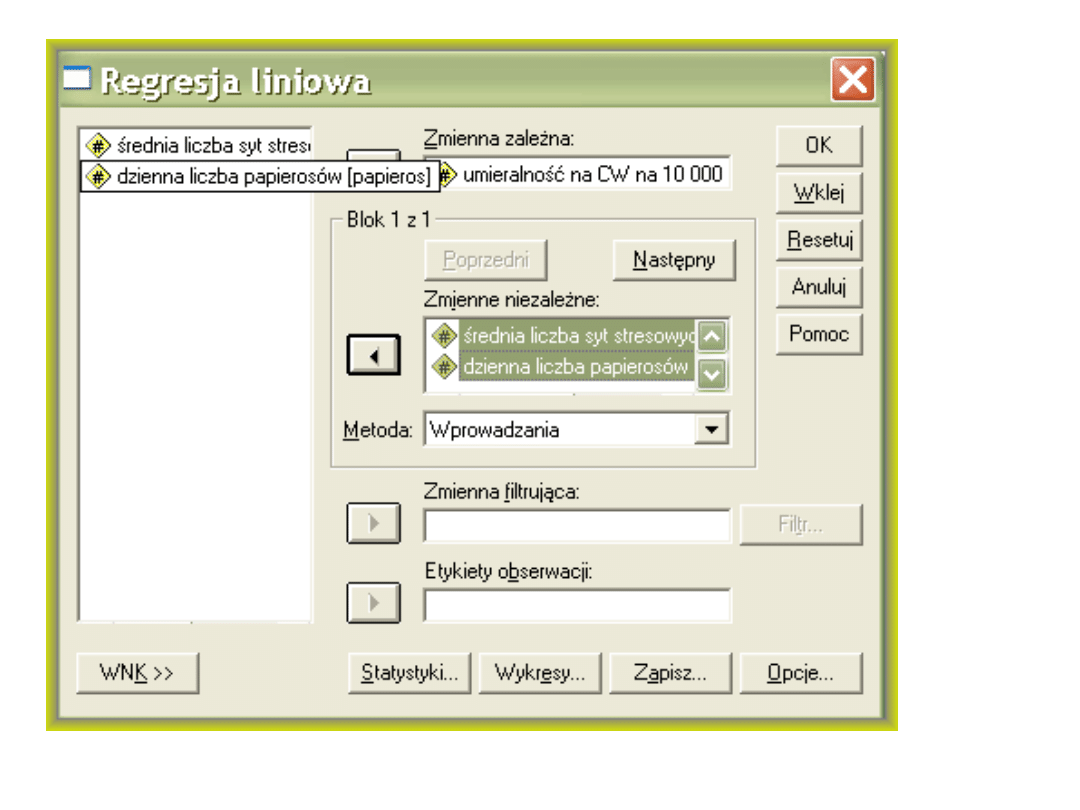
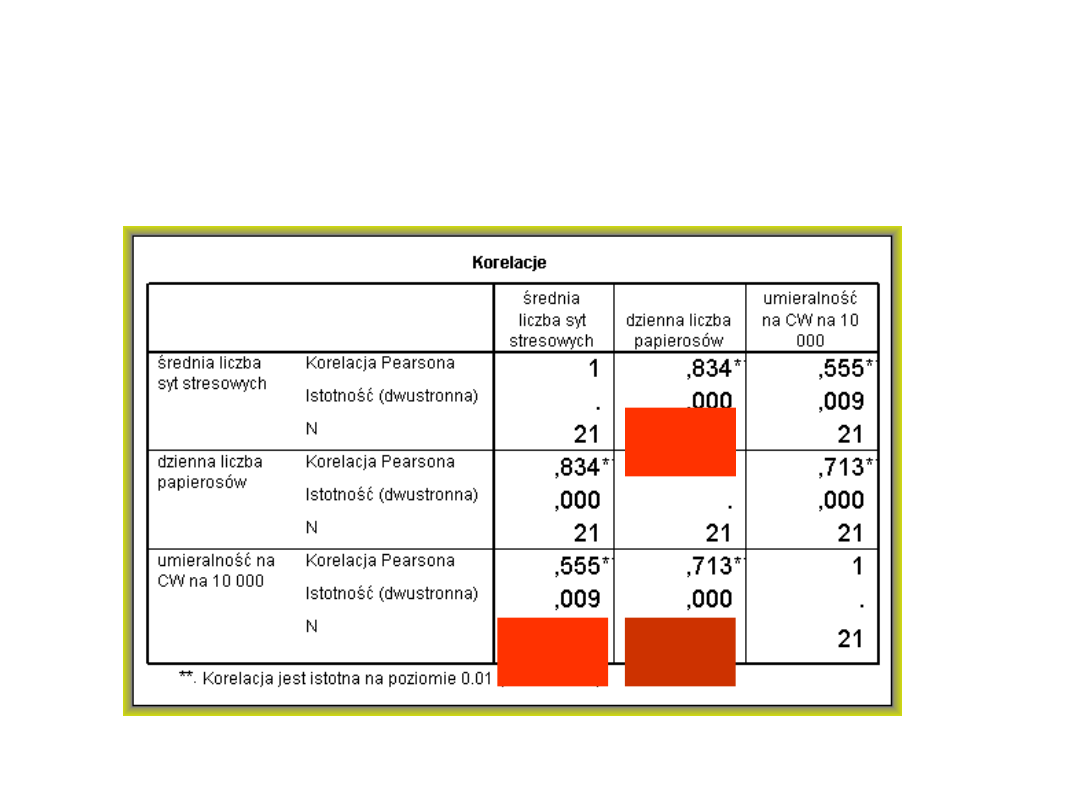
Obie zmienne sytuacje stresowe i liczba wypalanych papierosów są istotnie związane

z umieralnością na CW, ale również predyktory są ze sobą związane

Współczynnik korelacji

wielokrotnej

• Współczynnik analogiczny do r
• Zawsze oznaczany przez R
• Zawsze pozytywny

– Korelacja konstruktu stworzonego ze

wszystkich predyktorów łącznie ze
zmienna zależną

– Często zamiast R podaje się R

2

, które

łatwiej zinterpretować

R

2

Przy kilku predyktorach odczytujemy
Skorygowane R-kwadrat, gdyż R-kwadrat jest
przeszacowane wtedy, gdy więcej niż jeden
predyktor. Tutaj model regresji wyjaśnia 45%
zmienności zmiennej zależnej.

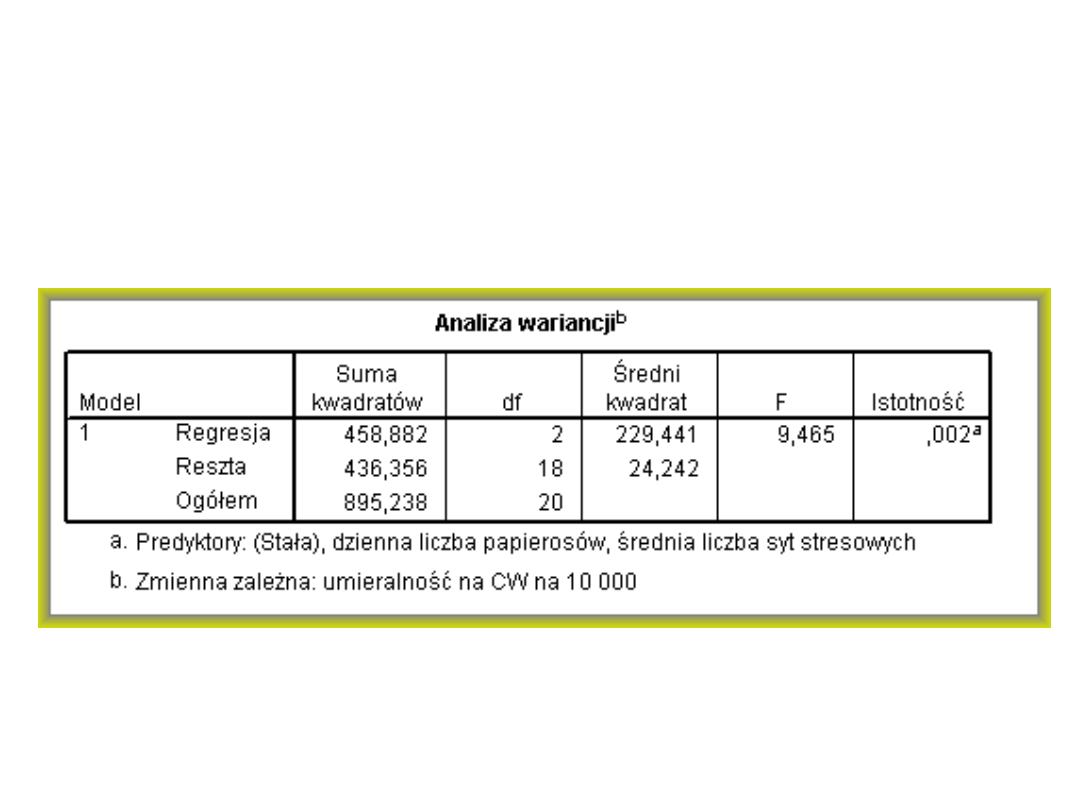
Czy model jest istotny?

Współczynniki regresji

• Stała i współczynniki dla każdego

predyktora

• Przy szacowaniu współczynnika dla

danej zmiennej wartości pozostałych
są utrzymywane na stałym poziomie

• Równanie regresji wielokrotnej jest

rozszerzeniem równania regresji
prostej o kolejne predyktory.

Równanie regresji

wielokrotnej

• W drugim równaniu nie mamy stałej, (stała = 0)
• Patrzenie na wystandaryzowane współczynniki –

sprowadzone do jednej skali pozwala na

porównywanie ich wkładu do modelu

2

2

1

1

0

2

2

1

1

Z

Z

Z

b

X

b

X

b

Y

y



















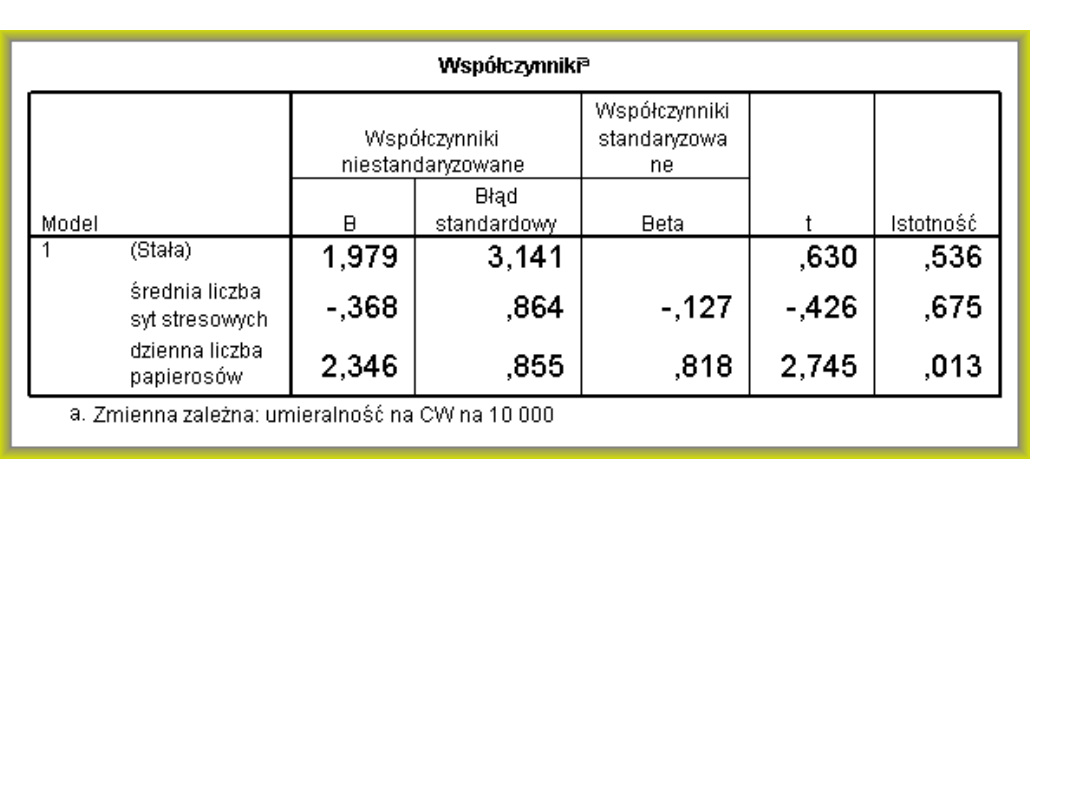
Odczytujemy, która zmienna jest istotnym
predyktorem umieralności na chorobę
wieńcową. Patrzymy na istotności
współczynników beta. Istotny jest tylko
współczynnik dla dziennej liczby papaierosów.
Zależność ta jest dodatnia i bardzo silna
(beta=0,818, p<0,05). Osoby, które duża palą są
też bardziej narażone na rozwój choroby
wieńcowej.

Równanie regresji

• A równaniu regresji uwzględniamy jedynie

istotne predyktory. A zatem w naszym
przykłądzie jedynie współczynnik
niestandaryzowane B dla zmiennej „liczba
wypalanych papierosów” oraz stałą. Co
prawda stała nie różni się istotnie od zera
więc też moglibyśmy pominąć ją w równaniu.

979

,

1

346

,

2

ˆ

0

2

2

1

1











pap

b

X

b

X

b

Y

Przewidywanie

Załóżmy, że:
• liczba papierosów = 10
• Liczba sytuacji stresowych = 5,
• Jakie jest ryzyko choroby wieńcowej

10000

44

,

25

979

,

1

46

,

23

ˆ

na

Y







979

,

1

346

,

2

ˆ

0

2

2

1

1











pap

b

X

b

X

b

Y

Dodatkowe założenie analizy

wielokrotnej

• Wielokrotna analizy regresji wymaga tego, żeby

predyktory nie były ze sobą skorelowane a więc

powinny być niezależne od siebie. Zależy nam

bowiem na tym, żeby wariancję zmiennej zależnej

wyjaśniać za pomocą niezależnych źródeł

predyktorów. Jeśli predyktory są ze sobą skorelowane

silnie, to znaczy, że de facto mierzą to samo

• Palenie papierosów i poziom stresu w gruncie rzeczy

mogą mierzyć tę samą tempEramentalną właściwość

– reaktywność. Jeśli ktoś jest reaktywny to nawet

słabe bodźce przysporzą mu stresu a jedną z form

jego rozładowania może być palenie. Więc obie te

zmienne wydają się mieć to samo źródło w postaci

innej zmiennej

Problem skorelowanych

predyktorów

• Korelacja cząstkowa –

– korelacja między dwiema zmiennymi Y i

X1, po odrzuceniu z obu zmiennych,

jakiejkolwiek wariancji, którą można

przypisać trzeciej zmiennej (X2).

– Patrzymy na związek dwóch zmiennych,

przy kontroli trzeciej

– Korelacja semicząstkowa – to co wyjaśnia

dany predyktor ze zmiennej wyjaśnianej

Silniejszy wygrywa?

R

2

=30,

8

R

2

=50,

8

R

2

=70

%

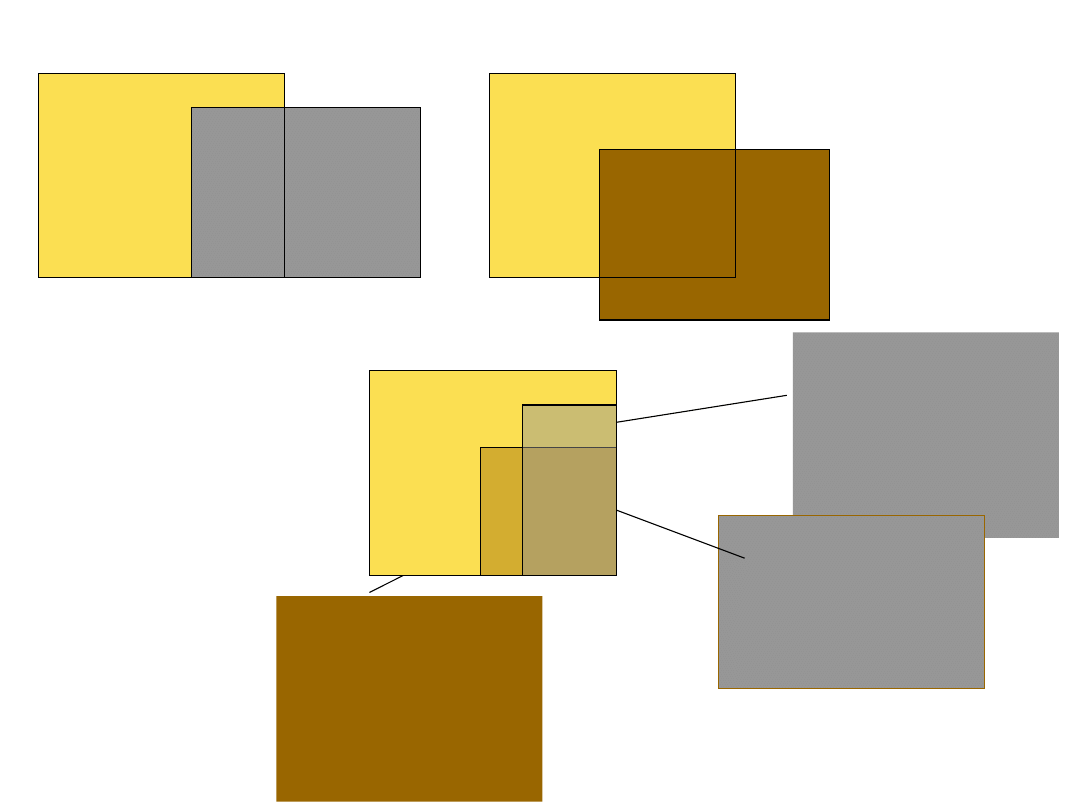
Idea korelacji cząstkowej

p

a

p

ie

ro

s

y

50,8%

Umieralność na CW

Syt. stresowe

30,8%

Unikalna
wariancja
w zmiennej
zależnej
wyjaśniona przez
papierosy

Unikalna
wariancja
w zmiennej
zależnej
wyjaśniona przez
syt. stresowe

Wariancja
w zmiennej
zależnej
wyjaśniona przez
oba predyktory

Przy korelacji
cząstkowej
kontrolujemy
efekt trzeciej
zmiennej na obie
pozostałe

Umieralność na CW

Umieralność na CW

1

2

3

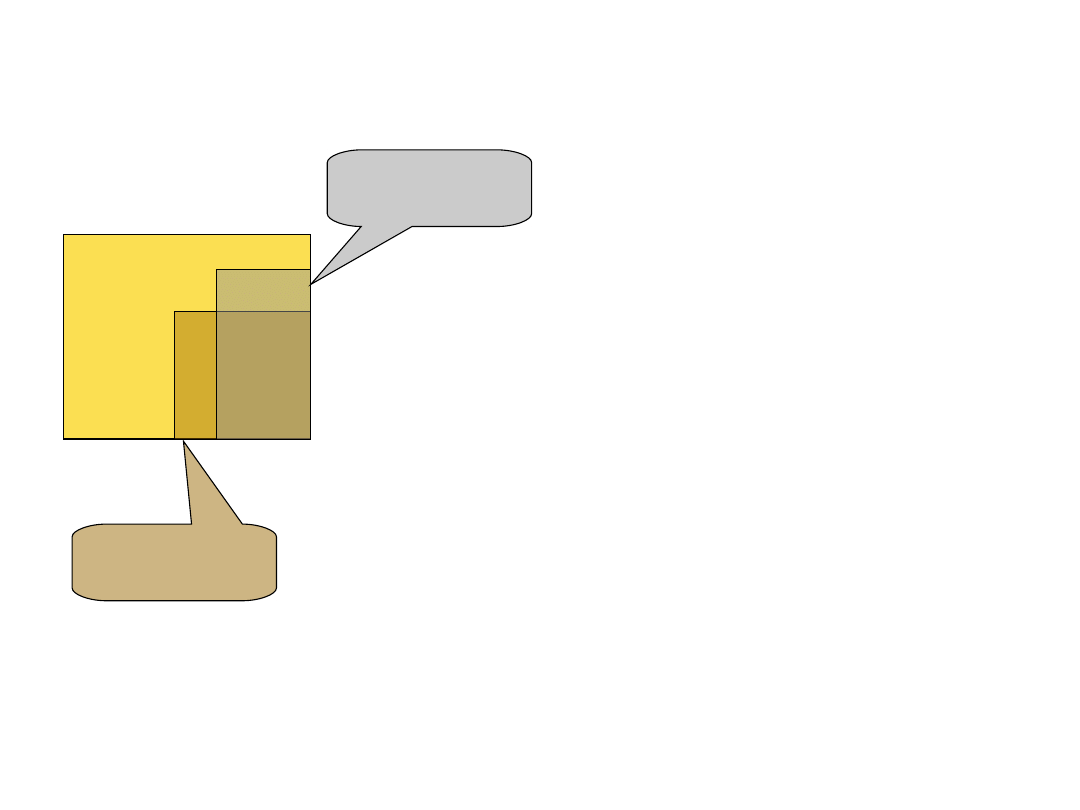
Idea korelacji cząstkoweji

semicząstkowej

Korelacja semicząstkowa
predyktora 1 to część
unikalna wyjaśniana
tylko przez ten predyktor
na tle tego co jest do
wyjaśnienia, czyli część
oznaczona numerem 1
do całego żółtego
kwadracika)
Korelacja cząstkowa
predyktora 1 to unikalna
cześć wyjaśniana przez
ten predyktor na tle
tego, czego ten drugi nie
wyjaśnia (część 1 na tle
1 i 4)

Umieralność na CW

1

2

3

Predykto

r2

Predykto

r1

4

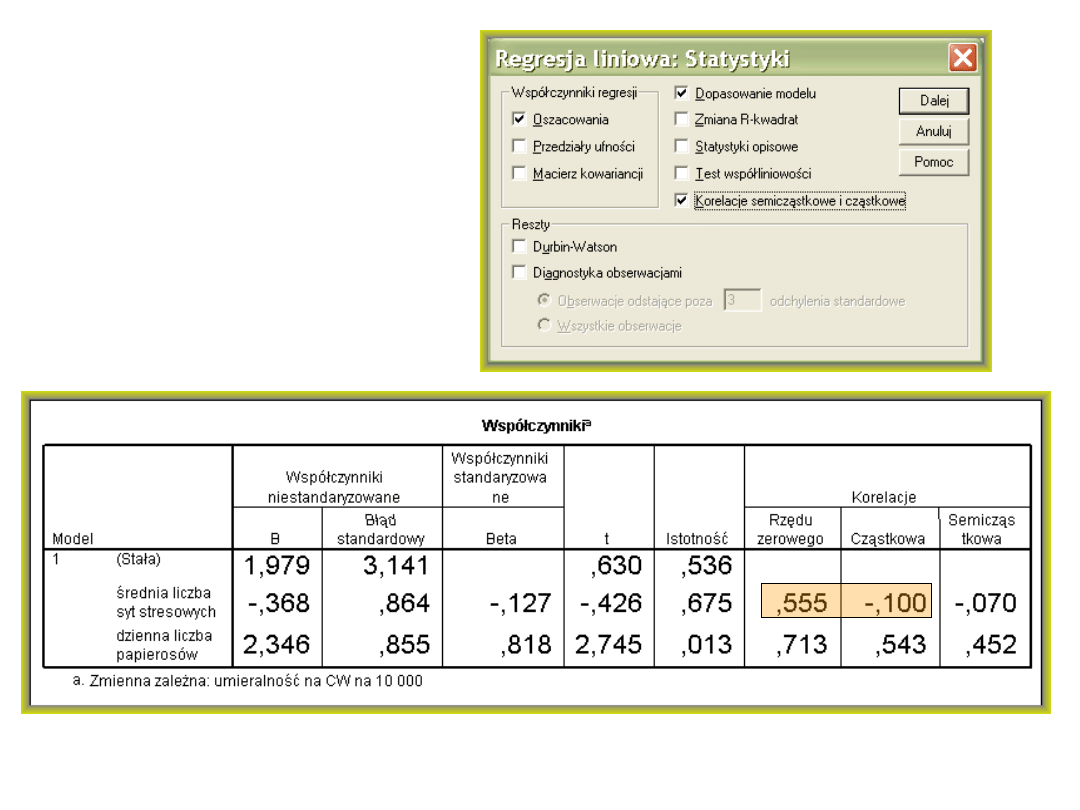
Korelacje
cząstkowe

Nasi sąsiedzi

• Jak widać, to, czy dana zmienna będzie dobrym

predyktorem zależy od sąsiedztwa z innymi

zmiennymi w modelu i tego, czy są one ze sobą

skorelowane

– (gdyby nie były, wtedy nie zmieniałyby się współczynniki

regresji w zależności od tego, która zmienna jest w

modelu. (ta informacja jest ważna przy stosowaniu różnych

metod wprowadzania danych).

• Patrząc na cząstkowe korelacje dostajemy czysty

obraz związku, przy kontroli innych zmiennych i

widać, które zmienne są lepszymi, a które gorszymi

predyktorami.

– Sugerowane jest zrobienie regresji jeszcze raz, tym razem

z uwzględnieniem w równaniu tylko istotnych predyktorów