Analiza regresji

wielokrotnej

Różne metody

„Metodologia i statystyka –

kurs zaawansowany”

Modelki

• Jak można przewidzieć

dochody modelek? Mamy
trzy zmienne: wiek, staż
pracy oraz urodę. Co się
stanie jeśli uwzględnimy te
trzy predyktory w
przewidywaniu dochodów
modelek.

Czy model analizy regresji jest

dobrze dopasowany?

• Wyniki analizy regresji wskazują, że

tak F(3,227)=17,07; p<0,001

Analiza wariancji

b

10871,964

3 3623,988

17,066

,000

a

48202,790

227

212,347

59074,754

230

Regresja
Reszta
Ogółem

Model
1

Suma

kwadratów

df

Średni

kwadrat

F

Istotność

Predyktory: (Stała), beauty, years, age

a.

Zmienna zależna: salary

b.

Współczynniki regresji

Współczynniki

a

-60,890

16,497

-3,691

,000

6,234

1,411

,942

4,418

,000

-5,561

2,122

-,548

-2,621

,009

-,196

,152

-,083

-1,289

,199

(Stała)
age
years
beauty

Model
1

B

Błąd

standardowy

Współczynniki

niestandaryzowane

Beta

Współczynniki

standaryzowa

ne

t

Istotność

Zmienna zależna: salary

a.

Model - Podsumowanie

,429

a

,184

,173

14,57213

Model
1

R

R-kwadrat

Skorygowane

R-kwadrat

Błąd

standardowy

oszacowania

Predyktory: (Stała), beauty, years, age

a.

Istotne

predyktory:

Wiek i lata pracy

Interpretacja:

Model wyjaśnia

17% wariancji

zarobków

Korelacje cząstkowe i

semicząstkowe

• Korelacje rzędu zerowego to korelacje r-

Pearsona

• Jeśli dwa predyktory są silnie ze sobą

skorelowane to korelacje cząstkowe i

semicząstkowe są dużo mniejsze niż beta lub

r-Pearsona.

Współczynniki

a

-36,182

7,315

-4,947

,000

2,630

,401

,397

6,555

,000

,397

,397

,397

-68,409

15,453

-4,427

,000

5,642

1,336

,853

4,222

,000

,397

,269

,254

-4,840

2,050

-,477

-2,361

,019

,337

-,154

-,142

(Stała)
age
(Stała)
age
years

Model
1

2

B

Błąd

standardowy

Współczynniki

niestandaryzowane

Beta

Współczynniki

standaryzowa

ne

t

Istotność

Rzędu

zerowego

Cząstkowa

Semicząs

tkowa

Korelacje

Zmienna zależna: salary

a.

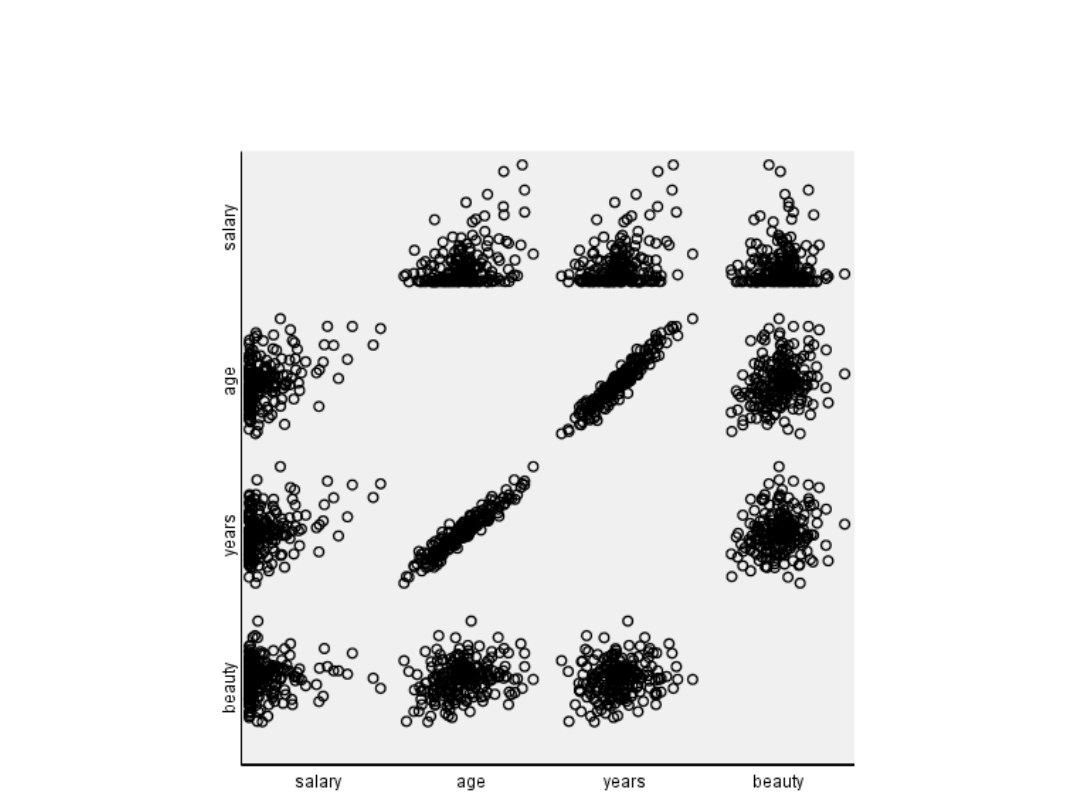
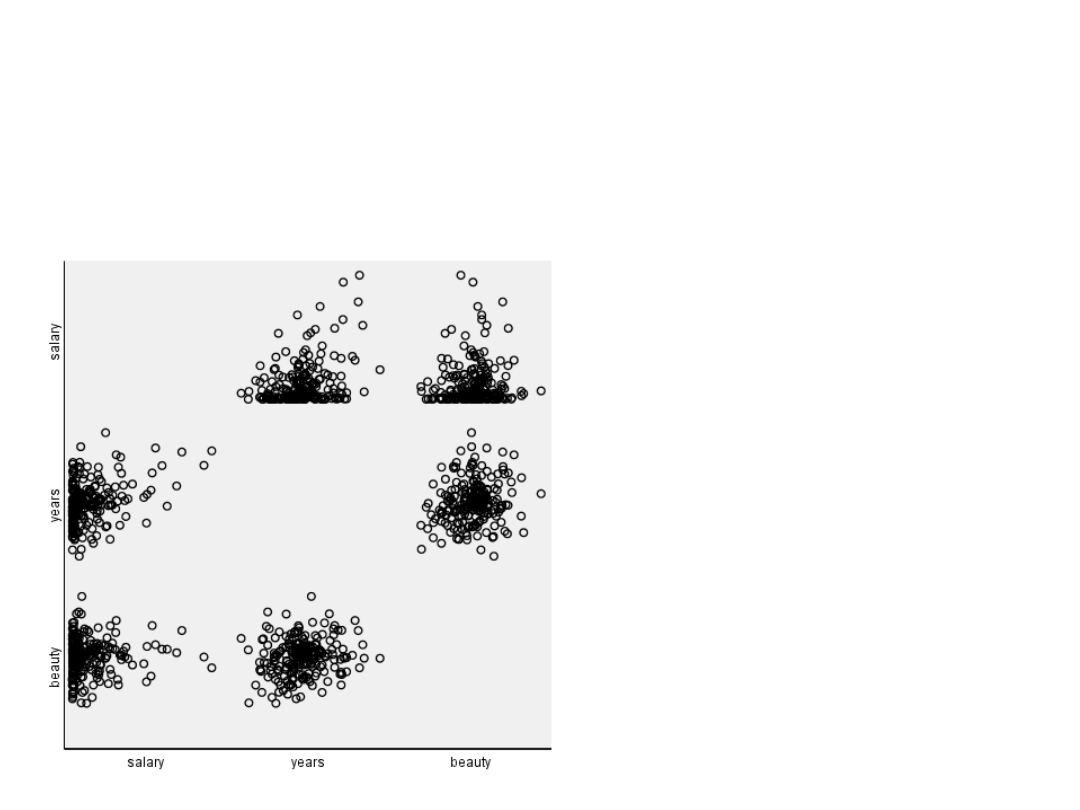
Wykres rozrzutu

macierzowy

Korelacje między

zmiennymi

• Ocena piękna modelki

nie jest skorelowana z
dochodami

• Wiek jest prawie

idealnie skorelowany
ze stażem pracy

Pytania:
1. Co z dewiantami?
2. Czy jest sens

uwzględniać
jednocześnie wiek i
staż pracy?

3. Czy można być

modelką będąc
brzydką?

Korelacje

1

,397**

,337**

,068

,000

,000

,304

231

231

231

231

,397**

1

,955**

,261**

,000

,000

,000

231

231

231

231

,337**

,955**

1

,173**

,000

,000

,008

231

231

231

231

,068

,261**

,173**

1

,304

,000

,008

231

231

231

231

Korelacja Pearsona
Istotność (dwustronna)
N
Korelacja Pearsona
Istotność (dwustronna)
N
Korelacja Pearsona
Istotność (dwustronna)
N
Korelacja Pearsona
Istotność (dwustronna)
N

salary

age

years

beauty

salary

age

years

beauty

Korelacja jest istotna na poziomie 0.01 (dwustronnie).

**.

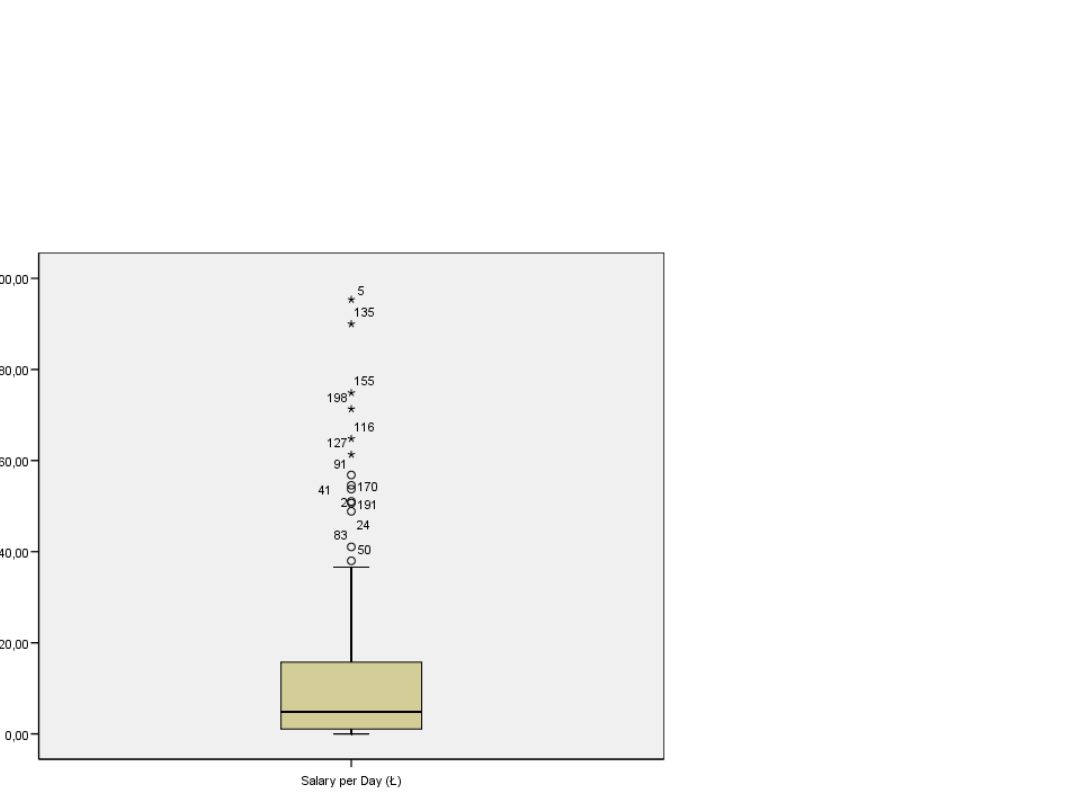
Wykres skrzynkowy dla

zmiennej zarobki

• Spora grupa

przypadków
nietypowych

• Rozkład dodatnio-

skośny – przewaga
niskich dochodów
nad wysokimi, bo
górny wąs wykresu
jest dłuższy niż
dolny a linia
oznaczająca
medianę jest
poniżej połowy
skrzynki.

Zmienne nie mogą się

dublować

• Odrzucamy zmienną

wiek i bierzemy pod
uwagę tylko staż
pracy. Jest także
możliwość zrobienia
łącznego wskaźnika
dla tych dwóch
zmiennych – można
tutaj zrobić
proporcję

Oglądamy współczynniki

korelacji

• Korelacje

istotne ale
znacznie
słabsze

Korelacje

1

,337**

,068

,000

,304

231

231

231

,337**

1

,173**

,000

,008

231

231

231

,068

,173**

1

,304

,008

231

231

231

Korelacja Pearsona
Istotność (dwustronna)
N
Korelacja Pearsona
Istotność (dwustronna)
N
Korelacja Pearsona
Istotność (dwustronna)
N

salary

years

beauty

salary

years

beauty

Korelacja jest istotna na poziomie 0.01 (dwustronnie).

**.

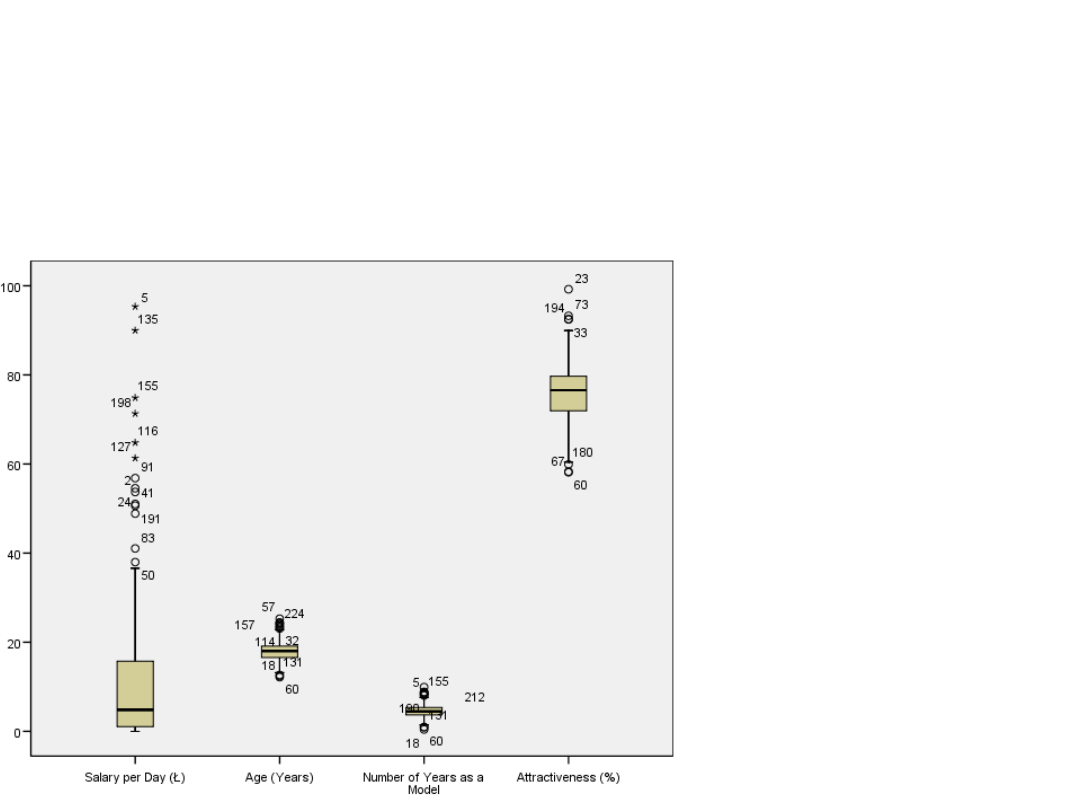
Wykresy skrzynkowe dla

wszystkich zmiennych

• Rozkład

atrakcyjności

modelek jest

normalny ale

atrakcyjność

oceniana w

procentach jest

bardzo wysoka –

wariancja dość

mała

• Bardzo małe

wariancje

pozostałych

zmiennych – wieku i

stażu pracy

Dewianci – analiza odrębna

• Dewianci mogą zostac usunięci ze zbioru

danych i całkowicie pominięci w analizach.

Informujemy wtedy ilu jest dewiantów i

jakie było kryterium ich wyodrębniania.

• Dewianci mogą także zostać potraktowani

jako osoby pochodzące z innej populacji i

analizowani osobno – tutaj dewianci to

populacja top-modelek. Analiza zostanie

wykonana oddzielnie dla całej grupy

modelek i osobno dla top-modelek.

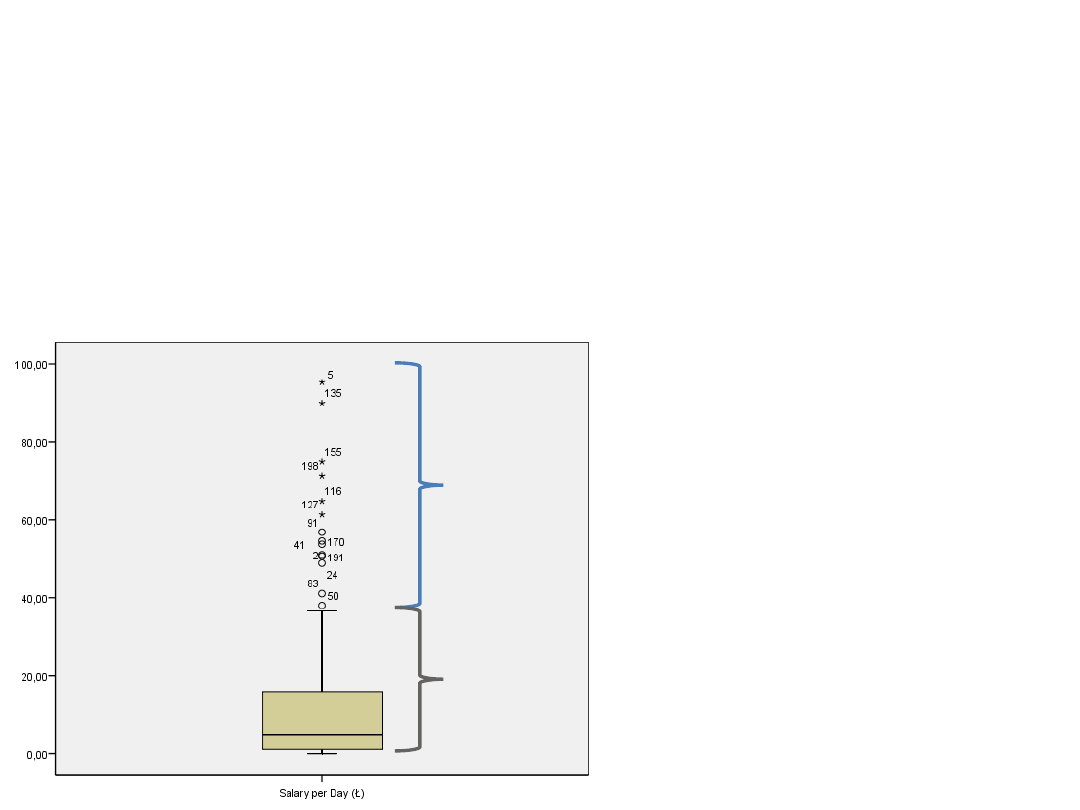
Wykres skrzynkowy dla

zmiennej zarobki

Top-modelki

–

osoby
zarabiające
powyżej 36
funtów dziennie

Modelki –

osoby

zarabiające
poniżej 36
funtów dziennie

Opcja –

Opcja –

wybierz

wybierz

obserwacje

obserwacje

Wyniki dla modelek (gorzej

zarabiających)

• Sprawdzamy czy model regresji jest

dobrze dopasowany do danych.

• Analiza wariancji wskazuje, że model

jest dobrze dopasowany do danych
F(2, 213)=4,20; p<0,05

Analiza wariancji

b

681,786

2

340,893

4,203

,016

a

17276,832

213

81,112

17958,618

215

Regresja
Reszta
Ogółem

Model
1

Suma

kwadratów

df

Średni

kwadrat

F

Istotność

Predyktory: (Stała), beauty, years

a.

Zmienna zależna: salary

b.

Współczynniki regresji

• Modelka jako

„chodzący

wieszak”

Współczynniki

a

-,534

6,888

-,078

,938

1,125

,410

,187

2,742

,007

,046

,091

,034

,507

,613

(Stała)
years
beauty

Model
1

B

Błąd

standardowy

Współczynniki

niestandaryzowane

Beta

Współczynniki

standaryzowa

ne

t

Istotność

Zmienna zależna: salary

a.

Model - Podsumowanie

b

,195

a

,038

,029

9,00621

Model
1

R

R-kwadrat

Skorygowane

R-kwadrat

Błąd

standardowy

oszacowania

Predyktory: (Stała), beauty, years

a.

Zmienna zależna: salary

b.

Istotne

predyktory:

lata pracy

beta=0,187;

p<0,01

Interpretacja:

Model wyjaśnia

3% wariancji

zarobków

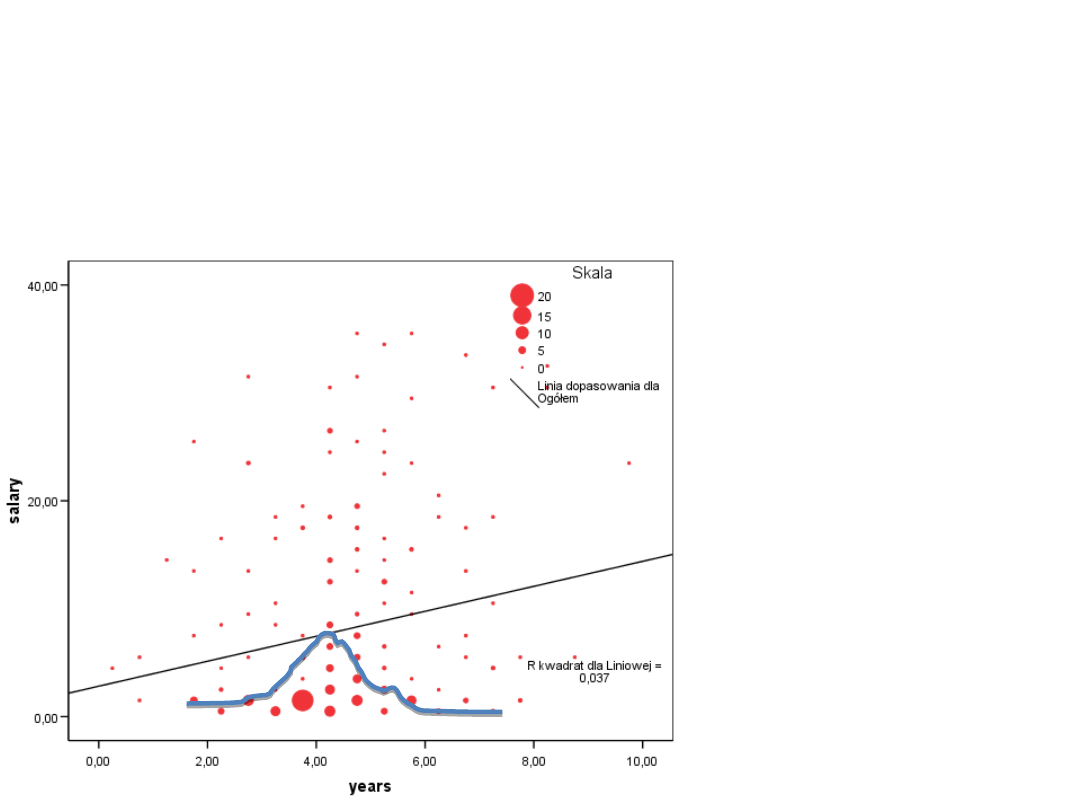
Wizualizacja

• Należałob

y chyba
zastosowa
ć inny
kształt niż
linia
prosta

Regresja dla top modelek

• Analiza regresji jest dobrze

dopasowana do danych F(2,
12)=4,803; p<0,05

Analiza wariancji

b

1900,570

2

950,285

4,803

,029

a

2374,451

12

197,871

4275,021

14

Regresja
Reszta
Ogółem

Model
1

Suma

kwadratów

df

Średni

kwadrat

F

Istotność

Predyktory: (Stała), beauty, years

a.

Zmienna zależna: salary

b.

Współczynniki dla top-

modelek

Współczynniki

a

68,785

49,716

1,384

,192

6,935

2,246

,722

3,087

,009

-,667

,693

-,225

-,963

,355

(Stała)
years
beauty

Model
1

B

Błąd

standardowy

Współczynniki

niestandaryzowane

Beta

Współczynniki

standaryzowa

ne

t

Istotność

Zmienna zależna: salary

a.

Model - Podsumowanie

b

,667

a

,445

,352

14,06666

Model
1

R

R-kwadrat

Skorygowane

R-kwadrat

Błąd

standardowy

oszacowania

Predyktory: (Stała), beauty, years

a.

Zmienna zależna: salary

b.

Istotny predyktor:

lata pracy

beta=0,722;

p<0,01

Interpretacja:

Model wyjaśnia

35% wariancji

zarobków

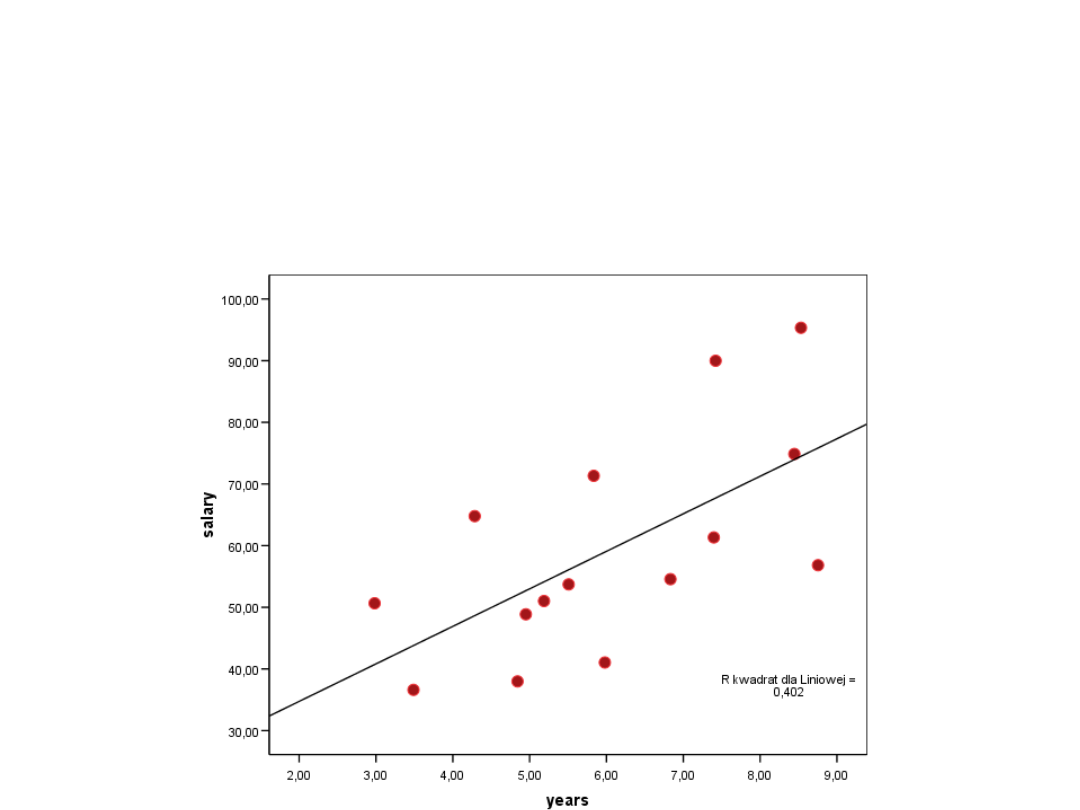
Wizualizacja zależności

Metody regresji – kolejność

wprowadzania zmiennych do

modelu

• Metoda wprowadzania (Enter)
• Metoda eliminacji wstecznej (Backward)
• Metoda selekcji postępującej (Forward)
• Metoda krokowa (Stepwise)
• Hierarchiczna analiza regresji

(Hierarchic)

• Segmentowa analiza regresji

Metoda eliminacji wstecznej

• Analiza przeprowadzana jest w kolejnych krokach –

najpierw wprowadzane są wszystkie predyktory a

potem kolejno usuwane są najsłabsze. Kryterium jest

poziom istotności >=0,1

• Analiza predyktorów konstruktywnego stylu radzenia

sobie w konflikcie. Predyktory to sześć rodzajów

kompetencji społecznych: wrażliwość społeczna,

wrażliwość emocjonalna, kontrola społeczna,

kontrola emocjonalna, ekspresywność społeczna,

ekspresywność emocjonalna. Zakładamy, że

predyktory wiążą się prostoliniowo ze zmienną

zależną a więc im wyższy poziom predyktora tym

większa tendencja do rozwiązywania konfliktów w

sposób konstruktywny

• Czy zawsze ta zależność musi być prostoliniowa?

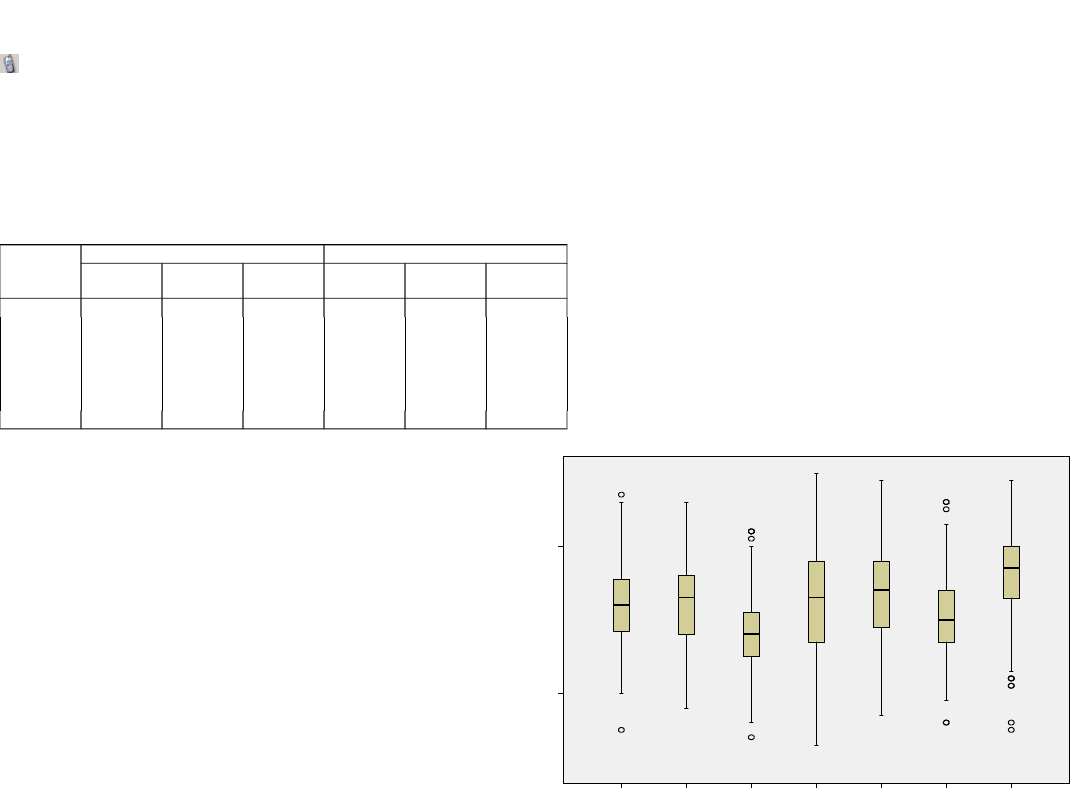
Testowanie założeń

Kołmogorow-Smirnow(a)

Shapiro-Wilk

Statystyk
a

df

Istotność

Statystyk

a

df

Istotność

ekspr_e

,054

236

,098

,995

236

,565

wraz_e

,072

236

,004

,989

236

,066

kontr_e

,063

236

,023

,991

236

,159

ekspr_s

,048

236

,200(*)

,993

236

,320

wraz_s

,062

236

,029

,989

236

,066

kontr_s

,078

236

,001

,987

236

,033

konstruk

,111

236

,000

,975

236

,000

konstruk

kontr_s

wraz_s

ekspr_s

kontr_e

wraz_e

ekspr_e

40

20

21

213

256

262

9

96

94

28

30 89

269

52

60

123

145

172

74

122

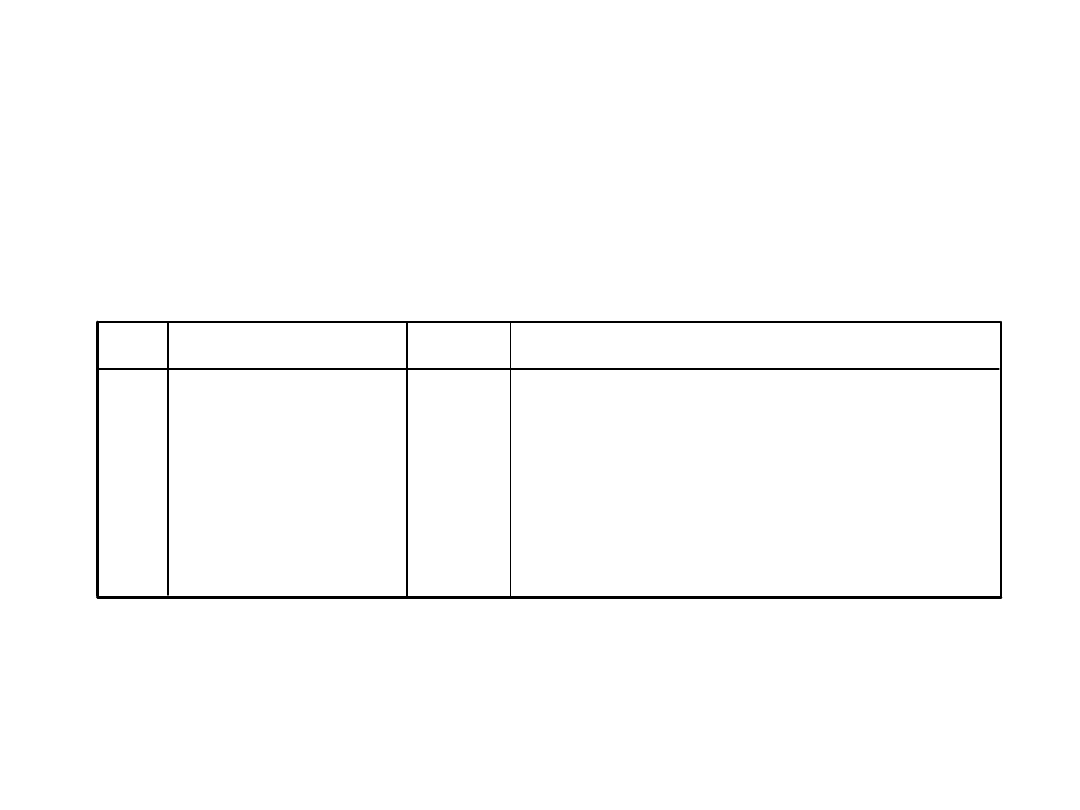
Które zmienne są usuwane w

kolejnych krokach?

Zmienne wprowadzone/usunięte

b

kontr_s, kontr_e, wraz_s,
ekspr_e, wraz_e, ekspr_s

a

.

Wprowadzanie

.

ekspr_s

Eliminacja wsteczna (Kryterium: Prawdopodobieństwo
F-usunięcia >= ,100).

.

kontr_s

Eliminacja wsteczna (Kryterium: Prawdopodobieństwo
F-usunięcia >= ,100).

.

ekspr_e

Eliminacja wsteczna (Kryterium: Prawdopodobieństwo
F-usunięcia >= ,100).

.

kontr_e

Eliminacja wsteczna (Kryterium: Prawdopodobieństwo
F-usunięcia >= ,100).

Model
1

2

3

4

5

Zmienne wprowadzone

Zmienne

usunięte

Metoda

Wszystkie wyspecyfikowane zmienne zostały wprowadzone.

a.

Zmienna zależna: konstruk

b.

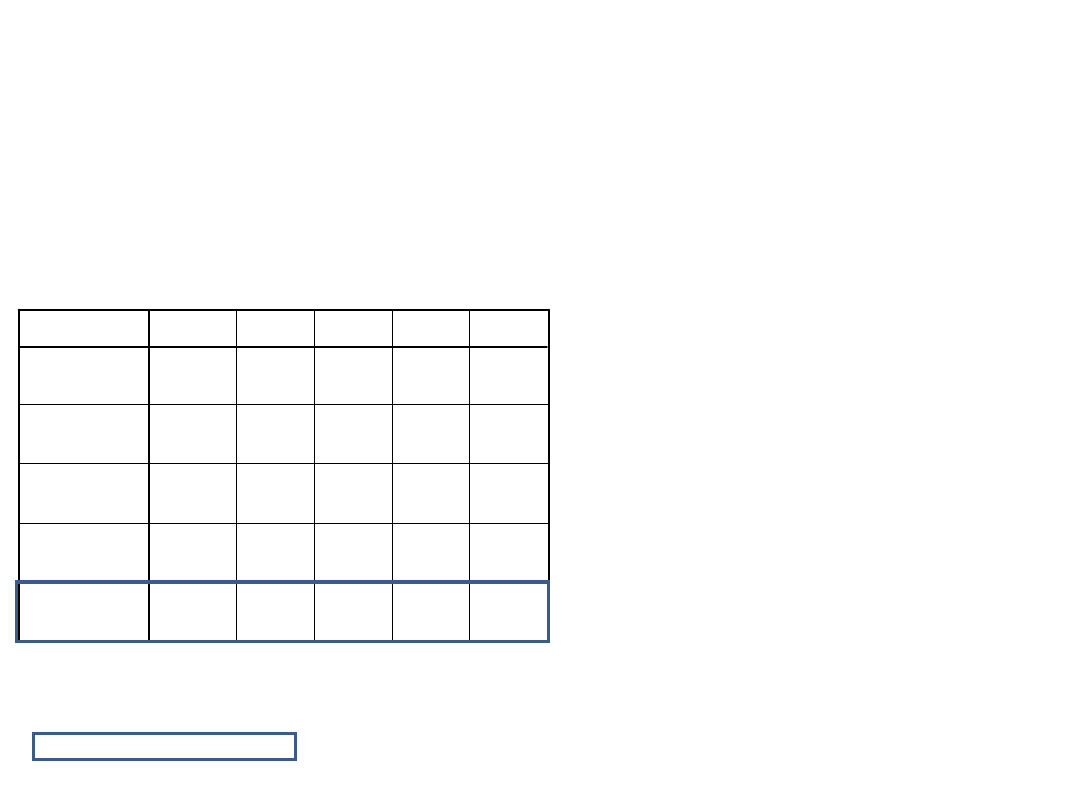
Dopasowania kolejnych

modeli

• Który model

wybieramy?
Ostatni istotny
– zerkamy
wtedy, które
zmienne są w
tym modelu
istotne

Analiza wariancji

f

1453,108

6

242,185

7,034

,000

a

7884,062

229

34,428

9337,169

235

1453,100

5

290,620

8,478

,000

b

7884,070

230

34,279

9337,169

235

1406,256

4

351,564

10,240

,000

c

7930,914

231

34,333

9337,169

235

1344,153

3

448,051

13,005

,000

d

7993,017

232

34,453

9337,169

235

1312,798

2

656,399

19,060

,000

e

8024,372

233

34,439

9337,169

235

Regresja
Reszta
Ogółem
Regresja
Reszta
Ogółem
Regresja
Reszta
Ogółem
Regresja
Reszta
Ogółem
Regresja
Reszta
Ogółem

Model
1

2

3

4

5

Suma

kwadratów

df

Średni

kwadrat

F

Istotność

Predyktory: (Stała), kontr_s, kontr_e, wraz_s, ekspr_e, wraz_e, ekspr_s

a.

Predyktory: (Stała), kontr_s, kontr_e, wraz_s, ekspr_e, wraz_e

b.

Predyktory: (Stała), kontr_e, wraz_s, ekspr_e, wraz_e

c.

Predyktory: (Stała), kontr_e, wraz_s, wraz_e

d.

Predyktory: (Stała), wraz_s, wraz_e

e.

Zmienna zależna: konstruk

f.

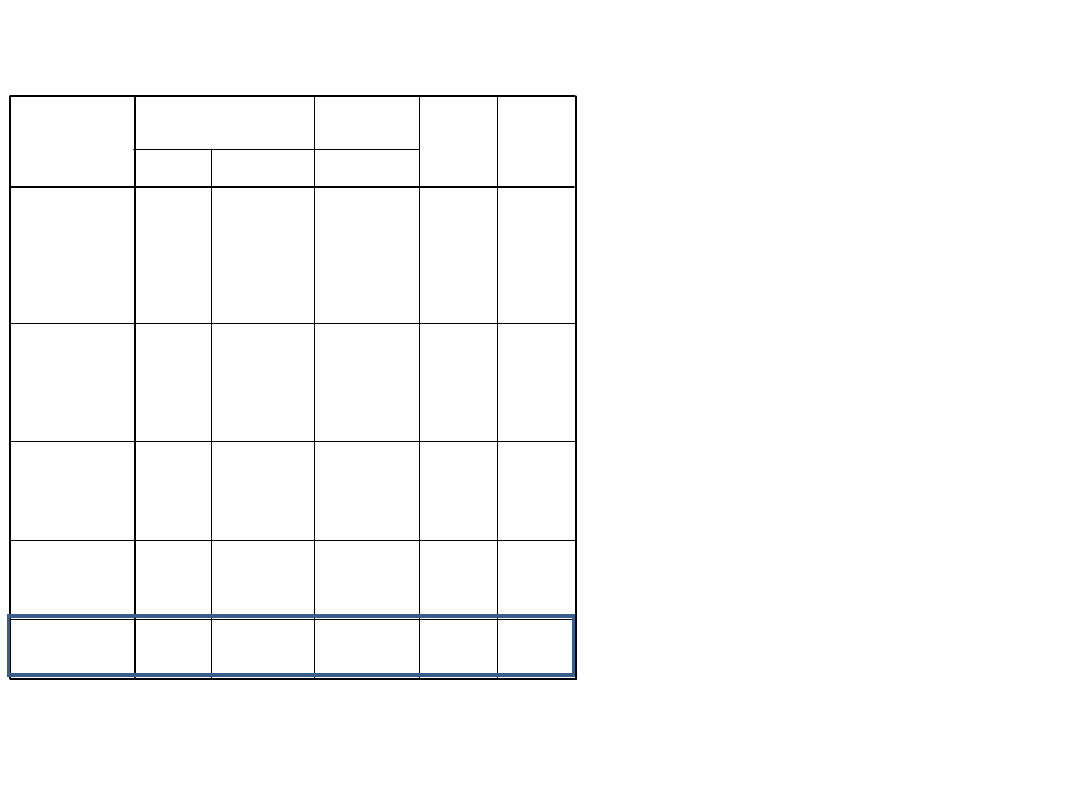
Współczynni

ki

• Opisujemy

współczynniki
dla ostatniego
modelu. Dla
tego modelu
zapisujemy
model
równania:

Współczynniki

a

23,342

4,314

5,411

,000

-,146

,092

-,121

-1,587

,114

,346

,089

,293

3,869

,000

-,123

,082

-,100

-1,509

,133

-,001

,070

-,001

-,015

,988

,202

,071

,198

2,857

,005

,092

,096

,078

,960

,338

23,338

4,295

5,434

,000

-,147

,090

-,122

-1,630

,104

,346

,089

,293

3,877

,000

-,123

,081

-,100

-1,522

,129

,202

,071

,198

2,865

,005

,091

,078

,077

1,169

,244

24,970

4,065

6,143

,000

-,116

,086

-,096

-1,345

,180

,358

,089

,303

4,037

,000

-,110

,080

-,089

-1,368

,173

,184

,069

,181

2,673

,008

21,833

3,335

6,547

,000

,306

,080

,260

3,825

,000

-,072

,075

-,058

-,954

,341

,186

,069

,183

2,700

,007

19,897

2,646

7,521

,000

,298

,080

,252

3,740

,000

,193

,069

,189

2,806

,005

(Stała)
ekspr_e
wraz_e
kontr_e
ekspr_s
wraz_s
kontr_s
(Stała)
ekspr_e
wraz_e
kontr_e
wraz_s
kontr_s
(Stała)
ekspr_e
wraz_e
kontr_e
wraz_s
(Stała)
wraz_e
kontr_e
wraz_s
(Stała)
wraz_e
wraz_s

Model
1

2

3

4

5

B

Błąd

standardowy

Współczynniki

niestandaryzowane

Beta

Współczynniki

standaryzowa

ne

t

Istotność

Zmienna zależna: konstruk

a.

Y

k

=0,198*X

WE

+0,193*X

WS

+ 19,897

Siła poszczególnych modeli

• Usuwanie kolejnych

predyktorów nie

powoduje

znaczących zmian w

obrębie R

2

skorygowanego.

• Zawsze lepszy

modelem jest ten,

który zawiera

maksymalnie mało

predyktorów

Model - Podsumowanie

,394

a

,156

,134

5,86756

,394

b

,156

,137

5,85479

,388

c

,151

,136

5,85943

,379

d

,144

,133

5,86964

,375

e

,141

,133

5,86851

Model
1
2
3
4
5

R

R-kwadrat

Skorygowane

R-kwadrat

Błąd

standardowy

oszacowania

Predyktory: (Stała), kontr_s, kontr_e, wraz_s, ekspr_e, wraz_
e, ekspr_s

a.

Predyktory: (Stała), kontr_s, kontr_e, wraz_s, ekspr_e, wraz_
e

b.

Predyktory: (Stała), kontr_e, wraz_s, ekspr_e, wraz_e

c.

Predyktory: (Stała), kontr_e, wraz_s, wraz_e

d.

Predyktory: (Stała), wraz_s, wraz_e

e.

Metoda selekcji

postępującej

• W metodzie selekcji postępującej

najpierw wybierany jest najsilniejszy
predyktor i ten predyktor jest
testowany. Otrzymujemy wydruk ze
statystykami tego modelu. Następnie
do modelu wprowadzany jest kolejny
predyktor. Kolejne kroki mają na celu
dodanie istotnych predyktorów – w
każdym kroku jeden predyktor.

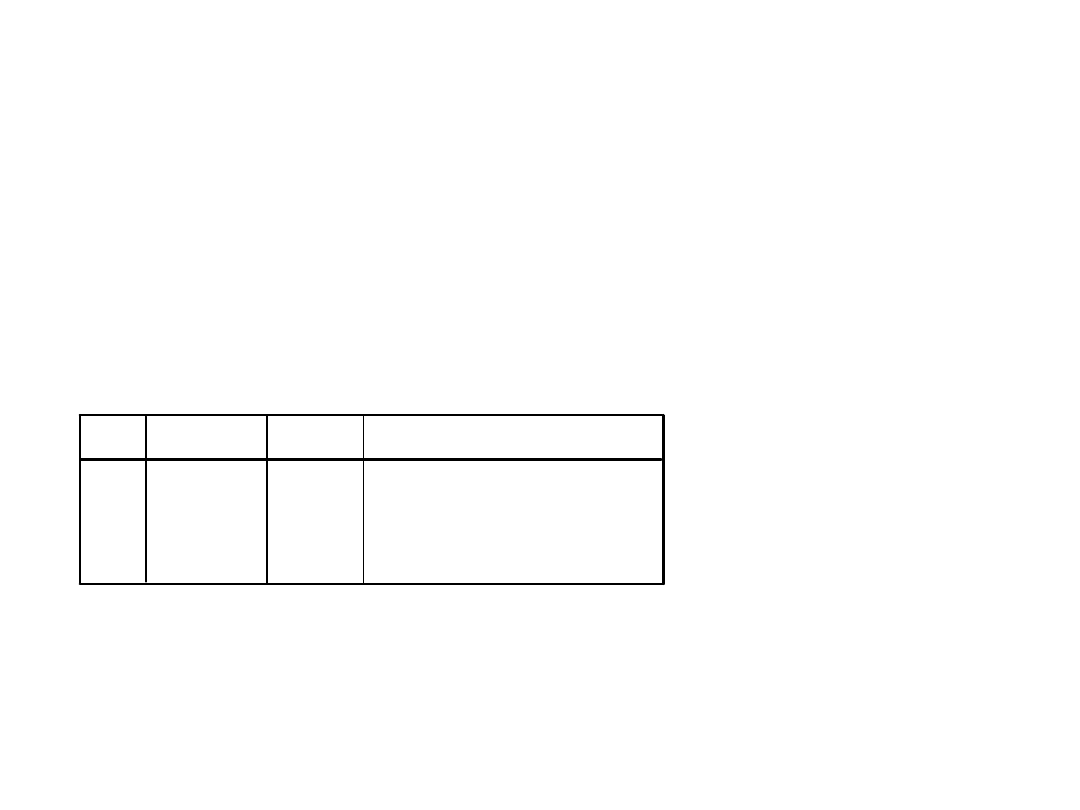
Dla selekcji postępującej

• Informacja o zmiennych

wprowadzonych i kryterium
wprowadzenia

Zmienne wprowadzone/usunięte

a

wraz_e

.

Selekcja postępująca (Kryterium:
Prawdopodobieństwo F-wprowadzenia
<= ,050).

wraz_s

.

Selekcja postępująca (Kryterium:
Prawdopodobieństwo F-wprowadzenia
<= ,050).

Model
1

2

Zmienne

wprowadzone

Zmienne

usunięte

Metoda

Zmienna zależna: konstruk

a.

Statystyki dopasowania

modeli

• Musimy wybrać któryś z modeli. Jak to zrobić?
• Najlepiej posłużyć się statystyką zmiana R

2

Analiza wariancji

c

1041,721

1 1041,721

29,385

,000

a

8295,448

234

35,451

9337,169

235

1312,798

2

656,399

19,060

,000

b

8024,372

233

34,439

9337,169

235

Regresja
Reszta
Ogółem
Regresja
Reszta
Ogółem

Model
1

2

Suma

kwadratów

df

Średni

kwadrat

F

Istotność

Predyktory: (Stała), wraz_e

a.

Predyktory: (Stała), wraz_e, wraz_s

b.

Zmienna zależna: konstruk

c.

Istotność zmiany R

2

• W tabeli zmiana R

2

dla modelu 2 jest

istotna. Zatem udaje nam się za pomocą

drugiego modelu wyjaśnić istotny kawałek

zmienności zmiennej zależnej. Tak więc

lepiej pokazywać drugi model niż pierwszy.

Model - Podsumowanie

,334

a

,112

,108

5,95404

,112

29,385

1

234

,000

,375

b

,141

,133

5,86851

,029

7,871

1

233

,005

Model
1
2

R

R-kwadrat

Skorygowane

R-kwadrat

Błąd

standardowy

oszacowania

Zmiana

R-kwadrat

Zmiana F

df1

df2

Istotność

zmiany F

Statystyki zmiany

Predyktory: (Stała), wraz_e

a.

Predyktory: (Stała), wraz_e, wraz_s

b.

Współczynniki regresji

Współczynniki

a

23,205

2,403

9,657

,000

,394

,073

,334

5,421

,000

19,897

2,646

7,521

,000

,298

,080

,252

3,740

,000

,193

,069

,189

2,806

,005

(Stała)
wraz_e
(Stała)
wraz_e
wraz_s

Model
1

2

B

Błąd

standardowy

Współczynniki

niestandaryzowane

Beta

Współczynniki

standaryzowa

ne

t

Istotność

Zmienna zależna: konstruk

a.

Istotne predyktory:

wrażliwość

społeczna

(beta=0,189,

-<0,01) i

emocjonalna

(beta=0,252;

p<0,001

Interpretacja:

Wybór metody

• Analiza regresji ma serię różnych

metod. Ich wybór nie jest prosty.
Niekiedy wszystkie te analizy dają
identyczne wyniki. Czasem jednak
dzieje się tak, że jedna metoda
zaprzecza drugiej. Często jest tak
wtedy, gdy predyktory są silnie ze
sobą skorelowane.