
ĆWICZENIE 8 i 9
(9.12.) (16.12.)
Zginanie poprzeczne z wykładową częścią
( )
( )
( )
z
y
xz
y
Q S
z
z
J b z
τ
=
Dyskusja wzoru na napr
ężenia styczne.
Uśrednione naprężenie styczne
( )
( ) ( )
( )
,
z
y
xz
y
Q
x S
z
x z
J b z
τ
=
jest funkcją dwóch zmiennych:
x- położenia przekroju w konstrukcji
z- położenia punktu na przekroju.
Dla ustalonego przekroju
o
x w konstrukcji dla którego znamy wartość funkcji siły
przekrojowej
( )
z
o
Q x
należy przeprowadzić badanie zmienności funkcji
( )
( )
y
S
z
b z
w celu znalezienia punktów o
maksymalnej wartości naprężeń stycznych. Wiadomo, że niezależnie od rodzaju przekroju
funkcja
( )
y
S
z
jest zawsze funkcją wypukłą o wartości maksymalnej dla punktów należących
do osi głównej centralnej i miejscami zerowymi dla włókien skrajnych.
Typowe przekroje występujące w budownictwie charakteryzują się skokową zmiennością
szerokości. Poniżej przedstawiono analizę przebiegu badanych funkcji dla dwóch typów
przekrojów.
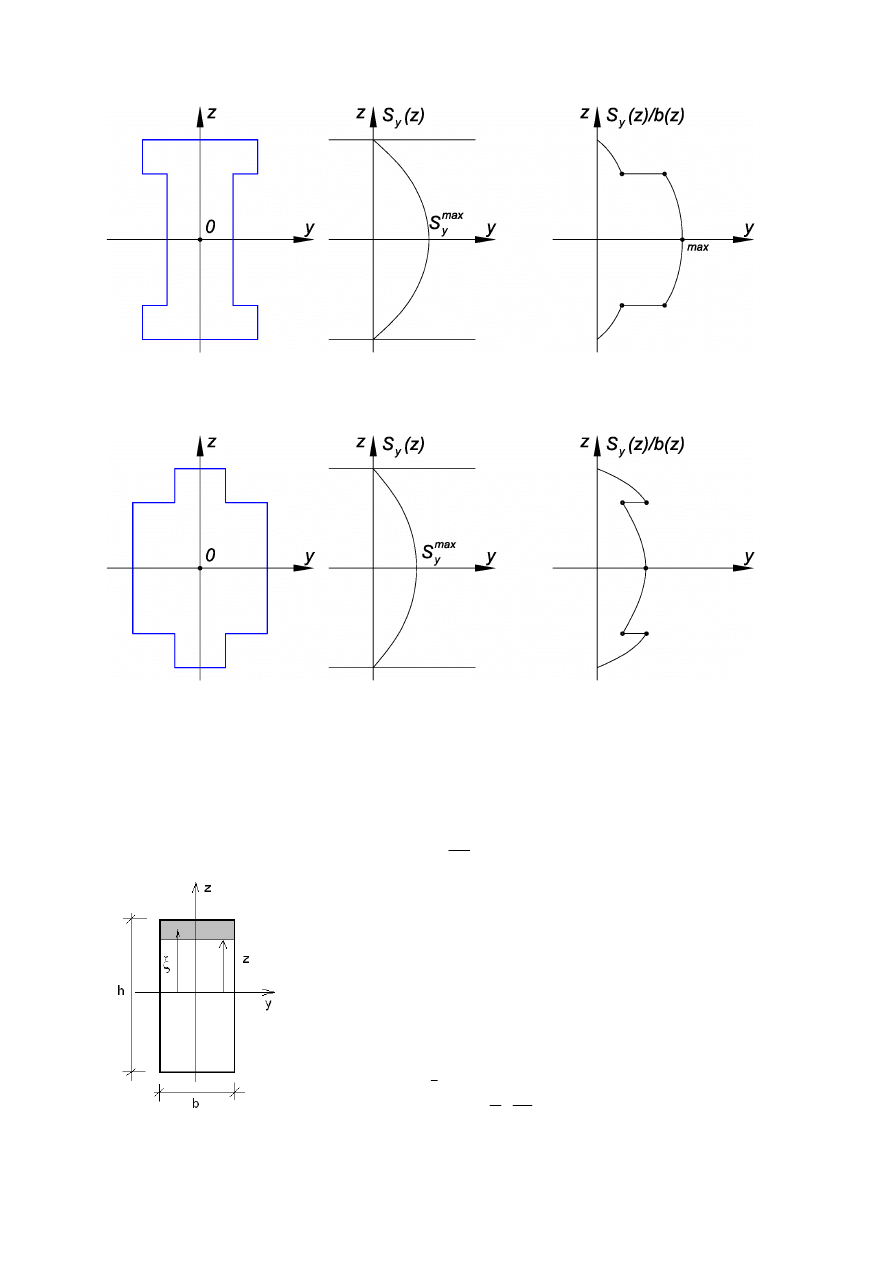
Typ 1. o szerokości wzrastającej wraz z oddalaniem się od środka przekroju.
Dla powyższego przekroju oczywiste jest, że naprężenia styczne o wartości maksymalnej leżą
na osi y.
Typ 2. o szerokości malejącej wraz z oddalaniem się od środka przekroju.
Dla powyższego przekroju należy policzyć naprężenia dla punktów które leżą na osi y oraz
pozostałych dwóch punktów na wykresie podejrzanych o występowanie w nich wartości
maksymalnych. Porównanie wyników obliczeń prowadzi do wskazania punktów w których
naprężenia styczne osiągają wartość maksymalną.
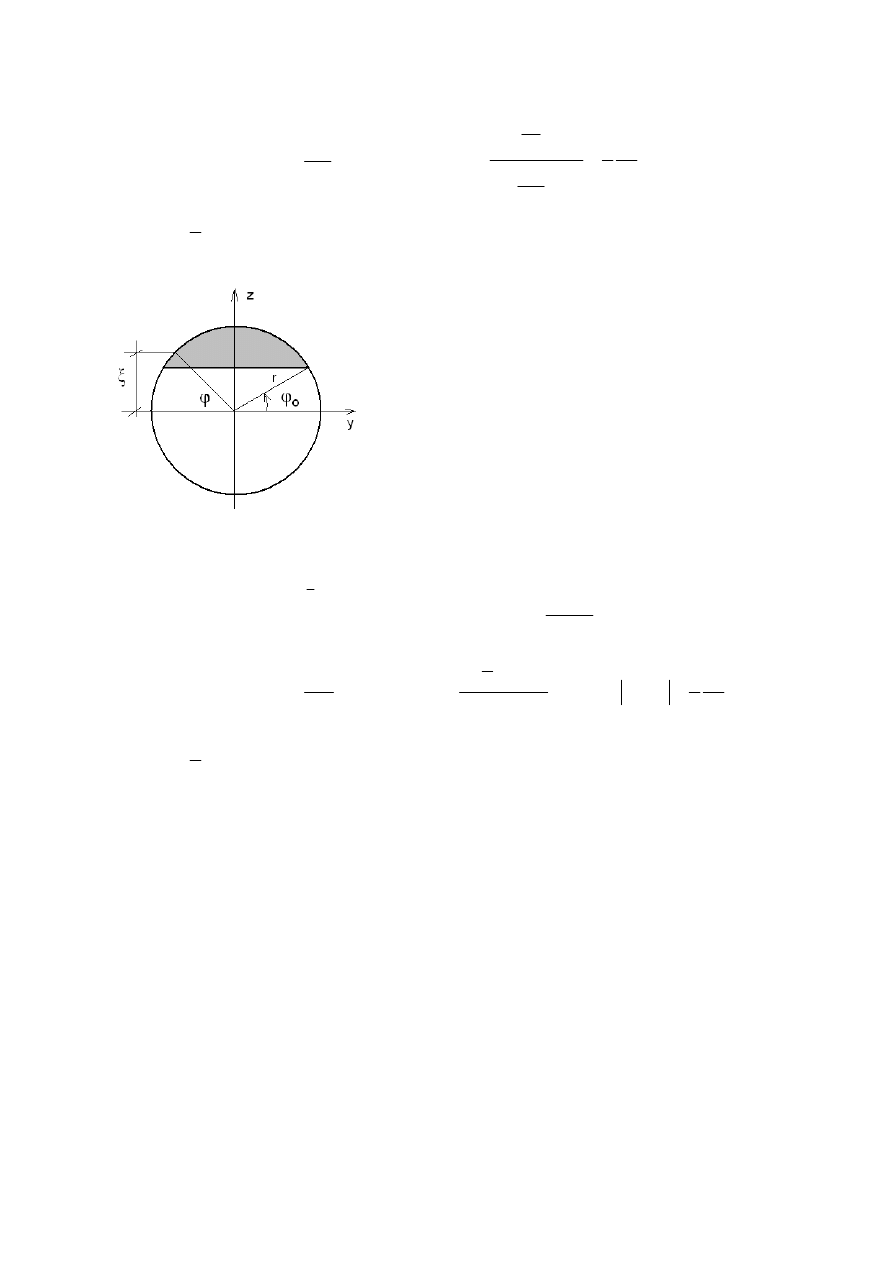
TYPOWE PRZEKROJE
( )
z
xz
Q
z
k
F
τ
=
( )
( )
2
2
2
2
4
h
y
A z
z
b h
S
z
dF
b
d
z
ξ
ξ ξ
=
=
=
−
∫∫
∫
F
bh
=
3
12
y
bh
J
=
( )
2
2
3
4
3
2
12
z
z
xz
h
Q
z
Q
z
bh
bh
b
τ
−
=
=
3
2
k
=
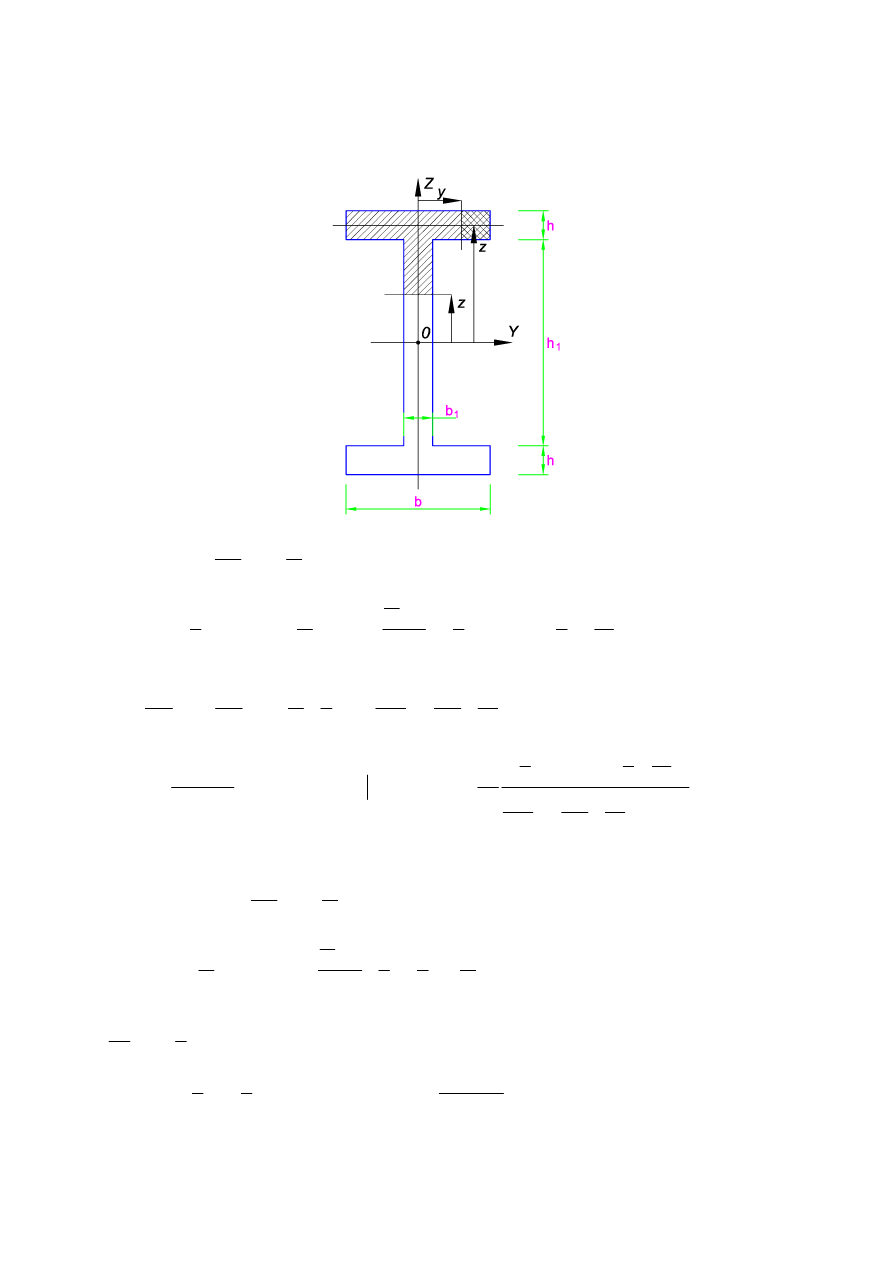
sin
r
ξ
ϕ
=
( )
2
cos
b z
r
ϕ
=
⋅
sin
o
z
r
ϕ
=
cos
d
r
d
ξ
ϕ ϕ
=
⋅
( )
2
2
2
cos
cos
2
cos
dF
b z
d
r
r
d
r
d
ϕ
ϕ
ϕ ϕ
ϕ ϕ
=
⋅
= ⋅
⋅ ⋅
⋅
=
⋅
( )
( )
2
2
2
2
3
cos
sin
2
cos
....
2
3
o
y
A z
S
z
dF
b r
r
d
r
π
ϕ
ϕ
ξ
ϕ
ϕ ϕ
=
=
⋅
=
=
∫∫
∫
2
F
r
π
=
4
4
y
r
J
π
=
( )
2
4
cos
3
z
o
xz
Q
z
F
ϕ
τ
=
( )
4
max
3
z
xz
Q
z
F
τ
=
4
3
k
=
Zadanie.
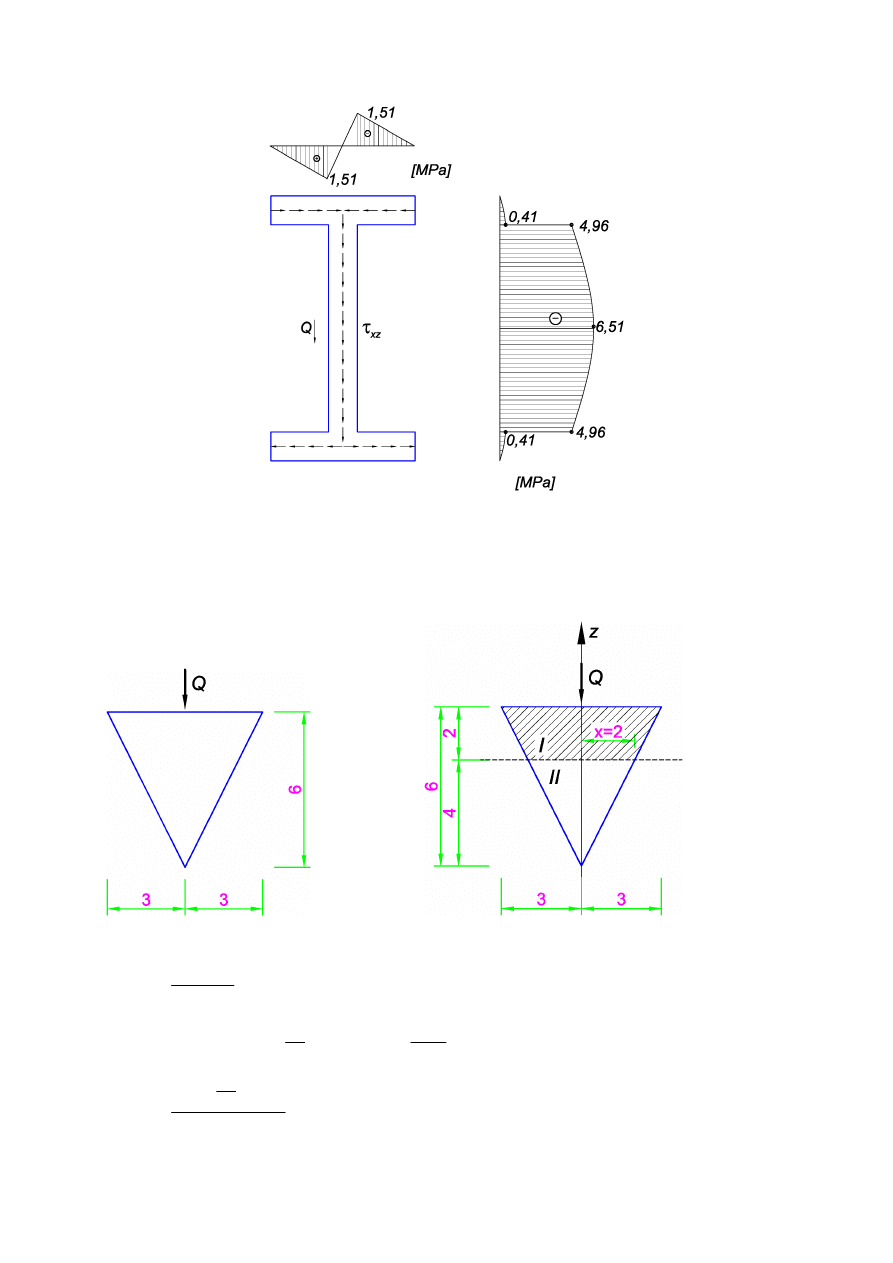
Wyznaczyć rozkład naprężeń stycznych w przekroju dwuteowym. Jaką część siły poprzecznej
oraz momentu zginającego przenoszą półki i środnik?
Środnik
1
1
2
2
h
h
z
− ≤ ≤
( )
(
)
(
)
1
2
2
1
1
1
1
1
1
1
1
1
2
2
2
2
2
2
4
y
h
z
h
h
S
z
bh
h h
b
z
z
bh h h
b
z
−
=
+
+
−
+
=
+
+
−
(
)
2
3
3
3
2
1 1
1
1 1
1
1
2
2
12
12
2
2
12
12
2
y
b h
h
b h
bh
bh
h
bh
J
bh
h h
=
+
+
+
=
+
+
+
( )
( )
( )
z
y
xz
y
Q S
z
z
J b z
τ
=
( )
(
)
(
)
2
1
1
1
3
3
0
2
1 1
1
1
1
1
2
2
4
max
2
12
12
2
z
xz
xz
z
h
bh h h
b
Q
z
b h
bh
bh
b
h
h
τ
τ
=
+
+
=
=
+
+
+
Półki
1
1
2
2
h
h
h
z
h
−
− +
≤ ≤ +
( )
1
2
2
1
1
1
2
2
2
2
2
2
y
h
h
h
h
z
S
z
b
h
z
z
b
h
z
+
=
+
−
+
−
=
+
−
2
2
b
b
z
− ≤ ≤
( )
(
)
1
1
2
2
y
b
S
y
h
y
h
h
=
−
+
( )
( )
z
y
xy
y
Q S
y
y
J h
τ
=
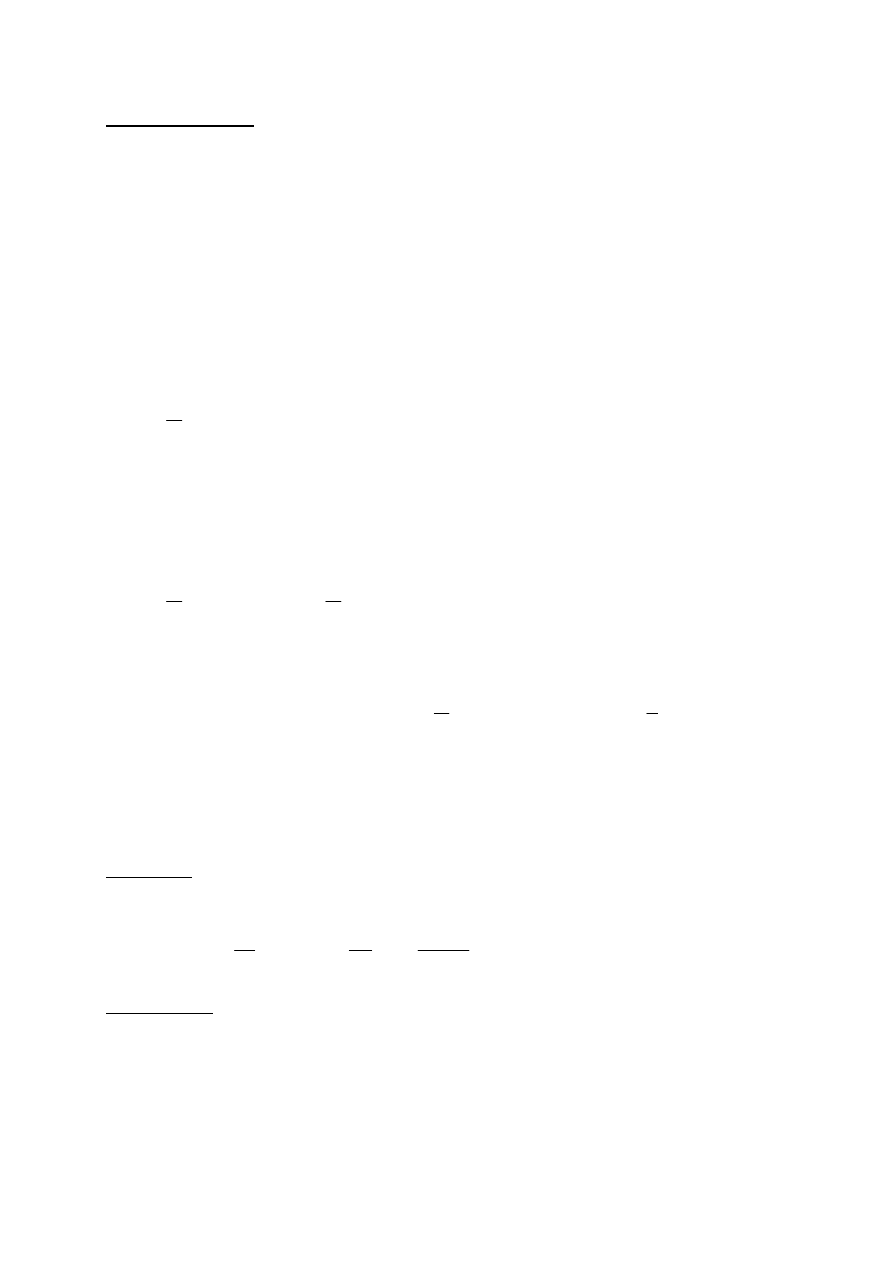
Przykład liczbowy:
dwuteownik 220
1
19.56 cm
h
=
1.22 cm
h
=
1
0.81 cm
b
=
9.80 cm
b
=
4
3089 cm
y
J
=
Środnik:
( )
4
3
2
3
1.63 10
4.05 10
m
y
S
z
z
−
−
=
⋅
−
⋅
( )
(
)
2
651.46 16186.5
xz
z
Q
z
τ
=
−
(
)
max
0
651.5
xz
xz
z
Q
τ
τ
=
=
=
1
496.6
2
xz
h
z
Q
τ
=
=
Półki:
( )
4
3
2
3
5.93 10
49.0 10
m
y
S
z
z
−
−
=
⋅
−
⋅
( )
(
)
2
195.9 16186.5
xz
z
Q
z
τ
=
−
1
0
2
xz
h
z
h
τ
= +
=
1
41.1
2
xz
h
z
Q
τ
=
=
( )
(
)
3
1.27 10
0.049
y
S
y
y
−
=
⋅
−
( )
(
)
3370.0 0.049
xy
y
y Q
τ
=
−
1
151.5
2
xy
b
y
Q
τ
=
=
0
2
xy
b
y
τ
=
=
Siła poprzeczna przenoszona przez środnik:
651.46
16186.5
1.032
0.082
0.95
s
s
s
xz
s
y
A
Q
dA
Q A
Q J
Q
Q
Q
τ
=
=
−
=
−
=
∫∫
s
Q =0.95 Q
Moment zginający przenoszony przez półki:
2
2584.3
0.84
3089.0
s
p
p
y
p
x
y
y
A
A
J
M
M
zdA
z dA
M
M
M
J
J
σ
=
=
=
=
⋅
=
∫∫
∫∫
0.84
p
M
M
=
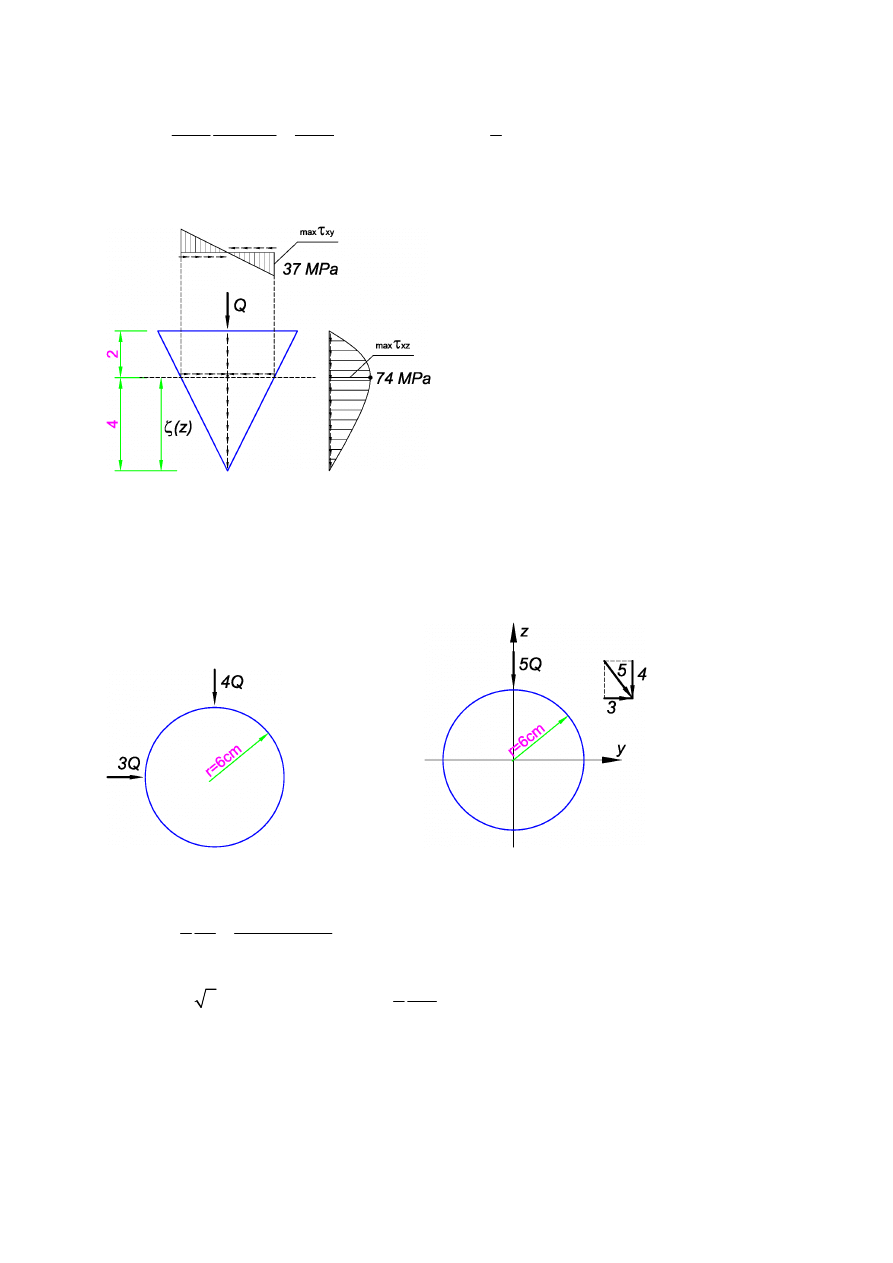
Zadanie.
Wyznaczyć rozkład naprężeń stycznych dla podanego przekroju trójkątnego jeżeli
100 kN
Q
=
.
( )
( )
( )
z
y
xz
y
Q S
z
z
J b z
τ
=
( )
4
b z
=
( )
3
32
cm
3
II
y
S
z
=
3
3
6 6
cm
36
y
J
⋅
=
( )
6
8
2
32
100
10
3
74 MPa
36 10
4 10
xz
z
τ
−
−
−
⋅
⋅
=
=
⋅
⋅ ⋅
( )
( )
( )
( )
( ) ( )
z
y
xy
xz
y
Q S
z
y
y
z
z
z
J b z
z
τ
τ
ζ
ζ
=
=
( )
2
74
37 MPa
4
xy
z
τ
=
=
Zadanie.
Wyznaczyć rozkład naprężeń stycznych dla podanego przekroju kołowego jeżeli
100 kN
Q
=
.
Przekrój jest osiowosymetryczny, stąd obieramy korzystne do opisu położenie osi.
2
4
4 500
max
58.94 MPa
3
3 3.14 0.06
z
xz
Q
A
τ
⋅
=
=
=
⋅
⋅
dla
3 2
y
z
= =
4
4
max
29.5 MPa
3
z
xy
Q
y z
r
τ
π
=
⋅ =
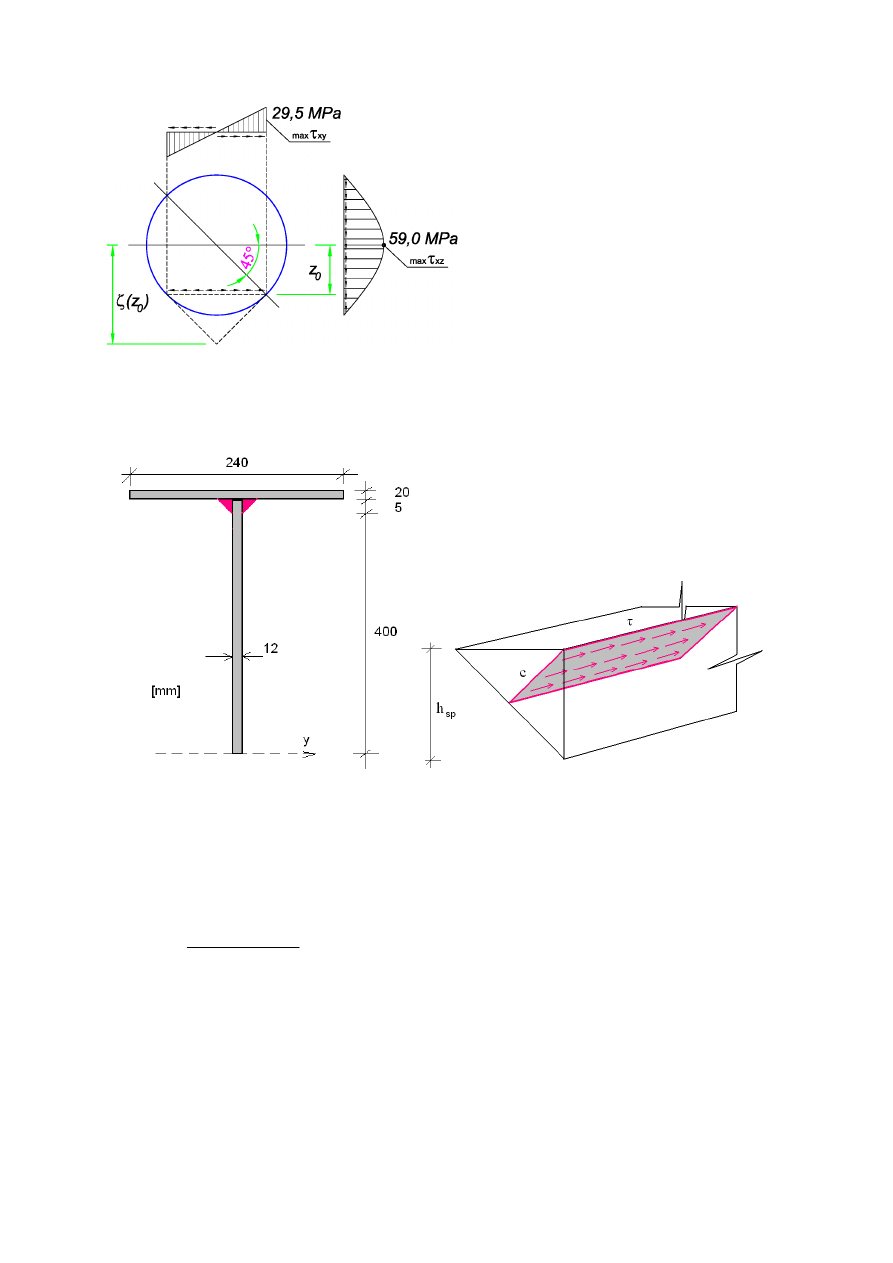
SPOINY - PRZYKŁAD
640
z
Q
kN
=
4
3
19.70 10
pó ki
y
S
m
τ
−
=
⋅
4
4
21.40 10
y
J
m
−
=
⋅
100
R
MPa
τ
=
0.7
sp
c
h
≅
⋅
3
5 10
sp
h
m
−
= ⋅
( )
(
)
,
84
100
2 0.7
pó ki
z
y
spoiny
xz
y
sp
Q S
x z
MPa
MPa
R
J
h
τ
τ
τ
=
=
<
=
⋅ ⋅
⋅
Zginanie poprzeczne
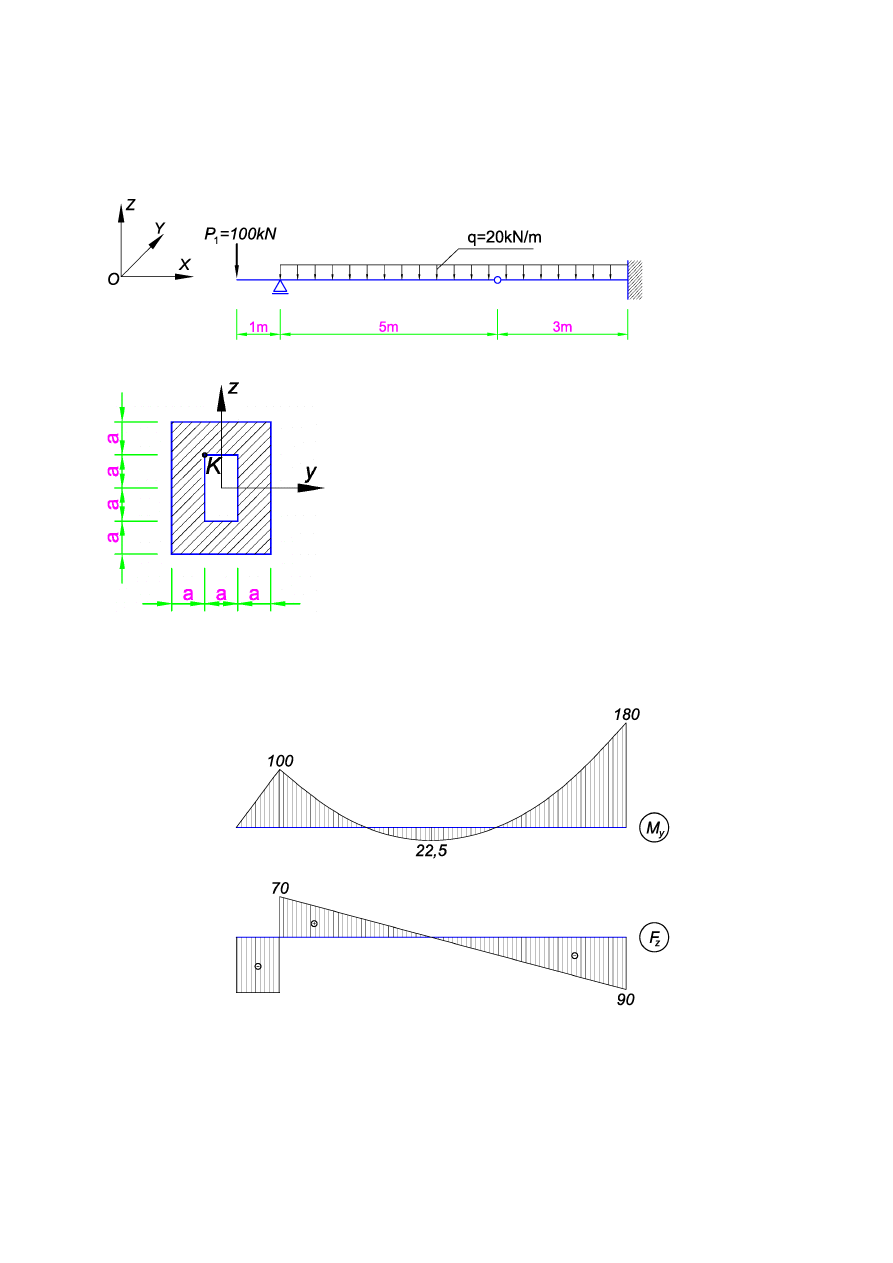
Zadanie
Zadaniem jest zaprojektowanie belki stalowej o podanym profilu i schemacie statycznym
oraz określenie stanu naprężeń w zadanym punkcie K.
Dane:
MPa
150
f
d
=
,
MPa
90
f
=
τ
1. Pierwszym krokiem jest sporządzenie wykresów sił przekrojowych
2. Charakterystyki geometryczne przekroju:

(
)
3
2
5
.
5
2
2
3
0
a
a
a
a
a
a
z
S
y
=
−
⋅
⋅
=
=
,
4
3
3
33
.
15
12
8
64
3
a
a
a
a
a
J
y
=
⋅
−
⋅
=
3
4
67
.
7
2
33
.
15
max
a
a
a
z
J
W
y
y
=
=
=
m
10
38
.
5
kPa
10
150
67
.
7
kNm
180
2
3
3
max
−
⋅
=
⇒
⋅
≤
=
a
a
σ
do obliczeń przyjęto:
m
10
4
.
5
2
−
⋅
=
a
3. Obliczenie naprężeń
( )
MPa
149
kPa
10
149
10
4
.
5
67
.
7
kNm
180
3
6
3
2
max
=
⋅
=
⋅
=
−
=
a
z
σ
(
)
(
)
(
)
MPa
15
.
6
kPa
10
15
.
6
m
10
5.4
2
m
10
4
.
5
33
.
15
m
10
5.4
5.5
kN
100
3
2
-
4
4
2
3
3
-2
0
max
=
⋅
=
⋅
⋅
⋅
⋅
⋅
⋅
⋅
=
−
=
z
τ
Dla punktu K leżącego w przekroju utwierdzenia naprężenia wynoszą:
( )
( )
MPa
6
.
74
kPa
10
6
.
74
10
4
.
5
33
.
15
m
10
5.4
kNm
180
3
6
3
-2
=
⋅
=
⋅
⋅
⋅
+
=
−
K
σ
( )
(
)
(
)
(
)
MPa
53
.
4
kPa
10
53
.
4
m
10
5.4
2
m
10
4
.
5
33
.
15
m
10
5.4
1.5
m
10
5.4
3
kN
90
3
2
-
4
4
2
-2
2
2
-2
−
=
⋅
=
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
−
=
−
K
τ
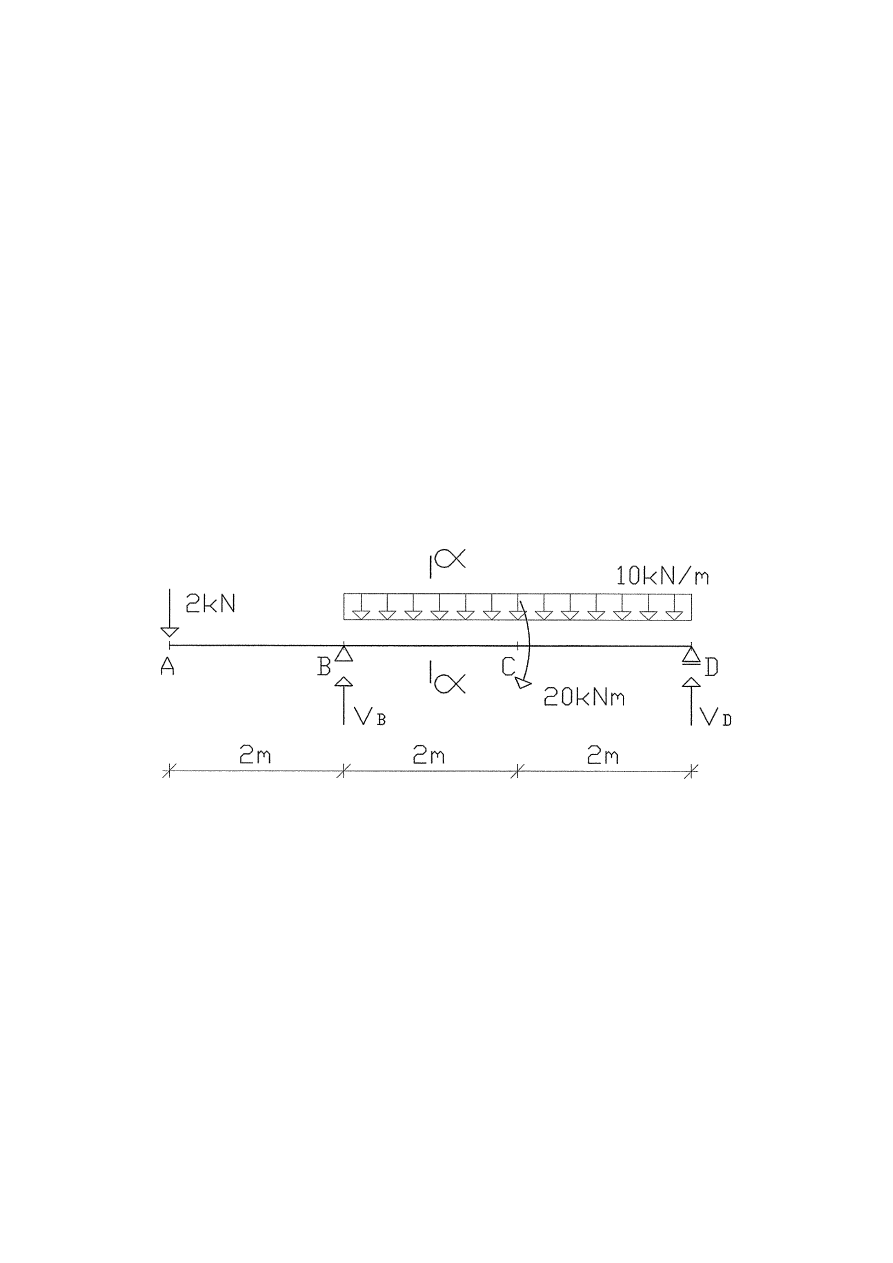
P R O J E K T
Projekt belki zginanej poprzecznie
Zaprojektować wymiary przekroju poprzecznego zginanej belki ze względu na stan graniczny
nośności i użytkowania.
Po zaprojektowaniu wyznaczyć rozkład naprężeń normalnych i stycznych w przekroju
α
-
α
oraz obliczyć naprężenia główne i ich kierunki w punkcie K przekroju.
Otrzymane wyniki sprawdzić programami komputerowymi STATYKA i PRZEKRÓJ,
załączyć wydruki rezultatów obliczeń.
R = 175 MPa
R
t
= 0.6
⋅⋅⋅⋅
R
f
dop
= l
max
/ 250
E = 205 GPa
STATYKA
Σ
M(B) = 0
Σ
M(D) = 0
V
D
⋅
4 + 2
⋅
2 – 20 – 10
⋅
4
⋅
2 = 0
2
⋅
6 + 10
⋅
4
⋅
2 – V
B
⋅
4 – 20 = 0
V
D
= (100 – 4) : 4
4
⋅
V
B
= 72
V
D
= 24
V
B
= 18
Spr. Σ ”Z” = 0
–10
⋅
4 – 2 + 24 + 18 = 0
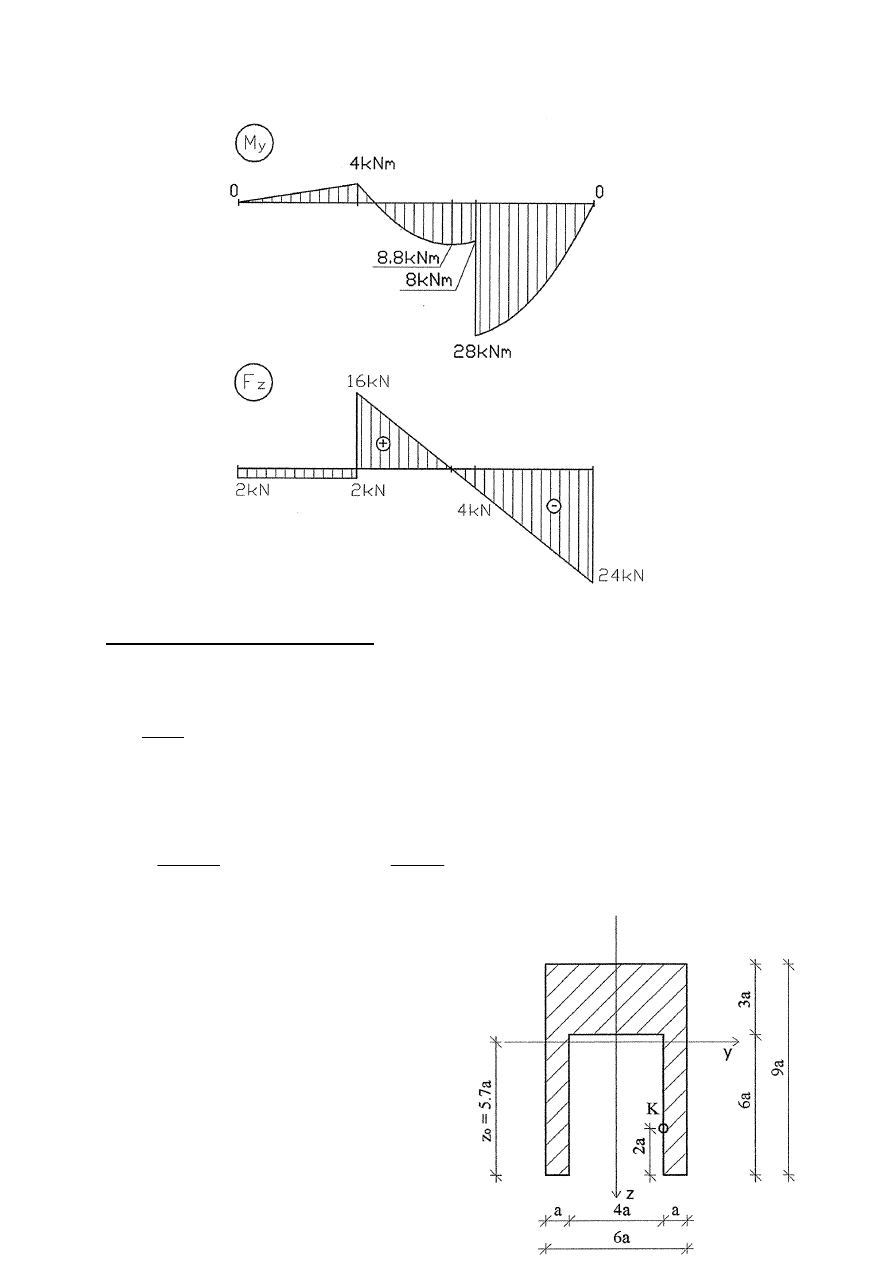
M(A) = 0
M(B) = –2
⋅
2 = –4
M(C)
L
= –2
⋅
4 + 18
⋅
2 + 10
⋅
2
⋅
1 = –8 + 36 – 20 = 8
M(C)
P
= 24
⋅
2 – 10
⋅
2
⋅
1 = 48 – 20 = 28
M(D)
= 0
F
z
(A) = –2
F
z
(B)
L
= –2
F
z
(B)
P
= –2 + 18 = 16
F
z
(C) = –24 + 20 = –4
F
z
(D) = –24
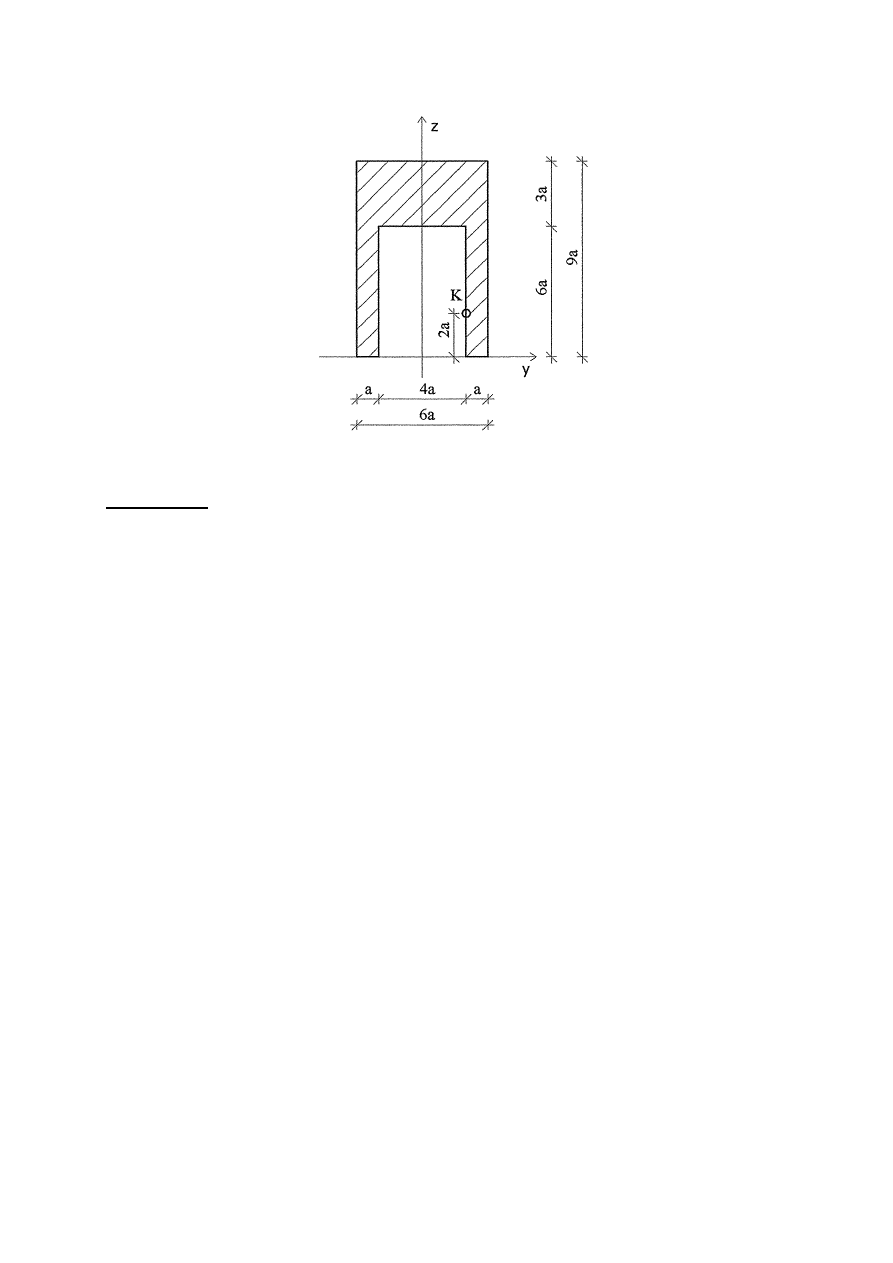
GEOMETRIA PRZEKROJU
F = 2
⋅
(a
⋅
6a) + 3a
⋅
6a = 12a² + 18a² = 30a²
S
y
= 2
⋅
(a
⋅
6a
⋅
3a) + 3a
⋅
6a
⋅
7.5a = 36a³ + 135a³ = 171a³
z
o
=
²
30
³
171
a
a
= 5.7a
MOMENT BEZWŁADNOŚCI
J
yo
= [
12
(3a)³
6a
⋅
+ 6a
⋅
3a
⋅
(1.8)² ] + 2
⋅
[
12
(6a)³
a
⋅
+ a
⋅
6a
⋅
(2.7)²] =
= [ 13.5a + 58.32 ] a
4
+ 2
⋅
[ 18 +
43.74 ] a
4
= 71.82a
4
+ 123.48a
4
= 195.3a
4
WSKAŹNIK WYTRZYMAŁOŚCI
| z
max
| = 5.7a
W
y
= J
yo
/ | z
max
| = 195.33a
4
/ 5.7a = 34.26a³
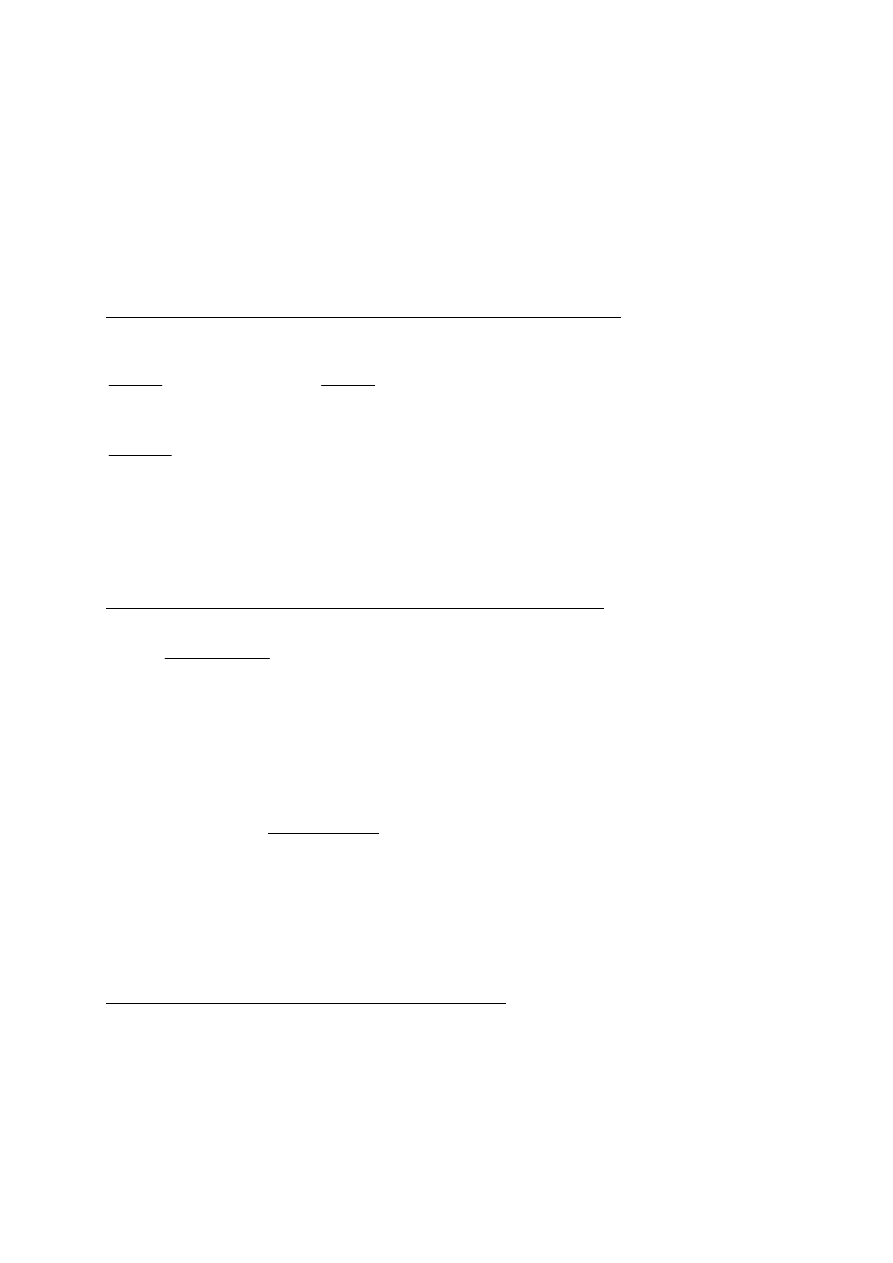
Warunek projektowania ze względu na naprężenie normalne:
Wy
max
M
≤ R
=>
R
M max
≤ W
y
MPa
kNm
175
28
≤ 34.26a³
28
⋅
10³ Nm ≤ 175
⋅
10
6
⋅
N/m²
⋅
34.26 a³
0.16
⋅
10
-3
: 34.26 m³ ≤ a³
a
≥ 1.67 cm
Warunek projektowania ze względu na naprężenia styczne:
τ
max
=
)
0
(
Jyo
)
0
(
max
Fz
b
Sy
⋅
⋅
S
y
(0) = 2
⋅
(a
⋅
0.3a
⋅
0.15a) + 3a
⋅
6a
⋅
1.8a = 0.09a³ + 32.4a³ = 32.49a³
b(0) = 2a
F
z max
= 24 kN
τ
max
≤ R
t
=>
2a
4
3
.
195
³
49
.
32
kN
28
⋅
⋅
a
a
≤ 0.6
⋅
R
1.9963
⋅
10
3
m² ≤ 105
⋅
10
6
⋅
a²
a
≥ 0.435 cm
Warunek projektowania ze względu na ugięcia:
M(x) = – 2
⋅
x
|
AB
+ 18
⋅
(x–2) – 10
⋅
½
⋅
(x–2)
2
|
BC
+ 20
⋅
(x–4)
0
|
CD
EJ
y
w’’(x) = 2
⋅
x
|
AB
– 18
⋅
(x–2) + 5
⋅
(x–2)
2
|
BC
– 20
⋅
(x–4)
0
|
CD

EJ
y
w’(x) = C + x
2
|
AB
– 9
⋅
(x–2)
2
+ 5/3
⋅
(x–2)
3
|
BC
– 20
⋅
(x–4)
1
|
CD
EJ
y
w(x) = D + C
⋅
x + 1/3
⋅
x
3
|
AB
– 9/3
⋅
(x–2)
3
+ 5/12
⋅
(x–2)
4
|
BC
– 20/2
⋅
(x–4)
2
|
CD
EJ
y
w(x) = D + C
⋅
x + 0.33
⋅
x
3
|
AB
– 3
⋅
(x–2)
3
+ 0.4166
⋅
(x–2)
4
|
BC
– 10
⋅
(x–4)
2
|
CD
Kinematyczne Warunki Brzegowe:
w(2) = 0
0 = D + 2
⋅
C + 0.33
⋅
8
0 = D + 2
⋅
C + 2.66
w(6) = 0
0 = D + 6
⋅
C + 0.33(3)
⋅
216 – 3
⋅
64 + 0.416(6)
⋅
256 – 10
⋅
4
0 = D + 6
⋅
C + 72 – 192 + 106.66 – 40
0 = D + 6
⋅
C – 53.34
0 = D + 2
⋅
C + 2.66
0 = D + 6
⋅
C – 53.34
0 = –4
⋅
C + 56
0 = D + 2
⋅
14 + 2.66
4
⋅
C = 56
–D = 30.66
C = 14
D = –30.66
EJ
y
w’(x) = 14 + x
2
|
AB
– 9
⋅
(x–2)
2
+ 1.66
⋅
(x–2)
3
|
BC
– 20
⋅
(x–4)
1
|
CD
EJ
y
w(x) = –30.66 + 14
⋅
x + 0.33
⋅
x
3
|
AB
– 3
⋅
(x–2)
3
+ 0.4166
⋅
(x–2)
4
|
BC
– 10
⋅
(x–4)
2
|
CD
pkt A
x = 0
EJ
y
w’(0) = 14
EJ
y
w(0) = –30.66
x = 1
EJ
y
w’(1) = 14 + 1
2
= 15
EJ
y
w(1) = –30.66 + 14
⋅
1 + 0.33
⋅
1
3
= –16.33
pkt B
x = 2
EJ
y
w’(2) = 14 + 2
2
= 18
EJ
y
w(2) = 0
x = 3
EJ
y
w’(3) = 14 + 3
2
– 9
⋅
(3–2)
2
+ 1.66
⋅
(3–2)
3
= 15.66
EJ
y
w(3) = –30.66 + 14
⋅
3 + 0.33
⋅
3
3
– 3
⋅
(3–2)
3
+ 0.4166
⋅
(3–2)
4
= 17.66
pkt C
x = 4
EJ
y
w’(4) = 14 + 4
2
– 9
⋅
(4–2)
2
+ 1.66
⋅
(4–2)
3
= 7.28
EJ
y
w(4) = –30.66 + 14
⋅
4 + 0.33
⋅
4
3
– 3
⋅
(4–2)
3
+ 0.4166
⋅
(4–2)
4
= 29.12
x = 5
EJ
y
w’(5) = 14 + 5
2
– 9
⋅
(5–2)
2
+ 1.66
⋅
(5–2)
3
– 20
⋅
(5–4) = –17.18
EJ
y
w(5) = –30.66 + 14
⋅
5 + 0.33
⋅
5
3
– 3
⋅
(5–2)
3
+ 0.4166
⋅
(5–2)
4
– 10
⋅
(5–4)
2
= 23.33
pkt D
x = 6
EJ
y
w’(6) = 14 + 6
2
– 9
⋅
(6–2)
2
+ 1.66
⋅
(6–2)
3
– 20
⋅
(6–4) = –27.76
EJ
y
w(6) = 0
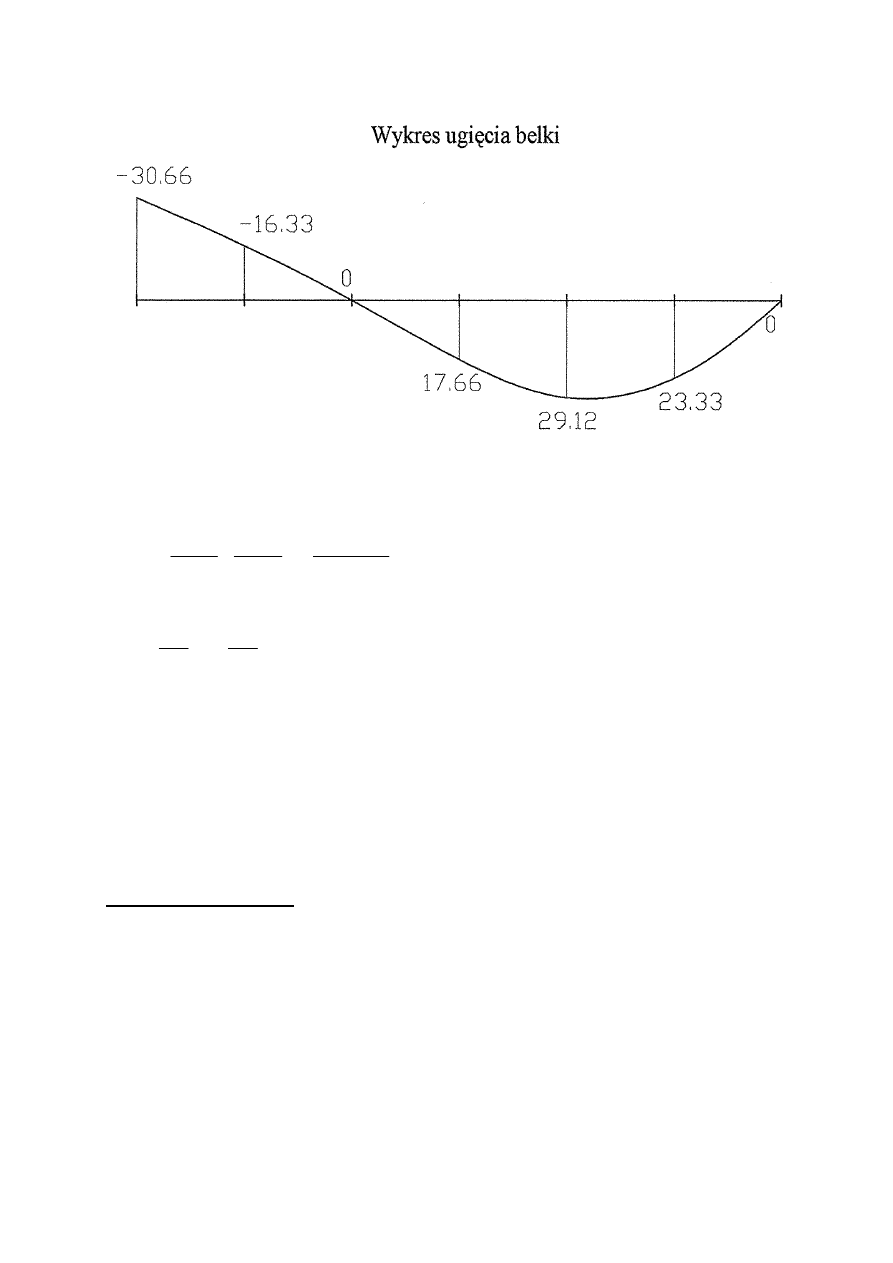
w
max
≤ w
dop
w
max
=
Jy
E
30.66
[
GPa
kNm³
] =
195.3
205
30.66
⋅
⋅
10
-6
⋅
a
-4
⋅
m
5
= 0.0007658
⋅
10
-4
⋅
a
-4
⋅
m
5
=
= 7.658
⋅
10
-10
⋅
a
-4
⋅
m
5
w
dop
=
250
l
m =
250
6
m = 0.024 m
7.658
⋅
10
-10
⋅
a
-4
⋅
m
5
≤ 0.024 m
7.658
⋅
10
-10
⋅
m
4
≤ 0.024
⋅
a
4
2.4
⋅
10
-2
⋅
a
4
≥ 7.658
⋅
10
-10
⋅
m
4
a ≥ 1.33
⋅
10
-2
⋅
m
a
≥ 1.33 cm
PODSUMOWANIE:
a
≥ 1.67 cm
٨
a
≥ 0.435 cm
٨
a
≥ 1.33 cm
Przyjmujemy do obliczeń:
a = 1.7cm
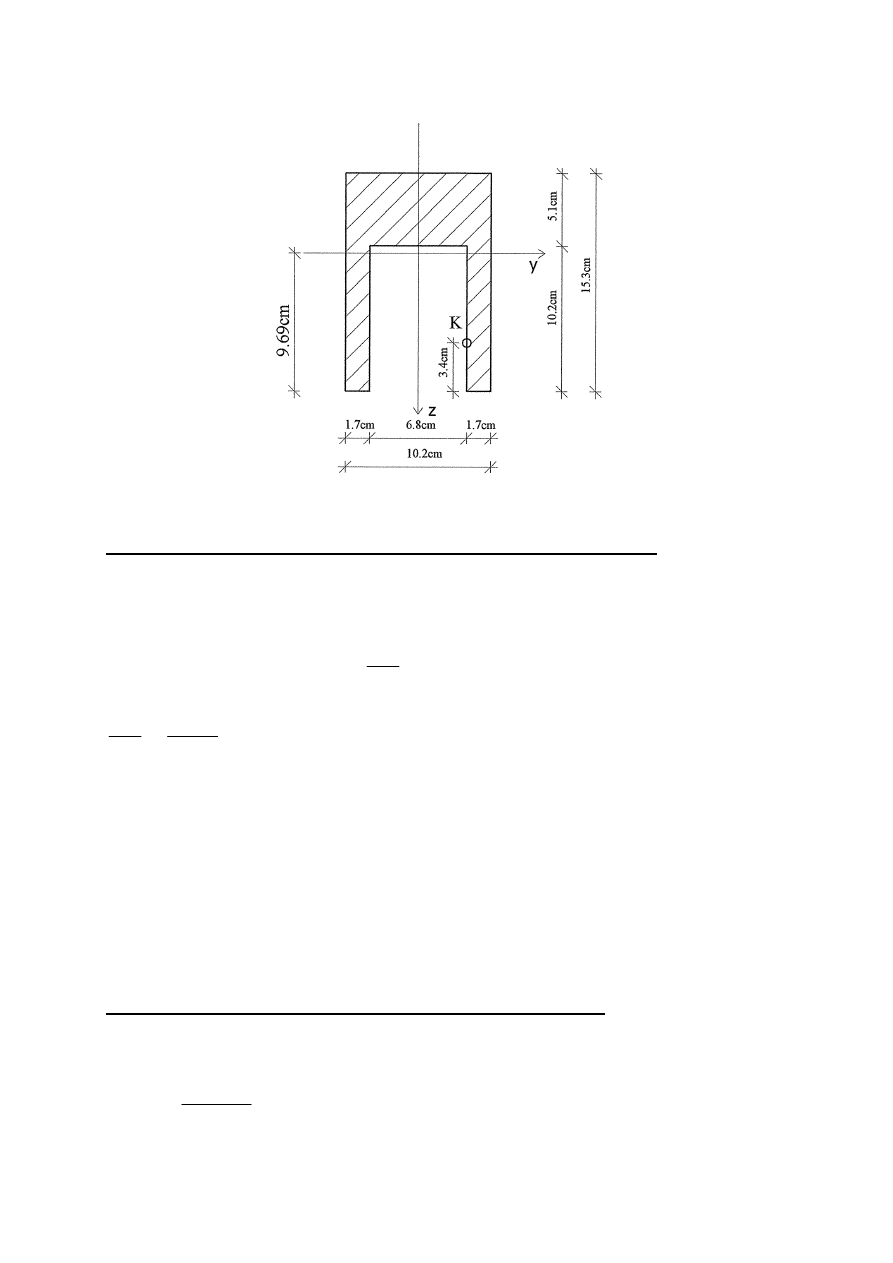
ROZKŁAD NAPR
ĘŻEŃ NORMALNYCH W PRZEKROJU
α
-α
J
yo
= 195.3
⋅
a
4
= 195.3
⋅
(1.7)
4
⋅
10
-8
m
4
= 195.3
⋅
(1.7)
4
⋅
10
-8
m
4
=
= 1631.16
⋅
10
-8
m
4
= 0.1631
⋅
10
-4
m
4
M
α
-α
= 7 kNm
σ
x
=
Jy
My
⋅
z,
Jy
My
=
0.1631
7
⋅
10
7
⋅
N
⋅
m
-3
= – 42.92
⋅
10
7
⋅
N
⋅
m
-3
= – 4.292
⋅
10
8
⋅
N
⋅
m
-3
σ
x
(z = 10.2) = –4.292
⋅
10
8
⋅
N
⋅
m
-3
⋅
0.102 m = 0.4377
⋅
10
8
⋅
N
⋅
m
-2
= –43.77 MPa
σ
x
(z = 0.51) = –4.292
⋅
10
8
⋅
N
⋅
m
-3
⋅
(–0.0051) m = 0.02188
⋅
10
8
⋅
N
⋅
m
-2
= 2.188 MPa
σ
x
(z = -5.61) = –4.292
⋅
10
8
⋅
N
⋅
m
-3
⋅
(–0.0561) m = –0.2407
⋅
10
8
⋅
N
⋅
m
-2
= 24.07 MPa
ROZKŁAD NAPR
ĘŻEŃ STYCZNYCH PRZEKROJU
α
-α
J
yo
= 0.1631
⋅
10
-4
m
4
F
z
α
-α
= 6 kN
τ
max
(z) =
)
(
Jyo
)
(
Fz
z
b
z
Sy
⋅
⋅
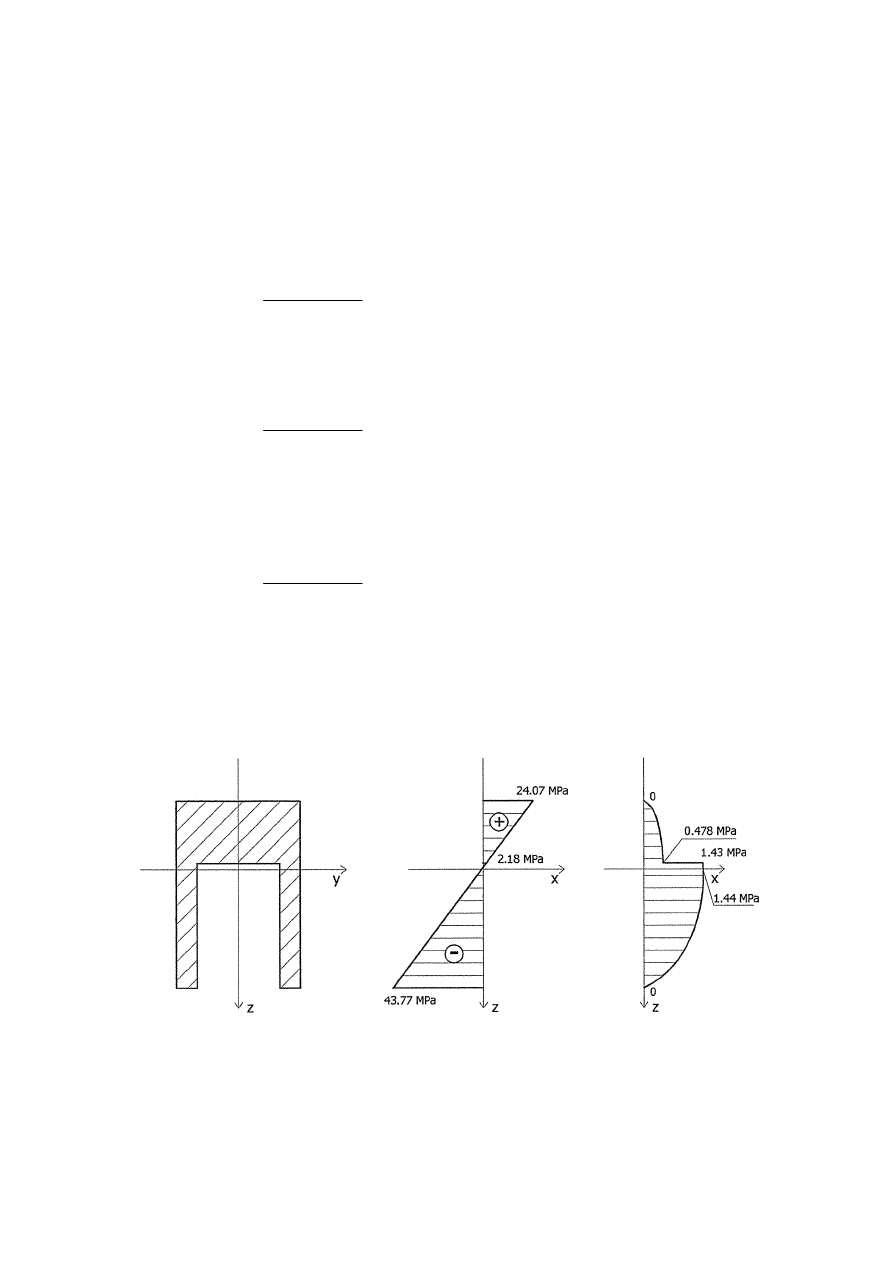
z = –0.0561 m
b = 0.102 m
S
y
(–5.61cm) = 0
τ
max
= 0
z = –0.0051 m
b = 0.102 m
S
y
(–0.51cm) = 10.2
⋅
5.1
⋅
2.55
⋅
10
-6
m
3
= 132.651
⋅
10
-6
m
3
τ
max
=
102
.
0
1631
.
0
651
.
132
6
⋅
⋅
⋅
10 Pa = 4.78
⋅
10
4
⋅
10 Pa = 0.478 MPa
z = –0.0051 m
b = 0.034 m
S
y
(–0.51cm) = 132.651
⋅
10
-6
m
3
τ
max
=
034
.
0
1631
.
0
651
.
132
6
⋅
⋅
⋅
10 Pa = 1.43
⋅
10
5
⋅
10 Pa = 1.43 MPa
z = 0 m
b = 0.034 m
S
y
(0) = 132.651
⋅
10
-6
+ 2
⋅
(1.7
⋅
0.3
⋅
1.7
⋅
0.255) m
3
=
= 132.651
⋅
10
-6
+ 0.4421
⋅
10
-6
m
3
= 133.093
⋅
10
-6
m
3
τ
max
=
034
.
0
1631
.
0
093
.
133
6
⋅
⋅
⋅
10 Pa = 1.44
⋅
10
5
⋅
10 Pa = 1.44 Mpa
z = 0.0969 m
b = 0.034 m
S
y
(9.69cm) = 0
τ
max
= 0
Wydać testy komputerowe przygotowujące do egzaminu
Wyszukiwarka
Podobne podstrony:
mechanika inzynieria id 291479 Nieznany
inzynieria id 219563 Nieznany
Grafika inzynierska 2 id 194765 Nieznany
Grafika inzynierska id 194762 Nieznany
Inzynieria wzory1 id 219676 Nieznany
3 Podstawy obl inzynierskich id Nieznany (2)
Biotechnologia i inzyniera id 8 Nieznany (2)
Abolicja podatkowa id 50334 Nieznany (2)
4 LIDER MENEDZER id 37733 Nieznany (2)
katechezy MB id 233498 Nieznany
metro sciaga id 296943 Nieznany
perf id 354744 Nieznany
interbase id 92028 Nieznany
Mbaku id 289860 Nieznany
Probiotyki antybiotyki id 66316 Nieznany
miedziowanie cz 2 id 113259 Nieznany
LTC1729 id 273494 Nieznany
D11B7AOver0400 id 130434 Nieznany
więcej podobnych podstron