Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 2

Nr: 1

Metody obliczeniowe

• wykład nr 2

– metody rozwiązywania równań nieliniowych

– zadanie optymalizacji

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 2

Nr: 2

Posta

ć

równania nieliniowego

Równanie nieliniowe jednej zmiennej o ogólnej postaci:

f(x)=0

–

rozwiązanie analityczne : znalezienie takiej wartości

x

0

dla której

f(x

0

)=0

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 2

Nr: 3

Posta

ć

równania nieliniowego

Równanie nieliniowe jednej zmiennej o ogólnej postaci:

f(x)=0

–

rozwiązanie analityczne : znalezienie takiej wartości

x

0

dla której

f(x

0

)=0

–

rozwiązanie przybliżone :

•

skomplikowana postać funkcji

f(x)=0

uniemożliwia znalezienie

rozwiązania analitycznego (dokładnego)

•

2 etapy:

–

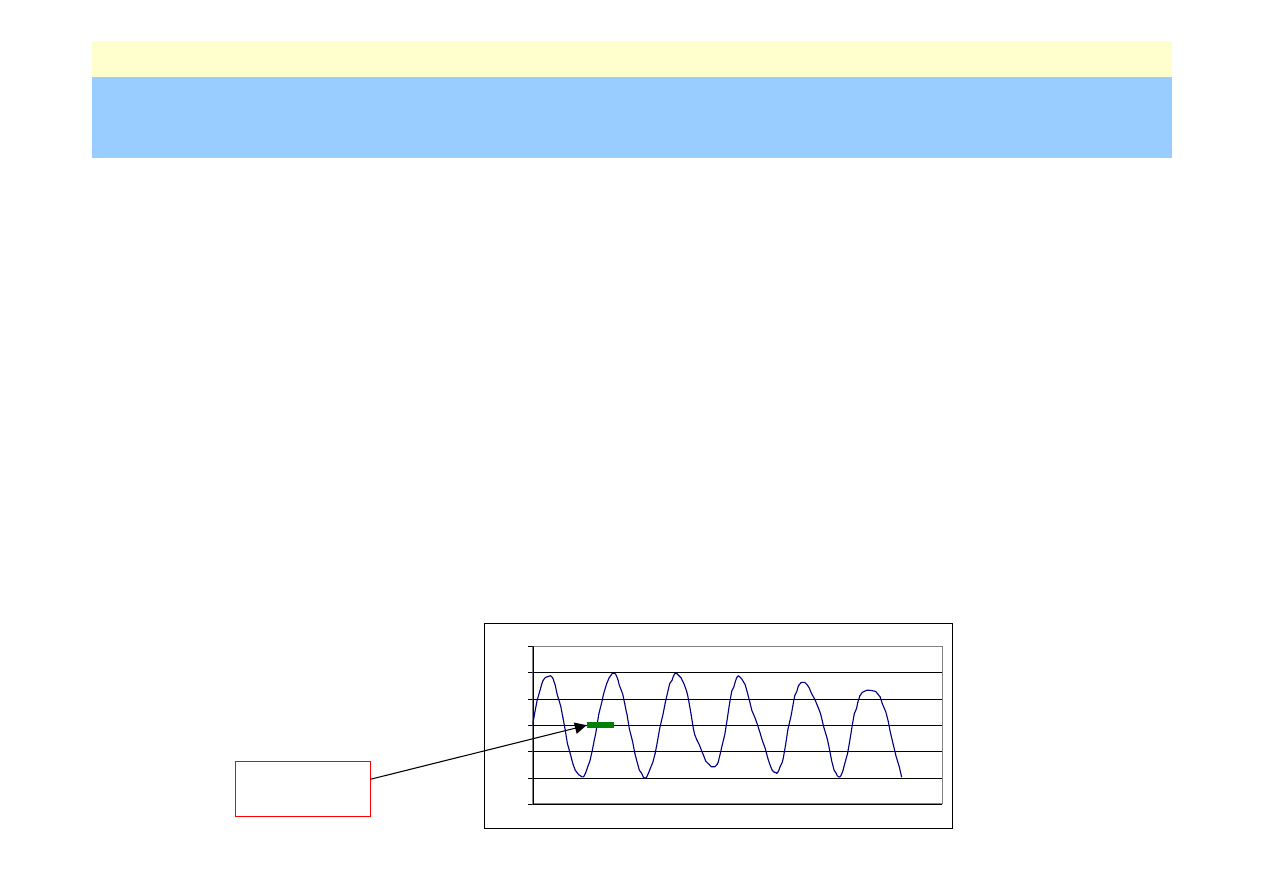
lokalizacja pierwiastków odosobnionych (określenie tzw. przedziałów izolacji w
których znajdują się pojedyncze pierwiastki)

–

znajdywanie z zadaną dokładnością pierwiastków metodami przybliżonymi
(iteracyjnymi)

-1.5

-1

-0.5

0

0.5

1

1.5

przedział

izolacji

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 2

Nr: 4

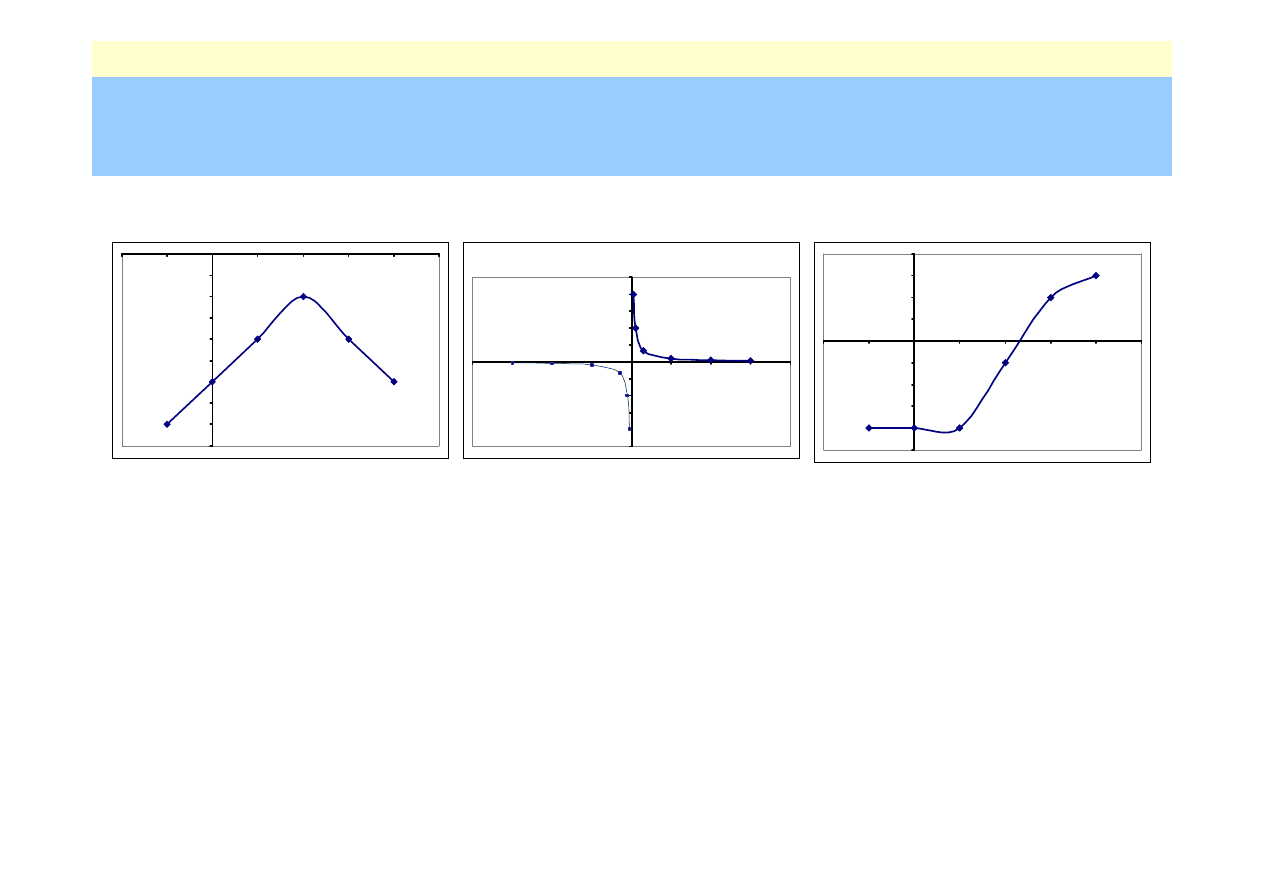
Równanie nieliniowe

Metody przybliżone rozwiązań

– metody iteracyjne:

– startują z przybliżenia początkowego

x

(0)

– polegają na konstrukcji nieskończonego ciągu rozwiązań

przybliżonych, zbieżnych do szukanego rozwiązania,

x

(0)

→

→

→

→

x

(1)

→

→

→

→

x

(2)

→

→

→

→

...

– przerywane w momencie osiągnięcia żądanej dokładności

|f (x

(i)

)|<

εεεε

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 2

Nr: 5

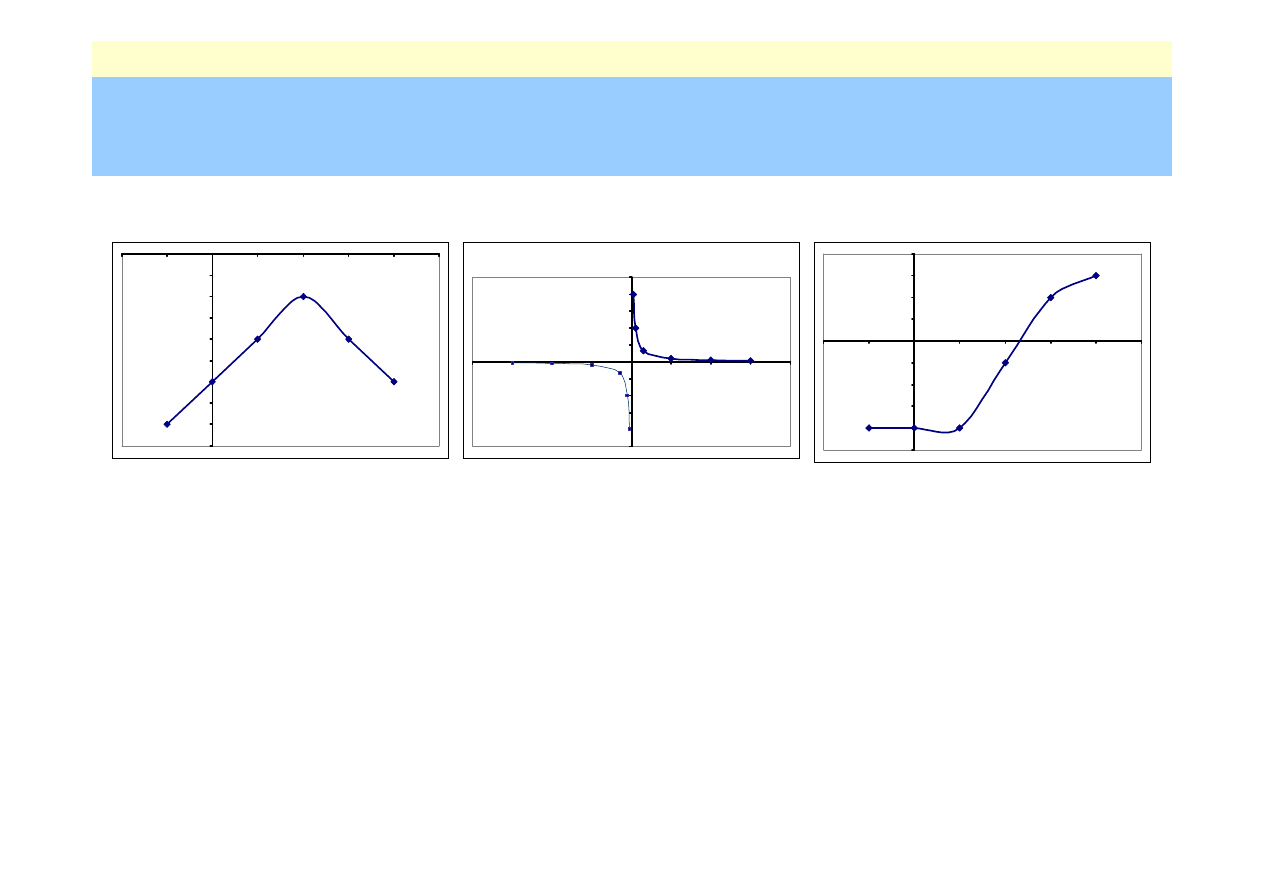
Równanie nieliniowe

Dana jest funkcja

f(x),

oraz przedział

[a,b]

funkc ja f(x) = 1/x - nie c iąg ło ś ć funkc ji w 0

-25

-20

-15

-10

-5

0

5

10

15

20

25

-4

-3

-2

-1

0

1

2

3

4

-4,5

-4

-3,5

-3

-2,5

-2

-1,5

-1

-0,5

0

-2

-1

0

1

2

3

4

5

-5

-4

-3

-2

-1

0

1

2

3

4

-2

-1

0

1

2

3

4

5

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 2

Nr: 6

Równanie nieliniowe

Dana jest funkcja

f(x),

oraz przedział

[a,b]

funkc ja f(x) = 1/x - nie c iąg ło ś ć funkc ji w 0

-25

-20

-15

-10

-5

0

5

10

15

20

25

-4

-3

-2

-1

0

1

2

3

4

-4,5

-4

-3,5

-3

-2,5

-2

-1,5

-1

-0,5

0

-2

-1

0

1

2

3

4

5

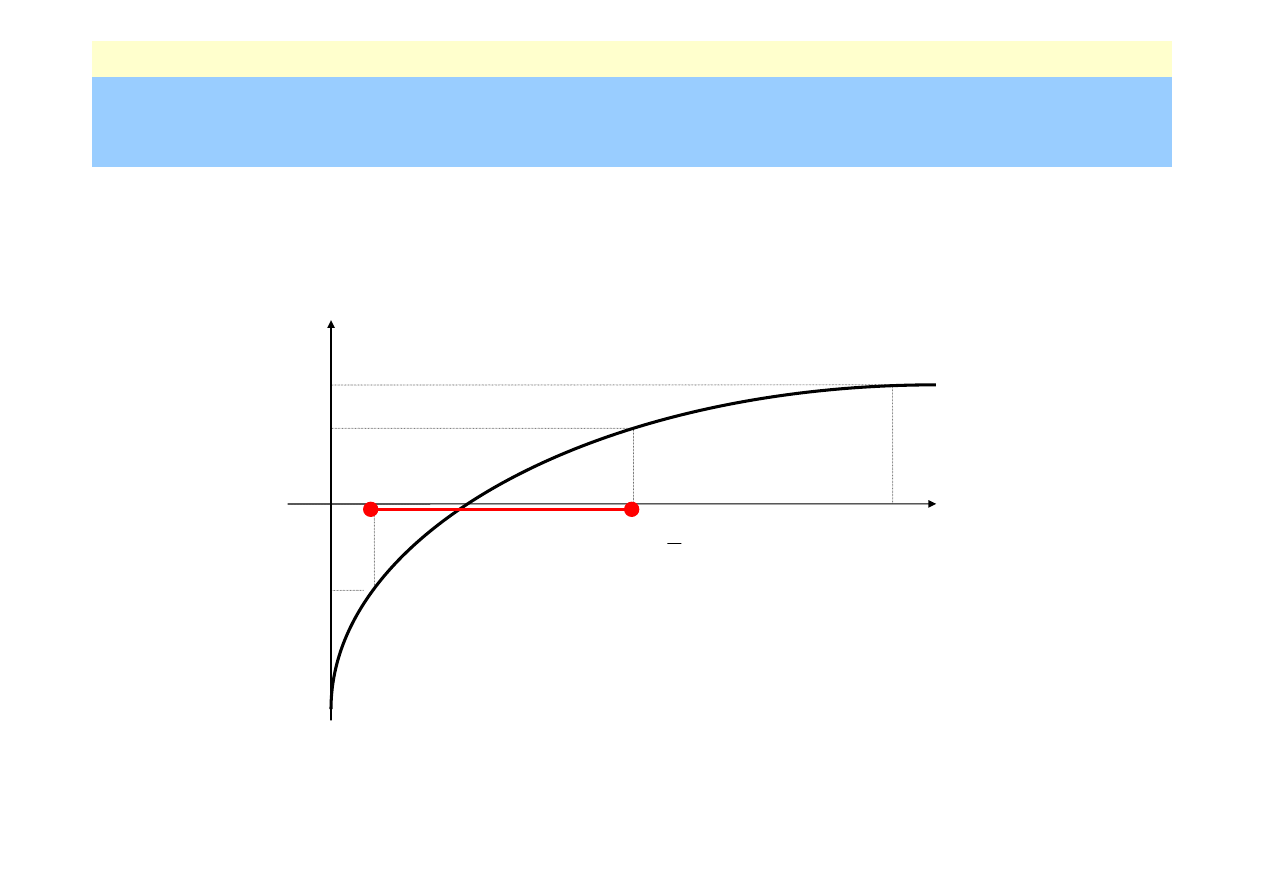
Funkcja

f(x)

– jest ciągła na przedziale

[a,b]

– spełnia warunek

f(a)·f(b)< 0

– posiada w przedziale

[a,b]

tylko jeden pierwiastek

x

0

równania

f(x)=0

-5

-4

-3

-2

-1

0

1

2

3

4

-2

-1

0

1

2

3

4

5

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 2

Nr: 7

Równanie nieliniowe – metody rozwi

ą

za

ń

• Metoda bisekcji

(pierwsza iteracja)

(

)

b

a

x

+

=

2

1

a

b

( )

b

f

( )

x

f

( )

a

f

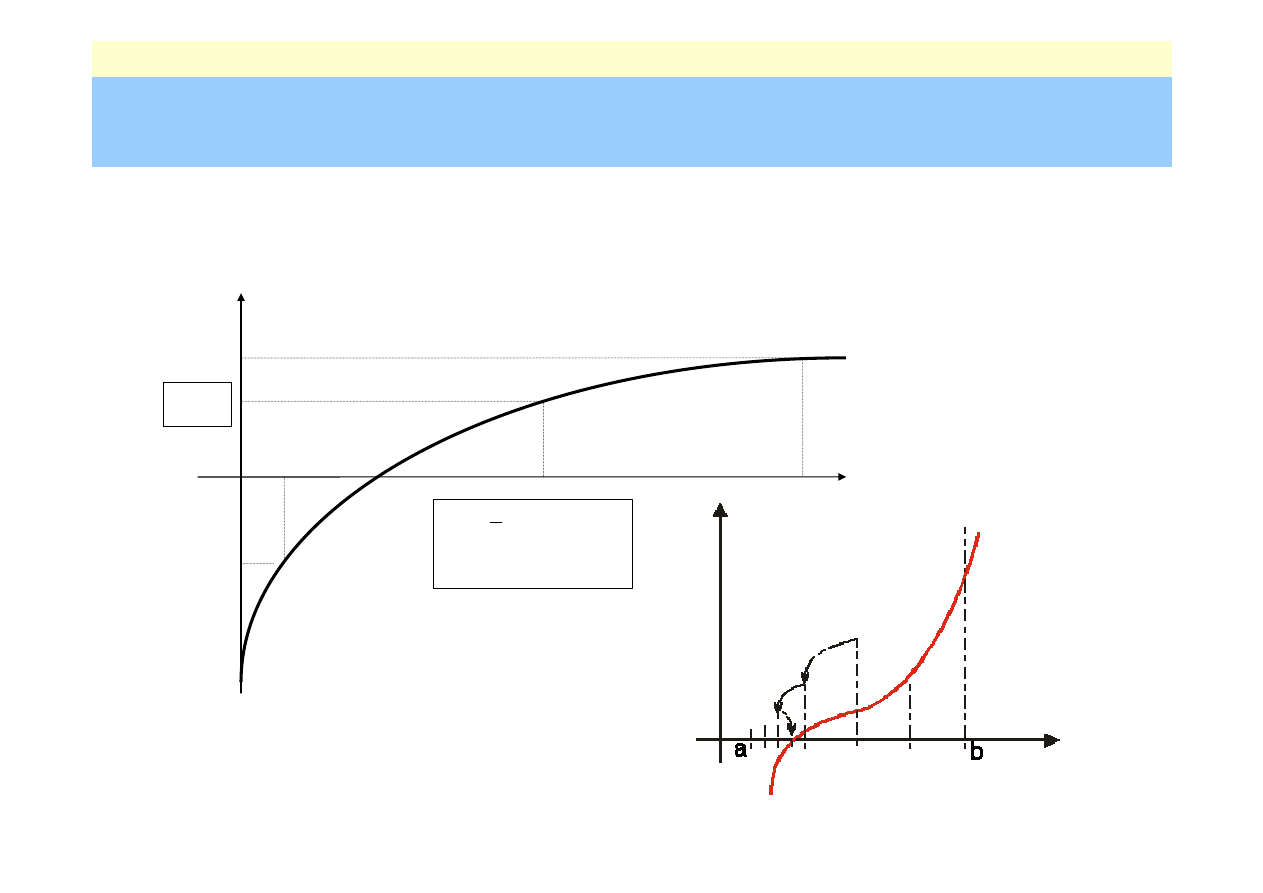
Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 2

Nr: 8

Metoda bisekcji

• i – ty krok iteracji

(

)

i

i

i

i

i

x

b

b

a

x

=

+

=

−

−

1

1

2

1

b

i

−

1

( )

f b

i

−

1

( )

i

x

f

( )

f a

i

−

1

i

b

a

a

i

i

−

=

1

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 2

Nr: 9

Metoda bisekcji

w i-tym kroku metody

:

– znajdujemy środek przedziału

– jeśli

|f(x

i

)|<

εεεε

⇒

znaleźliśmy pierwiastek

=

x

i

– w przeciwnym razie (gdy

|f(x

i

)|

≥≥≥≥ εεεε

)

wyznaczamy nowy przedział do podziału

– powtarzamy procedurę podziału

[

] [

]

( ) ( )

[

]

( ) ( )







>

<

=

−

−

−

−

0

,

0

,

,

1

1

1

1

i

i

i

i

i

i

i

i

i

i

x

f

a

f

gdy

b

x

x

f

a

f

gdy

x

a

b

a

;

2

1

1

−

−

+

=

i

i

i

b

a

x

x = (a + b)/2

while abs(f(x)) >= eps

if f(a)*f(x) < 0

b = x

else

a = x

end

x = (a + b)/2

end

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 2

Nr: 10

Metoda bisekcji

Własności metody

• prosta idea metody
• metoda jest zawsze zbieżna

– kontynuując podziały odpowiednio długo otrzymamy

ZAWSZE

wynik z żądaną dokładnością

• szybkość metody nie zależy od postaci funkcji

f

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 2

Nr: 11

Metoda bisekcji

Własności metody

• prosta idea metody
• metoda jest zawsze zbieżna

– kontynuując podziały odpowiednio długo otrzymamy

ZAWSZE

wynik z żądaną dokładnością

• szybkość metody nie zależy od postaci funkcji

f

• wady

– metoda wolno zbieżna (jedną cyfrę dziesiętną zyskuje się średnio

w 3,3 krokach)

• stosowana często do przybliżeń początkowych

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 2

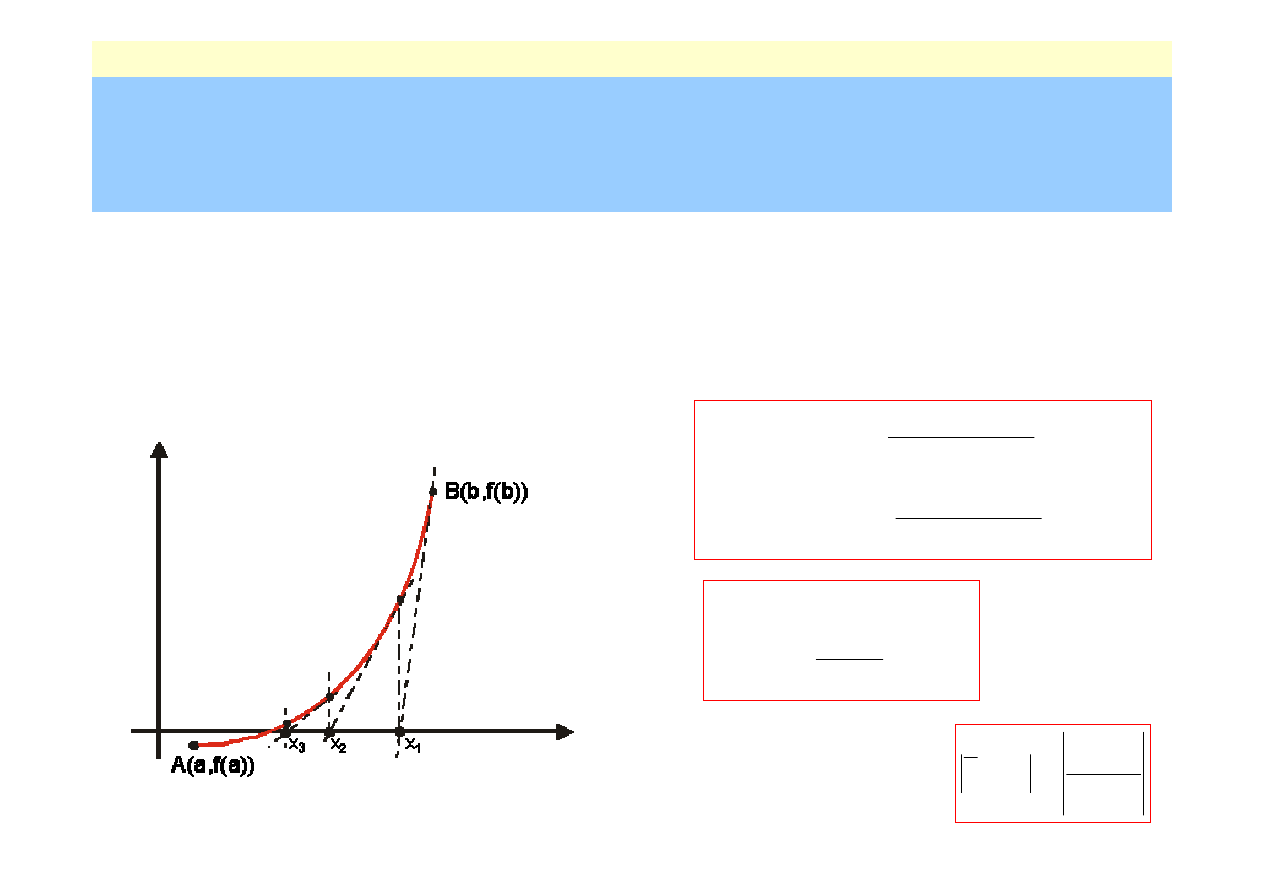
Nr: 12

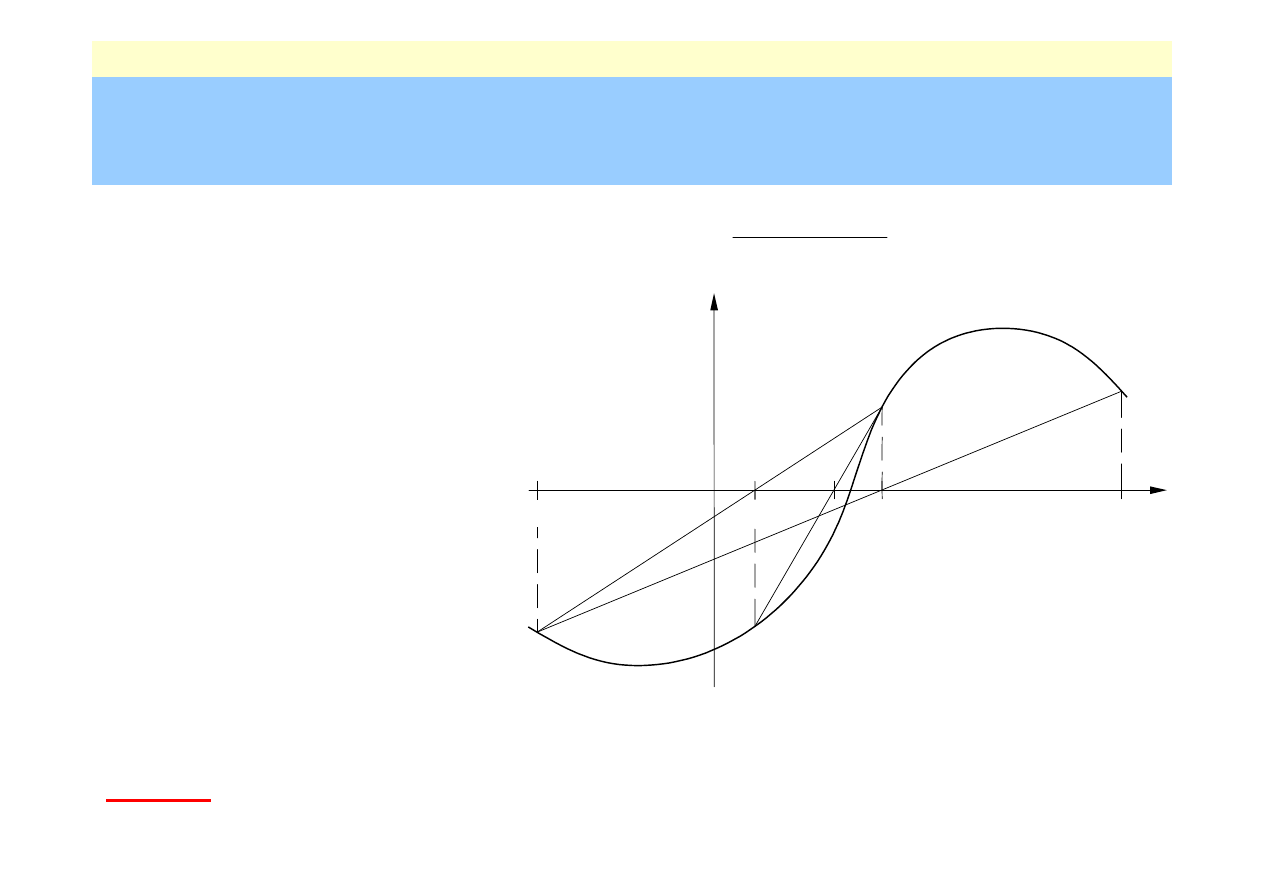
Regula falsi

(

regula - linia,

falsus - fa

ł

szywy

)

y

x

b

x

1

a

x

2

x

3

y=f(x)

1)

przez punkty

(a,f(a))

i

(b,f(b))

prowadzimy cięciwę o równaniu:

2)

przybliżeniem pierwiastka jest punkt
przecięcia tej cięciwy z osią OX

3)

jeśli

f(x

1

)=0

(lub

|f(x

1

)|<

εεεε

)

to

x

1

jest szukanym pierwiastkiem

4)

jeśli

f(a)f(x

1

)<0

to przyjmujemy

b=x

1

,

w przeciwnym przypadku

a=x

1

powracamy do punktu 1)

)

(

)

(

)

(

)

(

a

x

a

b

a

f

b

f

a

f

y

−

−

−

=

−

Zadanie: zapisz kod programu realizujący metodę, pokazujący oszacowanie błędu

(wykonaj obliczenia dla przykładu – slajd 26)

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 2

Nr: 13

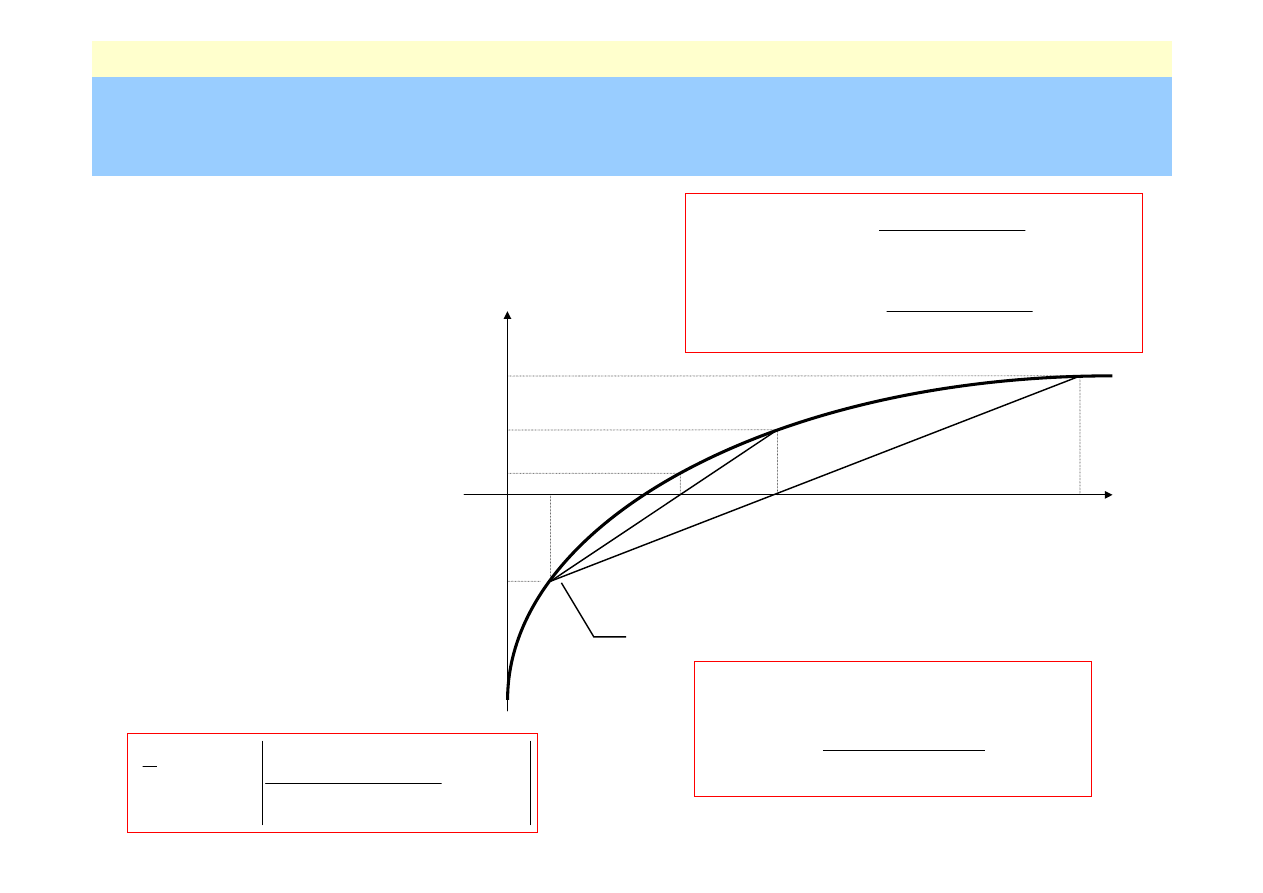
Regula falsi

założenia dodatkowe

– funkcja jest klasy

C

2

[a,b]

– pierwsza i druga

pochodna

f

mają

stały znak

metoda ma stały punkt

iteracji (

ff’’>0)

( )

f x

1

( )

f x

2

( )

f x

3

( )

f x

0

( ) ( )

f x

f

x

0

0

0

"

>

x

0

x

3

x

2

x

1

( )

( ) ( )(

)

0

0

1

1

0

,

x

x

x

f

x

f

x

f

x

x

b

x

a

x

i

i

i

i

i

−

−

−

=

=

=

+

( ) ( )(

)

( ) ( )(

)

i

i

i

i

i

i

i

i

i

i

i

x

x

x

x

x

f

x

f

x

f

x

x

x

x

x

f

x

f

x

f

x

f

−

−

−

=

−

⇒

−

−

−

=

−

+

+

+

1

0

0

1

0

0

1

)

(

)

(

)

(

( ) ( ) ( )

1

1

1

1

|

|

+

+

+

+

−

−

≈

−

i

i

i

i

i

i

x

f

x

f

x

f

x

x

x

x

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 2

Nr: 14

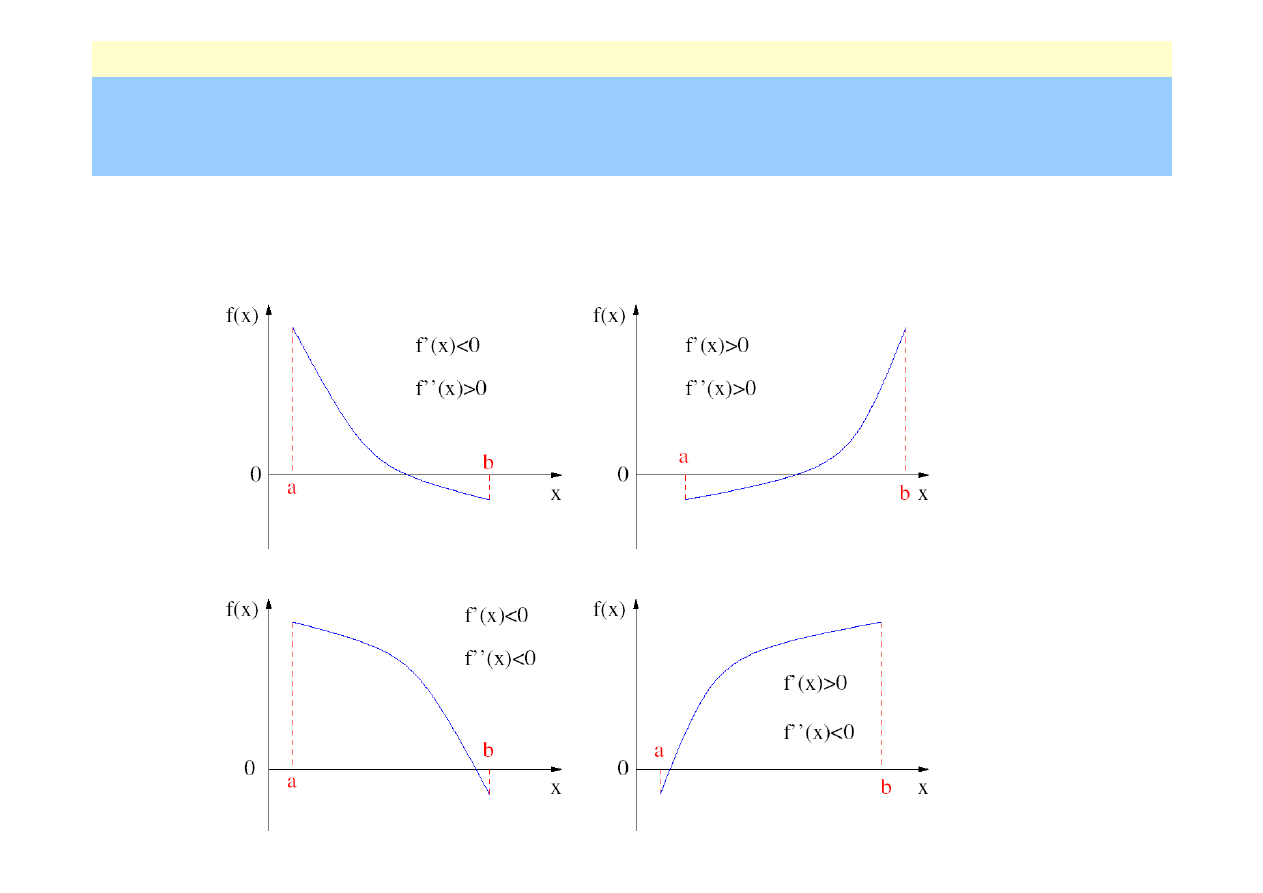
Regula falsi

przy

dodatkowych założeniach

otrzymujemy jeden z możliwych przypadków:

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 2

Nr: 15

Regula falsi

Własności metody

– w kolejnych punktach wytyczających cięciwę funkcja

f

ma różne znaki

– jest zbieżna dla funkcji ciągłej na

[a,b]

jeśli

f’(x)

jest

ograniczona i różna od zera w otoczeniu pierwiastka

– jeśli

f’’(x)

ma stały znak w

[a,b]

to ten punkt skrajny

w którym

ff’’>0

jest punktem stałym iteracji

– metoda jest wolno zbieżna

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 2

Nr: 16

Metoda Newtona-Raphsona (stycznych)

• zakładamy dodatkowo iż
• dla oszacowania błędu przyjmujemy iż
oraz pierwsza i druga pochodna mają stały znak w

[a,b]

– styczną do wykresu funkcji

f(x)

prowadzimy od końca

przedziału w którym

ff’’>0

( )

( )

[ ]

f x

C

a b

∈

1

,

( )

( )

[ ]

b

a

C

x

f

,

2

∈

( )

( )

( )

( )

i

i

i

i

i

i

i

i

x

f

x

f

x

x

x

x

x

f

x

f

'

)

(

'

1

1

−

=

−

=

−

+

+

( )

( )

i

i

i

x

f

x

f

x

x

'

≈

−

( ) ( )(

)

( ) ( )(

)

i

i

i

i

i

i

i

i

i

i

i

x

x

x

x

x

f

x

f

x

f

x

x

x

x

x

f

x

f

x

f

x

f

−

−

−

=

−

⇒

−

−

−

=

−

+

+

+

1

0

0

1

0

0

1

)

(

)

(

)

(

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 2

Nr: 17

Metoda Newtona-Raphsona (stycznych)

• Przykład braku zbieżności

druga pochodna funkcji

f

zmienia znak,

(cyframi 0,1,...,4 oznaczono kolejne przybliżenia pierwiastka)

0

1

2

4

3

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 2

Nr: 18

Metoda Newtona-Raphsona

Własności metody

– metoda jest zbieżna warunkowo (lokalne ekstrema, punkty

przegięcia)

Jeżeli

• w pewnym przedziale

[a,b], f(a)

i

f(b)

mają przeciwne

znaki,

• f’’

jest ciągła i nie zmienia znaku na

[a,b],

• styczne do krzywej

y=f(x)

poprowadzone w punktach o

odciętych

a

i

b

przecinają oś OX wewnątrz przedziału

[a,b]

to równanie

f(x)=0

ma dokładnie jeden pierwiastek w

[a,b]

i

metoda Newtona-Raphsona jest zbieżna do tego pierwiastka dla
dowolnego punktu startowego

x

0

∈

∈

∈

∈

[a,b]

– jest stosunkowo szybko zbieżna (jeśli algorytm jest zbieżny)
– wymaga tylko jednego punktu startowego
– konieczność obliczania pochodnej funkcji

f

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 2

Nr: 19

Metoda Newtona-Raphsona

uogólnienie metody (wyprowadzenie z wzoru Taylora)

•

Jeżeli pierwiastkiem równania jest

ξξξξ

, a

x

i

jest jego przybliżeniem, to

•

zaniedbując wyrazy rzędu większego niż p otrzymujemy równanie do
wyznaczenia kolejnego przybliżenia

–

dla

p=1

(metoda Newtona-Raphsona stopnia I):

–

dla

p=2

(metoda Newtona-Raphsona stopnia II):

L

+

−

+

−

+

−

+

=

=

)

(

!

3

)

(

)

(

''

!

2

)

(

)

(

'

)

(

)

(

0

)

(

)

3

(

3

2

i

i

i

i

i

i

i

x

f

x

x

f

x

x

f

x

x

f

f

ξ

ξ

ξ

ξ

)

x

(

'

f

)

x

x

(

)

x

(

f

i

i

i

i

−−−−

++++

====

++++

1

0

)

x

(

'

f

)

x

(

f

x

x

i

i

i

i

−−−−

====

++++

1

)

x

(

'

'

f

!

)

x

x

(

)

x

(

'

f

)

x

x

(

)

x

(

f

i

i

i

i

i

i

i

2

0

2

1

1

−−−−

++++

−−−−

++++

====

++++

++++

)

(

''

)

(

''

)

(

2

)

(

'

)

(

'

2

1

i

i

i

i

i

i

i

x

f

x

f

x

f

x

f

x

f

x

x

−

±

−

=

+

Zadanie: zapisz kod programu realizujący metodę Newtona-Raphsona stopnia II

(wykonaj obliczenia dla przykładu – slajd 26)

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 2

Nr: 20

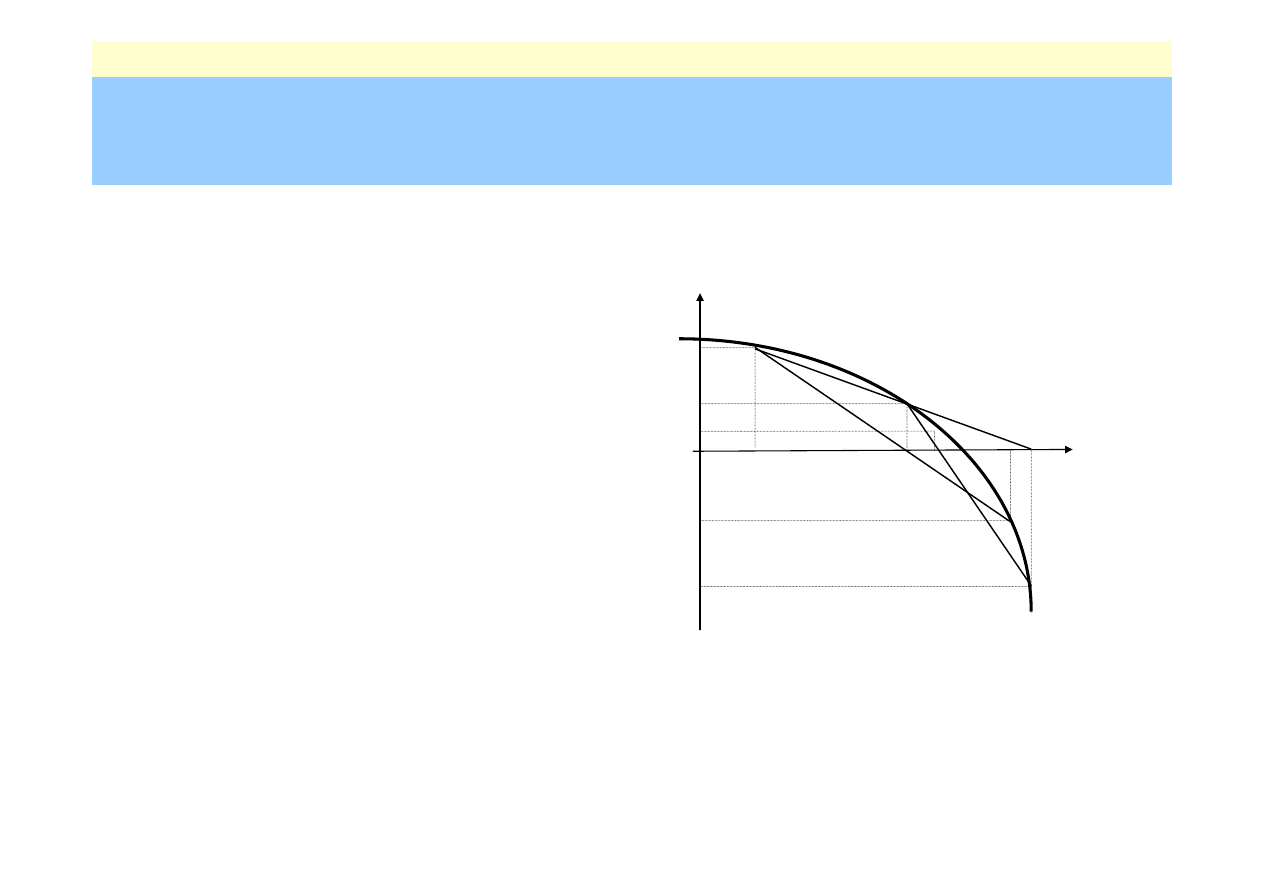
Metoda siecznych

• pochodna funkcji

f(x)

jest przybliżana ilorazem

różnicowym

• w i-tym kroku prowadzimy

sieczną

do wykresu funkcji w

punktach o odciętych

x

i

i

x

i-1

, a jako kolejne przybliżenie

x

i+1

przyjmujemy jej punkt przecięcia z osią OX

• nie jest wymagane aby w punktach wyznaczających kolejną

sieczną funkcja miała różne znaki (warunek obowiązuje dla
pierwszej stycznej)

(

)

( ) ( ) ( )

i

i

i

i

i

i

i

x

f

x

f

x

f

x

x

x

x

1

1

1

−

−

+

−

−

−

=

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 2

Nr: 21

Metoda siecznych

Własności metody

– zbieżność na ogół szybsza

niż dla regula falsi

– gdy

|x

i

-x

i-1

|

jest tego

samego rzędu co
oszacowanie błędu, następne
przybliżenie może nie być
poprawne

– gdy początkowe przybliżenia

nie leżą dostatecznie blisko
pierwiastka, metoda może
nie być zbieżna

– jeśli w trakcie obliczeń

odległości między kolejnymi
przybliżeniami zaczynają
wzrastać, należy je przerwać
i zawęzić przedział izolacji

( )

f x

1

( )

f x

2

( )

f x

4

( )

f x

0

( )

f x

3

x

1

x

2

x

4

x

0

x

3

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 2

Nr: 22

Metoda siecznych

• Przykład braku zbieżności

druga pochodna funkcji

f

zmienia znak

0

1

2

3

4

5

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 2

Nr: 23

Metoda siecznych - modyfikacje

• metoda Steffensena

– szybciej zbieżna niż metoda siecznych
– wymagająca obliczeń dwóch wartości funkcji

f(x)

– nie korzystająca z pochodnych
– dana wzorem :

( )

( )

(

)

( )

i

i

i

i

i

i

i

i

i

x

f

x

f

x

f

x

f

x

g

x

g

x

f

x

x

)

(

)

(

)

(

,

1

−

+

=

−

=

+

Zadanie: zapisz kod programu realizujący metodę (wykonaj

obliczenia dla przykładu – slajd 26)

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 2

Nr: 24

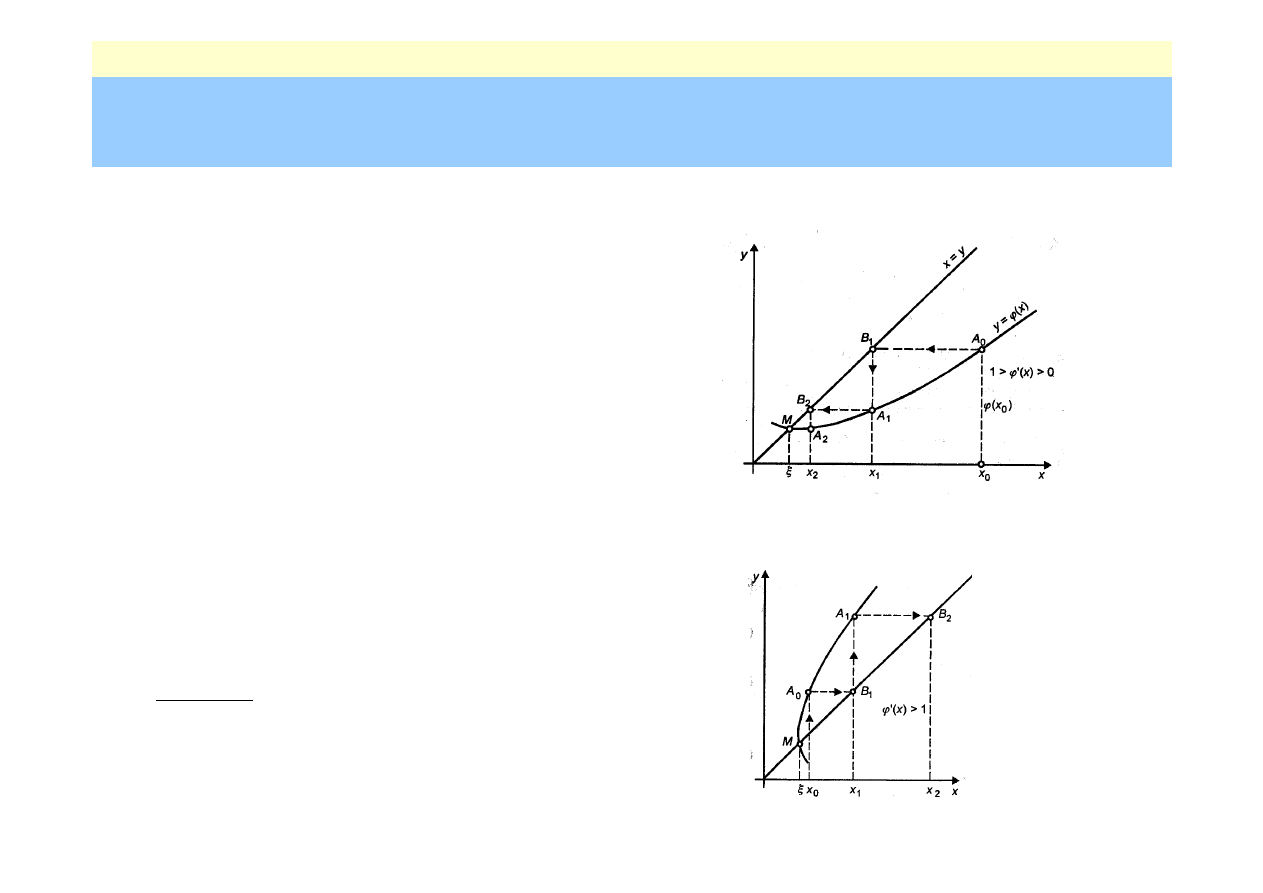
Metoda iteracji prostej

•

Równanie

f(x)=0

przekształcamy do

równania równoważnego

x=

ϕϕϕϕ

(x)

•

pierwsze przybliżenie obliczamy

x

1

=

ϕϕϕϕ

(x

0

), x

0

-

rozwiązanie początkowe

•

kolejne przybliżenia obliczamy

x

k

=

ϕϕϕϕ

(x

k-1

)

•

problemy

–

jak znaleźć funkcję

ϕϕϕϕ

?

–

przy jakich warunkach ciąg rozwiązań jest
zbieżny?

jeśli istnieje q takie, że

|

ϕϕϕϕ

’(x)|

≤≤≤≤

q <1 x

∈

∈

∈

∈

[a,b]

to proces iteracji prostej jest zbieżny niezależnie

od przybliżenia początkowego

x

0

∈

∈

∈

∈

[a,b].

Przykład

f(x)=x+ln(x)

⇒

ϕϕϕϕ

(x)=-ln(x)

x

k

= -ln(x

k-1

)

przypadek zbieżny

przypadek rozbieżny

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 2

Nr: 25

Rz

ą

d metod przybli

ż

onego obliczania pierwiastków

Metoda jest

rzędu p

(ma

wykładnik zbieżności równy p

)

jeżeli istnieje stała

K

taka, że dla dwu kolejnych przybliżeń

x

i

i

x

i+1

zachodzi nierówność

|

x

i+1

-

α

|

≤

K |

x

i

-

α

|

p

2

Steffensena

≈≈≈≈

1,62

siecznych

2

Netona

1

regula falsi

1

bisekcji

Rz

ą

d

Metoda

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 2

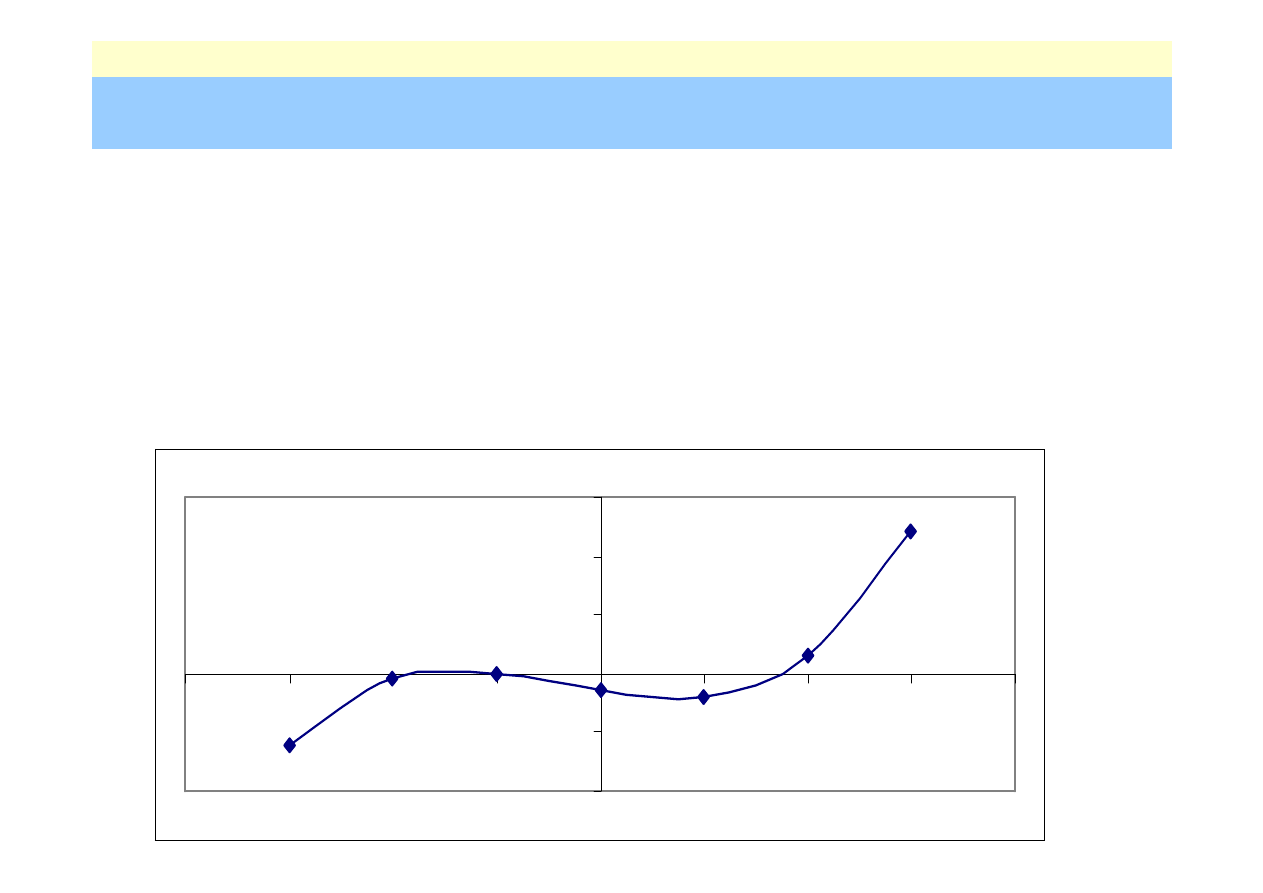
Nr: 26

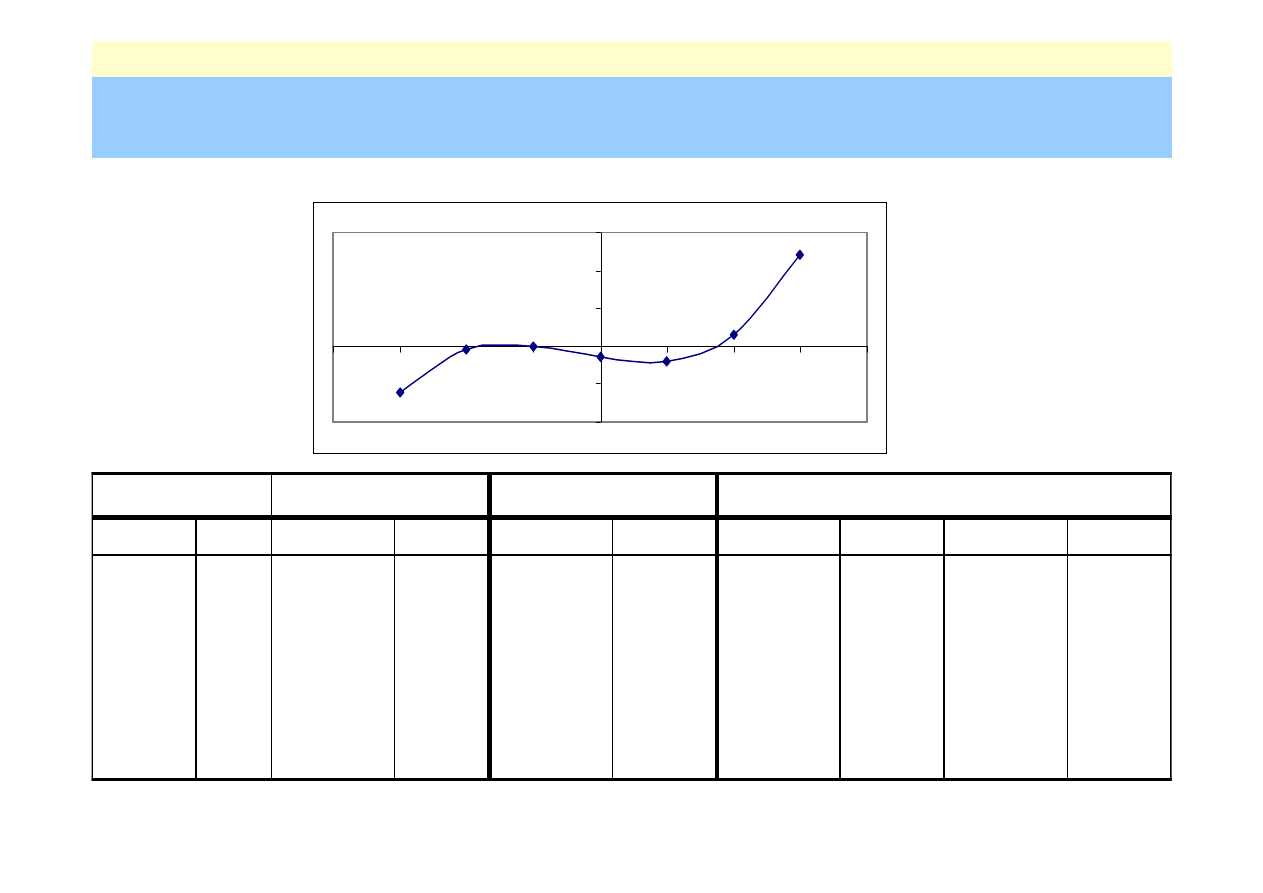
Przykład – porównanie zbie

ż

no

ś

ci metod

•

Szukamy dodatniego pierwiastka
równania

•

otrzymujemy

0

3

3

)

(

2

3

=

−

−

+

=

x

x

x

x

f

2

6

)

(

''

3

2

3

)

(

'

2

+

=

−

+

=

x

x

f

x

x

x

f

-20

-10

0

10

20

30

-4

-3

-2

-1

0

1

2

3

4

•

przedziałem izolacji może być

[1,2]

•

obie pochodne są w tym przedziale
dodatnie

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 2

Nr: 27

Przykład – porównanie zbie

ż

no

ś

ci metod – cd.

a = 1

b = 2

x

1

= 1,5

x

2

= 1,75

x

3

=1,625

x

4

= 1,687

x

5

= 1,719

x

Metoda bisekcji

-4

3

-1,875

0,172

-0,943

-0,409

-0,124

f(x)

3

0,36048

0,00823

-0,000008

f(x)

x

0

= 2

x

1

= 1,76923

x

2

= 1,73292

x

3

= 1,73205

x

Metoda Newtona

-4

24

5,88800

0,98899

0,24782

-0,00095

x

0

= 1

x

1

= 3

x

2

= 2,2

x

3

= 1,83015

x

4

= 1,7578

x

5

= 1,73195

-4

3

-1,36449

-0,24784

0,02920

0,000576

a = 1

b = 2

x

1

= 1,57142

x

2

= 1,70540

x

3

= 1,73513

x

4

= 1,73199

-4

3

-1,36449

-0,24784

-0,03936

-0,00615

a = 1

b = 2

x

1

= 1,57142

x

2

= 1,70540

x

3

= 1,72788

x

4

= 1,73240

f(x)

x

f(x)

x

f(x)

x

Metoda siecznych

Regula falsi

-20

-10

0

10

20

30

-4

-3

-2

-1

0

1

2

3

4

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 2

Nr: 28

Układy równa

ń

nieliniowych

Metoda Newtona

•

dla równania nieliniowego

– x

jest zmienną rzeczywistą

( )

0

x

=

f

)

x

(

'

f

)

x

x

(

)

x

(

f

i

i

i

i

−−−−

++++

====

++++

1

0

( )









































=

n

n

n

n

n

n

i

x

f

x

f

x

f

x

f

x

f

x

f

x

f

x

f

x

f

∂

∂

∂

∂

∂

∂

∂

∂

∂

∂

∂

∂

∂

∂

∂

∂

∂

∂

...

...

...

...

...

...

...

2

1

2

2

2

1

2

1

2

1

1

1

)

(

x

J

)

(

)

(

)

(

0

)

(

)

(

)

1

(

)

(

i

i

i

i

x

J

x

x

x

f

−

+

=

+

•

równanie nieliniowe

•

układ równań nieliniowych

(

)

(

)











=

=

0

0

n

n

n

x

x

f

x

x

f

,....,

,....,

1

1

1

( )

)

,...,

(

)

,...,

(

,

1

1

n

n

x

x

x

f

f

f

f

=

=

=

0

x

( )

0

x

=

f

( )

)

,...,

(

)

,...,

(

,

1

1

n

n

x

x

x

f

f

f

f

=

=

=

0

x

•

dla układu równań nieliniowych

– x

jest wektorem

n-

wymiarowym

(macierz Jacobiego)

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 2

Nr: 29

-5

-4

-3

-2

-1

0

1

2

3

4

5

3

7

1 1

1 5

1 9

2 3

2 7

3 1

3 5

3 9

Układy równa

ń

nieliniowych – rozwi

ą

zanie w SciLabie

wykorzystanie funkcji

fsolve(punkt_startowy, funkcja)

( )

0

4

2

0

8

cos

2

1

1

2

1

2

=

−

−

−

=

−

−

x

x

x

x

x













=













−

−

+

























−

+

























−

+

























−

2

1

2

1

2

2

1

2

1

4

8

)

cos(

0

0

0

1

0

1

0

0

1

2

1

0

y

y

x

x

x

x

x

x

( )

2

2

1

1

2

1

1

2

4

2

8

cos

y

x

x

x

y

x

x

=

−

−

−

=

−

−













=













−

−

=













−

=













−

=













−

=













=

=

+

⋅

+

+

2

1

2

1

2

,

4

8

,

0

0

0

1

,

0

1

0

0

,

1

2

1

0

,

)

cos(

y

y

Y

d

c

b

a

x

x

X

Y

d

X

c

bX

aX

function [Y]=fst(X)

// w definiowanej funkcji przyjmujemy X=[x

1

;x

2

], Y=[y

1

;y

2

]

a=[0,1;-2,1]; b=[0,0;-1,0]; c=[-1,0;0,0]; d=[-8;-4];

Y= a*X +b*X^2 + c*cos(X) + d

endfunction

// lub inny sposób:

function [Y]=fst(X)

Y= [X(2)-cos(X(1))-8; X(2)-2*X(1)-X(1)^2-4 ]

endfunction

// u

ż

ycie funkcji fsolve() – pocz

ą

tkowym rozwi

ą

zaniem punkt (0,0)

xy1=fsolve([0;0],fst);

// znalezione rozwi

ą

zanie: xy1=[ 1.2959523; 8.2713968]

xy2=fsolve([-3;0],fst);

// znalezione rozwi

ą

zanie: xy2=[ - 3.0024159; 7.0096695]

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 2

Nr: 30

Metody optymalizacji

Metody wyznaczania

optymalnych rozwiązań

– rozwiązanie optymalne to rozwiązanie najlepsze ze

względu na

przyjęte kryterium

– różne kryteria prowadzą na ogół do odmiennych

rozwiązań

– kryterium ściśle związane z rozwiązywanym zadaniem
– postać zadania:

• wyznaczenie minimum (maksimum) danej funkcji

f(x)

(tzw.

funkcji celu

)

,

gdzie

x=[x

1

,x

2

,...,x

n

]

jest

wektorem

• uwzględnienie warunków ograniczających:

– równania

A

i

(x)= b

i

dla

i=1,...,m

– nierówności

C

i

(x

i

)

≥≥≥≥

c

i

dla

i=1,...,p

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 2

Nr: 31

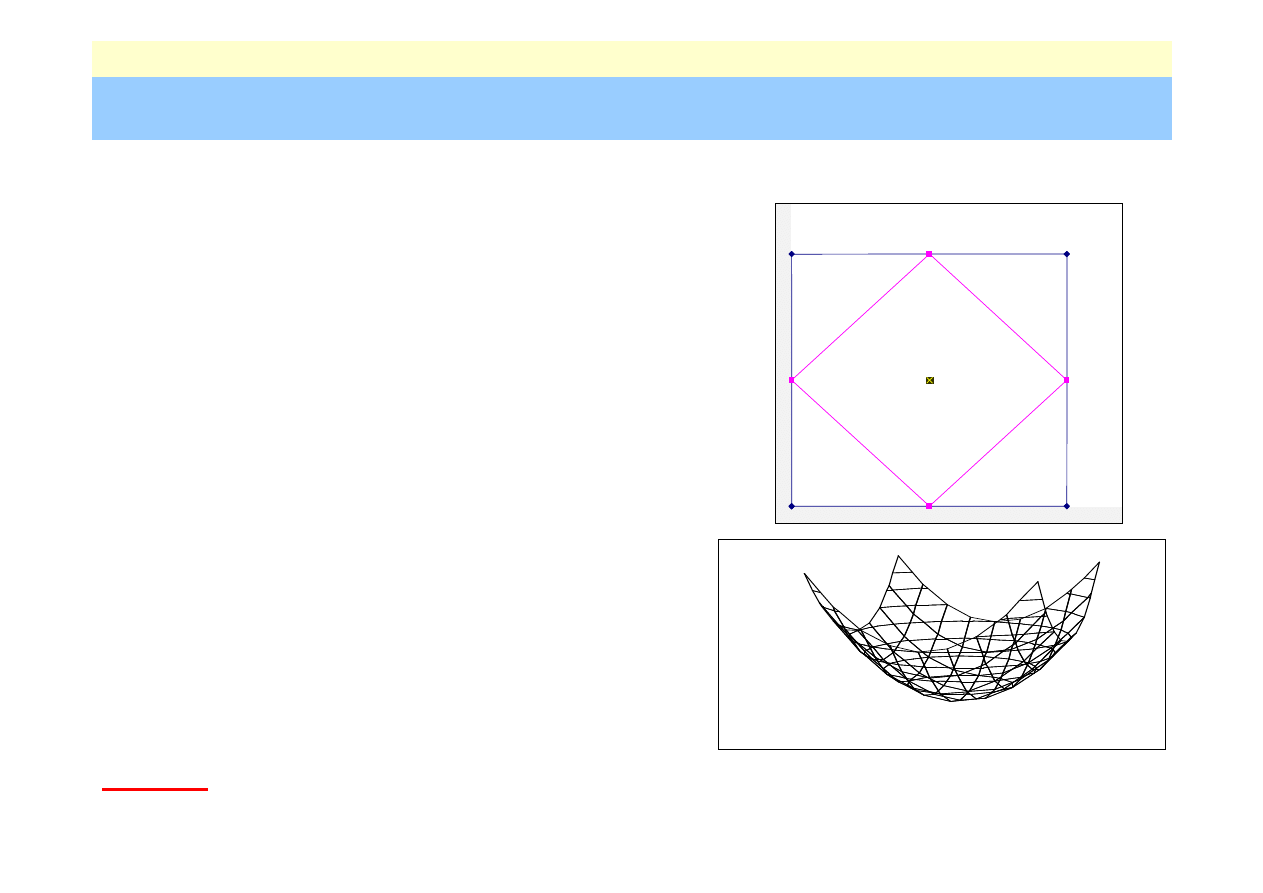
Metody optymalizacji – przykład

Zadanie transportowe

Dana jest sieć

m

punktów wytwarzających

określony produkt i

wysyłających go do

n

punktów odbiorczych

. Określono

•

x

ij

– ilość produktu wysłanego z punktu

i-

tego

(

i=1,...,m

) do

j-

tego (

j=1,...,n

)

•

a

i

– ilość produktu wytwarzana przez i-ty punkt,

•

b

i

– ilość zapotrzebowania na produkt przez j-ty punkt,

•

c

ij

– koszt transportu jednostki produktu z punktu i-tego do

punktu j-tego

•

łączne zapotrzebowanie jest równe całości produkcji, tzn.

Należy

znaleźć takie wartości

x

ij

aby całkowity koszt

transportu był

jak najmniejszy

. Szukamy minimum

wyrażenia

przy warunkach

∑

∑

=

=

=

n

j

j

m

i

i

b

a

1

1

∑∑

=

=

=

m

i

n

j

ij

ij

x

c

x

f

1

1

)

(

n

j

m

i

x

n

j

x

b

m

i

x

a

ij

m

i

ij

j

n

j

ij

i

,...,

1

;

,...,

1

,

0

,...,

1

,

;

,...,

1

,

1

1

=

=

≥

=

=

=

=

∑

∑

=

=

P_1

a

1

P_2

a

2

P_m

a

m

O_1

b

1

O_2

b

2

O_n

b

n

x

12

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 2

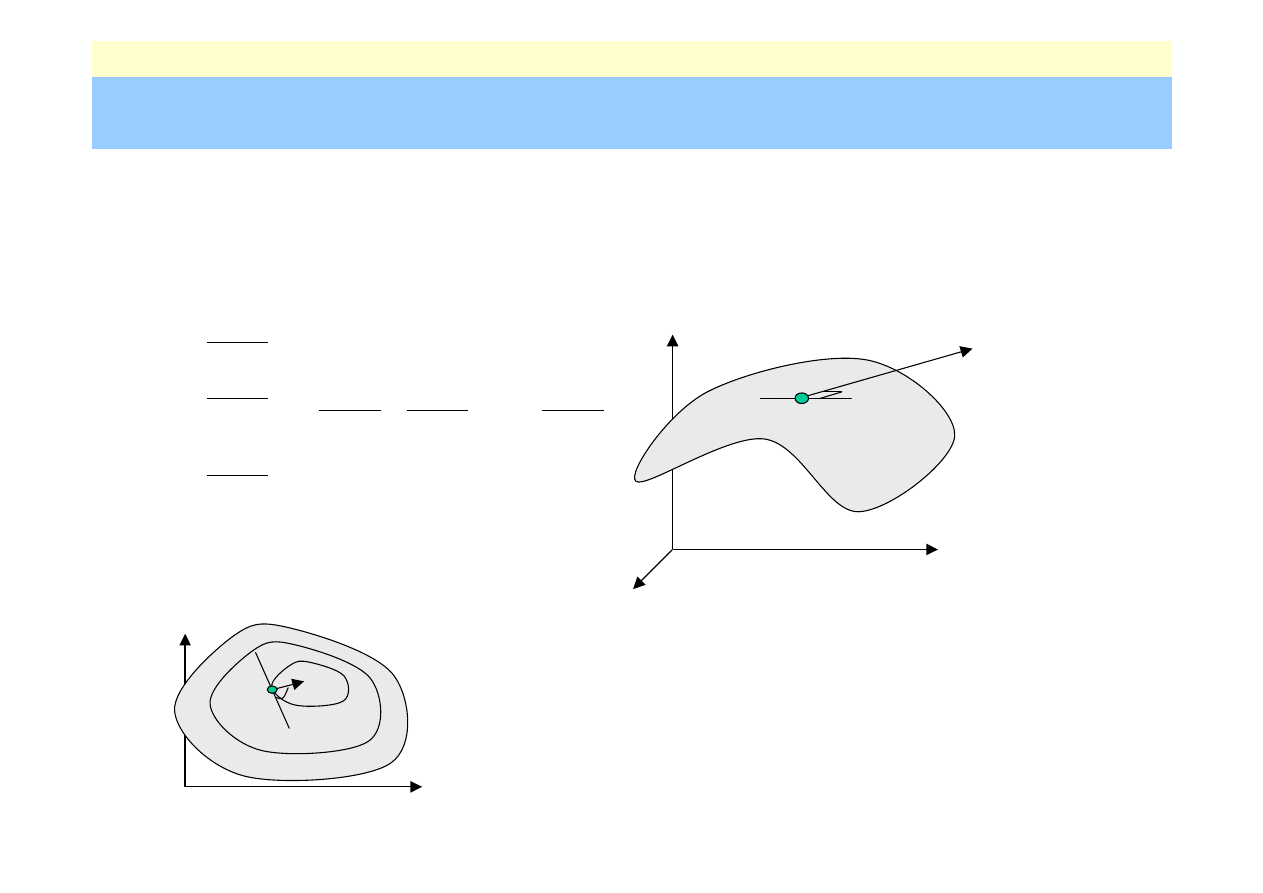
Nr: 32

Metoda spadku wzgl

ę

dem współrz

ę

dnych

Przykład – minimalizujemy funkcję

f(x,y)

1.

(x

0

,y

0

) –

punkt startowy

2.

ustalamy krok

k

3.

sprawdzamy wartości funkcji w 4 punktach:

(x

0

,y

0

+k),(x

0

,y

0

-k),(x

0

+k,y

0

),(x

0

-k,y

0

)

4.

jeżeli w jednym z punktów wartość funkcji

f(x,y)

jest

mniejsza niż w punkcie

(x

0

,y

0

)

(„jest położony niżej”)

to „przenosimy się do niego” i powtarzamy procedurę w
kroku 3.

5.

jeśli w punkcie 4. nie znaleziono takiego punktu to
zmniejszamy krok (np. 2-krotnie) i powtarzamy punkt 3.

(x

0

+k,y

0

)

(x

0

-k,y

0

)

(x

0

,y

0

-k)

(x

0

,y

0

+k)

(x

0

,y

0

)

Zadanie: zapisz kod programu realizujący metodę,
przetestować dla f(x

1

,x

2

)=-4x

1

2

-(2x

2

+3)

2

)

• kierunek poszukiwań nie zależy od postaci funkcji

• metoda zawodna w przypadku istnienia wielu
minimów lokalnych funkcji

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 2

Nr: 33

Metody gradientowe - sposoby poszukiwania rozwi

ą

za

ń

Metody gradientowe

- kierunek poszukiwań wyznaczany w każdym kolejnym kroku

•

niech funkcja

f(x)(x=[x

1

,x

2

,...,x

n

]

jest wektorem) jest klasy

C

1

.

•

Gradientem funkcji

f(x)

nazywamy wektor:

•

gradient określa kierunek największego

wzrostu funkcji

f(x)

T

x

x

f

x

x

f

x

x

f

x

x

f

x

x

f

x

x

f

x

f













∂

∂

∂

∂

∂

∂

=





































∂

∂

∂

∂

∂

∂

=

∇

n

2

1

n

2

1

)

(

)

(

)

(

)

(

)

(

)

(

)

(

L

M

x

3

x

1

X

ˆ

)

ˆ

( X

f

∇

Przykład (obliczenie gradientu):

f(x

1

,x

2

)=-(x

1

-2)

2

-(x

2

-3)

2

∇

∇

∇

∇

f(x)= [-2(x

1

-2),-2(x

2

-3)]

T

∇

∇

∇

∇

f((1,2))=[2,2]

T

x

1

x

2

)

ˆ

( X

f

∇

X

ˆ

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 2

Nr: 34

Metody optymalizacji - sposoby poszukiwania rozwi

ą

za

ń

Metody gradientowe

•

Procesy iteracyjne – kolejne przybliżenie

– x

k+1

= x

k

+ h

k

ξξξξ

k

• x

k

poprzednie przybliżenie (wektor n-wymiarowy),

• h

k

długość kroku (liczba rzeczywista),

•

ξξξξ

k

wektor (n-wymiarowy), określający kierunek poszukiwań.

– jeśli funkcja

f(x)(x=[x

1

,x

2

,...,x

n

])

ma

więcej niż jedno minimum

lokalne,

otrzymany wynik może zależeć od punktu startowego

,

– wybierając różne punkty startowe, porównując kolejne wartości, możemy

wybrać najlepsze z otrzymanych rozwiązań

– w sytuacjach gdy istnieje

wiele minimów lokalnych

wykorzystuje się sposoby

dające możliwość wyjścia z optimum lokalnego – rozszerzenie lokalnych
poszukiwań

– zatrzymanie obliczeń

• po zadanej liczbie iteracji, lub po upływie określonego czasu obliczeń,
• gdy wartość

f(x

k

)

(lub względna zmiana wartości ) spadnie poniżej zadanego

poziomu,

• gdy długość gradientu

||

∇

f(x

k

)||

spadnie poniżej zadanego poziomu.

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 2

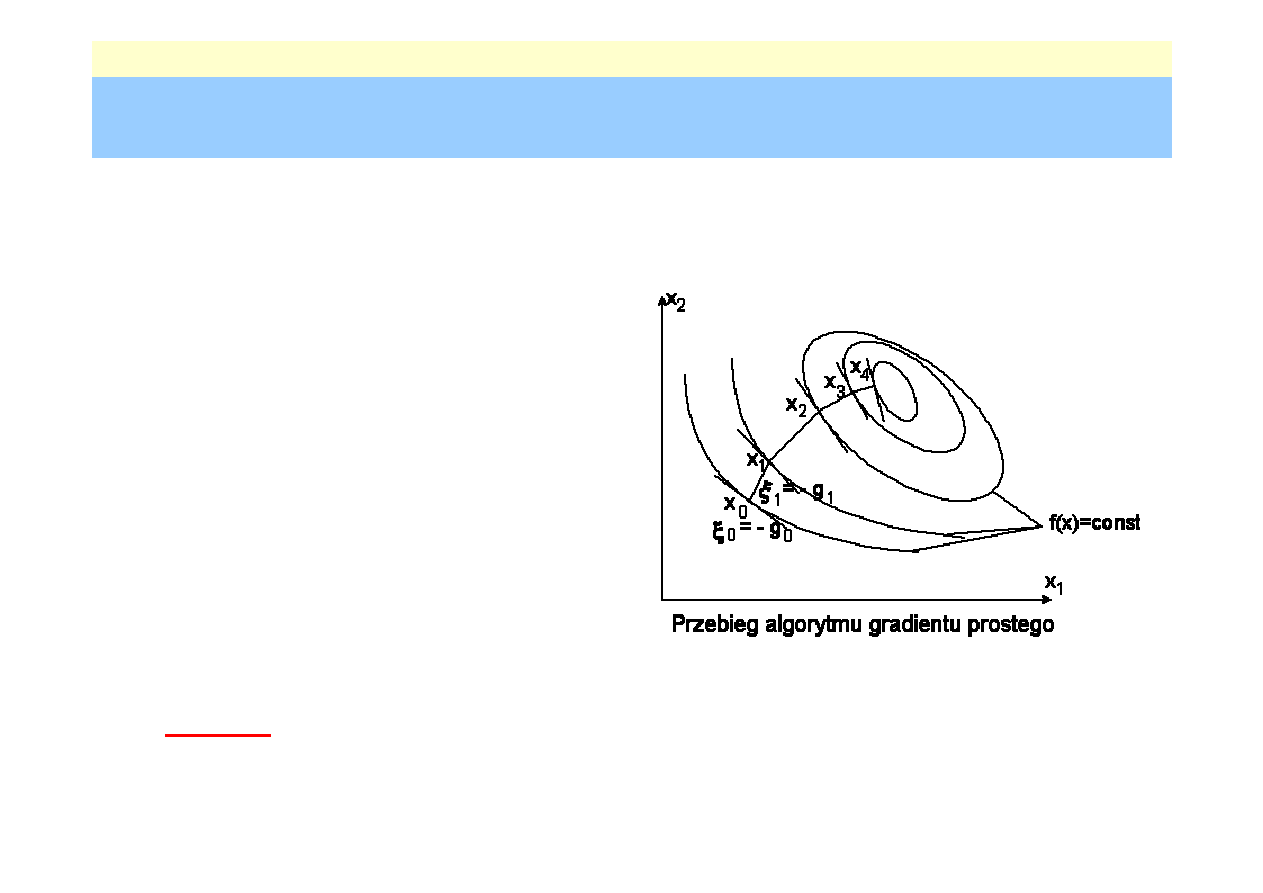
Nr: 35

Metody gradientowe -

Metoda gradientu prostego

Algorytm obliczeń :

1.

Obliczanie w punkcie startowym

x

0

wartość funkcji

f(x

0

)

oraz jej gradientu

g

0

= g(x

0

)

2.

Wyznaczenie kierunku poszukiwań

ξξξξ

=-g

0

3.

Wzdłuż kierunku

ξξξξ

wykonujemy krok o długości

h

oraz

określamy współrzędne nowego punktu :

x

i+1

=x

i

+h

*

ξξξξ

4.

Obliczenie w nowym punkcie wartość funkcji

f(x

i+1

)

oraz gradientu

g= g(x

i+1

),

jeżeli krok był pomyślny,

tzn.

f(x

i+1

)

<

f(x

i

)

to powtarzamy od punktu 2

podstawiając

g

(gradient) w miejsce

g

0

5.

Jeżeli nie osiągnięto minimum, należy wrócić do
poprzedniego punktu podstawiając :

x

i

=x

i+1

-h

*

ξξξξ

oraz zmniejszamy krok (np. 2-krotnie) i przechodzimy
do punktu 3.

Zadanie: zapisz kod programu realizujący metodę,

(przyjąć funkcje f, g jako znane – przetestować dla f(x

1

,x

2

)=-2x

1

2

-(x

2

-1)

2

)

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 2

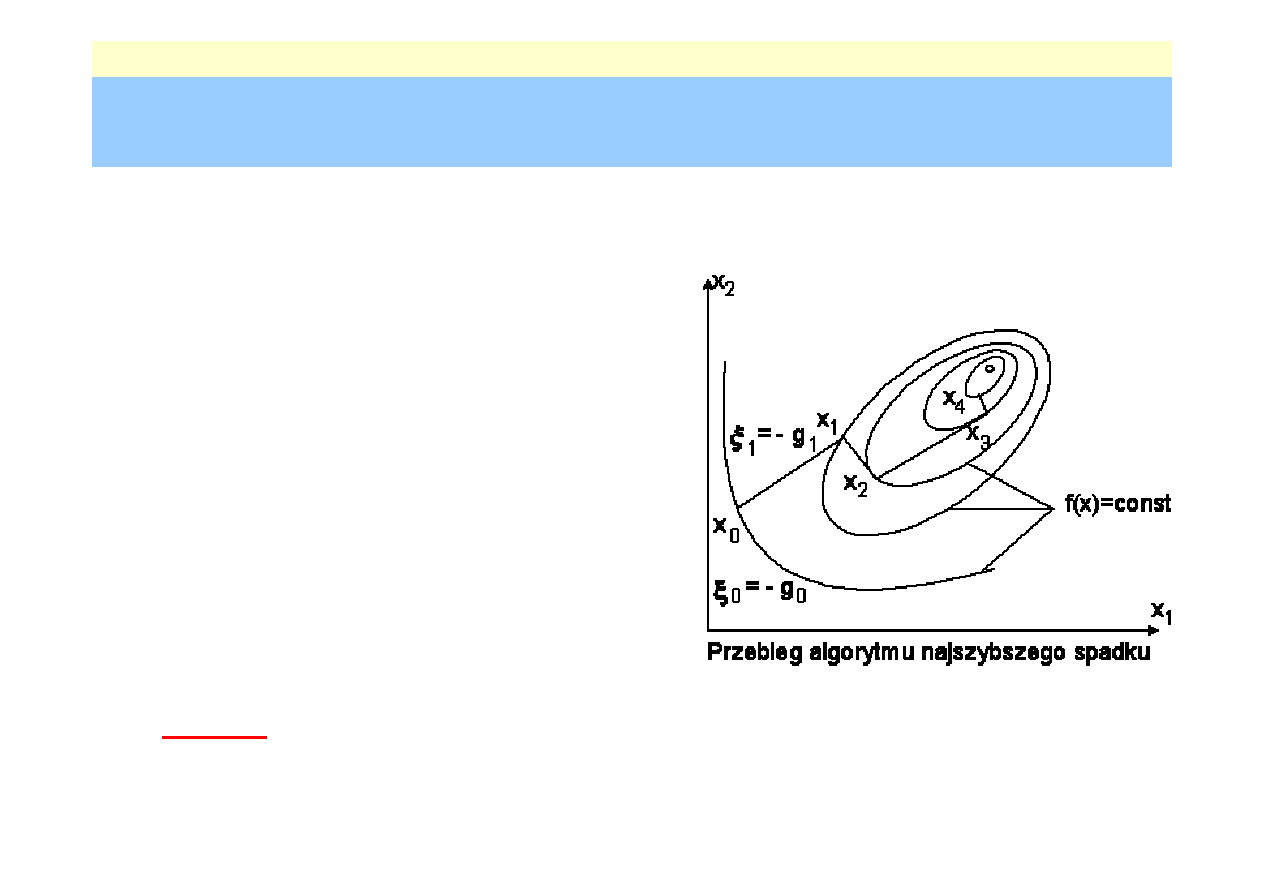
Nr: 36

Metody gradientowe –

Metoda najszybszego spadku

Algorytm obliczeń :

1.

Obliczenie w punkcie startowym

x

0

wartości

funkcji

f(x

0

)

oraz jej gradientu

g

0

= g(x

0

),

przyjmujemy

i=0

2.

Wyznaczenie kierunku poszukiwań

ξξξξ

=-g

i

3.

Wzdłuż kierunku

ξξξξ

określamy

λλλλ

i

takie dla której

wartość

f(x

i-1

+

ξξξξ

i

λλλλ

i

) osiąga minimum.

Współrzędne nowego punktu

x

i

= x

i-1

+

ξξξξ

i

λλλλ

i

4.

Obliczenie w nowym punkcie wartość funkcji

f(x

i+1

)

oraz gradientu

g= g(x

i+1

),

jeżeli

nie osiągnięto minimum, powrót do punktu 2.

Zadanie: zapisz kod programu realizujący metodę

(przyjąć funkcje f, g jako znane – przetestować dla f(x

1

,x

2

)=-x

1

2

-(2x

2

-3)

4

)

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 2

Nr: 37

Metoda najszybszego spadku - przykład

Znajdujemy minimum funkcji:

f(x

1

,x

2

)=x

1

2

+ x

2

2

Punkt startowy:

(x

1

(1)

,x

2

(1)

)= [1,1]

T

Gradient:

∇

∇

∇

∇

f(x

1

,x

2

)= [2x

1

,2x

2

]

T

Szukamy przybliżenia postaci:

x

(2)

= x

(1)

+h

(1)

·(-

∇

∇

∇

∇

f(x

(1)

))

-2

-1

0

1

2

-2

-0.5

1

0

1

2

3

4

5

6

7

8

wielkość

h

0

- miejsce w którym funkcja

f(x

1

,x

2

)

na wyznaczonym przez gradient kierunku

przyjmuje minimalną wartość):

h

0

= min

h

(f(x

(1)

-h·

∇

∇

∇

∇

f(x

(1)

)

)

)

Znajdujemy wielkość

h

0

- definiujemy pomocniczą funkcję

H

(1)

(h)

, znajdujemy jej minimum

H

(1)

(h) =f(x

(1)

-h·

∇

∇

∇

∇

f(x

(1)

))=

=f([1,1]

T

-h·[2,2]

T

)= f([1-2h,1-2h]

T

)=

=(1-2h)

2

+(1-2h)

2

= 2(1-2h)

2

H

(1)’

(h)= 2·2(1-2h)·(-2) = -8(1-2h)

H

(1)’

(h)=0

⇔

⇔

⇔

⇔

h=1/2

x

(2)

= [1,1]

T

+1/2·(-[2,2

]

T

)=[0,0]

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 2

Nr: 38

Inne (ulepszone) metody gradientowe

metoda sprzężonych gradientów

•

Kierunki poszukiwań tworzone są tak, aby każdy kolejny był sprzężony do wszystkich
poprzednich. Dwa kierunki

ξξξξ

i

oraz

ξξξξ

j

są wzajemnie sprzężone względem dodatnio

określonej macierzy A, jeżeli

ξξξξ

i

T

A

ξξξξ

j

=0

dla

i <> j

•

kierunki wzajemnie sprzężone są liniowo niezależne.

•

tworzenie kierunków sprzężonych :

•

pierwszy krok

: minus gradient :

ξξξξ

1

=-

∇

∇

∇

∇

f(x

1

)=-A*x

1

-b

(dobieramy macierz

A

i

wektor

b

tak by spełniona była powyższa równość)

–

minimalizacja

f(x)

wzdłuż tego kierunku : z równania

(

ξ

1

)

T

*[A(x

1

+

ββββ

1

*

ξ

1

+b]=0

otrzymujemy wartość

ββββ

1

, następnie określamy punkt

x

2

=x

1

+

ββββ

1

*

ξ

1

•

i-ty krok

: nowy kierunek w punkcie

x

i

jest wyznaczany według reguły :

ξ

i

=-

∇

∇

∇

∇

f(x

i

) +

ββββ

i

*

ξ

i-1

- współczynnik

ββββ

i

jest tak dobierany aby kierunki

ξ

i

,

ξ

i-1

były

sprzężone (punkt

x

i+1

wyznaczamy minimalizując

f(x)

wzdłuż tego kierunku) :

)

(

)

(

)

(

)

(

1

1

−

−

∇

⋅

∇

∇

⋅

∇

=

i

T

i

i

T

i

i

x

f

x

f

x

f

x

f

β

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 2

Nr: 39

Metody optymalizacji globalnej

•

Konwencjonalne metody poszukiwania minimum

–

startują z obranego punktu początkowego,

–

poszukując w jego pobliżu mniejszej (niż poprzednia) wartości funkcji celu, zmierzają
do minimum,

–

poszukiwanie takie

uzależnione jest od obranego punktu startowego

i nie zawsze

kończy się w

minimum globalnym

.

•

Algorytmy globalnej optymalizacji

–

ukierunkowane są na zwiększenie prawdopodobieństwa osiągnięcia

minimum

globalnego

,

–

wykorzystywane są w tym celu różne metody stochastyczne, lub algorytmy genetyczne

–

nie gwarantują uzyskania rozwiązania optymalnego, jednak prawdopodobieństwo błędu
można uczynić bardzo małym.

–

w metodach optymalizacji globalnej obliczane są wartości funkcji celu dla pewnego
zestawu stochastycznie wybranych punktów - różne metody to różne strategie doboru
zestawu punktów,

–

skuteczność konkretnej metody zależy od właściwości danej funkcji celu, dlatego nie
można mówić o metodach globalnej optymalizacji ogólnego zastosowania. Metoda i jej
parametry muszą być dopasowane do specyfiki problemu.

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 2

Nr: 40

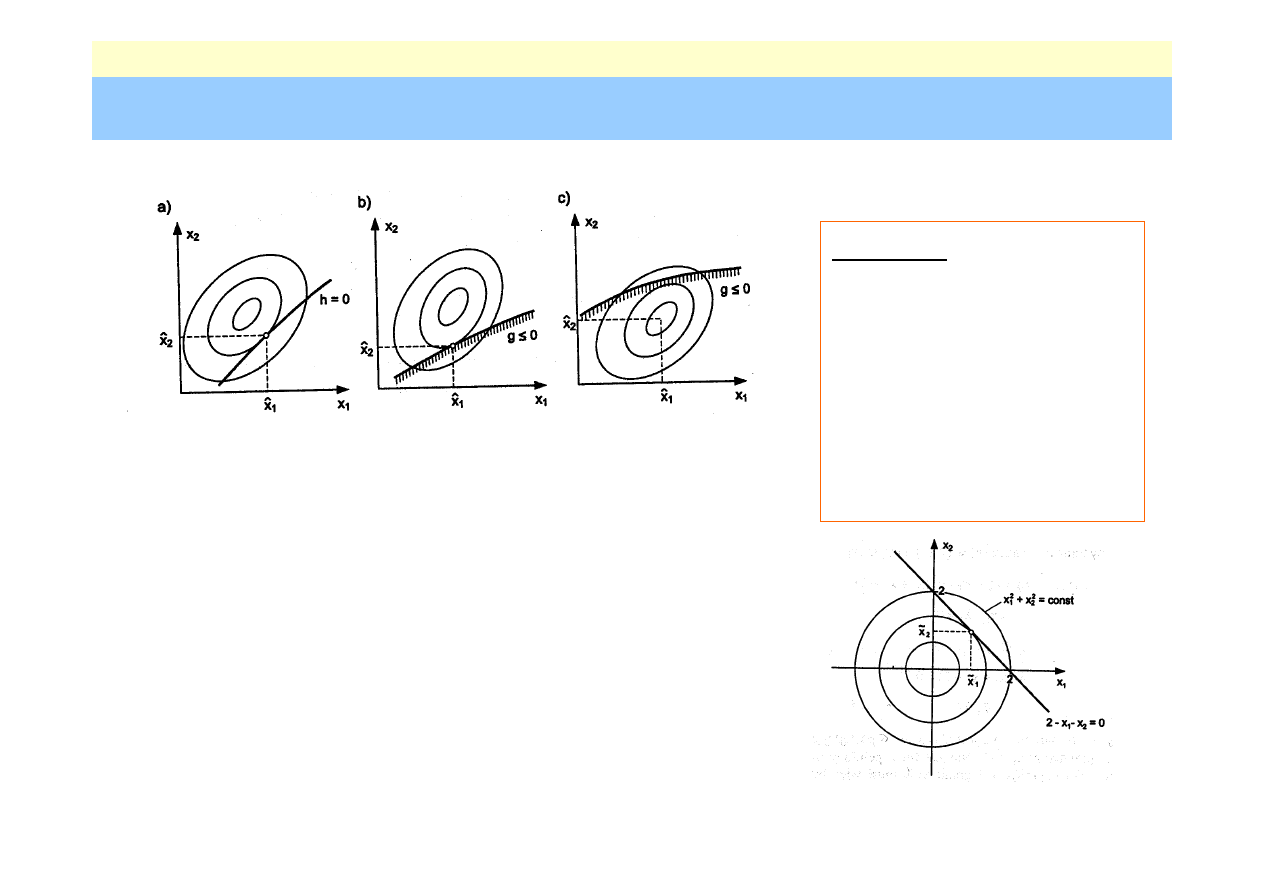
Metody optymalizacji –

przy zadanych ograniczeniach

Zadanie minimalizacji
a)

ograniczenie równościowe

h(x

1

,x

2

)=0

b)

ograniczenie nierównościowe (aktywne)

g(x

1

,x

2

)

≤≤≤≤

0

c)

ograniczenie nierównościowe (nieaktywne)

g(x

1

,x

2

)

≤≤≤≤

0

Przykład:

znaleźć minimum
funkcji

f(x

1

,x

2

)=x

1

2

+ x

2

2

z warunkiem

2-x

1

-x

2

=0

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 2

Nr: 41

Metody optymalizacji -

Programowanie liniowe

Programowanie liniowe –

funkcja celu

f(x)

i funkcje ograniczeń są

liniowe

Metoda simplex –

jedna z podstawowych metod rozwiązywania zadań

programowania liniowego

Postać zadania programowania liniowego

}

,

,

0

,

:

{

}

)

(

{

min

n

m

R

b

x

b

Ax

R

x

X

x

c

x

f

m

n

T

X

x

≤

∈

≥

=

∈

=

=

∈

}

,

,

0

,

:

{

}

)

(

{

min

n

m

R

b

x

b

Ax

R

x

X

x

c

x

f

m

n

T

X

x

≤

∈

≥

≤

∈

=

=

∈

ograniczenie nierównościowe można sprowadzić do równościowego

wprowadzając pomocniczą zmienną:

• x

1

+ 2x

2

≤≤≤≤

3

,

x

1

≥≥≥≥

0, x

2

≥≥≥≥

0

•

wprowadzamy pomocniczą zmienną

x

3

≥≥≥≥

0

zapisując

x

1

+ 2x

2

+ x

3

= 3

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 2

Nr: 42

Programowanie liniowe

Zadanie optymalnego wyboru asortymentu produkcji

W fabryce wytwarzanych jest

m

produktów. Każdy produkt wytwarzany jest z

n

surowców.

Określono

•

x

i

– ilość wytworzonych jednostek

i-

tego (

i=1,...,m)

produktu,

•

a

i

– zysk osiągnięty ze sprzedaży

i-

tego (

i=1,...,m)

produktu,

•

b

j

– ilość dziennej dostawy jednostek

j-

tego (

j=1,...,n)

surowca,

•

c

ij

– ilość jednostek

j-

tego (

j=1,...,n)

surowca potrzebna do wytworzenia jednostki

i-

tego

(

i=1,...,m)

produktu

Należy

znaleźć takie wartości

x

i

aby osiągnięty zysk dzienny był jak największy. Szukamy

maksimum wyrażenia

przy warunkach

∑

=

=

m

i

i

i

x

a

x

f

1

)

(

;

,...,

1

,

0

,...,

1

,

1

m

i

x

n

j

b

x

c

i

j

m

i

i

ij

=

≥

=

≤

∑

=

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 2

Nr: 43

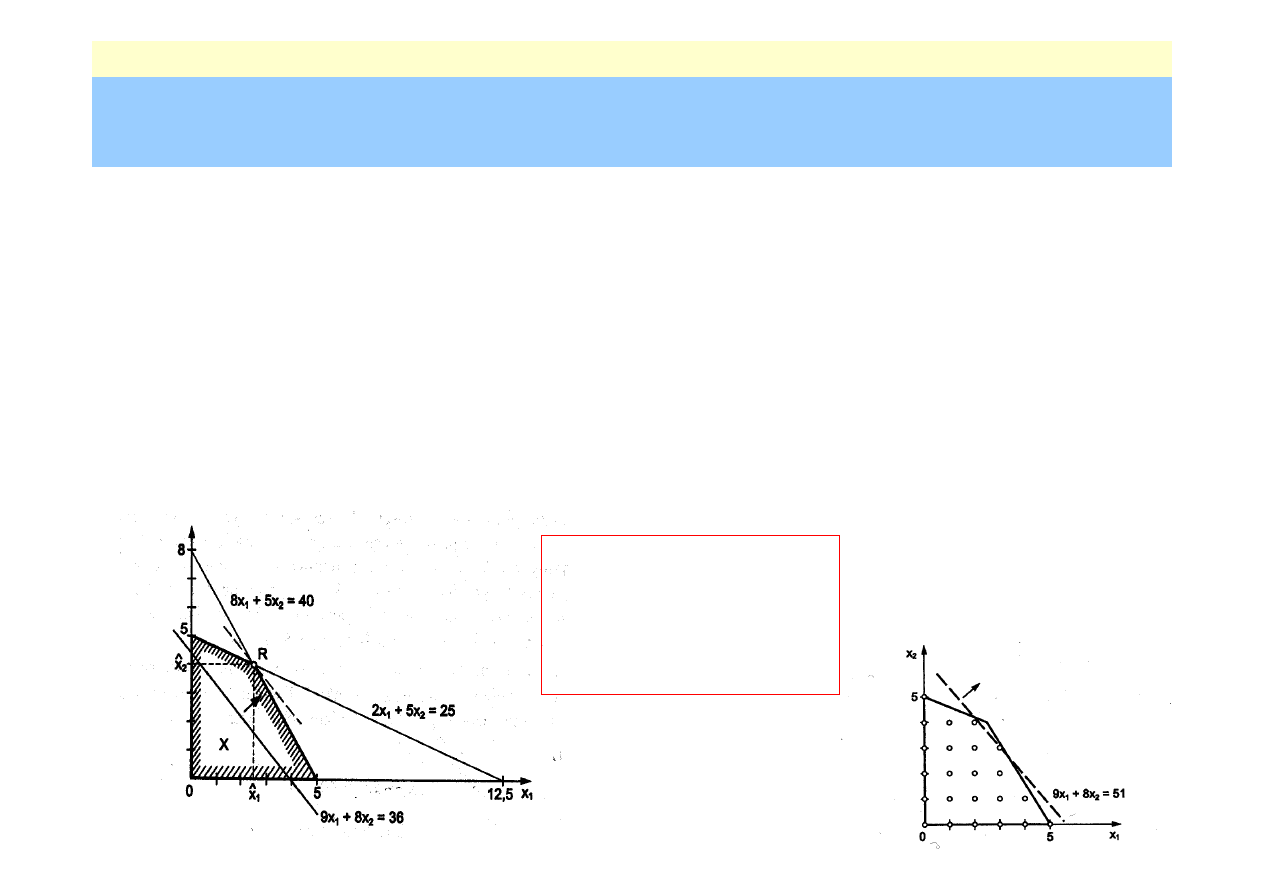
Programowanie liniowe – przykład liczbowy

Zadanie optymalnego wyboru asortymentu produkcji

Niech

m=2

, (w fabryce wytwarzane są 2 produkty),

n=2

(do wytworzenia jednego produktu potrzebne są 2

surowce).

–

do wytworzenia produktu I potrzeba 8 jednostek surowca A, oraz 2 jednostki surowca B,

–

do wytworzenia produktu II potrzeba 5 jednostek surowca A, oraz 5 jednostek surowca B.

Zysk ze sprzedaży : (szukamy największego zysku)

–

jednostki produktu I - 9 złotych

–

jednostki produktu II -8 złotych

Wielkość dziennej dostawy

–

surowca A – 40 jednostek

–

surowca B – 25 jednostek

Zadanie (X –zbiór rozwiązań dopuszczalnych, warstwicami funkcji

f(x)

są linie proste

9x

1

+8x

2

= const.)

25

5

2

:

40

5

8

:

0

,

0

max

8

9

)

(

2

1

2

1

2

1

2

1

≤

+

≤

+

≥

≥

→

+

=

x

x

B

x

x

A

x

x

x

x

x

f

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 2

Nr: 44

Zastąpienie kryteriów nierównościowych kryteriami równościowymi

•

wprowadzamy dodatkowe zmienne x

3

, x

4:

•

zadanie (ograniczenia równościowe) opisujemy układem równań

0

,

,

,

25

5

2

25

5

2

:

40

5

8

40

5

8

:

4

3

2

1

4

2

1

2

1

3

2

1

2

1

≥

=

+

+

≤

+

⇒

=

+

+

≤

+

x

x

x

x

x

x

x

x

x

B

x

x

x

x

x

A

[

]













=

⋅













=

25

40

1

0

5

2

0

1

5

8

:

4

3

2

1

T

x

x

x

x

b

Ax

Programowanie liniowe – przykład liczbowy

Zadanie optymalnego wyboru asortymentu produkcji

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 2

Nr: 45

25

5

2

:

40

5

8

:

0

,

0

max

8

9

)

(

2

1

2

1

2

1

2

1

≤

+

≤

+

≥

≥

→

+

=

x

x

B

x

x

A

x

x

x

x

x

f

[x, lagr, f] = linpro(p, C, b, ci, cs)

f(X)= p

T

*X ->

minimum













≤













≤













⇒

≤

≤













≤

























⇒

≤













−

−

=

⇒

−

=













=

1000

1000

0

0

25

40

*

5

2

5

8

*

*

]

8

,

9

[

)

(

*

)

(

2

1

2

1

2

1

2

1

x

x

cs

X

ci

x

x

b

X

C

x

x

X

f

X

p

X

f

x

x

X

T

[x, lagr, f]=-linpro([-9;-8],[8,5;2,5],[40;25],[0;0],[1000;1000])

// x=[2.5;4], f=54.5

Programowanie liniowe – przykład liczbowy

Zadanie optymalnego wyboru asortymentu produkcji

funkcja

linpro()

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 2

Nr: 46

Programowanie kwadratowe – przykład liczbowy

funkcja

quapro()

25

5

2

:

40

5

8

:

0

,

0

min

)

(

2

1

2

1

2

1

2

1

2

1

≤

+

≤

+

≥

≥

→

−

−

=

x

x

B

x

x

A

x

x

x

x

x

x

f

[x, lagr, f] = quapro(Q, p, C, b, ci, cs)

f(X)= 0.5*X

T

*Q*X + p

T

*X ->

minimum

[

]

[

]

[

]

[

]













≤













≤













⇒

≤

≤













≤

























⇒

≤













−

−

+

























=













+

























=













=

1000

1000

0

0

25

40

*

5

2

5

8

*

*

1

1

*

0

0

0

2

*

*

5

.

0

)

(

*

*

*

*

5

.

0

)

(

2

1

2

1

2

1

2

1

2

1

2

1

2

1

2

1

22

21

12

11

2

1

2

1

x

x

cs

X

ci

x

x

b

X

C

x

x

x

x

x

x

X

f

x

x

p

p

x

x

q

q

q

q

x

x

X

f

x

x

X

[x,lagr,f]=quapro([2,0;0,0],[-1;-1],[8,5;2,5],[40;25],[0;0],[1000;1000])

// x=[0.3;4.88]; f=-5.09

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 2

Nr: 47

Przykład zastosowania funkcji

optim()

Znajdź największą wartość funkcji (punkt startowy:

[1,1,1]

):

f(x,y,z)=sin(xy)+cos(xz)+sin(y-z)

na obszarze ograniczonym poprzez nierówności:

x

≥≥≥≥

0, y

≥≥≥≥

0, z

≥≥≥≥

0, x

≤≤≤≤

10, y

≤≤≤≤

10, z

≤≤≤≤

10

// zdefiniowanie funkcji SciLaba która b

ę

dzie optymalizowana:

// zmienne (x

1

,x

2

,x

3

) zapisane zostaj

ą

w postaci wektora x

//

f - zwraca warto

ść

funkcji

//

g - zwraca gradient funkcji

//

ind - parametr wymagany w funkcji optim()

function [f,g,ind]=fst(x,ind)

f = sin(x(1)*x(2))+cos(x(1)*x(3))+sin(x(2)-x(3))

g = [0;0;0]

g(1)= x(2)*cos(x(1)*x(2))-x(3)*sin(x(1)*x(3))

g(2)= x(1)*cos(x(1)*x(2))+cos(x(2)-x(3))

g(3)= -x(1)*sin(x(1)*x(3))-cos(x(2)-x(3))

endfunction

// u

ż

ycie

optim(fst

, [

’b’

]

, start,

[

ograniczenie_dolne,ograniczenie_górne

]

)

// wart – optymalna (minimalna) warto

ść

poszukiwanej funkcji,

// xp – punkt (wektor 3 współrz

ę

dnych) w którym warto

ść

zostaje obliczona

[wart,xp]=optim(fst,

'b',[0;0;0],[10;10;10],

[1;1;1])

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 2

Nr: 48

Programowanie liniowe -

Problem przydziału maszyn

Dany zakład produkcyjny mający

m

maszyn, wytwarzających

n

wyrobów.

Określono

•

x

ij

– ilość

j-

tego (

j=1,...,n

) produktu wytworzonego na

i-

tej (

i=1,...,m

) maszynie w danym okresie czasu;

•

a

ij

– czas potrzebny do wyprodukowania jednostki produktu

j-

tego (

j=1,...,n

) na

i-

tej (

i=1,...,m

) maszynie;

•

a

i

– dysponowany czas pracy

i-

tej (

i=1,...,m

) maszyny

•

b

j

– ilość produktu

j-

tego (

j=1,...,n

), który powinien być

wytworzony;

•

c

ij

– koszt wytworzenia jednostki produktu

j

(

j=1,...,n

)

na

i-

tej (

i=1,...,m

) maszynie;

Należy

znaleźć takie (nieujemne) wartości

x

ij

minimalizujący

wskaźnik jakości (najniższy koszt wytworzenia określonej

liczby wyrobów)

przy warunkach

∑∑

=

=

=

m

i

n

j

ij

ij

x

c

x

f

1

1

)

(

n

j

b

x

m

i

a

x

a

m

i

j

ij

i

n

j

ij

ij

,...,

1

,...,

1

,

1

1

=

=

=

≤

∑

∑

=

=

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 2

Nr: 49

Programowanie liniowe

Problem optymalnego mieszania surowców

Określono (mieszając n surowców otrzymujemy m produktów)

•

a

ij

– zawartość

j-

tego (

j=1,...,n

) składnika w jednostce

i-

tego

(

i=1,...,m

) produktu;

•

b

j

– wymagana zawartość

j-

tego (

j=1,...,n

) składnika w całości produktów;

•

c

i

– cena jednostki

i-

tego (

i=1,...,m

) produktu

Zadanie polega na wyznaczeniu

nieujemnych wielkości otrzymanych produktów

x

i

które minimalizują całkowity koszt

przy warunkach

∑

=

=

m

i

i

i

x

c

x

f

1

)

(

n

j

b

x

a

j

m

i

i

ij

,...,

1

,

1

=

≥

∑

=

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 2

Nr: 50

Programowanie liniowe -

Zadanie załadunku (plecakowe)

Spośród

n

ładunków ważących odpowiednio

a

1

, a

2

, ..., a

n

o

wartościach

c

1

, ...,c

n

należy załadować na samochód o

dopuszczalnych ładowności

b

takie, aby łączna ich wartość była jak

największa.

oznaczamy zmienne

x

i

(i=1,...,n)

:

– 1: gdy i-ty ładunek jest załadowany

– 0: w przeciwnym przypadku

zadanie przyjmuje postać:

n

i

x

b

x

a

x

c

x

f

i

n

i

i

i

n

i

i

i

,...,

1

},

1

,

0

{

max

)

(

1

1

=

∈

≤

→

=

∑

∑

=

=

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 2

Nr: 51

Programowanie liniowe -

Zadanie rozkroju

Zadanie polega na minimalizacji odpadów powstających podczas np. rozkroju arkusza na

części.

arkusz o szerokości

w

ma być pocięty na wstęgi o szerokościach odpowiednio

b

1

,b

2

,...,b

m

. Mamy wyróżnionych

n

sposobów).

Zadanie można sformułować (wyznaczenie krotności każdego ze sposobów rozkroju, tak

by zmieścić się w tolerancji zapotrzebowań i zminimalizować łączny odpad):

gdzie

z

j

– minimalne,

y

j

– maksymalne zapotrzebowanie na wstęgi o szerokościach

b

j

c

i

– odpad powstający w

i-

tym sposobie rozkroju

s

ij

– (całkowita) liczba wstęg o szerokości

b

j

wyciętych z arkusza w

i-

tym

sposobie rozkroju

n

i

x

m

j

y

x

s

z

n

i

b

s

w

c

x

c

x

f

i

j

n

i

i

ij

j

m

j

j

ij

i

n

i

i

i

,...,

1

,

0

,...,

1

,...,

1

min,

)

(

1

1

1

=

≥

=

≤

≤

=

−

=

→

=

∑

∑

∑

=

=

=

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 2

Nr: 52

Programowanie liniowe -

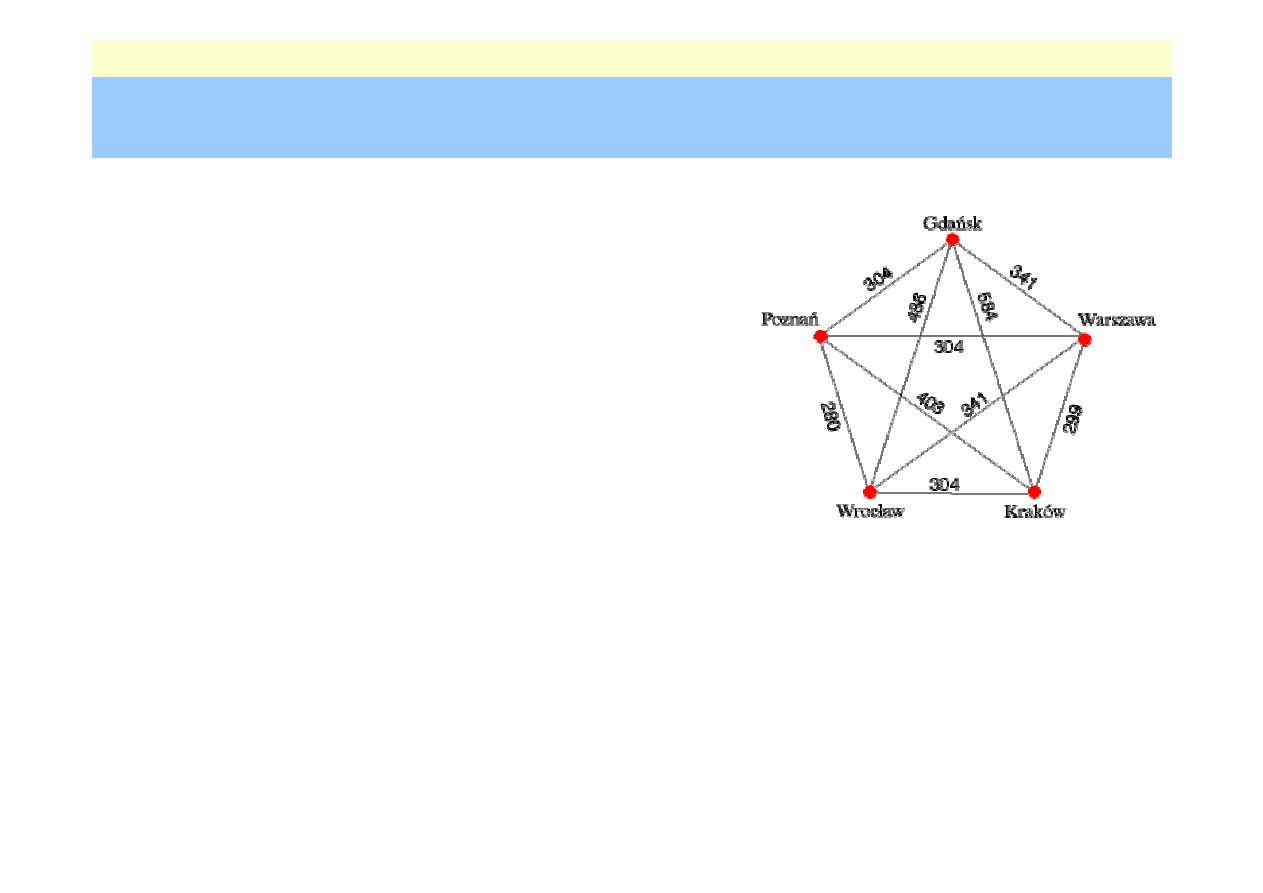
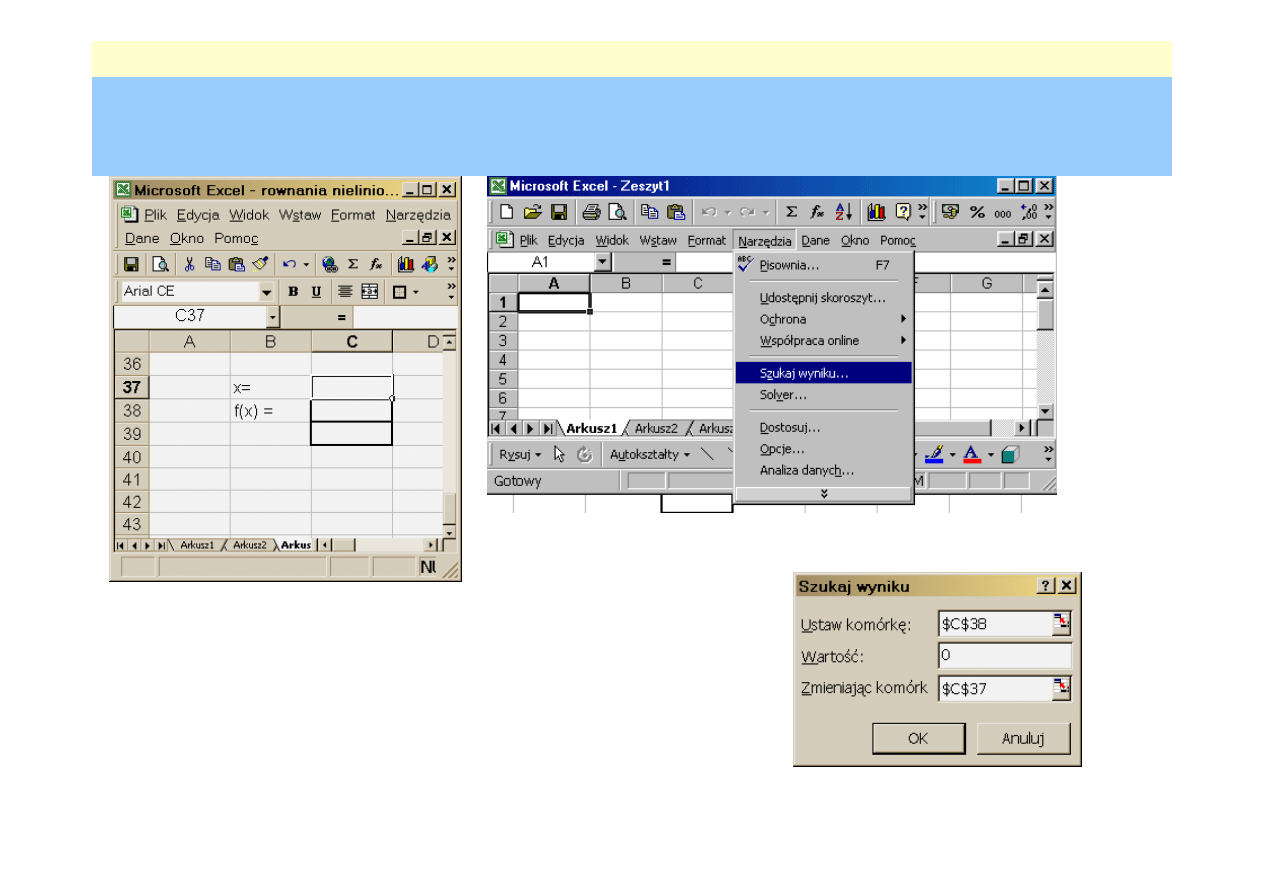
Zadanie komiwoja

ż

era

Komiwojażer startując z miasta nr 1 ma odwiedzić

(n-1)

miast i wrócić do punktu startu. Należy

ustalić,

w jakiej kolejności ma on odwiedzić te

miasta, aby przebyta droga była jak
najkrótsza

.

c

ij

– odległość miasta

i

od miasta

j

niech

x

ij

=1

jeśli komiwojażer przejeżdża z miasta

i

do miasta

j

,

x

ij

=0

w przeciwnym przypadku

Zadanie formułujemy:

)

(

,...,

2

,

,

1

)

3

(

,...,

1

;

,...,

1

},

1

,

0

{

,...,

1

,

1

)

2

(

,...,

1

,

1

)

1

(

min

)

(

1

1

1

1

j

i

n

j

i

n

nx

z

z

n

j

n

i

x

n

i

x

n

j

x

x

c

x

f

ij

j

i

ij

n

j

ij

n

i

ij

n

i

n

j

ij

ij

≠

=

−

≤

+

−

=

=

∈

=

=

=

=

→

=

∑

∑

∑∑

=

=

=

=

1.

komiwojażer do każdego
miasta tylko raz,

2.

wyjeżdża z każdego miasta
tylko raz,

3.

droga komiwojażera składa
się z jednego cyklu

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 2

Nr: 53

MS Excel – rozwi

ą

zywanie równa

ń

nieliniowych

narz

ę

dzie: Szukaj wyniku

1.

wpis początkowej wartości do komórki C37

2.

wpis formuły która ma przyjąć określoną wartość do
komórki C38

3.

wpis do okna

Szukaj wyniku

określonej wartości którą

ma przyjąć formuła wpisana do komórki C38

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 2

Nr: 54

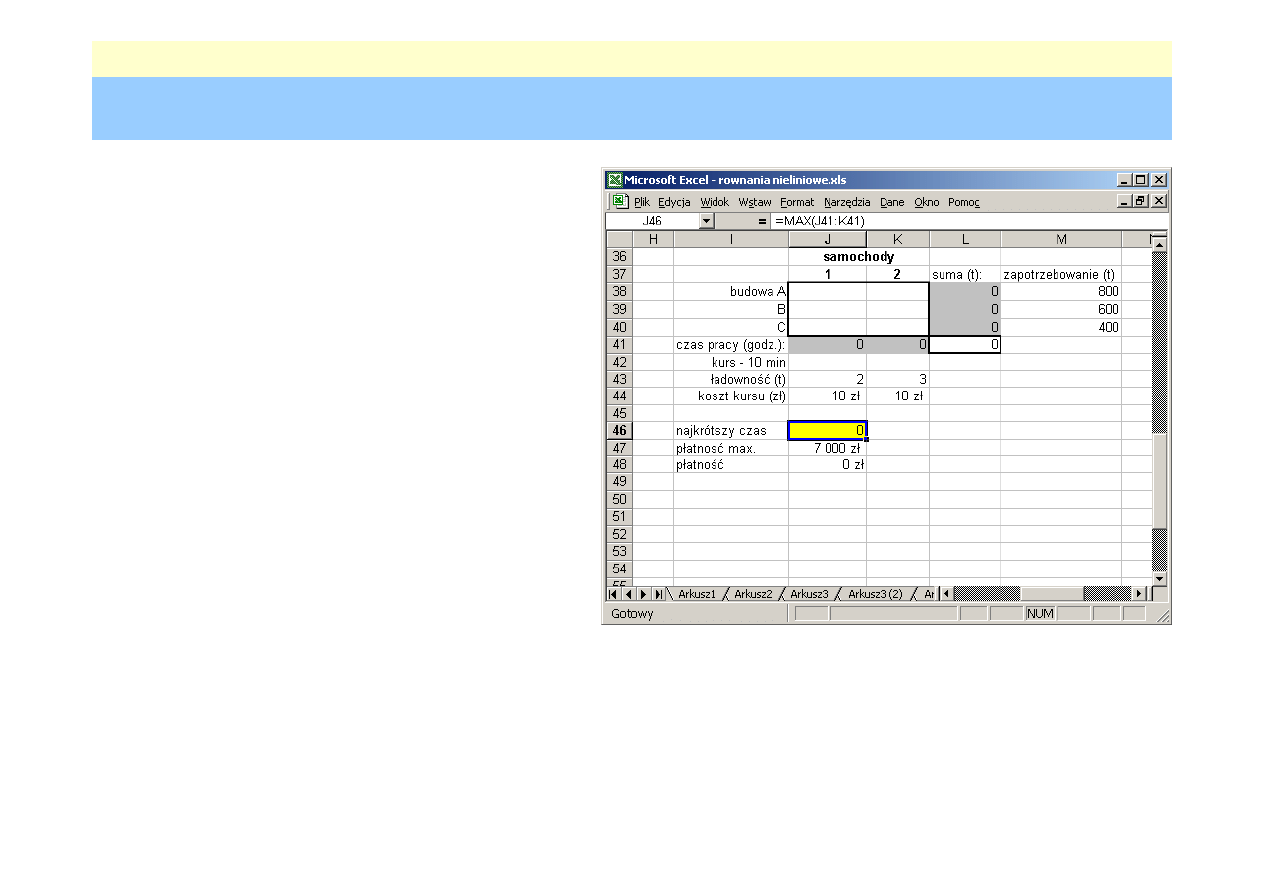
Zadanie transportowe

– przykład rozwi

ą

zania w MS Excel

2 samochody

dostarczają cement na

3 budowy

(budowa A, budowa B, budowa C)

zapotrzebowanie cementu:
•

budowa A

800 t

•

budowa B

600 t

•

budowa C

400 t

Ładowność samochodów:
•

samochód 1

2 t

•

samochód 2

3 t

Ile kursów na poszczególne budowy musiałby wykonać każdy
z pojazdów, wiedząc że koszt jednego kursu wynosi 10 zł,
czas dojazdu 10 minut, tak aby

•

czas w którym zostanie dostarczony beton był jak najkrótszy

•

koszt transportu nie przekroczyłby 7000 zł.

Oznaczenia:

•

x

ij

– ilość kursów

i-

tego pojazdu (

i=1,2

)

na

j-

tą budowę (

j=1,2,3

)

3

,

2

,

1

;

2

,

1

,

0

min

}

6

/

)

(

,

6

/

)

max{(

7000

)

(

10

400

3

2

600

3

2

800

3

2

23

22

21

13

12

11

23

13

22

12

21

11

23

13

22

12

21

11

=

=

≥

→

+

+

+

+

=

≤

+

+

+

+

+

⋅

=

=

+

=

+

=

+

j

i

x

x

x

x

x

x

x

czas

x

x

x

x

x

x

koszt

x

x

x

x

x

x

ij

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 2

Nr: 55

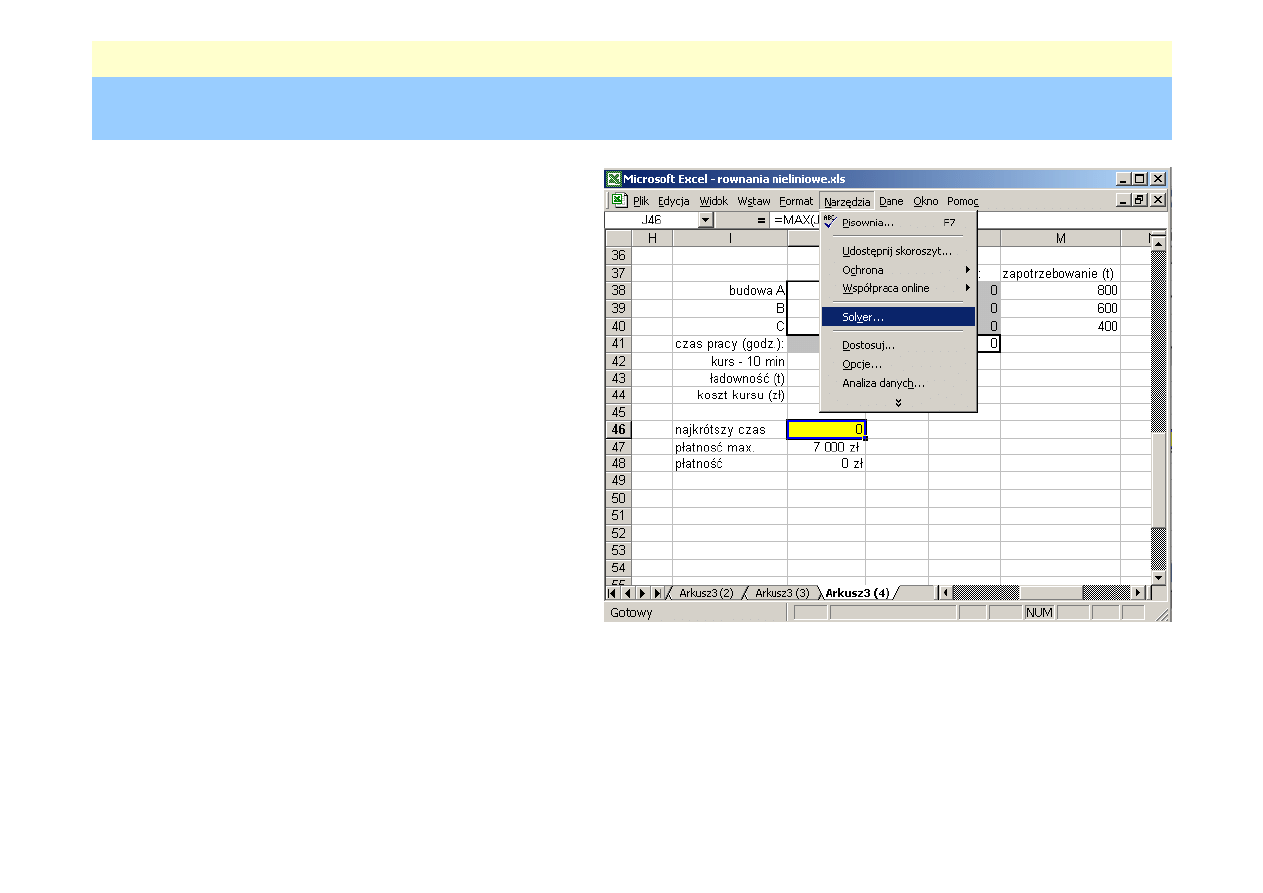
Zadanie transportowe

– przykład rozwi

ą

zania w MS Excel

2 samochody

dostarczają cement na

3 budowy

(budowa A, budowa B, budowa C)

zapotrzebowanie cementu:
•

budowa A

800 t

•

budowa B

600 t

•

budowa C

400 t

Ładowność samochodów:
•

samochód 1

2 t

•

samochód 2

3 t

Ile kursów na poszczególne budowy musiałby wykonać
każdy z pojazdów, wiedząc że koszt jednego kursu
wynosi 10 zł, czas dojazdu 10 minut, tak aby

•

czas w którym zostanie dostarczony beton był jak
najkrótszy

•

koszt transportu nie przekroczyłby 7000 zł.

Oznaczenia:

•

x

ij

– ilość kursów

i-

tego pojazdu (

i=1,2

)

na

j-

tą budowę (

j=1,2,3

)

3

,

2

,

1

;

2

,

1

,

0

min

}

6

/

)

(

,

6

/

)

max{(

7000

)

(

10

400

3

2

600

3

2

800

3

2

23

22

21

13

12

11

23

13

22

12

21

11

23

13

22

12

21

11

=

=

≥

→

+

+

+

+

=

≤

+

+

+

+

+

⋅

=

=

+

=

+

=

+

j

i

x

x

x

x

x

x

x

czas

x

x

x

x

x

x

koszt

x

x

x

x

x

x

ij

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 2

Nr: 56

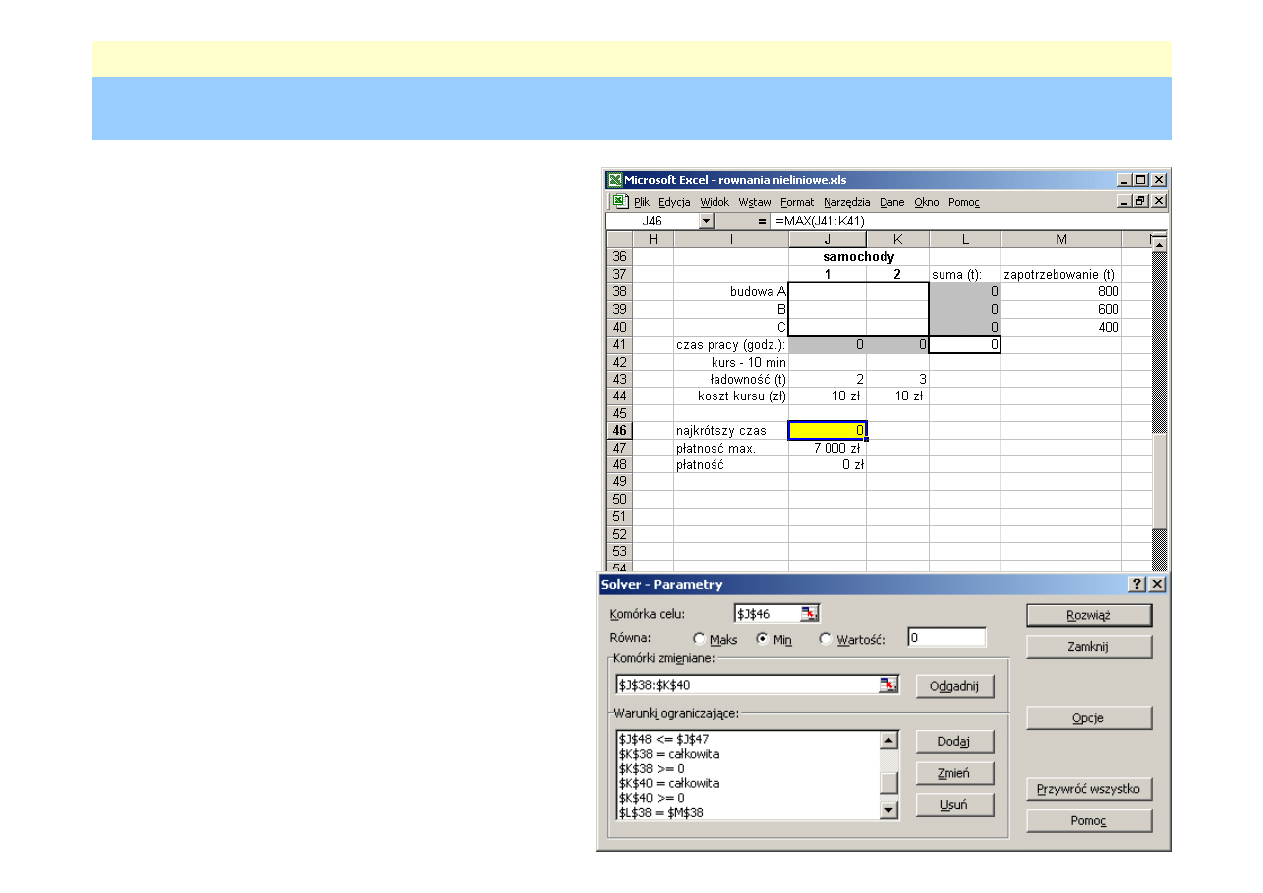
Zadanie transportowe

– przykład rozwi

ą

zania w MS Excel

2 samochody

dostarczają cement na

3 budowy

(budowa A, budowa B, budowa C)

zapotrzebowanie cementu:
•

budowa A

800 t

•

budowa B

600 t

•

budowa C

400 t

Ładowność samochodów:
•

samochód 1

2 t

•

samochód 2

3 t

Ile kursów na poszczególne budowy musiałby wykonać
każdy z pojazdów, wiedząc że koszt jednego kursu
wynosi 10 zł, czas dojazdu 10 minut, tak aby

•

czas w którym zostanie dostarczony beton był jak
najkrótszy

•

koszt transportu nie przekroczyłby 7000 zł.

Oznaczenia:

•

x

ij

– ilość kursów

i-

tego pojazdu (

i=1,2

)

na

j-

tą budowę (

j=1,2,3

)

3

,

2

,

1

;

2

,

1

,

0

min

}

6

/

)

(

,

6

/

)

max{(

7000

)

(

10

400

3

2

600

3

2

800

3

2

23

22

21

13

12

11

23

13

22

12

21

11

23

13

22

12

21

11

=

=

≥

→

+

+

+

+

=

≤

+

+

+

+

+

⋅

=

=

+

=

+

=

+

j

i

x

x

x

x

x

x

x

czas

x

x

x

x

x

x

koszt

x

x

x

x

x

x

ij

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 2

Nr: 57

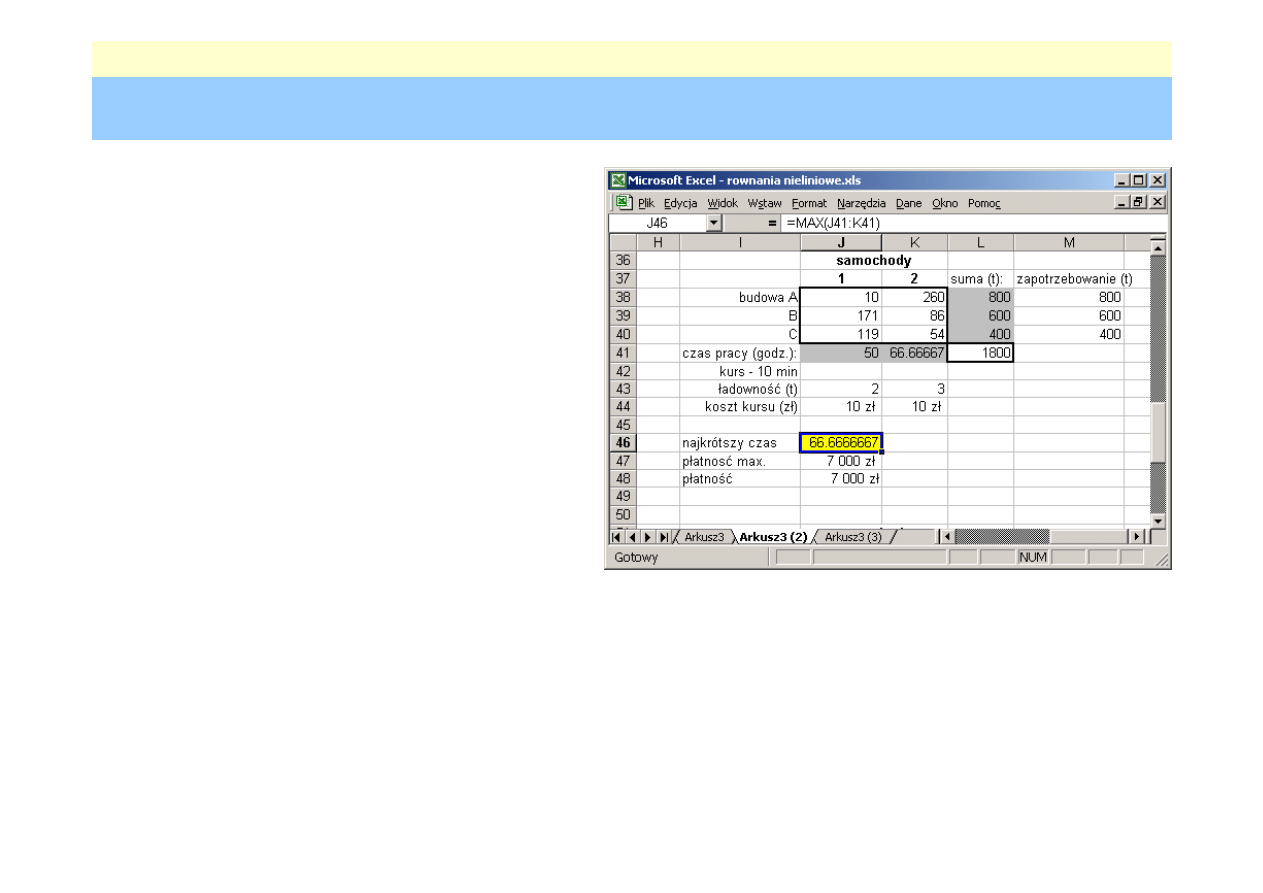
Zadanie transportowe

– przykład rozwi

ą

zania w MS Excel

2 samochody

dostarczają cement na

3 budowy

(budowa A, budowa B, budowa C)

zapotrzebowanie cementu:
•

budowa A

800 t

•

budowa B

600 t

•

budowa C

400 t

Ładowność samochodów:
•

samochód 1

2 t

•

samochód 2

3 t

Ile kursów na poszczególne budowy musiałby wykonać
każdy z pojazdów, wiedząc że koszt jednego kursu
wynosi 10 zł, czas dojazdu 10 minut, tak aby

•

czas w którym zostanie dostarczony beton był jak
najkrótszy

•

koszt transportu nie przekroczyłby 7000 zł.

Oznaczenia:

•

x

ij

– ilość kursów

i-

tego pojazdu (

i=1,2

)

na

j-

tą budowę (

j=1,2,3

)

3

,

2

,

1

;

2

,

1

,

0

min

}

6

/

)

(

,

6

/

)

max{(

7000

)

(

10

400

3

2

600

3

2

800

3

2

23

22

21

13

12

11

23

13

22

12

21

11

23

13

22

12

21

11

=

=

≥

→

+

+

+

+

=

≤

+

+

+

+

+

⋅

=

=

+

=

+

=

+

j

i

x

x

x

x

x

x

x

czas

x

x

x

x

x

x

koszt

x

x

x

x

x

x

ij

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 2

Nr: 58

Zadanie transportowe

– przykład rozwi

ą

zania w MS Excel

2 samochody

dostarczają cement na

3 budowy

(budowa A, budowa B, budowa C)

zapotrzebowanie cementu:
•

budowa A

800 t

•

budowa B

600 t

•

budowa C

400 t

Ładowność samochodów:
•

samochód 1

2 t

•

samochód 2

3 t

Ile kursów na poszczególne budowy musiałby wykonać
każdy z pojazdów, wiedząc że koszt jednego kursu
wynosi 10 zł, czas dojazdu 10 minut, tak aby

•

czas w którym zostanie dostarczony beton był jak
najkrótszy

•

koszt transportu nie przekroczyłby 7000 zł.

Oznaczenia:

•

x

ij

– ilość kursów

i-

tego pojazdu (

i=1,2

)

na

j-

tą budowę (

j=1,2,3

)

3

,

2

,

1

;

2

,

1

,

0

min

}

6

/

)

(

,

6

/

)

max{(

7000

)

(

10

400

3

2

600

3

2

800

3

2

23

22

21

13

12

11

23

13

22

12

21

11

23

13

22

12

21

11

=

=

≥

→

+

+

+

+

=

≤

+

+

+

+

+

⋅

=

=

+

=

+

=

+

j

i

x

x

x

x

x

x

x

czas

x

x

x

x

x

x

koszt

x

x

x

x

x

x

ij

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 2

Nr: 59

Równanie nieliniowe, zadanie optymalizacji – funkcje

SciLaba

• fsolve

() – funkcja rozwiązująca układ równań

nieliniowych

• linpro

() – narzędzie rozwiązywania zadań programowania

liniowego

• quapro

() – narzędzie rozwiązywania zadań

programowania kwadratowego

• optim

() – funkcja rozwiązująca nieliniowe zadania

optymalizacji

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 2

Nr: 60

Podsumowanie

Metody rozwi

ą

zywania równa

ń

nieliniowych.

Zadanie optymalizacji

•

Rozwiązywanie równań nieliniowych

–

Postać równania nieliniowego

–

Iteracyjne metody rozwiązań

•

idee poszczególnych metod,

•

sposób wyznaczania kolejnych przybliżeń,

•

własności

–

Metoda bisekcji

–

Regula falsi
Metoda Newtona-Raphsona (stycznych)

–

Metoda siecznych i jej modyfikacje

–

Porównanie metod rozwiązania

–

pojęcie rzędu metody

•

Układy równań nieliniowych – sposoby rozwiązania

•

Metody optymalizacji – postać zadania

–

sposoby poszukiwania rozwiązań

•

Metoda spadku względem współrzędnych

•

Metody gradientowe – własności, sposoby wyznaczania kierunków poszukiwań

•

Metoda gradientu prostego

•

Metoda najszybszego spadku

•

metoda Newtona

•

metoda sprzężonych gradientów

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 2

Nr: 61

Podsumowanie cd.

Metody rozwi

ą

zywania równa

ń

nieliniowych.

Zadanie optymalizacji

•

Zadanie programowania liniowego

–

sposób rozwiązywania metodą simplex

–

Przykłady standardowych zadań programowania liniowego

•

Zadanie transportowe

•

Zadanie optymalnego wyboru asortymentu produkcji

•

Problem przydziału maszyn

•

Problem optymalnego mieszania surowców

•

Zadanie załadunku

•

Zadanie rozkroju

•

Zadanie komiwojażera

•

Możliwości rozwiązania zadań optymalizacji przy użyciu arkusza
kalkulacyjnego MS Excel i programu SciLab