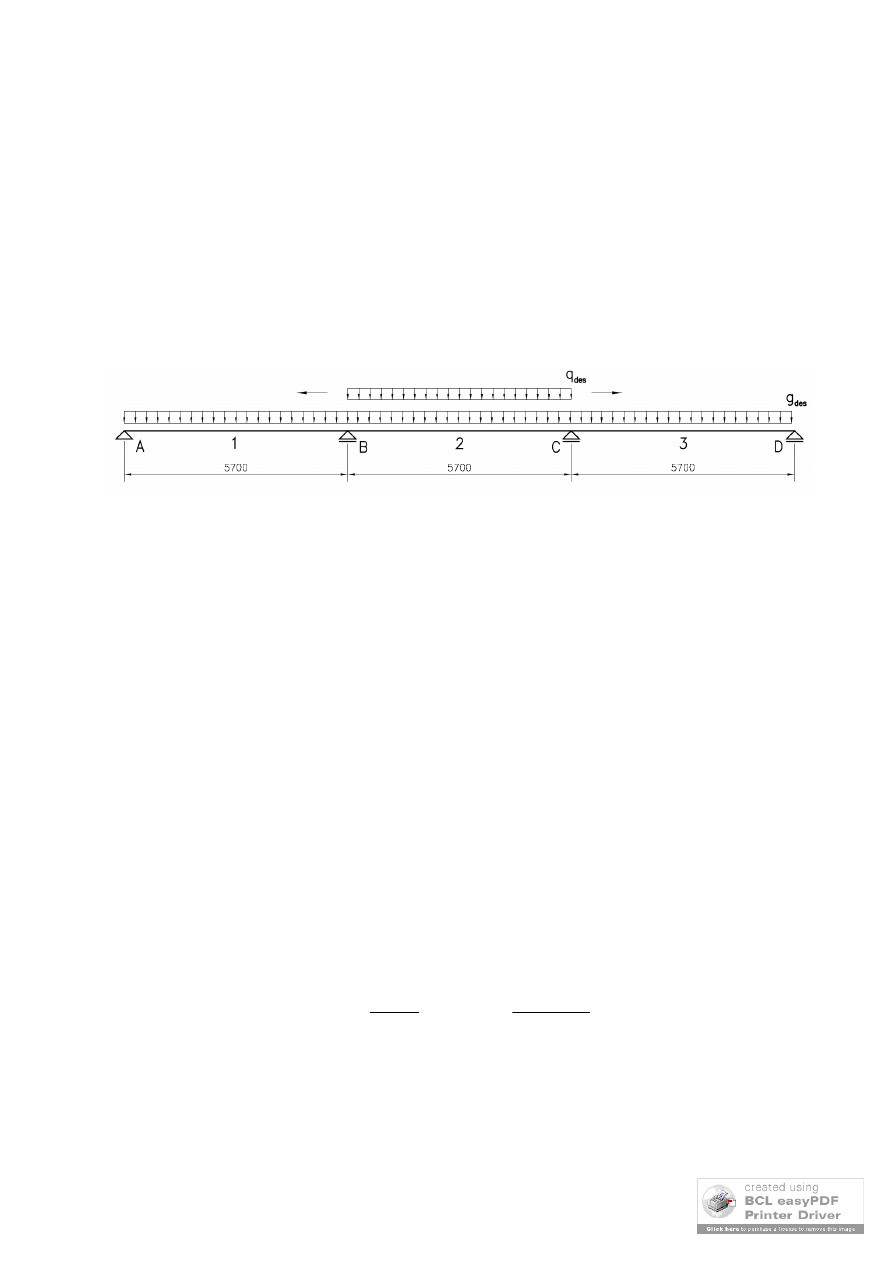
Poz.3.2. Żebro
Poz.3.2.1. Schemat statyczny i geometria przekroju
Zgodnie z planem stropu (rys.1.) żebro jest belką trójprzęsłową
(rys.5.)
Rozstaw osiowy podciągów (stanowiących podpory dla żeber) wynosi
5,70 m.
wymiary przekroju żebra: b = 0,30 m i h = 0,45 m
wymiary przekroju podciągu: b = 0,45 m i h = 1,00 m
Rys. 5. Schemat statyczny żebra
rozpiętość żeber w świetle podciągów
l
n
= 5,70 – 0,45 = 5,25 m
a
A
= min {0,5h ; 0,5t} = min {0,5
0,45 ; 0,5 0,45} = 0,225 m
a
B
= min {0,5h ; 0,5t} = min {0,5
0,45 ; 0,5 0,45} = 0,225 m
a
C
= a
B
= 0,175 m
rozpiętości obliczeniowe
l
ABeff
= l
n
+ a
A
+ a
B
= 5,25 + 2
0,225 = 5,70 m
l
BCeff
= l
n
+ a
B
+ a
C
= 5,25 + 2
0,225 = 5,70 m
wysokość użyteczna przekroju:
w przęśle
d = h – c
nom
– 0,5
–
s
= 450 – 20 – 0,5
20 – 8 = 412 mm
w osi podpór z uwzględnieniem sosu ukrytego
d = h – c
nom
– 0,5
–
s
+
3
5
0
t
,
= 412 +
3
450
5
0
,
= 487 mm
efektywna szerokość półki przekrojów teowych
b
eff
= min{b
w
+ 0,2
l
0
; b
w
+ 12 · h
f
; b
w
+ b
1
+ b
2
}
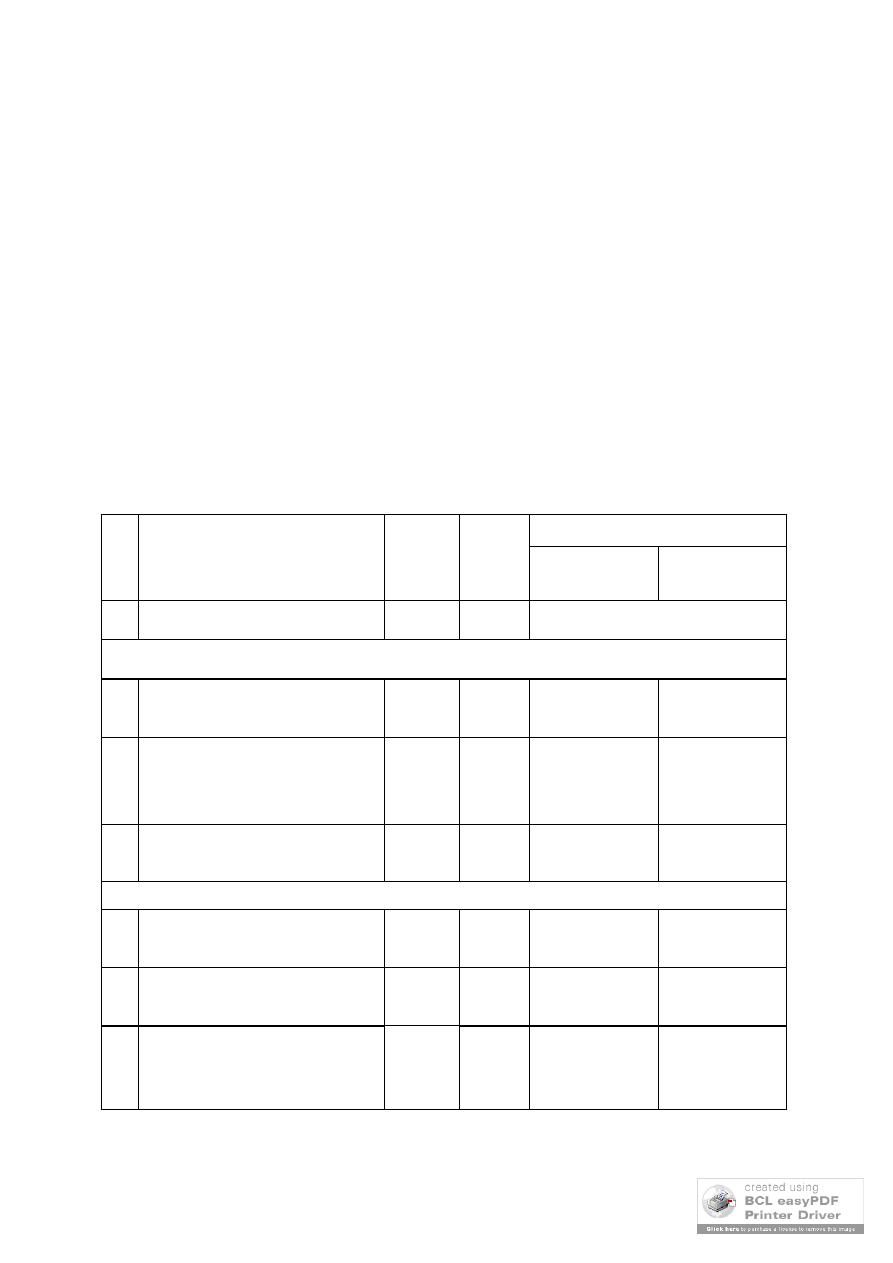
dla przęsła skrajnego
l
0
= 0,85 · l
eff
= 0,85 · 5,70 = 4,845 m
b
eff,AB
= min{b
w
+ 0,2
l
0
; b
w
+ 12 · h
f
; b
w
+ b
1
+ b
2
} =
= min{0,30 + 0,2
4,845 ; 0,30 + 12 · 0,1 ; 0,30 + 1,688} =
= min{1,269 ; 1,500 ; 1,988} = 1,27 m
dla przęsła środkowego
l
0
= 0,70 · l
eff
= 0,70 · 5,70 = 3,990 m
b
eff,BC
= min{b
w
+ 0,2
l
0
; b
w
+ 12 · h
f
; b
w
+ b
1
+ b
2
} =
= min{0,30 + 0,2
3,990 ; 0,30 + 12 · 0,1 ; 0,30 + 1,688} =
= min{1,098 ; 1,500 ; 1,988} = 1,10 m
Poz.3.2.2. Zestawienie obciążeń
Na żebro działają obciążenia z pasma o szerokości 1,988 m
Obciążenie obliczeniowe
Lp Rodzaj obciążenia
i jego wartość
charakterystyczna
f
> 1
f
< 1
f
> 1
f
< 1
[kN/m
2
]
[kN/m
2
]
OBCIĄŻENIA STAŁE (g)
1 ciężar płyty + warstwy
3,63
1,988 = 7,22
4,20
1,988
= 8,35
3,16
1,988
= 6,28
2 żebro
0,30
(0,45 – 0,10)
25,0 = 2,62
1,1
0,9
2,89
2,36
Razem obciążenie stałe
g
k
= 9,84
g
des,1
=
11,24
g
des,2
=
8,64
OBCIĄŻENIA ZMIENNE (q)
3 grunt (piaski grube)
18,05
1,988 = 35,88
1,1
0
39,47
-
4 śnieg
0,7
1,988 = 1,39
1,4
0
1,95
-
Razem obciążenie
zmienne
q
k
= 37,27
q
des
= 41,42
-

Poz.3.2.3. Siły wewnętrzne
Wartości momentów w żebrze policzono w kolejnych przekrojach w
przęsłach skrajnych poczynając od przęseł skrajnych oraz środkowym
co 0,2
l
eff
posługując się wartościami współczynników podanych w
tablicach Winklera.
Momenty zginające w przęśle skrajnym
M
0,2max
= 0,060
11,24 5,70
2
+ 0,070
41,42 5,70
2
= 116,11 kNm
M
0,4max
= 0,080
11,24 5,70
2
+ 0,100
41,42 5,70
2
= 163,79 kNm
M
0,5max
= 0,075
11,24 5,70
2
+ 0,100
41,42 5,70
2
= 161,96 kNm
M
0,6max
= 0,060
11,24 5,70
2
+ 0,090
41,42 5,70
2
= 143,03 kNm
M
0,8max
= 0,000
11,24 5,70
2
+ 0,04022
41,42 5,70
2
= 54,12 kNm
M
0,2min
= 0,060
8,64 5,70
2
– 0,010
41,42 5,70
2
= 3,38 kNm
M
0,4min
= 0,080
8,64 5,70
2
– 0,020
41,42 5,70
2
= –4,46 kNm
M
0,6min
= 0,060
8,64 5,70
2
– 0,030
41,42 5,70
2
= –23,53 kNm
M
0,8min
= 0,000
8,64 5,70
2
– 0,04022
41,42 5,70
2
= –54,16 kNm
Momenty zginające w osi podpory B
M
Bmin
= –0,100
11,24 5,70
2
– 0,1167
41,42 5,70
2
= –193,53 kNm
Momenty zginające w przęśle środkowym (licząc od podpory B)
M
0,2max
= 0,000
11,24 5,70
2
+ 0,050
41,42 5,70
2
= 67,29 kNm
M
0,4max
= 0,020
11,24 5,70
2
+ 0,070
41,42 5,70
2
= 101,50 kNm
M
0,5max
= 0,025
11,24 5,70
2
+ 0,075
41,42 5,70
2
= 110,06 kNm
M
0,2min
= 0,000
8,64 5,70
2
– 0,050
41,42 5,70
2
= –67,29 kNm
M
0,4min
= 0,020
8,64 5,70
2
– 0,050
41,42 5,70
2
= –61,67 kNm
M
0,5min
= 0,025
8,64 5,70
2
– 0,050
41,42 5,70
2
= –60,27 kNm
dalej symetrycznie
Siła poprzeczna przy podporze skrajnej A
V
A
= 0,400 · 11,24
5,70 + 0,450 41,42 5,70 = 131,87 kN

Siła poprzeczna przy podporze B
V
Bl
= –0,600 · 11,24
5,70 – 0,6167 41,42 5,70 = –184,04 kN
V
Bp
= 0,500 · 11,24
5,70 + 0,5833 41,42 5,70 = 168,75 kN
Poz.3.2.4. Stan graniczny nośności – zginanie
beton B37: f
cd
= 20,0 MPa,
cc
= 0,85
stal A-III: f
yd
= 350 MPa
Moment graniczny przenoszony przez półkę
243
0
412
0
100
0
,
,
,
d
h
f
M
Rdp,eff
=
(1 – 0,5
)
d
2
b
eff
f
cd
=
= 0,243
(1 – 0,5 0,243) 0,412
2
1,10 0,85 20,0 = 0,6776 MNm
M
Rdp,eff
= 677,6 kNm > M
max
= 163,79 kNm
całe żebro pracuje jak belka pozornie teowa
Przęsło skrajne
M
Sd
= M
0,4max
= 163,79 kNm
b
eff
= 1,27 m, d = 0,412 m
2
2
cm
27
2
m
000227
0
412
0
30
0
410
9
2
26
0
26
0
,
,
,
,
,
,
d
b
f
f
,
A
w
yk
ctm
min
.
s
045
0
412
0
27
1
20
85
0
10
79
163
2
3
2
,
,
,
,
,
d
b
f
M
eff
cd
cc
Sd
eff
z tablicy 3.10 odczytano
eff
= 0,973 i
eff
= 0,05 <
eff,lim
= 0,53
2
2
3
1
cm
67
11
m
001167
0
350
412
0
973
0
10
79
163
,
,
,
,
,
f
d
M
A
yd
eff
Sd
s
przyjęto 4
20 A
s,prov
= 12,57 cm
2
> A
s,min
= 2,36 cm
2
Przęsło środkowe
M
Sd
= M
0,5max
= 110,06 kNm
b
eff
= 1,10 m, d = 0,412 m

035
0
412
0
10
1
20
85
0
10
06
110
2
3
2
,
,
,
,
,
d
b
f
M
eff
cd
cc
Sd
eff
z tablicy 3.10 odczytano
eff
= 0,982 i
eff
= 0,04 <
eff,lim
= 0,53
2
2
3
1
cm
77
7
m
000777
0
350
412
0
982
0
10
06
110
,
,
,
,
,
f
d
M
A
yd
eff
Sd
s
przyjęto 4
16 A
s,prov
= 8,04 cm
2
> A
s,min
= 2,36 cm
2
Podpora B
w osi podpory
M
Sd
= M
Bmin
= 193,53 kNm
b
w
= 0,30 m, d = 0,487 m
2
2
cm
69
2
m
000269
0
487
0
30
0
410
9
2
26
0
26
0
,
,
,
,
,
,
d
b
f
f
,
A
w
yk
ctm
min
.
s
160
0
487
0
30
0
20
85
0
10
53
193
2
3
2
,
,
,
,
,
d
b
f
M
w
cd
cc
Sd
eff
z tablicy 3.10 odczytano
eff
= 0,938 i
eff
= 0,12 <
eff,lim
= 0,53
2
2
3
1
cm
10
12
m
001210
0
350
487
0
938
0
10
53
193
,
,
,
,
,
f
d
M
A
yd
eff
Sd
s
przyjęto 4
20 A
s,prov
= 12,57 cm
2
> A
s,min
= 2,69 cm
2
w licu podciągu
M
Sd
= M
Bmin
+ V
Bp
(0,5 b
wP
) – 0,5
(g
des,1
+ q
des
)
(0,5 b
wP
)
2
=
= –193,53 + 168,75
(0,5 0,45) – 0,5 (11,24 +41,42) (0,5 0,45)
2
=
= 156,89 kNm
b
w
= 0,30 m, d = 0,412 m
181
0
412
0
30
0
20
85
0
10
89
156
2
3
2
,
,
,
,
,
d
b
f
M
w
cd
cc
Sd
eff
z tablicy 3.10 odczytano
eff
= 0,900 i
eff
= 0,20 <
eff,lim
= 0,53

2
2
3
1
cm
09
12
m
001209
0
350
412
0
900
0
10
89
156
,
,
,
,
,
f
d
M
A
yd
eff
Sd
s
przyjęto zbrojenie jak w osi podpory: 4
20 A
s,prov
= 12,57 cm
2
Poz.3.2.5. Stan graniczny nośności – ścinanie
beton B37: f
cd
= 20,0 MPa, f
ctd
= 1,33 MPa, f
ck
= 30 MPa
zbrojenie główne A-III: f
ywd2
= 350 MPa
strzemiona A-I: f
ywd1
= 210 MPa, f
yk
= 240 MPa
Minimalny stopień zbrojenia strzemionami
240
30
08
0
08
0
,
f
f
,
yk
ck
min
,
w
= 0,18%
Maksymalny rozstaw strzemion
s
max
= min{0,75
d ; 400 mm} = min{0,75 412 ; 400} = 309 mm
przyjęto s
max
= 300mm
Poz.3.2.5.1. Podpora A
Siła poprzeczna w odległości d od lica podpory
V
SdA
= V
A
– (g
des,1
+ q
des
)
(a
A
+ d) =
= 131,87 - (11,24 +41,42)
(0,225 + 0,412) = 98,32 kN
Wyznaczenie nośności przekroju nie zbrojonego na ścinanie – V
Rd1
V
Rd1
= 0,35
k f
ctd
(1,2 + 40
L
)
b
w
d
Przyjęto, że do podpory doprowadzono dołem 2
20
A
sL
= 12,57 cm
2
L
=
d
b
A
w
sL
=
2
41
30
57
12
,
,
= 0,010
0,01
k = 1,6 – d = 1,6 – 0,412 = 1,188 > 1,0

V
Rd1
= 0,35
k f
ctd
(1,2 + 40
L
)
b
w
d =
= 0,35
1,188 1,33 10
3
(1,2 + 40 0,01) 0,30 0,412 = 109,36 kN
V
SdA
= 100,96 kN < V
Rd1
= 98,32 kN - odcinek pierwszego rodzaju
Zbrojenie na ścinanie należy przyjąć z warunków konstrukcyjnych
(rozstaw s
max
= 300 mm).
Nośności krzyżulców betonowych – V
Rd2
V
Rd2
= 0,5
f
cd
b
w
z
= 0,6
(1 – f
ck
/ 250) = 0,6
(1 – 30 / 250) = 0,528
z = 0,9
d = 0,9 0,412 = 0,371 m
V
Rd2
= 0,5
f
cd
b
w
z = 0,5 0,528 20 10
3
0,30 0,371 =
= 587,66 kN
V
SdA
= 98,32 kN < V
Rd2
= 587,66 kN – warunek spełniony
Poz.3.2.5.2. Podpora B z lewej strony
Siła poprzeczna w odległości d od lica podpory
V
Sd,ab
= V
Bl
– (g
des,1
+ q
des
)
(a
B
+ d) =
= 184,04 - (11,24 +41,42)
(0,225 + 0,412) = 150,50 kN
Wyznaczenie nośności przekroju nie zbrojonego na ścinanie – V
Rd1
V
Rd1
= 0,35
k f
ctd
(1,2 + 40
L
)
b
w
d
Przyjęto, że do podpory doprowadzono górą co najmniej 3
20
A
sL
= 9,43 cm
2
L
=
d
b
A
w
sL
=
2
41
30
43
9
,
,
= 0,008 < 0,01
V
Rd1
= 0,35
k f
ctd
(1,2 + 40
L
)
b
w
d =
= 0,35
1,188 1,33 10
3
(1,2 + 40 0,008) 0,30 0,412 = 103,9 kN
V
Sd,ab
= 150,50 kN > V
Rd1
= 103,9 kN - odcinek drugiego rodzaju
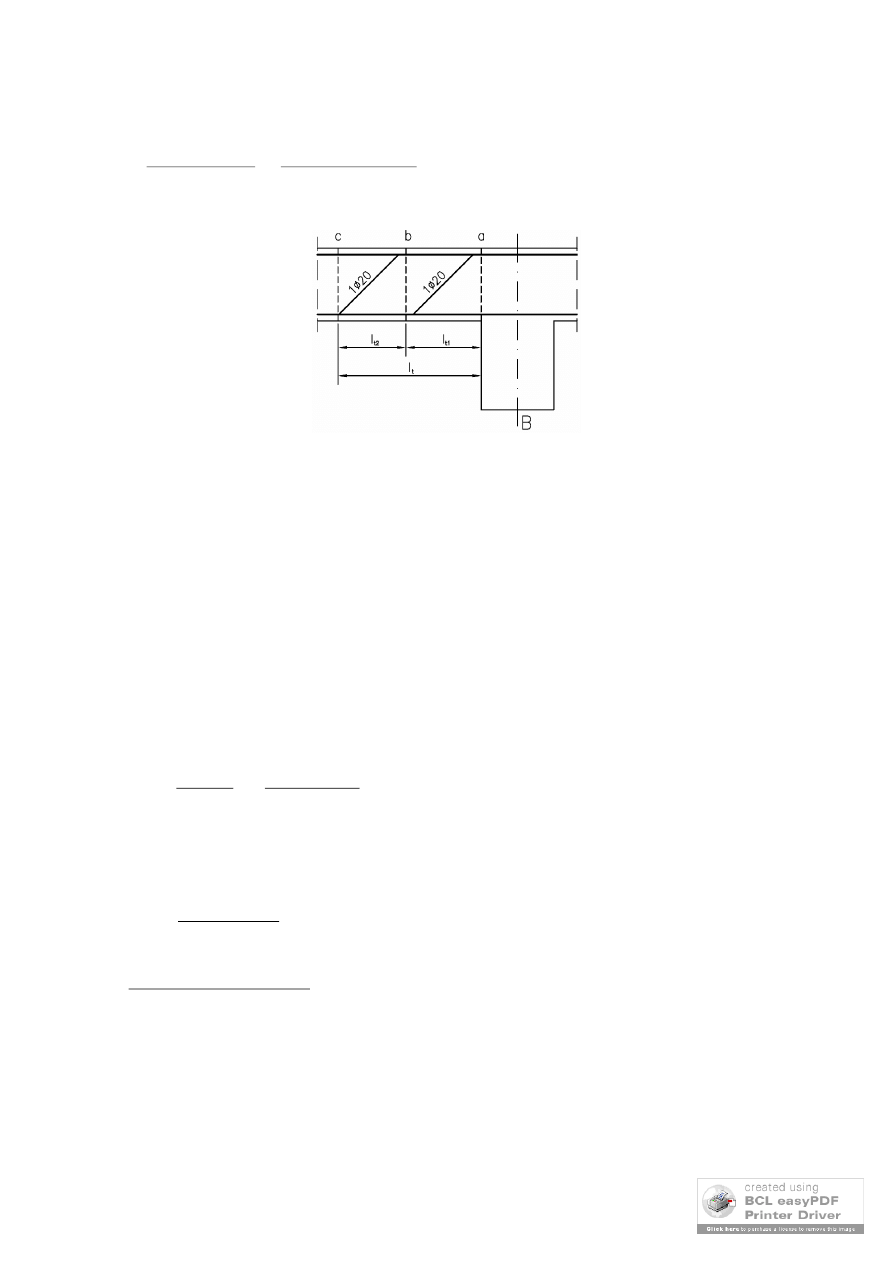
długość odcinka drugiego rodzaju
m
885
0
42
41
24
11
9
103
50
150
1
1
,
,
,
,
,
q
g
V
V
l
des
,
des
Rd
ab
,
Sd
t
Rys. __.6. Podział na odcinki przy podporze B
Na odcinku l
t
założono zbrojenie w postaci strzemionami dwuciętych
o średnicy
8 (A
sw1
= 1,00 cm
2
). Na długości odcinka dwa razy po
jednym pręcie
20 (A
sw2
= 3,14 cm
2
) pod kątem
= 45
. Odcinek
podzielono na trzy odcinki (rys. __.6)
Odcinek ab
l
t1
= s
a
+ d – a
2
s
a
= min{50 mm ; 0,2
h} = min{50 ; 0,2 450} = 50 mm
s
b
= 0,2
h = 0,2 450 = 90 mm
l
t1
= s
a
+ d – a
2
= 0,05 + 0,412 – 0,038 = 0,424 m
ctg
=
d
,
l
t
9
0
1
=
412
0
9
0
424
0
,
,
,
= 1,143 1 < ctg
< 2
Siła przenoszona przez pręt odgięty – V
Rd32
sin
ctg
ctg
z
s
f
A
V
ywd
sw
Rd
)
(
2
2
2
32
=
=
707
0
)
1
,143
1
(
412
0
9
0
464
0
10
350
10
14
3
3
4
,
,
,
,
,
= 133,06 kN
V
Rd32
= 133,06 kN > 0,5
V
Sd,ab
= 0,5
150,50 = 75,25 kN
Ponieważ strzemiona muszą przenosić co najmniej 50% siły
poprzecznej dlatego należy je zaprojektować na siłę V
Rd31
= 75,25 kN
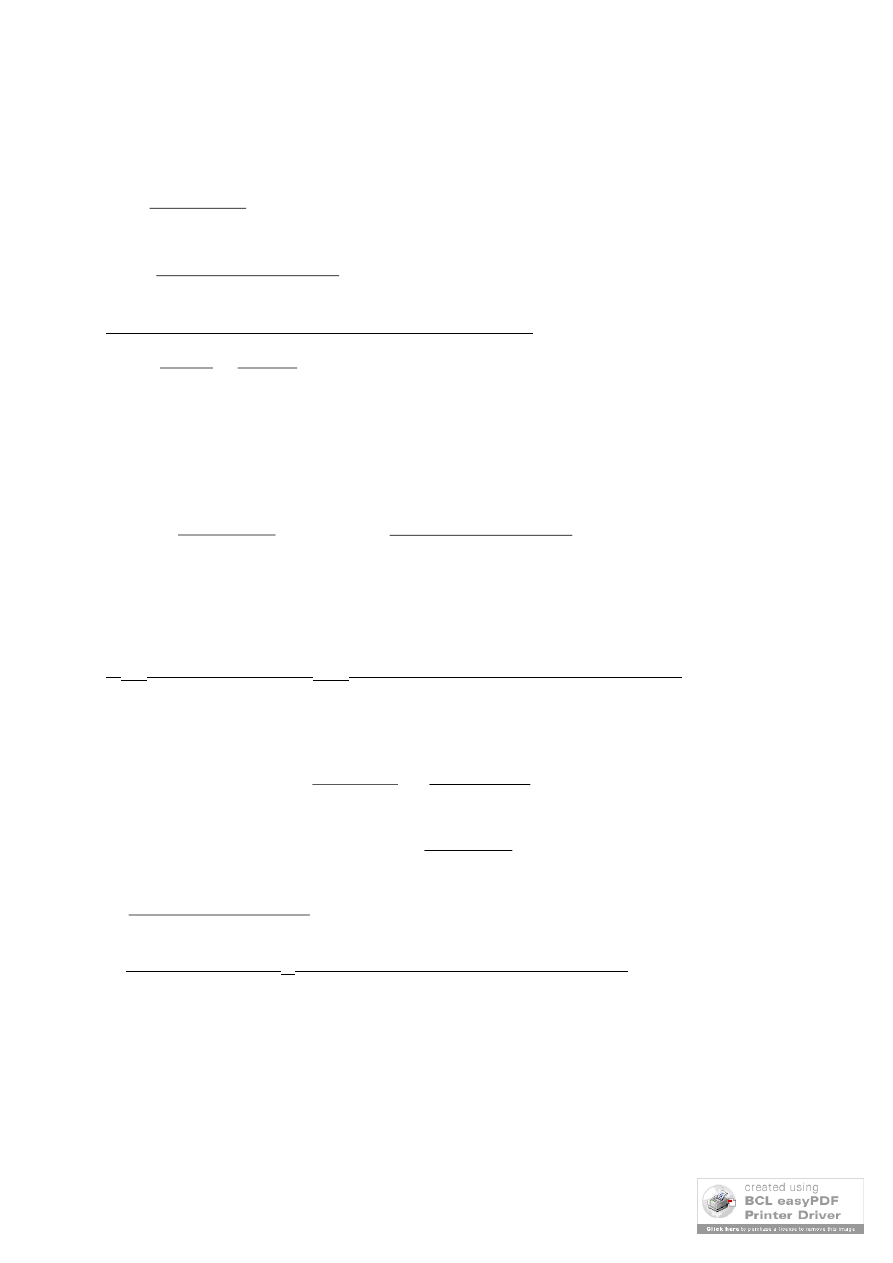
Rozstaw strzemion – s
1
ctg
z
V
f
A
s
Rd
ywd
sw
31
1
1
1
,143
1
412
0
9
0
25
75
10
210
10
00
1
3
4
1
,
,
,
,
s
= 0,118 m
przyjęto strzemiona dwucięte
8 co 100 mm
30
10
00
1
1
1
,
b
s
A
w
sw
w
= 0,33% >
w,min
= 0,18%
Sprawdzenie warunku: V
Sd
V
Rd3
ctg
z
s
f
A
V
ywd
sw
Rd
1
1
1
31
=
,143
1
412
0
9
0
100
0
10
210
10
00
1
3
4
,
,
,
,
=
89,00 kN
V
Rd3
= V
Rd31
+ V
Rd32
= 89,00 + 133,06 = 222,06 kN
V
Rd3
= 222,06 kN > V
Sd,ab
= 150,50 kN – warunek spełniony
Sprawdzenie nośności krzyżulców betonowych: V
Sd
V
Rd2
V
Rd2
=
f
cd
b
w
z
2
1 ctg
ctg
+
cos
z
s
f
A
ywd
sw
2
2
2
=
= 0,528
20 10
3
0,30 0,371
2
143
1
1
143
1
,
,
+
+
707
0
371
0
464
0
10
350
10
14
3
3
4
,
,
,
,
= 582,45 + 62,13 =
= 644,58 kN >> V
Bl
= 184,04 kN – warunek spełniony
Jednocześnie

f
cd
b
w
z
ctg
ctg
ctg
ctg
ctg
2
1
2
= 0,528
20 10
3
0,30
0,371
1
143
1
2
1
143
1
1
143
1
2
,
,
,
= 177,25 kN >
cos
z
s
f
A
V
ywd
sw
Rd
2
2
2
= 62,13 kN
Sprawdzenie nośności zbrojenia głównego przy ścinaniu
ctg
V
V
ctg
V
,
z
M
F
Rd
Rd
*
Sd
*
Sd
td
3
32
5
0
< F
t,max
Siła poprzeczna w licu podpory:
V
Sd
*
= V
Bl
– (g
des,1
+ q
des
)
a
B
=
= 184,04 - (11,24 +41,42)
0,225 = 172,19 kN
Moment zginający w licu podpory:
M
Sd
*
= M
Bmin
+ V
Bp
(0,5 b
wP
) – 0,5
(g
des,1
+ q
des
)
(0,5 b
wP
)
2
=
= –193,53 + 168,75
(0,5 0,45) – 0,5 (11,24 +41,42) (0,5 0,45)
2
=
= 156,89 kNm
1
06
222
06
133
143
1
19
172
5
0
412
0
9
0
89
156
,
,
,
,
,
,
,
,
F
td
= 469,93 kN
F
t,max
= A
s
f
yd
= 12,57
10
–4
350 10
3
= 439,95 kN
F
td
= 469,93 kN < F
t,max
= 439,95 kN – warunek spełniony
Odcinek bc
l
t2
= l
t
– l
t1
= 0,885 – 0,424 = 0,461 m
Na odcinku bc założono zbrojenie jak na odcinku ab.
V
Sd,bc
= V
Bl
– (g
des,1
+ q
des
)
(a
B
+ l
t1
) =
= 184,04 - (11,24 +41,42)
(0,225 + 0,424) = 149,86 kN

Ponieważ V
Sd,bc
V
Sd,ab
(różnica nie przekracza 1%) na odcinku bc
przyjęto zbrojenie jak na odcinku ab: strzemiona dwucięte
8 co
100mm i pręt odgięty
20.
Poz.3.2.5.3. Podpora B z prawej strony
Różnica sił poprzecznych z obu stron podpory B nie przekracza 10%.
Dlatego bez wykonywania szczegółowych obliczeń przyjęto zbrojenie
takie samo jak po lewej stronie podpory B.
Poz.3.2.5.4. Sprawdzenie ścinania między środnikiem i półką dla
półki w strefie ściskanej
Przęsło skrajne
warunek nośności:
ctg
f
s
A
V
z
V
v
yd
f
sf
Rd
Sd
f
Sd
3
długość rozpatrywanego odcinka:
4 ·
x = 0,85 · l
ABeff
= 0,85 · 5,70 = 4,845 m
x = 1,211 m
stosunek siły normalnej przenoszonej przez beton w półce po jednej
stronie środnika do całkowitej siły w rozpatrywanym przekroju:
f
=
AB
eff
AB
eff
b
b
,
,
1
=
27
,
1
5
,
0
)
30
,
0
27
,
1
(
= 0,382
ramię sił wewnętrznych:
z = 0,9 · d = 0,9 · 0,412 = 0,371 m
uśredniona wartość siły poprzecznej na rozpatrywanym odcinku:
V
Sd
= 0,75 · V
A
= 0,75 · 131,87 = 98,90 kN
podłużna siła ścinająca:
v
Sd
=
371
,
0
90
,
98
382
,
0
z
V
Sd
f
= 101,83 kN/m
zbrojenie płyty (dolne) -
8 co 90 mm:
f
sf
s
A
= 5,59 cm
2
ctg
f
s
A
V
yd
f
sf
Rd
3
= 5,59 · 10
-4
· 210 · 10
3
· 2 = 234,78 kN/m

v
Sd
= 101,83 kN/m
V
Rd3
= 234,78 kN/m – warunek spełniony
Ponieważ na drugim odcinku
x przęsła skrajnego występują dużo
mniejsze siły tnące a nośność półki na ścinanie pozostaje bez zmian,
nie przeprowadzano szczegółowych obliczeń.
Przęsło środkowe
x = 0,25 · 0,7 · l
BCeff
= 0,25 · 0,7 · 5,70 = 0,997 m
f
=
BC
eff
BC
eff
b
b
,
,
1
=
10
,
1
5
,
0
)
30
,
0
10
,
1
(
= 0,364
uśredniona wartość siły poprzecznej na rozpatrywanym odcinku:
V
Sd
=
BCeff
Bp
l
x
V
5
,
0
5
,
1
=
70
,
5
5
,
0
997
,
0
5
,
1
75
,
168
= 88,55 kN
v
Sd
=
371
,
0
55
,
88
364
,
0
z
V
Sd
f
= 86,88 kN/m
zbrojenie płyty (dolne) -
8 co 120 mm:
f
sf
s
A
= 4,19 cm
2
ctg
f
s
A
V
yd
f
sf
Rd
3
= 4,19 · 10
-4
· 210 · 10
3
· 2 = 175,98 kN/m
v
Sd
= 86,88 kN/m < V
Rd3
= 175,98 kN/m – warunek spełniony
Poz.3.2.6. Stan graniczny użytkowania – ugięcie
wg tabeli 13 PN-B-03264:2002
przęsło skrajne
moment od charakterystycznych obciążeń długotrwałych:
M
Sdk1,lt
= 0,060
9,84 5,70
2
+ 0,090
35,88 5,70
2
= 124,10 kNm
A
s,prov
= 12,57 cm
2
, d = 0,412 m, l
eff
= 5,70 m
2
41
30
57
12
,
,
d
b
A
w
prov
,
s
= 1,02 % dla
> 1,0 % –
= 0,80
4
3
1
10
57
12
412
0
8
0
10
1
124
,
,
,
,
A
d
M
prov
,
s
lt
,
Sdk
s
= 299,5 MPa

z tablicy 13 odczytano:
d
l
eff
max = 22 (dla
s
= 250 MPa)
d
l
eff
max = 22
5
299
250
,
= 18 >
412
0
70
5
,
,
d
l
eff
= 14
można nie przeprowadzać szczegółowych obliczeń
przęsło środkowe
moment od charakterystycznych obciążeń długotrwałych:
M
Sdk2,lt
= 0,025
9,84 5,70
2
+ 0,075
35,88 5,70
2
= 95,42 kNm
A
s,prov
= 8,04 cm
2
, d = 0,412 m, l
eff
= 5,70 m
2
41
30
04
8
,
,
d
b
A
w
prov
,
s
= 0,65 % –
= 0,85
4
3
1
10
04
8
412
0
85
0
10
42
94
,
,
,
,
A
d
M
prov
,
s
lt
,
Sdk
s
= 335,3 MPa
z tablicy 13 odczytano:
d
l
eff
max = 32 (dla
s
= 250 MPa)
d
l
eff
max = 32
3
335
250
,
= 24 >
412
0
70
5
,
,
d
l
eff
= 14
można nie przeprowadzać szczegółowych obliczeń
Poz.3.2.7. Stan graniczny użytkowania – rysy prostopadłe;
wg tabeli D.1 PN-B-03264:2002
przęsło skrajne
Dla
s
= 300 MPa oraz
= 0,65 % maksymalna średnica prętów przy
której szerokość rozwarcia rys prostopadłych jest ograniczona do w
lim
= 0,3 mm wynosi
max
= 28 mm >
prov
= 20 mm
można nie przeprowadzać szczegółowych obliczeń
przęsło środkowe
Dla
s
= 335 MPa oraz
= 1,02 % maksymalna średnica prętów przy
której szerokość rozwarcia rys prostopadłych jest ograniczona do w
lim
= 0,3 mm wynosi
max
= 18 mm >
prov
= 16 mm

można nie przeprowadzać szczegółowych obliczeń
Poz.3.2.8. Stan graniczny użytkowania – rysy ukośne;
Sprawdzenie przeprowadzono dla najbardziej wytężonego odcinka ab
po lewej stronie podpory B.
w
k
=
ck
s
w
f
E
2
4
< w
lim
= 0,3 mm
Siła poprzeczna od obciążeń charakterystycznych
V
Sdk1,lt
= –0,600 · 9,84
5,70 – 0,6167 39,47 5,70 = –172,40 kN
Siła poprzeczna w odległości d od lica podpory
V
Sdk1,lt,ab
= V
Sdk1,lt
– (g
k
+ q
k,lt
)
(a
B
+ d) =
= 172,40 - (9,84 +39,47)
(0,225 + 0,412) = 139,76 kN
stopień zbrojenia:
strzemiona dwucięte
8 co 100mm:
30
10
00
1
1
1
1
,
b
s
A
w
sw
w
= 0,33%
pręt odgięty
20:
707
0
30
4
46
14
3
2
2
2
,
,
,
sin
b
s
A
w
sw
w
= 0,32%
w
=
w1
+
w2
= 0,33 + 0,32 = 0,65%
naprężenia tnące:
412
0
30
0
76
139
1
,
,
,
d
b
V
w
ab
,
lt
,
Sdk
= 1,131 MPa
1
2
2
2
1
1
1
3
1
w
w
=
1
02
0
7
0
0032
0
008
0
0
1
0033
0
3
1
,
,
,
,
,
,
= 0,520 m
szerokość rys ukośnych:
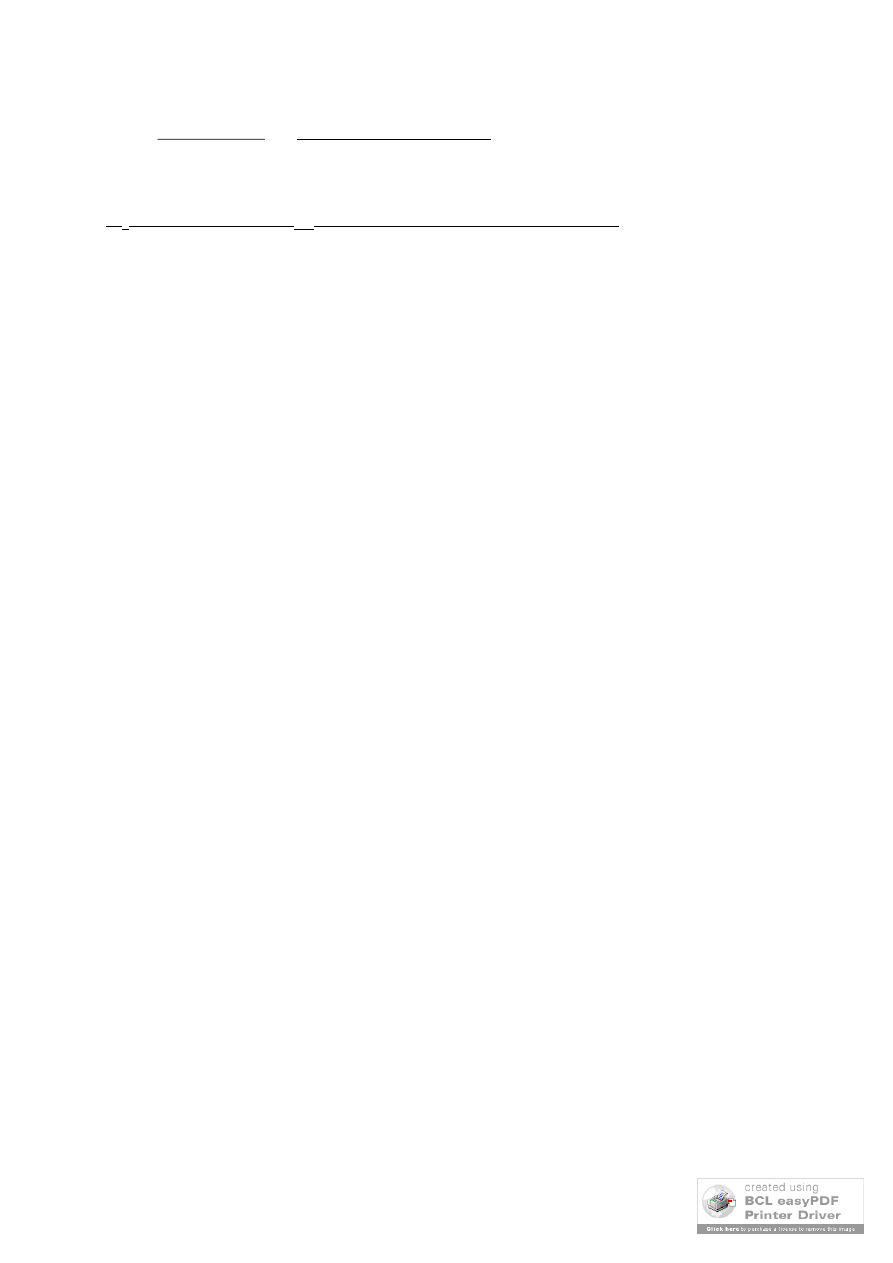
w
k
=
ck
s
w
f
E
2
4
=
30
10
200
0065
0
52
0
131
1
4
3
2
,
,
,
= 0,068 mm
w
k
= 0,068 mm < w
lim
= 0,3 mm – warunek spełniony
Wyszukiwarka
Podobne podstrony:
obliczenia zebro
3 Obliczenia dla stropu gęstożebrowego?rt60 obciążonego ścianką działową prostopadłą żebro podwójnex
6a.ŻEBRO, obc. obliczeniowe
Część obliczeniowa zbrojenie zszywające połączenie żebro podciąg
6a ŻEBRO obc obliczeniowe
Obliczenie belki żelbetowej żebro
cw 06 Zebro obliczenia statyczne i zginanie
Prezentacja JMichalska PSP w obliczu zagrozen cywilizacyjn 10 2007
3 ANALITYCZNE METODY OBLICZANIA PŁYWÓW
Obliczanie masy cząsteczkowej
Obliczanie powierzchni
2 Podstawy obliczania
3 2 Ćwiczenie Obliczanie siatki kartograficznej Merkatora
GEOMETRIA OBLICZENIOWA I
67 Sposoby obliczania sił kształtowania plastycznego ppt
więcej podobnych podstron