Mechanika płynów 1

MECHANIKA PŁYNÓW

Płyn - Każda substancja, która może płynąć, tj. pod wpływem

znikomo małych sił dowolnie zmieniać swój kształt w
zależności od naczynia, w którym się znajduje, oraz może
swobodnie się przemieszczać (przepływać), np. być
przepompowywana przez rury.

Pojęcia płynu nie należy utożsamiać tylko z cieczą, gdyż płynami są nie
tylko ciecze, ale także wszystkie gazy, a nawet takie mieszaniny różnych
faz fizycznych jak piana, emulsja, zawiesina i pasta.

Mierzalną cechą płynów jest ich lepkość, czyli miara oporu
wewnętrznego, jaki stawia płyn poddawany naprężeniom ścinającym
zmuszającym go do przepływu. Tej właściwości płynów jednak nie
weźmiemy pod uwagę w naszych rozważaniach.

W płynach siły nie występują przy deformacji kształtu, ale tylko przy
zmianie objętości. Dlatego siły działające na dowolnie usytuowaną
powierzchnię w płynie, zwane siłami parcia, są do niej prostopadłe.


Parcie - Siła nacisku, jaką płyn wywiera na daną powierzchnię.

Ciśnienie - Stosunek siły parcia na dowolną powierzchnię w płynie do

wielkości tej powierzchni.

Jednostki ciśnienia

paskal

bar

at

atm

Tr

paskal (Pa),

2

1 Pa 1 N/m

=

1

5

10

−

5

1,02 10

−

×

5

0,987 10

−

×

3

7,5 10

−

×

bar,

5

1 bar 10 Pa

=

5

10

1

1,02 0,987

750

atmosfera techniczna (at),

2

1 at 1 kG/cm

=

5

0,981 10

×

0,981

1

0,968

736

atmosfera fizyczna (atm),

1 atm 760 Tr

=

5

1,013 10

×

1,013

1,033

1

760

tor, 1 Tr 1 mm Hg

=

133

3

1,33 10

−

×

3

1,36 10

−

×

3

1,32 10

−

×

1

Mechanika płynów 2

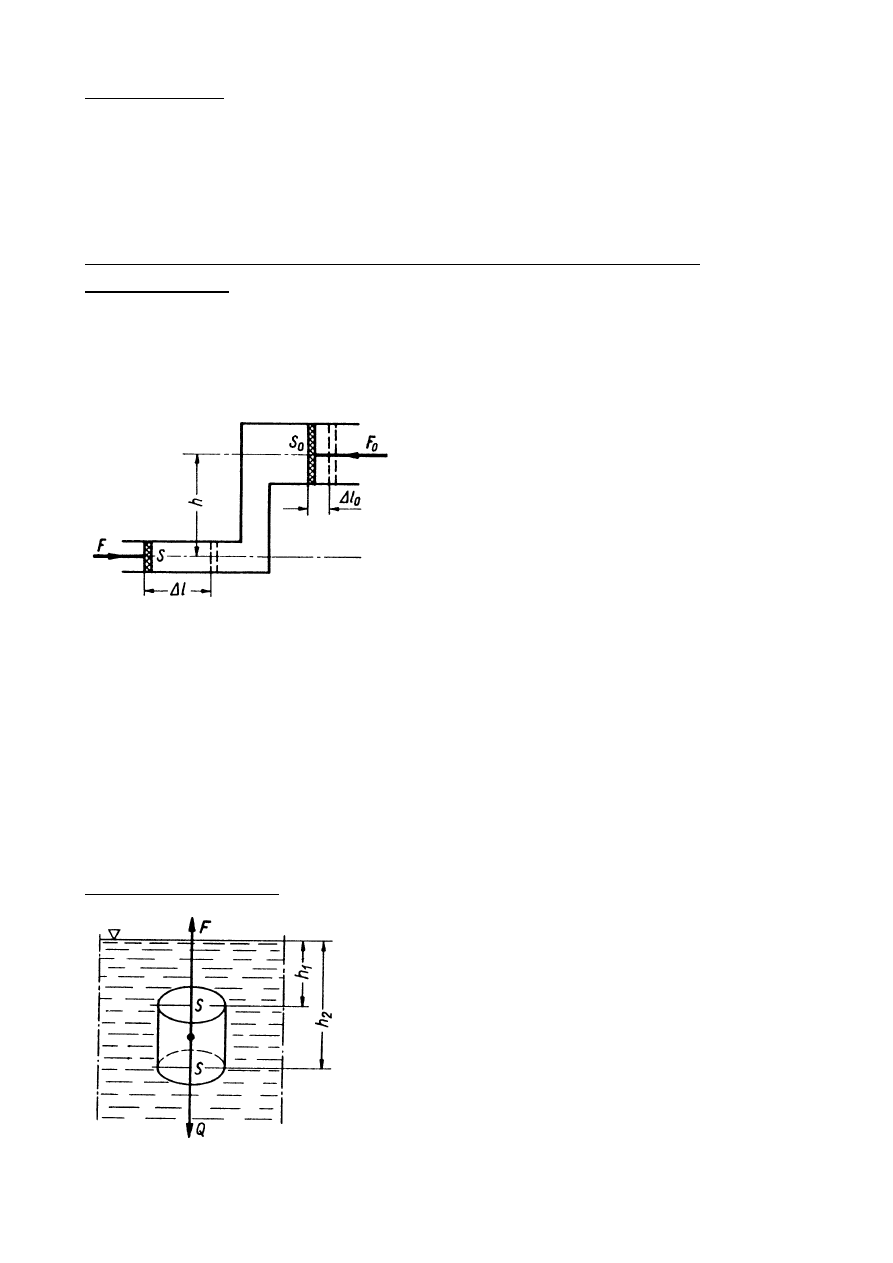
Prawo Pascala

Ciśnienie zewnętrzne wywierane na płyn jest przenoszone we
wszystkich kierunkach jednakowo.

Ciśnienie na pewnej głębokości w cieczy znajdującej się w polu
grawitacyjnym

Grawitacja wywołuje zmianę ciśnienia w zależności od głębokości - im
niżej tym większe ciśnienie. Wzrost ciśnienia wywołujany jest naciskiem
(ciężarem) ze strony słupa cieczy położonego nad punktem pomiaru.

Przyjmijmy:

ρ

- gęstość cieczy

g - przyspieszenie ziemskie

0

p - ciśnienie na poziomie górnym

p - ciśnienie na głębokości

h

Zachodzi:

0

0

0

0

0

0

0

0

0

0

F l

F

l

S

l

g h

F

p S

p

p

g h

F

p S

S l

S

l

ρ

ρ

∆ − ∆ = ∆





=

 ⇒ = +



=





∆ = ∆



Prawo Archimedesa

Siły działające na boczne ścianki cylindra są
skierowane prostopadle do ścianek i znoszą
się. Siły działające na dolną i górną
powierzchnię:

2

0

2

(

)

S p

S p

gh

ρ

=

+

1

0

1

(

)

S p

S p

gh

ρ

=

+

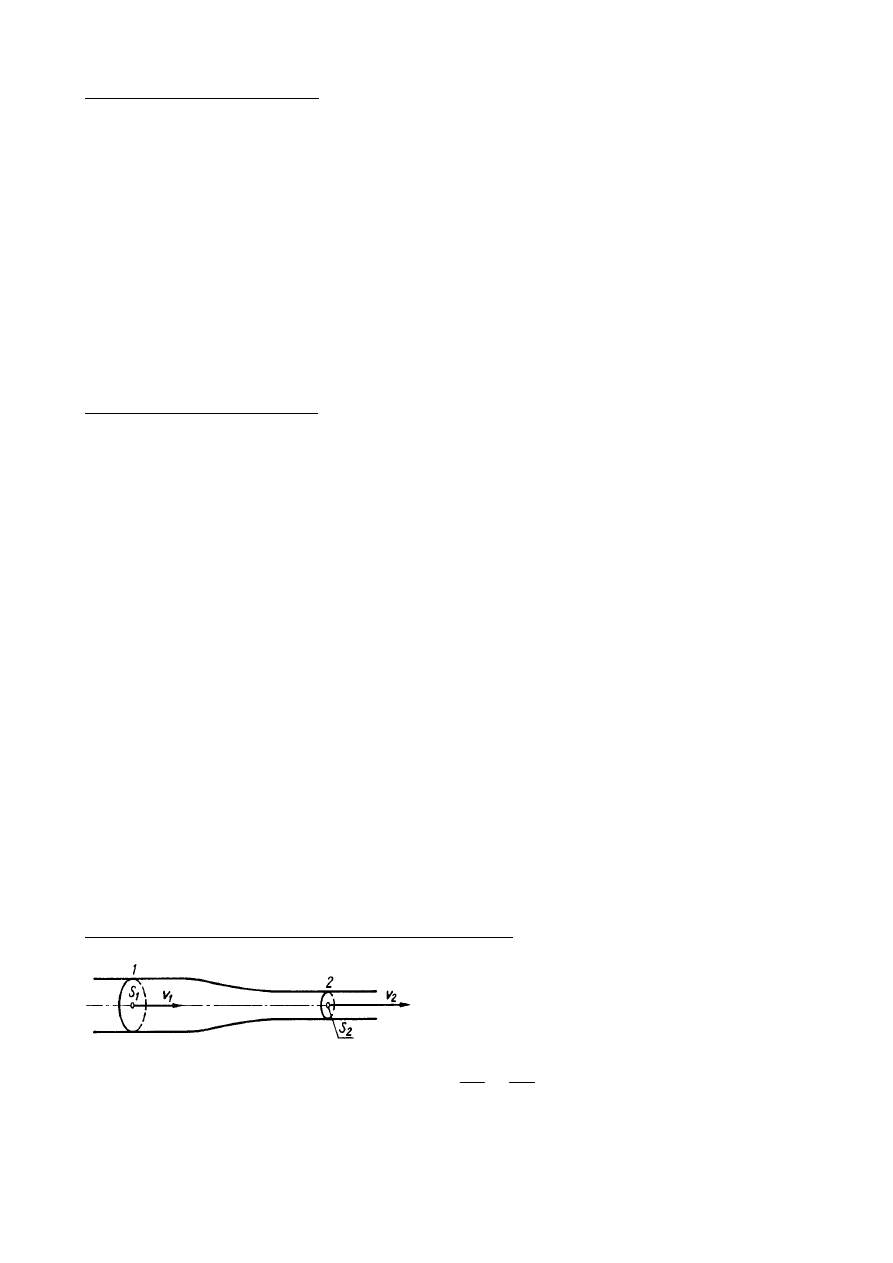
Mechanika płynów 3

Prawo Archimedesa, cd.

2

0

2

(

)

S p

S p

gh

ρ

=

+

,

1

0

1

(

)

S p

S p

gh

ρ

=

+

Siła wypadkowa:

0

2

0

1

(

)

(

)

W

S p

gh

S p

gh

gV

ρ

ρ

ρ

=

+

−

+

=

,

2

1

(

)

V

S h

h

=

−

Na ciało zanurzone w cieczy działa siła wyporu równa ciężarowi
wypartej przez to ciało cieczy.

Przepływ (ruch) płynów

Strumień, struga - Uporządkowany ruch cząstek płynu poruszających

się jednym kierunku

Przepływ

-

laminarny

Przepływ jest laminarny, jeśli strumień płynu może
być rozłożony na warstwy, w których wektor
prędkości jest równoległy do kierunku przepływu.
Tory sąsiednich warstw płynu są w tym przypadku
równoległe. Nie występuje mieszanie się sąsiednich
warstw płynu.

Przepływ

-

turbulentny

W przepływie turbulentnym zachodzi mieszanie się
poszczególnych warstw płynu.

Przepływ ustalony,-
(stacjonarny)

W danym punkcie przestrzeni prędkość
przepływającego płynu nie zależy od czasu.

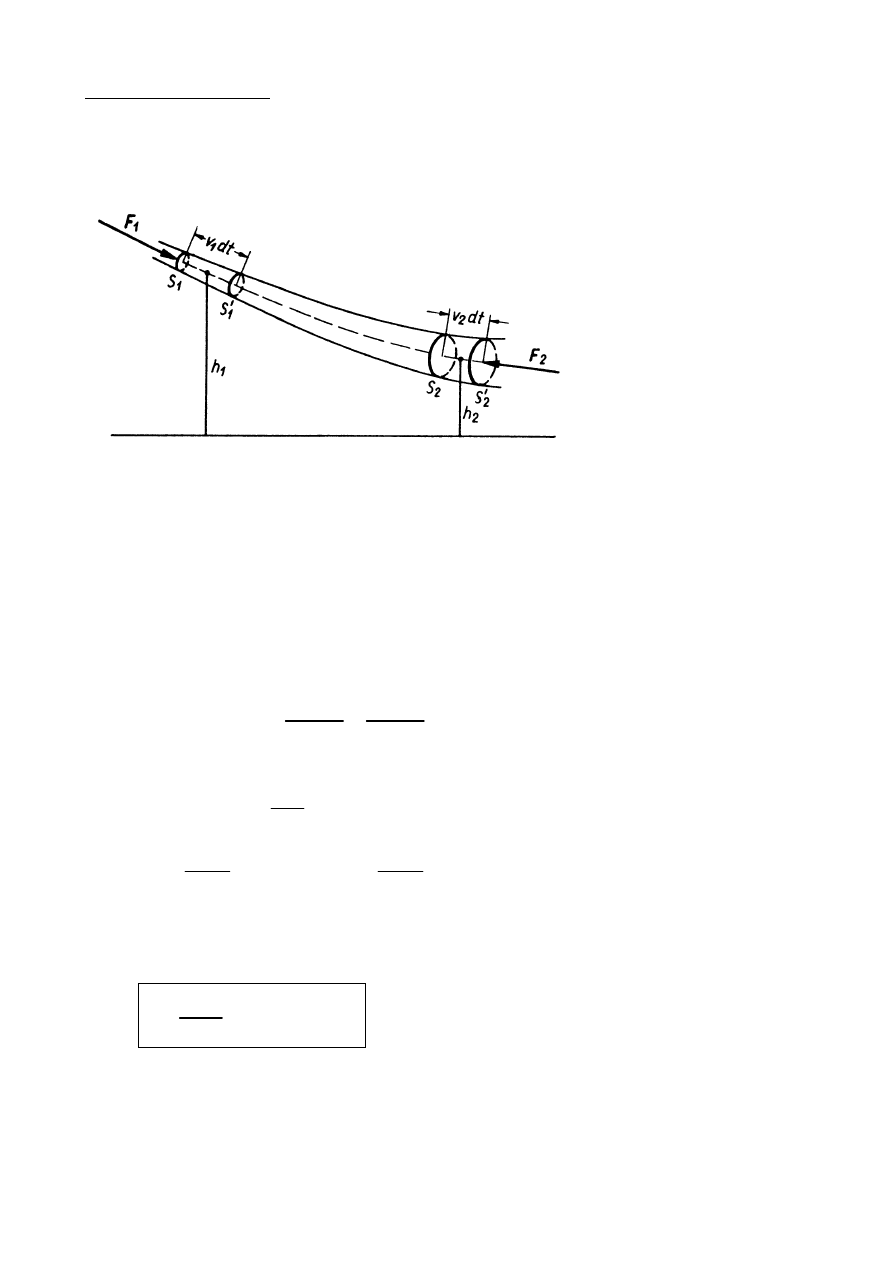
Równanie ciągłości dla cieczy nieściśliwych

Załóżmy, że przepływ jest stacjonarny.
Przez przekrój "1" i "2" w czasie

dt

przepływają te same objętości cieczy.

1 1

2

2

S

dt

S

dt

υ

υ

=

⇒

1

2

2

1

S

S

υ

υ

=

Prędkości cieczy w strudze są odwrotnie proporcjonalne do
powierzchni przekrojów strugi.

Mechanika płynów 4

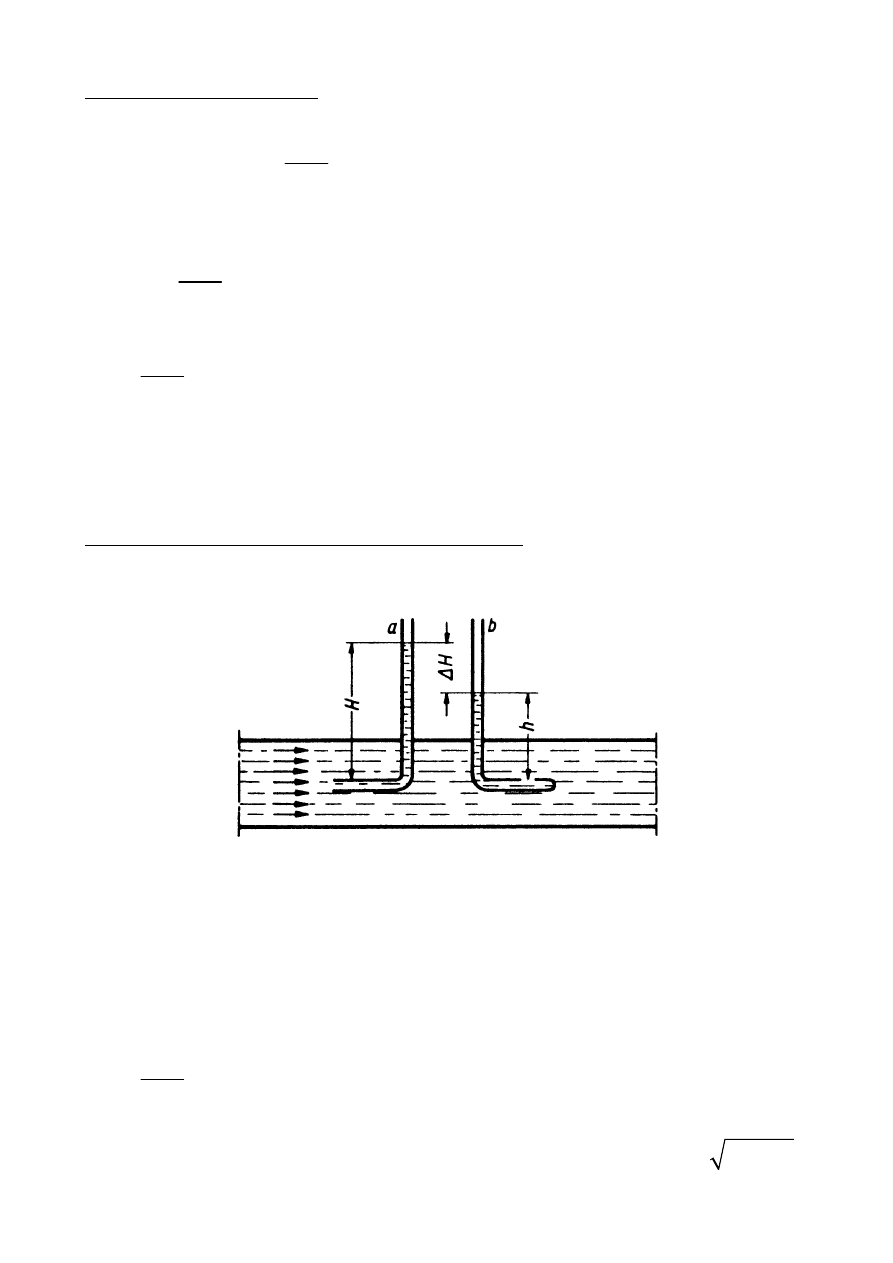
Prawo Benoulliego

Załóżmy, że przepływ cieczy doskonałej (w której nie występują siły
lepkości) następuje od przekroju

1

S do przekroju

2

S

Siły parcia:

1

1

1

F

p S

=

2

2

2

F

p S

=

Obliczmy pracę sił parcia w odcinku czasu

dt

1 1

2

2

1

1 1

2

2

2

1

2

(

)

p

dA

F

dt

F

dt

p S

dt

p S

dt

p

p

dV

υ

υ

υ

υ

=

−

=

−

=

−

W nieobecności sił lepkości praca ta równa jest zmianie energii
kinetycznej i potencjalnej mas

dm

cieczy zawartej między przekrojami

1

1

i

S

S

′

oraz

2

2

i

S

S

′

,

p

k

p

dA

dE

dE

=

+

, czyli

2

2

2

1

1

2

2

1

(

)

2

2

dm

dm

p

p

dV

dm g h

dm g h

υ

υ

−

=

−

+

−

Uwzględniając, że

dm

dV

ρ

=

, gdzie

ρ

jest gęstością cieczy, otrzymujemy

2

2

1

2

1

1

2

2

2

2

p

g h

p

g h

ρυ

ρυ

ρ

ρ

+

+

=

+

+

Ogólnie możemy więc napisać

2

const

2

p

gh

ρυ

ρ

+

+

=

równanie

Bernoulliego

Suma ciśnienia oraz energii kinetycznej i potencjalnej jednostki
objętości ustalonego przepływu cieczy doskonałej jest wielkością
stałą.

Mechanika płynów 5

Prawo Bernoulliego, cd.

Otrzymaliśmy

2

const

2

p

gh

ρυ

ρ

+

+

=

W przypadku pomijalnie małych zmian wysokości przepływu zachodzi:

2

0

const

2

p

p

ρυ

+

=

=

(inna postać równania Bernoulliego)

p -

ciśnienie statyczne

2

2

ρυ

- ciśnienie dynamiczne

0

p -

ciśnienie całkowite

Pomiar ciśnienia dynamicznego i statycznego

Pomiary tych ciśnień wykonuje się za pomocą układu rurek Pitota.









Rurki są zgięte pod kątem prostym, a części rurek zanurzone w cieczy są
ustawione wzdłuż strumienia. Powierzchnia otworu rurki a , służącej do
pomiaru ciśnienia całkowitego, jest skierowana prostopadle do wektora
prędkości przepływającej cieczy. Powierzchnia otworu rurki

b

jest do tego

wektora równoległa. Różnica wysokości H

∆

wskazań obu rurek

umożliwia wyznaczenie ciśnienia dynamicznego

2

0

2

p

p

g H

ρυ

ρ

=

− =

∆

Można stąd wyznaczyć prędkość przepływającej cieczy:

2 g H

υ

=

∆

.