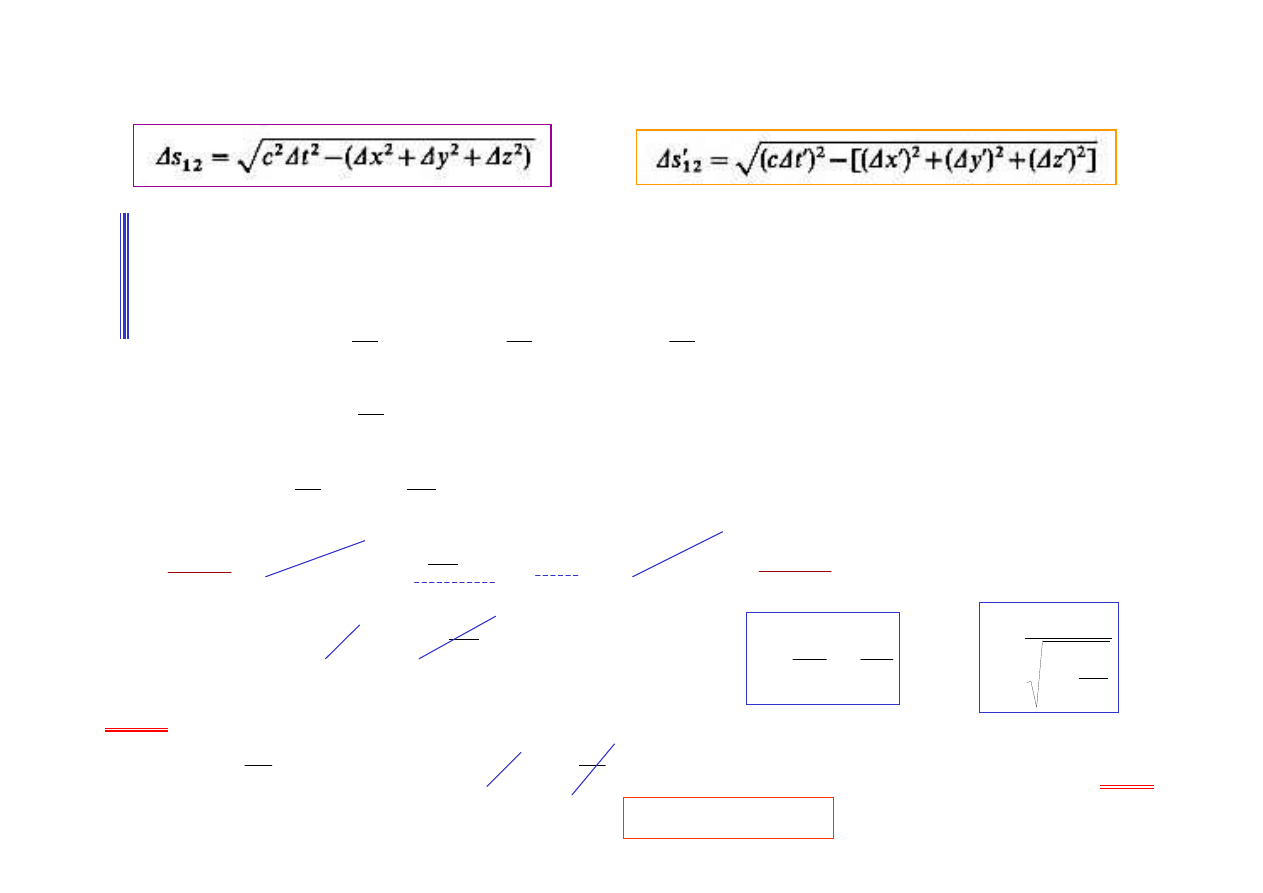
)

t

u

x

(

t

u

x

ut

x

ut

x

)

ut

x

(

)

ut

x

(

'

x

'

x

'

x

1

1

2

2

1

1

2

2

1

2

∆∆∆∆

−−−−

∆∆∆∆

γγγγ

====

∆∆∆∆

γγγγ

−−−−

∆∆∆∆

γγγγ

====

γγγγ

++++

γγγγ

−−−−

γγγγ

−−−−

γγγγ

====

−−−−

γγγγ

−−−−

−−−−

γγγγ

====

−−−−

====

∆∆∆∆

y

y

y

'

y

'

y

'

y

1

2

1

2

∆∆∆∆

====

−−−−

====

−−−−

====

∆∆∆∆

z

z

z

'

z

'

z

'

z

1

2

1

2

∆∆∆∆

====

−−−−

====

−−−−

====

∆∆∆∆

)

x

c

u

t

(

)

x

c

u

t

(

)

x

c

u

t

(

'

t

'

t

'

t

2

1

2

1

2

2

2

1

2

∆∆∆∆

−−−−

∆∆∆∆

γγγγ

====

−−−−

γγγγ

−−−−

−−−−

γγγγ

====

−−−−

====

∆∆∆∆

2

12

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

12

)

s

(

z

y

x

t

c

z

y

x

1

c

t

z

y

x

)

c

u

1

(

c

t

z

y

x

)

u

c

(

t

)

'

s

(

∆∆∆∆

====

∆∆∆∆

−−−−

∆∆∆∆

−−−−

∆∆∆∆

−−−−

∆∆∆∆

====

∆∆∆∆

−−−−

∆∆∆∆

−−−−

∆∆∆∆

−−−−

γγγγ

∆∆∆∆

γγγγ

====

∆∆∆∆

−−−−

∆∆∆∆

−−−−

∆∆∆∆

−−−−

−−−−

∆∆∆∆

γγγγ

====

====

∆∆∆∆

−−−−

∆∆∆∆

−−−−

∆∆∆∆

−−−−

−−−−

∆∆∆∆

γγγγ

====

∆∆∆∆

∆∆∆∆

s’

12

=

∆∆∆∆

s

12

Zadanie:

sprawdzić, czy ma miejsce równość:

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

4

2

2

2

2

2

2

2

2

2

2

2

2

2

2

12

z

y

)

c

u

1

(

x

)

u

c

(

t

z

y

t

u

t

x

u

2

x

x

c

u

x

t

u

2

t

c

z

y

)

t

u

t

x

u

2

x

(

)

x

c

u

x

t

c

u

2

t

(

c

z

y

)

t

u

x

(

)

x

c

u

t

(

c

)

'

s

(

∆∆∆∆

−−−−

∆∆∆∆

−−−−

−−−−

∆∆∆∆

γγγγ

−−−−

−−−−

∆∆∆∆

γγγγ

====

====

∆∆∆∆

−−−−

∆∆∆∆

−−−−

∆∆∆∆

γγγγ

−−−−

∆∆∆∆

∆∆∆∆

γγγγ

++++

∆∆∆∆

γγγγ

−−−−

∆∆∆∆

γγγγ

++++

∆∆∆∆

∆∆∆∆

γγγγ

−−−−

∆∆∆∆

γγγγ

====

====

∆∆∆∆

−−−−

∆∆∆∆

−−−−

∆∆∆∆

++++

∆∆∆∆

∆∆∆∆

−−−−

∆∆∆∆

γγγγ

−−−−

∆∆∆∆

++++

∆∆∆∆

∆∆∆∆

−−−−

∆∆∆∆

γγγγ

====

====

∆∆∆∆

−−−−

∆∆∆∆

−−−−

∆∆∆∆

−−−−

∆∆∆∆

γγγγ

−−−−

∆∆∆∆

−−−−

∆∆∆∆

γγγγ

====

∆∆∆∆

=

?

2

2

c

u

1

1

−−−−

====

γγγγ

2

2

2

1

c

u

1

γγγγ

====

−−−−

bo

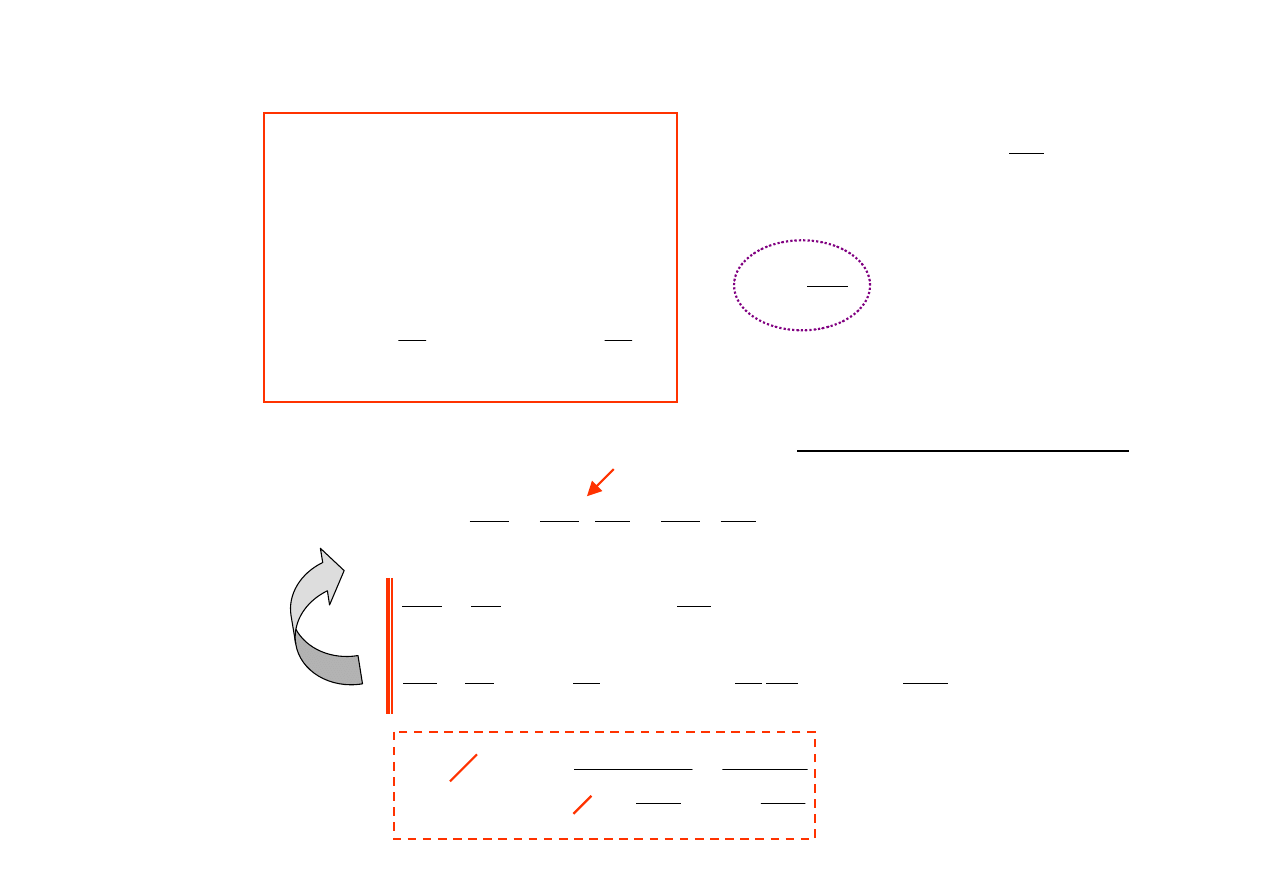
Relatywistyczne dodawanie prędkości

Obliczamy pochodne dla x’=

γγγγ

(x – ut) oraz t’=f(t) z transformacji Lorentza

O’

→

→

→

→

O

O

→

→

→

→

O’

x’ =

γγγγ

(x − ut)

x =

γγγγ

(x’ + ut’)

y’ = y

y = y’

z’ = z

z = z’

t’ =

t =













−−−−

γγγγ

x

c

u

t

2













++++

γγγγ

'

x

c

u

'

t

2

((((

))))

u

v

u

dt

dx

)]

ut

x

(

[

dt

d

dt

'

dx

x

−−−−

γγγγ

====













−−−−

γγγγ

====

−−−−

γγγγ

====













−−−−

γγγγ

====













−−−−

γγγγ

====

























−−−−

γγγγ

====

2

x

2

2

c

uv

1

dt

dx

c

u

1

x

c

u

t

dt

d

dt

'

dt

2

x

x

2

x

x

x

c

uv

1

u

v

)

c

uv

1

(

1

)

u

v

(

'

v

−−−−

−−−−

====

−−−−

γγγγ

⋅⋅⋅⋅

−−−−

γγγγ

====

dt

'

dt

:

dt

'

dx

'

dt

dt

dt

'

dx

'

dt

'

dx

'

v

x

====

⋅⋅⋅⋅

====

====

W układzie O:

W układzie O’:

t’ = f(t)

dt

dx

v

x

====

)

v

(

f

'

v

'

dt

'

dx

'

v

x

x

x

?

====







→

→

→

→









====

Tr

an

sf

or

m

ac

ja

Lo

re

nt

za

Relatywistycznie:

Klasycznie:

v’=v

−−−−

u