PARA SIŁ Para sił to układ 2 sił równoległych równych, co do wartości i mających przeciwne zwroty. Wektor mom pary sił jest wektorem prostopadłym do płaszczyzny, w której leży para sił. Jest to wektor swobodny, ponieważ nie zależy od pkt na płaszczyźnie względem, którego jest obliczana. Parę sił można przenieść dowolnie w płaszczyźnie ich działania. 2 pary sił leżące w jednej płaszczyźnie i mające równe mom są sobie równoważne i mogą być zamieniane jedna na drugą. REDUKCJA SIŁ DO PKT Przesunięciu siły z jednego pkt do 2 towarzyszy dodanie mom siły zależnego od pkt końcowego przesunięcia. Wektor mom pary sił jest prostopadły do płaszczyzny odpowiedniej pary sił. REDUKCJA UKŁ SIŁ DO PKT Każdą siłę ukł przenosi się do śr redukcji (pkt O) wprowadzając odpowiedni wektor mom. Po geometrycznym dodaniu wektorów sił i wektorów mom otrzymujemy 2 wektory wypadkowe. Pary sił zastępujemy odpowiednimi mom par. po dodaniu wszystkich wektorów sił otrzymujemy gł wektor sił.
Po dodaniu wszystkich wektorów mom otrzymujemy wektor gł mom.
W ogólnym przypadku gł wektor sił i wektor gł mom leżą na kierunkach o dowolnym nachyleniu względem siebie. NIEZMIENNIKI UKŁ SIŁ Wektor gł siły, który nie zależy od wyboru śr redukcji (wektor mom gł) zależy od wyboru pkt, O, ponieważ ze zmianą śr redukcji zmieniają się również mom poszczególnych sił. Iloczyn skalarny gł wektora sił i wektora gł mom.
ROZWIĄZ ZŁOŻONYCH UKŁ PŁASKICH (USTROJÓW) Ustrojem nazywamy ukł ciał połączonych ze sobą wiązaniami. Warunek statecznej wyznaczalności ustroju:
z-liczba składowych reakcji zew, w-liczba składowych reakcji wew, n-liczba ciał tworzących ustrój, m=0 (ustrój statecznie wyznaczalny), m>0 (ustrój przesztywniony), m<0 (ustrój chwiejny). Metoda przecięć-rozwiązując tą metodą izolujemy poszczególne ciała z ustroju. Polega to na zerwaniu więzów i zastąpieniu ich odpowiednimi reakcjami oraz wykorzystaniu warunków równowagi dla każdego ciała z osobna. Metoda rozwiązania na podstawie dodatkowego warunku równowagi, jakiego dostarcza przegub. W przypadku ustrojów, dla których możliwy jest przekrój układów przez przegub, w wyniku, czego ustrój dzieli się na 2 niezależne części, dysponujemy dodatkowym warunkiem równowagi. Suma algebraiczna mom wszystkich sił działających po jednej stronie przegubu względem tego przegubu jest równa 0. KLASYFIKACJA RUCHÓW BRYŁ

Rodzaj ruchu	Przesunięcie				Obrót
		x	y	z	X		y	z
Postępowy charakteryzuje się stałym kierunkiem wektora prędkości wszystkich punktów bryły	+	-	-	-		-	-
Obrotowy występuje w nim stała oś obrotu, a leżący na niej wektor prędkości obrotowej może mieć wartość dowolną	-	-	-	-		-	+
Śrubowy w tym ruchu ruch postępowy jest nałożony na ruch obrotowy przy zachowaniu stałej osi obu wektorów prędkości	-	-	+	-		-	+
Równoległy ruch odbywający się po linii krzywej, przy czym tory wszystkich punktów są do siebie przystające	+	+	+	-		-	-
Płaski w ruchu tym wszystkie wektory prędkości są równoległe do stałej płaszczyzny	+	+	-	-		-	+
Kulisty w ruchu tym jeden punkt bryły jest stale nieruchomy	-	-	-	+		+	+
Ogólny w ruchu tym bryła zmienia swoje położenie przy 6 stopniach swobody, ruch ten możemy traktować jako złożony	+	+	+	+		+	+

CAŁKOWANIE RÓWNAŃ RÓŻNICZKOWYCH RUCHU PKT MAT Z II prawa Newtona wektorowe równanie różniczkowe ruchu pkt mat o masie m, na który działa siła wypadkowa F przedstawia się następująco: 1)
,
. Rzutując równanie 1) na osie ukł odniesienia otrzymamy 3 rów skalarne: 2)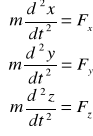
,
,
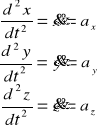
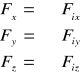
. F_z,F_y,F_z to długości składowych wektora siły F; a_x,a_y,a_z to długości składowe wektora przyspieszenia. Równania 2) są równaniami różniczkowymi (dynamicznymi) ruchu pkt mat. Rozwiązanie tych równań na drodze dwukrotnego całkowania pozwala na określenie nieznanych funkcji zależnych od czasu w postaci: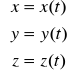
, funkcje te stanowią kinematyczne rów ruchu. Znalezienie rozwiązania ogólnych ukł równań różniczkowych 2) jest na ogół trudne i tylko w niektórych szczególnych przypadkach rozwiązania te można wyrazić za pomocą funkcji elementarnych

---