1)Podział mechaniki-Mech Płynów i Mech Ciała Stalego[Mechanika ciała odkształcalnego ,,wytrzymałość materiałów” i Mechanika ciała nieodkształcalnego ,,mechanika ogólna”(statyka,dynamika,kinematyka)]
Mechanika-zajmuje się ustalaniem ogólnych praw ruchu i równowagi ciał materialnych oraz zastosowaniem tych praw do pewnych wyidealizowanych schematów ciał materialnych, takich jak punkt materialny i ciało doskonale sztywne
Wytrz. Materiałów- jest nauką stosowaną, zjmującą się badaniem zjawisk występujących w ciałach rzeczywistych (odkształcalnych). Głównym jej zadaniem jest określenie wytrzymałości i sztywności urządzenia, konstrukcji lub elementu maszyny, czyli określenie odporności na zniszczenie.
Kinematyka-zajmuje się ilościowym badaniem ruchu ciał, bez uwzględniania czynników fizycznych wywołujących ten ruch, jest więc pewnego rodzaju geometrią ruchu w czasie
Dynamika - dzieli się na statykę i kinetykę.
Statyka - jest szczególnym przypadkiem dynamiki polegającym na tym,
że siły działające na ciało materialne znajdują się w
równowadze, co oznacza, że ciało jest w spoczynku lub porusza
się ruchem jednostajnym prostoliniowym.
Kinetyka - jest tym działem dynamiki, który ustala prawa zachowania się
ciał materialnych, na które działa niezrównoważony układ sil.
Ciała materialne znajdują się wtedy w ruchu.
2)Prawa ruchu Newtona-Pr. I:Każde ciało trwa w stanie spoczynku lub ruchu jednostajnego prostoliniowego, dopóki siły na nie działające tego stanu nie zmienią. Pr. II: Zmiana ilości ruchu (czyli pędu lub impulsu) jest proporcjonalna względem siły działającej i ma kierunek prostej, wzdłuż której ta siła działa. Pr. III: Każdemu działaniu towarzyszy równe i przeciwnie zwrócone przeciwdziałanie, czyli siły wzajemnych oddziaływań dwóch ciał są zawsze równe i skierowane przeciwnie. Pr. IV: Jeżeli na pkt materialny o masie m działa jednocześnie kilka sił, to każda z nich działa niezależnie, a wszystkie razem działają tak, jak jedna siła równa wektorowej sumie wektorów danych sił. Pr. V (grawitacji):Każde dwa pkt materialne przyciągają się wzajemnie z siłą wprost proporcjonalną do iloczynu ich mas (m1, m2) i odwrotnie proporcjonalną do kwadratu odległości r między nimi. Kierunek siły leży na prostej łączącej te punkty. P=(k*m1*m2)/r2 , k-stała grawitacji
3)Rodzaje sił-Masowe lub objętościowe(proporcjonalne do masy rozłożonej w objętości, działające na wszystkie punkty ciała) Powierzchniowe(powstające przy bezpośrednim zetknięciu się jednego ciała z drugim) Zewnętrzne(pochodzące od pkt lub ciał nie należących do rozpatrywanego układu mechanicznego) Wewnętrzne (pochodzące od punktów lub ciał należących do rozpatrywanego układu mech) Czynne,,obciążenia zewnętrzne”(mogące wywołać ruch) Bierne(powstające pod wpływem sił czynnych)
![]()
4)Zasady statyki-1.Działanie dwóch sił P1 i P2 można zastąpić działaniem jednej siły R, której wartość wynosi:
2.Jeśli do ciała przyłożone są dwie siły, to równoważą się one tylko wtedy, gdy mają tę samą linię działania, wartości liczbowe i przeciwne zwroty.
3.Skutek działania dowolnego układu sił, przyłożonego do ciała nie zmieni się, jeśli do tego układu dodamy lub odejmiemy dowolny układ równoważących się sił P2 i -P2 czyli tzw. układ zerowy.
4.Zasada zesztywnienia-Jeżeli ciało odkształcone znajduje się w równowadze pod działaniem pewnego układu sił, to również pozostanie w równowadze ciało
doskonale sztywne (nieodkształcalne) identyczne z poprzednim, pod działaniem tego samego układu sił.
5.Zasada działania i przeciwdziałania-Każdemu działaniu towarzyszy równe co do wartości o przeciwnym zwrocie i leżące na tej samej prostej przeciwdziałanie.
6. Zasada oswobodzenia od więzów-Każde ciało można oswobodzić z więzów, zastępując ich działanie reakcjami, a następnie rozpatrując jako ciało swobodne, znajdujące się pod działaniem sił czynnych i biernych (reakcji więzów)
Stopniem swobody (l) - nazywa się możliwość wykonania ruchu ciała
niezależnego od innych ruchów.
Punkt materialny - ma na płaszczyźnie dwa, a w przestrzeni trzy stopnie
swobody.
Ciało doskonale sztywne - ma na płaszczyźnie
Rozróżniamy trzy rodzaje wektorów:
- wektory związane z punktem ( wektory uczepione)
- wektory związane z prostą (wektory ślizgające się, wektory posuwne)
- wersor (wektor jednostkowy) \a0\= a0 = 1
- wersory związane z osiami układu prostokątnego
![]()
![]()
5)Działania na wektorach-Suma: ![]()
, Iloczyn skalarny: ![]()
(analityczne wyrażenie iloczynu skalarnego wektorów, , ),
![]()
![]()
Iloczyn wektorowy: ![]()
, (analityczne wyrażenie iloczynu wektorowego dwóch wektorów , )
![]()
6)Redukcja zbieżnego układu sił-Układ sił, których linie działania przecinają się w jednym punkcie. Płaski lub przestrzenny ukł sił zbieżnych przyłożonych do jednego punktu 0 można zastąpić jedną siłą wypadkową przyłożoną w tym punkcie i równą sumie geometrycznej tych sił. Ukł sił można zredukować za pomocą metody: równoległoboku, wieloboku.
7)Równowaga zbieżnego układu sił-zbieżny układ sił jest w równowadze jeżeli wielobok sił tego układu jest zamknięty. Jest to tzw. wykreślny warunek równowagi sił zbieżnych.
8)Analityczne składanie sił zbieżnych-Analityczne warunki równowagi zbieżnego układu sił:
![]()
![]()
![]()
9)Moment siły względem punktu-nazywamy odłożony z punktu 0 wektor Mo, równy iloczynowi wektorowemu promienia wektora r i wektora siły P ![]()
Twierdzenie Varignona.-Moment siły wypadkowej P przestrzennego układu sił zbieżnych względem dowolnego punktu 0 jest równy sumie geometrycznej
momentów tych sił względem tego samego punktu.
10)Wypadkowa sił równoległych-wartość siły wypadkowej równa się sumie lub różnicy (w zależności od zwrotu wektora) wartości sił składowych.
![]()
![]()
11)Redukcja płaskiego układu sił-Dowolny ukł sił, działających na ciało sztywne, o liniach działania leżących w jednej płaszczyźnie możemy zastąpić wektorem głównym R, przyłożonym do dowolnie wybranego środka redukcji O oraz momentem głównym Mo względem środka redukcji O. Wektor główny R jest równy sumie geometrycznej wszystkich sił układu. Wartość wektora głównego oraz kąt α, jaki wektor ten tworzy z osią Ox, wyznaczamy ze wzorów
12)Redukcja układu sił metodą wieloboku sznurowego- zbieżny układ sił jest w równowadze jeżeli wielobok sił tego układu jest zamknięty. Jest to tzw. wykreślny warunek równowagi sił zbieżnych.
![]()
13)Rozwiązywanie belek metodą analityczną i graficzną- Analityczna-reakcje podpór w belkach obciążonych płaskim układem sił wyznaczamy z 3 równań równowagi:1.Suma rzutów wszystkich sił na oś x musi być równa zero ΣPix=0, 2.ΣPiy=0, 3.Suma momentów względem dowolnie wybranego bieguna musi być równa zero ΣMiA=0
14)Charakterystyka kratownic płaskich-rzeczywiste kratownice charakteryzowane są przez: Kształt obrysu zew, Ukł prętów wew, Sposób podparcia kratownicy, Sposób obciążenia, Kształt i wymiary przekrojów poprzecznych prętów.
15)Rozwiązywanie kratownic metodą równoważenia węzłów- polega na oddzielnym rozpatrzeniu każdego węzła kratownicy, jako płaskiego zbieżnego ukł sił, dla którego zapisujemy warunki równowagi. Należy:1.Sprawdzić warunek statycznej wyznaczalności p=2w-3. 2.Narysować zwroty sił wewnętrznych w węzłach(wstępnie zakładamy,że wszystkie pręty są rozciągane, w przypadku ściskanych otrzymamy ujemne wartości sił) 3.Zapisujemy warunki równowagi sił zewnętrznych w celu wyznaczenia reakcji podpór. 4.Zapisujemy warunki równowagi dla kolejnych węzłów, zaczynając od tych, w których występują tylko dwie niewiadome siły. 5.Rozwiązujemy układy równań i wyznaczamy siły wewnętrzne w prętach.
16)Rozwiązywanie kratownic za pomocą planu Cremony- jest to metoda wykreślną polegającą na budowaniu wieloboków sił dla poszczególnych węzłów, zaczynając od węzła, w którym połączone są dwa pręty. Zasady postępowania: 1.Przyjmujemy skalę sił i skalę dł, po czym wykreślamy kratownicę w przyjętej skali dł. 2.Wszystkie siły zewnętrzne i reakcje podpór rysujemy na zewnątrz konturu kratownicy. 3.Wyznaczamy wykreślnie reakcje podpór. Rysujemy wielobok sił zewnętrznych i reakcji podpór kratownicy. Siły rysujemy w skali i w kolejności 4.Dla kolejnych węzłów rysujemy wielobok sił, składający się z
sił zewnętrznych, reakcji i sił wewnętrznych. Siły rysujemy w
kolejności ich występowania. Pręty i odpowiadające im siły
numerujemy. 5.Wykreślanie wieloboku sił zaczynamy od węzła, w którym występują tylko dwie siły wew. Rozpoczynając od znanej siły zewn, wyznaczamy zwroty sił wew i zaznaczamy je na rysunku kratownicy. W przypadku gdy siła jest skierowana do węzła, to pręt jest ściskany, natomiast gdy od węzła, rozciągany.
17)Rozwiązywanie kratownic metodą Rittera-Jeśli w kratownicy nie ma wiązań 2 prętowych, stosujemy metodę Rittera, która służy do wyznaczenia sił wewnętrznych w 3 prętach, których osie nie przecinają się w jednym punkcie i nie są równoległe. Tok postępowania: 1.Odcinamy kratownice w interesujących nas prętach. 2.Odrzucamy jedną część kratownicy i zastępujemy ją siłami działającymi wzdłuż prętów. 3.Rozwiązujemy równania równowagi.
18)Zjawisko tarcia ślizgowego i tocznego-jest to zjawisko powstawania sił stycznych do powierzchni styku dwóch ciał. Siły te można zdefiniować jako siły oporu zapobiegające ruchowi, który by powstał, gdyby nie było tarcia. Są one siłami biernymi i składowymi reakcji, które wystąpią dla zachowania równowagi stykających się ciał. Przyczyną powstania sił tarcia jest chropowatość powierzchni ciał, które pod wpływem obciążeń zewnętrznych przesuwają się względem siebie. Jeżeli wartość liczbowa chropowatości maleje to maleje siła tarcia.
19)Doświadczenie Coulomba-prawa tarcia ślizgowego
I prawo tarcia-siła tarcia ślizgowego między dwoma ciałami jest proporcjonalna do składowej normalnej siły utrzymującej ciała w zetknięciu, co wyraża wzór T=µ*N, N-siła dociskająca powierz. Trące, prostopadła do styku ciał, µ-współ. Tarcia. Jeżeli pozostają w spoczynku względem siebie, to siła tarcia równoważy działającą siłę. Siła tarcia statycznego ma kierunek działania siły równoległej do trących powierzchni i przeciwny do niej zwrot.
IIPT-Siła tarcia ślizgowego nie zależy od wielkości powierzchni zetknięcia ciał. III-Z chwilą wprowadzenia ciała w ruch, siła tarcia nie zależy od prędkości.
20)Tarcie ślizgowe statyczne i kinetyczne-Tarcie spoczynkowe (statyczne)-tarcie ślizgowe, występujące między dwoma ciałami gdy nie przemieszczają się względem siebie. Siła tarcia równoważy siłę działającą na ciało. Max siła tarcia jest proporcjonalna do siły, z jaką ciało naciska na podłoże.
Tarciem kinetycznym-nazywa się tarcie zewnętrzne, gdy dwa ciała ślizgają się lub toczą po sobie. Siła tarcia przeciwstawia się wówczas ruchowi.
![]()
21)Prawa tarcia tocznego-powstaje przy przetaczaniu walca o ciężarze G po poziomej płaszczyźnie. Toczenie walca wystąpi, gdy wartość siły tarcia tocznego T będzie mniejsza od wartości siły tarcia ślizgowego μN rozwiniętego, co wyraża się nierównością:
23)Środek sił równoległych-jest to punkt C mający własność, że przechodzi przez niego wypadkowa danego ukł sił równoległych. Współrzędne punktu obliczamy opierając się na twierdzeniu o momencie wypadkowej układu sił, według którego moment wypadkowej R względem dowolnej osi równy jest sumie momentów poszczególnych sił względem tej osi.
24)Modele ciał rzeczywistych
25)Moment statyczny pola względem pewnej osi nazywamy sumę iloczynów pól i odległości od tej osi. Jeżeli na tarcze będzie działać w jej płaszczyźnie siła P to nastąpi obrót tarczy wokół punktu O zwanego biegunem. M=P*a
26)Środek masy-punkt określony przez rozkład mas w danym ciele lub układzie ciał. Położenie środka masy wyraża się wzorem……….., mk i rk-odpowiednio masy i promienie wodzące poszczególnych punktowych ciał składających się na dany obiekt.
27)Środek ciężkości bryły materialnej
![]()
![]()
![]()
![]()
![]()
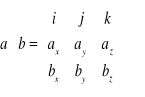
![]()
![]()
![]()
Wyszukiwarka
Podobne podstrony:
Mechanika 1- opracowanie (3), PWR, MiBM WME, ściągi, ściągi, mechanika 1
Mechanika 1 - opracowanie (2), PWR, MiBM WME, ściągi, mechanika 1
Mechanika 1 - opracowanie, PWR, MiBM WME, ściągi, ściągi, mechanika 1
mechanika sciaga 3, PWR, MiBM WME, Mechanika, ściągi mech
mechanika sciaga 2, PWR, MiBM WME, Mechanika, ściągi mech
środek masy, PWR, MiBM WME, Mechanika, ściągi mech
równania ruchu, PWR, MiBM WME, Mechanika, ściągi mech
mater, PWR, MiBM WME, P Materiały
Gotowa ściaga- mechanika budowli, BUDOWNICTWO, Mechanika budowli
ŚCIĄGI, Sciaga 1, Mechanika płynów - część mechaniki teoretycznej, zajmuje się badaniem ruchu płynów
ściąga na chemie [Jasiorski], Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Chemia materiałów
sciaga (Odzyskany), PWr, Podstawy telkom Krzysztofik, podstawy telekomunikacji, Podstawy telekomunik
Gotowa ściaga na obsługę, Ściągi, Fizyka
2 kolo z analitycznej laborki sciaga, Biotechnologia PWR, Semestr 4, Podstawy chemii analitycznej -
Fifyka komputerowa, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, fiza
więcej podobnych podstron