Konspekt nr 4 z laboratoriów „Statystyka i rachunek prawdopodobieństwa”

1

Elementy statystyki matematycznej

1.

Wstęp

Poprzednie trzy konspekty, przygotowane na zajęcia, dotyczyły rachunku prawdopodo-

bieństwa. Teraz przejdziemy do statystyki matematycznej, a więc nauki zajmującej się opisy-

waniem zjawisk masowych przy użyciu metod rachunku prawdopodobieństwa.

Aby łatwiej było nam zrozumieć zagadnienia występujące w statystyce, musimy najpierw

zdefiniować sobie pewne podstawowe pojęcia tam występujące.

Wyobraźmy sobie, że mamy pewien zbiór Z, którego elementy podlegają badaniu ze

względu na jedną lub więcej cech. Jeśli zbiór Z ma przynajmniej jedną cechę wspólną dla
wszystkich jego elementów,

oraz przynajmniej jedną właściwość, ze względu na którą ele-

menty tego zbioru

mogą się różnić między sobą, to taki zbiór nazywać będziemy populacją

(

zbiorowością) generalną, lub krócej populacją.

PRZYKŁAD 1.1. Przykładem populacji może być zbiór składający się ze studentów uczelni. Cechą wspólną

dla wszystkich elementów (studentów) tego zbioru

może być np. wzrost, waga, wiek. Ale np. nazwa wojewódz-

twa, w którym dany

student urodził się niekoniecznie musi być cechą wspólną wszystkich studentów. Może

przecież okazać się, że ktoś urodził się za granicą.

Badać można wszystkie elementy zbioru Z albo tylko ich część. W pierwszym przypadku

mówimy, że badanie jest kompletne (stuprocentowe, całkowite), w drugim, że jest częściowe.

Badanie kompletne dostarcza pełnej informacji o pewnej właściwości badanej populacji. Czę-

sto jednak badań kompletnych nie wykonuje się. Na przykład, gdy takie badanie jest czaso-

chłonne, kosztowne, elementy ulegają zniszczeniu podczas badania (np. trzeba wyciąć próbkę

z odlewu do oceny twardości, wytrzymałości na rozciąganie itp.), zbiór Z nie zawiera ściśle

określonej liczby elementów (np. w produkcji seryjnej przez cały czas do zbioru dochodzą
nowe elementy) itp. Badaniami kompletnymi statystyka rzadko za

jmuje się. Głównym bo-

wiem jej zadaniem jest wnioskowanie o pewnych

właściwościach zbioru Z, na podstawie in-

formacji uzyskanych z oceny

tych samach właściwości pewnego skończonego podzbioru z

1

zbioru

Z. Taki skończony podzbiór będziemy nazywać próbką (próbą). Oczywiście próbka

powinna stanowić reprezentację całej populacji w tym sensie, że częstości występowania
w

próbce każdej z badanych cech nie powinny znacznie różnić od częstości występowania

tych cech w populacji. Aby to osiągnąć, elementy próbki losuje się spośród elementów zbioru

Z. Tak otrzymany zbiór będziemy nazywać próbką (próbą) losową.

Gdy n-elementowa próbka losowana jest ze zbioru

Z w taki sposób, że prawdopodobień-

s

two trafienia każdego elementu do próbki jest takie samo, to będziemy nazywać ją

n-

elementową próbką (próbą) prostą.

W dalszej części konspektu zostaną przedstawione podstawowe pojęcia statystyki opiso-

wej, czyli

działu statystyki matematycznej zajmującego się wstępnym opracowaniem próbki

bez posługiwania się rachunkiem prawdopodobieństwa.

2. Szereg rozdzielczy

W

yobraźmy sobie, że mamy przeanalizować dużą próbkę losową

(I

(I)

Za dużą próbkę losową, umownie przyjmuje się gdy liczy ona co najmniej 30 elementów (n≥30)

)

. W takim przypadku

zamiast analizować wszystkie wyniki pojedynczo, co może być żmudne i pracochłonne, gru-

puje się je w tzw. klasy. Klasy są to nic innego jak przedziały, najczęściej o jednakowej dłu-

gości, do których „wrzuca” się poszczególne wartości próbki losowej.

Konspekt nr 4 z laboratoriów „Statystyka i rachunek prawdopodobieństwa”

2

PRZYKŁAD 2.1. Wyobraźmy sobie, że mamy próbkę losową zawierającą następujące pięć elementów: 2.5,

2.6,

2.3, 2.4, 2.6. Odstąpmy na razie od zasady mówiącej, że klasy tworzy się dla próbek dużych. Załóżmy, że

dla naszej próbki utworzyliśmy dwie klasy tj. przedział pierwszy [2.25; 2.45) oraz drugi [2.45; 2.65). W takim
razie do klasy pier

wszej będą należeć wartości: 2.3, 2.4; natomiast do drugiej klasy: 2.5, 2.6, 2.6. Zwróćmy

uwagę, że w klasie drugiej występuje dwa razy wartość 2.6. Może przecież tak zdarzyć się, że podczas przepro-
wadzania pomiarów

, kilka razy uzyskamy tą samą wartość. W takim przypadku uwzględniamy ten wynik

w

naszej próbce tyle razy ile on wystąpił.

Jak tworzyć takie klasy zostanie pokazane poniżej.
Mamy

pewną n-elementową próbę losową w postaci

n

x

x ,...,

1

(1)

gdzie x

j

dla j = 1, 2,...,n

oznaczają poszczególne wartości mierzonej cechy w próbce losowej.

Taką cechą może być np. wartość masy, natężenie prądu itp. Rozstępem badanej cechy
w próbie (1)

będziemy nazywać różnicę

min

max

x

x

R

−

=

(2),

gdzie x

max

i x

min

oznaczają odpowiednio największą i najmniejszą wartość badanej cechy

w próbce (1).

Ilość klas uzależniona jest od liczności próbki. Istnieje kilka reguł wyznaczania orienta-

cyjnej liczby k klas

n

k

ln

5

≤

(3),

n

k

ln

322

.

3

1

+

=

(4),

n

k

=

(5).

Otrzymaną wartość k z któregoś powyższego wzoru należy zaokrąglić do najbliższej licz-

by całkowitej.

Przybliżoną długość (szerokość) klasy wyliczamy z następującej zależności

k

R

b

≈

(6),

zaokrąglając otrzymaną wartość b w górę do wartość b’ tak aby b’·k ≥ R.

Punkty graniczne

przedziałów wyznacza się w następujący sposób. W pierwszej kolejno-

ści należy wyznaczyć dolną granicę x

d

z zależności

α

2

1

min

−

= x

x

d

(7),

gdzie

α oznacza dokładność

(II

1

)

z jaką zostały wyznaczone wartości próbki. Następnie wyzna-

czamy lewe granice x

l,i

. Dla i-tego

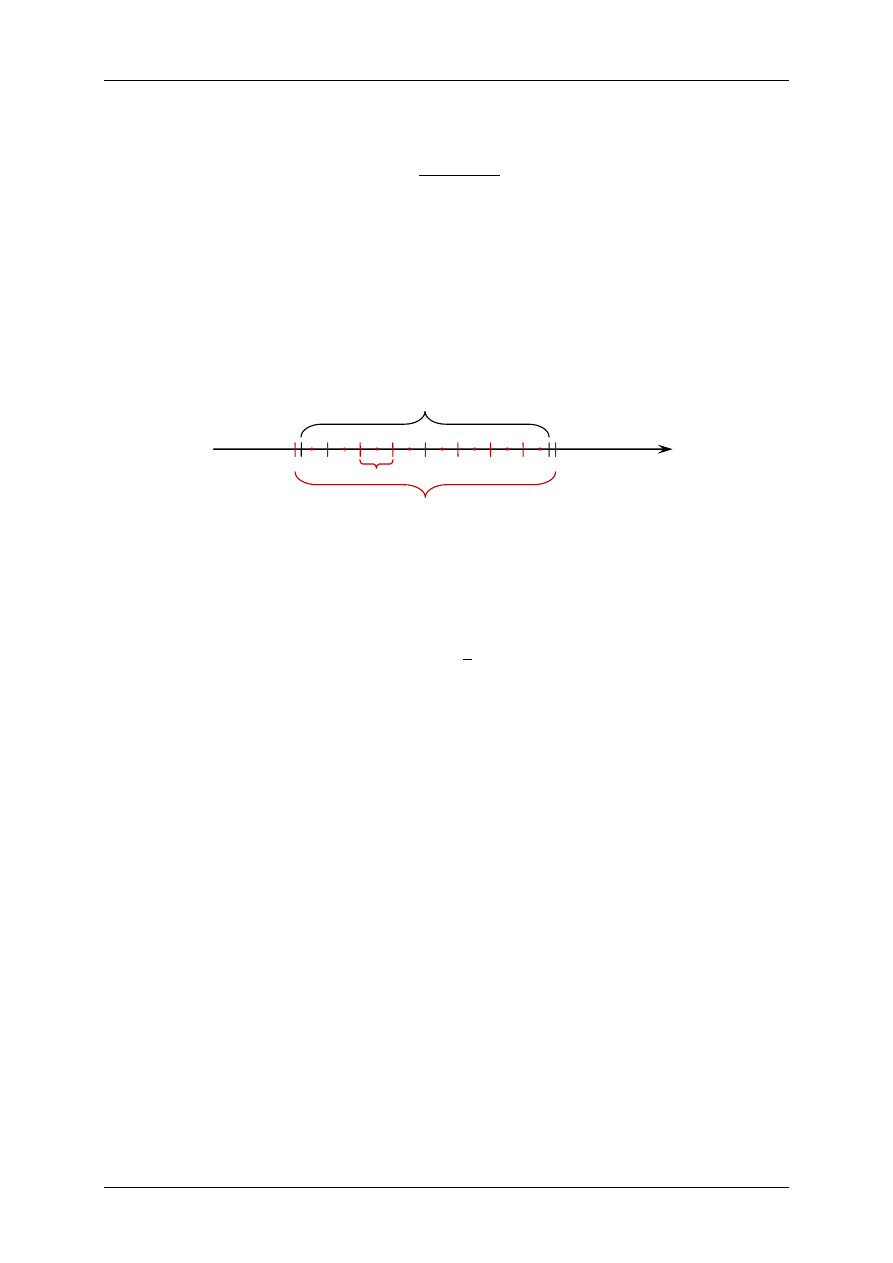
przedziału (patrz rys. ) wylicza się ją następująco

(

)







>

−

+

=

=

1

'

1

1

,

i

dla

b

i

x

i

dla

x

x

d

d

i

l

(8).

Pozostaje jeszcze wyliczyć prawe granice x

p,i

i środki przedziałów x

s,i

. Dla i-tego przedzia-

łu można to zrobić korzystając z poniższych prostych zależności

(II)

Gdy próbka zawiera np. dane: 2.48, 2.44, 2.59, 2.33, 2.78 to α = 0.01. Natomiast dla próbki z danymi: 2.5,

3.0, 2.0, 3.5, 1.5 dokładność α wynosi 0.5.

Konspekt nr 4 z laboratoriów „Statystyka i rachunek prawdopodobieństwa”

3

'

,

b

i

x

x

d

i

p

⋅

+

=

(9),

2

,

,

,

i

l

i

p

i

s

x

x

x

+

=

(10).

Wartość x

j

z próby losowej będziemy zaliczać do i-tej klasy jeśli spełniona będzie nastę-

pu

jąca nierówność

n

j

k

i

x

x

x

i

p

j

i

l

,...,

1

;

,...,

1

dla

,

,

,

=

=

<

≤

(11).

Ilość wartości x

j

próbki (1)

, które trafiają do i-tej klasy będziemy nazywać licznością (li-

czebnością) klasy i oznaczać symbolem n

i

. Jeśli liczność n

i

i-tej klasy podzielimy przez licz-

ność n całej próby losowej, to dostaniemy tzw. częstość w

i

i-tej klasy.

Rys 1.

Schemat ilustrujący sposób wyznaczania granic poszczególnych klas (czerwone

kropki –

środki przedziałów)

Jeżeli jakaś próba losowa x

1

,…,x

n

kwalifikuje się do podziału na k klas, to pod dokonaniu

grupowania jej wyników do poszczególnych klas

otrzymuje się tzw. szereg rozdzielczy. Sze-

reg rozdzielczy stanowią pary liczb o środkach

i

x

w kolejnych klasach oraz ich liczności n

i

(lub częstości w

i

), i = 1,…,k.

PRZYKŁAD 2.2. Z populacji generalnej pobrano próbę losową zawierającą n = 60 elementów i przebadano

ją ze względu na cechę X. Poszczególne wartości próby losowej są następujące: 5.1; 3.4; 6.2; 5.3; 3.9; 3.4; 4.6;
3.1; 5.2; 5.0; 6.2; 6.1; 3.9; 5.1; 5.5; 5.1; 6.0; 4.7; 5.5; 6.6; 5.1; 5.4; 4.2; 5.4; 4.5; 4.4; 5.7; 4.4; 5.6; 4.0; 5.5; 5.3;
7.2; 6.8; 5.4; 6.0; 6.5; 5.1; 5.1; 5.6; 5.6; 5.5; 4.0; 5.7; 6.7; 3.4; 3.7; 4.6; 5.6; 4.6; 5.7; 4.5; 5.7; 5.1; 3.8; 5.2; 5.6;
4.5; 4.1; 4.1.

Należy sporządzić szereg rozdzielczy dla danej próby losowej.

Znajdźmy w pierwszej kolejności wartość maksymalną i minimalną w naszej próbce. Wynoszą one odpo-

wiednio: x

max

= 7.2 oraz x

min

= 3.1. Następnie wyliczmy rozstęp R z równania (2). Po wyliczeniu dostajemy

R = 4.1.

Wszystkie 60 wartości naszej próbki musimy posegregować do k klas. Ilość tych klas obliczymy korzystając

np. ze wzoru (5)

. Dostajemy przybliżoną wartość k ≈ 7.75. Zaokrąglamy ją do najbliższej liczby całkowitej.

A

więc k = 8. Teraz cały odcinek o długości R = 4.1 dzielimy na k klas (przedziałów). Otrzymujemy przybliżoną

szerokość przedziału (równanie (6)) b = 0.5125. Zaokrąglimy tą wartość w górę do wartości b’ = 0.52 tak aby

spełniona była nierówność b’·k ≥ R.

Wartości w naszej próbce wyznaczone są z dokładnością α = 0.1. Dolną granicę, która jednocześnie równa

jest lewej granicy pierwszego przedziału, liczymy z zależności (7), dostając jako wynik 3.05. Pozostałe punkty

graniczne tj. granice lewe, prawe oraz środki wyliczono z zależności (8), (9) oraz (10) i zestawiono w tabeli 1.

R = k·b

x

min

x

max

b’·k

x

l,1

=

x

d

b’

x

x

l,i

=x

p,i-1

x

s,i

x

g

=

x

p,k

Konspekt nr 4 z laboratoriów „Statystyka i rachunek prawdopodobieństwa”

4

Tab. 1. Zestawienie

wyników obliczeń z przykładu

Nr klasy

i

Granice przedziałów Grupowanie warto-

ści próby

(gwiazdki oznaczają ile

wartości x

j

należy do danej

klasy)

Szereg rozdzielczy

x

l,i

x

p,i

Środki

klas

x

s,i

Liczności

klas

n

i

Częstości

klas

w

i

1

3.05

3.57

****

3.31

4

0.067

2

3.57

4.09

******

3.83

6

0.100

3

4.09

4.61

***********

4.35

11

0.183

4

4.61

5.13

*********

4.87

9

0.150

5

5.13

5.65

****************

5.39

16

0.267

6

5.65

6.17

*******

5.91

7

0.117

7

6.17

6.69

****

6.43

4

0.067

8

6.69

7.21

***

6.95

3

0.050

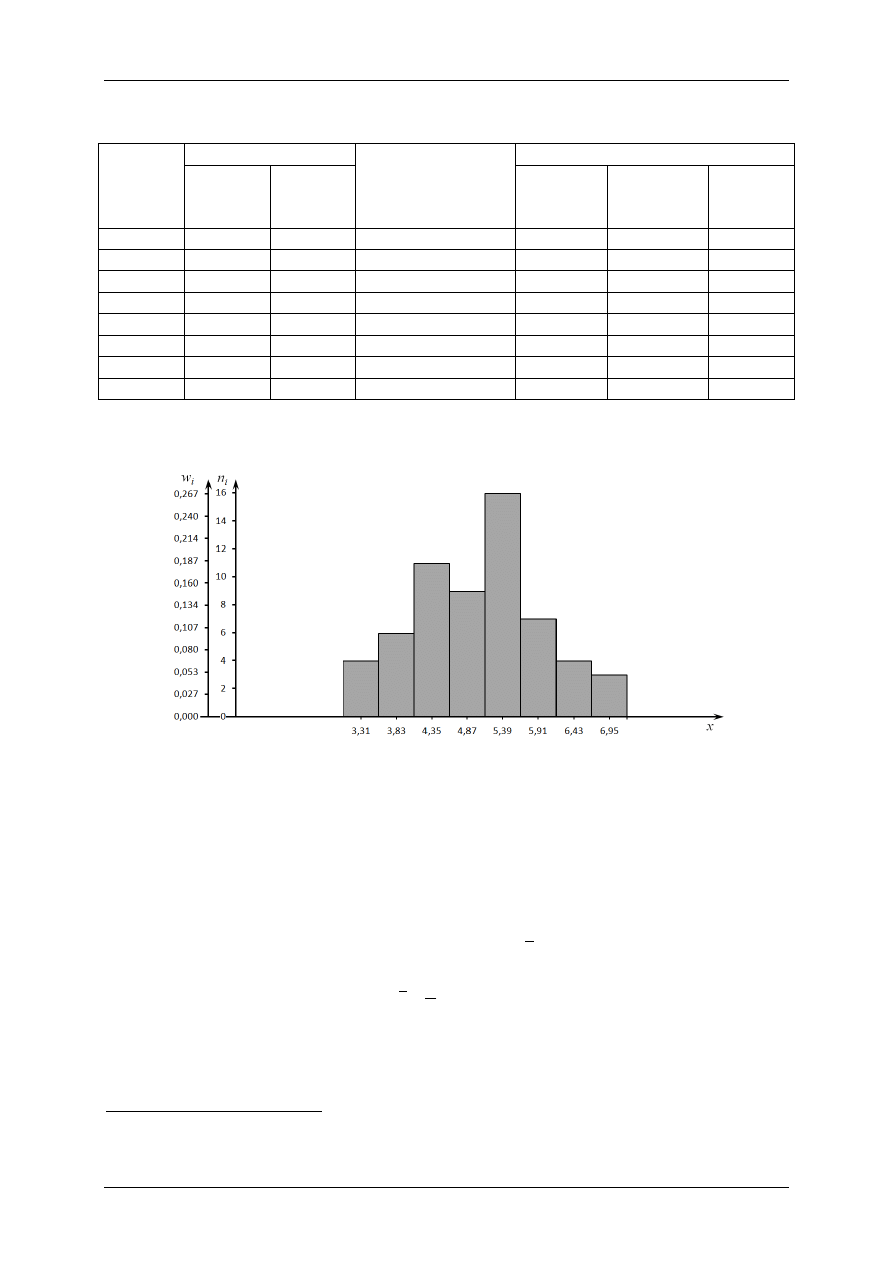
Otrzymany szereg można przedstawić w postaci histogramu (rys. 2). Na osi poziomej zaznacza się środki

klas

a na osi pionowej liczności n

i

i

częstości w

i

.

Rys. 2. Szereg rozdzielczy przedstawiony w postaci histogramu

3.

Miary położenia

Miary położenia, zwane czasami wartościami przeciętnymi, służą do określenia położenia

rozkładu empirycznego (w naszym przypadku szeregu rozdzielczego) na osi liczb rzeczywi-

stych. Poniżej zostaną przedstawione dwa typy położenia, mianowicie średnie

(III

3.1. Średnia arytmetyczna

)

i tzw. prze-

ciętne pozycyjne (mediana i moda).

Średnią arytmetyczną liczb x

1

,…,x

n

nazywamy liczbę

x

określoną wzorem

∑

=

=

n

i

i

x

n

x

1

1

(12).

(III)

W niniejszym konspekcie przedstawiono tylko niektóre rodzaje średnich. Istnieją jeszcze kilka innych śred-

nich takich jak: średnia harmoniczna ważona, średnia geometryczna ważona oraz średnia potęgowa rzędu r.

Konspekt nr 4 z laboratoriów „Statystyka i rachunek prawdopodobieństwa”

5

Jeżeli w próbie losowej wynik pomiaru x

i

wystąpił n

i

razy, gdzie i = 1,…,k oraz

∑

=

=

k

i

i

n

n

1

,

to średnią daną poniższym wzorem

∑

=

=

k

i

i

i

n

x

n

x

1

1

(13)

będziemy nazywać średnią arytmetyczną ważoną.

Średnia arytmetyczna ważona, często interpretowana jest jako współrzędna środka masy

układu punktów materialnych o masach n

i

, umieszczonych na osi liczbowej w punktach

o

współrzędnych x

i

.

Średnia arytmetyczna ma następujące właściwości

max

min

x

x

x

≤

≤

(14),

(

)

0

1

=

−

∑

=

n

i

i

x

x

(15).

Średnią arytmetyczną można obliczyć korzystając z funkcji ŚREDNIA znajdującej się w ar-

kuszu kalkulacyjnym MS Excel.
3.2. Średnia harmoniczna

Średnią harmoniczną liczb x

i

,...,x

n

różnych od zera, nazywamy liczbę h daną wzorem

∑

=

=

n

i

i

x

n

h

1

1

(16).

Podobnie jak w przy

padku średniej arytmetycznej aby obliczyć średnią harmoniczną moż-

na skorzystać z funkcji ŚREDNIA.HARMONICZNA w Excelu.
3.3. Średnia geometryczna

Średnia geometryczna liczb x

i

,..,x

n

większych od zera dana jest wzorem

n

n

i

i

x

g

∏

=

=

1

(17).

Analogicznie do dwóch pozostałych średnich, średnią geometryczną wyliczyć można przy

użyciu funkcji ŚREDNIA.GEOMETRYCZNA.
3.4. Mediana

Medianą lub wartością środkową nazywamy taką liczbę m

e

, dla której połowa realizacji

zmienn

ej losowej ma wartości nie przekraczające m

e

, natomiast druga połowa – wartości

wyższe niż m

e

. Aby wyznaczyć medianę, w pierwszej kolejności należy uporządkować

wszystkie wartości x

j

(j = 1,..,n

) zmiennej losowej w kolejności od najmniejszej do najwięk-

szej. W drugim kroku postępowania stosuje się jeden z poniższych wzorów. Jeśli n jest liczbą

nieparzystą, to

2

1

+

=

n

e

x

m

(18).

W przypadku gdy n jest parzyste, to korzystamy ze wzoru

Konspekt nr 4 z laboratoriów „Statystyka i rachunek prawdopodobieństwa”

6













+

=

+

2

1

2

2

1

n

n

e

x

x

m

(19).

Funkcja wyliczająca medianę w Excelu ma nazwę MEDIANA.

PRZYKŁAD 3.1. Obliczyć medianę próbki z przykładu 2.2.
Przedstawmy

wyniki próbki w postaci uporządkowanej w tabeli 2. Ponieważ n = 60 (jest parzyste) należy

zastosować wzór (19).

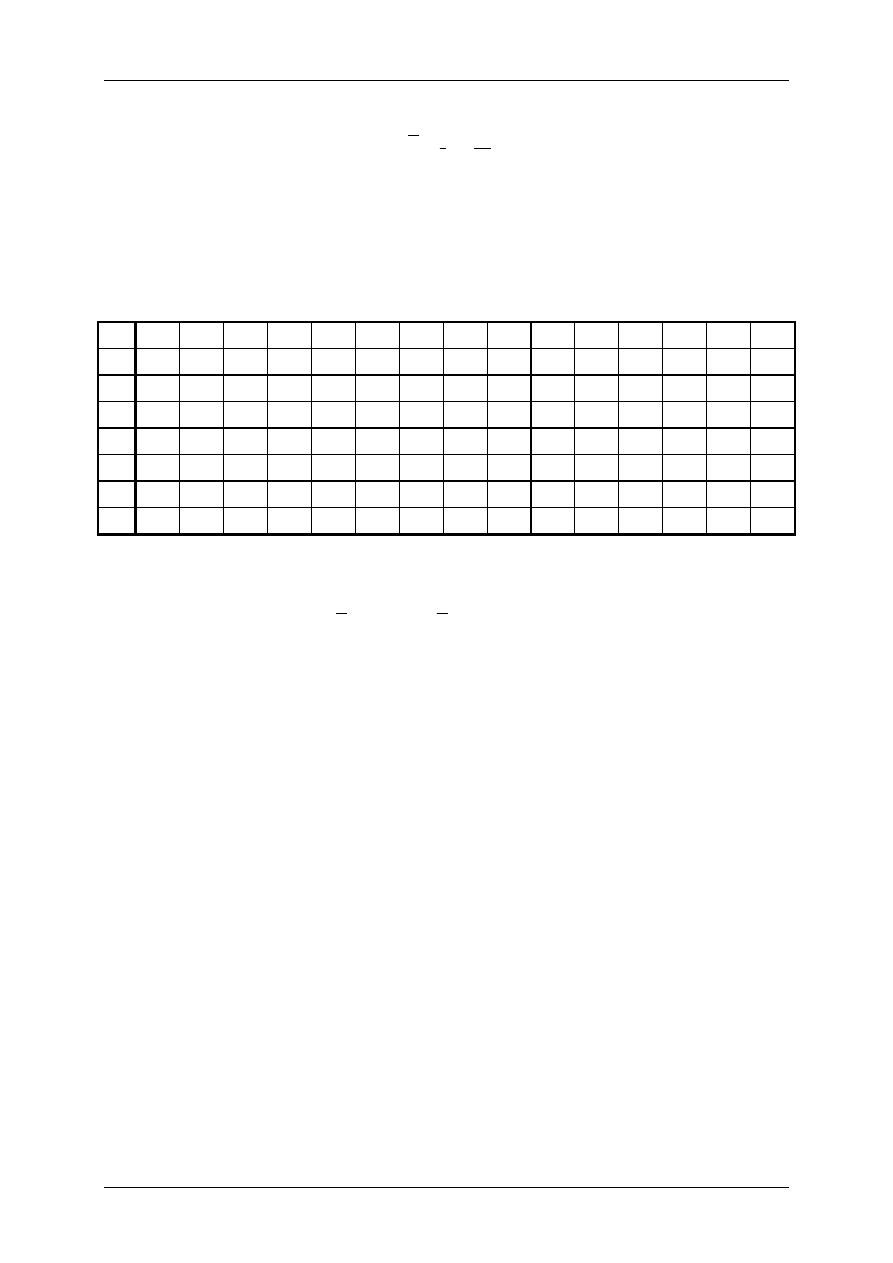
Tab. 2

. Zestawienie uporządkowanych wyników próbki

j

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

x

j

3.1

3.4

3.4

3.4

3.7

3.8

3.9

3.9

4.0

4

4.1

4.1

4.2

4.4

4.4

j

16

17

18

19

20

21

22

23

24

25

26

27

28

29

30

x

j

4.5

4.5

4.5

4.6

4.6

4.6

4.7

5

5.1

5.1

5.1

5.1

5.1

5.1

5.1

j

31

32

33

34

35

36

37

38

39

40

41

42

43

44

45

x

j

5.2

5.2

5.3

5.3

5.4

5.4

5.4

5.5

5.5

5.5

5.5

5.6

5.6

5.6

5.6

j

46

47

48

49

50

51

52

53

54

55

56

57

58

59

60

x

j

5.6

5.7

5.7

5.7

5.7

6

6

6.1

6.2

6.2

6.5

6.6

6.7

6.8

7.2

Z tabeli 2 odczytujemy x

30

= 5.1, x

31

= 5.2. Podstawiając do wzoru otrzymujemy

(

)

(

)

15

.

5

2

.

5

1

.

5

2

1

2

1

31

30

=

+

=

+

=

x

x

m

e

.

3.5. Moda

Modą (wartością modalną, dominantą) m

o

próbki (1)

nazywamy najczęściej powtarzającą

się wartość, o ile istnieje.

PRZYKŁAD 3.2. Wyznaczyć modę dla próbki z przykładu 2.2.

Zadanie można rozwiązać wykorzystując arkusz kalkulacyjny MS Excel. Funkcja obliczająca modę ma na-

zwę WYST.NAJCZĘŚCIEJ(zakres). Zmienna zakres jest zakresem komórek, w których znajdują się wyniki próbki.

Przykładowo może to być A1:A60. Jeśli w próbce wszystkie wartości byłyby różne, to oczywiście moda nie
istnieje i funkcja

WYST.NAJCZĘŚCIEJ zwraca wynik #N/D!. Wartością m

o

w naszym przykładzie jest liczba 5.1.

Można to sprawdzić analizując wyniki w tabeli 2.

Konspekt nr 4 z laboratoriów „Statystyka i rachunek prawdopodobieństwa”

7

LITERATURA

W. Krysicki, J. Bartos, W. Dysza, K. Królikowska, M. Wasilewska: Rachunek prawdopo-

dobieństwa i statystyka matematyczna w zadaniach. Wydawnictwo Naukowe PWN, Warsza-
wa 2005.

A. Iwasiewicz, A. Paszek: Statystyka z elementami statystycznych metod monitorowania

procesów. Wydawnictwo Akademii Ekonomicznej w Krakowie, Kraków 2004.

W. Kordecki:

Rachunek prawdopodobieństwa i statystyka matematyczny. Oficyna Wy-

dawnicza GiS,

Wrocław 2003.