1/6

Przedmiot:

Krystalografia

Lab. 6

Temat lab.: Obliczanie parametrów sieci dla układu regularnego Fe

α

i Fe

γ

Cel dwiczenia:

Umiejętnośd obliczania parametru sieci dla układu regularnego

Przebieg dwiczenia:

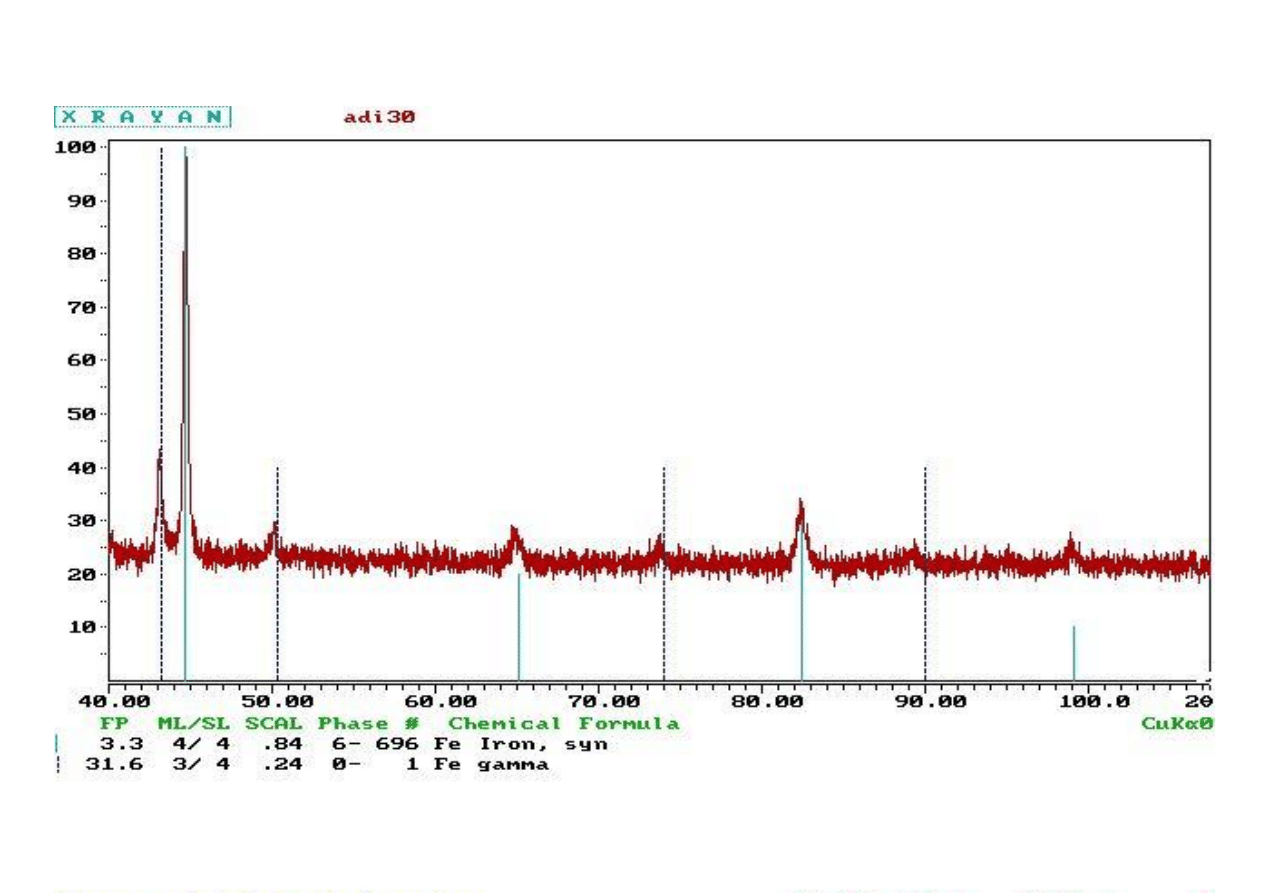
Na podstawie wykonanego dyfraktogramu rentgenowskiego żeliwa ADI oblicz

parametr sieci dla żelaza Fe

α

i Fe

γ

(Fe

α

- ferryt i Fe

γ

- austenit)

Dane do obliczeo:





sin

2

;



l

hk

d

(1)

gdzie:

d

hkl

– odległośd międzypłaszczyznowa *Å = 10

-10

m],

λ – długośd fali promieniowania elektromagnetycznego *Å+, λ(Cu

Kα1

) = 1,5405 Å,

Θ – kat odbicia *˚ +.

Parametr sieci (parametr swobodny - a) dla układu regularnego obliczmy z

następującego wzoru:

2

2

2

2

2

2

l

k

h

d

a

l

k

h

a

d

hkl

hkl

















(2)

gdzie:

h, k, l – wskaźniki Millera

Funkcja ekstrapolacyjna Taylora i Sinclaira (T-S) jest obliczana wg. poniższego wzoru:





























2

2

cos

sin

cos

2

1

)

(

S

T

(3)

Θ – kat odbicia w tym wypadku musi byd przeliczony na radiany

Przeliczenie wartości kąta ze stopni na radiany:

360

2









rd

(4)

gdzie:

π = 3,1415 ...

W celu wyznaczenia a

0

należy narysowad zależnośd a = f(T-S) i dopasowad prostą

regresji liniowej w postaci y = ax +b, gdzie parametr b = a

0

2/6

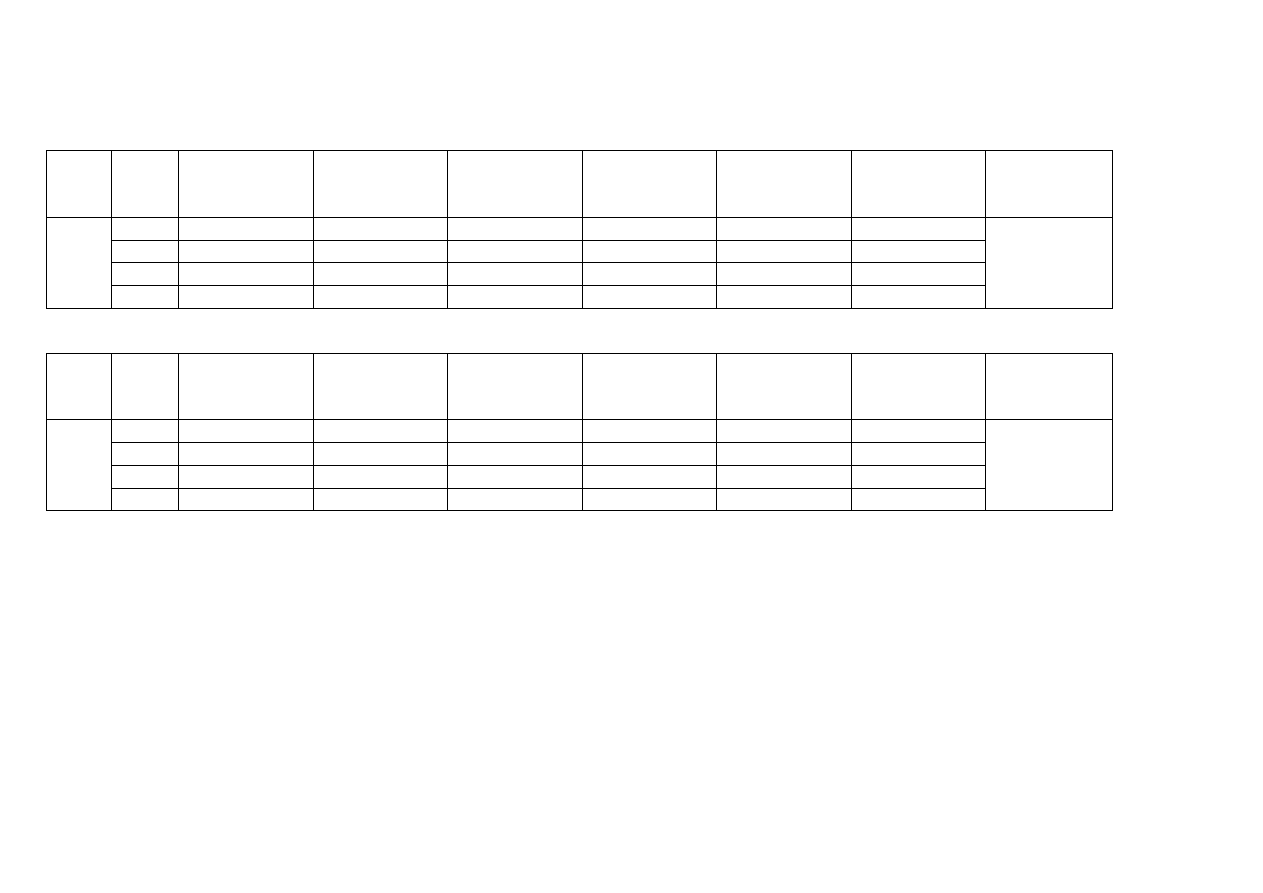
Tab. 1. Obliczenie parametru a

0

sieci krystalograficznej dla układu regularnego Fe

α

(sied A2)

Nazwa
fazy

hkl

Odczytaj 2Θ *˚ + Oblicz Θ *˚ +

Oblicz wg. (4) Θ
[rd]

Oblicz wg. (1)
d

hkl

*Å+

Oblicz wg. (3)
(T-S) lub
odczytaj z tab. 3

Oblicz wg. (2)
a *Å+

Wyznacz

a

0

z dopasowania
funkcji liniowej

Fe

α

110

200

211

220

Tab.2. Obliczenie parametru a

0

sieci krystalograficznej dla układu regularnego Fe

γ

(sied A1)

Nazwa
fazy

hkl

Odczytaj 2Θ *˚ + Oblicz Θ *˚ +

Oblicz wg. (4) Θ
[rd]

Oblicz wg. (1)
d

hkl

*Å+

Oblicz wg. (3)
(T-S) lub
odczytaj z tab. 3

Oblicz wg. (2)
a *Å+

Wyznacz

a

0

z dopasowania
funkcji liniowej

Fe

γ

111

200

220

311

3/6

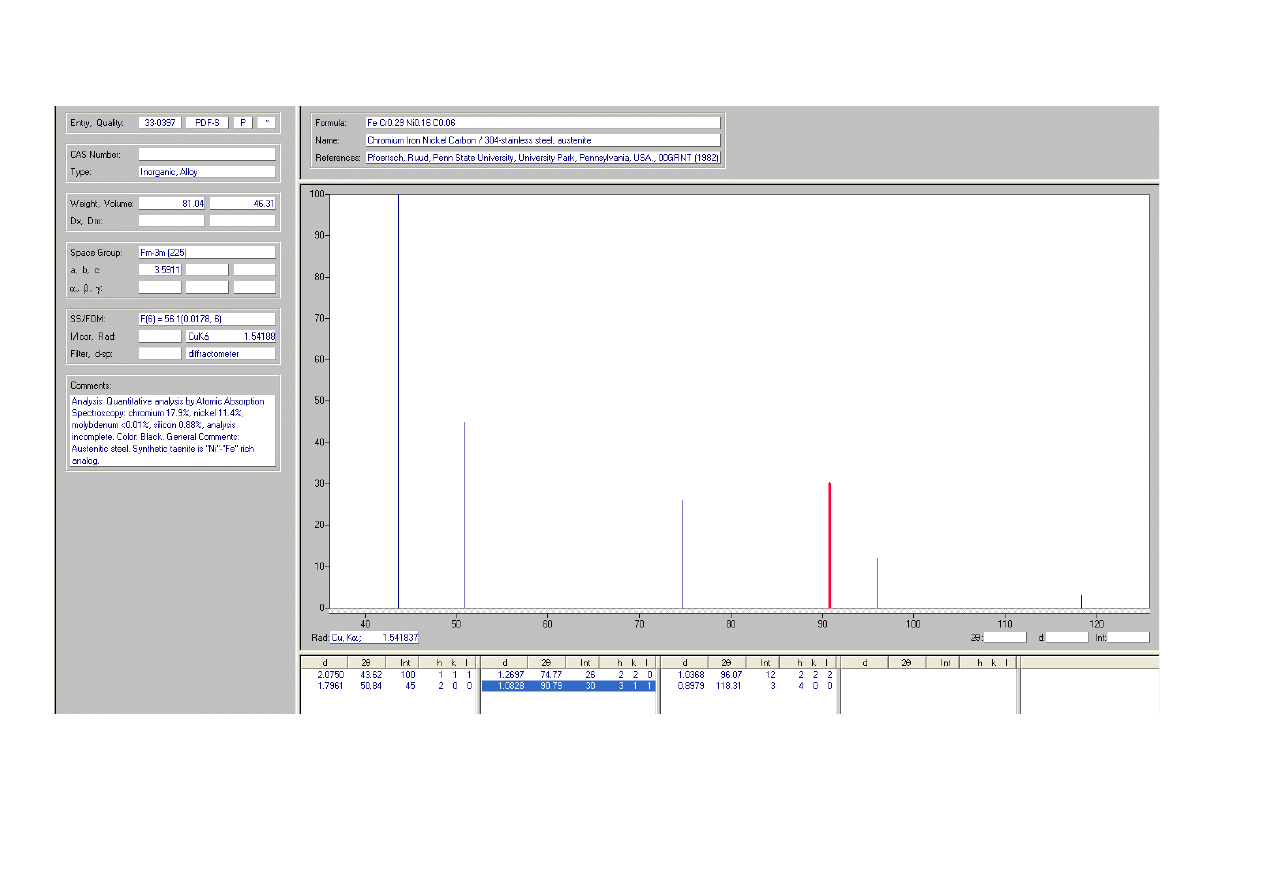
Fe



(110)

Fe



(111)

Fe



(200)

Fe



(220)

Fe



(311)

Fe



(200)

Fe



(211)

Fe



(220)

4/6

Tab. 3. Funkcja ekstrapolacyjna Taylora i Sinclaira (T-S)

Θ *˚ +

0.0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

10

5.571

5.513

5.456

5.399

5.344

5.290

5.237

5.185

5.134

5.084

11

5.035

4.986

4.938

4.892

4.846

4.800

4.756

4.712

4.669

4.627

12

4.585

4.544

4.504

4.464

4.425

4.386

4.348

4.311

4.274

4.238

13

4.202

4.167

4.133

4.098

4.065

4.032

3.999

3.967

3.935

3.903

14

3.872

3.842

3.812

3.782

3.753

3.724

3.695

3.667

3.639

3.612

15

3.584

3.558

3.531

3.505

3.479

3.454

3.428

3.404

3.379

3.355

16

3.331

3.307

3.283

3.260

3.237

3.215

3.192

3.170

3.148

3.127

17

3.105

3.084

3.063

3.042

3.022

3.001

2.981

2.961

2.942

2.922

18

2.903

2.884

2.865

2.847

2.828

2.810

2.792

2.774

2.756

2.738

19

2.721

2.704

2.687

2.670

2.653

2.636

2.620

2.604

2.588

2.572

20

2.556

2.540

2.524

2.509

2.494

2.479

2.464

2.449

2.434

2.419

21

2.405

2.391

2.376

2.362

2.348

2.334

2.321

2.307

2.294

2.280

22

2.267

2.254

2.241

2.228

2.215

2.202

2.189

2.177

2.164

2.152

23

2.140

2.128

2.115

2.103

2.092

2.080

2.068

2.056

2.045

2.033

24

2.022

2.011

2.000

1.989

1.978

1.967

1.956

1.945

1.934

1.924

25

1.913

1.903

1.892

1.882

1.872

1.861

1.851

1.841

1.831

1.821

26

1.812

1.802

1.792

1.782

1.773

1.763

1.754

1.744

1.735

1.726

27

1.717

1.708

1.698

1.689

1.680

1.672

1.663

1.654

1.645

1.637

28

1.628

1.619

1.611

1.602

1.594

1.586

1.577

1.569

1.561

1.553

29

1.545

1.537

1.529

1.521

1.513

1.505

1.497

1.489

1.482

1.474

30

1.466

1.459

1.451

1.444

1.436

1.429

1.421

1.414

1.407

1.399

31

1.392

1.385

1.378

1.371

1.364

1.357

1.350

1.343

1.336

1.329

32

1.322

1.316

1.309

1.302

1.296

1.289

1.282

1.276

1.269

1.263

33

1.256

1.250

1.244

1.237

1.231

1.225

1.218

1.212

1.206

1.200

34

1.194

1.188

1.182

1.175

1.169

1.164

1.158

1.152

1.146

1.140

35

1.134

1.128

1.123

1.117

1.111

1.106

1.100

1.094

1.089

1.083

36

1.078

1.072

1.067

1.061

1.056

1.050

1.045

1.040

1.034

1.029

37

1.024

1.019

1.013

1.008

1.003

0.998

0.993

0.988

0.983

0.977

38

0.972

0.967

0.962

0.958

0.953

0.948

0.943

0.938

0.933

0.928

39

0.923

0.919

0.914

0.909

0.905

0.900

0.895

0.891

0.886

0.881

40

0.877

0.872

0.868

0.863

0.859

0.854

0.850

0.845

0.841

0.836

41

0.832

0.828

0.823

0.819

0.815

0.810

0.806

0.802

0.798

0.794

42

0.789

0.785

0.781

0.777

0.773

0.769

0.765

0.761

0.757

0.753

43

0.748

0.745

0.741

0.737

0.733

0.729

0.725

0.721

0.717

0.713

44

0.709

0.706

0.702

0.698

0.694

0.690

0.687

0.683

0.679

0.676

45

0.672

0.668

0.665

0.661

0.657

0.654

0.650

0.647

0.643

0.639

46

0.636

0.632

0.629

0.625

0.622

0.619

0.615

0.612

0.608

0.605

47

0.601

0.598

0.595

0.591

0.588

0.585

0.582

0.578

0.575

0.572

48

0.568

0.565

0.562

0.559

0.556

0.552

0.549

0.546

0.543

0.540

49

0.537

0.534

0.531

0.528

0.524

0.521

0.518

0.515

0.512

0.509

50

0.506

0.503

0.500

0.498

0.495

0.492

0.489

0.486

0.483

0.480

51

0.477

0.474

0.472

0.469

0.466

0.463

0.460

0.458

0.455

0.452

52

0.449

0.447

0.444

0.441

0.438

0.436

0.433

0.430

0.428

0.425

53

0.423

0.420

0.417

0.415

0.412

0.410

0.407

0.404

0.402

0.399

54

0.397

0.394

0.392

0.389

0.387

0.384

0.382

0.379

0.377

0.375

55

0.372

0.370

0.367

0.365

0.363

0.360

0.358

0.356

0.353

0.351

56

0.349

0.346

0.344

0.342

0.339

0.337

0.335

0.333

0.330

0.328

57

0.326

0.324

0.322

0.319

0.317

0.315

0.313

0.311

0.309

0.306

58

0.304

0.302

0.300

0.298

0.296

0.294

0.292

0.290

0.288

0.286

59

0.284

0.282

0.279

0.277

0.275

0.274

0.272

0.270

0.268

0.266

60

0.264

0.262

0.260

0.258

0.256

0.254

0.252

0.250

0.248

0.247

5/6

6/6