1

Integralność konstrukcji

Wykład Nr 2

Inżynierska i rzeczywista krzywa rozciągania

Wydział Inżynierii Mechanicznej i Robotyki
Katedra Wytrzymałości, Zmęczenia Materiałów i Konstrukcji

2

2.1 NAPRĘŻENIA I ODKSZTAŁCENIA INŻYNIERSKIE

Oparte są na początkowych nie zdeformowanych wymiarach próbek

Oznaczenia:



,



R , początek

szyjki

(



f

,



f

)

R , płynięcie

(b)

(a)

(a)

(b)





(c)

(d)

(c)

(d)

0



u

m

e

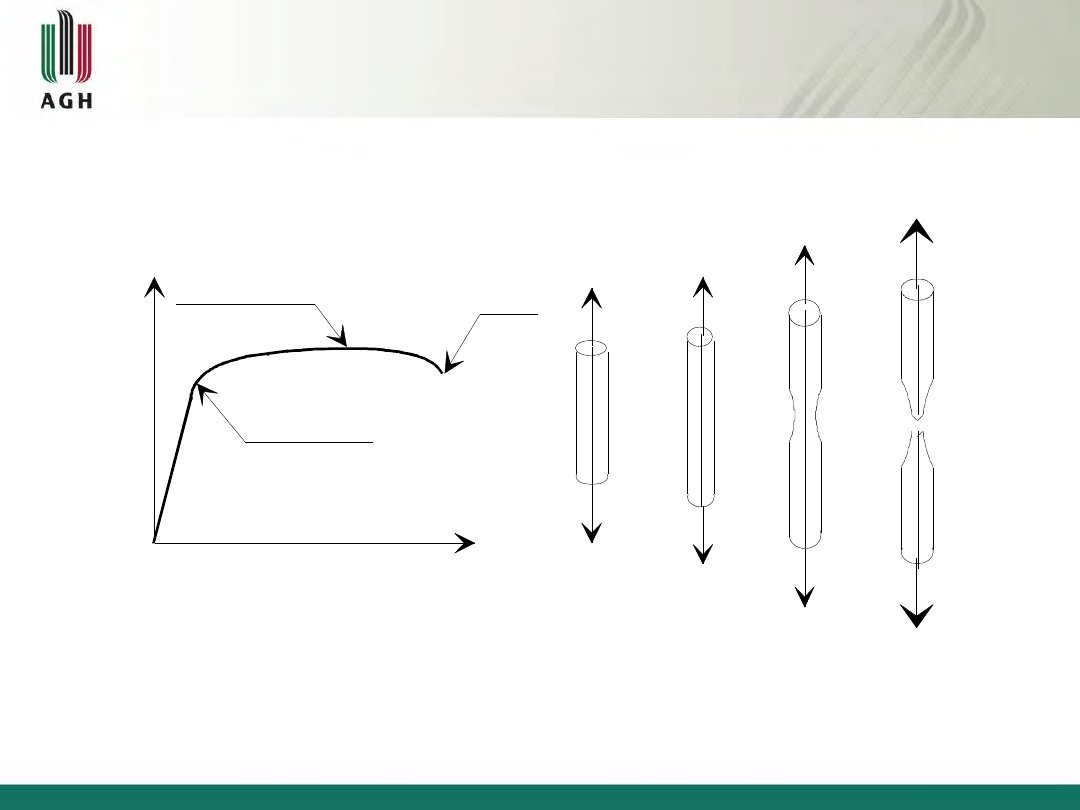
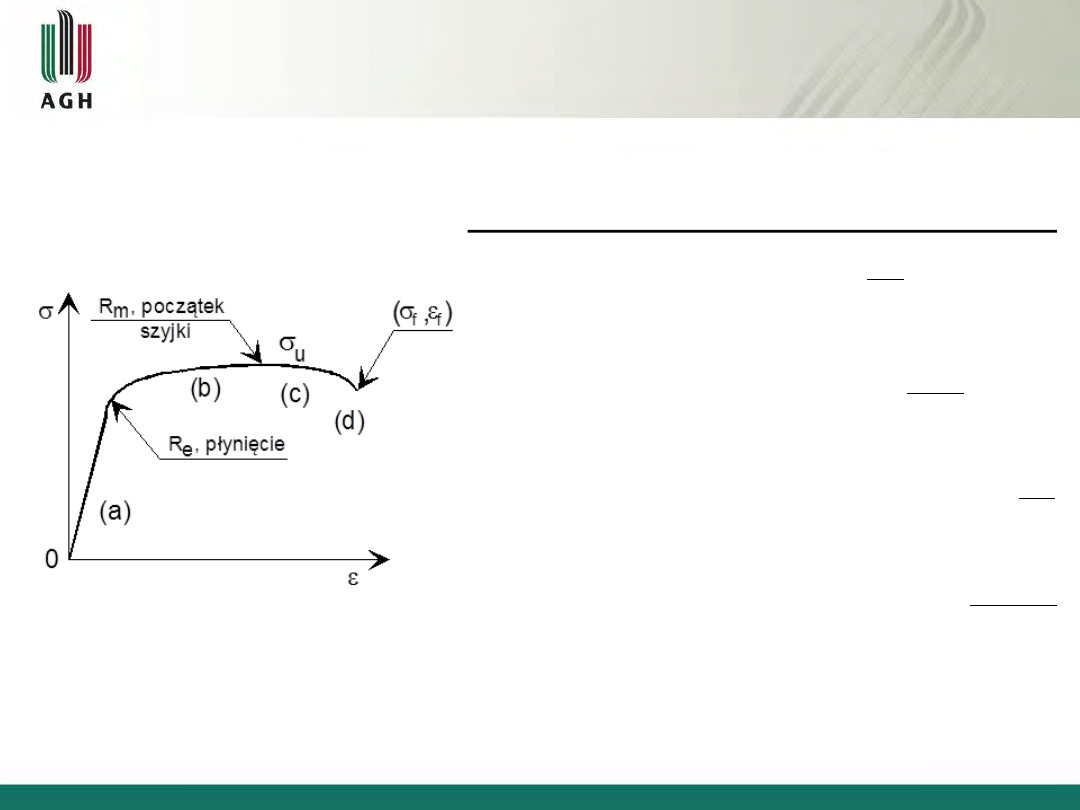
Rys.2.1 Schemat inżynierskiej krzywej rozciągania typowego materiału ciągliwego

(cechy charakterystyczne: płynięcie, zazwyczaj szyjka).

3

2.1 NAPRĘŻENIA I ODKSZTAŁCENIA INŻYNIERSKIE

Oparte są na początkowych nie zdeformowanych wymiarach próbek

Oznaczenia:



,



o

e

e

A

P

R



o

m

A

P

R

max



o

f

f

A

P





o

o

f

f

L

L

L







Stałe materiałowe o charakterze inżynierskim:



wytrzymałość doraźna:



inżynierskie naprężenie niszczące:



inżynierskie odkształcenie niszczące:

gdzie: A

o

- początkowa powierzchnia przekroju

L

o

(L

f

)- długość pomiarowa początkowa (końcowa)



granica plastyczności:

4

2.1 NAPRĘŻENIA I ODKSZTAŁCENIA INŻYNIERSKIE

R

eg













(a)

(b)

(c)





p

A

B

E

p



p

=?

E

t



pl

0.002

0

0

0

R

e 0.2

R

ed

R

e 0.2

R

e 0.2

=

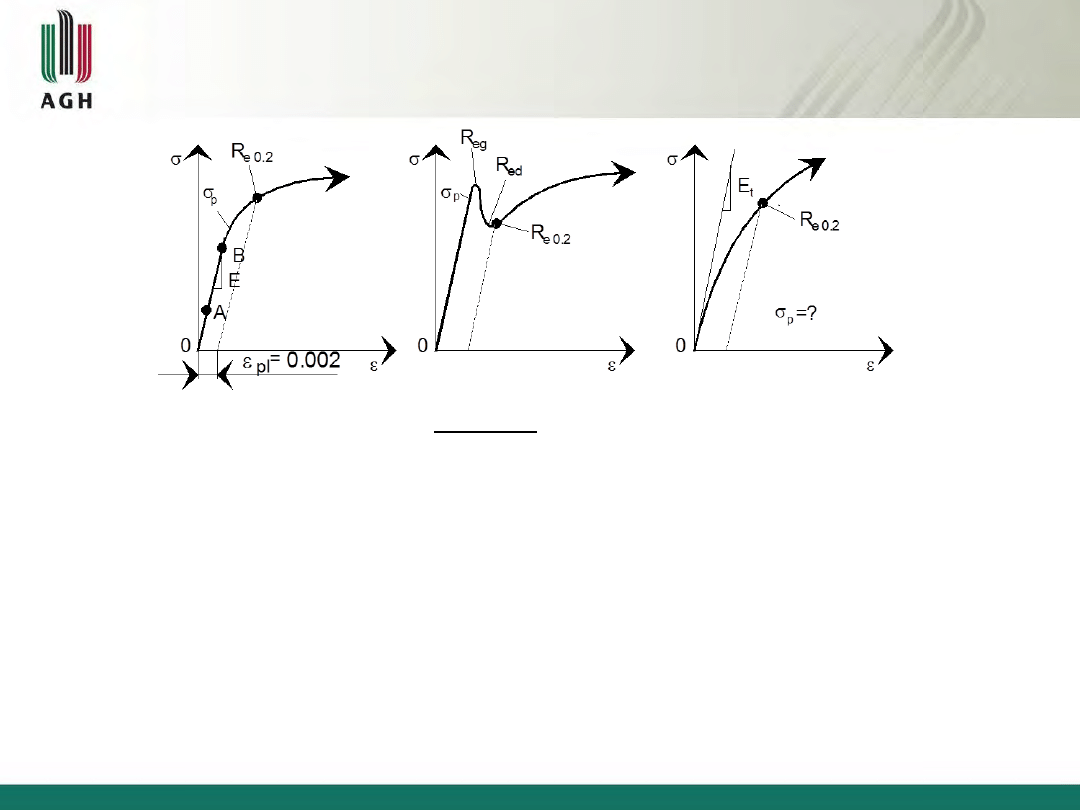
Rys.2.2 Kształt początkowej części krzywej rozciągania: a) większość metali i stopów; b)

z górną i dolną granicą plastyczności (np. stal miękka); c) bez zakresu liniowego

5

2.1 NAPRĘŻENIA I ODKSZTAŁCENIA INŻYNIERSKIE



E - moduł Younga: - tylko przypadek a) i b)



granica proporcjonalności:



P

- tylko przypadek a) i b)



umowna granica plastyczności: R

e0,2

jest najdogodniejszym parametrem do zidentyfikowania początku

odkształceń plastycznych (przy



= R

e02

;



pl

= 0,002)



górna i dolna granica plastyczności: R

eg

i R

ed

(R

eg

- duży rozrzut, R

ed



R

e 0,2

).

A

B

A

B

E















6

2.1 NAPRĘŻENIA I ODKSZTAŁCENIA INŻYNIERSKIE

Ciągliwość: zdolność materiału do akomodacji odkształceń plastycznych
bez zniszczenia

Materiały ciągliwe: zniszczenie poprzedzone znacznymi odkształceniami
plastycznymi, duża energia potrzebna do zniszczenia
(energia - pole pod wykresem



-



), często R

m

>



f

Materiały kruche: zniszczenie bez makroskopowych odkształceń
plastycznych, mała energia potrzebna do zniszczenia, R

m

=



f

7

2.1 NAPRĘŻENIA I ODKSZTAŁCENIA INŻYNIERSKIE

o

f

o

A

A

A



100

(b)

(a)

(a)

(b)

R





m

Miary ciągliwości:


wydłużenie procentowe: 100



f

,

(materiał kruchy:



f



5 % ; materiał ciągliwy:



f

> 5 % )



przewężenie procentowe:

gdzie:
A

f

- końcowa powierzchnia przekroju.

Posługiwanie się naprężeniami i odkształceniami inżynierskimi jest

korzystne, gdy zmiany wymiarów próbki są niewielkie. Przy dużych

odkształceniach plastycznych właściwsze jest używanie naprężeń i

odkształceń rzeczywistych.

Rys.2.3. Krzywa rozciągania materiału

kruchego

Oznaczenia:

Naprężenia rzeczywiste
gdzie: A - bieżąca powierzchnia przekroju


Odkształcenie rzeczywiste:


gdzie: zmiana długości mierzona jest w małych przyrostach



l

1

,



l

2

,



l

3

itd.,

a aktualna długość pomiarowa l

1

, l

2

, l

3

, itd. jest użyta do obliczenia

odkształcenia dla każdego przyrostu

Gdy



l

j

są bardzo małe:

gdzie: l = l

o

+



l - długość końcowa, l

o

- długość początkowa.

8

2.2 NAPRĘŻENIA I ODKSZTAŁCENIA RZECZYWISTE

~



~



A

P





~

j

j

l

l









~

(2.2)

(2.1)







l

l

o

o

l

l

l

dl

ln

~



(2.3)

Ponieważ odkształcenia inżynierskie:

to na podstawie (2.3) i (2.4) otrzymujemy:




Ponieważ przy dużych odkształceniach
plastycznych objętość pozostaje niezmienna, tzn.:

to na podstawie (2.3) i (2.6):

9

2.2 NAPRĘŻENIA I ODKSZTAŁCENIA RZECZYWISTE

(2.5)

(2.4)

(2.6)

o

l

l













l

l

o

o

l

l

l

dl

ln

~



(2.3)

































1

ln

1

ln

ln

~

o

o

o

l

l

l

l

l

0









ldA

Adl

const

l

A

d

d

A

A

A

A

A

dA

A

A

0

0

0

ln

2

ln

~

ln

~

0

















(2.7)

Z definicji i :


a uwzględniając (2.6):



otrzymamy:

10

2.2 NAPRĘŻENIA I ODKSZTAŁCENIA RZECZYWISTE

(2.9)

(2.8)



~



A

A

o









~

0









ldA

Adl

const

l

A





























1

~

o

o

o

l

l

l

l

l

11

2.2 NAPRĘŻENIA I ODKSZTAŁCENIA RZECZYWISTE





























1

~

o

o

o

l

l

l

l

l

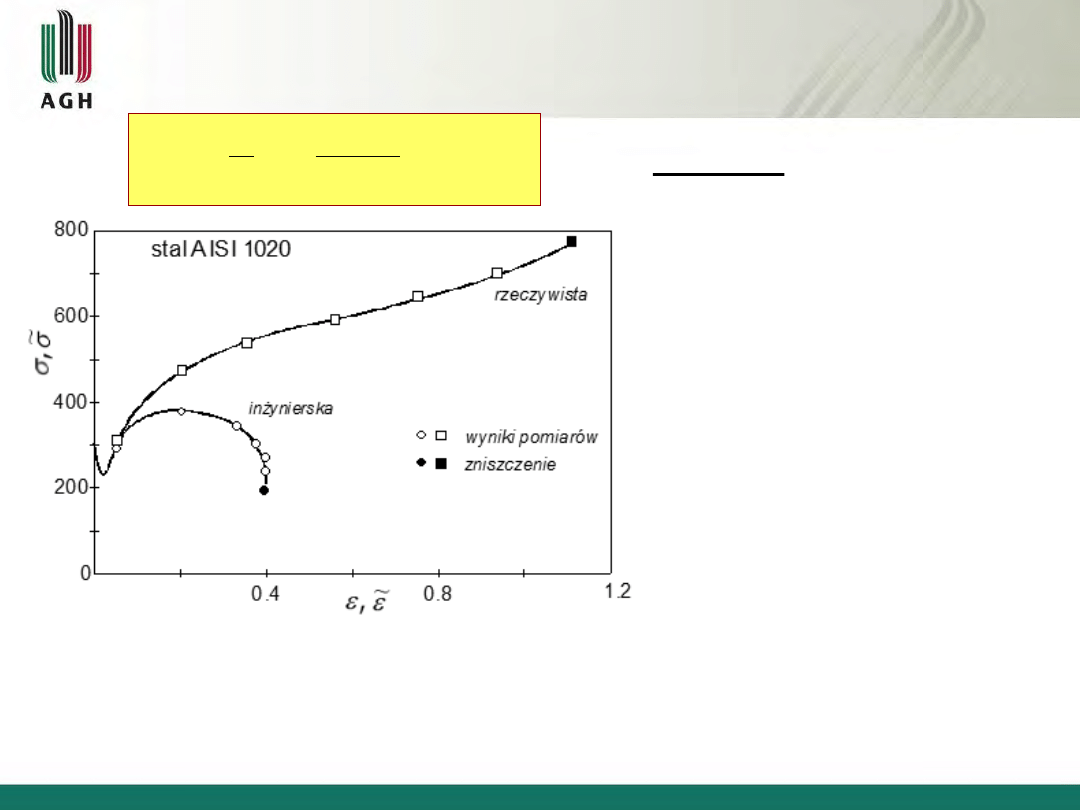
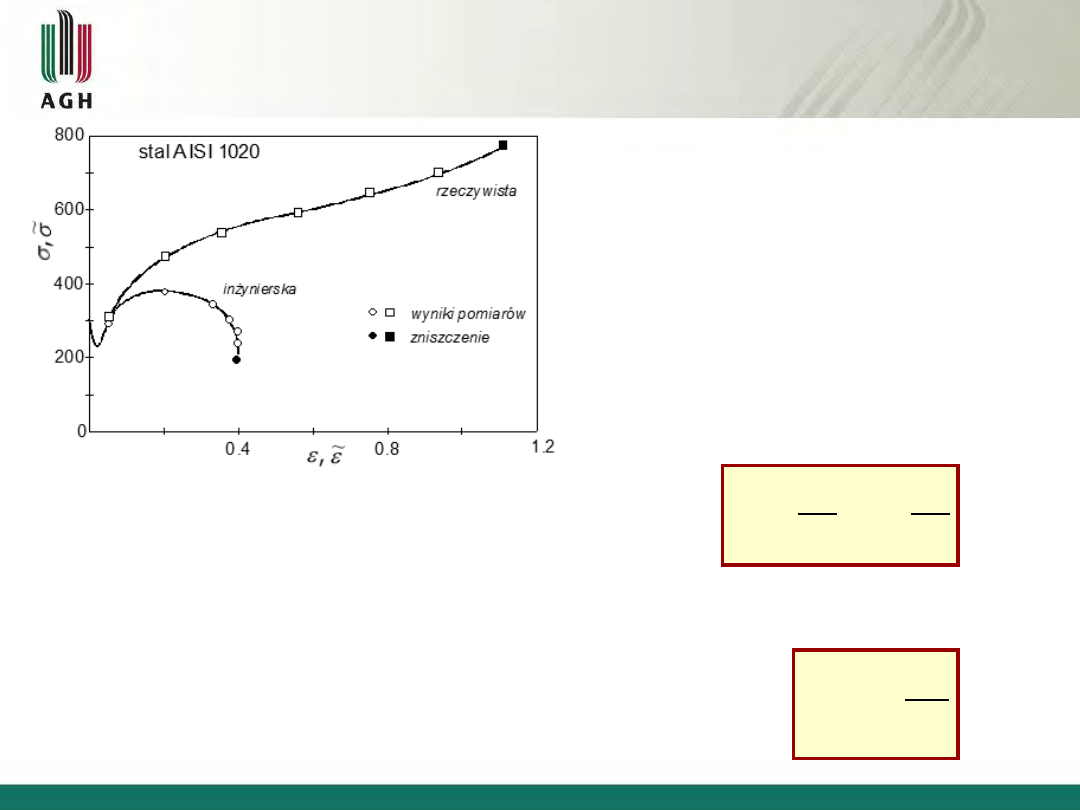
Rys. 2.4 Porównanie rzeczywistej i inżynierskiej krzywej

rozciągania dla stali miękkiej

Wnioski:
zawsze większe niż



=



do utworzenia się szyjki

potem >>



~



~



~



12

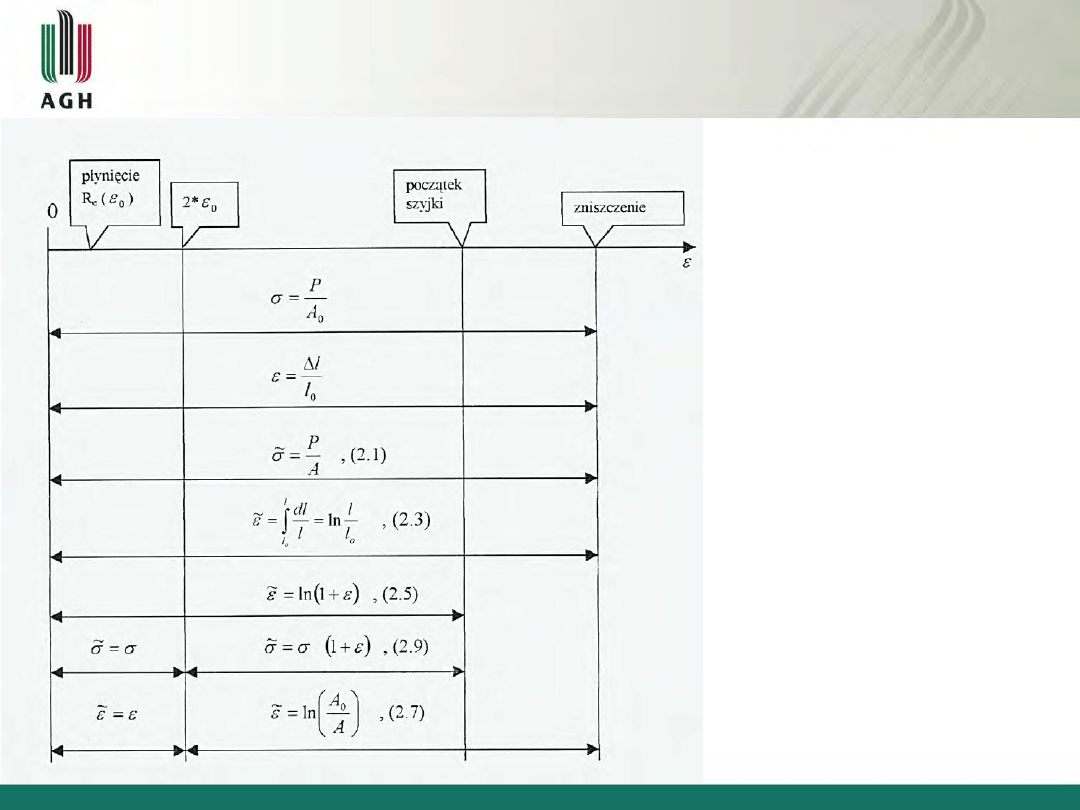
2.2 NAPRĘŻENIA I ODKSZTAŁCENIA RZECZYWISTE



rzeczywiste naprężenia niszczące (J):

gdzie:



f

- współrzędna



punktu



na krzywej inżynierskiej,

A

o

, A

f

- przekrój odpowiednio początkowy i po zniszczeniu



rzeczywiste odkształcenie niszczące (por. rów. 2.7):

Własności materiału o charakterze

rzeczywistym:

(współrzędne i punktu)



~



~

f

o

f

f

f

f

A

A

A

P









~

(2.10)

f

o

f

A

A

ln

~





(2.11)

f



~

13

2.2 NAPRĘŻENIA I ODKSZTAŁCENIA RZECZYWISTE

Zakres ważności różnych wzorów z próby rozciągania

Równania (2.5) i (2.9):

można stosować tylko do utworzenia się

szyjki, bo potem wydłużenie nie jest

równomierne na długości pomiarowej

Po utworzeniu się szyjki:

tylko równania (2.1) i (2.7)

Równanie (2.9):

może być stosowane przy dość

znacznych odkształceniach plastycznych

bo oparte jest na założeniu stałej

objętości materiału (2.6).

14

2.3. MATEMATYCZNY OPIS KRZYWEJ ROZCIĄGANIA DLA

METALI

n

p

e

H

E

1

~

~

~

~

~































, - odpowiednio sprężysta i plastyczna

składowa odkształcenia,

n - wykładnik umocnienia
H - współczynnik wytrzymałości

~



e

~



p

Stałe materiałowe H i n wyznacza się przedstawiając otrzymane doświadczalnie punkty
we współrzędnych podwójnie logarytmicznych

 





~

,

~

(2.12)

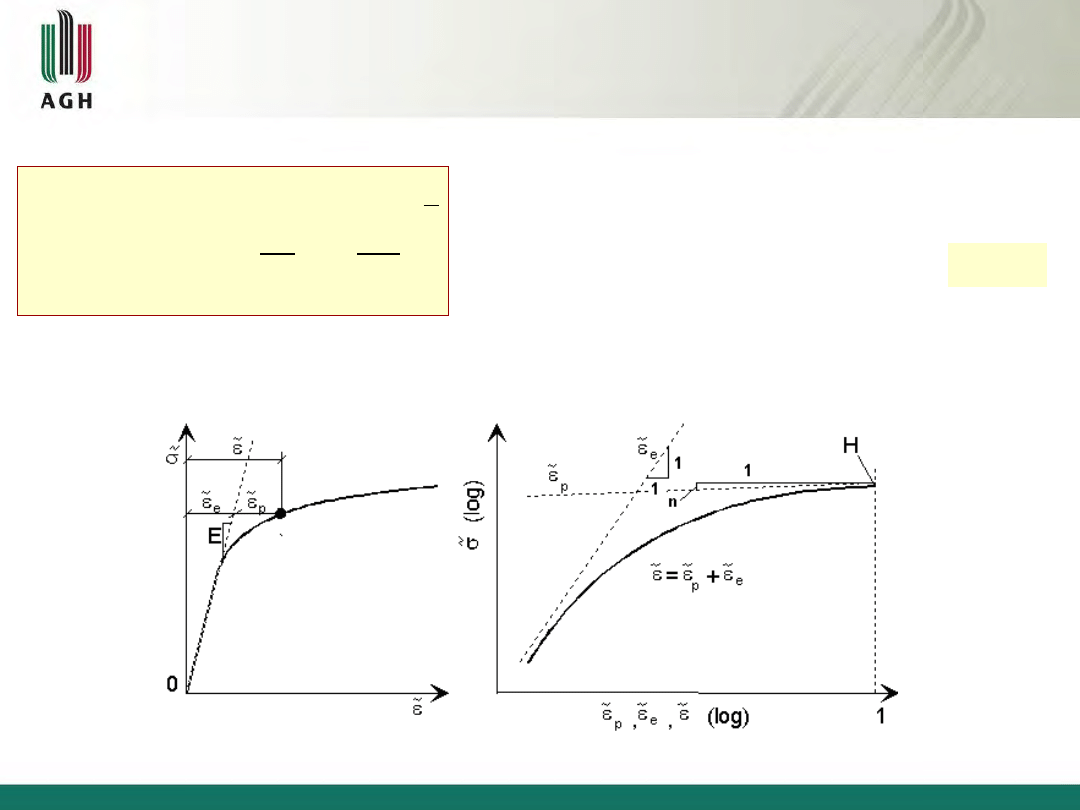
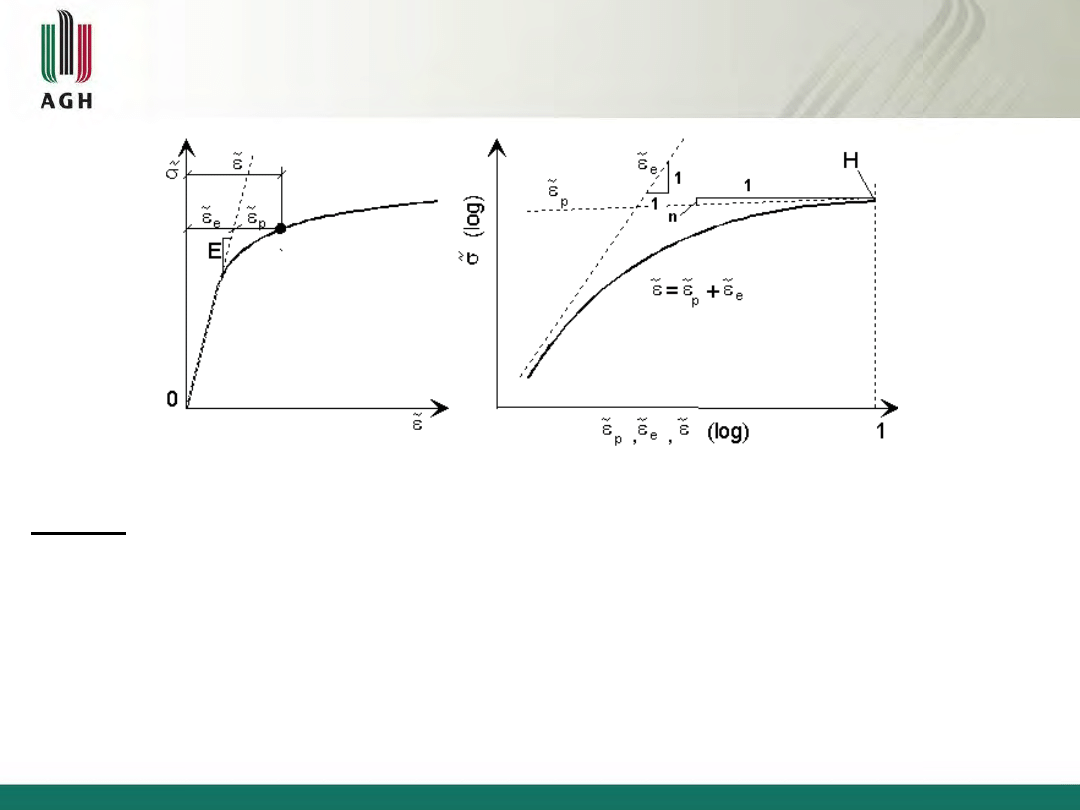
Rys. 2.5 Rzeczywista krzywa odkształcenia we współrzędnych: a) liniowych; b) podwójnie logarytmicznych

15

2.3. MATEMATYCZNY OPIS KRZYWEJ ROZCIĄGANIA DLA

METALI

Rys. 2.5 Rzeczywista krzywa odkształcenia we współrzędnych: a) liniowych; b) podwójnie logarytmicznych

Uwaga! We współrzędnych podwójnie logarytmicznych:


wykres jest linią prostą o współczynniku kierunkowym 1:



wykres jest linią prostą o współczynniku kierunkowym n:

e





~

~



e

E





~

log

log

~

log





p





~

~



log~ log

log~









H n

p

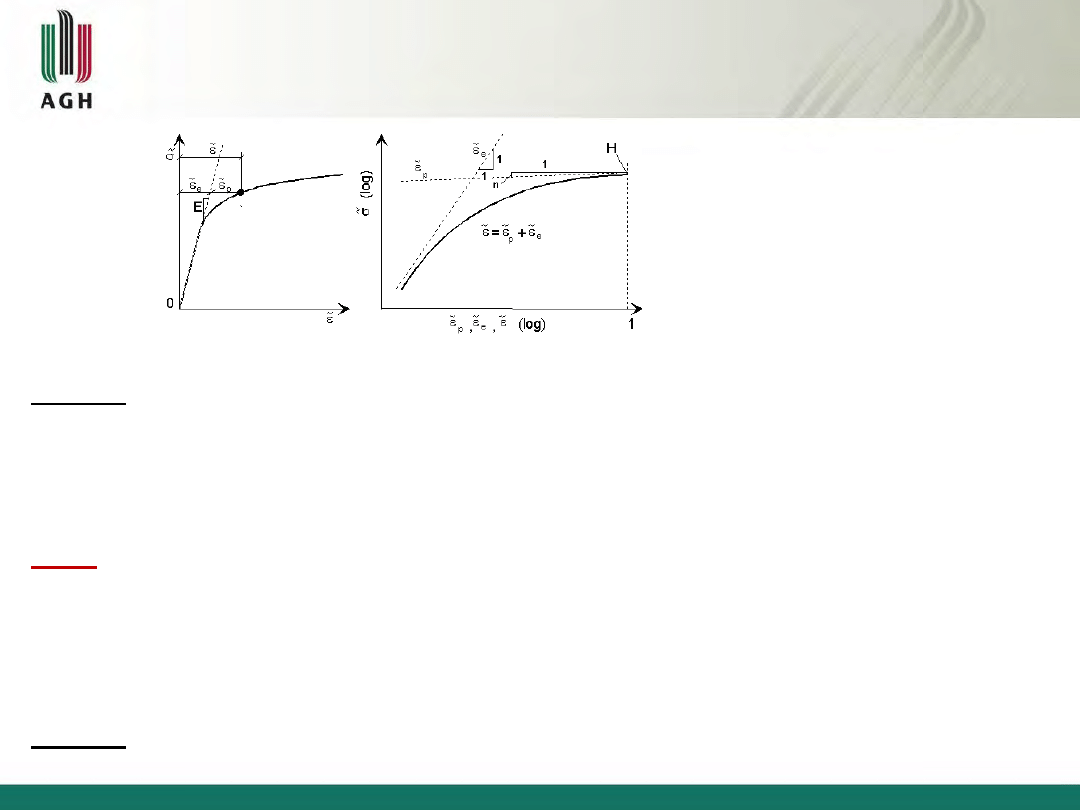
Uwaga! We współrzędnych podwójnie logarytmicznych:


wykres jest linią prostą o współczynniku kierunkowym 1:



wykres jest linią prostą o współczynniku kierunkowym n:

16

2.3. MATEMATYCZNY OPIS KRZYWEJ ROZCIĄGANIA DLA

METALI

Rys. 2.5 Rzeczywista krzywa odkształcenia we współrzędnych: a) liniowych; b) podwójnie logarytmicznych

e





~

~



e

E





~

log

log

~

log





p





~

~



log~ log

log~









H n

p

Stąd:

E – wartość przy , ; H - wartość przy
Zakres małych odkształceń: wykres wypadkowy bliski wykresowi
Zakres dużych odkształceń: wykres wypadkowy bliski wykresowi

Uwaga: zależność jest ważna od aż do zniszczenia



~

1

~



e





~

1

~



p



e





~

~



p





~

~



n

p

H





~

~



0

~



p



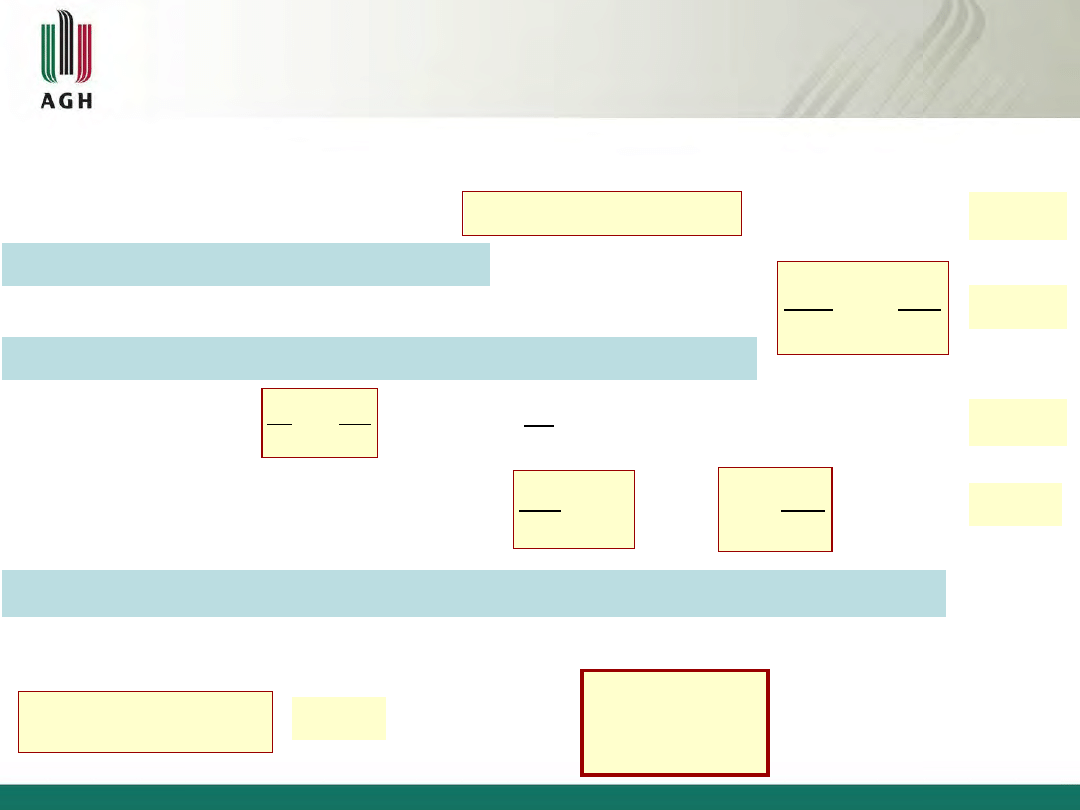
(C)* Ponieważ w chwili tworzenia się szyjki można przyjąć:

17

2.3. MATEMATYCZNY OPIS KRZYWEJ ROZCIĄGANIA DLA

METALI

Wyznaczenie wykładnika umocnienia „n” w równaniu na podstawie
inżynierskiej krzywej

n

p

H

)

~

(

~













A

P







~





~

~

Ad

dA

dP







(2.13)

(A)* W chwili utworzenia się szyjki dP=0

Na podstawie (2.13) i (A)*:

A

dA

d









~

~

(2.14)

(B)* Przy odkształceniach plastycznych V=A



l=const, tzn. dV=0

(B)*



Adl+ldA=0



A

dA

l

dl





(2.15)

gdzie:



~

d

l

dl

df



stąd, uwzględniając (2.14) i (2.15)

w chwili tworzenie sią szyjki:







~

~

~

d

d



lub







~

~

~

d

d



(2.16)







~

p





~

~



Równanie

n

p

H

)

~

(

~







uwzględniając (C*) oraz (2.15) ma postać:

1

~

)

~

(





n

p

n

p

Hn

H





(2.17)

stąd:

p

n



~



18

2.4. EFEKT BAUSCHINGERA (1880)

Jeżeli przy obciążaniu materiału wykazującego efekt umocnienia naprężenie przekroczyło

granicę plastyczności przy monotonicznym rozciąganiu (R

er

)

, to przy zmianie kierunku

obciążenia (odciążaniu) uplastycznianie występuje przy naprężeniu



K

powyżej poziomu

granicy plastyczności przy monotonicznym ściskaniu (R

ec

)

Dla metali można z dobrym przybliżeniem przyjąć, że gdy materiał został obciążony do

poziomu



>R

e

, to zmiana naprężeń potrzebna do spowodowania płynięcia przy odciążeniu

wynosi:



= 2R

e







monotoniczne

rozciąganie

monotoniczne

ściskanie

K







= f(



)

er

R

ec

R

Rys. 2.6 Ilustracja efektu Bauschingera

pojawienie się odkształceń plastycznych przy odciążaniu

(początek tzw. odwróconego płynięcia - „reversed yielding”)

19

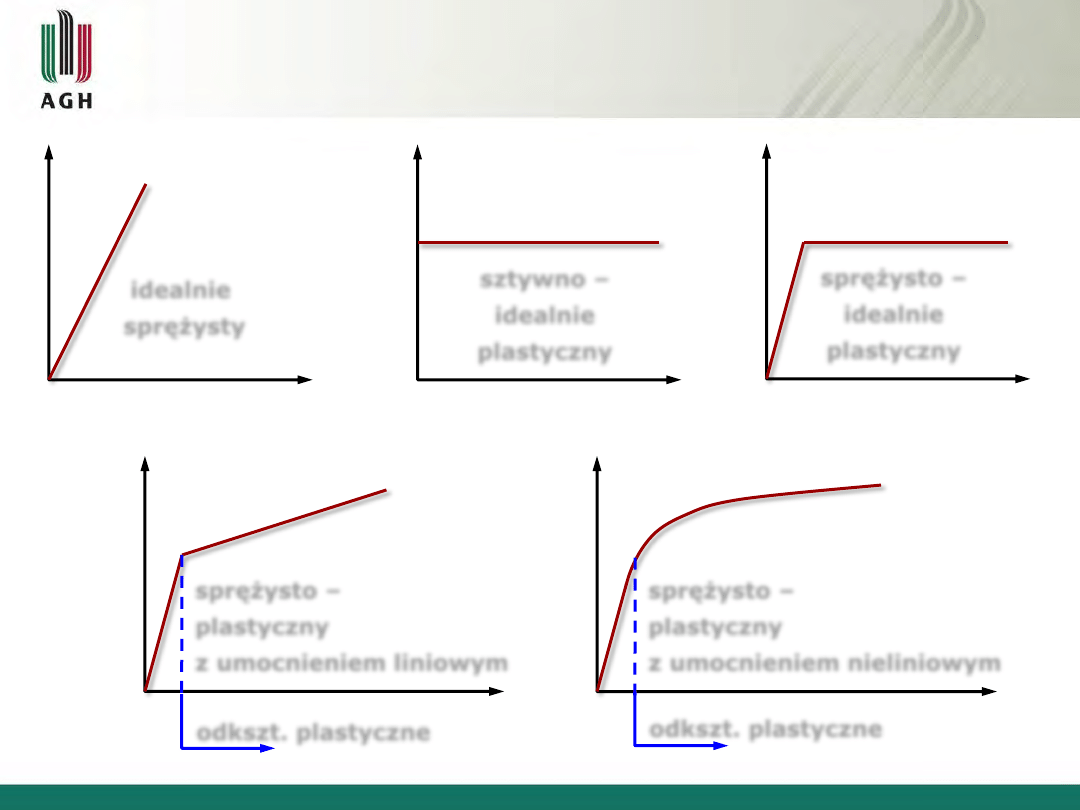
2.5. Modele materiałów

idealnie

sprężysty





sztywno –

idealnie

plastyczny





sprężysto –

idealnie

plastyczny





sprężysto –
plastyczny
z umocnieniem liniowym





odkszt. plastyczne



~



~

sprężysto –
plastyczny
z umocnieniem nieliniowym

odkszt. plastyczne