PODSTAWY
ANALIZY
NIEZAWODNOŚCI

dr inż. Marek Matyjewski

Politechnika Warszawska

Wydz. Mechaniczny Energetyki i Lotnictwa

Ryzyko w systemie C-T-O









⋅









=









zagrożenia

miara

zawodności

miara

ryzyka

miara

Człowiek

Technika

Środowisko

PODSTAWOWE POJĘCIA

Zdarzenie niepożądane jest to zdarzenie, którego
zajście w rozpatrywanym systemie C-T-O wywołuje w
efekcie zagrożenie dla chronionych dóbr.

Niesprawność jest to zdarzenie niepożądane
pojawiające się w ramach podsystemu C-T.

Niesprawność obiektu jest to każde zdarzenie
uniemożliwiające fizycznie lub umownie spełnianie
przewidzianych dla niego funkcji.

Uszkodzenie, awaria

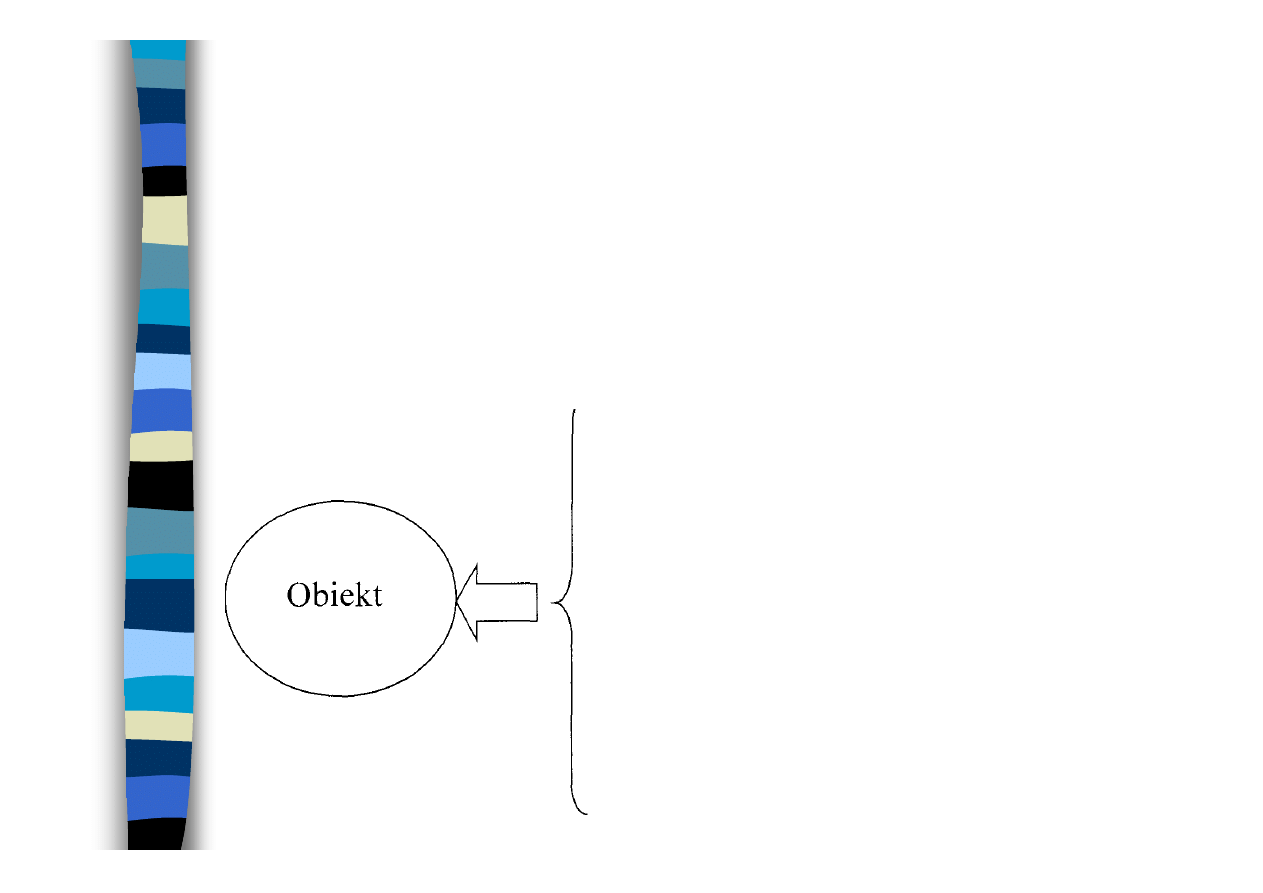
PODSTAWOWE POJĘCIA

Niezawodność - zdolność obiektu do prawidłowego
funkcjonowania w określonym czasie bez niesprawności.

System C-T

Człowiek (np. operator)

Zespół ludzi

Obiekt techniczny

Podzespół obiektu technicznego

Element obiektu technicznego

…

Stan niezawodnościowy obiektu

stan zdatno

stan zdatno

ś

ś

ci, stan niezdatno

ci, stan niezdatno

ś

ś

ci

ci

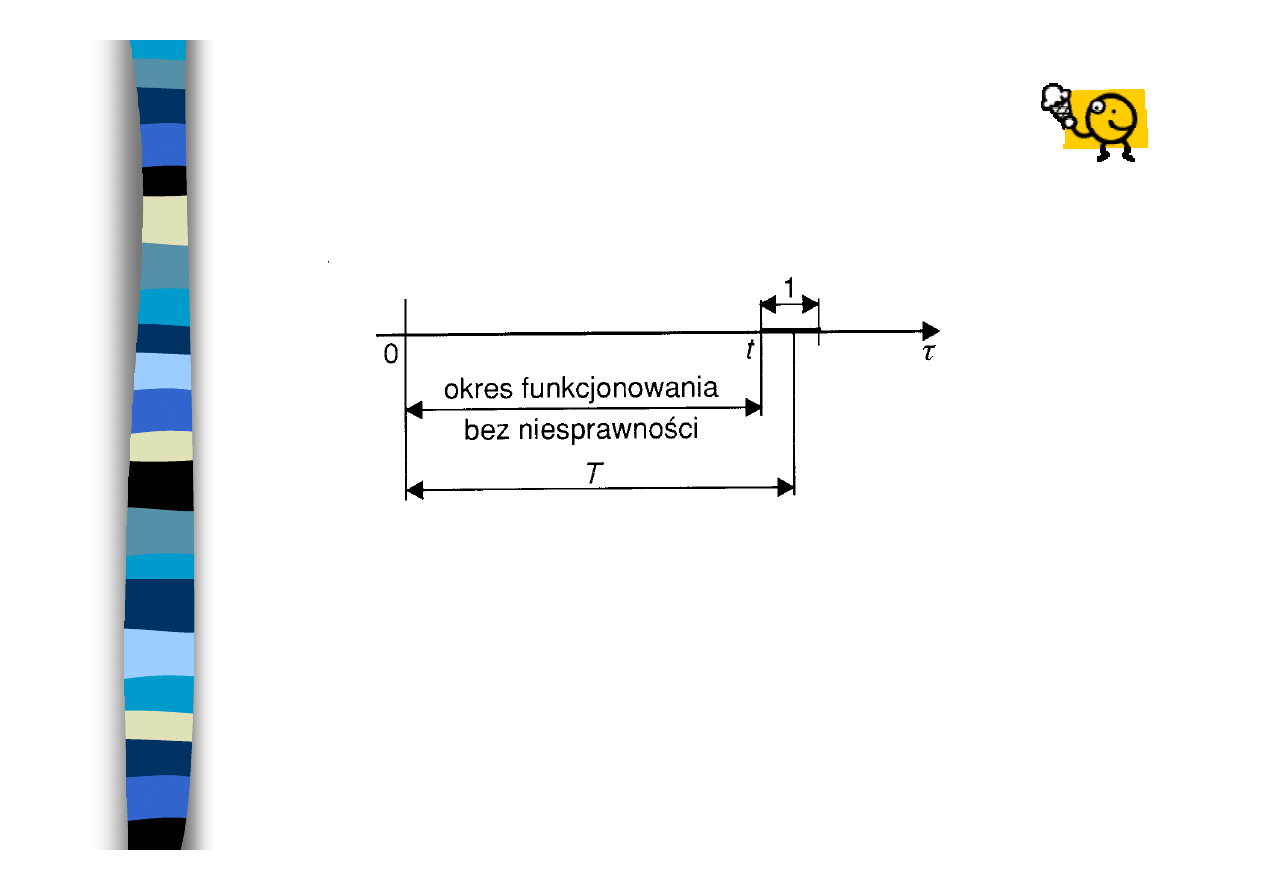
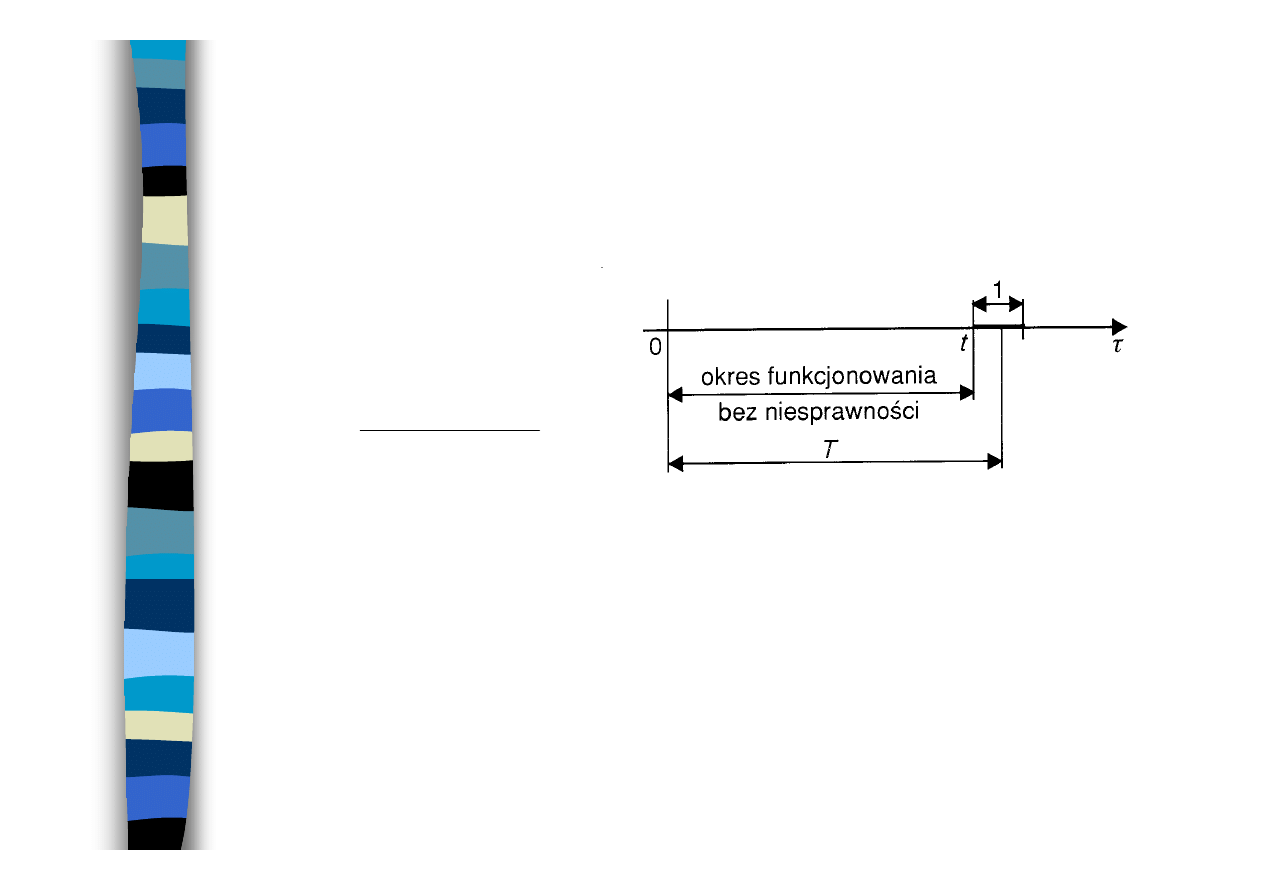
Czas funkcjonowania -

τ

Czas odnawiania

-

ϑ

Trwałość

-

t

rw

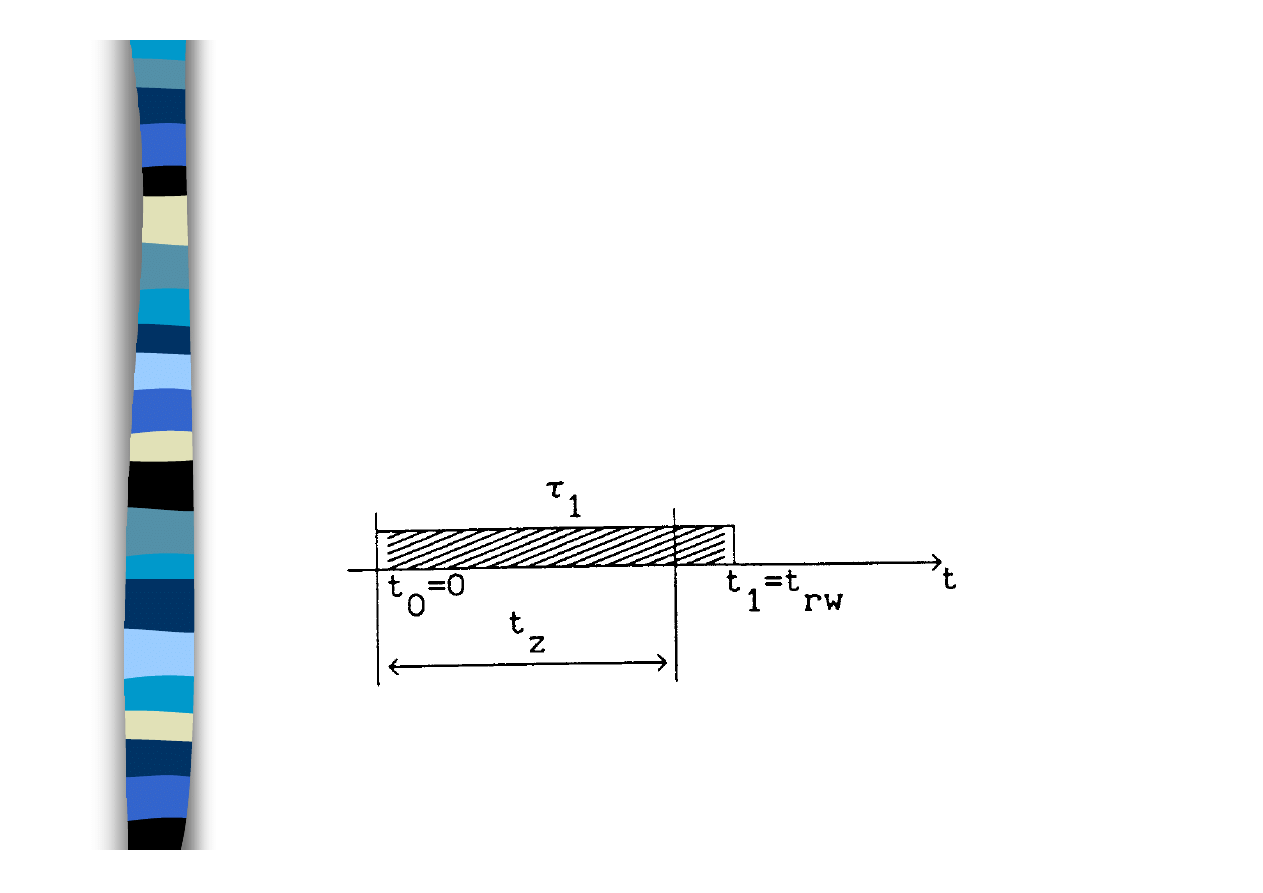
Przebieg procesu eksploatacji
obiektu

obiekt

nie

odnawiany

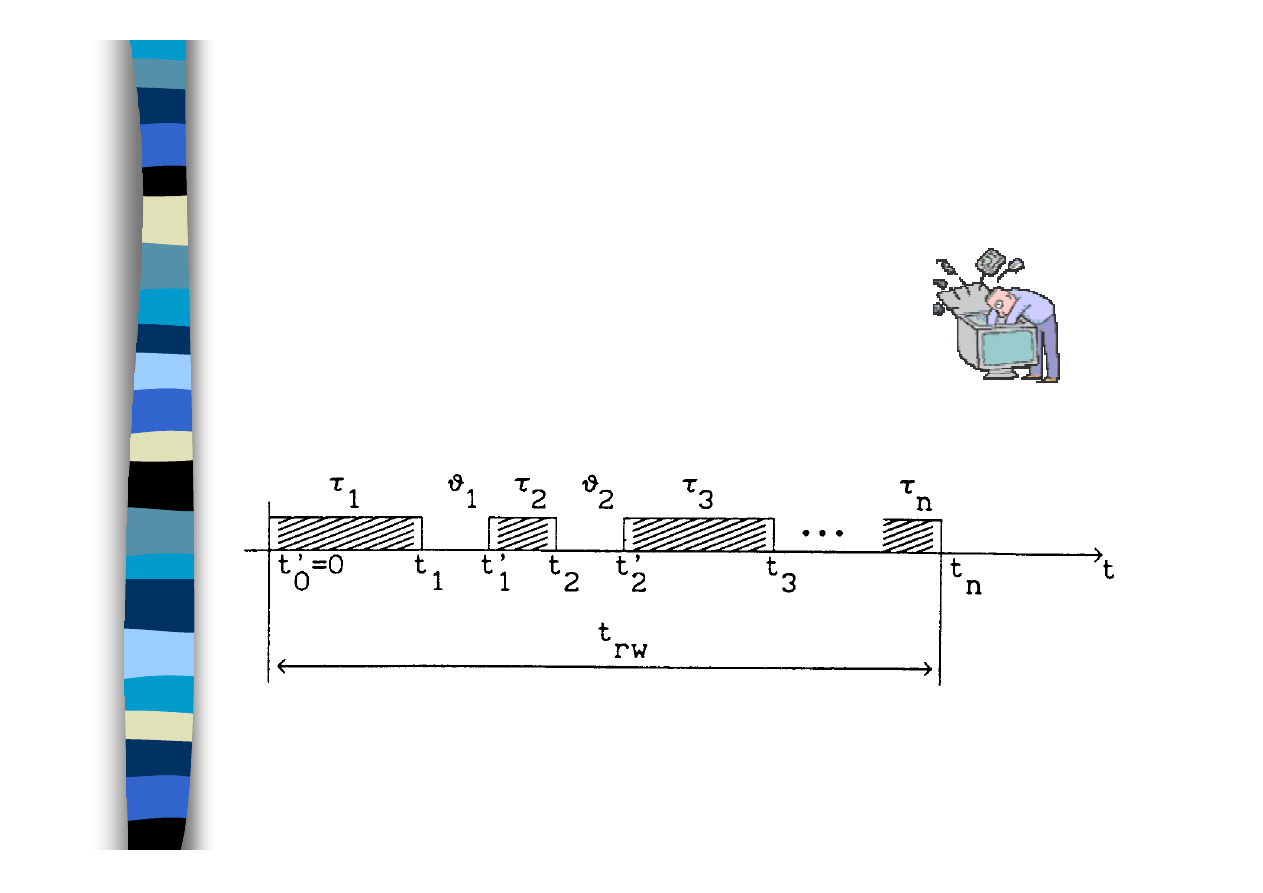
Przebieg procesu eksploatacji
obiektu

obiekt odnawiany

MIARY NIEZAWODNOŚCI

R(t) = P{

R(t) = P{

T

T

> t}

> t}

Przykłady realizacji czasu funkcjonowania
obiektu do wystąpienia niesprawności

MIARY NIEZAWODNOŚCI

R(t) = P{

R(t) = P{

T

T

> t}

> t}

Q(t) = 1 - R(t)

o

n

)

(

b

1

)

(

Rˆ

t

t

−

=

estymator funkcji niezawodno

estymator funkcji niezawodno

ś

ś

ci

ci

n

o

- liczebność próbki

b(t)

- liczba uszkodzonych obiektów do chwili t

Intensywność niesprawności

Intensywność niesprawności

λλλλ

λλλλ

to prawdopodobieństwo

wystąpienia niesprawności obiektu w jednostce czasu
następującej bezpośrednio po chwili

t

t, pod warunkiem że w chwili

t

t obiekt jest zdatny do funkcjonowania.

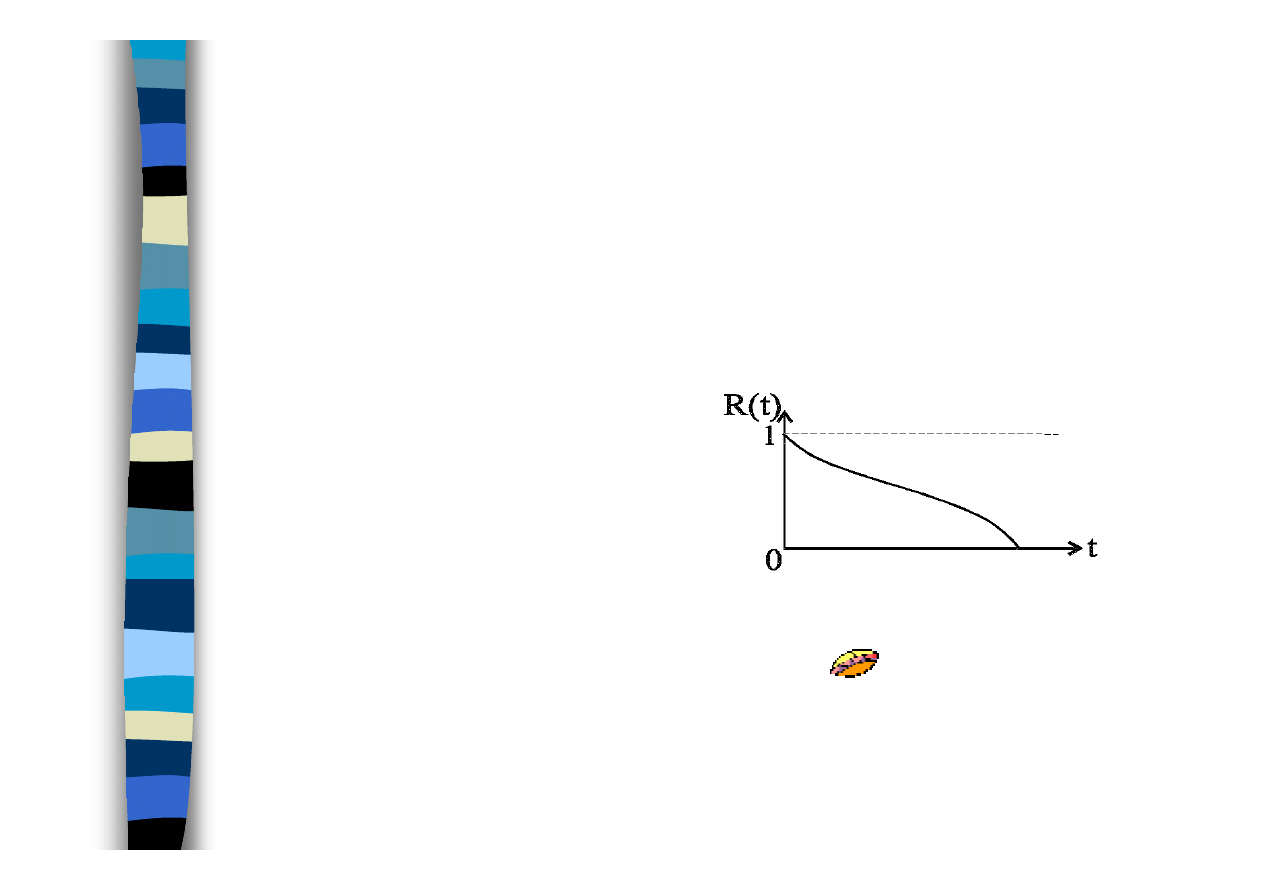
Intensywność niesprawności

( )

∫

=

−

t

τ

τ

0

)

(

d

e

t

R

λ

Gdy

λλλλ=const

t

)

(

λ

−

= e

t

R

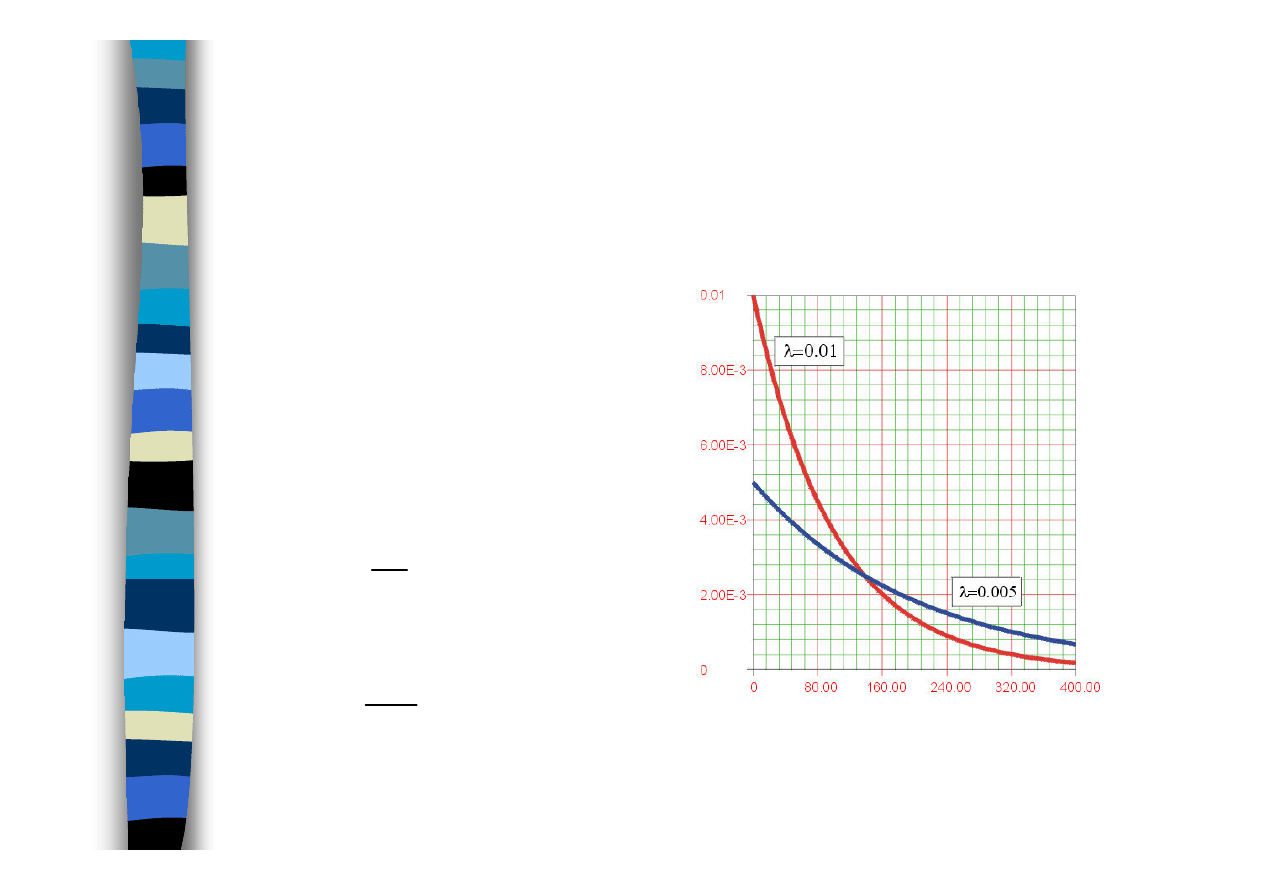
Rozkład wykładniczy

( )

( )

( )

;

1

;

1

;

;

1

2

λ

λ

λ

λ

λ

λ

=

=

=

−

=

=

−

−

−

VT

ET

e

t

f

e

t

Q

e

t

R

t

t

t

krzywa gęstości rozkładu wykładniczego
w zależności od parametru

λ = const.

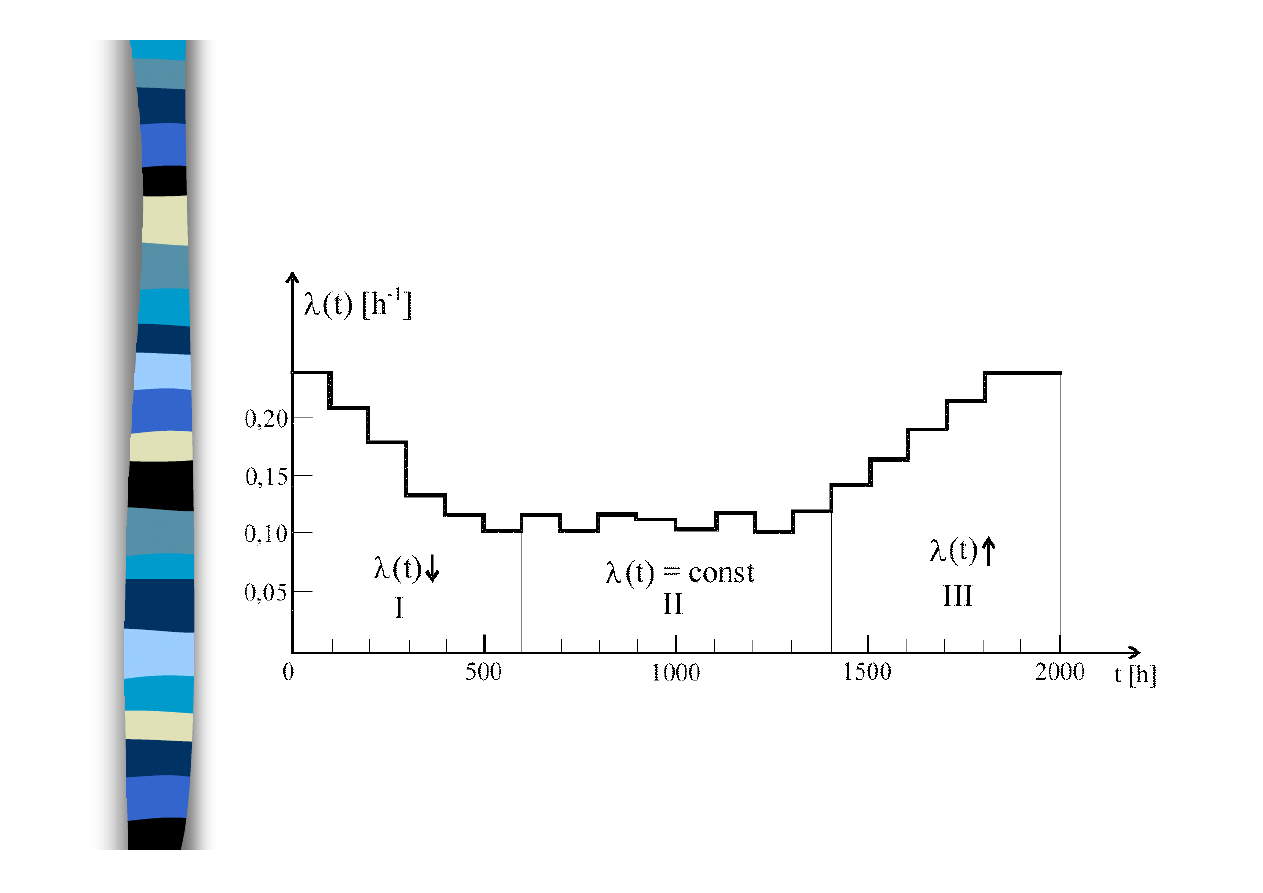
Intensywność niesprawności

Estymator
intensywności niesprawności

n(t) - liczebność próbki w chwili t

b(t,t+

∆t) - liczba obiektów, które uległy niesprawnościom

w okresie (t,t+

∆t)

( )

( )

t

t

n

t

t

t

b

t

∆

⋅

∆

+

=

)

,

(

ˆ

λ

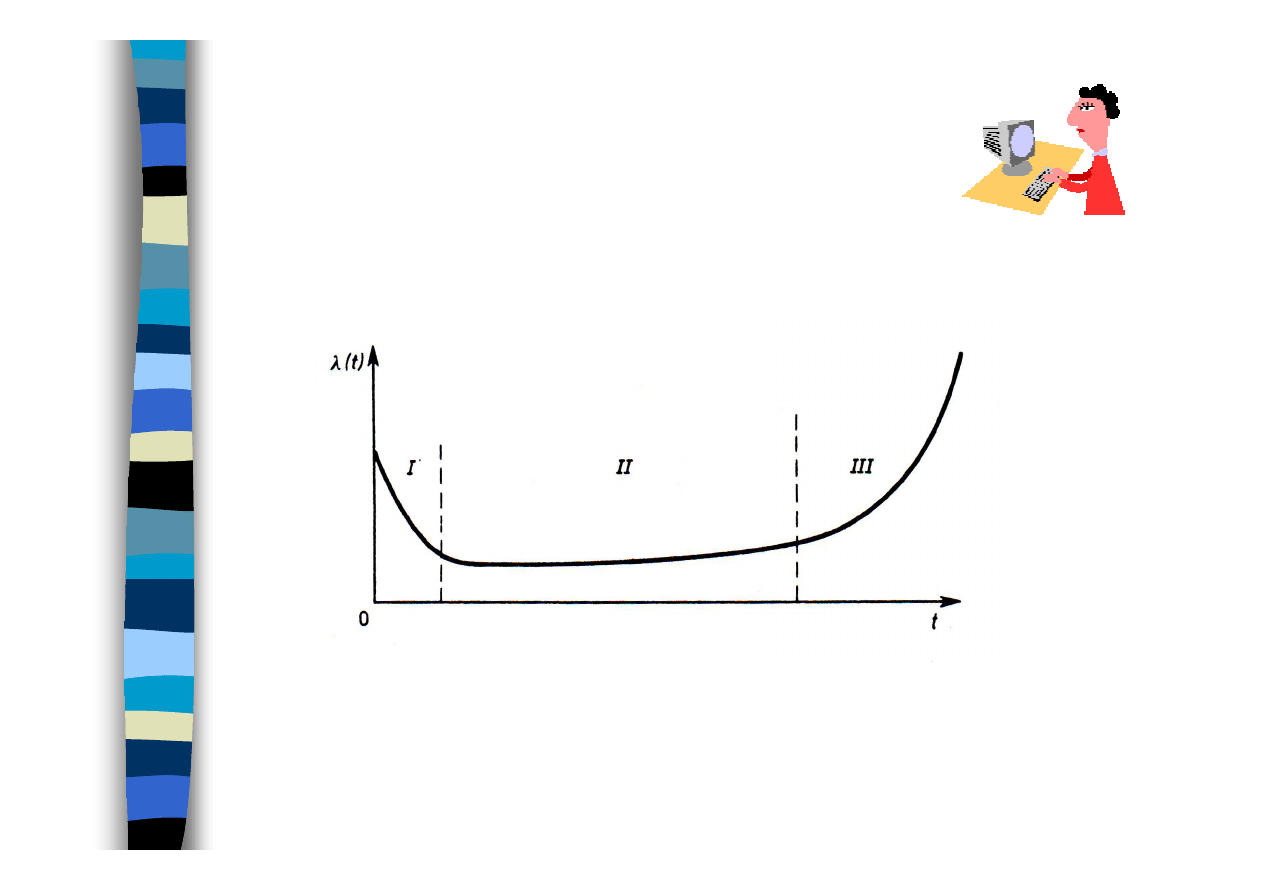
Przebieg intensywności
niesprawności

Typowy przebieg intensywności niesprawności obiektu technicznego

Zadanie

Intensywność uszkodzeń przekładni zębatej jest
stała (obiekt się nie starzeje) i wynosi 10

-5

[1/h].

Przewidywany czas pracy przekładni 10 000 [h].
Jakie jest prawdopodobieństwo funkcjonowania
przekładni bez uszkodzeń w ciągu:
•Pierwszych 100 h
•Przewidywanego czasu pracy
•Ostatnich 100 h

0,999
0,9048
0,999

t

)

(

λ

−

= e

t

R

999

0

001

0

100

00001

0

,

)

(

,

,

=

=

=

−

⋅

−

e

e

t

R

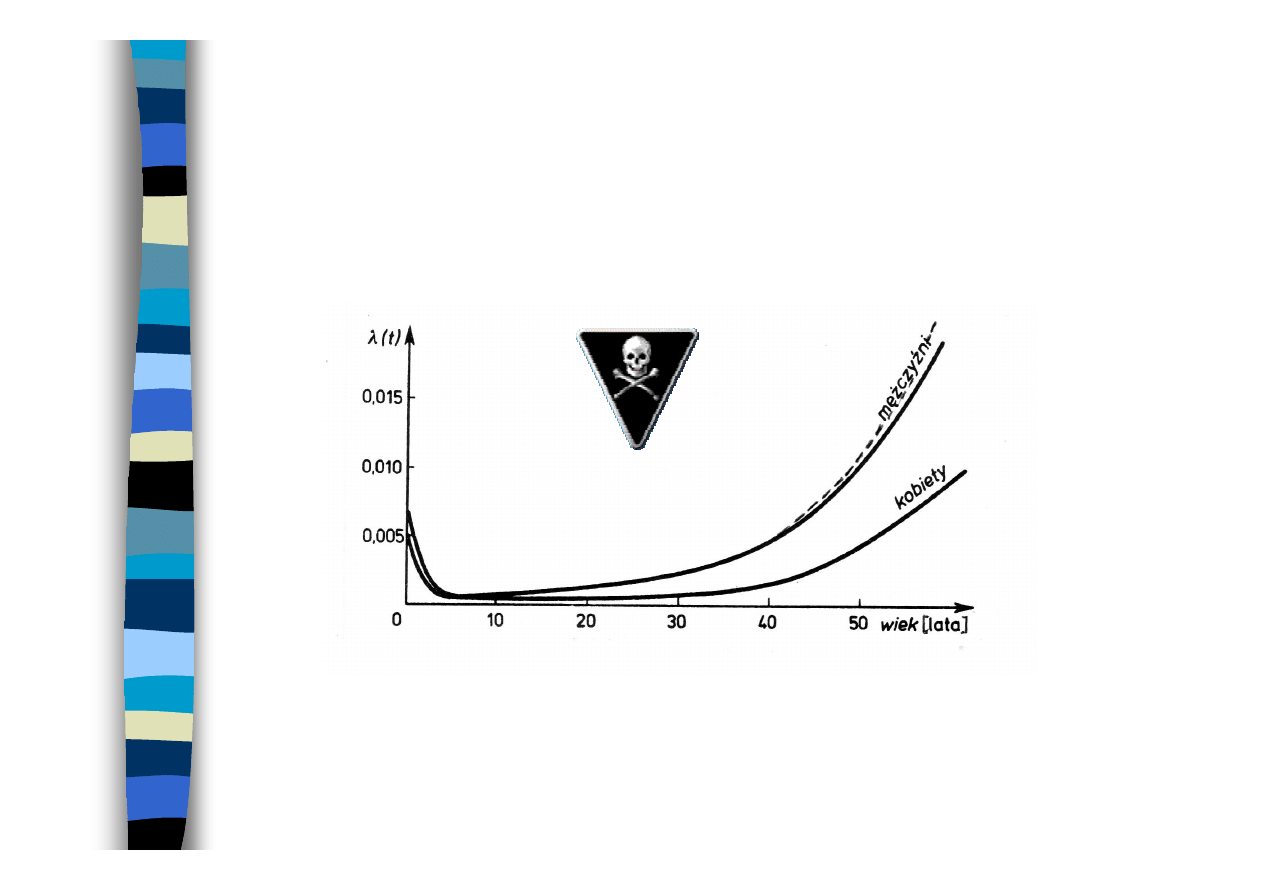
Przebieg intensywności
niesprawności

Przebieg intensywności zgonów mężczyzn (— 1978, --- 1994)
i kobiet (— 1978, 1994) w Polsce

MTTF & MTBF

∫

∫

∞

∞

=

⋅

=

0

0

)

(

)

(

dt

t

R

dt

t

f

t

EΤ

E

E

T

T

–

–

M

M

ean

ean

T

T

ime

ime

T

T

o

o

F

F

ailure

ailure

Dla obiektów

nie

odnawianych

E

E

T

T

–

–

M

M

ean

ean

T

T

ime

ime

B

B

etween

etween

F

F

ailures

ailures

T – zmienna losowa,

w analizie niezawodności

time

time

-

-

to failure

to failure

Dla obiektów odnawianych

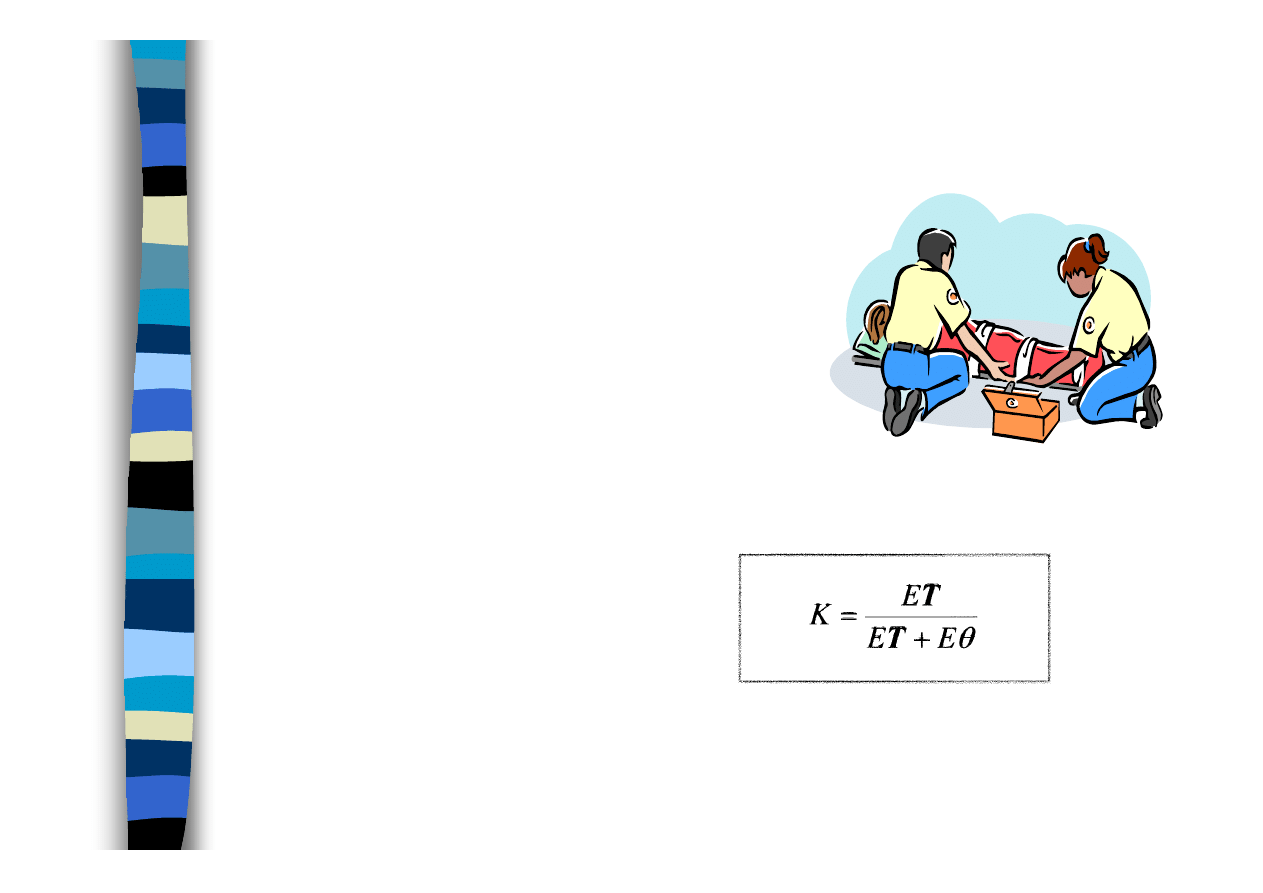
Miary niezawodności charakterystyczne
dla obiektów odnawianych

Gotowo

Gotowo

ść

ść - ważna cecha systemów

przeciwdzia

przeciwdzia

ł

ł

ania

ania

zagro

zagro

ż

ż

eniom

eniom

(np. systemów ratownictwa)

Wsp

Wsp

ó

ó

ł

ł

czynnik gotowo

czynnik gotowo

ś

ś

ci

ci

K

K –

prawdopodobieństwo przebywania obiektu w stanie
zdatności w dowolnej chwili

ET i E

θθθθ

- wartości oczekiwane (średnie) czasów przebywania

obiektu w stanie zdatności i w stanie niezdatności

MTTF =

12

,

λ =

0.083

[1/rok]

0

0,1

0,2

0,3

0,4

0,5

0,6

0,7

0,8

0,9

1

0

5

10

15

20

R(t)

czas [lata]

12

t

e

−

Zadanie

Zauważono, że średni czas użytkowania zakrętomierzy

w szybowcach wynosi 12 lat. Wiedząc, że czas

zdatności tych zakrętomierzy ma rozkład wykładniczy

należy określić:

ƒ

czas, po którym niezawodność zakrętomierzy spadnie

do 0,5 (zapas zdatności)

ƒ

niezawodność zakrętomierzy w ciągu 5 lat

R(

5

) =

0.66

t (

0.5

) =

8.32

lat

Zadanie

Samolot bezzałogowy musi mieć niezawodność powyżej

0,99

w czasie misji trwającej

10 godzin

.

Jaki powinien mieć co najmniej średni czas do
uszkodzenia (

MTTF

), przy założeniu rozkładu

wykładniczego ?

R(

10

)

≥

0.99

ET =1/

λ ≥

995 h

STRUKTURA
NIEZAWODNOŚCIOWA

Struktura niezawodno

Struktura niezawodno

ś

ś

ciowa

ciowa określa zależność

niezawodności obiektu od niezawodności jego
elementów

Sposoby graficznego przedstawiania struktur
niezawodnościowych:

•

schematy blokowe

•

drzewa niesprawności

STRUKTURA
NIEZAWODNOŚCIOWA

Podstawowe struktury niezawodnościowe

¾

szeregowe

¾

równoległe

¾

„k z m”

¾

z rezerwą

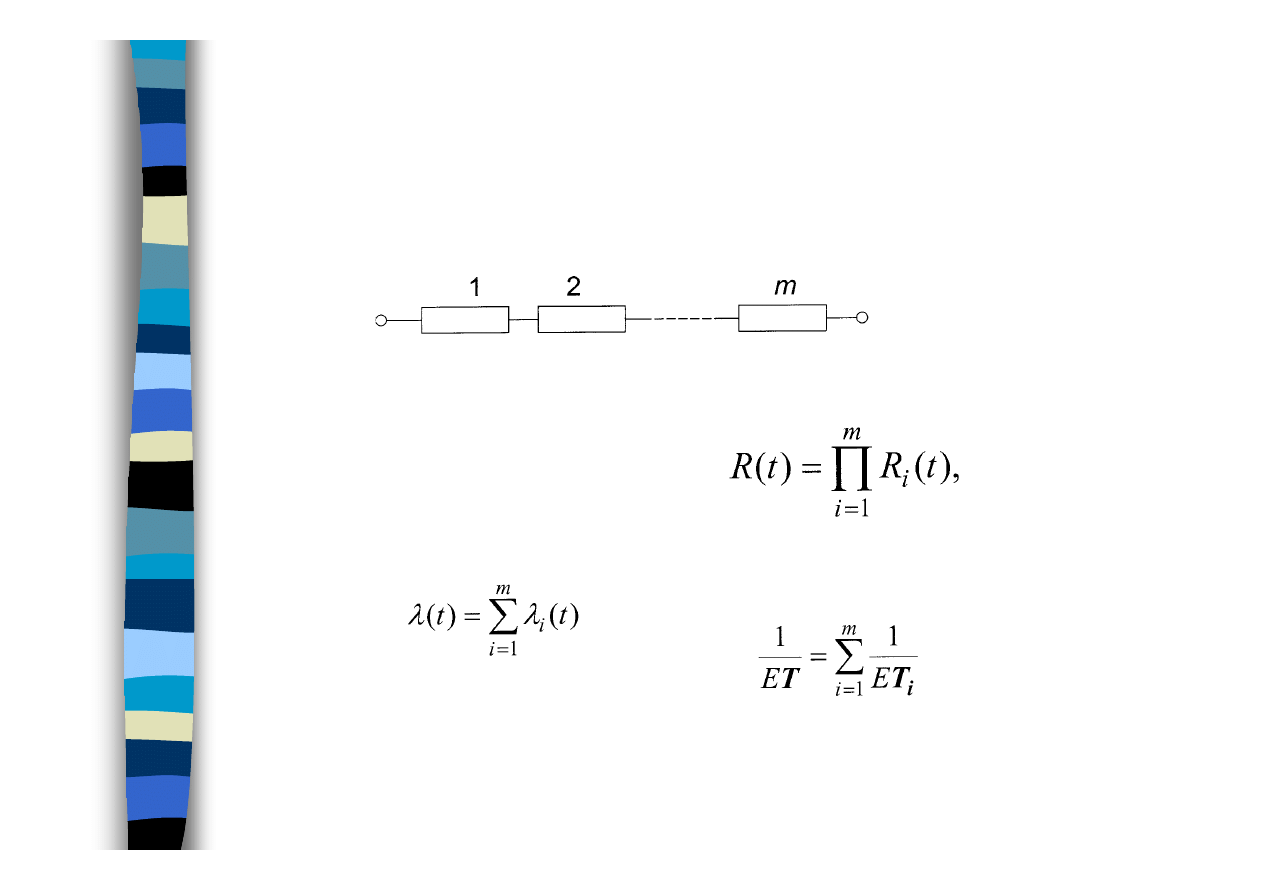
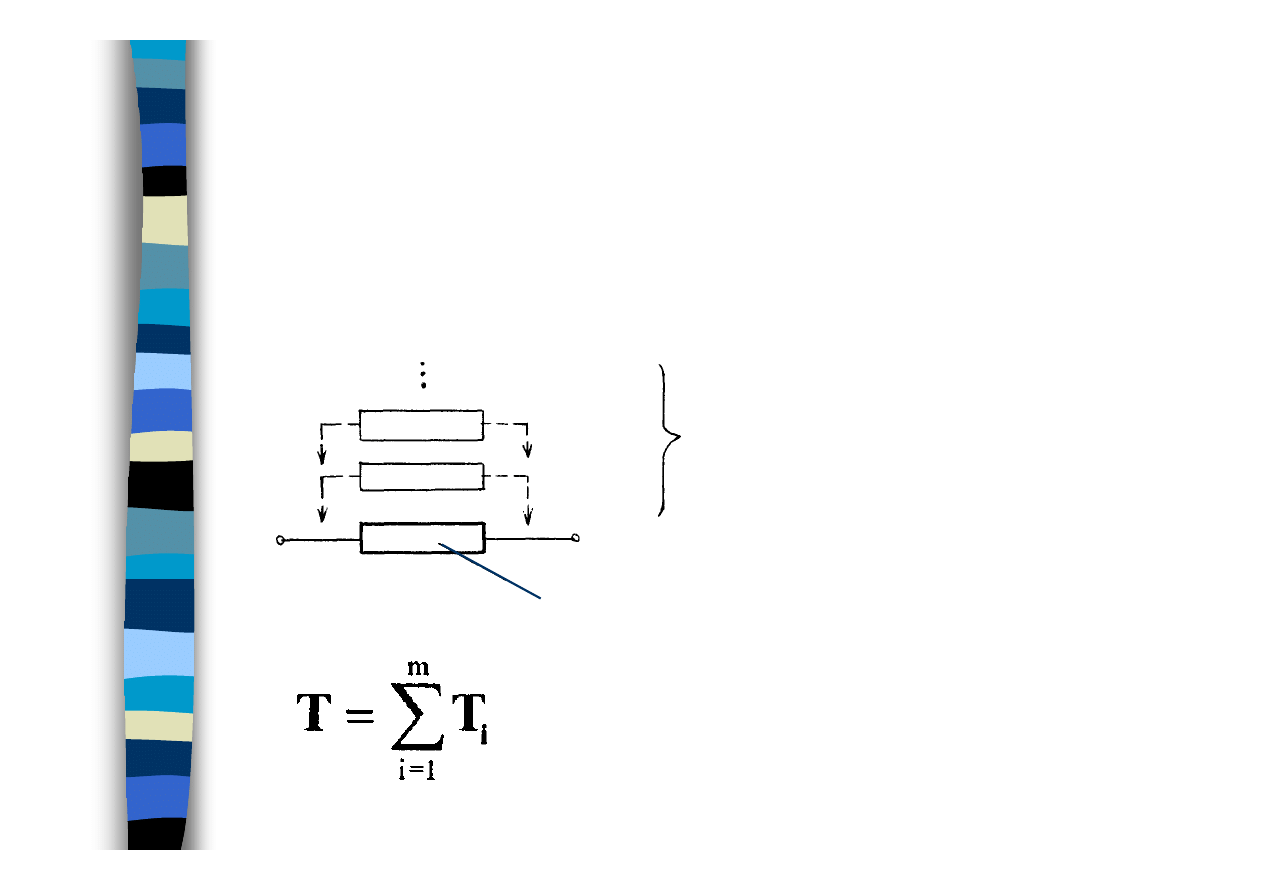
Struktura szeregowa

T, T

i

(i = 1, 2, ..., m)

Przykłady: ..., pracownik-obrabiarka, zespół ludzi wykonujących
określone zadanie, ...

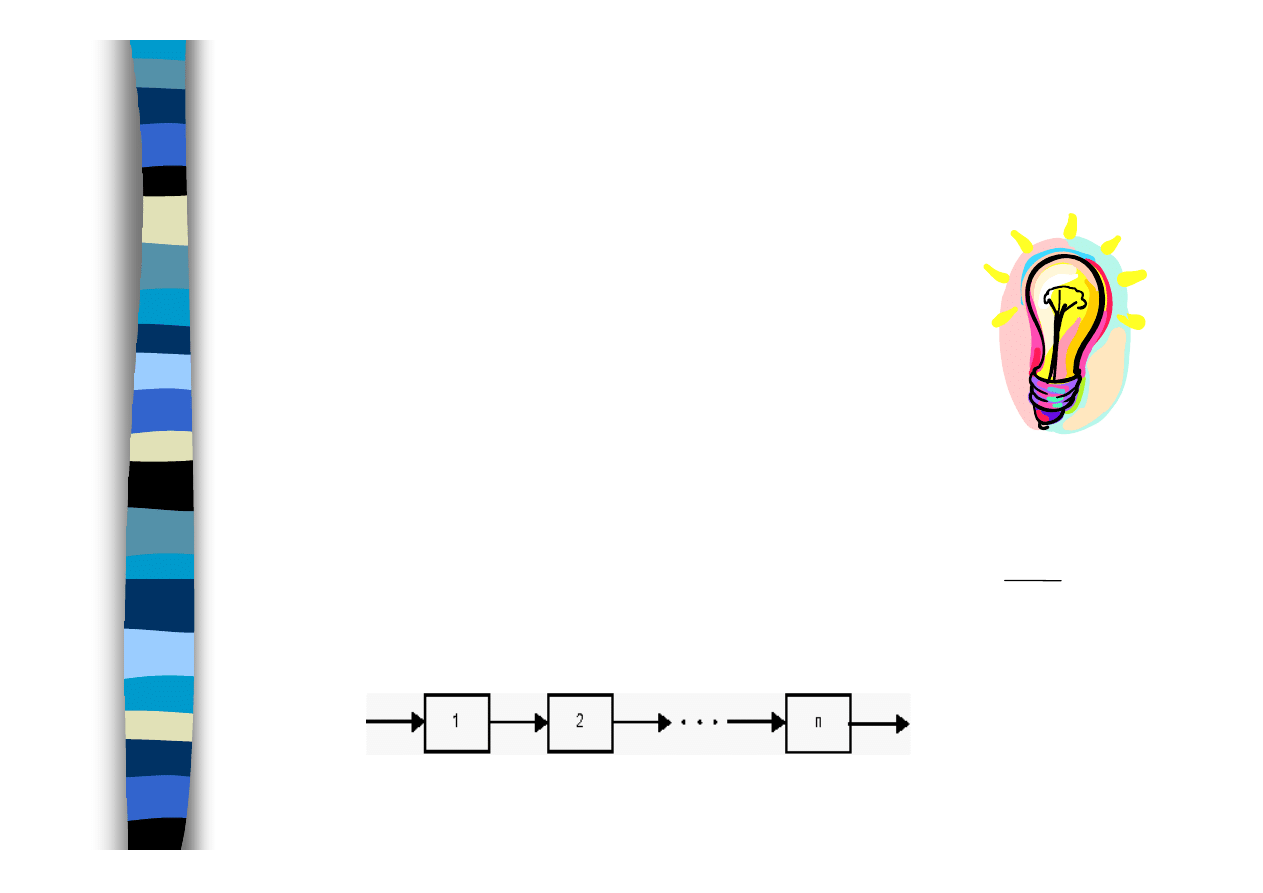
Przykład struktury szeregowej

Przykład:

5

identycznych żarówek o ET

i

=

100 h

ET = 100/5 = 20 h

m

ET

ET

i

=

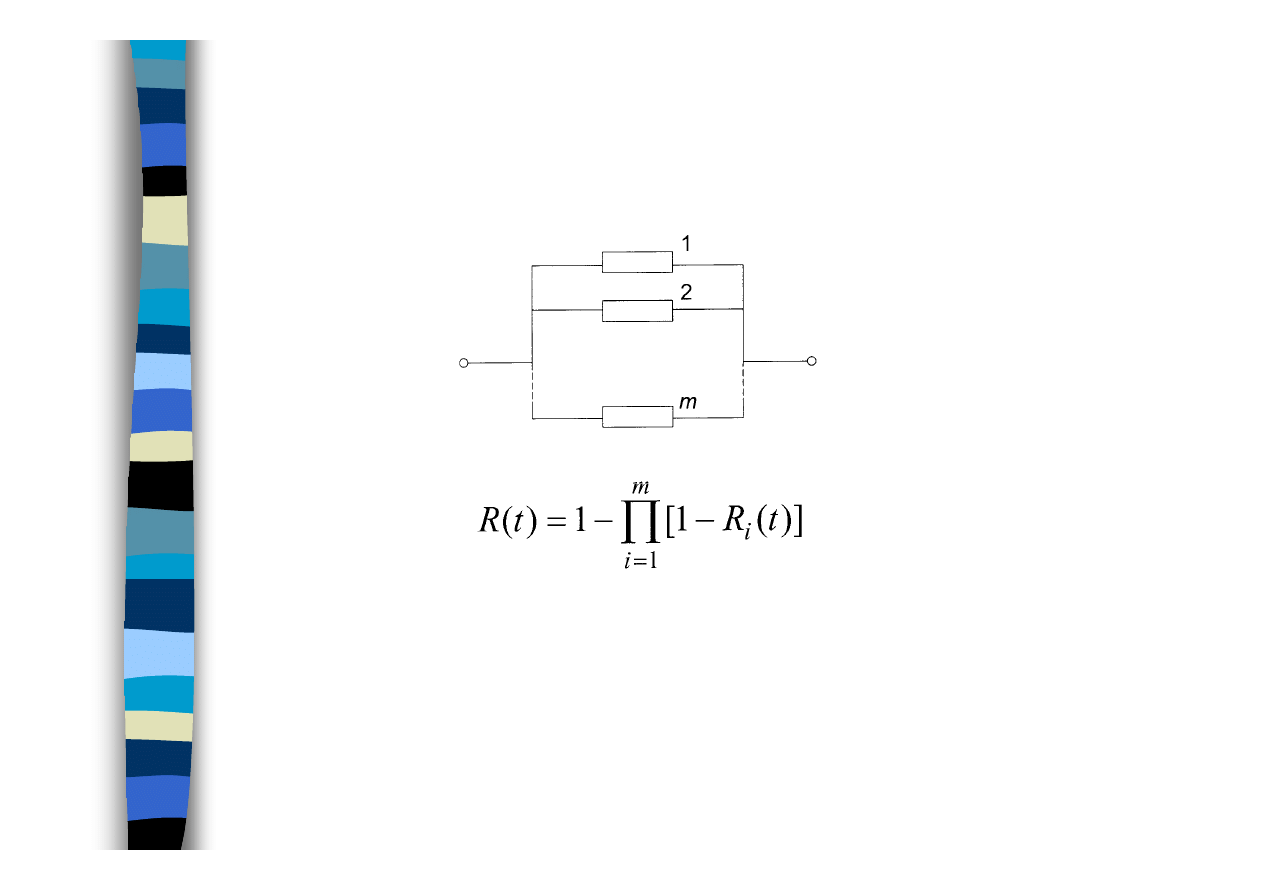
Struktura równoległa

∏

=

=

m

i

t

1

i

Q

Q(t)

)

(

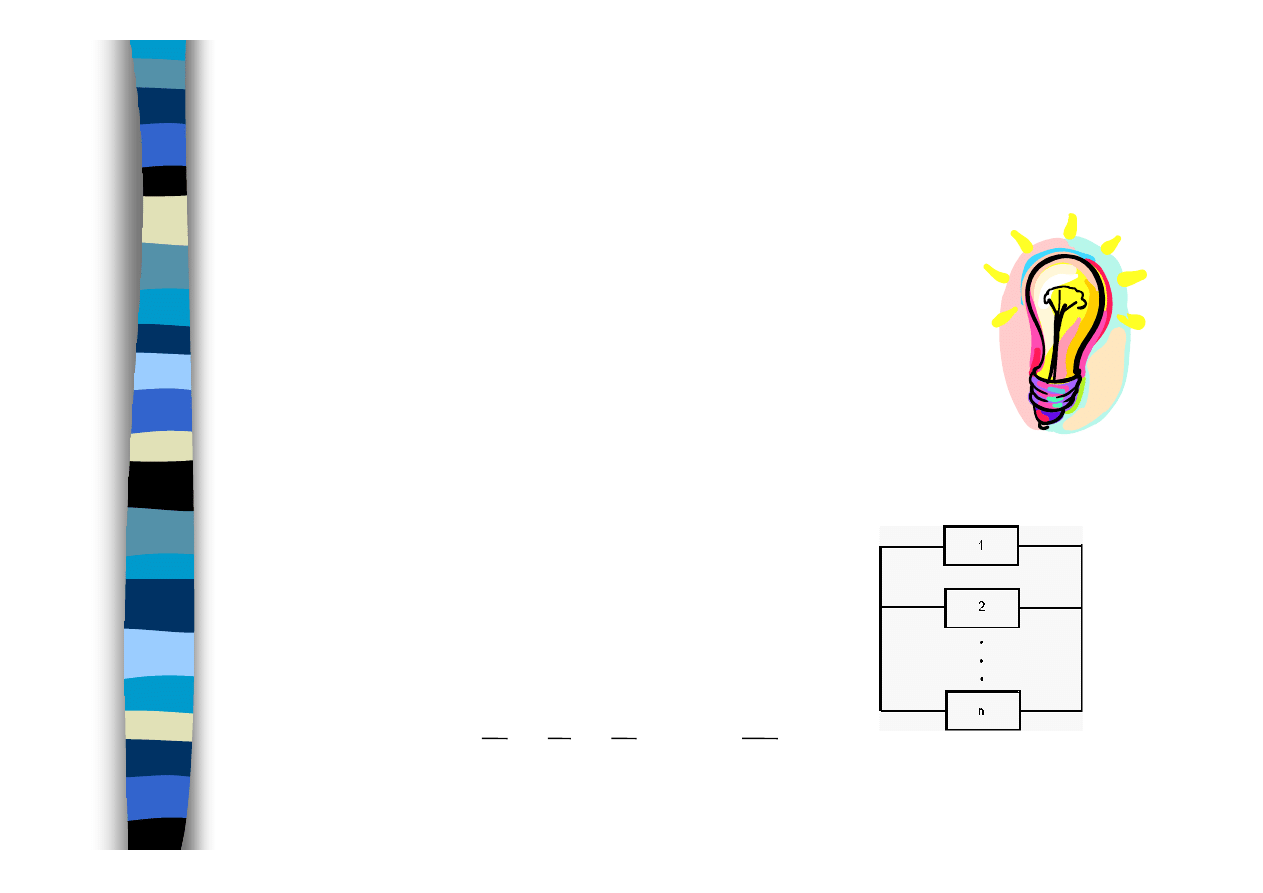
Przykład struktury równoległej

Przykład:

5

identycznych żarówek o ET

i

=

100 h

ET = 100(1+1/2+1/3+1/4+1/5) = 228 h













+

+

+

+

+

=

m

ET

ET

i

1

...

4

1

3

1

2

1

1

Struktura z rezerwą

elementy rezerwowe

element podstawowy

Rezerwa nieobci

Rezerwa nieobci

ąż

ąż

ona

ona

Przykład struktury z rezerwą

Przykład:

5

identycznych żarówek o ET

i

=

100 h

ET = 5*100 = 500 h

ET

m

ET

s

⋅

=

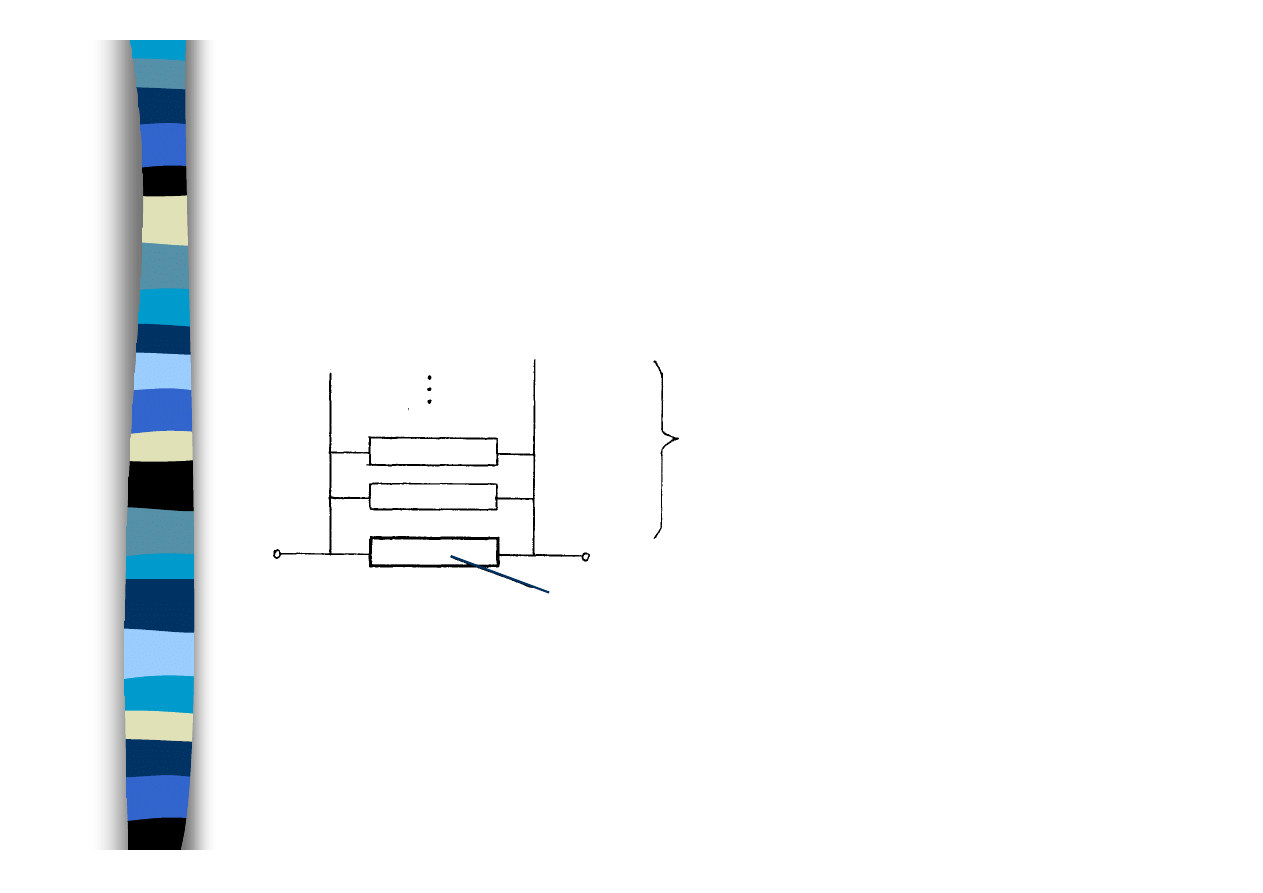
Struktura z rezerwą

elementy rezerwowe

element podstawowy

Rezerwa obci

Rezerwa obci

ąż

ąż

ona

ona

Rezerwa ulgowa

Przykłady: ...; systemy, w których niesprawności mogą stwarzać

duże zagrożenie (duże instalacje chemiczne,
elektrownie jądrowe, systemy ratownictwa)

Zadanie

System o strukturze szeregowej składa się z m
identycznych elementów o niezawodności
R(t

k

)=

0,95

. Z ilu elementów może składać się ten

system, aby jego niezawodność R

s

(t

k

)>=

0,8

?

m = ?

m = 5.47,

m = 5

Zadanie

System składa się z 2 identycznych elementów o
intensywności λ=

0,01

[1/h]. Określić wartości

oczekiwane czasów zdatności oraz niezawodności
systemu dla czasu t=

24

[h] dla struktury:

•Szeregowej
•Równoległej

ET=100 h, R (24)=0,787

Sz. ET

s

=100/2 = 50 h, R

s

=0,619

R. ET

s

= 150 h, R

s

=0,954

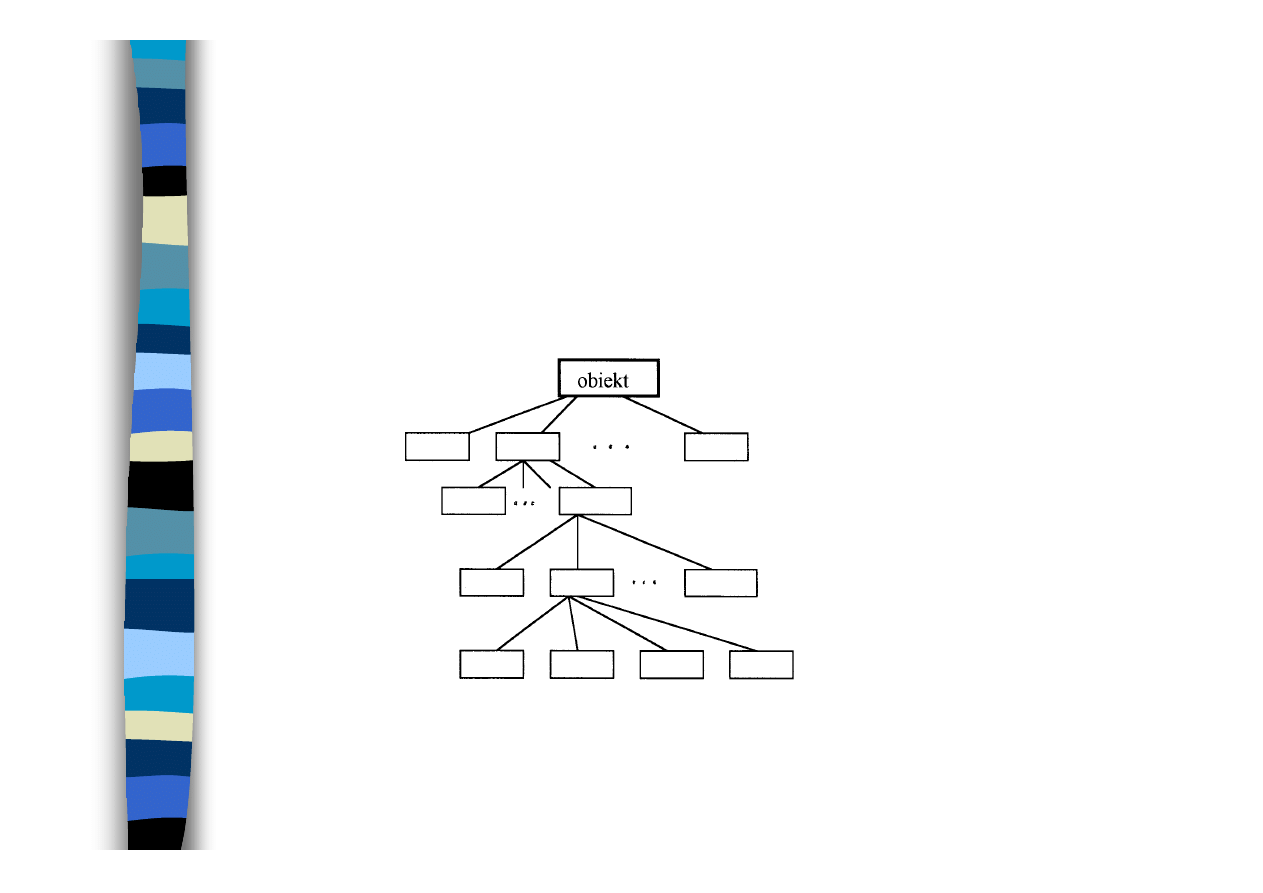
Procedura modelowania
struktury niezawodnościowej obiektu

1. dokonanie dekompozycji obiektu (podziału na elementy)

2. ustalenie kryteriów niesprawności obiektu

(definicji niesprawności obiektu)

3. wybór struktury niezawodnościowej

zespoły

podzespoły

elementy

fragmenty elementów

głę

boko

ść

deko

m

poz

yc

ji

METODY DRZEW
W ANALIZACH RYZYKA

Do opisu i analiz

Do opisu i analiz

zawodności
zagrożeń

stosuje się także

drzewa niesprawności

metody drzew

drzewa zdarzeń

ryzyka

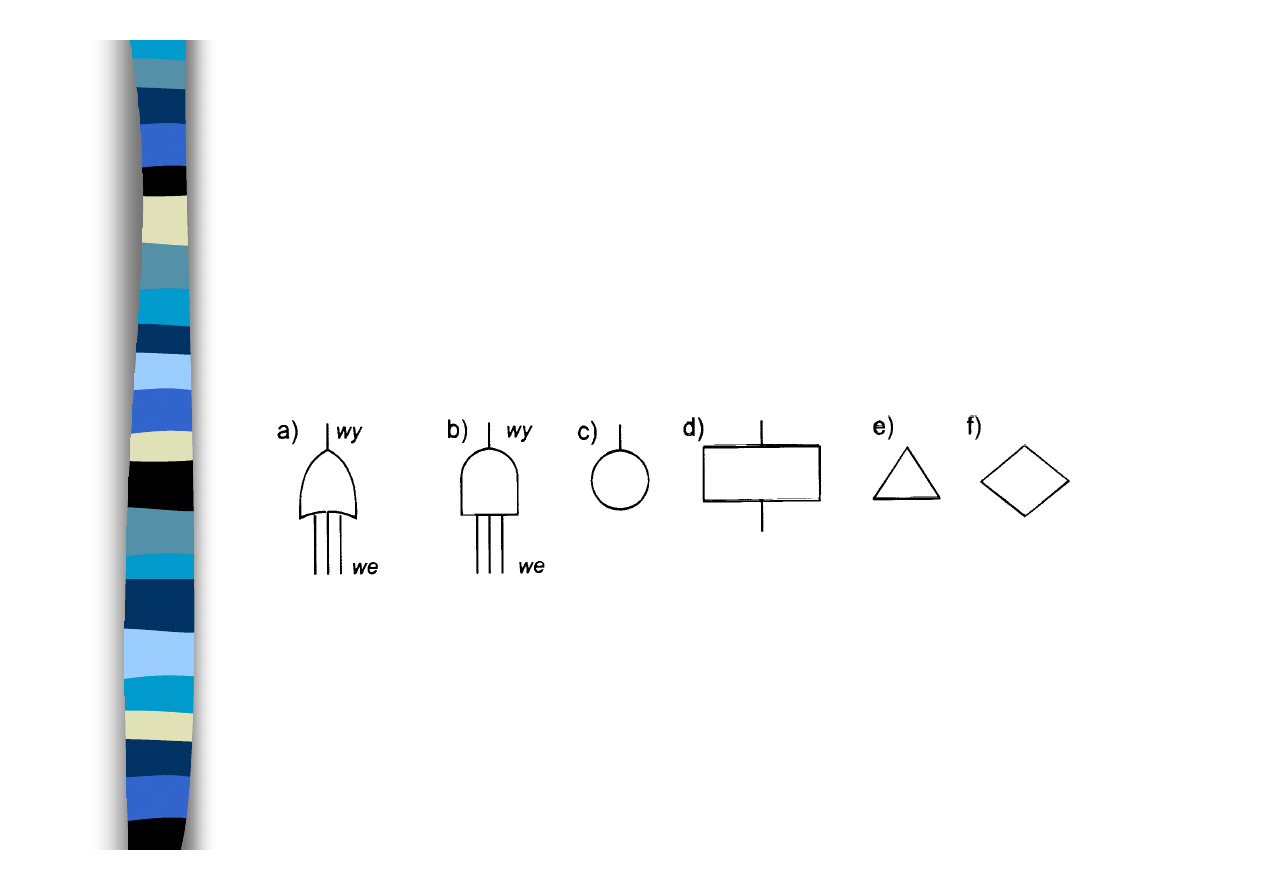
Drzewo niesprawności

Drzewo niesprawności - graficzny sposób przedstawiania
kombinacji zdarzeń niepożądanych (w tym niesprawności),
jako przyczyn rozpatrywanego zdarzenia niepożądanego

Podstawowe symbole zdarzeń i operacji logicznych:

a)

a) sumy logicznej („lub"),

b)

b) iloczynu logicznego („i"),

c)

c) zdarzenia

podstawowego,

d)

d) zdarzenia pośredniego będącego rezultatem

operacji logicznych,

e)

e) przeniesienia kontynuacji drzewa,

f)

f) zdarzenia chwilowo nierozwijanego

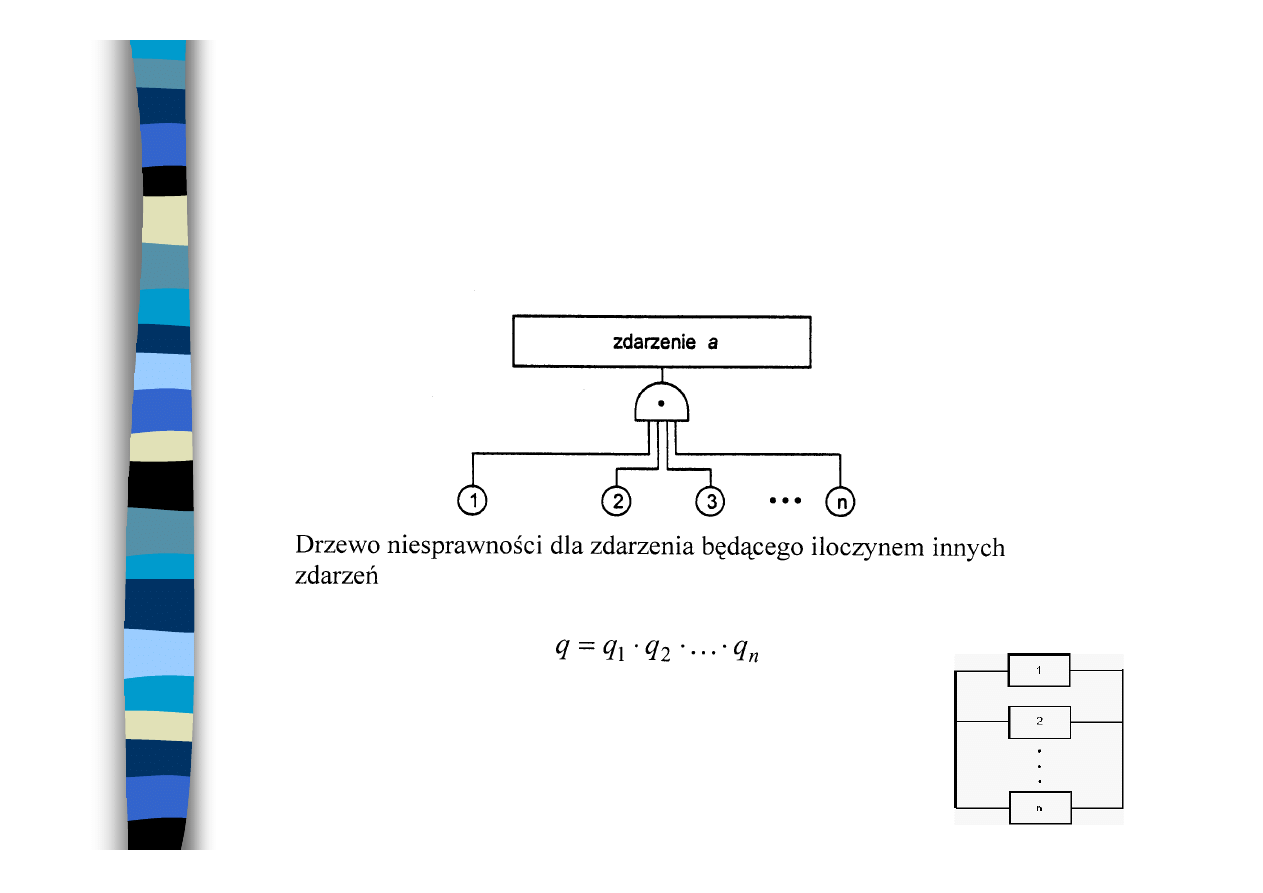
Iloczyn zdarzeń

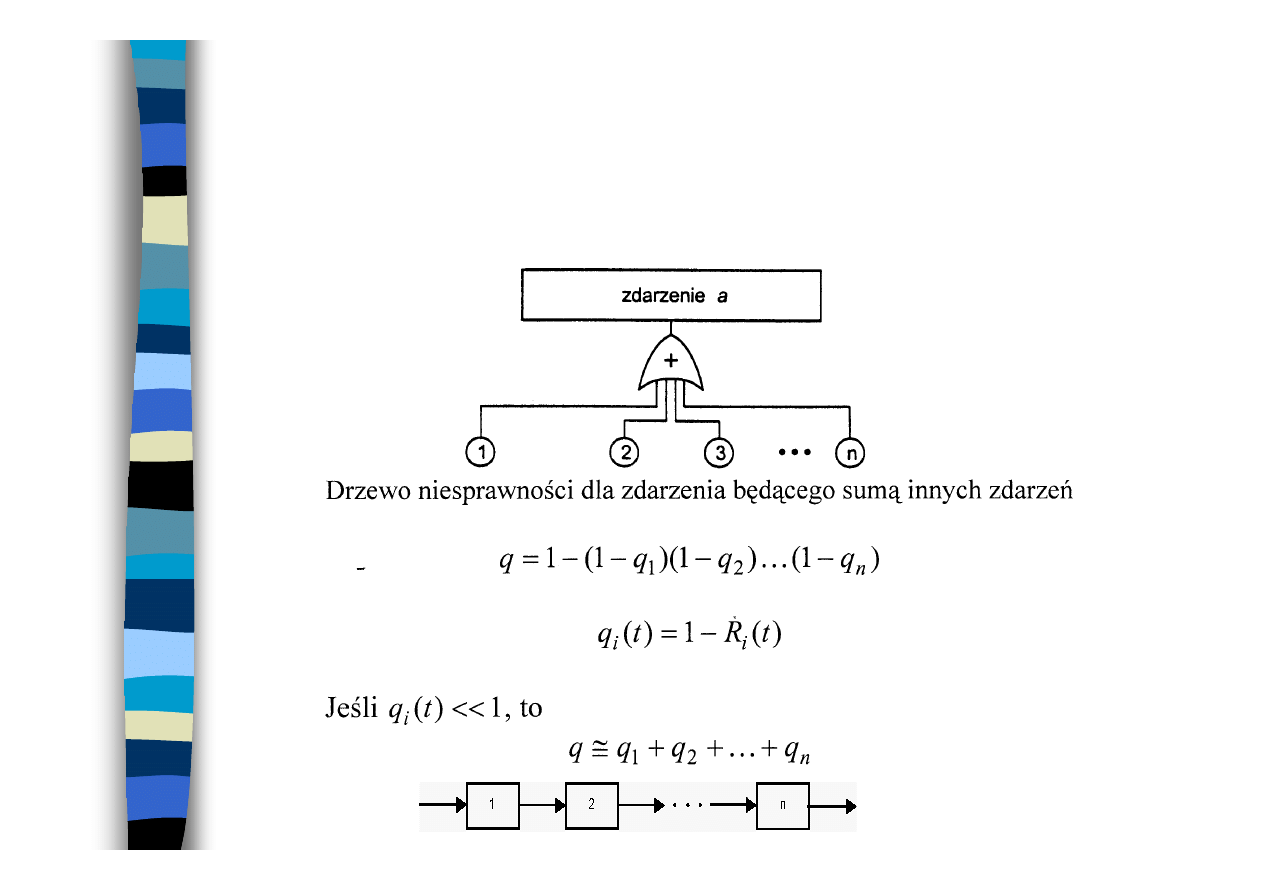
Suma zdarzeń

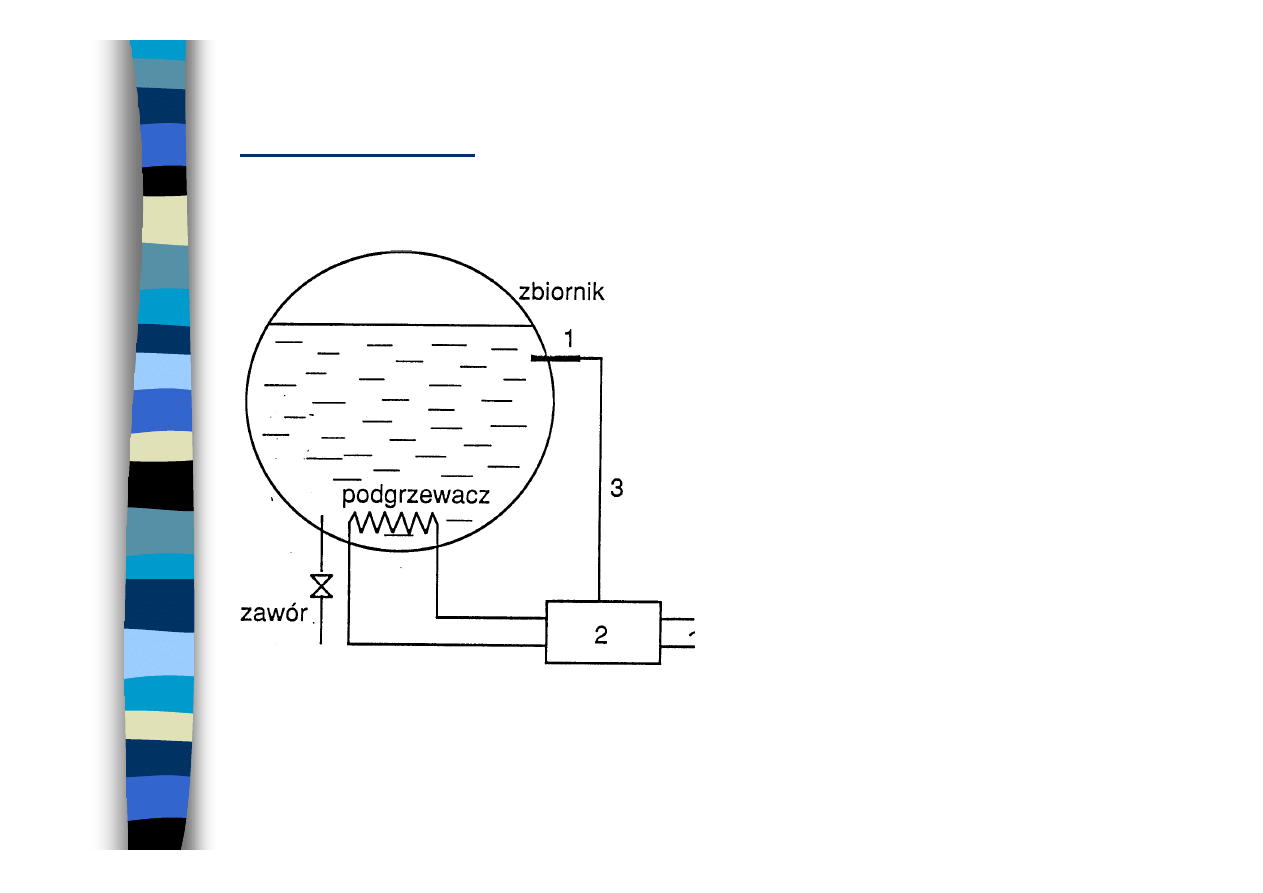
Przykład
tworzenia drzewa niesprawności

Instalacja chemiczna

Instalacja chemiczna

1 - czujnik temperatury,

2 - regulator temperatury,

3 - przewód

Wskazanie analizowanego zdarzenia niepożądanego A

(k)

,

którego prawdopodobieństwo Q

(k)

(1) zamierza się określić

A

A

(k)

(k)

=

=

(

(

T

T

>

>

T

T

dop

dop

)

)

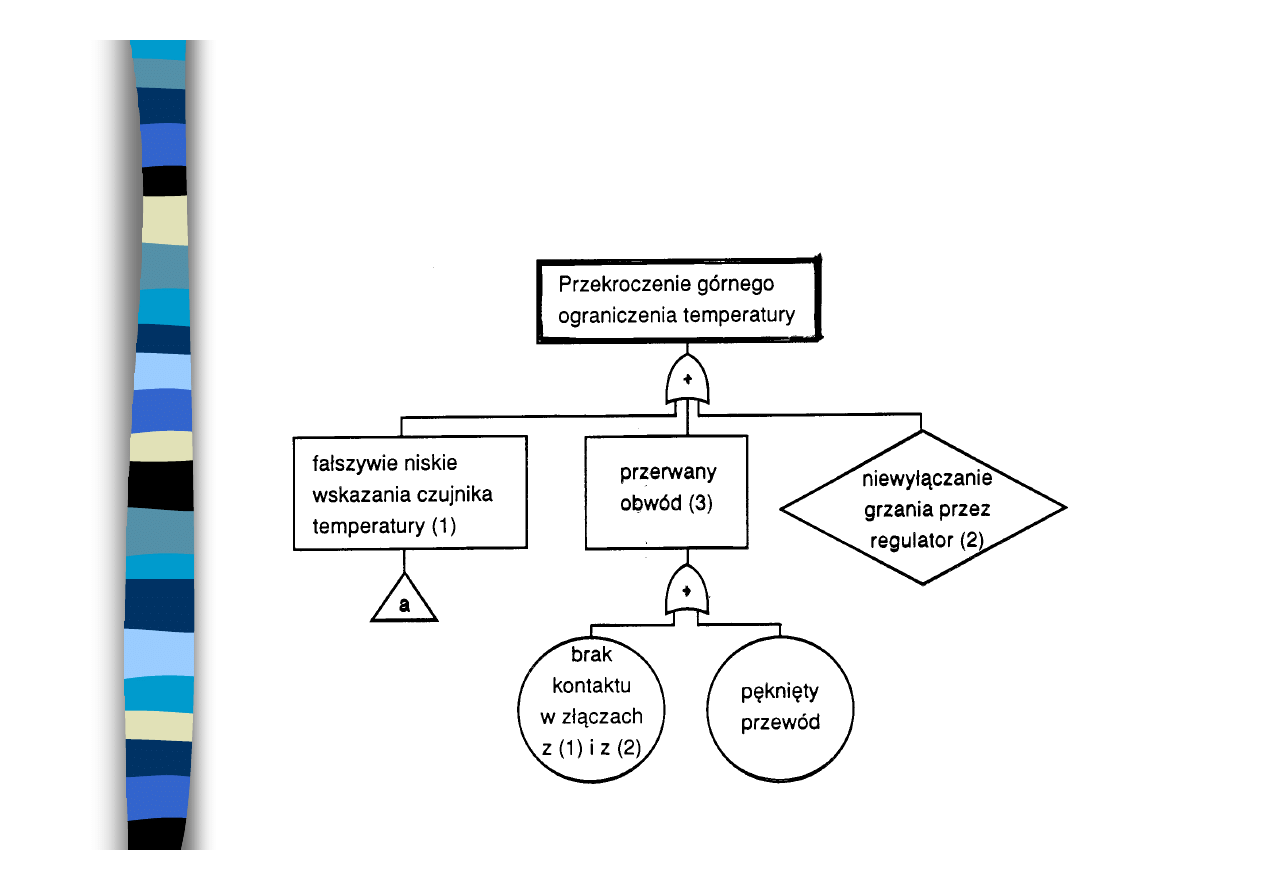
Przykład drzewa niesprawności

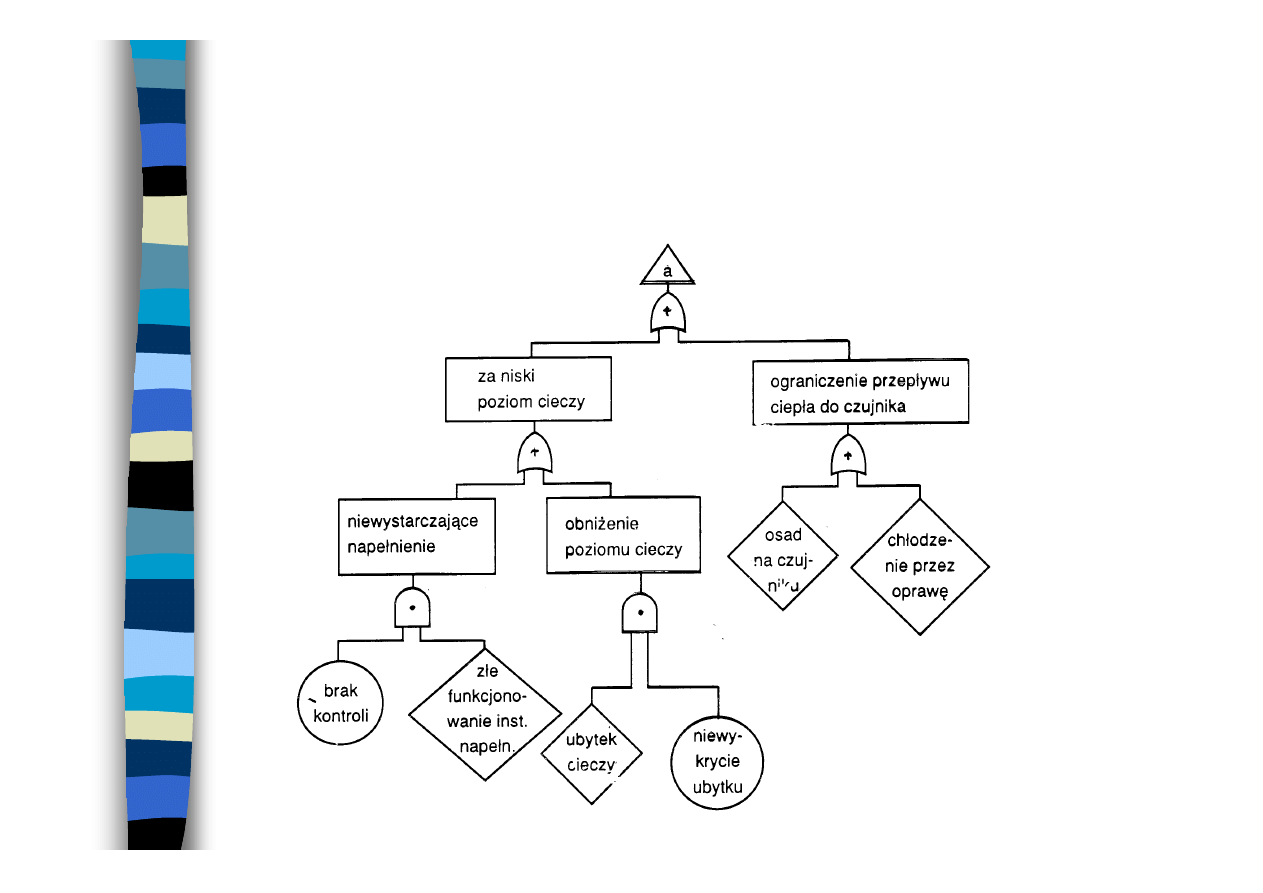
Przykład drzewa niesprawności

Drzewo niesprawności

opis struktury niezawodno

opis struktury niezawodno

ś

ś

ciowej

ciowej

Zalety

S

prócz informacji graficznej informacja słowna

S

zawiera postacie zdarzeń niepożądanych, które

mogą się pojawiać we fragmentach obiektu
(elementów)

S

bardziej szczegółowy opis niezawodności

obiektu

Zastosowanie metody drzewa
niesprawności

T

jakościowa analiza niezawodności, prowadzona
w celu eliminowania przyczyn niesprawności

T

ilościowe szacowanie i analiza niezawodności, ...

T

szacowanie i analiza ryzyka

prawdopodobieństwa zdarzeń na
najniższym poziomie

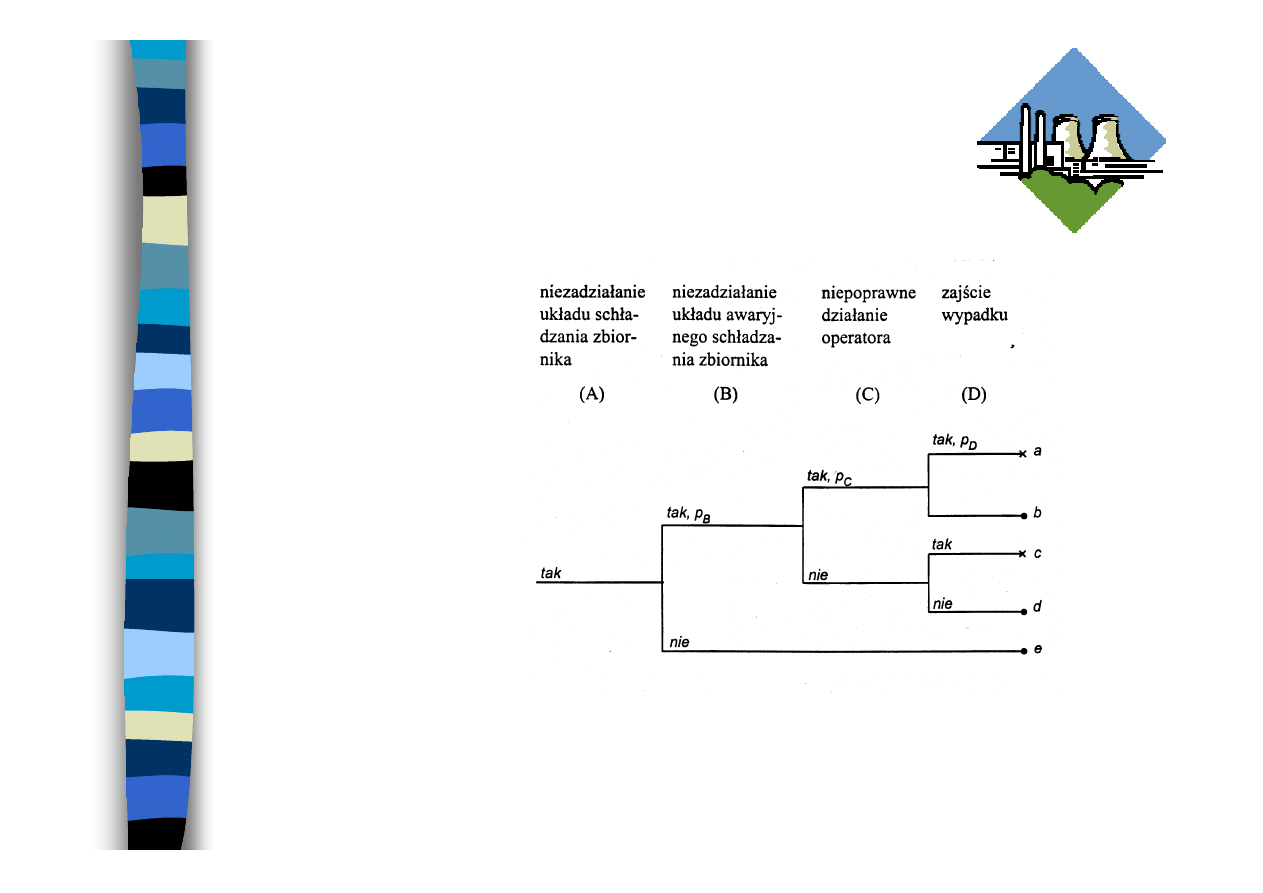
Drzewo zdarzeń

Drzewo zdarzeń - graficzny sposób przedstawienia
chronologicznego ciągu zdarzeń, istotnych ze względu na
funkcjonowanie obiektu, występujących po wybranej
niesprawności.

niesprawność instalacji chemicznej

Drzewo zdarzeń dla
instalacji chemicznej

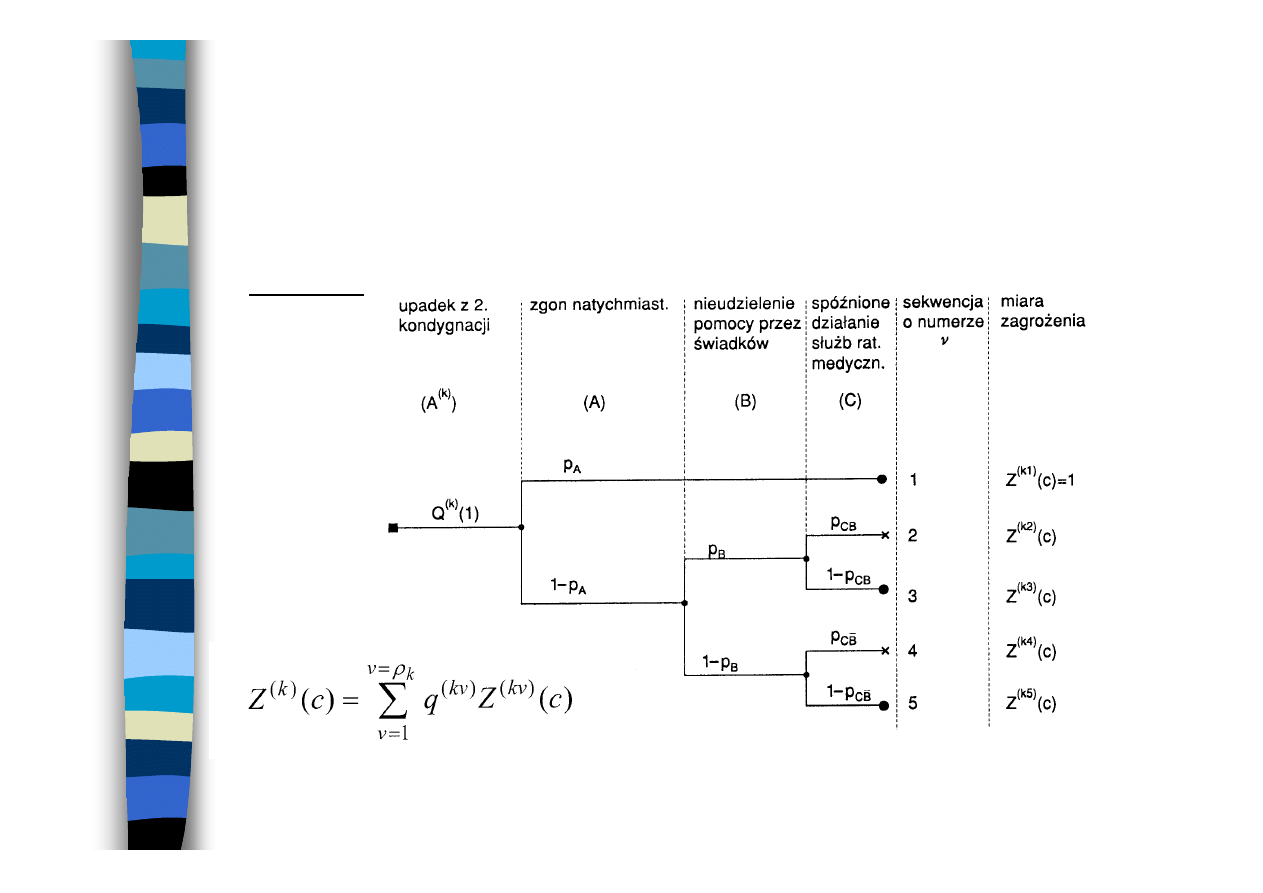
Modelowanie zagrożeń
przy użyciu techniki drzewa zdarzeń

Przykład

ρ

k

- liczba sekwencji w drzewie zdarzeń,

q

(k

ν

)

- prawdopodobieństwo zajścia v-tej sekwencji

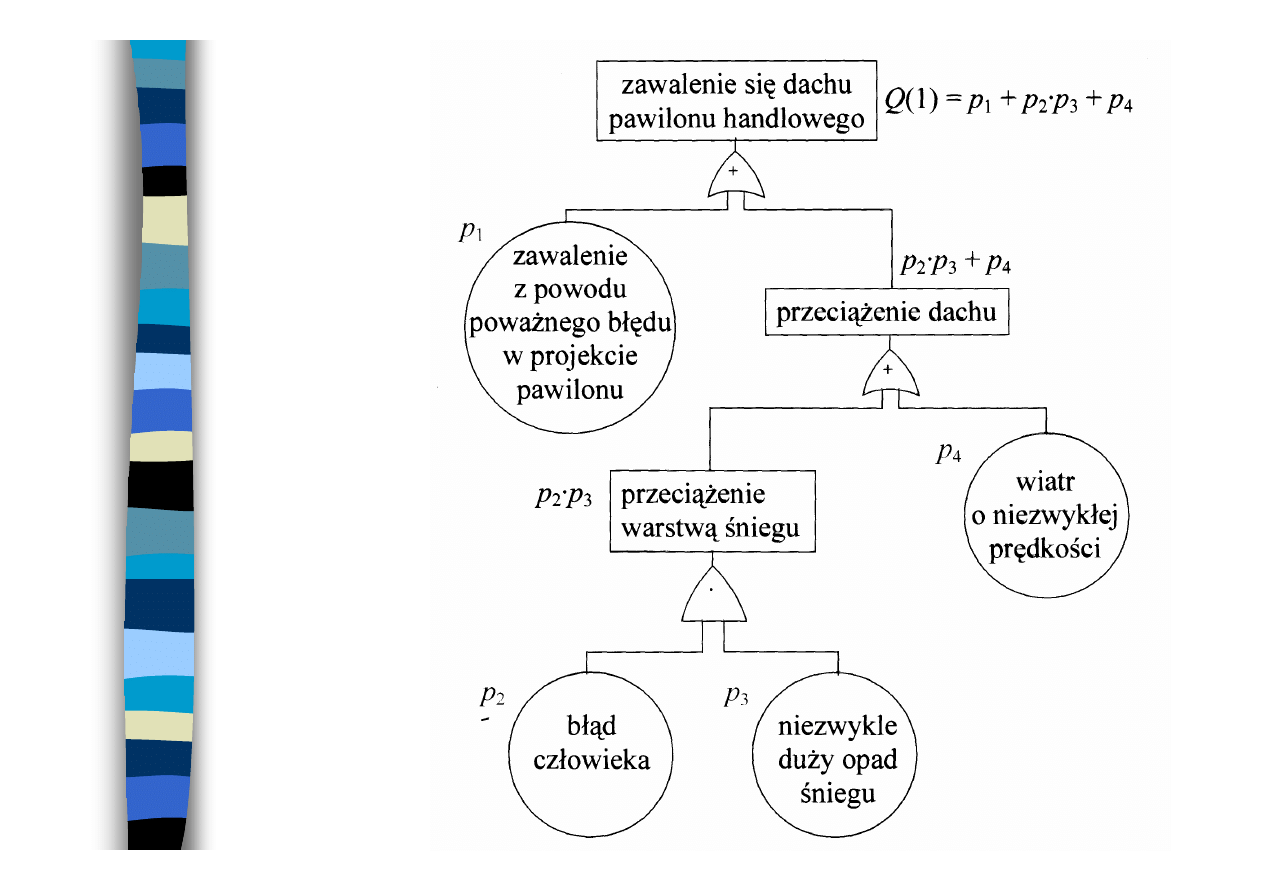
Przykład

Przykład obliczeń
prawdopodobieństwa
zdarzenia
szczytowego

Przykład obliczeń prawdopodobieństwa
zdarzenia szczytowego (cd.)

Potrzebne dane liczbowe:

np.

p

p

1

1

,p

,p

2

2

, p

, p

3

3

, p

, p

4

4

Metody pozyskiwania danych:

• statystyczne

• eksperckie

literatura

internet

rejestry wypadków

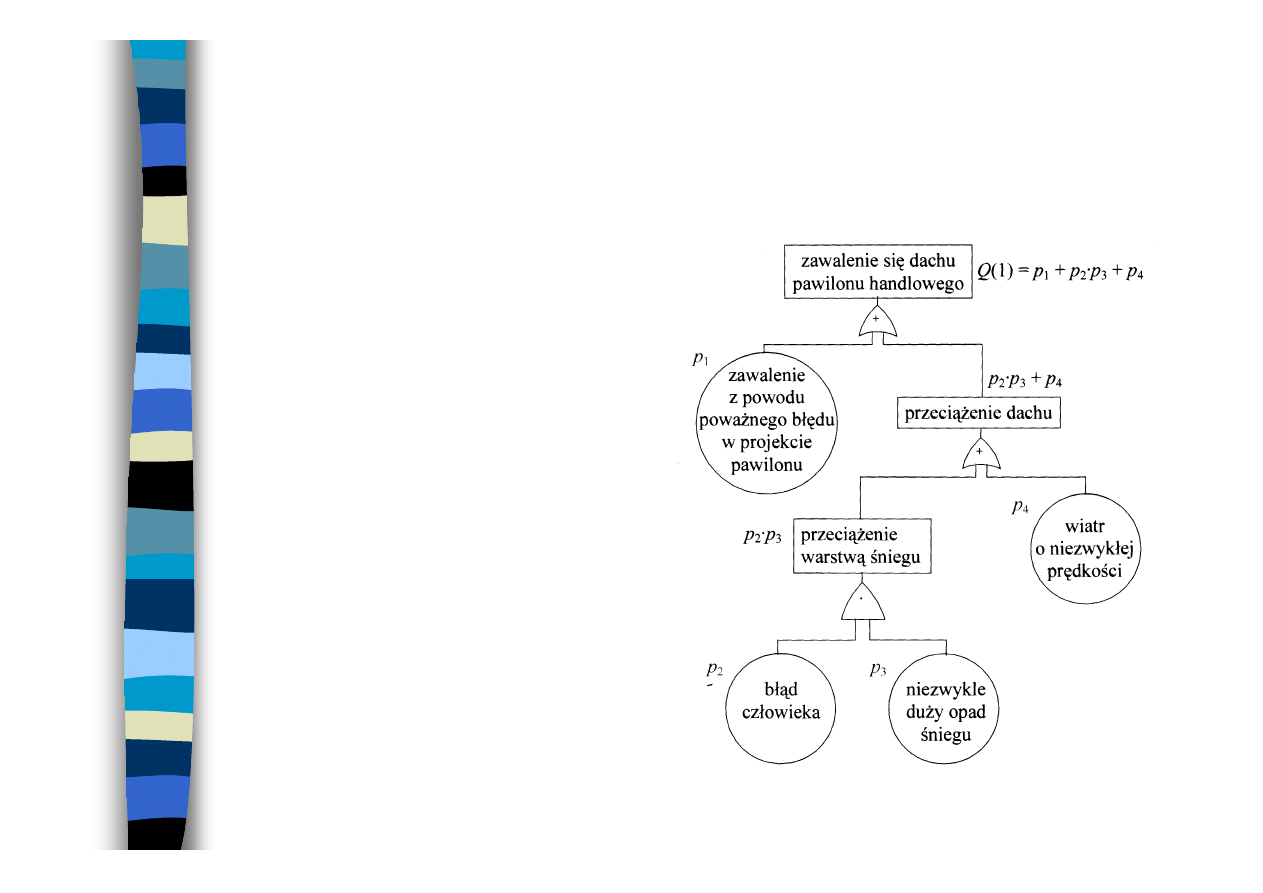
Przykład obliczeń prawdopodobieństwa
zdarzenia szczytowego (cd.)

Np.

p

1

= 0,008 = 8

⋅10

-3

w 1 roku

p

2

= 0,10

p

3

= 0,005 = 5

⋅10

-3

w 1 roku

p

4

= 0,020 = 20

⋅10

-3

w 1 roku

Q(1)

Q(1) = p

1

+ p

2

p

3

+ p

4

= 8

⋅10

-3

+ 0,5

⋅10

-3

+20

⋅10

-3

=

28,5

28,5

⋅⋅⋅⋅

⋅⋅⋅⋅

10

10

-

-

3

3

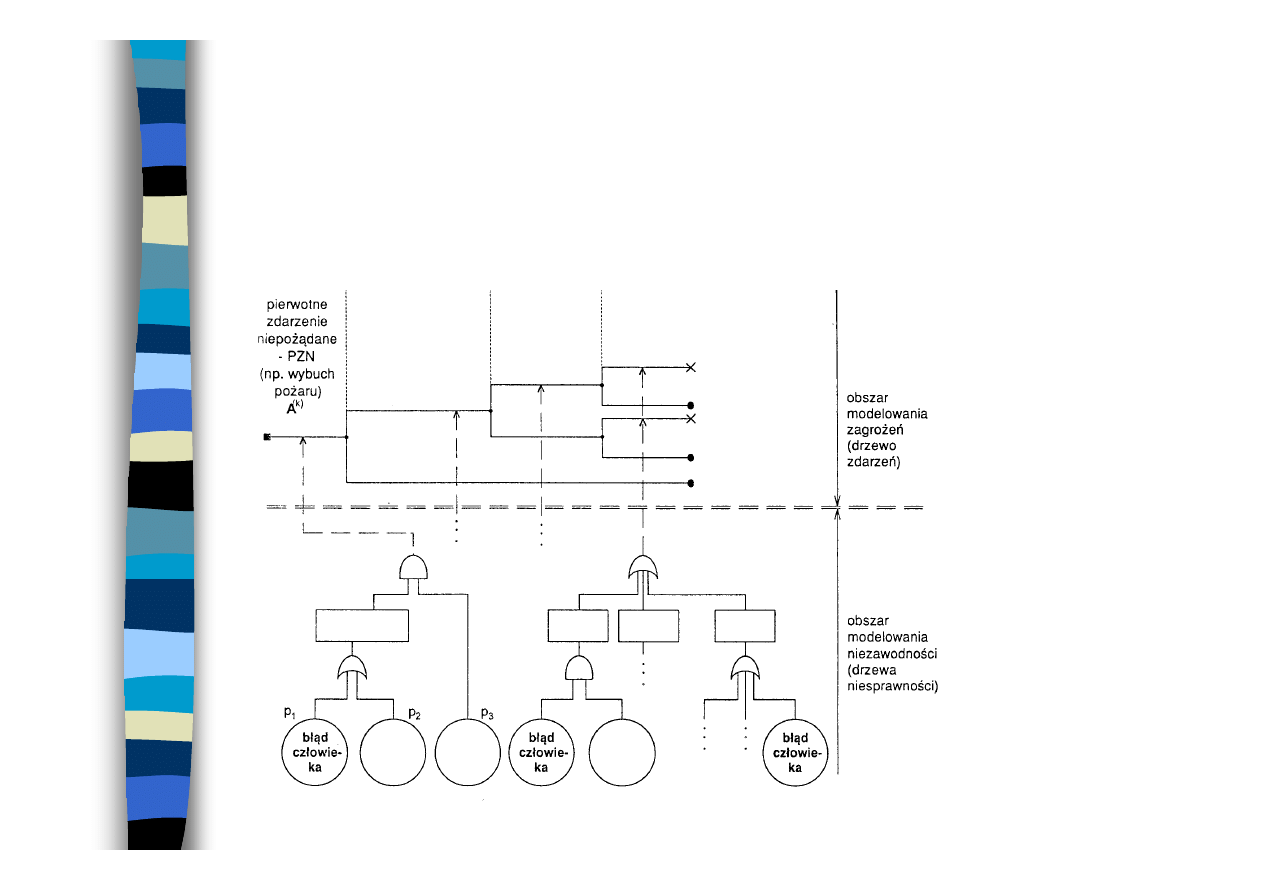
Koncepcja metody
modelowania i analizy ryzyka
przy użyciu technik drzew

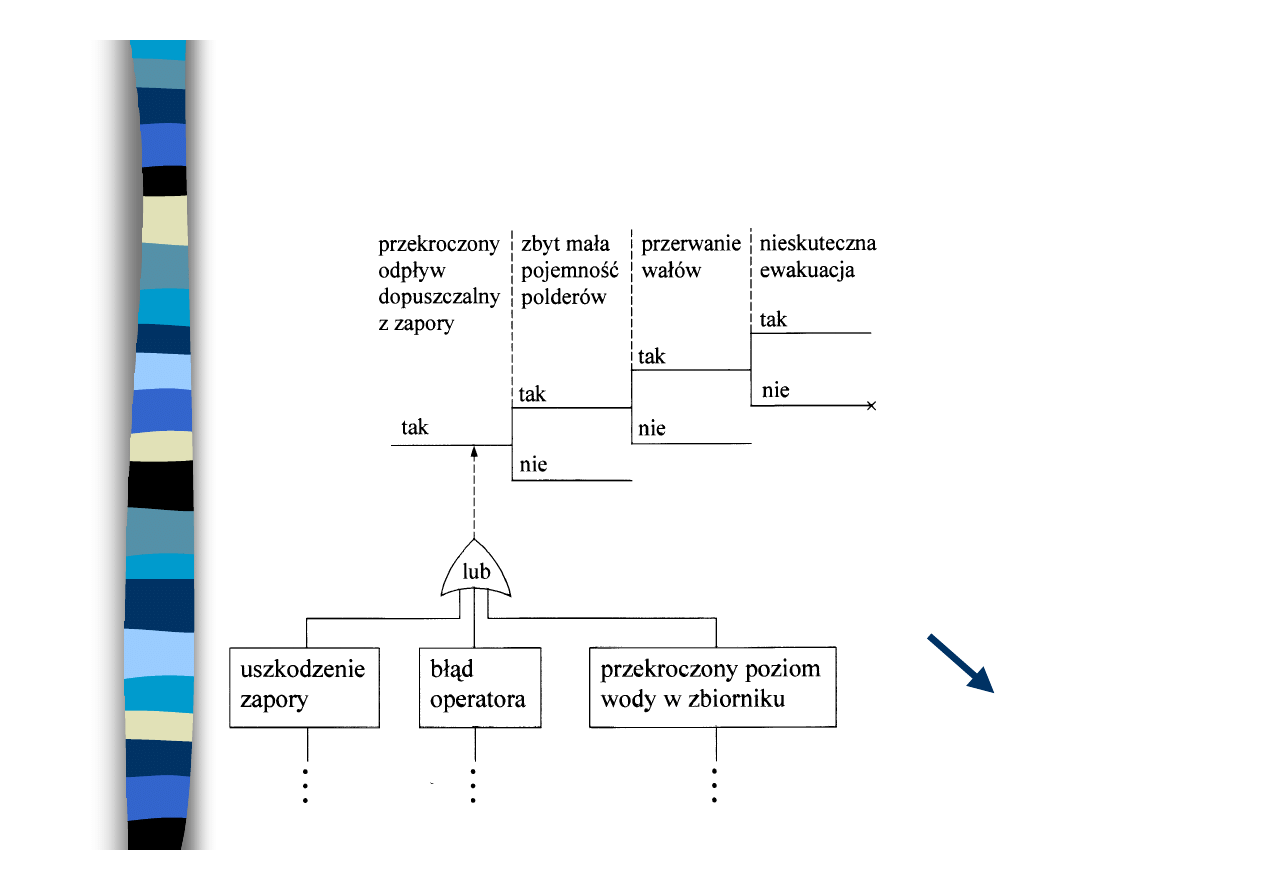
Przykład zastosowania metod drzew do
modelowania i analizy ryzyka powodziowego

• Szacowanie ryzyka
• Analiza wpływu czynników

uwzględnionych w modelu na
ryzyko strat

podstawa decyzji, np.

o rozsunięciu wałów

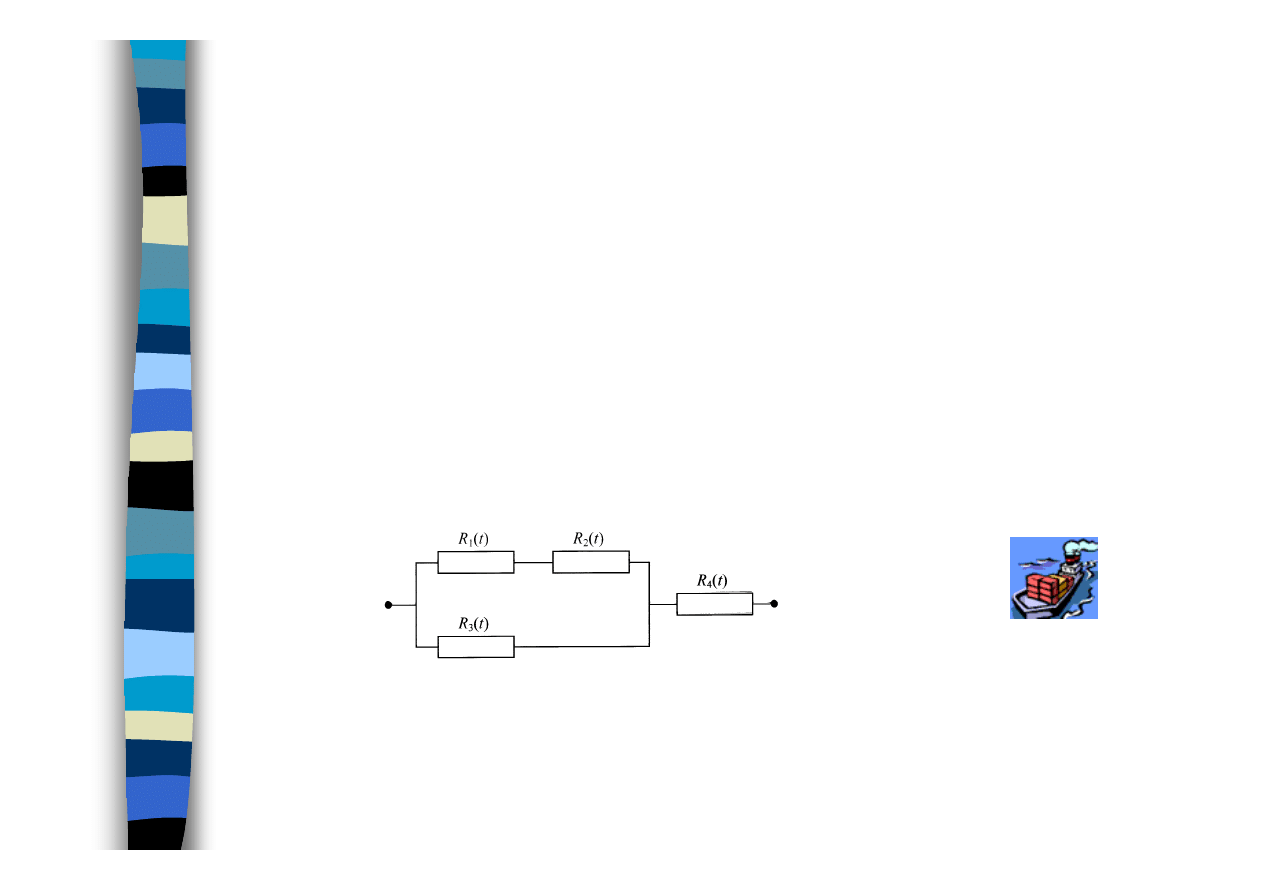
MODELOWANIE NIEZAWODNOŚCI

Niezawodno

Niezawodno

ś

ś

ciowy model obiektu

ciowy model obiektu

- układ, który pod

względem niezawodności odwzorowuje obiekt
rzeczywisty i zastępuje go w planowanych analizach
niezawodności

1. Model struktury niezawodnościowej

S

w formie schematu blokowego

Np.

R(t) = R

4

(t)

⋅

{1-[1- R

3

(t)][1- R

1

(t)R

2

(t)]}

S

w formie drzewa niesprawności

MODELOWANIE NIEZAWODNOŚCI

2. Modele niezawodności człowieka

3. Modele zjawisk, które mogą prowadzić do

niesprawności

m

p

X

t

X

Lt

v

t

<

+

=

)

(

)

(

c

X

X

0

}

)

(

{

}

{

)

(

m

X

t

P

t

P

t

R

<

=

>

=

X

T















+

−

−

Φ

=

2

)

)(

(

)

(

)

(

Lt

v

V

V

Lt

v

E

E

X

t

R

p

p

m

c

X

c

X

0

0

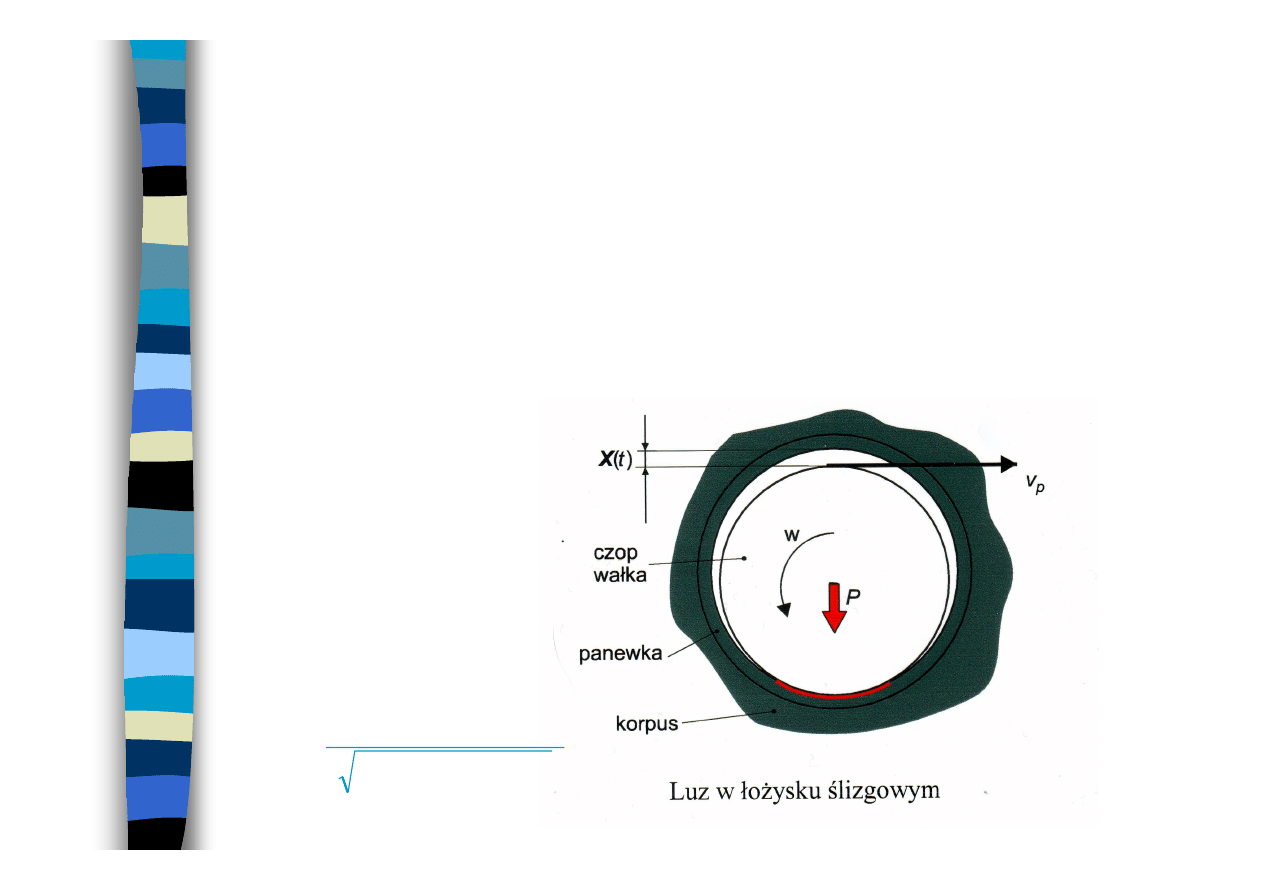
Łożysko ślizgowe

shaft

housing

bushing

m

p

X

t

X

Lt

v

t

<

+

=

)

(

)

(

0

c

X

X

METODY SZACOWANIA
I BADAŃ NIEZAWODNOŚCI

METODY SZACOWANIA
I BADAŃ NIEZAWODNOŚCI

Metody oparte na modelach mogą być stosowane
między innymi do badań niezawodności systemów:

S

zapobiegania zdarzeniom niepożądanym

S

przeciwdziałania zagrożeniom

S

ratownictwa

Np. badania symulacyjne różnych wariantów akcji
ratowniczych w celu oceny ich niezawodności itd.

W analizach ryzyka zawodowego

Metody

Metody

•

wykorzystujące modele niezawodności (zawodności)

• statystyczne

• eksperckie

Metody wykorzystujące modele

T

Stosowane głównie do analizy wpływu czynników
uwzględnianych przez model na niezawodność

T

Trudniejsze niż metody statystyczne i metody
eksperckie

T

Mogą być używane zwłaszcza do stanowisk pracy,
z którymi związane są duże zagrożenia

Metody statystyczne

Oparte na danych statystycznych o zdarzeniach

literatura

internet

raporty PIP, GUS

rejestr wypadków w przedsiębiorstwie

W(

∆τ) - zarejestrowana liczba wypadków, spowodowanych przez

zdarzenia A w okresie

∆τ na N rozważanych stanowiskach pracy

f - współczynnik wypadkowości (f < 1)

Metody eksperckie

Opinie ekspertów

Zespół ekspertów

Ankiety

wiedza

doświadczenie

intuicja

Metoda bezpośredniego szacowania

Cel --> Q(1) dla zdarzenia A

Opinie o częstości występowania zdarzenia A

w

w

i

i

= 3

= 3

razy w ciągu 10 lat

n - liczba ekspertów

w

e

- częstość podana przez e. eksperta

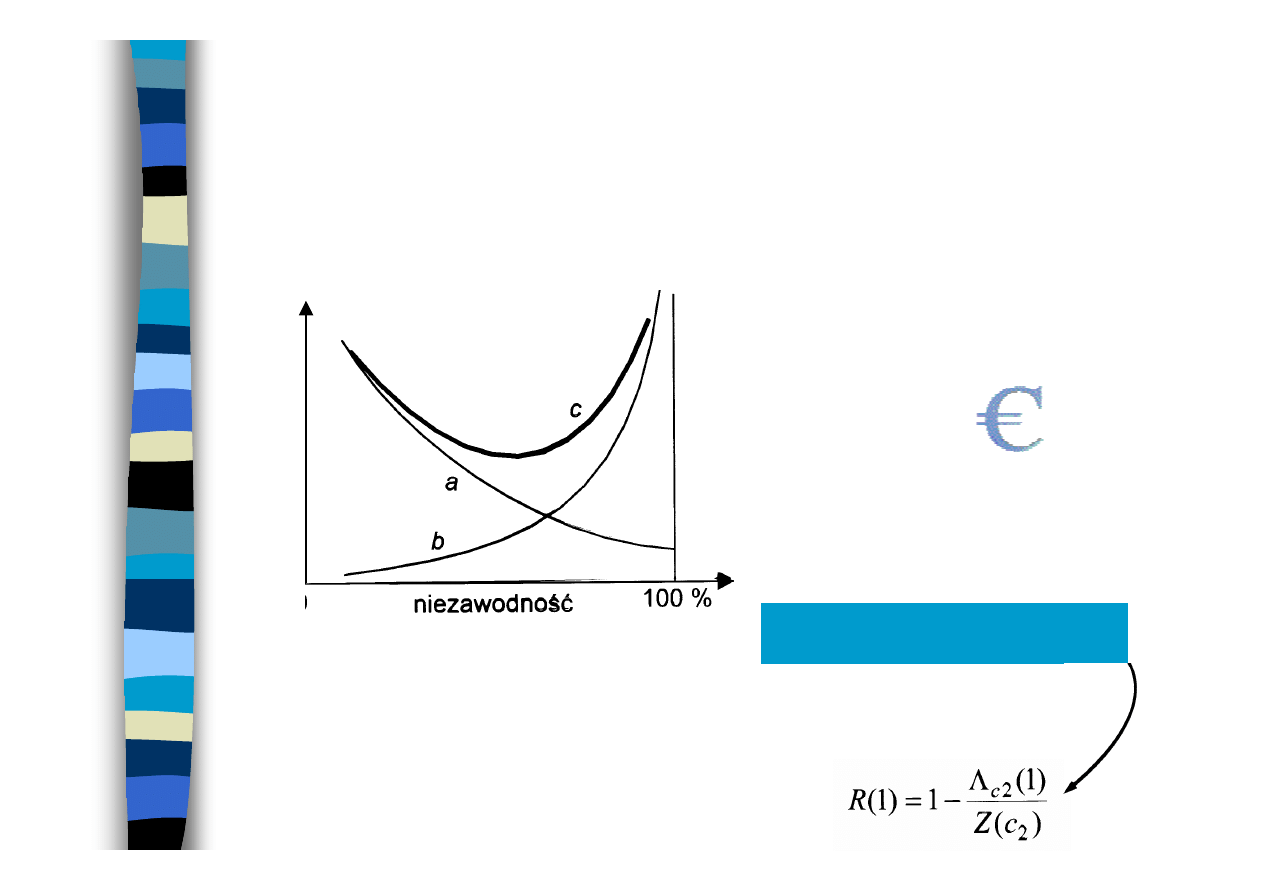
WYBÓR POZIOMU NIEZAWODNOŚCI

Zale

Zale

ż

ż

no

no

ść

ść

wydatk

wydatk

ó

ó

w od niezawodno

w od niezawodno

ś

ś

ci

ci

wy

d

at

ki

0

Λ

c

(1) = Q(1) · Z(c)

Pożądany poziom niezawodności

WYBÓR POZIOMU NIEZAWODNOŚCI

ZAGADNIENIA ODNOWY

Rodzaje odnawiania:

Y

po wystąpieniu niesprawności

Y

profilaktyczne

Cel odnawiania profilaktycznego:

zmniejszanie możliwości powstania niesprawności

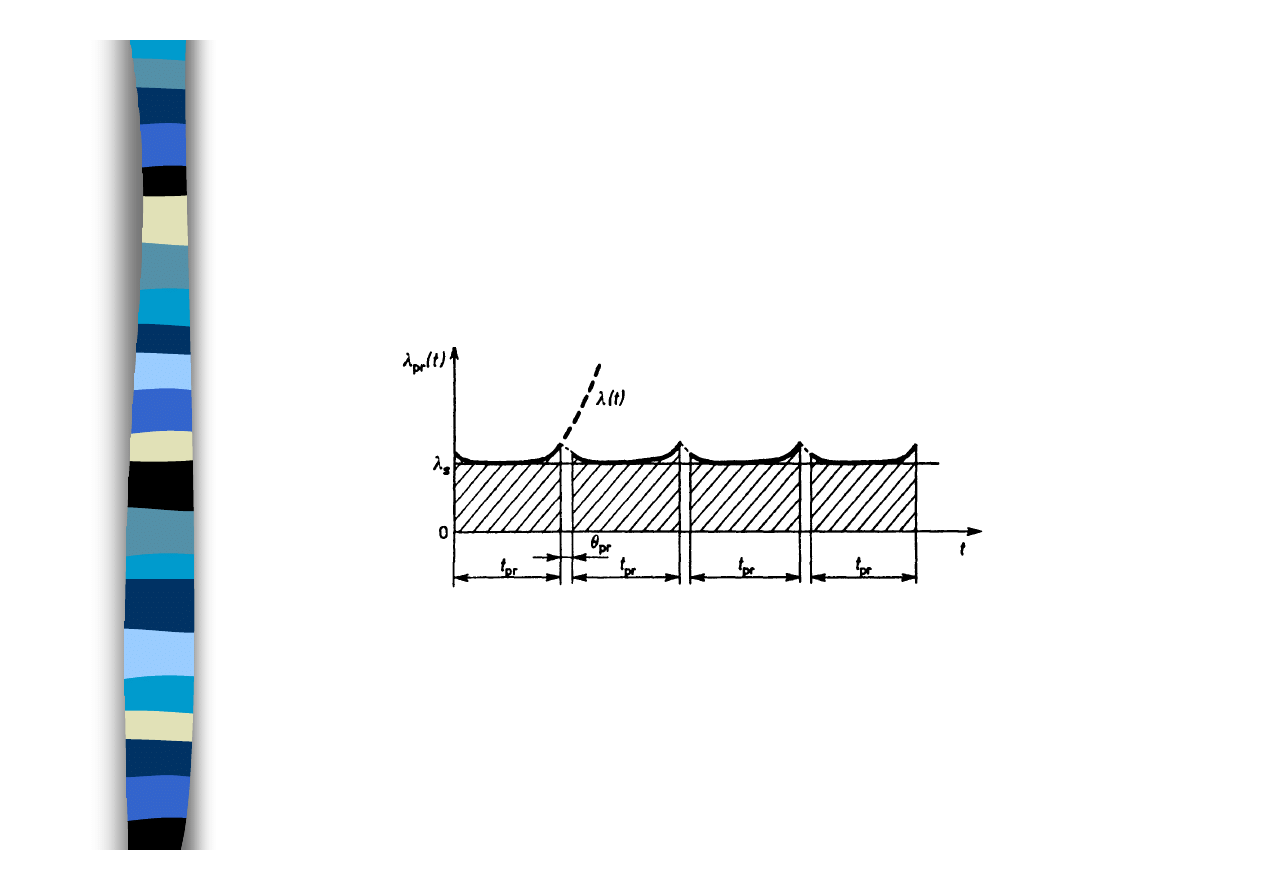
ZAGADNIENIA ODNOWY

Wpływ odnawiania profilaktycznego na niezawodność obiektu

* Analiza sensowności przeprowadzania odnawiania

profilaktycznego

* Optymalizacja strategii odnawiania

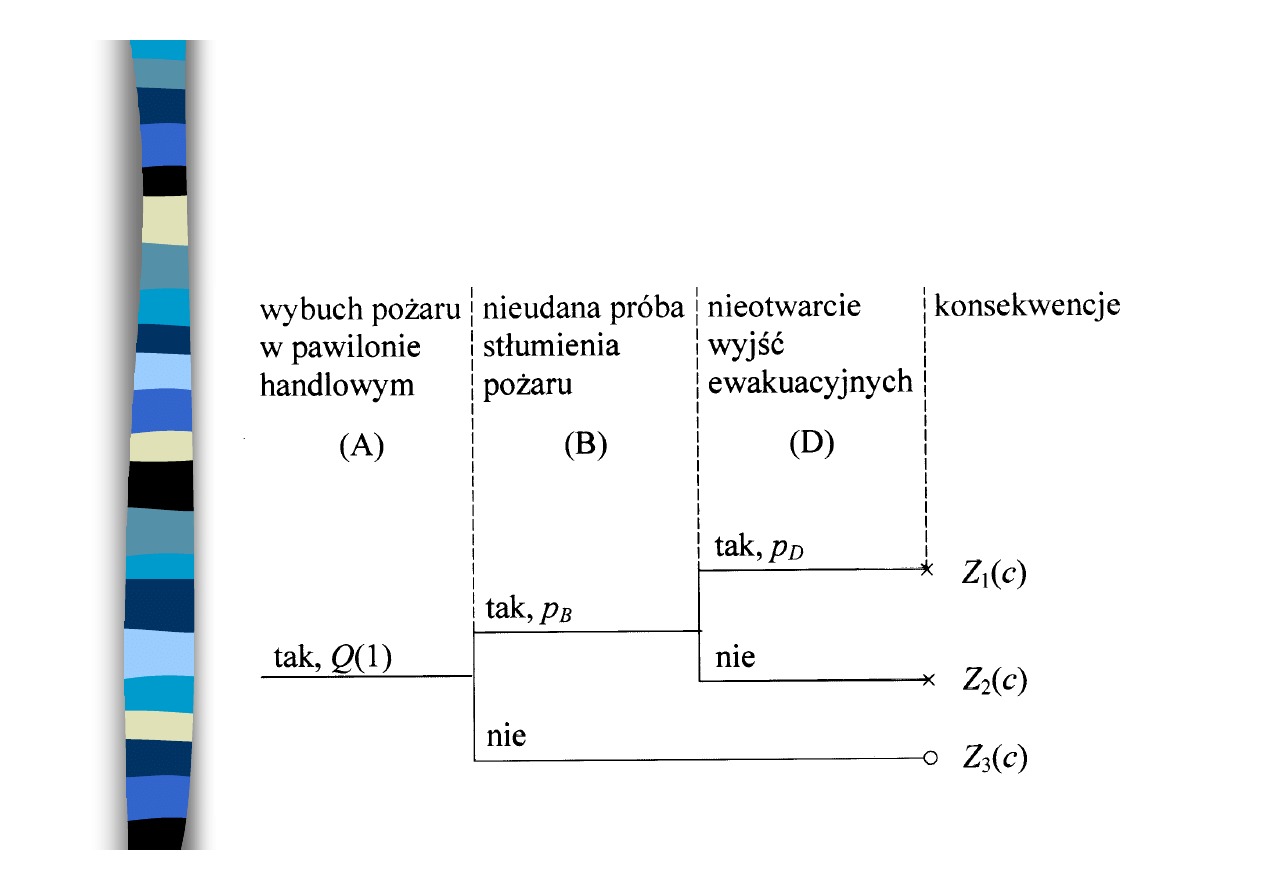
Przykład drzewa zdarzeń