12 Microactuators

Actuators are energy converters, which usually convert electric energy into me-
chanical energy. A voltage or current regulating system (e.g. power electronics)
and possibly a gear is as well part of the actuator together with the essential elec-
tromechanical converter. The tight coupling of the electromechanical energy con-
version and the integrated control electronics is frequently expressed by the techni-
cal term “Mechatronics” (mechanics and electronics) [8].

The application range of actuators is extremely wide and varied and is growing

steadily. Examples are robotics, handling equipments, micromanipulators, medical
technology, medical electronics, minimal invasive surgery, dosimetry, analysis
technology, measuring techniques, consumer and entertainment technology,
switches, automotive engineering and household technology. The market potential
for microactuators is very high due to their wide application that practically en-
compasses all areas of life [5, 6, 7, 18].

In the following, fundamental physical characteristics of energy conversion and

the available converter principles are treated. Further, the characteristics of the
most common types of actuator are analysed in some detail and checked for their
suitability for microsystems applications. It is seen that in the micro range, a larger
variety is justified [18] than that in the macro range, which is dominated by elec-
tromagnetic converters. Some microactuators are however inefficient under energy
criteria. Finally, we deal briefly on the importance of friction and the associated
wear.

12.1
Energy conversion

The goal of microactuation is the generation of forces which will produce a me-
chanical motion. Therefore, the different principles of actuation have to be judged
according to their ability to work, i.e. the usable mechanical energy. Beside the
electromagnetic energy conversion, predominating in traditional drive engineering,
for microactuation a multiplicity of different principles are common, which do not
play a role due to functional or cost arguments in macro technology. Clearly, in
microsystem technology the applicable materials and the realization in planar
technology are of fundamental importance.

The fundamental relation for ability to work is given by the change of the stored

energy

W

of the system, which leads to a force

F

:

12.1 Energy conversion

321

F

dW

ds

=

(12.1)

If the energy content changes between two states

W

1

and

W

2

we get:

F

W

s

W

W

s

=

=

−

∆

∆

∆

1

2

(12.2)

If we further assume that one of the two states achieves an energy content of zero

W

2

0

=

, then the realizable force becomes directly proportional to stored energy.

F

W

~

(12.3)

For this reason, the stored energy and/or the energy density is of crucial impor-
tance for the ability to work of an actuator. The attainable energy density is com-
pared in the table 12.1 for different forms of energy. Since each transformation
between different forms of energy is accompanied with losses, ability to work is
also proportional to the efficiency

η

, with which a form of energy can be con-

verted into mechanical energy. Power conversion, i.e. the work done per unit time,
is determined from ability to work and the time necessary for charging or discharg-
ing the energy store. This time interval can be assessed by a time constant, which
is characteristic for the specific actuator principle. The decision on a converter
principle has to be taken by considering the attainable energy density, the speed of
the state change (time constant

τ

) and the energy efficiency

η

. In dependence of

Table 12.1. Forms of energy and typical values for the energy density [12].

Form

Energy density

[

]

Ws m

3

Gravity Gravitational

force

w

g h

= ρ

10

3

Gold,

5mm

=

h

Mechanical Kinetic energy w

v

= ρ

2

2

10

4

Gold,

m/s

1

=

v

Electric

Electric field energy

E

D

w

5

.

0

=

4 10

5

⋅

E

= ⋅

3 10

5

V mm

Magnetic

Magnetic field energy

H

B

w

5

.

0

=

10

6

T

6

.

1

=

B

Mechanical Elasticity

ε

σ

=

5

.

0

w

10

7

Silicon, Fracture limit

Thermal Phase

transition

w

h

= ρ∆

2 10

7

⋅

Water, Evaporation

Biological

Energy currency of cells

7

10

6

⋅

ATP

a ADP

Thermal Heat

capacity

w

c

T

p

= ρ ∆

10

8

Silicon,

K

60

=

∆

T

Chemical

Electrochemical battery

10

9

Lithium battery

Chemical Combustion

10

10

Gasoline

Nuclear Nuclear

fuel

10

15

Uranium

Mass

w

c

= ρ

2

10

21

12 Microactuators

322

these quantities the power

P

of a system is given by:

P

dW

dt

dW

ds

ds
dt

F

=

=

= ⋅

v ~

W

η

τ

∆

(12.4)

If we consider the rotation around a fixed shaft, as with motors, then the change of
angle has to be considered.

ω

=

ϕ

ϕ

=

=

M

dt

d

d

dW

dt

dW

P

(12.5)

For instance, the important energy forms of electric

e

w and magnetic energy den-

sity

m

w result from the corresponding field quantities by the following integrals:

W

w dV

e

e

V

=

∫∫∫

w

E dD

e

D

=

∫

0

(12.6)

W

w dV

m

m

V

=

∫∫∫

w

H dB

m

B

=

∫

0

(12.7)

Especially, for constant (i.e. independent of field strength) material properties

µ

ε

,

energy density is given by:

w

E D

e

=

1
2

w

H B

m

=

1
2

(12.8)

The above relations suggest, that the energy content increases with the volume

V

and thus with the third power of the length scale

λ

, while the force scales with the

second power of length (similarity relation). However, since in some important
cases the attainable energy density also dependents on the dimensions, this de-
pendence on the third power of the dimensions is not always correct. For microsys-
tems, this leads to the important fact, that energy conversion principles become
attractive in the micro range, which are not appropriate for the macro range.

Generally, the connection between force

F

and length scale

λ

can be de-

scribed by the relation

F

n

~

λ

. Typical values of the exponent

n are indicated for

different conversion principles in table 12.2. The listed principles differ regarding
the attainable energy density, time constant and power efficiency. These quantities
determine the attainable force and power density. The typical energy density for
the majority of the conversion principles used today, lies within the range of

w

≈

−

10

5

10 Ws / m

6

3

. However, since the operating speed, expressed by a time

constant

τ

typical for a charging-discharging cycle of the energy store, differs

strongly, power density

τ

/

w

varies in a much wider range. The power density

ranges from

10

-6

to

10

0

W/cm³, thereby hydraulic and pneumatic actuators

achieve the highest power densities, however, no actuators with high power den-
sity exist in the micro range. [15]. The usable mechanical energy results from the
product of energy density and efficiency. The efficiency depends on the principle

12.2 Electromagnetic actuators

323

of operation and on the dimensions, therefore in the micro range some principles
exhibit a similar ability to work.

12.2
Electromagnetic actuators

In electromechanical engineering, machines of power

P

with at least 100 W are

designed with the help of a performance index, sometimes termed as Esson num-
ber

C

, which is a measure of power per unit volume.

P

C D

n p

=

2

2

l

(12.9)

Where

D

is the inside diameter of the stator,

l is the rotor length (iron length), n

is the number of revolutions and

p is the number of pole pairs. Typical values for

the Esson number lie within the range of

C

= − ⋅

5 25 10

4

Ws / m

3

[16].

This design is essentially based on the fact, that the attainable magnetic flux

density is limited due to saturation in the iron. The typical magnetization curve
represented in Fig. 12.1 shows that the permeability strongly decreases for a flux
density of approx. T

1

or higher. At higher magnetic flux density, this leads to

strongly increasing exciting current for the magnetization and increased losses in
the winding and the iron core. For this reason attainable, practical magnetic flux
density is limited to approximately

T

6

.

1

max

≤

B

.

Since magnetic field strength is very small inside the iron due to the high per-

meability, the magnetic field energy mainly concentrates in the air gap between
stator and rotor. Therefore, the attainable energy density becomes:

w

B

m

=

≈ ⋅

1
2

1 10

2

0

6

max

µ

Ws

m

3

(12.10)

Table 12.2. Common energy conversion principles and typical values for the energy density, the
time constant and the efficiency of microactuators [10, 15, 17].

Effect Energy

density

[

]

Ws m

3

Force scaling

F

n

~

λ

with

n

=

Time constant

τ

[ ]

ms

Efficiency

η

Piezoelectric

2 10

5

⋅

2

<< τ

mech

0.3

Electromagnetic

10

5

(2 to) 4

<< τ

mech

<0.01

Electrostatic

10

4

2

<< τ

mech

0.5

Bimetal

10

6

2 <

50

10

4

−

Thermopneumatic

< ⋅

5 10

5

2 10

0.1

Shape memory alloys

5

10

5

.

3

⋅

2 <

50

0.01

12 Microactuators

324

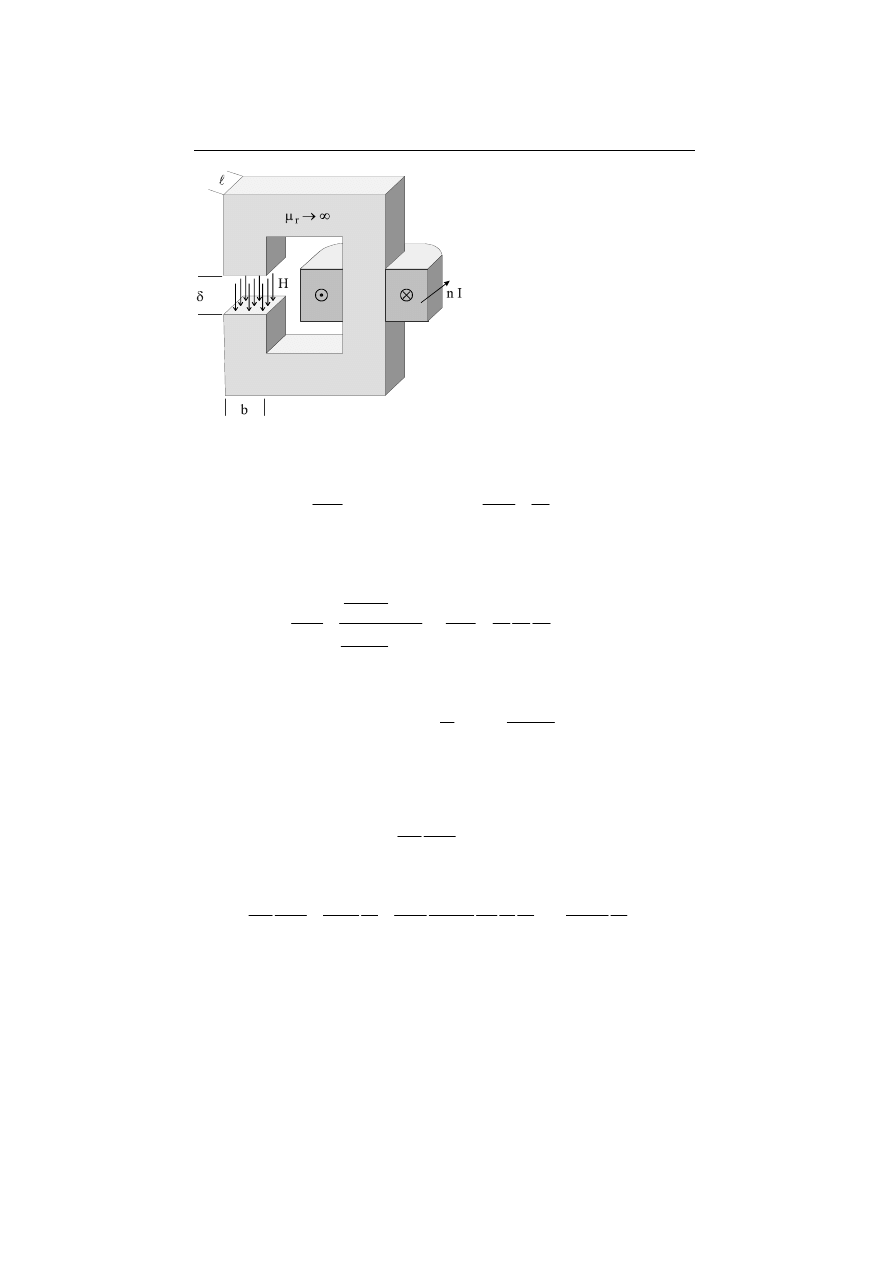
The idealized magnetic circuit in Fig. 12.2 is adequate for deriving the most im-
portant connections. Hereafter we neglected the magnetomotive force in the iron.
Applying Ampere’s law we receive the magnetic field strength

H

in the air gap

for the number

n of turns. Together with eq. (12.8) we compute the energy den-

sity.

H

n I

δ =

w

n

I

m

=

1
2

2

2

2

0

δ

µ

(12.11)

The magnetic field energy stored in the air gap of volume

V

b

= δ

l , results in:

W

n

I

b

m

=

1
2

2

2

2

0

δ

µ δ

l

(12.12)

As with the design of conventional electromagnetic machine we first assume a
constant magnetic flux density in the air gap, independent of the dimensions

l, ,

b

δ

of the system.

Am

Vs

10

4

T

6

.

1

.

7

0

max

−

⋅

π

≈

µ

=

=

B

const

H

(12.13)

For two realizations with the length ratio

λ

given by,

l

l

1

2

1

2

1

2

=

=

=

b

b

δ

δ

λ

(12.14)

the magnetomotive force

n I (ampere turns) decreases proportionally with the

dimensions.

Fig. 12.1. Magnetization curve of dynamo sheet. Continuous curve and left scale for relative
permeability, dotted curve and right scale for field strength in dependence of the magnetic flux
density.

12.2 Electromagnetic actuators

325

B

n I

max

µ

δ

0

=

⇒

n I

n I

1 1

2

2

1

2

=

=

δ

δ

λ

(12.15)

The assertion results in the scaling of the total energy content in the air gap region,
which is proportional to volume:

(

)

(

)

W

W

n I

b

n I

b

n I

n I

b

b

m

m

1

2

1 1

2

1

1

1

2 2

2

2

2

2

1 1

2 2

2

1

2

2

1

1

2

3

=

= 







=

δ

δ

δ

δ

λ

l

l

l

l

(12.16)

The thermal energy dissipated by the winding is given by:

P

U I

v

=

where:

U

I

R

n

b

A

= =

+

2(

)

l

κ

(12.17)

Where

A

is the conductor cross-section and

κ

is the electric conductivity. In

order to achieve the same efficiency, the ratio of losses to the active power must be
constant.

P

P

W

W

v

v

m

m

1

2

2

1

1

=

(12.18)

Together with eq. (12.15) and (12.17) we get:

P

P

W

W

U I

U I

n I

n I

b
b

A

A

I

I

n A

n A

v

v

m

m

1

2

2

1

1 1

2 2

3

1 1

2 2

1

1

2

2

2

1

1

2

3

3

2

2

1

1

3

1

1

1

=

=

+
+

=

λ

λ

λ

λ

l

l

(12.19)

Fig. 12.2. Magnetic circuit.

12 Microactuators

326

Therefore, the expression

winding

A

A

n

=

,

(12.20)

which represents the total winding area, should be constant, i.e. independent of the
other dimensions. This shows that something is wrong in our assumptions. Obvi-
ously, the above assumptions cannot be fulfilled simultaneously in scaling. From
the foregoing equations the quantity

P W

v

m

, which is important for efficiency,

results in:

P

W

I R
W

I n

b

A

n I

b

n A

b

b

v

m

m

=

=

+

=

+

2

2

2

2

0

0

1 2

1
2

4

1

κ

δ

µ

κ µ

δ

(

)

(

)

l

l

l

l

(12.21)

This relationship shows that it is not possible to achieve high efficiency at small
dimensions with electromagnetic actuators. The general expression for the effi-
ciency

η

, in dependence of the scaling factor

λ

and a constant

K

, is given by:

η

η

λ

1

2

2

1

1

=

+

−

K

(12.22)

For small dimensions, the first term of the denominator can be neglected, and
efficiency is proportional to the second power of the scaling factor.

If we give up the assumption of constant energy density, the alternative is to

proceed from maximum current density

J

max

, which either arises as a result of

thermal considerations (constant density of energy dissipation) or from the limit of
electromigration (

2

6

A/cm

10

5

.

1

⋅

≈

). The magnetic field strength now is given by:

H

n I

J

n A

=

=

δ

δ

(12.23)

With constant current density

J and a winding area n A , which scales according

to the dimensions, magnetic field strength gives:

H

H

J

J

n A

n A

1

2

1

2

1

1

2

2

2

1

2

1

1

=

= ⋅

=

δ

δ

λ

λ

λ

(12.24)

In this case, the magnetic field strength must decrease for small dimensions and
energy density the scales as:

w

w

H
H

m

m

1

2

1

2

0

2

2

0

2

=

=

µ
µ

λ

(12.25)

Finally, the total energy content results in:

W

W

w

w

V

V

m

m

m

m

1

2

1

2

1

2

5

=

= λ

(12.26)

12.3 Electrostatic micromotors

327

This dependence quantitatively matches with the relations (12.16) and (12.22). For
both cases the ability to work

m

W

η

shows a length scale dependence of

λ

5

. The

scaling law indicates that magnetic micromotors exhibit both, poor efficiency and
a relatively small power. If the fact that the current density is limited would be
ignored and under the assumption that current density increased in a way that tem-
perature keeps constant, a more favourable scaling law results [17].

It is known also in conventional electromagnetic machine design, that the per-

formance index (Esson number

C

) is not independent of size. Comparing different

motors, over a wide range of rated power, reveals that output power approximately
increases with the fourth order of the dimension, whereby the efficiency for small
machines clearly decreases [16]. The deviation from the relationship found here is
due to the fact that small machines obey a change in the design. This expresses as
an increase of the current density, a decrease of power density, a higher switching
frequency and/or speed and an enlargement of the winding area, possibly even by
complete suppression of the soft-magnetic iron part. Additionally, small machines
use almost exclusively permanent magnets for the generation of the magnetic field.
However, the efficiency of small magnetic motors is already extremely low (per-
cent range). In microsystems various realisations of electromagnetic actuators have
been proposed, however, they were not designed for efficiency and consequently
show very low efficiency of

η <

1% .

12.3
Electrostatic micromotors

The attractiveness of the magnetic field in actuator design arises from high attain-
able energy density in the macroscopic range. This results from the saturation of
the soft-magnetic material as the limiting factor. Breakdown field strength is the
limiting factor for the electric field. At atmospheric pressure
(

Pa

10

013

.

1

atm

1

5

⋅

=

) the breakdown field strength is approx. 10

4

V mm . There-

fore, the attainable energy density

w

e

is:

3

2

12

2

7

m

Ws

10

5

.

4

m

V

s

A

10

854

.

8

m

V

10

2

1

2

1

⋅

≈

⋅

⋅









=

=

−

ED

w

e

(12.27)

This energy density is almost four orders of magnitude smaller than the magnetic
field energy. However, according to the Paschen-law this applies only to dimen-
sions larger than 100

µm. In the case of further reduction in the dimensions, the

breakdown voltage rises to approx. 10

3

V for a dimension of 1

µm, which corre-

sponds to an electric field strength of

10

6

V / mm

. As a result the attainable en-

ergy densities, becomes comparable with that of the magnetic field

w

m

≈ ⋅

1 10

6

Ws m

3

at small dimensions.

3

6

m

Ws

10

5

.

4

⋅

≈

e

w

for

E

=

1000 V

m

µ

(12.28)

12 Microactuators

328

According to the Paschen-law the breakdown voltage depends on the product of
electrode gap and gas pressure. At smaller pressures, in vacuum or in other gases
(e.g. SF

6

) a substantially higher breakdown voltage can be achieved. From ex-

perimental investigations it is found that the actual behaviour deviates from the
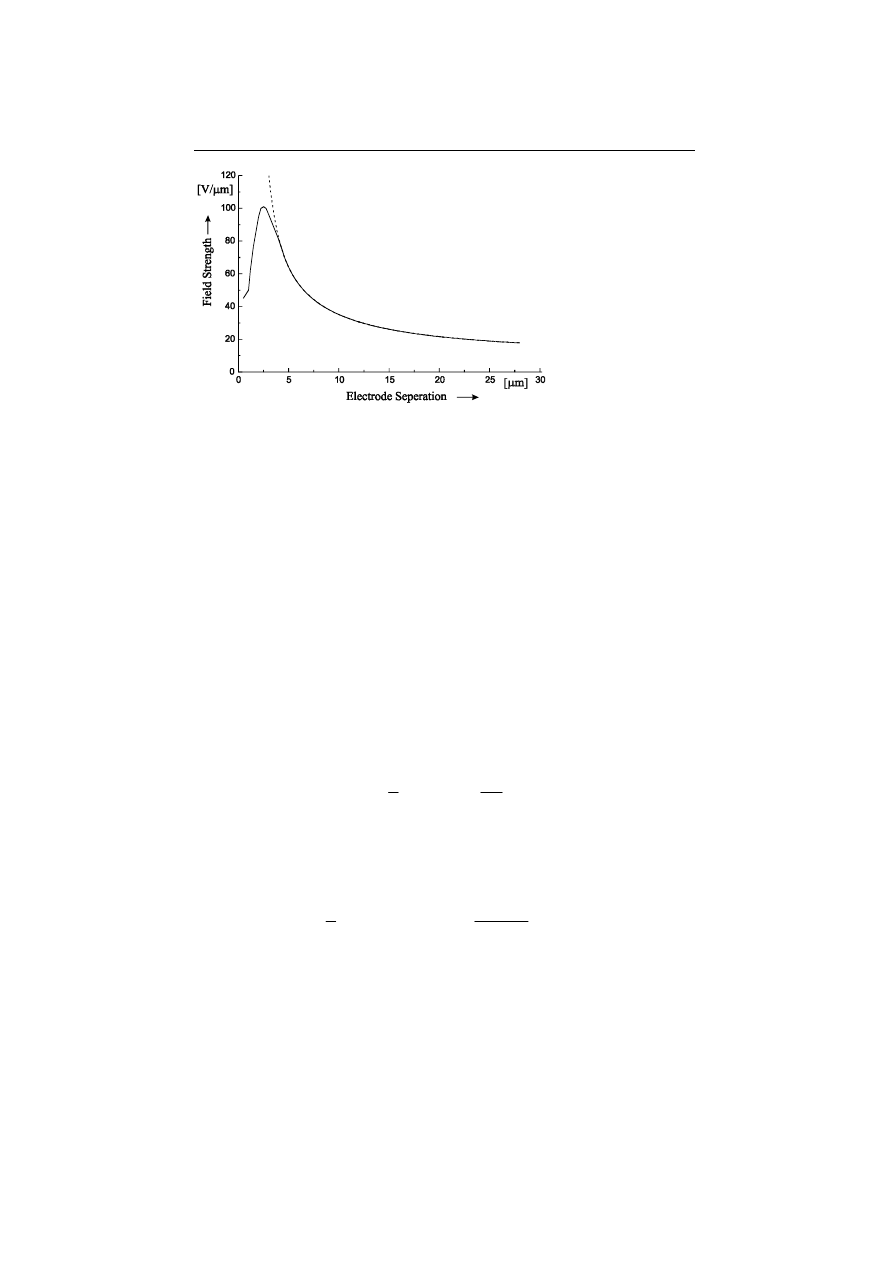
Paschen-law, below a gap width of approx. 4 µm, the breakdown field strength
becomes independent of the pressure and decreases again for small dimensions, as
represented in Fig. 12.3. The surface roughness seems to be crucial for the devia-
tions from the Paschen-law at small distances [19].

The relatively high energy density of the electrostatic field for small dimensions

makes this form of energy attractive for microactuators. In addition, the design
requirements are relatively easy to accomplish with microsystem technologies.
Since the attainable electric field strength is limited by the available voltage sup-
ply, often a clearly smaller energy density is used in the actual realization. If for
example the voltage is limited to 100 V, in the case of an air gap of

δ

µ

=

5 m , the

energy density is given by:

w

ED

e

=

≈ ⋅

1
2

18 10

2

Ws

m

3

(12.29)

The reluctance principle forms the basis of most electrostatic actuators. Here we
use the position-dependent change of energy content of capacitor arrangements.
For capacitor plates with a separation

y , the width w , depth

l and with the mis-

alignment

x energy density and forces are given by (stray fields neglected):

W

CU

e

=

1
2

2

(

)

C

w x

y

≈

−

ε

l

(12.30)

Fig. 12.3. Dependence of breakdown field strength on the electrode separation for air at standard
pressure. The dotted curve represents the Paschen-law, the continuous curve follows from meas-
urements obtained in [19].

12.3 Electrostatic micromotors

329

F

d W

d x

d

d x

CU

U

y

x

e

=

=







 =

−







1
2

1
2

2

2

ε

l

(12.31)

(

)

2

2

2

2

1

2

1

y

x

w

U

U

C

y

d

d

y

d

W

d

F

e

y

l

−

ε

−

=









=

=

(12.32)

Usually the normal force is larger than the tangential force

F

y

>

F

x

, since the elec-

trode width is larger than the spacing, and only in this case it is permissible to
neglect of stray field. The normal force cannot be used for the generation of a
continuous movement, since the operation range is limited to small displacements
by the electrode gap. Moreover, the force depends non-linearly on the position,
which is unflattering for many applications. Therefore, this form is used only for
incremental movement, e.g. for the position control in (acceleration-) sensors. In
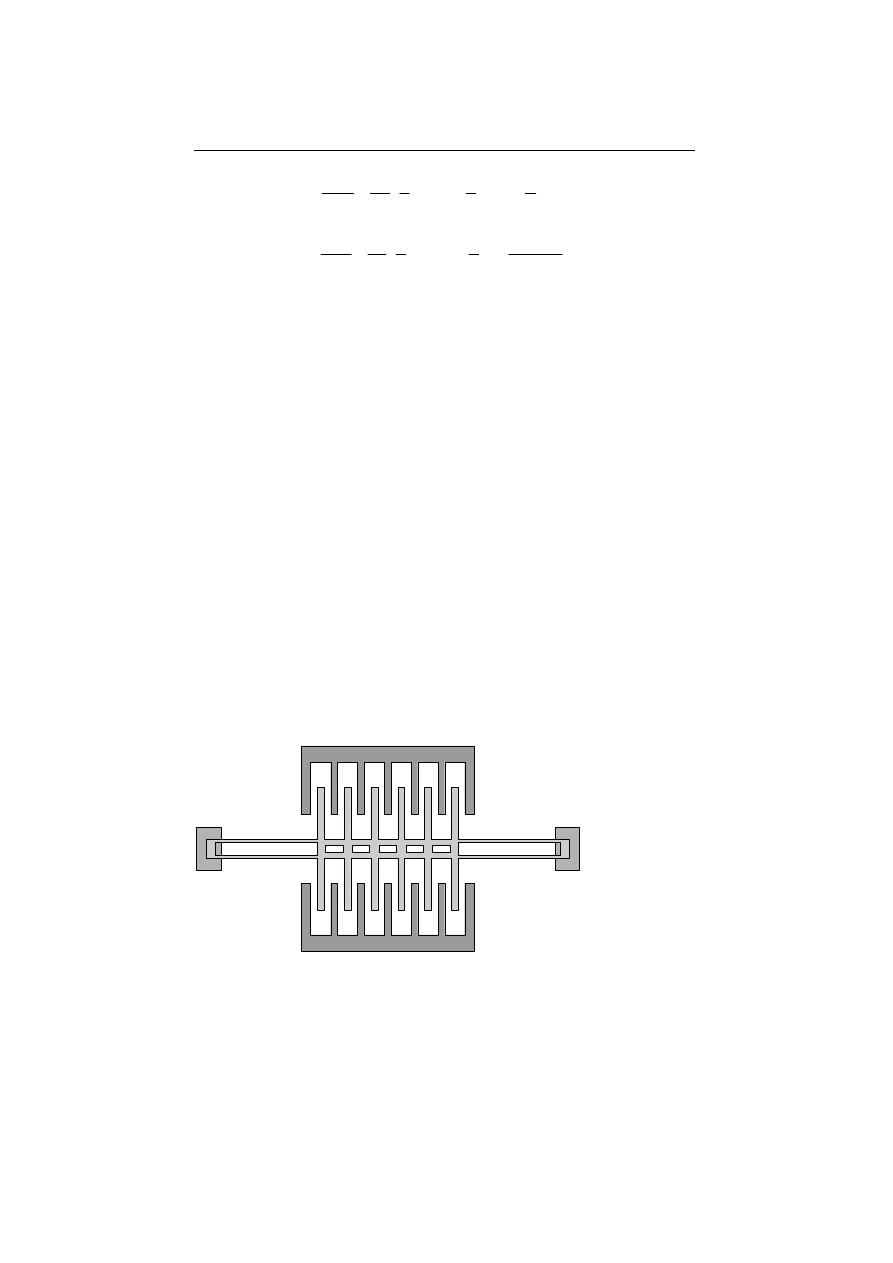
surface micromaching, structures as shown in Fig. 12.4 are common, which consist
of a multiplicity of interdigital parallel capacitors. The electrodes can be made of
polysilicon or electroplated structures, whereby the movable electrode is formed
by use of a sacrificial layer technique. The stray field mostly cannot be neglected.
For a high capacitance, larger layer thickness is required.

In electrostatic fields, the force between the electrodes always acts attractive –

independently of the polarity of the voltage supply. Therefore, an alternating
movement requires at least two phases (voltage supplies). A continuous linear or
rotary movement needs at least three phases.

Electrostatic motors execute a rotary motion around a fixed shaft. The reluc-

tance principle is commonly used, due to the simple construction and less stringent
material requirement. However, also asynchronous or electret motors can be real-
ized by use of the electric field [11]. For reluctance motors, stator and rotor mostly
consist of conductive materials, in addition, sufficiently large forces can be created
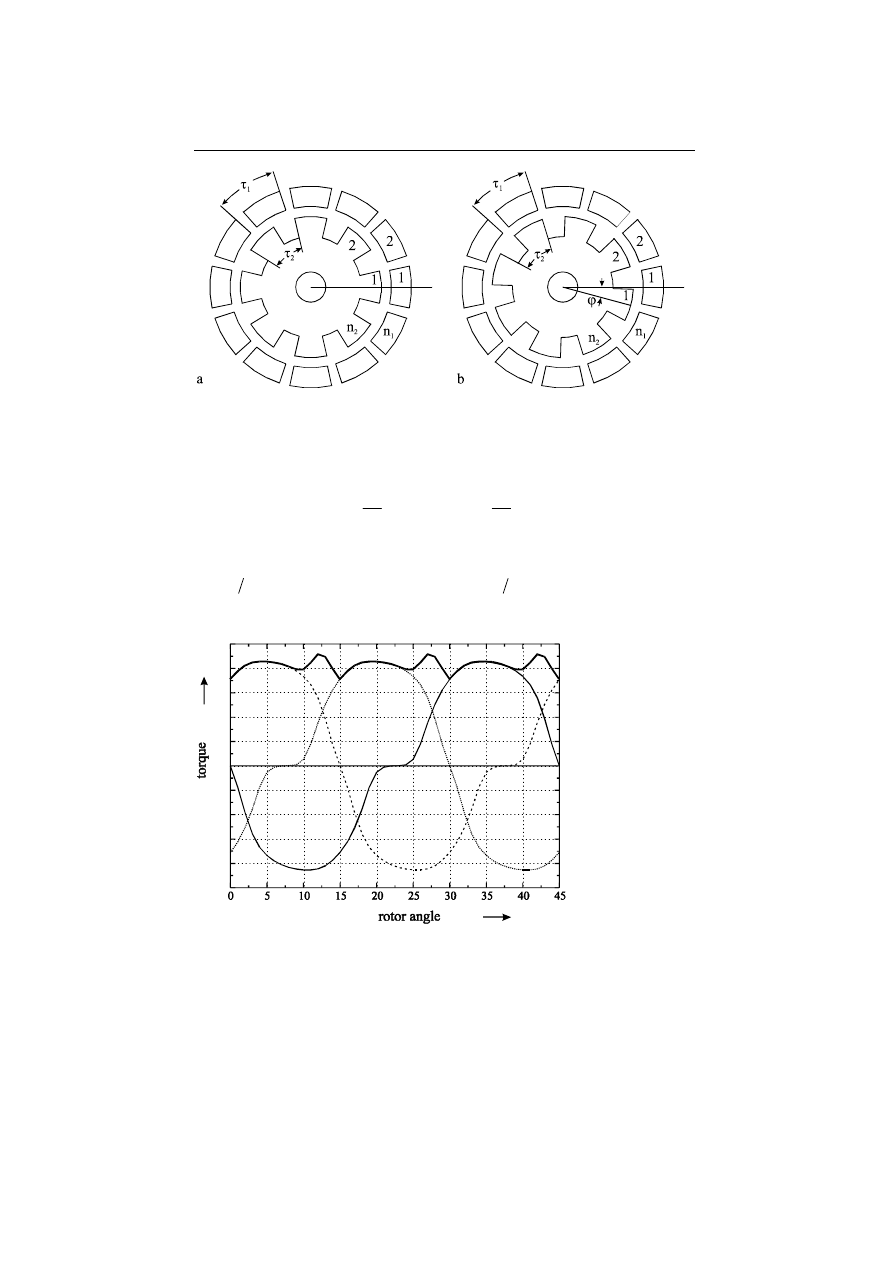
by materials with high dielectric constant. Figure 12.5 represented a reluctance
motor, where the stator has

n

1

and rotor has

n

2

poles. The distance between the

suspension

electrode A

electrode B

movable electrode

Fig. 12.4. Comb structure for a linear actuator in surface micromechanics.

12 Microactuators

330

poles is called pole pitch

τ

. The following relations hold for the motor:

τ

π

1

1

2

=

n

τ

π

2

2

2

=

n

(12.33)

Starting form the equilibrium condition in Fig. 12.5(a), if a voltage is applied to the
pole 1, a negative torque results for a position of the rotor at an angle of

ϕ =

0 to

ϕ τ

=

2

2 and a positive torque results for

ϕ τ

=

2

2 to

ϕ τ

=

2

. The numerically

Fig. 12.5. Reluctance motor with n

1

12

=

stator and n

2

8

=

rotor poles. (a) Rest position with

excitation at pole 1, (b) rest position with excitation at pole 2, with the rotor angle

ϕ

τ

= −

s

.

Fig. 12.6. Process of the torque for an electrostatic reluctance motor with n

1

12

=

and n

2

8

=

.

The torque of the three phases is represented in dependence of the rotor position together with
the torque resulting from the sum of respective positive components.

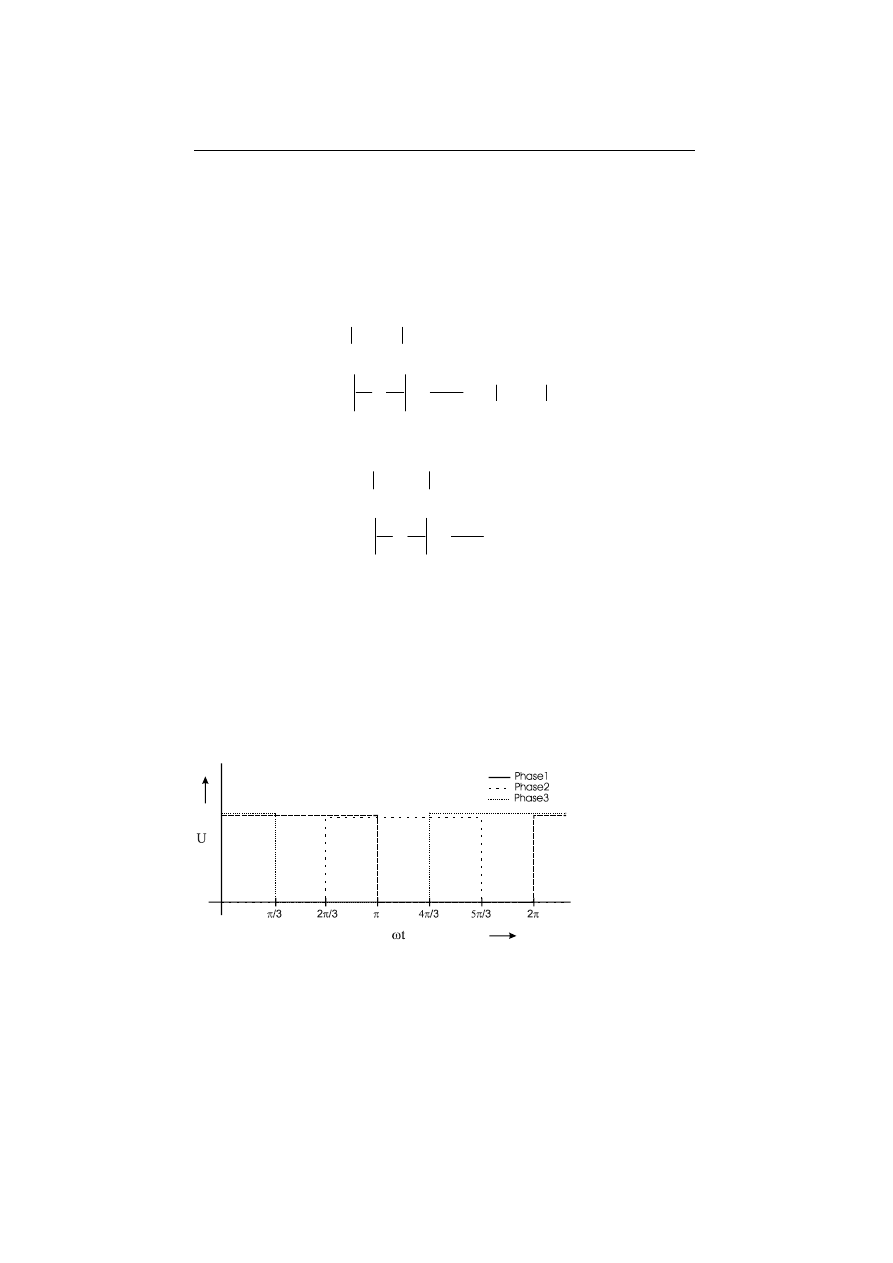
12.3 Electrostatic micromotors

331

computed curve of the torque of the motor from Fig. 12.5 is represented in Fig.
12.6.

If the voltage is switched to the next stator pole, then the rotor position changes

by the smallest possible angle such that again a stable position is achieved. This
angle

τ

s

is called step angle. Depending on the number of poles, the rotor can

rotate either in the direction of the field or in the opposite direction. The step angle
is found, if we switch the stimulation of the stator forward by one pole and then
looks for the rotor pole that is next to the excited stator pole.

{

}

[

]

τ

τ

τ

s

i

i

i

n

=

−

∈

−

min

,

1

2

2

0

1

(12.34)

{

}

=

−













=

−

2

1

2

1

2

1

2

2

1

π

π

min

min

i

i

n

i

n

n n

n

in

(12.35)

If we increase by

j

q

∈

−

[ ,

]

1

1

stator poles in each case, then the step angle results

in a similar way (

q

=

number of phases):

{

}

[

]

τ

τ

τ

s

i

j

i

i

n

=

−

∈

−

min

,

1

1

2

0

1

(12.36)

{

}

=

−













=

−

2

2

1

2

1

2

2

1

π

π

min

min

i

i

j

n

i

n

n n

j n

i n

(12.37)

For a machine with at least

q

=

5 phases, the switching sequence can be chosen in

a way that multiples of the smallest step angle are possible. Then with the same
switching frequency different speeds are possible depending upon the switching
order. If the poles are driven with rectangular voltages of the frequency

f, which

are shifted by the phase angles 2

π

/

q for the individual poles as shown in Fig.

12.7, the resulting rotational speed

n is given by:

Fig. 12.7. Switching sequence of the phases. Each of the phases remains active for the period of
180°, for which the torque exhibits a positive sign.

12 Microactuators

332

n

q

f

s

= 






−

2

1

π

τ

(12.38)

Example:

For a motor with

n

1

12

=

stator poles (stator pole pitch

τ

1

30

= °

) and

q

=

3

phases, the values for the rotor pole pitch and the step angle are indicated for dif-
ferent numbers of rotor poles

2

n in the following table. For n

2

6

=

and

n

2

18

=

an unstable equilibrium position results, and the direction of rotation is not
uniquely defined.

n

2

4 6 8 11 13 16 18 20

τ

2

90° 60° 45° 32.7°

27.7°

22.5° 20 18°

τ

s

30°

±

30°

-15° -2.7° 2.3° 7.5°

±

10°

-6°

For the design of reluctance motors the question arises, which poles shape is to be
selected, so that an optimal operation is achieved. We start with the simple capac-
ity model. The torque results from the change in capacitance during a step to:

M

W

C

U

s

=

=

∆

∆ϕ

∆

τ

1
2

2

(12.39)

Firstly it is seen, that a high torque results, if the step angle is small. Particularly
small step angles and therefore high torque can be obtained for

n

n

2

1

1

=

±

. To

achieve a large change in capacitance, the air gap should be as small as possible
and the difference of the radii of pole and pole gap should be as high as possible.
This prerequisite can only be fulfilled up to reasonable limits resulting from tech-
nological and possibly also the material strength restrictions.

To simplify the following consideration, we use the linear motor represented in

Fig. 12.8. However, all results can easily be transferred to the case of a rotating
motor considered before. The pole widths

w w

1

2

,

and the pole pitches

p p

1

2

,

and/or the step width

p

p

p

s

=

−

1

2

are to be chosen such that the resulting force

Fig. 12.8. Designation and dimensions of a linear electrostatic motor.

12.3 Electrostatic micromotors

333

is as uniform as possible.

For this we investigate three cases as depicted in Fig. 12.9. In the first case, the

poles of stator and rotor completely overlap, if the supply is switched to the next
pole after reaching the rest position. In this case, the force is very low. The geo-
metrical condition for this case is given by:

p

w

p

w

1

1

2

2

2

2

−

<

−

or

w

w

p

s

1

2

2

−

>

(12.40)

In the second case, rotor and stator poles partly overlap each other, so that the
change in capacitance becomes

dC dx

d

/

/

= ε

l

and thus force achieves its maxi-

mum value.

In the third case, there is no overlapping of the poles, therefore a relatively low

force results. The following condition holds for this case:

p

w

p

w

1

1

2

2

2

2

−

>

+

or

w

w

p

s

1

2

2

+

<

(12.41)

For a good design, the dimensions, i.e. the pole width should be selected according
to the second case. Then:

w

w

p

w

w

s

1

2

1

2

2

−

<

<

+

(12.42)

If instead of the pole width, the pole coverage

α

is used, as it is common for rotat-

ing motors,

α

1

1

1

=

w

p

,

α

2

2

2

=

w

p

(12.43)

we get the relation:

Fig. 12.9. Field distribution in the air gap of a reluctance motor. Left column in the rest position
(no force) and right column after switching to the next phase. In the right column, the rotor and
stator poles overlap completely, partly or not at all, from top to bottom.

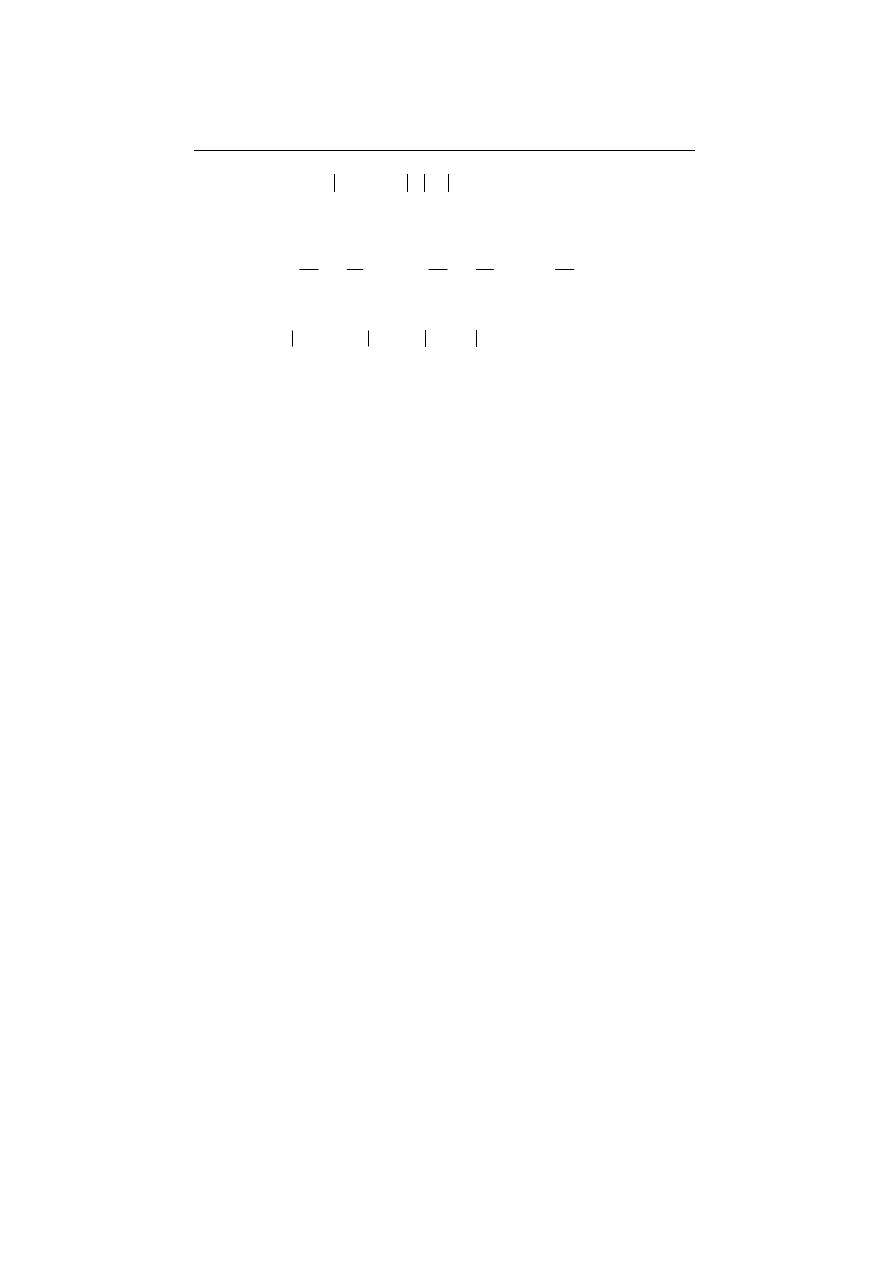
12 Microactuators

334

α

α

α

α

1 1

2 2

1 1

2 2

2

p

p

p

p

p

s

−

<

<

+

(12.44)

If we further replace the linear pole pitch

p by the angular pole pitch

τ

and the

radius

R

,

p

R

R

n

1

1

1

2

=

=

τ

π

,

p

R

R

n

2

2

2

2

=

=

τ

π

,

p

R

s

s

= τ

π

2

(12.45)

after a few transformations the expression becomes:

α

α

α

α

1 2

2

1

2

1

1 2

2 1

2

n

n

n

in

n

n

i

−

<

−

<

+

min{

}

(12.46)

This relationship gives a condition for the pole coverage depending on the pole
numbers, which can be easily checked. The connection only gives necessary condi-
tions for a partial overlap between rotor and stator poles. Whether a design fulfils
all requirements has to be checked for each specific case. For

n

n

2

1

1

=

±

the re-

quirements can be fulfilled without difficulty.

12.4
Piezoelectric actuators

Piezoelectric materials are characterized by the appearance of a polarization
charge when these materials are under mechanical stress. Conversely, piezoelectric
materials show a length variation when they are brought into an electric field. The
electric polarization P

D

E

= − ε

0

, which is related to the surface charge, increases

linearly with the mechanical stress

σ

in first-order approximation. The material

law is expressed by:

D

P

E

d

= +

=

ε

0

σ

(12.47)

The electric flux density

D

and field strength

E

are vectors, the mechanical stress

σ

and strain

ε

are tensors of rank two. Therefore, the piezoelectric coefficient

d

is a rank-three tensor. Since the stress tensor is symmetrical, the tensor of the pie-
zoelectric coefficient in general case has

3 6

18

⋅ =

independent entries. In compo-

nent notation we get the following relationship according to the definition in chap-
ter 3.1.

D

=















 =

















































D

D
D

d

d

d

d

d

d

d

d

d

d

d

d

d

d

d

d

d

d

1

2

3

11

12

13

14

15

16

21

22

23

24

25

26

31

32

33

34

35

36

1

2

3

4

5

6

σ

σ

σ

σ

σ

σ

(12.48)

The indices

3

,

2

,

1

refer to the crystal axes and can be equated with the coordinate

directions

z

y

x ,

,

at suitable orientation. For instance, a positive value of

d

33

12.4 Piezoelectric actuators

335

means that a tensile stress in z-direction leads to a positive charge on the surface
lying in z-direction.

The converse or indirect piezoelectric effect gives the relation between the elec-

tric field strength

E

and mechanical strain

ε

.

ε

ε
ε
ε

ε
ε

1

2

3

4

5

6

11

21

31

12

22

32

13

23

33

14

24

34

15

25

35

16

26

36

1

2

3





































=





















































d

d

d

d

d

d

d

d

d

d

d

d

d

d

d

d

d

d

E

E
E

(12.49)

The coefficients

d

ij

are identical to the direct piezoelectric effect. Electrostriction is

defined as the second order effect, which depends on the square of the electric
field strength and is described by a tensor of rank four.

ε

ε
ε
ε

ε
ε

γ

γ

γ

γ

γ

γ

γ

γ

γ

γ

γ

γ

γ

γ

γ

γ

γ

γ

γ

γ

γ

γ

γ

γ

1

2

3

4

5

6

11

21

31

12

22

32

13

23

33

14

24

34

15

25

35

16

26

36

1

2

3

11

12

13

14

15

16

21

22

23

24

25

26

31

32

33

34

35

36

41

42

43

44

45

46





































=



















































 +

d

d

d

d

d

d

d

d

d

d

d

d

d

d

d

d

d

d

E

E
E

γ

γ

γ

γ

γ

γ

γ

γ

γ

γ

γ

γ

51

52

53

54

55

56

61

62

63

64

65

66

1

2

2

2

3

2

2

3

3

1

1

2









































































E
E
E

E E

E E
E E

(12.50)

For the piezoelectric effect, a reversal of the electric field causes the transition
form tensile to compressive stress. The electrostrictive effect is related to the
square of the field strength and therefore does not depend on polarity.

In dependence on the crystal structure, some of the piezoelectric coefficients

become zero or have to be equated with others. The actual structure of the piezo-
electric material tensor follows from the associated crystal class. Crystalline quartz
belongs to the trigonal class with

d

d

11

12

= −

;

d

d

14

25

= −

;

d

d

26

11

2

= −

, the further

coefficients disappear. Zinc oxide and aluminium nitride belong to the hexagonal
class, here only the coefficients

d

d

31

32

=

;

d

33

and

d

d

24

15

=

are different from

zero. Crystals with a center of symmetry (like silicon) or isotropic materials do not
exhibit a piezoelectric effect, however, electrostriction occurs in all, also isotropic
materials.

Many of the piezoelectric materials are concurrently ferroelectric or pyroelec-

tric, i.e. they have a high permittivity, possess a hysteretic behaviour comparable
to ferromagnetic materials or show a polarization charge caused by a temperature
change. All ferroelectric materials are piezoelectric and pyroelectric, but not all
piezoelectric materials are ferroelectric (e.g..

Si O

2

, Zn O ). Similarly, pyroelectric

materials (e.g. turmalin) are not necessarily ferroelectric.

Particularly high piezoelectric coefficients are exhibited by ferroelectric ceram-

ics with perovskite crystalline structure A B O

3

.

A

and

B

are a divalent and a

12 Microactuators

336

tetravalent component, examples are

3

O

Ti

Ba

,

3

O

Ti

Pb

,

3

O

Zr

Pb

. For these

materials, the effect of the electrostriction can be neglected at field strength lower
than approximately E

<

10

4

V / m .

The characteristic of the ferroelectric material is that they change their material

properties at the Curie point

C

T . At temperature

C

T

T

>

the crystal does not ex-

hibit ferroelectricity, while for

C

T

T

<

it is ferroelectric. Most crystals can appear

in several crystalline phases, which are stable at different temperature and pressure
ranges. The transition between phases is accompanied by a change of the thermo-
dynamic characteristics (elastic, optical, thermal properties, volume, entropy, etc.).
During transition atoms are relocated, so that the crystal changes from one crystal
class to another. In general, transition occurs at different temperatures when heat-
ing and cooling (temperature hysteresis). The phase transition of the first order is
distinguished by strong and abrupt changes in the crystalline structure. During the
transition of the second order, the changes are less strong, and the transition is
continuous. Phase transitions of the second order do not possess a temperature
hysteresis. Phase transitions are often accompanied by the occurrence of new
physical phenomena (ferroelectricity, ferromagnetism, superconductivity, …). For

BaTiO

3

the Curie point is 120°C. Above this temperature BaTiO

3

belongs to the

cubic crystal class and loses thereby its ferroelectric and piezoelectric characteris-
tics, below the Curie point the crystal is tetragonal, at 0°C and -70°C further phase
transitions occur, with the orthorhombic and trigonal crystal classes. The change of
the crystal symmetry group connected to the phase transition causes the occurrence
of new coefficients in the material tensors.

The materials with usable length variation cover minerals, monocrystalline sub-

stances and polymers. Usually the piezoelectric effect is most strongly pronounced
in monocrystalline substances.

For materials usable in microsystems, the piezoelectric coefficients typically lie

within the range

1

100 10

12

−

⋅

−

m / V

. At a maximum field strength of

E

=

10

7

V / m

this leads to a length variation of

ε =

=

−

−

−

∆

l l

/

10

10

3

5

. In con-

Table 12.3. Characteristics of some piezoelectric materials. Relative permittivity

ε

r

, Curie

point T

C

and coupling factor k

p

[13, 14].

material / chem. Symbol

piezoelectric coefficient 10

12

−









m
V

ε

r

T

C

[

°

C]

k

p

quartz Si O

2

67

.

0

3

.

2

14

11

−

=

=

d

d

4.5

570

0.1

zinc oxide

Zn O

3

.

8

1

.

5

3

.

12

15

31

33

−

=

−

=

=

d

d

d

8.2

-

0.23

aluminium nitride Al N

d

d

d

33

31

15

5

2

4

=

= −

=

11.4

-

0.17

PZT-5A Pb Ti Zr

O

x

-x

3

(

)

1

584

171

374

15

31

33

=

−

=

=

d

d

d

1700

365

0.6

PZT-4 Pb Ti Zr

O

x

-x

3

(

)

1

d

d

d

33

31

15

289

123

496

=

= −

=

1300

328

0.6

polyvinylidenflourid P V D F

9

.

0

20

27

32

31

33

=

=

−

=

d

d

d

12

80

0.2

12.5 Thermomechanical actuators

337

sequence, the attainable control range is small. However, the motion can be con-
trolled very precisely by the voltage. In contrast to most other actuator principles,
there is no lower limit given by the atomic structure. This characteristic is ex-
ploited with the scanning tunnel or atomic force microscope, to resolve ranges
below an atomic diameter (

<

−

10

10

m ) to approx. 10

12

−

m .

The electromechanical coupling factor k

p

indicates the fraction at which en-

ergy is converted between mechanical and electrical forms in the material. It ap-
plies to the direct as well as to the converse piezoelectric effect.

energy

stored

energy

converted

2

=

p

k

(12.51)

For an effective energy conversion, naturally a high coupling coefficient is to be
achieved. The coupling factor is however not to be equated with the efficiency.
Since it is in principle possible to recover the stored energy; efficiency can be
clearly higher than the coupling factor.

Usually piezoactuators show small operating range but high forces. It is possible

to achieved a larger operating rage by utilising a suitable mechanical transmission.
Frequently piezoelectric converters are operated in resonance, in order to excite
acoustic waves. Here high frequencies up to the gigahertz range can be achieved
(e.g. surface acoustic wave filter, see Chap. 13). The acoustic waves can be used as
an energy converter or for measurement purposes.

A further important application is micro-dosing. Here a liquid filled capillary is

exposed to a short pressure pulse, whereby the capillary forces, with which the
liquid adheres to the nozzle, are overcome. The size of droplets mainly depends on
the diameter of the nozzle and the viscosity of the liquid. The volume of liquid
droplets typically lies within the range of some picoliters. High repetition rates
(over 1 kHz) can be achieved with this principle, which is used for example with
ink jet print heads.

12.5
Thermomechanical actuators

Thermomechanical actuators use the linear or volumetric expansion as well as the
shape deformation by the bimetallic effect, which occur due to a temperature
change [9]. On the one hand, the attractiveness of this type of actuator is based on
its simple structure. As operating components only a resistor heater and a layered
structure is required for the use of the bimetallic effect. On the other hand, thermal
actuators become attractive due to the favourable scaling law in the micro range,
since according to the Fourier number, the operating speed increases quadratically
with smaller dimensions. Almost any materials are applicable as active compo-
nents, apart from different coefficients of expansion only a sufficient strength is
required. Usually a meander-shaped resistor is used as heater, which can be real-
ized easily in thin film or thick film technology. Generally, sufficient large force

12 Microactuators

338

densities can be achieved, however, ability to work is often not satisfactory due to
the low efficiency.

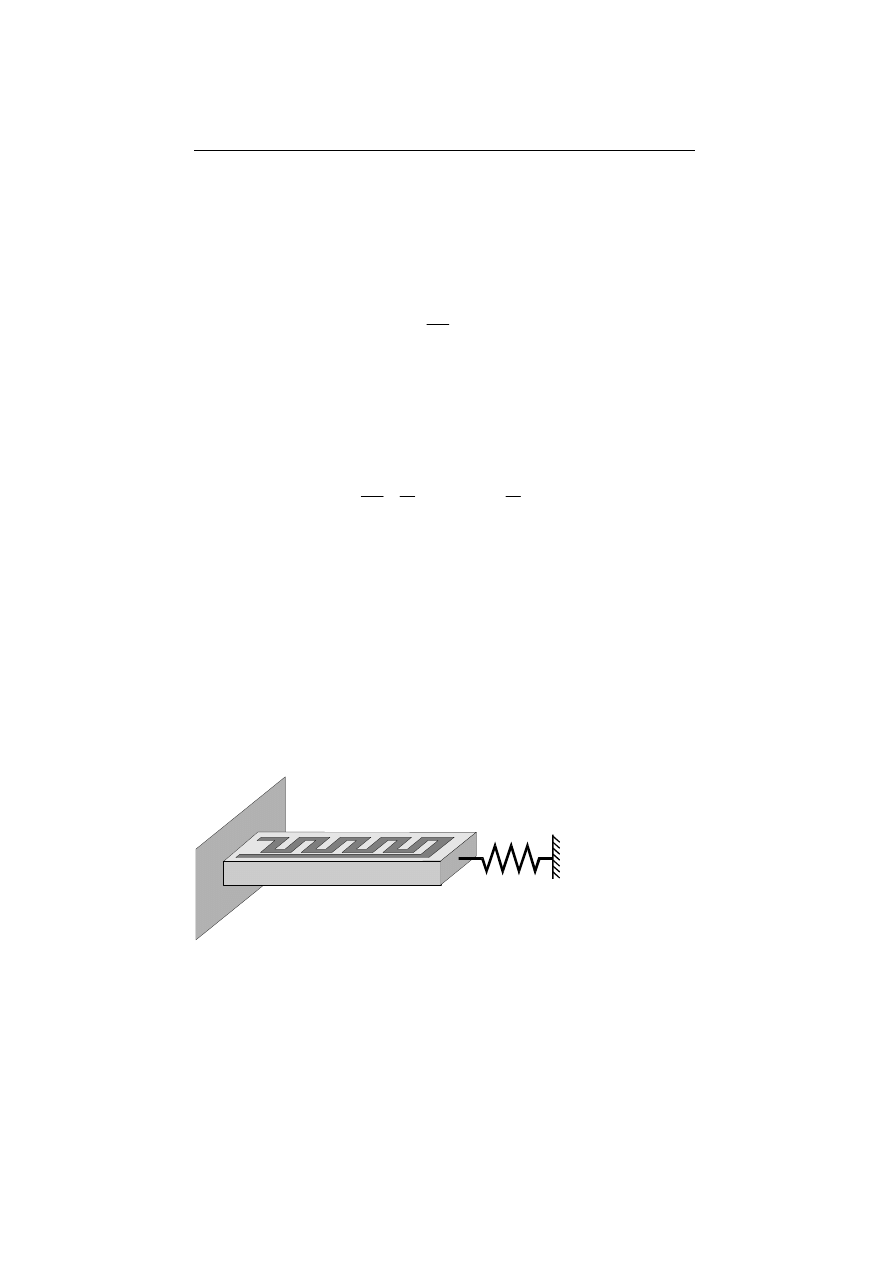
For the investigation of the thermal and mechanical transient behaviour, we first

examine the simplified arrangement from Fig. 12.10. The heating resistor is sup-
plied with an electrical power

P

el

, which is transformed to heat. By the Fourier

law, the removed thermal power results with the thermal resistor

R

ϑ

and the am-

bient temperature

T

T

T

0

= − ∆

:

P

T

R

v

= ∆

ϑ

(12.52)

If we assume that the entire volume

V of the actuator is at a uniform temperature,

then the stored thermal energy

Q is given by:

Q

c V T

p

= ρ

∆

(12.53)

With the abbreviation C

c V

p

ϑ

ρ

=

for the heat capacity, the energy balance results

in:

P

P

P

T

R

d

dt

Q W

d

dt

C

T

W

el

v

el

mech

mech

−

=

−

=

+

=

+

∆

∆

ϑ

ϑ

(

)

(

)

(12.54)

In order to simplify the transient solution of the differential equation, we neglect
the mechanical energy

mech

W

stored in the spring. This is only justified if the ratio

of the mechanical to the thermal energy is small. In the following we will see, that
this ratio, which determines the efficiency, is small for typical applications, hence
the assumption is reasonable. The resulting relation corresponds to the equivalent
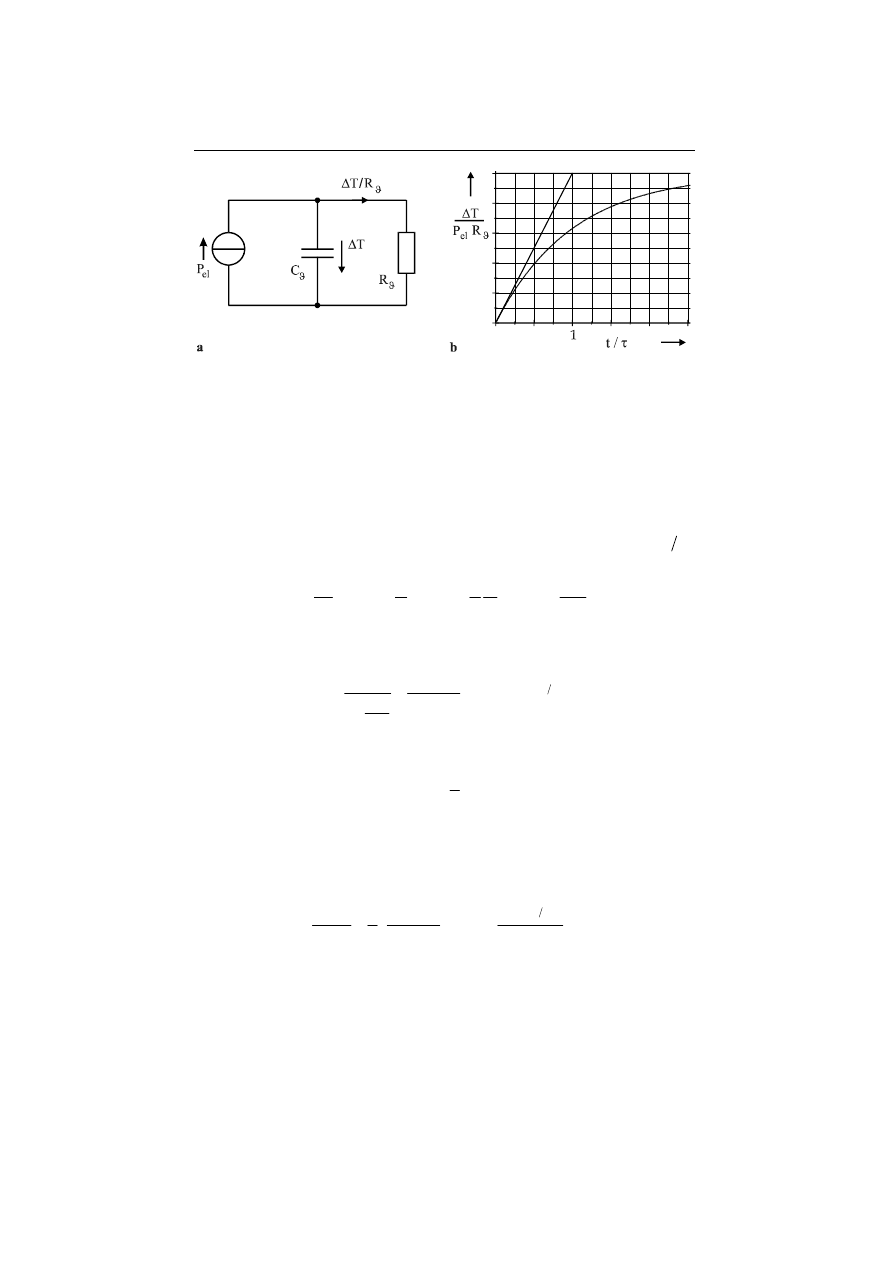
electric circuit represented in Fig. 12.11. The solution of the differential equation
(12.54) is found by integrating:

(

)

∆

T t

P R

e

el

t

( )

/

=

−

−

ϑ

τ

1

with

τ =

C R

ϑ

ϑ

(12.55)

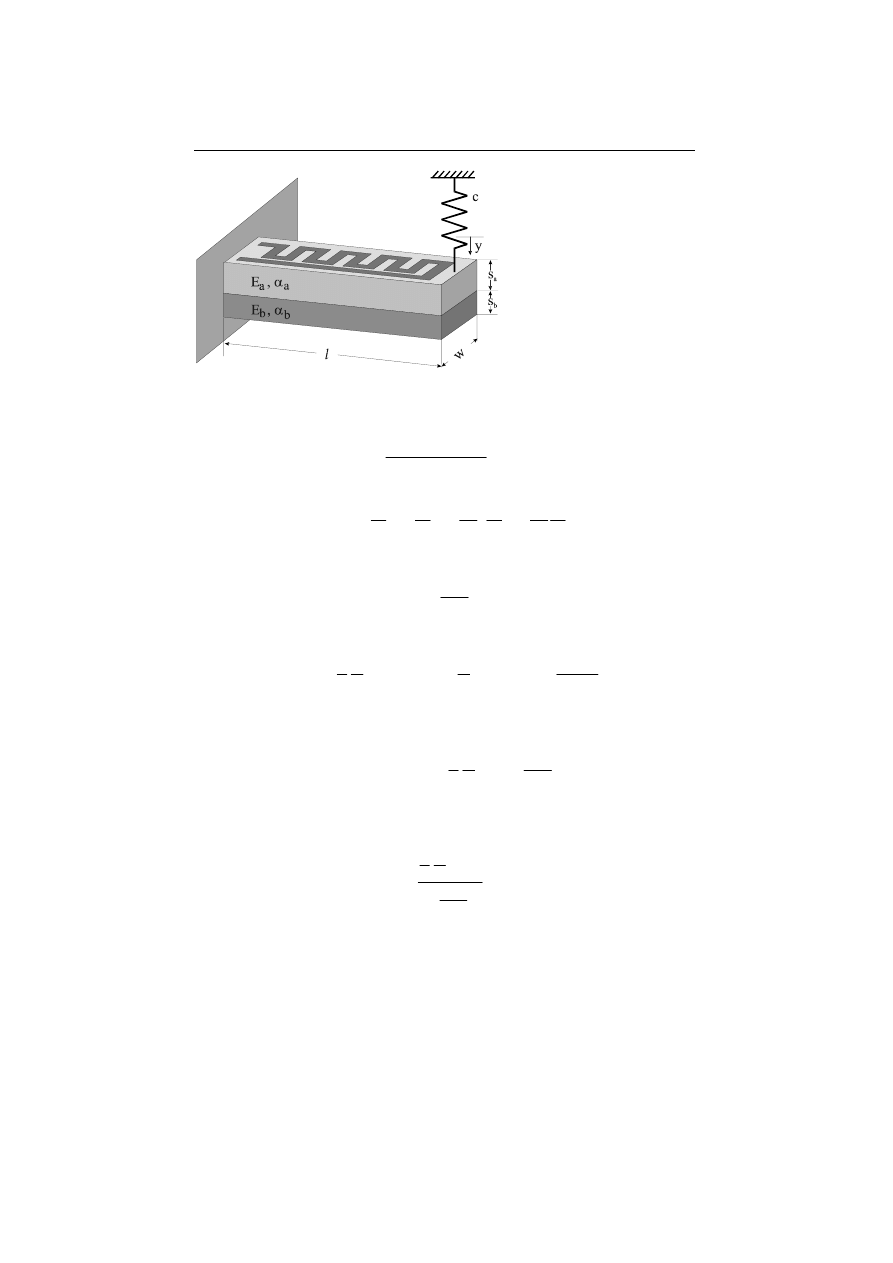
Fig. 12.10. Cantilever with heater structure as a model for a thermomechanical actuator. By
thermal expansion a mechanical work is performed in the spring.

12.5 Thermomechanical actuators

339

The speed of the process depends on the time constant

τ =

C R

ϑ

ϑ

. The attainable

final temperature is proportional to the electrically supplied heat and the thermal
resistance. The assumption of a uniform temperature in the volume presupposes
that the thermal transient process within the volume is fast in comparison to the
time constants

τ

(heat diffusion).

Thermal expansion leads to a strain in the material

ε α

= ∆

T , which interacts

with the spring. The spring is compressed according to the Hook’s law

ε σ

=

E .

The superposition of both components results in:

ε

α

σ α

α

=

=

− =

−

=

−

∆

∆

∆

∆

∆

l

l

l

T

E

T

E

F

A

T

c

E A

1

(12.56)

Here

c is the spring constant,

F

is the force,

A

is the cross-sectional area and

α

is the linear thermal expansion coefficient. The change in length is given by:

(

)

∆

∆

l

l

l

l

l

=

+

=

+

−

−

α

α

ϑ

τ

T

c

E A

E A

E A c

P R

e

el

t

1

1

(12.57)

The mechanical work equals to the energy stored in the spring:

W

c

mech

=

2

2

∆

l

(12.58)

The applied electrical energy is given by:

W

P t

el

el

=

(12.59)

Therefore, the efficiency of the actuation results in:

(

)

η

α

ϑ

τ

=

=

+







−

−

W

W

c

E V

E A c

R P

e

t

mech

el

el

t

2

1

2

2

2

l

(12.60)

Fig. 12.11. Transient behaviour of a thermomechanical actuator. (a) Equivalent electrical circuit
and (b) transient temperature behaviour.

12 Microactuators

340

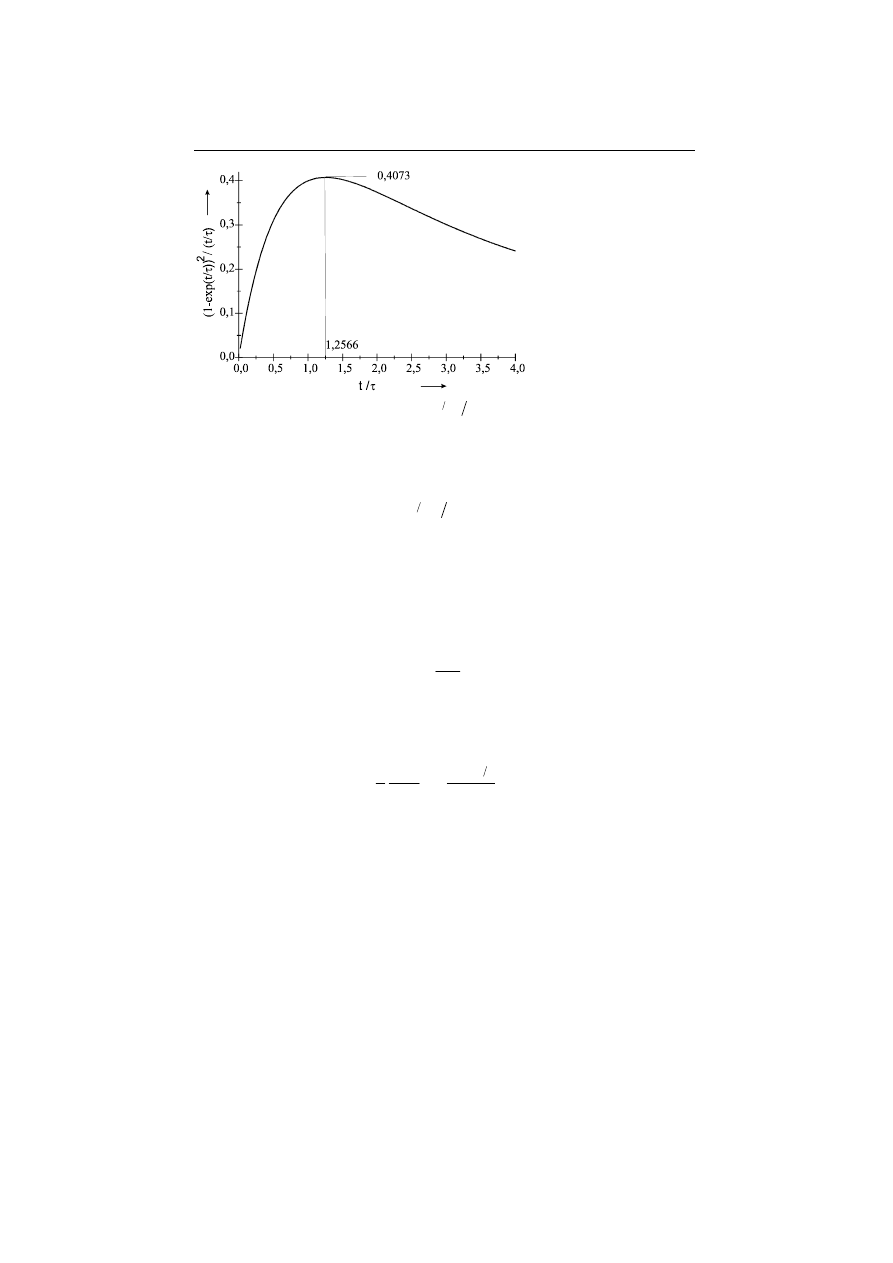
If we assume that the electric heating power is fixed, then it is favourable to termi-
nate the heating process after the time

τ

≈

25

,

1

t

, which corresponds to the maxi-

mum value of the function (

)

( / )

1

2

−

−

e

t

t

τ

τ

(Fig. 12.12) . If we consider the

heating power as a free design variable, which is to be determined from the tem-
perature and the heating duration according to eq. (12.55), then a short heating
duration leads to the highest possible efficiency. However, the necessary heating
power grows inversely to the heating duration. For practical reasons a typical heat-
ing duration of

τ

⋅

−

=

0

.

1

5

.

0

t

is most plausible.

From the relationship (12.60) it follows that the efficiency reaches its maxi-

mum, if we select the spring constant

c as follows:

c

E A

=

l

(12.61)

Thereby, the spring dilatation is halved compared to the unloaded case. Now, if we
use the material dependencies, then the following expression results for the effi-
ciency:

η

α

ρ

τ

τ

=

−

−

1
8

1

2

E

c

T

e

t

p

t

∆

/

(12.62)

This relationship explicitly gives the dependence on the material parameters. The
computation of the efficiency for typical materials for the arrangement in Fig.
12.10 results in insufficient values within the range of

10

10

4

6

−

−

−

. The very small

efficiency justifies the simplification we use before in deriving the transient ther-
mal behaviour.

Bimetal actuators of the type in Fig. 12.13 have a similar dependence and bad

efficiency. The behaviour can be computed analogous to a simple bending beam, if
the flexure rigidity

EI

is replaced by the following expression [20].

Fig. 12.12. Behaviour of the function (

)

( / )

1

2

−

−

e

t

t

τ

τ

, which determines the efficiency of

thermomechanical actuators in dependence of the heating duration.

12.5 Thermomechanical actuators

341

E I

w s s E E

s E

s E

K

a

b

a

b

a

a

b

b

=

+

3

1

12(

)

(12.63)

K

s
s

s
s

E
E

s
s

E
E

s
s

a

b

a

b

a

b

a

b

b

a

b

a

1

2

3

4

6

4

= +

+ 







+









+

(12.64)

Deflection due to a force is given by:

y

F

E I

l

mech

=

3

3

(12.65)

The bimetallic effect results in a deflection of [20].

y

s

T l

therm

=

1
2

2

α ∆

with

α

α

α

s

s

s

s K

b

a

a

b

b

=

−

+

6

2

1

(

)

(12.66)

For the calculation of resulting deflection

y , we assume that both components can

be superimposed, which applies to small deflections.

y

y

y

s

T l

F

E I

l

therm

mech

=

−

=

−

1
2

3

2

3

α ∆

(12.67)

Since the bimetal actuator operates on a spring, the force is proportional to deflec-
tion

F

c y

=

. Therefore, the dependence is given by:

y

s

T l

c

E I

l

=

+

1
2

1

3

2

3

α ∆

(12.68)

The transient thermal behaviour is the same as before, described by the relations
(12.52)-(12.55) above.

Fig. 12.13. Bimetal bending actuator.

12 Microactuators

342

Example: Bimetal actuator silicon / aluminium

Dimensions

s

Si

=

4

µ

m

m

8

.

1

µ

=

Al

s

l

=

200

µ

m

w

=

40

µ

m

Material data

K

1

10

3

.

3

6

−

⋅

=

α

Si

α

Al

= ⋅

−

23 10

6

1

K

K

kg

Ws

10

71

.

0

3

⋅

=

Si

p

c

K

kg

Ws

10

9

.

0

3

⋅

=

Al

p

c

3

3

m

kg

10

33

.

2

⋅

=

ρ

Si

3

3

m

kg

10

70

.

2

⋅

=

ρ

Al

E

Si

=

⋅

150 10

9

N

m

2

E

Al

=

⋅

70 10

9

N

m

2

κ

Si

=

150

W

m K

κ

Al

=

230

W

m K

Heat capacity:

K

Ws

10

8

.

8

8

−

ϑ

ϑ

ϑ

⋅

=

+

=

Al

Si

C

C

C

The switching speed is chosen to

τ =

10ms . Thus, the thermal resistance results

form:

W

K

10

13

.

1

5

⋅

=

τ

=

ϑ

ϑ

C

R

With the help of the heat diffusion length

δ

, the assumption of a uniform tempera-

ture of the cantilever can be checked.

δ

λ

ρ

τ

=

2

c

p

For silicon a heat diffusion length of 1.8 mm results, for aluminium the value is
1.95 mm. The heat diffusion length is large in comparison to all dimensions of the
cantilever. Therefore, the hypothesis of the constant temperature is justified.

Temperature difference (chosen):

∆

T t

(

)

= =

τ

50 K

Electrical heating power

(

)

∆

T t

P R

e

el

(

)

=

=

−

−

τ

ϑ

1

1

mW

70

.

0

=

el

P

The maximum possible temperature rise for this heating power is:

K

1

.

79

max

=

=

∆

ϑ

el

P

R

T

The thermal expansion of the cantilever (without spring force) results with

8

.

60

1

=

K

according to eq. (12.64) and

K

m

1

48

.

3

=

α

s

according to eq. (12.66) in:

12.6 Friction and wear

343

m

48

.

3

2

1

2

µ

=

∆

α

=

l

T

s

y

therm

In order to achieve an optimal efficiency, the spring constant

c is chosen such that

the counteracting force halves the deflection.

m

74

.

1

3

3

2

3

3

µ

=

=

=

=

l

I

E

y

c

l

I

E

F

y

y

them

mech

For this deflection, the spring constant results in

N/m

6

.

25

=

c

and the flexure

rigidity is

2

12

Nm

10

4

.

68

−

⋅

=

I

E

. The stress in the material is smaller than

2

6

N/m

10

50

⋅

and so does not lead to damage (fracture limit). The mechanical

work, which is exerted on the load (spring) results in:

Ws

10

8

.

38

2

12

2

−

⋅

=

=

y

c

W

mech

The electric energy supplied for this mechanical work is:

Ws

10

7

ms

10

mW

7

.

0

6

−

⋅

=

⋅

=

=

t

P

W

el

el

Thus, efficiency results in:

6

10

5

.

5

−

⋅

=

=

η

el

mech

W

W

The example shows that thermomechanical actuators can create relatively high
forces, but represent no design alternative seen from the angle of energy effi-
ciency. The result becomes more favourable with rising difference in the thermal
expansion coefficients

α

and higher temperature changes

T

∆

, the attainable

efficiency however remains relatively small. Gases and liquids show much higher
thermal expansion coefficient than solid, which can be used in thermopneumatic
actuators.

Shape memory alloys convert likewise thermal energy into mechanical energy

[5]. By exceeding a specific temperature, dependent on the material composition, a
phase transition occurs in the material, which is connected with a shape variation.
Temperature hysteresis is 10 K to 40 K. Shape memory alloys too exhibit a rela-
tively low efficiency. A further limitation results from the fact that the deformation
work of shape memory alloys decreases with the number of cycles (fatigue).

12.6
Friction and wear

Scaling laws lead to the fact that surface forces attain a larger importance com-
pared with volume forces in the micro range. From the mere fact, it is evident that
friction has high significance for microactuators. In addition, due to their small
volume, micromechanical components exhibit a small inertial force, which leads to
highly dynamic characteristics, so they often work with high operating frequencies
or speeds. [6]. Since microsystem technology mainly uses planar processes, the
design of micromechanical components is restricted in the layout and construction
of functional elements. For this reason a set of measures are not applicable, which

12 Microactuators

344

are common to control friction in macro technology. This applies in particular to
the application of the rolling friction using ball bearings. Rather in microsystem
technology we use sliding friction with plain bearings.

Friction on the one hand leads to losses, which causes an impairment of the

component function and wear the other hand, which affects the functional behav-
iour likewise negatively and leads to accelerated aging and eventually failure of
the component. Friction is a crucial factor that determines not only efficiency but
also durability. However, friction is not always accompanied by wear, on the con-
trary wearless friction is possible.

Friction is a phenomenon, acting at the surface layer of the material and which

practically is not affected by volume characteristics. It is a result of the interaction
between the contact regions and consequently the surface. Significant factors of
influence are the surface condition, surface topology and the interacting materials
[1].

In contrast to conventional mechanical engineering, in microsystems solid fric-

tion (dry friction) appears. With sleeve bearing the relatively large clearance and
the predominating start stop operation – due to the small inertia of micromechani-
cal devices – prevent the formation of a closed and supporting lubricating film.
The transition between dry friction and lubricant friction is characterized by the
Sommerfeld number.

So

p

=

ψ

η ω

2

(12.69)

Here

p

F

d

=

/ (

)

l is the load pressure,

ψ =

−

(

)

D d d is the relative radial clear-

ance,

D

is the outside radius of the journal and

d is the inside radius of the bear-

ing,

η

is the viscosity of the lubricant,

ω

is the speed and

l is the length of the

bearing. For a Sommerfeld number bigger than one, dry friction is present, this is
the prevailing domain of precision engineering and micromechanical devices.
Therefore, hydrodynamic sleeve bearings, where the shaft runs on a closed lubri-
cating film, are not applicable. Additionally, for micro motors the force resulting
from surface tension is already so large that it substantially affects the operation.
Therefore, dry-friction bearing is used for sleeve bearings, which however can be
provided with a molecular lubricant film in order to reduce friction and wear. In
this case, new characteristics of the lubricant and the contact surface become pre-
dominant. On the one hand material characteristics of the lubricants for films of
molecular thickness change, and on the other hand, adhesion of the lubricant to the
surface, which is explained by physisorption and chemisorption, receives higher
importance. However, today still no generally applicable method exists for apply-
ing the molecular films with a thickness of some nanometers. For the effectiveness
of these layers, naturally, the surface roughness plays a significant role, which is
relatively large in comparison to the film thickness with thin films used in
microsystems and lies within the range of some 10 up to some 100 nm.

12.6 Friction and wear

345

The classical engineering model of macroscopic friction has the following sali-

ent characteristics:

1. The friction force only depends on the normal force

F

n

and always acts in the

direction opposite the direction of motion.

2. Friction force is independent of the apparent contact surface.
3. Friction force is independent of the sliding speed.
4. Static friction force is larger than the kinetic friction force (static friction >

sliding friction).

5. Frictional forces depend on the two materials that are sliding past each other.

The following relation, also termed as Coulomb-Amonton law, represents these
ascertainments:

F

F

t

n

= µ

(12.70)

Where

F

t

and

F

n

are the tangential- and the normal force respectively and

µ

is

the kinetic coefficient of friction. Some coefficients of friction

µ

for dry sliding

friction and various material combinations are contained in the table 12.4.

Every surface exhibits roughness and surface waviness, which lead to the fact

that the actual area of contact, always consists of individual contact points. The
contact points or asperities only form a low fraction of the total area, dependent on
the loading (Fig. 12.14). Since solely the contact points contribute to force genera-
tion, the stress in the contact points is accordingly high and yield stress

m

σ

of the

material can be achieved with relatively small forces. Within the contact points
elastic or plastic deformations occur, whereby the resulting total contact area

A

becomes proportional to the pressure and inversely proportional to yield stress

m

p

A

σ

=

/

. In the contact areas interatomic cohesive forces act between adjacent

portions of matter over a short range, which withstand the shear stress

σ

s

. Friction

forces are only transferred in the contact areas. Thus, the friction force becomes
proportional to the actual contact area and the coefficient of friction results from

m

s

σ

σ

=

µ

/

. This model representation is able to explain the coulomb friction,

since friction becomes proportional to load and is independent of the apparent area.
The sum of point areas in actual contact increases with load by putting more area
in true adhesive contact by distortion. The model also explains why different mate-
rial surfaces have different coefficient of friction – the atomic surfaces have differ-

Table 12.4. Coefficient of kinetic friction (dry friction) of different material combinations [2, 4].

Material

µ

Material

µ

Aluminium / Aluminium

1.0-1.4

Teflon / Steel

0.04

Nickel / Nickel

0.53-0.8

Al

2

O

3

/ Al

2

O

3

0.4

Steel / Steel

0.42-0.57

Silicon / Al

2

O

3

0.18

Diamond / Diamond

0.1-0.15

Steel / Sapphire

0.15

Copper / Copper

1.2-1.5

Nickel /Tungsten

0.3

12 Microactuators

346

ent cohesions. Some application of this idea may verify conclusion that rough
surfaces may have less friction than the super-fine finishes, since a larger surface
fraction comes into contact. The main role of a lubricant is to keep the surfaces
apart.

Wear, which is accompanying friction, partially can be made plausible within

this picture. Within the contact points a high material load occurs, which leads to
plastic deformations on the one hand and on the other hand by adhering contact
partners to the formation of cracks, erosion at the contact surface and finally a non-
reversible material modification. The wear is attributed to the following mecha-
nisms [21, 22]:

−

Adhesion,

−

Abrasion,

−

Erosion by rupture of oxide coatings,

−

Fatigue.

Interatomic interactions are the result of breaking and reforming atomic bonds.
Within the range of the contact areas due to adhesive force a material transfer
between the contact points and restructuring in the crystalline lattice may occur.
The material transfer is more pronounced, with combinations of material, which
have larger mutual adhesive affinity or chemical solubility, making wear greater
for the contact of similar materials than for dissimilar. In abrasive wear, material is
removed due to the surface roughness of the partner or hard particles. Basically,
the harder material removes a volume from the softer material during a contact
path. Since the surface of metallic materials is covered with an oxide film, the
locally high loads can lead to rupture the oxide film. This leads to opening the
metallic surface and finally to the formation of a new oxide coating. Fatigue results
from stress cycling, which causes a plastic deformation of the surface.

The study of friction at the atomic level is called nanotribology, investigations

are accomplished by friction force measurements with the raster force microscope
[2, 3]. New concepts and sometimes intriguing but counter intuitive results have
been discovered since these techniques were first introduced in the late 1980s.
Friction forces produce harmonic atomic lattice vibrating, which varies with the
two materials. The mechanical oscillation energy ultimately produces heat. It is
shown that friction on atomic plane is a material dependent quantity and is propor-

Fig. 12.14. Model representation for the increase of the actual contact surface. (a) Contact area
with low pressure and (b) contact area with high load.

12.6 Friction and wear

347

tional to the actual instead of to the apparent contact area. The force is further
proportionally to the degree of their irreversibility, i.e. it depends on the ratio be-
tween the ease with which two areas adhere on each other. The ideal material to
prevent friction would resist forming chemical bonds with the widest variety of
materials. This chemical inertness is found in some materials like Teflon. At the
atomic level it has been determined that dry friction sometimes is less than wet
friction because the fluid allows more intimate contact between the surface and the
fluid resulting in a lot of adhesive friction. Texturing can be used primary to re-
duce stiction and static friction, since more irregular surfaces have lower stiction.
Texturing may also provide some support for the lubricant.

References

[1] Ando, Yasuhisa; Ino, Jiro: Friction and pull-off force on silicon surface modified by FIB.

Sensors and Actuators, A57 (1996) p. 83-89

[2] Bhushan, Bharat (ed.): Handbook of Micro/ Nanotribology. CRC Press, Boca Raton, New

York, London (1995)

[3] Bhushan, Bharat; Koinkar, Vilas N.: Microtribological studies of doped single-crystal

silicon and polysilicon films for MEMS devices. Sensors and Actuators, A57 (1996) p. 83-
89

[4] Bolz, Ray E.; Tuve, George L. (eds.): CRC Handbook of tables for Applied Engineering

Science. CRC Press, Boca Raton, 2. ed. (1987)

[5] Fatikow, Sergej; Rembold, Ulrich: Microsystem Technology and Microrobotics. Springer,

Berlin, Heidelberg, New York (1997)

[6] Fujimasa Iwao: Micromachines: a new era in mechanical engineering. Oxford University

Press, Oxford, New York, Tokyo (1996)

[7] Gerlach, Gerald; Dötzel, Wolfram: Grundlagen der Mikrosystemtechnik. Hanser, München,

Wien (1997)

[8] Heimann, Bodo; Gerth, Wilfried; Popp, Karl: Mechatronik: eine Einführung in die Kompo-

nenten zur Synthese und die Methoden zur Analyse mechatronischer Systeme. Hanser, Mün-
chen, Wien (1998)

[9] Janocha, Hartmut (Hrsg.): Aktoren: Grundlagen und Anwendungen. Springer, Berlin, Hei-

delberg, New York (1992)

[10] Jendritza, Daniel J.; Bölter, Ralf; Fleischer, Maximilian u. a.: Technischer Einsatz neuer

Aktoren: Grundlagen, Werkstoffe, Designregeln und Anwendungsbeispiele. expert, Rennin-
gen-Malmsheim (1995)

[11] Kasper, Manfred: Electrostatic Motors. Actuator 90, Proceedings of the 2nd International

Technology-Transfer Congress Bremen (1990), S. 195-198.

[12] Koenemann, Paul B.; Busch-Vishniac, Ilene J.; Wood, Kristin L.: Feasibility of Micro

Power Supplies for MEMS. Journal of Microelectromechanical Systems, Vol. 6 (1997) p.
355-362

[13] Landolt-Börnstein Neue Serie Gruppe III: Kristall- und Festkörperphysik, Bd. 11, Elasti-

sche, piezoelektrische, pyroelektrische, piezooptische, elektrooptische Konstanten und
nichtlineare dielektrische Suszeptibilitäten von Kristallen. Springer, Berlin, Heidelberg,
New York (1979)

[14] Landolt-Börnstein Neue Serie Gruppe III: Kristall- und Festkörperphysik, Bd. 16a, Ferro-

electrics and related Substances, Subvol. a: Oxides. Springer, Berlin, Heidelberg, New
York (1981)

[15] Madou, Marc: Fundamentals of Microfabrication. CRC Press, Boca Raton (1997)
[16] Nürnberg, Werner: Die Asynchronmaschine. Springer, Berlin, Heidelberg, New York, 2.

Aufl. (1979)

12 Microactuators

348

[17] Trimmer, William S.: Microrobots and Micromechanical Systems. Sensors and Acuators,

19 (1989) p. 267-287

[18] Trimmer, William S. (ed.): Micromechanics and MEMS: classical and seminal papers to

1990. IEEE Press, New York (1996)

[19] Torres, J. M.; Dhariwal, R. S..: Electric Field Breakdown at Micrometer Separations in Air

and Vacuum. In: Reichl, Herbert; Obermeier, Ernst (Hrsg.): Micro System Technologies 98,
6th int. Conference, vde Verlag, Berlin, Offenbach (1998)

[20] Young, Warren C.: Roark’s Formulas for Stress and Stain. McGraw-Hill, New York, St.

Louis, San Francisco, 6. ed. (1989)

[21] Zum Gahr, K. H. (Hrsg.):Reibung und Verschleiß, Mechanismen – Prüftechnik – Werk-

stoffeigenschaften. Deutsche Gesellschaft für Metallkunde, Oberursel (1983)

[22] Zum Gahr, Karl-Heinz: Microtribology. Interdisciplinary Science Review, Vol. 18 (1993)

p. 259-266