3. CECHOWANIE TERMOPAR W NISKICH TEMPERATURACH
Rozróżnia się następujące zjawiska termoelektryczne:



zjawisko Seebecka – powstanie siły termoelektrycznej w zamkniętym obwodzie składającym się
z dwóch różnych metali, o ile miejsca styku tych metali znajdują się w różnych temperaturach,



zjawisko Peltiera – gdy prąd elektryczny przepływa, przez miejsce złączenia dwóch różnych
metali, to zależnie od kierunku przepływu złącze to nagrzewa się lub oziębia (poza wydzielającym
się oczywiście w każdym przewodzie ciepłem Joule'a),



zjawisko Thomsona – to zjawisko nagrzewania lub oziębiania pod wpływem przepływu prądu
występujące również w jednorodnym przewodniku, którego końce znajdują się w różnych
temperaturach; jest zależne od rodzaju metalu i od kierunku przepływu prądu.

Zjawiska Peltiera i Thomsona dotyczą jedynie wydzielania się lub pochłaniania ciepła i nie

powodują generowania sił termoelektrycznych. Są to, więc zjawiska dotyczące jedynie efektów
cieplnych towarzyszących przepływowi prądu elektrycznego.

W praktyce prądy płynące w obwodzie termoelektrycznym są tak małe, że zjawiska Peltier

i Thomsona mogą być pominięte.

Ze wszystkich zjawisk termoelektrycznych jedynie zjawisko Seebecka jest źródłem

powstawania siły termoelektrycznej. Wynika ona z nierównomiernego rozkładu elektronów
w przewodzie o zróżnicowanej na długości temperaturze.

3.1. Zjawisko termoelektryczne

Wielkością fizyczną wykorzystywaną do pomiaru temperatury jest siła termoelektryczna.

Stykając ze sobą powierzchnie dwóch różnych metali występuje kontaktowa różnica potencjałów
uwarunkowanej różnymi wartościami energii Fermiego dla metali (Rys. 1).

Termopara jest najprostszą odmianą termometru termoelektrycznego, w której wykorzystuje się

zależność kontaktowej różnicy potencjałów od temperatury. Przy posługiwaniu się termoparami
sporządza się dwa spojenia odniesienia, z których jedno utrzymuje się w stałej temperaturze, drugie
spojenie jest w kontakcie cieplnym z miejscem, którego temperaturę wyznaczamy. Wielkością
fizyczną wykorzystywaną do wyznaczania temperatury jest siła termoelektryczna (SEM).

Rys.1. Powstanie kontaktowej różnicy potencjałów



k

przez połączenie dwóch metali A i B.

Jeżeli z metali A i B trudno przygotować długie druty bez naprężeń wewnętrznych do

podłączenia termopary z przyrządem pomiarowym, wtedy można trzeci metal C połączyć w dwu
miejscach o wspólnej temperaturze T

1

. Różnica potencjałów na końcach drutów C stanowi nadal

bezpośrednią miarę termoelektrycznej różnicy potencjałów między spojeniami AB o temperaturze T

0

oraz spojeniem AB o temperaturze T

1

.

Gdy elektron porusza się w obwodzie przedstawionym na Rys. 2 w kierunku zgodnym z ruchem

wskazówek zegara, ciepło wydzielone w złączu 1 będzie równe



AB

(T

1

), natomiast ciepło wydzielone

w złączu 2



BA

(T

2

), przy czym



BA

(T

2

)=-



AB

(T

2

). Wielkość



AB

(T), nazywana jest współczynnikiem

Peltiera złącza AB i zależy od temperatury T złącza. Współczynnik ten ma wymiar potencjału i jest
określony jako energia przypadająca na jednostkowy ładunek.

Wielkość różnicy potencjałów wywołanej przez różnicę temperatur na złączach, mierzona

w obwodzie w kierunku zgodnym z ruchem wskazówek zegara wynosi:

CECHOWANIE TERMOPAR W NISKICH TEMPERATURACH

io



zl

=



AB

(T

1

)+



BA

(T

2

)=



AB

(T

1

)-



AB

(T

2

).

Rys. 2. Siła termoelektryczna w termoparze utworzonej przez połączenie dwóch metali A i B.

Jeśli np., dwa końce przewodnika A będą się znajdować w różnych temperaturach T

1

i T

2

, to

pojawi się różnica średnich energii cieplnych elektronów na obu końcach tego przewodnika.
W wyniku, czego elektrony będą przemieszczać się ze złącza o wyższej temperaturze do złącza
o niższej temperaturze i między złączami przewodnika wytworzy się różnica potencjałów. Tę różnicę
potencjałów, która przeciwstawia się różnicy energii cieplnej elektronów można przedstawić
w następujący sposób:

 









2

T

1

T

A

A

T

dT

)

T

(

przy czym wielkość ta jest dodatnia jeśli T

2

jest większe od T

1

. Wielkość



A

(T) nazywana

współczynnikiem Thomsona dla metalu A w temperaturze T jest równa różnicy potencjałów dla
dwóch punktów przewodnika o jednostkowej różnicy temperatur.

Całkowita różnica potencjałów termopary przy obiegu zgodnym z ruchem wskazówek zegara

jest określona następująco:

=

zl

+(



T

)

A

-(



T

)

B

=

=



AB

(T

1

)-



AB

(T

2

)+





2

T

1

T

A

dT

)

T

(

-





2

T

1

T

B

dT

)

T

(

,

lub

=

zl

+(



T

)

A

-(



T

)

B

=

=



AB

(T

1

)-



AB

(T

2

)+













2

T

1

T

B

A

dT

)

T

(

)

T

(

.

Dla obiegu zgodnego z ruchem wskazówek zegara siłę termoelektryczną można zapisać w postaci:





























1

T

1

2

T

B

A

1

T

2

T

AB

dT

)

T

(

)

T

(

dT

dT

)

T

(

d

d

.

Zjawisko unoszenia elektronów przez fonony jest jeszcze jednym źródłem siły

termoelektrycznej. Jeżeli w ciele stałym istnieje gradient temperatur, to liczba fononów poruszających
się od złącza o wyższej temperaturze do złącza o niższej temperaturze będzie większa od liczby
fononów poruszających się w kierunku przeciwnym. Podczas ruch fonony w wyniku zderzeń
z elektronami będą je unosiły z sobą i na złączu o niższej temperaturze będzie gromadził się ładunek

2

CECHOWANIE TERMOPAR W NISKICH TEMPERATURACH

io

ujemny, aż powstająca w ten sposób różnica potencjałów zrównoważy zjawiska unoszenia. Efekt ten
wprowadza dodatkową składową siły termoelektrycznej w niskich temperaturach, w których dominuje
rozpraszanie fonon-elektron.

Efekt unoszenia fononowego jest maksymalny w temperaturach od 5 do 50K, zaś dla

temperatur niższych niż 1K - zanika. W temperaturach wysokich, gdzie zaczyna dominować
rozpraszanie fonon-fonon, unoszenie fononowe jest równoważone przez efekt rozpraszania typu
Umklapp.

Materiały wykorzystane do budowy termoelementów powinny charakteryzować się:

-

wysoką czułością, tzn. dużą siłą termoelektryczną przy określonej różnicy temperatur,

-

ciągła i liniową zależnością siły termoelektrycznej od temperatury,

-

wysoką temperaturą topnienia,

-

szerokim temperaturowym zakresem pracy ciągłej,

-

odpornością na warunki otoczenia,

-

stałością własności w czasie i ich powtarzalnością,

-

możliwie małą rezystancją,

Na wskazania wartości siły termoelektrycznej mają wpływ takie czynniki jak:
 konstrukcja złącza,
 zewnętrzne warunki pracy,
 niejednorodność materiałów, z których wykonano termopary,



czas i temperatura pracy,

dlatego należy cechowali termopary i wystrzegać się skalowania miernika wartości siły
termoelektrycznej w jednostkach temperatury.

Typowe termoelementy:



platyna-10% rod/platyna (Pt-Rh10-Pt) - o zakresie pracy od 300K do 2000K. Jest najbardziej
rozpowszechnionym zestawem wśród termoelementów z metali szlachetnych. Stosowany jest jako
termoelement wzorcowy przy odtwarzaniu międzynarodowej skali temperatur,



platyna-13% rod/platyna (Pt-Rh13-Pt),



żelazo/miedź-nikiel (Fe-CuNi) – (żelazo-konstantan) jest powszechnie stosowany ze względu na
niską cenę, stosunkowo dużą wartość siły termoelektrycznej i możliwość stosowania zarówno
w atmosferze utleniającej jak i redukującej. Zakres stosowania od 100K do 1200K,



miedź/miedź-nikiel (Cu-60CuNi) – (miedź-konstantan) zakres pracy: od 70K do 700K. Najczęściej
jest używany w pomiarach laboratoryjnych. Staranny dobór drutów termoparowych pozwala na
uzyskanie dokładności ok. 0.1K ze względu na dużą jednorodnośc tych metali w porównaniu
z innymi,



nikiel-chrom/miedź-nikiel (NiCr-CuNi)

– (chromel-konstantan 90Ni 10Cr-55Cu 45Ni)

charakteryzuje się największą siła termoelektryczną spośród termoelementów metalowych.
Stosowany jest w zakresie od 70K do 1200K w atmosferach redukujących i utleniających,



nikiel-chrom/nikiel-aluminium (NiCr-NiAl) – (chromel-alumel 90Ni 10Cr-94Ni 3Mn 2Al 1Si) ma
prawie prostoliniową charakterystykę termoelektryczną.

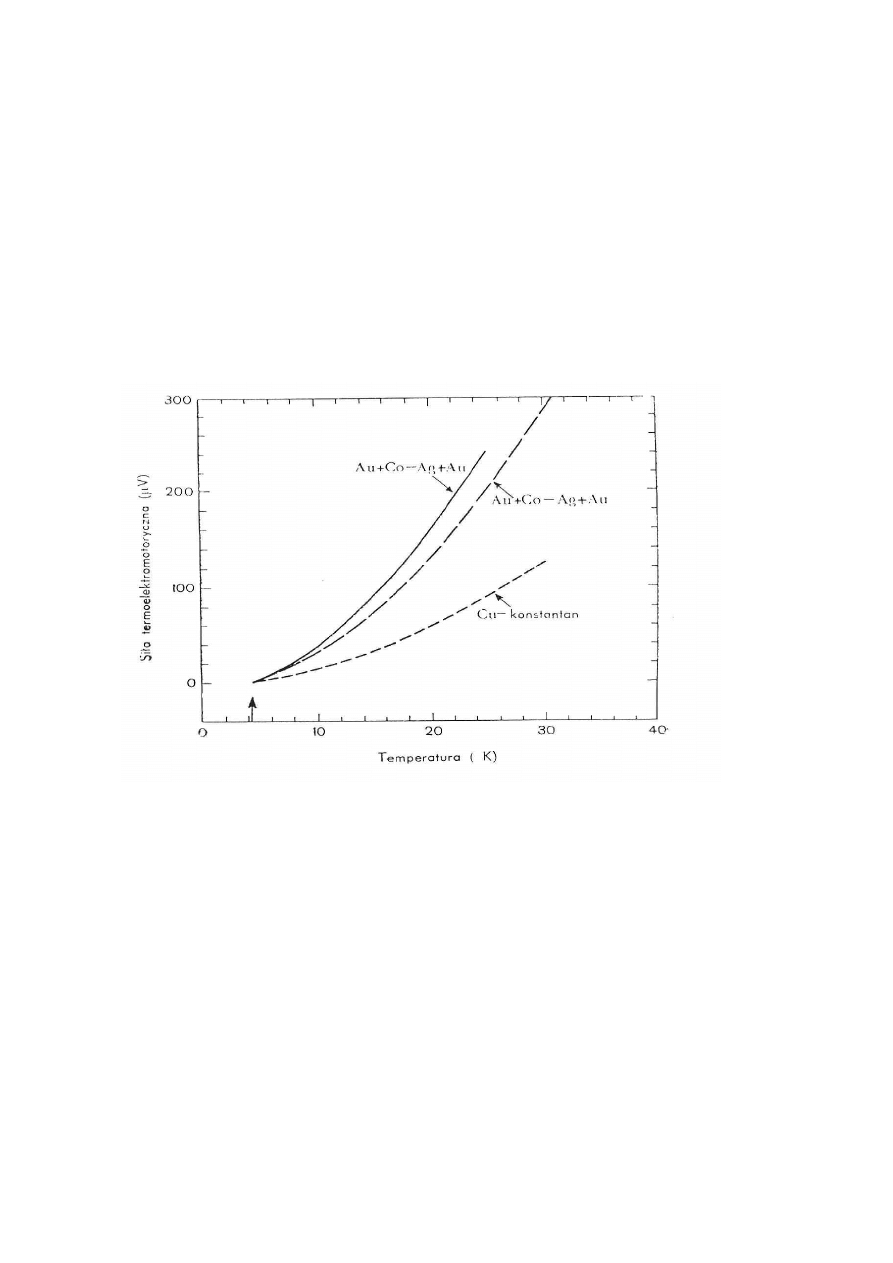
Najbardziej rozpowszechnionymi termoparami pozwalającymi mierzyć temperaturę od 300 K

do 25K są termopary Cu-konstantan oraz Fe-konstantan, ponieważ charakteryzują się dużą czułością.
Czułość termopary Cu-konstantan dla złącza odniesienia w T

0

=273K wynosi:



40

V/K w temperaturze T=300K,



17

V/K w temperaturze 90K,



5

V/K w temperaturze 20K.

3

CECHOWANIE TERMOPAR W NISKICH TEMPERATURACH

io

Istnieją materiały o wysokiej czułości w niskich temperaturach. Duża czułość termopar czyni je

przydatnymi do pomiaru temperatur aż do 1K. Sporządza się dwa rodzaje stopów na druty
termoparowe:
- stop złota z kobaltem (Au+2.1%).
- stop Au+Fe (od 0.02 do 0.07%).

Termopary za stopu Au+Co posiadają wysoką czułość w niskich temperaturach, jednakże stop

ten nie jest stabilnym roztworem i wykazuje niedostateczną jednorodność i powtarzalność.

3.2. Termopara

Termopary wyróżniają się bardzo małymi rozmiarami elementu termoelektrycznego, dzięki

czemu umożliwiają prawie punktowy pomiar temperatury. Zakłócenie temperatury w miejscu
zetknięcia spojenia termopary z ośrodkiem jest na ogół bardzo małe, jeśli druty użyte do budowy
termopar są odpowiednio cienkie (poniżej 50

m) a pomiar przeprowadza się metodą kompensacyjną.

Przy posługiwaniu się termoparami sporządza się dwa spojenia, z których jedno utrzymuje się

w stałej temperaturze (spojenie odniesienia), a drugie spojenie jest w kontakcie cieplnym z miejscem,
którego temperaturę wyznaczamy.

Rys. 3. Typowe połączenia metali typu A, B i C [4].

Jeżeli z dwóch rodzajów metali - A i B - trudno przygotować długie druty bez naprężeń

wewnętrznych (w celu podłączenia termopary do przyrządu pomiarowego) wtedy można odpowiedni
trzeci metal C połączyć w dwu miejscach o wspólnej temperaturze T

1

. Różnica potencjałów na

końcach drutów C stanowi nadal bezpośrednią miarę termoelektrycznej różnicy potencjałów między
spojeniami AB o temperaturze T

0

oraz spojeniem AB o temperaturze T

1

.

Wielkością charakteryzującą termopary jest czułość określana jako wartość siły

termoelektrycznej przypadająca na jednostkową zmianę temperatury złącza (dE/dT).

Zalety termopar:

-

nie wymagają zewnętrznego zasilania,

-

niski koszt,

-

szybkość działania,

-

ciągła rejestracja temperatury,

-

wygoda odczytu,

-

mała ilość ciepła wydzielonego w spojeniach,

-

mała pojemność cieplna,

-

proste i niezawodne w użyciu.

Wady termopar:

-

mała wartość siły termoelektrycznej,

-

zmniejszenie czułości wraz z obniżeniem temperatury,

-

prawie punktowy pomiar temperatury,

-

powstawanie pasożytniczych SEM wzdłuż przewodów (ponieważ druty termoparowe wykonane ze
stopu są mniej jednorodne niż z czystego metalu),

-

dokładność wyznaczania temperatury:

 0.1K,

-

konieczność utrzymania złącza odniesienia w ściśle określonej temperaturze.

4

CECHOWANIE TERMOPAR W NISKICH TEMPERATURACH

io

Najczęściej przytaczane równanie wzorcowe służące do opisu zależności SEM od różnicy

temperatur T-T

0

pomiędzy spojeniami termopary, ma postać:

3

0

2

0

0

)

T

T

(

C

)

T

T

(

B

)

T

T

(

A

E













.

Stałe A, B i C wyznacza się przez pomiar siły termoelektrycznej E termopary w trzech znanych
temperaturach.

Jeśli jedno spojenie termopary np. Cu-konstantan utrzymujemy w temperaturze mieszaniny

wody z lodem, to pomiar temperatury poniżej 100K drugim spojeniem obarczony jest dużym błędem,
jeśli nie stosuje się precyzyjnych układów pomiarowych. Dokładność pomiaru temperatury może być
zwiększona, jeśli spojenia odniesienia utrzymywać np. w temperaturze ciekłego azotu lub helu.
Pozwala to na pomiar mniejszych wartości bezwzględnych sił termoelektrycznych (ze znacznie
większą dokładnością) oraz eliminuje się możliwość powstawania pasożytniczych SEM, jakie zawsze
występują przy znacznych gradientach temperatur wzdłuż przewodów.

Rys. 4. Zależność SEM od temperatury dla spojenia odniesienia w temperaturze 4.2K [1].

3.3. Termostos

Istnieje możliwość ulepszenia termopar o małej różnicy potencjałów (kosztem prostoty

i wygody w użyciu). W tym celu należy połączyć kilka termopar szeregowo. Taki układ nazywa się
termostosem (lub termelem).

5

CECHOWANIE TERMOPAR W NISKICH TEMPERATURACH

io

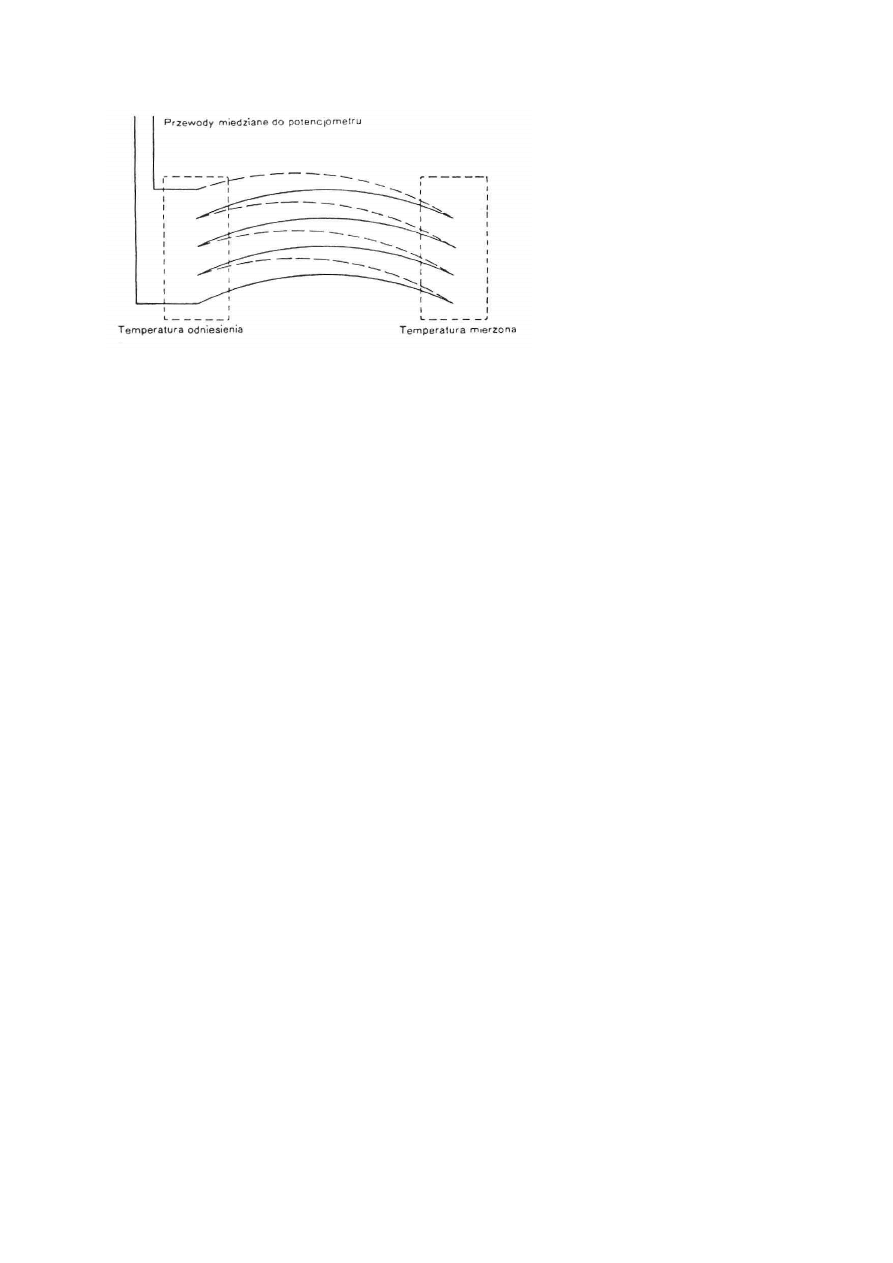
Rys. 5. Termel o spojeniach wielokrotnych: _________ - miedź, _ _ _ _ _ _ - konstantan [2].

Termel o 2n elementach wytwarza SEM n-krotnie większą od pojedynczej termopary.

Ponieważ SEM wywołane niejednorodnościami w różnych częściach drutu mogą się zarówno
redukować jak i dodawać to przypuszczalny błąd w wielkości SEM tylko (n)

1/2

większy niż w

przypadku pojedynczej termopary. Z tego powodu błąd temperatury będzie zredukowany o czynnik
(n)

-1/2

.

3.4. Literatura

1.

Scott R. B. Technika Niskich Temperatur, WNT Warszawa, 1963.

2.

White G. K. Technika doświadczalna w fizyce niskich temperatur, PWN, Warszawa, 1965.

3.

Blatt F. J. Fizyka zjawisk elektronowych w metalach i półprzewodnikach, PWN, Warszawa 1973.

4.

Michalski L., Eckersdorf K., Kucharski J. Termometria. Przyrządy i metody, Wydawnictwo PŁ,
Łódź, 1998.

6