ELEMENTY TEORII BŁEDÓW POMIARÓW

Każdy pomiar wielkości fizycznej wymaga oszacowania błędu, którym jestobarczony wynik tzn.
podania z jaką dokładnością dana wielkość została wyznaczona. Obowiązuje nas to także w
laboratorium. W procesie pomiaru można wyróżnić trzy etapy:
1. wyznaczenie szukanej wielkości fizycznej,
2. określenie błędu pomiaru,
3. podanie przypuszczalnych przyczyn błędów.
Ogólnie błędy dzielimy na:

•

błędy grube wynikłe z nieuwagi i z pomyłek eksperymentatora ( np. przy odczycie lub w
zapisie wyniku). Często są jednorazowe i mogą być bardzo duże.

•

błędy systematyczne wynikłe ze złego (mało dokładnego) ustawienia samego eksperymentu(nie
uwzględnienie pewnych poprawek np. siły wyporu powietrza przy dokładnym ważeniu), wad
urządzeń pomiarowych (przykładem może być źle wyskalowany przyrząd), ze stanu
zewnętrznych warunków pomiaru (np. zbyt wysoka temperatura w pomieszczeniu) jak i z błędu
eksperymentatora (np. znany błąd paralaksy). Błąd systematyczny charakteryzuje się stałą lub
zmieniającą się według określonego prawa odchyłką wartości wyznaczanej w doświadczeniu w
porównaniu z wielkością rzeczywistą. Przyczyny błędów systematycznych mogą być poznane i
usunięte.

•

błędy przypadkowe wynikłe z niedokładności odczytu, fluktuacji warunków pomiaru, z
nieokreślenia samej mierzonej wielkości fizycznej itd. Błędy te odznaczają się tym, że w serii
pomiarów jednego i tego samego stanu danej wielkości fizycznej wykonywanej w określonych
warunkach, wyniki zmieniają się w sposób losowy (przypadkowy). Nie można ich uniknąć
(usunąć), gdyż nie znamy ich przyczyn. Nie można więc wykonać bezbłędnego wyznaczenia
wielkości fizycznej - pomiaru absolutnie dokładnego.

Ze względu na źródła ich powstania rozróżniamy następujące rodzaje błędów pomiarowych:
1. błędy powodowane przez przyrządy pomiarowe, np. skończona rezystancja wewnętrzna

woltomierzy, nieliniowość wskazań przyrządów pomiarowych lub niedoskonałość ich
wzorcowania,

2. błędy powodowane przez metody pomiarowe,
3. błędy powodowane przez mierzącego, np. brak doświadczenia, skłonności, zmęczenie, nawyki,
4. błędy powodowane przez obliczenia - błędy przy niewłaściwym zaokrągleniu, niewłaściwe

metody wyrównywania błędów,

5. błędy powodowane przez wpływ otoczenia na mierzącego, na przyrządy i na mierzoną wielkość.

Czynniki wywołujące te błędy to temperatura, ciśnienie, wilgotność powietrza, zakłócenia
elektromagnetyczne.

W naszym laboratorium przy prowadzeniu obliczeń zakładamy, że nie występują błędy
systematyczne. Rachunek błędów będzie się sprowadzał do określenia tylko błędów przypadkowych
(Co nie oznacza, że w rzeczywistości błędy systematyczne nie występują).
Znane są pojęcia :
1) błędu bezwzględnego

∆

X definiowanego jako różnica wyniku X i wartości rzeczywistej X

R

.

∆X = X – X

R

(1)

2) błędu względnego

δ

x

definiowanego jako stosunku błędu bezwzględnego

∆

X do wartości

rzeczywistej.

δ

x

=

∆X / X

R

=X / X

R

– 1

(2)

Pojęcie wartości rzeczywistej jest tu czysto teoretyczne, gdyż praktycznie nie znamy jej. Powyższe
pojęcia są więc dla nas bezużyteczne. W oparciu o statystyczną teorię błędów przypadkowych
można jednak oszacować przybliżone wartości tych błędów, a tym samym dokładność otrzymanych

wyników pomiarowych. Te przybliżone wartości błędów noszą nazwę wskaźników dokładności
pomiarów.

1. Błędy przypadkowe w pomiarach bezpośrednich

Probabilistyczna teoria błędów Gaussa

Z jednego pomiaru nie możemy wnioskować o jego dokładności. Do tego konieczna jest ich seria.
Otrzymujemy ją przez kilkukrotne, niezależne powtórzenie rozpatrywanego pomiaru. Wyniki w
serii będą różnić się losowo. Oznaczmy je X

1

,X

2

,X

3

, ....... X

N

gdzie N jest ilością powtórzeń pomiaru

w serii i powinna wynosić przynajmniej 10. Wartości rzeczywistej nie znamy. Ale z serii pomiarów
wartością najbardziej zbliżoną do wartości rzeczywistej jest średnia arytmetyczna:

X =

1
N

∑

i

=1

N

X

i

(3)

Jest to podstawowe twierdzenie teorii błędów tzw. pierwszy postulat Gaussa. Wynika on z faktu
równości prawdopodobieństw tak zawyżenia wielkości mierzonej jak i jej zaniżenia. Tym samym
błędy powinny kompensować się. Jednak przy skończonej ilości pomiarów, może się zdarzyć, że
wyniki nie rozłożą się równomiernie wokół wartości rzeczywistej. Tym samym wartość średnia

X jest jedynie blisko położona wielkości rzeczywistej X

R

, ale nie równa jej. Zbliżenie to jest tym

lepsze im dłuższa jest seria pomiarowa. Równość 

X

= X

R

moglibyśmy napisać tylko dla serii

nieskończenie długiej pomiarów, ale przecież wykonanie takiej serii jest praktycznie niemożliwe.
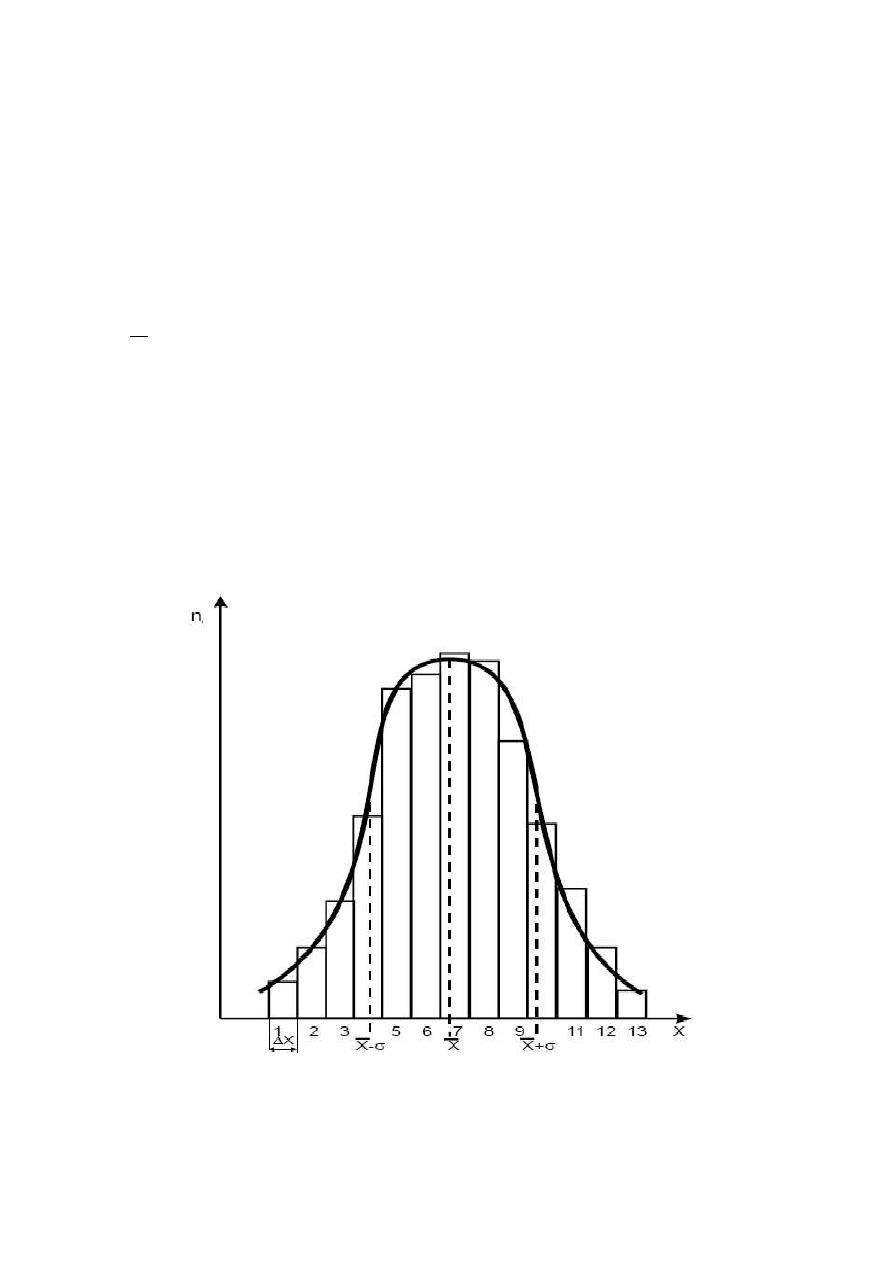
Wyniki pomiarów w serii rozkładają się wokół wartości średniej w tzw. krzywą Gaussa - mówi się
o rozkładzie Gaussa. Aby się o tym przekonać należy zakres pomiarowy podzielić na przedziały o
równej szerokości

∆X i obliczyć ile pomiarów z serii zmieściło się w każdym z nich (rys. 1).

Rys.1. Rozkład Gaussa.

Oczywiście zwiększając N możemy pozwolić sobie na zmniejszenie szerokości poszczególnych
schodków rozkładu, ale nadal zachowa on charakter dyskretny. Obwiednia dzwonowa
poprowadzona po środkach schodków jak na rys. 1 jest pewnym wyidealizowaniem - pokazuje jak

rozkład normalny wyglądałby gdyby był funkcją ciągłą (dla N =

Ą ). Taka postać łatwiej poddaje się

analizie matematycznej i dlatego często jest stosowana, ale nigdy nie należy zapominać, że realny
rozkład normalny ma strukturę ziarnistą. Ciągły rozkład Gaussa jest następującą funkcją
matematyczną:

P

 X =

1

⋅



2



e

− X − X 

2

2

⋅

2

(4)

przy czym parametr

σ zwany odchyleniem standardowym określa rozmycie rozkładu wokół

wartości średniej.
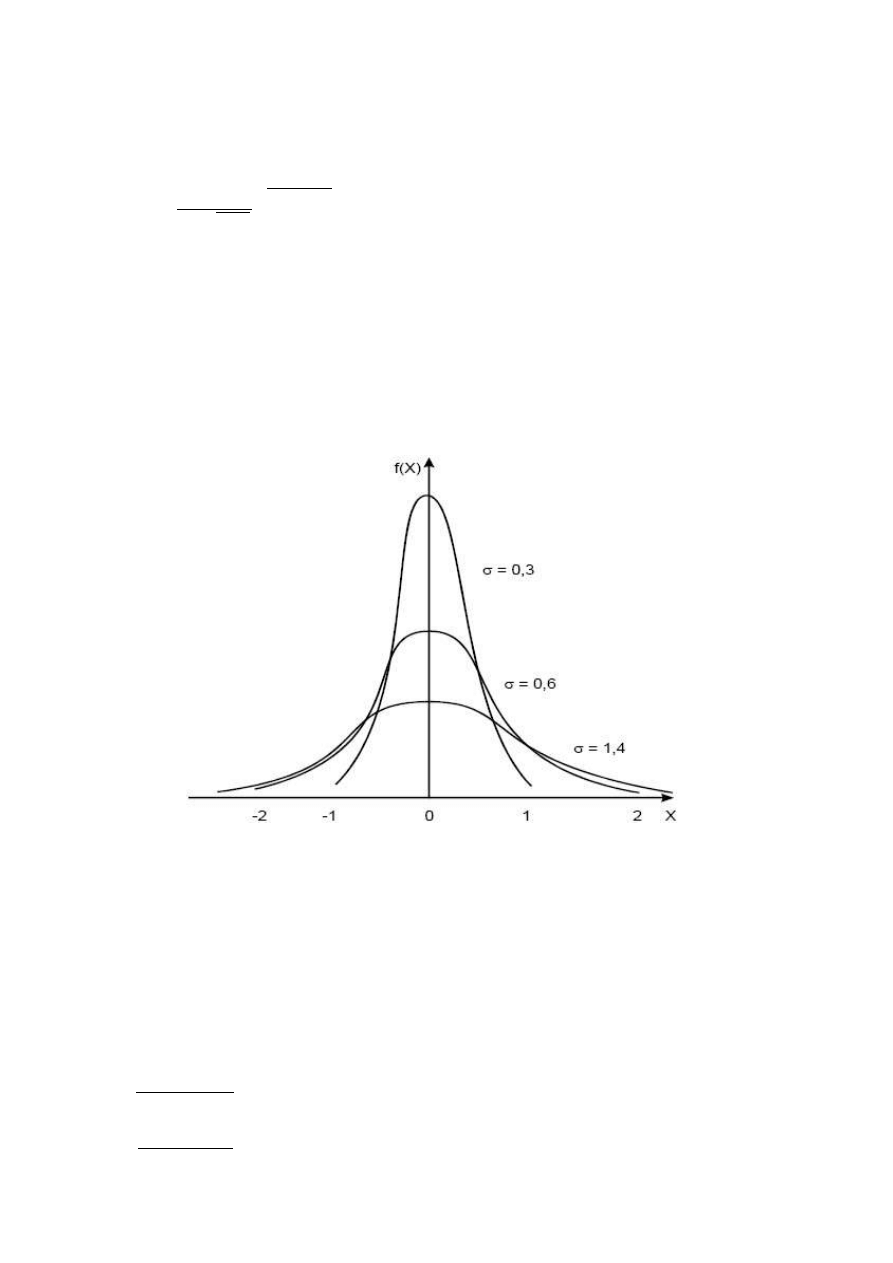
Kształt krzywej Gaussa, zwanej również krzywą dzwonową, bardzo silnie zależy od odchylenia
standardowego

σ. Na rys. 2 pokazano przebiegi krzywej Gaussa dla kilku różnych wartości

odchylenia standardowego. Im większe jest odchylenie standardowe, tym bardziej płaska jest
krzywa; dla bardzo małych odchyleń standardowych krzywa jest bardzo stroma i odchylenia od
wartości oczekiwanej są bardzo małe. Zauważmy, że na krzywej Gaussa można wyróżnić obszary o
przeciwnie skierowanej krzywiźnie. W okolicy maksimum krzywa jest wypukła, a daleko poza
maksimum staje się krzywą wklęsłą. Oczywiście obszary takie są oddzielone punktami przegięcia.
Odpowiadają one punktom 

X

− i X 

na osi odciętych.

Rys. 2. Przebieg krzywej ciągłego rozkładu normalnego w zależności od odchylenia standardowego.

Ponieważ rozkład Gaussa opisuje zjawisko probabilistyczne, a więc można określić jedynie
prawdopodobieństwo, że dowolny wynik pomiaru X

i

(i=1,2,3....N) znajdzie się w aktualnie

interesującym nas przedziale wartości < X

a

, X

b

>. I tak np.:

W przedziale < 

X

− , X  >

mieści się 68,26% wyników z serii.

W przedziale <

X −2

,

X 2

> mieści się 95,45% wyników z serii.

W przedziale < 

X

−3 , X 3 >

mieści się 99,73% wyników z serii.

Często operuje się prawdopodobieństwem, z jakim w zadanym przedziale znajdzie się dowolny
pomiar z serii. Prawdopodobieństwo to nazywa się poziomem ufności, a przedział przedziałem
ufności.
Odchylenie standardowe w teorii błędów nazywa się średnim błędem kwadratowym i oblicza się go
z wyrażenia:

=



∑

i

=1

N

 X

i

− X 

2

 N −1 

(5)

Występujący w tym wyrażeniu czynnik N – 1 można uzasadnić w ten sposób, że ponieważ część
informacji zawartej w serii je X

1

,X

2

,X

3

, ....... X

N

została wykorzystana do określenia wartości

średniej 

X , uśrednianie związane z odchyleniem standardowym następuje z mniejszą liczbą

punktów swobody i stąd podzielenie przez N – 1 zamiast przez N.
Najczęściej wyznaczany jest jednak jako optymalny średni błąd kwadratowy

σ (wzór 5), a z niego

średni błąd kwadratowy wartości średniej:



X

=





N

(6)

Z wzorów 5 i 6 otrzymujemy wyrażenie:

=



∑

i

=1

N

 X

i

− X 

2

N

⋅ N −1 

(7)

Błąd średni kwadratowy jest najważniejszym i najczęściej stosowanym wskaźnikiem dokładności
pomiaru. Dzieje się tak dlatego, że jest to błąd policzony optymalnie - najdokładniej z danej serii
pomiarowej.
Prawdopodobieństwo, że dany pomiar z serii pomiarowej znajdzie się w przedziale
< 

X

− , X  > wynosi 0,683. W interpretacji graficznej prawdopodobieństwu temu

odpowiada pole pod krzywą Gaussa odcięte tym przedziałem przy założeniu, że pole pod całą
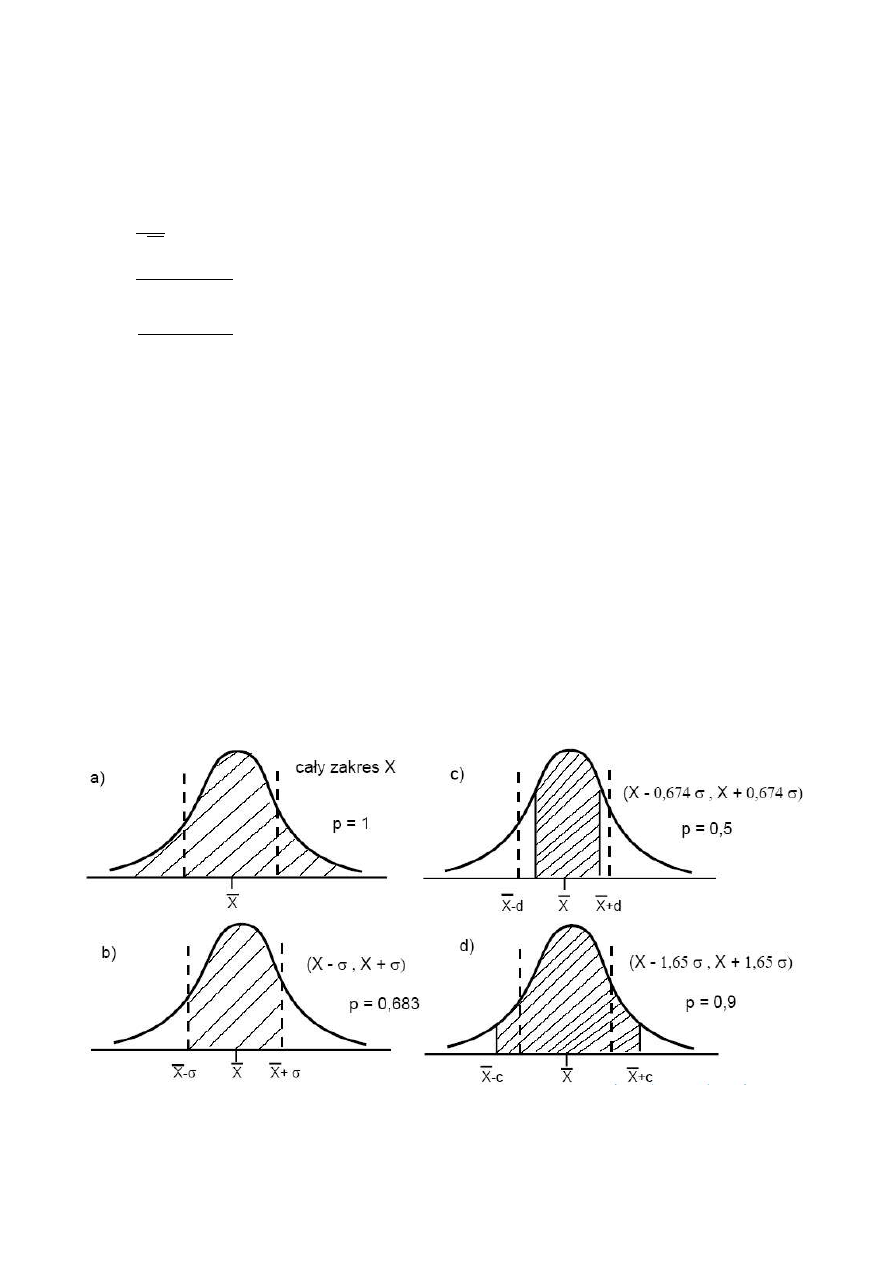
krzywą równa się jeden. Przedstawia to rys. 3ab. W eksperymencie oczywiście chcielibyśmy, żeby
błąd wyniku (przedział ufności) był jak najmniejszy przy możliwie dużym wyżej opisanym
prawdopodobieństwie (poziomie ufności).
Analizując kształt krzywej dzwonowej dochodzimy do wniosku, że optymalność przedziału
< 

X

− , X  >, wynika z faktu, że jest on wyznaczony przez punkty przegięcia krzywej.

Gdybyśmy chcieli sztucznie zmniejszyć ten przedział ufności do < 

X

−d , X d >

, (rys. 3c),

to znacznie stracimy na poziomie ufności (o pole pod krzywą Gaussa odcięte przedziałami
< 

X

− , X −d >, < X d , X  > które jest duże, bo na tych odcinkach krzywa

dzwonowa jest wypukła). Gdybyśmy z kolei chcieli sztucznie podnieść poziom ufności (rys. 3d), to
jest to możliwe tylko przez znaczne poszerzenie tego przedziału ufności do < 

X

−c , X c >,

gdyż pola pod krzywą w przedziałach oddalonych od średniej 

X dalej niż o

σ wnoszą już mały

wkład do poziomu ufności.

Rys. 3. Interpretacja graficzna przedziałów ufności i poziomów ufności p oraz

współzależność między nimi.

2. Błędy przypadkowe w pomiarach pośrednich

Załóżmy, że chcemy wyznaczyć pewną wielkość fizyczną A, ale nie możemy jej zmierzyć
bezpośrednio. Wiemy natomiast, że jest ona związana z K innymi wielkościami fizycznymi X

1

, X

2

,...X

K ,

które można już zmierzyć bezpośrednio, następującą zależnością:

A = f(X

1

, X

2

, ..., X

K

)

(8)

Po wykonaniu pomiarów wyniki i błędy pomiarowe wielkości X

1

, X

2

,...X

K

są znane i wynoszą

odpowiednio:



X

1

± 

X

1



X

2

± 

X

2

..................



X

K

± 

X

K

Wynikową wartość wielkości A łatwo jest znaleźć z zależności 8:

A= f  

X

1

, 

X

2

,... , 

X

K



(9)

Podstawowe pytanie brzmi jakim błędem

∆A obarczony jest w ten sposób otrzymany wynik. Można

zaproponować następujące metody postępowania:
1. Jeżeli ∆ 

X

i

( i = 1,2,...,K ) są średnimi błędami kwadratowymi





X

i

wartości średnich X

i

,

to otrzymujemy optymalnie znaleziony średni błąd kwadratowy z wyrażenia:



A

i

=



[

 A

 X

1





X

1

]

2

[

 A

 X

2





X

2

]

2

...[

 A

 X

K





X

K

]

2

(10)

Prawdopodobieństwo znalezienia się rzeczywistej wartości wielkości fizycznej A

R

w przedziale

<

A−

A

,

A

A

>

, wynosi 0,683.

2. Jeżeli błędy ∆ 

X

i

są błędami granicznymi (maksymalnymi) ∆ 

X

i max

, to w najmniej

korzystnym przypadku otrzymujemy błąd maksymalny pomiaru:

 

A

gr

=∣

 A

 X

1

 

X

1 max

∣∣

 A

 X

2

 

X

2 max

∣...∣

 A

 X

K

 

X

Kmax

∣

(11)

Prawdopodobieństwo znalezienia wartości rzeczywistej A

R

w przedziale

<

A− 

A

gr

,

A 

A

gr

> wynosi 0,999.

3. Jeżeli błędy

∆ 

X

i

są błędami granicznymi (maksymalnymi) ∆ 

X

i max

to w najbardziej

prawdopodobnym przypadku (optymistyczniejszym w porównaniu z przypadkiem poprzednim)
otrzymamy nieco mniejsze prawdopodobieństwo (w przybliżeniu 0,95) znalezienia wartości
rzeczywistej

A

R

, ale i w mniejszym przedziale ufności:

S

A

=



[

 A

 X

1

 

X

1 max

]

2

[

 A

 X

2

 

X

2 max

]

2

...[

 A

 X

K

 

X

Kmax

]

2

(12)

Jest to tzw. metoda różniczki zupełnej stosowana często, gdy błędy ∆ 

X

i max

są błędami

szacowanymi przy pomiarach jednorazowych, np. na podstawie dokładności skali przyrządu
pomiarowego, a zależy nam na zminimalizowaniu błędu wyniku końcowego.
Prawidłowo przeprowadzony rachunek błędów, automatycznie odpowiada na pytania:

•

które wielkości fizyczne (pośród X

i

) należy zmierzyć z większą dokładnością, jeśli chce się

uzyskać mniejszy błąd na wielkości wynikowej A;

•

który z błędów ∆ 

X

i

wnosi największy wkład do błędu ∆ A .

Otrzymane wnioski są więc ważne i pouczające, pozwalając na ewentualne powtórzenie
doświadczenia z mniejszym błędem.

L i t e r a t u r a

[1] J. Kilias, T. Kostrzyński, S. Wojciechowski.: Podstawy fizyki dla studentów informatyki, WAT,
Warszawa 2000.
[2] Reif E.: Fizyka statystyczna, PWN, Warszawa 1975.